Active dendrites enable strong but sparse inputs to determine orientation selectivity

Significance

An active pyramidal cell model, constrained by physiological and anatomical data, was used to simulate dendritic integration in vivo. The model shows that small numbers of strong excitatory synapses can trigger dendritic Na⁺ and NMDA spikes. Moreover, only a few dendritic spikes are sufficient to drive a single output action potential. As a consequence, as few as 1% of the synaptic inputs to a neuron can determine the tuning of somatic output in vivo. These results suggest that dendritic spikes can help to make sensory representations more efficient and flexible: they require fewer connections to sustain them, and only a small number of connections need to be changed to encode a different stimulus and alter the response properties of a neuron.

Abstract

The dendrites of neocortical pyramidal neurons are excitable. However, it is unknown how synaptic inputs engage nonlinear dendritic mechanisms during sensory processing in vivo, and how they in turn influence action potential output. Here, we provide a quantitative account of the relationship between synaptic inputs, nonlinear dendritic events, and action potential output. We developed a detailed pyramidal neuron model constrained by in vivo dendritic recordings. We drive this model with realistic input patterns constrained by sensory responses measured in vivo and connectivity measured in vitro. We show mechanistically that under realistic conditions, dendritic Na⁺ and NMDA spikes are the major determinants of neuronal output in vivo. We demonstrate that these dendritic spikes can be triggered by a surprisingly small number of strong synaptic inputs, in some cases even by single synapses. We predict that dendritic excitability allows the 1% strongest synaptic inputs of a neuron to control the tuning of its output. Active dendrites therefore allow smaller subcircuits consisting of only a few strongly connected neurons to achieve selectivity for specific sensory features.

There is longstanding evidence from in vitro experiments that dendrites of mammalian neurons are electrically excitable (1, 2), and theoretical work has demonstrated that these active properties can be exploited for computations so that single neurons can perform functions that could otherwise only be performed by a network (3–7). Recently, technical breakthroughs have enabled dendritic integration to be studied in vivo using both imaging and electrophysiological techniques (8, 9). These experiments have revealed that the integration of synaptic events in vivo can be highly nonlinear and that this process influences the response properties of single neurons and neuronal populations in vivo (10–16). For example, patch-clamp recordings from dendrites in mouse primary visual cortex (V1) have demonstrated that dendritic spikes are triggered by visual input and that they may contribute to the orientation selectivity of somatic membrane potential (17). However, important mechanistic questions are still unanswered. How many synaptic inputs must be locally coactive on a dendrite to recruit dendritic spikes? What is the contribution of individual dendritic spikes to somatic action potential (AP) output and its orientation selectivity? Moreover, we do not understand how the answers to these questions depend on the type of dendritic spike. Finally, how do active dendrites, by supporting dendritic spikes, influence which synaptic inputs control AP output and its tuning?

These issues are extremely challenging to address experimentally. We have therefore taken a modeling approach, constrained by in vitro and in vivo experimental data, in order to provide a quantitative understanding of the relationship between synaptic input, dendritic spikes, and AP output during sensory processing in V1. We constructed a detailed active model of a layer (L) 2/3 pyramidal neuron in mouse V1 and combined this with a model of the presynaptic inputs it receives during visual stimulation with drifting gratings in vivo (17–21).

Our model reproduces key features of the experimental data on dendritic and somatic responses to visual stimulation as observed in vivo and allows us to identify the synaptic inputs that trigger dendritic Na⁺ spikes and NMDA spikes. We also provide a quantitative explanation for how these dendritic spikes determine neuronal output in vivo. Our results show that dendritic spikes can be triggered by a surprisingly small number of synaptic inputs—in some cases even by single synapses. We also find that during sensory processing, already few dendritic spikes are effective at driving somatic output. Overall, this strategy allows a remarkably small number of strong synaptic inputs to dominate neural output, which may reduce the number of neurons required to represent a given sensory feature.

Results

An Active Dendritic Model Reproduces Responses to Visual Stimulation.

To study the mechanisms of synaptic integration during visual stimulation in vivo, we built and combined models of the sensory-evoked synaptic input and the postsynaptic pyramidal neuron (Fig. 1 A and B; Materials and Methods). The postsynaptic model satisfies a large set of experimental constraints obtained in vitro (22, 23) and in vivo (21, 23, 24) (SI Appendix, Fig. S1). In particular, we constrained dendritic excitability and membrane potential dynamics during sensory processing by taking advantage of direct patch-clamp recordings from the dendrites of L2/3 pyramidal neurons in mouse V1 in vivo (17).

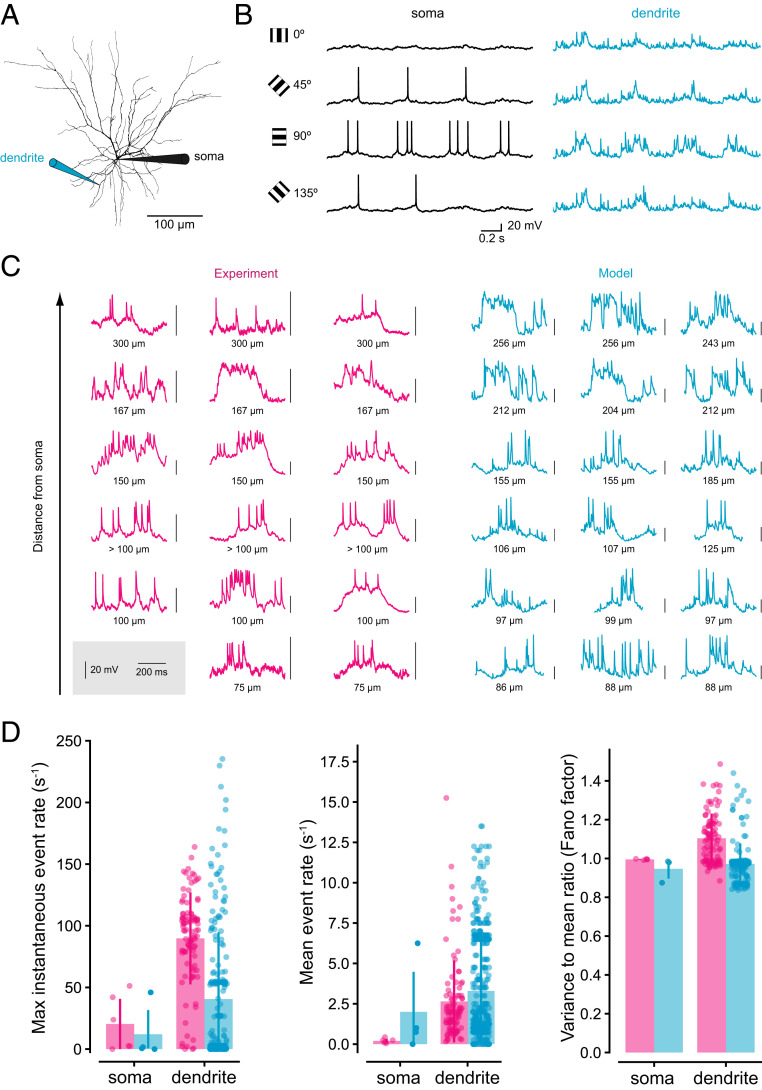
Fig. 1.

A pyramidal cell model with active dendrites reproduces dendritic responses to visual stimulation in vivo. (A) Morphology of the L2/3 pyramidal neuron used for the model, with pipettes indicating the locations of the recordings shown in B. (B) Example of somatic (Left) and dendritic (light blue, Right) responses of the postsynaptic model neuron to simulated synaptic inputs corresponding to visual stimuli with orientations 0°, 45°, 90°, and 135°, where 90° is the preferred orientation of the model neuron. (C) Comparison of dendritic patch-clamp recordings in vivo [pink, Left; data from Smith et al. (17)] with dendritic recordings in the model neuron (light blue, Right). Note that vertical scale bars differ between traces. (D) Comparison of event rates in the experiment [pink; using data from Smith et al. (17)] and model (light blue). Events are defined as episodes of monotonically rising membrane potential with a baseline-to-peak difference of more than 10 mV.

The synaptic input model (SI Appendix, Fig. S2) satisfies constraints set by the experimentally measured distribution of firing rates of the presynaptic neuron population (17), the overall number of synaptic inputs to the neuron (25), the mean number of synaptic contacts per connection (2.8) (19), and the connection probability (26) and strength (18) as a function of the difference in orientation preference of the pre- and postsynaptic neurons (Materials and Methods). A key assumption of the synaptic input model is the lognormal distribution of synaptic weights, which is supported by experimental studies (27–31) reporting a small number of relatively strong connections among many weaker ones. Since no direct and complete recordings of the synaptic input received by a L2/3 neuron in vivo are available, and there is conflicting evidence regarding the spatial and temporal structure of active synapses (32–37), we chose an approach in which different synaptic inputs are activated independently of each other so that any spatial or temporal clustering occurs by chance. We also tested an alternative synaptic input model in which synaptic inputs with similar tuning are spatially clustered.

The combined model reproduced somatic and dendritic responses to visual stimulation in vivo, including their orientation tuning (17) (Fig. 1B). In particular, the model exhibited a range of dendritic spikes and plateau potentials at different dendritic locations, which closely resembled the visually evoked events observed in experimental dendritic recordings (Fig. 1C). Using the same definition of events (SI Appendix, Fig. S3), the maximum instantaneous and mean rates of somatic and dendritic events, as well as the variance-to-mean ratio (Fano factor) of the distribution of event counts in a given time interval, were within the same range in model and experiment (Fig. 1D).

Biophysical Definition of Dendritic Na⁺ Spikes and NMDA Spikes.

Identifying and discriminating different types of active dendritic events is difficult in experimental dendritic recordings, especially in vivo where it has not yet been possible to record dendritic and somatic voltages simultaneously. This means that the signals arising from synaptic inputs, locally generated dendritic spikes and backpropagating APs (bAPs), are difficult to separate. In the model, the ability to accurately track all of the relevant variables, namely synaptic currents, membrane potentials, and the activation state of voltage-gated conductances, allowed us to develop detectors for dendritic Na⁺ spikes, NMDA spikes, and bAPs based on a rigorous biophysical definition of individual events (reference SI Appendix).

We detected local dendritic Na⁺ spikes using a conductance density threshold of 0.3 mS/cm². To validate this threshold, we compared simulations in our fully active model and a model in which dendritic Na_v conductances were switched off (38) (Fig. 2A, SI Appendix, Fig. S4, and Materials and Methods). We defined dendritic Na⁺ spikes by an increase in local dendritic event amplitude of >10% from passive to active, which was well predicted by a local dendritic g_Na of more than 0.3 mS/cm² (SI Appendix, Fig. S4C). Notably, actively backpropagating APs can also reach this conductance threshold. To prevent erroneous classification of bAPs as local Na⁺ spikes, we first identified a characteristic spatiotemporal bAP profile (latency and halfwidth) for each dendrite. Any dendritic event detected following a recent somatic AP and matching the bAP profile for that dendrite was then classified as a bAP, rather than as a locally generated Na⁺ spike.

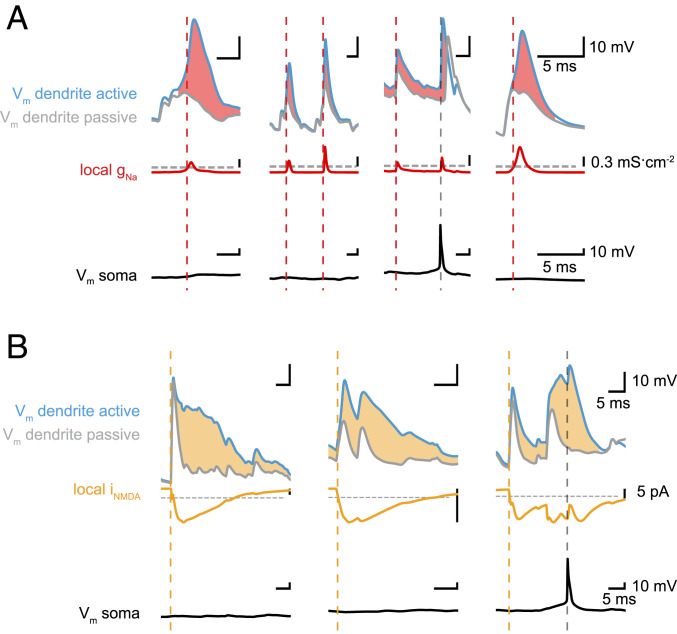
Fig. 2.

Detecting dendritic Na⁺ spikes and NMDA spikes. (A) Four examples of local dendritic Na⁺ spikes showing dendritic membrane potential (Top), dendritic Na⁺ conductance (Center), and somatic membrane potential (Bottom). We compared simulations in a fully active (light blue) and a passive dendrite (gray) with identical synaptic input. Dendritic Na⁺ spikes (initiation indicated by dashed red lines) are characterized by a >10% voltage amplitude difference (light red shading) between active and passive simulations. We use a threshold (gray horizontal dashed line) on the local Na⁺ conductance (Center, red) as a proxy to efficiently detect dendritic Na⁺ spikes in all following simulations. By simultaneously monitoring somatic V_m, we can distinguish local events from bAPs (gray vertical dashed lines; Materials and Methods). (B) Three examples of local dendritic NMDA spikes showing dendritic membrane potential (Top), local NMDA current (Center), and somatic membrane potential (Bottom). We compared simulations in a dendrite with voltage-dependent NMDA conductances (light blue) and the same dendrite with NMDA conductances frozen at the resting potential (gray), with identical synaptic input. Dendritic NMDA spikes (initiation indicated by dashed orange lines) are characterized by a >10% voltage amplitude difference (light orange shading) between active and passive simulations. We use a threshold (gray horizontal dashed line) on the local NMDA current (Center, orange) and a threshold on the local dendritic membrane potential, as well as a threshold on the total charge delivered during a spike, as a proxy to efficiently detect dendritic NMDA spikes in all following simulations (Materials and Methods).

We detected dendritic NMDA spikes using both a voltage criterion and an NMDA current criterion, scaled by synaptic weight (reference SI Appendix). The voltage criterion is fulfilled if the local dendritic membrane potential exceeds a threshold of –40 mV for at least 26 ms (compare τ_NMDA = 26 ms). The current criterion combines an NMDA current threshold, equivalent to synaptic weight multiplied by 30% of the peak NMDA conductance at –40 mV, and a charge threshold of –0.1 nA ms. For NMDA spike detection, both the current and voltage criteria have to be met within a spatial window of ±50 µm. We verified these criteria using fully active simulations and simulations in which NMDA conductances were frozen at their resting potential (38) (Fig. 2B).

Multiple Dendritic Na⁺ Spikes and NMDA Spikes Are Initiated Near Simultaneously across the Dendritic Tree.

The relationship between dendritic spike initiation and the output of the neuron under in vivo conditions is unknown and is critical for defining the input–output function of the neuron. Our simulations allow us to provide a quantitative account of this transformation, as we can track the initiation and propagation of all dendritic spikes and their relationship with output APs in the axon. Fig. 3A shows membrane potential traces from different dendritic recording locations as mapped onto the neuronal morphology during presentation of a preferred stimulus. SI Appendix, Fig. S5 shows a similar plot, providing more widespread dendritic recording locations together with the activation of synapses on the dendrite from which the recording has been made. These simulations indicate that multiple distinct local dendritic Na⁺ spikes and NMDA spikes can be triggered near simultaneously on different dendrites across the morphology.

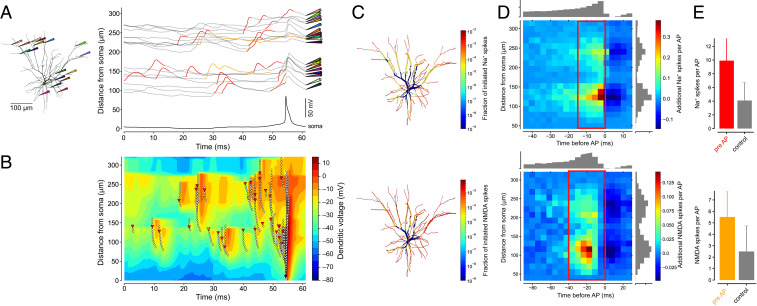
Fig. 3.

Dendritic Na⁺ spikes and NMDA spikes precede AP output. (A) Example recordings of local dendritic voltage at the location of dendritic Na⁺ spikes (red) and NMDA spikes (orange). Recording locations are shown on morphology (Left) with corresponding pipette colors. The intersection of voltage traces with the left vertical axis indicates distance from soma, while the scale bar shows the voltage scale. (B) Example snapshot of dendritic membrane potential as a function of space and time (same spatial and temporal extent as in A). Multiple dendritic Na⁺ spikes (initiation at red triangles; propagation indicated by white diamonds) and NMDA spikes (initiation at orange triangles) initiate and propagate across the dendritic tree. A bAP (blue triangle and white diamonds) occurs near time (t) = 54 ms. Contours are lines of equal membrane potential (maximum projection across all dendrites at this distance from the soma). (C) Distribution of the probability of initiating a dendritic Na⁺ spike (Top) or dendritic NMDA spike (Bottom) across the dendritic tree. (D) Spatiotemporal AP-triggered averages of dendritic Na⁺ spikes (Top) and NMDA spikes (Bottom), with BG dendritic spiking activity subtracted. Values in the red rectangles sum to the average numbers of dendritic events (shown in E) preceding a single AP. (E) Number of dendritic Na⁺ spikes (mean ± SD; red, Top) and NMDA spikes (mean ± SD; orange, Bottom) preceding a single AP compared to random time points (control, gray).

Such representations provide us with a useful snapshot of membrane potential at different locations in the neuron, yielding information which is not available from single-site electrophysiological recordings. However, it is still difficult to use such plots to assess the quantitative relationship between near-simultaneous events in different dendrites and their link to APs at the soma. We therefore developed a representation of the overall spatiotemporal dynamics of membrane potential across the entire neuron by plotting a maximum membrane potential projection against time, with individual dendritic Na⁺ spikes and NMDA spikes and their propagation identified using our detectors. These spatiotemporal panoramas allow us to track the evolution of individual events in space and time and determine their relationship with each other. Fig. 3B shows an example of such a panorama, which represents the same events as shown in Fig. 3A, except across the entire morphology. An even more powerful representation of the spatiotemporal interactions between synaptic inputs, dendritic spikes, and APs is provided by animating such a spatiotemporal snapshot and annotating it with active synapses (Movie S1). Such a movie allows the evolution of membrane potential to be linked to the location of synaptic inputs on the morphology.

Next, we quantified where in the morphology dendritic Na⁺ spikes and NMDA spikes are initiated by plotting the fraction of spikes generated across the morphology during prolonged simulations (Fig. 3C). This analysis indicates that most dendritic branches in the L2/3 pyramidal cell morphology support the generation of both dendritic Na⁺ spikes and NMDA spikes. The frequency of initiation was approximately dependent on the distance from the soma, with the majority of dendritic events being initiated in the most distal dendrites, and the most proximal dendrites (<50 µm from the soma) representing unfavorable locations for initiation of dendritic spikes. These simulations also indicate that it is unlikely that there exist discrete morphological “hotspots” in the dendritic tree where dendritic spike initiation is particularly favorable, but rather that spike initiation probability is graded across the morphology.

AP Output Strongly Depends on Dendritic Na⁺ Spikes and NMDA Spikes.

We linked dendritic spike initiation and AP output by developing an approach for quantifying the spatial and temporal footprint of dendritic spikes that precede APs during a preferred sensory stimulus. This involves detecting somatic APs and dendritic spikes and then computing the spatiotemporal somatic AP-triggered average of the dendritic spikes (Fig. 3D), taking into account the background (BG) frequency of dendritic spikes not associated with an AP. The resulting plot shows that dendritic Na⁺ spikes that are linked to output of the neuron (i.e., a somatic AP) can occur at all distances from the soma (aside from the most proximal 50 µm, a region which is generally unfavorable for triggering local dendritic spikes; Fig. 3C). The largest number of spikes occur in a zone ∼100 to 150 µm from the soma (which includes some terminal branches). With respect to timing, the majority of dendritic Na⁺ spikes occurred in the 5 ms prior to the AP, with a long “foothill” of tens of milliseconds where dendritic Na⁺ spikes could still influence axonal AP initiation (Fig. 3D, Top). For NMDA spikes, the spatial distribution was comparable to that of dendritic Na⁺ spikes, while the timing relationship was broader with the peak shifted to more negative values (Fig. 3D, Bottom). The latter effect is due to the much longer duration of the NMDA spikes, which allows them to exert their effect on AP initiation over a longer time window. In summary, the dendritic spikes associated with the triggering of an AP can originate and cooperate over almost the entire dendritic tree.

How many dendritic spikes are involved in triggering a single AP? To provide an estimate, we counted the number of dendritic spikes occurring across the dendritic tree in a spatiotemporal window corresponding to the peak temporal influence of the respective spike types (Fig. 3D, red rectangles). This count revealed that 9.9 ± 3.2 dendritic Na⁺ spikes occurred in the neuron in the 15 ms prior to each AP (compared to 4.1 ± 2.6 spikes in a randomly selected control window of the same duration and spatial extent; Fig. 3E, Top). In contrast, 5.5 ± 2.3 NMDA spikes occurred in the 40 ms prior to each AP (compared to 2.5 ± 2.3 NMDA spikes in a randomly selected control window; Fig. 3E, Bottom). These results indicate that a surge in dendritic spike activity across the dendritic tree leads to initiation of an AP, with a 2.4- and 2.2-fold increase above baseline for dendritic Na⁺ spikes and NMDA spikes, respectively. Both types of dendritic spike tended to be triggered in concert with each other (69.0 ± 2.7% of dendritic NMDA spikes were triggered within 20 ms of a dendritic Na⁺ spike, and 12.7 ± 0.8% of dendritic Na⁺ spikes occurred within 20 ms of a dendritic NMDA spike).

A Causal Link between Dendritic Spikes and Output APs.

In the previous figure we showed that output APs are associated with an increase in dendritic spikes preceding these APs. To demonstrate that these additional dendritic Na⁺ spikes and NMDA spikes causally drive somatic AP output, we selectively deleted the dendritic voltage-gated conductances (mediated by voltage-gated sodium [Na_v] channels and NMDA receptors) that are driving the Na⁺ spikes and NMDA spikes, respectively. First, we removed dendritic Na_v channels to prevent dendritic Na⁺ spikes and examined the consequences for AP output using identical synaptic input. Preventing dendritic Na⁺ spikes substantially reduced, on average from 6.0 to 2.3 Hz, but did not abolish output APs (Fig. 4 A and B). Second, we blocked NMDA spikes by freezing the NMDA conductance at its resting potential value, thus removing NMDA-based regenerative events while preserving an ohmic synaptic NMDA conductance. This completely abolished output APs (Fig. 4 A and B), implying that NMDA spikes are more efficient than dendritic Na⁺ spikes at driving AP output. Notably, AP output was abolished even while the mean depolarization at the soma was maintained by constant somatic current injection. This suggests that NMDA spikes mainly drive APs not via their contribution to the average membrane potential but rather by their contribution to large transient somatic depolarizations (39) that have been shown to precede APs in vivo (40, 41).

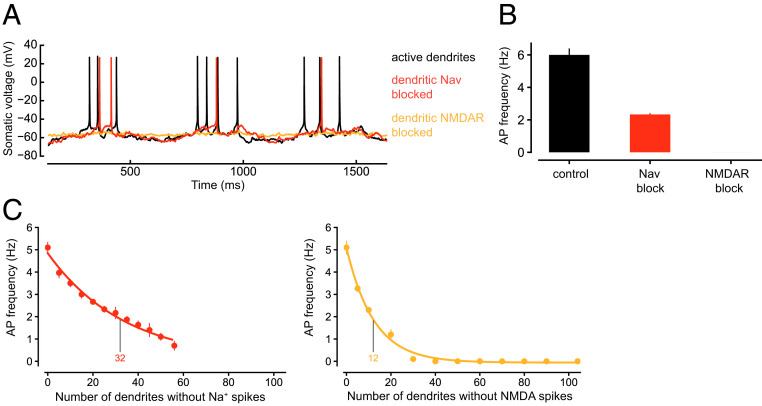
Fig. 4.

Causal role of dendritic Na⁺ spikes and NMDA spikes in triggering AP output. (A) Example recordings from the soma with a fully active dendritic tree (black), or when blocking dendritic Na⁺ spikes (red), or NMDA spikes (orange) by blocking dendritic Na_v channels, or freezing the voltage dependence of the NMDA conductance at the resting potential, respectively, while maintaining the mean somatic membrane potential by somatic current injection. (B) Blocking dendritic Na⁺ spikes (red) and NMDA spikes (orange) in the entire dendritic tree reduces AP output relative to a fully active dendritic tree (black). Mean somatic membrane potential was maintained as in A. (C) Blocking dendritic Na⁺ spikes (red, Left) and NMDA spikes (orange, Right) in an increasing number of randomly chosen individual dendrites leads to a decrease in AP output frequency that can be fit with an exponential decay. Mean somatic membrane potential was kept constant as in A.

Removing dendritic Na⁺ spikes or NMDA spikes from progressively larger numbers of dendritic branches (while again maintaining the mean somatic membrane potential by constant somatic current injection) revealed a nonlinear relationship between the number of manipulated branches and the output firing rate (Fig. 4C). In both cases, the relationship was described by an exponential decay, which was steeper for NMDA spike removal than for dendritic Na⁺ spike removal (on average, freezing the NMDA conductance in only 12 dendritic branches reduced the somatic output rate to 1/e of the control value, while deletion of Na_v channels in 32 dendritic branches was necessary to achieve the same effect at the soma). The stronger impact of NMDA conductance freezing compared with Na_v removal is consistent with our simulations using spatially widespread manipulations (Fig. 4 A and B), as well as with experimental results on the impact of dendritic NMDARs on neuronal output (13, 17).

Which Synaptic Inputs Are Most Important for Triggering Dendritic Spikes?

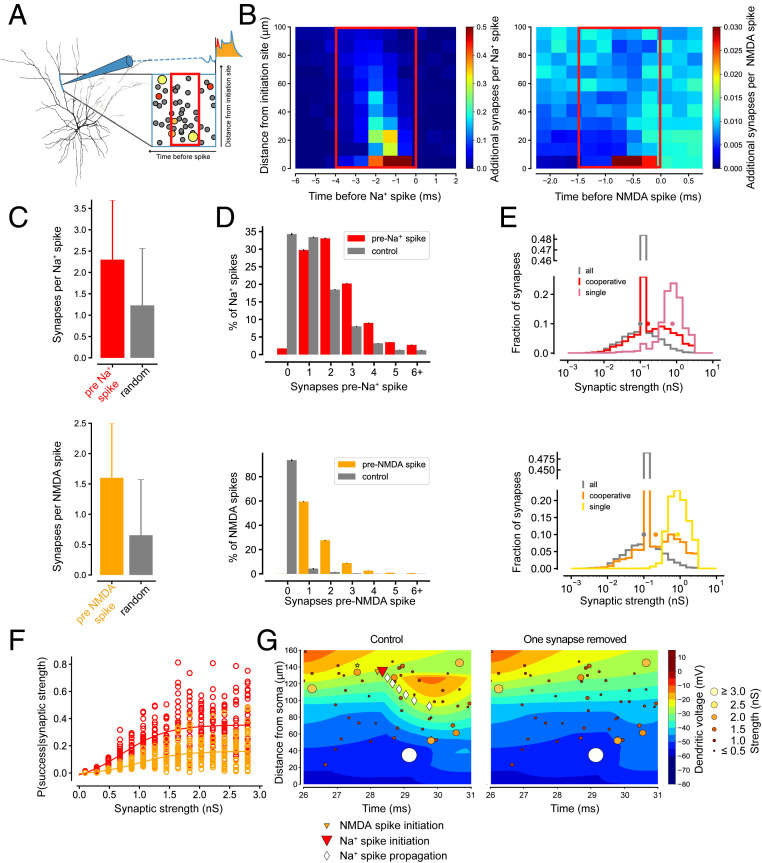
We next turned to the question which constellations of active synapses are most successful in triggering dendritic spikes. To determine the spatial and temporal scale over which synapses interact to trigger a dendritic spike, we first mapped the locations and timing of excitatory synaptic inputs relative to the initiation of a dendritic Na⁺ spike or NMDA spike (Fig. 5A). This was quantified and visualized using spatiotemporal dendritic spike–triggered averages (STA) for dendritic Na⁺ spikes (Fig. 5B, Left) and NMDA spikes (Fig. 5B, Right). In the case of dendritic Na⁺ spikes, most active synapses were located within ∼20 µm of the initiation site, and their activation preceded the initiation of the spike by less than 2 ms (Fig. 5B, Left). Most NMDA spikes were triggered by synapses located at the initiation site and were activated less than 1 ms before spike initiation (Fig. 5B, Right).

Fig. 5.

Surprisingly few synaptic inputs are required to trigger dendritic spikes. (A) Schematic of the spatiotemporal dendritic STA used in B. Circles of increasing diameter and increasingly “hot” colors indicate synaptic inputs with increasing synaptic strength (scale in G). (B) STA for dendritic Na⁺ spikes (Left) and dendritic NMDA spikes (Right), with the BG level of synaptic activity subtracted. Colormaps are clipped. Red rectangles indicate spatiotemporal windows for counting synaptic inputs in C. (C) Number of excitatory synaptic inputs active before dendritic Na⁺ spikes (mean ± SD; red, Top) and NMDA spikes (mean ± SD; orange, Bottom), compared to the number of active synapses in control spatiotemporal windows placed at random time points (gray; Materials and Methods). (D) Dendritic Na⁺ spikes (red, Top) and NMDA spikes (orange, Bottom) broken down by the number of synapses that triggered them. Gray bars show the distribution of the number of active inputs in control spatiotemporal windows. (E) Distribution of the strength of synapses activated preceding a random control timepoint (gray), dendritic Na⁺ spikes (Top, red colors), and NMDA spikes (Bottom, orange colors). For dendritic Na⁺ spikes and NMDA spikes, this distribution can be further split into cooperative trigger synapses (red and orange) and individual trigger synapses (magenta and yellow). The dots represent the mean values of the respective distribution. Note the peak at 0.1 nS resulting from BG synapses (w = 0.1 nS) that contribute to dendritic Na⁺ spikes and NMDA spikes. “Cooperative synapses” are synapses where more than one synapse was active in the spatiotemporal window preceding the dendritic spike, whereas if only a single synapse was active during this window, we call this an “individual trigger synapse.” (F) Average probability for a synapse to trigger a local dendritic Na⁺ spike (red) or NMDA spike (orange) as a function of synaptic strength. (G, Left) Snapshot of synaptic inputs across the dendritic tree (circles; brighter color indicates larger synaptic weight) contributing to the initiation of a dendritic Na⁺ spike. (Right) Silencing a strong trigger synapse (yellow circle at t = 27.6 ms, marked with a star on the Left) abolishes the dendritic Na⁺ spike. Contours are lines of equal membrane potential (maximum projection across all dendrites at this distance from soma, as in Fig. 3B).

To determine how many active excitatory synapses are required to trigger a dendritic spike, we counted the number of active synapses in a spatiotemporal window containing the peak temporal incidence of synaptic activation preceding dendritic spike initiation (Fig. 5B, red rectangles: up to 100 µm from the initiation site and 4 or 1.5 ms before the initiation of a Na⁺ spike or NMDA spike, respectively). On average, a single dendritic Na⁺ spike was triggered by 2.3 ± 1.4 active excitatory synapses, and a single NMDA spike was triggered by 1.6 ± 0.9 active excitatory synapses (Fig. 5C). In some cases, even a single synapse is sufficient to trigger either a dendritic Na⁺ spike or an NMDA spike (Fig. 5D).

Strong but Sparse Synaptic Inputs Trigger Dendritic Spikes.

Are all synapses equal in their ability to trigger dendritic spikes, or are there “privileged” synapses with respect to dendritic spike initiation? We plotted the probability that activation of a synapse leads to successful initiation of a dendritic spike as a function of peak synaptic conductance (Fig. 5F). This revealed a sigmoidal relationship: the probability of success is low for synapses with less than 0.5 nS peak conductance, increases severalfold from 0.5 to 2 nS peak conductance, and saturates for larger conductances. Thus, synaptic conductance is the major determinant of the efficacy of a synapse in evoking dendritic spikes. However, the scatter in the relationship indicates that other factors, such as dendritic morphology, dendritic location of the synapse, and in particular the number of cooperating synapses are also important. Notably, synapses which trigger dendritic spikes in cooperation with other synapses can include both strong and weak synapses (Fig. 5E, red and orange). However, synapses which can single-handedly trigger local dendritic spikes originate exclusively from the large-conductance tail of the lognormal synaptic weight distribution (Fig. 5E, magenta and yellow). In these cases, the dendritic spike was initiated at the location of this synapse (Fig. 5G). What is the functional impact of this subset of strong synapses, which we show have disproportional power in triggering dendritic spikes?

Dendritic Spikes Enable the Strongest 1% of Synapses to Determine Orientation Tuning of AP Output.

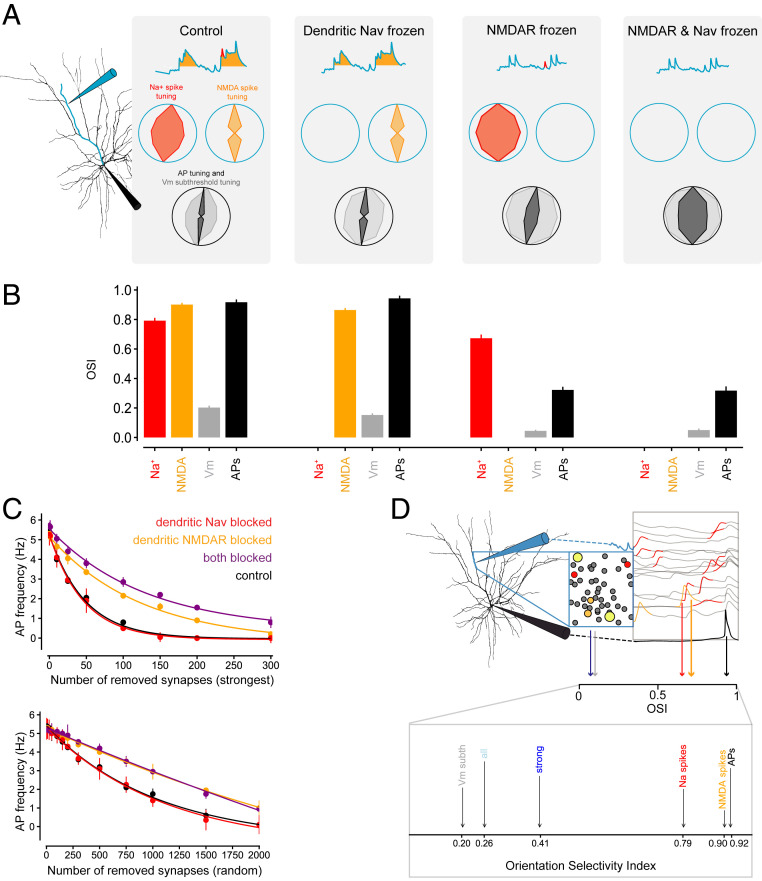
Since the generation of APs involves a threshold, they are often more sharply tuned than the average of the synaptic inputs triggering them, a phenomenon known as the “iceberg effect” (42, 43). This effect has previously been observed for orientation selectivity in L2/3 neurons in V1 (33, 36) and is reproduced by the model (SI Appendix, Fig. S6). Can dendritic spikes contribute to sharpening of AP tuning by nonlinearly amplifying and selectively weighting different synaptic inputs? To investigate this, we measured the orientation tuning of dendritic Na⁺ spikes, NMDA spikes, subthreshold membrane potential at the soma, and the AP output. As shown in Fig. 6 A and B, orientation selectivity index (OSI) values—with the exception of somatic V_mOSI, which is low both in the experiment (17) and in our model as it reflects the subthreshold tuning before application of the somatic iceberg effect—increase progressively from synaptic input via dendritic Na⁺ spikes and NMDA spikes to AP output (see also SI Appendix, Fig. S7 for full OSI distributions). This progression indicates that active dendrites enable two iceberg effects to enhance tuned responses to in vivo synaptic inputs: the first is the conversion of synaptic input to dendritic spikes, and the second involves their transformation into output APs.

Fig. 6.

Dendritic spikes enhance control of AP output and its tuning by a small number of strong synaptic inputs. (A) Example of the tuning of dendritic Na⁺ spikes (red) and NMDA spikes (orange) as well as subthreshold somatic membrane potential (gray) and APs (black), under control conditions and with dendritic Na⁺ spikes (second from Left), NMDA spikes (third from Left), or both (Right) blocked. (B) Mean OSI of dendritic Na⁺ spikes (red), NMDA spikes (orange), somatic V_m (gray), and APs (black) under control conditions (Left), with Na_v channels blocked (second from Left), with NMDA conductances frozen (third from Left), or both (Right). (C, Top) Removing strong synapses decreases AP frequency in response to a preferred visual stimulus in the full model (black) and under Na_v channel block (red). The decrease can be fit with an exponential decay and is less steep when NMDARs only (orange) or NMDARs and Na_v channels (purple) are blocked. Constant current was injected at the soma to maintain AP frequency at control levels with zero synapses removed. This was done to engage the somatic output nonlinearity at the same starting point as in control. (Bottom) Removing random synapses decreases AP frequency in response to a preferred visual stimulus in the full model (black) and under Na_v channel block (red). The decrease can be fit with an exponential decay. When NMDARs only (orange) or NMDARs and Na_v channels (purple) are blocked, the decrease can be fit linearly and is less steep. (D, Top) Schematic of the composition of spatiotemporal STAs of synaptic activity (see Fig. 5 A and B) and a spatiotemporal AP-triggered average of dendritic spikes (see Fig. 3 A and D). We used these tools to dissect the spatiotemporal constellations of synaptic inputs that evoke dendritic spikes and the effect of such dendritic spikes on AP output. (Bottom) OSI increases from synaptic input via dendritic spikes to AP output. We show the OSI of synaptic inputs (light blue: all synapses; dark blue: strong synapses), dendritic Na⁺ spikes (red), and NMDA spikes (orange) as well as subthreshold somatic membrane potential (gray) and APs (black).

To test this model, we directly measured the impact of dendritic spikes on the orientation tuning of AP output. We abolished either dendritic Na⁺ spikes by blocking dendritic Na⁺ conductances (Fig. 6 A and B, Center Left and SI Appendix, Fig. S7B) or NMDA spikes by freezing the voltage dependence of the NMDA conductance (Fig. 6 A and B, Center Right and SI Appendix, Fig. S7C) while maintaining the mean AP frequency by somatic current injection. When NMDA spikes were blocked, both the somatic subthreshold membrane potential tuning (as measured by the membrane potential OSI, V_mOSI) and the tuning of AP output were weakened compared to control conditions (Fig. 6 A and B, Left and Center Right and SI Appendix, Fig. S7C). Blocking dendritic Na⁺ spikes did not strongly affect V_mOSI nor AP output OSI (Fig. 6 A and B, Center Left and SI Appendix, Fig. S7B). However, simultaneous block of dendritic Na⁺ spikes and NMDA spikes strongly reduced both V_mOSI and output OSI (Fig. 6 A and B, Right and SI Appendix, Fig. S7D), indicating that dendritic spikes contribute substantially to the orientation tuning of AP output. Fig. 6B also shows that the tuning of dendritic Na⁺ spikes and NMDA spikes is reduced when the other type of dendritic spike is blocked, respectively, suggesting that they act cooperatively. A hallmark of this cooperativity, the combined contribution of dendritic Na⁺ spikes and NMDA spikes to AP output, exceeds the linear sum of their individual contributions (Fig. 4B): the firing rates when either dendritic spike is blocked (2.3 and 0 Hz) sum to less than the rate when they are both present (6.0 Hz).

These results suggest that sharply tuned, strong synaptic inputs, selectively amplified by dendritic spikes, have a disproportionate effect on the tuning of somatic output. To test this idea, we “deleted” inputs from the preferred input pool and measured the effect on AP output (Fig. 6C, Top). In all conditions, the relationship was described by an exponential decay, which was less steep when the NMDAR conductance was frozen alone or in combination with a block of Na_v, making the dendritic tree passive. We found that on average, removing as few as 46 of the strongest synapses, corresponding to less than 1% of the total synaptic input population, reduced AP output to 1/e of the initial value in the active model. Importantly, this effect relied on dendritic NMDA spikes: when the NMDA conductance was frozen to its value at the resting potential, twice the number (82 synapses) needed to be deleted to achieve the same reduction in AP output (Fig. 6C, Top). When dendritic Na_v was blocked in addition to freezing the NMDA conductance, the number of synapses to be deleted increased further to on average 95. Interestingly, the relationship was much more linear when random synaptic inputs as opposed to the strongest ones were removed (Fig. 6C, Bottom). Thus, compared to passive dendritic integration, dendritic spikes further amplify the efficacy of strong synapses in triggering APs at the soma.

Discussion

We have developed a realistic model of dendritic integration during sensory processing in vivo to address a longstanding question in neuroscience: how do active dendrites contribute to determining the stimulus selectivity of a neuron? Despite decades of work (44, 45), we still lack a good understanding of how neurons in primary sensory cortex respond selectively to a particular stimulus feature given a barrage of weakly selective inputs. Our model provides a mechanistic explanation for how narrowly tuned orientation-selective responses can arise from dendritic integration of weakly tuned synaptic input: a few strong synapses, which provide input from similarly tuned presynaptic neurons, preferentially trigger dendritic spikes. Dendritic spikes in turn are more narrowly tuned to orientation than the synaptic input and efficiently drive the majority of somatic AP output. Thus, by triggering dendritic spikes, a small subset of strong synapses drives amplification of orientation-selective signals, effectively determining the tuning of neuronal output. They do so in the context of the activity of other excitatory and inhibitory synapses on nearby dendrites, which can modulate their gain and thus implement a rich spectrum of nonlinear computations in dendrites (4, 46–48). These results indicate that active dendrites play an essential role in shaping stimulus selectivity in cortical circuits and have important implications for coding and connectivity in sensory cortex.

An Active Dendritic Model of In Vivo Synaptic Integration.

To study the mechanisms of synaptic integration during visual stimulation in vivo, we have built and combined models of synaptic input and the postsynaptic pyramidal neuron that are constrained by a large set of experimental data obtained in vitro (18, 22, 23, 49) and in vivo (17, 18, 20, 21, 23, 24). As with all biophysical models of neurons, biological variability in parameters including morphology, conductance densities, and synaptic weights leads to different parameter combinations that generate similar neural responses (50, 51) by relying on compensatory effects. The properties of real neurons will therefore differ from each other and from our model, allowing alternative scenarios for dendritic integration. The combined model reproduced characteristic dendritic spike waveforms and event statistics by using the sparse in vivo synaptic input patterns that are implied by recent experiments (20, 52). A key assumption was to use a lognormal distribution of synaptic weights, based on recordings from synaptically connected pairs of neurons (18, 31), with strong synapses preferentially tuned to a similar orientation as the postsynaptic neuron (18).

Because no direct and complete recordings of the synaptic input received by an L2/3 neuron in mouse V1 are available, we used patch-clamp recordings from the dendrites of L2/3 pyramidal neurons in mouse V1 in vivo (17) to constrain dendritic excitability and membrane potential dynamics during sensory processing. These dendritic recordings (see also ref. 12) present especially valuable sets of constraints because they allow dendritic events to be recorded directly with high resolution and because the spatial and temporal structure of synaptic input during sensory processing is still actively debated. In particular, evidence for spatial clustering of active synapses varies between different cell types, brain regions, and species (32–37, 53, 54). We therefore followed an approach in which synaptic inputs are placed randomly across the dendritic tree and activated independently of each other, with any spatial or temporal clustering occurring by chance. Our simulations show that this is sufficient to reproduce the pattern of dendritic Na⁺ spikes and NMDA spikes observed in vivo. We also show that implementing spatial clustering of cotuned excitatory inputs (32, 35, 36) has only a small effect on the orientation selectivity of dendritic spikes in our model (SI Appendix, Fig. S8), with the exception of the orientation selectivity of dendritic Na⁺ spikes, which increased with clustering when dendritic NMDA spikes were blocked. Thus, spatial clustering of cotuned synaptic input does not fundamentally change our conclusions about the relationship between synaptic input, dendritic spikes, and AP output.

Few Synaptic Inputs Are Sufficient to Drive Dendritic Spikes In Vivo.

The relationship between synaptic input in vivo and dendritic spikes in vivo is unknown. Here, we show that a small number of synaptic inputs can be sufficient to trigger a dendritic spike under in vivo conditions. In contrast, previous experimental work on pyramidal cells in brain slices suggested that many synaptic inputs are required to engage dendritic nonlinearities (39, 55, 56). Even with synchronous activation of inputs, activation of several tens of synapses was required to trigger dendritic spikes (57, 58). While early theoretical work suggested that single synapses could trigger regenerative events confined to a single spine head, these studies used very high spine neck resistances (59–61). More recent theoretical work has suggested that larger numbers of synchronized synaptic inputs are needed to initiate regenerative NMDA events in dendrites (39, 62) and to reproduce experimentally observed AP firing patterns in cortical pyramidal neurons (63, 64).

Our work complements these findings and suggests that during sensory processing, surprisingly few, but strong synaptic inputs—acting on top of BG depolarization provided by randomly activated synapses elsewhere in the dendritic tree (SI Appendix, Fig. S9)—can be sufficient to trigger local dendritic Na⁺ spikes and NMDA spikes. The discrepancy with previous experimental and theoretical work can be explained by the properties of the synaptic input that is present in vivo but absent in slices. Earlier attempts to include in vivo–like synaptic input to dendrites (39, 65–69) did not use realistic input weight distributions, which we have constrained using recent experimental data (18), featuring a tail of strong synapses among many weaker ones, a key element of our synaptic input model. Moreover, the advent of direct dendritic recordings of membrane potential in vivo during sensory processing (17) has now allowed us to provide more rigorous constraints on the frequencies and properties of active dendritic events in vivo. However, our results do not rule out alternative scenarios in which larger numbers of coactive, weaker synapses cooperate to generate dendritic spikes.

Dendritic Spikes Strongly Influence AP Output In Vivo.

How many dendritic Na⁺ spikes and NMDA spikes are required to trigger a single somatic AP? We used spatiotemporal AP-triggered averaging to identify dendritic events leading up to a somatic AP. On average, 5.5 ± 2.3 NMDA spikes and 9.9 ± 3.2 dendritic Na⁺ spikes occurred in the relevant time windows before a single AP. Recent in vivo two-photon imaging studies have suggested that local dendritic events are almost always part of a synchronized, multibranch depolarization of the dendrites that is associated with somatic AP firing (54, 70). Our results indicate that dendritic events often drive somatic APs, which explains these findings; however, we also find isolated dendritic events that would be more difficult to detect using calcium imaging methods. Our modeling approach also allows us to show that dendritic Na⁺ spikes and NMDA spikes provide different contributions to AP generation and AP tuning: NMDA spikes are good amplifiers even of single inputs, and a small number of spikes can drive somatic AP output (Fig. 3), which inherits their tuning (Fig. 6). Conversely, each dendritic Na⁺ spike represents integration over a larger number of synaptic inputs, forming an average of their sensory tuning—and in turn more dendritic Na⁺ spikes are required to drive a single somatic AP.

Our simulations also explain an apparently paradoxical experimental finding: using intracellular MK-801 to block NMDA receptors almost completely prevents AP output, while mean somatic membrane potential is little affected (11, 13, 17). Our model reproduces these results (Fig. 4 A and B), and using a cumulative block of NMDA spikes in individual dendrites, (Fig. 4C) we provide a causal link between NMDA spike generation and AP output at the soma. Specifically, NMDA spikes in individual dendritic branches provide substantial amplification of membrane potential transients so they reach threshold for triggering APs, without strongly affecting the mean membrane potential at the soma.

Output Tuning Is Determined by Dendritic Spikes.

The prevailing view of synaptic integration is that the preferred orientation, and the tuning width of the output of a neuron, are set by the sum of its synaptic inputs and the nonlinearity of AP generation (33, 37, 71–73). Even in models where the distribution of synaptic weights is taken into account (18, 74), a predominantly linear sum of those inputs drives somatic membrane potential fluctuations (75), and the sharpness of output tuning is effectively set by the somatic AP threshold. However, this single “iceberg effect” (42, 43) at the soma cannot explain the almost complete suppression of AP output by intracellular MK-801 block of NMDAR-mediated synaptic nonlinearities observed in vivo (11, 13, 17). Furthermore, direct dendritic recordings from neurons in mouse V1 show a progressive increase in orientation selectivity from synaptic input via dendritic spikes to AP output, while subthreshold somatic membrane potential remains weakly tuned (17). Here, we demonstrate a mechanism that provides an explanation for these results: well-tuned, strong synapses are privileged in their ability to trigger dendritic spikes, which in turn drive AP output. This mechanism effectively corresponds to two iceberg effects in series (Fig. 6D): the first being dendritic (and thus implemented locally and in parallel in different dendritic branches), resulting from the selective amplification of synaptic inputs by dendritic spikes, and the second being axosomatic, a global threshold for neuronal output. It is likely that the nonlinearities underlying these two iceberg effects can implement more general dendritic computations beyond orientation tuning (76). To demonstrate this mechanism directly, we performed simulations in which we blocked dendritic Na⁺ spikes or NMDA spikes while matching the mean somatic firing rate by constant somatic current injection. In this case, output tuning selectivity is degraded (Fig. 6 A and B). In summary, dendritic spikes are an essential step in the transformation of synaptic input tuning to neuronal output tuning. Importantly, we show that active dendrites strongly reduce the number of synapses that are required to determine output tuning, compared to a model without dendrites (18).

Implications for Circuit Function.

We demonstrate that a small fraction of strong synaptic inputs can determine postsynaptic output and its tuning. What are the implications of such a sparse input representation for the function of single neurons and for the operation of the circuit? First, sparser synaptic connectivity allows more robust storage of a given number of patterns in recurrent neural networks (77). Second, heavy-tailed synaptic weight distributions allow neural circuits to respond faster, have a larger dynamical range, and be less sensitive to random fluctuations in synaptic activity (74), compared to networks with normally distributed synaptic weights. Finally, computational and empirical evidence suggests that sparse, strong synapses embedded within a large pool of weak synaptic inputs might allow the neuron to “reside one synaptic input away from the threshold” (78). The resulting strong correlations in activity between pre- and postsynaptic neurons connected by strong synapses have indeed been observed in vivo (18) and may be both cause and consequence of the synaptic plasticity creating and maintaining the functional architecture of the circuit.

By amplifying the effect of strong synaptic inputs and helping them to reach threshold for the somatic AP, active dendrites enable an even sparser input representation than passive dendrites (Fig. 6C). Active dendrites therefore provide several advantages. First, encoding stimulus features with a smaller number of active neurons further increases the energy efficiency of the circuit (79), as chemical synaptic transmission is energetically costly (80) and AP propagation in presynaptic axons is more expensive than having active dendrites (81). Second, the large number of “background” synapses with small weights could provide the neuron with a reservoir to represent new stimuli through synaptic plasticity. For example, a recent model of learning (82) suggests that in the absence of dendritic amplification, weak synaptic input only minimally affects AP output, while plateau potentials not only drive somatic output but also lead to synaptic weight updates (83). Finally, nonlinear subunits in active dendrites increase the number of input patterns that can be stored and nonlinearly discriminated (76).

Given that a small number of strong inputs can determine output tuning, this leaves open the question of the immediate functional role of the majority of weaker synaptic inputs. First, they can provide weakly or untuned BG depolarization (18) to allow dendritic spikes—which are driven by the sparse, highly tuned input—to trigger output APs. Second, they might be involved in a distributed representation of more complex visual stimuli, such as natural scenes (53). In this way, they could allow dendritic mechanisms to implement computations that had previously been ascribed to network function, such as complex cell responses (7) and binocular disparity (3). Third, they could carry additional information about brain state and modulate postsynaptic response properties depending on the level of attention or motion of the animal (20, 84, 85). Finally, coactivation of local groups of weaker synapses could emulate the activation of a strong synapse (37), also in the recruitment of dendritic spikes (39, 86, 87).

We expect the mechanism described here to generalize to neurons in any neural circuit where sparse synaptic inputs engage postsynaptic dendritic nonlinearities. It should be particularly relevant in sensory systems where different sensory features are represented by a subnetwork of strongly coupled neurons with similar response properties, such as in barrel cortex (88, 89). While our quantitative predictions are based on responses in well-tuned L2/3 pyramidal neurons in mouse V1, the NMDA spikes and dendritic Na⁺ spikes studied here illustrate a more general principle of single neuron computation: dendritic excitability serves to selectively amplify the impact of a subset of strong synaptic inputs. In cells that do not support dendritic Na⁺ spikes or NMDA plateau potentials, NMDA current boosting (90) might provide sufficient input amplification to cross threshold for AP generation. This amplification could also be performed by other nonlinear dendritic mechanisms, such as dendritic Ca²⁺ spikes (91) or BAC firing (92).

Experimentally Testable Predictions.

Our results lead to several experimentally testable predictions. First, our model predicts that activating a small number of strong synaptic inputs in addition to a sensory stimulus 45° off from the preferred orientation should increase AP output to match the original sensory response to the preferred orientation. This number should be insufficient if randomly chosen synaptic inputs of average weight are activated, or if dendritic spikes are inactivated, for example, using targeted pharmacological intervention (13). The necessary experiment would require mapping the orientation selectivity of presynaptic neurons and a postsynaptic neuron and targeted photostimulation (93, 94) of a set of presynaptic neurons whose tuning is similar to that of the postsynaptic neuron.

Second, we predict that the response to a preferred grating orientation should decrease to a level corresponding to 45° off the preferred orientation when a small number of strong synapses coding for the preferred orientation are successively “removed,” or inactivated. Importantly, this effect should be absent if the same number of random synapses are inactivated or if dendritic spikes are pharmacologically inactivated. To test this prediction, one could characterize the sensory response properties of presynaptic neurons, then progressively inactivate those presynaptic neurons whose response properties are most similar to those of the postsynaptic neuron using targeted optogenetics (93, 94), with or without block of NMDA spikes by postsynaptic MK-801 (11, 13, 17). The effect on AP output could then be compared to the predictions of our model (Fig. 6C).

Finally, the quantitative relationships we predict between synaptic input, dendritic spikes, and somatic output may eventually be directly experimentally testable. This would require simultaneously measuring synaptic input patterns and dendritic voltage across the entire dendritic tree in vivo, while monitoring somatic output. This is an unprecedented experiment, which represents a major technical challenge, but recent developments in rapid three-dimensional two-photon imaging techniques (95–99), in combination with the use of new generations of genetically encoded sensors of glutamate (100) and voltage (101), may allow the decisive measurements to be made.

Conclusions

By synthesizing the latest data on synaptic connectivity, synaptic weight distributions, and dendritic excitability in V1 in vivo, we have shown that the selective amplification of the strongest 1% of synaptic inputs by dendritic spikes enables them to determine somatic AP output and its tuning. This occurs in a two-step process, whereby a small number of strong synapses trigger local dendritic NMDA spikes and Na⁺ spikes, and few dendritic spikes in turn are sufficient to drive AP output. As a consequence, many synapses are freed up to encode other input features, increasing the computational capacity of the postsynaptic neuron and the surrounding circuit. Ultimately, this design provides the local network with great flexibility for learning: only a small number of connections need to be changed to encode a different stimulus and alter the response properties of a neuron.

Materials and Methods

L2/3 Pyramidal Cell Compartmental Model.

All simulations were performed using NEURON [version 7.4 (102)] and Python (version 2.7/IPython version 5.1). We used a detailed morphology of a L2/3 pyramidal neuron filled with horseradish peroxidase (neuromorpho.org, archive Martin, NMO_00904), as used in Smith et al. (17). To improve the fit between model and in vivo experiments, we added an axon initial segment and axon hillock (reference SI Appendix, Table S1 for parameters). Passive parameters were C_m = 1.0 μF/cm², R_m = 15,000 Ω cm², and R_a = 150 Ω cm. We used voltage-activated Na⁺ channels (103), fast and slow voltage-activated K⁺ channels (104), M-type K⁺ channels, high- and low-voltage–activated Ca²⁺ channels, and Ca²⁺-activated K⁺ channels (reference SI Appendix, Table S1 for parameters and channel model references). Conductance densities in the axon, axon initial segment and hillock, soma, and dendrites are given in SI Appendix, Table S1. Reversal potentials were E_leak = −80 mV, E_Na = 60 mV, E_K = –80 mV, and E_Ca = 140 mV. The voltage dependence of activation and inactivation of all voltage-gated ion channels was shifted by 18.5 mV in the soma and by 13.5 mV in the axon and dendrites, and kinetics were scaled for a nominal temperature of 37 °C. The passive and active model properties satisfy a large range of constraints from experiments in vitro and in vivo (SI Appendix, Fig. S1).

In Vivo Synaptic Input Model.

We used numerous experimental findings to constrain our synaptic input model. Briefly, we calculated the average single synaptic conductance based on experimentally measured somatic excitatory postsynaptic potential (EPSP) amplitudes (18), taking into account dendritic morphology (our simulations) and the number of synapses per contact (19, 105). The conductances of individual excitatory signal synapses were then drawn from a lognormal distribution (28, 31) with this mean value, and each synapse was assigned a mean presynaptic firing rate for each sensory stimulus condition. The time-averaged total synaptic conductance was kept consistent with measurements obtained from in vivo whole-cell voltage-clamp recordings (20, 52). Under a realistic overall firing rate distribution (17, 18) this yielded a total number of synaptic inputs consistent with anatomical data. Regarding the spatial and temporal distribution of synaptic inputs on the dendritic tree, we make the simplest possible (and conservative) assumption that synaptic inputs are independent of each other, and are randomly distributed in space across the postsynaptic dendrites, as well as randomly activated in time (Discussion). The random placement of synapses in the dendritic tree is consistent with the recent results of Park et al. (106), who used ablation of L2/3 pyramidal neuron dendrites to show that there is no “master dendrite” which controls orientation selectivity.

Number and spatial distribution of synapses.

The model L2/3 neuron receives 5,001 synaptic contacts, of which 25% are inhibitory (25). Furthermore, 50% of inhibitory synapses were located perisomatically (107). To achieve a random spatial distribution of excitatory synapses on the dendritic tree (49), we proceeded as follows: for any given synapse, a dendrite was randomly chosen with a probability matching its fractional surface area, and a location on the dendrite was chosen from a uniform distribution of relative positions along its length (ranging from 0 to 1). For inhibitory synapses, 50% were randomly distributed across the dendritic tree according to the same rules as excitatory synapses. Of the remaining inhibitory synapses, 80% were placed directly on the soma and 20% were randomly distributed on the four dendrites branching off the soma.

Functional clustering of synapses.

To reproduce experimental results from Wilson et al. (36), we simulated functionally clustered synaptic inputs in a subset of simulations. To match the dispersion of orientation preferences of synaptic inputs along the dendrite measured by Wilson and colleagues (36), we fitted a Gaussian to the spiking response of each synapse, to four different orientations, 0°, 45°, 90°, and 135°, and calculated its preferred orientation. We then calculated the difference in orientation preference across all synapses. To generate clusters of similarly tuned synapses, we split the dendritic tree into regions of interest (ROIs) of ∼20-µm length (mean ± SD = 19.9 ± 3.6 µm) within which experimental work has identified clustering or apparently random synaptic organization (33, 36, 37, 53, 54). We then calculated the circular dispersion (36) of the orientation preferences of synapses in each ROI. Next, we swapped the location of the synapse with the highest contribution to the circular dispersion with another randomly chosen synapse; we then recalculated the circular dispersion for all synapses in the two ROIs affected by the new locations generated by the swap: if the new locations reduced the mean circular dispersion, we accepted them, but if the new locations increased or did not change the mean circular dispersion, we rejected the swap. We repeated this swapping procedure until the mean circular dispersion of all synapses was equal to or less than 15°. Our final “clustered” model had a circular dispersion of 15.0° ± 6.7° (mean ± SD), in agreement with experimental data (36).

In vivo–like synaptic activation.

Two thirds of synapses (“signal synapses”) were driven by an inhomogeneous Poisson process (108), with a mean firing rate of 1.37 ± 0.23 Hz (excitatory) or 6.0 Hz (inhibitory), consistent with refs 17 and 20. Notably, a characteristic feature of synaptic input during visual stimulation in vivo is the ratio of the tuned (F1) to the untuned postsynaptic response (F0) it evokes (refer to ref. 18, Fig. 4 A–D). We therefore modulated the firing rate of all synaptic inputs by a sine function of time to mimic an oscillating visual stimulus. We adjusted the scaling and offset of the sine oscillation to match experimentally observed F0:F1 ratios (17, 18). All other synapses (“background synapses”) were active at a constant rate of 1.0 Hz (excitatory) or 6.0 Hz (inhibitory) (20, 21, 24, 28). Overall, the total time-averaged excitatory and inhibitory synaptic conductance received by the postsynaptic neuron during visual stimulation was consistent with the experimentally measured values (20).

Synaptic weight distribution.

The weights of excitatory signal synapses followed a lognormal distribution (27–29, 31) (reference SI Appendix, Fig. S2B). We used the mean, median, and SD of the distribution of somatic EPSP amplitudes (in mV) recently measured by ref. 18 between pairs of L2/3 pyramidal neurons in mouse visual cortex (19, 109, 110) to fit a lognormal distribution (SI Appendix, Fig. S2B, Top) with parameters µ = –1.51 and σ = 1.14 as the mean and SD of the underlying normal distribution, respectively.

To translate the measured mean somatic EPSP amplitude into the peak conductance of a single synaptic contact (30), we simulated the activation of a single contact, determined the resulting somatic EPSP amplitude, and averaged the results of iterating this procedure over all dendritic locations where the single active contact was placed (SI Appendix, Fig. S2A). We then adjusted the peak synaptic conductance of this single contact to match the experimentally measured somatic EPSP amplitude divided by the number of synaptic contacts per connection between L2/3 pyramidal neurons (2.8) (19, 105). We used a fixed number of synaptic contacts per connection for this conversion since the correlation between the number of synaptic contacts per connection and the somatic EPSP amplitude is weak (19, 30), and other factors, such as dendritic location, presynaptic release probability, and postsynaptic conductance per synaptic contact are more important determinants of somatic EPSP amplitude. As this procedure assumes a release probability of 1, it yields a conservative estimate of the conductance of an average synaptic contact of 0.203 nS for excitatory signal synapses.

Finally, we obtained the lognormal distribution of synaptic conductances with this mean value (SI Appendix, Fig. S2B, Top) by linearly scaling the distribution of somatic EPSP amplitudes. BG excitatory synapses had a fixed conductance of 0.1 nS. Furthermore, we used an NMDA:AMPA ratio = 1 (17) for all excitatory synapses and verified that this produced results consistent with experimental data (ref. 111, Fig. 6 A and B) (ref. 112, Fig. 3). The GABA peak conductance was 0.1 nS, GABA reversal potential was –80 mV, and kinetics as in ref. 17, with the exception of τ_riseAMPA = 0.5 ms and τ_decayNMDA = 26 ms (111).

Implementation of synaptic input for different visual stimulus orientations.

Neurons with similar receptive field (RF) properties are more likely to be connected and share stronger synaptic connections than neurons with unrelated RF properties (18, 113). To emulate both findings in the synaptic input model, we first distributed the 3,000 excitatory signal synapses into 16 bins according to an empirical function of their spatial RF correlation with the postsynaptic neuron (SI Appendix, Fig. S2B, blue bars) following the distribution of pairwise RF correlations observed in the experiment (ref. 18 Fig. 2G, blue histogram). We then implemented the dependence of somatic EPSP amplitude on spatial RF correlation observed in the experiment by repeatedly swapping synaptic conductance values between pairs of spatial RF correlation bins and accepting a swap if the mean synaptic weight in each spatial RF correlation bin improved the approximation of the exponential relationship (ref. 18, refer to Extended Data Fig. 5D). The number of swaps was chosen to approximate the scatter in ref. 18 (refer to Fig. 2G, circles). This procedure results in stronger conductances being preferentially, but not exclusively, assigned to synapses with larger spatial RF correlations with the postsynaptic neuron (SI Appendix, Fig. S2B, Bottom) while the overall distribution of synaptic conductances remains lognormal (SI Appendix, Fig. S2B, Top).

Spatial RFs computed by reverse correlation with natural images using the pseudoinverse method employed by Cossell et al. (18) have been shown to predict the optimum orientation of the same cells in response to drifting gratings with high accuracy (114). However, spatial RF correlation can be small and even negative for two neurons with similar orientation preference (18). Thus, the procedure of assigning conductance values to synapses binned according to spatial RF correlation (SI Appendix, Fig. S2B, Bottom) introduces additional variability in synaptic conductance to inputs that may in fact have similar orientation preference.

Finally, the orientation of the visual stimulus was defined by different empirical distributions of firing rates of the presynaptic inputs (SI Appendix, Fig. S2C, cityscape histograms). During presentation of a stimulus at the preferred orientation of the postsynaptic neuron, 90°, synapses with a similar orientation preference as the postsynaptic neuron (and consequently higher weights on average) were activated at higher rates, while synapses preferring the orthogonal orientation were activated at lower rates, and vice versa (SI Appendix, Fig. S2C). Overall, synaptic input firing rates followed a normal distribution with a mean of 7.5 Hz (3.75 Hz for nonpreferred) and SD of 4 Hz (2 Hz for nonpreferred). Distributed across synapses of different synaptic weights, this achieves the average synaptic firing rates described under In vivo–like synaptic activation above.

Implementation of Pharmacological Block of Na_v Channels and NMDARs.

To compare our model responses to pharmacological experiments (13, 17), we mimicked the block of Na_v channels and NMDARs by setting g_Na = 0 or freezing the voltage dependence of NMDARs at the resting potential, respectively. For the Na_v channel block, we applied g_Na = 0 only to dendrites at a distance d > 50 µm from the soma to maintain the somatic resting membrane potential and AP threshold of the model.

AP-Triggered Averages of Dendritic Spikes.

Detectors for dendritic Na⁺ spikes, NMDA spikes, and bAPs are described in SI Appendix. We used STA to determine spatiotemporal windows during which dendritic Na⁺ spikes and NMDA spikes can drive AP output. We found that windows relative to AP onset from –15 to 0 ms for Na⁺ spikes and windows from –40 to 0 ms for NMDA spikes over the space of the whole dendritic tree were sufficient to capture dendritic activity preceding somatic APs (Fig. 3D). We then used these windows to count the number of dendritic Na⁺ spikes and NMDA spikes preceding a single AP. As a control, we counted dendritic Na⁺ spikes and NMDA spikes in the same spatiotemporal windows placed at random times during the visual response (see Fig. 3D).

Dendritic STAs of Synaptic Inputs.

Analogous to the AP-triggered averages of dendritic spikes, we performed dendritic STAs of synaptic inputs. Here, we found that spatiotemporal windows of −4 ms from the dendritic Na⁺ spike initiation time and −1.5 ms from the NMDA spike initiation time, as well as 100 µm from the Na⁺ spike initiation site and NMDA spike initiation site, covered all synaptic inputs integrated by the dendritic spike (Fig. 5B). We used these windows to count the number of excitatory synaptic inputs that can generate a local dendritic Na⁺ spike or NMDA spike, respectively. As a control, we used the same spatiotemporal windows but triggered on permuted spike initiation times while keeping the original spike initiation sites, taking into account the spatial and temporal statistics of spike initiation across the dendritic tree. The control values at random times are consistent with a back-of-the-envelope calculation of the expected number of active synapses in the detection window for Na⁺ spikes (1.32 synapses/window) and NMDA spikes (0.49 synapses/window), taking into account the mean firing rate (1.88 Hz) during the 200-ms peak in input firing, during which most APs are triggered, mean synapse density on the dendritic tree (0.53 synapses/µm³, see also refs. 115 and 116), as well as the spatial and temporal dimensions of the detection window (332 µm² dendritic surface area and 4 or 1.5 ms duration for Na⁺ spikes and NMDA spikes, respectively).

Measurement of Orientation Tuning.

We used the OSI to determine orientation tuning of synaptic input, dendritic spikes, somatic APs, and subthreshold membrane potential at the soma (V_mOSI) (17). OSI is defined as follows:

$$\text{OSI}=\frac{Rp-Ro}{Rp+Ro},$$

where Rp and Ro denote the response in the preferred and orthogonal direction, respectively. We define “OSI tuned,” shown in Fig. 6 A, B, and D, as the OSI including only events that display orientation tuning, that is, where the difference between a fitted Gaussian and the data are less than 15% of the peak response value (17). For the subthreshold dendritic response—an approximation to the charge delivered to the dendrite—the response is the product of the synaptic strength and presynaptic firing rate, summed over all synapses. For synaptic inputs, dendritic Na⁺ spikes and NMDA spikes, as well as somatic APs and V_m, we fitted a Gaussian to the orientation tuning curve (117), which consisted of the number of events during 0°, 45°, 90°, and 135° orientation for dendritic spikes and somatic APs, and the peak-to-trough amplitude of the cycle average for somatic V_m (17).

Removing Synapses.

To “remove” n strong excitatory synapses from the input configuration in the preferred orientation, we first sorted all excitatory synapses by descending synaptic weights and then set the firing rates of the strongest n excitatory synapses to 0 Hz. In addition, we also set the rates of a matched number of randomly chosen inhibitory synapses to 0 Hz. To remove n random excitatory synapses from the input configuration in the preferred orientation, we randomly selected n synaptic inputs and set their firing rates to 0 Hz. Error bars show SD unless stated otherwise.

Data Availability

There are no data underlying this work.