Tracking the impacts of El Niño drought and fire in human-modified Amazonian forests

Significance

Amazonia is experiencing an increase in the frequency of extreme droughts and wildfires. However, the duration of their impacts on plant mortality and carbon stocks are poorly known, and it is unclear whether impacts are amplified in forests with a history of previous human disturbance. We show that plant mortality rates remain above baseline levels for over 3 y in forests affected by drought and 2.5 y in forests affected by both drought and fire. A history of human disturbance led to greater plant mortality in forests simultaneously affected by drought and fire. Our assessment of an area covering 1.2% of the Brazilian Amazon shows that regional drought and fires can have globally relevant impacts on the world’s carbon balance.

Abstract

With humanity facing an unprecedented climate crisis, the conservation of tropical forests has never been so important – their vast terrestrial carbon stocks can be turned into emissions by climatic and human disturbances. However, the duration of these effects is poorly understood, and it is unclear whether impacts are amplified in forests with a history of previous human disturbance. Here, we focus on the Amazonian epicenter of the 2015–16 El Niño, a region that encompasses 1.2% of the Brazilian Amazon. We quantify, at high temporal resolution, the impacts of an extreme El Niño (EN) drought and extensive forest fires on plant mortality and carbon loss in undisturbed and human-modified forests. Mortality remained higher than pre-El Niño levels for 36 mo in EN-drought–affected forests and for 30 mo in EN-fire–affected forests. In EN-fire–affected forests, human disturbance significantly increased plant mortality. Our investigation of the ecological and physiological predictors of tree mortality showed that trees with lower wood density, bark thickness and leaf nitrogen content, as well as those that experienced greater fire intensity, were more vulnerable. Across the region, the 2015–16 El Niño led to the death of an estimated 2.5 ± 0.3 billion stems, resulting in emissions of 495 ± 94 Tg CO₂. Three years after the El Niño, plant growth and recruitment had offset only 37% of emissions. Our results show that limiting forest disturbance will not only help maintain carbon stocks, but will also maximize the resistance of Amazonian forests if fires do occur.^*

The Amazon basin is critically important for climate regulation, biodiversity conservation, and for supporting the livelihoods of millions of people (1). However, all these can be affected by the climate crisis (2, 3). One way to mitigate the impacts of climate change is through preserving the Amazon biome, which can act as an important carbon sink, sequestering more carbon via photosynthesis than emitting via decomposition and respiration (4). Nevertheless, this sink can become a source due to elevated plant mortality during extreme droughts (5, 6) or as a consequence of direct anthropogenic disturbances [e.g., selective logging and forest fires (7, 8)], which now affect an area much greater than that deforested (9). While the individual influence of extreme droughts and anthropogenic disturbances on carbon stocks are increasingly well known (10, 11), the combined effects of these two stressors remain poorly understood (12). Furthermore, in years of extreme drought, there is an increase in the occurrence of forest fires (7) as more fires escape agricultural lands and burn surrounding forests (13), which become temporary flammable due to drought conditions (14). According to climate predictions, extreme droughts and forest fires will become more frequent in much of Amazonia (15, 16), being exacerbated by increasing temperatures (17), and could herald the start of large-scale forest dieback (2). It is therefore vital to understand the severity and the duration of drought and fire effects on plant mortality and subsequent carbon loss.

Although increased plant mortality is the main mechanism by which the Amazon can switch from a carbon sink to a source, it is unclear what ecological and physiological factors can increase mortality in forests affected simultaneously by an extreme drought and anthropogenic disturbance. During a severe drought, the mortality of plants due to carbon starvation or hydraulic failure (18) can be heightened by morphological traits (e.g., stem size, height, and wood density), competition for water with other individuals, or attacks by herbivores (19). Similarly, local anthropogenic disturbance events can lead to increased mortality of a nonrandom portion of the plant community—for example, selective logging disproportionately impacts larger trees with high wood density because of their timber value (20). However, mortality from forest fires—which were largely unprecedented during the evolution of the Amazon’s flora—is less understood (21) and has been mostly attributed to cambium damage resulting from the lack of protection offered by the thin bark of Amazonian trees (22). Determining what predictors influence plant mortality during drought and fire events in undisturbed and human-modified forests, as well as the duration of each factor’s effect, will advance our understanding of the resilience of Amazonian forests in the Anthropocene.

Here, we address these knowledge gaps by examining 1) the duration of the effects of the 2015 to 16 El Niño–driven drought and fires on plant mortality and carbon stocks, 2) whether previous anthropogenic disturbance affects the El Niño impacts on plot-level stem mortality and carbon stocks, and 3) the ecological and physiological predictors of tree mortality over time. Finally, we 4) scale up our results to our study region—the Lower Tapajós—comparing the CO₂ emissions resulting from the 2015 to 16 El Niño with the annual CO₂ fluxes resulting from forest growth and loss across the entire Brazilian Amazon (see Methods).

Study Region and Plot Network

The Lower Tapajós, a 6.5-million hectare region of Eastern Amazonia, is composed of a mix of undisturbed and human-modified forests, which have experienced selective logging and wildfires in the past (23)—a landscape configuration very common in many parts of Amazonia (SI Appendix, Fig. S1). In 2015 to 16, the Lower Tapajós was the Amazonian epicenter of that year’s El Niño event—temperature anomalies were between 1.5 to 2 °C higher than observed in previous El Niños (17), the maximum climatological water deficit (a measure of dry season intensity) peaked at −448 mm, the highest deficit in the 19-y record (i.e., 2000 to 2018—see Methods), and the climatological water deficit (a measure of dry season length) remained negative for 8 mo, 2 mo longer than usual (SI Appendix, Fig. S2). These hot and extremely dry conditions contributed to unprecedented mega-wildfires, burning one million hectares of forests throughout the dry season (SI Appendix, Fig. S3A). To investigate the impacts of the El Niño drought and fires on undisturbed and human-modified forests, we conducted quarterly surveys from October 2015 to October 2018 in which we monitored the fate of 6,117 stems in 21 long-term plots. The plots were distributed along a gradient of pre-El Niño human disturbance, including undisturbed, logged, logged-and-burned, and secondary forests (hereafter referred to as pre-EN forest disturbance classes; SI Appendix, Table S1). During the El Niño, 13 plots were only affected by drought (EN-drought-affected, hereafter), while eight were also affected by wildfires, burning between the last week of November 2015 and the first of January 2016 (SI Appendix, Fig. S3B). We use the term “EN-fire-affected” for these plots but recognize that they suffered both drought and fire effects.

The Duration of El Niño Effects on Plant Mortality and Carbon Loss

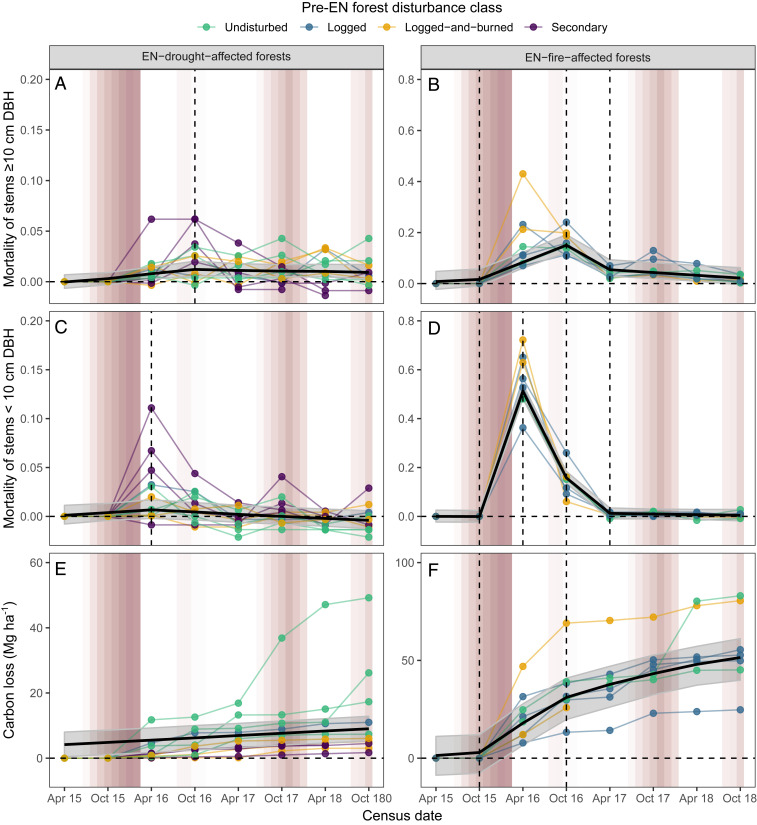
Our first analysis evaluated the magnitude and duration of the El Niño effects on stem mortality and carbon loss using a Bayesian change point model, a useful technique for examining changes in trends over time (see Methods). We found that in EN-drought–affected forests, there was a small increase in the mortality of stems ≥10 cm in diameter at breast height (DBH), which persisted for the whole 3 y of continued monitoring (Fig. 1A). No significant drought response was detected for stems <10 cm DBH (Fig. 1C), with mortality rates continuing similar to those of baseline levels. Over the whole sampling period, cumulative El Niño-mediated mortality of stems ≥10 cm DBH and <10 cm DBH in EN-drought–affected forests averaged 10 and 7%, respectively. In EN-fire–affected forests, mortality remained above baseline levels for 30 mo for stems ≥10 cm DBH and for 1 y for stems <10 cm DBH (Fig. 1 B and D). On average, we observed a mortality of 47% of stems ≥10 cm DBH and of 73% of stems <10 cm DBH in EN-fire–affected forests. These high levels of overall stem mortality explain why mortality rates went back to baseline levels in EN-fire–affected forests—there were not many stems left from the original plant stock, and although fire-driven mortality persisted, it was not enough to surpass baseline levels.

Fig. 1.

El Niño–driven carbon loss and plant mortality. Cumulative mortality of (A and B) stems ≥ 10 cm DBH and (C and D) stems 2 ≤ DBH < 10 cm; and (E and F) cumulative carbon loss between April 2015 and October 2018 in EN-drought–affected (A, C, and E) and EN-fire–affected forests (B, D, and F). Mortality was defined as the proportion of stems lost in census after discounting for baseline (i.e., pre-EN) levels of mortality (represented by the horizontal dashed line). Points show plot-level results and are colored by pre-EN forest disturbance classes. The solid black line shows the median estimate from the Bayesian piecewise linear change point model. The gray band shows the 95% credible interval. Vertical dashed lines show the changepoints (see Methods). The white/red background displays the CWD for the Lower Tapajós region from 0 (white) to −448 (dark red) mm.

The El Niño drought led to a median loss of 9.0 Mg ⋅ C ⋅ ha⁻¹ (95% credible interval: 5.2 to 12.9) over the whole sampling period, a figure 5.7 times smaller than in EN-fire–affected forests (51.5 Mg ⋅ C ⋅ ha⁻¹; 95% credible interval: 39.8 to 61.1). In EN-drought–affected forests, the pattern of carbon loss remained unchanged throughout the 3 y despite a peak in plant mortality immediately after the El Niño (Fig. 1 A, C, and E). In EN-fire–affected forests, carbon loss increased substantially in the first year after the El Niño (Fig. 1F), driven by the large spike in stem mortality (Fig. 1 B and D).

El Niño Impacts on Undisturbed and Human-Modified Forests

We used Bayesian ANOVA to assess whether the effects of the El Niño on plant mortality and carbon loss were higher in human-modified forests than in undisturbed controls (SI Appendix, Fig. S4). This plot-level assessment of plant mortality revealed two cases in which previous disturbance amplified the El Niño effect: for stems <10 cm DBH, mortality from drought alone was significantly higher in secondary forests (SI Appendix, Fig. S4C and Table S2); while for stems ≥10 cm DBH, the impact from drought and fire combined was higher across all human-modified forests (SI Appendix, Fig. S4B and Table S2). The results for carbon loss were very different from those for mortality. In EN-drought–affected forests, carbon loss was significantly higher in undisturbed controls despite all forest classes presenting similar levels of absolute and relative stem mortality (SI Appendix, Fig. S4A). In EN-fire–affected forests, relative and absolute carbon loss was similar across all pre-EN forest disturbance classes (SI Appendix, Fig. S4B), even though a greater number of stems ≥10 cm DBH died in human-modified forests. These apparently contradictory results can be explained by differences in size structure—in human-modified forests, stems are smaller and shorter than in undisturbed controls (SI Appendix, Table S1), and their mortality results in the loss of less carbon. Conversely, the death of a few very large stems, which are either absent or much rarer in human-modified forests, can lead to the loss of a disproportionate amount of carbon in pre-EN undisturbed forests.

Identifying Predictors of Tree Mortality

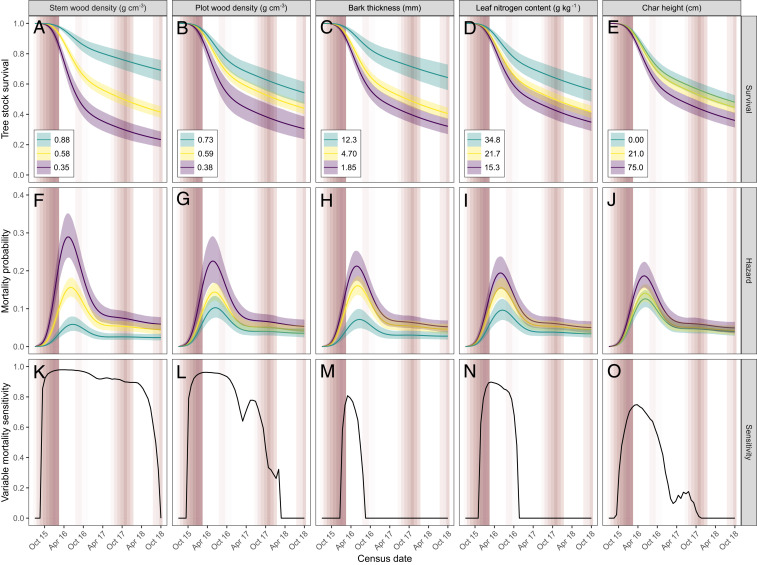
We employed Bayesian survival analysis to examine 11 potential ecological and physiological predictors of mortality for trees ≥10 cm DBH (n = 2,476). To increase statistical power and find generalizable trends, we substituted our pre-EN forest disturbance classes with a continuous variable that acts as a strong proxy of the intensity of previous human disturbance—plot-level mean wood density (24). We expected that postdrought and postfire mortality would be positively influenced by a) previous anthropogenic disturbance (low plot-level mean wood density), b) traits that can lead to either carbon starvation or hydraulic failure (taller and larger trees, those with low wood density, and trees with leaves with high specific leaf area and high nitrogen and phosphorus content), c) competition (higher levels of liana loads), d) higher levels of herbivory, e) lower stem protection (thinner bark), and f) greater fire intensity (char height) in the case of EN-fire–affected forests (19, 24). Last, we used the survival analysis to evaluate the mortality sensitivity of trees to variation in the mortality predictors.

Stem wood density was the only predictor of large tree mortality in EN-drought–affected forests, with lower wood density trees being less likely to survive (SI Appendix, Fig. S5 A and B and Table S3). This variable led to an increase in mortality sensitivity for 30 mo (SI Appendix, Fig. S5C). In EN-fire–affected forests, five variables predicted mortality (Fig. 2). Among these, stem wood density was the most influential—stems in the fifth percentile of the observed gradient of wood density values were more than three times as likely to have died by the end of the time series as those in the 95th percentile. Stem wood density raised the mortality sensitivity throughout almost the entire time series (Fig. 2K). Pre-EN plot-level mean wood density (a continuous variable that acts as a proxy for previous human disturbance; see Methods) was the second most important mortality predictor in EN-fire-affected forests, driving mortality for 30 mo. Trees with thinner bark, lower leaf nitrogen content, and higher char height (a proxy of fire intensity) were also more likely to die in EN-fire–affected sites, although these variables had much weaker and time-limited effects (Fig. 2 and SI Appendix, Table S3). All mortality predictors had their greatest effect in the first year following the El Niño fires (SI Appendix, Fig. S6).

Fig. 2.

Physiological and ecological predictors of tree mortality during and after the 2015 to 16 El Niño. The five significantly important predictors influencing (A–E) the proportion of live trees from the initial stock, (F–J) the instantaneous mortality probability (i.e., hazard), and (K–O) the tree mortality sensitivity in relation to each predictor. The results are for forests affected by fire and drought during the 2015 to 16 El Niño, which were sampled between October 2015 to 2018. Tree survival and hazard are shown for the fifth, 50th, and 95th percentiles of the observed variable gradient, while other variables were held at their mean values. The solid lines show the median estimate, and the bands show the 95% credible intervals. Mortality sensitivity quantifies the change in a variable from its baseline levels required to return a substantial increase in stem mortality. The baseline levels were defined as the mean of each variable found across all trees in undisturbed forests before the onset of the El Niño (i.e., in the absence of both a climatic or anthropogenic disturbance). The median char height, however, was defined as the mean found in undisturbed forests after the El Niño fires. A value of 0 indicates that no change in the variable mean influenced tree mortality at a given time (i.e., the variable does not act as a predictor of mortality); a value of 1 indicates that any change in the variable returned a substantial mortality increase. Mortality sensitivity thus quantifies a variable’s time-varying importance (see Methods for full details). The white/red background displays the CWD for the Lower Tapajós region from 0 (white) to −448 (dark red) mm.

Regional Impacts of the El Niño on Plant Mortality and CO₂ Emissions

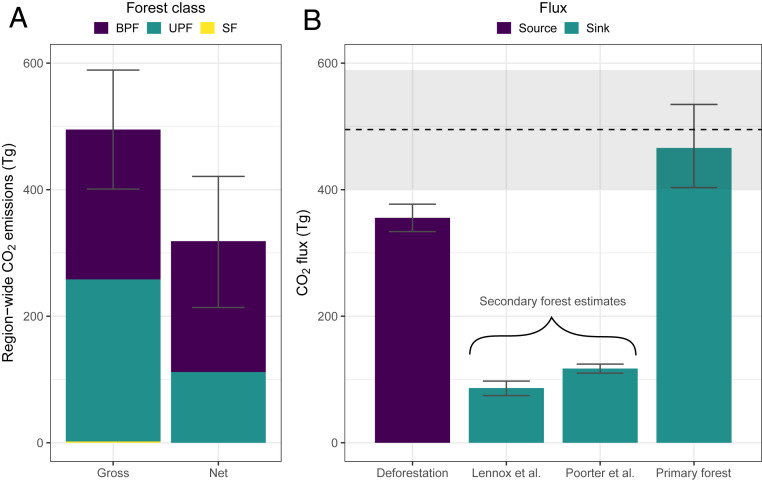
Extrapolating our results of plant mortality and carbon loss to the entire 6.5-million hectare region (i.e., the Lower Tapajós), we estimate that the 2015 to 16 El Niño killed 447 ± 50 million stems ≥10 cm DBH and 2.5 ± 0.3 billion stems <10 cm DBH (SI Appendix, Fig. S7), leading to the emission of 495 ± 94 Tg CO₂ over 3 y (Fig. 3A). Net emissions (i.e., when accounting for post-El Niño growth and recruitment measured in November 2018—see Methods) were 35.9% smaller than gross. The contribution of EN-drought–affected forests and EN-fire–affected forests to the regional CO₂ emissions were similar, as the large difference in the magnitude of drought and fire effects (Fig. 1 E and F) was compensated for by the area that was affected (4.6 million ha of EN-drought–affected primary forests compared to 978,000 ha of EN-fire–affected forests).

Fig. 3.

Region-wide carbon loss and CO₂ emissions. (A) Gross and net CO₂ emissions from burned primary (BPF), unburned primary (UPF), and secondary (SF) forests distributed across the epicenter of the 2015 to 16 El Niño in Amazonia. These figures include immediate (49) and committed CO₂ emissions (see Methods). (B) Comparison between the gross CO₂ emissions from our study region (dashed line with 95% credible interval as a gray band) with the major CO₂ sources and sinks in the Brazilian Amazon. The sources include the emissions arising from annual deforestation between 2009 and 2018 (51). The sinks include CO₂ sequestration by secondary and primary forests, using a locally derived (53), a neotropical (54), and an Amazonian (4) estimate of carbon uptake. Bars show mean values, while error bars show the SE.

Although our study region covers just 1.2% of the Brazilian Amazon, the emissions resulting from this single El Niño event were larger than the mean annual CO₂ emissions from deforestation across the whole of the Brazilian Amazon between 2009 and 2018 (Fig. 3B). Offsetting these emissions is challenging; for example, it would require, in the absence of any climatic or anthropogenic disturbance, either the continued carbon accumulation of the 10.5 million hectares of secondary forests for a period of 3.3 to 7.9 y or the continued carbon accumulation of the 334 million hectares of primary forests distributed across the Brazilian Amazon for 9 to 18 mo (Fig. 3B). If included in the national carbon accounting, the emissions resulting from the 2015 to 16 El Niño would represent an important setback to Brazil’s international commitments to mitigate climate change.

Conclusion

We provide evidence of the long-lasting impacts of the El Niño drought and fires on plant mortality, which remained elevated for up to 3 y, resulting in substantial carbon loss. Consequently, forest inventories conducted in the first year after extreme droughts or fires (e.g., refs. 5 and 23) will not fully capture these impacts, underestimating carbon loss in Amazonia. We also show that human disturbance can amplify the impacts of El Niño fires, significantly increasing both plot- and stem-level mortality. While previous research has shown that human-modified forests may be more susceptible to fires (14, 25), our results show that they are also more sensitive. Finally, our results show that extreme events—such as the 2015 to 16 El Niño—can have globally significant outcomes even if their main effects are concentrated in a relatively small area. Taken together, these findings suggest that country-level estimates of CO₂ emissions and global climate–vegetation models could be improved by including the duration and regional intensity of extreme drought and fire events as well as the previous disturbance history of affected forests. They also provide insights into management priorities in a changing world. While the next El Niño cannot be avoided, further human disturbance can—the resilience of the Amazon in the Anthropocene could be improved by curbing illegal logging operations and investing in improved fire management and combat.

Methods

Study Design.

In 2010, we established 21 plots (10 × 250 m) in the municipalities of Belterra, Mojuí dos Campos, and Santarém in the Lower Tapajós (Eastern Amazonia). Plots were distributed along a gradient of human-modified forests (SI Appendix, Fig. S3B) and located at least 100 m away from forest edges and between 1.5 to 97 km apart. Plots were distributed into four forest classes: undisturbed primary forests (n = 6), logged primary forests (n = 5), logged-and-burned primary forests (n = 5), and secondary forests (n = 5). Forest classes were established using a combination of physical evidence of past human disturbance found during field surveys (e.g., pieces of charcoal, tree stumps) and a visual analysis of a chronosequence of Landsat images ranging from 1988 until 2010 (23). We found no evidence of pre-Columbian settlements across our plots, such as dark earth or mounds.

Plot Census.

The first plant census took place in 2010. In each study plot, all trees and palms ≥10 cm DBH (1.3 m) were measured and identified to species level as well as all lianas ≥10 cm in diameter at 1.3 m from their main rooting point. Five subplots (5 × 20 m) were established in each plot in which all trees and palms ≥2 cm DBH and all lianas ≥2 cm in diameter at 1.3 m from their main rooting point were measured and identified.

Plot Recensuses and Mortality Assessments.

Plots were first recensused in 2014 and then again in 2018, measuring the DBH of every stem and the height of every tree and palm, noting when a stem was dead. During the recensus, we also recorded how much of a tree crown was covered by lianas (0, 1 to 25, 26 to 50, 51 to 75, and 76 to 100%). Between October 2015 and October 2018, we conducted quarterly mortality surveys of all stems in all 21 plots, including the eight plots that burned during the 2015 to 16 El Niño (SI Appendix, Table S1).

Carbon-Stocks Estimates.

Plot-level carbon stocks were calculated using biomass equations. For all trees, except Cecropia spp., we used Chave’s 2014 equation (model four), which includes tree DBH, height, and wood density (26). Tree DBH and height were assessed during the full vegetation census. Species-level wood density was extracted from the Global Wood Density Database (27) filtered for South American tropical regions. When a species was not present in the database, we used the mean wood density value at the lowest available taxonomic level. For Cecropia spp., we applied a genus-specific biomass equation (28) that accounts for their hollow stems. For palms, we applied different equations for individuals ≥10 cm DBH (29) and <10 cm DBH (30). Liana biomass was estimated using Amazonian-specific equations (31). Carbon was assumed to account for 50% of biomass (8, 32–34).

Physiological and Ecological Drivers of Tree Mortality.

In 2014, we sampled bark thickness in all trees ≥10 cm DBH across all 21 plots, taking two samples at 30 cm from the ground from opposite sides of each stem. In 2015, prior to the El Niño, we sampled leaf functional traits and invertebrate-mediated leaf herbivory in 20 study plots (all but one undisturbed forest in order to have an equal sample size across forest classes). For sampling, we first selected all species that contributed to 80% of each plot’s basal area. For each selected species, we then sampled a maximum of three individuals per plot, always selecting those with the largest DBH. For each individual, we sampled two branches fully exposed to the sun. From one branch, we collected three healthy adult leaves, carefully removing any dirt, moss, or lichen present on their surfaces. To calculate specific leaf area, we scanned each fresh leaf separately and then dried the leaves until constant weight. After drying, each leaf was ground, and its nitrogen and phosphorus content were analyzed. Total leaf nitrogen was determined using a CN Vario Max (35). The phosphorus content was extracted by nitroperchloric digestion (36) and subsequently determined by the Shimadzu spectrophotometer using the ammonium molybdate method (37). On the second branch, we counted the total number of leaves for those trees with simple leaves or the total number of leaflets for those trees with compound leaves. We then counted the number of leaves/leaflets that were chewed and then randomly selected 30 chewed leaves/leaflets to be scanned. Each leaf/leaflet had its original area reconstructed with imagery software (ImageJ) so we could estimate the proportion of area lost due to herbivory (38). The mean area lost across the scanned leaves was extrapolated to all other chewed leaves of each individual, and the mean percentage of herbivory per branch also incorporated the number of unaffected leaves. For individuals in which we did not sample their leaf traits, we attributed the mean trait value from that same species in the same forest class. After the El Niño fires, we measured the maximum char height in all trees ≥10 cm DBH in the EN-fire–affected plots. Finally, to estimate plot-level wood density, we calculated the mean wood density value of all trees ≥10 cm DBH in each plot.

Climatological Water Deficit.

The monthly climatological water deficit (CWD) between January 2000 and April 2019 was calculated as the precipitation of a given month [in millimeters, sourced from the Climate Hazards Group InfraRed Precipitation with Stations (CHIRPS) dataset (39)], minus evapotranspiration [in millimeters, sourced from TerraClimate (40)], plus the CWD of the previous month (41).

Data Analysis.

Accounting for expected mortality.

To account for pre-EN mortality levels (i.e., stem mortality in the absence of extreme climate events), we calculated the quarterly mortality rate between our 2010 and 2014 census. Quarterly mortality rates were calculated separately for each forest class (i.e., undisturbed, logged, logged-and-burned, and secondary forests). We then subtracted, for each forest class, its pre-EN mortality rate from all post-El Niño mortality rates.

Temporal dynamics of stem mortality and carbon loss.

We used a Bayesian multisite piecewise linear model (hereafter “change point model”) to assess the temporal dynamics of tree mortality and cumulative carbon loss across the census period. Change point analyses are ideal for investigating significant changes in the rate of an event through time; in this case, plant mortality and carbon loss.

The model is given by

$$y_{it}={\alpha }_i+{\displaystyle \sum }_j^{k+1}{\beta }_j{\left(t-{\theta }_j\right)}_{+}+{\tau }_i,$$

where $y_{it}$ is the value of the independent variable (stem mortality or cumulative carbon loss) at site $i$ at time $t$, and ${\alpha }_s$ is the site-specific intercept, which is modeled hierarchically as a random normal variable with a mean equal to the common intercept, ${\alpha }_0,$ and unknown variance [i.e., ${\alpha }_i\sim N({\alpha }_0,{\sigma }_1^2)$]. Similarly, ${\tau }_i$ is the site-specific error term, modeled hierarchically as $N({\mathit{ϵ}}_i,{\sigma }_2^2)$, to allow for correlated errors across sites. The change point model is comprised of up to $k+1$ linear coefficients, $\beta$, and corresponding changepoints, $\theta$.

A Bayesian model comparison with reversible jump Markov chain Monte Carlo (MCMC) simulations (42) was used to average multiple piecewise linear models (43). The number and location of changepoints were assigned hierarchical prior distributions that included zero changepoints: for example, binomial (3, 0.5). This approach is equivalent to averaging over multiple model structures, each with a different number and location of changepoints, using marginal likelihoods to weight models (43). The resulting posterior distributions yielded model-averaged parameter estimates and credible intervals that account for uncertainties about model structure. We assessed models which allowed for up to five changepoints and selected the most parsimonious as that with the lowest deviance information criterion score. We assumed strong evidence for a change point for posterior probabilities greater than 0.75.

The combined effects of prior forest disturbance and extreme climate events.

We assessed whether prior forest disturbance influenced the effects of the 2015 to 16 El Niño using a Bayesian analysis of variance. Separately for each pre-EN forest disturbance class in EN drought–affected forests and EN fire–affected forests, we calculated the total stem mortality and total carbon loss at the end of the census period. We then used one-way ANOVA within a Bayesian framework to assess the evidence for differences in mean mortality and carbon loss across forest classes using, in all cases, uninformative priors. To account for variation in initial conditions (e.g., less disturbed forests have larger carbon pools than more disturbed forests), we ran the ANOVA both for absolute mortality and carbon loss as well as mortality and carbon loss as a proportion of, respectively, the initial stem and carbon stocks. As above, we assumed evidence of a difference in class means for a posterior probability >0.75 (posterior probabilities are given in SI Appendix, Table S2).

Predictors of tree mortality.

We used a Bayesian survival model to investigate the roles of the potential physiological and ecological predictors of mortality. Survival analyses are recommended when investigating the duration of time until an event happens; in this case, tree death. Specifically, we fitted a semiparametric proportional odds model and used spike-and-slab variable selection to determine the important mortality predictors, using default uninformative priors (see ref. 44 for full details). All predictors deemed important (the standardized posterior 95% variable effect size credible interval excluded 0) were included in the final model. As stem height and DBH were highly correlated ($r\hspace{1em}=$ 0.76, SI Appendix, Fig. S8), we ran the initial model twice, including only one of them. However, neither variable met the criteria for inclusion in the final model. Using the final model, we determined cumulative mortality across the census period as well as the mortality hazard (probability of death at a given time) at each census. We also determined the marginal effect of each variable across its gradient, with all other variables held constant at their mean values (SI Appendix, Fig. S6).

In the survival analysis, we used plot-level wood density (i.e., the mean wood density of all stems in a given plot) as a continuous measure of prior anthropogenic disturbance (24)—that is, the more disturbed a forest, the lower its wood density (SI Appendix, Table S1). This significantly simplifies an interpretation of model results compared to the situation in which prior disturbance is a categorical variable with many classes.

Finally, we derived a time-varying measure of variable importance using the survival hazards. For each variable in the final model and at each point in time, we determined the change in variable from the mean observed in undisturbed forests required to return a substantial increase in mortality probability. We defined a “substantial increase in mortality probability” to mean that the 95% hazard credible intervals did not overlap. We refer to this measure as the variable’s mortality sensitivity, and we scaled it to lie between 0 and 1. A value of 0 indicates that no change in the variable returned a substantial mortality increase at a given time, and as such, the variable does not act as a mortality driver at that time. A value of 1 means that the smallest change considered returned a substantial mortality increase, and as such, the variable acts as a strong mortality driver at the given time. We consider a range of variable values in this analysis by scaling the undisturbed forest mean by 1 to 10 in increments of 0.1, accounting for the direction of the variable’s effect (i.e., if decreases in the variable led to increases in the mortality probability, we scaled the variable downward. Conversely, if increases led to increased mortality probability, we scaled the variable upwards).

For all Bayesian models, model parameters were estimated from 100,000 reversible jump MCMC iterations after 20,000 burn-in iterations. Chain-history and Gelman–Rubin statistics confirmed adequate MCMC mixing and convergence (45).

Scaling up to region-wide consequences of the 2015 to 2016 El Niño.

We focus on a 6.5-million hectare region around our study plots that was also the epicenter of rainfall anomalies in the Amazon during the 2015 to 16 El Niño (17). This extrapolation has a ratio of 1.2 M hectares for each sampled hectare being higher than that used in basin-wide assessments of Amazonian forests (4, 5, 46, 47) and is supported by two main reasons: 1) the whole 6.5-million hectare region, including our study plots, experienced the same climatic anomalies during the 2015 to 16 El Niño (17); 2) the similarity of our findings with those from an additional 13 human-modified permanent forest plots inventoried in 2016 and in 2018 (SI Appendix, Fig. S9).

To scale up our results, we first mapped total forest area in our 6.5-M hectare region in 2015, classifying forests into primary or secondary according to MapBiomas 3.1 (48). Over this forest map, we overlayed a map of forests that burned and did not burn during the El Niño (49), which allowed us to calculate the amount of primary and secondary forests that burned (i.e., drought- and fire-affected forests) and did not burn (i.e., drought-affected forests) during the El Niño. We used the four forest categories that we obtained (i.e., unburned primary, burned primary, unburned secondary, and burned secondary forests) to estimate gross and net carbon emissions and total stem mortality across the whole study region. For this, we extrapolated our plot-level estimates of carbon loss, carbon gain, and stem mortality to the whole area occupied by each of the four categories. Finally, we summed values across the classes, accounting for error propagation. To estimate gross carbon emissions, we converted our carbon loss estimates to CO₂ using a conversion factor of 44/12 (50). To estimate net CO₂ emissions, we applied the same procedure detailed above for stem growth and recruitment and subtracted total values across the study region from total gross emissions, again accounting for error propagation. We compared gross emissions to three types of annual Brazilian Amazon CO₂ fluxes: 1) emissions from deforestation, 2) sequestration from secondary, and 3) sequestration from primary forests. Annual deforestation extents were obtained from the Brazilian Space Agency (51) and converted to tCO₂ using a factor of 18.1 following Azevedo et al. (52). The rates of carbon uptake in primary forests came from Amazon-wide estimates (4), while those in secondary forests came from a locally derived (53) and a Neotropical estimate (54). The rates of carbon uptake were converted to CO₂ by also using a factor of 44/12 (50).

Data Availability

Data available at: https://doi.org/10.6084/m9.figshare.14839521.v1.