Significance
In vision research, oriented gratings are classical stimuli that drive a large population of neurons in the primary visual cortex, but it is unclear whether mice—a recently popular model animal for visual decision-making—can be trained in a task based on the comparison between orientations. Furthermore, it is unclear which strategies they would use and how these strategies would be affected by engagement in the task. Here, we demonstrate that mice can perform a relative orientation discrimination task with high levels of acuity. Using a probabilistic model of choice, we explored the animals’ choice strategies, as well as history biases and their dependency on engagement.
Keywords: animal behavior, probabilistic modeling, orientation discrimination
Abstract
During perceptual decision-making, the brain encodes the upcoming decision and the stimulus information in a mixed representation. Paradigms suitable for studying decision computations in isolation rely on stimulus comparisons, with choices depending on relative rather than absolute properties of the stimuli. The adoption of tasks requiring relative perceptual judgments in mice would be advantageous in view of the powerful tools available for the dissection of brain circuits. However, whether and how mice can perform a relative visual discrimination task has not yet been fully established. Here, we show that mice can solve a complex orientation discrimination task in which the choices are decoupled from the orientation of individual stimuli. Moreover, we demonstrate a typical discrimination acuity of 9°, challenging the common belief that mice are poor visual discriminators. We reached these conclusions by introducing a probabilistic choice model that explained behavioral strategies in 40 mice and demonstrated that the circularity of the stimulus space is an additional source of choice variability for trials with fixed difficulty. Furthermore, history biases in the model changed with task engagement, demonstrating behavioral sensitivity to the availability of cognitive resources. In conclusion, our results reveal that mice adopt a diverse set of strategies in a task that decouples decision-relevant information from stimulus-specific information, thus demonstrating their usefulness as an animal model for studying neural representations of relative categories in perceptual decision-making research.
The focus of perceptual decision-making research is to reveal the processes by which sensory information is used to inform decisions and guide behavior (1). When considering the neural underpinnings of these processes, both sensory and decision information are often found to be encoded by the same neural populations, making the identification of unique neural signatures of decision-making challenging (2–4). To overcome this problem, behavioral tasks that rely on relative rather than absolute values of stimulus properties can be advantageous (5–8). In these tasks, the same amount of information about the correct choice can be given by many combinations of stimuli, which allows the separation of the sensory and decision components of neural activity. Effectively, these tasks introduce invariance of choice categories with respect to specific stimuli.
In visual decision-making, a task with these characteristics is an orientation discrimination task featuring invariance with respect to specific orientations, which requires a subject to make relative orientation comparisons of stimuli. The convenience of this task relates to the well-characterized neural encoding of stimulus orientations in the striatal visual cortex of all mammalian species (9, 10). The mouse animal model, which features an unmatched abundant set of experimental tools for the dissection of neural circuits (11–13), performing a relative orientation discrimination task could be a promising study system for examining the neural mechanisms underlying sensory decision-making. However, whether mice can be trained in a relative orientation discrimination task, and which strategies they may adopt in this task, have been unknown.
Here, we implemented a two-alternative forced-choice (2AFC) discrimination task for mice in which they had to report the more vertical orientation of two simultaneously presented grating stimuli. Importantly, the vertical orientation was not shown in the majority of trials, and the same value of “relative verticality” was given by many pairs of oriented gratings. Animals could adopt similar but not optimal choice strategies, albeit at the cost of water reward, which allowed us to explore a continuum of naturally arising strategies. To characterize these strategies, we designed a probabilistic choice model that quantified how animals combined information from the two stimuli. We expanded the model to account for trial history–induced biases and analyzed the dependence of these biases on the engagement state of the animal. Finally, with the help of the model, we estimated orientation discrimination acuity and showed that mice perform this task with high levels of accuracy and sensitivity to small differences in orientation.
While the use of complex visual discrimination tasks in mice can be challenging because of the difficulty in training animals, modeling their choice strategies, parameterizing visual objects, and finding their neural representations, our complex discrimination task addresses these problems by extending the existing orientation discrimination protocols (14–18). We suggest that our task will allow for the exploration of links between neural and behavioral variability (19) in the context of heuristics and suboptimal choice strategies in rodent perceptual decision-making (20).
Results
Relative Orientation Discrimination Task.
Task details.
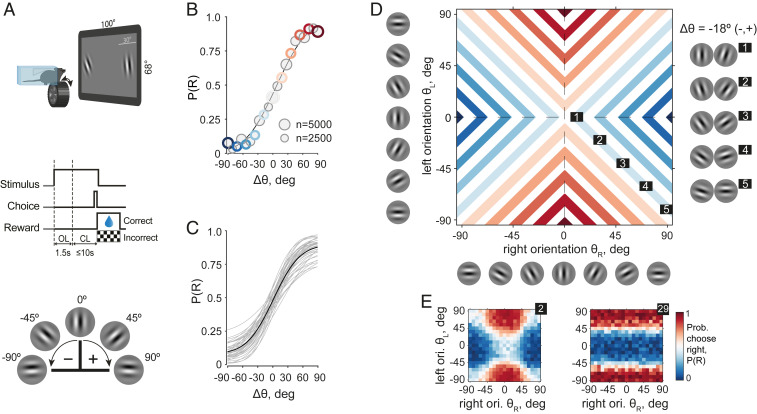
We trained transgenic mice (n = 40) in a 2AFC orientation discrimination task using an automated setup in which animals voluntarily fixed their heads to initiate an experimental session (Fig. 1 A, Top), as previously described (21). In this task, two oriented Gabor patches were simultaneously shown on the left and right sides of a screen; to obtain water, animals had to identify the patch that was more vertically oriented (n = 28; more horizontally, n = 12) and move it to the center of the screen by rotating a wheel manipulator (7, 21). Crucially, because the target in most trials was not vertical, the animals had to compare the angular distance to the vertical (verticality) of the two orientations. The same physical stimulus could thus be a target or a nontarget in different trials, thereby making the task invariant relative to the orientation of individual stimuli (Fig. 1 A, Middle). The orientations of both stimuli were sampled at random from angles between −90° and 90°, with a minimal angular difference of 9° (3° for one animal) and positive and negative angles corresponding to clockwise and counterclockwise orientations relative to vertical (Fig. 1 A, Bottom). We used this 9° spacing for most animals to sample a high number of responses for every angle condition, which was important for subsequent imaging experiments (not shown in this study). We analyzed a total of 1,313,355 trials, ranging from 4,591 to 82,065 per animal, with an average of 32,834 ± 2,962 trials per animal (mean ± SE) in 256 ± 22.28 sessions of 128.02 ± 1.34 trials each (SI Appendix, Fig. S1 and Table S1).
Fig. 1.
Mice were trained in an invariant orientation discrimination task. (A, Top) Schematic of a mouse during an experimental session. (Middle) Epochs of one trial. OL: open loop, during which the wheel manipulator did not move the stimuli on the screen. CL: closed loop, during which the wheel manipulator did move the stimuli. (Bottom) Convention for the angle signs. (B) Psychometric curve of an example animal. Solid line: best fit of the cumulative Gaussian psychometric function. Circles: data points, circle sizes represent numbers of trials, colors correspond to colors in D, and gray circles are data points not explicitly marked in D. (C) Psychometric curves for all animals in the study. Solid black line: population average. (D) Many orientation pairs give the same task-relevant information quantified by angular separation or difficulty (). Conditions with a fixed in the 2D stimulus space (colored lines) correspond to conditions (circles) of the same color in B. (Right) Five example stimuli for one of the four branches of constant = −18° ( ≤ 0, ≥ 0). (E) Probability of right choice of example animals 2 (Left) and 29 (Right) in the stimulus space as in D. Reference SI Appendix, Fig. S3 for other examples.
Mice achieved a high success rate in a relative orientation discrimination task.
As an initial step in the analysis of choice behavior, we quantified performance as a function of task difficulty using a standard cumulative Gaussian psychometric function (22). We modeled the probability of choosing the right stimulus, P(R), as a function of the angular separation between the two orientations, where denotes the distance from vertical ( = 0°), with small angular separations corresponding to difficult conditions and large angular separations corresponding to easy conditions. An angular separation ° corresponds to two equally vertical orientations, which are not necessarily parallel. Conditions with and correspond to a more vertical orientation on, respectively, the left and right sides (example animal, Fig. 1B; population, Fig. 1C). Mice reached an average performance of 74.7 ± 0.7% correct, with an average sensitivity parameter of the psychometric curve = 42.93 ± 1.18°. Animals retained their performance level after introducing changes in spatial frequencies and stimulus sizes, suggesting their decision-making strategy did not rely upon these low-level statistical properties of the stimuli (average psychometric curves over the three sessions before and after changing either of these parameters did not differ from each other, SI Appendix, Fig. S2).
As this task disentangles any given probability of choice from specific orientations, a fixed difficulty corresponding to one point on the psychometric curve is given by many possible pairs of orientations. For example, = 30° corresponds to orientation pairs (30°, 0°), (−60°, 30°) and many others (Fig. 1D). Conversely, no given orientation was always rewarded because for any orientation (except 0°) there was a possibility that the other orientation was more vertical. For equally vertical orientation pairs, a randomly chosen side was rewarded. Consequently, this task design compels the animal to estimate the verticality of the left and right orientations and and compare their estimates rather than detect a learned orientation.
Animals may not strictly adhere to this ideal strategy, so long as they obtain a sufficient amount of water reward in each experimental session. This amount can be difficult to estimate precisely because it varies significantly from animal to animal and depends on age, sex, food intake, and genetic background. For instance, with the help of the choice model described in-depth in the next sections, we computed choice variability associated with one orientation (as a geometric mean of two model-derived concentrations; see Success Rate with a One-Sided Strategy) and used it to estimate that an animal looking at only one of the two stimuli will perform at 63.1 ± 0.6% correct. The animal will thus exceed the 50% chance level but, on average, will not be able to maintain its weight at the pretraining level, assumed to be a heathy reference baseline. In the following section, we introduce in more detail the model that quantifies how animals combine information from the two orientations and capture the broad spectrum of strategies from nearly ideal (Fig. 1 E, Left, example animal no. 2) to a predominantly one-sided strategy (Fig. 1 E, Right, example animal no. 29).
Probabilistic Choice Model.
Accounting for stimulus space and biases in the model.
The psychometric curve quantifies an animal’s behavior along a single dimension of difficulty, . However, given the task structure, the complete representation of the stimulus space is two-dimensional (2D), with a unique stimulus condition corresponding to a pair of angles . In this space, a fixed is given by all stimulus conditions along the iso-difficulty lines (branches) that lie in the four quadrants of the space and correspond to four different combinations of angle signs (Fig. 1D). We therefore considered the probability of choosing the right orientation, P(R), for all stimulus conditions in this space.
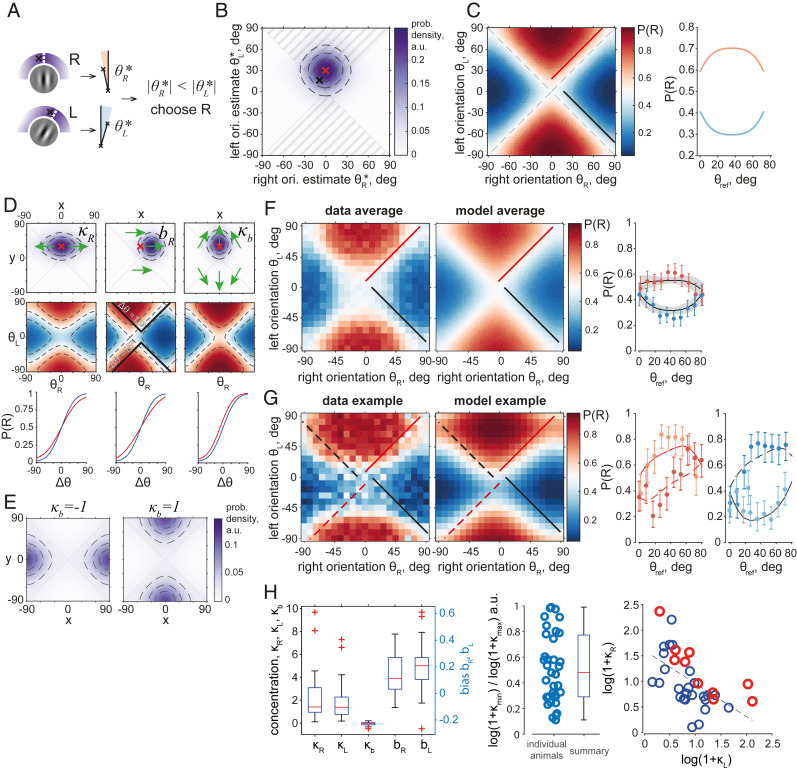
To gain better insight into the factors that affect the animals’ choices, we developed a psychometric model that provides functional mapping from the 2D stimulus space to the probability of the right choice, P(R). We assume that in every trial, a mouse makes noisy estimates of both orientations , compares their verticalities (,), and makes a choice (Fig. 2A). The probability of a right-side choice P(R) in this procedure is expressed as an integral of the distribution of estimates over the subspace (Fig. 2B) (see Materials and Methods, Eqs. 1–4). The shape of the P(R) surface over the stimulus space (Fig. 2 C, Left) is thus determined only by the parameters of the distribution , which we represent as a product of the animal’s likelihood function over percepts and its prior distribution.
Fig. 2.
The choice model characterizes individual biases and strategies and predicts variation of performance with reference orientation, as found in the data. (A) Choice model schematic. The angles of two oriented Gabor patches (white dashed lines, Left Column) are estimated as samples from circular distributions (density: purple, estimates: black crosses). Their absolute values are measured as angular distances to the vertical and compared with each other (Middle Column), which generates a choice. (B) Distribution of orientation estimates, as in A, in 2D space for (red cross) in an unbiased model with , and a sample from this distribution (black cross). Probability mass inside the shaded areas () is equal to the probability of right choice P(R). Dashed lines: distribution quartiles. (C, Left) P(R) of model in B evaluated at all stimulus pairs . Red and black lines are one example branch of and , respectively. (Right) P(R) along the branches of constant marked on the Left with red and black lines. (D) Effect of model parameters on animals’ likelihood distributions over percepts (Top Row), P(R) surface assuming uniform priors (Middle Row), and the corresponding psychometric curves (Bottom Row). Red crosses: distribution means before parameter manipulation; green arrows: transformation of the distributions with parameter change; blue psychometric curves: before parameter change; red curves: after parameter change. The Center panel in the Middle Column shows P(R) values displaced relative to isolines (solid black: example isoline for = 15°). (E) Choice priors with equal to −1 (Left; left-choice bias) and 1 (Right; right-choice bias). (F, Left) Population average P(R) (n = 40 mice), with an example branch of and marked with red and black lines, respectively. (Center) Population average of the model P(R), n = 40. (Right) P(R) values along the branches in data (dots with error bars represent mean ± CI) and model (black lines with shaded areas are mean ± CI). Reference SI Appendix, Fig. S3 for P(R) of every animal. (G) Example mouse, Left to Right: 1) data P(R); 2) P(R) of the fitted model; 3) P(R) along the red dashed and solid lines on the Left predicted by the model (lines) and computed from the data (dots with error bars, darker dots correspond to the dashed line); and 4) P(R) along the black dashed and solid lines on the Left, as predicted by the model (lines) and computed from the data (dots with error bars, darker dots correspond to the dashed line). Reference SI Appendix, Fig. S3D for the model of P(R) for every animal. (H, Left) Population summary of model parameters fitted to all mice (n = 35; n = 5 animals with or estimated on the edge of the allowed range of values are excluded). (Middle) Ratio of and with the smaller of the two values divided by the larger value for each mouse (n = 35). Circles: individual animals; Box plot: population summary; Red line: median value; Box borders: 25th and 75th percentiles. Whiskers are up to most extreme parameter values. Red crosses: outliers. (Right) and across the population are significantly anticorrelated. Linear regression line for all animals together. Red circles: 10 mice with best performance.
We model the likelihood as a product of circular von Mises functions and centered at the values of and equal to the true orientations and with variability for each target quantified by the concentration parameters and . High concentrations correspond to low variability in the percepts, and is thus qualitatively inverse to the SD and can be interpreted as the certainty (23, 24). For example, a distribution of percepts is broader and shallower along the axis of lower concentration (Fig. 2 D, Left Column, Top), making P(R) more independent of the respective stimulus (Fig. 2 D, Left Column, Middle).
Percepts of each orientation can be systematically biased, with an animal consistently making choices as if the right or left orientation were rotated more clockwise or counterclockwise. These systematic errors are accounted for by translational biases and (Fig. 2 D, Center Column, example: > 0, = 0), which move and consequently the P(R) surface relative to the angle axes without changing their values.
Both the translational biases and the certainty parameters change the slope of the psychometric curve but not its left–right choice bias (Fig. 2 D, Bottom Row), with the effects generally indistinguishable in the space as opposed to the complete stimulus space. A lower or higher certainty results in a shallower or steeper P(R), respectively, as well as a shallower or steeper psychometric curve. Conversely, a translational bias displaces the entire P(R) surface, decreasing overall performance for every in the space of the psychometric curve.
To model a choice bias toward the right or left, we introduced a family of prior distribution functions, or choice priors , parameterized by prior concentrations (Fig. 2E). These choice priors cause an orientation on the right or left to effectively appear more vertical—as opposed to more clockwise or counterclockwise—or equivalently make an animal more certain about the verticality of that stimulus or can be associated with procedural factors that similarly bias choices (Fig. 2 D, Right Column) (Materials and Methods, Eq. 2). For example, the choice prior for a right-side bias has a peak at (90°, 0°) (Fig. 2 E, Right, ) and increases the probability of a right-side choice for any pair of orientations (Fig. 2 D, Right Column) by biasing to the region (Fig. 2 D, Right Column, green arrows).
Concentrations, translational biases, and a prior concentration thus determined our model of choice, which allows for a more complete analysis of P(R) than the psychometric curve. The model predicts a previously unexplored property of P(R)—its variation along the branches of a fixed . A model with zero biases and an equal certainty for both orientations () predicts a decrease in P(R) whenever either orientation is close to 0° or 90° and an increase when close to 45° (Fig. 2 B and C). We parameterized this variation using the reference orientation (i.e., the orientation of the more vertical stimulus). The source of this variation is clear from the position of relative to the category boundary when considered along one branch of a fixed (Fig. 2B); the probability mass of orientation estimates that result in error judgments (e.g., when ) is higher around = 0° and = 90° than around = 45°. This effect arises from the variability in both orientation estimates and their interaction with the category boundary in the circular space and cannot be replicated by a psychometric curve with a single input variable of .
In summary, by combining information from two orientations, our model predicts a dependency of probability of choice on not only difficulty but also reference orientation. This latter variability necessarily follows from the circularity in the input stimulus space, given a limited certainty in orientation estimates.
The model captures the animals’ choices.
Next, we analyzed the choices of the mice in the 2D stimulus space. For the population of animals, P(R) varied with difficulty , as expected from the psychometric curves (Fig. 1 B and C), and with the reference (Fig. 2F, population average, n = 40), as predicted by our model (Fig. 2 B and C). For a fixed , P(R) was higher (and choices were more often correct) when the orientations were far from horizontal or vertical (Fig. 2F), while for , P(R) was smaller (and the choices were also more often correct) when the orientations were far from horizontal or vertical.
The model reproduced this performance variation for individual animals (Fig. 2G, example animal). However, due to individual biases, the P(R) curves for fixed were more distorted than in the unbiased case (cf. Fig. 2 C, Right). Counterintuitively, P(R) for the same in different quadrants of the stimulus space could represent, on average, opposite choices (Fig. 2 G, Two Right Panels), which our model accounted for thanks to translational biases. The model successfully captured animal-specific differences in choice probabilities (SI Appendix, Fig. S3), explained the data significantly better than the psychometric curve (ΔAIC [Akaike Information Criterion] = 798.8 ± 141.9; ΔAIC > 0 for all animals), and explained significantly more deviance (25) (fraction of deviance explained [ΔFDE] = 9.03 ± 1.48%, p = 1.07 10−6, signed-rank test).
Across the population of animals, the average stimulus concentration values were high and positive ( = 2.22 ± 0.69, p = 3.73 10−7; = 1.76 ± 0.52, p = 1.34 10−7, t tests) (Fig. 2 H, Left), showing that the animals used both targets for the decision. The bias concentration was small ( = −0.06 ± 0.05, p = 0.01), indicating a mixed bias across the population. The translational biases ( = 0.14 ± 0.05, p = 3.71 10−6; = 0.19 ± 0.05, p = 1.21 10−7) were similarly small but significant.
Although the stimulus protocol, reward sizes, and session schedules were designed to motivate animals to use information about both orientations equally, we found that the strategies of individual animals ranged from a balanced orientation comparison to a reliance on one target more than the other. We quantified this range of strategies with the ratio of the log of the concentrations and , with ratios closer to 1 representing more balanced strategies (Fig. 2 H, Center). The right and left concentrations were significantly anticorrelated (ρ = − 0.57, p = 4.45 10−4; t test, criterion α = 5 10−3 corrected for multiple comparisons), reflecting a trade-off in animals that preferentially used information from one of the stimuli (Fig. 2 H, Right). Despite this trade-off, the best-performing animals also had higher concentrations overall (p < 0.05; analysis of covariance, F-test of intercept with fixed slope), showing that while the task permitted relative flexibility in choice strategies, a more accurate estimation of the orientations was necessary to achieve a high success rate. Other parameters of the model did not significantly correlate with each other or with the concentration ratios.
In summary, our model accounted for biases in the animals’ behavior and explained the performance variation with . Individual animals weighted sensory information from the two orientations differently, following strategies that were sufficient to obtain needed amounts of the water reward, but were not perfectly aligned with the true stimulus–reward space. These sufficiently good strategies can be interpreted as approximations of the true task structure that subjects resort to in cases of complex problems (19). Nevertheless, while left and right concentrations were anticorrelated across the population, high success rates required overall high levels of certainty in the orientation estimates.
Discrimination acuity.
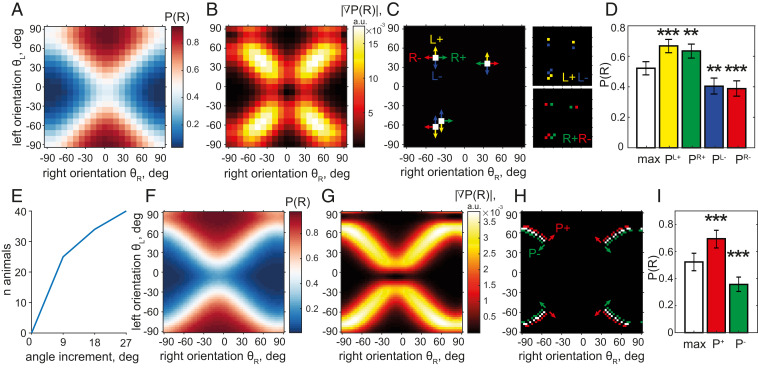
We next used our model to estimate the minimal orientation difference that the animals could reliably discriminate. A change in a pair of orientations that results in a significant change in P(R) is the smallest for conditions with the largest gradient of P(R). Because the numerical gradient directly computed from the data can be too noisy, we used our model to more accurately find the maximum gradient conditions. However, after identifying these conditions, we used experimentally obtained trial outcomes to test the significance of P(R) change.
Following this procedure, we compared the probability of a right-side choice in stimulus conditions with the highest gradient and in neighboring conditions (Fig. 3). Specifically, for every animal, using the model P(R) (Fig. 3A, example animal), we computed the absolute value of the numerical gradient |∇P(R)| (Fig. 3B) and identified orientation pairs with the top 5% largest gradient values and a nearly chance performance (maximum gradient conditions; Fig. 3C, white), which differed across animals due to differences in biases and concentrations. We then examined the four pooled neighboring conditions in which either the left or right orientation differed from the maximum gradient pair of stimuli by 9° and which we grouped by an increase or a decrease in P(R) (Fig. 3C, four colors for four neighboring conditions). For this example animal, all four neighboring conditions had a P(R) significantly different from the maximum gradient one (Fig. 3D). We found that a change in either left or right orientation by 9° with respect to the maximum gradient conditions resulted in a significant change in P(R) for 62.5% (n = 25) of the animals, and a change of 27° resulted in a significant change for all of the animals (n = 40; Fig. 3E). For the only animal tested with a 3° sampling of stimuli (Fig. 3 F–I), we found that conditions in which both orientations changed by 3° relative to the maximum gradient conditions—amounting to a total change of 6°—resulted in a significantly different P(R) (p < 0.0005 for directions both along and against the gradient).
Fig. 3.
Mice reach a typical orientation acuity of 9°. (A–D) Steps of acuity analysis for an example animal. (A) P(R) model surface of an example mouse. (B) |∇P(R)| absolute value of the gradient of P(R) surface in A. (C) Four stimulus conditions (white) with |∇P(R)| in the top 5% of values and P(R) close to chance level (0.48 < P(R) < 0.52). Arrows of the same color show angle change yielding one group of neighboring conditions: PL+ (yellow; L+ for left stimulus change that increases P(R)), PR+ (green), PL− (blue), PR− (red). Insets (Right) show these conditions in the stimulus space. (D) Pooled P(R) in maximum gradient conditions (white), P0.5 = 0.52 ± 0.04, differs from P(R) in the four neighboring conditions PL+ = 0.67 ± 0.04, p < 2.5 10−4 (yellow), PR+ = 0.63 ± 0.05, p < 2.5 10−3 (green), PL− = 0.40 ± 0.05, p < 2.5 10−3 (blue), PR− = 0.39 ± 0.05, p < 2.5 10−4 (red) (binomial CIs, χ2 test, df = 1, n = 4 comparisons). (E) Population summary of analysis in A through D: cumulative number of animals for which at least one direction of angle change gives a P(R) significantly different from P0.5 as a function of angle change magnitude. (F and G) Similar to A and B for an animal trained with 3° angle binning. (H) Maximum gradient conditions (white, same criteria as in C) and neighboring conditions obtained by changing both angles by ±3° in the direction of P(R) increase (P+, red) and decrease (P−, green). (I) Pooled P(R) in three groups highlighted in H: P0.5 = 0.52 ± 0.04, P+ = 0.69 ± 0.07 (red), P− = 0.36 ± 0.05 (green), both different from P0.5 with p < 0.0005 (χ2 test, df = 1; n = 2 comparisons).
In summary, our model allowed for an in-depth analysis of discrimination acuity by utilizing a complete picture of the P(R) gradient and identifying stimulus conditions in which the sensitivity to angle change was the highest. We found that the typical orientation discrimination acuity was 9°, given that in most animals, an angle change of this magnitude could be significantly detected based on the change of the probability of choice. Furthermore, we found that individual animals can exhibit even finer discrimination acuity, demonstrating that one animal exhibited significantly different behavior in conditions that differed by 6°.
Effects of trial history.
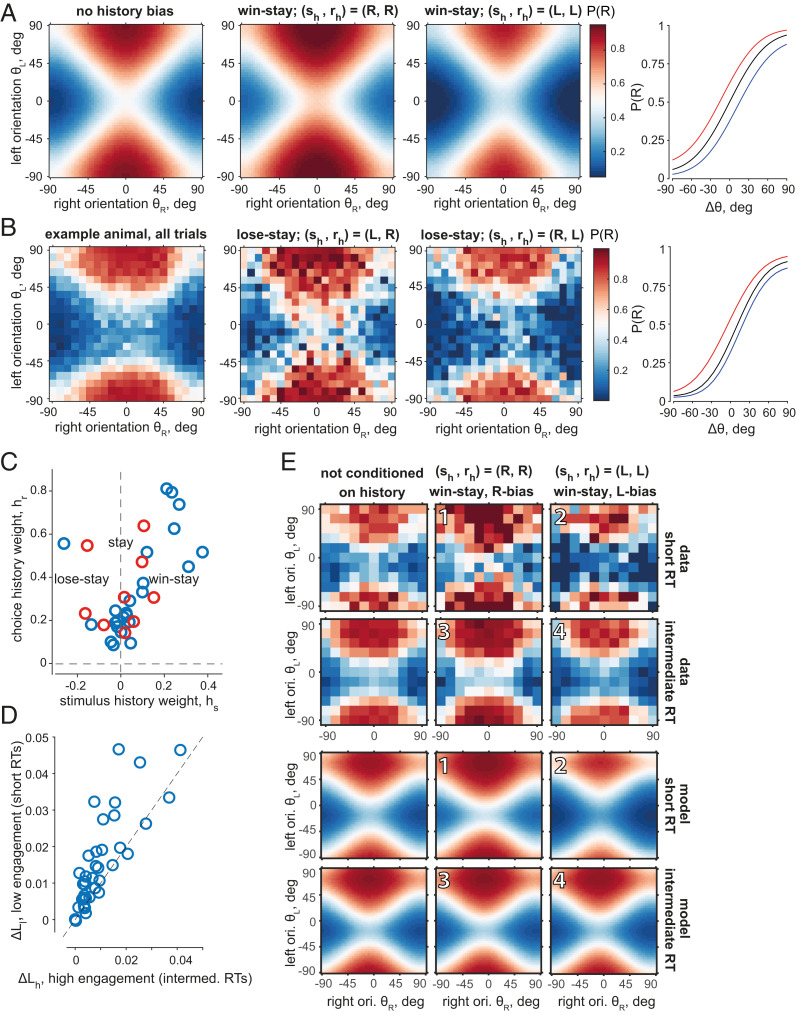
Choice strategies are determined not only by preferential weighting of available sensory information but also by trial history (6, 26–29). To account for history-related biases, we included a history prior , parameterized with a concentration parameter and a term that linearly depended on the choice and target orientation in the previous trial, through history weights (26, 27) . A pair of weights determined the choice strategy of an animal, such as win stay (Fig. 4A, model example) or lose stay (Fig. 4B, example animal) throughout all trials and in combination with the choice and target of the previous trial (, ) resulted in the history-dependent change of the P(R) (SI Appendix, Fig. S4 A–E) and the psychometric curve (Fig. 4 A and B) (26).
Fig. 4.
The probability of choice is affected by the choice and reward on the previous trial, with a larger effect during periods of lower task engagement. (A) P(R) of an unbiased example model with a win–stay strategy ; from Left to Right: 1) without history bias (after a neutral trial, ); 2) after a successful right choice with P(R) biased to the right choices as a result; 3) after a successful left choice with P(R) biased to the left choices; and 4) psychometric curves corresponding to 1 through 3 without a history effect (black), after a correct right choice (red), and after a correct left choice (blue). (B) P(R) of an example animal with large history biases (lose–stay strategy); from Left to Right: 1) average P(R) on all trials; 2) P(R) after an unsuccessful right choice biased to right choices; 3) P(R) after an unsuccessful left choice biased to left choices; where P(R) of all conditions in 2 and 3 with fewer than n = 5 trials was set to the average P(R) of its neighbors, and 2 and 3 are conditioned on preceding errors and thus had a relatively low number of trials since the performance of all mice exceeded a 65% success rate; and 4) psychometric curves of the corresponding surfaces; colors as in A. (C) History weights and corresponding strategies of all animals (four outliers not shown); stay and win–stay strategies are predominant, with few examples of lose stay. Blue circles: animals trained to detect a more vertical orientation; red circles: a more horizontal orientation. (D) The increase in the log likelihood due to inclusion of history terms was greater for low-engagement trials (10% shortest RT) than high-engagement trials (intermediate RT). Each circle is an animal. Abscissa: difference () between average log likelihood under the model with history () and without history () of high-engagement trial outcomes (), . Ordinate: difference () between average log likelihood under the model with and without history of the low-engagement trial outcomes (), . (E) History affects choices more strongly during periods of low engagement than high engagement. Example win–stay animal. (Left Column) P(R) not conditioned on history. (Center Column) P(R) after a correct right choice. (Right Column) P(R) after a correct left choice. (Top Two Rows) Data averages in low (Top) and high (Bottom) engagement trials; angles downsampled for presentation only. (Two Bottom Rows) Model P(R) fitted to high- and low-engagement trials separately. Change in P(R) is more pronounced between 1 and 2 (low engagement) than between 3 and 4 (high engagement). Color scale as in A and B.
Through the flexible family of history priors, our model captured a variety of strategies in addition to win stay (SI Appendix, Fig. S4F). Most of our mice showed a mild tendency toward the stay strategy, followed by win stay and, rarely, lose stay (Fig. 4C), which is largely consistent with a previous report (30). The history-dependent model explained the data significantly better than the history-independent model (ΔAIC = 211.8 ± 40.1; ΔAIC > 0 for all but four animals), and it also explained significantly more deviance (ΔFDE = 5.07 ± 0.98%, p = 8.1 10−6, signed-rank test).
We investigated whether the animals relied on history to a different extent during periods of relatively high and low engagement in the task, which we identified based on reaction times (RT). Long RTs are indicative of a lower task engagement due to, for example, lower arousal (31, 32). Very short RTs can also be a sign of lower task engagement accompanied by impulsive behavior and a hyperaroused state (31, 33, 34). Indeed, trials with intermediate RTs had higher success rates, on average, than trials with short RTs (p = 9.9 10−4, Wilcoxon test; SI Appendix, Fig. S5D) or long RTs (p = 1.9 10−7, Wilcoxon test; SI Appendix, Fig. S5E). We thus considered trials with the shortest 10% and the longest 10% RTs in every session and tested if the inclusion of history terms gave a significantly larger increase in the explanatory power compared to the trials with intermediate RTs. We found that the difference between the trial-average log likelihoods of the models with and without a history prior was larger for the trials with very short RTs (low engagement, ) than for trials with intermediate RTs (high engagement, ) (, p = 3.9 10−5, Wilcoxon test; Fig. 4D), and we found a similar qualitative tendency for long RTs (p = 0.088, Wilcoxon text; SI Appendix, Fig. S5A). The greater influence of history biases appeared visually as a stronger modulation of history-conditioned P(R) maps computed from short RT trials versus intermediate RT trials (Fig. 4E, cf. 1 to 2 modulation [short RT] and 3 to 4 modulation [intermediate RT]).
Fluctuations in performance could be another indicator of changes in engagement, and we found that choices were indeed more affected by history biases during periods of relatively low performance (, p = 2.12 10−7, Wilcoxon test; SI Appendix, Fig. S5 B and C).
In summary, after expanding our model to capture history-dependent biases, we found that the most prominent strategies were win stay and stay, and choices were affected by history biases to a greater extent during periods of lower engagement. Our observations demonstrate that choice heuristics can fluctuate together with the cognitive state of the subject.
Discussion
Using high-throughput automated cages with voluntary head fixation, we trained a large cohort of mice (n = 40; 1,313,355 trials) in a complex variant of a 2AFC orientation discrimination task. The task required the mice to measure the relative orientations of two stimuli, thereby decoupling choice from the particular orientation of an individual stimulus. We quantified their behavior with a model of choice that accounted for the circularity of the stimulus space and for individual choice biases and strategies. The model explained variations in the probability of choice not only with task difficulty but also with the reference orientation , an effect not reported previously. With the help of the model, we found that the typical maximum acuity of orientation discrimination in expert animals is 9° and can be as small as 6° in individual animals. Our model could be easily extended to examine history biases that are ubiquitous in human and animal psychophysical experiments (6, 26–29), revealing that a modulation of history components due to the animals’ engagement affects choices more strongly when engagement is relatively low. Our work responds to the need for a visual task that depends on relative choice categories and is invariant to specific visual stimuli but that can be performed by mice, relies on basic visual features, and allows for straightforward quantification within a probabilistic modeling framework. We argue that in addition to these advantages, our task can be useful in engaging higher visual areas in the computation of decision (35) and can provide valuable insight into the relationship between neural and behavioral variability (19, 24, 36–38).
Behavioral Assays for Studies of Perceptual Invariances and Their Quantifications.
Our task will be particularly advantageous for the study of the neural mechanisms underlying perceptual invariances. With its availability of unique experimental toolboxes, the mouse is currently the animal model of choice for the dissection of neural circuits (11–13). However, while visual behaviors elicited by low-level visual features have been well characterized (10, 39), intermediate (e.g., textures) and high-level visual features (e.g., objects) are largely unexplored in this species. Therefore, mouse studies that utilize complex visual stimuli are challenged by 1) the well-known difficulty of parameterizing complex objects (35, 40, 41); 2) the unknown neural substrate that encodes these parameters; 3) the uncertainty about whether mice can be trained in the task within a reasonable time, if at all; and 4) the difficulty of inferring behavioral strategies given the parametric complexity of the stimulus space (42, 43). Our task represents a convenient solution: it builds upon existing orientation discrimination tasks in mice (14–18) in which a specific orientation is to be chosen over a distractor orientation (14, 16–18, 44–46), or in which a change relative to a specific orientation is to be detected (47–50). However, it complicates discrimination by introducing well-controlled invariances (to specific orientations, spatial frequency, and stimulus size), exploring stimulus dimensions that are easy to parameterize and that have a clear neural representation, and can be learned by mice in a reasonable time.
Our model helped estimate the typical orientation discrimination acuity at a 9° angle difference, reaching 6° for one mouse tested with the smallest angular separation of 3°. The orientation discrimination acuity of mice has previously been measured in a 2AFC task with a distractor (17) and change detection tasks (47–50). Acuity measures have been reported as thresholds or just noticeable differences (JNDs) and have commonly relied on model-derived values, such as the model-based inverse of a certain success rate (47, 48), the mean of the fitted Gaussian (49, 50), or times its SD (49, 50). We developed an acuity estimation procedure suitable for our stimulus space in which we identified stimulus conditions with the highest gradient of model-predicted P(R) and compared the performance in these and neighboring conditions. Our approach took advantage of the complete stimulus space representation of P(R) instead of relying on a cruder psychometric model to compute a JND or threshold value.
Task- and Behavior-Related Factors Influencing Choice.
By parameterizing biases, history effects, and orientation certainties, our model showed that the animals largely followed the intended choice strategy. This was apparent from concentration values that were significantly different from zero in most animals, indicating that, overall, the mice used information from both stimuli. However, model parameters also exhibited variations that could be interpreted as animal-specific choice heuristics. One such heuristic was evident in the trade-off of concentration values, with some animals unequally weighting stimulus information. Accuracy of orientation estimation was still necessary for high success rates, but even among the best-performing animals, right and left concentrations were anticorrelated. This trade-off demonstrates that the animals followed a range of sufficiently good strategies for solving the discrimination problem.
Such strategies can be interpreted as examples of suboptimal or approximate inference in an uncertain environment. Suboptimal inference is sometimes thought of as an adaptive phenomenon, a way for a subject to deal with the complexity of the task at hand by constructing and acting upon its approximate model (19). Adherence to a suboptimal strategy can be linked to limited cognitive resources (51, 52), which in our task fluctuated together with task engagement. Indeed, we found that history-dependent biases—another manifestation of suboptimal behavior—are stronger during periods of lower engagement characterized by impulsive wheel rotations immediately after stimulus onset. We demonstrated this by introducing history priors—in a form that allows for their analytical inclusion in our model—which increased the explanatory power of the model more in periods of lower engagement than in periods of higher engagement. In addition, we obtained a congruent result if the task engagement was defined based on streaks of relatively good or bad performance. These fluctuations of the history biases are driven by the internal state of the animal, are independent of the stimulus protocol, and will thus occur in addition to difficulty- or confidence-dependent fluctuations, as recently described (53). During periods of decreased performance, higher explanatory power of history terms is not guaranteed, but it is consistent with switching between history-driven and stimulus-driven choice modes (54).
Limitations of Our Approach.
Although we believe that our work substantially advances the understanding of mouse behavior during complex orientation discrimination, our approach has limitations at the level of model design and strategy interpretation. First, our model assumes fixed psychometric parameters across sessions and trials, and thus a more flexible, dynamically parameterized model could provide better insight into the biases and choice strategies of mice. Second, the goodness of fit of the model with respect to the variation of P(R) with could be further improved; in some animals, this variation was larger than the model prediction (SI Appendix, Fig. S6, example animal), which could be explained by a dependency of and on the proximity to the category boundary () (55). Finally, the interpretation of concentration values might not be directly relatable to perceptual sensitivity, since the concentration values were likely decreased by nonsensory factors, such as noise in the decision computation (19, 24, 56), inherent priors (57), and choice heuristics (19, 20).
Future Directions and Potential Implications.
Because our task relies on perceptual invariances and decouples the decision information from specific sensory stimuli, it can be useful for exploring the neural basis of decision-making in future studies. A similar task design relying on combinations of stimuli has been used extensively in the body of decision-making literature (3, 58–62), but it has not been reported in mouse orientation discrimination experiments.
Furthermore, our task can provide valuable insight into the relationship between neural and behavioral variability. Whether behavioral variability arises predominantly from sensory sources (37) or from the deterministic or stochastic suboptimality of decision computation (19) is one of the central questions in the neuroscience of decision-making. The complexity of our orientation discrimination task will increase the role of suboptimal decision computation, as has been predicted theoretically (19, 20, 51), and will provide an opportunity to study the correlates of this suboptimality in neural responses.
Finally, our task is well suited for isolating the contributions of visual cortical areas in the computation of decisions. The importance of a particular visual area for decision-making depends on the type of task (63); mice with a lesioned or silenced visual cortex have shown better-than-chance performance in detection paradigms (47, 64), possibly reflecting a predominant role of the superior colliculus (49), while for orientation discrimination tasks with a distractor, the visual cortex is necessary (45, 46, 65). Our incrementally more complex version of the orientation discrimination task could provide further insight into the role of primary visual cortex (V1) and downstream visual areas in the computation of decisions (35) and could therefore be a useful addition to common behavioral protocols for mice.
Materials and Methods
Experimental Model and Subject Details.
All surgical and experimental procedures were approved by the Support Unit for Animal Resources Development of The Institute of Physical and Chemical Research (Japan) (RIKEN) Center for Brain Science. We used n = 40 transgenic mice: Thy1-GCaMP6f (n = 37), Camk2-tTA TRE-GCaMP6s (n = 2), Emx1-tTA TRE-GCaMP6s (n = 1), with a total of 30 male and 10 female animals, aged 4 to 25 mo. Animals were implanted with a coverslip and a head post. After the implantation of the head post and recovery from the surgery, for 2 wk mice were placed in habituation cages with enriched environment, where they learned to obtain water from an apparatus similar to the automatically latching part of the behavioral setup. Next, mice were placed under a water restriction plan for 2 wk, obtaining 3 mL water a day during the first week and 2 mL during the second, with a target of maintaining their body weight at 75 to 80% of the initial weight. If at this or any later point their weight dropped below the target level, mice were given additional water proportionate to the weight to be restored. After 2 wk, animals were moved to the training cages. For further details, reference SI Appendix, Supplementary Methods.
Behavioral Training.
During training, animals were housed in individual cages connected to automated setups (21) (O’Hara & CO., LTD., https://ohara-time.co.jp/) where two experimental sessions per animal per day were carried out. Sessions were initiated by animals themselves as they entered the setup and their head plate was automatically latched. Animals were trained in a 2AFC orientation discrimination task. Two oriented Gabor patches (20° visual angle static sinusoidal gratings, sf = 0.08 cpd, with randomized spatial phase, and windowed by a 2D Gaussian envelope with 4 equal to stimulus diameter) were shown on the left and right side of a screen positioned in front of the animal (liquid crystal display monitor, 25 cm distance from the animal, 33.6 cm × 59.8 cm [∼58°×100°dva], 1,080 × 1,920 pixels, PROLITE B2776HDS-B1, IIYAMA) at ±35° eccentricity relative to the body’s midline. Mice reported which of the two stimuli was more vertical (more horizontal for n = 12 animals; task details in SI Appendix, Phases of training) by rotating a rubber wheel with their front paws, which shifted the stimuli horizontally on the screen. For a response to be correct, the target stimulus had to be shifted to the center of the screen, upon which the animal was rewarded with 4 µL water (amount adjusted for a few animals with nontypical weight and age). Incorrect responses were discouraged with a prolonged (10 s) intertrial interval (ITI) and a flickering checkerboard stimulus (2 Hz). If no response was made within 10 s (time-out trials), neither reward nor discouragement was given.
All trials consisted of an open-loop period (OL, 1.5 s) during which the wheel manipulator did not move the stimuli on the screen and a closed-loop period (CL: 0 to 10 s) during which the wheel controlled their position. Intertrial interval was randomized (ITI: 3 to 5 s). Stimuli appeared on the screen at the beginning of the OL.
Data Selection.
We analyzed trials from sessions in which the average success rate was at least 60%, and the proportion of time-out trials did not exceed 20%. We only used animals that had reached the minimal angular difference of 9° and included the choice data from preceding sessions with minimal differences starting from 30°. We excluded the first trial of every session, all time-out trials, and every trial that followed a time-out. The two dimensions of the stimulus space were flipped for horizontal-reporting animals when fitting our model. Same stimulus space transformation was done for all the population summaries where mice trained on horizontal targets were pooled together with mice trained on vertical targets.
Psychometric Curve.
We fitted the animal’s probability of making a right choice P(R) as a function of task difficulty using a psychometric function where is a Gaussian cumulative probability function, and are the mean and SD, and are left and right (L/R) lapse rates, and is the difference in the angular distance to the vertical, . CIs were computed by bootstrapping (n = 999).
Model Design.
On each trial , the animal was shown a pair of stimuli { and made a right or a left choice , which we set by convention to be or , respectively. We denote response and correct target on the previous trial as and , respectively, with or if the animal chose left or right, respectively, and or if the correct answer was respectively left or right, and if targets had an equal verticality.
A choice in trial i was based on animal’s estimates of the presented stimulus orientations . We model and as random variables distributed according to a posterior distribution obtained after combining an animal’s likelihood distribution over percepts with prior terms and that model choice bias and history-dependent bias, respectively. We reserve the () notation for the random variables modeling percepts and biases and () to refer specifically to the posterior over animal’s estimates, to which the decision rule is applied. We model the likelihood as a product of von Mises distributions and centered at and , respectively, with additional angle estimation biases (translational biases) and with concentrations , (high concentration means smaller spread, with analogous to of a normal distribution; only were allowed) (Fig. 2 B and D):
| [1] |
where , and is modified Bessel function of order 0. A bias prior that induces choice bias for right or left stimuli, and a history prior that models choice dependency on previous choice and stimulus ( and ), are modeled as follows:
| [2] |
| [3] |
Here, is a concentration parameter that regulates the strength and sign of choice bias, is a concentration parameter of history prior, determines the influence of the previous stimulus and choice with respective weights and fixed for a given animal, and and are normalization constants.
Since by convention we set vertical orientation to zero, the angle with the smaller absolute value is the correct choice. Hence, the probability of choosing right on a given trial is given by the following:
| [4] |
Overall, the model has eight fitted parameters () or five parameters () when we fit a history-free model. All angles were converted from (−90°, 90°) range to (−180°, 180°) to satisfy periodicity.
Our model design follows similar models of perceptual inference (23, 57, 66) with two distinctions. First, since our animals never report point estimates of the observed orientations—usually modeled as maximum a posteriori—estimates only enter our model as not directly observed random variables. Second, since all orientations in our study are presented at 100% contrast, without added noise or any other form of stochasticity, and are displayed for the full duration of the trial (11.5 s or less if the choice is made earlier), we assume that the sensory evidence given by a specific orientation is the same on all trials.
Optimization.
To fit the model, we minimize the log-likelihood cost function:
| [5] |
using MATLAB built-in function fmincon. At every iteration of the optimizer we evaluated Eq. 4, first computing values of all probability densities on a grid of 300 by 300 points in the 2D domain and integrating numerically using MATLAB function trapz over for the numerator and over the whole domain for the denominator. We ran these calculations on GPU (NVIDIA RTX 2080Ti) using MATLAB Parallel Computing Toolbox.
Success Rate with a One-Sided Strategy.
We estimated the success rate that animals could reach when taking into account only one stimulus by first computing P(R) for every trial using a model where one concentration was set to zero and the other one to of that animal. We sampled choices using the stimulus conditions as they appeared in the experimental dataset 1,000 times and computed an average percent correct over repetitions and an average across animals.
Maximum Perceptual Acuity.
By analogy with a one-dimensional psychometric curve, we defined points of maximum perceptual acuity in the stimulus space as conditions (pairs of angles) where the change in was the largest for a small fixed change in the stimuli. We found these conditions from the probability surface given by the full model by computing the squared norm of the gradient vector, , and selecting conditions for which the values of g were in the top 5%. Among these conditions, we analyzed those with P(R) ≈ 0.5 (0.48 ≤ P(R) ≤ 0.52), which we call maximum gradient conditions (Fig. 3 C and H, white) with a pooled right-choice probability of P0.5. For n = 28 animals this procedure gave at least three unique maximum gradient conditions. For n = 12 animals, the initial criterion gave fewer than three maximum gradient conditions, and we expanded the allowed range to have at least three: we set (0.47 ≤ P(R) ≤ 0.53) for n = 7 animals, (0.46 ≤ P(R) ≤ 0.54) for n = 1, (0.42 ≤ P(R) ≤ 0.58) for n = 1, (0.40 ≤ P(R) ≤ 0.60) for n = 1, (0.38 ≤ P(R) ≤ 0.62) for n = 1, and (0.28 ≤ P(R) ≤ 0.72) for n = 1.
We then determined the neighboring conditions by changing one orientation at a time by 9°, which resulted in an increase (“+”) or decrease (“−”) of P(R) relative to P0.5 (Fig. 3C). For example, PR- corresponded to the probability of right choice pooled from all conditions in which changed relative to maximum gradient conditions in the direction of P(R) decrease. Here, the stimulus space was binned to a 9° grid. In a separate analysis, for an animal with 3° condition binning, we changed both orientations simultaneously by +−3°, “along” and “against” the gradient of P(R), and obtaining P+ and P+, respectively (Fig. 3H).
We tested that probabilities in the neighboring conditions (PL+, PR+, PL-, PR- in case of 9°-binned conditions, and P+, P− in case of 3°-binned conditions) were significantly different from maximum gradient probabilities P0.5 using a two-tailed test with df = 1 and doing pairwise comparisons of right-choice frequencies, with a correction for multiple comparisons. For a population summary (Fig. 3E), we computed PL+, PR+, PL-, PR- with increasing angle increments of 9°, 18°, and 27° and reported the cumulative number of animals for which at least one of the four probabilities was significantly different from P0.5, using a two-tailed test with df = 1 and a criterion α = 0.05/4.
History Biases during High and Low Engagement.
We first identified periods of high and low engagement in every session. For a given session, we computed a running estimate of the RT in a sliding window of 10 trials. RTs were defined as the first rotation of the wheel after stimulus presentation, with trials that had wheel rotations before the stimulus excluded from the analysis. Low and high RTs were defined as the lower and upper 10% of the distribution of RTs of every session and intermediate RTs as the remaining values. We considered trials with intermediate RTs as trials with a relatively high engagement, and trials with short and long RTs as low-engagement trials.
In a complementary analysis (SI Appendix, Fig. S5 B and C), we identified periods of high and low engagement based on the success rate. We computed a running estimate of the success rate in a sliding window of 10 trials and centered the running estimate by subtracting the mean success rate of the session. All trials with the centered success rate estimate exceeding a fixed threshold of 10% were labeled as high engagement, and all trials in which the centered success rate estimate was lower than −10% were labeled as low engagement. We confirmed the stability of our results using threshold values of 5%, 15%, and 20%. When identifying engagement epochs, time-out trials were counted as failures, but we discarded these trials for all the analysis that followed, consistently with the rest of this study.
Next, for both the main (RT-based) and the alternative (performance-based) engagement criterion, we computed the log-likelihood of outcomes in high- and low-engagement trials ( and , respectively) given the probabilities predicted by the full model that accounted for trial history and by a history-free model fitted separately ( and , respectively) (see Model Design). For binary outcomes and model-derived probabilities , we computed trial wise the log likelihood using the formula with stimulus conditions binned to a 9° grid. Applying two different trial selections and two different models, we obtained for the log likelihoods of high-engagement trial outcomes given the model with history, for the log likelihoods of low-engagement trial outcomes given the model with history, for the log likelihoods of high-engagement trials given the history-free model, and for the log likelihoods of low-engagement trials given the history-free model. We next computed the differences of log-likelihood averages between models with and without history terms, using high-engagement trials, and low-engagement trials, , (Fig. 4D).
For SI Appendix, Fig. S5C, we computed the average of each of these log likelihoods across all trials for every pair of orientations thus obtaining maps of as a function of orientations . We discarded any stimulus conditions where the number of trials was < 10. We computed the difference between history-dependent and history-free maps of separately for high- and low-performance trials, that is, and , and for all trials together, . For the population summary (SI Appendix, Fig. S5C) of , , and , we normalized maps of every animal by the SD across all stimulus conditions and averaged the resulting maps across animals.
Model Comparison.
AIC.
We compared the cumulative Gaussian psychometric model to our history-free model, and the history-free model to the model with history priors, using the Akaike Information Criterion (AIC) defined as where is the number of parameters (4 for Gaussian model, 5 for the history-free model, 8 for model with history) and is the log-likelihood value of the best fit. We computed using the following binomial log-likelihood formula:
where corresponds to a 9°-binned unique stimulus condition defined by for the history-free to Gaussian model comparison and for the history-free to the history-dependent model comparison, is the proportion of successes, is the total number of trials, and is the success rate given by either one of three models. We computed and reported and for the final quantification.
Fraction of explained deviance.
To estimate how much explanatory power is gained by fitting the history-free model in comparison to the Gaussian psychometric model, and by the history-dependent model in comparison to the history-free model, we computed the fraction of explained deviance. Deviance is defined as two times the log of the ratio of the saturated model likelihood to optimal model likelihood :
| [6] |
where are observations, are estimated parameters, and are parameters of the saturated model.
For binomial data, deviance is as follows:
| [7] |
where is the number of successes for stimulus condition , is the number of trials, and is the probability of success in condition given by the fitted model with parameters . For the cumulative Gaussian psychometric function , a stimulus condition is defined by a pair of angles in a history-free model and a pair of angles with trial history in a model with history.
We first computed the deviance of the null model, with the same P(R) = rate for all conditions (computed as a grand average P(R) across trials). We then used the formula for deviance [7], with when computing null deviance , as predicted by history-free model when computing history-free deviance , as predicted by the history-dependent model when computing history-dependent deviance , and as predicted by the Gaussian model when computing Gaussian deviance . Here, a condition corresponded to a unique pair of orientations when comparing the Gaussian model with the history-free model and to a pair of orientations together with history inputs when comparing the history-free model and the history-dependent model; the fraction of right choices and the total number of trials per condition changed accordingly. We computed the fraction of explained deviance () for the three models as , , and , and finally, we computed difference in the fraction of deviance explained as or . For this analysis, we trained each model on 50% randomly sampled trials and computed deviances from the other 50% of trials. We tested the significance of for a population of animals using the Wilcoxon signed-rank test.
Supplementary Material
Acknowledgments
We thank Yuki Goya and Rie Nishiyama for their support with behavioral training. We thank O’Hara & Co., Ltd., for their support with the equipment. This work was funded by RIKEN Brain Science Institute and RIKEN CBS institutional funding, JSPS (Japan Society for the Promotion of Science) Grants 26290011, 17H06037, and C0219129 to A.B., and a Fujitsu collaborative grant.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2103952118/-/DCSupplemental.
Data Availability
Code and Data have been deposited on GitHub and Zenodo (67) and are publicly accessible at https://github.com/CBS-NCB/mouseChoice and https://zenodo.org/record/5091324#.YPbo0ehKiHs, respectively.
References
- 1.Gold J. I., Shadlen M. N., The neural basis of decision making. Annu. Rev. Neurosci. 30, 535–574 (2007). [DOI] [PubMed] [Google Scholar]
- 2.Pho G. N., Goard M. J., Woodson J., Crawford B., Sur M., Task-dependent representations of stimulus and choice in mouse parietal cortex. Nat. Commun. 9, 2596 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Steinmetz N. A., Zatka-Haas P., Carandini M., Harris K. D., Distributed coding of choice, action and engagement across the mouse brain. Nature 576, 266–273 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mante V., Sussillo D., Shenoy K. V., Newsome W. T., Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Romo R., Brody C. D., Hernández A., Lemus L., Neuronal correlates of parametric working memory in the prefrontal cortex. Nature 399, 470–473 (1999). [DOI] [PubMed] [Google Scholar]
- 6.Akrami A., Kopec C. D., Diamond M. E., Brody C. D., Posterior parietal cortex represents sensory history and mediates its effects on behaviour. Nature 554, 368–372 (2018). [DOI] [PubMed] [Google Scholar]
- 7.Burgess C. P., et al., High-yield methods for accurate two-alternative visual psychophysics in head-fixed mice. Cell Rep. 20, 2513–2524 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dakin S. C., Tibber M. S., Greenwood J. A., Kingdom F. A. A., Morgan M. J., A common visual metric for approximate number and density. Proc. Natl. Acad. Sci. U.S.A. 108, 19552–19557 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hubel D. H., Wiesel T. N., Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol. 160, 106–154 (1962). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Huberman A. D., Niell C. M., What can mice tell us about how vision works? Trends Neurosci. 34, 464–473 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Abbott L. F., et al., The mind of a mouse. Cell 182, 1372–1376 (2020). [DOI] [PubMed] [Google Scholar]
- 12.Luo L., Callaway E. M., Svoboda K., Genetic dissection of neural circuits: A decade of progress. Neuron 98, 256–281 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Madisen L., et al., Transgenic mice for intersectional targeting of neural sensors and effectors with high specificity and performance. Neuron 85, 942–958 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Andermann M. L., Kerlin A. M., Reid R. C., Chronic cellular imaging of mouse visual cortex during operant behavior and passive viewing. Front. Cell. Neurosci. 4, 3 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Goard M. J., Pho G. N., Woodson J., Sur M., Distinct roles of visual, parietal, and frontal motor cortices in memory-guided sensorimotor decisions. eLife 5, 1–30 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Long M., Jiang W., Liu D., Yao H., Contrast-dependent orientation discrimination in the mouse. Sci. Rep. 5, 15830 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Reuter J. H., Tilt discrimination in the mouse. Behav. Brain Res. 24, 81–84 (1987). [DOI] [PubMed] [Google Scholar]
- 18.You W.-K., Mysore S. P., Endogenous and exogenous control of visuospatial selective attention in freely behaving mice. Nat. Commun. 11, 1986 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Beck J. M., Ma W. J., Pitkow X., Latham P. E., Pouget A., Not noisy, just wrong: The role of suboptimal inference in behavioral variability. Neuron 74, 30–39 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gardner J. L., Optimality and heuristics in perceptual neuroscience. Nat. Neurosci. 22, 514–523 (2019). [DOI] [PubMed] [Google Scholar]
- 21.Aoki R., Tsubota T., Goya Y., Benucci A., An automated platform for high-throughput mouse behavior and physiology with voluntary head-fixation. Nat. Commun. 8, 1196 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wichmann F. A., Hill N. J., The psychometric function: I. Fitting, sampling, and goodness of fit. Percept. Psychophys. 63, 1293–1313 (2001). [DOI] [PubMed] [Google Scholar]
- 23.Laquitaine S., Gardner J. L., A switching observer for human perceptual estimation. Neuron 97, 462–474.e6 (2018). [DOI] [PubMed] [Google Scholar]
- 24.Drugowitsch J., Wyart V., Devauchelle A.-D., Koechlin E., Computational precision of mental inference as critical source of human choice suboptimality. Neuron 92, 1398–1411 (2016). [DOI] [PubMed] [Google Scholar]
- 25.Agresti A., Categorical Data Analysis (John Wiley & Sons, 2003). [Google Scholar]
- 26.Fründ I., Wichmann F. A., Macke J. H., Quantifying the effect of intertrial dependence on perceptual decisions. J. Vis. 14, 9 (2014). [DOI] [PubMed] [Google Scholar]
- 27.Busse L., et al., The detection of visual contrast in the behaving mouse. J. Neurosci. 31, 11351–11361 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Urai A. E., Braun A., Donner T. H., Pupil-linked arousal is driven by decision uncertainty and alters serial choice bias. Nat. Commun. 8, 14637 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Abrahamyan A., Silva L. L., Dakin S. C., Carandini M., Gardner J. L., Adaptable history biases in human perceptual decisions. Proc. Natl. Acad. Sci. U.S.A. 113, E3548–E3557 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Odoemene O., Pisupati S., Nguyen H., Churchland A. K., Visual evidence accumulation guides decision-making in unrestrained mice. J. Neurosci. 38, 10143–10155 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yerkes R. M., Dodson J. D., The relation of strength of stimulus to rapidity of habit-formation. J. Comp. Neurol. Psychol. 18, 459–482 (1908). [Google Scholar]
- 32.Ratcliff R., A theory of memory retrieval. Psychol. Rev. 85, 59–108 (1978). [Google Scholar]
- 33.Shevinsky C. A., Reinagel P., The interaction between elapsed time and decision accuracy differs between humans and rats. Front. Neurosci. 13, 1211 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Robbins T. W., The 5-choice serial reaction time task: Behavioural pharmacology and functional neurochemistry. Psychopharmacology (Berl.) 163, 362–380 (2002). [DOI] [PubMed] [Google Scholar]
- 35.DiCarlo J. J., Cox D. D., Untangling invariant object recognition. Trends Cogn. Sci. 11, 333–341 (2007). [DOI] [PubMed] [Google Scholar]
- 36.Britten K. H., Newsome W. T., Shadlen M. N., Celebrini S., Movshon J. A., A relationship between behavioral choice and the visual responses of neurons in macaque MT. Vis. Neurosci. 13, 87–100 (1996). [DOI] [PubMed] [Google Scholar]
- 37.Brunton B. W., Botvinick M. M., Brody C. D., Rats and humans can optimally accumulate evidence for decision-making. Science 340, 95–98 (2013). [DOI] [PubMed] [Google Scholar]
- 38.Renart A., Machens C. K., Variability in neural activity and behavior. Curr. Opin. Neurobiol. 25, 211–220 (2014). [DOI] [PubMed] [Google Scholar]
- 39.Zoccolan D., Cox D. D., Benucci A., Editorial: What can simple brains teach us about how vision works. Front. Neural Circuits 9, 51 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.DiCarlo J. J., Zoccolan D., Rust N. C., How does the brain solve visual object recognition? Neuron 73, 415–434 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Riesenhuber M., Poggio T., Models of object recognition. Nat. Neurosci. 3 (suppl.), 1199–1204 (2000). [DOI] [PubMed] [Google Scholar]
- 42.Vermaercke B., Op de Beeck H. P., A multivariate approach reveals the behavioral templates underlying visual discrimination in rats. Curr. Biol. 22, 50–55 (2012). [DOI] [PubMed] [Google Scholar]
- 43.Alemi-Neissi A., Rosselli F. B., Zoccolan D., Multifeatural shape processing in rats engaged in invariant visual object recognition. J. Neurosci. 33, 5939–5956 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Pinto L., et al., Fast modulation of visual perception by basal forebrain cholinergic neurons. Nat. Neurosci. 16, 1857–1863 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Poort J., et al., Learning enhances sensory and multiple non-sensory representations in primary visual cortex. Neuron 86, 1478–1490 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Resulaj A., Ruediger S., Olsen S. R., Scanziani M., First spikes in visual cortex enable perceptual discrimination. eLife 7, e34044 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Glickfeld L. L., Histed M. H., Maunsell J. H. R., Mouse primary visual cortex is used to detect both orientation and contrast changes. J. Neurosci. 33, 19416–19422 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jin M., Beck J. M., Glickfeld L. L., Neuronal adaptation reveals a suboptimal decoding of orientation tuned populations in the mouse visual cortex. J. Neurosci. 39, 3867–3881 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wang L., McAlonan K., Goldstein S., Gerfen C. R., Krauzlis R. J., A causal role for mouse superior colliculus in visual perceptual decision-making. J. Neurosci. 40, 3768–3782 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wang L., Rangarajan K. V., Gerfen C. R., Krauzlis R. J., Activation of striatal neurons causes a perceptual decision bias during visual change detection in mice. Neuron 97, 1369–1381.e5 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Whiteley L., Sahani M., Attention in a Bayesian framework. Front. Hum. Neurosci. 6, 100 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wyart V., Koechlin E., Choice variability and suboptimality in uncertain environments. Curr. Opin. Behav. Sci. 11, 109–115 (2016). [Google Scholar]
- 53.Lak A., et al., Reinforcement biases subsequent perceptual decisions when confidence is low, a widespread behavioral phenomenon. eLife 9, e49834 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ashwood Z. C., et al., Mice alternate between discrete strategies during perceptual decision-making. bioRxiv [Preprint] (2020). 10.1101/2020.10.19.346353 (Accessed 1 February 2021). [DOI] [PMC free article] [PubMed]
- 55.Jazayeri M., Movshon J. A., A new perceptual illusion reveals mechanisms of sensory decoding. Nature 446, 912–915 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Dosher B. A., Lu Z. L., Perceptual learning reflects external noise filtering and internal noise reduction through channel reweighting. Proc. Natl. Acad. Sci. U.S.A. 95, 13988–13993 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Girshick A. R., Landy M. S., Simoncelli E. P., Cardinal rules: Visual orientation perception reflects knowledge of environmental statistics. Nat. Neurosci. 14, 926–932 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Hernández A., Salinas E., García R., Romo R., Discrimination in the sense of flutter: New psychophysical measurements in monkeys. J. Neurosci. 17, 6391–6400 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Scott B. B., Constantinople C. M., Erlich J. C., Tank D. W., Brody C. D., Sources of noise during accumulation of evidence in unrestrained and voluntarily head-restrained rats. eLife 4, e11308 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Pinto L., et al., An accumulation-of-evidence task using visual pulses for mice navigating in virtual reality. Front. Behav. Neurosci. 12, 36 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Constantinople C. M., Piet A. T., Brody C. D., An analysis of decision under risk in rats. Curr. Biol. 29, 2066–2074.e5 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Jogan M., Stocker A. A., A new two-alternative forced choice method for the unbiased characterization of perceptual bias and discriminability. J. Vis. 14, 20 (2014). [DOI] [PubMed] [Google Scholar]
- 63.Pinto L., et al., Task-dependent changes in the large-scale dynamics and necessity of cortical regions. Neuron 104, 810–824.e9 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Prusky G. T., Douglas R. M., Characterization of mouse cortical spatial vision. Vision Res. 44, 3411–3418 (2004). [DOI] [PubMed] [Google Scholar]
- 65.Jurjut O., Georgieva P., Busse L., Katzner S., Learning enhances sensory processing in mouse V1 before improving behavior. J. Neurosci. 37, 6460–6474 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Stocker A. A., Simoncelli E. P., Noise characteristics and prior expectations in human visual speed perception. Nat. Neurosci. 9, 578–585 (2006). [DOI] [PubMed] [Google Scholar]
- 67.Lyamzin D. R., Aoki R., Abdolrahmani M., Benucci A., Behavioral Data. Zenodo. https://zenodo.org/record/5091324#.YPXSGehKiHs. Deposited 12 July 2021. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Code and Data have been deposited on GitHub and Zenodo (67) and are publicly accessible at https://github.com/CBS-NCB/mouseChoice and https://zenodo.org/record/5091324#.YPbo0ehKiHs, respectively.