Assessing the effectiveness of the Italian risk-zones policy during the second wave of COVID-19

Abstract

On 4 November 2020 the Italian government introduced a new policy to address the second wave of COVID-19. Based on a battery of indicators, the 21 administrative regions of Italy were assigned a risk level among yellow, orange, red, and, starting on 6 November 2020, different type of restrictions were applied accordingly. This event represents a natural experiment that allows the evaluation of the effects of non-pharmaceutical interventions, free from those nuisance factors affecting cross-national studies.

In this work, we extract the daily growth rate of new cases, hospitalizations and patients in ICU from official data using an unobserved components model and assess how the different restrictions had different impacts in reducing the speed of spread of the virus.

We find that all the three packages of restrictions have an effect on the speed of spread of the disease, but while the mildest (yellow) policy leads to a constant number of hospitalizations (zero growth rate), the strictest (red) policy is able to halve the number of accesses to regular wards and intensive care units in about one month. The effects of the intermediate (orange) policy are more volatile and seem to be only slightly more effective than the milder (yellow) policy.

1. Introduction

In October 2020 Italy found itself in the second wave of COVID-19 infections. New cases were increasing with daily rates above 5% and hospitals were quickly reopening COVID-19 wards closed during the Summer and preparing new intensive care units (ICUs). On 24 October the Italian government introduced a new regulation [21] that imposed many restrictions, the most important being the use of masks everywhere outside private households, the closing time for restaurants, cafes and pubs set at 6 PM, the closure of gyms, swimming pools and game rooms, forbidding public events, introducing limitations on the number of students allowed into high schools and universities, stopping private visits in nursing homes, limiting the attendance to weddings and funerals.

On 4 November 2020, the government issued a new ordinance [22] to come into effect on 6 November that introduced three different policies to be implemented in regions according to their local risk as measured by pooling 21 indicators. The 21 indicators, computed for each of the 21 regions (the Region Trentino-South Tyrol is split into its two autonomous provinces Bozen and Trento), provide information about the probability/speed of spread, the impact on hospitals, ICUs and nursing homes, the resilience of the regional health system and the reliability of available data.

The measures of the three policies introduced by the ordinance, named yellow, orange and red, are summarized below [we rely on the excellent English translation and synthesis produced by the International Centre for Theoretical Physics 15].

Yellow

• •Between 10 PM and 5 AM, only persons with valid work (e.g. commuting to/from work), health or other urgent reasons may be out of home. In any case, it is strongly recommended at any point of the day that persons do not leave their homes except for work, health or other urgent reasons or to engage in physical activity or to make use of any ongoing services. Streets or squares in urban centers prone to the formation of crowds may be closed all or part of the day, though allowing access to legitimate commercial activities and private residences.
• •Teaching activities from the 9th year of schooling and in higher education will be provided remotely for 100% of the students.
• •Malls, shopping centers, and markets are closed on weekends and holidays; pharmacies, newsstands, tobacco shops and shops selling foodstuffs inside shopping centers and markets may remain open.
• •Arcades, betting rooms, bingo halls, and casinos are closed and such activities are prohibited in any other type of facility.
• •Museums, theaters, cinemas and other cultural institutions are closed.
• •Trains, trams, and buses may be filled to a maximum of 50% of their capacity.
• •Cruise services of Italian-flagged passenger ships are suspended.

Orange Like yellow but with the following further restrictions.

• •Nobody is allowed in or out of the region, except for work, health or other urgent reasons, for school attendance as allowed by the present decree, or to return to one’s legal residence. Passing through orange zones to reach one’s legal residence is allowed.
• •Leaving one’s municipality is also not allowed, except for the above stated reasons.
• •Food service activities (including cafes, restaurants, pubs, ice cream parlors, and pastry shops) are suspended. However, delivery continues to be allowed at all times while takeaway until 10 PM. Food service activities at rest stops along highways, in hospitals, and in airports may continue.

Red Like orange but with the following further restrictions.

• •All movements are prohibited except for work, health or other urgent reasons, for school attendance as allowed by the present decree, or to return to one’s legal residence. Passing through red zones to reach one’s legal residence is allowed.
• •Commercial activities are suspended, with the exception of those selling foodstuffs and basic necessities. Markets are also closed, with the exception of stands exclusively selling food. Newsstands, tobacco shops, and pharmacies remain open.
• •Teaching activities from the 7th year of schooling and in higher education will be provided remotely for 100% of the students.
• •Foodservice activities (including cafes, restaurants, pubs, ice cream parlors, and pastry shops) are suspended. However, delivery continues to be allowed at all times and takeaway until 10 PM. Foodservice activities at rest stops along highways, in hospitals, and in airports may continue.
• •Outdoor sports clubs and centers are closed. Individual outdoor exercise is exclusively allowed in the near vicinity of one’s residence and with the use of a mask.
• •Personal services are suspended, with few exceptions. Activities suspended include hair salons, barber shops, and beauty salons.
• •Public employers shall reduce in-person activities to those that cannot be postponed and cannot be performed remotely.

On 6 November 2020 each of the 21 regions was assigned one of three colors and, until 29 November 2020, regions were to keep their starting color or move to a stricter policy color according to the updated values of the 21 indicators.

Using this event and the official data published by Dipartimento di Protezione Civile we want to measure the effect of the different policies on the speed of spread of the virus and rate of growth of hospitalizations in regular wards and ICU.

The basic measurement on which we base our analysis is the daily growth rate (of new cases and hospitalizations). For comparison purposes we report also estimates of the effective reproduction number $R_t$, however, for various reasons we prefer to carry out our analysis on the daily growth rates: indeed, i) daily growth rates can be easily projected into short-term predictions of hospital occupancy, while the same operation is not immediate in terms of $R_t$, ii) $R_t$ is model-based and its estimate based on strong assumptions, while the estimation of growth rates entails only denoising and adjusting for seasonal effects (e.g., diagnostics tests and data transmission are reduced on weekends), iii) common procedures for the estimation of $R_t$ require data on the date of appearance of the first symptoms and such a time series has to be built retrospectively based on declarations and estimates and, therefore, is less reliable and not fit for policies that have to be adjusted in real time. Similar conclusions about the use of daily growth instead of $R_t$ for policy purposes can be found in Bonifazi et al. [4].

There is a vast literature on the effects of nonpharmaceutical interventions (NPIs) of various measures on the speed of spread of COVID-19 [10]. According to Perra [20], just considering the first twelve months since the beginning of the pandemic, around 350 articles were published in international journals about COVID-19-related NPIs. National and local Governments adopted many NPIs to reduce the transmission of the COVID-19 among the population and limit the damages. Examples of the most common measures are social distancing, educational institutes closures, travel restrictions, wearing masks in public spaces and early detection and isolation of cases. Many studies have proven the effectiveness of these measures in reducing the spread of severe acute forms of COVID-19 [14] and reducing the transmission of other respiratory infections [2]. See, for example, the study by Leung et al. [18], which discusses the role of surgical face masks for infected people in reducing onward transmission of influenza to other individuals. Considering international measures, the most relevant virus containment results have been achieved by interrupting entrance and departure via aeroplanes and transportation. Regarding mainland China’s specific case, travel restrictions delayed the overall epidemic progression and the importations from abroad were reduced by nearly 80% at the peak of the crisis in February 2020 [7]. However, early detection and isolation of cases prevented more infections than did travel restrictions and contact reductions, but a combination of nonpharmaceutical interventions achieved the most substantial and most rapid effect [17].

Most of the recent empirical papers investigating the effectiveness of NPIs during the COVID-19 pandemic apply a cross-country approach. In these works the effectiveness of NPIs is inferred by relating the policy implemented in different countries to the course of the epidemic in these contexts. To some extent, one could interpret this way of addressing the issue as a horizontally-oriented approach, in which the focus is on the cross-sectional difference between the effects of policies across countries over the entire period analysed and not on their temporal evolution. This last feature is instead the main emphasis of a vertical approach, such as the one proposed in this paper. Among others, a valid reason for not choosing cross-sectional studies is the high heterogeneity among nations concerning testing strategies, counting COVID cases and deaths [8] and in the access to PPE and medical aids. As stated by Brauner et al. [5], the worldwide responses to COVID-19 spread were heterogeneous and weakly coordinated as the national governments implemented different sets of NPIs, at different times, in different orders. The lack of policy coordination has been particularly evident even in politically harmonized settings, such as the European Union, in which every country disposed of independent policies. In Brauner et al. [5], the authors investigated the effect on the $R_t$ index of several NPIs disposed in forty-one countries, both European and non-European, between January and May 2020. The authors considered the case of common nonpharmaceutical interventions, such as social distancing, mask-wearing, educational institutes closing and stay-at-home orders. According to their findings, different NPIs are associated with stronger or weaker effects. In particular, closing schools and universities, as well as high-risk businesses, were very effective, while closing most other businesses had limited benefits. Furthermore, both Brauner et al. [5] and Flaxman et al. [11] suggest that all the considered countries could have achieved a value of the $R_t$ index below one without implementing more rigorous NPIs.

Other studies propose alternative specifications of the spreading mechanism of the virus and the growth rate of new cases and hospitalised people. A very popular epidemiological framework is the so-called Susceptible-Infected-Recovered (SIR) model (and extensions), which describes the number of infected and susceptible individuals as a set of difference equations [24]. The SIR and its extensions allow the derivation of essential quantities, such as the daily growth rate, starting from the original equation. This class of models have been applied by [2] to estimate the COVID-19 transmission rate in the US comparing the period before and during the NPI period. Using laboratory data, it is estimated that NPIs can reduce transmission of COVID-related respiratory syndromes by up to 20%, but that use of the interventions may suffer from complex interactions with seasonal effects that can distort efficacy.

With respect to the above illustrated frameworks, our work has some substantive differences in the aims and methods. Indeed, in our analysis, we assess how three well-defined packages of NPIs affect the daily growth rates of new infections and hospitalisations in Italy during an observational period of one month. In particular, we assess i) how quickly growth rates decrease as a consequence of the different restrictions (deceleration), ii) what is the speed of spread to which each risk-zone policy converges (steady-state speed). In other words, the steady-state rate (or $R_t$) of point ii) represents the speed of reduction (if the rate is negative) of the infection if the region had to remain under that policy for a long time, while the deceleration of point i) indicates how much the rate of growth (or $R_t$) decreases in a given time span, provided that the same policy is constantly applied for the whole time span.

The features of our study that differentiate it from the existing literature are the following.

Type of NPIs. We do not consider the effects of single measures, but the overall effects of three well-determined packages of measures with increasing restrictions implemented by the Italian government and that are expected to be operate until the end of the COVID-19 waves. The drawback of this is that we are not isolating the effect of each NPI, but the advantage is that we are not neglecting interactions among NPIs. Assessing the impact of these packages of measure is extremely relevant for Italy, but it is interesting also for countries that apply or consider the implementation of similar policies.

Territory and timing. We limit our study to the 21 administrative regions of Italy. The fact that the Italian territory on 6 November 2020 was split into three policy-homogeneous risk-zones offered the scientific community the chance to study a really unique natural experiment. Indeed, most confounding variables that typically affect international cross-sectional or panel studies become harmless. Indeed, the NPIs we are observing are identically defined in the whole country, the timing is the same, the way of administrating COVID tests, counting the number of new cases, hospitalizations and deaths is homogeneous. Furthermore, during the one-month period we consider, no other significant policy changes or seasonal effects (i.e., holidays, vacations, extreme weather conditions) were altering the natural course of events.

Cross-country studies should appropriately take into account the different way of measuring the variables of interest. For instance, Corrao et al. [8] point out the differences in the definition of deaths due to COVID-19 in various countries. Of course, one-country studies are not affected by these regulatory differences.

Methods. The data we analyze are time series and, thus, we have to take into account the dynamic nature of the effects of NPIs on these data. In measuring changes in the speed of spread of a disease time is a key variable. Any policy affecting the speed of transmission implies three elements: a starting speed, the new (lower) speed induced by the policy and the time to decelerate from the starting speed to the new speed. Over the limited period of time of our sample, herd immunity effects are negligible and, thus, changes in the speed of spread are to be attributed just to the policies. While many of the cited studies make use of compartmental models to derive the quantities of interest (generally, the $R_t$), in our study we try to be as much model-agnostic as possible. Indeed, our approach is based on extracting the signal daily growth rate of new cases and hospitalizations from the noisy data. We just assume that there is a time-varying daily growth rate of the quantities of interest that evolve over time according to a simple random process. The growth rate is not directly observable because data are collected and communicated with some noise and weekly patterns. The signal of the non-observable growth rate is extracted using well known Kalman filtering and smoothing techniques. The growth rates extracted in each Region of Italy are than grouped according to the three policy rules and analyzed under two aspects: the deceleration and the convergence to a lower speed of spread caused by each package of restrictions. All differences are tested for significance using a non parametric analogue of the analysis of variance (ANOVA) that takes ordering in consideration.

For this kind of assessment, keeping a model-agnostic approach has several advantages over model-based analyses. Firstly, measured data do not correspond to the theoretical quantities represented in epidemic models. Secondly, by choosing one specific model the analyst is conditioning his/her results on that model being the true data generating process, but different models can produce different estimates of the quantities of interest (e.g., the $R_t$). Thirdly, available data are typically not enough informative to estimate all the unknown parameters in the model and, so, important assumptions have to be based on conjectures or analogies in the available literature. These assumptions (e.g., the shape of the distribution of the transmission of the virus by a single infected person over time) are generally held fixed, neglecting the fact that NPIs may also affect them.

For comparison purposes, we convert our inference on growth rates into estimates of the effective reproduction number $R_t$, using the approach of [4], which seems to provide a very good approximation of the official time series published (just for Italy) by the Italian National Institute of Health (Istituto Superiore di Sanità).

The remainder of the paper is organized as follows. Section 2 introduces the method we use to extract the growth rates of the number of new cases, hospitalizations and patients in ICU. Section 3 contains the results of the analysis. Section 4 discusses the results and 5 draws some conclusions.

2. Materials and methods

We illustrate the statistical methods used in our analysis in a technical and in an intuitive way so that different type of readers can fully understand our approach.

2.1. Technical presentation

Let $y_t$, for $t=1,2,\dots ,n$, be the daily time series of interest (number of new cases, number of hospitalized patients, number of patients in intensive care units). Since official time series tend to show a weekly seasonal pattern and, for various reasons, can be rather noisy, we assume $y_t$ to be the product of three components: the level $m_t$, the weekly seasonal factor $g_t$ and the noise $e_t$,

$$y_t=m_t{g}_t{e}_t,$$ (1)

or, equivalently

$$\ln \left(y_t\right)={\mu }_t+{\gamma }_t+{\epsilon }_t,$$ (2)

with ${\mu }_t=\ln \left(m_t\right),{\gamma }_t=\ln \left(g_t\right),{\epsilon }_t=\ln \left(e_t\right)$.

In our analysis we are interested in the daily rate of growth of the level $m_t$, which is given by

$${\beta }_t={\mu }_{t+1}-{\mu }_t=\log \left(\frac{m_{t+1}}{m_t}\right)\approx \frac{m_{t+1}-m_t}{m_t}.$$ (3)

Notice that we are defining ${\beta }_t={\mu }_{t+1}-{\mu }_t$ instead of the more natural ${\beta }_t={\mu }_t-{\mu }_{t-1}$ because we have to cast the model in state space form. Thus, ${\beta }_t$ represents the rate of growth that takes place when moving from time $t$ to time $t+1$. If ${\beta }_t>0$ (${\beta }_t<0$) the number of cases or hospitalizations increases (decreases), while when $\beta =1$ the number of new cases or hospitalizations remains constant.

Since our analysis is short-term, based on past data, and we want to be model-agnostic and just use this setup to extract the signal (i.e., the growth rate ${\beta }_t$) from available data, we will not assume any compartmental epidemic model. We relay on an unobserved components model just as a reliable tool for signal extraction. In particular, we assume ${\beta }_t$ to evolve as a random walk, ${\beta }_{t+1}={\beta }_t+{\zeta }_t,$ where ${\zeta }_t$ is Gaussian white noise with variance ${\sigma }_{\zeta }^2$. So, the specification for the log-level is that of an integrated random walk (also called smooth trend):

$$\begin{array}{ccc}\hfill {\mu }_{t+1}& =& {\mu }_t+{\beta }_t\hfill \\ \hfill {\beta }_{t+1}& =& {\beta }_t+{\zeta }_t,{\zeta }_t\sim \mathit{NID}(0,{\sigma }_{\zeta }^2),\hfill \end{array}$$

where $NID(\mu ,{\sigma }^2)$ has to be read as normally independently distributed with mean $\mu$ and variance ${\sigma }^2$.

For the weekly seasonal component we rely on the stochastic dummy approach, in which the sum of seven consecutive values is equal to a Gaussian white noise:

$${\gamma }_t=-{\gamma }_{t-1}-{\gamma }_{t-2}-\dots -{\gamma }_{t-6}+{\omega }_t,{\xi }_t\sim NID(0,{\sigma }_{\omega }^2).$$

Finally, the noise component for the additive model is, again, a Gaussian white noise: ${\epsilon }_t\sim NID(0,{\sigma }_{\epsilon }^2)$.

In this model $\ln \left(y_t\right)$ is assumed Gaussian and, thus, $y_t$ is log-normal. Of course, the data that we are about to analyze are counts and log-normality can only be considered an approximation. We estimated also a model in which $y_t$ is negative binomial with mean $\exp ({\mu }_t+{\gamma }_t)$, but the results where virtually identical and, so, we decided to proceed with the computationally simpler log-normal model.

The above model can be easily cast is state space form, the variances ${\sigma }_{\zeta }^2$, ${\sigma }_{\omega }^2$, ${\sigma }_{\epsilon }^2$ estimated by maximum likelihood and the unobserved components extracted using Kalman filtering and smoothing algorithms [for details refer to the monographs by  [9], [13], [19]]. In particular, conditionally on the estimated variances, the smoothing algorithm returns the following quantities

$$\begin{array}{ccc}\hfill {\mathit{a}}_{t|n}& =& \mathbb{E}({\mathit{\alpha }}_t|y_1,y_2,\dots ,y_n)\hfill \\ \hfill {\mathit{P}}_{t|n}& =& \mathbb{E}({\mathit{\alpha }}_t-{\mathit{a}}_{t|n}){({\mathit{\alpha }}_t-{\mathit{a}}_{t|n})}^{\top }\hfill \end{array}$$

where ${\mathit{\alpha }}_t$ is the vector containing all the unobserved components: in our application ${\mathit{\alpha }}_t={\left[\begin{array}{ccc}{\mu }_t& {\beta }_t& {\gamma }_t\end{array}\right]}^{\top }.$ The vector ${\mathit{a}}_{t|n}$ contains the optimal predictions of the state variables based on the whole time series, $y_1,y_2,\dots ,y_n$, and the diagonal of ${\mathit{P}}_{t|n}$ contains the mean squared errors of those predictions.

2.2. Intuitive presentation

We assume that the daily quantity of interest, as measured by official data, say $y_t$, is obtained as product of three factors: an underlying average level $m_t$, a weekly pattern $g_t$ mainly due to the fact that on weekends the number of tests and hospitalizations are generally lower than in the rest of the week, and an accidental component $e_t$ that summarizes all other random effect:

$$y_t=m_t{g}_t{e}_t.$$

We are interested in the level $m_t$, while the other two components are just nuisance factors in our analysis. The choice of a multiplicative rather than additive model is due to the fact that the oscillations around the average level $m_t$ are larger when the level is high and smaller when the level is close to zero. Indeed, both $g_t$ and $e_t$ should vary slightly around 1, signalling if on a given day the observed number $y_t$ was larger ($g_t{e}_t>1$) or smaller ($g_t{e}_t<1$) than average. The movements generated by the components $g_t$ and $e_t$ are proportional to those of the level $m_t$. For example, if on Sundays the level of measured new cases is 15% lower than average, then $g_t=1-0.15=0.85$. When the level is $m_t=100$, then the decrease on Sundays is by 15 units ($=100·0.15$), while if the level is $m_t=1000$, then the reduction on Sundays is by 150 units ($=1000·0.15$).

All the component are let evolve over time. The accidental component $e_t$ oscillates randomly around the value of 1. The periodic component $g_t$ repeats itself (almost) identically every 7 days and its (geometric) average is 1, so that its effect disappears over a period of 7 contiguous days. The level component evolves with growth rate ${\beta }_t$,

$$m_{t+1}=m_t(1+{\beta }_t),$$

and the increment of growth rate over time is random, that is, the growth rate at time $t+1$ is equal to the growth rate a time $t$ plus a random shock.

Given the above information on the way the components evolve, thanks to a set of algorithms (the Kalman filter and the smoother), we are able to extract the unobservable components $m_t$ and ${\beta }_t$ from the observed values $y_t$. One can think of the estimates of the time series $m_t$ as some kind of weighted moving average of the neighbouring values $\{\dots ,y_{t-2},y_{t-1},y_t,y_{t+1},y_{t+2},\dots \}$ and as ${\beta }_t$ being the growth rate of the extracted $m_t$: ${\beta }_t=(m_{t+1}-m_t)/m_t$.

2.3. An example application to the COVID-19 data of Lombardy

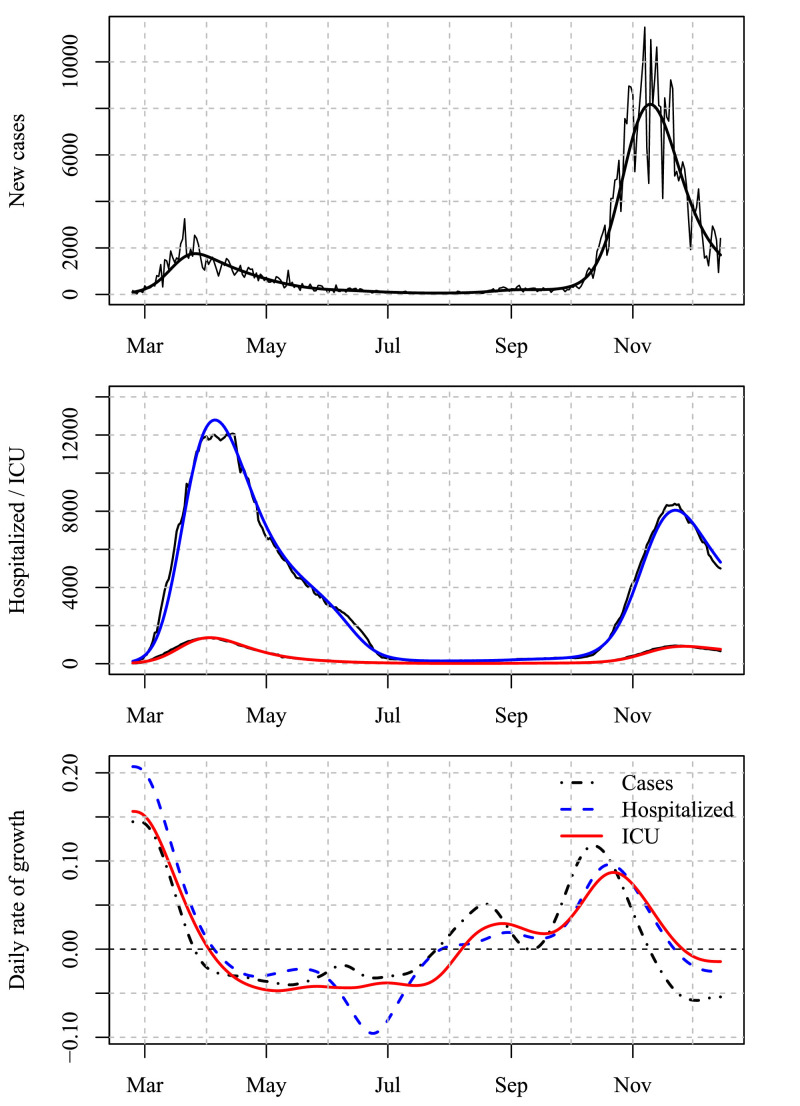
Figure 1 depicts the time series of the number of new cases, hospitalizations and COVID-19 patients in ICU in Lombardy with the extracted component $m_t$ and the daily rate of growth ${\beta }_t$ for the time span 24 Feb 2020 – 15 Dec 2020. The number of cases during the first wave appears to be much lower than that in the second wave, however the number of tests carried out during the first wave was significantly smaller. During the period we are going to analyze (6 November - 13 December) the number of tests has been roughly constant around 200,000 per day (country wise) with drops on weekends. These drops appear evident in the top graph of Fig. 1, however the smoothed estimate of the level plotted in the same graph is clearly free of any seasonal pattern.

Fig. 1.

Components extracted on the number of new cases in Lombardy. Top: new cases with level. Mid: hospitalized and ICU with levels. Bottom: daily rates of growth.

Analogous estimates for Italy, its 21 regions and 107 provinces are updated on a daily basis on the website https://bicocca-datalab.shinyapps.io/covid19/

The data used for producing Fig. 1 and used in the rest of the analysis are published by Dipartimento di Protezione Civile and available at https://github.com/pcm-dpc/COVID-19. The variables we analyze are nuovi_positivi (new cases), ricoverati_con_sintomi (hospitalized with symptoms) and terapia_intensiva (patients in ICU).

2.4. Derivation of the effective reproduction number from the growth rates

Even though, for reasons explained in the introductory section, we base our analysis on growth rates, for comparison purposes we report also estimates of the effective reproduction number $R_t$ and its changes due to the restriction policies. Our regional $R_t$ estimates are based on the method of Bonifazi et al. [4], who derive the mapping between the daily growth rate of new cases and the $R_t$ under common assumptions. In particular, if the distribution of the number of contagions generated by an infected person with respect to time is well approximated by a Gamma density function, then the $R_t$ can be computed as

$$R_t={(1+\theta {\beta }_t)}^{\kappa },$$ (4)

where ${\beta }_t$ is the growth rate and $\theta >0$ and $\kappa >0$ are the two parameters of the Gamma distribution. The Italian National Institute of Health (Istituto Superiore di Sanità) for its official estimates of the effective reproduction number sets $\theta =1.87$ and $\kappa =3.57$ as determined by Cereda et al. [6]. We rely on the same values in our analysis. For the period under scrutiny, our $R_t$ estimates for Italy are rather close to the official ones (which are regularly published only for the whole Italian territory). The reader interested in the comparison of the method proposed by Cereda et al. [6] with other popular methods used in epidemiology applied to Italian COVID-19 data should refer to the dashboard at https://covid19.infn.it/.

As expected, since the parameters $\theta$ and $\kappa$ are positive,

$$\begin{array}{cc}\hfill {\beta }_t>0& ⟺R_t>1\hfill \\ \hfill {\beta }_t=0& ⟺R_t=1\hfill \\ \hfill {\beta }_t<0& ⟺R_t<1.\hfill \end{array}$$

However, as mentioned in the introductory section, the derivation of the $R_t$ requires further assumptions on the shape of the distribution of the contagions generated by a positive individuals over time (Gamma) and its parameters ($\theta$ and $\kappa$). Moreover, most of the quantities that are necessary for health policies, such as the projection of the number of new cases and hospitalizations in the next few days or the halving time of the number of patients in ICUs or regular wards, can be easily derived directly from the growth rate and not from $R_t$ (unless additional assumptions are made and a formula such as (4) is implemented).

3. Results

The three policies (yellow, orange and red) to be assigned to the Italian regions on the basis of their risk were introduced on 6 November 2020 and, until 29 November 2020, the risk class and policy attributed to every region either remained unchanged or switched to a severer policy (i.e., darker color). In particular, all five red regions and the two orange regions remained such until 29 November 2020, while 9 out of 14 yellow regions switched color. The color assignments of 6 November and their later switches are synthesized in the second column of Table 1 using the following notation:

Table 1.

Reduction in the daily percentage growth rates of new cases, hospitalizations, ICU and $R_t$ changes, and percentage steady-state rates and $R_t$. Regions are ordered by the rate of reduction of new cases. Zones column entries have to be interpreted as region’s color on 6 November followed by day (of November) of change and color of landing. For instance, Toscana since 6 Nov was yellow, since 11 Nov was orange and since 15 Nov was red.

		Rate reduction				Steady rate
Region	Zones	Cases	Hosp.	ICU	$R_t$	Cases	Hosp.	ICU	$R_t$
Basilicata	y 11 o	8.8	5.4	10.2	0.60	$-$5.4	$-$1.8	$-$3.3	0.69
P.A. Bolzano	r	7.5	8.7	7.7	0.47	$-$5.2	$-$3.7	$-$2.4	0.70
Piemonte	r	7.5	6.5	7.7	0.47	$-$5.3	$-$1.7	$-$2.1	0.69
Calabria	r	7.4	6	9.3	0.50	$-$4.1	$-$0.7	$-$3.1	0.75
Lombardia	r	7.3	8	7.3	0.44	$-$5.8	$-$2.5	$-$1.4	0.66
Valle d’Aosta	r	7.2	7.2	6.7	0.41	$-$7.4	$-$3.5	$-$2.8	0.59
Abruzzo	y 11 o 18 r	7	3.9	5.6	0.45	$-$5.3	$-$0.3	$-$0.8	0.69
Toscana	y 11 o 15 r	6.7	6.1	5.8	0.40	$-$5.9	$-$2.1	$-$1.6	0.66
Campania	y 15 r	6.4	3.7	4.1	0.39	$-$5.2	$-$1.1	$-$2.2	0.70
Molise	y	6	4.9	6.2	0.41	$-$3.6	0	$-$1.2	0.78
Emilia-Rom.	y 15 o	5.5	4.4	4.9	0.38	$-$2.2	0.3	$-$0.7	0.86
Lazio	y	5.1	3.7	2.9	0.33	$-$3.2	$-$0.6	0.2	0.80
Umbria	y 11 o	5	3.9	6	0.29	$-$5.1	$-$1.2	$-$2.1	0.70
Sicilia	o	4.9	4.3	4.9	0.34	$-$2.2	$-$1.1	$-$1.3	0.86
Liguria	y 11 o	4.5	5	6.4	0.27	$-$4.7	$-$2.3	$-$2.4	0.72
Sardegna	y	4.1	1.9	3.1	0.28	$-$2.6	0.6	$-$0.7	0.84
Puglia	o	4	3.7	5.2	0.29	$-$1.1	0.2	$-$0.4	0.93
Friuli V.G.	y 15 o	3.8	5.7	3	0.28	$-$0.4	0.7	0.2	0.98
Marche	y 15 o	3.8	5.6	5.4	0.25	$-$2.1	$-$1.2	$-$0.5	0.87
Veneto	y	2.8	4.3	4.4	0.20	0.3	0.8	0.8	1.02
P.A. Trento	y	2.2	7.4	8.6	0.15	$-$0.8	$-$0.3	0.5	0.95
Mean of red		7.4	7.3	7.7	0.46	$-$5.6	$-$2.4	$-$2.3	0.68
Mean of to-red		6.7	4.6	5.2	0.41	$-$5.5	$-$1.2	$-$1.5	0.68
Mean of orange		4.4	4	5.4	0.31	$-$1.7	$-$0.5	$-$0.8	0.89
Mean of to-orange		5.2	5.1	6	0.34	$-$3.3	$-$0.9	$-$1.5	0.80
Mean of yellow		4	4.4	5	0.28	$-$2	0.1	$-$0.1	0.88
St.Dev. of red		0.1	1.1	1	0.04	1.2	1.3	0.6	0.06
St.Dev. of to-red		0.3	1.3	0.9	0.03	0.4	0.9	0.7	0.02
St.Dev. of orange		0.6	0.4	0.2	0.03	0.8	1	0.7	0.05
St.Dev. of to-orange		1.9	0.8	2.4	0.13	2	1.2	1.3	0.12
St.Dev. of yellow		1.6	2	2.4	0.10	1.7	0.6	0.8	0.10

[initial color] [date of change] [new color] [date of change] [new color]

As all changes took place in November 2020, in [date of change] only the day of the month is reported.

We relabeled the 21 regions according to the following rules:

• •yellow: regions that remained in the yellow zone from 6 Nov to 29 Nov;
• •to-orange: regions assigned to the yellow zone on 6 Nov, which ended up in the orange zone;
• •orange: regions that remained in the orange zone from 6 Nov to 29 Nov;
• •to-red: regions assigned to the yellow zone on 6 Nov, which ended up in the red zone;
• •red: regions that remained in the red zone from 6 Nov to 29 Nov.

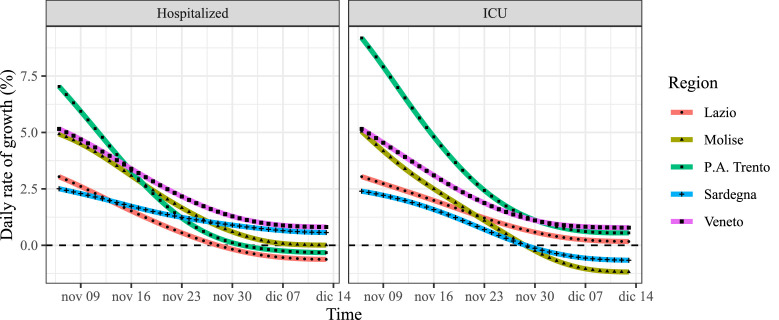
Then, we analyzed the daily rate of growth (the ${\beta }_t$ of Eq. (3)) of new cases, hospitalizations and patients in ICU for each region over two different time spans. Since almost every region shifted to a lower risk zone on 29 No. 2020, we observed the number of new cases over the period 6 Nov – 29 Nov. For the number of COVID-19 hospitalizations in regular wards and ICU, we extended the observation period by 14 days, since in our data we can observe an average delay of the peak of these time series with respect to new cases of approximately 14 days. For example, in Lombardy this delay can be observed in the bottom graph of Fig. 1: in November the blue (dashed) line and the red (continuous) line cross the $x$-axis later than the black (dash-dot) line. Thus, hospitalizations and ICU patients are monitored over the period 6 Nov – 13 Dec.

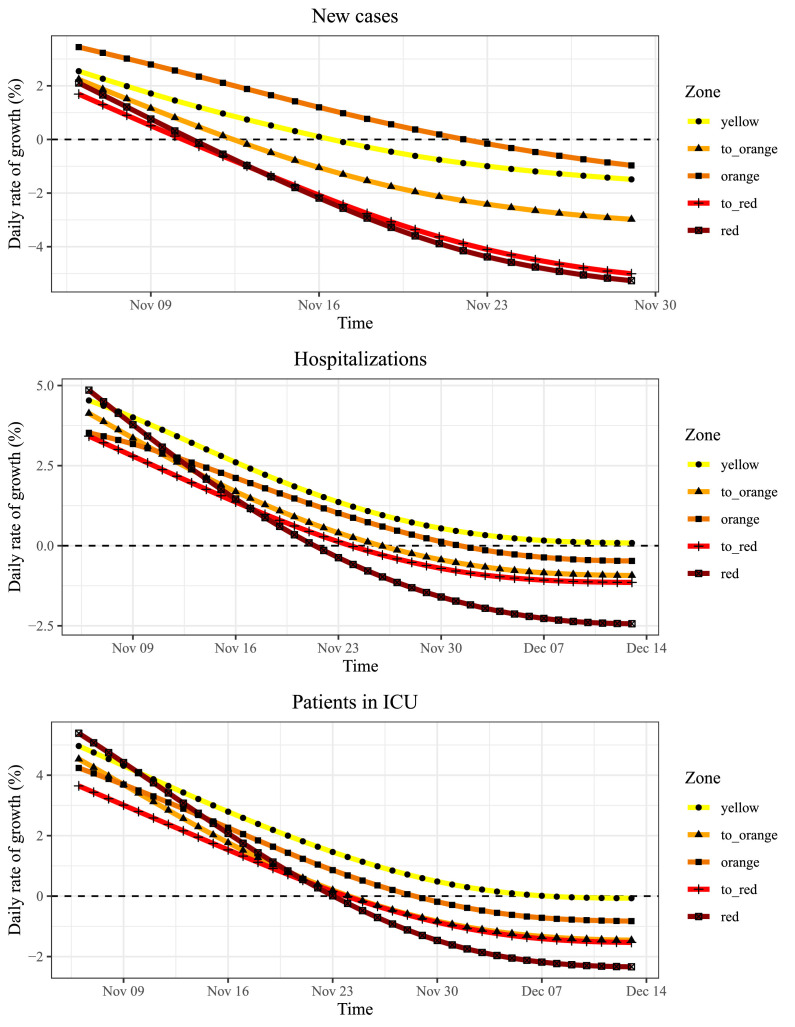
The average daily rates of growth in each group for the three time series are plotted in Fig. 2 . All the rates where positive and decreasing on 6 Nov. All (average) growth rates of new cases fell below zero in the observed time span, so at the end of this period the number of new COVID-19 cases were geometrically decreasing. Regions in the red and to-red zones were the first to reach the peak (i.e., growth rate crossing the zero level), followed by regions in the to-orange, yellow and orange zones. The behaviors of the average growth rates of hospitalizations and ICU patients appear similar: four time series fall below zero, while the rate of the yellow zone stops at zero. Hospitals in yellow zones reached the peak of hospitalizations but this peak looks like a plateau: the number of patients in regular wards and ICUs remains constant. In these two cases, the order of zero-crossing is the expected one: red zones first, orange zones second and the yellow zone last.

Fig. 2.

Mean growth rates by risk zone.

In order to assess how effective were the various zones in reducing the rates of growth of the three time series, we computed the cumulative rates of growth as ${\beta }_{start}-{\beta }_{end}$, where start is 6 Nov for all time series and end is 29 Nov for new cases and 13 Dec for the other two time series. Since ${\beta }_t$ are continuously compounded rates, they have the nice property of being additive: the composite rate is obtained as sum of the daily rates.1 We computed also discrete-time rates and (as expected) results are similar.

The four columns with header Rate reduction in Table 1 report these (percentage growth rate and $R_t$ reduction) values for all time series. Regions are decreasingly ordered by growth rate reduction of new cases. With the exception of Basilicata, all regions in top rows belong to the red zone (positions 2 through 6) or ended up in the red zone (positions 7 through 9). The growth rate reduction for hospitalizations and ICU patients are a bit more variable. Partially inconsistent data communicated by the Region Basilicata to the Government made the Scientific Committee consulting the Government doubt about their quality [cf. 3]. The placement and the figures of Basilicata in Table 1 seem to confirm the anomaly.

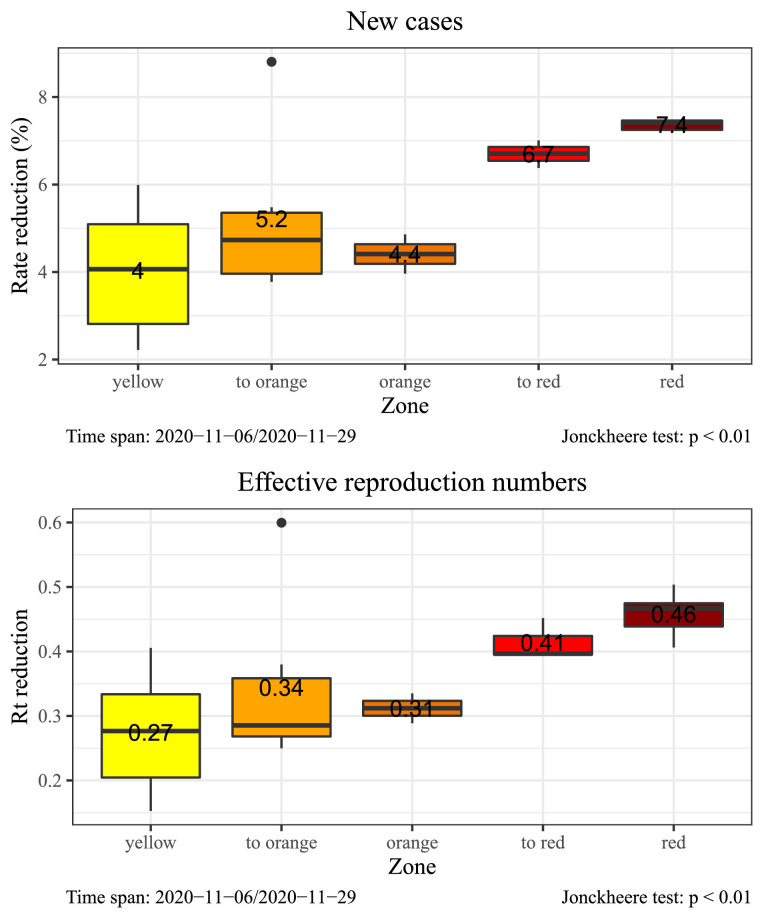
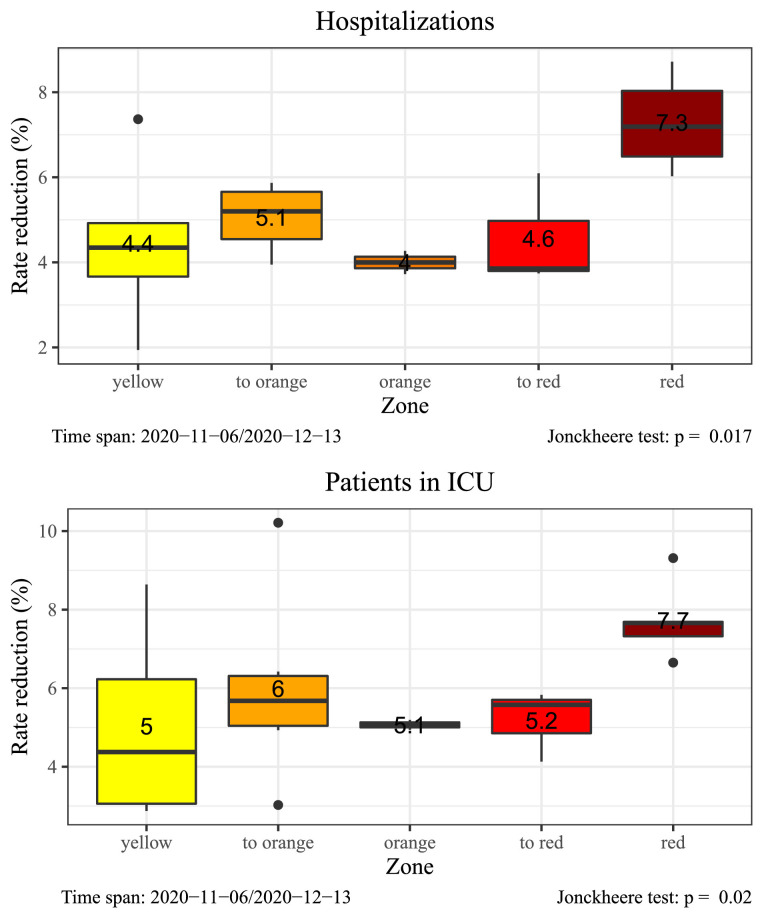
Figure 3 depicts box-plots of the reduction in growth rates and $R_t$ for new cases, while Fig. 4 plots the distribution of the growth rates for hospital-related quantities. In the same graphs we report the $p$-value of Jonckheere’s test [16], [23] for the null hypothesis that all median reductions are equal across zones (Jonckheere’s test is a nonparametric alternative to ANOVA $F$-test where the grouping variable is ordered): the null is rejected for all time series at 5% level, indicating that the differences in speed of reduction are significant. Red and to-red regions seem to have been very effective in reducing new cases, while for hospitalizations in regular wards and ICU only those regions in the red zone from the beginning where superior in reducing the growth rate. Regions in the other four groups showed similar reduction rates. The yellow group has highest dispersion, followed by the to-orange group. In those regions local governments have sometimes implemented further restrictions that may explain this differences among regions in the same risk zone. Moreover, some of these regions may have enjoyed positive side-effects from neighbors in stricter policy-zones.

Fig. 3.

New cases: distribution of regional growth rate and $R_t$ reductions by risk zone. The mean value of the group is expressed as text.

Fig. 4.

Hospitalizations: distribution of regional growth rate reductions by risk zone. The mean value of the group is expressed as text.

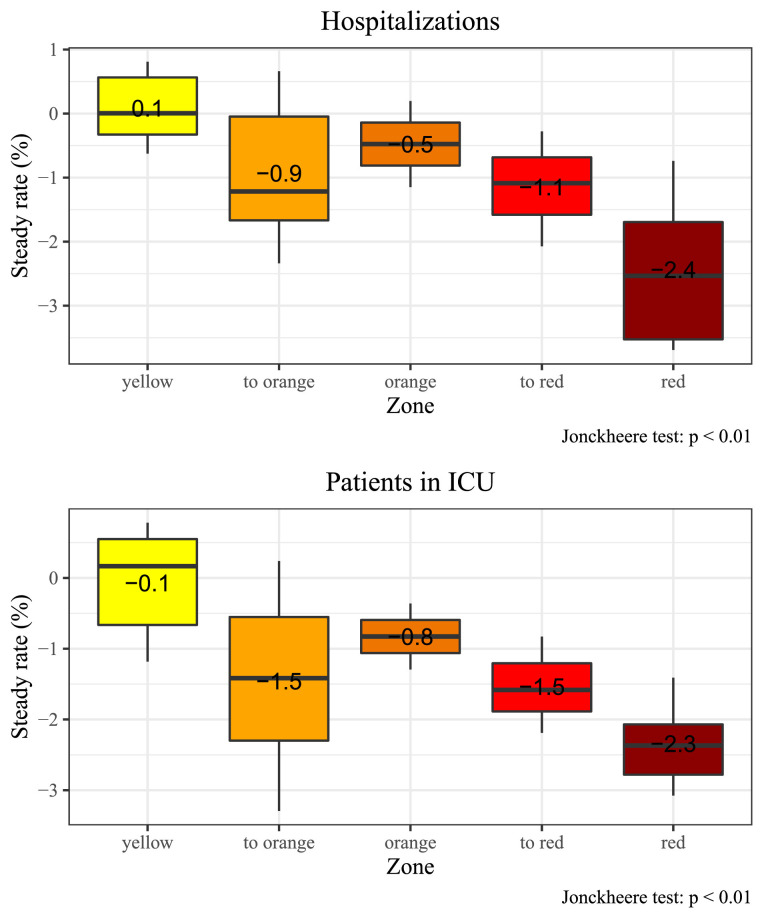
From Fig. 2 it appears clear that growth rates tend to converge to a steady-state value that may be different across zones. Indeed, each package of restrictions implies a different speed of spread of the disease. The last four columns of Table 1 report the daily percentage growth rates and $R_t$ after convergence to the steady-state. The steady-state growth rates computed for new cases can be considered reliable estimates as they were generally reached at most few days after the date of 29 November, in which zone assignment showed significant changes. The analogous estimates for hospitalizations (also ICU) may suffer from two limitations: i) at the moment of starting to write this paper only time series up to 15 December 2020 were available and the persistence of these time series [12, reports an average hospital stay of COVID-19 patients around 12 days with a long right tail] may have caused the steady-state to be reached later on, ii) due to the change of many risk zones on 29 November, waiting too long for the steady-state of these time series to come can confound the risk zone effects. For these reasons, we decided to look for the steady-state of hospitalizations only up to 15 December and to report the value at that date if no previous date was identified as convergent. Thus, the steady-state rate estimates for hospitalizations and ICU are less reliable than those of new cases.

Figures 5-6 depict the distribution of the steady-state rates and $R_t$ grouped by color-zone label. In principle, the steady-state rate should be the same for to-red and red zones and for to-orange and orange zones, and this fact is evident for new cases (Fig. 5). For hospitalizations and ICUs red zones seem to have a lower steady rate than to-red regions, meaning that full convergence to the steady-state was not reached in to-red zones. The negative trend of steady rates with respect to risk-zone with increasing restrictions is evident and confirmed by the fact that all Jonckheere tests are significant. If a region remains long enough under red-zone restrictions, the number of new cases reduces by around 5% per day. In orange zones, the volatility of the steady rates is higher, but in all regions the value is negative. In yellow regions the mean value is also negative (-2%), but not all steady rates are negative (the steady rate of Veneto is +0.3%). If we look at hospitalizations (both types), the steady rate is negative for red and orange regions, while yellow regions cluster around the value 0. This means that in yellow zones the number of patients tend to remain constant over time (cf. also Fig. 7 ).

Fig. 5.

New cases: distribution of regional steady-state growth rates and reproduction numbers by risk zone. The mean value of the group is expressed as text.

Fig. 6.

Hospitalizations: distribution of regional steady-state growth rates by risk zone. The mean value of the group is expressed as text.

Fig. 7.

Growth rates oh hospitalizations in regular wards and ICU for yellow regions. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

Our aim was measuring the effect of the Italian government three-color policy on the speed of spread of COVID-19 during the second wave.

4.1. Limitations

The limitations of our study are due to the following confounding factors.

• •At the beginning of the period under study, starting on 6 November, all rates of growth were already decreasing. This first slowdown was very probably due to the restrictions promulgated in the 24 October decree [21]. Furthermore, few regional governments had implemented stricter limitations on school attendances.
• •Only 11 out of 21 regions kept the same color during the whole period, while the others changed color once or twice (cf. Table 1). Our regrouping of these 10 regions cannot take into account all their slightly different histories.
• •Regions following stricter policies (as red regions) may have brought benefits to neighboring regions in a couple of ways: movements between regions of different colors were not allowed (with some exceptions), hospitals close to red region boundaries received a decreasing number of patients from those regions.
• •The initial allocation of the risk-zones was based on 21 structural and epidemiological indicators and, thus, this might have influenced the potential for change in growth rates. However, as Fig. 2 illustrates, the initial growth rates were not too different among the zones and the assignments were mostly based on the incidence compared to the level of saturation of regular wards and ICUs in local hospitals. Therefore, the possible effect of confounding between disease status and policy interventions should be weak.2

4.2. Evidence and policy implications

By looking at Fig. 2, all growth rates seem to be converging to a constant value. This convergence was expected as, far from herd immunity, social behaviors imposed by the three different regulations should imply different speeds of transmission of the virus and, in our analysis, speed of transmission is measured through the growth rate ${\beta }_t$. This steady-state value is negative for most time series, meaning that, if the restrictions persist, infections will eventually die-out (indeed, very slowly in yellow zones). However, the average growth rate for hospitalizations and patients in ICU is approximately zero in yellow regions, thus, in those regions hospitals are taking care of a constant number of COVID-19 patients both in regular wards and ICU. Fig. 7 depicts these growth rates for each region in the yellow group. At the end of the period under scrutiny, all time series seem to have reached a constant value and all these values are very close to zero.

In particular, Veneto’s growth rate is still above zero for both time series. One reason that kept Veneto in the yellow risk-zone, notwithstanding the speed of transmission, was the large number of ICU beds: with 20.4 ICU beds per 100,000 resident, Veneto is by far the best equipped region in Italy. However, at the moment of writing (end December 2020) the situation in Veneto is the least improving in the whole country [1].

From our analysis we can affirm that the introduction of the risk zones policy to counteract the evolution of the COVID-19 spread have generated noticeable positive effects in preventing regional health systems from collapsing, as happened during the first wave of March 2020 in Lombardy. In particular, the red zone policy was by far the most successful in reducing the rate of growth of new cases, hospitalizations in regular wards and ICUs.

In order to make the implications of our analysis more intelligible to policy makers, we can turn the steady-state rates into the number of days needed to half the quantities of interest. It is easy to show that, if the daily steady-state rate is $\beta <0$, then the quantity that changes with such a rate will be halved in $\tau =-\ln \left(2\right)/\beta$ days. If the rate is non-negative (i.e., $\beta \ge 0$), then the halving time is, of course, infinite.

Table 2 reports the median and the mean number of days to halve new cases, hospitalizations and ICU patients in the three risk zones (we merged to-orange and orange). The mean is infinite if at least one of the rates is positive, while the median is infinite if at least half of the rates are positive. The distribution of days is right-skewed and, so, the mean is always larger than the median.

Table 2.

Median and mean number of days to reduce quantity by one half.

	Median			Mean
Zone	Cases	Hosp.	ICU	Cases	Hosp.	ICU
yellow	27	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$
orange	31	59	75	48	$\infty$	$\infty$
red	13	27	29	13	40	32

The strong message of Table 2 is that if the red policy, which strongly limits movements and activities, is applied for a prolonged period of time, the number of registered cases and hospitalizations (and consequently also deaths, being strongly correlated) drop very quickly. Indeed, new cases are expected to halve every 13 days while the number of patients in regular wards and ICU halves every 30–40 days.

If a region is kept under orange restrictions for a prolonged period of time, the number of new cases is expected to halve every 31–48 days, hospitalizations are expected to halve every two months and ICU every 75 days. The infinite mean values on the right side of Table 2 are due to few regions that did not reach a negative growth in the considered period of time probably due to a too short sampling time.

Hospital in regions that remain under yellow restrictions for a long time are expected to reach a plateau which keeps a constant number of patients in regulars wards and ICU. Thus, the yellow policy is to be considered a maintenance policy to be applied in situations in which hospitals are well below saturation: the number of patients entering the hospitals is roughly equal to the number of hospitalized individuals exiting (alive or dead) the wards. Under this condition the daily number of deaths is expected to remain constant over time and, so, ethical considerations should also guide the decisions of policy makers.

In a nutshell, ceteris paribus, from the summary values it can be argued that if the authorities intend to halve the number of hospitalizations, one month of red zone is equivalent to two months of orange zone. On the other hand, if the authorities want to reduce the overall number of cases, one month of yellow or orange zone is equivalent to two weeks of red zone.

Of course, the differences between the restrictions in terms of social and economic effects are not negligible and lead to considerations about the trade-offs they might generate. Recall that, from the ministerial decrees, the substantial difference between orange and red areas is represented by the closure of commercial activities and the introduction of strong travel limitations, while the main difference between yellow and orange rules are represented by the suspension of food service activities (in presence).

Depending on the initial severity and available resources (e.g. health care facilities and hospitals saturation) and the intended goals of the authorities, the three policies have different consequences for the regions in which they are applied. On the one hand, the yellow zone, which imposes milder restrictions on movement and economic activities, is a policy that prevents the regional health system from collapsing, provided the health system is not close to saturation. If the level of hospitalizations is not already too high, the yellow zone makes it possible to maintain a constant level of admissions to the hospitals, tolerating a constant number of deaths over time. On the other hand, the red zone is an instrument that makes it possible to rapidly bring down cases and the speed of transmission of the virus and consequently both hospitalizations and deaths (being very correlated). However, it implies severe social and economic consequences due to forced economic activity suspensions and restrictions on the freedom of movement. Therefore, this choice can be considered as a tool of last resort in cases of dramatic spread of the epidemic or when the local health system is close to the collapse.

We found no significant difference in the deceleration of the yellow and the orange policies (by post-hoc tests). In particular, considering the 23 days under scrutiny, the decrease in rate of growth of new cases was very close to 7.4% for all red regions. If we scale this value to a single week, the average reduction is around 2.3% per week, even though the reduction is quicker in the first two weeks (cf. Fig. 2). For new cases, regions that ended in red (i.e., to-red regions) enjoyed almost the same deceleration as regions that were red from the beginning. The difference in the deceleration of the rate of growth of red regions with respect to yellow, to-orange and orange regions is, on average, circa 3%. Indeed, yellow, to-orange and orange zones decrease by 4–5% in 23 days, that is, by 1.2-1.5% per week. For example, if the rate of growth of new cases is 5% per day, in a red zone some 15 days should be sufficient to bring the growth rate to zero or below (or $R_t$ to 1 or below), while in a yellow or orange zone the same result would be reached in more than four weeks.

If we consider the longer time span (37 days) for hospitalizations (also in ICU), the average reduction in red zones is, again, around 7.5%, even though the dispersion is slightly higher. The average reduction over time is 1.4% per week, even though the first three weeks show a quicker decrease. In these last two cases, deceleration in to-red regions is similar to that of yellow and orange regions. For example, if the rate of growth of hospitalizations is 5% per day, in a red zone some 24 days should be sufficient to bring the growth rate to zero or below, while in a yellow or orange zone the same result would be reached in 31–37 days.

Finally, the fact that the growth rates of many of the regions were already decreasing on 6 November (cf. Fig. 2) proves that also the measures contained in the 24 October decree were having a decelerating effect when the new three-color regulation started operating. This effect may have been slightly amplified by the smoothing algorithm, which does not allow sharp jumps in the extractions of growth rates. However, we can assert without doubt that the measures in the 24 October degree were insufficient to bring the growth rate of the three quantities under scrutiny below zero and, thus, the $R_t$ below one.

5. Conclusions

The empirical analysis of the effects of the 4 November decree of the Italian government [22], which introduced the three risk-zones policy, proves its success in moderating the speed of transmission of COVID-19 infections and in keeping hospitals and ICUs below their levels of saturation.

The package of measures contained in the red policy well responds to the need of quickly reducing the speed of transmission of COVID-19 and consequent hospitalizations. The yellow and orange policies show variable effects in the regions of application and, on the average, tend to have similar outcomes in terms of deceleration. This suggests that the effect of closing restaurants and cafes also at Noon and the reduction of intra-municipal mobility are mostly negligible in the deceleration of the growth rates. However, in most regions belonging to the yellow risk-zone, hospitalizations in regular wards and ICU tend to reach their maximum in the form of a plateau rather than a sharp peak. Thus, the measures contained in the yellow policy should be used only in situations, in which hospitals and ICUs are not close to saturation, in order to let the virus circulate at a manageable speed. After the initial deceleration, orange and red zones lead to a negative daily rate of growth for new cases and hospitalizations (also in ICUs). However, while all regions in red and to-red zones reached a negative steady-state rate, among orange and to-orange there were few exceptions: for example, the rate of Friuli Venezia Giulia (in to-orange zone) did non converge to a negative value neither for hospitalizations nor to ICUs. One possible explanation for this is that the only internal boundary of Friuli Venezia Giulia is with Veneto (in yellow zone), whose steady-state rates remained all positive.

We can summarize the effects of risk-zone policies in the following way.

• •Once a region is assigned to a risk zone, the growth rates of new cases, hospitalizations and ICUs drop until they reach a steady state value.
• •The deceleration is quicker in red zones (-2.3% per week) and more gradual (-1.3% per week) in orange and yellow zones.
• •After deceleration, the risk zones imply different steady-state rates of growth that are negative in red zones, mostly negative in orange zones and close to zero in yellow zones.
• •Steady-state growth rates can be turned into estimates of the number of days needed to halve the quantities of interest. The uncertainty about these estimate is large. However, in a prolonged red zone we can expect the number of new cases to halve every two weeks and the number of patients in hospitals and ICU to halve in one month. In orange zones the variability of these estimate is even higher and new cases are expected to halve in a time between one and two months, while the number of patients in hospitals and ICUs should drop by one half in more than two months. As already remarked, yellow zones lead to a constant number of patients in hospitals and ICUs.