Interpreting Interaction Effects in Generalized Linear Models of Nonlinear Probabilities and Counts

Abstract

Psychology research frequently involves the study of probabilities and counts. These are typically analyzed using generalized linear models (GLMs), which can produce these quantities via nonlinear transformation of model parameters. Interactions are central within many research applications of these models. To date, typical practice in evaluating interactions for probabilities or counts extends directly from linear approaches, in which evidence of an interaction effect is supported by using the product term coefficient between variables of interest. However, unlike linear models, interaction effects in GLMs describing probabilities and counts are not equal to product terms between predictor variables. Instead, interactions may be functions of the predictors of a model, requiring nontraditional approaches for interpreting these effects accurately. Here, we define interactions as change in a marginal effect of one variable as a function of change in another variable, and describe the use of partial derivatives and discrete differences for quantifying these effects. Using guidelines and simulated examples, we then use these approaches to describe how interaction effects should be estimated and interpreted for GLMs on probability and count scales. We conclude with an example using the Adolescent Brain Cognitive Development Study demonstrating how to correctly evaluate interaction effects in a logistic model.

Introduction

Many studies in psychology seek to understand factors influencing the probability or count of a particular behavior. Common examples include evaluating the likelihood of a condition being present or absent (such as a clinical disorder) or assessing how frequently a behavior occurred. Evaluating these outcomes typically involves analyzing dependent variables that are binary or discrete counts. Although linear models serve as the analytic foundation for much of psychological science, linear approaches may be inappropriate for evaluating these variables given they are generated as discrete quantities. For instance, binary variables can assume only two values, and count outcomes are bounded at zero and assume strictly integer values. Because of these features, analysis of binary and count dependent variables via traditional linear regression typically leads to violations of assumptions (i.e. heteroscedastic and non-normal residual values; Gardner et al., 1995) and are often suboptimal for characterizing these outcomes.

To address this limitation, many researchers analyze these outcomes using generalized linear models (GLMs). GLMs provide a flexible framework that can characterize non-normal dependent variables by relating predictors to these outcomes through a nonlinear function (Nelder & Wedderburn, 1972). In so doing, GLMs can represent binary and count outcomes by modeling different conditional distributions and functional relations between variables (for reviews, see Coxe et al., 2013; Nelder & Wedderburn, 1972). The analyst then has several options for interpreting the effects produced by this model. First, one can retain the transformed scaling of the model and interpret the linear coefficients on this scale (e.g., log-odds or log-counts). The analyst can also transform the estimates produced by these models to recover a more natural scale of the outcome variable (e.g., probabilities and counts; Breen et al., 2018; Mize, 2019). These scales may have greater interpretive value given they can describe more meaningful real-world quantities. In this sense, a unique feature of GLMs relative to linear models is the distinction between the transformed scale in which the parameters are linearly specified versus the natural scale in which the model may be more meaningfully interpreted. Given the advantages of natural scales, analysts often favor the natural scale in describing research findings.

Central to many applications of probability and count models are interaction hypotheses, which address whether the effect of a focal predictor on an outcome of interest depends on a third variable (i.e. a moderator). Common examples include evaluating whether a given effect differs across groups or as a function of some continuous factor. For instance, the effect of stress exposure on psychopathology might differ across groups (such as biological sex) or as a function of age (Monroe & Simons, 1991). In linear models, interactions are tested using product term coefficients, which are then interpreted as the degree to which the effect of a focal predictor on the outcome changes for every unit change in the other variable (and vice-versa). The magnitude, direction, and statistical significance of this coefficient can then be evaluated to determine the presence and nature of the interaction (Bauer & Curran, 2005; McCabe et al., 2018). Interactions can then be probed to describe how the effect of a focal predictor on an outcome changes at particular levels of a moderator (Aiken & West, 1991).

In GLMs, interactions on natural scales can be quantified and probed using marginal effects (Long, 1997; Long & Freese, 2014). Marginal effects are often used as a flexible approach to characterize the rate-of-change in an outcome variable for a change in a predictor, holding all else constant. Hence, marginal effects are useful to characterize the effect of a predictor on the outcome in its natural scale of probabilities or counts. For instance, in the case of regression models that are linear in the predictors, marginal effects equal the coefficients of the specified model, which represent change in the outcome for every one-unit increase in a predictor. For GLMs of natural scales such as probability and count models, however, these coefficients do not capture marginal effects in the natural scale because they describe linear change in the transformed (e.g., logit or log) scale. Instead, as we describe in detail later, marginal effects use partial derivatives to quantify rates-of-change for nonlinear relations. In this sense, marginal effects represent a general approach for describing change in a naturally scaled outcome as a function of predictors and model parameters that can accommodate models with nonlinear design (Kim & McCabe, 2020), including GLMs of probabilities and counts. Using this conceptualization, an interaction effect can therefore be understood as change in the marginal effect for a focal variable for a change in the moderating variable.

Despite the utility of using marginal effects, interactions for GLMs are not typically quantified using marginal effects in published psychological research. Instead, tests of interaction are conducted in the same way as in linear models (i.e. via product terms). If the analyst describes their effects on the transformed scale (e.g., log-odds and log-counts), this is an appropriate practice given the linear specification of these scales. However, these terms do not quantify interaction effects when describing GLMs on their natural response scales. In brief, this is because transforming the scaling of the specified model introduces nonlinearity, which renders product term coefficients insufficient to quantify rate-of-change in a marginal effect on the natural response scale. Rather, a given interaction effect on natural scales is a function which must be interpreted with respect to other variables, as opposed to a constant quantified by the product term coefficient. This substantially increases the complexity involved in drawing straightforward inferences from these effects, and one cannot use methods developed to interpret interactions in linear models to evaluate interactions on the natural scale.

The issues and approaches we detail in this manuscript are not new to the social sciences, particularly in the context of nonlinear probability (e.g., logit) models. Others (Ai & Norton, 2003; Berry et al., 2010; Karaca-Mandic et al., 2012; Long & Mustillo, 2018; Norton et al., 2004; Tsai & Gill, 2013) have provided statistical formulations of interaction describing this issue for logit and probit models of economics data. Several texts (Long, 1997; Long & Freese, 2014) have also detailed approaches to computing marginal effects that parallel several of the solutions we describe here. Most recently, Mize (2019) provided a practical guide for characterizing interactions in nonlinear models, with emphasis on the pragmatics of describing these effects using data visualization and discrete differences in applied sociological research.

Despite this extensive literature, we have found that solutions for interaction effects in GLMs of probabilities and counts have not been widely adopted in the field of psychology. We conducted an online search in which we randomly sampled 100 articles published between 2009 and 2019 across seven high-impact journals in psychology that used either a logit or count model in analysis to describe changes in probabilities, odds, or counts and mentioned interaction effects in-text. We then examined whether the considerations for GLM interaction we describe in this paper were addressed in these manuscripts. Of these, 41 articles met our specific criteria of interest.¹ In addition to these articles, we also included a prior study led by the first author testing interaction using GLMs (McCabe et al., 2015). Consistent with similarly dismaying reviews in economics (Ai & Norton, 2003) and sociology (Mize, 2019), our results showed that none of the 42 articles reviewed (including the first author’s) interpreted the estimated interaction effect appropriately with respect to the natural scale in which they described their results. That is, despite having described effects on probability and count scales, all who inferred the presence of interaction supported their inference using the coefficient of the product term alone to provide a singular estimate of the interaction effect.

The overarching goal of this article is to address pervasive misconceptions in psychology regarding the interpretation of interaction effects in probability and count GLMs. Although theoretical frameworks (Ai & Norton, 2003; Berry et al., 2010; Karaca-Mandic et al., 2012; Norton et al., 2004; Tsai & Gill, 2013) and recommendations for presenting these effects (Mize, 2019) have been provided outside psychology, our aim is to bridge theoretical foundations with implications for testing and interpreting interaction effects for nonlinear probabilities and counts in psychological science. We pursue this by linking statistical accounts with actionable recommendations for estimating, interpreting, and presenting interaction effects for GLMs of nonlinear probabilities and counts. In so doing, we hope to provide a comprehensive resource for psychologists that describes how interaction hypotheses may be pursued within a generalizable framework for estimating interactions across linear and nonlinear scales using marginal effects.

We begin by reviewing GLMs and guiding readers through the formal definitions of interaction in these models using language more familiar to psychological scientists. We then provide computational solutions for estimating interactions in GLMs on the natural scale, with special focus on logistic, Poisson, and negative binomial models for probabilities and counts given their popularity in psychology. Using simulated examples, we then discuss how typical analytic approaches in psychology can lead to serious errors in modeling and interpreting interaction effects, and provide concrete guidelines for improving inferential practices. Finally, using Adolescent Brain Cognitive Development (ABCD) Study data (https://abcdstudy.org/), we then provide an empirical example of how to analyze and interpret interaction effects appropriately in the metric of probabilities in a large and publicly-available dataset.

Background

Generalized linear models

Overview

Generalized linear modeling provides a flexible framework that can model nonlinear scales (Nelder & Wedderburn, 1972). We begin by defining the form of a GLM generically as follows using a generalized substantive regression framework (Kim & McCabe, 2020):

$$g(\mathbb{E}[Y\mid x])=d{(x)}^T\beta .$$ (1)

Above, we define x as a p × 1 vector of observed predictors and β is an m × 1 vector of regression coefficients. The term $\mathbb{E}[Y\mid x]$ is the conditional expectation of some dependent variable Y on a fixed set of predictor variables x.

The function d(·) transforms x into a vector of m regressor variables, which includes an intercept and any desired product terms. We use this formulation to simplify notation for the equations presented later in the manuscript. For example, if x = [x₁ x₂]^T, then a possible design vector could be d(·) = [1 x₁ x₂ x₁x₂]^T. Note that although we have only two predictor variables involved in the model (x₁ and x₂), the inclusion of the intercept and product term via d(·) yields a total of four regressor variables (i.e. the intercept, predictors x₁ and x₂, and their product).² d(·) is analogous to a design matrix in the ANOVA framework, where one substantive categorical variable is split into a set of binary variables that actually serve as regressors in a model.

The GLM is distinguished from the traditional linear model due to the inclusion of the nonlinear link function g(·).³ We define $g(\mathbb{E}[Y\mid x])$ as the transformed scale, which allows the model to be estimated while retaining linearity in the parameters (Breen et al., 2018). However, it is very often the case that analysts seek to describe results in a more natural scale of a variable rather than the transformed one (Agresti, 2002; Breen et al., 2018; Long, 1997; Mize, 2019). For logit and count models, natural scales refer to probabilities and counts for their respective models. Relative to transformed scales, natural scales can be more intuitive and often more directly correspond with the motivating research question (Long, 1997; Mize, 2019; G. King et al., 2000; though see Breen et al., [2018] and Agresti, [2002] for discussions on competing perspectives). As such, analysts typically convert GLMs into their natural scales by inverting the link function, which is what renders most⁴ GLMs nonlinear in the natural scale:

$$\mathbb{E}[Y\mid x]=g^{-1}\left(d{(x)}^T\beta \right).$$ (2)

By performing this transformation, regressors are now associated with the outcome through g⁻¹(·). In other words, although this transformation allows us to recover the natural response scale, the relation between $\mathbb{E}[Y\mid x]$ and d(x)^Tβ is no longer linear as a consequence.

The logistic model

The logistic regression model is among the most frequently-used GLMs in psychology for binary dependent variables. Since Y is binary in these models, $\mathbb{E}[Y\mid x]$ refers to the probability of Y, and regressors are related to this quantity using a logit link function. The logit model can therefore be represented as:

$$\text{log}\left(\frac{\mathbb{E}[Y\mid x]}{1-\mathbb{E}[Y\mid x]}\right)=d{(x)}^T\beta .$$ (3)

This model states that the log-odds of $\mathbb{E}[Y\mid x]$ (i.e. the transformed scale) is the linear combination of our regressor variables (Figure 1a).

Figure 1.

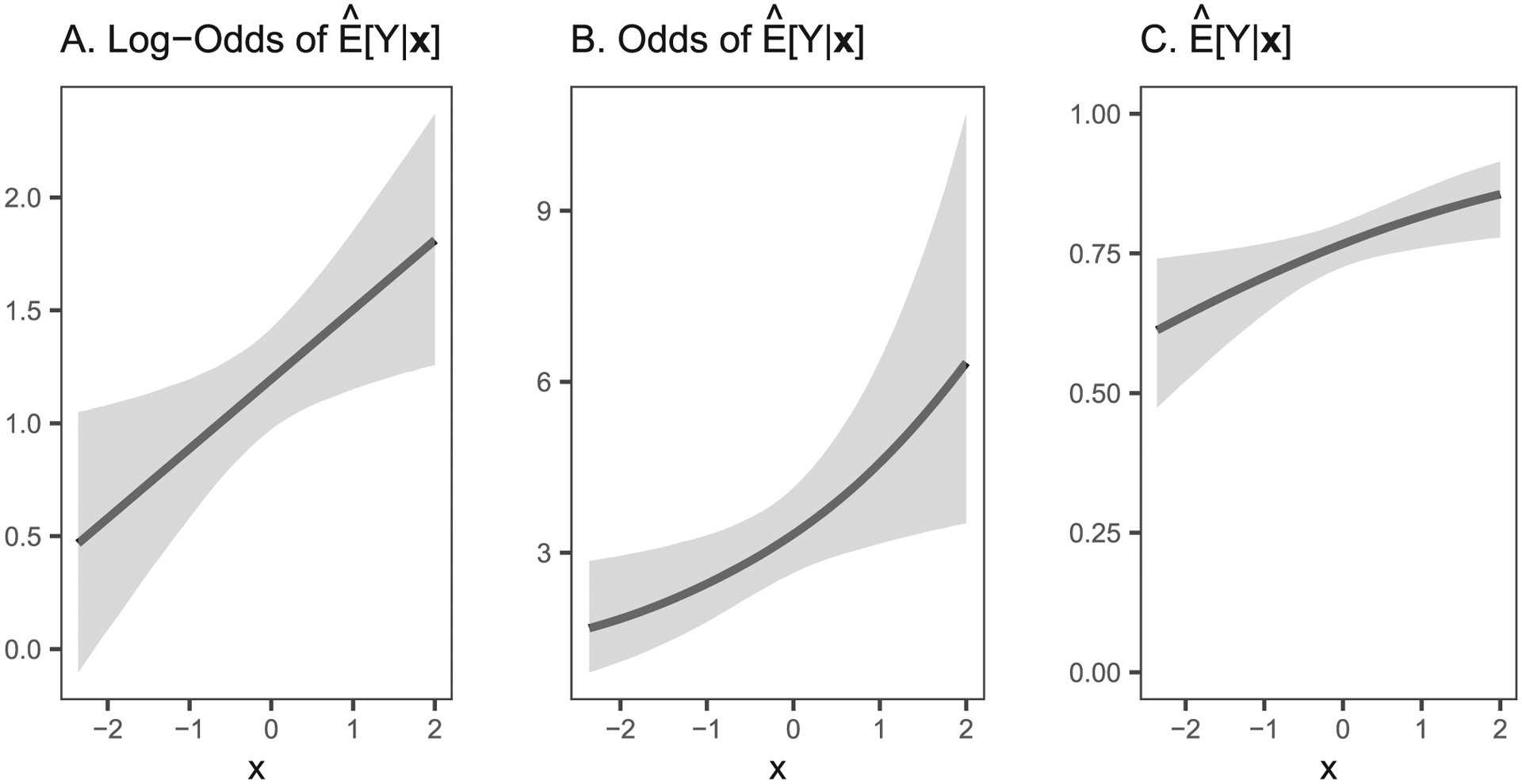
Logistic model regressing differing scales of a dependent variable on a predictor.

Note. Gray areas indicate 95% confidence regions.

A common practice in these models is to exponentiate both sides of the regression equation to rescale the model into odds, which may be somewhat easier to interpret (Figure 1b). This model can be represented as:

$$\frac{\mathbb{E}[Y\mid x]}{1-\mathbb{E}[Y\mid x]}=\text{exp}\left(d{(x)}^T\beta \right).$$ (4)

This model describes how regressors are associated with factor increases in the odds of a binary outcome occurring, which follow an exponential scale (Figure 1b). However, a second transformation can relate predictors directly to the natural scale of probability (Figure 1c):

$$\mathbb{E}[Y\mid x]=\frac{1}{1+\text{exp}\left(-d{(x)}^T\beta \right)}.$$ (5)

Note that although the functions relating the regressors to odds is also nonlinear (e.g., Figures 1b and 1c), we can use Equation 5 to describe how the predictors relate to the natural scale of probabilities. Relating predictors to this scale is often favored over other scales such as log-odds or odds due to their greater intuitive meaning and interpretability (e.g., Sackett et al., 1996).

Count models

Poisson and negative binomial models are commonly-used models of count data in psychological science.⁵ These models accommodate the assumption that Y is a discrete count (e.g., defined by non-negative integers) by relating predictors to the expected count on a log scale, as follows:

$$\text{log}(\mathbb{E}[Y\mid x])=d{(x)}^T\beta .$$ (6)

Here, we can state that the log-count is the transformed scale and is the linear combination of our regressors (e.g., Figure 2a). To obtain estimates on the natural (i.e. count) scale, the analyst may then convert this model by exponentiating both sides of the regression equation:

$$\mathbb{E}[Y\mid x]=\text{exp}\left(d{(x)}^T\beta \right).$$ (7)

This model states that predictors are associated with the count of Y on an exponential scale (e.g., Figure 2b).

Figure 2.

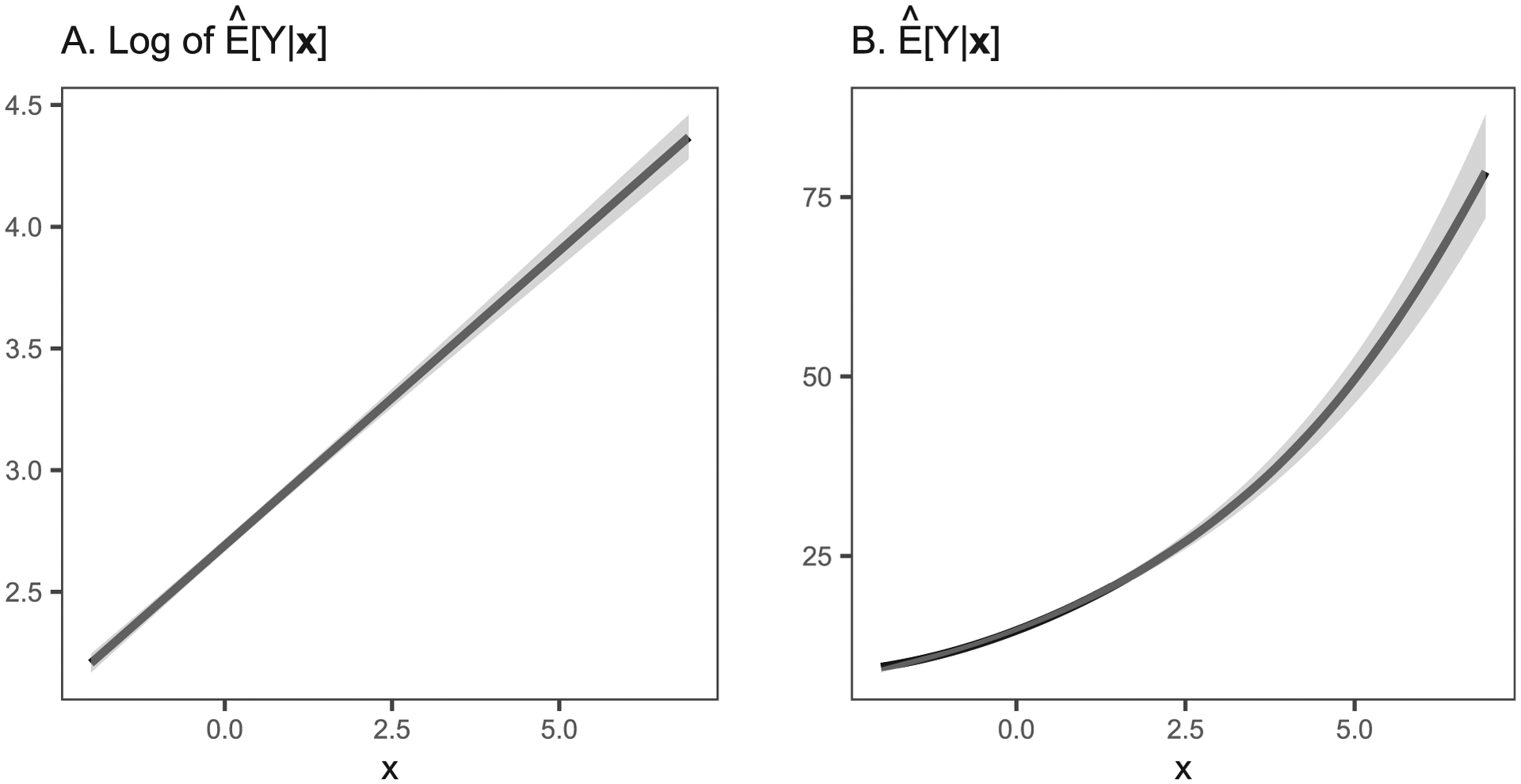
Poisson model regressing differing scales of a dependent variable on a predictor.

Note. Gray areas indicate 95% confidence regions.

Summary

Logistic and count models are common GLMs that can accommodate the analysis of discrete data. In its linear form (Equation 1), the scaling of the response is on a transformed metric that may be less valuable to the motivating research question relative to the natural response scale (e.g., Halvorson et al., in press). As we describe in the next section, however, such transformations introduce additional analytic complexities for estimating and interpreting interaction effects.

Interaction effects

Definition

We use a partial derivative approach (see also Kim & McCabe, 2020) and discrete differences (Long, 1997; Long & Freese, 2014) to define GLM effects on the natural scale described in the current paper. These formulations are very similar to those provided by Ai and Norton (2003) and others. We review them here in more detail to provide a context for discussing their implications later in the manuscript.

Partial derivatives and discrete differences describe how a function changes with respect to a given argument, holding all others constant. We may begin, for instance, by defining a marginal effect for a continuous variable using partial derivatives, which summarizes how $\mathbb{E}[Y\mid x]$ changes with respect to a variable of interest (e.g., x_j). Defining γ_j as the marginal effect of x_j on $\mathbb{E}[Y\mid x]$:

$${\gamma }_j=\frac{\partial \mathbb{E}[Y\mid x]}{\partial x_j}.$$ (8)

In the case of a linear regression model without nonlinear regressors, this is identical to deriving β_j from a regression model using calculus. For example, assume the following regression equation:

$$\mathbb{E}[Y\mid x]={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2.$$ (9)

Therefore, taking the derivative with respect to x₁:

$${\gamma }_1=\frac{\partial \mathbb{E}[Y\mid x]}{\partial x_1}={\beta }_1.$$ (10)

We note that in this simple case, the marginal effect is identical to β₁. This may mirror the intuition held by many readers familiar with linear regression models (Cohen et al., 2003): in this case, β₁ sufficiently quantifies how much $\mathbb{E}[Y\mid x]$ changes for every one unit increase in x₁, holding all else constant.

For categorical predictors, we can apply discrete differences to define a marginal effect as the difference between two points on a regression function (i.e. f(b) – f(a)). We note that discrete differences can also describe meaningful change in a continuous variable when choosing two relevant levels of the predictor (e.g., changing from the mean of a predictor to +1 standard deviation above the mean of this predictor; see Long & Freese, [2014]). For instance, assuming x_j is a categorical variable and $\underset{x_j:a,b}{\Delta }f(x)$ denotes the discrete difference of f(x) from a to b (i.e. $\underset{x:a,b}{\Delta }f(x)=f(b)-f(a)$):

$${\gamma }_j=\underset{x_j:a,b}{\Delta }\mathbb{E}[Y\mid x],$$ (11)

where a, b are categories of x_j.

For illustrative purposes using the linear model in Equation (9), we may assume x₂ is a dummy variable representing sex in which 0 = female (F) and 1 = male (M). We can then apply this definition to compute the marginal effect of sex as follows:

$$\begin{gathered} {\gamma }_2=\underset{x_2:\text{F},\text{M}}{\Delta }\mathbb{E}[Y\mid x]=\underset{x_2=\text{M}}{\underbrace{\left({\beta }_0+{\beta }_1{x}_1+{\beta }_2\right)}}-\underset{x_2=\text{F}}{\underbrace{\left({\beta }_0+{\beta }_1{x}_1\right)}} \\ ={\beta }_2. \end{gathered}$$ (12)

In other words, the marginal effect for sex using discrete differences is the expected value of Y for males minus the expected value for females. Similar to the preceding continuous variable example, this is conveniently quantified by the coefficient for sex β₂ by virtue of the fact that the model was linear (Cohen et al., 2003).

We extend the concept of marginal effects to provide a more general definition of interaction between variables: interaction effects represent change in a marginal effect of one predictor for a change in another predictor.⁶ We use this definition to encompass the concept of interaction (e.g., how the relation between a predictor and an outcome changes with respect to another predictor), and distinguish this definition from product term coefficients (see also Mize, 2019). We emphasize this distinction because, as we describe later in this paper, typical definitions of interactions are not appropriate for describing interaction effects in GLMs on the natural scale. Hence, following the notation for marginal effects used above, we define the interaction effect between two variables x_j and x_k using partial derivatives and discrete differences as follows:

$${\gamma }_{jk}^2≔\{\begin{array}{ll}\frac{{\partial }^2\mathbb{E}[Y\mid x]}{\partial x_j\partial x_k}\hfill & \text{if}{x}_j\text{and}{x}_k\text{are}\text{both}\text{continuous}\hfill \\ \underset{x_j:a,b}{\Delta }\frac{\partial \mathbb{E}[Y\mid x]}{\partial x_k}\hfill & \text{if}{x}_j\text{is}\text{discrete}\text{and}{x}_k\text{is}\text{continuous}\hfill \\ \underset{x_j:a,b}{\Delta }\underset{x_k:c,d}{\Delta }\mathbb{E}[Y\mid x]\hfill & \text{if}{x}_j\text{and}{x}_k\text{are}\text{both}\text{discrete},\hfill \end{array}$$ (13)

where a, b and c, d are categories for x_j and x_k, respectively, and $\underset{x_j:a,b}{\Delta }f(x)$ denotes the discrete difference of f(x) from a to b as introduced in Equation (11).

We use ${\gamma }_{jk}^2$ to generically denote the interaction effect between variables x_j and x_k, and use the three definitions provided in Equation (13) to define the interaction based on whether one or both variables are continuous or discrete. In the case where both variables are continuous (e.g., first line of Equation (13)), ${\gamma }_{jk}^2$ describes the rate-of-change in the marginal effect of one predictor for a change in another (i.e. the second-order cross-partial derivative; Ai & Norton, 2003). When one variable is continuous and the other is discrete (e.g., second line of Equation 13), we define ${\gamma }_{jk}^2$ as the difference in the marginal effect of the continuous predictor between two selected values of the discrete predictor (i.e. the discrete difference in the partial derivative; Ai & Norton, 2003). Finally, when both predictors are discrete (e.g., third line of Equation (13)), we define ${\gamma }_{jk}^2$ as the difference between the model evaluated at two categories of one variable (a, b) minus the difference in this model evaluated at two categories of another variable (c, d; i.e. the discrete double difference; Norton et al., 2004).

Linear models

We use the definitions provided above to show that, in linear models, the interaction effect between two variables is equal to the product term coefficient between these variables. Assume a model involving two continuous variables and a product term between them:

$$\mathbb{E}[Y\mid x]={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_{12}{x}_1{x}_2.$$ (14)

Applying the definition of the interaction effect to this linear case:

$${\gamma }_{12}^2=\frac{{\partial }^2\mathbb{E}[Y\mid x]}{\partial x_1\partial x_2}={\beta }_{12}.$$ (15)

In other words, Equation (15) takes the second-order cross-partial derivative of $\mathbb{E}[Y\mid x]$ with respect to both x₁ and x₂ to obtain the interaction effect β₁₂. Note that because ${\gamma }_{12}^2$ reduces to β₁₂ in this case, β₁₂ can be directly interpreted as the extent to which the effect of x₁ on $\mathbb{E}[Y\mid x]$ changes for every one-unit increase in x₂ (and vice versa), holding all else constant (Cohen et al., 2003). Fundamentally, we believe that this convenient fact has led to the misconception that product term coefficients are synonymous with interaction effects, and have thus been treated as a measure of the interaction effect in GLMs for nonlinear probabilities and counts. We demonstrate next how this is not the case.

GLMs

As we described in the Background section above, producing a model relating predictors to the scale of probabilities or counts requires that the link function be inverted to produce interaction effects in the natural response scale. Although the interaction is quantified appropriately by the product term coefficient when interpreting effects on the scale of log-odds or log-counts, the interaction effect will not reduce to the coefficient of the product term when describing effects on the natural response scale because of this transformation (Ai & Norton, 2003; Karaca-Mandic et al., 2012; Norton et al., 2004). For instance, taking the example of a GLM involving continuous predictors (as in Equation (14)), this model represented on the natural response scale would be defined as follows:

$$\mathbb{E}[Y\mid x]=g^{-1}\left({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_{12}{x}_1{x}_2\right).$$ (16)

We then aim to compute an interaction between x₁ and x₂ $\left({\gamma }_{12}^2\right)$ using Equation (13). In contrast to the linear model, the presence of the inverse link function g⁻¹(·) means that the chain rule⁷ must be applied when deriving ${\gamma }_{jk}^2$. This is because we are now taking the derivative of a composition of two functions: g⁻¹(·) and β₀ + β₁x₁ + β₂x₂ + β₁₂x₁x₂. As a result, applying Equation (13) to this case results in the following:

$$\begin{gathered} {\gamma }_{12}^2=\frac{{\partial }^2\mathbb{E}[Y\mid x]}{\partial x_1\partial x_2} \\ ={\beta }_{12}{\dot{g}}^{-1}\left(d{(x)}^T\beta \right)+\left({\beta }_1+{\beta }_{12}{x}_2\right)\left({\beta }_2+{\beta }_{12}{x}_1\right){\ddot{g}}^{-1}\left(d{(x)}^T\beta \right). \end{gathered}$$ (17)

Note that ${\dot{g}}^{-1}$ and ${\ddot{g}}^{-1}$ are the first and second derivatives of the inverse link function, respectively.

We may further apply Equation (13) to define an interaction effect when one or both interacting predictor(s) are binary. In the case where x₁ is binary and x₂ is continuous, this amounts to taking the derivative of $\mathbb{E}[Y\mid x]$ with respect to x₂ at the two observed values of x₁, and defining the interaction effect as the difference between the derivatives at each of these x₁ categories. For instance, noting that x₁ was binary, the interaction effect is the partial derivative of $\mathbb{E}[Y\mid x]$ with respect to x₂ when x₁ is 1 minus the function when x₁ is zero:

$$\begin{gathered} {\gamma }_{12}^2=\underset{x_1:0,1}{\Delta }\frac{\partial \mathbb{E}[Y\mid x]}{\partial x_2} \\ =\underset{\frac{\partial \mathbb{E}[Y\mid \mathit{x}]}{\partial x_2}\text{when}{x}_1=1}{\underbrace{\left({\beta }_2+{\beta }_{12}\right){\dot{g}}^{-1}\left(\left({\beta }_2+{\beta }_{12}\right)x_2+{\beta }_0+{\beta }_1\right)}}-\underset{\frac{\partial \mathbb{E}[Y\mid \mathit{x}]}{\partial x_2}\text{when}{x}_1=0}{\underbrace{{\beta }_2{\dot{g}}^{-1}\left({\beta }_0+{\beta }_2{x}_2\right)}}. \end{gathered}$$ (18)

When x₁ and x₂ are both binary, the interaction effect is the double discrete difference (Norton et al., 2004; Shang et al., 2018). In practical terms, this involves computing $\mathbb{E}[Y\mid x]$ for each combination of categories and taking the difference across all of these combinations. Noting again that x₁ and x₂ are binary, this can be done in the following manner:

$${\gamma }_{12}^2=\underset{x_1:0,1}{\Delta }\underset{x_2:0,1}{\Delta }\mathbb{E}[Y\mid x]=\underset{\Delta x_2\text{when}{x}_1=1}{\underbrace{\left[\underset{x_1=1,x_2=1}{\underbrace{g^{-1}\left({\beta }_0+{\beta }_1+{\beta }_2+{\beta }_{12}\right)}}-\underset{x_1=1,x_2=0}{\underbrace{g^{-1}\left({\beta }_0+{\beta }_1\right)}}\right]}}-\underset{\Delta x_2\text{when}{x}_1=0}{\underbrace{\left[\underset{x_1=0,x_2=1}{\underbrace{g^{-1}\left({\beta }_0+{\beta }_2\right)}}-\underset{x_1=0,x_2=0}{\underbrace{g^{-1}\left({\beta }_0\right)}}\right]}}.$$ (19)

In Equation (19) above, the terms in the left square brackets denote the difference in $\mathbb{E}[Y\mid x]$ between x₂ categories, holding x₁ at the category represented by 1. The terms in the right square brackets represent this same difference when x₁ is held at the category denoted by 0. Taking the difference between these two quantities defines the interaction effect.

We see in Equations (17) through (19) above that the interaction effect ${\gamma }_{12}^2$ is no longer equivalent to the product term coefficient (β₁₂). Rather, this coefficient is strictly a single term that contributes to this quantity, and the interaction effect may instead be a function of this term and all other terms involved in the model.

For estimation, we assume $\widehat{\beta }$ is obtained via maximum likelihood (ML) and propose our estimate of $\widehat{\mathbb{E}}[Y\mid x]$ and ${\widehat{\gamma }}_{jk}^2$ to be a simple plug-in estimator using $\widehat{\beta }$. Given that ML estimates are asymptotically normal and that ${\widehat{\gamma }}_{jk}^2$ is a function of $\widehat{\beta }$, standard errors for ${\widehat{\gamma }}_{jk}^2$ can be obtained using the delta method (Ferguson, 2017). Alternatively, standard errors can be obtained using sampling methods such as bootstrapping (Efron & Tibshirani, 1994; Robert & Casella, 2013) or via draws from a posterior distribution estimated with Markov Chain Monte Carlo (e.g., Alfaro et al., 2003; Efron, 2011) in the case of Bayesian models. The delta method uses Taylor expansion to determine the asymptotic variance of a function of asymptotically normal random variables. Bootstrapping approaches can involve re-sampling data directly (e.g., non-parametric bootstrap; Efron & Tibshirani, 1994) or sampling parameter estimates from a parametric distribution (e.g., parametric bootstrap; King et al., 2000) to generate draws of $\widehat{\beta }$ in order to approximate sampling variation in ${\widehat{\gamma }}_{jk}^2$.

Summary

To date, the vast majority of psychological researchers have extended established interaction practices from linear regression to GLMs irrespective of the scale in which they characterize results – that is, by using the product term coefficient provided by the estimated model to test interactions. We believe that this confusion has arisen because the product term has been treated as a synonym for the interaction effect, given the product term coefficient appropriately quantifies the interaction effect in models with linear specification. For instance, we highlight that product term coefficients quantify interaction effects when GLMs are described on their transformed scales (e.g., log-odds and log-counts). Nonetheless, we have shown that this is not the case when describing interaction effects on natural scales (e.g., probabilities and counts).

Misconceptions for interactions in GLMs

The presence of additional terms in computing ${\gamma }_{jk}^2$ for nonlinear probability and count GLMs fundamentally alters how interaction effects should be represented and interpreted on these scales. Below, we detail common misconceptions and practical guidelines for better representing interactions for these scales.

Misconception 1: The point estimate and standard error of interaction in the natural scale can be interpreted in an identical fashion as linear models, regardless of the levels of other predictors.

Probabilities and counts are nonlinear functions of the regressors in GLMs. Therefore, interactions may vary as a function of some of the other regressors involved in the specified model, such that quantifying and testing the estimate of interaction for GLMs in the scale of probabilities and counts do not follow from linear models.⁸ To evaluate the interaction function, specific values of predictors must instead be selected to derive point estimates. As a result, depending on the specific levels of the predictor variables, these estimates may vary in magnitude and sign across observations. This also implies that the standard errors of point estimate values (as well as their corresponding statistical significance) may also vary as a function of the predictors. Obtaining meaningful and straightforward point estimates of the interaction effect will thus require approaches that can accommodate this conditional nature of interaction in these models.

To illustrate, assume the following model holds in the population:

$$\text{log}(\mathbb{E}[Y\mid x])={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_3{x}_3+{\beta }_{13}{x}_1{x}_3,$$ (20)

such that $Y\mid x~\text{Poisson}(\mathbb{E}[Y\mid x])$, predictors x₁ and x₂ were drawn from a standard bivariate normal distribution with moderate correlation $\left(r_{x_1{x}_2}=.5\right)$, and x₃ was a dichotomous predictor with proportions equal to .5 for each category. Parameters were β₀ = −3.8, β₁ = 0.38, β₂ = 0.90, β₃ = 1.10, and β₁₃ = 0.20. For the purposes of illustration, assume further that x₃ is dummy coded and reflects biological sex at birth such that 1 = female. Drawing n = 1,000 samples from this population yielded estimates ${\widehat{\beta }}_0=-3.19$, ${\widehat{\beta }}_1=0.40$, ${\widehat{\beta }}_2=1.10$, ${\widehat{\beta }}_3=1.08$, and ${\widehat{\beta }}_{13}=0.01$.

In this example, we seek to examine the interaction between x₁ and biological sex. Treating biological sex as a binary predictor, we may therefore represent this interaction function as the discrete difference in the marginal effect of x₁ with respect to biological sex (see the second part of Equation (13), or Equation (18)). In other words, we define the interaction as the difference between the marginal effect of x₁ for females versus males:

$${\widehat{\gamma }}_{13}^2=\underset{x_3=\text{female}}{\underbrace{\left({\widehat{\beta }}_1+{\widehat{\beta }}_{13}\right)\ast \text{exp}\left(\left({\widehat{\beta }}_1+{\widehat{\beta }}_{13}\right)x_1+{\widehat{\beta }}_0+{\widehat{\beta }}_2{x}_2+{\widehat{\beta }}_3\right)}}-\underset{x_3=\text{male}}{\underbrace{{\widehat{\beta }}_1\ast \text{exp}\left({\widehat{\beta }}_0+{\widehat{\beta }}_1{x}_1+{\widehat{\beta }}_2{x}_2\right)}}.$$ (21)

We highlight that the conditional nature of this interaction function is illustrated by the presence of x₁ and x₂ in Equation (21): specific values for x₁ and x₂ must be chosen to evaluate this function in order to compute ${\widehat{\gamma }}_{13}^2$. One may do so using several approaches, noting that each are extensions of methods developed previously to summarize marginal effects (King et al., 2000; Long & Freese, 2014; Williams, 2012).

First, the analyst can evaluate the function at different values of covariates to determine the interaction at one or more hypothetical scenarios of interest (i.e. the interaction at representative values; Williams, 2012; King et al., 2000). This is done by selecting hypothetical values for each covariate and computing the interaction effect for each scenario. For instance, we can first define the interaction function for scenarios where x₂ assumes several values of interest, such as the 25th (x₂ = −0.69), 50^th (i.e. median; x₂ = 0.00), and 75^th (x₂ = 0.67) percentiles. Plugging in the obtained model estimates and x₂ values selected, we can define the interaction at these percentiles as:

$${\widehat{\gamma }}_{13}^2=\{\begin{array}{ll}0.41\ast \text{exp}\left(0.41x_1-2.87\right)-0.40\ast \text{exp}\left(0.40x_1-3.95\right)\hfill & \text{ if }{x}_2=-0.69\hfill \\ 0.41\ast \text{exp}\left(0.41x_1-2.11\right)-0.40\ast \text{exp}\left(0.40x_1-3.19\right)\hfill & \text{ if }{x}_2=0.00\hfill \\ 0.41\ast \text{exp}\left(0.41x_1-1.37\right)-0.40\ast \text{exp}\left(0.40x_1-2.45\right)\hfill & \text{ if }{x}_2=\mathrm{0.67.}\hfill \end{array}$$ (22)

We depict these effects in Figure 3. This plot illustrates that the effect of x₁ on the expected count of Y is stronger among females than males across all percentiles of x₂, though this effect is more pronounced as x₂ increases from the 25^th to the 75^th percentile. Assuming that the mean of x₁ (−0.06) is a value of substantive interest, we can also evaluate Equation (22) by entering sample mean values of x₁ into this equation, resulting in point estimates of 0.01, 0.03, and 0.06 at the 25th, 50th, and 75th percentiles of x₂, respectively. Applying the delta method to compute standard errors of these quantities, findings suggested that the interaction was significant and positive across all three x₂ percentiles.⁹ We note from these three values that, consistent with the effects depicted in Figure 3, the point estimate of the interaction effect varied as a function of the covariate x₂. Note that it may be most useful to represent the interaction across multiple values of interest of x₂ (as above) to gain a better substantive understanding of the interaction.

Figure 3.

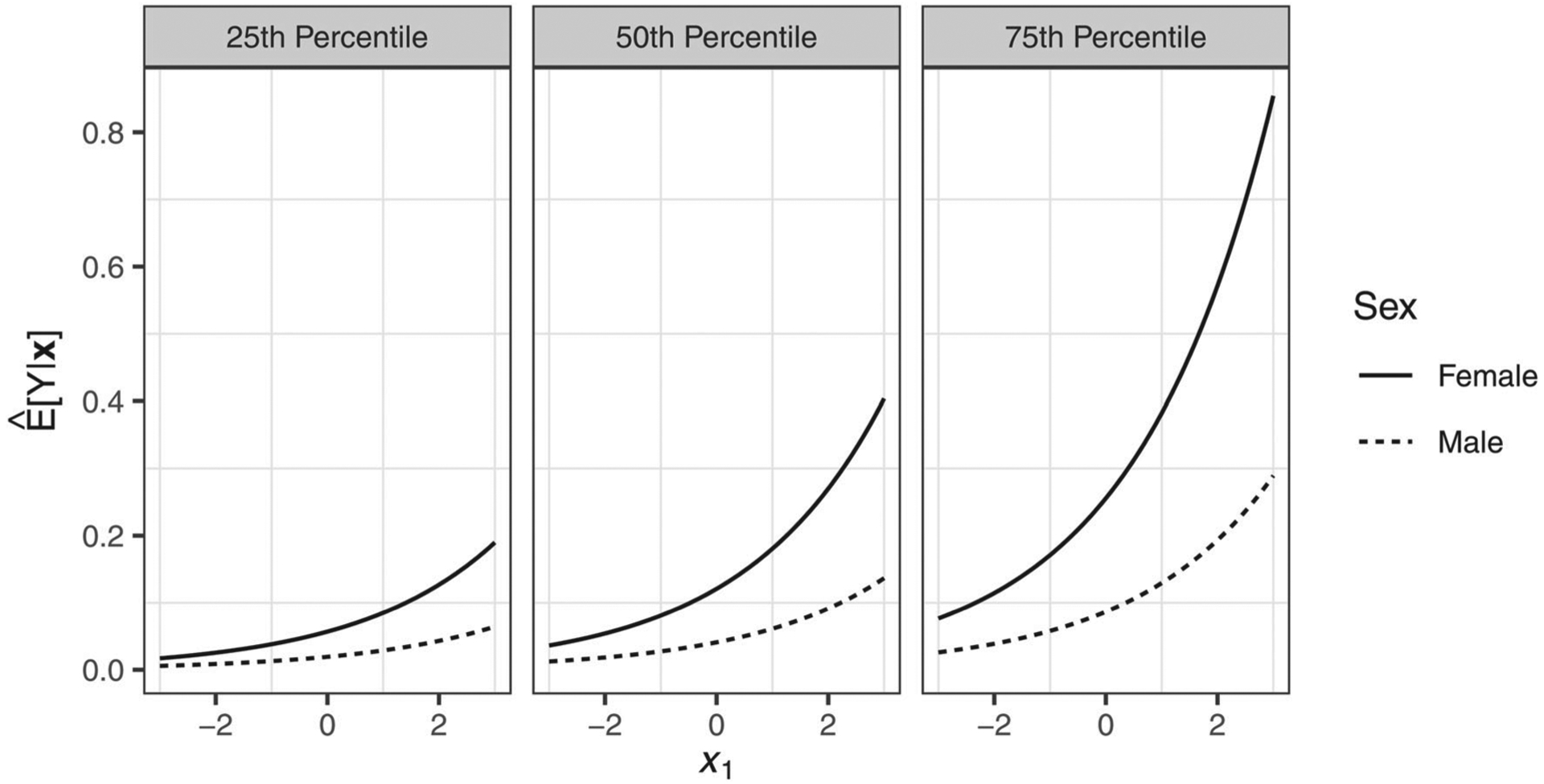
The relation between $\widehat{\mathbb{E}}[Y\mid x]$ and x₁ across low, median, and high levels of x₂ by biological sex.

As a starting place, it is common practice to use hypothetical average values of all covariates (i.e. interaction effects at the means; Williams, 2012), so long as these values are meaningful in the data. In the above example, we may (for instance) report the coefficient estimate at the mean of all covariates (${\widehat{\gamma }}_{13}^2=0.03$, 95% CI = [0.01, 0.05]) in the results section of a manuscript as a single estimate for a hypothetical average observation. For continuous variables that are unimodal, such an approach using either the mean or median value may be appropriate. However, we caution that in the case of discrete or multi-modal variables, these values may represent few if any real observations in the data (Mize, 2019; Williams, 2012). For instance, evaluating an interaction at the mean of a bi-modal variable may reflect an effect for an individual representing a scenario where few observations exist in the data. One may choose to represent the interaction function separately at various modes in these instances, or utilize an approach based on the observed data described below.

The analyst may also compute the interaction effect for each individual observation in a similar fashion (Figure 4) that more directly incorporates the observed data. Given that observations are likely to reflect a unique permutation of predictor variable values (e.g., each observation may reflect mostly unique combinations of values for x₁, x₂, and biological sex), this approach can be used to describe similar variation in the interaction effect. For instance, significant ${\widehat{\gamma }}_{13}^2$ values for each observation indicate that the interaction between x₁ and biological sex was significant for 85.8% of the observations in the sample. These effects also varied substantially in the sample for those reporting higher versus lower values of x₂ (e.g., comparing observed values above and below the median of x₂ in Figure 4). Specifically, point estimates ranged from 0.001 to 0.042 among observations below the median of x₂ values and from 0.015 to 0.589 above the median of x₂. These point estimates were also generally larger among observations above the median, as depicted on the righthand side in Figure 4. Similarly, point estimates varied with regard to whether or not they were statistically significant: though interaction effects for certain observations were particularly large compared to others, several of these effects remained non-significant in the sample due to their large standard errors (e.g., several large effects above the median of x₂ values were non-significant in Figure 4). The analyst can produce a single estimate summarizing these effects by taking the mean of the interaction coefficients across observations (i.e. the average interaction effect; Williams, 2012) and can conduct inference on this value by computing its standard error. In the example above, for instance, the mean ${\widehat{\gamma }}_{13}^2$ value across the observed data is 0.07. Utilizing the delta method, we can further derive the standard error for this value (0.03) and compute its 95% confidence interval ([0.01, 0.13]). Thus, we may conclude that the average interaction effect was significant and positive across the sample.

Figure 4.

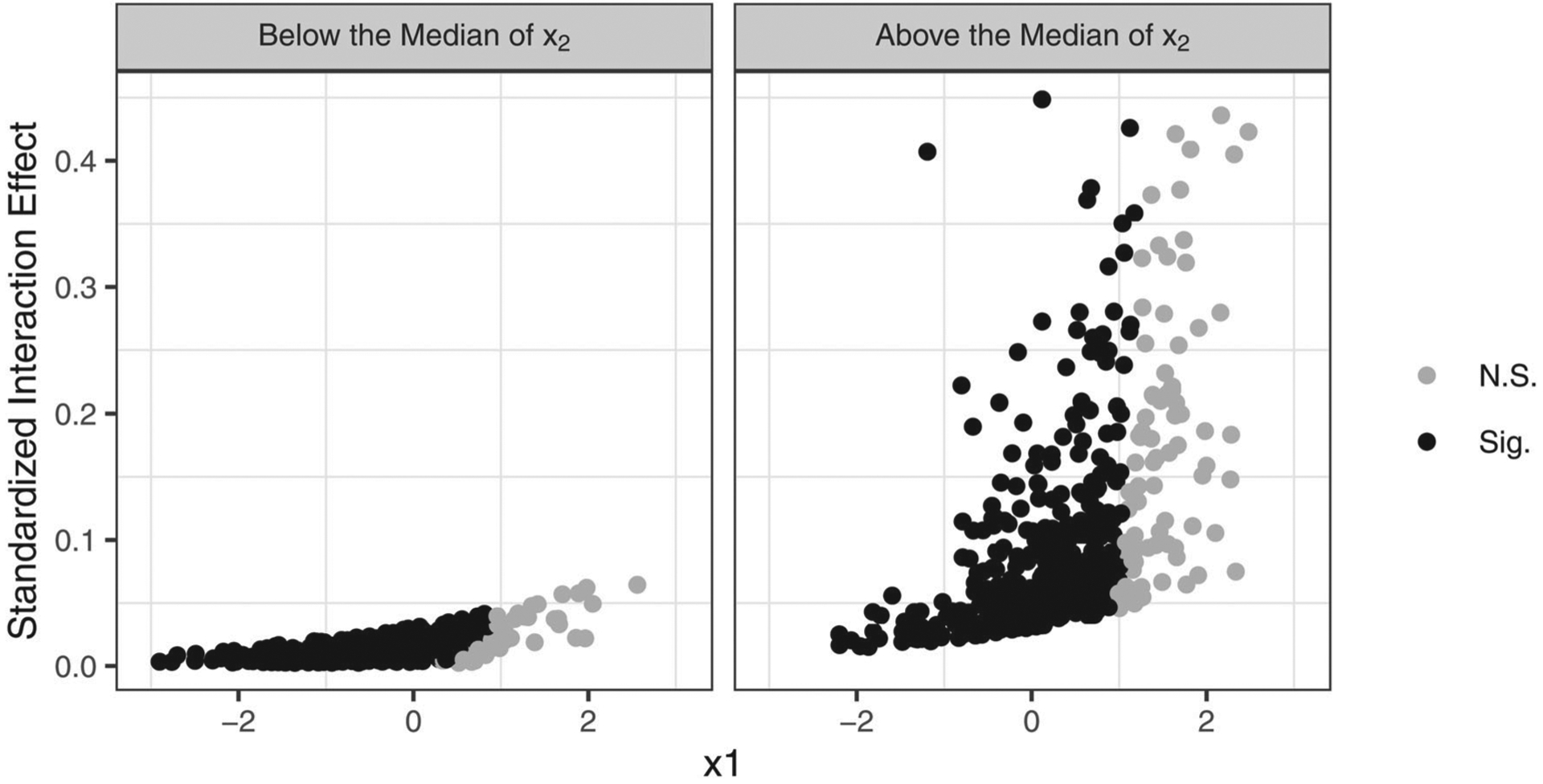
Interaction between x₁ and biological sex as a function of x₁ plotted at low (below median) and high (above median) values of x₂.

Note. Black points indicate significant effects and gray points indicate non-significant effects at α = 0.05. This figure illustrates that the interaction effect between x₁ and biological sex varied across observations, such that the effect was larger for observations with high values of the covariate x₂. This highlights that the interaction effect (as well as its statistical significance) may be conditioned on predictors involved in the model. N.S. = Not Significant, Sig. = Significant.

In sum, the interaction effect in GLMs may not reduce to a single value. Instead, this effect may be a function of predictors included in a model, and its value may vary depending on the specific levels of predictor values. Evaluating the function at hypothetical predictor levels of interest, computing the interaction for each case in the observed data, and/or summarizing the average interaction effect across observations can all provide helpful approaches to accurately summarize these effects. These approaches can generate greater evidence of the robustness of an interaction effect, as well as aid in detecting the conditions under which the effect is absent or varying in magnitude within a single sample.

Practical considerations

We note the distinction between the average interaction effect (${\widehat{\gamma }}_{13}^2=0.07$, 95% CI = [0.01, 0.13]) versus the interaction effect at the sample means of the substantive predictors (${\widehat{\gamma }}_{13}^2=0.03$, 95% CI = [0.01, 0.05]) described earlier in this section. Though the prevailing approach is using hypothetical means, whether one should use one or the other approach will depend on the goals of the analyst. On the one hand, the average interaction effect describes the interaction for the whole sample and may be most helpful in generating inferences about the population of interest (Hanmer & Kalkan, 2013). On the other, representing the interaction using hypothetical values can be useful in generating estimates of the interaction for hypothetical scenarios of interest (e.g., computing the interaction effect for particular groups of interest or for a prototypical predictor using sample means). Whichever approach is applied, we nonetheless advocate that researchers evaluate and report the range in the interaction effect within the observed sample as a standard approach. This is essential in describing variability in the interaction effect and evaluating whether the interaction is non-significant (or even of differing signs) among observations in the same data.

Misconception 2: The coefficient of the product term between two predictors of interest is sufficient and necessary to fully describe the interaction between the two variables on natural response scales.

There are two prevalent misconceptions in psychology regarding the nature of product term coefficients in GLMs of natural response scales. First, whereas using the product term coefficient alone is often treated as a comprehensive measure of an interaction effect between two variables on natural scales, this coefficient by itself is insufficient to quantify the interaction effect on these scales. This is exemplified in Equations (17) through (19) above: although the interaction effect in these equations includes the product term coefficient (β₁₂), the interaction effect may also involve other coefficients in the model (e.g., in Equation (18), note the additional presence of β₀, β₁ and β₂ within the first derivative functions). Second, whereas it is common practice to specify a product term for interaction effects on the natural scale, these effects can exist even when the product term is omitted (or the product term coefficient is zero). For instance, note in the continuous variable case in Equation (17), if β₁₂ is zero, the interaction effect reduces to ${\beta }_1{\beta }_2{\ddot{g}}^{-1}\left(d{(x)}^T\beta \right)$, which may yet be non-zero.

We first illustrate that product term coefficients are insufficient to fully describe an interaction effect in a simulated example in Figure 5. Assume the following model held in the population,

$$\text{log}\left(\frac{\mathbb{E}[Y\mid x]}{1-\mathbb{E}[Y\mid x]}\right)={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_{12}{x}_1{x}_2=\eta .$$ (23)

Figure 5.

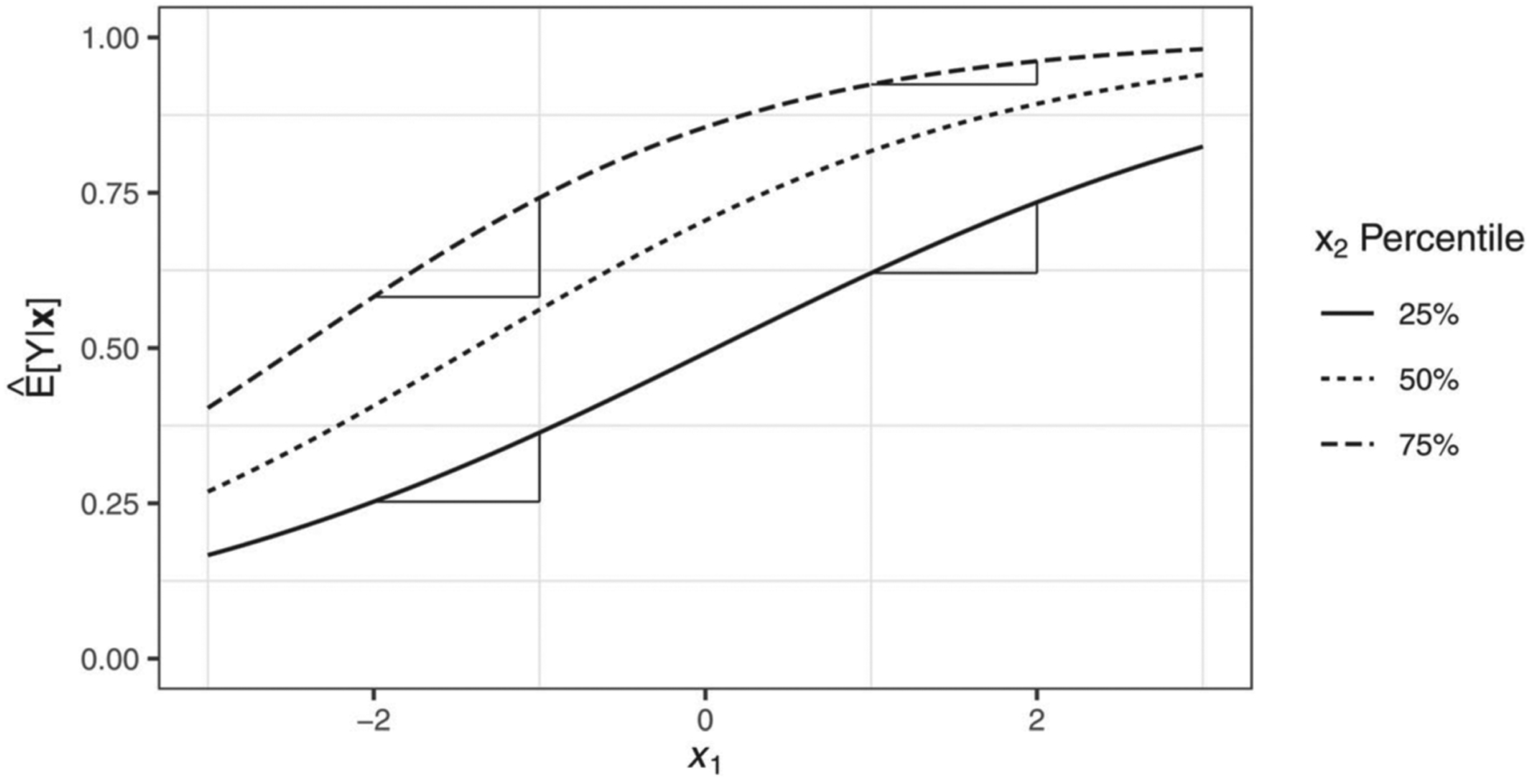
The relation between $\widehat{\mathbb{E}}[Y\mid x]$ and x₁ across low, median, and high levels of x₂ in a logistic model.

Note. This figure represents multiple interaction effects of opposite sign present within the data. We illustrate this is using one-unit rates of change. For instance, in describing one-unit rates of change, $\widehat{\mathbb{E}}[Y\mid x]$ increases by 0.037 as x₁ increases from 1 to 2 when x₂ is at the 75^th percentile, but this increase is over 3 times larger (0.114) when examined at the 25^th percentile of x₂. In contrast, at the lower end of the x₁ range, $\widehat{\mathbb{E}}[Y\mid x]$ increases by 0.160 units as x₁ increases from −2 to −1 at the 75^th percentile of x₂, but the increase is smaller (0.111) at the 25^th percentile of x₂. This illustrates that interactions can have differing signs in the same model resulting from the nonlinear nature of the model.

We defined this model as η for brevity of notation. Further, $Y\mid x~\text{Bernoulli}(\mathbb{E}[Y\mid x])$, and predictors were drawn from a standard bivariate normal distribution and had moderate correlation $\left(r_{x_1{x}_2}=.5\right)$. Parameters were β₀ = 1.00, β₁ = 0.70, β₂ = 1.50, and β₁₂ = 0.10. Generating n = 10,000 samples from the population model described above yielded estimates ${\widehat{\beta }}_0=0.85$, ${\widehat{\beta }}_1=0.62$, ${\widehat{\beta }}_2=1.32$, and ${\widehat{\beta }}_{12}=0.14$. Applying the continuous variable definition of interaction in Equation (17) resulted in the following:

$${\widehat{\gamma }}_{12}^2={\beta }_{12}\frac{e^{\eta }}{{\left(1+e^{\eta }\right)}^2}+\left({\beta }_1+{\beta }_{12}{x}_2\right)\left({\beta }_2+{\beta }_{12}{x}_1\right)\frac{e^{\eta }\left(1-e^{\eta }\right)}{{\left(1+e^{\eta }\right)}^3}.$$ (24)

Evaluating this function showed that despite a significant and positive product term coefficient (95% CI = [0.068, 0.219]), the interaction effect was significant in opposing directions in the sample depending on levels of x₁ and x₂: the effect was significant and negative for 56.0% of the sample (ranging from −0.066 to −0.001) and significant and positive for 33.8% (ranging from 0.004 to 0.079), illustrated using one-unit rates of change in Figure 5. Moreover, despite a positive product term coefficient, the interaction effect was significant and negative (${\widehat{\gamma }}_{12}^2=-0.041$, 95% CI = [−0.06, −0.02]) when represented at the hypothetical mean of all predictors. Note that the product term coefficient failed to represent the multiple signs of the interaction effect present. Further, if the natural and transformed scales were conflated in this example, the product term coefficient also implied a positive interaction effect when the interaction was negative at the hypothetical mean of predictors, suggesting that the product term coefficient alone was an insufficient representation of the interaction effect on the natural scale.

Moreover, a product term specified in a model is not a necessary condition for interaction to exist on the natural scale. For instance, assume the following model holds in the population,

$$\text{log}(\mathbb{E}[Y\mid x])={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2,$$ (25)

such that $Y\mid x~\text{Poisson}(\mathbb{E}[Y\mid x])$ and predictors were drawn from a bivariate standard normal distribution with moderate correlation $\left(r_{x_1{x}_2}=.5\right)$, β₀ = 1.00, β₁ = 0.70, and β₂ = 1.50. Parameters were β₀ = −3.80, β₁ = 0.35, and β₂ = 0.90. Generating n = 10,000 samples from this population model yielded estimates ${\widehat{\beta }}_0=-3.34$, ${\widehat{\beta }}_1=0.28$, and ${\widehat{\beta }}_2=1.02$.

Using these estimates, applying the continuous variable definition of interaction in Equation (17) with respect to x₁ and x₂ resulted in:

$${\widehat{\gamma }}_{12}^2={\beta }_1{\beta }_2\ast \text{exp}\left({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2\right).$$ (26)

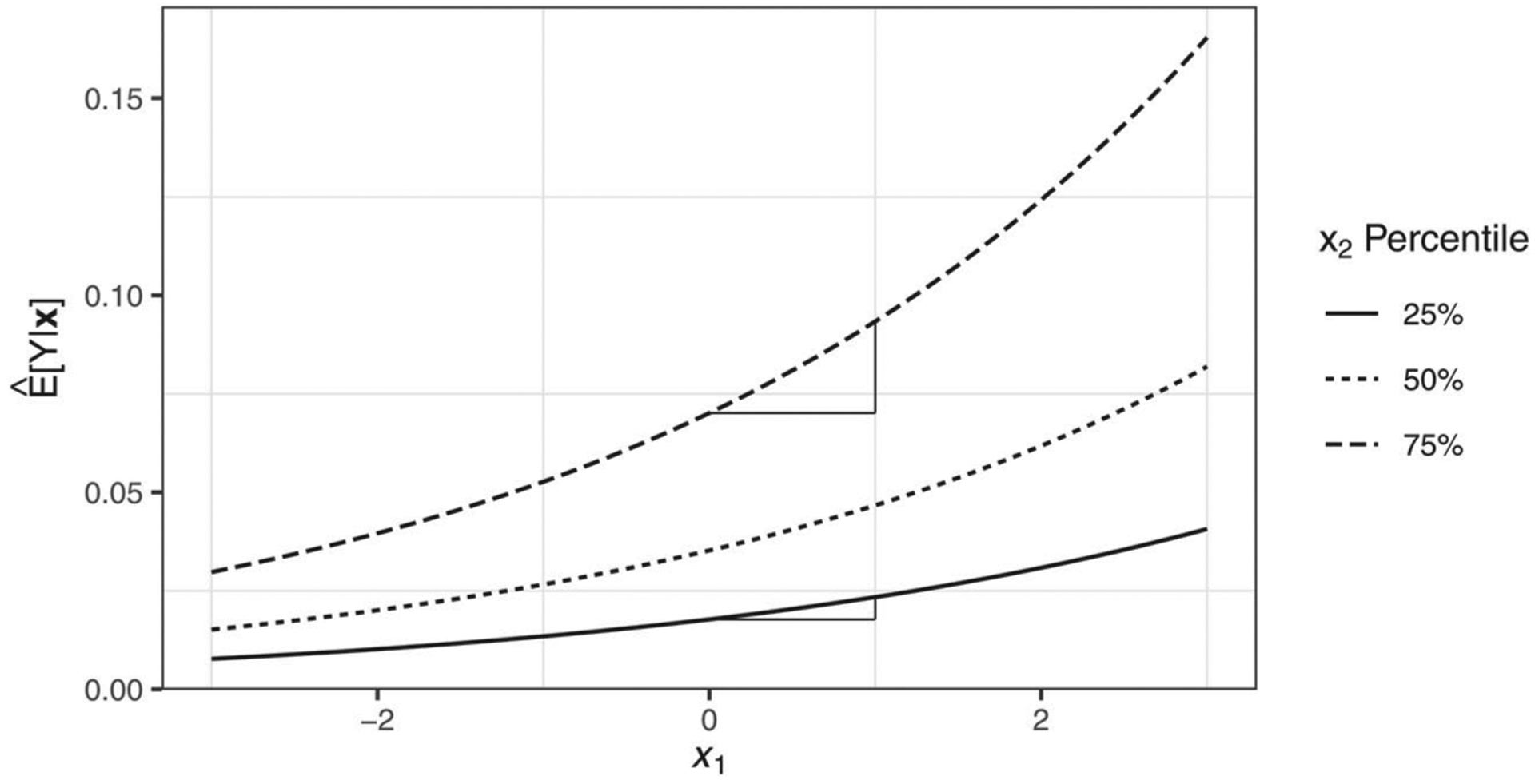
Evaluating this effect across observations showed that the interaction was significant and positive for all observations (ranging from 0.001 to 0.708) with an average interaction effect of 0.021 (95% CI = [0.01, 0.03]), illustrating that interaction was introduced automatically due to the exponential nature of the model despite no specification of a product term. We can observe this in Figure 6 by noting that, beginning at the lowest value of x₁, the expected count of Y is higher at the 75th percentile compared to the 25th percentile. In other words, due to the interaction effect, the single-unit change as x₁ increases also compounds more quickly at the 75th (versus the 25th) percentile of x₂.

Figure 6.

The relation between $\widehat{\mathbb{E}}[Y\mid x]$ and x₁ across low, median, and high levels of x₂ in a Poisson model.

Note. This figure represents the interaction effect in a Poisson model despite omission of a product term. For instance, the effect of a one-unit increase in x₁ from 0 to 1 on $\widehat{\mathbb{E}}[Y\mid x]$ was greater at higher levels of x₂ (0.023 at the 75^th percentile of x₂) compared to lower levels (0.006 at the 25^th percentile of x₂).

Note that this and the preceding example highlight two crucial implications for how testing interactions on natural scales is distinguished from traditional linear approaches, which involves the direct interpretation of the product term coefficient. First, in the logistic example, the marginal effect of x₁ on the natural scale was stronger or weaker depending on the level of x₂ despite a singular positive estimate provided by the product term coefficient. Second, in the Poisson example, interaction was present between variables on the natural count scale despite no specification of a product term. Taken together, these illustrate that product terms are neither sufficient nor necessary in testing interaction on natural response scales. Rather, relying on product term coefficients may result in a failure to estimate the correct magnitude and sign of interaction on these natural scales (i.e. a Type M or S error; Gelman & Carlin, 2014).

Practical considerations

There is some debate on role of product terms in GLMs on the natural response scale. In the logit case, for instance, some have considered it unnecessary to include a product term if theory dictates that interaction between two variables is solely produced by model-inherent nonlinearity (Berry et al., 2010). Others have characterized the issue as one of model fitting, such that the product term should be retained if this term is significant via asymptotic z-test on the product term coefficient (see also Karaca-Mandic et al., 2012). However, more recent work has stated that failing to include a product term can produce bias toward discovering interaction when none truly exists under certain model misspecifications (i.e. a Type I Error), and recommended that researchers include the product term irrespective of theory so that one’s theoretical argument is more vulnerable to the observed data (Rainey, 2016).

There are several considerations one must make in evaluating the inclusion of a product term. First, the product term can serve a central role in the specification of an interaction effect, such that if a researcher has strong substantive theory and subject matter knowledge, this term can capture interaction between variables on the multiplicative scale (Tsai & Gill, 2013). If the researcher has weak subject matter knowledge regarding the interaction effect on the multiplicative scale, then the inclusion of the product term may be evaluated by model fit (e.g., Karaca-Mandic et al., 2012). Under some conditions, specifying a product term can lead to a higher probability of detecting interaction effects that exist in the population in spite of certain kinds of model misspecification (Rainey, 2016). However, several aspects of model performance must also be considered when product terms are included. First, including a product term may decrease the precision of the interaction effect if this coefficient is truly zero in the population, as may be the case with including any irrelevant regressor in the model (Fomby, 1981). This may be of little practical consequence in situations where a model is sufficiently powered and overfitting is adequately managed. That said, because psychological science has long been criticized for its use of small, underpowered samples (Sedlmeier & Gigerenzer, 1992; K. M. King et al., 2019), we generally advise that the inclusion of product terms be motivated by substantive hypotheses.

Misconception 3: The product term coefficient is an appropriate estimator for the interaction effect on natural response scales.

We described in Misconception 2 above how the nonlinear nature of GLMs on the natural scale must be accounted for in estimating interaction, and in itself may also be sufficient to establish the presence of interaction. Yet, nonlinearity between predictors can also be introduced into the interaction effect through specification of a product term in the design function of the model (e.g., β_jk in Equations (17) through (19); Tsai & Gill, 2013). Despite its presence in the interaction function, however, it is inappropriate practice to use the product term coefficient alone to determine the presence and nature of an interaction effect on the natural scale of GLMs. Nonetheless, we have noted that this is common practice in psychology because transformed and natural scales are frequently conflated when testing interaction. That is, typical practice involves evaluating evidence of interaction based on significance of product term coefficients on the transformed scale. Then, coefficients are transformed to interpret effects on the natural scale. Although product term coefficients are sufficient estimates of interaction effects when interpreting effects on the transformed scale, this raises the question of what potential consequences may result from confounding the product term with an appropriate estimator of the interaction effect on the natural scale.

To illustrate these consequences, we conducted a simulation with nine conditions where product term coefficients (β₁₂) were included in a logistic regression. We assumed the following model held in the population:

$$\text{log}\left(\frac{\mathbb{E}[Y\mid x]}{1-\mathbb{E}[Y\mid x]}\right)={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+{\beta }_{12}{x}_1{x}_2,$$ (27)

where x₁ and x₂ were continuous variables drawn from a standard bivariate normal distribution and had moderate correlation $\left(r_{x_1{x}_2}=.5\right)$. Values of β₀, β₁, and β₂ were fixed to 1.0, 0.7, and 1.5, respectively, and β₁₂ values were set at −0.20, −0.15, −0.10, −0.05, 0.00, 0.05, 0.10, 0.15, and 0.20. For each condition, we simulated 10,000 datasets with n = 1,000. In each dataset, we estimated the product term coefficient $\left({\widehat{\beta }}_{12}\right)$ as well as the interaction effect for each observation $\left({\widehat{\gamma }}_{12}^2\right)$. We assessed the performance of ${\widehat{\beta }}_{12}$ and ${\widehat{\gamma }}_{12}^2$ as estimators of ${\gamma }_{12}^2$ by comparing their sample average empirical biases and empirical mean square errors (MSEs). We structured the comparison of these estimators in this manner to reflect how interaction effects are generally tested and interpreted in-practice in psychological science describing effects on natural scales: by using ${\widehat{\beta }}_{12}$ under the (incorrect) assumption that it is an estimate of ${\gamma }_{12}^2$.

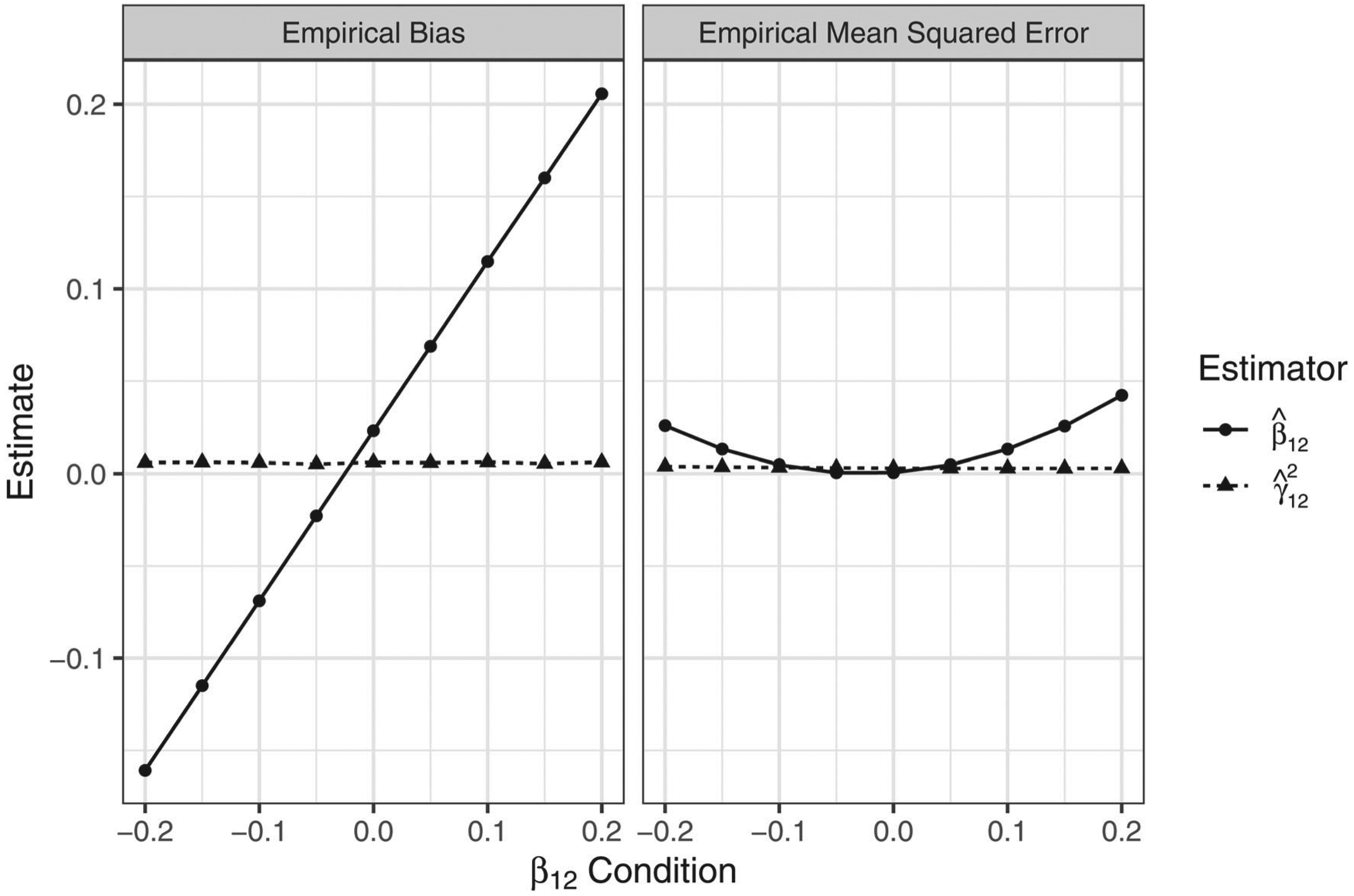
Figure 7 displays the average empirical biases and MSEs of each estimator for each β₁₂ condition. Whereas ${\widehat{\gamma }}_{12}^2$ was a generally unbiased estimator of ${\gamma }_{12}^2$, bias using ${\widehat{\beta }}_{12}$ as an estimator exhibited a linear trend (e.g., the positive linear trend in left panel of Figure 7). The MSEs of each estimator suggested that, whereas ${\widehat{\gamma }}_{12}^2$ was generally an efficient estimator of ${\gamma }_{12}^2$, using ${\widehat{\beta }}_{12}$ as an estimator lead to greater inflation in the variance of the estimator as the absolute magnitude of β₁₂ increased (e.g., the parabolic shape in the right panel of Figure 7). These values indicated that, particularly in conditions where β₁₂ is non-zero, ${\widehat{\beta }}_{12}$ may represent a biased and less efficient estimator of ${\gamma }_{12}^2$.

Figure 7.

Empirical bias and mean squared error for ${\widehat{\gamma }}_{12}^2$ and ${\widehat{\beta }}_{12}$ as estimators of ${\gamma }_{12}^2$ across conditions of β₁₂.

Note. Points represent values of each estimate averaged across 10,000 simulated datasets for each β₁₂ condition.

Demonstrating a worst-case scenario, we extended the above simulation to a Poisson model with an identical parameterization as the above. Values of β₀, β₁, and β₂ were again fixed to 1.0, 0.7, and 1.5, respectively, while β₁₂ was set at −0.20 for illustration.¹⁰ Coefficient estimates obtained from this model were ${\widehat{\beta }}_0=1.43$, ${\widehat{\beta }}_1=0.76$, ${\widehat{\beta }}_2=1.47$, and ${\widehat{\beta }}_{12}=-0.29$. Here, ${\widehat{\beta }}_{12}$ was significant and negative (95% CI = [−0.31, −0.27]), such that one might infer an antagonistic interaction between x₁ and x₂ given both lower-order terms indicated positive associations with the outcome. If the analyst sought to interpret this effect on the log-count scale, this coefficient sufficiently quantifies the interaction effect on this transformed scale, such that evidence of an antagonistic interaction on this scale is supported. However, this is not the case when describing results in the scale of counts. Namely, the average interaction effect was 2.48 across observations (95% CI = [1.99, 2.97]) with 98.5% indicating a significant positive (i.e. synergistic) interaction effect on the count scale. Producing a visual of these relations makes this distinction clear (Figure 8): in the count scale, the rate-of-change of x₁ on the count of $\widehat{Y}$ strengthens as x₂ increases, yet the rate-of-change weakens as x₂ increases when describing relations on the log-count scale. In other words, the nature of the interaction depended on the scaling chosen to describe the effects. On the one hand, there was evidence of an antagonistic interaction on the log-count scale – an effect that was sufficiently quantified by the product term coefficient. On the other, the interaction was synergistic when interpreted on the count scale, such that the product term coefficient implied an interaction effect that was of incorrect magnitude and the opposite sign for nearly the entirety of observations on this scale.

Figure 8.

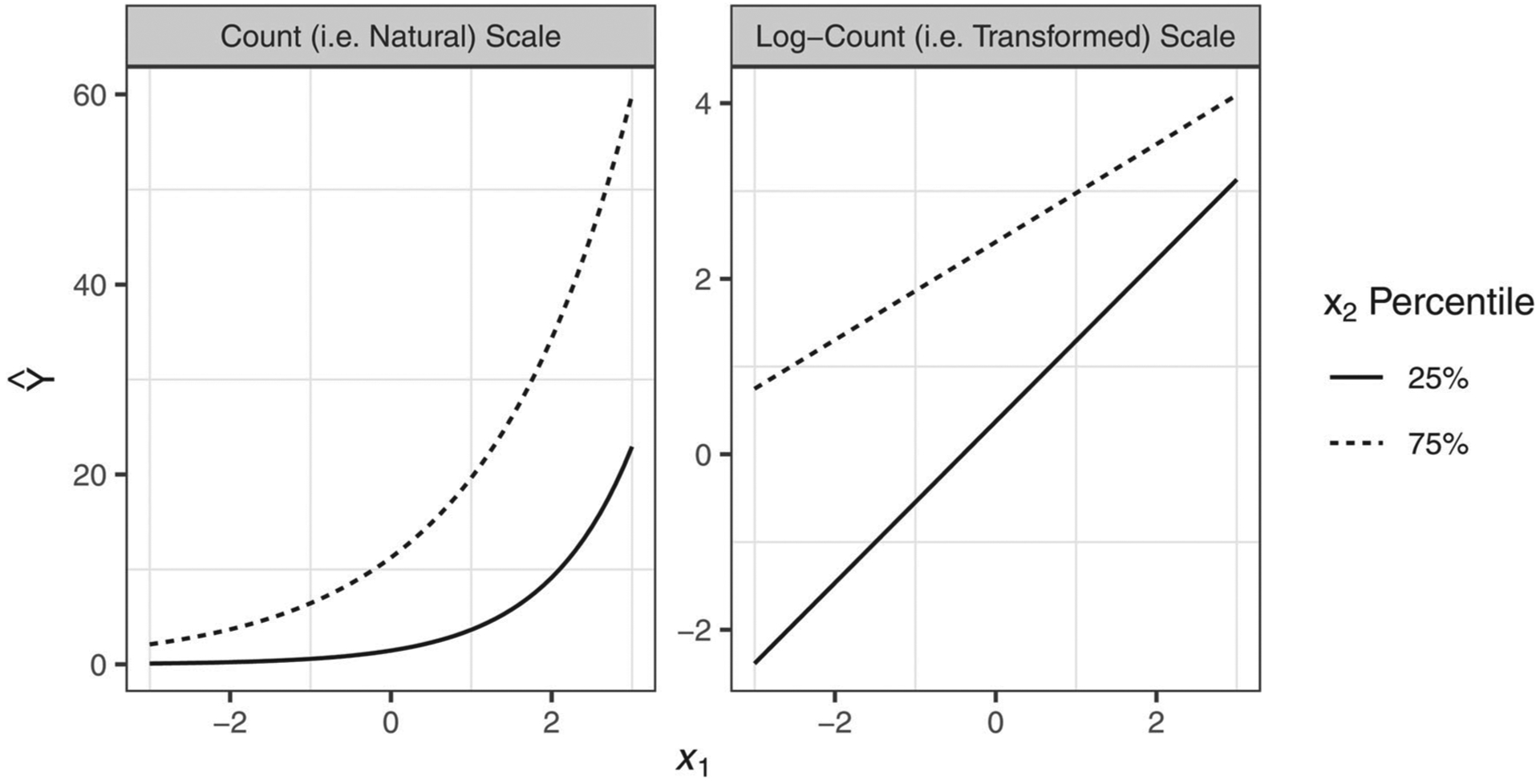
Marginal effects of x₁ plotted against different scalings of $\widehat{Y}$ at low and high values of x₂.

Note. This figure illustrates how interaction effects can be of opposite sign depending on the scaling choice for inference. For instance, in the count scale (left-hand side), the curves presented are growing farther apart as x₁ increases, indicating the synergistic interaction on the natural scale. By contrast, on the log-count scale (right hand side), the lines are coming closer together as x₁ increases, indicating the antagonistic interaction on the transformed scale.

These results illustrate that as a result of conflating interaction effects on transformed and natural scales, using only the product term to draw inferences about an interaction effect can severely compromise the performance of estimation when describing effects on natural scales. At worst, this can imply that an interaction effect is of the opposite sign from what is true in the population when there is a mismatch between the GLM scale used for interpretation and the estimator used for quantifying interaction. When describing effects on the transformed scale, the product term coefficient is an appropriate estimator of an interaction effect. In contrast, when results are interpreted on the natural scale, evaluating interactions using the partial derivative and discrete difference approaches is a better-performing estimator of the interaction effect relative to the product term coefficient.

Real data example

We illustrate the approaches described above by examining alcohol sipping behavior among youth (ages 8–11 years) using the Adolescent Brain Cognitive Development (ABCD) Study (https://abcdstudy.org), a large multisite study of long-term brain development and child health. We focused our analyses on assessing the effects of social and environmental factors on the lifetime occurrence of alcohol sipping behavior measured by the ABCD Substance Use and Culture and Environment modules (see Lisdahl et al., 2018 and Zucker et al., 2018 for in-depth descriptions of these modules).

The focus of our analyses was on the influences of social and environmental risk factors on the level of non-religious alcohol sipping in late childhood. Prior research has demonstrated that both low parental monitoring (e.g., Steinberg et al., 1994) and greater school disengagement (e.g., Bryant et al., 2003) were associated with a higher likelihood of substance use involvement in youth, and these factors are thought to interact across these multiple levels of environmental influence to characterize heightened risk among youth (Pantin et al., 2004; Szapocznik & Coatsworth, 1999). As such, we hypothesized that the interaction between lower parental monitoring and greater school disengagement would characterize a higher likelihood of alcohol sipping among youth.

Method

We used baseline assessments from ABCD to address hypotheses (data release 2.0). The study was approved by the institutional review board at the University of California, San Diego and at each individual participating site (see Clark et al., 2018 for details). We specified a nonhierarchical logistic model assuming uncorrelated errors at the initial stage of model estimation. We then applied a sandwich variance estimator to the variance-covariance estimates obtained by this model to account for correlation within sites (Miglioretti & Heagerty, 2007) using the “ClusterRobustSE” package (Huh, 2020). For simplicity and purposes of illustration, we used listwise deletion to address missingness among study variables, which resulted in minimal loss of data (1.7%). The remaining n = 11,642 observations were included for analysis. Additional study design and recruitment details are described by Garavan et al. (2018).

Sipping behaviors were measured using the iSay Sip Inventory (Jackson et al., 2015) using the binary response item “Have you ever had alcohol not as part of a religious ceremony such as in church or at a Seder dinner?”. Consistent with prior estimates (e.g., Donovan & Molina, 2004), a total of 17% of youth (n = 1,991) reported lifetime alcohol sipping. Parental monitoring was measured using five items adapted from Karoly et al. (2016). School disengagement was measured as a sum of two items adapted from Arthur et al. (2007) in which youth rated agreement with the statements “usually, school bores me” and “getting good grades is not so important to me” on 4-point Likert scales. Additional covariates included in the model were age, sex, ethnicity (Hispanic vs. non-Hispanic) and race (White vs. nonwhite). Additional descriptive summaries of study variables are provided in Table 1.

Table 1.

Sample correlations and descriptive statistics.

	1	2	3	4	5	6	Mean	SD	Min.	Max.
1. Alcohol Sipping (Yes vs. No)	1.00						0.17	0.38	0.00	1.00
2. Age	0.04	1.00					9.48	0.51	8.00	11.00
3. White	0.11	0.00	1.00				0.74	0.44	0.00	1.00
4. Hispanic	−0.03	−0.02	−0.07	1.00			0.21	0.40	0.00	1.00
5. Male	0.05	0.02	0.02	0.00	1.00		0.52	0.50	0.00	1.00
6. Parental Monitoring	−0.01	0.08	0.06	−0.03	−0.17	1.00	4.38	0.52	1.00	5.00
7. School Disengagement	0.06	−0.01	0.01	−0.03	0.15	−0.22	3.74	1.46	2.00	8.00

We specified a logistic regression model using the base stats package in R (R Core Team, 2019) to estimate the following model:

$$\mathbb{E}[Y\mid x]=\frac{1}{1+\text{exp}\left(-d{(x)}^T\beta \right)}.$$ (28)

In this model, Y was a binary random variable indicating the presence or absence of sipping; x was comprised of parental monitoring and school disengagement variables, as well as age, sex, ethnicity, and race; and d(·) adds an intercept and product term between parental monitoring and school disengagement to x. We included the product term to capture the multiplicative interaction between parental monitoring and school disengagement. Variables included in the product term (i.e. parental monitoring and school disengagement) were standardized to facilitate interpretation.

Results

We provide a summary generated by our model output in Table 2. This model suggests the presence of interaction between parental monitoring and school disengagement on the log-odds scale, as evidenced by the statistical significance of the product term coefficient (${\widehat{\beta }}_{PM\times SD}=0.08$, p = 0.008). Thus, if one uses the transformed scale for inference, then a one-unit increase in school disengagement reduces the protective effect of parental monitoring on the log-odds of alcohol sipping by 0.08 units, holding all else constant.

Table 2.

Logistic regression results for alcohol sipping.

Parameter	Estimate	SE	95% CI	p
Intercept	−4.29
Age	0.21	0.05	[0.12, 0.31]	<0.001
White	0.74	0.06	[0.61,0.87]	<0.001
Hispanic	−0.14	0.06	[−0.26, −0.01]	0.035
Male	0.17	0.05	[0.07, 0.27]	<0.001
Parental Monitoring	−0.03	0.03	[−0.08, 0.02]	0.226
School Disengagement	0.15	0.03	[0.10, 0.20]	<0.001
Parental Monitoring × School Disengagement	0.06	0.02	[0.02, 0.11]	0.008

Note. Parental monitoring and school disengagement are standardized variables.

However, if the analyst sought to describe these effects on the natural scale, computing and interpreting ${\widehat{\gamma }}_{12}^2$ effects provides a more nuanced depiction of the interaction effect in its direct association with the probability of alcohol sipping behavior. For instance, though the point estimates of the interaction effect were positive for all observations, they were significant for only 82.2% of the sample, ranging in magnitude among observations from 0.003 to 0.021 with an average interaction effect of 0.008 (95% CI = [0.002, 0.014]), suggesting a near-zero average effect in the sample. We may also choose to represent the interaction effect at particular categories to further address how the interaction effect varies within the sample. Conditioning the effect using (for instance) the sample mean age, female, and Hispanic identity as scenarios of interest, the interaction effect was significant and positive among White Hispanic females (${\widehat{\gamma }}_{12}^2=0.009$, 95% CI = [0.001, 0.017]) though fell short of significance among nonwhite Hispanic females (${\widehat{\gamma }}_{12}^2=0.005$, 95% CI = [0.000, 0.010]), exemplified in Figure 9. This level of description makes evident how this interaction varies as a function of participant characteristics, which may help delimit the scope of these research findings in informing public policy on early alcohol exposure risk. Taken together, these findings highlight that the effect of parental monitoring on the probability of alcohol sipping was enhanced by school disengagement, with variability in the magnitude of this effect as a function of sex, race, and/or ethnic identity.

Figure 9.

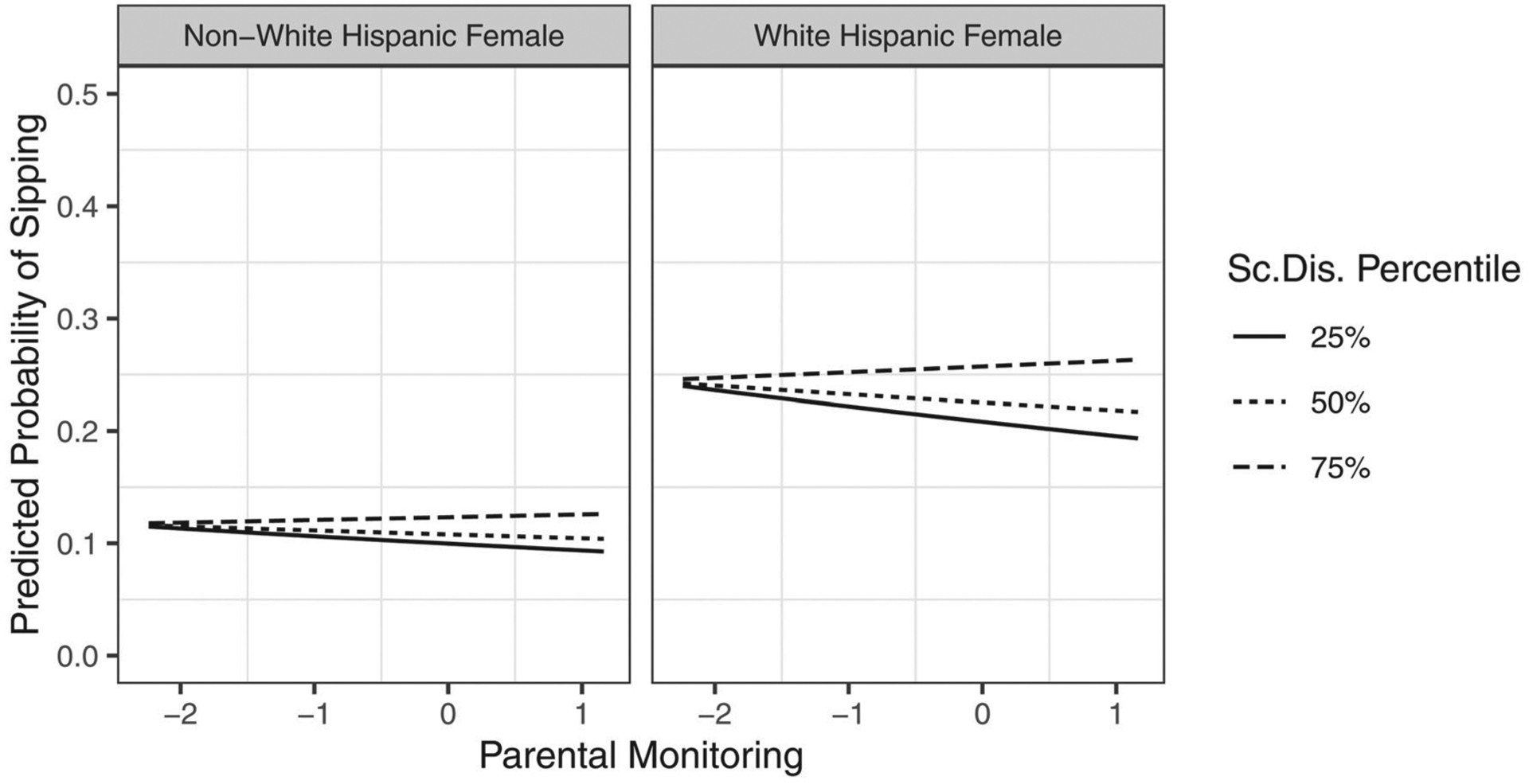
The relation between the predicted probability of alcohol sipping and parental monitoring across low, median, and high levels of school disengagement among Hispanic females by race.

Note. Sc.Dis. = School Disengagement.

Discussion

GLMs are being increasingly utilized in pursuit of interaction hypotheses when analyzing probability and count dependent variables. Although typical practice is to test interactions by applying approaches from linear models, we have demonstrated that these practices are insufficient for representing interactions in GLMs on these natural response scales. We have reviewed partial derivative and finite difference approaches for estimating the interaction effect in GLMs of probabilities and counts. We have also articulated how standard practices (i.e. using the product term coefficient as an estimator of interaction) can lead to bias and inefficiency in estimating the interaction effect on natural scales, as well as how serious errors in inference can occur if scales are conflated when evaluating interaction effects. We further provided guidelines and examples of how to interpret these models in the analysis of real and simulated data. Our hope is that this work will aid researchers in increasing the validity of interaction analyses when GLMs are utilized, and ultimately improve the methodological rigor and replicability of pursuing such hypotheses. To aid in the dissemination of this work, we have also developed R functions adapted from Ai and Norton’s Stata software (Norton et al., 2004) and the R package “DAMisc” (Armstrong, 2020). These functions accommodate the analysis of interaction effects in both binary and count models by incorporating the applications described above. Open-source code for these functions and instructions for using them are available at https://github.com/connorjmccabe/modglm.

Future directions

Despite the recommendations and solutions we have provided here, we consider this work to be a first step in improving the evaluation of interactions in GLMs of psychological data. For instance, data visualization approaches for interaction effects such as those in linear models (e.g., Bauer & Curran, 2005; McCabe et al., 2018) could aid substantially in interpreting and communicating these effects in GLMs. Such approaches summarize the nature of interaction for non-expert consumers of research involving GLMs, while providing a means of assessing research findings given the observed data. Similarly, computing and communicating quantities such as first differences and rate ratios (Halvorson et al., in press; King et al., 2000) can help translate interaction effects into more concrete and interpretable metrics. Although we have employed some of these approaches to describe effects in the current paper, research describing their application more broadly will help facilitate their widespread adaptation into published studies. Further, there remains an ongoing and pressing need to improve the accessibility of these approaches for use among methodological non-experts (King et al., 2019; Sharpe, 2013). We provide computational and inferential solutions developed in this paper through open-source R code. Mize’s data visualization software for marginal effects is also an excellent resource for plotting marginal effects in the Stata framework, available at https://trentonmize.com/software/cleanplots (Mize, 2019). However, the continued development and refinement of analytic tools and tutorials are essential to increase the accessibility of these advanced approaches in data analysis and interpretation.

We note that partial derivatives and discrete differences are highly flexible tools that can be applied to improve inferences in other modeling frameworks that involve nonlinear design (Kim & McCabe, 2020). We describe them here as a means of understanding and interpreting the interaction function when nonlinearity is introduced via the link function of a GLM, yet nonlinearity introduced via any other element of a model may similarly obscure the straightforward interpretation of parameters produced by these models. Notable examples include linear regression models involving nonlinear transformations of predictor variables (e.g., power, log, or exponentially transformed variables), machine learning approaches (e.g., linear spline models; Friedman et al., 2001), or combinations of these involving multiple forms of nonlinear design. We hope that the misconceptions and solutions we reviewed here will stimulate future applications of partial derivatives and discrete differences in addressing substantive questions in these and other more intensive nonlinear models.

Conclusion

This manuscript aimed to correct pervasive misconceptions regarding the estimation and interpretation of interaction effects in probability and count GLMs. As a concept, interactions test nonlinear association between a given predictor and an outcome as a function of other variables, yet we have shown that there are several aspects of modeling design in GLMs that induce nonlinearity and render a test of this concept less than straightforward. For instance, reporting the results of GLMs in terms of natural scales can improve readers’ understanding of research results and the translation of research findings to practice, yet this also introduces complexities that make interpreting model coefficients much more difficult. We have highlighted numerous decision points that reflect this and other such design choices, such as selecting a GLM appropriately matched to one’s outcome and theory; seeking to understand associations on the natural scale of these models; and/or choosing among several plausible options for probing and presenting such effects. Each of these design choices must be weighed delicately in determining the most appropriate test of an interaction theory given the analyst’s specific research question. As such, we urge researchers to think carefully on how each of these choices affect the theoretical concepts they wish to test. Even subtle choices in model design and interpretation may have significant impact on inference.