Mapping Cell Viability Quantitatively and Independently from Cell Density in 3D Gels Noninvasively

Abstract

Objective:

In biomanufacturing there is a need for quantitative methods to map cell viability and density inside 3D bioreactors to assess health and proliferation over time. Recently, noninvasive MRI readouts of cell density have been achieved. However, the ratio of live to dead cells was not varied. Herein we present an approach for measuring the viability of cells embedded in a hydrogel independently from cell density to map cell number and health.

Methods:

Independent quantification of cell viability and density was achieved by calibrating the ¹H magnetization transfer- (MT) and diffusion-weighted NMR signals to samples of known cell density and viability using a multivariate approach. Maps of cell viability and density were generated by weighting NMR images by these parameters post-calibration.

Results:

Using this method, the limits of detection (LODs) of total cell density and viable cell density were found to be 3.88×10⁸ cells · mL⁻¹ · Hz^−1/2 and 2.36×10⁹ viable cells · mL⁻¹ · Hz^−1/2 respectively.

Conclusion:

This mapping technique provides a noninvasive means of visualizing cell viability and number density within optically opaque bioreactors.

Significance:

We anticipate that such nondestructive readouts will provide valuable feedback for monitoring and controlling cell populations in bioreactors.

I. Introduction

AS larger and increasingly complex engineered tissues are developed for use in medicine and research, novel methods are being investigated to measure indicators of successful growth of engineered tissue. Recently, magnetic resonance imaging (MRI) was used to spatially quantify cell density in thick, three-dimensional (3D) gels. It was found that three nuclear magnetic resonance (NMR) weightings: T₂ relaxation, magnetization transfer (MT), and diffusion could be calibrated to measure live cell density [1]. MRI’s unlimited imaging depth allows thick samples to be fully profiled without invasive physical sectioning. Recent developments in MR compatible bioreactor and incubator systems [2], [3] provide additional motivation for developing novel MRI methods for noninvasive, real-time evaluation of engineered tissue or 3D cell culture.

Spatially resolved cell density maps (e.g., as demonstrated in [1]) display growth within a tissue culture but do not provide a fully comprehensive profile of tissue health. Indicators of tissue health are critical for predicting the culture’s outcome. Success of an engineered tissue may not be discernable until days or weeks post implantation. Measurements of viability have commercial and scientific value since they serve as early indicators of a successful product and a more immediate indicator of potential cell growth. The extent to which MRI has previously been employed to detect cellular viability is limited. In a few studies, MRI was used to track viable cell transplants [4], [5]. In these cases, cells that were transplanted in vivo were labelled with a viability sensitive contrast agent such as MnCl₂ or gadolinium liposomes (Gd-MSCs). When evaluated in vitro, the MR signal generated from the Gd-MSCs labelled cells could quantify cell density in suspensions containing either completely viable or completely non-viable cells. However, partially viable cell populations were not examined to determine whether the viable fraction was quantifiable [4].

In addition to studying cells prepared in vitro, researchers have used contrast agents to target and image necrotic tissue in vivo. Several contrast enhanced techniques have been used to distinguish regions of viable and non-viable myocardium following infarction [6]–[8]. Contrast enhanced diffusion-weighted MRI was used to differentiate irradiated and non-irradiated regions of liver tumors [9]. In another study, it was found that the nitroxide 4-trimethylammonium-2,2,6,6-tetramethylpiperidine-1-oxyl iodide (Cat-1) could be used as a necrosis sensitive contrast agent in muscle [10]. In ischemic stroke patients, Røhl et al. employed gradient-echo echo-planar imaging of a gadodiamide bolus, referred to as perfusion-weighted MRI, to map relative cerebral blood flow (rCBF), or the ratio of CBF in the lesion to CBF on the contralateral side of the brain. It was found that an rCBF cutoff of 0.59 could be used to distinguish regions of the penumbra that will recover from those that will progress to infarction [11]. Lastly, Gröhn et al. exploited the dependence of T₂ relaxation on dissolved O₂ in the brain following ischemic stroke to identify the mismatch between oxygen delivery and metabolic consumption of O₂. This technique could be used to distinguish metabolically active and viable brain tissue from genuine ischemia [12].

Several contrast agent-free techniques have been used to image necrosis in vivo. T₂-weighted MRI was used to accurately identify lesions induced by ultrasound in rabbit brains [13]. Another study found a decrease in ³⁹K MRI signal correlated to necrotic cardiac tissue following infarction [14]. Neither of these techniques provided quantitative viability data. Two studies were able to quantify necrosis using contrast agent-free MRI. In order to overcome geometric distortion, chemical shift artifacts, and spatial resolution limitations associated with single shot MRI, which limit its quantitative potential, Deng et al. used a multishot periodically rotated overlapping parallel lines with enhanced reconstruction (PROPELLER) approach, and found that diffusion-weighted PROPELLER MRI measurements quantitatively correlated with the necrotic fraction of liver tumors [15]. However, in this case the necrotic fraction was defined as the ratio of the histologically defined necrotic region to the total tumor area. In the other study using a fibrosarcoma tumor model, it was found that multispectral analysis using apparent diffusion coefficient, T₂, proton density, and a k-means clustering algorithm could identify tissue necrotic fraction (TNF) [16]. Good correlations between k-means determined- and histologically determined-TNF volume were found, but this method also relies on the binary classification of macroscopic tissue regions as either totally viable or necrotic.

Although these techniques have the potential to assist in clinical decision making, they are not quantitative measurements of the viable fraction of cells within a population. Rather, they are used to distinguish distinct regions of clinically viable tissue from clinically necrotic regions. This requires the partitioning of tissue into two well-defined regions: a viable and necrotic region. It does not allow for quantitating of volumes containing a mixture of both live and dead cells. Maps of viable cell fraction distribution within a culture are relevant in the context of tissue engineering, where this distribution is expected to be dependent on culture conditions such as nutrient delivery [17], [18].

In this study, we examine closely the potential for MT and diffusion-weighted ¹H NMR signals to be used as means to quantify viability of mammalian cells embedded in agarose hydrogels independently from cell density. The separation of cell density and cell viability contributions to these NMR signals is non-trivial, as both signals reflect such contributions. We have accomplished this by exploiting key differences between how each weighting detects the presence of cells. The diffusion coefficient of water strongly depends on compartmentalization of water molecules caused by the presence of intact cell membranes [19], making it sensitive to cellular events such as apoptosis, necrosis, and even volume changes [20]–[22]. In contrast, MT-weighted imaging is strongly influenced by macromolecular content [23] and less so by intact membranes. It is expected that exploiting these differences to generate quantifiable maps of cell viability will provide valuable data about otherwise inaccessible thick, 3D cell cultures.

II. Materials and methods

A. Preparation of Viable Samples

B16-F10 cells were cultured in a 37°C, 5% CO₂ incubator in Dulbecco’s Modified Eagle Medium (DMEM) supplemented with 10% FBS, L-glutamine, and penicillin/streptomycin. Cells were harvested by incubating in trypsin for 5 minutes and neutralizing trypsin with DMEM containing 10% FBS. Dead cell populations with ruptured membranes were generated by suspending cells first in 2% paraformaldehyde and later in Hank’s Balanced Salt Solution containing 0.3% Triton-X and 0.05% Tween-20. Dead cells were washed twice with phosphate buffered saline (PBS) prior to use. Live and dead cell populations were counted using software developed by Arteta et al. [24] that was trained to recognize live and dead cells in transmission light micrographs of trypan blue stained populations suspended in disposable hemocytometers. Live and dead cell populations were combined in ratios and concentrated to generate final populations with the desired cell concentration and viable fraction.

It was noticed that every transfer step resulted in cell losses of 5–10%, and more dead cells were lost than live cells during transfers. This was likely due to cells adhering to the inner surface of serological pipettes. To account for this, cell populations were counted after the pipette that would be used to transfer them to their final tube was wetted with cell suspension. Live and dead cells were transferred to the final tube with a single transfer immediately after they were counted.

Mixed cell populations were pelleted in 50 mL conical tubes by centrifugation at 200 g for 5 min. Supernatant was aspirated down to 10 mL if applicable. The final volume of supernatant was poured off the cell pellet in one swift motion by inverting the tube to reduce cell losses caused by aspiration. Any drips remaining on the walls of the tube were aspirated with the tube inverted. Pellets prepared for NMR spectroscopy were then suspended in a 37°C liquid mixture containing a 1:1 ratio of cell culture media and 1.8% low gelling temperature agarose (Sigma, A9045-5G) dissolved in PBS. Gel cell suspensions were quickly mixed, cast in 5 mm NMR tubes, and allowed to anneal at room temperature for eight minutes. Annealed samples were reheated to 37°C and maintained at that temperature during data acquisition. All data was acquired immediately after sample preparation.

Samples containing layers of B16-F10 cells of various viable fractions were prepared by casting a small quantity of agarose gel containing the desired viability and density in a 5 mm NMR tube, allowing the layer to anneal, and then casting the next layer with a different viability/density on top of the first layer. This process was repeated until all four layers were cast. The regions of the NMR tube beneath and above the radiofrequency (RF) region were filled with acellular agarose. Serum free DMEM was used to rinse and encapsulate cells prepared for longer imaging acquisitions in order to slow down cell metabolism [25] and prevent CO₂ bubbles from forming during acquisition.

B. NMR Measurements

Spectroscopy measurements and images of B16-F10 cells were acquired in a Varian 400 MHz (9.4 T) spectrometer equipped with a 10 mm broadband probe and air-flow variable temperature (VT) control. MT- and diffusion-weighted spectroscopy and imaging data were collected with pulse sequences described previously [1]. Pulse sequence parameters including diffusion time, Δ, diffusion weighting value (b-value), and saturation pulse frequency offset were determined using methods similar to previous work [1]. Briefly, NMR acquisitions were carried out on pilot samples containing 0% and 100% viable cells at 1 × 10⁸ cells · mL⁻¹ and acellular agarose. On each sample, a total of 50 MT-weighted NMR spectra were acquired with saturation pulse frequency offsets arrayed at values spaced on a log scale from 0 to 200 MHz. Diffusion-weighted NMR spectra were acquired with Δ’s of 25, 30, 50, 100, 150, and 200 ms, and gradient strength, G, arrayed from 0 to 50 Gauss/cm at 1 Gauss/cm intervals for each value of Δ. Diffusion weighted spectra integrals were compared between the 0% and 100% viable samples for each combination of Δ and G, and the combination of values which led to the greatest difference in signal was selected as the most sensitive to viability. Since the MT-weighted signal was expected to be insensitive to changes in cell viability, MT weighted signal integrals were compared between the cell laden gels and acellular gels. The offset frequency found to be most sensitive to cell density was similar when comparing the 100% and 0% viable samples to the acellular sample.

C. Data Analysis

In this study, the MT-weighted signal, represented by S_MT, was generated by normalizing the signal generated from an MT pulse sequence acquisition with an offset optimized for generating contrast (S_MT,c) to a reference signal obtained from an MT pulse sequence acquisition using an offset frequency of 200 kHz (S_MT,0), so that $S_{MT}=\frac{S_{MT,c}}{S_{MT,0}}$. Similarly, the reported diffusion-weighted signal is equivalent to $S_{\mathit{\text{Diff}}}=\frac{S_{\mathit{\text{Diff}},c}}{S_{\mathit{\text{Diff}},0}}$ where S_Diff,c is the signal obtained from a Pulsed Field-Gradient STimulated-Echo (PFG-STE) sequence using a contrast optimized b-value, and S_Diff,0 is a reference signal obtained from the same pulse sequence without applying diffusion weighted gradients. Background diffusion and MT-weighted measurements of acellular agarose gels were obtained in the same way, such that $S_{MT,bg}=\frac{S_{MT,bg,c}}{S_{MT,bg,0}}$ and $S_{\mathit{\text{Diff}},bg}=\frac{S_{\mathit{\text{Diff}},bg,c}}{S_{\mathit{\text{Diff}},bg,0}}$. The background signals were subtracted from all cell measurements to isolate the change in diffusion- and MT-weighted signal caused solely by the presence of cell populations.

To determine the cell concentration and viability limits of detection (LODs), cell concentration and viability were plotted as a function of their measured diffusion- and MT-weighted NMR signals. Previous work established an exponential dependence of the diffusion-weighted signal and a linear dependence of the MT-weighted signal on cell density [1]. When generating concentration dependent linear MT fits and exponential diffusion fits at several different viabilities, we observed exponential dependencies of the fitted parameters on viability, suggesting that the dependence of the diffusion- and MT-weighted signals on cell density and viability include nested exponentials in the form $S_M=\left(c_1{e}^{c_2\cdot V}\right)C+c_3{e}^{c_4\cdot V}+c_5$ and $S_D=\left(c_6{e}^{c_7\cdot V}\right)e^{\left(c_8{e}^{c_9\cdot V}\right)C}+c_{10}$, where C and V are concentration in cells · mL⁻¹ and viability in % respectively; c₁, c₂, … c₁₀ are constants; and S_D and S_M represent the background corrected, normalized diffusion- and MT-weighted signals:

$$S_D\equiv S_{\mathit{\text{Diff}}}-S_{\mathit{\text{Diff}},bg}$$

and

$$S_M\equiv S_{MT}-S_{MT,bg}.$$

To quantifiably measure cell viability and density, C and V need to be expressed as functions of S_M and S_D. Because the expressions with nested exponentials have no analytical solution for C and V, surface models of the form of a second order power series approximation $(y=b_0+b_1{x}_1+b_2{x}_2+b_3{x}_1^2+b_4{x}_1{x}_2+b_5{x}_2^2)$ were fit to the data using a weighted Levenberg-Marquardt nonlinear least squares algorithm [26]. The LOD for the multivariate fits were calculated using the relationship, $\text{LOD}=3\overline{\sigma }\cdot \mathit{\text{b}}$ where b is the model coefficient vector, (b₁ b₂ b₃ b₄ b₅), and $\overline{\sigma }$ is the average standard deviation vector $({\overline{\sigma }}_{x_1}{\overline{\sigma }}_{x_2}{\overline{\sigma }}_{{\left(x_1\right)}^2}{\overline{\sigma }}_{x_1{x}_2}{\overline{\sigma }}_{{\left(x_2\right)}^2})$. Diffusion- and MT-weighted signals (represented here by x₁ and x₂) were collected for all samples in triplicate. Using ${\sigma }_{x_1,n}$ to represent the standard deviation of the measured x_1,n at a single data point, n, the average of the standard deviations of all data points from 1 to N is represented by ${\overline{\sigma }}_{x_1}$. Similarly, ${\overline{\sigma }}_{{\left(x_1\right)}^2}$ is the average of all the standard deviations of the value (x₁)², and the pattern continues for all other values in the average standard deviation vector. This LOD analysis is based on the International Union of Pure and Applied Chemistry (IUPAC) recommendations extended to a multivariate model [27].

Images were analyzed by manually drawing regions of interest (ROIs) around portions entirely within discrete layers. Average voxel intensities from each ROI were compared to each other with a 1-way analysis of variance (ANOVA) for images in which only one independent variable was changed or a 2-way ANOVA when both viability and density were varied between layers. Significance for pairwise group mean comparisons was obtained using Tukey’s honestly significant difference criterion [28]. Error bars displayed on mean ROI intensity plots were chosen to represent one standard error rather than one standard deviation to account for the greater voxel-to-voxel variation when compared to variation between NMR spectra acquired of the entire RF region (which is larger in volume by orders of magnitude).

III. Results

A. NMR Spectroscopic Viability and Density Calibrations

Plots of B16-F10 viability versus diffusion-weighted NMR spectrum intensity for three different cell densities are shown in Fig. 1 (a). A diffusion time, Δ, of 100 ms and diffusion weighting value (b-value) of 2800 s·mm⁻² were found to be most sensitive to B16-F10 viability. The diffusion-weighted signal was found to have an exponential dependence on cell viability at all cell densities studied, which is similar to previously established exponential dependence of diffusion-weighted signal on cell density [1]. The response of the MT-weighted signal to cell viability at three cell densities is shown in Fig. 1 (b). The optimal MT-weighted saturation pulse offset was found to be 3.3 kHz. It can be seen that the MT-weighted signal is linearly dependent on cell viability, but is less dependent on viability than it is on cell density as expected. The level of dependence on viability was also seen to depend on the density at which measurements were taken.

Fig. 1. Diffusion- and T₂-Weighted Viability Calibrations.

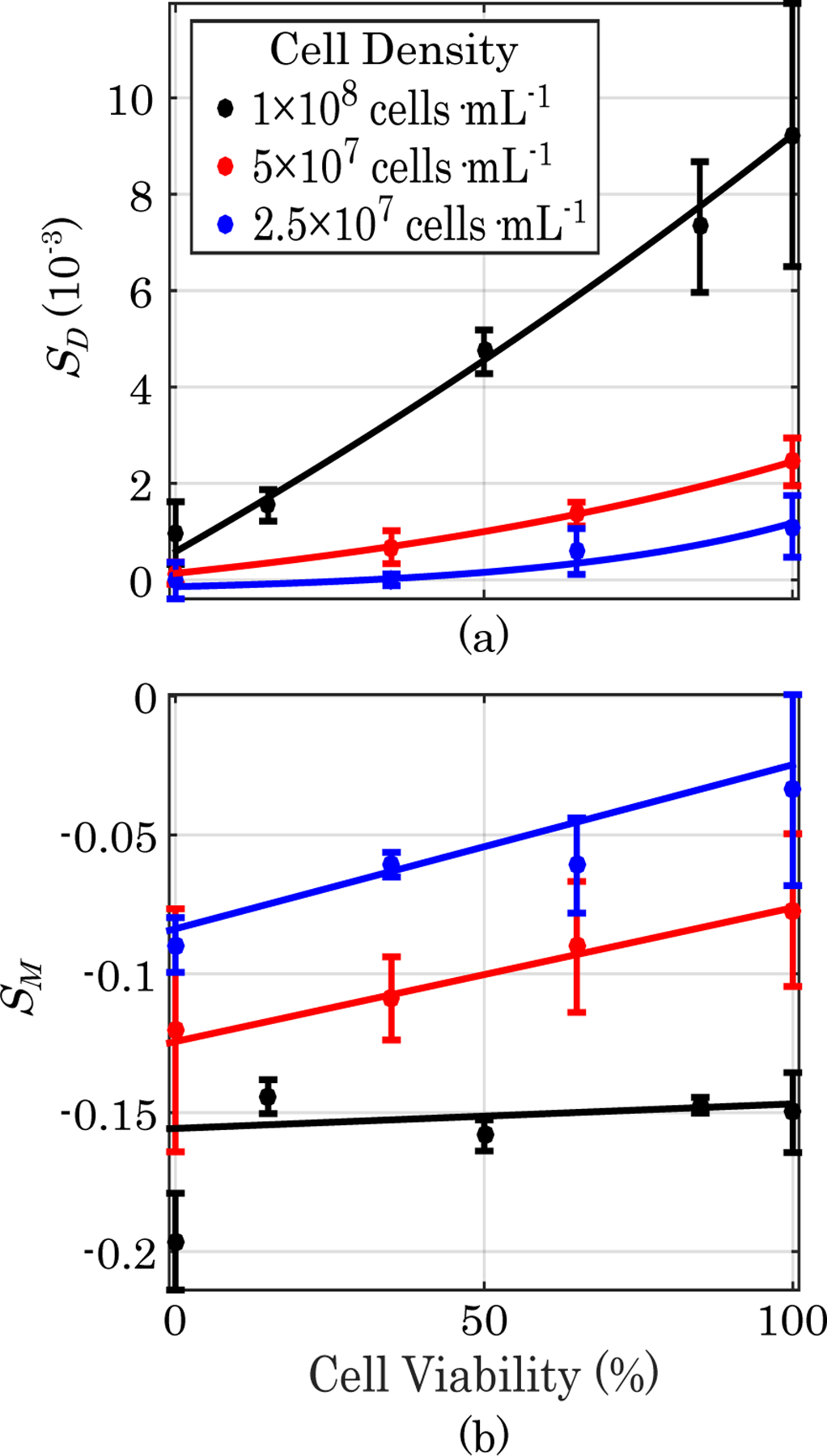
(a) Plots of B16-F10 cell viability versus diffusion-weighted NMR spectroscopy signal for three different cell densities. (b) Plots of B16-F10 cell viability versus MT-weighted signal for three different cell densities. Error bars represent one standard deviation (n=3).

A diffusion- and MT-weighted measurement was taken for each sample with a known viability and total density. Both NMR signals were dependent on both cell density and viability. In order to determine if viability and density can be measured independently from each other using a combination of their respective calibration curves, cell concentration and cell viability were plotted as a function of their diffusion- and MT-weighted signals in Fig. 2. The points were fitted to surfaces of the form of a second order power series of the form:

$$C\left(S_D,S_M\right)=C_0+C_1{S}_D+C_2{S}_M+C_3{S}_D^2+C_4{S}_D{S}_M+C_5{S}_M^2$$ (1)

$$V\left(S_D,S_M\right)=V_0+V_1{S}_D+V_2{S}_M+V_3{S}_D^2+V_4{S}_D{S}_M+V_5{S}_M^2,$$ (2)

where C₀, C₁, … C₅ are the coefficients of a power series expansion of second order concentration dependence and V₀, V₁, … V₅ are the coefficients of a power series expansion of second order viability dependence. The values of the fitted parameters are listed in Table I. The coefficients of determination (R²) for the concentration and viability fits are 0.952 and 0.965 respectively. Their fit p-values are 1.27×10⁻⁶ and 5.71 × 10⁻⁵, respectively.

Fig. 2. 3D Viability and Density Calibrations.

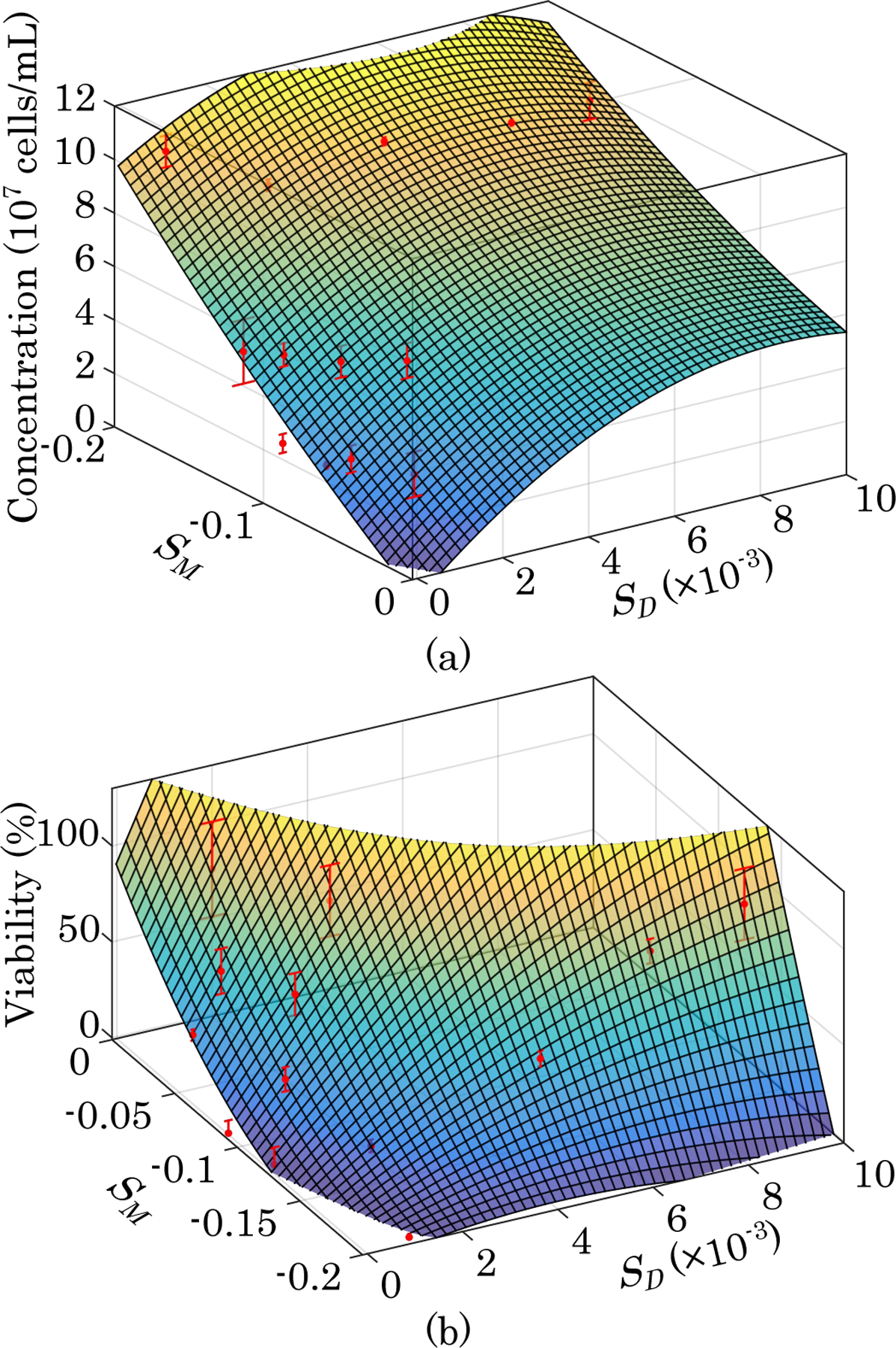
(a) Plot of calibration surface overlaid on data showing cell concentration as a function of diffusion- and MT-weighted signals. (b) Plot of calibration surface overlaid on data showing cell viability as a function of diffusion- and MT-weighted signals (n=3).

TABLE I.

Model Parameters

Concentration	Value	Viability	Value
C 0	−1.14 × 107	V 0	66.6
C 1	1.53 × 1010	V 1	5.27 × 104
C 2	−4.36 × 108	V 2	1.03 × 103
C 3	−8.69 × 1011	V 3	−6.41 × 105
C 4	2.34 × 1010	V 4	2.41 × 105
C 5	5.19 × 108	V 5	3.27 × 104

Using the parameters of the fitted surfaces and the multivariate LOD formula, $\text{LOD}=3\overline{\sigma }\cdot \mathit{\text{b}}$, the cell concentration LOD was determined to be 1.94 × 10⁷ cells · mL⁻¹, which is the same order of magnitude as determined previously for HEK 293 cells all with 100% viability [1]. The cell viability LOD was determined to be 607%, corresponding to 1.18×10⁸ viable cells · mL⁻¹ at the cell concentration detection limit. NMR signal to noise ratio improves in proportion to the square root of the number of scans that are averaged, which can be quantified by the amount of time required per scan. Here the dependence of the LOD on the quantity of time taken for acquiring multiple scans is accounted for by reporting the detection limit in cells · mL⁻¹ · Hz ^−1/2 (which is also cells · mL⁻¹ · s ^1/2). The total combined acquisition time for a diffusion- and MT-weighted sequence was 132.3 s. Given a total of three replicates, the cell concentration LOD per root bandwidth is 3.88×10⁸ cells · mL⁻¹ · Hz ^−1/2, and the viable cell concentration LOD per root bandwidth is 2.36×10⁹ viable cells · mL⁻¹ · Hz ^−1/2.

B. Viability Mapping

MR images of a B16-F10 cell viability gradient are shown in Fig. 3. Thirty diffusion-weighted contrast acquisitions were averaged to generate the image shown in (a). A gradient amplitude of 8.12 G/cm, b-value of 800 s·mm⁻², and Δ of 100 ms were used to generate contrast. A reference scan, to which the contrast-optimized scan was normalized, was generated using the same pulse sequence timing, but no diffusion weighted gradient. Two scans were averaged for the diffusion-weighted reference. The frequency offset used to generate contrast for the MT-weighted image shown in (b) was 3.3 kHz. A frequency offset of 200 kHz was used for the MT reference scan to which the contrast sensitive scan was normalized. The contrast and reference scans were both averaged from two acquisitions. The same imaging settings and pulse sequences were used for all other figures in this study.

Fig. 3. Viability Gradient MRI.

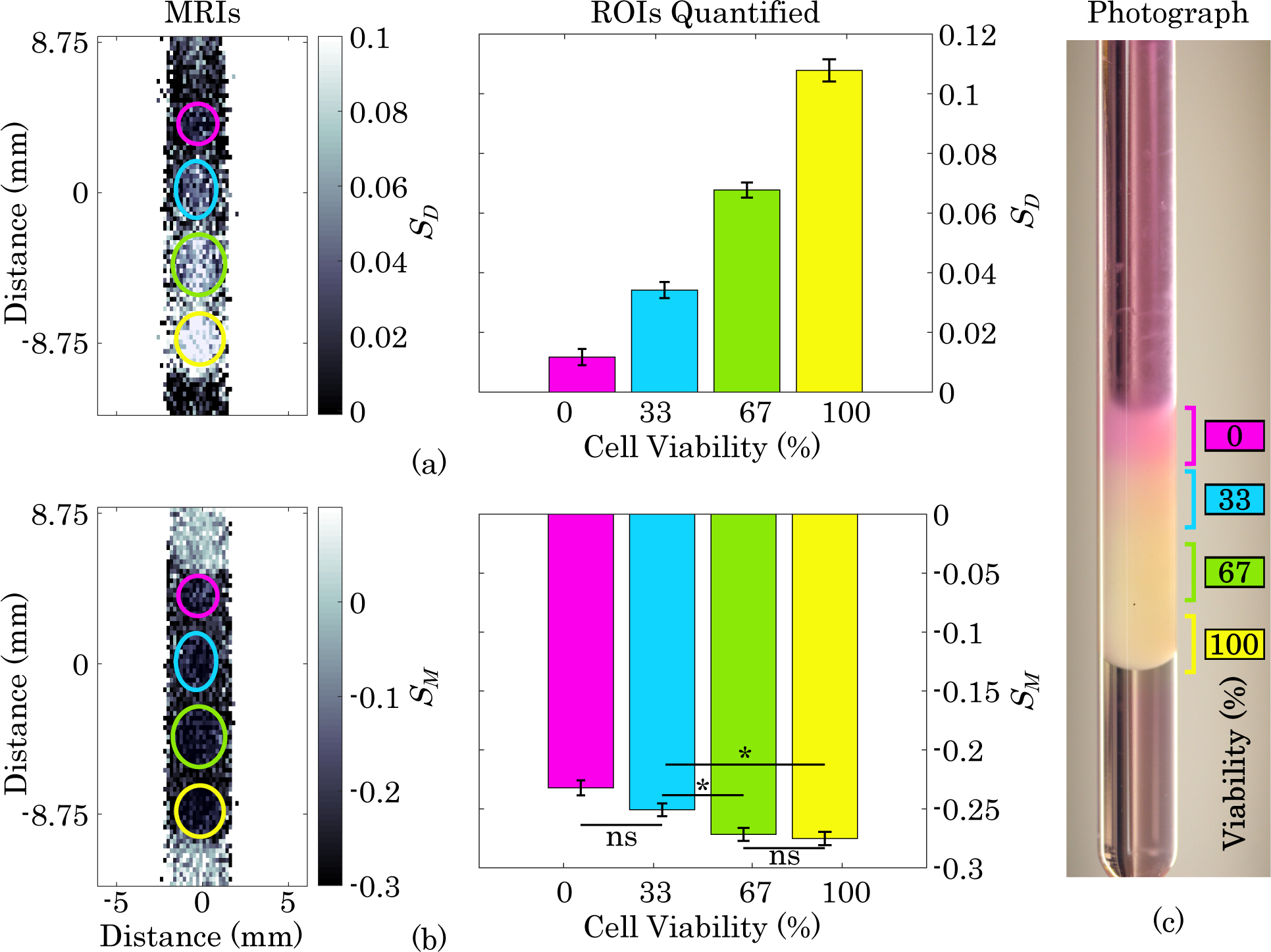
(a) Diffusion-weighted MRI and quantification of layers of gel containing, from top to bottom, 0%, 33%, 66%, and 100% viable B16-F10 cells with a constant total cell density of 2×10⁸ cells·mL⁻¹ Error bars represent one standard error. All groups have a statistically significant difference from each other (p<0.0001). (b) MT-weighted image and quantification of viability gradient sample. ns = not significant, * indicates significant difference (p <0.05), and all others are significantly different (p <0.0001). (c) Photograph of NMR tube containing viability gradient immediately after sample prep and prior to MRI acquisition.

In Fig. 3 (a), the diffusion-weighted image shows distinct layers of increasing signal intensity corresponding to increasing viability, whereas the MT-weighted image shows less sensitivity to the changing viability. In the diffusion-weighted image, all layers with viability greater than 0% are distinct from the baseline signal (acellular agarose above and below the layers). Despite being indistinguishable from each other, the layers in the MT-weighted image are clearly distinct from the acellular agarose region surrounding the layers, indicating that at this cell concentration, the MT weighting detects the presence of cells without being heavily impacted by viability. When the signals from each layer were quantified, all layers were found to be significantly different from each other in the diffusion-weighted image, whereas only four of the six pairwise comparisons between layers in the MT-weighted image were significantly different, and the difference was much less pronounced.

MR images of a B16-F10 cell density gradient are shown in Fig. 4. It can be seen that both diffusion- and MT-weighted signals are strongly dependent on cell density with the strength of the diffusion-weighted signal positively correlated with density and the strength of the MT-weighted signal inversely correlated with density (consistent with our previous findings in HEK 293 cells [1]). The signal intensities of each layer are all significantly different from each other in both weightings.

Fig. 4. Density Gradient MRI.

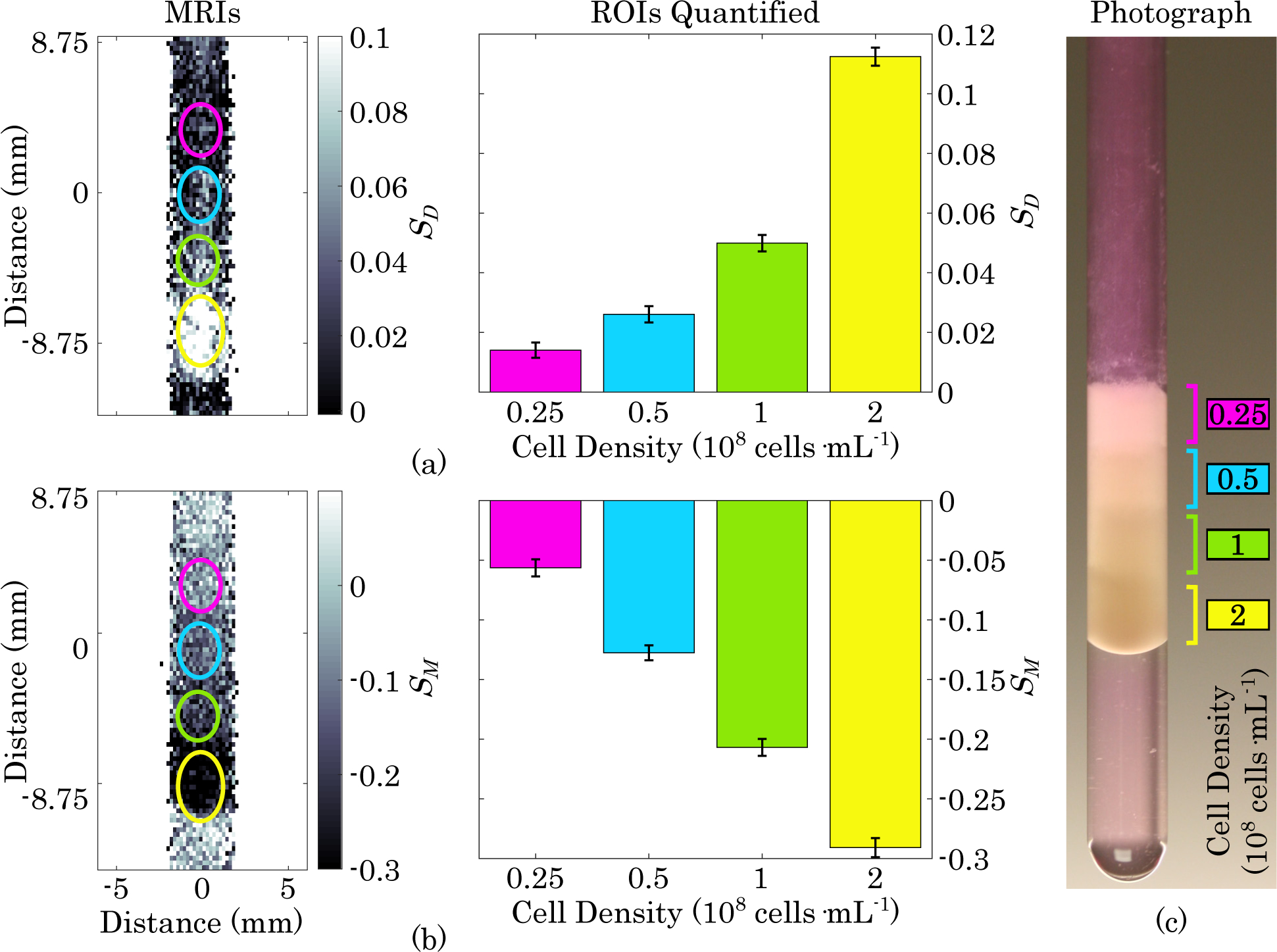
(a) Diffusion-weighted MRI and quantification of layers of gel containing, from top to bottom, 0.25, 0.5, 1, and 2 ×10⁸ cells · mL⁻¹ B16-F10 cells with 100% viability. Error bars represent one standard error. All layers have a statistically significant difference from each other (p <0.0001). (b) MT-weighted image and quantification of cell density gradient. All layers have a statistically significant difference from each other (p <0.0001). (c) Photograph of NMR tube containing cell density gradient immediately after sample prep and prior to MRI acquisition.

Finally, MR images of B16-F10 cells of four different combinations of viability and density are shown in Fig. 5. In the diffusion-weighted image shown in Fig. 5 (a), all layers were significantly different from each other except for the layer containing 2 × 10⁸ cells·mL⁻¹ at 50% viability and the layer containing 1×10⁸ cells·mL⁻¹ at 50% viability. Both of these layers contained the same concentration of viable cells (1×10⁸ viable cells·mL⁻¹). In the MT-weighted image shown in Fig. 5 (b), all layers were significantly different from each other, suggesting dependence on both cell density and viability.

Fig. 5. MRI of Viability and Density Combinations.

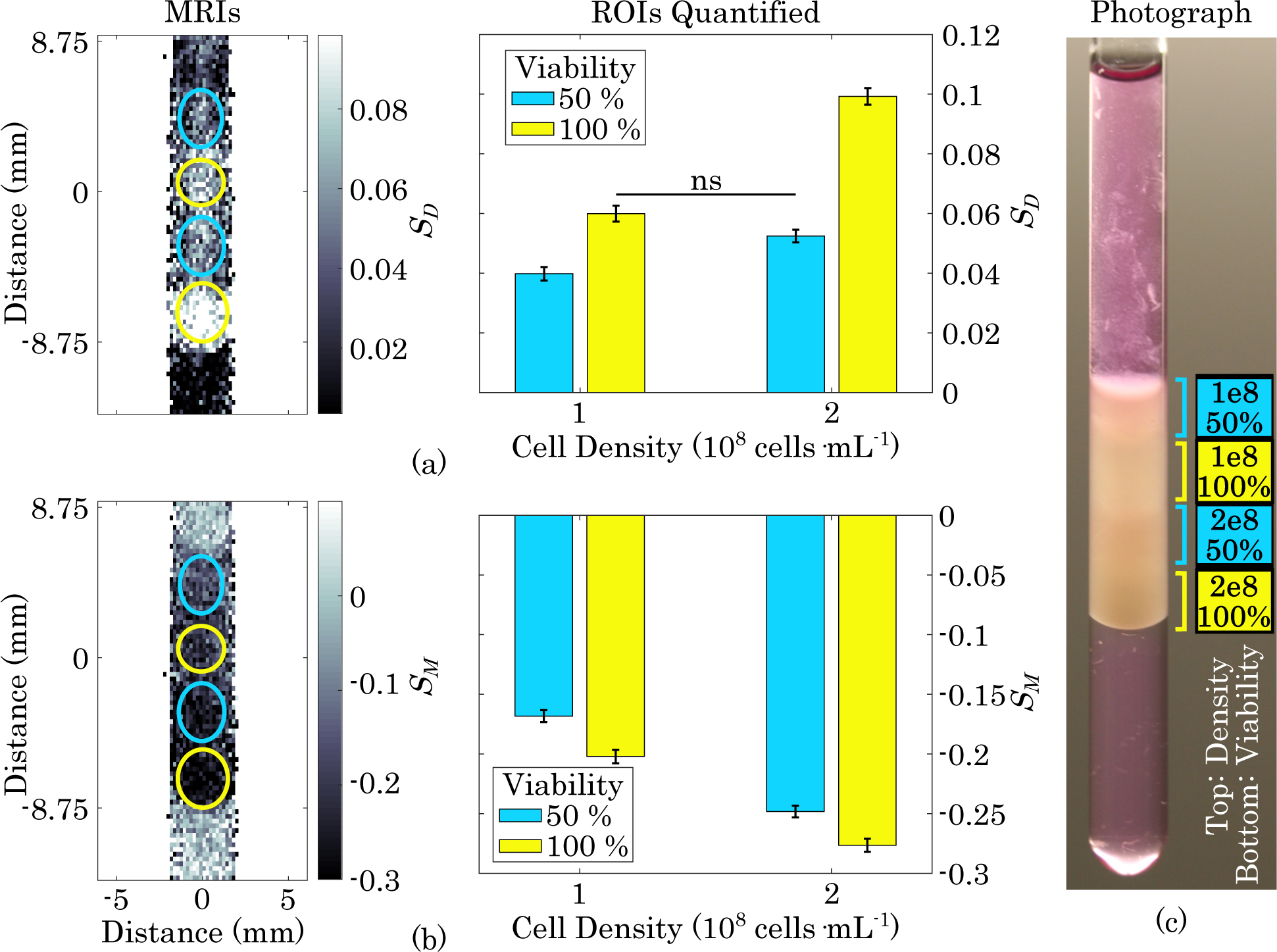
(a) Diffusion-weighted MRI and quantification of layers of gel containing, from top to bottom, B16-F10 densities of 1, 1, 2, and 2 ×10⁸ cells · mL⁻¹ and corresponding viabilities of 50, 100, 50, and 100% . Error bars represent one standard error. ns = not significant, all other layers are significantly different from each other (p <0.0001). (b) MT-weighted image and quantification of cell density and viability combinations. All layers are significantly different from each other (p <0.0001). (c) Photograph of NMR tube containing combinations of viability and density immediately after sample prep and prior to MRI acquisition.

After acquiring each image, the mean diffusion- and MT-weighted signal intensities from each ROI were fitted to viability and density calibration surfaces. The fitted equations for each image were then used to calculate the cell viability and cell density on a voxel-by-voxel basis. Images of cell density and viability are show in Fig. 6. With only four cell populated layers and an acellular background region, a power series with second order terms for both diffusion- and MT-weighted signal was not possible. One of the parameters needed to be restricted to first order terms in order to fit a surface. The results did not appear to depend on which parameter was restricted to first order. Fig. 6 shows that cell density images are clearly representative of the sample in all cases, but cell viability calibrations worked best when the layers contained a full range of viability to use in the calibration.

Fig. 6. Maps of Cell Density and Viability.

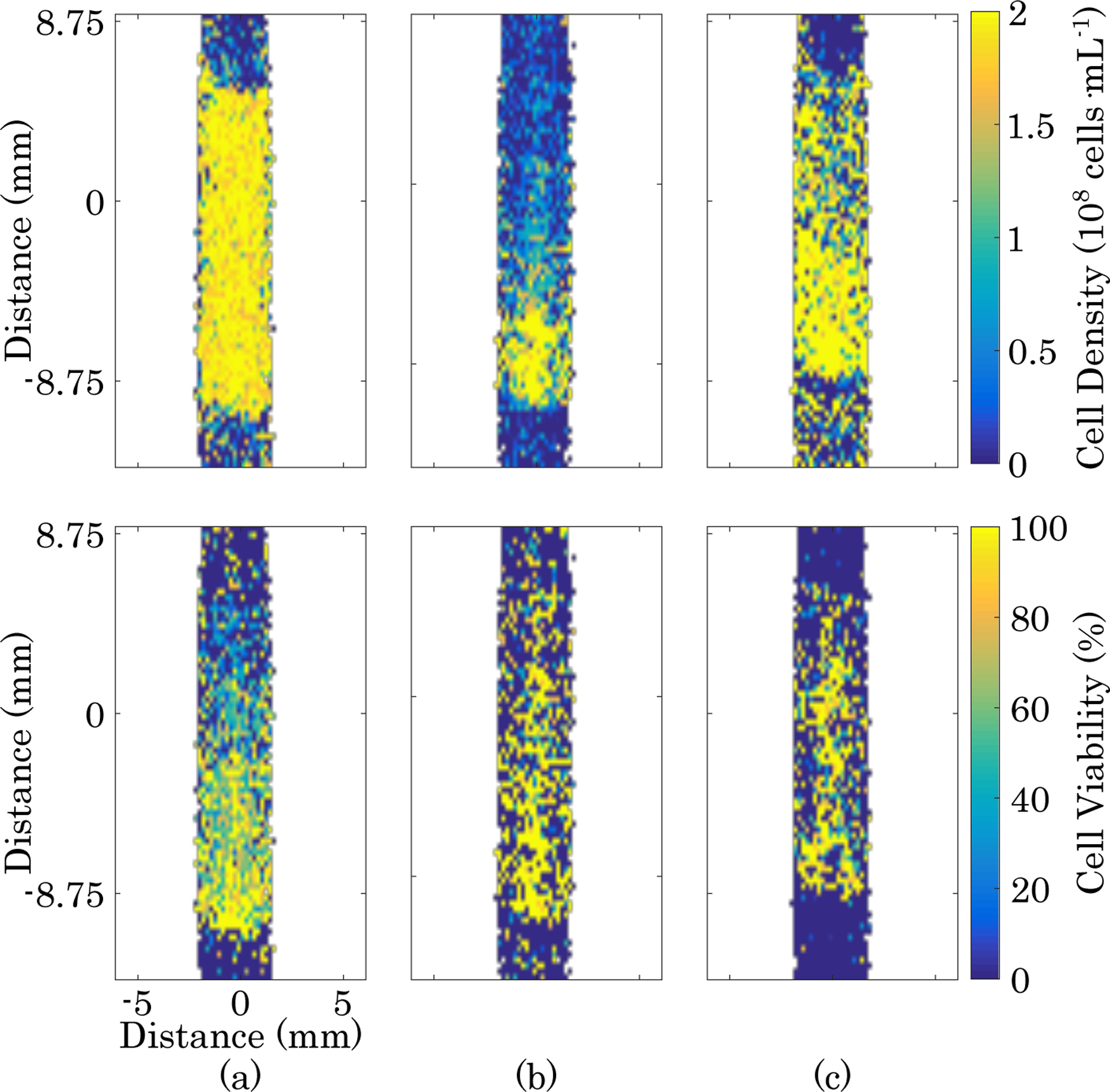
Top: cell density maps. Bottom: cell viability maps. (a) Cell viability gradient sample shown in Fig. 3. (b) Cell density gradient sample shown in Fig. 4. (c) Sample containing cell viability and density combinations shown in Fig. 5.

IV. Discussion

A. Decoupling Cell Viability from Cell Density

Our results suggest that the viability and density of a population of cells cultured in a hydrogel can be quantifiably mapped independently of each other without contrast agents using only diffusion- and MT-weighted MRI scans. From our data it can be seen that the diffusion-weighted signal is largely dependent on the number of viable cells, as measured by intact membranes detected with trypan blue. This is supported in both our NMR spectroscopy calibrations and our images which show increasing diffusion weighted signal with increasing numbers of viable cells. However, the presence of dead cells does have a slight influence on the diffusion weighted measurement, likely due to partially intact membranes and remaining macromolecular content restricting water motion to a lesser degree. For example, upon close examination of Fig. 1 (a), the sample with 100% viable cells at 5 × 10⁷ cells · mL⁻¹ has a lower diffusion weighted signal than the sample containing 50% viable cells at 1 × 10⁸ cells · mL⁻¹ despite the fact that they both have the same number of viable cells. Additionally, there is a pattern of increasing diffusion weighted signal with increasing cell density in the 0% viable cell samples.

Another notable observation is that the MT-weighted signal is mostly dependent on the total number of cells, but it is not completely independent of the viability of the cells. Fig. 1 (b) shows the magnitude of MT-weighted response decrease with increasing viability at low cell concentrations, meaning the non-viable cells are contributing more to the MT-weighted signal. At the greatest cell concentration in Fig. 1, 1×10⁸ cells · mL⁻¹, the MT-weighted signal has nearly zero dependence on cell viability. When imaging an even higher cell density of 2 × 10⁸ cells · mL⁻¹, the magnitude of the MT-weighted response increased with increasing viability. Therefore, the type of dependence of MT-weighted signal on cell density is dependent on the density of cells at which viability is being measured, but it consistently holds that the dependence of MT-weighted signal on viability is less than its dependence on cell density over the ranges examined.

The results of this study show a clear decrease in diffusion-weighted signal with decreasing viability, which is the inverse of the response of diffusion-weighted signal to lesions caused by acute ischemic stroke [29]–[31]. In this study, cells were fixed and permeabilized to replicate the stage of cell death in which membrane integrity is lost and the cell body remains intact, a state that is consistent with the state detected by optical viability assays based on dyes excluded by intact membranes [32], [33]. Prior to reaching this state, a series of pre-morbid cellular processes, referred to as cytotoxic edema, are known to influence diffusion-weighted NMR readings. These processes notably include hypoxia induced cell swelling [34], [35], which occurs in the brain following ischemic stroke [36]. Diffusion-weighted NMR signal will increase with increases in the fraction of intracellular water volume, whether it is due to increasing cell density or size of individual cells [37]. Therefore, cytotoxic cerebral edema causes an initial increase in diffusion-weighted signal of acute ischemic lesions, whereas the eventual permanent drop in diffusion-weighted signal due to cell death occurs approximately one week later [29]–[31].

In this study, permeabilization alone was unable to generate intact cells with ruptured membranes due to the complete dis-integration of cells without prior fixation. Despite the fixation step keeping cells intact, this process is known to result in a 20–30% loss of mass per cell, depending on the concentrations of fixative and detergent used [38]. Since MT is generally sensitive to macromolecular concentration, nonviable cells which have less macromolecular content should contribute less to the magnitude of the change in MT-weighted signal, which was the case at higher cell densities. At lower cell densities, the slight increase in the magnitude of the MT-weighted signal difference with decreasing viability (increasing fraction of nonviable cells) suggests another mechanism is contributing toward the MT-weighted viability dependence.

One possible explanation is the porousness of permeabilized membranes. Magnetization transfer is a process that depends on the exchange of nuclear saturation between protons interacting with macromolecules and protons in free water. Macromolecular protons are selectively saturated, but the final NMR signal is obtained by excitation of free water [39]. Therefore, factors that influence the exchange of magnetization between the two pools will influence MT-weighted signal in addition to the total quantity of macromolecular content. A factor that could influence the rate of exchange is the contact area between macromolecules and free water, which can be influenced by membrane permeabilization. Detergents form physical pores in cell membranes [19]. Adding detergents to phospholipid bilayers increases the total lipid surface area in contact with free water molecules [40], [41]. Increasing the lipid-water contact area would facilitate the transfer of magnetization between macromolecules and free water, leading to an increase in the MT-weighted response with decreasing viability. This pattern is seen at low cell densities. As cell density increases, intercellular macromolecular crowding may diminish this effect by reducing macromolecular interactions with free water.

Despite the interdependence of diffusion- and MT-weighted signals on both total cell number and the viable fraction of cells, measurements of cell density and viability can be obtained independently of each other with only a diffusion and MT-weighted acquisition and a multivariate calibration surface. This method applies both to NMR spectroscopy bulk measurements and spatially resolved MRI maps of cell populations on a voxel by voxel basis. Compared to cell density imaging, our results indicate that mapping cell viability requires a higher number of scans to resolve cell viability numbers in a reasonable range. To put it in perspective, three scans corresponded to a cell density LOD of 1.94×10⁷ cells · mL⁻¹ and a viable cell LOD of 1.18×10⁸ viable cells · mL⁻¹. The cell density LOD is in a practical range - the average physiologic hepatocellularity is 1.12×0⁸ cells · mL⁻¹ (based on a reported average hepatocellularity of 1.07×10⁸ cells·g⁻¹ [42] and an average hepatic density of 1.051 g·mL⁻¹ [43]) whereas engineered hepatic seeding densities have been reported with an upper range that is an order of magnitude less [44]. However, cell viability measurements require additional scans to achieve a measurement in a practical range. This is consistent with our imaging results which found that preparing a calibration standard with viability variation is more critical than cell density variation.

V. Conclusion

In this study, we showed that cell viability and cell density can be quantifiably mapped independently from each other in a hydrogel using diffusion and MT-weighted MRI. We showed that these two parameters have unique functional dependencies on viability and density which can be resolved with a multivariate second order power series calibration. Our findings showed that the quantity of time required to quantify viability is much greater than what is required for cell density, making it less practical for contrast-free implementation. The noninvasiveness of this technique makes it applicable for monitoring cell health and cell number in opaque 3D environments such as engineered tissues and perfusion bioreactors.