Propensity Score Weighting and Trimming Strategies for Reducing Variance and Bias of Treatment Effect Estimates: A Simulation Study

Abstract

To extend previous simulations on the performance of propensity score (PS) weighting and trimming methods to settings without and with unmeasured confounding, Poisson outcomes, and various strengths of treatment prediction (PS c statistic), we simulated studies with a binary intended treatment T as a function of 4 measured covariates. We mimicked treatment withheld and last-resort treatment by adding 2 “unmeasured” dichotomous factors that directed treatment to change for some patients in both tails of the PS distribution. The number of outcomes Y was simulated as a Poisson function of T and confounders. We estimated the PS as a function of measured covariates and trimmed the tails of the PS distribution using 3 strategies (“Crump,” “Stürmer,” and “Walker”). After trimming and reestimation, we used alternative PS weights to estimate the treatment effect (rate ratio): inverse probability of treatment weighting, standardized mortality ratio (SMR)-treated, SMR-untreated, the average treatment effect in the overlap population (ATO), matching, and entropy. With no unmeasured confounding, the ATO (123%) and “Crump” trimming (112%) improved relative efficiency compared with untrimmed inverse probability of treatment weighting. With unmeasured confounding, untrimmed estimates were biased irrespective of weighting method, and only Stürmer and Walker trimming consistently reduced bias. In settings where unmeasured confounding (e.g., frailty) may lead physicians to withhold treatment, Stürmer and Walker trimming should be considered before primary analysis.

Abbreviations

AUC

area under the receiver operating characteristic curve

IPTW

inverse probability of treatment weighting

PS

propensity score

RE

relative efficiency

RR

rate ratio

SMR

standardized mortality ratio

The propensity score (PS), proposed by Rosenbaum and Rubin in 1983 (1), allows pharmacoepidemiologists to focus on treatment decisions, including timing and alternatives, and highlights the importance of choosing an appropriate study population in the presence of treatment effect heterogeneity (2–4). Weighting of observations on the basis of some function of the PS allows researchers to balance covariates across treatment groups and hence estimate unconfounded treatment effects in defined populations. For dichotomous treatments, researchers commonly use weights to estimate treatment effects in 3 possible target populations: the treated and untreated combined (average treatment effect in the population), the treated population (average treatment effect in the treated), and a group that gets much less attention, the untreated population (average treatment effect in the untreated). Recently, additional balancing weights have been proposed, including matching weights (5), overlap weights (6), and entropy weights (7), which can increase efficiency and reduce imbalances if the PS model is misspecified but which have uncertain performance in the presence of unmeasured confounding.

Restricting the study population provides another way to reduce the variance of weighted estimates and to reduce bias from confounding in the tails of the PS distribution. Methodologists with different goals have proposed various methods of trimming the study population based on the PS or a function of the PS. Crump et al. (8) proposed reducing the variance of inverse probability of treatment weighting (IPTW) estimates of the average treatment effect in the overall population by trimming both tails of the PS distribution, thereby restricting the study population to observations without an extreme preference for one of the treatments compared. Motivated by studies that found both unmeasured confounding and treatment contrary to prediction to be more common in the tails of the PS distribution (9, 10), Stürmer et al. (11) proposed a different trimming approach to reduce confounding in settings where unmeasured factors may result in patients’ being treated contrary to prediction. Trimming by a function of the PS, the preference score, was extended to the setting of comparative effectiveness research by Walker et al. (12), to enhance validity through focus on comparison of subjects in treatment equipoise.

While trimming has been proposed to reduce the magnitude of unmeasured confounding in pharmacoepidemiology and comparative effectiveness research, the separate and joint effects of trimming and more recent weighting strategies that down-weight observations in the tails of the PS (i.e., matching weights, overlap weights, and entropy weights) have not been assessed with respect to their potential to reduce unmeasured confounding. Here we extend the simulations of Stürmer et al. (11), Yoshida et al. (13), and Li et al. (14) to the combination of all established weighting methods (IPTW, standardized mortality ratio (SMR)-treated, and SMR-untreated) and novel weighting methods (matching, overlap, and entropy) with all proposed trimming methods (Crump, Stürmer, and Walker) in the setting of a dichotomous treatment and a Poisson outcome more closely mimicking pharmacoepidemiologic settings, and with and without unmeasured confounding concentrated in the tails of the PS.

METHODS

Data generation

We used the same simulation setup as Stürmer et al. (11), outlined in Web Figure 1 (available online at https://doi.org/10.1093/aje/kwab041). In brief, we simulated 5,000 cohort studies with a sample size of n = 10,000 each and a binary intended treatment T as a function of 6 measured covariates—instruments (X₁ and X₄), risk factors (X₂ and X₅), and confounders (X₃ and X₆), each category being both dichotomous (X₁, X₂, and X₃) and continuous (X₄, X₅, and X₆). We then mimicked the overriding of the predicted treatment decision by adding 2 rare (prevalence approximately 1% each) “unmeasured” dichotomous confounders (X₇ and X₈) that directed treatment assignment to change for a small number of patients in both tails of the PS distribution. X₇ directed last-resort treatment, leading to treatment in some patients who are very unlikely to be treated (e.g., because they have a very bad prognosis) while strongly increasing the risk for the outcome. X₈ directed treatment withheld, leading to nontreatment of some patients who are very likely to be treated (e.g., because they are frail), again strongly increasing the risk for the outcome. X₇ was set to 1 (present) when a random uniform number was less than or equal to [γ − p(T|X₁–X₆)] and set to 0 otherwise. Thus, observations with a probability of intended treatment close to 0 would be most likely to have X₇ = 1, and no one with a probability of intended treatment greater than γ would have X₇ = 1. The values for γ ranged from 0.037 to 0.520, depending on the scenario (mostly, prevalence of treatment). X₈ was set to 1 (present) when a random uniform number was less than or equal to [p(T|X₁–X₆) − δ] and set to 0 (absent) otherwise. Thus, observations with a probability of intended treatment close to 1 would be most likely to have X₈ = 1, and no one with a probability of intended treatment less than δ would have X₈ = 1. The values for δ ranged from 0.285 to 0.967, depending on the scenario (again, mostly prevalence of treatment). The number of outcomes Y (over a constant follow-up period) was then simulated as a Poisson function of T (uniform treatment effect), all confounders (including unmeasured), and the 2 risk factors. Table 1 shows the prevalence (distribution) and effects on treatment and outcome of all measured and unmeasured covariates, and Web Figure 2 shows the distributions of the PS based on measured covariates according to treatment and to the c statistic of the PS model.

Table 1.

Parameters Covered in the Simulation Study and Their Values

Variable a	Distribution	OR T	RR γ
X 1	Binomial (10,000, 0.2)	2.0	1.0
X 2	Binomial (10,000, 0.2)	1.0	2.0
X 3	Binomial (10,000, 0.2)	0.2	0.2
X 4	Normal (0, 1)	1.5	1.0
X 5	Normal (0, 1)	1.0	1.5
X 6	Normal (0, 1)	0.5	0.5
X 7	Binomial (10,000, ~0.01)	1.0, 10.0	1.0, 10.0
X 8	Binomial (10,000, ~0.01)	1.0, 0.1	1.0, 10.0
T, P = 0.2, 0.5, 0.8	Binomial (10,000, P)		1.0, 2.0
Y|T = 0	Poisson (λ ~ 0.1)
AUC	0.75 (0.85, 0.65)

Abbreviations: AUC, area under the receiver operating characteristic curve; OR, odds ratio; RR, rate ratio.

^a  T, treatment; X₁–X₈, covariates; Y, outcome.

Estimands

In all studies, we estimated the PS with main-effects logistic regression as a function of measured covariates only (i.e., ignoring X₇ and X₈). We trimmed the tails of the PS distribution using 5 strategies (Table 2): 1) no trimming (i.e., allowing for PS tails containing only treated or only untreated (i.e., nonpositivity); 2) common range trimming (trimming observations below the lowest observed PS in the treated and above the highest observed PS in the untreated); 3) “Crump” trimming (trimming observations below a PS of 0.1 and above a PS of 0.9); 4) “Stürmer” trimming (trimming both treated and untreated observations below the fifth percentile of observed PS in the treated and above the 95th percentile of observed PS in the untreated); and 5) “Walker” trimming (trimming observations below a preference score of 0.3 and above a preference score of 0.7, where higher scores reflect higher preference for treatment given measured covariates and the logit of the preference score is defined as the logit of the PS minus the logit of the treatment prevalence). These trimming methods have recently been described and compared in detail with regard to the resulting study populations (15). While Crump et al. (8) and Walker et al. (12) proposed only 1 set of cutpoints, Stürmer et al. (11) originally proposed using a range of cutpoints (the first, 2.5th, and fifth percentiles of the treated and their complements on the upper end of the untreated PS distribution). For our simulations, we chose the fifth and 95th percentile trimming only, since Glynn et al. (15) used the fifth percentile cutpoint for Stürmer trimming when comparing the number trimmed (and remaining after trimming) across the 3 trimming strategies and Yoshida et al. (13) similarly compared the number trimmed for 3 treatments (using adapted but unique cutpoints).

Table 2.

Propensity Score Trimming Methods Implemented in the Simulation Study

Method	Term Used	Lower Cutpoint	Upper Cutpoint
No trimming	N/A	N/A	N/A
Remove nonpositivity regions	Common range	Lowest PS in the treated	Highest PS in the untreated
Stürmer et al. (11)	Stürmer	Fifth PS percentile in the treateda	95th PS percentile in the untreateda
Walker et al. (12)	Walker	Preference scoreb ≤0.3	Preference scoreb ≥0.7
Crump et al. (8)	Crump	PS ≤0.1	PS ≥0.9

Abbreviation: N/A, not applicable; PS, propensity score.

^a Stürmer et al. (11) also proposed first/99th and 2.5th/97.5th percentile cutpoints.

^b Logit(preference score) = logit(PS) − logit(treatment prevalence); this transformation makes it possible to use absolute cutpoints irrespective of the treatment prevalence.

After trimming (if applicable), we reestimated the PS to improve covariate balance. Reestimation of the PS in the trimmed populations is important, since the PS model estimated in the untrimmed population will be misspecified in the population remaining after trimming (16). We then implemented 6 different PS weights (Table 3) to estimate the treatment effect (rate ratio), including 3 defined populations: the overall population (i.e., both the treated and the untreated (average treatment effect in the population)), the treated (average treatment effect in the treated), and the untreated (average treatment effect in the untreated). Three alternatives targeted less well defined populations: overlap weights, which are proposed to increase efficiency by emphasizing the population with the most overlap in observed characteristics (6); matching weights, which mimic 1:1 matching without replacement and varying target populations depending on the treatment prevalence (5); and entropy weights, which were originally proposed as an iterative process to lead to better covariate balance (7). For our simulations, we used closed-form entropy weights, multiplying IPTW weights with a semicircular tilting function recently proposed by Zhou et al. (17).

Table 3.

Propensity Score Weighting Methods Implemented in the Simulation Study and Their Target Populations

Target Population	Term Used	Treated	Untreated
Combined	IPTW	1/PS	1/(1 − PS)
Treated	SMR-treated weights	1	PS/(1 − PS)
Untreated	SMR-untreated weights	(1 − PS)/PS	1
Overlap	Overlap weights	(1 − PS)	PS
Matched	Matching weights	min(PS, (1 − PS))/PS	min(PS, (1 − PS))/(1 − PS)
Combined	Entropy weights	−[PS × log(PS) + (1 − PS) × log(1 −  PS)]/PS	−[PS × log(PS) + (1 − PS) × log(1 −  PS)]/(1 − PS)

Abbreviations: IPTW, inverse probability of treatment weighting; PS, propensity score; SMR, standardized mortality ratio.

Performance measures

We report the exponent of the mean log rate ratio (RR) across simulations and used the empirical variance of the log(RR) across simulations to derive empirical 95% confidence intervals. The mean squared error was estimated as the mean (across simulations) of the squared bias within simulations. We used the within-simulation variance ignoring the estimation of the PS when assessing coverage probabilities. The relative efficiency (RE) of estimators versus untrimmed IPTW was calculated by multiplying the inverse of the empirical variance of the specific estimator by the empirical variance of the untrimmed IPTW (×100). Nonconvergence was defined as an estimated treatment effect | β | or its standard error being greater than 5; all values for such studies were set to missing.

RESULTS

All scenarios assessed had fewer than 20 out of 5,000 studies with nonconvergence. We present efficiency results without unmeasured confounding for the basic scenario in Figure 1 (for a treatment prevalence of 20%) and Web Table 1 (for all treatment prevalences). As expected, all estimates were unbiased. RE as compared with the untrimmed IPTW ranged from 61% (for SMR-untreated weights with Walker trimming) to 123% (for overlap weights without any trimming or with trimming to a common PS range). Crump trimming improved efficiency for IPTW (RE = 112%) but did not further increase efficiency for overlap weights (RE = 120% with Crump trimming vs. RE = 123% without prior trimming). With increasing treatment prevalence (Web Table 1), differences in RE generally became more pronounced while maintaining the patterns observed for a treatment prevalence of 20%. For a treatment prevalence of 80%, untrimmed IPTW is especially variable, leading to more pronounced efficiency gains with the untrimmed overlap, matching, SMR-untreated, and entropy weights (all >200%). This imprecision of the untrimmed IPTW is due to the simulation setup with an incidence rate ratio of 2.0 and an incidence in the unexposed of 0.1. This setup leads to few events in the unexposed and, in combination with large weights in those few unexposed with high propensity for treatment, an imprecise untrimmed IPTW estimator.

Figure 1.

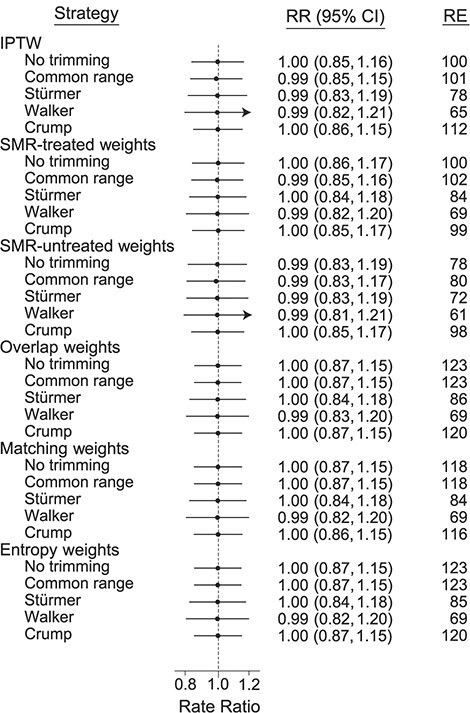
Mean rate ratios (RRs) and relative efficiency (RE) from 5,000 simulated studies without unmeasured confounding. RRs are exponentiated mean log(RRs) across simulations; 95% confidence intervals (CIs) are derived from the empirical variance of the log(RR) across simulations; and the REs of estimators versus untrimmed inverse probability of treatment weighting (IPTW) are calculated by multiplying the inverse of the empirical variance of the specific estimator by the empirical variance of the untrimmed IPTW (×100). True RR = 1.0; treatment prevalence = 20%. Bars, empirical 95% CIs. SMR, standardized mortality ratio.

In Web Tables 2 and 3, we present results without unmeasured confounding for the scenarios with stronger prediction of treatment (area under the receiver operating characteristic curve (AUC) (c statistic) = 0.85; Web Table 2) and weaker prediction of treatment (AUC = 0.65; Web Table 3). The differences in RE were greater with stronger predictors of treatment, but the patterns were again preserved. In these scenarios, Stürmer trimming increased efficiency for IPTW, SMR-treated weights, and SMR-untreated weights as compared with untrimmed estimators, but not for overlap weights, matching weights, and entropy weights. Stürmer trimming came close to Crump trimming for SMR-treated weights (treatment prevalence = 20%).

Figure 2 shows results for the basic scenario with unmeasured confounding due to treatment withheld (mimicking frailty) with a treatment prevalence of 20%, and Table 4 shows results for unmeasured confounding due to last-resort treatment, treatment withheld, and their combination. Since most of the differences were observed for treatment withheld (and similarly for the combination of the 2 unmeasured confounding patterns), we focus here on treatment withheld. Note that we simulated the unmeasured confounding scenarios with a true incidence rate ratio of 2.0. Unmeasured confounding due to treatment withheld led to a considerable bias in the direction opposite the bias due to measured confounding. All weighting approaches, when controlling only for the measured confounders, were biased without trimming. This included the 3 approaches that down-weight the tails of the PS distribution (overlap, matching, and entropy weights), which might be expected to reduce bias due to unmeasured confounding concentrated in the tails of the PS distribution. Without trimming, SMR-treated weights, matching weights, and entropy weights were most biased and SMR-untreated weights were least biased. Only Stürmer and Walker trimming consistently reduced bias from unmeasured confounding for all weighting approaches, whereas Crump trimming consistently did not reduce bias.

Figure 2.

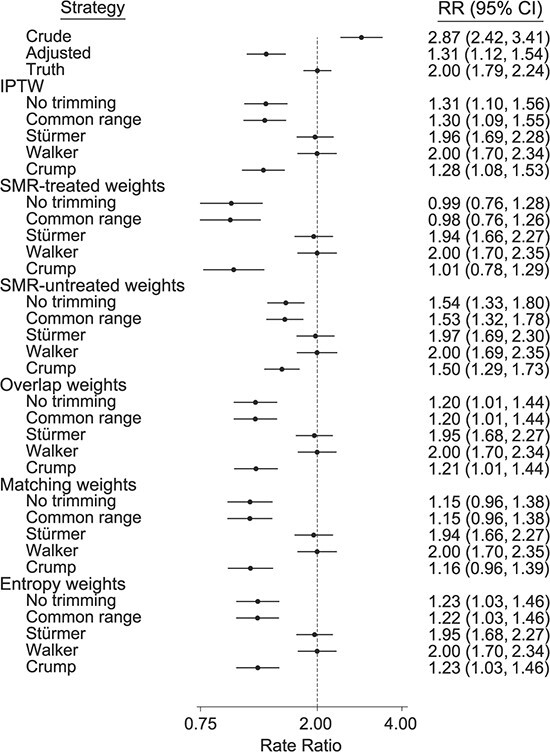
Mean rate ratios (RRs) from 5,000 simulated studies with unmeasured confounding due to treatment withheld, mimicking frailty. RRs are exponentiated mean log (RR) across simulations, and 95% confidence intervals (CIs) are derived from the empirical variance of the log(RR) across simulations. True RR = 2.0; treatment prevalence = 20%; area under the receiver operating characteristic curve (c statistic) = 0.75. Bars, empirical 95% CIs. IPTW, inverse probability of treatment weighting; SMR, standardized mortality ratio.

Table 4.

Mean Rate Ratios, Empirical Variance, Mean Squared Error, and Percent Coverage of 95% Confidence Intervals From 5,000 Simulated Studies With Unmeasured Confounding Leading to Treatment Contrary to Prediction According Pattern of Unmeasured Confounding^a

	Pattern of Unmeasured Confounding
	Last Resort Treatment				Treatment Withheld				Last Resort and Withheld
Weighting and Trimming Method	RR	Var b	MSE c	Cov, % d	RR	Var b	MSE c	Cov, % d	RR	Var b	MSE c	Cov, % d
Crude	3.50	0.0033	0.3181	0	2.87	0.0077	0.1386	0	2.88	0.0076	0.1397	0
Residual confounding	2.08	0.0033	0.0049	88	1.31	0.0067	0.1829	0	1.38	0.0068	0.1464	0
True outcome model	2.00	0.0031	0.0031	95	2.00	0.0034	0.0034	95	2.00	0.0034	0.0034	95
IPTW
No trimming	2.18	0.0049	0.0123	80	1.31	0.0082	0.1867	0	1.45	0.0088	0.1132	8
Common rangee	2.17	0.0049	0.0112	82	1.30	0.0080	0.1941	0	1.44	0.0086	0.1178	6
Stürmere	2.04	0.0051	0.0055	95	1.96	0.0060	0.0063	96	2.01	0.0063	0.0063	95
Walkere	2.00	0.0057	0.0057	96	2.00	0.0068	0.0068	96	2.00	0.0067	0.0067	96
Crumpe	2.00	0.0036	0.0036	96	1.28	0.0080	0.2040	0	1.31	0.0080	0.1896	0
SMR-treated weights
No trimming	2.06	0.0045	0.0054	94	0.99	0.0172	0.5157	0	1.05	0.0165	0.4312	0
Common range	2.05	0.0045	0.0050	95	0.98	0.0162	0.5264	0	1.04	0.0156	0.4415	0
Stürmer	2.01	0.0048	0.0049	96	1.94	0.0065	0.0074	94	1.97	0.0064	0.0067	95
Walker	2.00	0.0057	0.0057	96	2.00	0.0068	0.0068	96	2.00	0.0067	0.0067	96
Crump	2.00	0.0047	0.0047	96	1.01	0.0164	0.4876	0	1.02	0.0166	0.4702	0
SMR-untreated weights
No trimming	2.23	0.0065	0.0188	75	1.54	0.0061	0.0728	12	1.72	0.0077	0.0305	61
Common range	2.22	0.0064	0.0174	77	1.53	0.0060	0.0772	10	1.71	0.0076	0.0324	58
Stürmer	2.04	0.0057	0.0061	95	1.97	0.0063	0.0065	96	2.02	0.0068	0.0069	95
Walker	2.00	0.0060	0.0060	96	2.00	0.0071	0.0072	96	2.00	0.0071	0.0071	96
Crump	2.00	0.0040	0.0040	96	1.50	0.0055	0.0899	4	1.52	0.0055	0.0815	5
Overlap weights
No trimming	2.07	0.0035	0.0047	93	1.20	0.0083	0.2661	0	1.27	0.0083	0.2131	0
Common range	2.07	0.0035	0.0046	93	1.20	0.0082	0.2673	0	1.27	0.0082	0.2146	0
Stürmer	2.02	0.0046	0.0047	96	1.95	0.0060	0.0066	95	1.98	0.0060	0.0061	96
Walker	2.00	0.0055	0.0055	96	2.00	0.0066	0.0066	96	2.00	0.0065	0.0065	96
Crump	2.00	0.0036	0.0036	97	1.21	0.0083	0.2621	0	1.23	0.0083	0.2484	0
Matching weights
No trimming	2.06	0.0037	0.0045	94	1.15	0.0089	0.3141	0	1.20	0.0089	0.2672	0
Common range	2.06	0.0037	0.0045	94	1.15	0.0088	0.3154	0	1.20	0.0089	0.2688	0
Stürmer	2.01	0.0048	0.0049	96	1.94	0.0065	0.0074	94	1.97	0.0064	0.0067	95
Walker	2.00	0.0057	0.0057	96	2.00	0.0068	0.0068	96	2.00	0.0067	0.0067	96
Crump	2.00	0.0038	0.0038	96	1.16	0.0090	0.3102	0	1.17	0.0090	0.2961	0
Entropy weights
No trimming	2.09	0.0034	0.0052	91	1.23	0.0081	0.2472	0	1.31	0.0081	0.1899	0
Common range	2.08	0.0034	0.0051	91	1.22	0.0080	0.2489	0	1.30	0.0080	0.1916	0
Stürmer	2.02	0.0046	0.0047	96	1.95	0.0059	0.0064	95	1.99	0.0059	0.0059	95
Walker	2.00	0.0055	0.0055	96	2.00	0.0065	0.0065	96	2.00	0.0064	0.0064	96
Crump	2.00	0.0035	0.0035	97	1.23	0.0082	0.2468	0	1.24	0.0082	0.2329	0

Abbreviations: Cov, coverage; IPTW, inverse probability of treatment weighting; MSE, mean squared error; RR, rate ratio; SMR, standardized mortality ratio; Var, variance.

^a True RR = 2.0; area under the receiver operating characteristic curve (c statistic) = 0.75; treatment prevalence = 20%.

^b Variance of treatment effect estimates (log(RR)) over 5,000 simulated studies.

^c Mean of (log(RR) − log(2.0))² over 5,000 simulated studies.

^d Percentage of simulated studies in which the 95% confidence interval includes the true value (RR = 2.0).

^e Common range: restricting to positivity; Stürmer: asymmetrical trimming at fifth percentile of treated and 95th percentile of untreated; Walker: preference score trimming below 0.3 and above 0.7; Crump: propensity score trimming below 0.1 and above 0.9.

Web Tables 4 and 5 show results for the scenarios with treatment prevalences of 50% and 80%, respectively. Patterns were similar to the results with a treatment prevalence of 20% (Table 4), with a few notable exceptions. With a treatment prevalence of 50%, Crump trimming reduced bias, since the absolute PS cutpoints of 0.1 and 0.9 now trimmed away both tails of the PS distribution. With a treatment prevalence of 80%, Walker trimming outperformed Stürmer trimming with respect to mean bias but not mean squared error. Since bias is mainly due to treatment withheld, we focus here on X₈ for an explanation with results on its prevalence stemming from a single simulated data set with n = 200,000. We simulated X₈ to have an overall prevalence of close to 1% in all scenarios. Stürmer trimming effectively reduced the prevalence of X₈ in both treated and untreated persons to less than 0.05% (with little difference in prevalence, and therefore confounding remaining) with treatment prevalences of 20% and 50%. With a treatment prevalence of 80%, however, the prevalence of X₈ was reduced much less, leaving a more pronounced difference between the treated (X₈ prevalence of 0.14%) and the untreated (X₈ prevalence of 0.37%). In this situation, the prevalence of X₈, which is a strong risk factor for the outcome, is high enough to produce noticeable residual confounding. All weighting methods up-weight at least some of those who are treated contrary to prediction. After IPTW, X₈ had a prevalence of 1.29% in the untreated.

In Table 5, we present results for scenarios with unmeasured confounding due to treatment withheld (mimicking frailty) with a treatment prevalence of 20% according to the AUC of the PS model. Compared with the results from the basic scenario with an AUC of 0.75 (middle columns), a higher AUC (0.85) leads to similar patterns, with Stürmer and Walker trimming performing equally well. With a lower AUC (0.65), Stürmer trimming generally removes more bias than Walker trimming. In Web Table 6, we present results for unmeasured confounding due to treatment withheld according to the AUC of the PS model for a treatment prevalence of 50%. With a lower AUC (0.65), Stürmer trimming outperformed Walker trimming. With a higher AUC (0.85), Stürmer and Walker trimming removed all of the bias due to unmeasured confounding, and Crump trimming removed most of it. In this setting, SMR-untreated weights were least biased without trimming, followed by matching weights.

Table 5.

Mean Rate Ratios, Empirical Variance, Mean Squared Error, and Percent Coverage of 95% Confidence Intervals From 5,000 Simulated Studies With Unmeasured Confounding Leading to Treatment Withheld According to AUC of the Propensity Score Model^a

	AUC of the Propensity Score Model
	AUC = 0.65				AUC = 0.75 b				AUC = 0.85
Weighting and Trimming Method	RR	Var c	MSE d	Cov, % e	RR	Var c	MSE d	Cov, % e	RR	Var c	MSE d	Cov, % e
Crude	2.20	0.0053	0.0147	52	2.87	0.0077	0.1386	0	4.12	0.0068	0.5290	0
Residual confounding	1.52	0.0048	0.0796	92	1.31	0.0067	0.1829	0	1.37	0.0066	0.1472	0
True outcome model	2.00	0.0028	0.0028	96	2.00	0.0034	0.0034	95	2.00	0.0029	0.0029	96
IPTW
No trimming	1.57	0.0046	0.0620	7	1.31	0.0082	0.1867	0	1.19	0.0227	0.2883	2
Common rangef	1.57	0.0045	0.0625	7	1.30	0.0080	0.1941	0	1.15	0.0215	0.3259	1
Stürmerf	1.89	0.0043	0.0078	89	1.96	0.0060	0.0063	96	1.99	0.0069	0.0069	96
Walkerf	1.80	0.0043	0.0151	70	2.00	0.0068	0.0068	96	1.99	0.0095	0.0095	96
Crumpf	1.57	0.0046	0.0630	7	1.28	0.0080	0.2040	0	1.23	0.0119	0.2483	0
SMR-treated weights
No trimming	1.38	0.0074	0.1438	1	0.99	0.0172	0.5157	0	0.79	0.0444	0.9151	0
Common range	1.38	0.0072	0.1444	1	0.98	0.0162	0.5264	0	0.76	0.0411	0.9686	0
Stürmer	1.84	0.0049	0.0118	81	1.94	0.0065	0.0074	94	2.00	0.0067	0.0067	96
Walker	1.72	0.0053	0.0278	48	2.00	0.0068	0.0068	96	2.00	0.0094	0.0094	96
Crump	1.39	0.0073	0.1417	2	1.01	0.0164	0.4876	0	0.93	0.0220	0.6025	0
SMR-untreated weights
No trimming	1.65	0.0041	0.0415	19	1.54	0.0061	0.0728	12	1.76	0.0119	0.0289	78
Common range	1.65	0.0041	0.0419	19	1.53	0.0060	0.0772	10	1.70	0.0111	0.0372	68
Stürmer	1.90	0.0043	0.0070	91	1.97	0.0063	0.0065	96	1.99	0.0078	0.0078	96
Walker	1.83	0.0042	0.0123	77	2.00	0.0071	0.0072	96	1.99	0.0101	0.0101	96
Crump	1.64	0.0041	0.0427	17	1.50	0.0055	0.0899	4	1.63	0.0063	0.0475	32
Overlap weights
No trimming	1.47	0.0056	0.1013	2	1.20	0.0083	0.2661	0	1.25	0.0092	0.2293	0
Common range	1.47	0.0056	0.1014	2	1.20	0.0082	0.2673	0	1.25	0.0092	0.2297	0
Stürmer	1.86	0.0046	0.0102	84	1.95	0.0060	0.0066	95	2.00	0.0062	0.0062	96
Walker	1.75	0.0049	0.0225	55	2.00	0.0066	0.0066	96	1.99	0.0090	0.0090	96
Crump	1.47	0.0056	0.1005	2	1.21	0.0083	0.2621	0	1.30	0.0096	0.1957	1
Matching weights
No trimming	1.39	0.0070	0.1397	1	1.15	0.0089	0.3141	0	1.31	0.0084	0.1882	0
Common range	1.39	0.0069	0.1399	1	1.15	0.0088	0.3154	0	1.31	0.0084	0.1885	0
Stürmer	1.84	0.0049	0.0118	81	1.94	0.0065	0.0074	94	2.00	0.0067	0.0067	96
Walker	1.72	0.0053	0.0278	48	2.00	0.0068	0.0068	96	2.00	0.0094	0.0094	96
Crump	1.39	0.0070	0.1379	1	1.16	0.0090	0.3102	0	1.35	0.0088	0.1614	1
Entropy weights
No trimming	1.23	0.0101	0.2470	0	1.23	0.0081	0.2472	0	1.50	0.0053	0.0898	3
Common range	1.23	0.0100	0.2489	0	1.22	0.0080	0.2489	0	1.49	0.0052	0.0899	3
Stürmer	2.00	0.0062	0.0062	96	1.95	0.0059	0.0064	95	1.86	0.0045	0.0094	86
Walker	1.99	0.0090	0.0090	96	2.00	0.0065	0.0065	96	1.76	0.0047	0.0203	59
Crump	1.28	0.0100	0.2088	0	1.23	0.0082	0.2468	0	1.50	0.0053	0.0894	3

Abbreviations: AUC, area under the receiver operating characteristic curve; Cov, coverage; IPTW, inverse probability of treatment weighting; MSE, mean squared error; RR, rate ratio; SMR, standardized mortality ratio; Var, variance.

^a True RR = 2.0; treatment prevalence = 20%.

^b See Table 4.

^c Variance of treatment effect estimates (log(RR)) over 5,000 simulated studies.

^d Mean of (log(RR) − log(2.0))² over 5,000 simulated studies.

^e Percentage of simulated studies in which the 95% confidence interval includes the true value (RR = 2.0).

^f Common range: restricting to positivity; Stürmer: asymmetrical trimming at fifth percentile of treated and 95th percentile of untreated; Walker: preference score trimming below 0.3 and above 0.7; Crump: propensity score trimming below 0.1 and above 0.9.

DISCUSSION

Our simulations confirmed that overlap weights and Crump trimming of IPTW consistently reduce the variance of PS-weighted treatment effect estimates in comparison with untrimmed IPTW (14). Adding Crump trimming to overlap weights does not further reduce the variance, however. In settings where some treatment decisions are based on unmeasured confounders (e.g., frailty), only Stürmer and Walker trimming consistently reduced bias due to unmeasured confounding in the scenarios assessed, whereas overlap, matching, and entropy weights did not, despite the fact that they down-weight at least 1 tail of the PS distribution. Crump trimming, overlap, matching, and entropy weights were never intended to reduce bias from unmeasured confounding. That said, Crump trimming will do so when the relevant tail of the PS distribution falls into the range of trimming—that is, last-resort treatment with low treatment prevalence, treatment withheld with high treatment prevalence, or, to some extent, either type of confounding with a treatment prevalence close to 50%.

Assuming uniform treatment effects and no unmeasured confounding, all weighted treatment effect estimates will be the same and unbiased. The variance of weighted estimators will be driven by large weights assigned to those observations treated contrary to prediction—that is, the treated with a low PS and the untreated with a high PS. IPTW is most affected by large weights due to the need to up-weight both the treated at the low tail of the PS and the untreated at the high tail of the PS. With IPTW, Crump trimming removes observations with weights greater than 10 and therefore reduces variance. Overlap, matching, and entropy weights achieve similar efficiency gains by down-weighting both tails of the PS distribution. The effects of matching weights, however, will depend on the prevalence of the treatment, since matching weights mimic 1:1 matching without replacement but are generally more efficient (5, 13). With a low treatment prevalence, matching weights will mimic SMR-treated weights and mostly down-weight at the low end of the PS, whereas with a high treatment prevalence, matching weights will mimic SMR-untreated weights and down-weight at the high end of the PS distribution.

With nonuniform treatment effects and no unmeasured confounding, these different weighting estimators will obviously result in different treatment effect estimates. In such settings, the choice of estimator will largely depend on the scientific and public health question at hand rather than any potential efficiency gains. IPTW, SMR-treated weights, and SMR-untreated weights have obvious advantages in the sense that their target populations are clearly defined independent of additional parameters, at least under positivity. While matching weights and 1:1 matching without replacement will produce the average treatment effect in the treated when the treatment prevalence is low, a limited number of untreated subjects with higher PSs will result in the down-weighting (matching weights) or exclusion (1:1 matching) of some of those treated with the highest predicted probability of treatment. This means that the estimand will no longer be the average treatment effect in the treated. Similarly, overlap and entropy weights have less clearly defined target populations, which will vary depending not only on the prevalence of the treatment but also on the AUC (c statistic) of the PS. The latter issue introduces the problem that the target population will depend on the variables used to estimate the PS. Addition of an instrumental variable, for example, will increase the AUC of the PS and therefore increase the number of observations trimmed and reduce the number of those observations remaining in the trimmed population. This phenomenon will be more pronounced with Walker trimming than with Stürmer trimming (15).

With uniform treatment effects and unmeasured factors inducing physicians or patients to make different treatment decisions from those predicted by mismeasured PSs, trimming the tails of the PS or, equivalently, focusing on study populations with better equipoise between treatments will generally reduce bias due to unmeasured confounding. This concept was first proposed in 2010 by Stürmer et al. in the context of estimating a treatment effect versus no treatment (11) and was then extended by Walker et al. to the setting of comparative effectiveness research (12). These methods have recently been compared with each other (and Crump trimming) by Glynn et al. (15) with respect to the effects of the PS AUC (c statistic) on the number of observations remaining in the restricted cohorts. Here we extend these results to bias in estimating a simulated uniform treatment effect. Our finding that aggressive (fifth/95th percentiles) Stürmer and Walker trimming achieve comparable bias reduction in many settings is novel, as is the finding that Walker trimming outperforms Stürmer trimming when the prevalence of treatment is high. Glynn et al. have shown that AUCs or c statistics larger than about 0.67 lead to larger populations remaining after Stürmer trimming as compared with Walker trimming (15). The AUC was 0.75 in our basic scenario. In Figure 2, both trimming methods perform similarly with respect to bias reduction, since they both exclude the PS tails where the small number of observations for persons treated contrary to prediction reside. Nevertheless, there are differences even for an AUC of 0.75; this is most pronounced in Web Table 4 for treatment withheld and a treatment prevalence of 80%, where Walker trimming leads to less biased treatment effect estimates than Stürmer trimming. This difference occurs because Walker trimming removes more observations than Stürmer trimming and therefore more of those treated contrary to prediction in the upper tail of the PS. Assuming true uniform effects, the unclear definition of the target populations is not a problem. Unfortunately, we cannot use the data to test this assertion, since unmeasured confounding may lead to nonuniformity of the treatment effect estimate over the PS or mask real heterogeneity.

Finally, with nonuniform treatment effects and unmeasured confounding, it is impossible to estimate an unbiased treatment effect. Logic might help to separate true heterogeneity from unmeasured confounding in specific settings. In the striking example of apparent heterogeneity of treatment effects described by Kurth et al. (9), for instance, it may be very unlikely that thrombolysis would reduce mortality in any subgroup of patients with stroke based on pathophysiology and results from randomized trials. Recent proposals to abandon the concepts of internal versus external validity and to define bias as any deviation from the true treatment effect in the target population (18) might allow the use of trimming to reduce bias even in situations with true treatment effect heterogeneity. This idea, as well as the consideration to reweight trimmed populations to target populations of interest, clearly needs further research.

Yoshida et al. (13) observed that multinomial Stürmer and Walker trimming were more successful in bias reduction when the 3 treatment groups had very different sizes (10:10:80). Our simulation setup does not seem to lead to similar conclusions, as Stürmer trimming especially was less successful in reducing bias with a treatment prevalence of 80%. Yoshida et al. also observed a variance reduction with all trimming methods for IPTW but not with matching weights or overlap weights (13). This variance reduction was more successful with multinomial Crump and Stürmer trimming than with Walker trimming (13). We observed little or no variance reduction with either Sürmer trimming or Walker trimming for any of the weighting methods assessed, whereas we did reproduce the intended variance reduction of IPTW with Crump trimming. Interestingly, Crump trimming did not further decrease variance for SMR-treated weights, overlap weights, matching weights, and entropy weights in our basic scenario. Li et al. compared bias, variance (RE), and confidence interval coverage of overlap weights with Crump- and Stürmer-trimmed IPTW in the setting of uniform treatment effects on a continuous outcome without unmeasured confounding (14, 19). They demonstrated the validity of asymmetrical (Stürmer) trimming (bias and coverage) and the variance reduction with overlap weights in this setting (19).

Matching weights, overlap weights, and entropy weights have been shown to improve covariate balance as compared with IPTW in settings where the PS model is misspecified (17). Our result that these weighting methods do not reduce bias from unmeasured confounding concentrated in the tails of the PS as compared with IPTW indicates that this improved covariate balance provides no practical advantage in this setting. Potential reduction of model misspecification with respect to the measured confounders due to omission of unmeasured predictors of treatment (the unmeasured confounders) has no noticeable beneficial effect on bias.

Our simulation study had several limitations. As always, results were restricted by the limited number of scenarios and parameter values assessed. Most importantly, we assumed that unmeasured confounding was restricted to the tails of the PS distribution, mimicking the data presented by Kurth et al. (9), Lunt et al. (10), and Stürmer et al. (11). The data generation was based on the idea that an infrequent factor, such as frailty, would lead the physician (patient, caregiver) to override the treatment decision based on “usual” predictors of treatment, since more refined measures of frailty based on health-insurance claims data have been proposed and may capture some of this previously unmeasured confounding (20, 21). However, frailty will remain a construct that is difficult to measure in the absence of specific frailty assessments, and trimming might be needed to reduce confounding by frailty even in settings where some measures of frailty are available. We did not change the incidence of the outcome; in future work, researchers should assess the performance of weighting and trimming methods in settings with rare outcomes.

Our results on trimming for both precision of treatment effect estimates (without unmeasured confounding) and bias reduction (in the presence of unmeasured confounding concentrated in the tails of the PS) are dependent on the cutpoints for trimming chosen by the investigators. While Crump et al. (8) and Walker et al. (12) proposed only 1 set of cutpoints, Stürmer et al. (11) originally proposed using a range of cutpoints. Unfortunately, so far there has been no guidance on choosing the best cutpoint for Stürmer trimming. In settings where the treatment effect estimate changes with little trimming and remains stable with more aggressive trimming, researchers might feel comfortable choosing the minimum amount of trimming needed to “stabilize” the treatment effect. While we have seen such settings, it is straightforward to imagine settings where the unmeasured confounding is not largely concentrated in the tails of the PS or where the underlying treatment effect heterogeneity will not allow the treatment effect to stabilize with any amount of trimming. We need more guidance on how to identify trimming cutpoints along the lines of work on weight truncation (22). A useful sensitivity analysis could evaluate the effect of an alternative choice, and this might be most important if overlap of the PS distributions between treatment groups is limited (e.g., AUC (c statistic) > 0.7). We ignored the estimation of the PS when estimating coverage probabilities based on within-simulation variance of the treatment effect estimate. The coverage of the 95% confidence interval is close to nominal in the unbiased settings, and we therefore assume that any potential gain in precision by taking the estimation of the PS into account would be minimal.

In the presence of nonuniform treatment effects, the choice of weighting approach will depend on the population of interest. Whichever weighting method is selected, the addition of Stürmer and Walker trimming consistently reduces bias when unmeasured confounding is concentrated in the tails of the PS distribution. If the likelihood of unmeasured confounding in the tails of the PS distribution is high and particularly if overlap in the PS distributions of the compared treatment groups is limited, one might follow the advice of Walker et al. (11) and consider the treatment comparison in the trimmed study population with the chosen weights as the primary analysis.