Basics of Metabolic Reactions

Metabolism performs four essential functions for cells.

1. It provides energy by generating ATP to conduct cellular functions.

2. It converts nutrients, such as fat, protein, and sugar, into simpler structures, such as fatty acids, amino acids, and glucose, respectively (i.e., catabolism). This process can generate energy.

3. It converts simpler structures into macromolecules, such as nucleotides, lipids, and proteins (i.e., anabolism). This process requires energy.

4. It participates in cellular functions beyond energy, anabolism, and catabolism, such as cellular signaling and gene transcription. For example, metabolites serve as substrates for posttranslational modification of proteins to elicit changes in protein function or regulate epigenetics to invoke changes in gene expression.

As an example, the metabolism of acetyl-CoA fulfills all four of these functions (Fig. 1). Nutrients, such as fat, protein, and table sugar, are converted into simpler structures, such as fatty acids, amino acids, and glucose, respectively (i.e., catabolism). All three can generate acetyl-CoA, which can produce ATP in the mitochondria through the TCA cycle, also known as the citric acid cycle, or the Krebs cycle (i.e., energy). Acetyl-CoA can also be used to generate cholesterol, triacylglycerol, and phospholipids (i.e., anabolism). Acetyl-CoA is also a substrate for protein acetylation. Recent evidence indicates that protein acetylation is a robust posttranslational modification that alters protein function to change biological processes (i.e., signaling).

Figure 1.

Acetyl-CoA fulfills four functions of metabolism: (1) ATP generation, (2) catabolism, (3) anabolism, and (4) signaling.

Metabolic pathways are a series of connected reactions that can be linear, circular, or bifurcate into two directions. These pathways are found in different compartments of the cell, such as the mitochondria, endoplasmic reticulum, and cytosol, and these reactions use metabolites, enzymes, and energy. The small molecules that are the reactants and products of a reaction are called metabolites, and the catalysts that drive the reactions by converting reactants into products are enzymes. Reactions can either require (absorb energy) or release energy. The levels of metabolites and enzymes, along with availability of energy, influence whether a metabolic reaction will proceed:

$$\text{Reactants}\stackrel{\mathrm{Enzymes}}{---\to }\text{Products}(\mathrm{\Delta }\text{energy}).$$

It is important to realize that enzymes cannot determine the directionality of an individual reaction. Enzymes are proteins that serve as catalysts, which increase the rate of a reaction; they remain unaffected by the reaction itself. An enzyme will bind to a substrate and undergo a catalytic cycle that releases products. The enzyme itself remains intact and is poised to accept another substrate.

So, what determines whether a reaction requires or releases energy? Thermodynamics! I realize some readers are likely to shriek at the thought of thermodynamics. However, an appreciation of at least the basic thermodynamic principles is essential to understanding the directionality of metabolic pathways.

BASICS OF THERMODYNAMICS

Thermodynamics is the study of energy, which is defined as the ability to do work. Potential and kinetic energy are two major forms of energy. In simple terms, kinetic energy is the energy caused by motion, whereas potential energy is stored energy. The law of conservation of energy states that energy can neither be created nor destroyed. The total energy in a system remains constant as dictated by the first law of thermodynamics. However, energy can change from one form to another. For example, cellular respiration converts the energy stored within glucose (C₆H₁₂O₆) to ATP in the presence of oxygen (O₂) and to carbon dioxide (CO₂), and water (H₂O) as products of the reaction. ATP is the major form of energy that living organisms use to conduct reactions. The potential energy of ATP can be converted to kinetic energy (e.g., to contract muscles). In biology, an example of potential energy is bond energy, which is the amount of energy required to break a chemical bond.

In the 1870s, the American physicist Josiah Willard Gibbs integrated into an equation the concepts of thermodynamics to determine whether a reaction requires energy or releases it:

$$\mathrm{\Delta }G=\mathrm{\Delta }H-T\mathrm{\Delta }S.$$

At constant temperature and pressure, the Gibbs free-energy change, ΔG, has two components known as the enthalpy change, ΔH, and the entropy change, ΔS. Enthalpy is a measure of heat content and entropy is measure of randomness. In biological reactions, the enthalpy of reactants and products is equal to their respective bond energies, and the overall change in enthalpy, ΔH, is equal to the difference in bond energy between products and reactants. The current unit of measurement for enthalpy is the joule (J) in the International System of Units. However, most readers are likely familiar with the calorie as a unit of energy as it pertains to metabolism. A calorie is defined as the amount of heat energy required to increase the temperature of 1 g of water by 1°C at 1 atm of pressure. A calorie is ∼4.184 joules. Entropy, S, is a measure of the degree of randomness of a system. According to the second law of thermodynamics, all processes in the universe incline toward randomness without input of energy. Thus, the only way to prevent the natural course of disorder or randomness is to put energy into a system. For example, living organisms are made of highly ordered structures and thus tend to have low disorder or entropy. This is primarily a result of the consumption of nutrients that help generate energy to counteract the disorder and therefore sustain life. However, once an organism ceases to take in nutrients and energy generation (ATP) is diminished, disorder (entropy) increases, resulting in the eventual death of the organism. The entropy change, ΔS, of reactions is the change in randomness between products and reactants. At the cellular level, in catabolic reactions in which highly ordered structures, such as starch, are broken down, there is an increase in entropy (ΔS is positive), whereas in anabolic reactions, in which highly ordered structures, such as cholesterol, are generated, there is a decrease in entropy (ΔS is negative). Anabolic reactions require energy to counteract entropy for the generation of higher-order structures.

WHAT DETERMINES WHETHER A REACTION REQUIRES ENERGY OR RELEASES ENERGY?

In an initial solution of reactants and products, a reaction that proceeds to produce more products than reactants will have ΔG < 0, a reaction in which energy is released. This reaction is referred to as exergonic or exoergic. The bond energy of reactants is greater than the products and thus ΔH < 0. The products tend to be more disordered than the reactants; as a result, the reaction proceeds to a higher randomness state (ΔS > 0). Plugging a negative ΔH and positive ΔS at constant temperature, T, into the Gibbs free-energy equation yields ΔG < 0. The ΔG can be represented as the Gibbs free energy difference between products and reactants:

$$\begin{array}{rl}& \text{exergonic reaction}\left(\text{energy released}\right):\\ & \mathrm{\Delta }G=G_{\mathrm{products}}-G_{\mathrm{reactants}}<0.\end{array}$$

In an initial solution of reactants and products, a reaction that proceeds to produce more reactants than products will require external energy if the reaction is to accumulate products instead of reactants. This reaction is referred to as endergonic or endoergic. The bond energy of reactants is smaller than the products and thus ΔH > 0. The products tend to be more ordered than the reactants, and thus the reaction proceeds to a higher-ordered state (ΔS < 0). Plugging a positive ΔH and negative ΔS at constant temperature, T, into the Gibbs free-energy equation yields ΔG > 0:

$$\begin{array}{rl}& \text{endergonic reaction}\left(\text{energy required}\right):\\ & \mathrm{\Delta }G=G_{\mathrm{products}}-G_{\mathrm{reactants}}>0.\end{array}$$

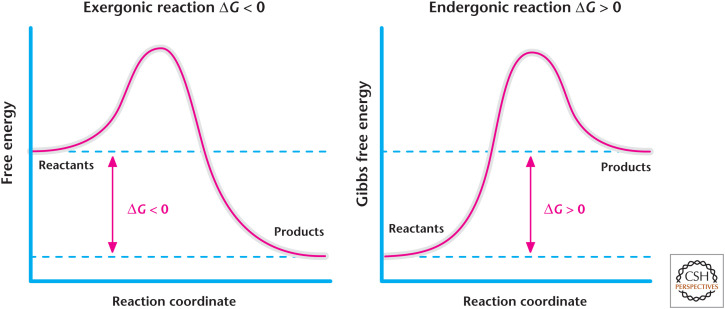
When the rates of forward and backward reactions are equal and the concentrations of products and reactions do not change, then ΔG = 0; that is, the reaction is at equilibrium. Gibbs free energy can be represented graphically (Fig. 2). Gibbs free energy of biological reactions is expressed as kJ/mol.

Figure 2.

Exergonic and endergonic reactions. The change in Gibbs free energy of a reaction is the energy difference between products and reactants. Exergonic reactions have a negative change in the Gibbs free energy and, thus, release energy. In contrast, endergonic reactions have a positive change in the Gibbs free energy and, thus, require energy.

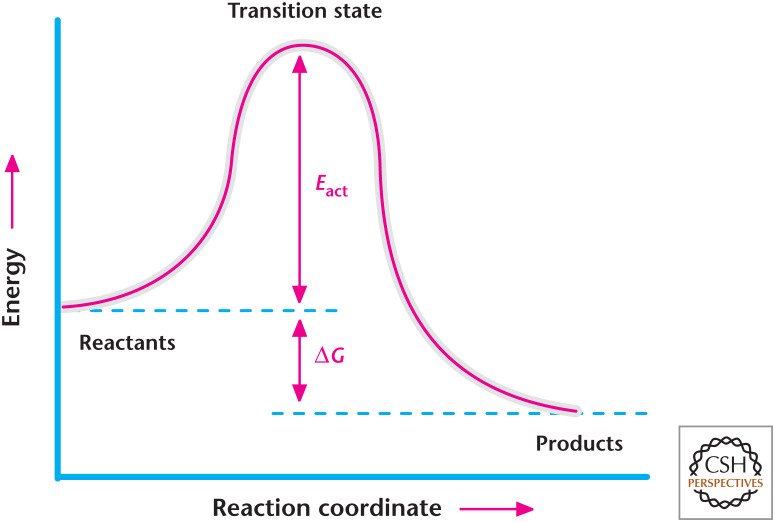
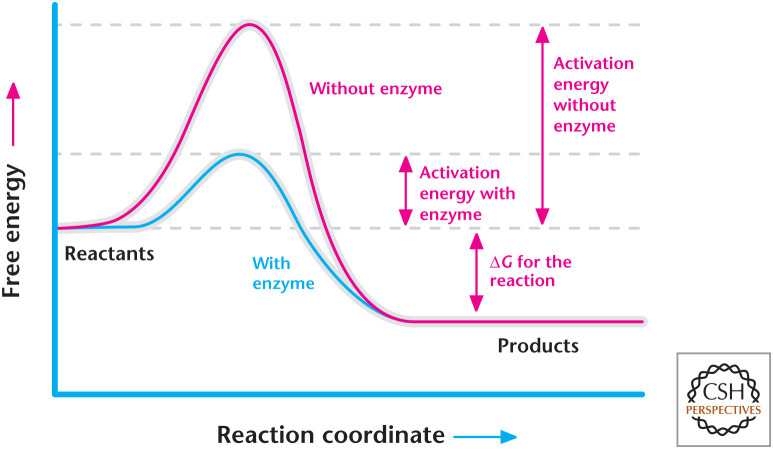
It is vital to realize that Gibbs free energy does not account for the time it takes for a reaction to occur; rather, it determines whether the reaction releases or requires energy. The rate of the reaction is governed by activation energy (E_act), expressed as kJ/mole, which is the energy required to push the reactants up to an activated complex known as the transition state. Hence, the activation energy is the energy difference between reactants and the activated complex. The peak of the energy profile is the transition state in which an activated complex can either go back to the reactants or go forward to the products (Fig. 3). The activation energy determines the rate of the reaction. Reactions with small activation energy proceed faster than reactions with high activation energy. Think of rolling a ball up a hill to the top. A smaller hill will require less time to roll the ball up than a larger hill. As we will learn later, enzymes as catalysts increase the rate of the reaction by lowering the activation energy (Fig. 4). Enzymes do not change the amount of Gibbs free energy of a reaction, but they do increase the rate of the reaction.

Figure 3.

Transition state. The transition state is the highest point of energy in which an activated complex can either go back to the reactants or forward to the products. Activation energy (E_act) is the energy difference between reactants and the transition state.

Figure 4.

Enzymes lower the activation energy to increase the rate of reaction but not the overall change in Gibbs free energy of the reaction.

CONCENTRATIONS OF PRODUCTS AND REACTANTS DETERMINE ΔG AS A RESULT OF THE LAW OF MASS ACTION

The law of mass action states that ΔG of a reaction depends not only on the difference in energy stored in the products versus reactants but also in the concentrations of these molecules. To appreciate how concentration of products and reactants affect the favorability of a reaction, we need to understand the equilibrium constant (K_eq) of a reaction. Most biological reactions are reversible with a forward (k₁) and reverse (k₋₁) rate constant, which is the speed of the reaction. For the single-step reaction,

$$\mathrm{A}+\mathrm{B}\underset{k_{-1}}{\overset{k_1}{\stackrel{⟶}{⟵}}}\mathrm{C}+\mathrm{D},$$

in which [A], [B], [C], and [D] are the molar concentrations of A, B, C, and D, respectively. The forward rate of a reaction is proportional to the product of the concentrations of A and B and is expressed as k₁[A][B]. The reverse rate of the reaction is proportional to the concentrations of C and D and is expressed as k₋₁[C][D].

At equilibrium, the forward rate of a reaction is equal to the reverse rate of the reaction:

$$k_1\left[\mathrm{A}\right]\left[\mathrm{B}\right]=k_{-1}\left[\mathrm{C}\right]\left[\mathrm{D}\right].$$

The equilibrium constant

$$K_{\mathrm{eq}}=k_1/k_{-1}=\left[\mathrm{C}\right]\left[\mathrm{D}\right]/\left[\mathrm{A}\right]\left[\mathrm{B}\right].$$

The equilibrium constant is often used in Le Chatelier's principle (1884), which states that “Every change of one of the factors of an equilibrium occasions a rearrangement of the system in such a direction that the factor in question experiences a change in a sense opposite to the original change.” In biological reactions, if the concentrations of products and reactants at equilibrium are changed, the equilibrium shifts in a direction that tends to restore the original concentrations (to counteract the change). For example, if you add the reactants A and B in the reaction, then the reaction goes forward. In contrast, if you add products C and D, then the reaction goes backward.

The actual free energy, ΔG (kJ/mol), of a given reaction is the standard free-energy change referred to as ΔG°′, which depends on the bond energy and disorder of the products and reactants, along with the concentration of the products and reactants. Gibbs derived the following equation to express this relationship:

$$\mathrm{\Delta }G=\mathrm{\Delta }{G}^{\circ \mathrm{\prime }}+\mathrm{RT}\ln \left[\mathrm{C}\right]\left[\mathrm{D}\right]/\left[\mathrm{A}\right]\left[\mathrm{B}\right],$$

in which R is the gas constant 8.315 J/mol · K and T is absolute temperature.

The ΔG°′ can be calculated by setting up a reaction under standard physiological conditions and then allowing it to proceed to equilibrium in which the concentrations of all reactants and products are measured. The change in actual free energy is 0 (ΔG = 0), and ΔG°′ can be calculated directly from K_eq:

$$\begin{array}{rl}0& =\mathrm{\Delta }{G}^{\circ \mathrm{\prime }}+\mathrm{RT}\ln \left[\mathrm{C}\right]\left[\mathrm{D}\right]/\left[\mathrm{A}\right]\left[\mathrm{B}\right],\\ \mathrm{\Delta }{G}^{\circ \mathrm{\prime }}& =-\mathrm{RT}\ln \left[\mathrm{C}\right]\left[\mathrm{D}\right]/\left[\mathrm{A}\right]\left[\mathrm{B}\right].\end{array}$$

HOW DO ENDERGONIC REACTIONS UNDER EQUILIBRIUM CONDITIONS BECOME EXERGONIC REACTIONS?

First, an endergonic reaction under equilibrium conditions (ΔG°′ > 0) in a cell can become exergonic if the concentration of products is very small compared with the concentration of reactants. In this scenario, [products]/[reactants], referred to as the mass-action ratio, will be <1. The natural log (ln) of a number that is <1 is a negative number and will result in the actual Gibbs free energy, ΔG, to be negative. Second, an endergonic reaction is coupled to an exergonic reaction. The conversion of ATP to ADP and P_i is a favorable reaction and is often used to drive unfavorable reaction. Let us look at the example of ATP → ADP + P_i to see how concentration of ATP/ADP can make the difference in the amount of Gibbs free energy available to drive unfavorable reactions.

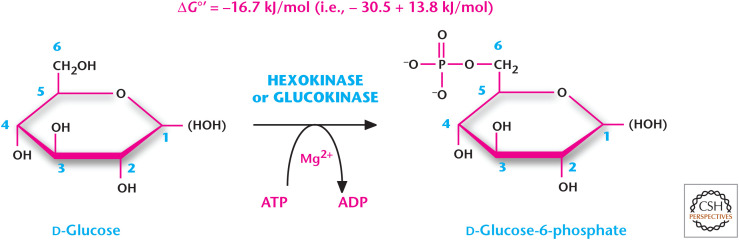
An example of an ATP-coupled reaction is (also see Fig. 5)

$$\begin{array}{c}\mathrm{\Delta }{G}^{\circ \mathrm{\prime }}\left(\text{kJ}/\text{mol}\right)\\ \text{Glucose}+{\text{P}}_{\mathrm{i}}\to \text{Glucose}-6-\text{phosphate}+{\text{H}}_2\text{O}+13.8\\ \text{ATP}+{\text{H}}_2\text{O}\to \text{ADP}+{\text{P}}_{\mathrm{i}}-30.5\\ --------------------------\\ \text{ATP}+\text{Glucose}\left(\text{Glu}\right)\to \text{Glucose}-6-\text{Phosphate}+\text{ADP}-16.7.\end{array}$$

Figure 5.

The first step of glycolysis is an example of an ATP coupled reaction.

This first reaction of glycolysis (see Chandel 2020a) is an irreversible reaction that commits glucose to this metabolic pathway. The conversion of glucose to glucose 6-phosphate is a reaction and has a ΔG°′ = +13.8. However, coupling this reaction to the conversion of ATP to ADP and P_i results in an exergonic reaction with a ΔG°′ =–30.5. Thus, under standard conditions, the ΔG°′ is –16.7, but remember that the overall ΔG for the reaction will be dependent on the ratio of products/reactants along with the ΔG°′. The overall ΔG is even more favorable because the reactants, glucose and ATP, are much more in excess than the products, glucose 6-phosphate and ADP. By knowing the ΔG°′ and metabolite concentration, we plug in these values to ΔG = ΔG°′ + RT ln (products/reactants). If we use a steady-state concentration of products (glucose 6-phosphate and ADP) and reactants (Glu and ATP) observed in red blood cells, then the equation looks like

$$\begin{array}{rl}\mathrm{\Delta }G& =\mathrm{\Delta }{G}^{\circ \mathrm{\prime }}\\ & +\mathrm{RT}\ln \frac{\left(\left[\text{Glucose 6 - phosphate}\right]\left[\mathrm{ADP}\right]\left[{\mathrm{P}}_{\mathrm{i}}\right]\right)}{\left(\left[\mathrm{Glu}\right]\left[\mathrm{ATP}\right]\right)},\\ \mathrm{\Delta }G& =-16.7\mathrm{kJ}/\mathrm{mol}\\ & +\left(8.314\mathrm{J}/\mathrm{mol}\mathrm{K}\right)\left(310\mathrm{K}\right)\ln \frac{\left(\left[0.083\right]\left[0.14\right]\left[1\right]\right)}{\left(\left[5\right]\left[1.85\right]\right)},\\ \mathrm{\Delta }G& =-33\mathrm{kJ}/\mathrm{mol}.\end{array}$$

Endergonic reactions can also be coupled to exergonic reactions involving NADH, FADH₂, and NADPH conversion into NAD⁺, FAD, and NADP⁺, respectively. A coupled oxidation–reduction reaction, also called a redox reaction, is one in which one molecule is oxidized (loses electrons) while a second is reduced (gains electrons). Accordingly, there is a loss of electrons in an oxidation reaction, whereas in a reduction reaction there is a gain of electrons. An oxidizing agent gains electrons during a redox reaction and is therefore reduced during reaction. Conversely, a reducing agent loses electrons during a redox reaction and is therefore oxidized during reaction. See Box 1 for an example of a coupled redox reaction.

BOX 1.

A COUPLED REDOX REACTION

An example of a coupled redox reaction is the conversion of pyruvate to lactate. The conversion of pyruvate to lactate is enzymatically catalyzed by lactate dehydrogenase. In this reaction, pyruvate gains two electrons and is reduced to lactate; that is, in the reduction half of the reaction, NADH loses two electrons and is oxidized to NAD⁺ (i.e., in the oxidizing half of the reaction).

This redox reaction consists of two half-reactions

$$\begin{array}{rl}& \mathbf{p}\mathbf{y}\mathbf{r}\mathbf{u}\mathbf{v}\mathbf{a}\mathbf{t}\mathbf{e}+\mathbf{2}{\mathbf{H}}^{+}+\mathbf{2}{\mathbf{e}}^{-}\to \mathbf{l}\mathbf{a}\mathbf{c}\mathbf{t}\mathbf{a}\mathbf{t}\mathbf{e}\left(\text{pyruvate gains}{\mathrm{e}}^{-}\right[\text{reduction half reaction}\left]\right),\\ & \mathbf{N}\mathbf{A}\mathbf{D}\mathbf{H}+{\mathbf{H}}^{+}\to \mathbf{N}\mathbf{A}{\mathbf{D}}^{+}+\mathbf{2}{\mathbf{H}}^{+}+\mathbf{2}{\mathbf{e}}^{-}\left(\text{NADH loses}{\mathrm{e}}^{-}\right[\text{oxidation half reaction}\left]\right),\\ & \mathbf{p}\mathbf{y}\mathbf{r}\mathbf{u}\mathbf{v}\mathbf{a}\mathbf{t}\mathbf{e}+\mathbf{N}\mathbf{A}\mathbf{D}\mathbf{H}+{\mathbf{H}}^{+}\to \mathbf{l}\mathbf{a}\mathbf{c}\mathbf{t}\mathbf{a}\mathbf{t}\mathbf{e}+\mathbf{N}\mathbf{A}{\mathbf{D}}^{+}\left(\mathrm{net}\mathrm{reaction}\right).\end{array}$$

NADH donates (or loses) two electrons and is oxidized to NAD⁺. NADH is the reducing agent. Pyruvate accepts (or gains) two electrons and is reduced. Pyruvate is the oxidizing agent. These half reactions, measured in volts, are the reduction potential, E°′, of a redox reaction. Reduction potential is a measure of the propensity of a metabolite to gain electrons. Thus, the E°′ of the two reduction half-reactions of pyruvate conversion to lactate are as follows:

$$\begin{array}{rl}& \left(1\right)\text{pyruvate}+2{\text{H}}^{+}+2{\text{e}}^{-}\to \text{lactate},E^{\circ \mathrm{\prime }}=-0.190\text{V},\\ & \left(2\right){\text{NAD}}^{+}+2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-}\to \text{NADH}+{\mathrm{H}}^{+},E^{\circ \mathrm{\prime }}=-0.320\mathrm{V}.\end{array}$$

The higher (less negative) the E°′, the more likely it has a propensity to gain electrons. The pyruvate/lactate pair has a higher E°′ than the NAD⁺/NADH pair and is likely to accept more electrons. Thus, the NAD⁺ reaction is reversed along with the sign of the reduction potential:

$$\left(2\text{reversed}\right)\text{NADH}+{\mathrm{H}}^{+}\to {\mathrm{NAD}}^{+}+2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-},E^{\circ \mathrm{\prime }}=0.320\mathrm{V}.$$

Then, reaction (1) and the reversed reaction (2) can be added together to arrive at the net redox reaction, and the ΔE°′ can be found by adding the reduction potential of the first half-reaction to the oxidation potential of the second half-reaction

$$\begin{array}{rl}\left(1\right)& \mathrm{pyruvate}+2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-}\to \mathrm{lactate},E^{\circ \mathrm{\prime }}=-0.190\mathrm{V},\\ \left(2\mathrm{reversed}\right)& \mathrm{NADH}+{\mathrm{H}}^{+}\to {\mathrm{NAD}}^{+}+2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-},E^{\circ \mathrm{\prime }}=0.320\mathrm{V},\\ & -----------------------------------------------------------------------\\ \left(\mathrm{sum}\right)& \mathrm{pyruvate}+\mathrm{NADH}+{\mathrm{H}}^{+}\to \mathrm{lactate}+{\mathrm{NAD}}^{+},\mathrm{\Delta }{E}^{\circ \mathrm{\prime }}=0.130\mathrm{V}\left(\mathrm{sum}\right).\end{array}$$

This ΔE°′ of the redox reaction can be converted into ΔG°′, in which n is the number of electrons involved in the reaction and F is the Faraday constant (96.5 kJ/volt*mol):

$$\mathrm{\Delta }{G}^{\circ \mathrm{\prime }}=-nF\mathrm{\Delta }{E}^{\circ \mathrm{\prime }}.$$

If we plug ΔE°′ = 0.130 V into the above equation

$$\mathrm{\Delta }{G}^{\circ \mathrm{\prime }}=-2\left(96.5\mathrm{KJ}/\mathrm{V}\mathrm{mol}\right)\left(0.130\mathrm{V}\right),$$

we get ΔG°′ = –25 kJ/mol. Because ΔG°′ < 0, this is a reaction that releases energy. Note that these redox reactions have a positive ΔE°′ and are reflected as negative ΔG°′. The equation above reflects standard conditions. Remember from the previous section that the actual ΔG in a cell will be determined by the ratio of the reactants (pyruvate and NADH) to products (lactate and NAD⁺). To calculate E of redox reactions taking into the concentrations of reactants and products, we use the Nernst equation:

$$\mathrm{\Delta }E=\mathrm{\Delta }{E}^{\circ \mathrm{\prime }}-\left(\mathrm{RT}/nF\right)\ln \left(\left[\mathrm{products}\right]/\left[\mathrm{reactants}\right]\right).$$

Subsequently, ΔG can be calculated by –nFΔE.

THE ENERGY CHARGE QUANTIFIES THE ENERGETIC STATE OF CELLS

It is essential that cells maintain an adequate ATP/ADP ratio to drive biological reactions. The ADP generated from these reactions is usually converted back to ATP by glycolysis in cytosol (Chandel 2020a) or oxidative phosphorylation (Chandel 2020b) in the mitochondria. If these sources of ATP production are compromised, then two molecules of rising ADP can be converted to ATP and AMP by adenylate kinase:

$$2\text{ADP}\leftrightarrow \text{AMP}+\text{ATP}.$$

This buffers the decrease of ATP levels and maintains an adequate ATP/ADP ratio. This reaction also increases AMP levels, which triggers the activation of AMP kinase (AMPK). This metabolic sensing kinase, which is sensitive to the AMP/ATP ratio, activates catabolic pathways to stimulate ATP production and inhibits anabolic pathways to prevent ATP consumption. Furthermore, high levels of AMP or ATP activate or inhibit, respectively, metabolic reactions involved in generating ATP.

In the 1960s, Daniel Atkinson developed a formula to quantitatively estimate the energy state of the cell based on the concentrations of ATP, ADP, and AMP, referred to as the energy charge:

$$\text{energy charge}=\frac{\left[\mathrm{ATP}\right]+\frac{1}{2}\left[\mathrm{ADP}\right]}{\left[\mathrm{ATP}\right]+\left[\mathrm{ADP}\right]+\left[\mathrm{AMP}\right]}.$$

An energy charge ranges from 0 (all AMP) to 1 (all ATP). If ATP, ADP, and AMP have the same concentration, then the energy charge is 0.5. Cells maintain an energy charge between 0.7 and 0.9 by regulating metabolic flux, which is the turnover rate of reactants and products through pathways that generate and consume ATP. An imbalance between rates of use and regeneration of ATP causes a decrease in the energy charge. Consequently, a lower energy charge value slows down macromolecular synthesis and growth. Atkinson's important insight was that cells counteract a decreasing energy charge by diminishing the rate of ATP-consuming reactions and increasing the rate of ATP-regenerating reactions.

ENZYMES CATALYZE METABOLIC PATHWAYS

Enzymes can be either a protein or a catalytic RNA, such as a ribozyme (RNA enzyme). Enzymes increase the rate of reactions by lowering the activation energy of reactions. The rate of reaction (k) is how fast a reactant gets used up or how fast a product gets produced. Without enzymes, the rate of metabolic reactions would proceed too slowly to deliver the necessary energy, as well as the biosynthesis of macromolecules to keep organisms alive. An important consideration to remember is that if a reaction is not thermodynamically favorable, then enzymes cannot make the reaction go forward. Enzymes do not alter the Gibbs free energy of a reaction (Fig. 4). Imagine pushing a heavy ball up a hill. It will take less time to push the ball over a smaller hill than a larger hill. However, the strength to push the ball over either hill is similar. If the person does not have the strength to push the ball, it does not matter if the hill is big or small.

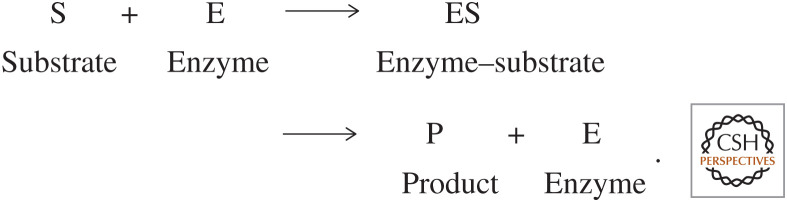
Many enzymes also require the presence of nonprotein molecules called cofactors for their catalytic activity. An inactive enzyme without the cofactor is designated as an apoenzyme, whereas an active enzyme bound with a cofactor is referred to as a holoenzyme. Cofactors, such as heme, that are permanently bound to enzymes are called prosthetic groups, and those, such as NAD⁺, that are not permanently bound are termed coenzymes. Many enzymes also use metal ions, such as iron, copper, or magnesium, for their catalytic activity. Enzymes show specificity to the reactions they catalyze. They usually have specific substrates (reactants); however, they are not consumed like a substrate of a reaction nor do they appear as reaction products. A substrate and an enzyme form a transient intermediate before the generation of the product. Once the product is generated, the enzyme returns to its original form poised to accept another substrate.

A basic enzymatic reaction is

However, most biological reactions are reversible; thus, the enzyme–substrate complex can either become a product or substrate, depending on their respective concentrations. Looking at this reaction, it is apparent that both the substrate and enzyme concentrations are going to affect the rate of the reaction. The other important factors that affect the rate of reactions are temperature, pH, and the presence of activators or inhibitors. Enzymes have a temperature and pH range at which their activity is greatest.

There are two important points regarding enzyme kinetics at a constant pH and temperature.

1. If there is unlimited substrate, then the rate of a reaction is proportional to enzyme concentration (Fig. 6).

2. If the enzyme concentration is constant, then the initial rate of the reaction (V₀) will increase as the substrate concentration increases from 0 until it reaches a maximum, defined as V_max. After this point, a further increase in the substrate concentration will not increase the rate. The K_m of the reaction is defined as the substrate concentration at ½V_max (Fig. 6). Quantitatively, this is illustrated in the Michaelis–Menten equation:

   $$v_0=\frac{V_{max}\left[\mathrm{S}\right]}{K_{\mathrm{m}}+\left[\mathrm{S}\right]}.$$

   Plugging in a substrate concentration [S] = K_m in the equation gives v₀ = V_max/2. The K_m is also referred to as the Michaelis–Menten constant.

Figure 6.

Rate of a reaction is dependent on the enzyme and substrate concentration.

The size of K_m tells us the following things about a particular enzyme.

• A small K_m indicates that the enzyme requires only a small amount of substrate to become saturated. Hence, the maximum velocity is reached at relatively low substrate concentrations.

• A large K_m indicates the need for high substrate concentrations to achieve maximum reaction velocity.

REGULATION OF ENZYMES AFFECTS THEIR CATALYTIC ACTIVITY

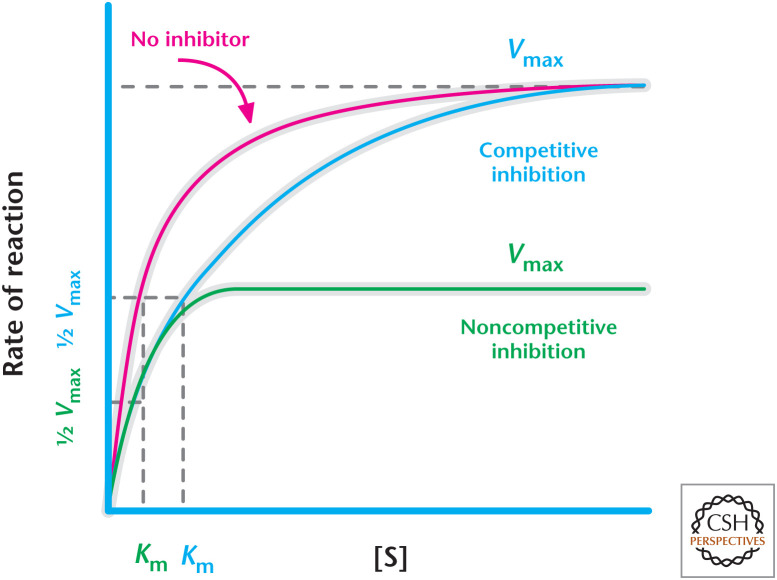
Aside from increasing rate of reaction and having specific substrates, enzymes are regulated so that they can go from a low- to a high-activity state. Enzymes have an active site in which the substrate binds to form the enzyme–substrate complex and an allosteric site at which metabolites, ions, and proteins can bind and affect the catalytic activity of the enzyme by increasing or decreasing the substrate–enzyme interaction. Allosteric enzymes, a special class of enzymes, oscillate between two conformations: a high-activity, high-affinity relaxed (R) state and a low-activity, low-affinity tense (T) state. These enzymes are made of multiple subunits and require an activator to bind all the subunits to stabilize the active form. There are also multiple mechanisms to inhibit enzyme activity, including feedback, competitive, and noncompetitive inhibitions (Fig. 7). Feedback inhibition is a mechanism by which product accumulation inhibits the enzyme. In competitive inhibition, an inhibitor mimics the substrate and competes for binding to the active site. This forces the natural substrate for the enzyme to increase its concentration to achieve V_max. However, the presence of the inhibitor does not change the V_max of the reaction because excess natural substrate would compete away the inhibitor. Thus, competitive inhibition results in an increase in K_m without changing V_max. In contrast, noncompetitive inhibition involves an inhibitor that binds to an allosteric site to deactivate the enzyme. The natural substrate can still bind to the enzyme, but as long as the inhibitor is bound to the allosteric site, the enzyme is essentially catalytically inactive. Thus, the noncompetitive inhibitor decreases V_max and addition of excess natural substrate cannot overcome inhibition.

Figure 7.

Competitive versus noncompetitive inhibition of enzymes. Competitive inhibition results in an increase in K_m without changing V_max, whereas noncompetitive inhibition causes a decrease in V_max without changing K_m.

ILLUSTRATION OF CONTROL OF FLUX THROUGH A HYPOTHETICAL METABOLIC PATHWAY

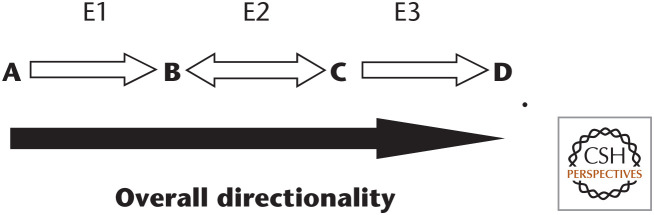
Let us take a look at a hypothetical simple metabolic pathway to integrate the concept of how enzymes and metabolites control flux, defined as rate of turnover of molecules through a metabolic pathway. A, B, C, and D are defined as metabolites and E1, E2, and E3 are their enzymes. The first step catalyzed by enzyme E1 is irreversible and commits the initial reactant A to this pathway. The irreversible steps catalyzed by E1 and E3 also become the regulatory steps in the pathway. The middle reaction, carried by E2, is reversible. Because C is quickly removed by E3, this forces B to become C. Alternatively, if E3 becomes inhibited at an allosteric site, then C would build up and be converted back to B because the E2-catalyzed reaction is reversible. This could prevent any further conversion of A to B by E1 because B could inhibit E1 (i.e., product inhibition):

In summary, always look at the concentration of the products and reactants, along with the enzyme activity, to get a sense of the direction of any given reaction.

WHAT DETERMINES THE METABOLIC FLUX OF A PATHWAY?

Metabolic flux through a particular direction within a pathway is regulated by four factors: (1) the availability of reactants, (2) the concentration of enzymes, (3) the posttranslational modifications that cause a change in the enzyme activities, and (4) the concentrations of the metabolites affecting the enzyme activity, including the reactants and products of the enzyme-catalyzed reaction. It is important to note enzyme function, and so metabolic flux through a pathway represents an integration of enzyme gene expression, protein translation, and posttranslational modification, as well as enzyme–metabolite interaction. Furthermore, multiple enzymes within a metabolic pathway are coordinately activated for optimal flux through the pathway. Therefore, one advantage of doing metabolomics is that it provides a functional readout of metabolic pathways compared with genomics and proteomics. In Chandel (2020a,b,c,d,e,f,g), the major regulation of enzymes discussed is restricted to how metabolites, such as adenine nucleotides, regulate enzyme function. Chandel (2020h,i) covers cover the signaling pathways and transcription factors that regulate gene expression, protein translation, and posttranslational modification of enzymes to control anabolic and catabolic processes.