Spatio-temporal performance in an incoherent holography lattice light-sheet microscope (IHLLS)

Abstract

We propose an Incoherent holography detection technique for lattice light-sheet (IHLLS) systems for 3D imaging without moving either the sample stage or the detection microscope objective, providing intrinsic instrumental simplicity and high accuracy when compared to the original LLS schemes. The approach is based on a modified dual-lens Fresnel Incoherent Correlation Holography technique to produce a complex hologram and to provide the focal distance needed for the hologram reconstruction. We report such an IHLLS microscope, including characterization of the sensor performance, and demonstrate a significant contrast improvement on beads and neuronal structures within a biological test sample as well as quantitative phase imaging. The IHLLS has similar or better transverse performances when compared to the LLS technique. In addition, the IHLLS allows for volume reconstruction from fewer z-galvo displacements, thus facilitating faster volume acquisition.

1. Introduction

Phase imaging of live cells and tissue opens several possibilities that have not been available to more established methods in microscopy [1–16]. The simplest example is the ability of holographic imaging to reconstruct 3-dimensional information by both effectively autofocusing and extending the depth of field from which valuable information can be gathered. As an example, neurons in situ are inherently 3-dimensional structures, with processes that extend through the nervous system in all dimensions. Volumetric imaging solutions that have been applied to this include confocal imaging, multiphoton imaging, and light sheet methods [17,18]. However, to reconstruct 3-dimensional structures the objective lens is invariably moved. Taking the nervous system as an example, in dendritic fields neurons receive information rapidly and often synchronously at different locations at various 3-dimensional planes. With conventional approaches it is not possible to image in the millisecond temporal range at multiple depths. This can now be achieved using holographic methods. Neurons also respond electrically to inputs. This activity is rapid (milliseconds duration) and spread throughout their complex 3D structure. Interestingly, changes in the entire cell membrane follow rapidly from localized electrical changes, and these can be detected in phase images in transmission or reflection imaging modalities [19,20].This opens the possibility of measuring excitability of nerve cells across the complex 3-dimensional structure of the neuron. At longer time scales, organelle and protein movement within cells change the local refractive index [11,12,15]. Since phase changes in reflection geometry do not include the refractive index difference between the cytoplasm and the medium, it implies that the movements restricted to structural changes, axonal transport, or vesicle recycling may be detected through the cell membrane dynamics using the reflection phase microscopy approach. The combination of lattice light-sheet (LLS) excitation targeting specific neurons with holographic phase imaging of selective fluorescent markers to detect fast events, or of electrical or structural changes of phase, creates many new approaches in imaging neuronal activity.

By providing excitation illumination along a different axis to viewing light emission, confocal theta microscopy provides improves z resolution [21]. The confocal PSF depends on the volume of intersection between the illumination and detection PSFs and with excitation and emission lens placed orthogonally, the intersection gives a much smaller effective sample volume compared to more conventional on axis systems. A rotation of these axes by 90° minimizes the overlap of the two PSFs giving similar resolution along the orthogonal axes. This approach represents the starting point for a similar orthogonal setup in Lattice Light-Sheet Microscopes (LLSM) [22–24]. In this modality the excitation in LLSM is confined to a plane defined by a lattice of intersecting Bessel beams that self-reinforce as they project through tissue and provides an adaptable low excitation imaging approach that penetrates diffractive tissue much better than traditional light sheets. The generation of the lattice light sheet is done in multiple steps. In the first step, the lattice light sheet is formed by stretching a linearly polarized circular laser input beam in the x axis with cylindrical lenses and compressing it in the z axis. The resultant sheet is projected to a spatial modulator (SLM) to generate optical lattice of Bessel beams. The next step is to generate a diffraction pattern of the optical lattice using a Fraunhofer lens and directed to a transparent annular mask to further eliminate the unwanted diffraction orders and lengthen the light sheet. After that, the optical lattice is dithered laterally using a galvanometer mirror (x-axis), to suppress the Bessel beams side lobes (which can degrade imaging contrast and induce photobleaching) and to create a uniform light sheet. The position of the resultant Bessel beam is also controlled by the z galvanometer (z-axis), which moves together with the detection objective. Fluorescence excited by this sheet is viewed orthogonally by an emission objective.

The Bessel beam excitation in LLS allows depth penetration with less disruption of the sheet than other light sheet approaches. Volumetric reconstruction is possible either by moving the light sheet (with the z-galvo mirror) and detection objective (Nikon, 25X, 1.1 NA, with the z-piezo stage), together through the specimen, or by translating the specimen with a second piezo stage through the stationary light sheet along an axis s in the plane of the specimen cover slip. Both the latter methods have disadvantages. Moving the sample precludes in situ studies combined with other modalities such as electrophysiology. Moving the objective slows the imaging and generates movement artifacts because of the mass of the objective. Furthermore, in the LLS a dithering mode is needed to move the Bessel beam in the x-plane using a x-galvo mirror to blur the edges of the lattice lines produced by the self-reinforcing Bessel beam making the resultant excitation more uniform.

Due to its thin illumination (∼ 400 nm) deep lattice sheet, lattice light-sheet microscopy enables high-resolution imaging in the z axis and either diffraction limited resolution in x and y or higher by creating structured illumination using phase rotations of the Bessel beam lattice. The approach also allows long-term live-cell imaging with an extremely low light dose and little photobleaching. This makes LLS an ideal fluorescence imaging system for many biological studies. However, the x and y dimensions are limited to approximately the dimensions of the lattice (up to 80µm with the Special Optics of 0.65 NA lens used). This can be enlarged for larger samples (up to 170 µm FOV is possible) by using a tile-scanning approach [25]. Unfortunately, while this scanning modality still utilizes the coherent properties of Bessel beams, the optical sectioning ability is lower when compared to the original LLS, because the expansion of the FOV is limited by the beam width of the excitation laser. Moreover, the in-vivo imaging capabilities using LLS are still limited by the need to move the bulky detection objective, and not always practical because the specimen may not tolerate the objective motion. Dispersion and distortion of the lattice and distortion of emitted light through the tissue are also inevitable at larger depths.

To overcome these limitations, we imaged emitted light using an adapted Fresnel Incoherent Correlation Holography (FINCH) arrangement that enables the expansion of the FOV by using the 3D information encoded in the Fresnel patterns while moving the z-galvanometer mirror at various depths in the sample. LLS beams are coherent, and the beams produce stronger modulation depth than incoherent patterned light sheets, but when combined with FINCH the depth information is encoded in the Fresnel patterns. FINCH [26,27], is based on the use of the self-interference property of the emitted fluorescent light, in which three or four interference patterns are created using a phase shifting technique to generate Fresnel holograms of a 3D object. This is similar to a Michelson interferometer, in which the self-interference property of the fluorescent light is addressed in a similar manner using spherical lenses, mirrors, and a beam splitter [28]. In FINCH, this approach is modified. The beam splitter of the interferometer is replaced by a spatial light modulator (SLM), so that each spherical beam propagating from each 3D object’s points is split into two spherical beams with different radii of curvature. FINCH uses three combinations of diffractive elements displayed on the SLM; one diffractive lens and a constant phase mask with shared pixels, two diffractive lenses of different focal lengths with shared pixels, and two diffractive lenses of different focal lengths with randomly selected pixels to achieve the maximum resolution. The last configuration gives the freedom to choose only one polarizer in the system to create the interference between the beams, which implies that lower doses of light could be used to image biological samples.

2. Principle

To address the problems indicated above we have developed an incoherent holography lattice light-sheet (IHLLS) system, as a second detection module on the original design of the LLS system [22]. This has the chief advantage of utilizing the incoherent properties of the fluorescence emission together with the coherent properties of LLS [Fig. 1]. The goal of the approach is to eliminate the need to move the emission objective, to provide volumetric imaging information at higher sample rates, and to increase the depth of view. Positioning of the z galvo at various depths in the samples coupled with FINCH technique will increase the optical sectioning ability of the IHLLS system.

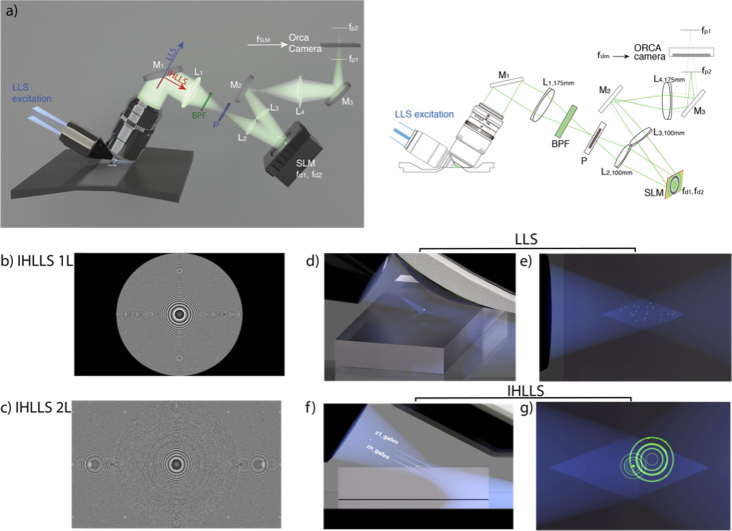
Fig. 1.

The IHLLS system. a) Schematics of the IHLLS systems with b) one diffractive lens of focal length, f_SLM = 400 mm at the phase shift θ₁ = 0, and c) two diffractive lenses with focal lengths f_d1 = 220 mm and f_d2 = 2356 mm, at the phase shift θ₁ = 0, superposed with a slight defocus to bring the objects in focus in the middle of the camera FOV; The system consists of a water immersed microscope objective MO (Nikon 25X, NA 1.1, WD 2 mm), lenses L₁=L₄ with focal lengths 175 mm, L₂=L₃ with focal lengths 100 mm; mirrors M₁, M₂, M₃; polarizer P; 520 center wavelength, 40 nm band pass filter BPF; spatial light modulator SLM. The light propagates through either pathway 1 (blue line in a) for the original LLS or pathway 2 (red line in a)) for IHLLS, depending on the orientation of sliding mirror. A collimated 30 Bessel beam is focused by an excitation objective lens (d, f) which generates a lattice light sheet. The vectors represent the x, y, z and s planes of the Bessel. z and x are moved by the z and x galvos. It excites only fluorophores in the focal plane (e) and in/off the focal plane (g) of the detection objective lens. While the z-galvo and z-piezo are moved along the z axis to acquire stacks in LLS (d-e), in IHLLS only the z-galvo is moved at various z positions (f-g), (Visualization 1 ^{(5.8MB, avi)} ). For IHLLS, the size of the beam coming out the objective is diminished in half by the relay lens system, L₁ and L₂, to fit the size of the SLM. The SLM plane is optically conjugated with the objective back-focal-plane. The diffraction mask was positioned for all experiments on the anulus of 0.55 outer NA and 0.48 inner NA. The CMOS camera, tube lens, filter, and detection objective lens are used for fluorescence detection. The detection magnification $M_{T-LLS}$=62.5 and the illumination wavelength ${\lambda }_{illumination}$ = 488 nm. The width of the light sheet in the center of the FOV is about 400 nm. x-axis is the direction of the x-galvo mirror motion, z-axis is the direction of the z-piezo mirror motion, and s-axis is the direction of excitation light propagation.

The approach we chose uses FINCH with two diffractive lenses of different focal lengths with randomly selected pixels to scan an extended sample area and to recover the phase/depth information in the microscope’s emission while scanning the depth in the excitation arm by the z-galvo mirror only (Visualization 1 ^{(5.8MB, avi)} ). This allows multiple planes of fluorescence to be acquired without emission lens focusing, to give high speed detection coupled with the low light volumetric imaging available from LLS microscopy.

In this configuration, emitted light from a point object located in the front focal plane of the detection objective is collimated into a plane wave after passing the objective. This wave is transformed into two beams due to the two diffractive lenses with different focal lengths, f_d1 and f_d2, uploaded on the SLM that focus at two focal points, f_p1 and f_p2. The beam is adjusted in size by using the two lens pairs, L₁, L₂ and L₃, L₄, to fit the SLM chip area. The SLM used here was a phase SLM (Meadowlark; 1920 × 1152 pixels, it was recalibrated to produce the desired focal lengths and phase shifts for a 520 nm wavelength and delivers a full 2π phase shift over its working range of 256 gray levels.

A hologram is obtained by the interference between the two positive spherical waves converging to the image points f_p1, and f_p2 (relative to the SLM-plane), [Fig. 1(a))], located at 109 mm and 289 mm from the CMOS ORCA camera plane, and with interference efficiency $\text{tan}(\phi )\le 0.04$ (Algorithm S1). The SLM transparency for the two diffractive lenses has the expression:

$$\left[C_{1}Q\left(-\frac{1}{f_{d1}}\right)+C_2\text{exp}(i\theta )Q\left(-\frac{1}{f_{d2}}\right)\right]$$ (1)

where $\text{Q(b)}=\text{exp}[\text{i}\pi \text{b}{\lambda }^{-1}\text{(}{x}^2\text{+}{y}^2\text{)]}$ is a quadratic phase function. $\theta$ is the phase shift of the SLM, and $C_1=C_2=0.5$ are constants. When $f_{d1}=\mathrm{\infty }$, the expression becomes:

$$\left[C_1+C_2\text{exp}(i\theta )Q\left(-\frac{1}{f_{SLM}}\right)\right]$$ (2)

This is the transparency for the system with only one diffractive lens, and $C_1=0.1$, $C_2=0.9$ . We uploaded a single diffractive lens on the SLM [Fig. 1(b))], for calibration purposes (IHLLS 1L), or dual diffractive lenses with randomly selected pixels (IHLLS 2L) for recording sample holograms [Fig. 1(c))].

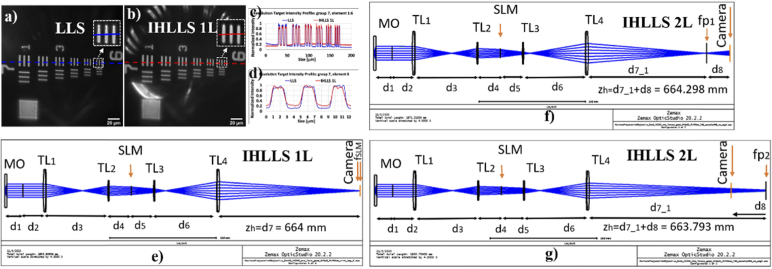
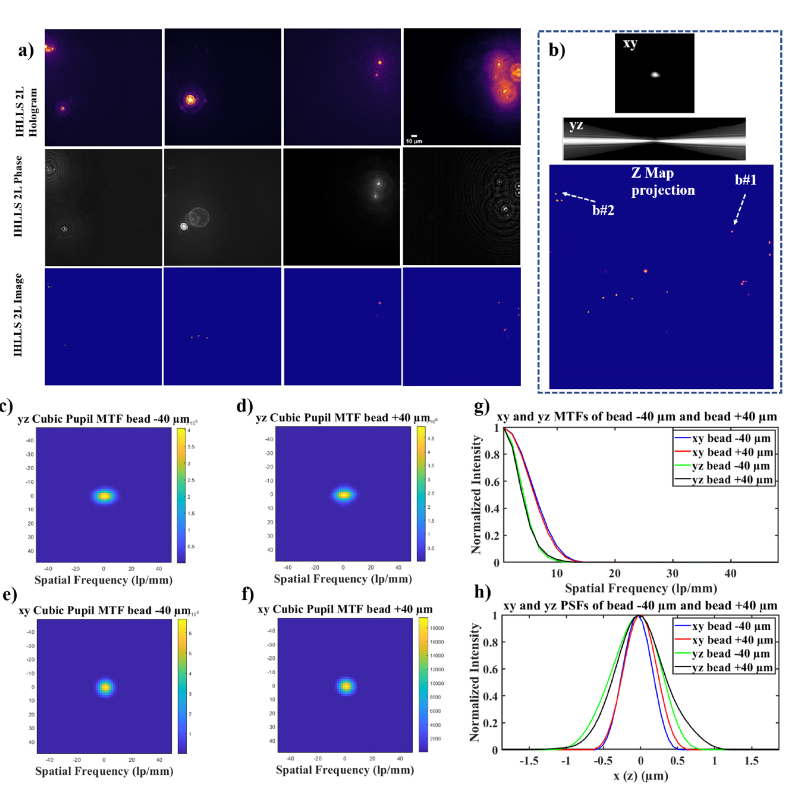
To overcome the limitations of the conventional (original) LLS hardware [Fig. 1(d), (e)], as described by Chen et al. [22], we implemented the IHLLS approach in four main steps. First, we matched the effective pixel size in both configurations, conventional LLS and IHLLS 1L [Fig. 1(f), (g)] by using a USAF 1951 resolution target [Fig. 2(a)-(d)] and Opticstudio (Zemax, LLC) optical design [Fig. 2(e)-(g)]. The Opticstudio software simulated the optical components, beams propagation from the sample plane to the camera plane and calculated the correct distances between each sequential optical component (Figure S1 for detailed measurements). Second, we demonstrated the 3D imaging capabilities of polystyrene beads by using both conventional LLS and IHLLS 1L for the diffractive lens with f_SLM = 400 mm at phase $\theta =0^o$ on the SLM, with x, z-galvo, and z-piezo motions [Fig. 3] for the calibration purposes. Third, we have recorded and reconstructed IHLLS 2L bead holograms at various z-galvo scanning depths, from $-40\mu m$ to $+40\mu m$ in steps of $10\mu m$, without moving the z-piezo, to assess the instrument performances in comparison to those of the conventional LLS [Fig. 3(e)-(h) and Fig. 5(p)-(t)]. Fourth, volumetric imaging of 500 nm and 200 nm beads [Fig. 4] and a nerve cell [Fig. 5(a)-(o)] are presented.

Fig. 2.

The IHLLS system calibration. a) The LLS resolution target imaging (a, c (blue), d (blue)) with $M_{T-LLS}$=62.5; b) The IHLLS resolution target imaging with one diffractive lens, IHLLS 1L, (b, c (red), d (red)) with $M_{T-IHLLS}$=62.5; c), d, Cross-sections of group 7 and element 6 respectively; e) Opticstudio simulation of IHLLS 1L, with the constraint $M_{T-IHLLS}$=62.5, to calculate the focal length (f_SLM = 400 mm) of a single diffractive lens uploaded on the SLM and the distances between each pair of optical components; f), g) These distances are kept constant for the simulation of IHLLS with two diffractive lenses, IHLLS 2L, to obtain the focal lengths of the two diffractive lenses on the SLM, f_d1 = 220 mm and f_d2 = 2356 mm.

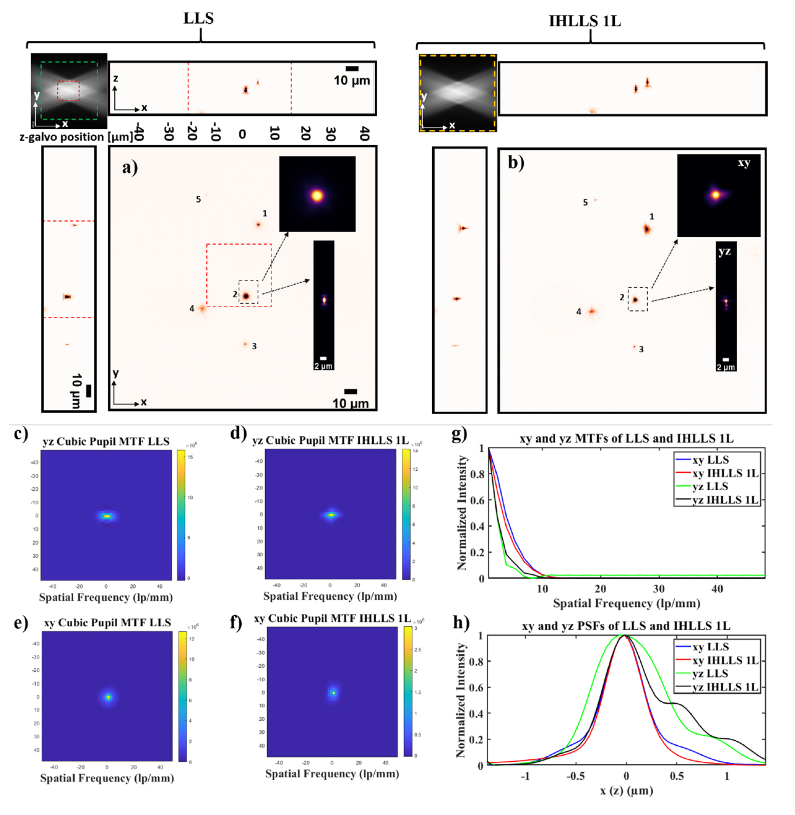
Fig. 3.

Tomographic imaging of 0.5 µm, FOV 208 µm², in a conventional LLS (a) and incoherent LLS with only one diffractive lens (IHLLS 1L) of focal length 400 nm (b), without deconvolution. On the sides and above are shown the max projections through the volume (400 Z-galvo steps). The Bessel beams are displayed in the upper left corner of each xy-projection to show the orientation of the beams (FOV 208 µm²) . The area enclosed inside the colored dashed rectangles are as follows: red- the scanning area for the original LLS (52 µm^2), green – the extended area mentioned in [21] of 120 µm^2, and yellow – the actual scanning area for the LLS, IHLLS 1L, and IHLLS 2L. The bead #2 in the black dashed rectangle that is in the middle of the lattice sheet is considered for calculating the resolution for the two instruments. The transverse MTFs of the two imaging techniques are shown in (c, d) and the axial MTFs are shown in (e, f); g) 1D xy and yz sections of the MTFs, h) 1D xy and yz of the PSFs. The FWHM of the curves are blue- 0.530 µm, red 0.495 µm, green 0.8341 µm, and black 0.9004 µm.

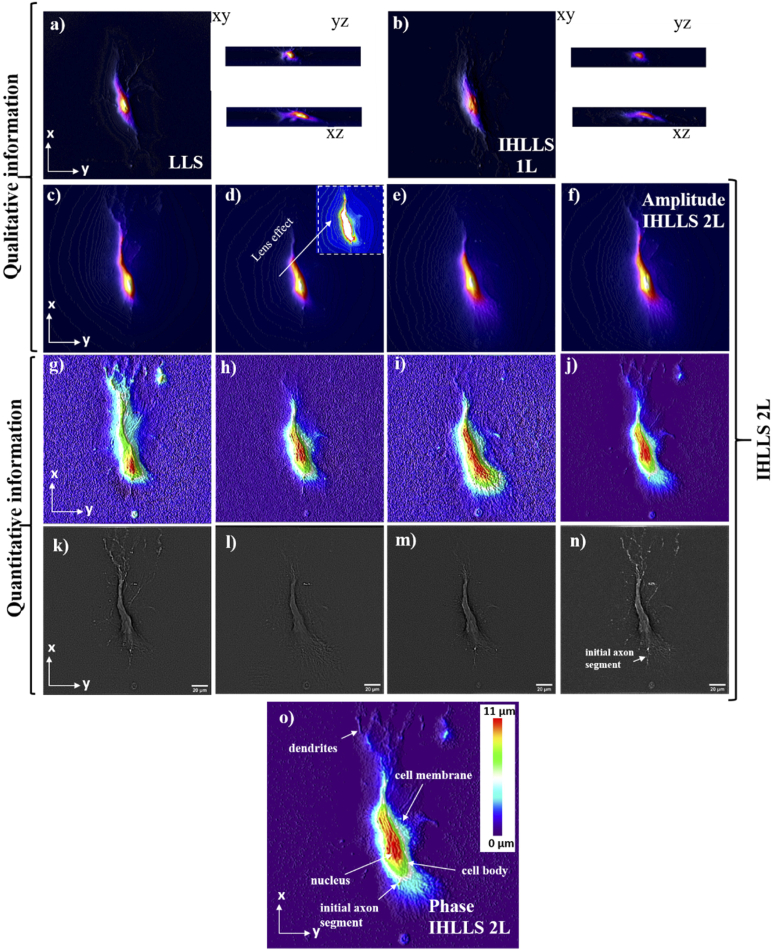
Fig. 5.

Lattice light-sheet imaging of a lamprey spinal cord ventral horn neuron with dendrites; a) Max projections through the volume (300 z-galvo steps) in a conventional LLSM without deconvolution; b) Max projections through the volume (300 z-galvo steps) in an incoherent LLSM without deconvolution using IHLLS 1L; Amplitude reconstruction of a neuronal cell at three z-galvo positions: c) +30µm, d) 0µm, e) −30µm, and f) the superposition of all three; Phase reconstruction of a neuronal cell at z-galvo positions: g) +30µm, h) 0µm, i) −30µm, and j) the superposition of all three; k)-n) Band-pass filter applied to the phase images from g)-j).

Fig. 4.

IHLLS 2L beads volume reconstruction; a) 500 nm beads holography $\pm 40\mu m,\pm 30\mu m$, holograms (first row), phase maps (second row), and reconstructed images (third row); b) The xy and yz cross-sections of a bead after the hologram reconstruction together with the z-max projection of all of the best z-reconstructed planes. The IHLLS phase images contain the depth dependent phase information derived from the IHLLS holograms and the reconstructed IHLLS images show the complex holograms propagated to the best focal plane. The max projection of the reconstructed volume of the 500 nm beads sample contains the z-galvo levels $\pm 40\mu m,\pm 30\mu m,$ $\pm 20\mu m,\text{and}0\mu m$. The transverse MTFs of the two beads b#1 and b#2 are shown in (c, d) and the axial MTFs are shown in (e, f); g) 1D xy and yz sections of the MTFs, h) 1D xy and yz of the PSFs. The FWHM of the curves are blue- 0.4534 µm, red 0.5118 µm, green 0.7663 µm, and black 0.7946 µm.

To achieve the best possible interference efficiency, the two beams from the two lenses, in the IHLLS 2L, must overlap exactly at the camera plane with foci in front and behind this plane. The constraint used for the optimization process by the optical design software, in Fig. 2(e)), was the transversal magnification, $M_{T-IHLLS}=M_{T-LLS}=62.5$. We obtained the gap between the last lens L₄ and camera $z_h=d_7=664mm$, and the focal length of the single diffractive lens $f_{SLM}=400mm$. Keeping all the distances $d_1$ to $d_7$ constant, we further designed a multi-configuration optical system with the condition that the height of the two beams was equal at the camera plane for a perfect overlap [Fig. 2(f), (g)]. After performing the optimization, we obtained the $f_{d1}=220mm$ and $f_{d2}=2356mm$.

3. Methods

3.1. System control

The entire system was controlled by the original LLS software based on LabView platform (National Instruments) with the diffractive SLM (Meadowlark Inc.) synchronized with the ORCA camera for the IHLLS module. The complex hologram is propagated and reconstructed at the best focal plane using a custom diffraction method routine in MATLAB (MathWorks, Inc.). The laser intensity and detector exposure time in IHLLS 2L were two times higher when compared to the LLS or IHLLS 1L.

3.2. Sample preparation

Fluorescent latex beads of 500 nm (${\lambda }_{exc}=488nm,{\lambda }_{em}=520nm$, 'F-8888, ThermoFisher Scientific, USA) were used as test objects. The bead solution (2% solids) was diluted 1:4000 with distilled water and briefly centrifuged in a desktop centrifuge for 1 min. Clean coverslips were prepared by applying 1 µL as a thin layer that was left to dry. After drying, the cover slip was mounted in the sample holder under distilled water.

Lamprey neurons were imaged in live intact isolated spinal cords. of larval lampreys (Petromyzon marinus). The animals were anesthetized with tricaine methanesulfonate (MS−222; 100 mg/l; Sigma, St. Louis, MO), decapitated, and dissected in a cold saline solution (Ringer) of the following composition (in mM): 100 NaCl, 2.1 KCl, 2.6 CaCl₂, 1.8 MgCl2 or 1.8 MgSO4, 4 glucose, 5 HEPES, adjusted to a pH of 7.60 with NaOH and to a final osmolarity of 270 ± 5 mOsm. The spinal cord was isolated and placed ventral side up in a cooled, small-volume chamber with a sylgard floor that is inserted under an upright water dipping objective on a fluorescence microscope. Spinal ventral horn neurons were impaled with sharp microelectrodes containing KC1 (500 mM), HEPES (5 mM) and dye (Alexa 488 hydrazide) titrated to a pH of 7.2. Dye was injected into up to 10 neurons per preparation. The chamber and spinal cord were then transferred onto the customized stage of the LLS microscope. The recording chamber was continually superfused with cold, oxygenated Ringer (8–10°C) for the duration of the experiment.

4. Results and discussions

To examine the effects of applying IHLLS holography, we performed three experiments for this study. The first was done using the conventional LLS pathway where the z-galvo was stepped in $\delta z_{LLS}=0.101\mu m$ increments through the focal plane of a 25x Nikon objective, which was simultaneously moved the same distance with a z-piezo controller for a displacement range of $\mathrm{\Delta }{z}_{galvo}=80\mu m$ [Fig. 3(a))] for scanning area of $208\times 208\mu m^2$. The second set of images was obtained using the IHLLS 1L with focal length $f_{SLM}=400mm$ displayed on the SLM, where both the z-galvo and z-piezo were again stepped with the same $\delta z_{LLS}=0.101\mu m$ increments through the focal plane of the objective for the same displacement $\mathrm{\Delta }{z}_{galvo}=80\mu m$ [Fig. 3(b))]. The scanning area in a conventional LLS is at best $52\times 52\mu m^2$ (red square in Fig. 3(a) and in the upper left corner of Fig. 3(a)), and it is still big for being illuminated by the Bessel beams. Therefore, to enlarge the scanned region these $52\times 52\mu m^2$ areas can be moved in a mosaic-fashion by moving the sample. However, this requires a substantially longer acquisition time and image registration. It also prevents simultaneous use of other recording modalities such as electrophysiology A recent more effective solution is to extend the scanning area to $170\times 170\mu m^2$ (green square in the upper left corner of Fig. 3(a)). This was achieved by superposing a spherical phase profile on the illumination wavefront at the pupil plane which requires 17 tiling positions [25], but with a lower axial resolution than the original LLS. The IHLLS 1L [Fig. 3(b), (d)], performs better than LLS by scanning a bigger area, but the resolution is lower in the axial directions due to the blurring effect of one of the lenses that is focused to infinity. Resolving fine structure in an image depends on both the shape and the extent of the spatial frequency support of the optical transfer function (OTF). To evaluate the relative imaging performance of IHLLS 1L compared with conventional LLSM techniques, the OTFs of these methods were computed in the following way. We calculated the xy- and yz- point spread functions of the two systems and compared them to the bead # 2’s transverse and axial images. The absolute values of the OTFs were calculated for the xy and yx cross-sections [Fig. 3(c)-(f)] by taking the Fourier transform of the 2D PSFs distributions. The 1D OTFs are shown in [Fig. 3(g))] and the corresponding PSFs in [Fig. 3(h))].

We calculated the FWHM in xy and yz directions for the two systems by fitting the PSFs from [Fig. 3(h))] with a 1D Gaussian function. The calculations for the 500 nm beads show a xy FWHM of 0.530 nm (LLS), 0.495 nm (IHLLS 1L) and yz FWHM of 834 nm (LLS) and 900 nm (IHLLS 1L). The IHLLS performs better within the scanning areas of $52\times 52\mu m^2$ and it gets worse outside this area due to the blurring effect of the second lens with infinite focal length.

We have chosen a different approach. We created a robust system that enables full complex-amplitude modulation of the emitted light for extended FOV and depth. This was achieved by combining the coherent properties of the Bessel beams with the incoherent properties of the fluorescent light emitted by each 3D point of the sample but made coherent in the self-interference process. This method was performed using the IHLLS pathway with two super-imposed diffractive lenses displayed on the SLM comprising randomly selected pixels (IHLLS 2L), where only the z-galvo was moved within the same $\mathrm{\Delta }{z}_{galvo}=40\mu m$ displacement range, above and below the reference focus position of the objective (which corresponds to the middle of the camera FOV), at $z_{galvo}=\pm 40\mu m$ $\pm 30\mu m$, $\pm 20\mu m$, $\pm 10\mu m$, and $0\mu m$.

The two wavefronts interfere with each other at the camera plane, to create Fresnel holograms. Four interference patterns were created using a phase shifting technique ($\theta =0^o,\theta =\pi /2^{\text{o}}$, $\theta ={\pi }^o,\theta =3\pi /2^o$) and further combined mathematically to obtain the complex amplitude of the object point at the camera plane:

$$\text{U}(\text{u},\text{v})=\text{A}(\text{u},\text{v})\text{exp}(\text{i}\varphi (\text{u},\text{v}))=\frac{1}{4}\{({\text{I}}_{\text{H}(\text{u},\text{v},0)}-{\text{I}}_{\text{H}(\text{u},\text{v},\pi )})+\text{i}({\text{I}}_{\text{H}(\text{u},\text{v},\pi /2)}-{\text{I}}_{\text{H}(\text{u},\text{v},3\pi /2)})\}$$ (3)

where: $A(u,v)$ is the amplitude of the image, ${\text{I}}_{\text{H}}$ are the hologram intensities, and phase:

$$\mathrm{\varnothing }(u,v)=arctan\left[\frac{I_H(u,v,0)-I_H(u,v,\pi )}{I_H(u,v,\pi /2)-I_H(u,v,3\pi /2)}\right].$$ (4)

The results are summarized in Figs. 4(a), (b), which depict the sample at four z-galvo planes, denoted $z_{galvo}=\pm 40\mu m,$ and $\pm 30\mu m$. The z-galvo planes correspond to the same relative depths in the sample. The reconstruction distance calibration from the image plane to the sample plane is $20mm$ in the IHLLS pathway for each $\pm 10\mu m$ displacement of the z-galvo mirror so, it means the conversion should be $80mmto\pm 40\mu m$. The monochrome SLM of the original LLSM instrument (this is different than the phase modulation SLM mounted in the incoherent arm) was used to generate the Bessel beams, and the beams were Fourier transformed and imaged onto the annular mask to block the zero-order diffracted beam. The image plane of the annular mask is conjugate to the back aperture of the LLSM excitation objective. The dimensions of the inner and outer rings determine the nature of the beams (Bessel-like beams or Gaussian-like beams) which are produced by the mask. In this optical setup we used an annular mask (outer NA = 0.55, inner NA = 0.48), which generated a Bessel beam with a FWHM sheet length of 15 µm. Choosing annuli with smaller ring diameters with lower NA we can obtain longer light sheets and deeper penetration depths, but the beams are more Gaussian-like beams. Using the LLS with this annular filter the z-galvo range is limited to about 30 µm, but the IHLLS 2L could scan up to about 80 µm for the same z-galvo range.

The IHLLS 2L holograms ($\theta =0^o$) for each z-galvo level are displayed in the upper row of Fig. 4(a)), and the phase corresponding to each hologram displayed in the second row. The phase images contain the depth dependent phase information derived from the IHLLS holograms. Then, the complex hologram is propagated and reconstructed at the best focal plane using a custom diffraction Angular Spectrum method (ASM) routine programmed in MATLAB (MathWorks, Inc.). These IHLLS 2L reconstructed images are shown in the third row of Fig. 4(a)). We chose the ASM and not the Fresnel reconstruction as the ASM can reconstruct the wave field at any distance from the hologram plane, without the minimum reconstruction distance requirement [2]. The max projection of all z-planes where the beads were found are displayed in Fig. 4(b)). They show the complex holograms propagated to the best focal plane. We performed scanning at other three z-galvo levels, $\pm 10\mu m$, and $0\mu m$, but the results are not shown in Fig. 4. Each column of Fig. 4(a)) results from images captured with the z-galvo positioned at a designated sample plane. Consequently, a sample plane at , contains the right layer of beads in this image, the sample plane at $z_{galvo}=-40\mu m$ contains the left layer and sample planes at $\pm 30\mu m$ $\pm 20\mu m$, and $0\mu m$, are equidistant between the two layers.

We also determined the distribution in transverse FWHM values for the 500 nm beads [Fig. 4]. In the original FINCH system, it was shown that using spatial incoherent light, such as fluorescent light, to form holograms, and producing images with better spatial resolution than conventional imaging, is possible, because the incoherent imaging systems break the Lagrange principle valid for classical imaging system.

This occurs in such a way that it magnifies the gap between two spots more than it magnifies the spots themselves [29–31]. While we have indeed achieved higher resolution with IHLLS-2L than with IHLLS-1L or LLS, we must still do more work to optimize the system. We need to determine how many galvanometric and hologram reconstruction steps before we draw the same conclusion here. Another factor to consider is to investigate the Lagrange principle with a larger area SLM without reducing and expanding the beam size. Nevertheless, from Fig. 4(g) and (h), we can draw the conclusion that IHLLS-2L provides a better method for finding the focal position of the objects than using analog glass optics.

Understanding the physiology and pathophysiology of neuronal cells provide the foundation for understanding many diseases in human brain, which requires the quantitative observation of cell structure and dynamics at cellular and subcellular resolutions. Wavefront phase imaging is a noninvasive contrast imaging technique besides the better-known and more commonly used fluorescence microscopy. Various quantitative phase microscopy (QPM) techniques using interferometry or holography have been developed. These approaches have been successful in mapping and dissecting the complex cellular processes [2–6]. Examples of quantitative information gained from this approach are the cellular dry mass [8–10], intracellular refractive index (RI) [11–15], and the cell volume [14] measurements.

LLS volumetric imaging [Fig. 5(a))] can provide only morphological measurements in any sample volume, but not complex cellular parameters such as the cellular dry mass or RI. These are features of cells that dynamically change in response to activity. As an example, the LLS is unable to account directly for potential contributions that might be provided to the surface area by subresolution features such as subdiffraction sized structure including microvilli [32], whose structure can be rapidly altered by Ca²⁺ entry [33–35] or the structure of cell membranes altered by voltage fluctuations [20].Therefore, quantitative analysis of membrane dynamics detected by using the IHLLS system will be of significance in understanding a range of cell functions.

The last step in our study is to demonstrate, for the first time, quantitative phase imaging of cells using IHLLS 2L. These findings would open a new avenue for light sheet imaging instruments.

For this step we chose a simple neuronal preparation in which a neuron could be readily labeled with fluorescent dye and maintained alive during imaging. Lamprey spinal cord ventral horn neurons have dendrites that are sufficiently large to cover the whole camera FOV of $208\mu m^2$. When performing tomographic imaging using the original LLS [Fig. 5(a))] or IHLLS 1L (phase ${\theta }^o$ in Fig. 5(b))), the sample outside of the maximum area of $78\times 78\mu m^2$ cannot be resolved, although the z-galvo mirror and the z-piezo stage objective were moved 300 steps in the range $60\mu m$. Deconvolution sharpening of the raw data is the standard solution for blur reduction and enhancement of fine image details in LLS image processing. When using the IHLLS 2L [Fig. 5(c)-(f)] the max projection of only three reconstructed amplitude images from IHLLS holograms recorded at $z_{galvo}=\pm 30\mu m$, and $0\mu m$, could give similar results as the LLS, and within a larger resolved sample area. In addition to the amplitude images, the IHLLS 2L can provide access to the reconstructed phase information [Fig. 5(g)-(j)] needed to understand the physiology and pathophysiology of various cells or other parts of samples under study. Applying further a band-pass filter to the above phase images other features could be identified [Fig. 5(k)-(n)].

Within biological samples, axial resolution enhancement is possible if the phase difference of two interfering wavefronts is known. The combination of the two lenses with focal lengths, f_d1 = 220 mm and f_d2 = 2356 mm, gave a reconstruction distance with a maximum $80mm$ above the reference plane (microscope objective position or the middle of the camera FOV) and 60 mm below the reference plane, but when converted to the z-galvo displacement the reconstructed distance was $30\mu m$ and $-30\mu m$ respectively, which results in a $30\mu m$ volume height. When the scanning range is increased to $\pm 40\mu m,$ the reconstruction distance increases to about $250mm$ above the reference plane and 80 mm below the reference plane, which correspond to z-galvo displacements of $40\mu m$ and $-40\mu m$ respectively, and a $80\mu m$ volume height.

3D perspective representation of the quantitative phase contrast image of the axon cell is displayed in Fig. 5(g)-(j). Each pixel represents a quantitative measurement of the cellular optical path length (OPL) of the fluorescently labeled neurons and their subcellular compartments. The scale (at right) in Fig. 5(o)) relates the OPL (in the color LUT) to the morphology (in µm). The IHLLS 2L and LLS techniques have similar transverse performances, but the axial performance is poorer for the IHLLS 2L, when moving the z-galvo in 7 or 9 steps along the 80 µm ranges. Therefore, we need to increase the number of z-galvo increments to achieve a better axial performance.

5. Conclusion

In summary, in addition to achieving a maximum detector FOV of $208\mu m^2$, the IHLLS is equipped with the capacity of faster volumetric acquisition and multi-plane imaging for probing the three-dimensional morphology and structure of biological samples. The axial resolution can be improved by recording and reconstructing images at multiple z-galvo steps and minimizing the hologram reconstruction increment, δz, to achieve better localization of the sample points. Because the objective position is fixed, images at the center of the z galvo range are brighter, therefore we modulated the laser power and exposure time in the z axis. While the system can improve rate of acquisition of 3D structure and allows phase imaging within these structures, light is necessarily lost in a required polarizer in the IHLLS. Nevertheless, the LLSM excitation provides a low light baseline on which to base this approach which still minimizes bleaching. Thus, the optical and mechanical design of the incoherent arm expands the applicability of the lattice light-sheet system and could open entirely new imaging modalities in all light sheet imaging instruments. The incoherent configuration could be added as an accessory or as an add-on feature.

Funding

National Institute of Mental Health10.13039/100000025 (DC017292, NS111749); National Institutes of Health10.13039/100000002 (R21 DC017292, RO1 NS111749).

Disclosures

The authors declare that they have no conflict of interest.

Data availability

The technical drawings of the beam geometry of both, conventional LLS and IHLLS are available in Visualization 1 ^{(5.8MB, avi)} . Detailed measurements of focal lengths and distances between each sequential optical component are available in Supplement 1 ^{(1.3MB, pdf)} . All other details required for setting up the complete system are provided in the Methods. Supporting data for Figs. 3–5 are available from the corresponding author on reasonable request. This is due to the size of the datasets being so large that they are not available on a public server.

Supplemental document

See Supplement 1 ^{(1.3MB, pdf)} for supporting content.