Abstract
This article discusses short term forecasting of the Novel Corona Virus (COVID −19) data for infected, recovered and active cases using the Machine learned hybrid Gaussian and ARIMA method for the spread in India. The Covid-19 data is obtained from the World meter and MOH (Ministry of Health, India). The data is analyzed for the period from January 30, 2020 (the first case reported) to October 15, 2020. Using ARIMA (2, 1, 0), we obtain the short forecast up to October 31, 2020. The several statistics parameters have tested for the goodness of fit to evaluate the forecasting methods but the results show that ARIMA (2, 1, 0) gives better forecast for the data system. It is observed that COVID 19 data follows quadratic behavior and in long run it spreads with high peak roughly estimated in September 18, 2020. Also, using nonlinear regression it is observed that the trend in long run follows the Gaussian mixture model. It is concluded that COVID 19 will follow secondary shock wave in the month of November 2020. In India we are approaching towards herd immunity. Also, it is observed that the impact of pandemic will be about 441 to 465 days and the pandemic will end in between April-May 2021. It is concluded that primary peak observed in September 2020 and the secondary shock wave to be around November 2020 with sharp peak. Thus, it is concluded that the people should follow precautionary measures and it is better to maintain social distancing with all safety measures as the pandemic situation is not in control due to non-availability of medicines.
Keywords: ARIMA, Nonlinear Regression, Gaussian Model, COVID 19, Global Health Security Index, Long term forecast
Introduction
When the world was celebrating New Year’s Eve in December 2019, China declared an outburst of a new virus in Wuhan city that is located in China’s Hubei region and a residence for approximately 11 million people. The virus, was found to be linked with the family of single-stranded RNA viruses generally known as coronaviridae, which affects the species like reptiles, mammals and birds [1]. It was named Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-coV-2), if a living body gets infected by this virus and develops a disease then the disease is called COVID-19. It’s transmission to humans have caused a panicking situation due to its virulent and pernicious effects on our bodies. A person having SARS-coV-2 virus may experience symptoms like: Cough; High body temperature; Shivering and fever; Breathlessness; Diarrhea; Headache and Body ache.
Further, it exhibits various astute qualities to sustain itself. Like travelling within us without getting detected (unless tested properly), infecting everything its host touches, reproducing itself liberally. However, its origin has not been confirmed till now [2]. Initially, it was suspected to be originated in Wuhan’s South China Seafood Wholesale Market and later on, new possible origins were supposed like some scientists claimed that the cross-species circulation may be from snakes to humans; however, this claim was disputed [3]. Coronaviruses (CV) are RNA viruses that are respiratory pathogens. Coronavirus transmission is defined as zoonotic i.e. between animals and people. They can cause benign seasonal illnesses like common cold to more severe public health emergencies like Severe Acute Respiratory Syndrome (SARS) and Middle East Respiratory Syndrome (MERS). A novel strain of Coronavirus disease has been identified in 2019 which was not previously identified in humans [4]. The death rate from Covid-19 is considered very low for many age groups; but, the virus has turned out to be deadly for people above the age of 60 and due to its spread in over 200 countries, World Health Organization (WHO) on 11th February. 2020 declared it as a pandemic [5].
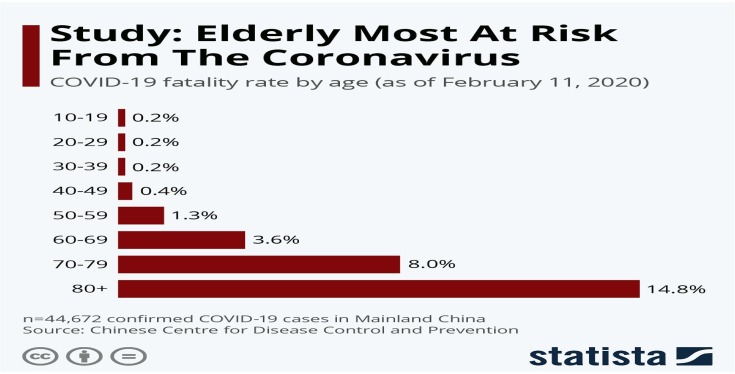
The COVID 19 fatality rate by age (as on February 11, 2020) was shown in Fig. 1 [6]. With an estimated reproduction number greater than 1 (range 2.6–4.7), early reports predicted a potential Coronavirus outbreak [7]. This novel Coronavirus was named COVID-19 by WHO on Feb 11, 2020. In India, first case of COVID-19 was discovered in Kerala. The patient was identified as a female of Indian nationality; she was a student of Wuhan University and was isolated & declared stable by doctors later on. After this incident, a rapid response team was called for an emergency meeting; the meeting discussed ways of preventing the community transmission of this virus [8]. India reported almost no new cases of the virus until one month after this incident. During the month of March 2020 India experienced the true outbreak of COVID-19 and the number of new cases has continued to rise exponentially since then. In history, the world has gone through many pandemics. The Global Health Security Index-2019, which ranks 195 countries on health security as on March 20, 2020 [9] is shown in Fig. 2 .
Fig. 1.
COVID 19 fatality rate by age.
Fig. 2.
Global Health Security Index 2019.
Corona viruses (Co-Vs) are majorly identified through respiratory in addition with the gastrointestinal- tract taints that can be hereditarily categorized as four key genera: Alpha coronavirus, Beta coronavirus, Gamma coronavirus, and Delta coronavirus. First two genera predominantly infected mammalia and last two primarily infect birds. Various kinds of human-destroying Co-Vs have been previously identified. These comprise of HCoV-NL63 and HCoV229E, that may belong towards Alpha coronavirus genus; and HCoV-OC43, HCoVHKU1, severe-acute-respiratory-syndrome-coronavirus (SARS-Co-V), and Middle-East-respiratory-syndrome- coronavirus (MERS-Co-V) belonging into Beta coronavirus genus. Coronaviruses were not globally known or recognized until the 2003-SARS pandemic followed by year-2012 MERS and, most recently, the 2019-nCoV outbreaks. SARS-CoV and MERS-CoV are considered highly virulent. Also, it is very probable that both SARS-CoV & MERS-CoV were communicated from bats to palm-civets & dromedary camels and further transferred ultimately to humans. Novel coronavirus (CoV)-‘‘2019 novel coronavirus’’/‘‘2019-nCoV’’ by the World Health Organization (WHO) is accountable for the recent pneumonia outbreak that started in early December 2019. The molecules that may perhaps enter into host cell and cause acute respiratory syndrome targeting towards coronavirus studied and forecasted impending COVID-19 spread cases for China plus some other regions using mathematical & traditional time-series prediction models [40]. Mathematical model-based prediction at an early stage achieved for the outburst of this particular virus in China [41]. Extensive exploration of pneumonia outbreak via corona-genome originating from bat species [42].
Effects of the virus
Coronavirus can have harmful effects on our bodies and livelihood. Some of them are:
-
1.
Forming Blood Clots in the Human Body Doctors and scientists across the globe are witnessing a surfeit of clotting-related disorders – ranging from innocuous skin bruise seen on the foot occasionally called as “Covid toe” to the life-threatening strokes & vain blockage. The issue is clear in clots that is thrombi, it forms in a patient’s arterial catheters and filters used to support the failing of kidneys. More dangerous the blood clots, more impeding of the blood circulation in the lungs and breathlessness.
-
2.
Causes Silent Hypoxia Researchers and doctors have revealed a medical condition known as “happy” or “silent” hypoxia, in this condition the patients have extremely low blood oxygen levels in their bodies and yet do not show any symptoms of breathlessness. They are now supporting for its early detection as a means to avoid a deadly disorder called “Covid pneumonia”, a malign condition found in patients that are severely affected by COVID-19. It is preceded by “silent hypoxia” that is a form of oxygen deprivation and is harder to elicit than regular hypoxia. In numerous cases the COVID-19 patients with silent hypoxia did not exhibit signs such as a lack of coughing or breaths until their oxygen levels fell to very low, at this point the risk of acute respiratory distress (ARDS) and organ failure is engendered.
Preventive measures
As the number of cases infected with Covid-19 disease reaches approximately 3 lakhs in India, it becomes more than ever important to prevent ourselves from the virus. Also, we can witness that many states are loosening the restrictions that were previously imposed to prevent the community spread. So, personal and individual hygiene is eminent [31]. Some of the measure that can ensure personal hygiene and safety are:
-
1.
Always sanitize your hands after coming in contact with anyone. It is crucial as many cases are asymptomatic and the virus can be transferred without getting noticed.
-
2.
Always wear hand gloves and a face mask. Wearing protective gear like hand gloves and face mask ensures that the molecules of the virus are contained within the infected person and prohibits them from entering the body of another in search of a new host.
-
3.
Avoid going in crowd places Going in crowed places highly increases the risk of getting infected with the COVID-19, it is because social distancing is not followed in these areas.
-
4.
Always stay updated about the virus with trusted sources Staying updated from trusted sources will help in maintaining your welfare and safety. [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37], [38]
Methodology
The different techniques and methodologies used for forecasting are given in flow chart [38] as Fig. 3 .
| (1) |
Fig. 3.
Descriptive Analysis Flow Diagram [23].
To control epidemiology the value of CFR should be minimum [22].
| (2) |
For control of pandemic the value of Cumulative active cases to be minimum with cumulative death cases as zero and cumulative recovered cases as maximum [18].
Nonlinear regression
Nonlinear regression is a type of regression examination wherein information is fit to a model and afterward communicated as a numerical capacity. Basic direct relapse relates two factors (X and Y) with a straight line (y = mx + b), while nonlinear regression relates the two factors in a nonlinear (curved) relationship. The objective of the model is to make the amount of the squares as little as could really be expected. The amount of squares is an action that tracks how far the Y perceptions differ from the nonlinear (curved) function that is utilized to foresee Y.
Box-Cox time transformation measure
The Box-Cox transformation is principally useful family of transformations [34], [35].
Theorem:
Suppose a sample of n response values t1. Letbe a value such that. Compute the set ofwith respect to tias:
| (3) |
where ,
Natural log is applied in the case of instead of the aforementioned formula. It helps to define the measure of normality of resulting transformation. It is meant to moderate non-normal dependent variable into normal contour. The measure computes the correlation coefficient of normal probability. Correlation is simulated for the variables of probability plot and a scale of linearity of probability plot. Vertical axis encapsulates correlation coefficient of normal probability and horizontal axis stands for the values of . This stationarity test is applied towards the positive and negative values [36], [37].
Autocorrelation & partial correlation function (ACF & PACF)
The statistics under consideration are said to have autocorrelation whenever the response variables, at time-domain, are determined to be correlated through the values, at time-domain, where, refers to the time increment that lies in the upcoming events [10], [11], [14], [15]. It can be observed that within the long memory-process, auto-correlation deteriorates over time resulting in the power-law trend written as
| (4) |
where, - constant and – autocorrelation-function having lag . Generalizing, consider set of responses as: at time: along with auto-correlation function is represented via:
| (5) |
where, .
The interpretations should be uniformly-sampled. Unlike cross-correlation, ACF result in a correlation-coefficient signifying degree of resemblance of two response variables at time, . ACF used to identify non-randomness in data and propagate appropriate time-repressiveness when data has no chaos. Whenever ACF is applied for locating apt time successive regression, there ACF gets charted.
Augmented Dickey-fuller stationarity test (ADF)
Basically, a unit root test to check stationarity as these unit roots can cause unpredictable results in the autoregressive models of time series analysis. Time series are different in comparison to the predictive modeling. As in modeling the assumptions exist that summary statistics of observations are consistent. In context to time series, these expectations are referred as time domain being stationary [19], [20], [33]. Time-series is taken to be stationary when it does not contain trend or seasonal effects. So, these summary statistics computed on time domain is said to be consistent over time. Thus, statistical modeling considers that stationarity in the series makes it effective [10], [12], [13]. In particular, it concludes how strongly a time series is defined by a trend.
Goodness of Fit, histogram and density function
Grading goodness-of-fit (GOF) for various-distributions one can get impressions for whichever distribution is satisfactory& whichever is not. From cumulative-distribution-function (CDF), derive histogram and the probability-density-function (PDF) [24], [25], [26].
Theorem The measurement of discrepancies among observed and fitted values is regarded the deviation. For Poisson-responses, deviances take this form:
| (6) |
First-term-identical towards binomial-deviance, demonstrating “twice a sum of observed times log of observed over fitted”. Second term is the sum of differences between observed and fitted values, is usually zero [16], [17], [21], [27].
Lemma For large-sections, distribution of deviation is nearly chi-squared with n-p degrees of freedom, whenever n considers no. of observations; p for no. of parameters. Thus, deviance can be utilized directly towards testing goodness-of-fit of this model.
Coefficient of determination (R2)
R-squared, the statistical measure of the closeness of data to look for fitted-regression-line. It is also known referred as coefficient of determination, coefficient of multi-determination for multi-regressors. Description of R-squared is fairly simple; it is the percentage of retort-variable having variation which usually described through the regression. R-squared lies between 0 and 1 where 0 indicates that model describes none of variability of this response data around the mean. 1 determines that the prototype describes all of the variability around response data of the mean [28], [29], [30], [32].
Results and discussions for model selection
For long term behavior, data sets of India from January 30, 2020 to October 15, 2020 is analyzed. The spread of COVID 19 in different states of India as on August 9, 2020 is shown in Fig. 4 [39]. Descriptive statistics for new cases; total cases; new deaths; total deaths; new recovered; total recovered; new active; total active and CFR is given in Table 1 with the details of correlation and coefficient of determination in Table-2. Parallel coordinate -plot for all cases is shown in Fig. 5 .Table 2
Fig. 4.
COVID 19 spread in different states of India.
Table 1.
Descriptive Statistics of COVID 19 of India.
| Statistic | Daily cases | Daily deaths | Daily recovered | Daily active | Total_cases | Total_deaths | TOTAL recovered | Total active | CFR |
|---|---|---|---|---|---|---|---|---|---|
| Range | 97894.000 | 2003.0 | 101468. | 51900.0 | 7307096.000 | 111266.000 | 6383441.000 | 1017754.000 | 0.03 |
| 1st Quartile | 506.000 | 10.500 | 32.500 | 1.500 | 3138.000 | 72.500 | 210.500 | 2855.000 | 0.02 |
| Median | 9971.000 | 287.000 | 5247.000 | 1532.000 | 256611.000 | 7135.000 | 123848.000 | 125628.000 | 0.02 |
| 3rd Quartile | 60969.0 | 855.000 | 53816.500 | 5768.000 | 2299156.500 | 45674.000 | 1,611,544 | 641938.500 | 0.03 |
| Sum | 7,307,097 | 111266. | 6382830.0 | 812399.0 | 377,905,886 | 6,793,432 | 291,430,686 | 79681767.0 | 5.29 |
| Mean | 28212.730 | 429.598 | 24644.131 | 3136.676 | 1459096.085 | 26229.467 | 1125215.004 | 307651.610 | 0.02 |
| Variance (n-1) | 1,072,500,058 | 189,361 | 982,772,956 | 47,687,169 | 4,529,384,296,503 | 1,146,730,168 | 3,106,697,485,596 | 126,928,747,047 | 0.00 |
| Standard deviation (n-1) | 32749.047 | 435.157 | 31349.210 | 6905.590 | 2128235.019 | 33863.405 | 1762582.618 | 356270.609 | 0.01 |
| Variation coefficient | 1.159 | 1.011 | 1.270 | 2.197 | 1.456 | 1.289 | 1.563 | 1.156 | 0.52 |
| Skewness (Pearson) | 0.773 | 0.609 | 0.943 | −0.139 | 1.412 | 1.145 | 1.580 | 0.785 | −0.78 |
| Skewness (Fisher) | 0.778 | 0.613 | 0.948 | −0.140 | 1.420 | 1.152 | 1.589 | 0.790 | −0.78 |
| Skewness (Bowley) | 0.687 | 0.345 | 0.806 | 0.469 | 0.779 | 0.690 | 0.847 | 0.616 | 0.08 |
| Kurtosis (Pearson) | −0.993 | −0.841 | −0.693 | 2.558 | 0.662 | −0.039 | 1.239 | −0.987 | −0.44 |
| Kurtosis (Fisher) | −0.989 | −0.834 | −0.683 | 2.631 | 0.699 | −0.017 | 1.287 | −0.983 | −0.43 |
| Standard error of the mean | 2034.927 | 27.039 | 1947.945 | 429.092 | 132242.090 | 2104.170 | 109521.555 | 22137.579 | 0.0 |
| Lower bound (95%) | 24205.549 | 376.353 | 20808.235 | 2291.706 | 1198684.779 | 22085.934 | 909545.006 | 264058.260 | 0.02 |
| Upper bound (95%) | 32219.910 | 482.844 | 28480.027 | 3981.645 | 1719507.391 | 30373.001 | 1340885.002 | 351244.960 | 0.02 |
Fig. 5.
Parallel Coordinate plot for confirmed (new; total); death (new, total); recovered (new, total); active (new, recovered); CFR cases from January 30, 2020 to October 15, 2020.
Table.
2. Correlation and coefficient of determination between the variables.
| Correlation Matrix (Pearson) with 0.05 significance level | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Variables | Dailycases | Daily Deaths | Dailyrecovered | Daily Active | Aggregate cases | Aggregate Deaths | Aggregate recovered | Aggregate active | CFR |
| New cases | 1 | 0.945 | 0.977 | 0.249 | 0.905 | 0.941 | 0.875 | 0.990 | −0.081 |
| Total cases | 0.945 | 1 | 0.910 | 0.284 | 0.822 | 0.873 | 0.786 | 0.937 | 0.030 |
| New deaths | 0.977 | 0.910 | 1 | 0.036 | 0.960 | 0.979 | 0.940 | 0.991 | −0.126 |
| Total deaths | 0.249 | 0.284 | 0.036 | 1 | −0.116 | −0.034 | −0.168 | 0.138 | 0.186 |
| Daily recovered | 0.905 | 0.822 | 0.960 | −0.116 | 1 | 0.993 | 0.998 | 0.944 | −0.158 |
| Total recovered | 0.941 | 0.873 | 0.979 | −0.034 | 0.993 | 1 | 0.983 | 0.972 | −0.123 |
| Daily active | 0.875 | 0.786 | 0.940 | −0.168 | 0.998 | 0.983 | 1 | 0.919 | −0.171 |
| Total active | 0.990 | 0.937 | 0.991 | 0.138 | 0.944 | 0.972 | 0.919 | 1 | −0.085 |
| CFR | −0.081 | 0.030 | −0.126 | 0.186 | −0.158 | −0.123 | −0.171 | −0.085 | 1 |
| Coefficients of determination (R2) | |||||||||
| new cases | 1 | 0.892 | 0.954 | 0.062 | 0.819 | 0.886 | 0.765 | 0.981 | 0.006 |
| total cases | 0.892 | 1 | 0.829 | 0.081 | 0.675 | 0.763 | 0.618 | 0.878 | 0.001 |
| new deaths | 0.954 | 0.829 | 1 | 0.001 | 0.921 | 0.958 | 0.883 | 0.983 | 0.016 |
| total deaths | 0.062 | 0.081 | 0.001 | 1 | 0.014 | 0.001 | 0.028 | 0.019 | 0.034 |
| daily recovered | 0.819 | 0.675 | 0.921 | 0.014 | 1 | 0.986 | 0.995 | 0.891 | 0.025 |
| total recovered | 0.886 | 0.763 | 0.958 | 0.001 | 0.986 | 1 | 0.967 | 0.945 | 0.015 |
| daily active | 0.765 | 0.618 | 0.883 | 0.028 | 0.995 | 0.967 | 1 | 0.844 | 0.029 |
| total active | 0.981 | 0.878 | 0.983 | 0.019 | 0.891 | 0.945 | 0.844 | 1 | 0.007 |
| CFR | 0.006 | 0.001 | 0.016 | 0.034 | 0.025 | 0.015 | 0.029 | 0.007 | 1 |
Cross correlation for total recovered cases with respect to dates are shown in Fig. 6 . The details of normality and white noise test for date; total recovered and date/ recovered cases are shown in Table 3 for different Statistics like Box-pieces for six degrees of freedom and 12 degrees of freedom; Liung Box for six degrees of freedom and 12 degrees of freedom; Mcleod Li for six degree of freedom and 12 degrees of freedom.
Fig. 6.
Cross correlation for total Recovered cases.
Table 3.
Goodness of fit statistics at 95% confidence interval.
| Statistic | date Value | total recovered | date/ total recovered |
|---|---|---|---|
| Box-Pierce (6) | 15.409 | 124.305 | 801.126 |
| Ljung-Box (6) | 1430.953 | 1363.071 | 818.537 |
| McLeod-Li (6) | 1461.418 | 1391.856 | 1535.401 |
| Box-Pierce (12) | 1461.419 | 1271.785 | 1668.301 |
| Ljung-Box (12) | 2662.032 | 2427.930 | 1725.859 |
| McLeod-Li (12) | 2748.909 | 2505.284 | 3015.533 |
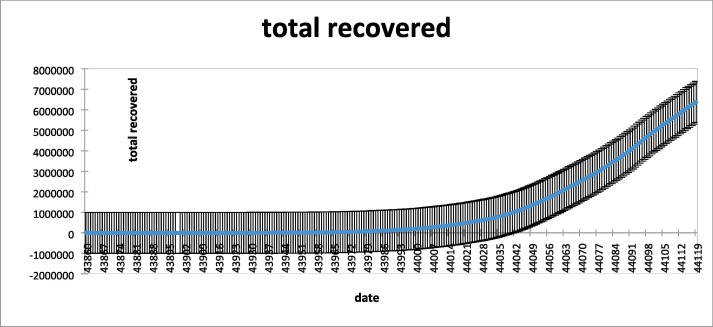
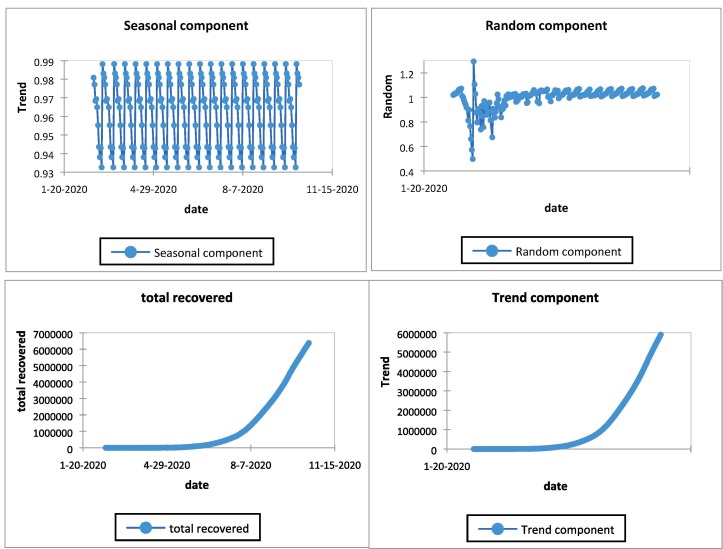
Mann- Kendall trend test of two tailed test for total recovered case is discussed at 95% confidence interval so value of alphas is 0.05. Test interpretation is considered as: H0: There is no trend in the series; Ha: There is a trend in the series. The value of Kendall’s tau is 0.994 with S as 33,008 and Variance of S as 1939506.667 with p value as less than 0.0001. As the computed p-value is lower than the significance level alpha = 0.05, one should reject the null hypothesis H0, and accept the alternative hypothesis Ha. The risk to reject the null hypothesis H0 while it is true is lower than 0.01%. Sen’s slope is 12,275 with confidence interval as ]10767.131, 13831.833 [. The Mann-Kendall trend for total recovered cases is shown in Fig. 7 and total error is depicted in Fig. 8 . For total recovered cases using Box Cox transformation, with lamda as zero as differencing as zero, polynomial regression is fitted with goodness of fit statistics R2 as 0.691; adjusted R2 as 0.69. In case of seasonal fitting goodness of fit statistics are R2 as 0.002; adjusted R2 as −0.046. All trends are shown in Fig. 9 and Fig. 10 . Fig. 11 shows the forecasted and trend analysis using ARIMA (2,1,0) model for total confirmed; total death; total recovered and total active cases with detailed values in Table 4 .
Fig. 7.
Mann- Kendall trend for total recovered cases.
Fig. 8.
Error Bars for total recovered cases.
Fig. 9.
Bos Cox Transformation and polynomial regression of total recovered cases.
Fig. 10.
Trend; seasonal and random component for total recovered cases.
Fig. 11.
Forecast and trend analysis using ARIMA (2,1,0).
Table 4.
Forecasting ARIMA (2,1,0) model where A -Actual, P- Predicted, F- forecasted.
| Actual & Predicted Values | |||||
|---|---|---|---|---|---|
| Date | status | Aggregate Cases | Aggregate Deaths | Aggregate Recovery | Aggregate Active |
| 08–10-2020 | A | 6,906,151 | 106,490 | 5,906,069 | 893,592 |
| P | 6,913,019 | 106,483 | 5,910,230 | 897,733 | |
| 09–10-2020 | A | 6,979,423 | 107,416 | 5,988,822 | 883,185 |
| P | 6,977,669 | 107,436 | 5,986,431 | 888,088 | |
| 10–10-2020 | A | 7,053,806 | 108,334 | 6,077,976 | 867,496 |
| P | 7,052,027 | 108,340 | 6,069,439 | 875,970 | |
| 11–10-2020 | A | 7,120,538 | 109,150 | 6,149,535 | 861,853 |
| P | 7,127,789 | 109,236 | 6,164,146 | 856,648 | |
| 12–10-2020 | A | 7,175,880 | 109,856 | 6,227,295 | 838,729 |
| P | 7,188,275 | 109,996 | 6,229,333 | 855,827 | |
| 13–10-2020 | A | 7,239,289 | 110,586 | 6,301,927 | 826,876 |
| P | 7,232,549 | 110,599 | 6,302,027 | 824,867 | |
| 14–10-2020 | A | 7,301,424 | 111,266 | 6,383,441 | 812,390 |
| P | 7,307,097 | 111,292 | 6,377,879 | 814,796 | |
| Forecasted Values | |||||
| 15–10-2020 | F | 7,363,474 | 111,997 | 6,453,080 | 805,557 |
| A | 7,365,509 | 112,161 | 6,453,779 | 803,999 | |
| 16–10-2020 | F | 7,425,310 | 112,691 | 6,528,494 | 797,824 |
| A | 7,430,635 | 112,998 | 6,524,995 | 795,256 | |
| 17–10-2020 | F | 7,486,968 | 113,379 | 6,603,673 | 791,669 |
| A | 7,494,551 | 114,031 | 6,597,209 | 783,544 | |
| 18–10-2020 | F | 7,548,444 | 114,058 | 6,678,825 | 786,781 |
| A | 7,550,273 | 114,610 | 6,663,608 | 772,977 | |
| 19–10-2020 | F | 7,609,739 | 114,731 | 6,753,853 | 783,006 |
| A | 7,597,063 | 115,197 | 6,733,328 | 748,154 | |
| 20–10-2020 | F | 7,670,855 | 115,396 | 6,828,804 | 780,178 |
| A | 7,651,107 | 115,940 | 6,795,103 | 739,932 | |
| 21–10-2020 | F | 7,731,793 | 116,054 | 6,903,656 | 776,850 |
| A | 7,706,946 | 116,616 | 6,874,518 | 715,869 | |
| 22–10-2020 | F | 7,792,553 | 116,705 | 6,978,418 | 777,794 |
| A | 7,761,312 | 117,306 | 6,948,497 | 695,233 | |
| 23–10-2020 | F | 7,853,137 | 117,350 | 7,053,087 | 782,088 |
| A | 7,814,682 | 117,956 | 7,016,046 | 681,355 | |
| 24–10-2020 | F | 7,913,545 | 117,989 | 7,127,665 | 790,283 |
| A | 7,864,811 | 118,534 | 7,078,123 | 668,844 | |
| 25–10-2020 | F | 7,973,778 | 118,621 | 7,202,152 | 800,049 |
| A | 7,909,959 | 119,014 | 7,137,228 | 655,263 | |
| 26–10-2020 | F | 8,033,838 | 119,247 | 7,276,546 | 810,667 |
| A | 7,946,429 | 119,502 | 7,201,070 | 626,868 | |
For nonlinear regression of total recovered cases, degree of freedom is 232 with coefficient of determination as 0.992. SSE as 11642055841827.9; MSE as 51513521424.02; RMSE as 226965.904 with 200 iterations. Nonlinear regression with residuals and trends is shown in Fig. 12 . According to the BIC criterion, the best mixture model is the Log-likelihood with 3 component(s). The EM algorithm did not converge. The maximum number of iterations should be increased for more than 50. Gaussian mixture model is used for the analysis of total cases.
-
•
For class 1: proportion 0.402; mean 406268.07, variance as 614729409104.276;
-
•
For class 2: proportion 0.401; mean 406268.08, variance as 614729409104.276;
-
•
For class 3: proportion 0.197; mean 4465173.27, variance as 614729409104.276.
Fig. 12.
Nonlinear regression forecasting.
As NEC is greater than 1 so there is no clustering in the data. MAP classification and fitted distribution using Gaussian Mixture Modelling is shown in Fig. 13 .
Fig. 13.
GMM for Total recovered cases.
From the figures and tables, it is observed that total confirmed, total death, total active and total recovered cases are highly correlated. For ARIMA (2,1,0) it is observed that the value of constant is zero for all cases. Total confirmed cases; total death cases; total recovered cases and total active cases are exactly fit to forecast using ARIMA (2,1,0) model but daily deaths initially show a perturbed or random pattern which is not perfectly fitted using ARIMA (2,1,0) model. But later it is showing similar patter as forecasted using ARIMA (2,1,0). It is observed that the actual and forecasted values using model ARIMA (2,1,0) from August 3, 2020 to August 11, 2020 are providing the better results. It is concluded that ARIMA (2,1,0) model gives the best fit for long term and short-term behavior. Nonlinear regression and Gaussian mixture model also show the same trend for total cases as forecasted using ARIMA (2,1,0). It is advised as number of cases are increasing so proper cautionary and health guidelines to be strictly adhered to fight with pandemic COVID 19 to remain healthy and safe.
Conclusion and future work
The forecasting of COVID 19 in order to prevalence as pandemic in India play an important role for the policy makers and health department to focus on the strengthening the surveillance system and reallocating the resources. It is observed that COVID 19 data follows quadratic behavior and in long run it spreads with high peak roughly estimated in July 2020. Also, using nonlinear regression it is observed that the trend in long run follows the Gaussian mixture model. It is concluded that COVID 19 will follow secondary shock wave in the month from October 2020 end to mid November 2020. In India we are approaching towards herd immunity. Also, it is observed that the impact of pandemic will be about 441 to 465 days. Thus, it is concluded that the people should follow precautionary measures and it is better to maintain social distancing with all safety measures as the pandemic situation is not in control due to non-availability of medicines.
The time series model plays the important role in the prediction and controlling of the disease. The results of the study can help the policymakers to reallocate the resources like hospitals, staff and the facilities required for the critically infected peoples. The cases everyday increasing in the country and there is a need to pay more attention and utilization of the available resources. The analysis helps in the understanding the complex nature of spread of the disease. For further research, this method can be compared by the other models like Neural Networks and machine learning.
CRediT authorship contribution statement
Shivam Bhardwaj: Conceptualization, Methodology, Software. Sunil Sharma: Formal analysis, Software, Validation, Writing – review & editing. Rashmi Bhardwaj: Investigation, Supervision, Visualization, Writing – original draft.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.World Health Organization. 2020. Available at: https://www.who.int/ith/2020-24-01-outbreak-of-Pneumonia-caused-by-new-coronavirus/en/ (accessed January 2020).
- 2.Ji W, Wang W, Zhao, X et al. J Med Virol 2020; In press. doi: 10.1002/fut.22099. [DOI] [PMC free article] [PubMed]
- 3.Callaway E & Cyranoski D. 2020. Available at: https://www.nature.com/articles/d41586-020-00180-8 (accessed January 2020).
- 4.https://www.who.int/health-topics/coronavirus.
- 5.https://www.thehindu.com/topic/coronavirus/.
- 6.https://www.weforum.org/agenda/2020/03/coronavirus-covid19-cov2-wuhan-china-virus-disease-risks-fatality-rates/.
- 7.Adhikari S.P., Meng S., Wu Y.-J., Mao Y.-P., Ye R.-X., Wang Q.-Z. Epidemiology, causes, clinical manifestation and diagnosis, prevention and control of coronavirus disease (COVID-19) during the early outbreak period: a scoping review. Infect Dis Poverty. 2020;9(1) doi: 10.1186/s40249-020-00646-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.https://www.thehindubusinessline.com/news/indias-first-case-of-coronavirus-reported-in-kerala/article30691210.ece.
- 9.Nicholas LePan, Visual Capitalist:2020 Ranked: Global Pandemic Preparedness by Country. Mar. 20, 2020, https://markets.businessinsider.com/news/stocks/global-pandemic-preparedness- ranked-1029018966.
- 10.Bhardwaj Rashmi, Datta, Debabrata. Consensus Algorithm. 71, “Studies in Big Data” pp 91-107. ISBN: 978-3-030-38676-4. Springer. 2020.
- 11.Bhardwaj Rashmi, Datta Debabrata, Bhardwaj Rajat, Bhardwaj Shivam, Sharma Sunil Kumar, Shehri Mohamad Al (2020): AN APPARATUS AND METHOD WITH IOT TO DETECT AND CONTROL TEMPERATURE CHANGE SIMULATION CASE. Date of Indian Patent Publication: June 26, 2020. Indian Patent Application No. 202011021339.
- 12.Aashima B., Rashmi B., Jayakumar K.V. River water quality estimation through Artificial Intelligence conjuncted with Wavelet Decomposition. 978-981-15-3214-6; Springer. ISBN: 2020. pp. 107–123. [Google Scholar]
- 13.Bhardwaj R., Bangia A. Springer Nature; 2019. Neuro-Fuzzy Analysis of Demonetization on NSE. 816, Soft Computing for Problem Solving; pp. 853–861. [Google Scholar]
- 14.Bhardwaj, Rashmi. (2019). Nonlinear Time Series Analysis of Environment Pollutants. Mathematical Modeling on Real World Problems: Interdisciplinary Studies in Applied Mathematics. 71-102. Publisher: NOVA Publisher, New York, USA.
- 15.Bhardwaj, Rashmi. Wavelets and Fractal Methods with environmental applications. Mathematical Models, Methods and Applications. pp. 173-195. ISBN: 978-981-287-971-4 Publisher: Springer. 2016.
- 16.Bhardwaj R., Das S. “Fractal Analysis of Indian Rhinoceros Poaching at Kaziranga”, JNANABHA, Vijnana Parishad of India, 48, 54-60. 2018.
- 17.Bhardwaj R., Duhoon V. Time Series Analysis of Heat Stroke, JNANABHA, Vijnana Parishad of India, 49(1), , 01-10. 2019.
- 18.Bhardwaj R., Bangia A. Data driven estimation of novel COVID-19 transmission risks through hybrid soft-computing techniques. Chaos Soliton Fractals. 2020;140:110152. doi: 10.1016/j.chaos.2020.110152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bhardwaj Rashmi, Chawla, Meenu. Convection dynamics of Nanofluids for temperature and magnetic field variations. “Advances in Intelligent Systems and Computing” pp 271-290. Publisher: Springer, ISBN: 978-981-15-5113-0. 2020.
- 20.Bhardwaj R., Das S. Synchronization of two three-species food chain system with Beddington- DeAngelis functional response using active controllers based on the Lyapunov function. Ital J Pure Appl Math. 2020;44:57–77. [Google Scholar]
- 21.Bhardwaj Rashmi, Datta Debabrata. Development of a Recommender System Health Mudra Using Blockchain for Prevention of Diabetes. “Recommender System with Machine Learning and Artificial Intelligence: Particle Tools and Applications in Medical and Agricultural Domains”. Pp 313-327. Publisher: Wiley & Sons, USA. ISBN: 978-1-119-71157-5. 2020.
- 22.Bhardwaj Rashmi, Datta Debabrata. Development of Epidemiological Modeling RD_COVID-19 of Coronavirus Infectious Disease and its Numerical Simulation. Mathematical Modelling and Analysis of Infectious Disease Problems (COVID-19). Editors: Praveen Agarwal, Juan J Nieto, Delfim F. M. Torres. Publisher: Springer. 2020.
- 23.Bhardwaj R., Datta D. Optimization Techniques. Revista INGLOMAYOR Ingeniena Global Mayor. 2020;18(A):54–82. [Google Scholar]
- 24.Bhardwaj R., Duhoon V. Auto-regressive integrated moving-averages model for daily rainfall forecasting. Int J Sci Technol Res. 2020;9(2):793–797. [Google Scholar]
- 25.Bhardwaj R., Pruthi D. Evolutionary techniques for optimizing air quality model. Procedia Comput Sci. 2020;167C:1872–1879. [Google Scholar]
- 26.Bhardwaj R., Pruthi D. Development of model for sustainable nitrogen dioxide prediction using neuronal networks. Int J Environ Sci Technol. 2020;17(5):2783–2792. [Google Scholar]
- 27.Bhardwaj R., Pruthi D. Variability analysis in PM2.5 monitoring. Data Brief. 2019;24:103774. doi: 10.1016/j.dib.2019.103774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bhardwaj Rashmi, Duhoon Varsha. Classification and Clustering of Time Series of Weather Data. Advances in Intelligent Systems and Computing. pp 257-270. Publisher: Springer, ISBN: 978-981-15-5113-0. 2020.
- 29.Bhardwaj Rashmi, Bangia Aashima, Mishra Jyoti. Complexity Analysis of Pathogenesis of Coronavirus Epidemiology Spread in the China region. Mathematical Modelling and Soft Computing in Epidemiology, Taylor & Francis Publisher. ISBN: 9781003038399. 2020.
- 30.Bhardwaj Shivam, Khanna Ashish, Gupta Deepak. Water Quality Evaluation Using Soft Computing Method”. Advances in Intelligent Systems and Computing volume 1166. 1043-1052. ISBN: 978-981-15-5147-5. Publisher: Springer. 2020.
- 31.Shivam B. How to remain composed during pandemic COVID-19. Revista INGLOMAYOR Ingeniena Global Mayor. 2020;18(B):04–12. [Google Scholar]
- 32.Rashmi B., Varsha D. DISPERSION ANALYSIS OF MONTHLY RAINFALL & TEMPERATURE TIME SERIES – 1901–2015. Indian J Ind Appl Math. 2020;11(1):91–100. [Google Scholar]
- 33.Datta Debabrata, Bhardwaj Rashmi. Fuzziness-Randomness modeling of Plasma Disruption in First Wall of Fusion Reactor Using Type I Fuzzy Random Set. An Introduction to Fuzzy Sets. Publisher: Nova publisher Inc. ISBN: 978-1-53618-012-1. 2020.
- 34.Durai V.R., Bhardwaj R. Evaluation of statistical bias correction methods for numerical weather prediction model (NWP) forecasts of maximum and minimum temperatures. Nat Hazards. 2014;73(3):1229–1254. [Google Scholar]
- 35.Durai V.R., Bhardwaj R. Improving precipitation forecasts skill over India using a multi-model ensemble technique. GEOFIZIKA. 2014;30(2):119–141. [Google Scholar]
- 36.Srivastava K., Bhardwaj R. Analysis and very short-range forecast of Cyclone “AILA” with radar data assimilation with rapid intermittent cycle using ARPS 3DVAR and cloud analysis techniques. Meteorol Atmos Phys. 2014;124(1-2):97–111. [Google Scholar]
- 37.Srivastava K., Bhardwaj R. Assimilation of Doppler weather Radar Data in WRF model for simulation of tropical cyclone Aila. Pure Appl Geophys. 2014;171(8):2043–2072. [Google Scholar]
- 38.Sharma S.K., Bhardwaj S., Alowaidi M., Bhardwaj R. Nonlinear time series analysis of pathogenesis of COVID-19 epidemiology spread in Saudi Arabia computers. Mater Continua. 2020;66(1):805–825. [Google Scholar]
- 39.https://en.wikipedia.org/wiki/COVID-19_pandemic_in_India.
- 40.Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet (London, England). 2020;395(10225):689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zhong L., Mu L., Li J., Wang J., Yin Z., Liu D. Early prediction of the 2019 novel coronavirus outbreak in the mainland china based on a simple mathematical model. IEEE Access. 2020;8:51761–51769. doi: 10.1109/ACCESS.2020.2979599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhou P., Yang X.-L., Wang X.-G., Hu B., Zhang L., Zhang W. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature. 2020;579(7798):270–273. doi: 10.1038/s41586-020-2012-7. [DOI] [PMC free article] [PubMed] [Google Scholar]