Value of Models for Membrane Budding

Abstract

The budding of membranes and curvature generation is common to many forms of trafficking in cells. Clathrin-mediated endocytosis, as a prototypical example of trafficking, has been studied in great detail using a variety of experimental systems and methods. Recently, advances in experimental methods have led to great strides in insights on the molecular mechanisms and the spatio-temporal dynamics of the protein machinery associated with membrane curvature generation. These advances have been ably supported by computational models, which have given us insights into the underlying mechanical principles of clathrin-mediated endocytosis. On the other hand, targeted experimental perturbation of membranes has lagged behind that of proteins in cells. In this area, modeling is especially critical to interpret experimental measurements in a mechanistic context. Here, we discuss the contributions made by these models to our understanding of endocytosis and identify opportunities to strengthen the connections between models and experiments.

Graphical Abstract

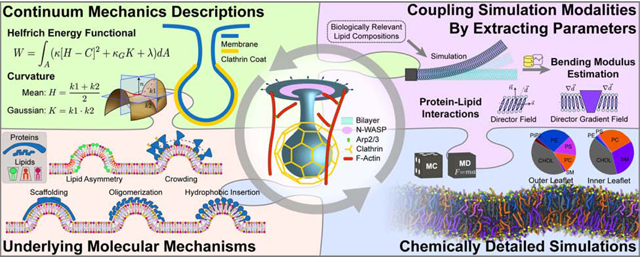
Model development for the different subprocesses of clathrin-mediated endocytosis (CME) can span different length scales. Like the pieces of a puzzle, these different modeling approaches at different scales contribute to our understanding of the mechanisms underlying CME.

Introduction

In the 1970s, two separate developments in two disparate fields took place: cell biologists discovered receptor-mediated endocytosis [1, 2]; meanwhile other researchers, investigating the mechanics of lipid bilayers (not biological membranes), generated a model that expresses the energy of a lipid bilayer as a function of its local curvatures [3, 4, 5]. While these two developments stem from what appear to be independent fields and methods, molecular and cell biological approaches to elucidate the molecular mechanisms of clathrin-mediated endocytosis (CME) and the non-trivial mathematics of differential geometry and thin shell theory for lipid mechanics models [6, 7], they have converged over the years to result in experimentally-informed models that have given us insight into the mechanics and energetics of CME [8, 9, 10, 11, 12, 13, 14]. Here, we summarize those models from the context of their predictive capabilities and discuss the value of modeling CME. We have organized these models, with a focus on bud formation, based on specific biophysical themes including identifying the role of membrane tension in CME, the spatial organization of endocytic proteins, and accounting for the heterogeneous composition of the plasma membrane (Figure 1A). Throughout our discussion we consider the following question: what is the value of the model?

Figure 1:

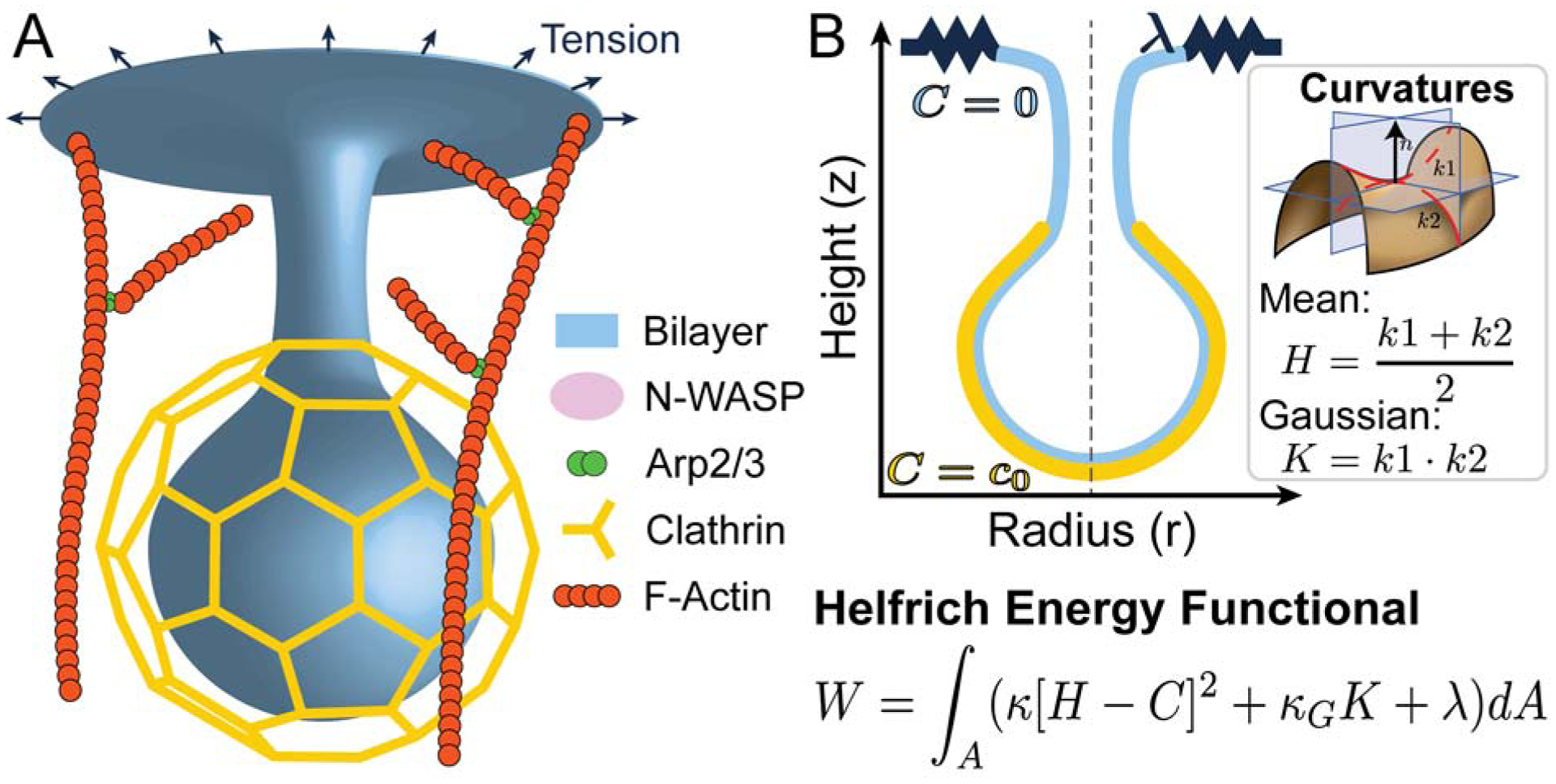
Schematic of endocytosis. A) 3D cartoon of an endocytic bud with protein machinery of interest. The localization of many of these molecules is being elucidated by advances in experimental imaging techniques. B) Equivalent 2D axisymmetric representation of the endocytic bud in A. In the Helfrich model, the contributions of the clathrin scaffold to membrane bending can be represented by a localized non-zero spontaneous curvature c₀. Here W is the total energy of the membrane, k is the bending modulus, H is the mean curvature of the membrane, which is the average of the two principal curvatures, C is the spontaneous curvature, k_G is the Gaussian modulus, K is the Gaussian curvature, which is the product of the two principal curvatures, λ is the membrane tension, and A is the total membrane surface area [15].

Membrane curvature generation in clathrin-mediated endocytosis - a mathematical description

As noted in a comprehensive review by Seifert [15], the mechanical models for membrane curvature generation were primarily biologically inspired physics (focused on lipid bilayer mechanics) as opposed to biophysically inspired (focused on cell membrane mechanics). Although such models make many simplifications, they lay the theoretical and computational foundations for biophysically inspired models. We first summarize the Helfrich model in the context of membrane budding in CME because it is the foundation for a vast majority of the current models of membrane curvature generation.

The principle behind the Helfrich model is as follows: while lipids can flow in the plane of the membrane, the bilayer is elastic in bending. Compared to the observed curvatures of membrane buds, the thickness of the bilayer (~ 5 nm) is very small and so the membrane can be thought of as a surface with negligible thickness. In this case, the bending energy can be written as a function of the curvatures of the surface [16, 17]. This bending energy density was proposed by Helfrich [4], Canham [3], and Evans [5] and is shown in (Figure 1B). To obtain the shape of the membrane for a given load, the bending energy must be minimized, often under the assumption is that the membrane is under mechanical equilibrium. This approach is commonly used to model buds in CME [8, 18, 12, 9, 11]; indeed one of the energy minimizing configurations that can be obtained from this model is the spherical vesicle associated with a bud in CME. We illustrate how this model has played an important role in addressing some critical phenomena in CME.

The role of membrane tension in CME

In general, the plasma membrane of animal cells is under tension as a result of in-plane stresses in the bilayer and connections between the membrane and the underlying actomyosin cortex [19, 20, 21, 22•]. Recent studies have shown that the membrane tension is heterogeneous in cells [23] and can be measured using a fluorescent sensor [22•]. Furthermore, membrane tension varies across cell types and plays an important role locally and globally [21, 23]. In CME, in particular, membrane tension plays a critical role in the progression of bud formation. Experiments have demonstrated that membrane tension opposes deformations to the membrane by curvature-generating proteins [24]. Elevated tension in combination with actin inhibitors causes clathrin-coated pits (CCPs) to exhibit longer lifetimes and stall at an open, U-shaped intermediate conformation [25, 26•, 27]. Similar observations have been made in a reconstituted system [28]. However, these observations did not explain the mechanical principles relating membrane tension to bud formation.

Using the Helfrich model described above, the role of membrane tension in regulating budding was investigated in recent studies by us and others [12, 10, 29•]. The curvature induced by the coat proteins was modeled using the spontaneous curvature term (Figure 1B). Such model representation allowed us to simulate a clathrin coat by tuning the area of the coat, spontaneous curvature, and the bending modulus of the coated region with respect to the uncoated membrane. Most of these values have been measured experimentally either in vitro or in cells [12, 18, 21, 20]. This model predicted that high tension is energetically unfavorable for bud formation, while low tension is favorable. More importantly, as the membrane tension was tuned, the model also predicted that there is a “jump” from the U-shaped bud to an Ω-shaped bud at intermediate, physiologically relevant [30], membrane tensions (Figure 2).

Figure 2:

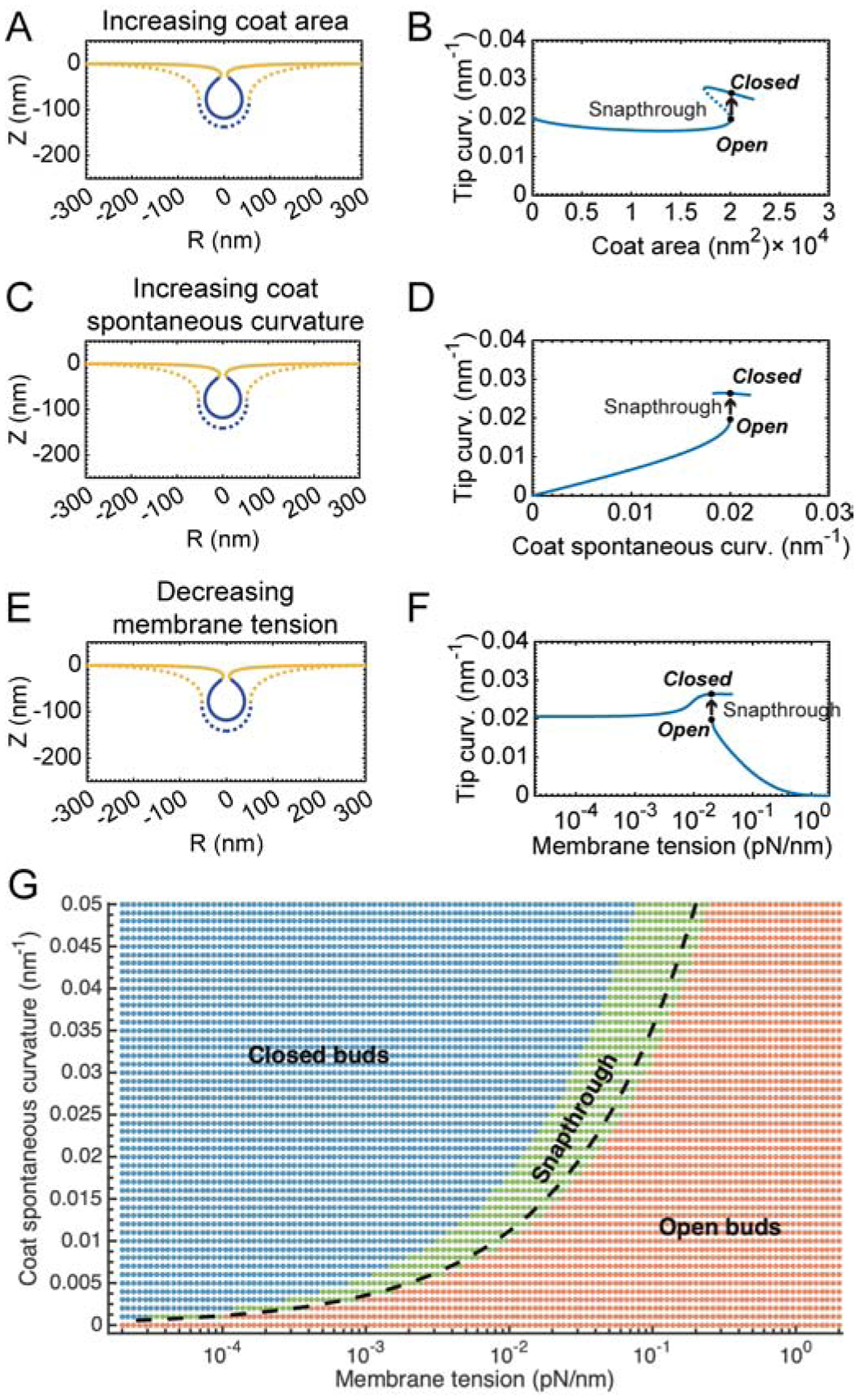
Transition from open to closed buds in CME is mediated by a snapthrough instability. This instability is observed as a function of coat area (A, B), coat curvature (C, D), and membrane tension (E,F). Membrane profiles of the bud morphology before (dashed line, A_coat = 20,065 nm²) and after (solid line, A_coat = 20,105 nm²) addition of a small amount of area to the coat, C₀ = 0.02 nm⁻¹ are shown in (A, B). Bud morphologies before (dashed line) and after (solid line) a snapthrough instability with increasing spontaneous curvature, A_coat = 20, 106 nm², C₀ = 0.02nm⁻¹ are shown in (C, D). Bud morphology before (dashed line) and after (solid line) a snapthrough instability with decreasing membrane tension, A_coat = 20, 106 nm², C₀ = 0.02nm⁻¹, λ₀ = 0.02 pN/nm is shown in (E, F). Phase diagram showing the range of membrane tension and spontaneous curvature variations and the regimes in which the membrane shape corresponds to open and closed buds (G). The green region indicates transitions with a “jump”. Adapted from Hassinger et al. [12] with permission pending.

This “jump” can be understood as follows. There are two stable branches of solutions of the equilibrium membrane shape equations. The lower branch consists of open, U-shaped buds while the upper branch consists of closed, Ω-shaped buds. The dashed portion of the curve indicates “unstable” solutions that are not accessible by simply increasing and decreasing the area of the coat. The marked positions on the curve denote the membrane profiles shown in (Fig. 2A). The transition between these two shapes is a snapthrough instability, in which the bud “snaps” closed upon a small addition to area of the coat. In other words, a small addition to the coat area, coat curvature, or tension does thermodynamic work on the system to enable access to a closed bud configuration. Thus, a continuum description of membrane budding synthesizes multiple factors that can deform the membrane and helps us interpret the transition from the open to closed bud shape from an energetic standpoint.

The spatial organization of endocytic proteins

The above models were useful in predicting the effect of membrane tension; however, their predictive power was limited to regimes where the molecular organization of the protein composition on the membrane could be simplified in terms of a spontaneous curvature. A critical step in CME is the assembly of a multicomponent protein coat that clusters cargo and bends the membrane into a budded morphology [31, 32, 33••, 34••]. The initiation of an endocytic patch is thought to be random and likely involves fluctuation-driven molecular binding and unbinding until a critical concentration is achieved [35]. Clathrin assembles into a lattice-like cage on the membrane with the assistance of adaptor proteins which directly bind lipids and membrane receptors [36, 37, 38, 29•]. This assembly is generally thought to act as a scaffold which restricts the fluctuations of the membrane curvature, similar to a Brownian ratchet, while the adaptor proteins such as AP2 and epsin may impose membrane curvature [39, 38, 40]. Recent work suggests that other components of the coat can also contribute to membrane bending through scaffolding by F-BAR domains, amphipathic helix insertion into the bilayer, and adaptor protein crowding [41, 42, 37,43]. The BAR domain proteins associated with CME and the details of their recruitment have been identified but how they synergize with coat components and their unique role relative to isotropic coat proteins (coat proteins that induce the same curvature in both principal directions) is yet to be investigated in detail or understood. From a structural standpoint, proteins containing BAR domains can induce two different curvatures along the membrane, allowing them to form tubes or neck-like (catenoidal) structures [44].

We consider two critical questions based on the above information: how can this level of detail be incorporated in a model, and what can be learned from such modeling efforts? From a modeling perspective, the simplest way to include the contributions of the many proteins discussed above has been to combine the contributions into a single measure of the curvature generating capability of the coat, or spontaneous curvature (Table 1), with an effective strength that depends on the local protein composition, density, and area coverage [4, 45]. Even with this simplification, when the localization of this spontaneous curvature on the membrane surface is considered, we and others have shown that this local protein-induced spontaneous curvature alters the membrane tension locally [46, 45, 24]. Spontaneous curvature only accounts for the isotropic curvature on the membrane surface such that the curvature induced in both principal directions is the same [4,45], such that the protein coats result in spherical buds or vesicles [4]. The curvatures induced by BAR-domain proteins, on the other hand, can be captured by using anisotropic spontaneous curvature [47, 48]. As summarized in Table 1, the radius of curvature induced by these proteins and their molecule numbers gives us a critical set of parameters to constrain more detailed models. Going beyond the spontaneous curvature term, the energetics of membrane-protein interactions can be directly considered in a more quantitative model for curvature generation in CME [49, 50, 51, 52, 53], where the contributions to the total energy of the system can be formulated to include the energy of the membrane-protein interactions and the energy of bending the membrane. While the exact form of the interaction energy with these proteins remains to be experimentally verified, based on thermodynamic arguments, a quadratic dependence of the energy on the local protein density has been proposed [50, 54, 51, 55, 56, 57, 52]. Using these thermodynamic arguments, the protein density on the membrane (number of molecules per unit area), the curvature generation capability (both isotropic and anisotropic), binding and unbinding kinetics, and diffusion of proteins on the membrane can be modeled. Over the years, we have extended this formulation to include heterogeneity in the membrane due to proteins [58, 50], flow of lipids along the plane of the membrane [46], membrane-protein interactions [59, 60], and diffusion of proteins in the plane of the membrane [52]. These studies have highlighted how adding layers of complexity to the models can give rise to emergent properties due to the interaction of multiple aspects in CME. Therefore, these heterogeneous, dynamic features are important not only because they are one way to capture the compositional complexity of biological membranes in CME but also because heterogeneity implies that membrane tension is a local and dynamic variable [23, 58, 12, 50, 45].

Table 1:

Preferred curvature and molecule numbers of select endocytic proteins.

Protein	Protein Class	Type of Curvature	Radius of Curvature (nm)	No. of Molecules
Clathrin	Coat scaffold	Isotropic	>15[61]	120 (40 triskelia)[61]
FCHo	F-BAR	Anisotropic	9–40[62]	20 (10 dimers)[63, 64••]
Epsin	Coat protein	Both	19[65]	20[63, 64••, 66]
Endophilin	N-BAR	Anisotropic	5[24]	10–20[67]
Amphiphysin	N-BAR	Anisotropic	3[68]	10–20[69]
SNX9	BAR	Anisotropic	5–10[70]	22–40[64••]
Dynamin	GTPase	Anisotropic	10 (unconstricted) 3.5 (constricted) 1.9 (superconstricted)[73]	20–60[71, 72]

Estimation of material properties to account for compositional heterogeneity of the membrane

Another important parameter in membrane curvature generation in CME is the bending modulus. This bending modulus, or rigidity, of the plasma membrane is a material property of the lipid bilayer describing its resistance to bending, and is function of the molecular composition [74]. Estimates of the membrane bending modulus for specific lipid compositions range from ~10–50 k_BT [75, 76]. Actin and microtubules, for reference, have bending rigidities on the order of ~2500 and ~350 000 k_BT respectively (given measured rigidities of 7.3 × 10⁻²⁶ Nm² and 2.1 × 10⁻²³ Nm² divided by approximate filament widths of 7 nm and 25 nm for actin and microtubules respectively [77]). Although cellular membranes have a heterogeneous composition that can vary dynamically with location, cell type, and cell stage. Particularly for CME, PIP2 is important for the progression of endocytosis since it interacts with binding sites in AP2 and other proteins involved in the coat assembly [78••, 79•]. The dynamics of phosphoinositide conversion specify the site of endocytosis [78••] and have been modeled using line tension as a model parameter [80]. Lipid composition variations can thus alter the membrane bending and Gaussian moduli along the membrane.

How can models incorporate the variation in membrane physical properties? If experimental measurements exist, then the modulus can be input as a heterogeneous parameter for the simulations [12, 18]. In the absence of such measurements, one method to estimate the membrane bending modulus is to use molecular dynamics simulations [75]. Recent advances in computational power and complexity of lipid force fields now allow for the simulation of realistic bilayers with complex lipid compositions and asymmetry at atomistic and/or coarse grained detail [81]. While MD simulations can be computationally intensive, Coarse Grained Molecular Dynamics (CGMD) models such as the MARTINI force field among others, coupled with advanced simulation and analysis schemes [82, 75, 83, 76], provide a good compromise between chemical detail and computational tractability to estimate properties such as area per lipid and bending moduli [81]. Given the diversity and heterogeneity of lipids in cell membranes, modeling the individual properties of the myriad compositions will be a challenge. Scaling laws for lipid mixtures such as those proposed by Kelley et al. [84•] which related the area per lipid to the bending modulus, area compression modulus, and the viscosity of the bilayer, can help create improved approaches for extracting membrane material properties from MD simulations while helping to interpolate the material properties between known lipid compositions in large length scale models of membrane bending.

Image-based modeling for CME

Finally, we discuss an emerging avenue for image-based modeling in CME. The explosive advances in microscopy have now given us high resolution and 3D images of an endocytic site. Can such data be used to inform quantitative models of CME? Conceptually, the shape of the membrane in an endocytic site can be considered as a reporter of applied forces [59]. This concept has been used to calculate the axial forces in membrane tethers drawn from a vesicle [85] and to estimate the magnitude of the Gaussian modulus [86]. 3D reconstructions of CME [87, 88, 33••] sites can be processed using image analysis and meshing software such as GAMer 2 [89] and the curvatures of the membrane along the endocytic pit can be calculated. From these curvatures, the traction forces acting along different portions of the membrane can be calculated [59] assuming that the Helfrich model is valid. Such calculations can be coupled to the molecular mechanism either from CGMD simulations [90, 91] or experimental analysis. We note that while it is difficult to assign a reaction coordinate or a temporal scheme from still images, the progression of endocytosis can be inferred from the changes to the membrane geometry [88]. One of the advantages of using electron micrographs of membrane structures in cells is that we can now bridge the gap between membrane mechanics, curvature studies, and realistic geometries in CME.

Summary

We are the cusp of a very exciting time in cell biology - quantitative experimental biology methods can be ably supported by quantitative models, especially in CME given its state of maturity. Success in such an endeavor requires a community-wide acknowledgment of the expanding role played by models and modelers in enhancing our understanding of cellular processes.

As a community, we also need to invest in two fronts to realize the promise of model-experiment collaboration in quantitative biology. The first investment requires a wider recognition that while models are not “real”, they are necessary to understand the physical mechanisms governing these cellular processes. A predictive model generally does not include all the known molecular details; after all, the goal is not to build the entire cell in a computer. With reasonable assumptions, a well-constrained model can generate experimentally testable hypotheses and, critically, eliminate hypotheses that are not physically plausible. These two features are what make for “good” and useful models. In order to achieve such a value proposition, we need to have more conversations about the bounds for what models can predict and what experiments can measure. Establishing metrics that can be compared between models and experiments, and between models of different scales will strengthen the connection and confidence in the iterative loop between models and experiments.

The second investment needed from the community, in order to realize the opportunities identified here, is to acknowledge the jargon barrier that arises from the differences in technical language used by cell biologists and theoreticians, which can be sometimes compounded by field-specific cultural differences. It is the corresponding author’s own experience in transitioning between engineering, biology, and back to engineering that while such communication barriers do exist, with good faith effort and interdisciplinary training, such barriers can be lowered. Ultimately, such efforts will bring fresh ideas and insights and strengthen our understanding of CME and membrane trafficking.

Highlights.

• Membrane curvature generation is a readout of the underlying biomechanical events

• Computational models help identify the physical principles behind membrane budding

• Tight connection between experiments and models will aid study of design principles

• New experiments should consider how measurements can be related to model parameters