Improving the Subtype Classification of Non-small Cell Lung Cancer by Elastic Deformation Based Machine Learning

Abstract

Non-invasive image-based machine learning models have been used to classify subtypes of non-small cell lung cancer (NSCLC). However, the classification performance is limited by the dataset size, because insufficient data cannot fully represent the characteristics of the tumor lesions. In this work, a data augmentation method named elastic deformation is proposed to artificially enlarge the image dataset of NSCLC patients with two subtypes (squamous cell carcinoma and large cell carcinoma) of 3158 images. Elastic deformation effectively expanded the dataset by generating new images, in which tumor lesions go through elastic shape transformation. To evaluate the proposed method, two classification models were trained on the original and augmented dataset, respectively. Using augmented dataset for training significantly increased classification metrics including area under the curve (AUC) values of receiver operating characteristics (ROC) curves, accuracy, sensitivity, specificity, and f₁-score, thus improved the NSCLC subtype classification performance. These results suggest that elastic deformation could be an effective data augmentation method for NSCLC tumor lesion images, and building classification models with the help of elastic deformation has the potential to serve for clinical lung cancer diagnosis and treatment design.

Supplementary Information

The online version contains supplementary material available at 10.1007/s10278-021-00455-0.

Introduction

Lung cancer is the leading cause of mortality worldwide [1–4], and non-small cell lung cancer (NSCLC) is the most common type of lung cancer (75—85%) [5, 6]. Major histology subtypes of NSCLC include adenocarcinoma, squamous cell carcinoma, and large cell carcinoma, separated by different genomic patterns [7, 8]. Previous works have shown that classifying NSCLC subtypes contributed to therapy plan design, cancer prognosis evaluation, increased drug response and survival time period [9–15].

The most common clinical method for classifying NSCLC subtypes is tumor tissue biopsy [5]. This approach is limited by several factors, including involuntary body movement due to breathing, risk of infection, unstable DNA quality [16], and poor time efficiency [14]. Recent researches have adopted a non-invasive, image-based method named radiomics for NSCLC subtype classification [17–20]. In the radiomics method, features are extracted from tumor lesion images and then used to predict the subtypes [21–23]. This method yielded promising results, but it also had limitations. Feature selecting parameters were often tuned by experience, which could have impact on the final predictions [24]. Some features may have high predictive power when used as a group, but each feature often offered limited information. These features could be neglected by the feature selection step so they could not contribute to classification [17]. In order to overcome these limitations, the end-to-end machine learning classification models could be used. These models take tumor images as input, automatically select features, and then output subtype predictions.

A limitation of using image-based models is the scarcity of data, which restricts the classification performance [20, 25, 26]. To solve this problem, a method named data augmentation could come in handy. Data augmentation enlarges the original dataset by creating new samples based on available data, helping reduce overfitting and improve classification results [27–29]. In order to expand the NSCLC datasets in this work, a data augmentation method called elastic deformation is proposed. This method was originally used to mimic the distortion of handwritten characters due to involuntary hand muscle tremor [30]. Being different from affine data augmentation methods including rotation, flipping, and rescaling, elastic deformation is non-linear so it has the potential to simulate the elastic shape change of soft biological tissue under compression from surrounding tissues [31, 32]. Previous studies have shown that elastic deformation had improved other image classification results [29, 33].

A number of studies have focused on differentiating adenocarcinoma and squamous cell carcinoma [26, 34–36]. As to squamous cell carcinoma and large cell carcinoma, previous works focused on comparing various biomarkers to analyze the drug response and prognosis of these two subtypes [37–41]. However, to the best of our knowledge, research on using image-based machine learning models to classify these two subtypes remains at an early stage. Thus, the objective of this work is to improve classification performance of NSCLC subtypes (squamous cell carcinoma vs. large cell carcinoma) by a machine learning approach with the help of elastic deformation.

The dataset in this study consisted of tumor lesion images (of squamous cell carcinoma and large cell carcinoma) from a public lung cancer CT image database. Our dataset was then augmented by both the traditional affine transformation and our proposed elastic deformation. Machine learning classification models were trained on original dataset and augmented dataset, respectively, and their classification performances on the test samples were compared. The results showed that using the augmented dataset from elastic deformation to train the model significantly improved the classification performance, compared with using the original dataset for training. This work provides encouragement for a new way to improve NSCLC subtype classification by using elastic deformation, and our approach could serve as a valuable tool for future studies on lung cancer detection and diagnosis.

Materials and Methods

Data

The public database (NSCLC-Radiomics-Lung1) contains the pretreatment CT scans of 422 NSCLC patients. Gross tumor volume and contour are delineated manually by oncologists, and the size of each original CT image is 512 × 512 pixels [42–44]. We have manually checked scans of each patient, selected tumor scans that belonged to the squamous cell carcinoma and large cell carcinoma, respectively. Finally, 169 patients were selected for this study (81 patients were diagnosed with squamous cell carcinoma, 88 patients were diagnosed with large cell carcinoma).

Rectangular regions of interest (ROIs) of tumor lesion were extracted from the CT scans of those 169 patients (Fig. 1 shows some example tumor ROIs of both subtypes). Three thousand one hundred and fifty-eight ROIs were selected for this study (consisting of 1579 squamous cell carcinoma ROIs and 1579 large cell carcinoma ROIs). These ROIs were adjusted to the same size (200 × 200 pixels). The pixel intensity level of each ROI was normalized to the range of $[0,1]$. Each ROI contained both the lesion and its surrounding area, which has been found to contain lesion information that contributes to classification [45, 46]. Each tumor lesion was cropped from original CT image by drawing a square box around it. The size of the square box was set as 125% of the largest axis of the tumor lesion. Therefore, each ROI captured the whole tumor lesion and its surrounding lung tissues and the ROI size was relative to the tumor lesion size.

Fig. 1.

Example images of lesions of NSCLC patients having squamous cell carcinoma (upper row) and large cell carcinoma (bottom row)

Elastic Deformation

The shapes of biological tissues change elastically when they are compressed by surrounding organs, because of their non-rigidity. Thus, the traditional spatial rigid data augmentation methods including rotating, flipping and re-scaling could not effectively capture the biological variance of medical image data [25]. Initially used for generating hand-written characters, the elastic deformation method has the potential to model this tissue shape change and simulate the tissue appearance.

In this paper, we have introduced the concept of elastic deformation into the augmentation of NSCLC datasets. In the elastic deformation method, two matrices M_x and M_y are created to store the offsets of each pixel along the x-axis and y-axis, respectively. First, each pixel is moved randomly in either direction for a distance d or remains unmoved,

$$M_{x_{\mathit{ij}}},M_{y_{\mathit{ij}}}\in \left\{-,d,,,0,,,d\right\}$$

Then the two matrices are convoluted with two one-dimensional Gaussian kernels with size n (n should be an odd number) and standard deviation σ [47]: every row of M_x and M_y is filtered with the first Gaussian kernel k_x,

$$k_x=\alpha \ast e^{{-\left(x,-,\left(n,-,1\right),/,2\right)}^2/\left(2,,\ast ,{\sigma }^2\right)}$$

where $x=0,\cdots ,n-1$ and α is the scale factor chosen so that ${\sum }_x{k}_x=1$.

Then every column of M_x and M_y is filtered with the second Gaussian kernel k_y,

$$k_y=\alpha \ast e^{{-\left(y,-,\left(n,-,1\right),/,2\right)}^2/\left(2,,\ast ,{\sigma }^2\right)}$$

where $y=0,\cdots ,n-1$ and α is the scale factor chosen so that ${\sum }_y{k}_y=1$.

Finally, each pixel of original image is moved according to the distances in M_x and M_y.

In previous work [30], the offset d was 1 on images of 28 × 28 pixels. Since characteristics of tumor lesion are more subtle than the hand-written digits, the offset d in this study was extended to one-tenth of the image size (d = 20 on 200 × 200 images). In order to decide the key parameters of elastic deformation (width of Gaussian kernel n and standard deviation σ), five values of n and three values of σ were chosen empirically, and their effects on deformation were compared. Based on the comparison results, four combinations of n and σ were used for data augmentation. After data augmentation, both original images and generated images were stored in the augmented dataset.

Training, Testing, and Evaluation Metrics

The whole image data set was later resized into the same size (32 × 32 pixels) before splitting into training set and test set, in which each class was equally represented. Images of each patient formed a group, in which images were mutually dependent. Due to this internal dependency, our data needed to be split in a way that training set and test set did not have images from the same patient, otherwise the probability distribution represented by the samples in the training set would “leak” to the test set, thus inflating the performance of machine learning models [48]. In this study, the dataset was split at the patient level and then all images from a patient went to either training set or test set.

Two methods were used to generate the training set and test set: k-fold cross-validation (KF) and random shuffle split (RS). The KF method (k = 5) took turns to take part of the original data as the test set, and finally each part of the whole original data could be used for testing, while the RS method which randomly generated the test set with multiple times (n = 5) could introduce more randomness. Both of the two methods were adopted in this study, which could fully evaluate the generalization performance of the model and avoid the performance interference caused by the unicity and special partition of the original data in the best way.

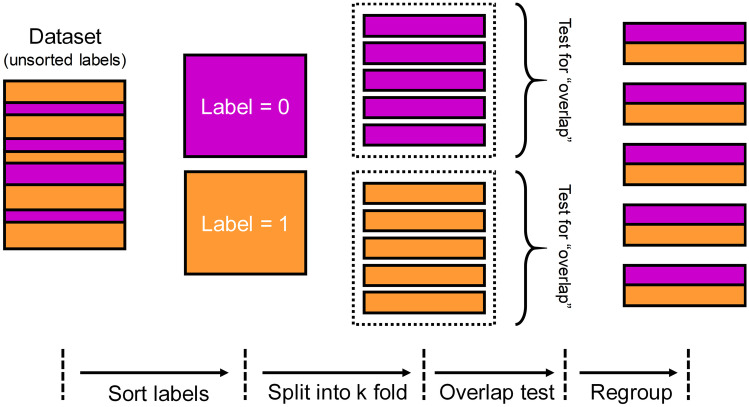
In the KF method, the dataset was split into k subsets, by GroupKFold function in scikit-learn package. In order to ensure the class balance in each subset, this method was implemented manually. As illustrated in Fig. 2, from left to right, the labels were unsorted in the dataset to be split. First, the dataset was separated according to label, resulting in two subgroups of the same size (shown in color of magenta and orange). Then, each subgroup was shuffled and then split into five folds. These folds were checked to guarantee that they did not have images from the same patients. Finally, one fold of label 0 and another fold of label 1 were combined into a complete fold. Five “complete folds” were generated. Note that each complete fold had nearly the same number of samples of label 0 or 1. In the cross-validation step, each complete fold was the test set, while the rest four complete folds formed the training set (training-to-test ratio was 4:1). In this way, five training set/test set pairs were generated, so the model could be trained and evaluated for five times.

Fig. 2.

Schematic illustration of KF method for separating training set and test set (k = 5)

In order to examine whether the method of separating training set and test set interfered with the classification results, RS method was also implemented to split the datasets. In the RS method, the dataset was shuffled randomly and then split into the training set and test set (training-to-test ratio was also 4:1), using the GroupShuffleSplit function in scikit-learn package [49]. The whole dataset was split for five times, resulting in five training/test pairs. All five pairs were examined, and they did not share any samples from the same patients.

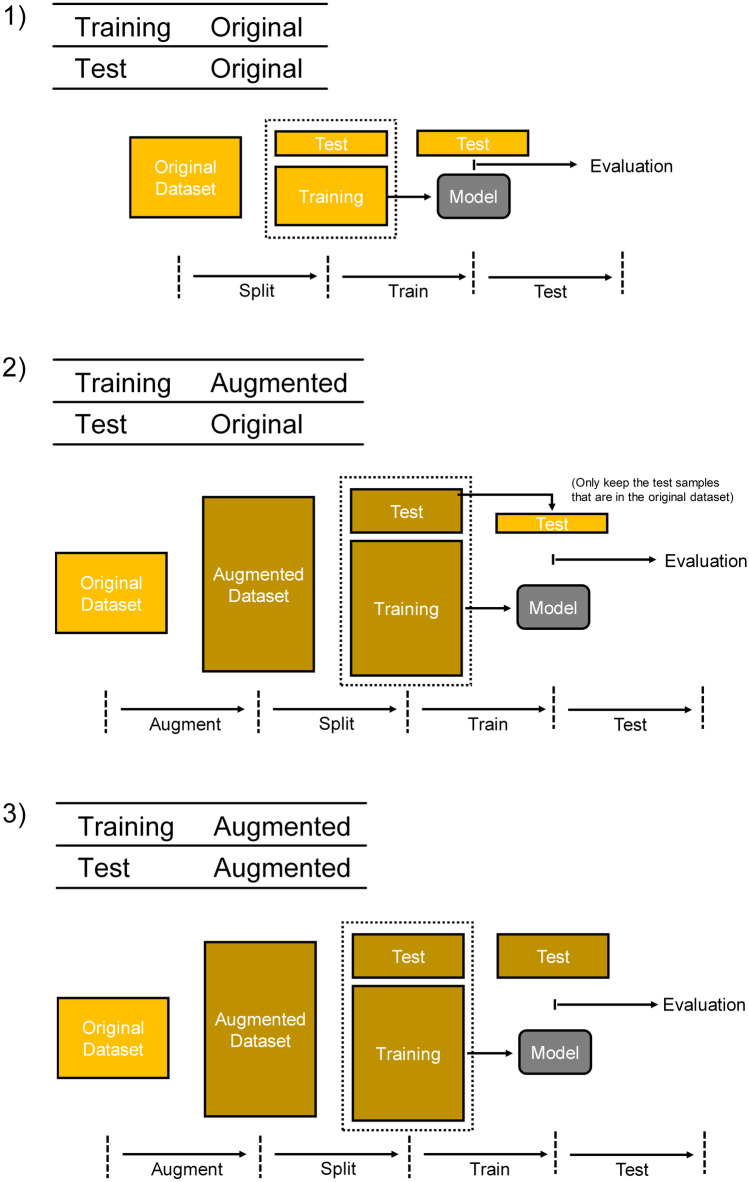
Then the training set obtained by KF method or RS method was used to train the classification models, whose performance was later evaluated on the test set. Different types of training set and test set were used in three combinations (Fig. 3): (1) training set was from original data, and test set was from original data; (2) training set was from augmented data, and test set was from original data; (3) training set was from augmented data, and test set was from augmented data. In combination 1, the original dataset was split into training set and test set directly. In combination 2, the augmented dataset was generated by elastic deformation and then split into training set and test set. Then, only the original images in this test set were kept and they formed a new test set, which was used for model evaluation. In combination 3, the augmented dataset was split into training set and test set, which was directly used for model evaluation.

Fig. 3.

Three combinations of training set and test set. (1) The original dataset was separated into training set and test set. (2) The augmented dataset was split into training set and test set. In the test set, only the original images were kept. These original images were used for model evaluation. (3) The augmented dataset was split into training set and test set, and they were used directly for training and evaluation

In conclusion, the original dataset was split into training set and test set (training-to-test was 4:1) by two methods (KF and RS) and performed five validations, then three different combinations were adopted for each data partition. A total of 30 (2×5×3) results could be obtained and enable this study to comprehensively compare the effects of elastic deformation augmentation.

The model establishment and evaluation were performed in scikit-learn package. The ensemble methods combine machine learning models to improve their performance [50]. Decision tree based ensemble models including random forests (RF) and gradient boosted regression trees (GBRT) showed the advantage of being less susceptible to over-fitting compared to models based on single decision tree [51]. In the present study, RF and GBRT models were both used.

The parameters max_features (max number of features in a node) and n_estimators (number of decision trees) were keys to RF, and the parameter max_depth (the max depth of each decision tree) was important to GBRT. Optimal parameters are results of the trade-off between model complexity and test performance [50]. For the RF models, the max_features was set to 32, n_estimators was set to 60. For the GBRT models, the max_depth was set to 10.

Classification metrics including accuracy (ACC), specificity (SPE), sensitivity (SEN), positive predictive value (PPV), negative predictive value (NPV), and f₁-score were used for model evaluation:

$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$

$$Specificity=\frac{\mathit{TN}}{TN+FP}$$

$$Sensitivity=\frac{\mathit{TP}}{TP+FN}$$

$$PPV=\frac{\mathit{TP}}{TP+FP}$$

$$NPV=\frac{\mathit{TN}}{TN+FN}$$

$$f_1-score=\frac{2·Sensitivity·PPV}{\left(S,e,n,s,i,t,i,v,i,t,y,+,P,P,V\right)}=\frac{2·TP}{2·TP+FN+FP}$$

where TP, TN, FP, and FN stand for true positive, true negative, false positive, and false negative, respectively.

Moreover, to take uncertainty into account, the model could be analyzed by changing the threshold that was used for making a classification decision and adjusting the trade-off of false positive rate (FPR) and true positive rate (TPR) (TPR is the same as sensitivity):

$$\begin{array}{c}FPR=\frac{\mathit{FP}}{FP+TN}\\ TPR=\frac{\mathit{TP}}{TP+FN}\end{array}$$

The relation between FPR and TPR was shown in the receiver operating characteristics (ROC) curve, and the area under the curve (AUC) of ROC was calculated.

Model performance metrics were expressed as mean and standard deviation. Mean and standard deviation were calculated using Excel 2016 (Microsoft Corp., Seattle, WA, USA).

Results

Elastic Deformation

Two parameters (n and σ) were experimented to find suitable combinations for elastic deformation.

Based on the results of various parameters, two values were selected for each parameter: Gaussian kernel width n = 11, 15 and standard deviation σ = 4, 8, resulting in four different parameter pairs (Fig. 4). Each image passed through the elastic deformation with these four parameter pairs, generating four new images, which were stored in the augmented dataset with original images. Notably, each generated image comes from only one original image, and it does not have information of other original images. The original dataset expanded for four times and there were 15,790 images in total (squamous cell carcinoma 7895, large cell carcinoma 7895), including the original images.

Fig. 4.

Elastic deformation results of an example original image with various parameters. a An original image of tumor lesion. b Images after elastic deformation with kernel size n = 3, 11, 15, 25, 45 and standard deviation σ = 4, 8, 12. Selected parameters for data augmentation in the present study were indicated by the dashed line box

Classification

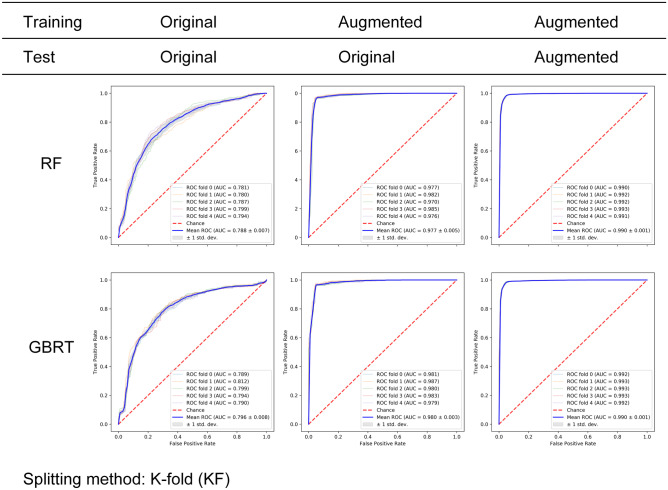
Three combinations were generated as described previously in the the “Training, Testing, and Evaluation Metrics” Section. On each of these combinations, classification models including RF and GBRT were trained, and then evaluated using five-fold cross-validation. ROC curves and their AUCs of the two models and three combinations are presented in Fig. 5. For the RF model (upper row, Fig. 5), training on the original images resulted in mean AUC that was around 0.788 (combination 1). Changing the training set to augmented images while keeping testing on original images significantly increased the mean AUC to 0.977, and kept the AUC variation among folds relatively small (0.005). Using augmented images for both training and testing further pushed the mean AUC up to 0.99 while limited standard deviation to 0.001. For the GBRT model, a similar pattern was observed (bottom row, Fig. 5).

Fig. 5.

Classification results of RF (upper row) and GBRT (lower row) on three combinations of training set and test set. The KF method was used for generating the training set and test set. The table above ROC subfigures indicated the

source of training set and test set: original dataset and augmented dataset. ROC curves of five folds were plotted (thin lines) along with the average ROC curve (thick blue line) and the standard deviation (gray area). For both RF and GBRT, training the model on augmented images (combination 2) led to significantly improved classification performance compared to training on original images (combination 1) (mean AUCs 0.788 to 0.977, 0.796 to 0.980). Training and testing on both augmented images (combination 3) further increased the AUCs

Classification metrics including ACC, f₁-score, SPE, SEN, PPV, and NPV were calculated (upper halves of Tables 1 and 2). Switching the training set to augmented images significantly increased all the six metrics (from near 0.740 to around 0.950), using both RF and GBRT models.

Table 1.

Classification metrics: accuracy (ACC), area under the curve (AUC) and f₁-score of three data combinations, two classification models (RF and GBRT), and two training/test splitting methods (KF and RS). In both KF and RS results, using combination 2 led to significantly improved accuracy (from ≤ 0.745 to ≥ 0.950), for both RF and GBRT. Combination 3 further increased the metrics. Similar pattern was observed for AUC and f₁-score: using combination 2 increased the results (AUC: from ≤ 0.813 to ≥ 0.972, f₁-score: from ≤ 0.747 to ≥ 0.950). Std. stands for standard deviation

Method		Data		Model	Mean ± std
		Training	Test		ACC	AUC	f1-score
KF	(1)	Ori	Ori	RF	0.726 ± 0.020	0.788 ± 0.007	0.726 ± 0.018
				GBRT	0.738 ± 0.009	0.797 ± 0.008	0.740 ± 0.009
	(2)	Aug	Ori	RF	0.955 ± 0.005	0.978 ± 0.005	0.955 ± 0.003
				GBRT	0.956 ± 0.004	0.982 ± 0.003	0.956 ± 0.003
	(3)	Aug	Aug	RF	0.966 ± 0.002	0.992 ± 0.001	0.966 ± 0.002
				GBRT	0.967 ± 0.002	0.993 ± 0.001	0.967 ± 0.002
RS	(1)	Ori	Ori	RF	0.692 ± 0.015	0.758 ± 0.019	0.671 ± 0.019
				GBRT	0.745 ± 0.012	0.813 ± 0.017	0.747 ± 0.012
	(2)	Aug	Ori	RF	0.950 ± 0.006	0.972 ± 0.007	0.950 ± 0.006
				GBRT	0.960 ± 0.005	0.984 ± 0.004	0.960 ± 0.004
	(3)	Aug	Aug	RF	0.950 ± 0.003	0.985 ± 0.002	0.950 ± 0.003
				GBRT	0.965 ± 0.003	0.992 ± 0.001	0.966 ± 0.003

Ori. original, Aug. augmented

Table 2.

Other classification metrics: specificity (SPE), sensitivity (SEN), positive predictive value (PPV), and negative predictive value (NPV) of three data combinations, two classification models (RF and GBRT), and two training/test splitting methods (KF and RS). For all five metrics, combination 2 showed better performance over combination 1, using both RF and GBRT model and both KF and RS method

Method		Data		Model	Mean ± std
		Training	Test		SPE	SEN	PPV	NPV
KF	(1)	Ori	Ori	RF	0.727 ± 0.030	0.725 ± 0.014	0.727 ± 0.024	0.725 ± 0.017
				GBRT	0.730 ± 0.010	0.746 ± 0.010	0.734 ± 0.009	0.742 ± 0.009
	(2)	Aug	Ori	RF	0.954 ± 0.005	0.955 ± 0.005	0.954 ± 0.003	0.955 ± 0.008
				GBRT	0.954 ± 0.002	0.958 ± 0.007	0.954 ± 0.002	0.958 ± 0.010
	(3)	Aug	Aug	RF	0.961 ± 0.004	0.971 ± 0.002	0.961 ± 0.004	0.970 ± 0.002
				GBRT	0.963 ± 0.005	0.971 ± 0.005	0.963 ± 0.004	0.971 ± 0.005
RS	(1)	Ori	Ori	RF	0.758 ± 0.019	0.626 ± 0.022	0.723 ± 0.024	0.668 ± 0.018
				GBRT	0.741 ± 0.016	0.750 ± 0.024	0.745 ± 0.017	0.746 ± 0.026
	(2)	Aug	Ori	RF	0.951 ± 0.016	0.950 ± 0.013	0.949 ± 0.017	0.951 ± 0.013
				GBRT	0.958 ± 0.013	0.963 ± 0.008	0.957 ± 0.014	0.964 ± 0.007
	(3)	Aug	Aug	RF	0.960 ± 0.004	0.940 ± 0.003	0.959 ± 0.004	0.940 ± 0.004
				GBRT	0.964 ± 0.004	0.967 ± 0.004	0.965 ± 0.004	0.966 ± 0.004

Ori. original, Aug. augmented

In order to examine whether the method of separating training set and test set interfered with the classification results, RS method was also implemented to split the datasets (both original and augmented). After each split, the size of test set and training set was 1:4, which was the same as the ratio in KF method (since k = 5). Three combinations were generated in the same way as in the KF method.

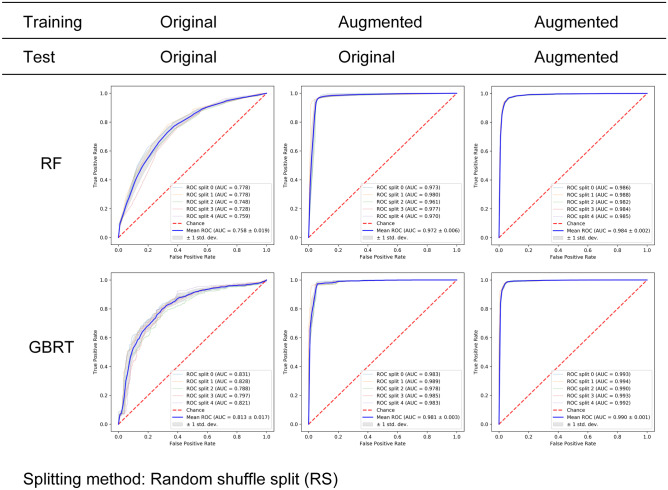
For each model and each combination, the dataset separation process was repeated for five times, in order to match the settings in five-fold cross-validation. ROC results of the RS method were summarized in Fig. 6. For the RF model (upper row, Fig. 6), changing training set from original images to augmented images significantly lifted the AUCs (from 0.758 to 0.977) while restraining the standard deviation (from 0.019 to 0.006). Using augmented dataset for both training and testing further increased the mean AUC to 0.984. The GBRT results showed a similar pattern (bottom row, Fig. 6). Note that GBRT model led to higher mean AUC compared to RF model, especially for combination 1 (0.813 vs. 0.758).

Fig. 6.

Classification results of RF (upper row) and GBRT (lower row) on three combinations of training set and test set. The RS method was used for generating the training set and test set. The table above ROC subfigures indicated the

source of training set and test set: original dataset and augmented dataset. ROC curves of five experiments were plotted (thin lines) along with the average ROC curve (thick blue line) and the standard deviation (gray area). For both RF and GBRT, training the model on augmented images (combination 2) led to significantly improved classification performance compared to training on original images (combination 1) (mean AUCs 0.758 to 0.972, 0.813 to 0.981). Training and testing on both augmented images (combination 3) further increased the AUCs

Classification metrics of the RS method were summarized in bottom halves of Tables 1 and 2. All metrics of combination 2 were significantly higher than those of combination 1. This increase in classification metrics was in line with the pattern of KF method results.

Results of both KF method and RS method pointed to the idea that training classification models on augmented images (generated by elastic deformation method) could significantly improve the performance of distinguishing NSCLC subtypes (squamous cell carcinoma and large cell carcinoma).

In Table 3, some of the state-of-the-art works for the classification of lung cancer subtypes was shown. The work of (1) to (5) used machine learning or deep learning to classify different lung cancer subtypes, and they obtained classification results of AUC 0.72–0.903, ACC 0.783–0.860. These works demonstrated the feasibility of using medical imaging data for quantitative feature analysis to predict lung cancer subtypes, but their classification results still needed to be improved to meet the actual clinical requirements. In this study (6), the elastic deformation method was used for the first time to carry out the subtype classification task of lung cancer, and quite good results were obtained (ACC 0.960 ± 0.005, AUC 0.984 ± 0.004; the GBRT algorithm based on the augmented images of the training set, the original images of the test set, and used RS method to split for 5 times).

Table 3.

Comparison with the state-of-the-art works for the classification of lung cancer subtypes. This work used the results of the GBRT algorithm based on the augmented images of the training set, the original images of the test set, and used RS method to split for 5 times

	Works	Lung subtypes	Samples	Methods	No. of features	Image modal	Results
(1)	Wu W [17]	ADC, SCC	350	Naive Bayes	440	CT	AUC 0.720
(2)	Saad M [18]	ADC, SCC, LCC	317	SVM	624	CT	ACC 0.783 AUC 0.863
(3)	E L [19]	NSCLC, SCLC	278	SVM	1695	CT	AUC 0.741
(4)	Liu J [58]	ADC, SCC, LCC, NOS	349	SVM	1029	CT	ACC 0.860
(5)	Han Y [60]	ADC, ACC	1419	VGG16	No feature extraction	PET/CT	ACC 0.841 AUC 0.903
(6)	This work	SCC, LCC	169	GBRT	No feature extraction	CT	ACC 0.960 ± 0.005 AUC 0.984 ± 0.004

ADC  adenocarcinoma, SCC squamous cell carcinoma, LCC large-cell carcinoma, NOS not otherwise specified, NSCLC non-small cell lung cancer, SCLC small cell lung cancer, ACC accuracy, AUC area under the curve, SVM support vector machine

Discussion

Classifying NSCLC subtypes is important for accurate diagnosis and therapy design. Our goal is to improve the classification performance of NSCLC subtypes (squamous cell carcinoma vs. large cell carcinoma) using machine learning models with the help of elastic deformation. The results suggest that using augmented dataset (created by elastic deformation) as the training set improved the performance of machine learning classifiers including RF and GBRT.

According to the clinical information of public NSCLC dataset, the subtypes “squamous cell carcinoma” and “large cell carcinoma” was determined by histology. After WHO modified NSCLC subtyping criteria, the term “large cell carcinoma” could include tumor subtypes that lack clear histology definition [52]. Our results provided an approach to distinguish a NSCLC subtype with clear definition (squamous cell carcinoma) from a NSCLC subtype of various content, which therefore is hard to define (large cell carcinoma).

Previous works on NSCLC subtype classification showed promising results, but they had been limited by the size of dataset, which is a common restriction in medical image researches. Training classification models on a relatively small dataset could lead to suboptimal performance. In this study, RF and GBRT models resulted in accuracy of mere 0.726 and 0.735 on the original dataset, respectively.

This limitation could be improved by the data augmentation method. Data augmentation generates new images based on original ones and enlarges dataset [28, 29]. Therefore, it improves the classification performance by providing the models with more information of the targets. As elastic deformation mimics the non-linear shape changes of in vivo biological tissue under compression, it has the potential to help with medical image classification tasks.

After the dataset was enlarged by elastic deformation, three data combinations were created and used in this study (Fig. 3). Combination 1 was created to test the classification performance of models that were trained on original images. Combination 2 used augmented images for training, note that these augmented images include both the original images and the generated images. For testing, combination 2 kept only original images (similar to the settings in previous work [32, 33, 53]). Note that the training set did not include images generated from the test set. In this way, combination 2 made test performance independent to the data augmentation process, thus removed possible disturbance. Combination 3 used augmented images for both training and testing. This combination was designed to measure possible “leakage” of elastic deformation details from training data to test data, which could lead to inflated classification results.

Combination 2 significantly improved the classification performance compared to combination 1 (Figs. 5 and 6; Tables 1 and 2). The mechanism behind this improvement could be that elastic deformation successfully kept the invariance of their subtype-specific details by creating new images of tumor lesions. Therefore, the augmented dataset covered a broader distribution of tumor lesion appearance, compared to the original dataset. As the result, the classification models learned more characteristics of subtypes and yielded better performances. Notably, affine data augmentation methods including rotation and flip did not improve the classification (see the Supplementary data section), suggesting that the non-linear details generated by elastic deformation contributed to the classification.

Combination 3 showed further improvement over combination 2 and achieved the highest metrics among three combinations (Figs. 5 and 6; Tables 1 and 2). However, these optimistic results might not fully come from the classification capability. In combination 3, when models recognized similar elastic deformation patterns in a generated image in the test set, they might use details of elastic deformation, rather than the details of the image itself, to predict the label of that image. Therefore, classification results could be inflated, and features related to tumor subtype physiology could be neglected. In this way, results of combination 2 should be regarded as the best one among three combinations, as the “improvement” of combination 3 over combination 2 could be triggered by the leakage of elastic deformation details from training set to test set. By the term “leakage”, we mean that the elastic deformation features, rather than the image features, were leaked from training to testing.

Moreover, although two models (RF and GBRT) in this study led to similar classification metrics, their training time showed significant differences. For instance, the training time per fold in GBRT model (1068.2 ± 25.9 s) was nearly 50 times as large as that in RF model (20.8 ± 0.7 s), when the augmented data (~ 12,630 images) were used for training, and KF method was used for dataset separation (Table 4). Although RF was not as accurate as GBRT (especially on combination 1), RF could be trained relatively fast (less than half a minute). This advantage makes it suitable for possible applications that require real-time classification results in clinical settings.

Table 4.

Training time of each fold using RF and GBRT. GBRT needed longer time to train (1068 s on average) compared to RF (20.8 s on average) (KF method was used for splitting the dataset and augmented images were used for training)

	Training time per fold (s)
	RF	GBRT
Fold 0	22	1039
Fold 1	21	1084
Fold 2	21	1111
Fold 3	20	1054
Fold 4	20	1053
Mean ± std	20.8 ± 0.7	1068.2 ± 25.9

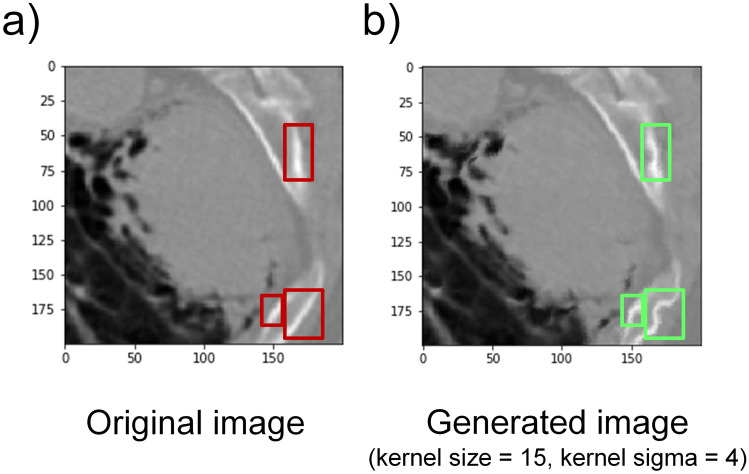
It is plausible that a number of limitations might have influenced our results. Firstly, as powerful as it may be, elastic deformation applies same level of deformation across the image. Therefore, applying elastic deformation on tissues of different elasticity could lead to distortion. For instance, the bone appeared like straight lines in original images, but after data augmentation, its shape became curvaceous, which would not happen in reality (Fig. 7). These distorted bone structures (green boxes, Fig. 7b) might interfere with the subtype related features and then compromise the classification performance. Furthermore, tumor ROI images that were fed into the models have different resolutions. Since the size of each raw ROI is proportional to the tumor, raw ROIs cropped from CT scans have different dimensions. Therefore, after being resized to the identical size, their resolutions are different.

Fig. 7.

Possible distortion after elastic deformation. a An original tumor lesion image. b A representative tumor lesion image generated by elastic deformation (with kernel size of 15 and kernel sigma of 4). Red rectangle boxes in a showed the original rib structure. Green boxes in b indicate the corresponding distortion

Future work will focus on implementing other non-linear or generative data augmentation methods including generative adversarial networks (GAN) on the lung cancer dataset and comparing their effects on classification performance. We also intend to explore ways to quantify the mechanisms of how data augmentation methods (especially non-linear ones such as elastic deformation) improved classification performance. The sample distribution after data augmentation could be studied and compared with that of the original dataset, in order to better understand the data augmentation mechanism quantitatively. Also, integrating other subtype-specific information, including NSCLC genomic data [42, 54–56], and lesion distance to the central lung region (this distance tends to be short for squamous cell carcinoma [57]) with the end-to-end classification models could be important to further enhance classification and help reveal model interpretability. In addition, the effectiveness of our proposed method needs to be further validated on independent NSCLC datasets. Last but not least, our method has the potential to help studies on multiple NSCLC subtype classification [58, 59] to overcome the problem of data scarcity.

Conclusions

The results of the present study indicate that NSCLC subtype classification (squamous cell carcinoma vs. large cell carcinoma) could be effectively improved by using elastic deformation. Artificially enlarged tumor image dataset can provide more NSCLC subtype characteristics to the classifiers and enhance their predictive power. For application, our method could be used to augment clinical NSCLC datasets and train classification models prior to diagnosis, so the models would be ready to classify NSCLC subtypes later for new patients. This approach also has the potential to provide validation for clinical subtype genomic tests and serve as a valuable image-based tool for both treatment strategy design and future lung cancer physiology studies.

Supplementary Information

Below is the link to the electronic supplementary material.

Funding

This work was partially supported by the National Natural Science Foundation of China (Nos. 61871251, 62027901 , 61601019, 61871022), the 111 Project (No. B13003), the Fundamental Research Funds for Central Universities, and the Beijing Natural Science Foundation (7202102).