Abstract
Age-related macular degeneration (AMD) is one of the leading causes of irreversible blindness and is characterized by fluid-related accumulations such as intra-retinal fluid (IRF), subretinal fluid (SRF), and pigment epithelial detachment (PED). Spectral-domain optical coherence tomography (SD-OCT) is the primary modality used to diagnose AMD, yet it does not have algorithms that directly detect and quantify the fluid. This work presents an improved convolutional neural network (CNN)-based architecture called RetFluidNet to segment three types of fluid abnormalities from SD-OCT images. The model assimilates different skip-connect operations and atrous spatial pyramid pooling (ASPP) to integrate multi-scale contextual information; thus, achieving the best performance. This work also investigates between consequential and comparatively inconsequential hyperparameters and skip-connect techniques for fluid segmentation from the SD-OCT image to indicate the starting choice for future related researches. RetFluidNet was trained and tested on SD-OCT images from 124 patients and achieved an accuracy of 80.05%, 92.74%, and 95.53% for IRF, PED, and SRF, respectively. RetFluidNet showed significant improvement over competitive works to be clinically applicable in reasonable accuracy and time efficiency. RetFluidNet is a fully automated method that can support early detection and follow-up of AMD.
Keywords: Age-related macular degeneration (AMD), Intra-retinal fluid (IRF), Subretinal fluid (SRF), Pigment epithelial detachment (PED), Retinal edema, Spectral-domain optical coherence tomography (SD-OCT)
Background
Age-related macular degeneration (AMD) is one of the leading causes of blindness in developed countries in which genetic and environmental factors play a large role in its development [1]. The typical sign of AMD is the occurrence of fluid types such as intra-retinal fluid (IRF), subretinal fluid (SRF), and pigment epithelial detachment (PED) (Fig. 1). AMD has an effective yet expensive treatment named anti-vascular endothelial growth factor (anti-VEGF) [2]. Anti-VEGF effectiveness depends on the early detection and frequent monitoring of the disease response to the treatment. Developing robust diagnostic technology for automated detection and quantification of fluid accumulation is vital to deliver efficient and cost-effective treatment.
Fig. 1.
Examples of B-scans containing Age-related macular degeneration (AMD) related fluids. (a) Intra-retinal fluid (IRF) (region within the green boundary). (b) Subretinal fluid (SRF) (area within the red boundary). (c) Pigment epithelial detachment (PED) and SRF regions with blue and red boundaries, respectively. (d) PED in the early stage (area within the blue boundary
The AMD diagnosis and follow-up commonly rely on multi-modal imaging tools; however, spectral-domain optical coherence tomography (SD-OCT) is the primary modality [3]. The recent advancements in the SD-OCT have aided in the better monitoring of disease response to the various treatments [4, 5]. SD-OCT is a non-invasive medical imaging tool capable of providing micrometer-resolution volumetric retinal images [6, 7]. Generally, in SD-OCT IRF, SRF and PED are shown as the well-circumscribed fluid accumulation in the macular region (Fig. 1a, b and c). In some cases, like the early stage of PED, the area is maybe shown as non-fluid material with bright elevation (Fig. 1d).
For retinal fluid segmentation, several automated approaches have been developed [8–19]. Quellec et al. [13] used the texture of suspected regions evaluation in subjection to features extracted from normal retinal layers to identify retinal abnormalities. To delineate the boundaries of fluid-associated pathologies, Novosel et al. [10] utilized the local attenuation coefficient contrast of retinal layers. These methods exploit the handcrafted feature; thus, it may not be generalized for different sized and shaped fluid regions. Xu et al. [11] integrated the layer segmentation and region stratification to find fluid areas from the retina. This method may work better on larger fluid regions yet may fail to detect small fluid pockets. In Shi et al. [15], the retinal layers were segmented, and then the empirically set threshold value for layers height variation was used to detect PED. However, the single threshold selection approach is not robust enough to accommodate unpredictable sizes of fluid regions.
There are also some research works based on graph-theory and the traditional machine learning approach. The kernel regression and graph theory were adopted in Chiu et al. [17] to find retinal layers and fluid-related abnormalities. Zhang et al. [16] presented a technique that combined 3D graph search and supervised voxel classification to segment the fluid-filled anomalies from eyes affected by AMD. Sun et al. [14] proposed the PED segmentation method using the AdaBoost classifier and shape-based graph-cut. The k-means cluster and 3D graph-cut were assimilated in Bekalo et al. [19] to segment SRF-related fluid from the SD-OCT image. These methods may provide better results but may not achieve the same performance for the 3D data and multiple-class representation. When the data gets bigger, the optimization function gets computationally more challenging for graph-based techniques and fails to find the optimal solution. Furthermore, the hard constraint selection and weight initialization in graph-based approaches are heuristics that may not be applicable for the unseen dataset. Furthermore, many of the approaches mentioned above focus on the segmentation of one or two fluid types and do not determine the fluid types.
The convolutional neural network (CNN) introduction enabled advancing retinal fluid segmentation [20–36]. A fully convolutional neural network (FCN)-based model presented in Lu et al. [20] uses the image data and distance map to segment retinal fluids. Arunkumar and Karthigaikumar [22] proposed a method that integrates the deep belief neural network and multi-class SVM classifier to segment retinal lesions, including AMD. Morley et al. [28] used a ResNet to segment fluid regions and refined the results by applying the graph-cut technique. Bai et al. [34] used a combination of FCN and a fully connected conditional random field for fluid segmentation. The works mentioned above showed significant improvement, but the method’s confines lay on the extensive pre- and post-processing techniques they have adopted. For example, to remove false-positive fluid regions, Lu et al. [20] used traditional machine learning approaches, whereas Morley et al. [28] used the graph-cut system and morphological operations. Besides the limitations mentioned above about the graph-based and traditional machine learning methods, as pre- and post-processing steps, these approaches undeniably impose additional computational cost; thus, the model may not be clinically serviceable. Kang et al. [26] presented a two-stepped neural network in which the first network is to segment fluid areas, whereas the latter network post-processes the result by accepting the original image and the corresponding prediction result from the early stage. This approach may achieve better performance, but it computationally costs since the same model runs several times.
Roy et al. [21] presented the architecture mainly focuses on retinal layer segmentation. They tested the model only on IRF segmentation in which the effectiveness of the work cannot be assertive for the segmentation of untested fluid types. Rashno et al. [24] presented a method for the segmentation of IRF, SRF, and PED. The segmentation of IRF and SRF utilizes a trained CNN model, while the PED detection relies on computing the elevation of the retinal pigment epithelium (RPE) layer. To tackle the effect of non-cysts regions like vitreous fluid, researchers in Rashno et al. [24] and Lee et al. [25] apply region of interest (ROI) extraction as the pre-processing stage. In many cases, to limit the ROI, the inner limiting membrane (ILM) and Bruch’s membrane (BM) layers are segmented using a graph-based approach. Since AMD is well-known for deteriorating intensity value distribution of layers, graph-based retina layer segmentation is prone to error. This is a very significant problem when severe PED detachment is available. Because in the case of severe PED, segmentation of the most needed BM layer is subjective to several empirically chosen parameters and weight initializations that may not be effective on different shaped and sized PED detachments. Lastly, to the best of our knowledge, existing works deploy CNN-based models for specific segmentation tasks, but none of them investigate the sensitivity of CNN architectures and its hyperparameters towards SD-OCT images.
In this work, we proposed a novel CNN architecture, called RetFluidNet, to segment retinal fluids from SD-OCT images. In contrast to all previously presented approaches, this work focuses on the following points.
This paper presents an improved semantic segmentation architecture well tested to segment three types of retinal fluids (IRF, SRF, and PED).
The method uses existing skip-connect approaches and integrates with Atrous Spatial Pyramid Pooling (ASPP) to achieve better performance without pre- or post-processing stages.
This work investigates between consequential and comparatively inconsequential hyperparameters to suggest future fluid segmentation tasks starting choice.
Finally, the work evaluates and presents the effect of different types of skip-connect techniques to judge their usefulness on the fluid segmentation from SD-OCT images.
The rest of this paper is structured as followed. In “Method,” we explain the architectural details of the proposed method. “Experimental Method” describes the experimental techniques include the details about datasets, comparative methods, and evaluation metrics. “Result Analysis” discusses the results in terms of qualitative and quantitative evaluations. In “RetFluidNet Architecture Analysis,” the architecture of the proposed method is evaluated to reveal the effects of skip-connect operations and respective hyperparameters. “Discussion” presents the discussion that elaborates the findings of this work while comparing the findings with previous studies. Finally, in “Conclusion,” we end with a brief conclusion and an outlook for future research.
Method
RetFluidNet follows the semantic segmentation approach that associates each pixel of an image with one of four class labels IRF, PED, SRF, or background. Figure 2 shows the illustrative diagram of RetFluidNet architecture. The model consists of encoding and decoding paths. The encoding path is the contracting path that extracts features and produces dense low-resolution feature-maps. The decoding path is the expansive path that restores the original size. The decoding path has an additional operation termed F–C (fuse-concatenate) to facilitate the precise localization. F–C combines high-resolution features from the encoding path with a similar-sized feature on the decoding side. The ASPP operation next to the decoding path is to incorporate the larger contextual information. Additionally, the model has an operation hereafter called A-R-C (A—average pooling, R—resize, and C—concatenation) that allows the reuse of features from different encoding path layers. The details of each operation are explained in the following sections.
Fig. 2.
The diagrammatic representation of RetFluidNet architecture. The blue boxes stand for the feature map with respective channel dimensionality written below the boxes. The purple box stands for the feature map after the ASPP operation. The channel size for the ASPP result is 42 which is the result of 14 channels from three parallel ASPP operations. P stands for the number of classes, and in this paper, it is 4 (three fluid types and background)
Encoding
The encoding part consists of layers in which each layer combines regular convolution and Relu activation function. After certain encoding layers, the A-R-C operation is induced to the model. The A-R-C operation is a type of skip-connect technique that is anticipated to encourage feature reuse from various levels of encoding layers. The A-R-C operation conducts average pooling on the output of the layer before the operation and resizes the outputs of all other preceding layers to have the same size as the output of average pooling (Fig. 3). In the end, outputs from average pooling and resizing operation are concatenated and fed to layer followed A-R-C operation. In other words, each layer that follows the A-R-C operation obtains additional resized inputs from all preceding layers, including the original image. For the image classification task with small training samples, this approach was used in Huang et al. [37] and showed significant improvement in reducing over-fitting.
Fig. 3.
The diagrammatic representation of A-R-C operation. Red rectangles are the input to A-R-C operation in which average pooling is applied. The green-colored rectangles including the original image are resized to attain the size of the average pooled result. Finally, all the results are concatenated. For the easy demonstration, the letters are given similar color with the representative rectangles. ln represents nth layer, d is the dimension feature channel, and x and y are the height and width of feature maps
For a given nth layer , the input is the output of A-R-C operation ( on Fig. 3), if the A-R-C operation precedes it; otherwise, the input is the output of the preceding convolutional layer (see Fig. 2). It is noteworthy to remark that only A-R-C operation reduces the input size by a factor of 2 in and directions because of 2 by 2 average pooling. For the convolution operation, the output feature-map size remains similar to its input. The stride value was set to 1 with the “same” padding to keep the spatial dimensions. The encoding path consists of seven layers, excluding the input layer ( on Fig. 3). The first layer has a channel size of 30, and in each successive layer, the channel size increases by 30.
Decoding
The series of convolutional layers and the A-R-C operation in the encoding phase produces dense and coarse features representation that may lack sharp details, limited positioning accuracy, and have a lesser spatial dimension. The decoding path is the expansive operation that intends to restore the resolution of the original image and try to regain the lost features. In this work, the repetitive deconvolution technique is applied to retain the original resolution, and the F–C method is implemented to restore the lost details. F–C is a set of operations that encapsulates the summation of feature maps followed by the concatenation. First, feature maps from the encoding path are fused (summed) to the similar-sized output in the decoding path, and then, the result from summation is again concatenated with output from the encoding path. F–C enables the maximum information flow from high-resolution features of encoding to decoding path. It doubles the features map channel of its input and feeds into the next layer. Since deconvolution reverses the forward and backward passes of convolution, to compensate for the size reduction in the A-R-C operation, the up-sampling stride was set to 2 for the deconvolution operation before F–C. In the decoding path, the feature maps’ channel size follows the reverse order of the encoding path except that the last layer of decoding has channel size of the number of classes (p in Fig. 2.).
Atrous Spatial Pyramid Pooling
The architecture so far can segment the edema region at a reasonable accuracy. However, since the three fluid types have similar intensity value distribution with slightly different shapes, many wrong class-labeling was observed. To solve this problem, the information about the region of fluid occurrence was incorporated using ASPP. Based on retinal fluids’ anatomy, the type of fluid is correlated to the closer retinal layers. For example, IRF appears in the relatively lower reflective region (between nerve fiber layer (NFL) and outer nuclear layer), whereas the PED and SRF are near to the brighter region (inner segment and the outer segment IS/OS). For SRF, the brighter region is the lower boundary, while PED has a brighter upper boundary. Using solely the intensity of pixels and its neighbors windowed by a standard convolutional kernel (with a dimension of 7 × 7 in this work) may not be good enough to extract all discriminative features to differentiate between three fluid types. Standard kernels often suffer from confusion categories and inconspicuous classes because of missing global context information [38]. ASPP captures multi-scale features so that the model can encode contextual information. The contextual information is an essential factor to segment objects with various scales and ambiguous pixels requiring a diverse range of contextual information [39]. In this work, the contextual information from ASPP assists the model to differentiate the fluid type more efficiently (see “RetFluidNet Architecture Analysis”).
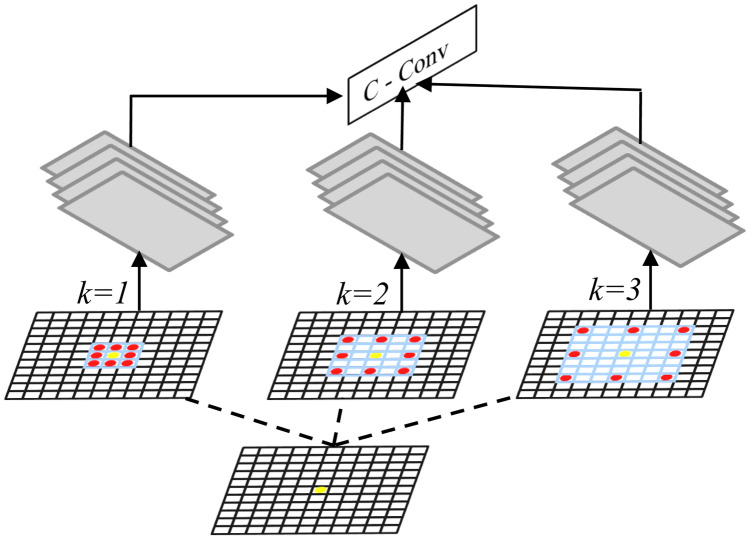
ASPP is a technique that uses a series of atrous (or dilated) convolutions with different dilation rates to capture information from an arbitrary scaled region. For a given pixel shown by yellow, consider a 3 × 3 convolution filter in Fig. 4 with the image size 11 × 11. When the dilation rate is equal to 1, the filter behaves as a standard convolution. If the dilation rate is set to the value of k, it enlarges the convolution kernel by padding k − 1 zeros between two consecutive non-zero values. ASPP adds feature responses from the broader context without increasing the number of parameters and the computational cost. In this work, ASPP contains three parallel operations with the dilation rates = 4, 8, and 12. Each ASPP operation produces a feature map with a channel size of 14 that is similar to the original input image. The output from ASPP is concatenated to the result from the decoding phase and followed by two convolution layers in which the last layer is to predict final class labels. Since the fluid segmentation in this work is formulated as a 4-class labeling problem (IRF, SRF, PED, and background), the final convolution layer contains four filters.
Fig. 4.
The pictorial representation of ASPP operation where the dilation rate k set to the values of 1, 2, and 3. The overlaid blue area represents the region covered by the kernel. The red dots are the neighborhood kernel values. The yellow dot is a pixel where a feature response is calculated for. The green stacked rectangles represent the result of the different rate values. C stands for the concatenation of results, whereas Conv is convolution
Experimental Method
Datasets
RetFluidNet and all the comparative methods were trained and tested on B-scans from 124 patients. The B-sans were obtained from a Cirrus SD-OCT machine (Carl Zeiss Meditec, Inc., Dublin, CA). Each SD-OCT cube has 128 B-scans, and a given B-scan contains 512 A-scans where each A-scan comprises 1024 pixels).
The models are evaluated in two different ways, named patient-dependent and patient-independent evaluations. For the patient-dependent evaluation, the B-scans from all patients were combined, and later the training, validation, and testing folds were chosen. The dataset consists of B-scans without fluid, only with IRF, PED, and SRF or in a combination of two or even three fluid types. For the unbiased selection, the B-scans were divided into eight categories: IRF, PED, SRF, IRF&PED, IRF&SRF, PED&SRF, IRF&PED&SRF, and B-scans without fluid. From each category, 70% of the B-scans were randomly selected for training. The evaluation and testing folds have 15% of the total images. It is essential to realize that in this evaluation, the B-scans from the same patient may be available in the training and testing datasets, which makes the experiment patient-dependent. This test enables us to evaluate the models’ ability to capture B-scans’ structural variability and correctly predict the result.
For the patient-independent evaluation, the datasets were divided in a random choice of patients rather than B-scans; thus, the training and testing sets are independent. Of 124 patients, 70% were used for training, and 30% were equally divided for validation and testing. This evaluates the model capability on the patient level instead of B-scans. Since the large image size increases both memory and computational complexity of the network, in both evaluation methods, the B-scans were resized through the “nearest” interpolation method to get B-scans of size 256 × 256.
Experimental Settings
The Adam optimizer was used to update the network weights and bias on a mini-batch size of 6 using the learning rate of 10–5. The combination of softmax activation function and the cross-entropy was applied to estimate the training loss. The model was trained for the 33,000 iteration steps. The kernel size for all convolution and deconvolution layers was set to 7 × 7. The weight and bias in the network were initialized using the Xavier scheme. During training, to overcome the overfitting, a dropout layer was inserted before the F–C operation with the probability of 0.5. In the testing stage, the dropout probability was set to 1 so that all the layers were kept to generate the prediction. The model was built on an open-source deep-learning toolbox named Tensorflow [40], and then, the experiments were run on an NVIDIA GeForceGTX 1080 GPU.
Comparative Methods and Evaluation Metrics
The performance of RetFluidNet was evaluated against existing methods named Deeplabv3 [41], fully convolutional network (FCN) [42], UNet++ [41], and an improved multi-scale parallel branch convolutional neural network (Im-MPB-CNN) [35]. RetFluidNet and comparative methods were set to have similar learning rate values, batch size, and the number of training iterations. All other hyperparameters of the comparative methods attain the default values suggested by the authors. The reason to choose the first three comparative methods was that the evaluation against these methods would help us demonstrate the advantages of the A-R-C, F–C, and ASPP since these comparative methods use one of the concepts in a different approach. For instance, to restore the lost details during the encoding phase, FCN uses features fusing, UNet++ utilizes concatenation to facilitate information flow, and Deeplabv3 uses ASPP to capture a wide range of information. Remember that we have integrated these concepts in different architecture to produce plausibly good results. Comparison against Im-MPB-CNN [35] is included to evaluate RetFluidNet with the method specifically designed for AMD fluid segmentation.
The accuracy of fluid volume segmentation is calculated in terms of overlap ratio (Overlap), overestimate ratio (Ovrest), underestimate ratio (Undest), and dice score. The overlap ratio indicates the amount of fluid region available in both the proposed method and manual segmentation. The overestimate ratio denotes the volume of fluid detected by the algorithm but not on the manual segmentation results. The underestimate ratio on another side measures the volume available on the manual result but not on the result of the algorithm. For the result of expert (A) and the proposed method (M), the accuracy metrics are calculated as follows:
| 1 |
| 2 |
| 3 |
| 4 |
where TP, FP, and FN represent true positive, false positive, and false negative, respectively. and indicate the complements of and , whereas the operator ∪ and ∩ are union and intersection operations, respectively.
Result Analysis
Qualitative Evaluations
The model trained to segment three types of fluid regions from the SD-OCT image. In this section, the qualitative comparison of results from RetFluidNet and the comparative methods are shown. From Fig. 5, we can see that RetFluidNet achieves (shown on the fifth column) visually comparable results with the ground truth (shown on the sixth column). The training dataset for non-fluid PED was smaller compared to others; nonetheless, RetFluidNet is capable of finding non-fluid PED even in the severe case where it appeared in combination with IRF (first row). RetFluidNet is also capable of segmenting small lesions, as shown in the last row. Followed by RetFluidNet, the Im-MPB-CNN model showed better results. In some cases, Im-MPB-CNN fails to segment early PED regions while over segmenting the NRD regions and PED with wrong boundary delineation (second and third rows). The typical limitations of UNet++ were the under segmentation and wrong class-labeling of the lesion regions, as indicated in the third column in Fig. 5. FCN and DeepLabv3 also experienced under-segmentation. In many cases, DeepLabv3 and UNet++ failed to segment small fluid regions (Fig. 5 last raw).
Fig. 5.
Sample results from RetFluidNet and the comparative methods. From the left to right column, it shows the results from FCN, DeepLabv3, UNet++ , Im_MPB_CNN, RetFluidNet, and the ground truth
Quantitative Evaluation: Patient-dependent
This section presents the qualitative evaluation of the models on the patient-dependent dataset. Table 1 shows each fluid type’s accuracy from the RetFluidNet and the comparative methods in terms of overlap, overestimate, underestimate ratios, and the dice score. The RetFluidNet demonstrates the highest accuracy for IRF, PED, and SRF. Im-MPB-CNN achieved better accuracy following the RetFluidNet. FCN has shown the lowest performance in all fluid types. Another difference between UNet++ and RetFluidNet is that UNet++ demands nearly twice the memory capacity compared to RetFluidNet.
Table 1.
Dice score, overlap, overestimated, and underestimate of three fluid types from the proposed method and comparative methods
| Fluid types | Metrics (%) | FCN [42] | DeepLabV3 [41] | UNet++ [43] | Im-MPB-CNN [35] | RetFluidNet |
|---|---|---|---|---|---|---|
| NRD | Dice | 87.47 | 94.24 | 94.79 | 94.71 | 95.53 |
| Overlap | 77.73 | 89.10 | 90.10 | 89.95 | 91.44 | |
| Undest | 17.86 | 5.80 | 6.14 | 5.09 | 5.02 | |
| Ovrest | 4.40 | 5.10 | 3.76 | 4.97 | 3.54 | |
| PED | Dice | 84.77 | 88.78 | 83.91 | 88.57 | 92.74 |
| Overlap | 73.56 | 79.82 | 72.27 | 79.48 | 86.46 | |
| Undest | 21.36 | 14.30 | 22.24 | 11.69 | 7.60 | |
| Ovrest | 5.08 | 5.88 | 5.49 | 8.83 | 5.94 | |
| IRF | Dice | 53.00 | 70.59 | 74.20 | 77.57 | 80.05 |
| Overlap | 36.05 | 54.55 | 58.98 | 63.36 | 66.74 | |
| Undest | 56.53 | 30.82 | 26.99 | 18.0 | 20.32 | |
| Ovrest | 7.41 | 14.6 | 14.04 | 18.63 | 12.94 |
From all the fluid types, IRF detection was challenging (as shown in Table 1, all the methods achieved lower performance in IRF accuracy). RetFluidNet yields reasonably good results in IRF identification with an accuracy of 80.05%, which has a substantial improvement over other comparative methods with an accuracy of 27.05%, 9.46%, 5.85%, and 2.48% over FCN, DeepLabv3, UNet++ , and Im-MPB-CNN, respectively, in terms of dice score. Overall, the quantitative evaluation shows that RetFluidNet outperformed the comparative methods.
Quantitative Evaluation: Patient-independent
In this section, the patient-independent evaluation is presented for the RetFluidNet and the comparative methods. The result of a patient-independent experiment is shown in Table 2. RetFluidNet achieved an accuracy of 78.95%, 90.90%, and 95.78% for IRF, PED, and SRF, respectively. Compared to the patient-dependent test, the accuracy of IRF and PED reduced by 1.1% and 1.84%, respectively, while SRF increased by 0.25%. RetFluidNet holds its outstanding position over the comparative methods in the patient-independent evaluation. Compared to a patient-dependent evaluation in “Quantitative Evaluation: Patient-Dependent,” all the comparative methods showed a decline for PED and excluding Im-MPB-CNN; other methods achieved trivial improvement over the accuracy of SRF segmentation. For IRF detection, FCN and UNet++ exhibited improvement, whereas DeepLabV3, Im-MPB-CNN, and RetFluidNet experienced lower accuracy.
Table 2.
The overlap, overestimate, underestimate, and dice score of the proposed method and comparative methods for patient-independent evaluation
| Fluid types | Metrics (%) | FCN [42] | DeepLabV3 [41] | UNet + + [43] | Im-MPB-CNN [35] | RetFluidNet |
|---|---|---|---|---|---|---|
| NRD | Dice | 88.21 | 95.10 | 95.69 | 94.20 | 95.78 |
| Overlap | 78.90 | 90.66 | 91.74 | 89.04 | 91.89 | |
| Undest | 16.00 | 5.07 | 3.35 | 7.80 | 6.11 | |
| Ovrest | 5.10 | 4.27 | 4.92 | 3.16 | 2.00 | |
| PED | Dice | 81.31 | 85.47 | 78.96 | 81.69 | 90.90 |
| Overlap | 68.51 | 74.63 | 65.23 | 69.05 | 83.32 | |
| Undest | 25.50 | 21.16 | 17.64 | 26.45 | 10.61 | |
| Ovrest | 5.99 | 4.21 | 17.13 | 4.49 | 6.07 | |
| IRF | Dice | 54.06 | 64.58 | 74.59 | 70.70 | 78.95 |
| Overlap | 37.04 | 47.69 | 59.47 | 54.68 | 65.22 | |
| Undest | 48.73 | 41.56 | 23.44 | 22.35 | 27.10 | |
| Ovrest | 14.22 | 10.76 | 17.09 | 22.97 | 7.68 |
RetFluidNet Architecture Analysis
Contributions of A-R-C, F–C, and ASPP
We investigated the effect of A-R-C, F–C, and ASPP operations on the final result of RetFluidNet. First, the basic network runs without any of the operations. Basic network means the RetFluidNet only with convolution and Relu layer on the encoding side and deconvolution and relu on the decoding path. The subsequent experiments run on the different combinations, as indicated in Table 3. The combinations of modules were represented by a number in Table 3, and the corresponding numbers are used in Table 4 to show the respective accuracy metrics results.
Table 3.
Different combinations of modules with the basic network
| Number | Combinations |
|---|---|
| 1 | Basic network |
| 2 | Basic network + A-R–C |
| 3 | Basic network + F–C |
| 4 | Basic network + A-R–C + F–C |
| 5 | Basic network + A-R–C + F–C + ASPP |
Table 4.
Dice score, overlap, overestimated, and underestimate of different module combination
| Fluid types | Metrics (%) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| NRD | Dice | 95.06 | 94.72 | 87.14 | 95.18 | 95.53 |
| Overlap | 90.59 | 89.97 | 77.22 | 90.80 | 91.44 | |
| Undest | 3.39 | 3.93 | 20.41 | 4.28 | 5.02 | |
| Ovrest | 6.02 | 6.11 | 2.37 | 4.92 | 3.54 | |
| PED | Dice | 89.50 | 90.02 | 90.47 | 91.96 | 92.74 |
| Overlap | 80.99 | 81.85 | 82.60 | 85.11 | 86.46 | |
| Undest | 2.87 | 11.34 | 11.67 | 6.40 | 7.60 | |
| Ovrest | 16.14 | 6.80 | 5.73 | 8.49 | 5.94 | |
| IRF | Dice | 76.77 | 74.10 | 64.85 | 78.36 | 80.05 |
| Overlap | 62.30 | 58.86 | 47.98 | 64.41 | 66.74 | |
| Undest | 13.09 | 17.81 | 43.34 | 18.12 | 20.32 | |
| Ovrest | 24.61 | 23.33 | 8.68 | 17.47 | 12.94 |
The basic network was able to segment SRF, yet the segmentation accuracy of IRF was not satisfactory. When the A-R-C and F–C modules were introduced independently, the accuracy of IRF and SRF were comparatively lower, and PED identification was better. The accuracy of all the fluid types increased when both A-R-C and F–C were integrated into the basic network. This demonstrates that assimilating the information flow in the different network stages has an essential effect on improving the final result. Another benefit of A-R-C and F–C operations is that even if the training dataset was relatively small, the model was capable of training for a larger number of iterations without being affected by overfitting.
Hyperparameters Selection
One of the significant challenges in CNN-based model development is hyperparameter tuning. In practice, the sensitive hyperparameter subset is different for various CNN architectures and the respective datasets. As CNN has many interdependent hyperparameters, it is experimentally quite expensive to show the effect of all hyperparameter and their dependence. In this work, we have tested the hyperparameters known to have a stimulating effect on deep learning architecture [44], including the learning rate, batch size, filter size, and number of layers.
The effect of hyperparameter was evaluated after finding the optimal result generating hyperparameters through a manual search approach. When the effect of a given hyperparameter was evaluated, the rest of the hyperparameters were kept fixed to the best value found via manual investigation. The hyperparameters effect was shown using a graphic representation of loss function (Fig. 6), accuracy metrics, and their effect on training and testing time per the B-scan (Tables 5 and 6). For the reported result, the model has seven layers on each encoding and decoding side that trained using a learning rate of 10–5 updated on a batch size of 6. The chosen filter size was 7 × 7. The model was trained for 12.05 h and took 0.06 s for testing.
Fig. 6.
The graphic representation of training loss response of RetFluidNet towards the change of different parameter values. (a) Training loss response for various batch sizes. (b) Training loss response for various learning rates. (c) Training loss response for different filter sizes. (d) Training loss response for the different number of layers. Note: the * shows the values used for the result reported in this paper
Table 5.
The response of the proposed method for changes in values of different hyperparameters. (TR.tm and TS.tm stand for training and testing time, respectively. h and s represent hours and second)
| Batch size | Learning rate | ||||||
|---|---|---|---|---|---|---|---|
| Fluid types | Metrics (%) | 2 | 10 | 14 | 10–4 | 10–6 | 10–7 |
| NRD | Dice | 94.00 | 95.15 | 95.53 | 95.51 | 91.70 | 67.93 |
| Overlap | 88.68 | 90.74 | 91.44 | 91.41 | 84.68 | 51.43 | |
| Undest | 2.82 | 2.61 | 5.02 | 4.23 | 3.01 | 3.69 | |
| Ovrest | 8.50 | 6.65 | 3.54 | 4.36 | 12.31 | 44.88 | |
| PED | Dice | 87.46 | 91.93 | 92.63 | 92.74 | 57.51 | 0.03 |
| Overlap | 77.71 | 85.07 | 86.26 | 86.46 | 40.36 | 0.01 | |
| Undest | 18.23 | 4.21 | 5.69 | 7.60 | 1.24 | 99.90 | |
| Ovrest | 4.06 | 10.72 | 8.04 | 5.94 | 58.40 | 0.08 | |
| IRF | Dice | 76.07 | 79.60 | 78.79 | 78.98 | 64.11 | 0.47 |
| Overlap | 61.38 | 66.12 | 65.00 | 65.26 | 47.17 | 0.23 | |
| Undest | 14.71 | 17.58 | 24.12 | 16.91 | 15.51 | 98.54 | |
| Ovrest | 23.91 | 16.31 | 10.88 | 17.83 | 37.31 | 1.23 | |
| TR.tm (h) | 5.03 | 15.97 | 18.53 | 12.01 | 12.97 | 12.42 | |
| TS.tm (s) | 0.06 | 0.06 | 0.06 | 0.06 | 0.07 | 0.07 | |
Table 6.
The response of the proposed method for changes in values of different hyperparameters. (TR.tm and TS.tm stand for training and testing time, respectively. h and s represent hours and second)
| No. of layers | Filter size | ||||||
|---|---|---|---|---|---|---|---|
| Fluid types | Metrics (%) | 3 | 5 | 9 | 3 | 5 | 9 |
| NRD | Dice | 81.09 | 94.19 | 94.16 | 86.41 | 95.25 | 95.22 |
| Overlap | 68.20 | 89.02 | 88.96 | 76.07 | 90.92 | 90.87 | |
| Undest | 21.51 | 7.23 | 2.47 | 14.68 | 5.14 | 2.86 | |
| Ovrest | 10.30 | 3.75 | 8.56 | 9.25 | 3.93 | 6.27 | |
| PED | Dice | 70.92 | 86.37 | 89.30 | 63.24 | 91.29 | 92.14 |
| Overlap | 54.94 | 76.01 | 80.66 | 46.24 | 83.97 | 85.43 | |
| Undest | 27.82 | 7.02 | 2.15 | 35.56 | 5.73 | 6.50 | |
| Ovrest | 17.24 | 16.97 | 17.19 | 18.20 | 10.30 | 8.07 | |
| IRF | Dice | 41.29 | 67.62 | 75.74 | 30.45 | 76.45 | 79.59 |
| Overlap | 26.02 | 51.08 | 60.95 | 17.96 | 61.87 | 66.10 | |
| Undest | 62.77 | 35.98 | 4.02 | 71.54 | 19.42 | 15.58 | |
| Ovrest | 11.22 | 12.94 | 35.03 | 10.50 | 18.71 | 18.32 | |
| TR.tm (h) | 6.16 | 10.58 | 13.45 | 3.18 | 5.60 | 18.37 | |
| TS.tm (s) | 0.03 | 0.05 | 0.08 | 0.017 | 0.036 | 0.112 | |
Including the chosen values of reported results, RetFluidNet was tested on four batch sizes. When batch-size increases, the model experiences stable training loss (Fig. 6a). The smallest batch size produced moderately the lowest accuracy, whereas the larger batch size showed better performance (Table 5). For the chosen training iteration steps (33,000), batch size 6 produced a better result. Increasing the training iteration step may improve the larger batch size results, but it requires larger memory and training hours. The experiment shows that increasing the batch size causes longer training hours though it does not affect the testing time.
We have seen that the learning rate is the most sensitive hyperparameter that needs to be chosen very carefully. Even if the training loss was stable (Fig. 6b), for very large or small values of the learning rate, the model exhibited the worst performance (Table 5). Another important observation is that the learning rate has nearly no effect on training and testing time.
Compared to batch size, learning rate, and the number of the layers, changes in the filter size showed a significant effect on the training and testing time (Table 6). When the filter size increases, both the training and testing time increase. Many CNN-based works used 3 × 3 filter sizes, but for RetFluidNet, it demonstrated quite unstable training loss (Fig. 6c) and the lowest accuracy compared to other filter sizes. For the reported result, we have used a filter size of 7 × 7, although 9 × 9 also produced a comparable result.
Finally, we have tested the effect of the number of layers (Fig. 6d). In this sense, the number of layers represents layers in the encoding and decoding path without changing the setup of ASPP. For instance, if a number of the layer was set to 3, then it means only the first three layers from encoding were used, and the decoding path was set as explained in “Method.” When the number of layers set to 9, we used the rule of expanding succeeding layers by 30. That means additional layers of size 270 and 300 were added. When the model size increases or decreases, its accuracy reduces (Table 6), which may be because of lower feature representation when layers are small and lesser training time for larger layer size.
The number of iterations specified in this work was selected after running the model on different iteration steps ranging from 15,000 to 45,000. The model showed over-fitting to the iteration numbers higher than 33,000 and under-fitting for less than this value.
Discussion
As shown in “Result Analysis”, RetFluidNet achieved the best result in terms of quantitative and qualitative evaluation. From Table 1, it can be seen that all the models attained the best performance on SRF detection. This may be because larger numbers of training datasets contain SRF, and compared to other fluid types, SRF has a predictable shape and occurrence region. The accuracy of PED is reasonably good; nevertheless, the representation of two types of PED (fluid-filled and non-fluid filled) as one class may affect its accuracy since a small number of training datasets have non-fluid filled compared to fluid-filled PED. The lower accuracy of IRF arguably emanated from two main reasons. The first reason is that the intensity value distribution similarity with SRF and PED and the extremely unpredictable shape leads to the wrong class-labeling. Secondly, it might be because of the over-segmentation or under-segmentation of the ground truth. The medical image interpretation is commonly prone to the expert’s visual judgment, leading to overestimation or underestimation. In this case, the training datasets found from multiple experts and averaging to represent the final training dataset may improve the result.
The patient-independent evaluation shows that the fluid types such as SRF with relatively predictable shapes and occurrence regions can be trained on smaller datasets to achieve good performance. However, as the fluid type has unpredictable shapes, it is vital to increase the training dataset with various disease severity levels to handle varied shapes. In a patient-independent test (Table 2), the accuracy of IRF (mostly with the unpredictable shape) and PED (with unpredictable shape in early-stage) was reduced. On the patient-dependent and patient-independent evaluations, nearly all the methods showed a higher underestimate ratio compared to the respective overestimate ratio. We have found this as an intriguing observation that requires investigation of further works.
Evaluation of the effects of different skip-connect techniques in “RetFluidNet Architecture Analysis” helps to judge their usefulness on the fluid segmentation from SD-OCT images. In its overall evaluation, the A-R-C, F–C, and ASPP modules raise the performance of the RetFluidNet in comparison to the comparative model, which used the above concepts in different ways. The existing works, like FCN and UNet++ concatenation and fuse, were used in the decoding phase, respectively. As already mentioned by the authors of these works, these skip-connect techniques help improve final results, which align with our experiment observation. Nevertheless, encouraging reuse of features in both the encoding and decoding phases provided better results (Table 4, column 6). Further improvement was observed when the ASPP module was induced to the model. From the combination number 5 of Tables 3 and 4, we can see that the contextual information has a beneficial effect on the success of RetFkuidNet. Moreover, the interesting observation is that even though vitreous fluid has similar intensity value distribution with the fluid cysts, the model can capture the structural difference and avoid false-positive segmentations without applying ROI extraction steps used by other works. We believe that ASPP plays a significant role in this achievement since it captures features from different spatial levels. RetFkuidNet also showed promising achievement in differentiating fluid and low reflective retinal regions (such as NFL).
Conclusion
This paper has proposed a semantic segmentation method named RetFluidNet to segment three retinal fluid types from the SD-OCT image. RetFluidNet consists of seven layers in the encoding and decoding path. The two special skip-connections, so-called A-R-C and F–C, were introduced to the architecture. The A-R-C operation was induced in the encoding path to permit the reuse of features throughout the network. F–C combines the high-resolution features from an encoding path with a similar-sized feature in the decoding side to restore the lost details in the encoding stage. RetFluidNet exploits the multi-scale context information integration ability of atrous spatial pyramid pooling (ASPP) to achieve a credible good result. ASPP is applied using the dilation rates of 4, 8, and 12. The main aim of incorporating ASPP is to assimilate nearby fluid layers’ information because the three fluids’ main difference is their region of occurrence.
In many previous works related to retinal fluid segmentation based on CNN, the models incorporate pre- and post-processing stages to improve the final result. Though pre- and post-processing can improve the results, these steps impose additional computational cost leading the method not to be clinically applicable. In the approaches that use layer segmentation as pre-processing, any layer segmentation error can be propagated to the fluid segmentation. RetFluidNet enjoys the multi-level field-of-view capability of ASPP instead of pre- and post-processing stages to attain higher accuracy. Additionally, contrary to the existing works, which mostly focus only on segmentation tasks, we have evaluated the effects of different hyperparameters and skip-connect operations in this work.
RetFluidNet yields reasonably good results on the SD-OCT image, yet since many clinical investigations use multi-modal imaging modalities, the model needs to be trained and improved to accommodate images from different modalities. RetFluidNet uses the 2D information; its performance may be improved if it can be extended to utilize the 3D information for volumetric images like SD-OCT and can be considered for further work. The effect of down-sampling on the small fluid regions is not studied in this work. Since it is likely to have small fluid pockets, especially for IRF, in the future work investigating the effect of down-sampling and coming up with an alternative image resizing approach is advisable.
It is also earnest to mention that this work’s main challenge was the extensiveness of the optimization process emanating because of the large number of hyperparameters and their interdependence. The model requires a GPU based computer for both training and testing with longer training time. Examining the effect of the hyperparameters value change requires more extended time and makes hyperparameters tuning very exhaustive and time-consuming. In future work, it is recommendable to apply the hyperparameter selection methods like BOHB [45] to search for an optimal combination of hyperparameter values so that the model may produce a better result.
Abbreviations
- AMD
age-related macular degeneration
- IRF
intra-retinal fluid
- SRF
subretinal fluid
- PED
pigment epithelial detachment
- SD-OCT
spectral-domain optical coherence tomography
- CNN
convolutional neural network
- FCN
fully convolutional neural network
- ROI
region of interest
- ILM
inner limiting membrane
- BM
Bruch’s membrane
- ASPP
Atrous spatial pyramid pooling
- A-R–C
a-average pooling, R-resize and C-concatenation
- F–C
fuse-concatenate
- TP
true positive
- FP
false positive
- FN
false negative
Funding
This work was supported by the National Natural Science Foundation of China (61671242, 61701222) and Key R&D Program of Jiangsu Provincial Department of Science and Technology (BE2018131).
Declarations
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Bressler NM. Age-related macular degeneration is the leading cause of blindness. JAMA. 2004;291(15):1900. doi: 10.1001/jama.291.15.1900. [DOI] [PubMed] [Google Scholar]
- 2.R. Deonandan, and S. Jones, "Anti-vascular endothelial growth factor drugs for the treatment of retinal conditions: a Review of the Safety," (2017). [PubMed]
- 3.A. Daruich, A. Matet, A. Dirani, E. Bousquet, M. Zhao, N. Farman, F. Jaisser, and F. Behar-Cohen, "Central serous chorioretinopathy: Recent findings and new physiopathology hypothesis," Prog. Retin. Eye Res. 48(82-118 (2015). [DOI] [PubMed]
- 4.Matsumoto H, Sato T, Kishi S. Outer nuclear layer thickness at the fovea determines visual outcomes in resolved central serous chorioretinopathy. Am J Ophthalmol. 2009;148(1):105–110.e101. doi: 10.1016/j.ajo.2009.01.018. [DOI] [PubMed] [Google Scholar]
- 5.Abouammoh MA. Advances in the treatment of central serous chorioretinopathy. Saudi J Ophthalmol. 2015;29(4):278–286. doi: 10.1016/j.sjopt.2015.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.R. F. Spaide, J. G. Fujimoto, and N. K. Waheed, "Optical coherence tomography angiography," Retina (Philadelphia, Pa.) 35(11), 2161 (2015). [DOI] [PMC free article] [PubMed]
- 7.Morgan JI. The fundus photo has met its match: optical coherence tomography and adaptive optics ophthalmoscopy are here to stay. Ophthalmic Physiol Opt. 2016;36(3):218–239. doi: 10.1111/opo.12289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wu M, Chen Q, He X, Li P, Fan W, Yuan S, Park H. Automatic subretinal fluid segmentation of retinal SD-OCT images with neurosensory retinal detachment guided by enface fundus imaging. Eng: IEEE Trans. Biomed; 2017. [DOI] [PubMed] [Google Scholar]
- 9.Fernandez DC. Delineating fluid-filled region boundaries in optical coherence tomography images of the retina. IEEE Trans Med Imag. 2005;24(8):929–945. doi: 10.1109/TMI.2005.848655. [DOI] [PubMed] [Google Scholar]
- 10.J. Novosel, Z. Wang, H. de Jong, M. van Velthoven, K. A. Vermeer, and L. J. van Vliet, "Locally-adaptive looselycoupled level sets for retinal layer and fluid segmentation in subjects with central serous retinopathy," Biomedical Imaging (ISBI), 2016 IEEE 13th International Symposium on 702-705 (2016).
- 11.Xu X, Lee K, Zhang L, Sonka M, Abràmoff MD. Stratified sampling voxel classification for segmentation of intraretinal and subretinal fluid in longitudinal clinical OCT data. IEEE Trans Med Imag. 2015;34(7):1616–1623. doi: 10.1109/TMI.2015.2408632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Xinjian C, Niemeijer M, Li Z, Kyungmoo L, Abramoff MD, Sonka M. Three-dimensional segmentation of fluid-associated abnormalities in retinal OCT: probability constrained graph-search-graph-cut. IEEE Trans Med Imag. 2012;31(8):1521–1531. doi: 10.1109/TMI.2012.2191302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Quellec G, Lee K, Dolejsi M, Garvin MK, Abràmoff MD, Sonka M. Three-dimensional analysis of retinal layer texture: identification of fluid-filled regions in SD-OCT of the macula. IEEE Trans Med Imag. 2010;29(6):1321–1330. doi: 10.1109/TMI.2010.2047023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Z. Sun, H. Chen, F. Shi, L. Wang, W. Zhu, D. Xiang, C. Yan, L. Li, and X. Chen, "An automated framework for 3D serous pigment epithelium detachment segmentation in SD-OCT images," Sci. Rep. 6((2016). [DOI] [PMC free article] [PubMed]
- 15.Shi F, Chen X, Zhao H, Zhu W, Xiang D, Gao E, Sonka M, Chen H. Automated 3-D retinal layer segmentation of macular optical coherence tomography images with serous pigment epithelial detachments. IEEE Tran Med Imag. 2015;34(2):441–452. doi: 10.1109/TMI.2014.2359980. [DOI] [PubMed] [Google Scholar]
- 16.Zhang L, Sonka M, Folk JC, Russell SR, Abramoff MD. Quantifying disrupted outer retinal-subretinal layer in SD-OCT images in choroidal neovascularization. Invest Ophthalmol Vis Sci. 2014;55(4):2329–2335. doi: 10.1167/iovs.13-13048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chiu SJ, Allingham MJ, Mettu PS, Cousins SW, Izatt JA, Farsiu S. Kernel regression based segmentation of optical coherence tomography images with diabetic macular edema. Biomed Opt Express. 2015;6(4):1172–1194. doi: 10.1364/BOE.6.001172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.M. Dolejší, M. D. Abràmoff, M. Sonka, and J. Kybic, "Semi-automated segmentation of symptomatic exudateassociated derangements (SEADs) in 3D OCT using layer segmentation," Biosignal (2010).
- 19.L. Bekalo, S. Niu, X. He, P. Li, I. P. Okuwobi, C. Yu, W. Fan, S. Yuan, and Q. Chen, "Automated 3-D retinal layer segmentation from SD-OCT images with neurosensory retinal detachment," IEEE Access 7(14894-14907 (2019).
- 20.D. Lu, M. Heisler, S. Lee, G. Ding, M. V. Sarunic, and M. F. Beg, "Retinal fluid segmentation and detection in optical coherence tomography images using fully convolutional neural network," arXiv preprint arXiv:1710.04778 (2017). [DOI] [PubMed]
- 21.Roy AG, Conjeti S, Karri SPK, Sheet D, Katouzian A, Wachinger C, Navab N. ReLayNet: retinal layer and fluid segmentation of macular optical coherence tomography using fully convolutional networks. Biomed Opt Express. 2017;8(8):3627–3642. doi: 10.1364/BOE.8.003627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Arunkumar R, Karthigaikumar P. Multi-retinal disease classification by reduced deep learning features. Neural Comput Appl. 2015;28(2):329–334. doi: 10.1007/s00521-015-2059-9. [DOI] [Google Scholar]
- 23.Montuoro A, Waldstein SM, Gerendas BS, Schmidt-Erfurth U, Bogunović H. Joint retinal layer and fluid segmentation in OCT scans of eyes with severe macular edema using unsupervised representation and auto-context. Biomed Opt Express. 2017;8(3):1874–1888. doi: 10.1364/BOE.8.001874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.A. Rashno, D. D. Koozekanani, and K. K. Parhi, "Oct fluid segmentation using graph shortest path and convolutional neural network," 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) 3426-3429 (2018). [DOI] [PubMed]
- 25.Lee CS, Tyring AJ, Deruyter NP, Wu Y, Rokem A, Lee AY. Deep-learning based, automated segmentation of macular edema in optical coherence tomography. Biomed Opt Express. 2017;8(7):3440–3448. doi: 10.1364/BOE.8.003440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.H. S. P. Sung Ho Kang, Jaeseong Jang and Kiwan Jeon1, "Deep neural networks for the detection and segmentation of the retinal fluid in OCT images.," MICCAI Retinal OCT Fluid Challenge (RETOUCH) (2017).
- 27.Venhuizen FG, van Ginneken B, Liefers B, van Asten F, Schreur V, Fauser S, Hoyng C, Theelen T, Sánchez CI. Deep learning approach for the detection and quantification of intraretinal cystoid fluid in multivendor optical coherence tomography. Biomed Opt Express. 2018;9(4):1545–1569. doi: 10.1364/BOE.9.001545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.D. Morley, H. Foroosh, S. Shaikh, and U. Bagci, "Simultaneous detection and quantification of retinal fluid with deep learning," arXiv preprint arXiv:1708.05464 (2017).
- 29.S. Apostolopoulos, C. Ciller, R. Sznitman, and S. De Zanet, "Simultaneous Classification and Segmentation of Cysts in Retinal OCT."
- 30.Girish G, Thakur B, Chowdhury SR, Kothari AR, Rajan J. Segmentation of intra-retinal cysts from optical coherence tomography images using a fully convolutional neural network model. IEEE J Biomed Health Inform. 2019;23(1):296–304. doi: 10.1109/JBHI.2018.2810379. [DOI] [PubMed] [Google Scholar]
- 31.Bogunović H, Venhuizen F, Klimscha S, Apostolopoulos S, Bab-Hadiashar A, Bagci U, Beg MF, Bekalo L, Chen Q, Ciller C. RETOUCH: The retinal OCT fluid detection and segmentation benchmark and challenge. IEEE Trans Med Imag. 2019;38(8):1858–1874. doi: 10.1109/TMI.2019.2901398. [DOI] [PubMed] [Google Scholar]
- 32.A. Rashno, D. D. Koozekanani, and K. K. Parhi, "Detection and segmentation of various types of fluids with graph shortest path and deep learning approaches," Proc. MICCAI Retinal OCT Fluid Challenge (RETOUCH) 54-62 (2017).
- 33.Gopinath K, Sivaswamy J. Segmentation of retinal cysts from optical coherence tomography volumes via selective enhancement. IEEE J Biomed Health Inform. 2019;23(1):273–282. doi: 10.1109/JBHI.2018.2793534. [DOI] [PubMed] [Google Scholar]
- 34.F. Bai, M. J. Marques, and S. J. Gibson, "Cystoid macular edema segmentation of Optical Coherence Tomography images using fully convolutional neural networks and fully connected CRFs," arXiv preprint arXiv:1709.05324 (2017).
- 35.J. Fang, Y. Zhang, K. Xie, S. Yuan, and Q. Chen, "An improved MPB-CNN segmentation method for edema area and neurosensory retinal detachment in SD-OCT images," International Workshop on Ophthalmic Medical Image Analysis 130-138 (2019).
- 36.Khan KB, Khaliq AA, Jalil A, Iftikhar MA, Ullah N, Aziz MW, Ullah K, Shahid M. A review of retinal blood vessels extraction techniques: challenges, taxonomy, and future trends. Pattern Anal Appl. 2019;22(3):767–802. doi: 10.1007/s10044-018-0754-8. [DOI] [Google Scholar]
- 37.G. Huang, Z. Liu, L. Van Der Maaten, and K. Q. Weinberger, "Densely Connected Convolutional Networks," in 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), IEEE (2017).
- 38.Y. Zhao, N. Barnes, B. Chen, R. Westermann, X. Kong, and C. Lin, Image and Graphics: 10th International Conference, ICIG 2019, Beijing, China, August 23–25, 2019, Proceedings, Springer Nature (2019).
- 39.M. Yang, K. Yu, C. Zhang, Z. Li, and K. Yang, "Denseaspp for semantic segmentation in street scenes," Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 3684-3692 (2018).
- 40.M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, and M. Devin, "Tensorflow: Large-scale machine learning on heterogeneous distributed systems," arXiv preprint arXiv:1603.04467 (2016).
- 41.L.-C. Chen, G. Papandreou, F. Schroff, and H. Adam, "Rethinking atrous convolution for semantic image segmentation," arXiv preprint arXiv:1706.05587 (2017).
- 42.J. Long, E. Shelhamer, and T. Darrell, "Fully convolutional networks for semantic segmentation," in 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), IEEE (2015). [DOI] [PubMed]
- 43.Z. Zhou, M. M. R. Siddiquee, N. Tajbakhsh, and J. Liang, "Unet++: A nested u-net architecture for medical image segmentation," in Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, pp. 3-11, Springer (2018). [DOI] [PMC free article] [PubMed]
- 44.Y. Bengio, "Practical Recommendations for Gradient-Based Training of Deep Architectures," in Lecture Notes in Computer Science, pp. 437-478, Springer Berlin Heidelberg (2012).
- 45.S. Falkner, A. Klein, and F. Hutter, "BOHB: Robust and efficient hyperparameter optimization at scale," arXiv preprint arXiv:1807.01774 (2018).