Abstract
Cardiovascular diseases (CVDs) are the top ten leading causes of death worldwide. Atherosclerosis disease in the arteries is the main cause of the CVD, leading to myocardial infarction and stroke. The two primary image-based phenotypes used for monitoring the atherosclerosis burden is carotid intima-media thickness (cIMT) and plaque area (PA). Earlier segmentation and measurement methods were based on ad hoc conventional and semi-automated digital imaging solutions, which are unreliable, tedious, slow, and not robust. This study reviews the modern and automated methods such as artificial intelligence (AI)-based. Machine learning (ML) and deep learning (DL) can provide automated techniques in the detection and measurement of cIMT and PA from carotid vascular images. Both ML and DL techniques are examples of supervised learning, i.e., learn from “ground truth” images and transformation of test images that are not part of the training. This review summarizes (1) the evolution and impact of the fast-changing AI technology on cIMT/PA measurement, (2) the mathematical representations of ML/DL methods, and (3) segmentation approaches for cIMT/PA regions in carotid scans based for (a) region-of-interest detection and (b) lumen-intima and media-adventitia interface detection using ML/DL frameworks. AI-based methods for cIMT/PA segmentation have emerged for CVD/stroke risk monitoring and may expand to the recommended parameters for atherosclerosis assessment by carotid ultrasound.
Keywords: Atherosclerosis, Carotid ultrasound, Plaque, Artificial intelligence, Machine learning, Deep learning, Carotid intima-media thickness, Carotid plaque area
Introduction
Cardiovascular disease (CVD)-related deaths in the United States of America (USA) were 17.6 million in 2016, and that is 14.5% higher than reported in 2006 [1]. The major causes of such an increase in fatalities can be attributed to an increase in tobacco use, physical inactivity, obesity, high blood pressure, diabetes, arthritis, coronary artery disease, and other disorders. This has deep economic implications on the US economy. It is estimated that the total direct and indirect costs were US $351.2B in 2014–2015, adjusting to inflation [1, 2].
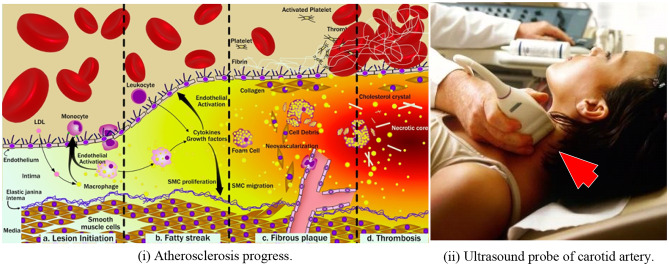
The main cause of CVD is the blood vessel inflammatory disease, called atherosclerosis [3, 4]. Atherosclerosis is initiated by endothelium dysfunction [4, 5], where the thin wall of the interior surface of blood vessels gets damaged leading to the formation of more complex lesions and fatty streak within arterial walls [1, 6–8]. Several studies have been conducted demonstrating how atherosclerosis progresses in the carotid arteries. One study on 68 asymptomatic patients with greater than 50% stenosis showed that the wall area increased by 2.2% per year over 18 months [9]. Another study that ran over months, consisting of 250 patients with asymptomatic plaques having 40–99% stenosis, showed a high percentage area of lipid-like matter. This risk factor caused subsequent cerebral infarction (hazard ratio = 4.4) [10]. Such a situation generally signifies a time bomb where the artery can no longer sustain the plaque burden leading to the rupture of the fibrous cap. This leads to the intrusion of plaque into the bloodstream causing thrombosis and finally resulting in a stroke [11–13] (shown in Fig. 1). Atherosclerosis has been also linked to neuronal diseases such as dementia [14], leukoaraiosis [15, 16], and Alzheimer’s [17], renal diseases [18, 19], arthritis [20], and coronary artery diseases [21].
Fig. 1.
(i) Left panel: atherosclerosis progression consisting of (a) endothelium dysfunction and lesion initiation, (b) formation of a fatty streak, (c) formation of fibrous plaque underlying fibrous cap, and (d) rupture and thrombosis. (ii) Right panel: ultrasound scanning of the carotid artery (both images courtesy of AtheroPoint™, Roseville, CA, USA)
The atherosclerotic disease can be quantified by tracking the carotid intima-media thickness (cIMT) and plaque area (PA) over time, so-called atherosclerotic disease monitoring or vascular screening [22]. The cIMT is the measured distance between lumen-intima (LI) and media-adventitia (MA) borders [23, 24] while the area covered between the LI and MA boundary walls typically refers to PA [25–32]. The role of cIMT/PA measurement has gone beyond is normal tracking of the atherosclerosis burden, but rather computing CVD composite risk estimation, unlike the traditional risk calculators such as Framingham [33], ASCVD [34], Reynold risk score (RRS) [35], United Kingdom Prospective Diabetes Study (UKPDS56) [36], UKPDS60 [37], QRISK2 [38], and Joint British Societies (JBS3) [39]. None of these conventional calculators used plaque burden as a risk factor. This changed recently when AtheroEdge Composite Risk Score (AECRS 1.0) [20] was developed that used an automated morphological-based CVD risk prediction tool that integrates both conventional and imaging-based phenotypes such as cIMT and PA. The image-based biomarkers are based on the scanning of carotid segments such as a common carotid artery, bulb, or internal carotid artery acquired using 2D B-mode ultrasound [5, 40, 41]. AECRS 2.0 is another class of image-based 10-year risk calculator that combines conventional risk factors, blood biomarkers, and image-based phenotypes. It is these image-based phenotypes that are an integral part of the risk calculators, and therefore, better understanding is needed on how cIMT/PA can be computed automatically in artificial intelligence (AI) framework. To get a better idea, one must therefore see how the cIMT/PA evolved over time.
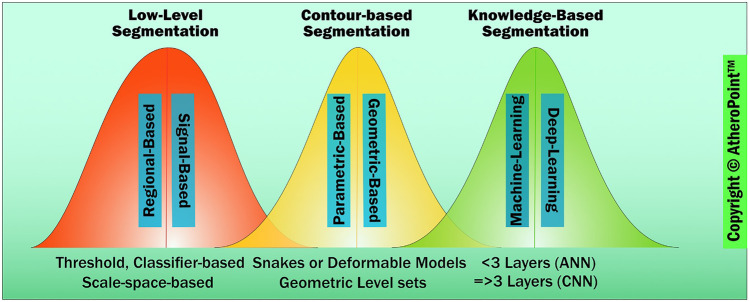
There are different school-of-thoughts (SOT) dealing with automated identification of the cIMT/PA region (so-called segmentation) for static (or frozen) and motion images; however, the scope of this work is only limited to static scans. These SOTs range from simple image morphology-based threshold techniques to deep learning (DL)-based AI systems developed over 50 years. Therefore, a generation-wise categorization is necessary. Thus, SOTs can be further divided into three generations based on how the ROI region is determined [42] and then how LI/MA is searched in this ROI region. The first-generation technologies were low-level segmentation techniques which used conventional image processing methods based on the primary threshold to get the edges of LI/MA and then use a caliper-based solution to measure the mean distance. The second-generation (or second kind of methods) used contour-based methods, which consisted of parametric curves or geometric curves. Some of these methods are semi-automated [43–46]. Further in the same class were a fusion of signal-processing-based methods (such as scale-space) and deformable models. These were categorized under the class of AtheroEdge™ models. They are completely and fully automated. Some methods were regional-based combined with deformable models under the fusion category in generation 2. These were also fully automated [47, 48]. The latest third-generation models use AI technology like machine learning (ML) [49] and DL [50] for both ROI estimation and LI/MA interface detection. All the three generations used some kind of distance measurement method such as shortest distance, centerline distance, Hausdorff distance [51], and more often adapted and called as “Suri’s polyline distance method” [52]. This review is focused on how ML and DL can be used for cIMT/PA measurements, which in turn requires LI/MA detection in plaque and non-plaque regions.
The layout of the paper is given as follows: the “Chronological Generations of cIMT Regional Segmentation and cIMT Measurement” section gives an overall overview of conventional and advanced techniques in joint carotid cIMT/PA estimation along with their classification. The “ML Application for cIMT and PA Measurement” section is dedicated to both ML and DL techniques applied for the segmentation of cIMT/PA regions. The “Deep Learning Application for cIMT and PA extraction” section provides different quantification techniques, and finally, the paper concludes in the “Discussion” section.
Chronological Generations of cIMT Regional Segmentation and cIMT Measurement
As already known, the carotid IMT is the surrogate biomarker for carotid/coronary artery disease [53]. Several first-generation computer vision and image-processing techniques have been developed for the low-level segmentation of the cIMT region (the region between LI and MA borders) and LI/MA interface detection, such as dynamic programming (DP) [54], Hough transform (HT) [55], Nakagami mixture modeling [56], active contour [57], edge detection [58], and gradient-based techniques [59].
These come under the class of computer-aided diagnosis [40, 60, 61]. The comparison of these methods has been presented previously [62–66]. Dynamic programming uses optimization techniques to minimize the cost function which is the summation of weighted terms of local estimations such as echo intensity, intensity gradient, and boundary continuity. All sets of spatial pixel points forming a polyline are considered. The polyline having the lowest cost is considered the cIMT vertices and such polylines constitute the boundary [54]. The HT of a line is a point in the (s, θ) plane where all the points on this line map into this single point. This fact is utilized to find different line segments through edge points which can be used to detect curves in an image. HT has been used for lumen segmentation in various works by Golemati et al. [67], Stoitis et al. [68], and Petroudi et al. [69], and Destrempes et al. [56] used Nakagami distribution and motion estimation to segment the cIMT region. This generation also involved the usage of signal processing techniques such as scale-space [70] to detect LI and MA boundaries [46]. Several version of cIMT segmentation methods with scale-space based augmented by second-generation methods (so-called [24, 71–73]).
In the second generation, the concept of active contour evolved that involves fitting a contour to local image information. Snakes or active contour are an example of active parametric contours [14] that were used for LI/MA estimation, followed by cIMT measurement [74]. In the same class, curve fitting models were a classic example of the cIMT estimation method [75]. Level sets topologically independent propagating zero level curves to settle at the interfaces of LI and MA were used to compute the LI/MA interfaces so-called as cIMT borders [76]. There has been a method which fuses first generation and second generation, such as fusion of scale-space [70] with deformable models [46]. Several version of cIMT segmentation methods with scale-space based augmented by second-generation methods (so-called [24, 71–73]). Edge detection techniques use a variation of grey levels and included image gradient to delineate cIMT borders [77]. Molinari et al. used a fusion of these approaches to segment the cIMT borders [78]. Elisa et al. [27] used an automated software AtheroEdge™ system [19, 66, 79] based on scale-space for computing cIMT and plaque area (PA) after computing LI-and MA boundary interfaces. The third-generation advanced techniques consist of intelligence-based techniques such as ML [49] and DL [50] techniques, primarily banking on neural network models. ML was based on hand-crafted features, while DL was more along the lines of automated feature extraction. Regarding the risk prediction of CVD, both ML and DL have been objective and methodologies that can be replicated with high diagnostic accuracy [80, 81]. A representation of technologies generation wise is shown in Fig. 2. A detailed discussion of general working of ML and DL follows next.
Fig. 2.
Three generations of cIMT/PA measurement evolution (color image) (courtesy of AtheroPoint™, Roseville, CA, USA)
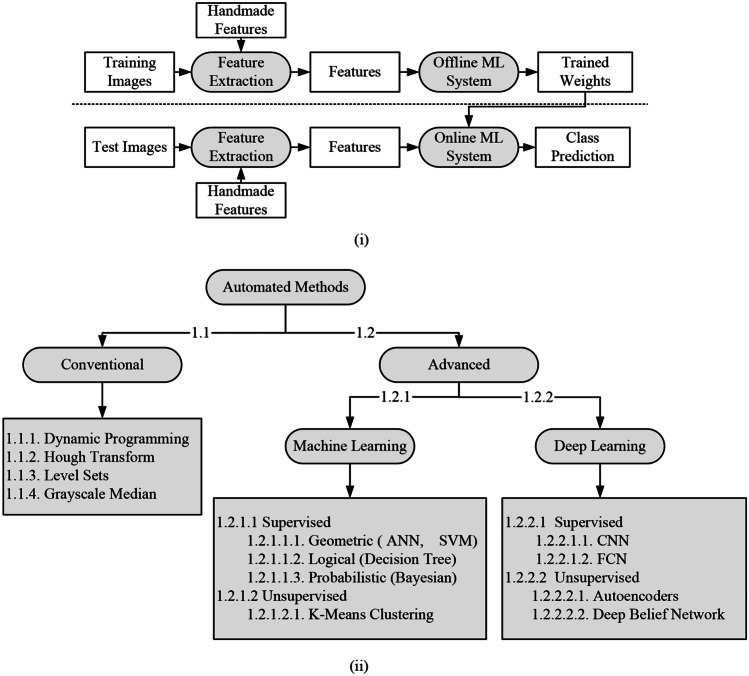
ML and DL differ in the methodology of feature derivation from instances. In the case of ML (details in Appendix 1), feature extraction is independent of the actual model of classification and is handcrafted (shown in Fig. 3 (i)), whereas, in DL, the feature extraction and model of characterization are indifferent from each other. ML models of classification mostly appear as a single statistical learning and inference technique to make accurate predictions using the extracted features [82, 83]. The DL models, on the other hand, apply multiple layers of statistical learning and inference techniques to extract features and make predictions. Hence, the DL techniques are costlier in terms of computation time and space, but are more robust and in some cases provide higher accuracy, when applied to a very large dataset [84]. ML techniques are more economical in both time and cost when compared with DL. Often these two techniques are clubbed together for better performance. An interesting characteristic is how ultrasound image noise (speckle noise, scattering noise) was handled by each of these generations. While the first two generations used various denoising techniques such as Gaussian filter, anisotropic diffusion, and smoothing, there was no evolution of such in third-generation [64, 65, 75, 85]. A brief outline of technologies generation wise is given in Table 1. Although technologies were divided generation wise, they were not water-tight compartments. Many models were a fusion of different technologies belonging to different generations to increase performance. In this regard, Molinari et al. [23] used a combination of first and second techniques to minimize the cIMT error.
Fig. 3.
(i) Generalized ML model and (ii) classification tree of different automated models
Table 1.
The three generations of cIMT regional segmentation
| SN | Attributes | First generation | Second generation | Third generation |
|---|---|---|---|---|
| 1 | Fields of engineering | Conventional image processing, signal processing/combined with image processing | Signal processing combined with image processing | Knowledge-based engineering |
| 2 | Computer vision methods or fusion of methods | Dynamic programming, Hough transform | Parametric (snakes) curves, geometric curves (level sets), scale-space, conventional classifiers | Machine learning and deep learning |
| 3 | Distance measurement methods or cIMT measurement methods | Vertical, shortest distance along with the columns of the image | Polyline distance method, centerline distance Method | Polyline Distance Method / Centerline Distance |
The PA biomarker received significant research focus after it was conclusively proven to be as important as cIMT in the works of Spence et al. [86, 87], Mathiesen et al. [88], and Saba et al. [79]. Mathematically, PA can be computed along with cIMT if LI/MA borders are known. It is computed by counting all pixels between LI and MA borders and then calibrating it to mm2. PA has been well adapted in AECRS 1.0 [89] and AECRS2.0 [18] systems.
ML Application for cIMT and PA Measurement
In the Appendix 1, a brief outline of ML techniques was given. The different AI methodologies are shown in Fig. 3 (ii) and their description is given in Table 2. This is categorized into conventional, machine learning, and deep learning strategies. In this section, we will study in detail about different ML techniques that are applied for cIMT/PA segmentation and measurements from CCA images. As stated earlier, features are needed to be extracted before the ML model is applied. Some part of the features is used for training the model, i.e., training data (, while the rest of it is used to test the model, i.e., test data ). The training process uses a feedback mechanism based on known and actual outputs, wherein the model parameters are changed based on the error. This training process repeats until the model parameters converge or do not change their values anymore, it is conceded that training is complete. Therefore, the model with trained parameters is tested on with outputs unknown to the model. Once model outputs are out, they are compared with actual outputs to check the performance of the model. Several applications of ML has been developed which uses the concept of offline and online system, such as arrhythmia [90] and diabetes [91]. Since they all use ground truth during cross-validation, we call them supervised learning, and is applied extensively in cIMT and PA computation from CCA images. There are two different SOTs (Rosa et al. [92, 93] and Molinari et al. [23]) regarding segmenting the cIMT region from ultrasound CCA images. Both SOTs extract the ROI before the application of ML paradigm for cIMT segmentation. They are given as follows:
Table 2.
Comparison between different cIMT regional segmentation methods for given attributes
| Attributes | Conventional methods (1.1) | Machine learning (1.2.1) | Deep learning (1.2.2) | ||
|---|---|---|---|---|---|
| Types | Active contour, level sets, edge detection, dynamic programming (1.1.*) | Supervised (1.2.1.1) | Geometric: ANN, SVM (1.2.1.1.1) | Supervised (1.2.2.1) | CNN, FCN (1.2.2.1.*) |
| Logical: decision trees (1.2.1.1.2) | |||||
| Probabilistic: Bayesian (1.2.1.1.3) | Unsupervised (1.2.1.2) | Auto-encoders, deep belief nets (1.2.2.2.*) | |||
| Unsupervised (1.2.1.2) | K-means clustering (1.2.1.2.1) | ||||
| Description | Techniques employing imaging features and processing for the cIMT regional segmentation | The two-stage intelligence-based paradigm in which image features are extracted and then used by the ML model for training and testing for the cIMT region identification | Mimics human visual cortex with numerous hierarchical network of neurons extracting high-level features directly from images for recognition of the cIMT region | ||
| Advantages |
1. Fastest among all methods for region estimation as no training and testing 2. Simple |
1. Uses intelligence in the form of learning from experience/training and applies to unknown instances 2. Somewhat generalized and can be applied to instances within the similar domain 3. Faster than deep learning |
1. Independent of feature extraction algorithms 2. Can be scaled up to recognize/characterize millions of images 3. Generalized and can be used to multiple domains |
||
| Disadvantages |
1. Task-specific and cannot be generalized 2. Low accuracy |
1. Dependent upon the quality of features for better accuracy 2. The accuracy curve diminishes when scaled up to a large number of instances |
1. Costly in terms of computation time and memory 2. Easily overfits and therefore requires different techniques for prevention of overfitting |
||
ANN Model for cIMT Region Detection
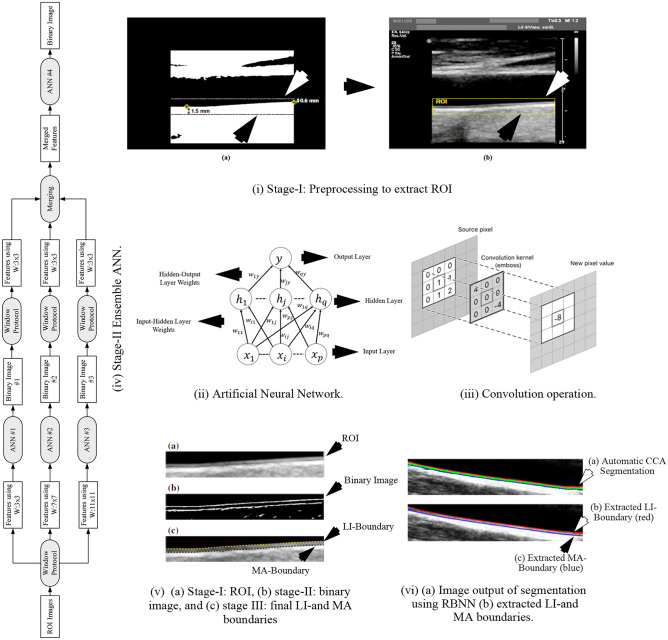
Rosa et al. [92] used three stages to acquire cIMT values from 60 B-mode ultrasound CCA images. In stage I, the CCA images were preprocessed to extract ROI, and stage-II is the AI-based classification stage where the IMT regional pixels were segregated from non-IMT regional pixels resulting in a binary image. Stage III consisted of delineation of LI and MA boundary from the binary image. The preprocessing stage consisted of the application of watershed transform [94–96] of the CCA to detect the lumen, wherein the lower limit of the lumen is assigned as the posterior wall. The final ROI in the region, where the uppermost point of the far wall was considered as 0.6 mm above the binary lumen, and the bottom boundary is fixed to 1.5 mm below the lowest point detected in the binary mask. Once the ROI is detected, its dimension is noted and extracted from the original image as shown in Fig. 4 (i). The extracted ROIs are input to the next stage for IMT border delineation. The next stage applies the ensemble of four artificial neural networks (ANNs) [97] to classify cIMT from non-cIMT region pixels. The ANN is in the form of a multi-layer perceptron consisting of three layers such as input, hidden, and output as shown in Fig. 4 (ii). In the ANN model, the computation is done by the nodes, whereas the “learning experience” is embedded in the weights between input-hidden and hidden-output layers. These weights generally are randomly initialized and converge to a stable value based on the feedback on the error propagation as the learning progresses. The computation is generally, multiplication of weights with the input values, thereafter, a sigmoid function is applied. Also, a bias term is added to each computed term. The output function is given by:
| 1 |
where and signify the weights between input-hidden, and hidden-output layers, respectively. The weight values () are optimized for each error propagation using the gradient (), given as:
| 2 |
where is the learning parameter. The input pattern to each ANN is the pixel intensities that are generated by a kernel process. For each image, three kernels of size 3 × 3, 7 × 7, and 11 × 11 were applied pixel-by-pixel through shifting, to collect contextual information of neighborhood pixel intensities. The process is also known as convolution and its operation using the kernel is shown in Fig. 4 (iii). The ground truth was the pixel class information collected through manual segmentation of CCA images and annotation of each pixel being cIMT boundary or not. Therefore, the inputs were passed through three ANNs, respectively, for training and testing. The output is in the form of another reconstructed binary image from each of the three ANNs. Thereafter, these three output binary images are merged and another kernel of size 3 × 3 is again applied to the merged image and this data is fed into the fourth ANN to get the final binary mask. A representative model of the entire process is shown in Fig. 4 (iv). In the final stage, LI and MA boundaries are identified (shown in Fig. 4 (v)) and cIMT is computed. The mean absolute distance, polyline distance, and centerline distance were mm, mm, and mm, respectively.
Fig. 4.
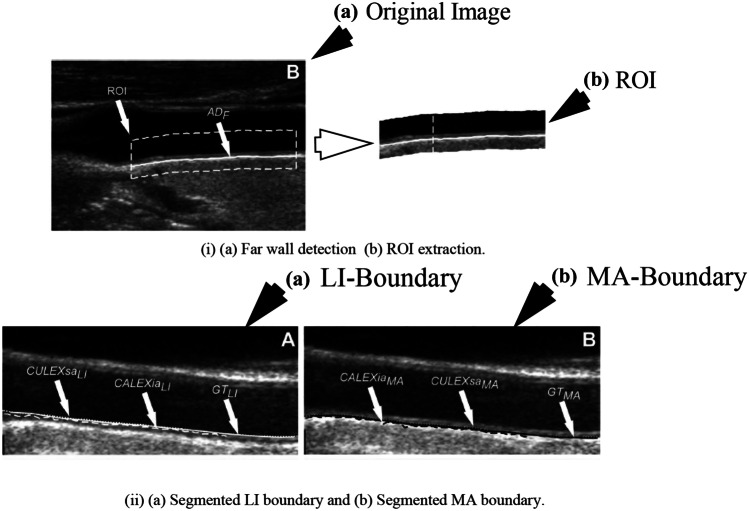
(i) ROI extraction (reproduced with permission), (ii) ANN, (iii) convolution operation, (iv) stage II ANN ensemble network, (v) outputs of [92] (reproduced with permission), (vi) segmentation using RBNN [93] (reproduced with permission)
Extreme Learning Machines-Radial Basis Neural Network Model for cIMT Region Detection
Rosa et al. [93] used radial basis neural network (RBNN) [98] for the estimation of the cIMT region from 25 ultrasound CCA images. RBNNs are single-layer feed-forward neural networks consisting of input, hidden, and output layers. One of the key differences between RBNN and ANN is that the number of hidden layers in RBNN is restricted to one. The working principle of RBNN lies in interpolating training points to their corresponding target variable . Therefore, the model output function for an input is given by:
| 3 |
where is the Gaussian radial basis function implemented by the hidden layer, is the weight between the hidden and output layer. The is the radial basis function which is given by:
| 4 |
where represents the width of the hidden neuron. Equation (3) can be reduced into a matrix notation and is given as:
| 5 |
where is the target vector. The weights can be found by standard matrix inversion
| 6 |
the initialization of hidden nodes’ Gaussian parameters (number of hidden nodes, centers, and deviation of each radial unit) are done using optimally pruned-extreme learning machine (OP-ELM) [99, 100]. The ground truth information and ROI of the 25 CCA images are extracted using the method mentioned in the “ANN Model for cIMT Region Detection” section. Similar to the previous method [92], the input pattern is generated by the kernel process. A comparative study was performed using varying kernel sizes in the range of 3 to 23. The optimized kernel window size was . The ground truth was manually traced by experienced radiologists. Three classes of pixels were considered for each CCA image, pixels of the LI boundary, pixels within the region between LI and MA boundary, and the pixels of the MA wall. Finally, each class of pixels were extracted and superimposed on the original image as shown in Fig. 4 (vi). The cIMT error for this experiment was mm.
Fuzzy K-means Classifier for cIMT Region Extraction
Molinari et al. [23] introduced the concept of unsupervised learning of fuzzy K-means clustering [101] (FKMC) to segregate a CCA image into three parts, i.e., plaque region, LI, and MA boundaries. This method is also called CULEXia. The FKMC is unsupervised in the sense that there is no ground truth for the pixels. The FKMC is similar to the K-means algorithm [102], where initially K random points denoting K cluster centers are initialized, and then all data points in the dataset are assigned to each of the K clusters based on the nearest mean. For each cluster centroid, represents the mean of all points in the cluster. The membership function of each point determining degree of its membership for each cluster , is given by:
| 7 |
where is a hyper-parameter controlling fuzziness.
In this work, the ROI is extracted from each CCA image by tracing the MA wall. The MA wall is traced by locating the brightest local maximum starting from the bottom of the image for each column. The upper limit of ROI is computed 1.25 mm and 0.625 mm above and below the MA wall, respectively as shown in Fig. 5 (i). Thereafter, in the next stage, three clusters of pixels are considered for each column in the ROI column-wise, i.e., lumen, LI, and MA wall. The pixels in each column are automatically assigned to each cluster using the FKMC algorithm. The sequence of LI and MA centroids for each column marks the delineation of respective walls in the ROI as shown in Fig. 5 (ii). This procedure was repeated for 200 ultrasound CCA images. The cIMT error for the method was mm. The ML models discussed covered cIMT measurement in brief; however, they did not consider plaque area until the DL work by Elisa et al. [103] in 2018 and joint cIMT and PA measurement by Biswas et al. [104] in 2020. A brief outline of DL in cIMT and PA measurement is given in the next section.
Fig. 5.
(i) Far wall detection and (ii) segmentation of LI (white) and MA (black) boundary (reproduced with permission) [23]
Deep Learning Application for cIMT and PA Extraction
There are several DL techniques used for image classification and segmentation [82, 105] such as CNN [50], deep belief networks (DBN) [106], autoencoders [107], and residual neural networks [108]. Fully convolutional network (FCN) [109] is a variation of CNN which excludes the connected network and is used specifically for segmentation. Three different SOTs are working on cIMT measurement using ultrasound CCA images. DL. Rosa et al. [110] used autoencoders for feature extraction before employing ANNs for LI and MA boundary delineation. Suri and his team used FCN both on whole [111] and patch [104] CCA ultrasound images for cIMT and PA [103] measurement while Del Mar et al. [112] used FCN for whole CCA images for cIMT estimation. The next few subsections deal with some of these works in detail for cIMT and PA measurement computed using CCA images.
ANN Autoencoder-Based cIMT Region Segmentation
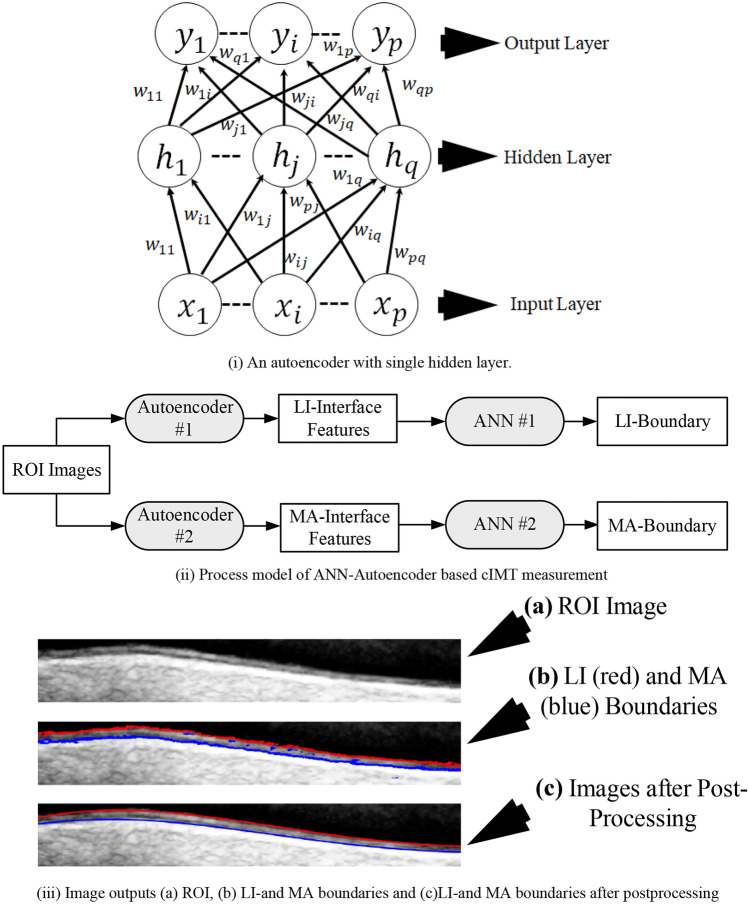
Rosa et al. [110] used ANN for characterizing LI and MA pixels belonging to 55 ultrasound CCA images. The authors used trained autoencoders [107] to extract features in the LI and MA interface. Autoencoders are neural networks designed to reproduce the input. They are generally used for unsupervised learning to understand complex relationships within input images. Given an input , the autoencoder maps it to a compressed representation using single or multiple hidden layers, using the mapping function similar to Eq. 3. Finally, the compressed representation is upsampled to its original dimension. It is done so to understand the essential structures and relationships with the input vector, and the training required to regenerate it. The compressed representation of neighborhood pixels denotes the features. An illustration of the autoencoder is shown in Fig. 6 (i). The ROI extraction approach is similar to [92]. The authors trained two autoencoders using five ground truth images. The neighborhood pixels of the LI and MA interface were used to train the two autoencoders. The LI and MA features were used to train two ANNs for pixel characterization. Finally, the offline CCA images were segmented, to extract the LI and MA boundary. Postprocessing was applied to discard the unnecessary LI and MA pixels. The system’s cIMT error was mm. The process model is shown in Fig. 6 (ii) while the results are shown in Fig. 6 (iii).
Fig. 6.
(i) An autoencoder, (ii) process model, (iii) image outputs (reproduced with permission) [110]
Fully Convolutional Network for cIMT Region Estimation
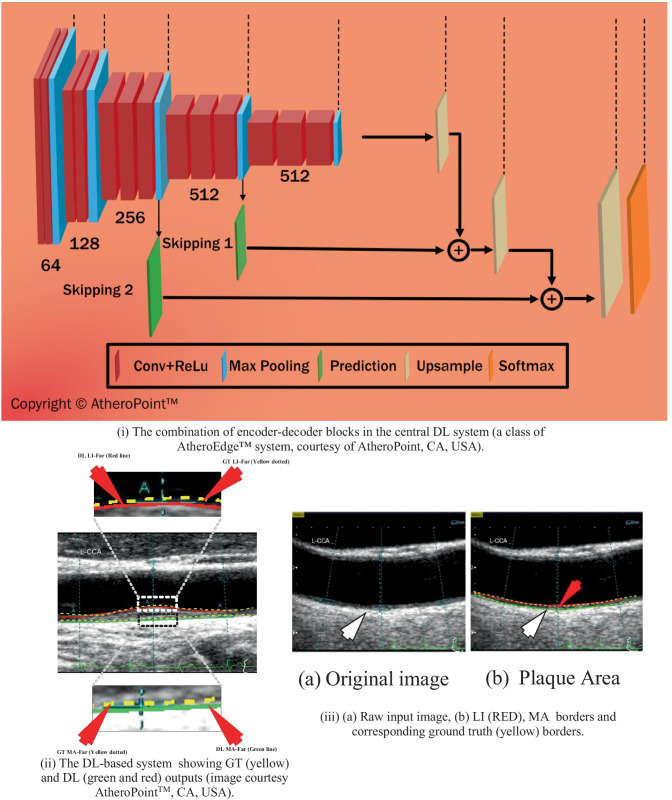
In the work by Biswas et al. [111], the LI and MA borders were extracted in three stages from 396 ultrasound CCA images. The ground truth was binary images obtained from tracings of LI and MA borders by two experienced radiologists using general-purpose tracing software AtheroEdge™ [66, 113, 114]. In the first multiresolution stage, the images were cropped 10% from each side to ensure that the low-contrast and the nonrelevant portion of the images do not affect learning in the second stage. This typically arises due to poor probe-to-neck contact or lack of gel during the image acquisition. In the second stage, FCN was applied to segment the cIMT region from the rest of the image. The FCN-based system consisted of two subsystems: (i) encoder and decoder (shown in Fig. 7 (i)). The encoder consisted of 13 layers of convolution (two layers of 64 (window size = 3 × 3) kernels + two layers of 128 (window size = 3 × 3) kernels + three layers of 256 (window size = 3 × 3) kernels + three layers of 512 (window size = 3 × 3) kernels + three layers of 512 (window size = 3 × 3) kernels), and five max-pooling layers to draw a downsampled representation or feature map of the image. The convolution operation (similar to as discussed in Sect. 3.1 by Rosa et al. [92]) applies kernel filters over the image pixel-by-pixel to extract contextual information and position invariant features of the cIMT wall region. Before every max-pooling operation, a 1 × 1 convolution operation is employed to reduce the feature maps to a single map. The decoder constitutes three upsampling layers to upsample the downsampled feature map, two intermediate skipping operations to merge intermediate feature maps and one softmax layer to make pixel-to-pixel comparison with the ground truth. Mathematically, the convolution operation is given as:
| 8 |
where is the output representation at the location (a,b), is the input image, is the kernel of size , represents the location of the pixel, and are dummy variables. The max-pooling operation is used for the downsampling of the feature map by retaining the most important information from each block of the image. The FCN model applied is shown in Fig. 7 (i). The encoder applies 13 layers of convolution (shown in red boxes), five max-pooling layers (shown in blue boxes) to obtain a feature map of (1/32nd) size of the original image as shown in Fig. 7 (i).The decoder using a series of three up-sampling layers (shown in gray boxes) and intermediate skipping operations (shown in green boxes) to perform dense softmax classification (shown in the orange box) with ground truth for each feature map pixel. The up-sampling operation is the inverse of convolution applied to the feature map at the end of the encoder. Three up-sampling layers were applied to expand the image to its original size. The skipping operations merged features maps from contracting layers of the encoder to the intermediate layers of the decoder to recover spatial information lost during the downsampling in the encoder. The cross-entropy loss function for the pixel-to-pixel characterization is given by:
| 9 |
where is the prediction, is the gold standard or GT, is the total number of classes, and is the total number of images. The softmax layer is used for final characterization where a pixel is assigned a class with the highest probability as given by:
| 10 |
Fig. 7.
(i) FCN model, (ii) IMT output using the FCN [111], and (iii) TPA output using the FCN [103]
where represents the output score of the instance for the ith class. The segmented images were computed by fixing the DL iterations to 20,000. Finally, in the third stage, refinement of MA boundary was done using calibration employing a matrix inverse operation [115]. The LI and MA borders along with their ground truth counterpart are shown in Fig. 7 (ii). The cIMT error obtained for this application using DL on the two ground truth values were and mm, respectively.
FCN for PA Measurement
Elisa et al. [103] used a similar strategy [111] discussed in the “ANN Autoencoder-Based cIMT Region Segmentation” section, to obtain the PA values for the same cohort using the same ground truth and drew important conclusions. The PA error values for the two ground truth values were mm2 and mm2, respectively. The coefficient of correlation between PA and cIMT using the outputs of DL for the two ground truths were and , respectively. The output image is shown in Fig. 7 (iii).
Two-Stage Patching-Based AI Model for cIMT and PA Measurement
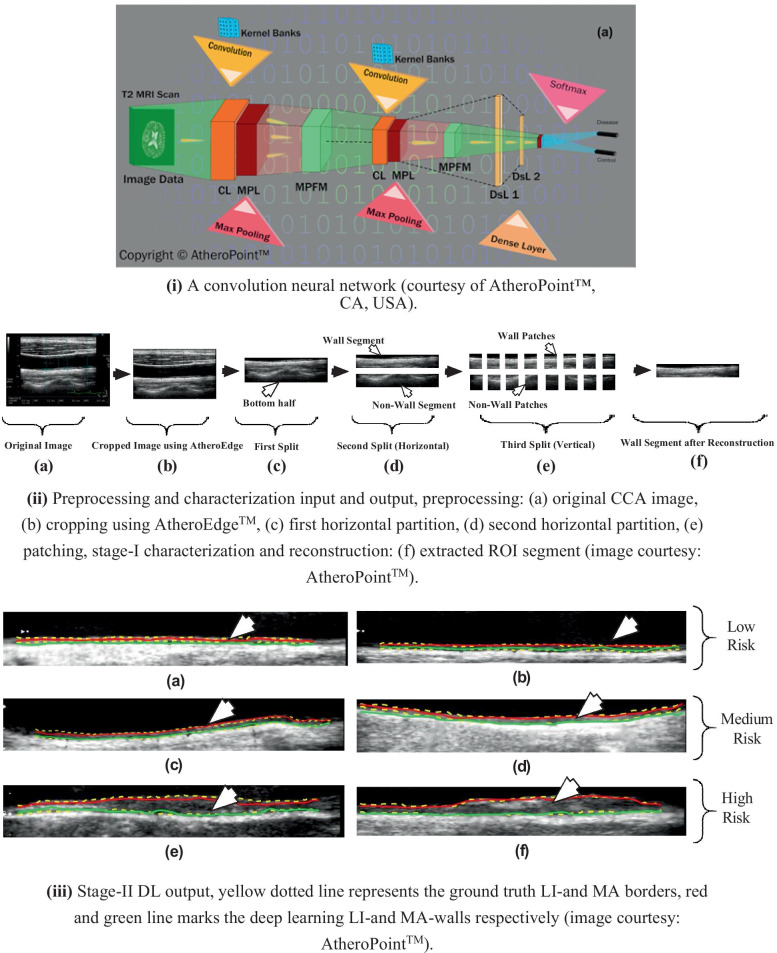
Recently, Biswas et al. [104] used a two-stage DL-based network for cIMT and PA measurement. In the first stage, a CNN was applied for extraction of ROI while in the second stage, an FCN similar to [111] was used for delineation of LI and MA borders and cIMT measurement. CNN is different from FCN in the way that CNN applies a neural network in the form of a fully connected layer for classification, whereas a trained FCN only applies convolution and subsequently upsampling to regenerate a feature map representing semantic segmentation of the actual image. A representative diagram of the 2-layer CNN model is shown in Fig. 8 (i). The softmax classification function (Eq. 12) is used for final characterization for the image. In this work, authors have used 22-deep layers [116] for the extraction of high-level features from the images. Initially, 250 CCA images of the diabetic cohort were collected. A preprocessing was performed using the AtheroEdge™ (AtheroPoint™, Roseville, CA, USA) system to crop the image to remove background information and ensure the lumen region is central to the cropped CCA image. The resultant cropped CCA image is split horizontally into two halves. The bottom half of the image consisting of the far-wall is taken out and further spit horizontally. The upper split in the bottom half consists of wall information whereas the lower split consisted of the tissue region. Both the upper and lower splits are divided column-wise into sixteen equal-sized patches. The patches form the input to the two-stage DL-based system. In the first stage, an independent 22-layered CNN network [116] is applied to characterize the input images into the wall and nonwall patches. The CNN accuracy performance for characterization was approximately 99.5%. Once the patches are characterized, the wall patches are combined patient-wise to generate the ROI segment. The preprocessing and DL stage I inputs and outputs are shown in Fig. 8 (ii). These ROI segments along with their binary ground truths are used to train the second stage DL. The second stage DL architecture is similar to the previous architecture [111]. Once trained, the second stage DL system partitions the ROI segment into plaque and nonplaque regions.
Fig. 8.
(i) A CNN model, (ii) patching and reconstruction process, and (ii) outputs of the two-stage DL model [104]
Thereafter, LI and MA boundaries are delineated from the plaque region, and cIMT and TPA are computed as shown in Fig. 8 (iii). The cIMT error, PA, and PA error was found to be mm, mm2, and mm2, respectively. A similar strategy [112] was applied to the whole CCA images using DenseNet [108] for the whole 331 images with cIMT mean error mm. Although the DL techniques are accurate, robust, and more scalable than ML techniques, the storage and computation costs are much higher. The several layers of neurons mean a huge number of parallel computations that need to take place which may not be possible in desktop CPU architectures but need graphic processor units (GPUs). Also, the storing of intermediate values requires a huge amount of memory space. Therefore, ML is more suited to small systems where faster results are needed and accuracy is not a high priority. DL on the other hand suited for industrial medical imaging purposes where there are large patient volumes and higher accuracy is a requirement.
Discussion
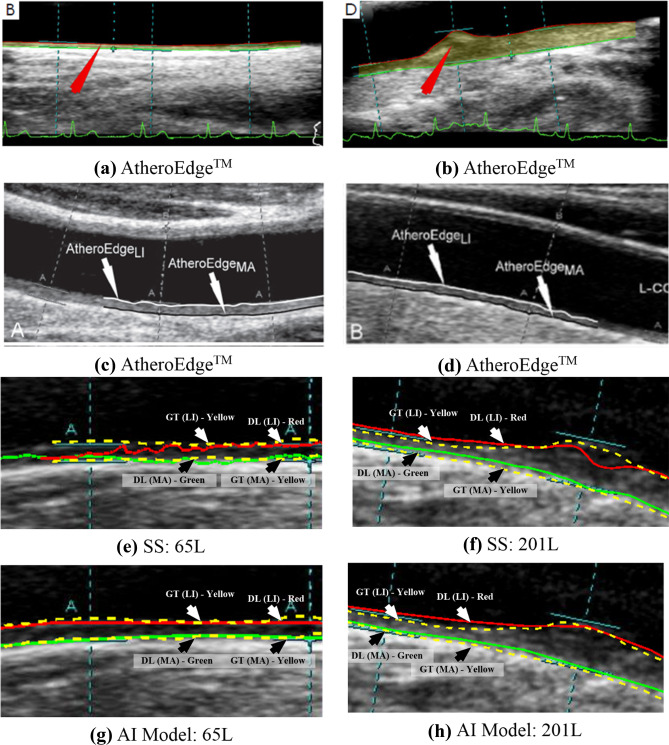
In this study, we have looked at several state-of-art AI techniques implemented in recent years for plaque burden quantification in the form of cIMT and PA using carotid ultrasound images. Although AI is a newer concept, it has a significant impact on the medical imaging industry due to its robustness and accuracy. The ML techniques introduced the notion of learning from training images which have been taken over by DL techniques recently. Even though forthcoming deep learning systems are superior to older stage systems, there is a price to pay on the hardware cost or computational time. We have yet to see more through comparison in terms of speed, accuracy, large cohort, and variability in the resolution of the carotid scans, applied to both CCA and bulb segments. In some works such as application of DL in liver implemented previously, it has been seen that the presence of noise or redundant information can affect the performance of deep learning significantly [117]. Hence, cropping was done to achieve significant performance levels. The training data size also significantly affects the training performance irrespective of the cross-validation protocol. A large training pool is always better for training DL models as it captures wider complexities and intricacies of the data pool. This helps in better performance when applied to unknown data. Further, this review sheds light on three generations of cIMT/PA evolution, followed in-depth analysis on several key ML and DL paradigms that computed cIMT and PA values directly from carotid ultrasound images without any human intervention. Note that since the scope of this study was meant for only static (or frozen) ultrasound scans, there was no attempt to study cIMT/PA in motion imagery. However, studies have been done using conventional (non-AI) methods for cIMT estimation in selected frames of the cardiac cycle for understanding the plaque movement [118–120]. A visual comparison of the AtheroEdge™, a patented software [121, 122], scale-space method [46], and AI-based model (Biswas et al. [111]) is shown in Fig. 9. The AtheroEdge™ model is based on splines and elastic contour and achieved fairly good results, and clear border tracing is achieved. However, it fails around noisy corners. On the other hand, a distinct and clear delineation is achieved by the AI model when compared with the scale-space model. The proposed AI model results are more aligned along the ground truth than the scale-space model for the same patient. The AI model parameters are trained to align along the LI-far and MA-far wall over several iterations leading to better learning. The better training means that the parameters have also included plausible noise around the walls and got around them to delineate correct borders. Low-level segmentation models such as scale-space have failed to include the noisy information in their computation and therefore give a lesser accurate delineation.
Fig. 9.
Comparison of AtheroEdgeTM (a and b [121], c and d [122] (reproduced with permission)), SS (e and f [46]) and AI (g and h) [111] delineation of LI-and MA borders
Benchmarking
The first- and second-generation techniques have been already briefly described by Molinari et al. [123]. In this section, we have presented Table 3 which shows the benchmarking table using first-, second- and third-generation techniques used in the last two decades. The first-generation techniques are discussed first. In the year 2000, Liang et al. [124] used DP to quantify cIMT from 50 images. Both Stein et al. [125] and Faita et al. [126] used edge detection techniques to measure cIMT from 50 and 150 CCA images, respectively, with cIMT error of and , respectively. Ikeda et al. [48] used bulb edge point detection technique to quantify cIMT from 649 images with bias between predicted and ground truth being . A fusion of first- and second-generation techniques are discussed next. Molinari et al. [72] used a combination of level set and morphological image processing to estimate cIMT from 200 images. The cIMT error was found to be mm. A similar fusion based patented techniques were developed by Molinari et al. in form of CARES [127], CAMES [24], CAUDLES [128], and FOAM [129], for cIMT estimation. The cIMT error for each of them were found to be , , , and from 647, 657, 630, and 665 images, respectively. Some of the second-generation techniques that were developed are discussed now. In 2002, Gutierrez et al. [130] developed active contour model for cIMT measurement from 180 images. Molinari et al. [131] developed snakes-based model for cIMT estimation from 200 images. In 2014 again, Molinari et al. [132] developed second-generation CALEX 1.0 model for estimating cIMT from 665 images. The cIMT error for the active contour, snakes, and CALEX 1.0 were , , and , respectively. Among the third-generation AI-based techniques, Rosa et al. [92] used ANN as the ML model for cIMT error from 60 ultrasound CCA images using three metrics, mean, Suri’s polyline, and centerline with average values of mm, mm, and mm, respectively. Further, Rosa et al. [93] used RBNN for cIMT error computation which was mm using the database of 25 CCA images. Molinari et al. [23] used unsupervised FKMC technique for cIMT computation from 200 ultrasound CCA scans. The cIMT error obtained was mm. Rosa et al. [110] further showed the combination of ML (ANN) and DL-autoencoder to compute cIMT from 55 ultrasound images having a mean cIMT error of mm. Biswas et al. [111] used the database of 396 carotid scans and demonstrated the DL paradigm using FCN for cIMT computation by taking ground truth taken from two different observers. The cIMT error when considering the two ground-truth was mm and mm, respectively. Elisa et al. [103] used the same FCN technique and obtained TPA of mm2 and mm2, respectively, using the two sets of ground truths. Biswas et al. [104] further again showed the usage of a two-stage (CNN + FCN) DL system to compute cIMT from 250 ultrasound CCA images. The authors used a patching-based approach to extract ROI from the first stage and delineate the LI and MA border in the second stage. The cIMT error was mm. The patch-based method was a unique solution in the sense that both stages were DL stages. In another study by Del Mar et al. [112], FCN was applied on 331 carotid ultrasound scans with a cumulative cIMT error of mm.
Table 3.
Benchmarking table showing ML/DL methods for cIMT/PA measurements
| SN | Gen | Author (year) | Method | Cross-validation protocol | Data size | cIMT/PA error | Performance (cIMT error and PA errors) |
|---|---|---|---|---|---|---|---|
| 1 | First | Liang et al. [124] (2000) | Dynamic programming | NA | 50 | cIMT | |
| 2 | Stein et al. [125] (2005) | Edge-detection | NA | 50 | cIMT | ||
| 3 | Faita et al. [126] (2008) | Edge-detection | NA | 150 | cIMT | ||
| 4 | Ikeda et al. [48] (2017) | BEP* detection | NA | 649 | cIMT | ||
| 5 | First + second | Molinari et al. [72] (2012) | Level set, morphological image processing | NA | 200 | cIMT | |
| 6 | Molinari et al. [127] (2011) | CARES | NA | 647 | cIMT | ||
| 7 | Molinari et al. [24] (2011) | CAMES 1.0 | NA | 657 | cIMT | ||
| 8 | Molinari et al. [128] (2011) | CAUDLES | NA | 630 | cIMT | ||
| 9 | Molinari et al. [129] (2011) | FOAM | NA | 665 | cIMT | ||
| 10 | Second | Gutierrez et al. [130] (2002) | Active contours | NA | 180 | cIMT | |
| 11 | Molinari et al. [131] (2009) | Snakes | NA | 200 | cIMT | ||
| 12 | Molinari et al. [132] (2014) | CALEX 1.0 | NA | 665 | cIMT | ||
| 13 | Third | Rosa et al. [92] (2013) | ANN | 60% training, 40% testing | 60 | cIMT |
mm (mean) mm (polyline) mm (center) |
| 14 | Rosa et al. [93] (2014) | RBNN | Jackknifing (Leave one out) | 25 | cIMT | mm | |
| 15 | Molinari et al. [23] (2010) | FKMC | K13 (92% training, 8% testing) | 200 | cIMT | mm (polyline) | |
| 16 | Rosa et al. [110] (2015) | ANN + autoencoder | K2 (50% Training, 50% Testing) | 55 | cIMT | mm | |
| 17 | Biswas et al. [111] (2018) | FCN | K10 (90% training, 10% testing) | 396 | cIMT |
mm (DL1) mm (DL2) |
|
| 18 | Elisa et al. [103] (2018) | FCN | K10 (90% training, 10% testing) | 396 | TPA |
mm2 (DL1) mm2 (DL2) |
|
| 19 | Biswas et al. [104] (2020) | CNN + FCN | K10 (90% training, 10% testing) | 250 | cIMT, TPA value, TPA | mm (cIMT error), mm2 (DL-TPA), mm2 (PA error) | |
| 20 | Del Mar et al. [112] 2020 | FCN | K10 (90% training, 10% testing) | 331 | cIMT error | mm |
In further reading, short notes on cardiovascular risk assessment, clinical impacts of AI on cIMT/PA techniques, inter- and intra-observer variability analysis, 10-year risk assessment, statistical power analysis and diagnostic odds ratio, and graphical processing units is given in Appendix 2.
Conclusions
The paper presented three generations for cIMT/PA measurement systems starting from conventional methods to intelligence-based methods using the machine and deep learning methods. The key reason for this wave is the ability to do the deeper number crunching to derive sophisticated information leading to better accuracy, reliability, and stability of the systems. The improved results also show that there is significant clinical viability of the systems. Deep learning powered by GPU has significantly impacted medical imaging ushering new horizons in automated diagnosis and treatment.
Appendix 1 Mathematical Representations of ML and DL Paradigms
The usage of the term learnability denotes the ability of computational models to discover patterns from unstructured data, infer logical constructs, and make decisions. Learning models, both ML and DL, have been thoroughly used in medical imaging to make life-saving decisions [82, 151–153]. In this review, we will delve deeper into ML and DL paradigms for carotid imaging and gauge the similarities and differences between them. Also, from this point onward, the first and second techniques for plaque segmentation will be referred to as conventional models. The third-generation techniques, ML, and DL will be addressed independently, which is the main focus of this study. A general discourse on ML is given in the next subsection.
Machine Learning: A Mathematical Representation
A mathematical approach to the concept of ML is as follows [154, 155]: if the instance space is denoted as and the label/class space is denoted by , then characterization job can be denoted by mapping of the function , where is an estimate of the true function , and, denotes the true class of an instance . The difference between the estimated version of the true function and the true function is used as a feedback to fine-tune the ML model to converge towards the correct output. The least-square (LS) method is the most common tool to compute the difference between the desired and actual output which is expressed mathematically as:
| 11 |
where is the output of the ML model is the input of the ML model. Different variations of error or loss-functions are employed in other AI paradigm. There are different variations of this form of learning, i.e., probability estimation, where the approximate function outputs a probability estimation over classes for any instance, i.e., . Regression is another learning job, where and where, , and , is an approximation function mapping from to . The instances are defined by their attributes or features. Therefore, the attribute space can be defined as a mapping of function from , i.e., from instance space to attribute domain . In other words, the instance space can be defined as the Cartesian product of attribute domains . In the case of ML, the features are needed to be extracted separately from the instances. The features are generally statistical information that can be categorized as quantitative, ordinal, and categorical. Since we are mainly dealing with different imaging modalities, features are generally quantitative. Some of the features extracted in general from these images deal with orientation, direction, scale, and texture, etc. ML models that estimate the function can be geometric, probabilistic, or logical. Geometric models are built directly in instance space using geometric concepts of lines, planes, and distances. These models work by drawing a hyperplane between two classes, i.e., K-nearest neighbors [156], support vector machines (SVMs) [157], artificial neural networks (ANNs) [158], etc. Probabilistic models take into consideration most likelihood of an instance belonging to a class by computing maximum posterior probability e.g., Bayesian classifier [159]. Logical models compute the likelihood of a class by developing a series of rules based on logical operations, i.e., decision trees [160]. The training and testing of ML as well as DL models (described in the next section) follow the same pattern except for the feature extraction part which is the same as the learning paradigm of the latter. Initially, the given model is trained using offline labeled data. Once trained, the ML model is tested on an unknown online data to test its performance. An illustration of training and testing is shown in Fig. 3 (i).
Deep Learning: A Mathematical Representation
Deep learning models draw their inspiration from the working of brain neural networks. Unlike ML, deep learning models generate feature space directly from instance space, without the requirement of third-party feature extraction algorithms. These features can be said to be a downsampled representation of the original instances. The feature space, also called as representation space for DL techniques, is generated by using many layers of similar kernel functions, resulting in dimensionality reduction of the original instance space to the desired dimensionality of feature space which is given as follows:
| 12 |
where, , , and are different kernels applied repeatedly on the instance . is the desired feature vector obtained after applications of , and . Therefore, the least square model (Eq. 11) can be used to backpropagate [161] the error within the network to fine-tune the DL model. Convolution neural networks (CNNs) [84] and fully convolutional networks (FCNs) [109] are the most common deep supervised learning models used widely in the characterization of carotid plaque and segmentation of the cIMT region. These networks apply a series of convolution and pooling operations to extract features from plaque images and characterize/segment them.
There is another form of learning in which outputs are not available and called unsupervised learning [162]. The unsupervised learning models try to find out interesting relationships within the input data to show important properties. K-means clustering [163] and autoencoders [107] are important ML and DL unsupervised learning algorithms, respectively. This review briefly describes all the models used in cIMT and PA measurement.
JS Suri, D Kumar, Medical image enhancement system, US Patent App. 11/609,743
Appendix 2 Mathematical Representations of ML and DL Paradigms
A Short Note on Cardiovascular Risk Assessment
The cardiovascular risk assessment or stratification using intelligence paradigms such as ML and DL can help in both monitoring the CVD risk. Many studies have shown a strong association between covariates such as blood biomarkers, and conventional risk factors like age, grayscale median values, and stroke risk [20, 79, 89, 133]. In addition to blood biomarkers, behavioral patterns such as smoking, diets, and other image-based phenotypes such as cIMT, and PA values can be combined to enhance stroke risk assessment.
A note on Clinical Impact of AI Methods on cIMT/PA Techniques
Note that DL has just started to penetrate in the vascular area, especially vascular ultrasound. The prototypes have been attempted recently and our group has been leading this field. While we are able to undergo the designs, these designs have not passed the stage of its application to clinical world, unlike our non-AI-based models which are already in clinical practice (see AtheroEdge™ 2.0, AtheroPoint™, Roseville, CA, USA [79, 89, 133–136]). We however believe, as time progresses, we will see more applications of TL/DL/RL will reach the clinical world where diagnostic ultrasound community would start using this. Some of the scientific validation can be accomplished by matching the plaque regional information between cross modalities using registration methods [137].
A Note on Inter- and Intra-Observer Variability Analysis on Evaluation of AI Models
Inter- and intra-observer variability is certainly an important consideration during the performance evaluation of the cIMT/PA systems. Our group has attempted the variability analysis on cIMT and other applications [138–140] using AtheroEdge™ 1.0 and 2.0 systems. Recently, Biswas et al. [141] showed the effect of inter-observer variability using deep learning systems. The authors demonstrated inter-operator variability of the DL system using three set of manual tracings on 407 ultrasound scans for lumen boundary detection and performance evaluation. Each DL system was trained using the manual tracings, which underwent cross-validation runs for training and testing protocol. Using the Suri’s polyline distance metric, the precision of merit for three DL systems over 407 US scans was 99.61%, 97.75%, and 99.89%, respectively. The Jaccard index of the DL lumen segmented region against three ground truth (GT) regions were 0.94, 0.94, and 0.93, while the Dice similarity was 0.97, 0.97, and 0.97, respectively. The corresponding AUC for three DL systems was 0.95, 0.91, and 0.93. This DL system demonstrated superior performance of proposed DL system over conventional methods in literature. In another recent DL method using patch-based technique [142], the authors did the variability analysis using two manual tracings taken from two vascular radiologists. The authors showed that the absolute cIMT error of their AI-based system was (i.e., 20% lesser than the earlier method [111]) using GT1 (i.e., ) and 18% lesser using GT2 (i.e., ), respectively. As part of performance evaluation of the system such as reliability, the authors in [48, 131] attempted studying the effect of ultrasound scanners on the performance of cIMT.
A Short Note on 10-year Risk Stimation Using cIMT and PA
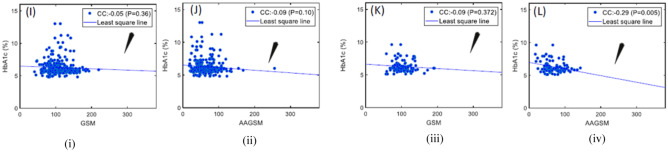
Many studies have shown that cIMT and PA values are linked with diabetes and cardiovascular risks [79]. Different risk measures and calculators have been developed to compute the 10-year risks. A new measure, age-adjusted grayscale median (AAGSM) [28], has been developed as a function of age, PA, and conventional GSM. An association of HbA1c, AAGSM, and GSM is shown in Fig. 10 which illustrated low CC: between HbA1c (male) and GSM, low CC: between HbA1c (male) and AAGSM, low CC: between HbA1c (female) and GSM, high CC: − 0 between HbA1c (female) and AAGSM. These relationships were instrumental in stratifying diabetes patients into low, medium, and high-risk groups.
Fig. 10.
(i) GSM vs. HbA1c for male; (ii) AAGSM vs. HbA1c for male; (iii) GSM vs. HbA1c for female and (iv) AAGSM vs. HbA1c for female (image courtesy AtheroPoint™)
In another study, cIMT [134] has been used to calculate the risk of diabetic cohorts using logistic regression. Another risk score “AtheroEdge Composite Risk Score 1.0” (AECRS1.010 yr) [89] computed the 10-year risk of carotid image phenotypes by integrating conventional cardiovascular risk factors and reported the highest area-under-the-curve of 0.927.
Statistical Power Analysis and Diagnostic Odds Ratio
Statistical power analysis is performed to validate sample size for training. If z* is the standardized value taken from the z-table, is the data proportion, and MoE is the margin of error, then the number of samples (n) required is computed as . This is used with a 95% confidence interval with a 5% margin of error and 0.5 data proportion. In some recent AI studies, power analysis was performed for training data size validation [143–145]. The diagnostic odds ratio (DOR) [146] presents a meta-analysis of the diagnosis. The DOR is given by:
| 13 |
where and refers to the sensitivity and specificity of the study, respectively. Another popular tool to understand the power of the diagnostic tool is to know the reduction rate of type II error (false negative) [147]. If refers to a false negative rate, then refers to the power of the study.
A Short Note on Graphical Processing Units
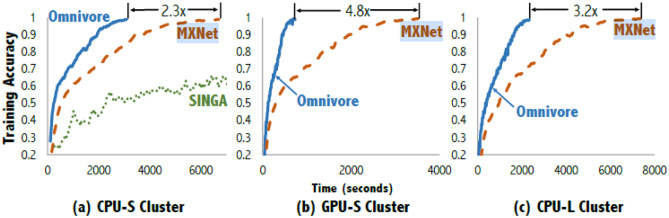
The AI growth is powered by the availability of graphical processing units (GPUs). As experienced by our group, the AI usually involves millions of complex computations which if performed sequentially in multicore CPUs that take large time (sometimes even several hours) to converge. In contrast, GPUs break the complex problems into thousands of simple problems to be divided among its thousands of cores to solve them in parallel and combine them at once. Hence, convergence is much faster in GPUs compared to CPUs. In a comparative analysis [148] of ImageNet8 [84] implementation by different deep learning libraries such as MXNet [149], SINGA [150], Omnivore [148] on CPU-S (nine cores), CPU-L (33 cores), and GPU-S (36 GPUs) cluster systems, the GPU-S converged faster than the CPU-S and CPU-L for both.
Omnivore and MXNet. Among the libraries, Omnivore performed best (2.3X-CPU-S, 4.8X-GPU-S, 3.2X-CPU-L) while the SINGA library performed worst, and was not implemented in CPU-L and GPU-S. The comparison graph is shown in Fig.11
Fig. 11.
ImageNet implementation using different libraries on CPU-S, GPU-S, and CPU-L cluster (reproduced with permission[148])
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Benjamin EJ, Muntner P, Bittencourt MS. Heart disease and stroke statistics-2019 update: a report from the American Heart Association. Circulation. 2019;139(10):e56–e528. doi: 10.1161/CIR.0000000000000659. [DOI] [PubMed] [Google Scholar]
- 2.Benjamin EJ, Virani SS, Callaway CW, Chamberlain AM, Chang AR, Cheng S, Chiuve SE, Cushman M, Delling FN, Deo R: Heart disease and stroke statistics—2018 update: a report from the American Heart Association. Circulation 2018. [DOI] [PubMed]
- 3.Ross R. Atherosclerosis—an inflammatory disease. New England journal of medicine. 1999;340(2):115–126. doi: 10.1056/NEJM199901143400207. [DOI] [PubMed] [Google Scholar]
- 4.Suri JS, Kathuria C, Molinari F: Atherosclerosis disease management: Springer Science & Business Media; 2010.
- 5.Saba L, Sanches JM, Pedro LM, Suri JS: Multi-modality atherosclerosis imaging and diagnosis: Springer; 2014.
- 6.Libby P: The heart in COVID19: primary target or secondary bystander? JACC: Basic to Translational Science 2020. [DOI] [PMC free article] [PubMed]
- 7.Basta G, Schmidt AM, De Caterina R. Advanced glycation end products and vascular inflammation: implications for accelerated atherosclerosis in diabetes. Cardiovascular research. 2004;63(4):582–592. doi: 10.1016/j.cardiores.2004.05.001. [DOI] [PubMed] [Google Scholar]
- 8.Colwell JA, Lopes-Virella M, Halushka PV. Pathogenesis of atherosclerosis in diabetes mellitus. Diabetes care. 1981;4(1):121–133. doi: 10.2337/diacare.4.1.121. [DOI] [PubMed] [Google Scholar]
- 9.Saam T, Yuan C, Chu B, Takaya N, Underhill H, Cai J, Tran N, Polissar NL, Neradilek B, Jarvik GP. Predictors of carotid atherosclerotic plaque progression as measured by noninvasive magnetic resonance imaging. Atherosclerosis. 2007;194(2):e34–e42. doi: 10.1016/j.atherosclerosis.2006.08.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hashimoto H, Tagaya M, Niki H, Etani H. Computer-assisted analysis of heterogeneity on B-mode imaging predicts instability of asymptomatic carotid plaque. Cerebrovascular diseases. 2009;28(4):357–364. doi: 10.1159/000229554. [DOI] [PubMed] [Google Scholar]
- 11.Ross R, Glomset JA. The pathogenesis of atherosclerosis. New England journal of medicine. 1976;295(7):369–377. doi: 10.1056/NEJM197608122950707. [DOI] [PubMed] [Google Scholar]
- 12.Ross R. The pathogenesis of atherosclerosis—an update. New England Journal of Medicine. 1986;314(8):488–500. doi: 10.1056/NEJM198602203140806. [DOI] [PubMed] [Google Scholar]
- 13.Carr S, Farb A, Pearce WH, Virmani R, Yao JS. Atherosclerotic plaque rupture in symptomatic carotid artery stenosis. Journal of vascular surgery. 1996;23(5):755–766. doi: 10.1016/S0741-5214(96)70237-9. [DOI] [PubMed] [Google Scholar]
- 14.Iadecola C: Revisiting atherosclerosis and dementia. Nature Neuroscience 2020:1–2. [DOI] [PMC free article] [PubMed]
- 15.Lucatelli P, Raz E, Saba L, Argiolas GM, Montisci R, Wintermark M, King KS, Molinari F, Ikeda N, Siotto P. Relationship between leukoaraiosis, carotid intima-media thickness and intima-media thickness variability: Preliminary results. European radiology. 2016;26(12):4423–4431. doi: 10.1007/s00330-016-4296-4. [DOI] [PubMed] [Google Scholar]
- 16.Saba L, Sanfilippo R, Balestrieri A, Zaccagna F, Argiolas GM, Suri JS, Montisci R. Relationship between Carotid Computed Tomography Dual-Energy and Brain Leukoaraiosis. Journal of Stroke and Cerebrovascular Diseases. 2017;26(8):1824–1830. doi: 10.1016/j.jstrokecerebrovasdis.2017.04.016. [DOI] [PubMed] [Google Scholar]
- 17.Wingo AP, Fan W, Duong DM, Gerasimov ES, Dammer EB, Liu Y, Harerimana NV, White B, Thambisetty M, Troncoso JC: Shared proteomic effects of cerebral atherosclerosis and Alzheimer’s disease on the human brain. Nature Neuroscience 2020:1–5. [DOI] [PMC free article] [PubMed]
- 18.Viswanathan V, Jamthikar AD, Gupta D, Puvvula A, Khanna NN, Saba L, Viskovic K, Mavrogeni S, Turk M, Laird JR: Integration of eGFR biomarker in image-based CV/Stroke risk calculator: a south Asian-Indian diabetes cohort with moderate chronic kidney disease. International Angiology: a Journal of the International Union of Angiology 2020. [DOI] [PubMed]
- 19.Puvvula A, Jamthikar AD, Gupta D, Khanna NN, Porcu M, Saba L, Viskovic K, Ajuluchukwu JN, Gupta A, Mavrogeni S: Morphological Carotid Plaque Area Is Associated With Glomerular Filtration Rate: A Study of South Asian Indian Patients With Diabetes and Chronic Kidney Disease. Angiology 2020:0003319720910660. [DOI] [PubMed]
- 20.Khanna NN, Jamthikar AD, Gupta D, Piga M, Saba L, Carcassi C, Giannopoulos AA, Nicolaides A, Laird JR, Suri HS. Rheumatoid arthritis: atherosclerosis imaging and cardiovascular risk assessment using machine and deep learning–based tissue characterization. Current atherosclerosis reports. 2019;21(2):7. doi: 10.1007/s11883-019-0766-x. [DOI] [PubMed] [Google Scholar]
- 21.Boi A, Jamthikar AD, Saba L, Gupta D, Sharma A, Loi B, Laird JR, Khanna NN, Suri JS. A survey on coronary atherosclerotic plaque tissue characterization in intravascular optical coherence tomography. Current atherosclerosis reports. 2018;20(7):33. doi: 10.1007/s11883-018-0736-8. [DOI] [PubMed] [Google Scholar]
- 22.Liu K, Suri JS: Automatic vessel indentification for angiographic screening. In.: Google Patents; 2005.
- 23.Molinari F, Zeng G, Suri JS. Intima-media thickness: setting a standard for a completely automated method of ultrasound measurement. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2010;57(5):1112–1124. doi: 10.1109/TUFFC.2010.1522. [DOI] [PubMed] [Google Scholar]
- 24.Molinari F, Pattichis CS, Zeng G, Saba L, Acharya UR, Sanfilippo R, Nicolaides A, Suri JS. Completely automated multiresolution edge snapper—a new technique for an accurate carotid ultrasound IMT measurement: clinical validation and benchmarking on a multi-institutional database. IEEE Transactions on image processing. 2011;21(3):1211–1222. doi: 10.1109/TIP.2011.2169270. [DOI] [PubMed] [Google Scholar]
- 25.Herder M, Johnsen SH, Arntzen KA, Mathiesen EB. Risk factors for progression of carotid intima-media thickness and total plaque area: a 13-year follow-up study: the Tromsø Study. Stroke. 2012;43(7):1818–1823. doi: 10.1161/STROKEAHA.111.646596. [DOI] [PubMed] [Google Scholar]
- 26.Moreno PR, Falk E, Palacios IF, Newell JB, Fuster V, Fallon JT. Macrophage infiltration in acute coronary syndromes. Implications for plaque rupture. Circulation. 1994;90(2):775–778. doi: 10.1161/01.cir.90.2.775. [DOI] [PubMed] [Google Scholar]
- 27.Cuadrado-Godia E, Maniruzzaman M, Araki T, Puvvula A, Rahman MJ, Saba L, Suri HS, Gupta A, Banchhor SK, Teji JS. Morphologic TPA (mTPA) and composite risk score for moderate carotid atherosclerotic plaque is strongly associated with HbA1c in diabetes cohort. Computers in biology and medicine. 2018;101:128–145. doi: 10.1016/j.compbiomed.2018.08.008. [DOI] [PubMed] [Google Scholar]
- 28.Kotsis V, Jamthikar AD, Araki T, Gupta D, Laird JR, Giannopoulos AA, Saba L, Suri HS, Mavrogeni S, Kitas GD. Echolucency-based phenotype in carotid atherosclerosis disease for risk stratification of diabetes patients. Diabetes research and clinical practice. 2018;143:322–331. doi: 10.1016/j.diabres.2018.07.028. [DOI] [PubMed] [Google Scholar]
- 29.Saba L, Banchhor SK, Londhe ND, Araki T, Laird JR, Gupta A, Nicolaides A, Suri JS. Web-based accurate measurements of carotid lumen diameter and stenosis severity: an ultrasound-based clinical tool for stroke risk assessment during multicenter clinical trials. Computers in Biology and Medicine. 2017;91:306–317. doi: 10.1016/j.compbiomed.2017.10.022. [DOI] [PubMed] [Google Scholar]
- 30.Baradaran H, Ng CR, Gupta A, Noor NM, Al-Dasuqi KW, Mtui EE, Rijal OM, Giannopoulos A, Nicolaides A, Laird JR. Extracranial internal carotid artery calcium volume measurement using computer tomography. International angiology: a journal of the International Union of Angiology. 2017;36(5):445–461. doi: 10.23736/S0392-9590.17.03811-1. [DOI] [PubMed] [Google Scholar]
- 31.Saba L, Than JC, Noor NM, Rijal OM, Kassim RM, Yunus A, Ng CR, Suri JS. Inter-observer variability analysis of automatic lung delineation in normal and disease patients. Journal of medical systems. 2016;40(6):142. doi: 10.1007/s10916-016-0504-7. [DOI] [PubMed] [Google Scholar]
- 32.Saba L, Bhavsar A, Gupta A, Mtui E, Giambrone A, Baradaran H, Lavra F, Laird J, Nicolaides A, Suri J. Automated calcium burden measurement in internal carotid artery plaque with CT: a hierarchical adaptive approach. International angiology: a journal of the International Union of Angiology. 2015;34(3):290–305. [PubMed] [Google Scholar]
- 33.Lloyd-Jones DM, Wilson PW, Larson MG, Beiser A, Leip EP, D'Agostino RB, Levy D. Framingham risk score and prediction of lifetime risk for coronary heart disease. The American journal of cardiology. 2004;94(1):20–24. doi: 10.1016/j.amjcard.2004.03.023. [DOI] [PubMed] [Google Scholar]
- 34.Preiss D, Kristensen SL. The new pooled cohort equations risk calculator. Canadian journal of Cardiology. 2015;31(5):613–619. doi: 10.1016/j.cjca.2015.02.001. [DOI] [PubMed] [Google Scholar]
- 35.Ridker PM, Buring JE, Rifai N, Cook NR. Development and validation of improved algorithms for the assessment of global cardiovascular risk in women: the Reynolds Risk Score. Jama. 2007;297(6):611–619. doi: 10.1001/jama.297.6.611. [DOI] [PubMed] [Google Scholar]
- 36.Stevens RJ, Kothari V, Adler AI, Stratton IM, Holman RR. Group UKPDS: The UKPDS risk engine: a model for the risk of coronary heart disease in Type II diabetes (UKPDS 56) Clinical science. 2001;101(6):671–679. doi: 10.1042/CS20000335. [DOI] [PubMed] [Google Scholar]
- 37.Kothari V, Stevens RJ, Adler AI, Stratton IM, Manley SE, Neil HA, Holman RR. UKPDS 60: risk of stroke in type 2 diabetes estimated by the UK Prospective Diabetes Study risk engine. Stroke. 2002;33(7):1776–1781. doi: 10.1161/01.STR.0000020091.07144.C7. [DOI] [PubMed] [Google Scholar]
- 38.Tillin T, Hughes AD, Whincup P, Mayet J, Sattar N, McKeigue PM, Chaturvedi N, Group SS Ethnicity and prediction of cardiovascular disease: performance of QRISK2 and Framingham scores in a UK tri-ethnic prospective cohort study (SABRE—Southall And Brent REvisited) Heart. 2014;100(1):60–67. doi: 10.1136/heartjnl-2013-304474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Board JBS: Joint British Societies’ consensus recommendations for the prevention of cardiovascular disease (JBS3). Heart 2014, 100(Suppl 2):ii1-ii67. [DOI] [PubMed]
- 40.Seabra J, Sanches J: Ultrasound Imaging: Advances and Applications. In.: New York: Springer; 2012.
- 41.Suri JS, Laxminarayan S: Angiography and plaque imaging: advanced segmentation techniques: CRC press; 2003.
- 42.Molinari F, M. Meiburger K, Zeng G, Acharya UR, Liboni W, Nicolaides A, Suri JS: Carotid artery recognition system: a comparison of three automated paradigms for ultrasound images. Medical physics 2012, 39(1):378–391. [DOI] [PubMed]
- 43.Molinari F, Meiburger KM, Acharya UR, Zeng G, Rodrigues PS, Saba L, Nicolaides A, Suri JS: CARES 3.0: a two stage system combining feature-based recognition and edge-based segmentation for CIMT measurement on a multi-institutional ultrasound database of 300 images. In: 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society: 2011. IEEE: 5149–5152. [DOI] [PubMed]
- 44.Wendelhag I, Liang Q, Gustavsson T, Wikstrand J. A new automated computerized analyzing system simplifies readings and reduces the variability in ultrasound measurement of intima-media thickness. Stroke. 1997;28(11):2195–2200. doi: 10.1161/01.STR.28.11.2195. [DOI] [PubMed] [Google Scholar]
- 45.Cheng D-c. Schmidt-Trucksäss A, Cheng K-s, Burkhardt H: Using snakes to detect the intimal and adventitial layers of the common carotid artery wall in sonographic images. Computer methods and programs in biomedicine. 2002;67(1):27–37. doi: 10.1016/S0169-2607(00)00149-8. [DOI] [PubMed] [Google Scholar]
- 46.Kumar PK, Araki T, Rajan J, Saba L, Lavra F, Ikeda N, Sharma AM, Shafique S, Nicolaides A, Laird JR. Accurate lumen diameter measurement in curved vessels in carotid ultrasound: an iterative scale-space and spatial transformation approach. Medical & biological engineering & computing. 2017;55(8):1415–1434. doi: 10.1007/s11517-016-1601-y. [DOI] [PubMed] [Google Scholar]
- 47.Ikeda N, Gupta A, Dey N, Bose S, Shafique S, Arak T, Godia EC, Saba L, Laird JR, Nicolaides AJUim et al: Improved correlation between carotid and coronary atherosclerosis SYNTAX score using automated ultrasound carotid bulb plaque IMT measurement. 2015, 41(5):1247–1262. [DOI] [PubMed]
- 48.Ikeda N, Dey N, Sharma A, Gupta A, Bose S, Acharjee S, Shafique S, Cuadrado-Godia E, Araki T, Saba L. Automated segmental-IMT measurement in thin/thick plaque with bulb presence in carotid ultrasound from multiple scanners: Stroke risk assessment. Computer methods and programs in biomedicine. 2017;141:73–81. doi: 10.1016/j.cmpb.2017.01.009. [DOI] [PubMed] [Google Scholar]
- 49.Han J, Pei J, Kamber M: Data mining: concepts and techniques: Elsevier; 2011.
- 50.LeCun Y. Bengio Y. Hinton G: Deep learning. nature. 2015;521(7553):436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 51.Eggleston HG. A property of Hausdorff measure. Duke Mathematical Journal. 1950;17(4):491–498. doi: 10.1215/S0012-7094-50-01743-1. [DOI] [Google Scholar]
- 52.Saba L, Molinari F, Meiburger K, Piga M, Zeng G, Rajendra UA, Nicolaides A, Suri J. What is the correct distance measurement metric when measuring carotid ultrasound intima-media thickness automatically? International angiology: a journal of the International Union of Angiology. 2012;31(5):483–489. [PubMed] [Google Scholar]
- 53.Bartels S, Franco AR, Rundek T. Carotid intima-media thickness (cIMT) and plaque from risk assessment and clinical use to genetic discoveries. Perspectives in Medicine. 2012;1(1–12):139–145. doi: 10.1016/j.permed.2012.01.006. [DOI] [Google Scholar]
- 54.Gustavsson T, Liang Q, Wendelhag I, Wikstrand J: A dynamic programming procedure for automated ultrasonic measurement of the carotid artery. In: Computers in Cardiology 1994: 1994. IEEE: 297–300.
- 55.Ballard DH: Generalizing the Hough transform to detect arbitrary shapes. In: Readings in computer vision. Elsevier; 1987: 714–725.
- 56.Destrempes F, Meunier J, Giroux M-F, Soulez G, Cloutier G. Segmentation of plaques in sequences of ultrasonic B-mode images of carotid arteries based on motion estimation and a Bayesian model. IEEE Transactions on Biomedical Engineering. 2011;58(8):2202–2211. doi: 10.1109/TBME.2011.2127476. [DOI] [PubMed] [Google Scholar]
- 57.Giraldi G, Rodrigues P, Suri J, Singh S: Dual active contour models for medical image segmentation. Image Segmentation 2011:129.
- 58.Suri JS, Haralick RM, Sheehan F, Jamin V: Effect of edge detection, pixel classification, and classification-edge fusion over LV calibration: A two stage automatic system. In: SCIA'97: 10th Scandinavian conference on image analysis (Lappeeranta, June 9–11, 1997): 1997. 197–204.
- 59.Hill PR, Canagarajah CN, Bull DR. Image segmentation using a texture gradient based watershed transform. IEEE Transactions on Image Processing. 2003;12(12):1618–1633. doi: 10.1109/TIP.2003.819311. [DOI] [PubMed] [Google Scholar]
- 60.El-Baz A, Suri JS: Lung imaging and computer aided diagnosis: CRC Press; 2011.
- 61.Radeva P, Suri JS: Vascular and Intravascular Imaging Trends, Analysis, and Challenges, Volume 2; Plaque characterization. vii2 2019.
- 62.Molinari F, Zeng G, Suri JS: Carotid wall segmentation and IMT measurement in longitudinal ultrasound images using morphological approach. In: International symposium on biomedical imaging, Rotterdam: 2010.
- 63.Molinari F, Meiburger KM, Saba L, Acharya UR, Ledda G, Zeng G, Ho SYS, Ahuja AT, Ho SC, Nicolaides A. Ultrasound IMT measurement on a multi-ethnic and multi-institutional database: our review and experience using four fully automated and one semi-automated methods. Computer methods and programs in biomedicine. 2012;108(3):946–960. doi: 10.1016/j.cmpb.2012.05.008. [DOI] [PubMed] [Google Scholar]
- 64.Patel AK, Suri HS, Singh J, Kumar D, Shafique S, Nicolaides A, Jain SK, Saba L, Gupta A, Laird JR. A review on atherosclerotic biology, wall stiffness, physics of elasticity, and its ultrasound-based measurement. Current atherosclerosis reports. 2016;18(12):83. doi: 10.1007/s11883-016-0635-9. [DOI] [PubMed] [Google Scholar]
- 65.Kumar PK, Araki T, Rajan J, Laird JR, Nicolaides A, Suri JS. State-of-the-art review on automated lumen and adventitial border delineation and its measurements in carotid ultrasound. Computer methods and programs in biomedicine. 2018;163:155–168. doi: 10.1016/j.cmpb.2018.05.015. [DOI] [PubMed] [Google Scholar]
- 66.Molinari F, Meiburger KM, Suri J: Automated high-performance cIMT measurement techniques using patented AtheroEdge™: A screening and home monitoring system. In: 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society: 2011. IEEE: 6651–6654. [DOI] [PubMed]
- 67.Golemati S, Stoitsis J, Sifakis EG, Balkizas T, Nikita KS. Using the Hough transform to segment ultrasound images of longitudinal and transverse sections of the carotid artery. Ultrasound in medicine & biology. 2007;33(12):1918–1932. doi: 10.1016/j.ultrasmedbio.2007.05.021. [DOI] [PubMed] [Google Scholar]
- 68.Stoitsis J, Golemati S, Kendros S, Nikita K: Automated detection of the carotid artery wall in B-mode ultrasound images using active contours initialized by the Hough transform. In: 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society: 2008. IEEE: 3146–3149. [DOI] [PubMed]
- 69.Petroudi S, Loizou CP, Pattichis CS: Atherosclerotic carotid wall segmentation in ultrasound images using Markov random fields. In: Proceedings of the 10th IEEE International Conference on Information Technology and Applications in Biomedicine: 2010. IEEE: 1–5.
- 70.Suri JS, Liu K, Reden L, Laxminarayan S. A review on MR vascular image processing algorithms: acquisition and prefiltering: part I. IEEE transactions on information technology in biomedicine: a publication of the IEEE Engineering in Medicine and Biology Society. 2002;6(4):324. doi: 10.1109/TITB.2002.804139. [DOI] [PubMed] [Google Scholar]
- 71.Delsanto S, Molinari F, Giustetto P, Liboni W, Badalamenti S: CULEX-completely user-independent layers extraction: ultrasonic carotid artery images segmentation. In: 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference: 2006. IEEE: 6468–6471. [DOI] [PubMed]
- 72.Molinari F, Krishnamurthi G, Acharya UR, Sree SV, Zeng G, Saba L, Nicolaides A, Suri JS. Hypothesis validation of far-wall brightness in carotid-artery ultrasound for feature-based IMT measurement using a combination of level-set segmentation and registration. IEEE Transactions on Instrumentation and measurement. 2012;61(4):1054–1063. doi: 10.1109/TIM.2011.2174901. [DOI] [Google Scholar]
- 73.Molinari F, Liboni W, Pantziaris M, Suri J. CALSFOAM-completed automated local statistics based first order absolute moment" for carotid wall recognition, segmentation and IMT measurement: validation and benchmarking on a 300 patient database. International angiology: a journal of the International Union of Angiology. 2011;30(3):227–241. [PubMed] [Google Scholar]
- 74.Kass M, Witkin A, Terzopoulos D. Snakes: Active contour models. International journal of computer vision. 1988;1(4):321–331. doi: 10.1007/BF00133570. [DOI] [Google Scholar]
- 75.Molinari F, Zeng G, Suri JS. An integrated approach to computer-based automated tracing and its validation for 200 common carotid arterial wall ultrasound images: A new technique. Journal of Ultrasound in Medicine. 2010;29(3):399–418. doi: 10.7863/jum.2010.29.3.399. [DOI] [PubMed] [Google Scholar]
- 76.Suri JS, Liu K, Singh S, Laxminarayan SN, Zeng X, Reden L. Shape recovery algorithms using level sets in 2-D/3-D medical imagery: a state-of-the-art review. IEEE Transactions on information technology in biomedicine. 2002;6(1):8–28. doi: 10.1109/4233.992158. [DOI] [PubMed] [Google Scholar]
- 77.Liguori C, Paolillo A, Pietrosanto A. An automatic measurement system for the evaluation of carotid intima-media thickness. IEEE Transactions on instrumentation and measurement. 2001;50(6):1684–1691. doi: 10.1109/19.982968. [DOI] [Google Scholar]
- 78.Molinari F, Zeng G, Suri JS: Inter-greedy technique for fusion of different segmentation strategies leading to high-performance carotid IMT measurement in ultrasound images. In: Atherosclerosis Disease Management. Springer; 2011: 253–279. [DOI] [PubMed]
- 79.Khanna NN, Jamthikar AD, Gupta D, Araki T, Piga M, Saba L, Carcassi C, Nicolaides A, Laird JR, Suri HS: Effect of carotid image-based phenotypes on cardiovascular risk calculator: AECRS1. 0. Medical & biological engineering & computing 2019, 57(7):1553–1566. [DOI] [PubMed]
- 80.Than MP, Pickering JW, Sandoval Y, Shah AS, Tsanas A, Apple FS, Blankenberg S, Cullen L, Mueller C, Neumann JT. Machine learning to predict the likelihood of acute myocardial infarction. Circulation. 2019;140(11):899–909. doi: 10.1161/CIRCULATIONAHA.119.041980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Ambale-Venkatesh B, Yang X, Wu CO, Liu K, Hundley WG, McClelland R, Gomes AS, Folsom AR, Shea S, Guallar E. Cardiovascular event prediction by machine learning: the multi-ethnic study of atherosclerosis. Circulation research. 2017;121(9):1092–1101. doi: 10.1161/CIRCRESAHA.117.311312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Biswas M, Kuppili V, Saba L, Edla DR, Suri HS, Cuadrado-Godia E, Laird J, Marinhoe R, Sanches J, Nicolaides A. State-of-the-art review on deep learning in medical imaging. Front Biosci (Landmark Ed) 2019;24:392–426. doi: 10.2741/4725. [DOI] [PubMed] [Google Scholar]
- 83.Bishop CM: Pattern recognition and machine learning: springer; 2006.
- 84.Krizhevsky A, Sutskever I, Hinton GE: Imagenet classification with deep convolutional neural networks. In: Advances in neural information processing systems: 2012. 1097–1105.
- 85.Naik V, Gamad R, Bansod P: Carotid artery segmentation in ultrasound images and measurement of intima-media thickness. BioMed research international 2013, 2013. [DOI] [PMC free article] [PubMed]
- 86.Spence JD, Eliasziw M, DiCicco M, Hackam DG, Galil R, Lohmann T. Carotid plaque area: a tool for targeting and evaluating vascular preventive therapy. Stroke. 2002;33(12):2916–2922. doi: 10.1161/01.STR.0000042207.16156.B9. [DOI] [PubMed] [Google Scholar]
- 87.Spence JD. Ultrasound measurement of carotid plaque as a surrogate outcome for coronary artery disease. The American journal of cardiology. 2002;89(4):10–15. doi: 10.1016/S0002-9149(01)02327-X. [DOI] [PubMed] [Google Scholar]
- 88.Mathiesen EB, Johnsen SH, Wilsgaard T, Bønaa KH, Løchen M-L, Njølstad I. Carotid plaque area and intima-media thickness in prediction of first-ever ischemic stroke: a 10-year follow-up of 6584 men and women: the Tromsø Study. Stroke. 2011;42(4):972–978. doi: 10.1161/STROKEAHA.110.589754. [DOI] [PubMed] [Google Scholar]
- 89.Khanna NN, Jamthikar AD, Gupta D, Nicolaides A, Araki T, Saba L, Cuadrado-Godia E, Sharma A, Omerzu T, Suri HS. Performance evaluation of 10-year ultrasound image-based stroke/cardiovascular (CV) risk calculator by comparing against ten conventional CV risk calculators: a diabetic study. Computers in biology and medicine. 2019;105:125–143. doi: 10.1016/j.compbiomed.2019.01.002. [DOI] [PubMed] [Google Scholar]
- 90.Martis RJ, Acharya UR, Prasad H, Chua CK, Lim CM, Suri JS. Application of higher order statistics for atrial arrhythmia classification. Biomedical signal processing and control. 2013;8(6):888–900. doi: 10.1016/j.bspc.2013.08.008. [DOI] [Google Scholar]
- 91.Maniruzzaman M, Kumar N, Menhazul Abedin M, Shaykhul Islam M, Suri HS, El-Baz AS, Suri JS. Comparative approaches for classification of diabetes mellitus data: Machine learning paradigm. Comput Methods Programs Biomed. 2017;152:23–34. doi: 10.1016/j.cmpb.2017.09.004. [DOI] [PubMed] [Google Scholar]
- 92.Menchón-Lara R-M, Bastida-Jumilla M-C, Morales-Sánchez J, Sancho-Gómez J-L. Automatic detection of the intima-media thickness in ultrasound images of the common carotid artery using neural networks. Medical & biological engineering & computing. 2014;52(2):169–181. doi: 10.1007/s11517-013-1128-4. [DOI] [PubMed] [Google Scholar]
- 93.Menchón-Lara R-M, Sancho-Gómez J-L: Ultrasound image processing based on machine learning for the fully automatic evaluation of the Carotid Intima-Media Thickness. In: 2014 12th International Workshop on Content-Based Multimedia Indexing (CBMI): 2014. IEEE: 1–4.
- 94.Meyer F. Topographic distance and watershed lines. Signal processing. 1994;38(1):113–125. doi: 10.1016/0165-1684(94)90060-4. [DOI] [Google Scholar]
- 95.Elnakib A, Gimel’farb G, Suri JS, El-Baz A: Medical image segmentation: a brief survey. In: Multi Modality State-of-the-Art Medical Image Segmentation and Registration Methodologies. Springer; 2011: 1–39.
- 96.Suri JS. Computer vision, pattern recognition and image processing in left ventricle segmentation: The last 50 years. Pattern Analysis & Applications. 2000;3(3):209–242. doi: 10.1007/s100440070008. [DOI] [Google Scholar]
- 97.Yegnanarayana B. Artificial neural networks for pattern recognition. Sadhana. 1994;19(2):189–238. doi: 10.1007/BF02811896. [DOI] [Google Scholar]
- 98.Schwenker F, Kestler HA, Palm G. Three learning phases for radial-basis-function networks. Neural networks. 2001;14(4–5):439–458. doi: 10.1016/S0893-6080(01)00027-2. [DOI] [PubMed] [Google Scholar]
- 99.Huang G-B, Zhu Q-Y, Siew C-K. Extreme learning machine: theory and applications. Neurocomputing. 2006;70(1–3):489–501. doi: 10.1016/j.neucom.2005.12.126. [DOI] [Google Scholar]
- 100.Miche Y, Sorjamaa A, Bas P, Simula O, Jutten C, Lendasse A. OP-ELM: optimally pruned extreme learning machine. IEEE transactions on neural networks. 2009;21(1):158–162. doi: 10.1109/TNN.2009.2036259. [DOI] [PubMed] [Google Scholar]
- 101.Dunn JC: A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. 1973.
- 102.Hartigan JA, Wong MA. Algorithm AS 136: A k-means clustering algorithm. Journal of the Royal Statistical Society Series C (Applied Statistics) 1979;28(1):100–108. [Google Scholar]
- 103.Cuadrado-Godia E, Srivastava SK, Saba L, Araki T, Suri HS, Giannopolulos A, Omerzu T, Laird J, Khanna NN, Mavrogeni S. Geometric total plaque area is an equally powerful phenotype compared with carotid intima-media thickness for stroke risk assessment: a deep learning approach. Journal for Vascular Ultrasound. 2018;42(4):162–188. doi: 10.1177/1544316718806421. [DOI] [Google Scholar]
- 104.Mainak Biswas LS, Shubhro Chakrabartty, Narender N Khanna, Hanjung Song,Harman S. Suri, Petros P. Sfikakis, Sophie Mavrogeni, Klaudija Viskovic, John R. Laird, Elisa Cuadrado-Godia, Andrew Nicolaides, Aditya Sharma, Vijay Viswanathan, Athanasios Protogerou, George Kitas, Gyan Pareek, Martin Miner, Jasjit S. Suri: Two-Stage Artificial Intelligence Model for Jointly Measurement of Atherosclerotic Wall Thickness and Plaque Burden in Carotid Ultrasound: A Screening Tool for Cardiovascular/Stroke Risk Assessment. Computers in biology and medicine 2020. [DOI] [PubMed]
- 105.Saba L, Biswas M, Kuppili V, Cuadrado Godia E, Suri HS, Edla DR, Omerzu T, Laird JR, Khanna NN, Mavrogeni S, et al. The present and future of deep learning in radiology. European Journal of Radiology. 2019;114:14–24. doi: 10.1016/j.ejrad.2019.02.038. [DOI] [PubMed] [Google Scholar]
- 106.Hinton GE. Deep belief networks. Scholarpedia. 2009;4(5):5947. [Google Scholar]
- 107.Baldi P: Autoencoders, unsupervised learning, and deep architectures. In: Proceedings of ICML workshop on unsupervised and transfer learning: 2012. 37–49.
- 108.He K, Zhang X, Ren S, Sun J: Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition: 2016. 770–778.
- 109.Long J, Shelhamer E, Darrell T: Fully convolutional networks for semantic segmentation. In: Proceedings of the IEEE conference on computer vision and pattern recognition: 2015. 3431–3440. [DOI] [PubMed]
- 110.Menchón-Lara R-M, Sancho-Gómez J-L. Fully automatic segmentation of ultrasound common carotid artery images based on machine learning. Neurocomputing. 2015;151:161–167. doi: 10.1016/j.neucom.2014.09.066. [DOI] [Google Scholar]
- 111.Biswas M, Kuppili V, Araki T, Edla DR, Godia EC, Saba L, Suri HS, Omerzu T, Laird JR, Khanna NN. Deep learning strategy for accurate carotid intima-media thickness measurement: an ultrasound study on Japanese diabetic cohort. Computers in biology and medicine. 2018;98:100–117. doi: 10.1016/j.compbiomed.2018.05.014. [DOI] [PubMed] [Google Scholar]
- 112.del Mar Vila M, Remeseiro B, Grau M, Elosua R, Betriu À, Fernandez-Giraldez E, Igual L. Semantic segmentation with DenseNets for carotid artery ultrasound plaque segmentation and CIMT estimation. Artificial Intelligence in Medicine. 2020;103:101784. doi: 10.1016/j.artmed.2019.101784. [DOI] [PubMed] [Google Scholar]
- 113.Molinari F, Meiburger KM, Saba L, Acharya UR, Famiglietti L, Georgiou N, Nicolaides A, Mamidi RS, Kuper H, Suri JS: Automated carotid IMT measurement and its validation in low contrast ultrasound database of 885 patient Indian population epidemiological study: results of AtheroEdge® software. In: Multi-modality atherosclerosis imaging and diagnosis. Springer; 2014: 209–219.
- 114.Saba L, Molinari F, Meiburger KM, Acharya UR, Nicolaides A, Suri JS. Inter-and intra-observer variability analysis of completely automated cIMT measurement software (AtheroEdge™) and its benchmarking against commercial ultrasound scanner and expert Readers. Computers in Biology and Medicine. 2013;43(9):1261–1272. doi: 10.1016/j.compbiomed.2013.06.012. [DOI] [PubMed] [Google Scholar]
- 115.Suri JS, Haralick RM, Sheehan FH. Greedy algorithm for error correction in automatically produced boundaries from low contrast ventriculograms. Pattern Analysis & Applications. 2000;3(1):39–60. doi: 10.1007/s100440050005. [DOI] [Google Scholar]
- 116.Biswas M, Kuppili V, Edla DR, Suri HS, Saba L, Marinhoe RT, Sanches JM, Suri JS. Symtosis: A liver ultrasound tissue characterization and risk stratification in optimized deep learning paradigm. Computer methods and programs in biomedicine. 2018;155:165–177. doi: 10.1016/j.cmpb.2017.12.016. [DOI] [PubMed] [Google Scholar]
- 117.Biswas M, Kuppili V, Edla DR, Suri HS, Saba L, Marinhoe RT. Sanches JM. Suri JSJCm, biomedicine pi: Symtosis: A liver ultrasound tissue characterization and risk stratification in optimized deep learning paradigm. 2018;155:165–177. doi: 10.1016/j.cmpb.2017.12.016. [DOI] [PubMed] [Google Scholar]
- 118.Carvalho DD, Akkus Z, van den Oord SC, Schinkel AF, van der Steen AF, Niessen WJ, Bosch JG, Klein S. Lumen segmentation and motion estimation in B-mode and contrast-enhanced ultrasound images of the carotid artery in patients with atherosclerotic plaque. IEEE transactions on medical imaging. 2014;34(4):983–993. doi: 10.1109/TMI.2014.2372784. [DOI] [PubMed] [Google Scholar]
- 119.Gastounioti A, Golemati S, Stoitsis J, Nikita K: Kalman-filter-based block matching for arterial wall motion estimation from B-mode ultrasound. In: 2010 IEEE International Conference on Imaging Systems and Techniques: 2010. IEEE: 234–239.
- 120.Ilea DE, Duffy C, Kavanagh L, Stanton A, Whelan PF. Fully automated segmentation and tracking of the intima media thickness in ultrasound video sequences of the common carotid artery. IEEE transactions on ultrasonics, ferroelectrics, and frequency control. 2012;60(1):158–177. doi: 10.1109/TUFFC.2013.2547. [DOI] [PubMed] [Google Scholar]
- 121.Araki T, Ikeda N, Molinari F, Dey N, Acharjee SM, Saba L, Nicolaides A. Suri JSJJoMI. Informatics H: Effect of geometric-based coronary calcium volume as a feature along with its shape-based attributes for cardiological risk prediction from low contrast intravascular ultrasound. 2014;4(2):255–261. [Google Scholar]
- 122.Jamthikar A, Gupta D, Khanna NN, Saba L, Araki T, Viskovic K, Suri HS, Gupta A, Mavrogeni S, Turk MJCd et al: A low-cost machine learning-based cardiovascular/stroke risk assessment system: integration of conventional factors with image phenotypes. 2019, 9(5):420. [DOI] [PMC free article] [PubMed]
- 123.Molinari F, Zeng G, Suri JS. A state of the art review on intima–media thickness (IMT) measurement and wall segmentation techniques for carotid ultrasound. Computer methods and programs in biomedicine. 2010;100(3):201–221. doi: 10.1016/j.cmpb.2010.04.007. [DOI] [PubMed] [Google Scholar]
- 124.Liang Q, Wendelhag I, Wikstrand J, Gustavsson T. A multiscale dynamic programming procedure for boundary detection in ultrasonic artery images. IEEE Transactions on medical imaging. 2000;19(2):127–142. doi: 10.1109/42.836372. [DOI] [PubMed] [Google Scholar]
- 125.Stein JH, Korcarz CE, Mays ME, Douglas PS, Palta M, Zhang H, LeCaire T, Paine D, Gustafson D, Fan L. A semiautomated ultrasound border detection program that facilitates clinical measurement of ultrasound carotid intima-media thickness. Journal of the American Society of Echocardiography. 2005;18(3):244–251. doi: 10.1016/j.echo.2004.12.002. [DOI] [PubMed] [Google Scholar]
- 126.Faita F, Gemignani V, Bianchini E, Giannarelli C, Ghiadoni L, Demi M. Real-time measurement system for evaluation of the carotid intima-media thickness with a robust edge operator. Journal of ultrasound in medicine. 2008;27(9):1353–1361. doi: 10.7863/jum.2008.27.9.1353. [DOI] [PubMed] [Google Scholar]
- 127.Molinari F, Acharya UR, Zeng G, Meiburger KM, Suri JS. Completely automated robust edge snapper for carotid ultrasound IMT measurement on a multi-institutional database of 300 images. Medical & biological engineering & computing. 2011;49(8):935–945. doi: 10.1007/s11517-011-0781-8. [DOI] [PubMed] [Google Scholar]
- 128.Molinari F, Meiburger KM, Zeng G, Nicolaides A, Suri JS. CAUDLES-EF: carotid automated ultrasound double line extraction system using edge flow. Journal of digital imaging. 2011;24(6):1059–1077. doi: 10.1007/s10278-011-9375-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Molinari F, Suri JS: Automated measurement of carotid artery intima-media thickness. In: Ultrasound and Carotid Bifurcation Atherosclerosis. Springer; 2011: 177–192.
- 130.Gutierrez MA, Pilon PE, Lage S, Kopel L, Carvalho R, Furuie S: Automatic measurement of carotid diameter and wall thickness in ultrasound images. In: Computers in Cardiology: 2002. IEEE: 359–362.
- 131.Molinari F, Liboni W, Giustetto P, Badalamenti S, Suri JS. Automatic computer-based tracings (ACT) in longitudinal 2-D ultrasound images using different scanners. Journal of Mechanics in Medicine and Biology. 2009;9(04):481–505. doi: 10.1142/S0219519409003115. [DOI] [Google Scholar]
- 132.Molinari F, Acharya UR, Saba L, Nicolaides A, Suri JS: Hypothesis Validation of Far Wall Brightness in Carotid Artery Ultrasound for Feature-Based IMT Measurement Using a Combination of Level Set Segmentation and Registration. In: Multi-Modality Atherosclerosis Imaging and Diagnosis. Springer; 2014: 255–267.
- 133.Khanna NN, Jamthikar AD, Araki T, Gupta D, Piga M, Saba L, Carcassi C, Nicolaides A, Laird JR, Suri HS. Nonlinear model for the carotid artery disease 10-year risk prediction by fusing conventional cardiovascular factors to carotid ultrasound image phenotypes: A Japanese diabetes cohort study. Echocardiography. 2019;36(2):345–361. doi: 10.1111/echo.14242. [DOI] [PubMed] [Google Scholar]
- 134.Cuadrado-Godia E, Jamthikar AD, Gupta D, Khanna NN, Araki T, Maniruzzaman M, Saba L, Nicolaides A, Sharma A, Omerzu T. Ranking of stroke and cardiovascular risk factors for an optimal risk calculator design: Logistic regression approach. Computers in biology and medicine. 2019;108:182–195. doi: 10.1016/j.compbiomed.2019.03.020. [DOI] [PubMed] [Google Scholar]
- 135.Jamthikar A, Gupta D, Saba L, Khanna NN, Viskovic K, Mavrogeni S, Laird JR, Sattar N, Johri AM, Pareek GJCiB et al: Artificial Intelligence Framework for Predictive Cardiovascular and Stroke Risk Assessment Models: A Narrative Review of Integrated Approaches using Carotid Ultrasound. 2020:104043. [DOI] [PubMed]
- 136.Jamthikar AD, Puvvula A, Gupta D, Johri AM, Nambi V, Khanna NN, Saba L, Mavrogeni S, Laird JR, Pareek G: Cardiovascular disease and stroke risk assessment in patients with chronic kidney disease using integration of estimated glomerular filtration rate, ultrasonic image phenotypes, and artificial intelligence: a narrative review. International Angiology: a Journal of the International Union of Angiology 2020. [DOI] [PubMed]
- 137.Narayanan R, Kurhanewicz J, Shinohara K, Crawford ED, Simoneau A, Suri JS: MRI-ultrasound registration for targeted prostate biopsy. In: 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro: 2009. IEEE: 991–994.
- 138.Saba L, Banchhor SK, Araki T, Viskovic K, Londhe ND, Laird JR, Suri HS, Suri JS. Intra-and inter-operator reproducibility of automated cloud-based carotid lumen diameter ultrasound measurement. Indian Heart Journal. 2018;70(5):649–664. doi: 10.1016/j.ihj.2018.01.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Saba L, Than JCM, Noor NM, Rijal OM, Kassim RM, Yunus A, Ng CR, Suri JS: Inter-observer Variability Analysis of Automatic Lung Delineation in Normal and Disease Patients. Journal of Medical Systems 2016, 40(6). [DOI] [PubMed]
- 140.Zhang S, Suri JS, Salvado O, Chen Y, Wacker FK, Wilson DL, Duerk JL, Lewin JS. Inter-and Intra-Observer Variability Assessment of in Vivo Carotid Plaque Burden Quantification Using Multi-Contrast Dark Blood MR Images. Studies in health technology and informatics. 2005;113:384–393. [PubMed] [Google Scholar]
- 141.Biswas M, Kuppili V, Saba L, Edla DR, Suri HS, Sharma A, Cuadrado-Godia E, Laird JR, Nicolaides A, Suri JSJM, et al. Deep learning fully convolution network for lumen characterization in diabetic patients using carotid ultrasound: a tool for stroke risk. 2019;57(2):543–564. doi: 10.1007/s11517-018-1897-x. [DOI] [PubMed] [Google Scholar]
- 142.Biswas M, Saba L, Chakrabartty S, Khanna NN, Song H, Suri HS, Sfikakis PP, Mavrogeni S, Viskovic K, Laird JR. Two-stage artificial intelligence model for jointly measurement of atherosclerotic wall thickness and plaque burden in carotid ultrasound: A screening tool for cardiovascular/stroke risk assessment. Computers in Biology and Medicine. 2020;123:103847. doi: 10.1016/j.compbiomed.2020.103847. [DOI] [PubMed] [Google Scholar]
- 143.Jamthikar A, Gupta D, Saba L, Khanna NN, Araki T, Viskovic K, Mavrogeni S, Laird JR, Pareek G, Miner M. Cardiovascular/stroke risk predictive calculators: a comparison between statistical and machine learning models. Cardiovascular Diagnosis and Therapy. 2020;10(4):919. doi: 10.21037/cdt.2020.01.07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Jamthikar A, Gupta D, Khanna NN, Saba L, Laird JR, Suri JS. Cardiovascular/stroke risk prevention: a new machine learning framework integrating carotid ultrasound image-based phenotypes and its harmonics with conventional risk factors. Indian heart journal. 2020;72(4):258–264. doi: 10.1016/j.ihj.2020.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Viswanathan V, Jamthikar AD, Gupta D, Shanu N, Puvvula A, Khanna NN, Saba L, Omerzum T, Viskovic K. Mavrogeni SJFiB: Low-cost preventive screening using carotid ultrasound in patients with diabetes. 2020;25:1132–1171. doi: 10.2741/4850. [DOI] [PubMed] [Google Scholar]
- 146.Glas AS, Lijmer JG, Prins MH, Bonsel GJ, Bossuyt PM. The diagnostic odds ratio: a single indicator of test performance. Journal of clinical epidemiology. 2003;56(11):1129–1135. doi: 10.1016/S0895-4356(03)00177-X. [DOI] [PubMed] [Google Scholar]
- 147.Kadam P, Bhalerao S. Sample size calculation. International journal of Ayurveda research. 2010;1(1):55. doi: 10.4103/0974-7788.59946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Hadjis S, Zhang C, Mitliagkas I, Iter D, Ré C: Omnivore: An optimizer for multi-device deep learning on cpus and gpus. arXiv preprint arXiv:160604487 2016.
- 149.Chen T, Li M, Li Y, Lin M, Wang N, Wang M, Xiao T, Xu B, Zhang C, Zhang Z: Mxnet: A flexible and efficient machine learning library for heterogeneous distributed systems. arXiv preprint arXiv:151201274 2015.
- 150.Ooi BC, Tan K-L, Wang S, Wang W, Cai Q, Chen G, Gao J, Luo Z, Tung AK, Wang Y: SINGA: A distributed deep learning platform. In: Proceedings of the 23rd ACM international conference on Multimedia: 2015. 685–688.
- 151.Saba L, Tiwari A, Biswas M, Gupta SK, Godia-Cuadrado E, Chaturvedi A, Turk M, Suri HS, Orru S, Sanches JM. Wilson's disease: A new perspective review on its genetics, diagnosis and treatment. Frontiers in bioscience (Elite edition) 2019;11:166–185. doi: 10.2741/E854. [DOI] [PubMed] [Google Scholar]
- 152.Tandel GS, Biswas M, Kakde OG, Tiwari A, Suri HS, Turk M, Laird JR, Asare CK, Ankrah AA, Khanna N. A review on a deep learning perspective in brain cancer classification. Cancers. 2019;11(1):111. doi: 10.3390/cancers11010111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Sharma AM, Gupta A, Kumar PK, Rajan J, Saba L, Nobutaka I, Laird JR, Nicolades A, Suri JS. A review on carotid ultrasound atherosclerotic tissue characterization and stroke risk stratification in machine learning framework. Current atherosclerosis reports. 2015;17(9):55. doi: 10.1007/s11883-015-0529-2. [DOI] [PubMed] [Google Scholar]
- 154.Flach P: The many faces of ROC analysis in machine learning. ICML Tutorial 2004.
- 155.Flach PA. On the state of the art in machine learning: A personal review. Artificial Intelligence. 2001;131(1–2):199–222. doi: 10.1016/S0004-3702(01)00125-4. [DOI] [Google Scholar]
- 156.Cover T, Hart P. Nearest neighbor pattern classification. IEEE transactions on information theory. 1967;13(1):21–27. doi: 10.1109/TIT.1967.1053964. [DOI] [Google Scholar]
- 157.Cortes C, Vapnik V. Support-vector networks. Machine learning. 1995;20(3):273–297. [Google Scholar]
- 158.Majumder M: Artificial Neural Network. In: Impact of Urbanization on Water Shortage in Face of Climatic Aberrations. Springer; 2015: 49–54.
- 159.Resnik P, Hardisty E. Gibbs sampling for the uninitiated. In.: Maryland Univ College Park Inst for Advanced Computer Studies; 2010. [Google Scholar]
- 160.Quinlan JR. Induction of decision trees. Machine learning. 1986;1(1):81–106. [Google Scholar]
- 161.LeCun Y, Touresky D, Hinton G, Sejnowski T: A theoretical framework for back-propagation. In: Proceedings of the 1988 connectionist models summer school: 1988. CMU, Pittsburgh, Pa: Morgan Kaufmann: 21–28.
- 162.Barlow HB. Unsupervised learning. Neural computation. 1989;1(3):295–311. doi: 10.1162/neco.1989.1.3.295. [DOI] [Google Scholar]
- 163.Alsabti K, Ranka S, Singh V: An efficient k-means clustering algorithm. 1997.