Are restricted mean survival time methods especially useful for Noninferiority Trials?

Abstract

Background:

Restricted mean survival time methods compare the areas under the Kaplan-Meier curves up to a time τ for the control and experimental treatments. Extraordinary claims have been made about the benefits (in terms of dramatically smaller required sample sizes) when using restricted mean survival time methods as compared to proportional hazards methods for analyzing noninferiority trials, even when the true survival distributions satisfy proportional hazards.

Methods:

Through some limited simulations and asymptotic power calculations, we compare the operating characteristics of restricted mean survival time and proportional hazards methods for analyzing both noninferiority and superiority trials under proportional hazards to understand what relative power benefits there are when using restricted mean survival time methods for noninferiority testing.

Results:

In the setting of low event rates, very large targeted noninferiority margins, and limited follow-up past τ, restricted mean survival time methods have more power than proportional hazards methods. For superiority testing, proportional hazards methods have more power. This is not a small-sample phenomenon but requires a low event rate and a large noninferiority margin.

Conclusion:

Although there are special settings where restricted mean survival time methods have a power advantage over proportional hazards methods for testing noninferiority, the larger issue in these settings is defining appropriate noninferiority margins. We find the restricted mean survival time methods lacking in these regards.

Introduction

The restricted mean survival time (RMST) methodology for comparing survival curves in a randomized clinical trial involves calculating the area between the Kaplan-Meier curves for the experimental and control groups up to a time τ.^1–6 (With no censoring and τ → ∞, the area between the curves is simply the difference in mean survival times between the treatment groups.) This area being large suggests the experimental treatment is better than the control treatment, and one can also calculate a p-value associated with the observed area. While this methodology has nonparametric appeal, its practical application is not straightforward. We have noted a number issues with prospective use of these methods⁷ and argued that RMST methods are not ready to be used as the primary analysis for definitive trials because of the difficulty in choosing an appropriate τ and in interpreting the results (although there is disagreement on this point^8–10). However, we have been intrigued by assertions that RMST methods were superior or greatly superior in terms of required sample sizes to standard methods for noninferiority trials.^5,11–21

As a specific example, in a discussion of the pros and cons of various alternatives to the hazard ratio for noninferiority trials, Uno et al.⁵ suggest that using RMST methods instead of proportional hazards methods results in dramatically lower required sample sizes for noninferiority trials. To demonstrate this, they consider some design alternatives for a completed trial of saxagliptin versus placebo for patients with type 2 diabetes; the endpoint was a time to a specified cardiac event.²² First, Uno et al.⁵ note that if the design had been a standard (proportional hazards) noninferiority design with a hazard-ratio margin of 1.3 (with 80% power for a one-sided 0.025 test), then 456 events would have been required. Then they calculate that using RMST with a noninferiority margin of 18 days (with τ =900 days), only 182 events would be required, quite a savings. However, this apples to oranges comparison is misleading: Using the assumed Weibull modeling assumptions,⁵ the 18-day noninferiority margin (with τ=900) corresponds to a hazard ratio of 1.45. If one had designed the trial using a standard proportional hazards analysis with a noninferiority margin hazard ratio of 1.45, 228 events would be required for 80% power, a 25% increase over using the RMST methods rather than the 250% increase suggested. (Note that the 25% increase in the number of events would translate into a 27% increase in the study sample size assuming the same accrual rate and study duration).

We were willing to attribute the suggestions of dramatic sample-size benefits from using RMST methods for noninferiority trials to the exuberance of RMST proponents, but we were given pause by some simulations done by Weir and Trinquart,¹⁶ which correctly matched the RMST and hazard-ratio noninferiority margins and showed some power benefits for the RMST methods. However, Appendix Figure 5 of Weir and Trinquart¹⁶ suggests that for some scenarios proportional hazards methods are better than RMST methods for testing noninferiority, making it unclear when, and to what extent, there are benefits of the RMST methods for testing noninferiority.

It would seem that the clinical trial community could benefit from some further explanation/quantification of the purported advantages of RMST over the proportional hazards analyses, especially as those claims extend to the proportional hazards settings. In an attempt to explain the sample-size/power advantage in the noninferiority setting (even under proportional hazards), a number of authors reference the dependence of proportional hazards model hazard ratio estimator on the number of events: “The precision of the hazard ratio estimate depends primarily on the number of observed events but not directly on exposure times or sample size of the study population.”⁵ While technically correct, this does not provide an explanation for why there are benefits for testing noninferiority that are not seen when testing superiority. Indeed, the theoretical sensitivity of RMST to longitudinal differences in survival distributions (as contrasted with scale-less nature of the rank tests used in proportional hazards model) was a key motivation for RMST development.² Yet how this may affect the relative performance of the tests in the specific (noninferiority) applications is not obvious. A more nuanced attempt to provide theoretical justification of lower required sample sizes when using RMST instead of standard methods for noninferiority trials is given in Zhao et al.:¹¹

“Moreover, for the low event rate case with fixed numbers of study subjects, when the event rates decrease, the precision of the Cox’s hazard ratio estimate decreases because the standard error of the hazard ratio estimate is approximately inversely related to the number of observed events, but its counterpart of the estimated integrated survival rate difference would increase. This interesting feature, coupled with its easy interpretation, makes the integrated survival rate difference a more desirable measure for the treatment contrast than its hazard ratio–based counterpart for equivalence or noninferiority studies. On the other hand, in the superiority study setting, as pointed out by a referee, the increasing precision of the estimated integrated survival rate difference does not necessarily mean increasing power for detecting the difference between the two survival curves. This is because the effect size of the integrated survival rate difference may also decrease when the number of observed events decreases.”

We are unable to follow the reasoning here, so in this article we investigate the potential power benefits of RMST methods over proportional hazards methods focusing on the noninferiority setting.

Methods

To evaluate the operating characteristics of RMST methods vis a vis proportional hazards methods, we performed some limited simulations for both noninferiority and superiority testing using two accrual patterns: In the first, accrual was instantaneous and all patient were followed for three years. In the second, accrual was uniform over three years with an additional three years of follow-up. For both patterns, we set τ equal to three years. (Additional simulations with τ equal to 5 years are provided in the appendix in the supplemental material.) Inclusion of the first setting was to provide the most relative benefit for the RMST methods (as there would be no additional events after three years entering into the proportional hazards analyses), whereas the second setting was included to be more representative of actual clinical trials. We choose to set τ to be fixed (at three years) with uniform accrual rather than setting equal to the (random) smallest of the largest observed time in each arm, as this corresponds to the advice given by Eaton et al.²³ that τ should be set at a clinically meaningful value. For each accrual pattern we considered three settings (all events were simulated using exponential distributions), where the experimental-arm survivals rates are high (90%), moderate (60%) or low (20%) for the power calculations. A range of noninferiority hazard-ratio (experimental over control) margins were evaluated (2, 1.75, 1.5 and 1.25), with the sample sizes chosen to achieve up to 80–90% power. Note that to provide an appropriate power comparison, the noninferiority margins for the RMST designs were calibrated to correspond to the difference between the restricted means (with the designated τ) for the exponential distributions with corresponding noninferiority margin hazard ratios.

To highlight the differences between the operating characteristics of noninferiority versus superiority testing, we use a parallel/matched structure for the simulations: For example, to compare with testing noninferiority with a noninferiority hazard ratio margin of 2 (control-arm three-year survival=90%, experimental-arm three-year survival=81%), we test superiority with a target hazard ratio of 0.5 (control-arm three-year survival=81%, experimental-arm three-year survival 90%).

For any test statistic, $\widehat{\theta }$, we reject (at the one-sided level of 0.025) the hypothesis that the survival curves are equal in favor of superiority when

$$\frac{\widehat{\theta }}{\widehat{SE}(\widehat{\theta })}>1.96$$

For noninferiority testing, we can declare noninferiority with a noninferiority margin of Δ if

$$\frac{\widehat{\theta }+\Delta }{\widehat{SE}(\widehat{\theta })}>1.96$$

For the proportional hazards analysis, $\widehat{\theta }$ is the log of the estimated hazard ratio, and is standard error is the square root of $\frac{1}{d_C}+\frac{1}{d_E}$ (where d_C and d_E are the number of events in control and experimental arms). An asymptotically equivalent test is obtained by using a log-rank test for testing superiority or a modified log-rank test for testing noninferiority (where the null hypothesis is the noninferiority margin²⁴).

For the RMST analysis, $\widehat{\theta }$ is the difference in the treatment-arm Kaplan-Meier curves up to τ. Note that with accrual patterns considered, any observation has three years of potential follow-up, so that the area under a treatment-arm Kaplan-Meier curve is simply the sample mean of the truncated variable z:

$$\begin{array}{ccc}& y_i\text{if}{y}_i<\tau & \\ Z_i=& & i=1,\dots ,n\\ & \tau \text{if}{y}_i\ge \tau & \end{array}$$

where y_i are the survival times and n is the sample size for that treatment arm. Thus, $\widehat{\theta }={\overline{Z}}_E-{\overline{Z}}_C$. Although there are choices,^23,25 the most commonly used nonparametric variance estimator for the RMST (for a single treatment arm) is:²⁶

$$\widehat{V}={\sum }_{i=1}^V{\left[{\int }_{t_i}^{\tau }\widehat{S}(t)dt\right]}^2\frac{v_i}{Y_i\left(Y_i-v_i\right)}$$

where $\widehat{S}$ is the Kaplan-Meier curve, and the sum is over the V event times (t₁, t₂, …), and where ν_i and Y_i are the number of events and number at risk at time t_i, respectively. In the present setting, this reduces to [(n − 1)/n] s²/n, where s² is the sample variance of the z_i.²⁵ The standard error of $\widehat{\theta }$ is thus given by $\sqrt{s_E^2/n_E+s_C^2/n_C}$.

We conducted our simulations under proportional hazards firstly because it allows elucidating the issue in its purest from. However, it is also important to note that the relative efficiency of RMST methods and log-rank methods changes with nonproportionality, with RMST methods reported to be more efficient with early differences in the survival curves and proportional hazards methods more efficient with later differences in the survival curves.^6,23,27 (We note in passing that later differences in survival curves are practically always more clinically relevant than earlier differences that evaporate, since the former imply an increase in the patient’s probability of cure while the latter represents a transient effect that does not improve the patient’s long-term prospects.)

To better understand the simulated power results, we consider analytic power formulas that use asymptotic variances for the instant accrual setting. The powers of the superiority and noninferiority tests are given by, respectively,

$$P_{\Delta }\left(\frac{\widehat{\theta }-\Delta }{\widehat{SE}(\widehat{\theta })}>1.96-\frac{\Delta }{\widehat{SE}(\widehat{\theta })}\right)\hspace{1em}\text{and}\hspace{1em}{P}_0\left(\frac{\widehat{\theta }}{\widehat{SE}(\widehat{\theta })}>1.96-\frac{\Delta }{\widehat{SE}(\widehat{\theta })}\right)$$

where the subscripts Δ and 0 refer to calculating these probabilities under the alternative Δ or when the survival curves are identical, respectively. For the proportional hazards analysis using exponential distribution, we substitute the expected value of d, n(1 – e^−λτ), for d in the variance formulas. For the RMST analysis, we substitute Var(Z) for s² in the variance formulas, where

$$Var(Z;\lambda )=\frac{1}{{\lambda }^2}-\frac{1}{{\lambda }^2}{e}^{-2\tau \lambda }-\frac{2}{\lambda }\tau e^{-\lambda \tau }$$

Assuming n_C = n_E = n, consider the values of the “noncentrality parameters” $\frac{\Delta }{\sqrt{n}SE(\widehat{\theta })}$ for testing superiority and noninferiority using a RMST or proportional hazards analysis. These values are given in Table 3. Asymptotic powers can then be calculated as the normal probability greater than the value of 1.96 minus the noncentrality parameter.

Table 3:

Noncentrality parameters for noninferiority testing and superiority testing using proportional hazards analyses or RMST analyses (instant accrual, τ =3); see text

	Proportional hazards analysis	RMST analysisa
Non-inferiority testing	$\frac{\text{log}\left(\frac{{\lambda }_E}{{\lambda }_C}\right)}{\sqrt{2{\left(1-e^{-{\lambda }_C\tau }\right)}^{-1}}}$	$\frac{\frac{1-e^{-{\lambda }_C\tau }}{{\lambda }_C}-\frac{1-e^{-{\lambda }_E\tau }}{{\lambda }_E}}{\sqrt{2Var\left(Z;{\lambda }_C\right)}}$
Superiority testing	$\frac{\text{log}\left(\frac{{\lambda }_E}{{\lambda }_C}\right)}{\sqrt{{\left(1-e^{-{\lambda }_C\tau }\right)}^{-1}+{\left(1-e^{-{\lambda }_E\tau }\right)}^{-1}}}$	$\frac{\frac{1-e^{-{\lambda }_C\tau }}{{\lambda }_C}-\frac{1-e^{-{\lambda }_E\tau }}{{\lambda }_E}}{\sqrt{Var\left(Z;{\lambda }_C\right)+Var\left(Z;{\lambda }_E\right)}}$

^(a)$Var(Z;\lambda )=\frac{1}{{\lambda }^2}-\frac{1}{{\lambda }^2}{e}^{-2\tau \lambda }-\frac{2}{\lambda }\tau e^{-\lambda \tau }$

Results

Tables 1 and 2 present the simulation results for testing noninferiority and superiority, respectively. For noninferiority testing, the RMST has better power than the proportional hazard analyses in the low-event rate setting, when the noninferiority margins are large, and there is instantaneous accrual or τ is close to maximum follow-up time. For superiority testing, the proportional hazards analyses uniformly have better power than the RMST methods, although the differences are negligible in the high-event rate setting. Per reviewer suggestion, we also conducted simulations for a “very rare” event setting with 4% 3-year event rate to represent a study concerned with rare adverse events (Tables 3A and 4A in the online appendix); the results are similar to the low-event rate setting. Note however, Kaplan-Meier estimates may not be appropriate for comparing adverse events in clinical trials.²⁸

Table 1:

Simulated rejection probabilities for noninferiority testing using proportional hazards (Cox) and RMST methods (τ=3) under three event-rate settings with instant or staggered accrual

Noninferiority designs
NI Margin		Sample size per arm	Simulated powers					Simulated levels
HR	RMST (years)		3-yr surv (Exp arm)	3-yr surv (Contr arm)	RMST	Proportional hazards	Proportional hazards Staggered*	3-yr surv (Exp arm)	3-yr surv (Contr arm)	RMST	Proportional hazards
	Low event-rate setting: 90% 3-year survival on the best arm(s)
2	.14	250	90%	90%	.846	.682	.834	81%	90%	.0278	.0254
1.75	.11	450	90%	90%	.856	.750	.889	83%	90%	.0269	.0255
1.5	.07	1000	90%	90%	.858	.816	.932	85%	90%	.0263	.0257
1.25	.04	3750	90%	90%	.841	.861	.957	88%	90%	.0250	.0253
	Moderate event-rate setting: 60% 3-year survival on the best arm(s)
2	.47	75	60%	60%	.848	.759	.863	36%	60%	.0243	.0252
1.75	.37	125	60%	60%	.851	.794	.892	41%	60%	.0249	.0259
1.5	.25	250	60%	60%	.836	.815	.907	46%	60%	.0249	.0252
1.25	.13	1000	60%	60%	.864	.885	.953	53%	60%	.0252	.0253
	High event-rate setting: 20% 3-year survival on the best arm(s)**
2	.60	50	20%	20%	.816	.868	.900	4%	20%	.0264	.0248
1.75	.49	75	20%	20%	.817	.861	.897	6%	20%	.0251	.0249
1.5	.36	150	20%	20%	.845	.880	.913	9%	20%	.0251	.0250
1.25	.20	450	20%	20%	.816	.849	.888	13%	20%	.0250	.0250

^*Proportional hazards analysis performed after 3 years of accrual followed by 3 years of follow-up (6 years after study activation)

^**In trial replications where the minimum of the longest observed times on each arm was less than 3 years τ was set to the minimum of the longest observed times on the two arms (Tian et al.³¹)

Table 2:

Simulated rejection probabilities for superiority testing using the proportional hazards (Cox) and RMST methods (τ=3) under three event-rate settings with instant accrual or staggered accrual

Superiority designs
Target effect		Sample size per arm	Simulated powers					Simulated levels
HR	RMST (years)		3-yr surv (Exp arm)	3-yr surv (Contr arm)	RMST	Proportional hazards	Proportional hazards Staggered*	3-yr surv (Exp arm)	3-yr surv (Contr arm)	RMST	Proportional hazards
	Low event-rate setting: 90% 3-year survival on the best arm(s)
½	.14	250	90%	81%	.721	.817	.933	81%	81%	.0247	.0239
1/1.75	.11	450	90%	83%	.759	.856	.954	83%	83%	.0253	.0244
1/1.5	.07	1000	90%	85%	.791	.884	.967	85%	85%	.0249	.0255
1/1.25	.04	3750	90%	88%	.804	.896	.973	88%	88%	.0248	.0247
	Moderate event-rate setting: 60% 3-year survival on the best arm(s)
½	.47	75	60%	36%	.800	.856	.925	36%	36%	.0268	.0244
1/1.75	.37	125	60%	41%	.808	.870	.937	41%	41%	.0263	.0248
1/1.5	.25	250	60%	46%	.802	.870	.939	46%	46%	.0256	.0245
1/1.25	.13	1000	60%	53%	.846	.909	.965	53%	53%	.0256	.0252
	High event-rate setting: 20% 3-year survival on the best arm(s)**
½	.60	50	20%	4%	.891	.898	.913	4%	4%	.0258	.0263
1/1.75	.49	75	20%	6%	.876	.890	.909	6%	6%	.0263	.0255
1/1.5	.36	150	20%	9%	.880	.901	.922	9%	9%	.0258	.0248
1/1.25	.20	450	20%	13%	.834	.863	.895	13%	13%	.0253	.0252

^*Proportional hazards analysis performed after 3 years of accrual followed by 3 years of follow-up (6 years after study activation)

^**In trial replications where the minimum of the longest observed times on each arm was less than 3 years τ was set to the minimum of the longest observed times on the two arms (Tian et al.³¹)

The distribution of the RMST test statistics can be far from their putative normal distributions when the sample sizes are small, especially for noninferiority testing;²⁹ the inflated type 1 error in the low-event rate setting demonstrates this (e.g., .0278 in the top line of Table 1). To ensure the relatively high power seen for this case is not just due to the inflated type 1 error, we reran this simulation using the variance estimator suggested by Lawrence et al.²⁹ that uses a t-distribution with a Satterthwaite degrees of freedom estimator instead of a normal-distribution cut-off. The simulated type 1 error was then 0.0253 and the simulated power remained high at 0.833.

The asymptotic powers calculated using the noncentrality parameters in Table 3 approximate very closely the empirical powers given in Tables 1 and 2 (not shown). For example, in the first line of Table 1 the asymptotic powers are calculated to be 0.847 and 0.688 for the RMST and proportional hazards analyses, respectively, which can be compared to the simulation powers of 0.846 and 0.682. Therefore, we can examine these noncentrality parameters to better understand the changes in relative powers over various survival settings when testing noninferiority and superiority. Figure 1 is a plot of the noncentrality parameters as a function of the hazard ratio for the settings given in Tables 1 and 2, with the control (experimental) arm event rates kept fixed for noninferiority (superiority) designs. For noninferiority testing, the denominators of the noncentrality parameters in the top row of Table 3 are fixed and we can focus on the numerators: The noncentrality parameter is a logarithmic function of the hazard ratio for the proportional hazard analysis but is an approximately linear function of the hazard ratio for the RMST analysis. In the low event-rate setting this leads to the RMST noncentraility parameter (red line) being larger than that for the proportional hazards analysis (blue line) for hazards ratios larger than 1.5 (Figure 1A) - resulting in the better power of RMST in this setting (top lines of Table 1). Note that the benefits of the RMST analyses in this setting is not a small-sample phenomenon, but instead depends on the noninferiority margin being large and the event rate being low. With superiority testing, the denominators as well as the numerators of the noncentrality parameters depend on the hazard ratio and the noncentrality parameter for the RMST test is always below that for proportional hazards method explaining why benefits of the RMST methods are lost (right-hand panels of Figure 1).

Figure 1:

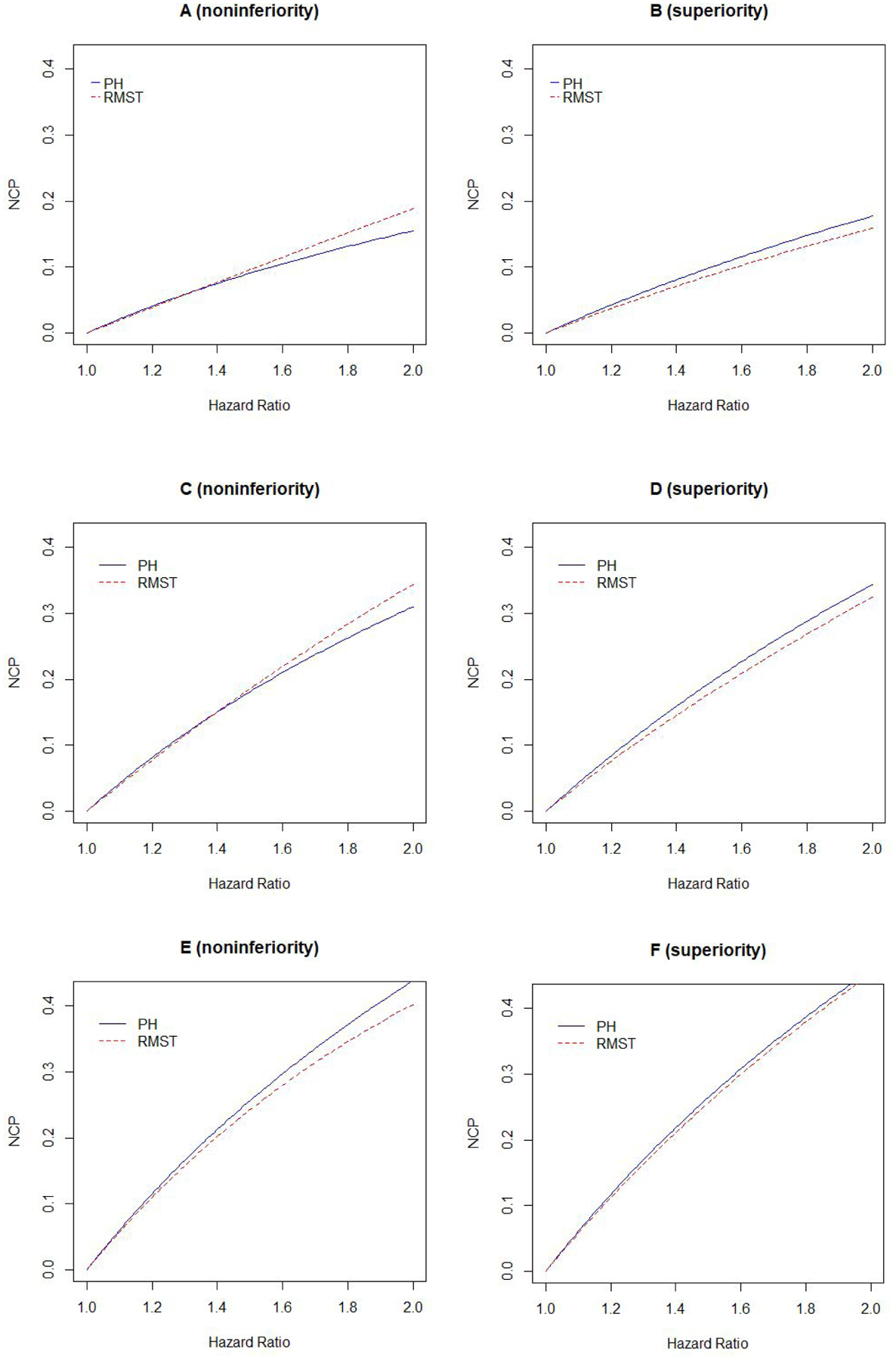
Noncentrality parameters for testing noninferiority (left panels) and superiority (right panels) using proportional hazards (blue solid lines) and RMST methods (red dashed lines). Top panels (A, B), middle panels (C, D) and lower panels (E, F) are for low, medium and high event rates as in Tables 1 and 2. Horizontal axes correspond to noninferiority margin hazard ratios for noninferiority panels (A,C,E) and the inverses of the targeted hazard ratio alternatives for the superiority panels (B, D, F).

Discussion

A summary of our simulation and asymptotic results suggest that the RMST power advantage over the proportional hazards methods for testing noninferiority is limited to the scenarios where (a) the survival rates are very high, (b) the targeted hazard ratio is large, and (c) few events are expected after the pre-specified τ. However, we caution that in these scenarios the bigger issue is choosing an appropriate noninferiority margin because a single summary measure may not accurately capture all clinically meaningful difference patterns in survival curves over a relevant time period (any summary measure would have to be interpreted in the context of the survival curves). Contrary to the suggestions that standard proportional hazards methods go awry because they do not account for differing baseline rates of events, we have found that in practice the targeted noninferiority hazard-ratio margin is frequently set with the baseline rates in mind. In the low event-rate setting, this is typically done by considering the margin as a difference in survival rates at a fixed time point. Note that in many low-event clinical settings like adjuvant cancer therapy differences in the long-term survival rates represent by far the most relevant summary measure of clinical benefit as the they reflect difference in cure rates. For example, in the TAILORx trial (NCT00310180),³⁰ a decrease in five-year disease-free survival from 90.0% to 87.0% was considered unacceptable. Assuming exponential distributions, this corresponds to a hazard ratio of 1.322, which was used as the noninferiority margin. In this setting, the hazard ratio has the simple interpretation of being approximately equal to the relative reduction in death rates at any fixed time point (8.0%/6.1%=1.31 at three years, 13%/10%=1.30 at five years, 20.0%/15.5%=1.29 at eight years). On the other hand, choosing a τ, and then choosing the number of days of RMST for this τ for a noninferiority margin seems less interpretable when the therapeutic goal is to preserve the long-term cure rate.