Abstract
The aims of this study were to describe the worst-case scenarios (WCS) in professional soccer players calculated by fixed length and rolling average methods with regards to each playing position. This was done, firstly, by comparing total distance (TD covered in the WCS; secondly, by comparing high-speed running distance (HSRD); and thirdly, by comparing sprint distance (SPD). The study was conducted over a three-mesocycle competitive period. The WCS of three distance-related variables (TD, HSRD, SPD) in four time windows (1, 3, 5, 10 minutes) were calculated according to playing position (central defender; full-back; midfielder, wide midfielder, and forward) using fixed length and rolling average methods. A significant effect of the type of method used to calculate the WCS in TD (F(1, 142) = 151.49, p < 0.001, ηp2 = 0.52), HSRD (F(1, 138) = 336.95, p < 0.001, ηp2 = 0.71) and SPD (F(1, 138) = 76.74, p < 0.001, ηp2 = 0.36) was observed. In addition, there was a significant interaction between type of method and WCS duration in TD (F(1.36, 193.53) = 41.95, p < 0.001, ηp2 = 0.23), HSRD (F(2.28, 315.11) = 21.77, p < 0.001, ηp2 = 0.14) and SPD (F(2.59, 358.41) = 6.93, p < 0.001, ηp2 = 0.05). In conclusion, the use of fixed length methods of different durations significantly underestimated the WCS of TD, HSRD and SPD across the most common playing positions in professional soccer players. Therefore, the application of rolling averages is recommended for an appropriate WCS analysis in professional soccer match-play.
Keywords: External load, GPS, Most demanding passage, Football, Performance
INTRODUCTION
Soccer is a team sport which combines intermittent high intensity periods of activity and longer periods of lower intensity activity [1–3]. In this context, strength and conditioning coaches are currently designing their training programmes based on match demands in order to prepare the players for the chaotic nature of the competition [4, 5]. However, from a practical perspective, it should be noted that the use of average demands may underestimate peak intensity periods of match-play [6]. In consequence, new methods have been developed recently aimed at quantifying peak intensity periods, which are also known as the most demanding passages (MDP) [5] or worst-case scenarios (WCS) [6].
The WCS are defined as the periods of 1, 3, 5 or 10 minutes of maximum physical output (distance covered at high speed running) throughout a match [4, 7]. The fixed length method was the first attempt to quantify the WCS [8] and consisted of splitting the total match into fixed periods from the start to the end of the match, for example, periods of 1 minute (0–59ʺ, 1–1.59ʺ, 2–2.59ʺ… until the end of the match); 3 minutes (0–2.59ʺ, 3–5.59ʺ… until the end of the match); 5 minutes (0–4.59ʺ, 5–9.59ʺ… until the end of the match); and 10 minutes (0–9.59ʺ, 10–19.59ʺ… until the end of the match). Nevertheless, the use of the rolling average method is currently considered more accurate for quantifying WCS [5] as this method detects the exact period (depending on the time selected for the analysis) in which the player is at peak intensity [6]. Thus, the WCS could be detected, for example, from the period 2ʹ53ʺ to 3ʹ53ʺ (1-minute WCS), from 2ʹ53ʺ to 5ʹ53ʺ (3 minutes), from 2ʹ53ʺ to 7ʹ53ʺ (5-minute WCS) or from 2ʹ53ʺ to 12ʹ53ʺ (10 minutes) [6].
In addition, the performance in the WCS is associated with different contextual variables (e.g., playing position, match location, match outcome, match half or congested calendars) [4, 5, 9–12]. For example, the WCS in soccer matches could be specifically analysed with regards to the playing position [4, 5, 9, 10]. It has recently been observed that midfielders (MF) and wide midfielders cover greater distance in WCS than other positions [4, 5], and when longer periods of WCS are analysed, there are even greater differences between playing positions [5]. Consequently, these differences are deemed important to optimally prescribe position-specific training load and therefore methodological studies are needed to analyse which analysis technique is more accurate to assess the physical demands of soccer players.
Despite the studies mentioned above, research on WCS has, to date, been limited. Methodological works on the comparison between the use of fixed length and rolling average methods are scarce in the literature. For example, a recent study found that the use of fixed length methods may underestimate WCS running demands [13]. However, variables including high-speed running actions such as sprinting distance (i.e., distance covered above 25.2 km/h), which are less frequent [5, 14, 15], were not analysed. Consequently, there is a risk of results misinterpretation since the use of fixed length methods may underestimate WCS in low- or medium-speed actions [6, 13] but it may be useful for high-speed actions.
Therefore, the main purpose of this study is to describe the WCS, in professional soccer players, calculated by fixed length and rolling average methods with regards to each playing position. This was done, firstly, by comparing total distance covered in the WCS; secondly, by comparing high speed running distance covered; and thirdly, by comparing sprint distance covered.
MATERIALS AND METHODS
A cohort study was conducted over an in-season three-mesocycle competitive period in LaLiga 123 with a total of twelve official professional soccer matches. The soccer matches were consecutive (one match per week) and played at home or away on Friday, Saturday or Sunday depending on the official calendar. The data were collected through wearable sensors (RealTrack Systems, Almería, Spain) to calculate players’ WCS. Four WCS periods were analysed: 1, 3, 5 and 10 minutes. Every soccer player was categorized according to their playing position: forward (FW), midfielder (MF), wide midfielder (WMF), full-back (FB) and central defender (CD).
Nineteen professional soccer players (mean ± SD; age, 26.78 ± 3.77 years old; body mass index, 23.1 ± 0.19) voluntarily participated in the study. The team playing formation was 4-2-3-1. Soccer players who did not complete the full match and goalkeepers were not included in the analysis. The data were derived from daily monitoring over the season and the club provided informed consent to use the dataset for research purposes. The study was also approved by the University of Almeria’s Ethics Board.
Total distance (TD), high speed running distance (HSRD, above 19.8 km/h) [5] and sprint distance (SPD, above 25.2 km/h) [5] were collected using WIMU Pro (RealTrack Systems, Almería, Spain). This is an inertial device with 3D accelerometers, gyroscopes and magnetometers which collects positioning data through a 10 Hz Global Positioning System (GPS). These tracking systems are considered as valid (bias in mean speed: 1.2–1.3 km/h; bias in distance: 2.3–4.3 m) and reliable (intraclass correlation coefficients: above 0.93) instruments for the analysis of time-motion parameters in soccer [16]. The devices were calibrated 30 minutes before the start of each match following the manufacturer’s instructions: first, the units were placed on a steady surface, then turned on, and finally, after waiting 30 seconds the recording of the session was started. The devices were then placed in a vertical position in the back pocket of a chest vest (Rasán, Valencia, Spain) designed for the players. Each player wore the same device in every match in order to avoid inter-unit error. Once the match had finished, the players returned the devices to the research team. The devices were placed on a Smart Station (RealTrack Systems, Almeria, Spain) and the data were transferred to the analysis software.
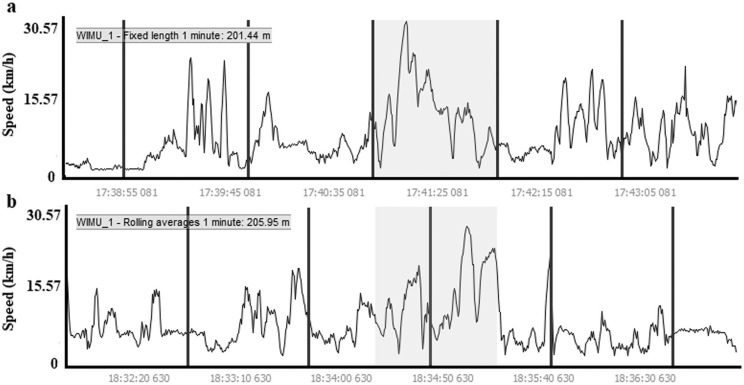
The data were analysed using SPro software (RealTrack Systems, Almeria, Spain). This software analyses GPS Speed raw data and two methods of analysis are applied: fixed-length and rolling-average. First, fixed length scenarios were obtained by splitting the total match into fixed periods, from the start to the end of the match, of 1, 3, 5 and 10 minutes (Figure 1a). Secondly, the rolling average method was used by means of an algorithm that detected and calculated the WCS of each variable at the four WCS durations (1, 3, 5 and 10 minutes). Given the 10 Hz sample frequency of the device (RealTrack Systems, Almería, Spain) and 1-minute WCS for instance (Figure 1b), the rolling average algorithm found the moment (60 seconds = 600 samples) when the player covered the greatest distance. Thus, the fixed length method calculated the WCS in static period samples (1–600, 601–1200, and so on).
FIG. 1.
Difference between fixed length (a) and rolling average methods (b) for WCS detection.
Regarding the statistical analysis, firstly, descriptive statistics were calculated for both methods (fixed length and rolling averages) based on playing positions (CD, FB, FW, MF, WMF) and WCS duration (1, 3, 5, 10 minutes). Secondly, the assumption of normality in each variable was analysed using the Shapiro-Wilk test. Thirdly, linear mixed models were performed using a 2 x 5 x 4 ANOVA design (methods*playing positions*WCS duration) to determine the difference between fixed and rolling average methods while accounting for potential effects and interactions with playing position and WCS duration. This analysis compares different means when there are two or more independent variables or factors, but at least one of the factors should be an intra-subject factor (e.g., method or WCS duration) and between-subjects factor (e.g., playing position). In addition, to assess the assumption of equal variance, Mauchly’s test of sphericity was performed using all the ANOVA results. A Greenhouse–Geisser correction was performed to adjust the degrees of freedom if the assumption was violated, while pairwise comparisons using a Bonferroni adjustment were employed if a significant main effect was observed. Effect sizes were also reported using partial eta-squared (ηp2). The level of significance was set at p ≤ 0.05 and the statistical analysis was carried out using IBM SPSS Statistics version 26 (IBM Corp., Armonk, NY, USA).
RESULTS
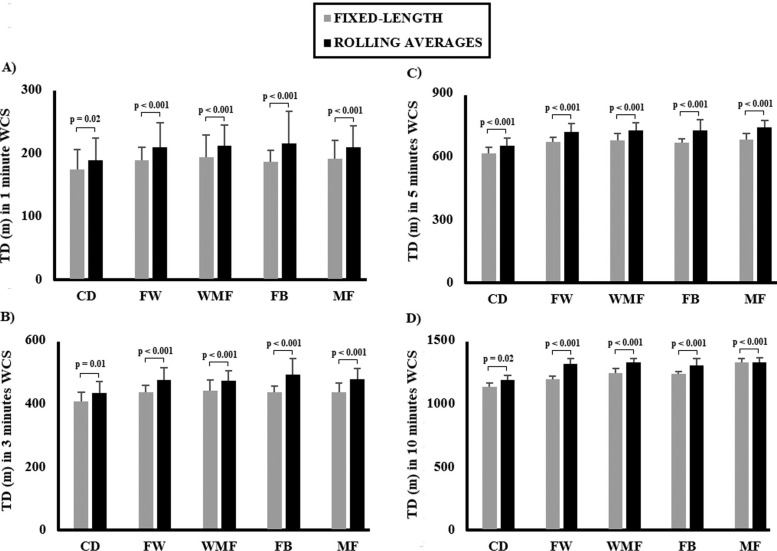
Figure 2 shows TD covered in meters for each WCS duration (1, 3, 5 and 10 minutes), which were calculated by fixed and rolling average methods. The rolling average method showed significantly greater TD (p < 0.05) than the fixed length method in all positions at each WCS duration. A significant effect of the type of method used to calculate the WCS in TD covered was observed (F(1, 142) = 151.49, p < 0.001, ηp2 = 0.52). In addition, there was a significant interaction between type of method and WCS duration (F(1.36, 193.53) = 41.95, p < 0.001, ηp2 = 0.23). The was no significant interaction between type of method and playing position (F(5, 142) = 1.13, p = 0.35, ηp2 = 0.04) or between method, playing position and WCS duration (F(6.81, 142) = 1.74, p = 0.11, ηp2 = 0.06).
FIG. 2.
Total distance (TD) covered in every WCS duration calculated for each playing position using fixed length and rolling averages.
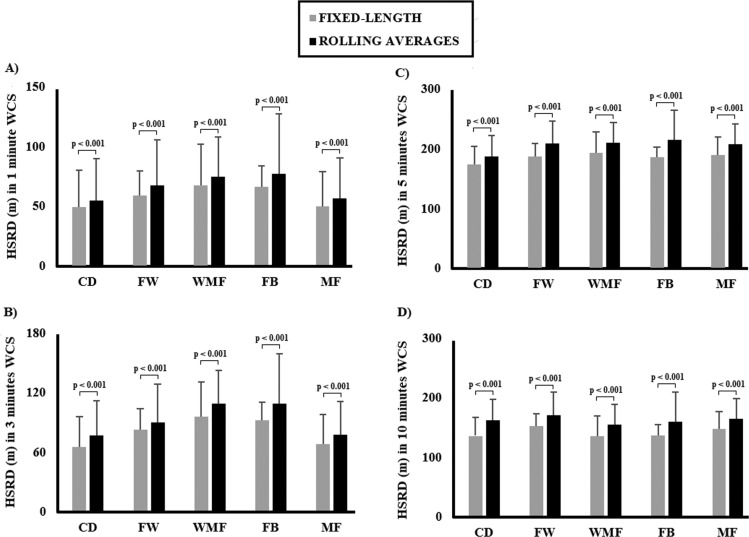
HSRD covered in meters for each WCS duration by fixed and rolling average methods is represented in Figure 3. The rolling average method showed significantly greater HSRD (p < 0.05) than the fixed length method in all positions at each WCS duration. A significant effect of the type of method used to calculate the WCS in HSRD covered was observed (F(1, 138) = 336.95, p < 0.001, ηp2 = 0.71). There was a significant interaction between method and playing position (F(5, 138) = 2.63, p = 0.03, ηp2 = 0.09) and between method and WCS duration (F(2.28, 315.11) = 21.77, p < 0.001, ηp2 = 0.14). However, the interaction method, playing position and WCS duration was not significant (F(11.41, 138) = 1.16, p = 0.30, ηp2 = 0.04).
FIG. 3.
High-speed running distance (HSRD) in every WCS duration calculated for each playing position using fixed length and rolling averages.
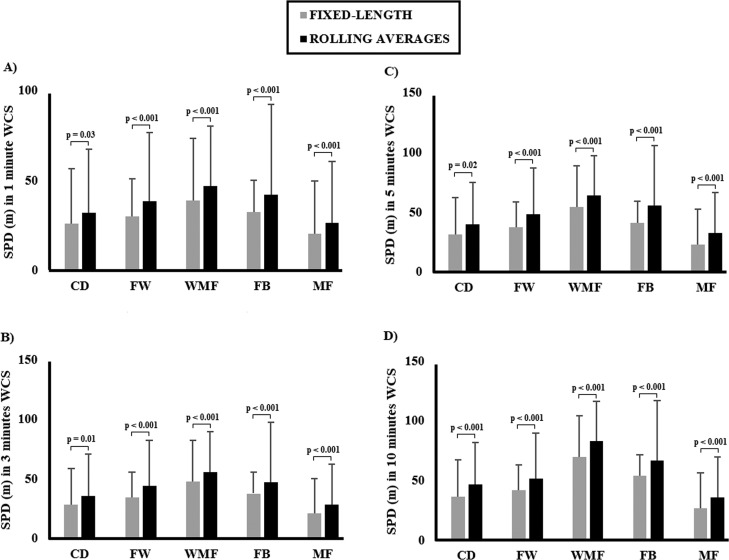
Subsequently and with regards to SPD covered (Figure 4), significant differences between fixed length and rolling averages were found for each WCS duration in all playing positions (p < 0.05). A significant effect of the type of method used to calculate the WCS in TD covered was found (F(1, 138) = 76.74, p < 0.001, ηp2 = 0.36). In addition, there was a significant interaction between type of method and WCS duration (F(2.59, 358.41) = 6.93, p < 0.001, ηp2 = 0.05). There was no significant interaction between type of method and playing position (F(5, 138) = 0.54, p = 0.75, ηp2 = 0.02) or between method, playing position and WCS duration (F(12.99, 138) = 0.91, p = 0.54, ηp2 = 0.03).
FIG. 4.
Sprint distance (SPD) covered in every WCS duration calculated for each playing position using fixed length and rolling averages.
DISCUSSION
This study compared the WCS calculated by fixed length and rolling average methods taking into consideration soccer playing positions and four WCS durations (1, 3, 5 and 10 minutes) in professional matches. From a practical perspective, it was necessary to investigate the interchangeability of both methods for the analysis of WCS in TD, HSRD and SPD, a methodology which had never been conducted in the scientific literature in relation to soccer. The main finding was that the use of fixed length methods of different durations significantly underestimated the WCS of TD, HSRD and SPD in all playing positions. In addition, a significant interaction between WCS duration and the method used to calculate the WCS was observed in all the external load variables.
Rolling averages calculated significantly greater TD (p < 0.05) than fixed length epochs in all positions at each WCS duration. Previous studies, which compared both methods in soccer players, also concluded that the fixed method produced significantly lower values compared to rolling averages in TD (10.1% difference) for 1 minute [13], 3 minutes (8.2% difference) [13], 5 minutes (7.5% difference and 25.2%, respectively) [13, 17], and 10 minutes (6.7% difference). This comparison has also been applied to rugby players, and the fixed length method underestimated the rolling averages WCS of TD for 1 minute (11.8% difference), 3 minutes (12.2% difference) and 5 minutes (11.4% difference) [6]. One of the main findings of this study was that WCS duration had a significant interaction with the method used to calculate the WCS (F(1.36, 193.53) = 41.95, p < 0.001, ηp2 = 0.23). Contrary to the findings of Ferraday et al. [13], which showed that the longer the WCS the lower the differences between methods, this study showed that the longer the WCS, the greater the differences between fixed length and rolling average methods in all playing positions. Since the same interaction was found but with different conclusions, future studies could investigate the association of WCS duration and type of method used to calculate the WCS and therefore replicate the results in a larger sample size.
In addition, MF, WMF and FB positions experienced higher peak demands in TD covered in soccer matches than positions such as FW and CD. This is consistent with previous research on the WCS of soccer matches which showed that there were positional differences in TD covered in 1-minute WCS (MF: ~204 m; WMF: ~201 m; FB: ~194 m; CD: ~181 m; FW: ~181 m), 3-minute WCS (MF: ~483 m; WMF: ~471 m; FB: ~453 m; CD: ~429 m; FW: ~414 m), 5-minute WCS (MF: ~750 m; WMF: ~730 m; FB: ~695 m; CD: ~665 m; FW: ~640 m) and 10-minute WCS (MF: ~1400 m; WMF: ~1350 m; FB: ~1280 m; ~CD: 1270 m; FW: ~1170 m) [5]. However, the results from our study showed that the interaction between the method used to calculate the WCS and playing position was not significant. Since the same results were obtained in a previous investigation [13], this suggests that soccer playing position does not have a significant influence on the method applied to calculate the WCS. Therefore, rolling averages are considered as the most appropriate method to quantify TD covered in WCS [4, 13, 18].
Regarding HSRD, a significant effect of the method was observed (F(1, 138) = 336.95, p < 0.001, ηp2 = 0.71). The rolling average method showed significantly greater HSRD covered (p < 0.05) than the fixed length method in all positions at each WCS duration. A few studies have previously compared HSRD using both methods in team sport matches [6, 13], but these authors obtained similar results to the current study. For example, HSRD was underestimated in WCS of 1 minute (10.6% and 11.7% difference, respectively) [6, 13], 3 minutes (19.5% and 21.1% difference, respectively) [6, 13], 5 minutes (21.3% and 22% difference, respectively) [6, 13], and 10 minutes (14.2% difference). Although there was a significant interaction between method and playing position, the effect size was small (F(5, 138) = 2.63, p = 0.03, ηp2 = 0.09). This implies that playing position does not have a meaningful impact on the differences between methods even though the effect of position on HSRD is higher than on TD. Perhaps this could be explained by the influence of high-speed variables on decreasing distance covered [5]. However, the interaction between method and WCS duration was significant (F(2.28, 315.11) = 21.77, p < 0.001, ηp2 = 0.14). The differences between methods were greater in longer WCS (p < 0.001), especially from 1 to 10 minutes. Consequently, the use of rolling averages for HSRD WCS detection is recommended and supported not only by previous research [4–6, 13, 19] but also by this study, which showed how HSRD was always underestimated using the fixed length method across all positions in every WCS duration.
Additionally, when SPD was analysed, rolling averages once again attained greater values than the fixed length method, with statistically significant differences for each WCS duration and playing position. This is the first study to compare both methods of WCS in SPD covered, and it is relevant to highlight that the only significant interaction observed was between WCS duration and method (F(2.59, 358.41) = 6.93, p < 0.001, ηp2 = 0.05). Given the nature of sprinting actions, in which the player needs to exceed 25.2 km/h, SPD might be time-dependent [4, 5, 19], which could explain why the effect of WCS duration on the differences between methods is lower in SPD compared to TD or HSRD. In addition, SPD might be position-dependent [5]. However, the results from our study showed that the interaction between the method used to calculate the WCS and playing position was not significant (F(5, 138) = 0.54, p = 0.75, ηp2 = 0.02), which implies that playing position does not have any significant effect on the method applied to calculate the WCS. Therefore, it could be concluded that SPD covered in WCS was directly dependent on the method used, suggesting rolling averages as the most appropriate method to quantify SPD.
This research has several limitations since it only analyses WCS of professional soccer players in four WCS durations (1, 3, 5 and 10 minutes) which were based on three variables (TD, HSRD and SPD). As this is the first research on the comparison between fixed length and rolling average methods, future studies are needed to provide more details about this analysis. Future research could focus on the analysis of shorter or longer WCS durations, analyse a different population (e.g., youth players) or include other variables such as accelerations/decelerations [20] and total of high intensity actions [21].
In conclusion, this study showed that fixed length methods underestimated the TD, HSRD and SPD covered in 1-minute, 3-minute, 5-minute, and 10-minute WCS across the most common playing positions in professional soccer players. Therefore, the use of rolling averages is recommended. Gaining knowledge on how technology is used to quantify WCS is important for applied practitioners who daily attempt to optimize performance through position-specific load management. For example, the values reported by rolling averages for TD, HSRD or SPD could serve as a reference when prescribing a 5-minute training drill trying to meet match WCS demands. However, the values reported by the fixed-length method would underestimate WCS across all playing positions. Thus, the results of this study also help to understand competitive match-play demands and plan strategies to prepare the players for official soccer matches.
Acknowledgements
José M. Oliva-Lozano was supported by a scholarship funded by the Spanish Ministry of Science, Innovation and Universities (FPU18/04434). Isabel Martín-Fuentes was supported by a scholarship funded by the Spanish Ministry of Science, Innovation and Universities (FPU17/03787).
Conflict of interest disclosure
The authors declare no conflicts of interest. All authors were involved in the research concept and study design; literature review, JM.O.L., I.M.F., and V.F.; data collection and interpretation, JM.O.L., I.M.F., and V.F.; statistical analyses, JM.O.L., JM.M.; writing, reviewing and editing of the manuscript, JM.O.L., and JM.M.
REFERENCES
- 1.Abbott W, Brickley G, Smeeton NJ. Positional differences in GPS outputs and perceived exertion during soccer training games and competition. J Strength Cond Res. 2018;32(11):3222–31. doi: 10.1519/JSC.0000000000002387. [DOI] [PubMed] [Google Scholar]
- 2.Rampinini E, Coutts A, Castagna C, Sassi R, Impellizzeri F. Variation in top level soccer match performance. Int J Sports Med. 2007;28(12):1018–24. doi: 10.1055/s-2007-965158. [DOI] [PubMed] [Google Scholar]
- 3.Oliva-Lozano JM, Gómez-Carmona CD, Pino-Ortega J, Moreno-Pérez V, Rodríguez-Pérez MA. Match and training high intensity activity-demands profile during a competitive mesocycle in youth elite soccer players. J Hum Kinet. 2020;75:1–11. doi: 10.2478/hukin-2020-0050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Delaney JA, Thornton HR, Rowell AE, Dascombe BJ, Aughey RJ, Duthie GM. Modelling the decrement in running intensity within professional soccer players. Sci Med Football. 2018;2(2):86–92. [Google Scholar]
- 5.Martin-Garcia A, Casamichana D, Diaz AG, Cos F, Gabbett TJ. Positional differences in the most demanding passages of play in football competition. J Sports Sci Med. 2018;17(4):563–70. [PMC free article] [PubMed] [Google Scholar]
- 6.Cunningham DJ, Shearer DA, Carter N, Drawer S, Pollard B, Bennett M, Eager R, Cook CJ, Farrell J, Russell M, Kilduff LP. Assessing worst case scenarios in movement demands derived from global positioning systems during international rugby union matches: Rolling averages versus fixed length epochs. PLOS ONE. 2018;13(4):1–14. doi: 10.1371/journal.pone.0195197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Reardon C, Tobin DP, Tierney P, Delahunt E. The worst case scenario: Locomotor and collision demands of the longest periods of gameplay in professional rugby union. PLOS ONE. 2017;12(5):1–11. doi: 10.1371/journal.pone.0177072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bradley PS, Sheldon W, Wooster B, Olsen P, Boanas P, Krustrup P. High-intensity running in English FA Premier League soccer matches. J Sports Sci. 2009;27(2):159–68. doi: 10.1080/02640410802512775. [DOI] [PubMed] [Google Scholar]
- 9.Oliva-Lozano JM, Fortes V, Muyor JM. The first, second, and third most demanding passages of play in professional soccer: a longitudinal study. Biol Sport. 2020;38(2):1–12. doi: 10.5114/biolsport.2020.97674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Oliva-Lozano JM, Rojas-Valverde D, Gómez-Carmona CD, Fortes V, Pino-Ortega J. Worst case scenario match analysis and contextual variables in professional soccer players: a longitudinal study. Biol Sport. 2020;37(4):1–10. doi: 10.5114/biolsport.2020.97067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Casamichana D, Castellano J, Díaz A, Gabbett T, Martin-Garcia A. The most demanding passages of play in football competition: a comparison between halves. Biol Sport. 2019;36(3):233–240. doi: 10.5114/biolsport.2019.86005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Castellano J, Martin-Garcia A, Casamichana D. Most running demand passages of match play in youth soccer congestion period. Biol Sport. 2020;37(4):367–73. doi: 10.5114/biolsport.2020.96853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fereday K, Hills SP, Russell M, Smith J, Cunningham DJ, Shearer D, McNarry M, Kilduff LP. A comparison of rolling averages versus discrete time epochs for assessing the worst-case scenario locomotor demands of professional soccer match-play. J Sci Med Sports. 2020;23(8):764–769. doi: 10.1016/j.jsams.2020.01.002. [DOI] [PubMed] [Google Scholar]
- 14.Palucci Vieira LH, Aquino R, Moura FA, Barros RML de, Arpini VM, Oliveira LP, Bedo BLS, Santiago PRP. Team dynamics, running, and skill-related performances of Brazilian u11 to professional soccer players during official matches. J Strength Cond Res. 2019;33(8):2202–16. doi: 10.1519/JSC.0000000000002577. [DOI] [PubMed] [Google Scholar]
- 15.Oliva-Lozano JM, Fortes V, Krustrup P, Muyor JM. Acceleration and sprint profiles of professional male football players in relation to playing position. PLOS ONE. 2020;15(8):1–18. doi: 10.1371/journal.pone.0236959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bastida Castillo A, Gómez Carmona CD, De la Cruz Sánchez E, Pino Ortega J. Accuracy, intra- and inter-unit reliability, and comparison between GPS and UWB-based position-tracking systems used for time–motion analyses in soccer. Eur J Sport Sci. 2018;31:1–8. doi: 10.1080/17461391.2018.1427796. [DOI] [PubMed] [Google Scholar]
- 17.Varley MC, Elias GP, Aughey RJ. Current match-analysis techniques’ underestimation of intense periods of high-velocity running. Int J Sports Physiol Perform. 2012;7(2):183–185. doi: 10.1123/ijspp.7.2.183. [DOI] [PubMed] [Google Scholar]
- 18.Martin-Garcia A, Castellano J, Diaz AG, Cos F, Casamichana D. Positional demands for various-sided games with goalkeepers according to the most demanding passages of match play in football. Biol Sport. 2019;36(2):171–180. doi: 10.5114/biolsport.2019.83507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lacome M, Simpson BM, Cholley Y, Lambert P, Buchheit M. Small-sided games in elite soccer: does one size fit all? Int J Sports Physiol Perform. 2018;13(5):568–76. doi: 10.1123/ijspp.2017-0214. [DOI] [PubMed] [Google Scholar]
- 20.Aamot IL, Karlsen T, Dalen H, Støylen A. long-term exercise adherence after high-intensity interval training in cardiac rehabilitation: a randomized study. Physiother Res Int. 2016;21(1):54–64. doi: 10.1002/pri.1619. [DOI] [PubMed] [Google Scholar]
- 21.Aquino R, Munhoz Martins GH, Palucci Vieira LH, Menezes RP. Influence of match location, quality of opponents, and match status on movement patterns in Brazilian professional football players. J Strength Cond Res. 2017;31(8):2155–2161. doi: 10.1519/JSC.0000000000001674. [DOI] [PubMed] [Google Scholar]