Ex vivo porcine iris stiffening due to drug stimulation

Abstract

The purpose of this study was to quantify how the elastic modulus of the ex vivo iris changes following stimulation by pilocarpine (PILO), phenylephrine (PE), and tropicamide (TROP). Irides (n = 20) were dissected from porcine eyes within 4 h post-mortem and tested uniaxially. Either the entire iris or sector thereof was used. The samples were stretched up to 40% Green strain. The radial modulus was calculated from the linear portion of the stress–strain curve, and the azimuthal modulus was fitted to a model treating the iris as a collection of circular elastic bands. One of the three drugs (n = 6 or 7) of interest was added (80 µg/ml) to the bath surrounding the tissue, and the test was repeated. Changes in pupil diameter of free-floating samples and isometric force of mounted samples confirmed that the tissue was responsive to the drugs. The untreated iris modulus for cut sections in radial extension was 4.0 ± 0.9 kPa (mean ± s.d., n = 20), and treated iris modulus was 7.7 ± 2.0 kPa (PILO, n = 7), 6.9 ± 2.2 kPa (PE, n = 6), and 8.4 ± 1.7 kPa (TROP, n = 7). Intact irides (n = 10) gave similar trends but values approximately 25% higher, presumably due to support from the nominally unloaded tissue. The azimuthal modulus of the untreated iris was 2.97 ± 1.3 kPa (n = 5), and that of the treated iris (PILO) was 5.34 ± 2.1 kPa. Although PILO, PE, and TROP work by different mechanisms, all three had similar results – an increase of modulus by a factor of two. These results suggest that in most normal situations the iris remains compliant at all pupil diameters.

1. Introduction

Most forms of glaucoma are associated with elevated intraocular pressure, but the mechanism of pressure increase varies with different forms of the disease. Of interest to us are the forms of glaucoma with a pathologically deformed iris contour. For example, in pigment dispersion syndrome and pigmentary glaucoma the iris is displaced posteriorly and rubs against the lens and zonules, releasing pigment that eventually becomes lodged in the trabecular meshwork (Farrar and Shields, 1993; Karickhoff, 1992; Potash et al., 1994; Ritch, 2004). Whereas in angle-closure glaucoma the iris is displaced anteriorly, obstructing the aqueous humor outflow pathway. One form of angle-closure glaucoma involves pupillary block (obstruction between the pupillary margin and the crystalline lens), with secondary anterior bowing of the iris and angle obstruction (Hong et al., 1996; Mapstone, 1978). While angle closure events are most likely to occur at mid-dilation, the exact role of iris mechanics in angle closure remains poorly understood. One possible explanation for the narrowing of the angle at middilation is extreme stiffening of the stretched iris dilator during pupil constriction, which at large strain might decrease the flexibility of the iris enough to bow forward when the pupil is constricted. It is possible that although constriction of the pupil increases pupillary block, stiffening of the iris could prevent significant anterior bowing. In evaluating this possibility, it is necessary to assess changes in iris stiffness with pupil size.

Changes in the mechanical interactions within the eye clearly play a role in the clinical conditions described above, but the detailed mechanical properties of the iris and other ocular components are not well understood. The ultrastructure of the iris has been well characterized (Bartholomew et al., 1997; Freddo, 1996), but to our knowledge, there has been little done on the mechanical characterization of the iris. The only previous studies regarding the mechanical behavior of the iris are a study measuring the relative magnitude of force induced in the iris periphery by pilocarpine and phenylephrine (Tabandeh et al.,1995), our previous mechanical characterization on the untreated cadaveric bovine iris (Heys and Barocas, 1999), and a more recent study measuring the mechanical properties of isometrically contracting or isotonically released the rabbit iris sphincter and dilator (Yamaji et al., 2003). The studies found that the iris generated a mean relative force of 27.5 ± 5.7 × 10⁻³ N when activated with pilocarpine and 23.3 ± 4.0 × 10⁻³ N with the application of phenylephrine (Tabandeh et al., 1995), the largest constrictive and dilative force occurred at the minimum and maximum pupil diameter (Yamaji et al., 2003), and the elastic passive modulus of a bovine iris is 9.6 ± 2.0 kPa (Heys and Barocas,1999) illustrating that actually very little known about the mechanical characterization of the iris tissue.

Mechanical analysis of the iris requires the consideration of its two constituent muscles: the inner sphincter iridis and the outer dilator pupillae, shown in Fig. 1. The sphincter and dilator are antagonistic muscle groups and maintain the delicate balance of forces necessary to allow rapid, tight control of pupil diameter. The dilator is a smooth muscle composed of modified pigment epithelial cells arranged radially and is sympathetically innervated. The sphincter, in contrast, is a typical smooth muscle arranged circumferentially and innervated by the parasympathetic nervous system (Vale and Cox, 1978). At maximum constriction the fibers of the sphincter iridis can shorten by a factor of eight, an amount seldom seen in any smooth or striated muscle in the body (Alexandridis, 1985).

Fig. 1.

Frontal view of the porcine iris: (a) schematic diagram of iris illustrating the constituent muscles, (b) dissected porcine iris, and a (c) light micrograph section of the iris.

The hypotheses tested in this work were (1) that stimulation of the iris muscles by pharmaceuticals produces a significant change in their mechanical properties, (2) that the change can be quantified by an elastic modulus measured in radial and circumferential tension, and (3) that such changes could have a significant effect on the mechanics of pupillary block.

2. Materials and methods

2.1. Tissue preparation

All experiments were conducted using isolated porcine irides received from Experimental Surgical Services or Visible Heart Research Laboratory at the University of Minnesota, in compliance with the ARVO statement for use of animals in ophthalmic and vision research. The porcine model was used for convenience, rapid post-mortem availability, size, and anatomical similarity to the human eye (Prince, 1960). Enucleated eyes were isolated and refrigerated in a modified Krebs–Ringer bicarbonate (KRB) buffer for testing within 4 h post-mortem. The KRB buffer used was of the following millimolar composition: 118 NaCl, 25 NaHCO₃, 4.7 KCL, 1.2 KH₂PO₄, 1.2 MgSO₄, 1.25 CaCl₂, and 10 glucose. Removal and dissection of the iris from the eye globe was done by making a small incision through the sclera, roughly 1 mm below the edge of the corneoscelera boundary, and cutting around the entire perimeter. The procedure was similar to the dissection technique for penetrating keratoplasty (Vajpayee et al., 1994). The anterior portion of the eye, containing the cornea, iris, and lens, was then removed, and the iris was peeled away from the sclera.

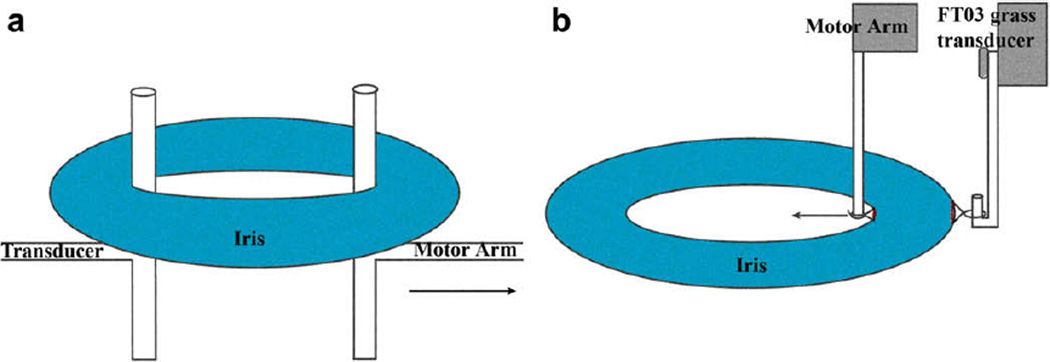
Intact (n = 10) and cut (n = 20) irides were mounted on one of two mechanical testing systems, circumferential or radial (Fig. 2), to measure force. The circumferential loop extension used a T-bar mounting system on a uniaxial MTS 895 Micro-Bionix Test System (MTS Systems Corp., Eden Prairie, MN). The MTS was equipped with a 0.5 N load cell and an LVDT with resolution 0.15 µm. The radial extension tests were performed using an in-house system equipped with an Aurora Scientific 318-B motor (Aurora Scientific Inc., Aurora, Ontario, Canada) and Grass FT-03 transducer with a 50 g load cell (Astro-Med, Inc. West Warwick, RI).

Fig. 2.

Mechanical testing experimental setup. An illustration of the mechanical test setup for the (a) circumferential extension and (b) radial extension.

During the experiment, the irides were submerged in KRB buffer temperature regulated at 37 °C using a Dagan TC-10 temperature controller (Dagan Instruments, Minneapolis, MN) and bubbled with 95% O₂ and 5% CO₂ to maintain a physiological pH of 7.5 to ensure muscle activation. Three common ophthalmic drugs activated the iris muscle, and muscle activation was verified by measuring pupil diameter changes in free-floating samples and isometric force changes on mounted samples. The initial and post-drug thicknesses was measured by taking ultrasound images (n = 5) of the iris in the globe before and after the application of the drugs and then using the ImageJ software (NIH) to quantify the average mid-iris thickness.

2.2. Radial extension

A resting tension of 0.5 gf was applied to the tissue to define the rest length L₀. The samples were then stretched to 40% Green strain (ε_g),

$${\epsilon }_{\mathrm{g}}=\frac{1}{2}[{\lambda }^2-1]$$ (1)

and the second Piola–Kirchhoff stress (σ_s) was calculated,

$${\sigma }_{\mathrm{S}}=\sigma {\left[\frac{1}{\lambda }\right]}^2$$ (2)

where λ = L/L₀ and L is the length of the stretched sample and σ is the Cauchy tensile stress (Bonet and Wood, 1997). Three to five preconditioning cycles were performed in order to ensure repeatable loading and unloading behavior in all trials. One of the three drugs (n = 6 or 7), pilocarpine (PILO), phenylephrine (PE), or tropicamide (TROP) was mixed (80 µg/ml) in the bath surrounding the tissue after the mechanical test was conducted first with no drug. Stretches were made using extension rates between 1 and 100 mm/min to assess viscoelasticity resistance to rapid extension (Fig. 3) and the experiments used to calculate the modulus were conducted at an extension rate of 10 mm/min. The radial extension modulus, E_r, was calculated from a linear fit of the stress–strain curve between 10 and 25% Green strain (ε_g).

Fig. 3.

Assessment of the viscoelastic response to variable extension rates. No significant differences were found in the results when the extension rates were increased from 1.0 (a), 5.0 (b), 10 (c), and 100 mm min⁻¹ (d) indicating negligible retardation.

The circumferential modulus, E_c, was calculated following the method of Heys and Barocas (1999) for cadaveric bovine irides. The model treated the iris as a collection of independent circular elastic bands of rest length L₀ = 2πr, where r is the radial position. The total force exerted by the iris at a given extension was then defined by the integral,

$$F=\underset{R_i}{\overset{R_o}{\int }}\sigma [L,L_o(r)]h\mathrm{d}r$$ (3)

where R_i and R₀ are the inner and outer radii of the iris, L is the stretched length (equal to twice the distance between the posts plus the circumference of the posts), and h is the thickness of the iris. Due to the large deformations involved, a neo-Hookean model was used yielding the following expression for the exerted stress at each radial position assuming the iris buckles and supports no load in compression:

$$\sigma [L,L_{\mathrm{o}}(r)]=\{\begin{array}{cc}0\hfill & L\le L_{\mathrm{o}}\hfill \\ \frac{E(r)}{3}[{\left(\frac{L}{L_{\mathrm{o}}}\right)}^2-\frac{L_o}{L}]\hfill & L>L_{\mathrm{o}}\hfill \end{array}$$ (4)

where E(r) is the elastic modulus (Heys and Barocas, 1999). In the current analysis, unlike the Heys and Barocas model, the modulus was assumed to be constant within both constituent iris muscles, the sphincter and dilator. The azimuthal modulus was then determined by a one-parameter fit of the force from Equations (3) and (4),

$$F=\frac{E_{\mathrm{c}}h{[L+\pi (R_{\mathrm{p}}-R_{\mathrm{i}})]}^2[2L+\pi (2R_{\mathrm{p}})]}{2{\pi }^2{R}_{\mathrm{i}}(L+\pi R_{\mathrm{p}})}$$ (5)

where E_c is the circumferential modulus and R_p is the radius of the post on which the iris was looped (R_p = 750 µm).

2.3. Drugs

The three drugs used in the experiment to stimulate pupil activation were 1% PILO for contraction and 2.5% PE, 1% TROP for dilation. Working as a muscarinic acetylcholine agonist, PILO simulates parasympathetic nerve activity and causes pupil constriction via the sphincter muscles. PE stimulates the sympathetic nerve activity causing pupil dilation. TROP, similar to PE, causes pupil dilation, but is an anticholinergic drug that blocks the responses of the sphincter muscle to cholinergic stimulation. During the experimental trials, after control measurements,100 µg/mL of drug stock solution was added to the KRB solution for stimulation.

2.4. Statistical analysis

Statistical analysis was performed using MacAnova, a statistical analysis software package. All measurements and calculated values are expressed as a mean ± SD. Analysis of variance (ANOVA) was performed on a six-by-six statistical block on the following factors: drug, sex and weight of pig, age of tissue postmortem, sample preparation (intact vs. cut), and carry-over drug effects. Student’s t-tests and pairwise comparisons were also made to determine whether significant differences existed among the three drug treatments. A value of p < 0.05 was classified as significant.

3. Results

3.1. Drug activation

Changes in pupil diameter of free-floating samples with the addition of 80 µg/mL of drug occurred instantaneously and are visually evident in Fig. 4. The addition of PILO, as expected, caused mydriasis, and PE and TROP caused miosis. The pupil diameter change (n = 5) in the response to pharmaceutical stimulation is shown in Fig. 5 and indicates that PILO had a greater effect on the pupil diameter compared to the other two drugs, a result assumed to be due to the unique characteristics of the sphincter and the lack of peripheral attachment. Fig. 5 also shows that PILO induced contraction at a velocity of approximately 20 mm/min, PE at 5 mm/min, and TROP at 50 mm/min. The maximum iris isometric force generated from a concentration of 80 µg/mL PILO was 0.16 gf. ANOVA analysis indicated that drugs and post-mortem tissue age after enucleation were significant, p < 0.05. At the time of testing the tissue age post-mortem was placed into four time blocks: 0–4, 4–8, 8–12, and 12þ h, and it was found that tissue older than 8 h was not activated by any of the drug treatments. Therefore only tissue less than 4 h post-mortem was used in this study (Fig. 6).

Fig. 4.

Drug effects of PILO and PE on free-floating porcine irides. The irides were submersed in a KRB buffer temperature regulated at 37 °C to ensure muscle activation: (a) No Drug (control), (b) PILO, and (c) PE.

Fig. 5.

Active iris response to pharmaceutical stimulation. There was an instantaneous change in the pupil diameter after addition of PILO, PE, and TROP. Iris diameter results are shown as average ± s.d. (n = 6).

Fig. 6.

Radial extension stress–strain diagram for intact and cut irides with the addition of PILO, PE, TROP. (a) A typical stress–strain relationship for intact-iris tests on passive (CONTROL) and active (PILO, PE, and TROP) irides. (b) A typical stress–strain relationship for the cut-iris tests on passive and active irides. The stress and strain measures are represented by Green strain (ε_g) and the second Piola-Kirchhoff stress (σ_s) for large deformation analysis.

3.2. Viscoelasticity

The radial and circumferential extension tests showed no significant change when the extension rate was increased from 1 to 100 mm/min, indicating negligible retardation, Fig. 3. These results, in combination with our previous findings (Heys and Barocas, 1999), support the assumption that viscoelasticity is a small factor in the mechanical analysis of the iris. Since the iris showed little viscoelastic response, variable velocities were not considered and testing was performed at a constant rate of 10 mm/min for all experiments. This rate was also consistent with the pupil velocities observed following drug administration.

3.3. Radial extension

A typical stress–strain curve for intact and cut radial extension experiments can be seen in Fig. 7; all three drugs caused an increase in tissue stiffness. For the cut irides in radial extension, the passive-iris modulus was 4.0 ± 0.9 kPa (n = 20), and the activated iris modulus was 7.7 ± 2.0 (PILO, n = 7), 6.9 ± 2.2 (PE, n = 6), and 8.4 ±1.7 (TROP, n = 7). Intact irides (n = 10) followed similar trends, but yielded approximately 25% higher values. Presumably this result occurred because the shape of the intact-iris made the stress and strain fields inhomogeneous within the sample. The radial modulus increased significantly (p < 0.05) with the addition of all three drugs, with the final value roughly twice the initial value. A summary of the intact and cut radial moduli can be seen in Fig. 8. No significant differences in the moduli were found between cut and intact samples or among the three drugs applied.

Fig. 7.

Radial modulus drug effect summary for intact and cut irides. No significant difference (p > 0.05) was found between strip and intact samples or between any three of the drug treatments PILO, PE, and TROP. The modulus increased significantly (*, p < 0.05) with the application of any drug resulting in a final value roughly twice the initial value. The maximum force and modulus were also dependent on the concentration of the drugs. Modulus values are average ± SEM. The sample size is illustrated at the base of each bar graph.

Fig. 8.

Azimuthal stress–strain diagram with the addition of PILO. A typical displacement–force curve for an intact-iris is shown. The passive (triangle) and PILO-treated (circle) curves are shown; and in each case the line represents a one-parameter fit of Equation (5).

3.4. Circumferential extension

A typical force–length curve for azimuthal extension before and after the application of PILO is shown in Fig. 8. The raw data was fit with Equation (5) with the modulus, E_c, as the fitting parameter. Unlike the radial extension tests, the force–length curve for azimuthal extension tests had a low slope in the small-extension region, attributed to the loop geometry, which did not place the tissue in tension immediately. The recruitment model fit the data extremely well with an R² value of 0.9981, yielding an average passive-iris azimuthal modulus of 2.97 kPa, and 5.33 kPa for the PILO-activated modulus. On average, the azimuthal modulus increased by a factor of 1.7, consistent with the results from the radial extension tests. The circumferential modulus values were significantly smaller (p < 0.05) than the radial modulus values.

4. Discussion

To our knowledge, our work represents the first experimental study evaluating mechanical changes (measured by a modulus) induced by stimulating the iris with ophthalmic drugs. A key result we found was an increase of the modulus two- to three-fold at maximum when either the sphincter or dilator was activated; supporting the hypothesis that dilation and contraction affects major structural components of the iris. Our results agree with Newsome and Loewenfeld (1971), who divided the iris into two portions an inner and outer ring, and visually tracked the change in surface area and radius of the two portions when the iris was stimulated. The changes in size and shape of the two iris regions were the same regardless of the method of activation; for example, parasympathetic, sympathetic, or adrenergic stimulation. Their study parallels our result that PILO, PE, and TROP all increased the passive modulus by a factor of two. This outcome is significant since our initial assumption was that different methods of activation (i.e. sphincter or dilator) would result in a measurable stiffness difference.

For the circumferential extensions the nonlinearity observed experimentally was consistently captured by a recruitment model using only one physical parameter (E_c) and unlike the cadaveric bovine irides mechanical tests (Heys and Barocas, 1999), the sphincter and dilator remained intact. The modulus was assumed to be constant throughout both muscles, but further analysis with the goal of separating the individual mechanical characteristics of the two constituent muscles requires further study. For the radial study, a detailed characterization of the mechanical behavior would clearly require a more sophisticated approach than the simple tangent modulus calculated here, but our goal was primarily to compare samples under different conditions, for which the tangent modulus is sufficient. A complete analysis of iris biomechanics would also have to account for the complex architecture of the iris, including the localization of the dilator to the posterior iris and potential mechanical differences between the dilator and stroma, which could not be evaluated in the current study because the dilator and stroma were loaded in parallel.

Our results for the untreated modulus of the iris (radial and circumferential) compare favorably with studies of other smooth muscles. In these studies, in a range of 1–100 kPa was observed (Azuma and Hasegawa, 1973; Murphy, 1980; Sarma et al., 2003). Herein, the untreated porcine iris modulus is similar to the reported bovine iris dilator muscle modulus of 9.6 ± 2.0 kPa (Heys and Barocas, 1999). The two-fold increase following muscle activation by pharmaceutical stimulation was surprisingly small. Other activated smooth muscle experiments have found that stiffness increased by a factor of 3.5 (Armentano et al., 1990) up to 10 (Murphy, 1980) with stimulation. In contrast, we found a smaller magnitude of response for the smooth muscle modulus in both the untreated and treated cases. This difference may be in part due to the unknown pharmaceuticals and anesthetization administered to the pigs prior to the enucleation of the eyes since other studies have found that vasoconstriction in large arteries was effected in anesthetized animals (Dobrin, 1984; Teranishi et al., 2000).

Deformation of the iris from the normal position occurs in many forms of glaucoma, e.g. angle closure or pigmentary glaucoma. Like any muscular tissue, the iris can deform actively due to muscle contraction or passively due to external stresses and pressure, i.e. the aqueous humor. We have made preliminary measurements of the active mechanical properties of the porcine iris. Although the ex vivo model has limitations (e.g. lack of blood flow and blood pressure, which could contribute to the measured stiffness), these results suggest that there is a statistically significant but fairly small change in the iris modulus when treated with pupil-active drugs. We conclude that pharmaceutical stimulation of the iris induces changes in the elastic modulus that is statistically significant, but that the effect may not be practically significant. Importantly, the observed mechanical change during pupil constriction would not be sufficient to prevent anterior bowing due to pupillary block since Heys et al. (2001) and Huang (2005) have shown that a five-fold change in iris stiffness has a negligible effect on iris contour.