Abstract
We report structural and computational studies of three α-aminophosphonates 4-XC6H4–NH–CH(4-BrC6H4)–P(O)(OiPr)2, namely diisopropyl((4-bromophenyl)(phenylamino)methyl)phosphonate (X = H, 1), diisopropyl((4-bromophenyl)((4-bromophenyl)amino)methyl)phosphonate (X = Br, 2) and diisopropyl((4-bromophenyl)((4-methoxyphenyl)amino)methyl)phosphonate (X = MeO, 3). The structures of 1–3 were fully confirmed by means of the 31P{1H} and 1H NMR spectroscopy. Crystal structures of 2 and 3 are isostructural and each contain two independent molecules in the asymmetric unit cell. Energy frameworks have been calculated to analyze the overall crystal packing of 1–3. The DFT calculations were performed to verify the structures of 1–3 as well as their electronic and optical properties. Molecular docking was applied to examine the influence of both the (S)- and (R)-enantiomers of 1–3 on a series of the SARS-CoV-2 proteins.
Keywords: Aminophosphonate, Crystal structure, Hirshfeld surface analysis, Computational studies, DFT, Molecular docking
Graphical abstract
We report structural and computational studies of three closely related α-aminophosphonates 4-XC6H4–NH–CH(4-BrC6H4)–P(O)(OiPr)2, namely diisopropyl((4-bromophenyl)(phenylamino)methyl)phosphonate (X = H, 1), diisopropyl((4-bromophenyl)((4-bromophenyl)amino)methyl)phosphonate (X = Br, 2) and diisopropyl((4-bromophenyl)((4-methoxyphenyl)amino)methyl)phosphonate (X = MeO, 3). The structures of 1–3 were fully confirmed by means of the 31P{1H} and 1H NMR spectroscopy. The geometrical parameters of all molecules are very similar. Two molecules in the crystal structures of 1–3 are interlinked through a pair of intermolecular N–H⋯O=P hydrogen bonds. Theoretical calculations based on density functional theory (DFT) were performed to verify the structures of 1–3 as well as their electronic and optical properties. The global chemical reactivity descriptors were estimated from the energy of the HOMO and LUMO. Molecular docking was applied to examine the influence of 1–3 on a series of the SARS-CoV-2 proteins. All the discussed aminophosphonates showed the best binding energies (−7.70 ÷ −8.00 kcal/mol) towards nonstructural protein 14 (nsp14 N7-MTase).

1. Introduction
α-Aminophosphonic acids are known to be close analogues of α-amino acids, where a less bulky and planar carboxyl group is replaced by a phosphonic acid group with a tetrahedral geometry (Chart 1). More than sixty years ago the biological activity of α-aminophosphonates was discovered [1,2], and nowadays both the chemistry and biology of α-aminophosphonates constantly attract a particular interest within the broad field of (organo)phosphorus chemistry [3]. Due to fascinating biological properties, α-aminophosphonates are of great interest and importance for practical application in many fields, such as agriculture, pharmacy, medicine, etc. [[4], [5], [6], [7], [8], [9], [10], [11], [12], [13]].
Chart 1.
Diagrams of α-aminophosphonic acid and α-amino acid.
One of the main structural features of α-aminophosphonates is the presence of the P–C–N backbone (Chart 1), which provides a broad structural modification of the resulting product, thus yielding a broad panel of biological properties [13]. Furthermore, the P–C–N fragment can also be chiral, producing certain stereoisomers. As such, one of the most efficient synthetic procedures towards α-aminophosphonates is the Kabachnik-Fields reaction [14]. This one-pot reaction involves three components, namely a primary amine, a carbonyl compound and a dialkylphosphite. Notably, when an aldehyde is used as a carbonyl compound, chiral α-aminophosphonates are obtained due to the generation of the chiral carbon center in the P–C–N backbone. Furthermore, α-aminophosphonates can possess an intriguing biological activity upon incorporation of aryl-containing functionalities in the structure of a molecule [15,16].
With all this in mind, we have also directed our attention towards α-aminophosphonates. In this work we focused on the synthesis, NMR and structural characterization of a series of closely related α-aminophosphonates of the common formula 4-XC6H4–NH–CH(4-BrC6H4)–P(O)(OiPr)2, namely diisopropyl((4-bromophenyl)(phenylamino)methyl)phosphonate (X = H, 1), diisopropyl((4-bromophenyl)((4-bromophenyl)amino)methyl)phosphonate (X = Br, 2) and diisopropyl((4-bromophenyl)((4-methoxyphenyl)amino)methyl)phosphonate (X = MeO, 3). We shed more light on the crystal structures of 1–3 using Hirshfeld surface analysis to in-depth examine non-covalent interactions responsible for crystal packing. Furthermore, energy frameworks have been calculated to study the overall crystal packing. Theoretical calculations based on density functional theory (DFT) were performed to verify the structures of 1–3 as well as their electronic and optical properties. The global chemical reactivity descriptors were estimated from the energy of the HOMO and LUMO. Using an in silico molecular docking method, we have explored the binding modes and interactions of 1–3 with binding sites of the SARS-CoV-2 proteins as targets at the atomic level.
2. Experimental
2.1. Physical measurements
NMR spectra in CDCl3 were recorded with a Bruker DPX FT/NMR-400 spectrometer at room temperature. Microanalyses were performed using a LECO-elemental analyzer.
2.2. Synthesis
A mixture of 4-bromobenzaldehyde (0.185 g, 1 mmol), diisopropylphosphite (0.166 g, 1 mmol) and aniline or 4-bromoaniline or 4-methoxyaniline (0.093, 0.172 and 0.123 g, respectively; 1 mmol) in toluene (8 mL) was heated under reflux for 12 h. The solvent was then removed in vacuo and the resulting crude product was recrystallized from a CH2Cl2/n-hexane (1:3, v/v) mixture.
2.2.1. Diisopropyl((4-bromophenyl)(phenylamino)methyl)phosphonate (1)
Yield: 0.371 g (87 %). 1H NMR: δ = 1.04 (d, 3 J H,H 6.2 Hz, 3H, CH3), 1.27 (d, 3 J H,H 6.2 Hz, 3H, CH3), 1.31 (d, 3 J H,H 6.1 Hz, 3H, CH3), 1.35 (d, 3 J H,H 6.1 Hz, 3H, CH3), 4.48–4.89 (m, 4H, OCH + C(H)NH), 6.60 (d, 3 J H,H 7.8 Hz, 2H, o-Ph), 6.74 (t, 3 J H,H 7.3 Hz, 2H, m-Ph), 7.14 (d, 3 J H,H 7.8 Hz, 1H, p-Ph), 7.39 (d. d, 3 J H,H 8.5 Hz, 4 J H,H 2.3 Hz, 2H, o-C6H4), 7.50 (d, 3 J H,H 8.4 Hz, 2H, m-C6H4) ppm. 31P{1H} NMR: δ = 20.0 ppm. Anal. calc. for C19H25BrNO3P (426.29): C 53.53, H 5.91 and N 3.29 %; found: С 53.75, Н 5.98 and N 3.18 %.
2.2.2. Diisopropyl((4-bromophenyl)((4-bromophenyl)amino)methyl)phosphonate (2)
Yield: 0.470 g (93 %). 1H NMR: δ = 1.01 (d, 3 J H,H 6.1 Hz, 3H, CH3), 1.22 (d, 3 J H,H 6.1 Hz, 3H, CH3), 1.27 (d, 3 J H,H 6.1 Hz, 3H, CH3), 1.32 (d, 3 J H,H 6.0 Hz, 3H, CH3), 4.40–4.86 (m, 4H, OCH + C(H)NH), 6.48 (d, 3 J H,H 8.6 Hz, 2H, o-C6H4N), 7.21 (d, 3 J H,H 8.7 Hz, 2H, m-C6H4N), 7.37 (d. d, 3 J H,H 8.4 Hz, 4 J H,H 2.2 Hz, 2H, o-C6H4), 7.48 (d, 3 J H,H 8.4 Hz, 2H, m-C6H4) ppm. 31P{1H} NMR: δ = 19.4 ppm. Anal. calc. for C19H24Br2NO3P (505.19): C 45.17, H 4.79 and N 2.77 %; found: С 45.02, Н 4.88 and N 2.69 %.
2.2.3. Diisopropyl((4-bromophenyl)((4-methoxyphenyl)amino)methyl)phosphonate (3)
Yield: 0.470 g (84 %). 1H NMR: δ = 1.05 (d, 3 J H,H 6.3 Hz, 3H, CH3), 1.23 (d, 3 J H,H 6.2 Hz, 3H, CH3), 1.28 (d, 3 J H,H 6.3 Hz, 3H, CH3), 1.37 (d, 3 J H,H 6.3 Hz, 3H, CH3), 3.68 (s, 3H, CH3O), 4.35–4.79 (m, 4H, OCH + C(H)NH), 6.54 (d, 3 J H,H 8.6 Hz, 2H, o-C6H4N), 6.77 (d, 3 J H,H 8.7 Hz, 2H, m-C6H4N), 7.33 (d. d, 3 J H,H 8.5 Hz, 4 J H,H 2.1 Hz, 2H, o-C6H4), 7.49 (d, 3 J H,H 8.4 Hz, 2H, m-C6H4) ppm. 31P{1H} NMR: δ = 20.2 ppm. Anal. calc. for C20H27BrNO4P (456.32): C 52.64, H 5.96 and N 3.07 %; found: С 52.51, Н 6.04 and N 3.01 %.
2.3. Computational details
Theoretical calculations of the ground state geometry of 1–3 were performed using the GaussView 6.0 molecular visualization program [17] and Gaussian 09, Revision D.01 program package [18] under the density functional theory (DFT) with B3LYP exchange-correlation functional [19,20] and 6–311++G(d,p) [19,21] basis set. The crystal structure geometry was used as a starting model for structural optimization. The vibration frequencies were calculated for the optimized structure in gas phase and no imaginary frequencies were obtained.
2.4. Single crystal X-ray diffraction
Diffraction data were collected at 173(2) K, using a STOE IPDS-II diffractometer with graphite-monochromatized Mo-Kα radiation (λ = 0.71073 Å). Images were indexed, integrated and scaled with the X-Area package [22]. Data were corrected for absorption with the PLATON program [23]. Structures were solved by direct methods with SHELXS-07 [24] and refined first isotropically and then anisotropically with SHELXL-97 [24]. The CH hydrogen atoms were refined with riding models, while the NH hydrogen atoms were freely refined.
2.4.1. Crystal data of 1
C19H25BrNO3P, M r = 426.27 g mol−1, monoclinic, space group P21/n, a = 13.3777(9), b = 9.6460(4), c = 16.0504(10) Å, α = 101.859(5)°, V = 2027.0(2) Å3, Z = 4, ρ = 1.397 g cm−3, μ(Mo-Kα) = 2.124 mm−1, reflections: 17938 collected, 3797 unique, R int = 0.052, R 1(all) = 0.0449, wR 2(all) = 0.0762, S = 1.000.
2.4.2. Crystal data of 2
C19H24Br2NO3P, M r = 505.18 g mol−1, triclinic, space group P–1, a = 8.1761(5), b = 14.9538(10), c = 18.0425(11) Å, α = 91.200(5), β = 96.771(5), γ = 101.618(6)°, V = 2143.4(2) Å3, Z = 4, ρ = 1.566 g cm−3, μ(Mo-Kα) = 3.874 mm−1, reflections: 38449 collected, 7564 unique, R int = 0.089, R 1(all) = 0.0898, wR 2(all) = 0.1968, S = 1.059.
2.4.3. Crystal data of 3
C20H27BrNO4P, M r = 456.31 g mol−1, triclinic, space group P–1, a = 8.1828(4), b = 15.0664(7), c = 18.2022(8) Å, α = 92.173(4), β = 94.830(4), γ = 99.222(4)°, V = 2204.18(18) Å3, Z = 4, ρ = 1.375 g cm−3, μ(Mo-Kα) = 1.961 mm−1, reflections: 71115 collected, 10890 unique, R int = 0.063, R 1(all) = 0.0559, wR 2(all) = 0.0964, S = 1.189.
CCDC 722386, 711117 and 711118 contain the supplementary crystallographic data. These data can be obtained free of charge via http://www.ccdc.cam.ac.uk/conts/retrieving.html, or from the Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB2 1EZ, UK; fax: (+44) 1223-336-033; or e-mail: deposit@ccdc.cam.ac.uk.
3. Results and discussion
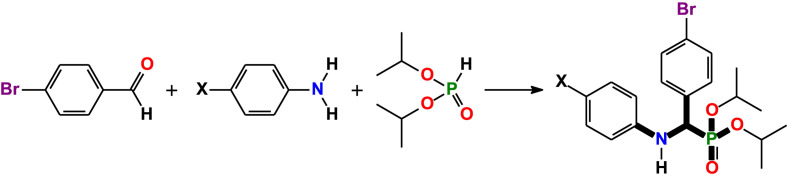
A one-pot reaction of 4-bromobenzaldehyde, diisopropylphosphite and aniline or 4-bromoaniline or 4-methoxyaniline has allowed to produce the corresponding α-aminophosphonates 1–3 with good yields (Scheme 1 ). The 31P{1H} NMR spectra of 1–3 in CDCl3 each contain a singlet at 19.4–20.2 ppm. The 1H NMR spectra of the obtained compounds in the same solvent each exhibit four doublets at 1.01–1.37 ppm with 3 J H,H = 6.0–6.3 Hz, corresponding to the methyl protons of the isopropyl groups. The signal for the OCH protons of the isopropyl groups is overlapped with the signals for the C(H)NH group and were found at 4.35–4.89 ppm. The phenyl protons in the 1H NMR spectrum of 1 are shown as two doublets at 6.6 and 7.14 ppm and one triplet at 6.74 ppm, corresponding to the o- and p-H-atoms, and m-H-atoms, respectively. The o- and m-H-atoms of the phenylene group attached to the amine nitrogen atom in the spectra of 2 and 3 are shown as two doublets at 6.48–6.54 and 6.77–7.21 ppm, respectively. The o- and m-H-atoms of the phenylene group attached to the C(H)N carbon atom are shifted to lower fields and are shown as one doublet of doublets at 7.33–7.39 ppm and one doublet at 7.48–7.50 ppm, respectively, in the spectra of all the reported α-aminophosphonates. Finally, the spectrum of 3 also contains a singlet for the methoxy hydrogen atoms at 3.68 ppm.
Scheme 1.
Synthesis of α-aminophosphonates 1 (X = H), 2 (X = Br) and 3 (X = MeO).
According to single-crystal X-ray diffraction, compounds 2 and 3 crystallize in triclinic space group P–1, while 1 crystallizes in monoclinic space group P21/n. Notably, the former two structures are isostructural and each contain two independent molecules in the asymmetric unit cell, namely 2-I and 2-II, and 3-I and 3-II. Furthermore, in the structure of 3-I one of the isopropyl groups is disordered over two positions with a 0.546(16) to 0.454(16) ratio. For the sake of brevity, we herein discuss only the major contributor of the disordering, while the minor one has almost the same results and was not considered.
The geometrical parameters are very similar in all the discussed molecules (Fig. 1 , Table 1 ). Particularly, the P–O bond lengths vary from 1.560(5) Å to 1.5848(19) Å, while the P=O bonds are about 0.1 Å shorter. The P–C and C(H)–N distances are 1.819(2)–1.833(7) Å and 1.444(9)–1.458(9) Å, respectively. The phosphorus atoms were found to be in a distorted CO3 tetrahedral environment with the O=P–O/C and O–P–O/C bond angles being 111.0(3)–118.4(3)° and 100.58(10)–107.4(3)°, respectively. Notably, the O=P–C–N fragment in all structures exhibits a Z conformation with the corresponding dihedral angles, compared by their magnitudes, varying from 46.90(18)° to 57.5(2)°. Furthermore, the aromatic rings in all the reported molecules are almost orthogonal to each other as evidenced from the corresponding dihedral angles being 84.60(14)–87.60(14)°. Furthermore, two molecules in the crystal structures of 1–3 are interlinked through a pair of intermolecular N–H⋯O=P hydrogen bonds (Fig. 1, Table 2 ), affording a centrosymmetric supramolecular dimer with a R 2 2(10) motif.
Fig. 1.
A hydrogen bonded centrosymmetric dimer in the crystal structure of 1 (thermal ellipsoids are drawn with 50 % probability; CH hydrogen atoms are omitted for clarity). Color code: H = black, C = gold, N = blue, O = red, Br = purple, P = green; N–H⋯O hydrogen bond = dashed cyan line. The same dimers are formed in the crystal structures of 2 and 3.
Table 1.
Experimental and calculated (DFT, B3LYP/6–311++G(d,p)) selected bond lengths (Å) and angles (°) in the structures of 1–3.a
|
1 |
2-I |
2-II |
3-I |
3-II |
||||
|---|---|---|---|---|---|---|---|---|
| Experimental | Calculated | Experimental | Calculated | Experimental | Calculated | |||
| Bond lengths | ||||||||
| C–Br | 1.906(2) | 1.9188 | 1.897(7), 1.901(9) | 1.898(8), 1.911(7) | 1.9179, 1.9198 | 1.916(3) | 1.915(3) | 1.9189 |
| P=O | 1.4698(18) | 1.4897 | 1.470(5) | 1.462(5) | 1.4895 | 1.472(2) | 1.4782(19) | 1.4900 |
| P–O | 1.5635(18), 1.5786(17) | 1.5989, 1.6143 | 1.567(6), 1.572(5) | 1.560(5), 1.576(6) | 1.5978, 1.6144 | 1.568(2), 1.580(3) | 1.5774(18), 1.5848(19) | 1.6001, 1.6149 |
| P–C | 1.819(2) | 1.8541 | 1.822(7) | 1.833(7) | 1.8556 | 1.830(3) | 1.827(2) | 1.8529 |
| C(H)–N | 1.454(3) | 1.4520 | 1.458(9) | 1.444(9) | 1.4520 | 1.453(3) | 1.449(3) | 1.4532 |
| Bond angles | ||||||||
| O=P–O | 113.86(10), 117.45(10) | 113.93, 118.17 | 114.7(3), 116.7(3) | 114.8(3), 118.4(3) | 113.93, 118.37 | 114.92(12), 117.99(13) | 114.62(10), 116.72(10) | 113.95, 118.09 |
| O–P–O | 103.14(10) | 102.39 | 103.8(3) | 101.5(3) | 102.38 | 101.92(12) | 103.38(10) | 102.25 |
| O=P–C | 114.52(10) | 112.89 | 113.0(3) | 111.0(3) | 112.55 | 111.54(11) | 112.92(11) | 112.85 |
| O–P–C | 100.58(10), 105.63(10) | 101.62, 106.35 | 102.0(3), 105.2(3) | 102.4(3), 107.4(3) | 101.68, 106.46 | 102.21(11), 106.87(12) | 102.14(11), 105.62(11) | 101.53, 106.70 |
| C–N–C | 119.5(2) | 123.44 | 121.2(6) | 121.8(6) | 123.79 | 121.7(2) | 121.1(2) | 122.56 |
| P–C–N | 107.47(15) | 103.91 | 107.1(5) | 105.9(5) | 103.82 | 104.95(17) | 107.22(17) | 103.89 |
| Dihedral anglesb | ||||||||
| O=P–C–N | 46.90(18) | 46.13 | −57.1(6) | −47.7(6) | −44.40 | −47.2(2) | −57.5(2) | −47.06 |
| C–C(H)–N–C | −68.8(3) | −69.29 | 73.5(9) | 66.2(9) | 69.80 | 68.3(3) | 73.5(3) | 66.92 |
| Cgbenzene⋯Cgbenzene | 85.40(12) | 88.66 | 84.6(4) | 86.5(4) | 88.79 | 87.60(14) | 84.60(14) | 89.32 |
Values with respect to the moieties marked in bold in Scheme 1.
The corresponding dihedral angles must be compared by their magnitudes.
Table 2.
Classic hydrogen bond lengths (Å) and angles (°) in the structures of 1–3.
| D–H⋯A | d(D–H) | d(H⋯A) | d(D⋯A) | ∠(DHA) | Symmetrycode | |
|---|---|---|---|---|---|---|
| 1 | N–H⋯O=P#1 | 0.77(3) | 2.31(3) | 3.065(3) | 166(3) | 1 – x, 1 – y, 1 – z |
| 2-I | N–H⋯O=P#2 | 0.91(8) | 2.15(7) | 2.991(8) | 154(7) | 1 – x, 2 – y, 1 – z |
| 2-II | N–H⋯O=P#3 | 0.87(6) | 2.16(6) | 3.014(8) | 166(8) | 1 – x, 1 – y, 2 – z |
| 3-I | N–H⋯O=P#1 | 0.84(3) | 2.27(3) | 3.058(3) | 157(3) | 1 – x, 1 – y, 1 – z |
| 3-II | N–H⋯O=P#4 | 0.92(3) | 2.18(3) | 3.079(3) | 164(2) | 1 – x, 2 – y, 2 – z |
Crystal packing of 1–3 was further studied by a Hirshfeld surface analysis [25], also resulted in the corresponding 2D fingerprint plots [26], which were generated using CrystalExplorer 17 [27]. Additionally, the enrichment ratios (E) [28] of the intermolecular contacts were also calculated to estimate the propensity of two chemical species to be in contact.
It was found that the Hirshfeld surfaces of 1, 2-I, 2-II, 3-I and 3-II, calculated over d norm, each contain two pairs of bright and faint red spots, corresponding to donors and acceptors of the reciprocal N–H⋯O=P and C–H⋯O=P intermolecular interactions (Fig. 2 ). Notably, the latter contacts in the structure of 1 are formed with one of the o-H-atoms of the phenylene fragment attached to the amine nitrogen atom, while in the structures of other molecules the same intermolecular contacts are formed with one of the o-H-atoms of the phenylene fragment attached to the C(H)N carbon atom. The donors and the acceptors of these interactions can be evidenced as blue and red regions around the participating atoms on the Hirshfeld surface mapped over shape index (Fig. 2). Moreover, no flat regions were observed on the Hirshfeld surfaces of 1, 2-I, 2-II, 3-I and 3-II, mapped over curved surfaces, indicating the absence of reasonable π⋯π interactions (Fig. 2).
Fig. 2.
Molecular Hirshfeld surfaces in the structures of 1–3 (top, middle, bottom denote normalized distance dnorm, shape index and curvedness, respectively).
An overwhelming majority of the Hirshfeld surface area of all the discussed molecules is occupied by intermolecular H⋯H (46.7–59.4 %) contacts, followed by H⋯C (16.7–17.7 %), H⋯Br (11.3–21.5 %) and H⋯O (5.8–11.8 %) contacts (Fig. 3 , Table 3 ). This is, obviously, due to the presence of the isopropyl fragments as well as due to the absence of intermolecular π⋯π stacking interactions. Notably, a proportion of the H⋯H contacts decreases from 1, 3-I and 3-II to 2-I and 2-II with the simultaneous increase of the H⋯Br contacts (Table 3), which is explained by the presence of the second bromine atom in the structures of the latter two molecules. Furthermore, the presence of the second bromine atom in the structures of 2-I and 2-II is also responsible for appearance of a perceptible proportion of the Br⋯Br contacts (3.3–3.8 %).
Fig. 3.
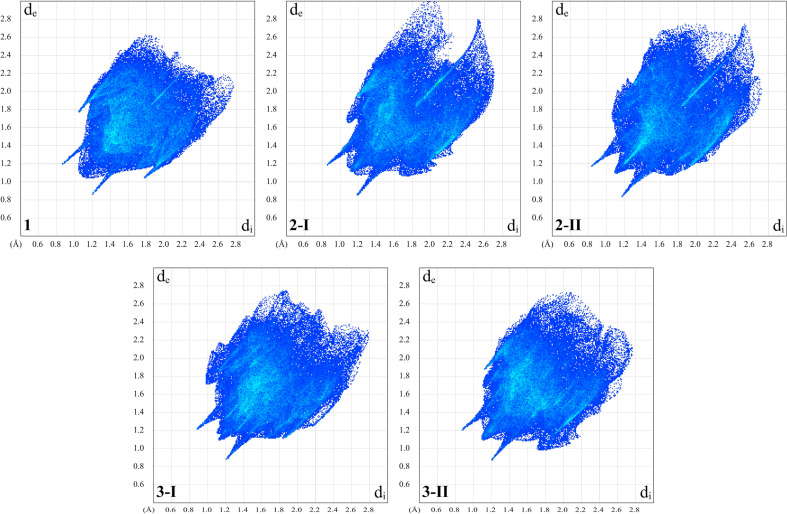
2D fingerprint plots of observed contacts in the structures of 1–3.
Table 3.
Hirshfeld contact surfaces and derived “random contacts” and “enrichment ratios” for structures of 1–3.
|
1 |
2-I |
2-II |
3-I |
3-II |
|||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H | C | N | O | Br | H | C | N | O | Br | H | C | N | O | Br | H | C | N | O | Br | H | C | N | O | Br | |
| Contacts (C, %)a | |||||||||||||||||||||||||
| H | 59.1 | – | – | – | – | 46.7 | – | – | – | – | 51.1 | – | – | – | – | 59.4 | – | – | – | – | 56.3 | – | – | – | – |
| C | 16.9 | 0.0 | – | – | – | 16.9 | 0.0 | – | – | – | 17.4 | 0.0 | – | – | – | 17.7 | 0.0 | – | – | – | 16.7 | 0.0 | – | – | – |
| N | 1.5 | 0.0 | 0.0 | – | – | 1.0 | 0.0 | 0.0 | – | – | 0.3 | 0.0 | 0.0 | – | – | 0.4 | 0.0 | 0.0 | – | – | 1.0 | 0.0 | 0.0 | – | – |
| O | 8.7 | 0.0 | 0.0 | 0.0 | – | 7.5 | 0.0 | 0.0 | 0.0 | – | 5.8 | 0.0 | 0.0 | 0.0 | – | 9.6 | 0.0 | 0.0 | 0.0 | – | 11.8 | 0.0 | 0.0 | 0.0 | – |
| Br | 13.1 | 0.0 | 0.0 | 0.0 | 0.8 | 21.5 | 1.5 | 0.0 | 1.0 | 3.8 | 19.5 | 1.6 | 0.0 | 0.9 | 3.3 | 11.3 | 0.4 | 0.0 | 1.2 | 0.0 | 12.6 | 0.3 | 0.0 | 1.3 | 0.0 |
| Surface (S, %) | |||||||||||||||||||||||||
| 79.2 | 8.5 | 0.8 | 4.4 | 7.4 | 70.2 | 9.2 | 0.5 | 4.3 | 15.8 | 72.6 | 9.5 | 0.2 | 3.4 | 14.3 | 78.9 | 9.1 | 0.2 | 5.4 | 6.5 | 77.4 | 8.5 | 0.5 | 6.6 | 7.1 | |
| Random contacts (R, %) | |||||||||||||||||||||||||
| H | 62.7 | – | – | – | – | 49.3 | – | – | – | – | 52.7 | – | – | – | – | 62.3 | – | – | – | – | 59.9 | – | – | – | – |
| C | 13.5 | 0.7 | – | – | – | 12.9 | 0.8 | – | – | – | 13.8 | 0.9 | – | – | – | 14.4 | 0.8 | – | – | – | 13.2 | 0.7 | – | – | – |
| N | 1.3 | 0.1 | 0.0 | – | – | 0.7 | 0.1 | 0.0 | – | – | 0.3 | 0.0 | 0.0 | – | – | 0.3 | 0.0 | 0.0 | – | – | 0.8 | 0.1 | 0.0 | – | – |
| O | 7.0 | 0.7 | 0.1 | 0.2 | – | 6.0 | 0.8 | 0.0 | 0.2 | – | 4.9 | 0.6 | 0.0 | 0.1 | – | 8.5 | 1.0 | 0.0 | 0.3 | – | 10.2 | 1.1 | 0.1 | 0.4 | – |
| Br | 11.7 | 1.3 | 0.1 | 0.7 | 0.5 | 22.2 | 2.9 | 0.2 | 1.4 | 2.5 | 20.8 | 2.7 | 0.1 | 1.0 | 2.0 | 10.3 | 1.2 | 0.0 | 0.7 | 0.4 | 11.0 | 1.2 | 0.1 | 0.9 | 0.5 |
| Enrichment (E)b | |||||||||||||||||||||||||
| H | 0.94 | – | – | – | – | 0.95 | – | – | – | – | 0.97 | – | – | – | – | 0.95 | – | – | – | – | 0.94 | – | – | – | – |
| C | 1.25 | – | – | – | – | 1.31 | – | – | – | – | 1.26 | – | – | – | – | 1.23 | – | – | – | – | 1.27 | – | – | – | – |
| N | 1.15 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – |
| O | 1.24 | – | – | – | – | 1.25 | – | – | – | – | 1.18 | – | – | – | – | 1.13 | 0.00 | – | – | – | 1.16 | 0.00 | – | – | – |
| Br | 1.12 | 0.00 | – | – | – | 0.97 | 0.52 | – | 0.71 | 1.52 | 0.94 | 0.59 | – | 0.90 | 1.65 | 1.10 | 0.33 | – | – | – | 1.15 | 0.25 | – | – | – |
The shortest H⋯H contacts are shown in the corresponding 2D fingerprint plots at d e + d i ≈ 2.2–2.3 Å (Figs. S1–S5 in the Supplementary Information) with a distinct splitting of the shortest H⋯H contacts in the 2D fingerprints of 2-I and 3-I, and less visible in the corresponding 2D fingerprint plot of 1, which is typical when interaction occurs between three atoms [25]. The H⋯O contacts in the corresponding 2D fingerprint plots of all molecules are shown as a pair of sharp horns with the shortest values at d e + d i ≈ 2.1–2.2 Å (Figs. S1–S5 in the Supplementary Information) due to the formation of strong N–H⋯O=P hydrogen bonds (Fig. 1, Table 2). All the H⋯X contacts in the structures of 1, 2-I, 2-II, 3-I and 3-II are favoured since the corresponding enrichment ratios E HX are close to or even higher than unity (Table 3). This is explained by a relatively higher proportion of these contacts on the total Hirshfeld surface area over a corresponding proportion of random contacts R HX (Table 3). In the structures of 2-I and 2-II the Br⋯Br contacts are also highly favoured (Table 3). Remaining observed intermolecular contacts are either much less favoured or even negligible (Table 3).
Voids in the crystal structures of 1–3 (Fig. 4 ) were calculated using CrystalExplorer 17 [27]. It was found that the void volume decreases from 3 through 2 to 1 and of 344.88, 307.04 and 293.65 Å3, respectively, and the corresponding surface area is 975.64, 936.70 and 846.19 Å2. With the porosity, the calculated void volume is 14.3–15.6 % (Table 4 ).
Fig. 4.
Void plots in the structures of 1–3 (results under 0.002 a.u. isovalue).
Table 4.
Voids in the crystal structures of 1–3, calculated using CrystalExplorer 17 [27].
| Void volume (Å3) | Void surface area (Å2) | Cell volume (Å3) | Porosity (%) | |
|---|---|---|---|---|
| 1 | 293.65 | 846.19 | 2027.0(2) | 14.5 |
| 2 | 307.04 | 936.70 | 2143.4(2) | 14.3 |
| 3 | 344.88 | 975.64 | 2204.18(18) | 15.6 |
We have also calculated energy frameworks using CrystalExplorer 17 [27] to further analyze the crystal packing of 1–3. A single-point molecular wavefunction at HF/3-21G was applied for a cluster of radius 3.8 Å to perform the energy calculation (Fig. 5 , Table 5 ). The overall topology of the energy distributions in the crystal structures was studied through the energy framework. It was established that all the structures are mainly characterized by the dispersion energy, followed by a less significant electrostatic energy contribution (Fig. 6 , Table 5).
Fig. 5.
The colour-coded interaction mapping within 3.8 Å of the centring molecule in the structures of 1–3, calculated from a single-point molecular wavefunction at HF/3-21G.
Table 5.
Interaction energies (kJ/mol) calculated at the HF/3-21G electron density for the crystal structures of 1–3.
Fig. 6.
Energy frameworks calculated for the crystal structures of 1–3, showing the (top) electrostatic potential force, (middle) dispersion force and (bottom) total energy diagrams. The cylindrical radii are proportional to the relative strength of the corresponding energies and they were adjusted to the same scale factor of 100 with a cut-off value of 5 kJ/mol.
The electronic structure of 1–3 was analyzed using the density functional theory (DFT). The ground state geometry of 1–3 was first fully optimized at the B3LYP/6–311++G(d,p) [[19], [20], [21]] level. The calculated values of bond lengths, bond angles and dihedral angles of the optimized structures are in good agreement with the values obtained from single crystal X-ray diffraction (Table 1). Some revealed insignificant differences between the calculated and experimental geometrical parameters are explained by the gas phase optimization approach.
According to the DFT calculations, the lowest total energy and the largest dipole moment of −177117.181858 eV and 4.917023 Debye, respectively, are observed for 2, whereas for the other optimized structures these values are found to be −107087.487936 eV and 3.412321 Debye for 1, and –110204.642597 eV and 3.103810 Debye for 3, respectively (Table 6 ). The calculated energies of the frontier molecular orbitals of 1–3 are in the range from −5.87276 eV to −5.37507 eV for the highest occupied molecular orbital (HOMO) and from −1.10750 eV to −0.95485 eV for the lowest unoccupied molecular orbital (LUMO), respectively (Table 6).
Table 6.
Total energies, dipole moments, frontier molecular orbitals, gap values and descriptors for 1–3 in gas phase, obtained by using the B3LYP/6–311++G(d,p) method.
| 1 | 2 | 3 | |
|---|---|---|---|
| Total energy (eV) | −107087.487936 | −177117.181858 | −110204.642597 |
| Dipole moment (Debye) | 3.412321 | 4.917023 | 3.103810 |
| EHOMO (eV) | −5.79957 | −5.87276 | −5.37507 |
| ELUMO (eV) | −0.98369 | −1.10750 | −0.95485 |
| ΔELUMO – HOMO = ELUMO – EHOMO (eV) | 4.81587 | 4.76526 | 4.42022 |
| Ionization energy, I = –EHOMO (eV) | 5.79957 | 5.87276 | 5.37507 |
| Electron affinity, A = –ELUMO (eV) | 0.98369 | 1.10750 | 0.95485 |
| Electronegativity, χ = (I + A)/2 (eV) | 3.39163 | 3.49013 | 3.16496 |
| Chemical potential, μ = –χ (eV) | −3.39163 | −3.49013 | −3.16496 |
| Global chemical hardness, η = (I – A)/2 (eV) | 2.40794 | 2.38263 | 2.21011 |
| Global chemical softness, S = 1/(2η) (eV−1) | 0.20765 | 0.20985 | 0.22623 |
| Global electrophilicity index, ω = μ2/(2η) (eV) | 2.38859 | 2.55622 | 2.26617 |
| Maximum additional electric charge, ΔNmax = –μ/ƞ | 1.40852 | 1.46482 | 1.43204 |
The HOMO and HOMO–1 orbitals of the optimized geometries for all the discussed structures are delocalized over the 4-XC6H4–NH–CH– and 4-BrC6H4–CH–P(O)O– fragments, respectively (Fig. 7 ). Interestingly, while the HOMO–2 and HOMO–3 orbitals in the optimized geometry of the structure of 1 are spread exclusively over the Ph and C6H4 rings, respectively, the former orbital in the optimized geometries of the structures of 2 and 3 is delocalized over the 4-XC6H4–NH–CH(C6H4)–P(O)O– moiety, and the latter orbital is spread over the C6H4 fragment linked to the nitrogen atom (Fig. 7). The LUMO, LUMO+1 and LUMO+2 orbitals in the optimized geometries of all the reported structures are mainly located over the C6H5/4–NH–CH(4-BrC6H4)–P fragment (Fig. 8 ). The LUMO+3 orbital in 1 and 2, and the LUMO+4 orbital in 2 and 3 are mainly spread over the 4-XC6H4–NH– fragment, while the LUMO+4 orbital in 1 and the LUMO+3 orbital in 3 are located over the 4-BrC6H4 fragment (Fig. 8). The observed delocalization of the reported molecular orbitals is obviously dictated by the presence of the 4-H, 4-Br or 4-MeO substituents, exhibiting different mesomeric and inductive effects in the aromatic ring attached to the amine nitrogen atom in the structures of 1–3, respectively.
Fig. 7.
Energy levels and views on the electronic isosurfaces of the selected high occupied molecular orbitals of the ground state of 1 (left), 2 (middle) and 3 (right), obtained by using the B3LYP/6–311++G(d,p) method.
Fig. 8.
Energy levels and views on the electronic isosurfaces of the selected lowest unoccupied molecular orbitals of the ground state of 1 (left), 2 (middle) and 3 (right), obtained by using the B3LYP/6–311++G(d,p) method.
The so-called ionization potential (I) and the electron affinity (A) value of the molecule were established as follows: I = –E HOMO and A = –E LUMO (Table 6) [29], which determine the electron donating ability and the ability to accept an electron, respectively. As such, as lower values of I as better donation of an electron, while as higher values of A as better ability to accept electrons. The I value is large and A value is relatively mean for 1–3 (Table 6), indicating that the reported aminophosphonates each exhibit low electron donating and pronounced electron accepting properties.
To estimate the relative reactivity of molecules of 1–3 we have further established values of the so-called global chemical reactivity descriptors derived from the HOMO-LUMO energy gap, which counts for 4.42022–4.81587 eV (Table 6). Chemical potential (μ) for 1–3 ranges from −3.49013 eV to −3.16496 eV, indicating the regular electron accepting ability and low donating ability, which is supported by the corresponding values of electronegativity, χ (Table 6). The chemical hardness (η) describes the resistance towards deformation/polarization of the electron cloud of the molecule upon a chemical reaction, while softness (S) is a reverse of chemical hardness [29]. Aminophosphonates 1–3 each are characterized by a low value of η (2.21011–2.40794 eV) and a relatively mean value of S (0.20765–0.22623 eV–1), respectively, indicating these compounds exhibit a remarkable tendency to exchange their electron clouds with surrounding environment. The descriptor electrophilicity index (ω) describes the energy of stabilization to accept electrons [29]. The ω values for 1–3 were found to be 2.26617–2.55622 eV, indicating the nucleophilic nature of 1–3. Finally, compounds 1–3 each can accept about 1.5 electrons as evidenced from the ΔNmax value (Table 6).
The electrophilic and nucleophilic sites in 1–3 were examined using the molecular electrostatic potential (MEP) analysis. The MEP surfaces of all the discussed structures were generated from the fully optimized ground state geometry obtained by using the B3LYP/6–311++G(d,p) method. The red and blue colours of the MEP surface correspond to electron rich (nucleophilic) and electron deficient (electrophilic) regions, respectively. On the MEP surfaces of 1–3 the most pronounced nucleophilic center is located on the P=O oxygen atom, while the other negative electrostatic potential sites are located on the bromine and methoxy oxygen atoms (Fig. 9 ). As the most electrophilic region the N(H)–C(H) fragment can be highlighted for the structures of 1–3 (Fig. 9).
Fig. 9.
Front (left) and rear (right) views of the molecular electrostatic potential surface of 1 (top), 2 (middle) and 3 (bottom), obtained by using the B3LYP/6–311++G(d,p) method.
The absorption spectra of the fully optimized ground state geometry of 1–3 were simulated at the TD-DFT/B3LYP/6–311++G(d,p) level. The calculated UV–vis spectrum of 1 exhibits an absorption band centered at about 237 nm, which mostly corresponds to the HOMO → LUMO+5, HOMO → LUMO+6 and HOMO → LUMO+7 transitions (Fig. 10 , Table 7 ). The UV–vis spectrum of 2 exhibits two intense absorption bands centered at about 244 nm and 250 nm, where the first band mainly corresponds to the HOMO → LUMO+5, HOMO → LUMO+6 and HOMO→LUMO+7 transitions and the second band mainly corresponds to the HOMO → LUMO+4 and HOMO → LUMO+5 transitions (Fig. 10, Table 7). As for the calculated UV–vis spectrum of 3, two intense absorption bands are observed at about 252 nm and 289 nm and mainly corresponds to the HOMO → LUMO+6 and HOMO → LUMO+7 transitions for the first band and to the HOMO → LUMO+2 and HOMO → LUMO+3 for the second band, respectively (Fig. 10, Table 7).
Fig. 10.
The calculated UV–vis spectra of the ground states of 1 (top), 2 (middle) and 3 (bottom), obtained by using the TD-DFT/B3LYP/6–311++G(d,p) method.
Table 7.
Values for the calculated UV–vis spectra of the ground state of 1–3 (Fig. 7, Fig. 8), obtained by using the TD-DFT/B3LYP/6–311++G(d,p) method.
|
1 |
2 |
3 |
||||||
|---|---|---|---|---|---|---|---|---|
| λmax(nm) | Oscillator strength | Transitions | λmax(nm) | Oscillator strength | Transitions | λmax(nm) | Oscillator strength | Transitions |
| 237.2 | 0.1502 | HOMO–2 → LUMO (2.6 %) | 238.6 | 0.0342 | HOMO–1 → LUMO (17.2 %) | 248.9 | 0.0016 | HOMO–3 → LUMO (24.2 %) |
| HOMO–2 → LUMO+3 (2.3 %) | HOMO–1 → LUMO+2 (6.1 %) | HOMO–1 → LUMO+1 (71.9 %) | ||||||
| HOMO–1 → LUMO (6.8 %) | HOMO–1 → LUMO+3 (52.5 %) | |||||||
| HOMO–1 → LUMO+2 (5.6 %) | HOMO–1 → LUMO+4 (9.6 %) | |||||||
| HOMO → LUMO+4 (4.3 %) | HOMO–1 → LUMO+5 (6.2 %) | |||||||
| HOMO → LUMO+5 (30.9 %) | ||||||||
| HOMO → LUMO+6 (16.1 %) | ||||||||
| HOMO → LUMO+7 (25.3 %) | ||||||||
| 239.3 | 0.0238 | HOMO–1 → LUMO (9.0 %) | 241.4 | 0.0365 | HOMO → LUMO+4 (3.9 %) | 250.1 | 0.0009 | HOMO → LUMO+4 (3.9 %) |
| HOMO–1 → LUMO+2 (62.5 %) | HOMO → LUMO+6 (25.1 %) | HOMO → LUMO+7 (16.9 %) | ||||||
| HOMO–1 → LUMO+3 (6.9 %) | HOMO → LUMO+7 (41.6 %) | HOMO → LUMO+8 (65.7 %) | ||||||
| HOMO–1 → LUMO+4 (8.4 %) | HOMO → LUMO+9 (21.7 %) | HOMO → LUMO+10 (3.4 %) | ||||||
| HOMO → LUMO+7 (4.3 %) | HOMO → LUMO+11 (2.1 %) | HOMO → LUMO+11 (4.2 %) | ||||||
| 240.1 | 0.0174 | HOMO–1 → LUMO+2 (2.6 %) | 243.8 | 0.1612 | HOMO–1 → LUMO (2.8 %) | 252.3 | 0.0334 | HOMO → LUMO+6 (50.5 %) |
| HOMO → LUMO+4 (2.6 %) | HOMO → LUMO+5 (35.7 %) | HOMO → LUMO+7 (31.2 %) | ||||||
| HOMO → LUMO+5 (3.6 %) | HOMO → LUMO+6 (26.9 %) | HOMO → LUMO+8 (8.8 %) | ||||||
| HOMO → LUMO+6 (38.5 %) | HOMO → LUMO+7 (14.7 %) | |||||||
| HOMO → LUMO+7 (29.3 %) | HOMO → LUMO+8 (3.2 %) | |||||||
| HOMO → LUMO+8 (9.1 %) | HOMO → LUMO+9 (7.7 %) | |||||||
| HOMO → LUMO+9 (7.4 %) | ||||||||
| HOMO → LUMO+10 (3.2 %) | ||||||||
| 242.9 | 0.0082 | HOMO → LUMO+2 (2.1 %) | 249.4 | 0.0065 | HOMO–3 → LUMO (21.8 %) | 259.0 | 0.0011 | HOMO → LUMO+6 (41.8 %) |
| HOMO → LUMO+4 (20.8 %) | HOMO–1 → LUMO+1 (68.4 %) | HOMO → LUMO+7 (39.3 %) | ||||||
| HOMO → LUMO+5 (28.4 %) | HOMO → LUMO+4 (3.9 %) | HOMO → LUMO+8 (11.4 %) | ||||||
| HOMO → LUMO+6 (21.2 %) | ||||||||
| HOMO → LUMO+7 (10.0 %) | ||||||||
| HOMO → LUMO+8 (3.2 %) | ||||||||
| 249.1 | 0.0014 | HOMO–3→ LUMO (25.0 %) | 250.3 | 0.1620 | HOMO–1 → LUMO+1 (4.1 %) | 265.4 | 0.0055 | HOMO → LUMO+4 (44.9 %) |
| HOMO–1→ LUMO+1 (72.2 %) | HOMO → LUMO+4 (59.5 %) | HOMO → LUMO+5 (45.4 %) | ||||||
| HOMO → LUMO+5 (18.3 %) | HOMO → LUMO+7 (5.1 %) | |||||||
| HOMO → LUMO+7 (3.3 %) | ||||||||
| HOMO → LUMO+8 (6.1 %) | ||||||||
| 250.6 | 0.0137 | HOMO → LUMO+2 (11.1 %) | 256.8 | 0.0361 | HOMO → LUMO+2 (2.2 %) | 273.4 | 0.0045 | HOMO → LUMO+2 (14.5 %) |
| HOMO → LUMO+3 (7.8 %) | HOMO → LUMO+3 (64.5 %) | HOMO → LUMO+3 (9.4 %) | ||||||
| HOMO → LUMO+4 (58.0 %) | HOMO → LUMO+4 (6.8 %) | HOMO → LUMO+4 (38.8 %) | ||||||
| HOMO → LUMO+5 (15.1 %) | HOMO → LUMO+5 (7.6 %) | HOMO → LUMO+5 (35.9 %) | ||||||
| HOMO → LUMO+6 (4.9 %) | HOMO → LUMO+6 (9.4 %) | |||||||
| HOMO → LUMO+8 (5.1 %) | ||||||||
| 260.1 | 0.0040 | HOMO → LUMO+2 (53.0 %) | 271.8 | 0.0005 | HOMO → LUMO+3 (29.5 %) | 282.7 | 0.0064 | HOMO → LUMO+2 (22.9 %) |
| HOMO → LUMO+3 (23.9 %) | HOMO → LUMO+4 (18.8 %) | HOMO → LUMO+3 (51.8 %) | ||||||
| HOMO → LUMO+4 (10.1 %) | HOMO → LUMO+5 (26.6 %) | HOMO → LUMO+4 (10.0 %) | ||||||
| HOMO → LUMO+5 (4.0 %) | HOMO → LUMO+6 (20.8 %) | HOMO → LUMO+5 (11.4 %) | ||||||
| HOMO → LUMO+6 (5.9 %) | ||||||||
| 266.1 | 0.0329 | HOMO–2→ LUMO+7 (2.8 %) | 278.0 | 0.0234 | HOMO–2 → LUMO+5 (2.5 %) | 288.7 | 0.0437 | HOMO–2 → LUMO+9 (2.4 %) |
| HOMO → LUMO+2 (31.3 %) | HOMO → LUMO+2 (91.2 %) | HOMO → LUMO+2 (59.4 %) | ||||||
| HOMO → LUMO+3 (57.6 %) | HOMO → LUMO+3 (33.4 %) | |||||||
| HOMO → LUMO+5 (2.0 %) | ||||||||
| 288.1 | 0.0017 | HOMO → LUMO+1 (99.2 %) | 288.4 | 0.0041 | HOMO → LUMO+1 (98.1 %) | 313.4 | 0.0017 | HOMO → LUMO+1 (99.4 %) |
| 299.5 | 0.0028 | HOMO → LUMO (98.7 %) | 301.0 | 0.0062 | HOMO → LUMO (97.9 %) | 326.8 | 0.0034 | HOMO → LUMO (98.9 %) |
We have further applied a molecular docking approach, performed with the AutoDock Vina software [30], to examine both the interaction efficiency and mechanism of 1–3 towards a series of the SARS-CoV-2 proteins (Table 8 ). Crystal structures of the applied proteins were extracted from the RCSB Protein Data Bank [31]. Both 1–3 and corresponding proteins were first prepared using BIOVIA Discovery Studio 2020 [32]. For comparison of potential biological activity, the initial ligands were also redocked with the applied proteins using the same approach.
Table 8.
The best poses of the (S)- and (R)-enantiomers of 1–3 inside the binding sites of the listed proteins.
It was found that the absolute values of binding energy for the (S)- and (R)-enantiomers of all the reported α-aminophosphonates are, in general, lower than those for the corresponding initial ligands, except for complexes with the nonstructural protein 3 (nsp3_range 207–379-MES) (marked by red bold in Table 8), of which the (R)-enantiomer of 3 was found to be the slightly more efficient ligand. Notably, no clearly defined preference of either the (S)- or (R)-enantiomer was revealed upon docking with the applied proteins as evidenced from the close comparable binding energies (Table 8). Considering only the (S)- and (R)-enantiomers of 1–3 the absolute values of binding energy with the nonstructural protein 14 (nsp14 N7-MTase) (marked by black bold in Table 8) are remarkably higher than those for the complexes with other proteins (Table 8). Moreover, somewhat higher absolute values of binding energy were found for the (R)-enantiomers of 1–3 upon docking with the nonstructural protein 14 (nsp14 N7-MTase) (marked by black bold in Table 8). All this is due to sets of intermolecular interactions formed between the enantiomers of 1–3 and the corresponding protein. Particularly, the main interactions between the (R)-enantiomer of 1 and nsp14 (N7-MTase) are two conventional hydrogen bonds with Asn388, one C⋯H bond with Cys387, one π-system⋯anion interactions with Asp352, two π-system⋯S interactions with Cys387, five alkyl interactions with Pro335, Arg289 and Val290, and five π-system⋯alkyl interactions with Trp292, Phe367, Phe426, Pro335 and Ala353 (Fig. 11 , Table S1 in the Supplementary Information). Interaction of the (R)-enantiomer of 2 with nsp14 (N7-MTase) is the most efficient, most likely due to the presence of two bromine substituents, and is characterized by two π⋯π interactions with Trp292 and Phe426, three alkyl interactions with Val290, Pro335 and Lys336, and eleven π-system⋯ alkyl interactions with Trp292, Trp385, Phe401, Tyr420, Phe426, Val290 and Pro335, respectively (Fig. 11, Table S1 in the Supplementary Information). Finally, the (R)-enantiomer of 3 interacts with nsp14 (N7-MTase) through one conventional hydrogen bond with Asn386, one π-system⋯cation interaction with Phe426, one π⋯π interaction with Phe426, and seven π-system⋯alkyl interactions with Trp292, Phe401, Tyr420, Phe426 and Pro335 (Fig. 11, Table S1 in the Supplementary Information). The docking poses of the (S)-enantiomers of 1–3 with the same nonstructural protein 14 (nsp14 N7-MTase), being less efficient, are described with their own set of interactions (Fig. S6 and Table S1 in the Supplementary Information).
Fig. 11.
3D (left) and 2D (right) views on the interaction of the (R)-enantiomers of 1 (top), 2 (middle) and 3 (bottom) with nsp14 (N7-MTase).
4. Conclusions
In summary, we report synthesis and in-depth structural and computational studies of three closely related α-aminophosphonates 4-XC6H4–NH–CH(4-BrC6H4)–P(O)(OiPr)2, namely diisopropyl((4-bromophenyl)(phenylamino)methyl)phosphonate (X = H, 1), diisopropyl((4-bromophenyl)((4-bromophenyl)amino)methyl)phosphonate (X = Br, 2) and diisopropyl((4-bromophenyl)((4-methoxyphenyl)amino)methyl)phosphonate (X = MeO, 3), which were readily obtained by a one-pot reaction of 4-bromobenzaldehyde, diisopropylphosphite and aniline or 4-bromoaniline or 4-methoxyaniline, respectively. The 31P{1H} and 1H NMR spectroscopy data fully support the formation of 1–3.
Single crystal X-ray diffraction revealed that 2 and 3 are isostructural and each contain two independent molecules in the asymmetric unit cell, namely herein as 2-I and 2-II, and 3-I and 3-II. Furthermore, the geometrical parameters of all molecules are very similar. The O=P–C–N fragment in all structures exhibits a Z conformation, while the aromatic rings are almost orthogonal to each other. Two molecules in the crystal structures of 1–3 are interlinked through a pair of intermolecular N–H⋯O=P hydrogen bonds, affording a centrosymmetric supramolecular dimer with a R 2 2(10) motif.
According to the Hirshfeld surface analysis an overwhelming majority of the molecular surfaces of 1, 2-I, 2-II, 3-I and 3-II is occupied by favoured intermolecular H⋯H contacts, followed by also favoured H⋯C, H⋯Br and H⋯O contacts, which is due to the presence of the isopropyl fragments as well as due to the absence of intermolecular π⋯π stacking interactions. Interestingly, a proportion of the H⋯H contacts decreases from 1, 3-I and 3-II to 2-I and 2-II with the simultaneous increase of the H⋯Br contacts, which is explained by the presence of the second bromine atom in the structures of the latter two molecules. The presence of the second bromine atom in the structures of 2-I and 2-II is also responsible for appearance of a perceptible proportion of the Br⋯Br contacts.
Energy frameworks have been calculated to additionally analyze the overall crystal packing of the discussed molecules. It was established that all the structures are mainly characterized by the dispersion energy, followed by a less significant electrostatic energy contribution.
According to the DFT calculation results, it was established that 1–3 each exhibit low electron donating and pronounced electron accepting properties. The most pronounced nucleophilic center is located on the P=O oxygen atom, while the other negative electrostatic potential sites are located on the bromine and methoxy oxygen atoms in 1–3. The most electrophilic region corresponds to the N(H)–C(H) fragment for all the structures.
In silico molecular docking was applied to probe interactions of both the (S)- and (R)-enantiomers of 1–3 with a series of the SARS-CoV-2 proteins. It was established that the absolute values of binding energy for the (S)- and (R)-enantiomers of 1–3 are, in general, lower than those for the corresponding initial ligands, except for complexes with the nonstructural protein 3, of which the (R)-enantiomer of 3 was found to be the slightly more efficient ligand. No clearly defined preference of either the (S)- or (R)-enantiomer was revealed. Considering only the (S)- and (R)-enantiomers of 1–3 the absolute values of binding energy with the nonstructural protein 14 (nsp14 N7-MTase) are remarkably higher than those for the complexes with other proteins, of which the compound 2 was found to be the most efficient one, most likely due to the presence of two bromine functions in a molecule. We hope that the results reported herein will be of value for future design of potential drugs against SARS-CoV-2.
Declaration of competing interest
There are no conflicts to declare.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.tet.2021.132376.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- 1.Hiroguchi M., Kandatsu M. Isolation of 2-aminoethane phosphonic acid from rumen Protozoa. Nature. 1959;184:901–902. doi: 10.1038/184901b0. [DOI] [PubMed] [Google Scholar]
- 2.Mastalerz P. Inhibition of glutamine synthetase by phosphonic analogues of glutamic acid. Arch. Immunol. Ter. Dosw. 1959;7:201–210. [Google Scholar]
- 3.Kukhar V.P., Hudson H.R. John Wiley & Sons; Chichester, U.K: 2000. Aminophosphonic and Aminophosphinic Acids: Chemistry and Biological Activity. [Google Scholar]
- 4.Kafarski P., Lejczak B. BIOLOGICAL ACTIVITY OF AMINOPHOSPHONIC ACIDS, phosphorus. Sulfur Silicon Relat. Elem. 1991;63:193–215. [Google Scholar]
- 5.Collinsová M., Jiráček J. Phosphinic acid compounds in biochemistry, biology and medicine. Curr. Med. Chem. 2000;7:629–647. doi: 10.2174/0929867003374831. [DOI] [PubMed] [Google Scholar]
- 6.Kafarski P., Lejczak B. Aminophosphonic acids of potential medical importance. Curr. Med. Chem. Anti Canc. Agents. 2001;1:301–312. doi: 10.2174/1568011013354543. [DOI] [PubMed] [Google Scholar]
- 7.Berlicki Ł., Kafarski P. Computer-aided analysis and design of phosphonic and phosphinic enzyme inhibitors as potential drugs and agrochemicals. Curr. Org. Chem. 2005;9:1829–1850. [Google Scholar]
- 8.Azema L., Baron R., Ladame S. Targeting enzymes with phosphonate-based inhibitors: mimics of tetrahedral transition states and stable isosteric analogues of phosphates. Curr. Enzym. Inhib. 2006;2:61–72. [Google Scholar]
- 9.Wardle N.J., Bligh S.W.A., Hudson H.R. ω -Phosphinyl-α -amino acids: synthesis, and development towards use as therapeutic agents. Curr. Org. Chem. 2007;11:1635–1651. [Google Scholar]
- 10.Ecker S.J., Erion M.D. Prodrugs of phosphates and phosphonates. J. Med. Chem. 2008;51:2328–2345. doi: 10.1021/jm701260b. [DOI] [PubMed] [Google Scholar]
- 11.Lejczak B., Kafarski P. Biological activity of aminophosphonic acids and their short peptides. Top. Heterocycl. Chem. 2009;20:31–63. [Google Scholar]
- 12.Orsini F., Sello G., Sisti M. Aminophosphonic acids and derivatives. Synthesis and biological applications. Curr. Med. Chem. 2010;17:264–289. doi: 10.2174/092986710790149729. [DOI] [PubMed] [Google Scholar]
- 13.Mucha A., Kafarski P., Berlicki Ł. Remarkable potential of the α-aminophosphonate/phosphinate structural motif in medicinal chemistry. J. Med. Chem. 2011;54:5955–5980. doi: 10.1021/jm200587f. [DOI] [PubMed] [Google Scholar]
- 14.Keglevich G., Bálint E. The Kabachnik-fields reaction: mechanism and synthetic use. Molecules. 2012;17:12821–12835. doi: 10.3390/molecules171112821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hamilton R., Walker B., Walker B.J. Synthesis and proteinase inhibitory properties of diphenyl phosphonate analogues of aspartic and glutamic acids. Bioorg. Med. Chem. Lett. 1998;8:1655–1660. doi: 10.1016/s0960-894x(98)00272-8. [DOI] [PubMed] [Google Scholar]
- 16.Burchacka E., Skoreński M., Sieńczyk M., Oleksyszyn J. Phosphonic analogues of glutamic acid as irreversible inhibitors of Staphylococcus aureus endoproteinase GluC: an efficient synthesis and inhibition of the human IgG degradation. Bioorg. Med. Chem. Lett. 2013;23:1412–1415. doi: 10.1016/j.bmcl.2012.12.074. [DOI] [PubMed] [Google Scholar]
- 17.Dennington R., Keith T.A., Millam J.M. Semichem Inc.; Shawnee Mission, KS: 2016. GaussView, Version 6.0. [Google Scholar]
- 18.Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V., Mennucci B., Petersson G.A., Nakatsuji H., Caricato M., Li X., Hratchian H.P., Izmaylov A.F., Bloino J., Zheng G., Sonnenberg J.L., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Montgomery J.A., Jr., Peralta J.E., Ogliaro F., Bearpark M., Heyd J.J., Brothers E., Kudin K.N., Staroverov V.N., Keith T., Kobayashi R., Normand J., Raghavachari K., Rendell A., Burant J.C., Iyengar S.S., Tomasi J., Cossi M., Rega N., Millam J.M., Klene M., Knox J.E., Cross J.B., Bakken V., Adamo C., Jaramillo J., Gomperts R., Stratmann R.E., Yazyev O., Austin A.J., Cammi R., Pomelli C., Ochterski J.W., Martin R.L., Morokuma K., Zakrzewski V.G., Voth G.A., Salvador P., Dannenberg J.J., Dapprich S., Daniels A.D., Farkas O., Foresman J.B., Ortiz J.V., Cioslowski J., Fox D.J. 2013. Gaussian 09, Revision D.01. [Google Scholar]
- 19.Krishnan R., Binkley J.S., Seeger R., Pople J.A. J. Chem. Phys. 1980;72:650–654. [Google Scholar]
- 20.Becke A.D. J. Chem. Phys. 1993;98:5648–5652. [Google Scholar]
- 21.Frisch M.J., Pople J.A., Binkley J.S. Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets. J. Chem. Phys. 1984;80:3265–3269. [Google Scholar]
- 22.Stoe & Cie. X-Area . Stoe & Cie; Darmstadt, Germany: 2001. Area-Detector Control and Integration Software. [Google Scholar]
- 23.Spek A.L. Single-crystal structure validation with the program PLATON. J. Appl. Crystallogr. 2003;A36:7–13. [Google Scholar]
- 24.Sheldrick G.M. A short history of SHELX. Acta Crystallogr. 2008;A64:112–122. doi: 10.1107/S0108767307043930. [DOI] [PubMed] [Google Scholar]
- 25.Spackman M.A., Jayatilaka D. Hirshfeld surface analysis. CrystEngComm. 2009;11:19–32. [Google Scholar]
- 26.Spackman M.A., McKinnon J.J. Fingerprinting intermolecular interactions in molecular crystals. CrystEngComm. 2002;4:378–392. [Google Scholar]
- 27.Turner M.J., McKinnon J.J., Wolff S.K., Grimwood D.J., Spackman P.R., Jayatilaka D., Spackman M.A. University of Western Australia; 2017. CrystalExplorer17.http://hirshfeldsurface.net [Google Scholar]
- 28.Jelsch C., Ejsmont K., Huder L. The enrichment ratio of atomic contacts in crystals, an indicator derived from the Hirshfeld surface analysis. IUCrJ. 2014;1:119–128. doi: 10.1107/S2052252514003327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Geerlings P., De Proft F., Langenaeker W. Conceptual density functional theory. Chem. Rev. 2003;103:1793–1874. doi: 10.1021/cr990029p. [DOI] [PubMed] [Google Scholar]
- 30.Trott O., Olson A.J., Vina AutoDock. Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010;31:455–461. doi: 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.https://www.rcsb.org/
- 32.BIOVIA, Dassault Systèmes . Dassault Systèmes; San Diego: 2020. BIOVIA Discovery Studio. 2020. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.