A BAYESIAN MARK INTERACTION MODEL FOR ANALYSIS OF TUMOR PATHOLOGY IMAGES

Abstract

With the advance of imaging technology, digital pathology imaging of tumor tissue slides is becoming a routine clinical procedure for cancer diagnosis. This process produces massive imaging data that capture histological details in high resolution. Recent developments in deep-learning methods have enabled us to identify and classify individual cells from digital pathology images at large scale. Reliable statistical approaches to model the spatial pattern of cells can provide new insight into tumor progression and shed light on the biological mechanisms of cancer. We consider the problem of modeling spatial correlations among three commonly seen cells observed in tumor pathology images. A novel geostatistical marking model with interpretable underlying parameters is proposed in a Bayesian framework. We use auxiliary variable MCMC algorithms to sample from the posterior distribution with an intractable normalizing constant. We demonstrate how this model-based analysis can lead to sharper inferences than ordinary exploratory analyses, by means of application to three benchmark datasets and a case study on the pathology images of 188 lung cancer patients. The case study shows that the spatial correlation between tumor and stromal cells predicts patient prognosis. This statistical methodology not only presents a new model for characterizing spatial correlations in a multitype spatial point pattern conditioning on the locations of the points, but also provides a new perspective for understanding the role of cell-cell interactions in cancer progression.

1. Introduction.

Cancer is a complex disease characterized by uncontrolled tumor cell growth. The pathological examination of hematoxylin and eosin (H&E)-stained tissue slides forms the basis of cancer diagnosis. It has been reported that cell growth patterns are associated with the survival outcome (Amin et al. (2002), Barletta, Yeap and Chirieac (2010), Borczuk et al. (2009), Gleason and Mellinger (2002)) and treatment response (Tsao et al. (2015)) of cancer patients. In addition, the interactions between tumor cells and other types of cells (e.g., immune cells) play important roles in the progression and metastasis of cancer (Gillies, Verduzco and Gatenby (2012), Hanahan and Weinberg (2011), Junttila and de Sauvage (2013), Mantovani et al. (2002), Merlo et al. (2006), Orimo et al. (2005), Polyak, Haviv and Campbell (2009)). Spatial variations among cell types and their association with patient prognosis have been previously reported in breast cancer (Mattfeldt et al. (2009)). Pathological examination of tissue slides requires a pathologist to match the observed image slides with his/her memory for certain patterns and features (such as tumor content, nuclei counts and tumor boundary). This process is laborious, tedious and subject to errors. More importantly, due to the limitations of the human brain in interpreting highly complex pathology images, it is hard for pathologists to systematically explore those subtle but important patterns, such as tumor cell distribution and interaction with the surrounding micro-environment. Pathological examination by the human eyes is insufficient to decipher the large amount of complex and comprehensive information harbored in the high resolution pathology images.

With the advance of imaging technology, H&E-stained pathology imaging is becoming a routine clinical procedure, which produces massive digital pathology images on a daily basis. Digital pathology image analyses have been proven to be valuable in clinical diagnosis and prognosis of various malignancies, including precancerous lesions in the esophagus (Sabo et al. (2006)), prostate cancer (Tabesh et al. (2007)), neuroblastoma (Sertel et al. (2009a)), lymphoma (Sertel et al. (2009b)), breast cancer (Beck et al. (2011), Yuan et al. (2012)) and recently, lung cancer (Luo et al. (2016), Yu et al. (2016)). However, current studies of pathology image analysis mainly focus on the morphology features, such as tissue texture and granularity. For example, Tabesh et al. (2007) aggregate color, texture and morphometric cues at the global and histological object levels to predict the malignancy level of prostate cancer. Both Yu et al. (2016) and Luo et al. (2016) used a large number of objective morphological features (e.g., cell size, shape, distribution of pixel intensity in the cells and nuclei, texture of the cells and nuclei, etc.) extracted by CellProfiler (Carpenter et al. (2006), Kamentsky et al. (2011)) to predict lung cancer prognosis. Yuan et al. (2012) even integrate histopathology and genomics information, extending approaches that only use morphological features to predict breast cancer patient survival. However, these imaging data, which capture histological details in high resolution, still leave unexplored more undiscovered knowledge. Computer vision and machine learning algorithms have enabled us to automatically identify individual cells from digital pathology images at large scale (e.g. Yuan et al. (2012)). Recent developments in deep-learning methods have greatly facilitated this process. We have developed a convolutional neural network (CNN) to identify individual cells and classify their types into three categories: lymphocyte, stromal and tumor.

Consequently, a pathology image is abstracted into a spatial map of marked points, where each cell belongs to one of the three distinct types. The analysis of pathology images thus becomes an investigation of those marked point pattern, which will provide a new perspective for the role of cell-cell interactions in cancer progression. Currently, a patient cohort usually contains hundreds of patients, and each patient has one or more pathology images. These rich datasets provide a great opportunity to study the cell-cell interactions in cancer. Recently, Li et al. (2017) developed a modified Potts model to study the spatial patterns observed in tumor pathology images, by projecting irregularly distributed cells into a square lattice. However, this approximate method relies on selection of an ad hoc lattice. More importantly, it models the interaction among different regions (small squares defined by the lattice), but not those among individual cells.

The study of interactions between objects, which results in the spatial correlation of marks, has been a primary focus in spatial statistics. It is a key aspect in population forestry (Stoyan and Penttinen (2000)) and ecology (Dale (2000)) theory, but receives little attention in biology. Illian et al. (2008) discussed in detail a large variety of numerical, functional and second-order summary characteristics, which can be used to describe the spatial dependency between different types of points in a planar region. The most common approaches are based on generalizing the standard distance-dependent G-, K-, J- and L-functions to their “cross-type” versions (see, e.g., Besag (1977), Diggle and Cox (1981), Lotwick and Silverman (1982), Ripley (1977), Vincent and Jeulin (1989), van Lieshout and Baddeley (1996, 1999)). Mark connection functions (MCFs) are another well recognized tool for qualitative marks, which are more suitable for the detection of mark correlation in an exploratory analysis (Wiegand and Moloney (2004)). The ad hoc testing of hypotheses, such as spatial independences of the marks, based on some suitable summary characteristics (e.g., K-functions) has also been discussed in the literature (Grabarnik, Myllymäki and Stoyan (2011)). However, model-based analysis, which may sharpen inferences about the spatial pattern, is lagging. Marked point process models are usually constructed by familiar devices, such as Cox, cluster and thinned processes (Gelfand et al. (2010)). For example, Diggle and Milne (1983) defined the class of bivariate Cox processes and investigated the structure of correlated bivariate Cox models. Gibbsian point processes are more appropriate to account for interaction between points than Cox models, which tend to reflect underlying environmental variation. Ogata and Tanemura (1985) and Diggle, Eglen and Troy (2006) formulated pairwise interaction models based on Gibbs distributions for bivariate marked point patterns and argued that model-based inference is statistically more efficient. Inference for those mark-dependent/independent pairwise interactions are mainly based on frequentist approaches, which can only provide for point estimation. Bayesian inference of marked point processes has been notably underrepresented in the literature (Bognar (2008)). For more detailed examples of modeling approaches for marked point processes, see Baddeley and Turner (2006).

In this paper, motivated by the emerging needs of tumor pathology images analysis, we develop a novel geostatistical marking model, which aims to study the mark formulation at a finite known set of points through a Bayesian framework. A local energy function of three groups of parameters, that is, first- and second-order intensities, and an exponential decay rate to the inter-point distance, is carefully defined, so is the related Gibbs distribution. The proposed model can serve as a novel model-based approach to characterize the spatial pattern/correlation among marks. We use the double Metropolis-Hastings (DMH) algorithm (Liang (2010)) to sample from the posterior distribution with an intractable normalizing constant in the Gibbs distribution. The model performs well in simulated studies and three benchmark datasets. We also conduct a case study on a large cohort of lung cancer pathology images. The result shows that the spatial correlation between tumor and stromal cells is associated with patient prognosis (P-value = 0.007). Although the morphological features of stroma in tumor regions have been discovered to be associated with patient survival, there is no strong statistical evidence to support this, due to a lack of rigorous statistical methodology. In the study, the proposed statistical methodology not only delivers a new perspective for understanding how marks (i.e., cell types in pathology images) formulate, given an independent unmarked point process, but also provides a refined statistical tool to characterize spatial interactions, which the existing approaches (e.g., MCF) may lack sufficient power to do so.

The remainder of the paper is organized as follows: Section 2 introduces the proposed modeling framework, including the local energy function and its related Gibbs distribution (i.e., the model likelihood), the choices of priors and the model interpretation. Section 3 describes the Markov chain Monte Carlo (MCMC) algorithm and discusses the resulting posterior inference. Section 4 assesses performance of the proposed model on simulated data. Section 5 analyzes three benchmark datasets and a large cohort of lung cancer pathology images from the National Lung Screening Trial (NLST). Section 6 concludes the paper with some remarks on future research directions.

2. Model.

We describe a spatial map of cells in a Cartesian coordinate system, with n observed cells indexed by i. We use $\left(x_i,y_i\right)\in {ℝ}^2$ to denote the x- and y-coordinates and z_i ∈ {1, … , Q}, Q ≥ 2 to denote the type of cell i. In spatial point pattern analysis, such data are considered as multitype point pattern data, where (x₁, y₁), … , (x_n, y_n) are the point locations in a compact subset of the 2-dimensional Euclidean space ${ℝ}^2$ (note that the proposed model can be easily extend to a general case of ${ℝ}^k$, k ≥ 3) and z₁, … , z_n are their associated qualitative (i.e., categorical or discrete) univariate marks. The mark attached to each point indicates which type/class it is (e.g., on/off, case/control, species, etc.). Without loss of generality, we assume that the data points are restricted within the unit square [0, 1]². This can be done by rescaling each pair of coordinates (x_i, y_i) to $\left(x_i^{\prime },y_i^{\prime }\right)$. Suppose all the points are within a known rectangle, with four vertices’ coordinates denoted by $\left(v_x^{\text{lwr}},v_y^{\text{lwr}}\right)$, $\left(v_x^{\text{upp}},v_y^{\text{lwr}}\right)$, $\left(v_x^{\text{upp}},v_y^{\text{upp }}\right)$ and $\left(v_x^{\text{lwr}},v_y^{\text{upp }}\right)$, then $x_i^{\prime }=\left(x_i-v_x^{\text{lwr}}\right)/L$ and $y_i^{\prime }=\left(y_i-v_y^{\text{lwr}}\right)/L$, where $L=\text{max}\left(v_x^{\text{upp }}-v_x^{\text{lwr }},v_y^{\text{upp }}-v_y^{\text{lwr }}\right)$.

Since our primary interest lies in the spatial correlations of different types of cells, we only treat the marks as random variables, conditional on their fixed locations within a bounded observation window. This removes the need to infer the unmarked point process, simplifying the modeling construction and eliminating error due to the estimation of point density. Baddeley (2010) argued that it is often appropriate to analyze a marked point pattern by conditioning on the locations and under some reasonable assumptions, the marks effectively constitute a random field.

2.1. Energy functions.

In the analysis of tumor pathology images, cell distribution and cell-cell interaction may reveal important messages about the tumor cell growth and its micro-environment. Therefore, it is of great interest to study the arrangements of cell types associated with the observed cells, given their locations. In spatial point pattern analysis, such a problem is called geostatistical marking (Illian et al. (2008)), which is to study the formulation of the marks z in a pattern, given the points (x, y). In this subsection, we explore the formulation of energy functions, accounting for both of the first- and second-order properties of the point data. The energy function (also known as the potential function) originates in statistical physics. It can be interpreted as the energy required to obtain a stable arrangement of z, which is contributed by each z_i as well as each pair of $\left(z_i,z_i^{\prime }\right)$.

At the initial stage, we assume that each point interacts with all other points in the space. A complete undirected graph G = (V, E) can be used to depict their relationships, with V denoting the set of points (i.e., the n observed cells) and E denoting the set of direct interactions (i.e., the (n − 1)n/2 cell-cell pairs). We define G as the interaction network and define its potential energy as

$$V(\mathit{\text{z}}|\mathit{\omega },\mathbf{\Theta })=\sum _q{\omega }_q\sum _{i}I\left(z_i=q\right)+\sum _q\sum _{q^{\prime }}{\theta }_{q{q}^{\prime }}\sum _{\left(i~i^{\prime }\right)\in E}I\left(z_i=q,z_{i^{\prime }}=q^{\prime }\right),$$ (2.1)

where the notation (i ~ i′) denotes that points i and i′ are the interacting pair in G (i.e., they are connected by an edge in G), and I denotes the indicator function. Note that θ_qq′ = θ_q′q as the edge between any pairs of points has no orientation. On the right-hand side of equation (2.1), the first term can be viewed as the weighted average of the numbers of points with different marks, while the second term can be viewed as the weighted average of the numbers of pairs connecting two points with the same or different marks. In the context of spatial point pattern analysis, the first and second terms are referred to the first- and second-order potentials/characteristics, respectively. Their corresponding parameters ω = (ω₁, … , ω_Q) and Θ = [θ_qq′]_Q×Q are defined as the first- and second-order intensities. These two groups of parameters control the enrichment of different marks and the spatial correlations among them simultaneously. A detailed interpretation of ω and Θ is discussed in Section 2.4.

In mathematical physics and statistical thermodynamics, the interaction energy between two points (i.e., particles and cells) is usually an exponential decay function with respect to the distance between the two points (see, e.g., Avalos and Bucci (2014), Chulaevsky (2014), Kashima (2010), Penrose and Lebowitz (1974), Rincón, Ganahl and Vidal (2015)). Similarly, exponential decay has also been observed in biological systems, such as cell-cell interactions (Hui and Bhatia (2007), Segal and Stephany (1984)) and gene-gene correlations (Xiao, Reilly and Khodursky (2009), Xiao, Wang and Khodursky (2011)). In this study, we assume the interaction energy between a pair of points decreases exponentially at a rate λ proportional to the distance,

$$\begin{gathered} V(\mathit{\text{z}}|\mathit{\omega },\mathbf{\Theta },\lambda )=\sum _q{\omega }_q\sum _{i}I\left(z_i=q\right) \\ +\sum _q\sum _{q^{\prime }}{\theta }_{q{q}^{\prime }}\sum _{\left(i~i^{\prime }\right)\in E}{e}^{-\lambda d_{i{i}^{\prime }}}I\left(z_i=q,z_{i^{\prime }}=q^{\prime }\right), \end{gathered}$$ (2.2)

where $d_{i{i}^{\prime }}=\sqrt{{\left(x_i-x_{i^{\prime }}\right)}^2+{\left(y_i-y_{i^{\prime }}\right)}^2}$ is the Euclidean distance between points i and i′. A larger value of the decay parameter λ makes the interaction energy vanish much more rapidly with the distance, while a smaller value leads to $e^{-\lambda d_{i{i}^{\prime }}}\approx 1$ and equation (2.2) → equation (2.1). See Figure S1 in the Supplementary Material (Li et al. (2019)) for examples of exponential decay functions with different values of parameter λ. The decay function makes our approach similar in spirit to the other literature on spatial prediction, which are built from a fairly simple concept: spatial correlation suggests that one should give more weight to observations near the prediction location than to those far away (Waller (2005)). In addition to the exponential decay, we can also consider the other decay forms under different scenarios and for different applications, such as the step decay I (d ≤ λ), 0 < λ < 1, the power-law decay d^−λ, λ > 0 and the power-exponential decay $e^{-\lambda d^{\beta }}$, λ > 0, β > 0. However, note that different choices of decay functions may result in different estimations on the second-order intensities.

As shown in equation (2.2), it needs to sum over n data points and (n − 1)n/2 pairs of data points to compute the potential energy, resulting in a tedious computation, especially when n is large. An alternative way is to obtain an approximate value of V(z|ω, Θ, λ) by neglecting those pairs with distance beyond a certain threshold c, c ∈ (0, 1). It can be illustrated that a point (i.e., a cell) can only interact with its nearby points within a certain range c. Therefore, the complete network G reduces to a sparse network G′ = (V, E′), with E′ ⊆ E denoting the set of edges joining pairs of points i and i′ in G′, if their distance d_ii′ is smaller than a threshold c. We write the potential energy of the interaction network G′ as

$$\begin{gathered} V(\mathit{\text{z}}|\mathit{\omega },\mathbf{\Theta },\lambda )=\sum _q{\omega }_q\sum _{i}I\left(z_i=q\right) \\ +\sum _q\sum _{q^{\prime }}{\theta }_{q{q}^{\prime }}\sum _{\left(i~i^{\prime }\right)\in E^{\prime }}{e}^{-\lambda d_{i{i}^{\prime }}}I\left(z_i=q,z_{i^{\prime }}=q^{\prime }\right). \end{gathered}$$ (2.3)

Note that c is not a model parameter, but a user-defined value. We may determine its value from a mark connection function analysis (discussed in Section 4) or from the subjective assessment of an experienced expert in the related field. The choice of a large c causes a considerably complex network, while a too small value results in a sparse network that may neglect some important spatial information. See Figure S2 in the Supplementary Material (Li et al. (2019)) for an example of three-type point pattern data (n = 100) and its corresponding mark interaction networks G′ under different choices of c. By introducing the sparse network G′, we not only reduce the computational cost, but also define a local spatial structure.

2.2. Data likelihood.

According to the fundamental Hammersley-Clifford theorem (Hammersley and Clifford (1971)), if we have a locally defined energy, such as equation (2.3), then a probability measure with a Markov property exists. This frequently seen measure in many problems of probability theory and statistical mechanics is called a Gibbs measure, which gives the probability of observing marks associated with their locations in a particular state,

$$p(\mathit{\text{z}}|\mathit{\omega },\mathbf{\Theta },\lambda )=\frac{\text{exp}(-V(\mathit{\text{z}}|\mathit{\omega },\mathbf{\Theta },\lambda ))}{{\sum }_{z^{\prime }}\text{exp}\left(-V\left({\mathit{\text{z}}}^{\prime }|\mathit{\omega },\mathbf{\Theta },\lambda \right)\right)}.$$ (2.4)

The normalizing constant C(ω, Θ, λ) = Σ_z′ exp(−V(z′|ω, Θ, λ)) is also called a partition function. An exact evaluation of C(ω, Θ, λ) needs to sum over the entire space of z, which consists of Qⁿ states. Thus, it is intractable even for a small size model. Take Q = 2 and n = 100, for example, it needs to sum over 2¹⁰⁰ ≈ 1.268 × 10³⁰ elements. To address this issue, we employ the double Metropolis-Hastings (DMH) algorithm (Liang (2010)) to make inference on the model parameters ω, Θ and λ. DMH is an auxiliary variable MCMC algorithm, which can make the normalizing constant ratio canceled by augmenting appropriate auxiliary variables through a short run of the ordinary Metropolis-Hastings (MH) algorithm. More details are given in Section 3.1.

Equation (2.4) serves as the full data likelihood. Since the model satisfies the local Markov property, we can also write the probability of observing point i belonging to class q conditional on its neighborhood configuration(s),

$$\begin{gathered} p\left(z_i=q|{\mathit{\text{z}}}_{-i},\mathit{\omega },\mathbf{\Theta },\lambda \right) \\ \propto \text{exp}\left(-{\omega }_q-\sum _{q^{\prime }}{\theta }_{q{q}^{\prime }}\sum _{\left\{i^{\prime }:\left(i~i^{\prime }\right)\in E^{\prime }\right\}}{e}^{-\lambda d_{i{i}^{\prime }}}I\left(z_{i^{\prime }}=q^{\prime }\right)\right), \end{gathered}$$ (2.5)

where z_−i denotes the collection of all marks excluding the ith one. According to equation (2.5), the conditional probability depends on the first-order intensity ω_q, the second-order intensities θ_qq′, q′ = 1, … , Q, the decay parameter λ, and the neighborhood of the points defined by c. Equation (2.5) is essentially a multinomial logistic regression and hence the parameters ω_q and θ_qq′ can be interpreted in terms of conditional odds ratios.

2.3. Parameter priors.

The proposed model in the Bayesian framework requires the specification of prior distributions for the unknown parameters. In this subsection, we specify the priors for all three groups of parameters: ω, Θ and λ. For the first- and second-order intensities ω and Θ, we notice that an identifiability problem arises from equation (2.4) or (2.5). For example, adding a nonzero constant, say s, into ω_q, q = 1, … , Q does not change the probability of observing point i belonging to class q. Similarly, the settings of Θ and $\mathbf{\Theta }+s\mathbb{1}$ lead to the same conditional probability, where $\mathbb{1}$ is a Q-by-Q matrix of ones. Therefore, imposing an appropriate constraint is necessary. Without loss of generality, suppose the points with mark Q have the largest population and we set ω_Q = 1 and θ_QQ = 1. For the other parameters in ω and Θ, we consider normal priors and set ${\omega }_q~\text{N}\left({\mu }_{\omega },{\sigma }_{\omega }^2\right)$, q = 1, … , Q − 1 and ${\theta }_{q{q}^{\prime }}~\text{N}\left({\mu }_{\theta },{\sigma }_{\theta }^2\right)$, q = 1, … , Q − 1, q′ = q, … , Q. We suggest users choose the standard normal distribution; that is, μ_ω = μ_θ = 0 and σ_ω = σ_θ = 1. For the decay parameter λ, we specify a gamma prior λ ~ Ga(a_λ, b_λ). One standard way of setting a weakly informative gamma prior is to choose small values for the two parameters, such as a_λ = b_λ = 0.001. The Ga(a, b) prior is an attempt at noninformativeness within the conditionally conjugate family, with both a and b set to a low value, such as 0.1, 0.01 and 0.001 (Gelman et al. (2014)).

2.4. Interpretation.

In this subsection, we aim to interpret the meanings of the model parameters ω and Θ. In order to understand the relationship between the estimated parameter values and the observed multitype point pattern.

Suppose there is only one point in the space. Then equation (2.5) reduces to p(z₁ = q|·) ∝ exp(−ω_q), which implies the probability of observing a point with mark q in this single-point system is equal to π_q = exp(−ω_q)/Σ_q exp(−ω_q). Note that the vector π = (π₁, … , π_Q) has a natural constraint; that is, Σ_q π_q = 1. Furthermore, suppose there are n points in the space and there are almost no mark interactions. This can be fulfilled by any one of the following conditions: (1) the distance between any pairs of two points is beyond the given value c, that is, d_ii′ > c, ∀(i ~ i′) ∈ E; (2) the second-order intensities are all equal, that is, $\mathbf{\Theta }=s\mathbb{1}$, $\exists s\in ℝ$ ; or (3) the decay parameter λ goes to infinity, that is, λ → ∞. Then equation (2.5) converges to p(z_i = q|z_−i, ω, Θ, λ) ∝ exp(−ω_q) = π_q, implying that the expected number of points with mark q is nπ_q. Thus, after transforming the first-order intensities ω to their probability measures π, we find a clear path to describe the abundance of different marks in the above simplified situations.

Suppose there are only two points 1 and 2 in the space, with the type of the second point known; say z₂ = q′. For convenience, we further assume ω₁ = ⋯ = ω_Q. We first consider the case of the two points being at the same location, that is, d₁₂ = 0. Then equation (2.5) turns out to be p(z₁ = q|z₂ = q′,·) ∝ exp(−θ_qq′), which implies the probability of observing the point with unknown mark belonging to type q, given the one with the known mark q′ (at the same location), is ϕ_qq′ = exp(−θ_qq′)/Σ_q exp(−θ_qq′). We use a Q-by-Q matrix ϕ to denote the collection of ϕ_qq′, q = 1, … , Q, q′ = 1, … , Q. Note that each column in ϕ should be summed to 1 and ϕ is not necessary to be a symmetric matrix as Θ. In this duo-point system (and more complex cases therein), the larger the value of ϕ_qq′, the more likely the points with mark q get attracted to the nearby points with mark q′. Thus, the spatial correlations among marks can be easily interpreted by the probability matrix ϕ.

In the aforementioned duo-point model with known parameters, if the assumption of equivalent first-order intensities is relaxed, then the probability of assigning mark q to point 1 conditional on the mark of point 2 is q′ is a strictly monotonic function of their distance d,

$${\text{MIF}}_{q|q^{\prime }}(d)=\frac{\text{exp}\left(-{\omega }_q-{\theta }_{q{q}^{\prime }}{e}^{-\lambda d}\right)}{{\sum }_{q^{″}}\text{exp}\left(-{\omega }_{q^{″}}-{\theta }_{q^{″}{q}^{\prime }}{e}^{-\lambda d}\right)}.$$ (2.6)

We call the above equation the mark interaction function (MIF) of mark q given mark q′. As the distance increases, its value ultimately converges to π_q. The plot of MIF is a more comprehensive way to describe the spatial correlation/interaction between marks.

In conclusion, π, ϕ and MIF directly characterize a single point behavior (i.e., the assignment of its mark) in a model with small size, such as n = 1 and 2. However, the observed multitype point pattern is a reflection of how each individual point reacts with its neighbors. Note that the mappings from ω to π and from Θ to ϕ are one-to-one/unique, so we can implement this step after obtaining the estimates of ω and Θ.

3. Model fitting.

In this section, we describe the MCMC algorithm for posterior inference. Our inferential strategy allows for simultaneously estimating (1) the first-order intensities ω, which reveal the abundance of different marks; (2) the second-order intensities Θ, which capture the spatial correlation among marks; and (3) the decay parameter λ. We first give the full details of our MCMC algorithm and then discuss the resulting posterior inference.

3.1. MCMC algorithm.

We are interested in estimating ω, Θ and λ, which define the Gibbs measure based on the local energy function. However, the data likelihood, as shown in equation (2.4), includes an intractable normalizing constant C(ω, Θ, λ), making the Metropolis-Hastings (MH) algorithm infeasible in practice. To address this issue, we use the double Metropolis-Hastings algorithm (DMH) proposed by Liang (2010). The DMH is an asymptotic algorithm, which has been shown to produce accurate results by various spatial models. Unlike other auxiliary variable MCMC algorithms (Møller et al. (2006), Murray, Ghahramani and MacKay (2012)) that also aim to have the normalizing constant ratio canceled, the DMH sampler is more efficient because: (1) it removes the need for exact sampling while it only needs to generate auxiliary variables through a short run of the MH algorithm initialized with the original observation; and (2) it does not require drawing the auxiliary variables from a perfect sampler, which can be very expensive or impossible for many models with intractable normalizing constants. Liang et al. (2016) also proposed an adaptive exchange algorithm, which generates auxiliary variables via an importance sampling procedure from a Markov chain running in parallel. However, this exact algorithm is computationally more intensive than the DMH. See the Appendix for details of our MCMC algorithm.

3.2. Posterior estimation.

We obtain posterior inference by summarizing the MCMC samples after burn-in. Suppose that we obtain sequences of MCMC samples for the model parameters, that is, ${\omega }_q^{(1)},\dots ,{\omega }_q^{(U)}$, 1 ≤ q ≤ Q, ${\theta }_{q{q}^{\prime }}^{(1)},\dots ,{\theta }_{q{q}^{\prime }}^{(U)}$, 1 ≤ q, q′ ≤ Q and λ⁽¹⁾, … , λ^(U), where U is the total number of iteration after burn-in, then an approximate Bayesian estimator of each parameter can be simply obtained by averaging over the samples, ${\widehat{\omega }}_q={\sum }_{u=1}^U{\omega }_q^{(u)}/U$, ${\widehat{\theta }}_{q{q}^{\prime }}={\sum }_{u=1}^U{\theta }_{q{q}^{\prime }}^{(u)}/U$ and $\widehat{\lambda }={\sum }_{u=1}^U{\lambda }^{\left(u\right)}/U$, where u indexes the iteration. We suggest to project the parameters (ω, Θ) to (π, Φ), or plot the MIFs as given in equation (2.6).

4. Simulation.

In this section, we use simulated data generated from the proposed model to assess performance of our strategy for posterior inference on the model parameters. In addition, we discuss how to choose the tunable parameter c based on the MCF plots and investigate the sensitivity of the model to the choice of c.

We considered to generate the points by using two different point processes: (1) a homogeneous Poisson process (HPP) with a constant intensity η = 2000 over the space [0, 1]²; and (2) a log Gaussian Cox process (LGCP) with an inhomogeneous intensity $\eta (x,y)=\text{exp}(6+|x-0.3|+|y-0.3|+\mathcal{G}\mathcal{P}(x,y))$, x ∈ [0, 1], y ∈ [0, 1] and $\mathcal{G}\mathcal{P}$ denotes a zero-mean Gaussian process with variance equal to 1 and scale equal to 1. The mark of each point, z_i ∈ {1, 2}, was simulated by using a Gibbs sampler based on equation (2.5). We ran 100,000 iterations with a random starting configuration of z. The true parameters were set as follows: (1) the decay parameter λ = 60 or λ = 0, and the threshold c = 0.05, which implies that any pair of points with distance large than 0.05 were not considered in the model construction; (2) the first-order intensities ω = (1, 1), which correspond to π = (0.5, 0.5); and (3) the second-order intensities Θ were set according to each of the five scenarios, as shown in Table S1 in the Supplementary Material (Li et al. (2019)). They represented the cases of high/low repulsion, complete randomness and high/low attraction. Attraction or inter-mark attraction is defined as the clustering of points with different marks, while repulsion (also known as inhibition or suppression) is defined vice versa. We repeated the above steps to generate 30 independent datasets for each point process and each setting of λ and Θ. See Figure S3 for examples of simulated data generated by the HPP under settings of Θ and λ = 60, and their mark connection functions (MCFs) and multitype K-functions. MCF is used to describe the spatial correlations of marks, where its quantity MCF_qq′ (d) is interpreted as the empirical probability that two points at distance d have marks q and q′. An upward trend in MCF_qq(d) with a downward trend in MCF_qq′ (d) indicates attraction, while the opposite case suggests repulsion. K-function is a standard tool for exploratory analysis of spatial point pattern data and (Lotwick and Silverman (1982)) defined its “cross” variant that is suitable in the bivariate case. Let ρ_q denote the expected number of points with mark q per unit area, then ρ_qK_q′,q(d) represents the expected number of additional points with mark q within distance d of an arbitrary point with mark q′. In the bivariate case, a similarity between K₁₁(d) and K₂₂(d) suggests that different types of points are generated by the same underlying process, while K₁₁(d) = K₂₂(d) = 0 reveals an inhibitory effect within each of the component patterns. For the rigorous definitions and detailed explanations of these two summary statistics, please refer to Baddeley (2010).

For the prior on ω₁, we used a normal distribution N(1, 1), corresponding that π₁ ∈ [0.125, 0.878] with 95% probability a priori. For the priors on θ₁₁ and θ₁₂, we used a standard normal distribution N(0, 1). Note that we set the constraints ω₂ = 1 and θ₂₂ = 1 to avoid the identifiability problem. We set the hyperparameters that control the gamma prior on the exponential decay to a_λ = b_λ = 0.001, which leads to a vague prior with variance equal to 1000. We chose the tunable parameter c = 0.05. Results we report below were obtained by running the MCMC chain with 50,000 iterations, discarding the first 50% sweeps as burn in. We started the chain from a model by randomly drawing ω₁, θ₁₁, θ₁₂ and λ from their priors and assigning a random configuration of z. All experiments were implemented in R with Rcpp package to accelerate computations on a Mac PC with 2.60 GHz CPU and 16 GB memory. In our implementation, the MCMC algorithm ran about half an hour for each dataset.

Table 1 summarizes the results of posterior inference on the model parameters, for simulated datasets from the HPP and λ = 60. For the results for the other scenarios, please see Table S2–S4 in the Supplementary Material (Li et al. (2019)). Each estimate was obtained by averaging over 30 independent datasets. Overall, the tables indicate that our model fitting strategy based on the DMH algorithm works well. However, we notice that the decay parameter λ was greatly overestimated in the complete randomness scenarios. This is not surprising because all z_i’s are completely irrelevant to each other (i.e., p(z_i = q|·) ∝ exp(−ω_q)) under this scenario. Therefore, λ was ill-defined when λ = 0. The observed large values of λ also indicate the weights, associated with the second-order intensities, decrease faster and thus explain why each mark was dominated by the first-order intensities. We also found that high repulsion scenarios had the worst performance on θ₁₂, which measures the interaction strength between different types of points. The reason is that we can only observe a small number of the interacting pairs between type 1 and 2 points. Take Figure S3(a) for example, such interacting pairs can be only seen near the border between the two clumps. Therefore, a biased estimation on θ₁₂ is expected.

Table 1.

Simulated datasets from the homogeneous Poisson process with λ = 60: Results of posterior inference on the model parameters. Values are averaged over 30 simulated datasets for each scenario, with standard deviations indicated in parentheses

	High repulsion	Low repulsion	Complete randomness	Low attraction	High attraction
ω1	1.0	1.0	1.0	1.0	1.0
${\widehat{\omega }}_1$	1.30 (0.39)	1.05 (0.12)	1.04 (0.09)	1.08 (0.18)	1.05 (0.19)
θ11	1.0	1.0	1.0	1.0	1.0
${\widehat{\theta }}_{11}$	0.71 (0.37)	0.97 (0.09)	0.84 (0.33)	0.94 (0.15)	0.95 (0.14)
θ12	3.2	1.9	1.0	0.2	−1.2
${\widehat{\theta }}_{12}$	2.52 (0.26)	1.82 (0.17)	0.81 (0.30)	0.05 (0.19)	−1.14 (0.20)
λ	60	60	60	60	60
$\widehat{\lambda }$	48.36 (6.79)	58.77 (7.49)	186.76 (118.09)	65.58 (11.82)	58.75 (4.81)

The proposed model contains a tunable parameter c, which defines the neighborhood for each point. A large value of c quadratically increases the computational cost, while a small value may cause biased estimates. We suggest users choose a value of 0.1 or less unless there is strong evidence in support of a larger value. Such evidence could be either subjective, such as an assessment from an experienced expert, or objective, such as MCF plots from the data. Take Figure S3 in the Supplementary Material (Li et al. (2019)), for example. For attraction scenarios, the MCF curve converged right after d passing over the true value of c. However, for repulsion scenarios, the curve tends to have a much bigger lag, especially for larger values of ϕ₁₂ or ϕ₂₁. We also conducted a sensitivity analysis. We fit each of the 120 simulated datasets generated from the HPP (30 for each scenario, excluding the complete randomness) into the proposed model with c = 0.03, 0.05 and 0.1. Figure S4 show the boxplots of the three estimates ${\widehat{\omega }}_1$, ${\widehat{\theta }}_{11}$ and ${\widehat{\theta }}_{12}$ under different values of c for each scenario. The model was quite robust to different choices of c.

5. Application.

In this section, we first investigate the performance of our methodology using three benchmark datasets. Then we apply the model to a large cohort of lung cancer pathology images, and the result reveals novel potential imaging biomarkers for lung cancer prognosis.

5.1. spatstat datasets.

R package spatstat is a major tool for spatial point pattern analyses. One of the basic data types offered by it is multitype point pattern data. We used two retinal cell datasets with marks on/off and one wood dataset with six species to quantify their attraction/repulsion characteristics using the proposed model.

Since 1970s, there has been considerable interest in studying the spatial pattern presented by particular types of mammalian retinal cell bodies (Wässle, Peichl and Boycott (1981), Wässle and Riemann (1978), Hughes (1981a, 1981b), Peichl and Wässle (1981), Rockhill, Euler and Masland (2000), Vaney, Peichl and Boycott (1981)). One of the two commonly used examples is the amacrine cells dataset (Diggle (1986)), consisting of two types of displaced amacrine cells within the retinal ganglion cell layer of a rabbit. The other is the betacells dataset (Wässle and Illing (1981)), composed of two types of beta cells that are associated with the resolution of fine details in the visual system of a cat. Figure 1 [left] and [middle] depict how the two different types of amacrine and beta cells distribute in restricted rectangular regions. Their MCF and multitype k-function plots are shown in Figure S5 in the supplemental material (Li et al. (2019)). Although the MCF plots clearly indicate strong attraction among cells with the different type and the interaction region radius around 0.1, no quantities can be accurately estimated further. We applied the proposed model with the same hyperparameter and algorithm settings as described in Section 4 and the choice of c = 0.2 for each dataset. We ran four independent MCMC chains and used the potential scale reduction factor (PSRF) (Gelman et al. (1992)) to evaluate convergence. PSRF is a statistic comparing the estimated between-chains and within-chain variances for each model parameter. Its value should be close to 1 if multiple chains have converged to the target posterior distribution. In this case, the PSRFs for all the model parameters were below 1.029, clearly suggesting that the MCMC chains converged. Then, for each dataset, we pooled together the outputs from the four chains and reported the estimated model parameters with their 95% credible interval in Figure S6 and S7. We plotted the estimated MIFs in Figure 2. Our method, as well as other methods (Diggle (1986), van Lieshout and Baddeley (1999)), suggest attraction between the cells (i.e., most cells have a nearest neighbor of the opposite type). The message about oppositely labeled pairs between neighbor cells would strengthen the assumption that there are two separate channels for brightness and darkness as postulated by Hering in 1874. Furthermore, our method is able to provide an accurate quantitative description, which can benefit the development and retinal sampling efficiency.

Fig. 1.

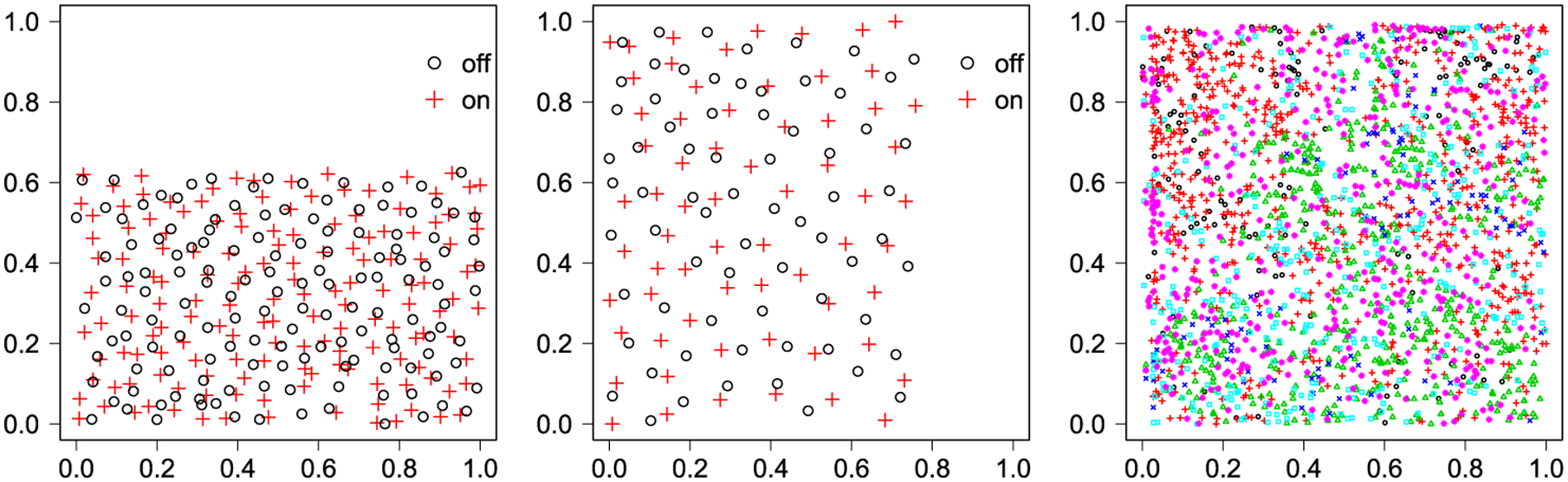
The plots of the rescaled marked points of [left]: amacrine with a unit standing for approximate 1000 μm, including 142 “light-off” cells (○) and 152 “light-on” cells (+); [middle]: betacells with a unit standing for approximate 1000 μm, including 70 “light-off” cells (○) and 65 “light-on” cells (+); [right]: lansing with a unit standing for approximate 282 m (≈ 924 ft), including 135 black oaks (○), 703 hickories (+), 514 maples (Δ), 105 miscellaneous trees (×), 346 red oaks (◻) and 448 white oaks (*).

Fig. 2.

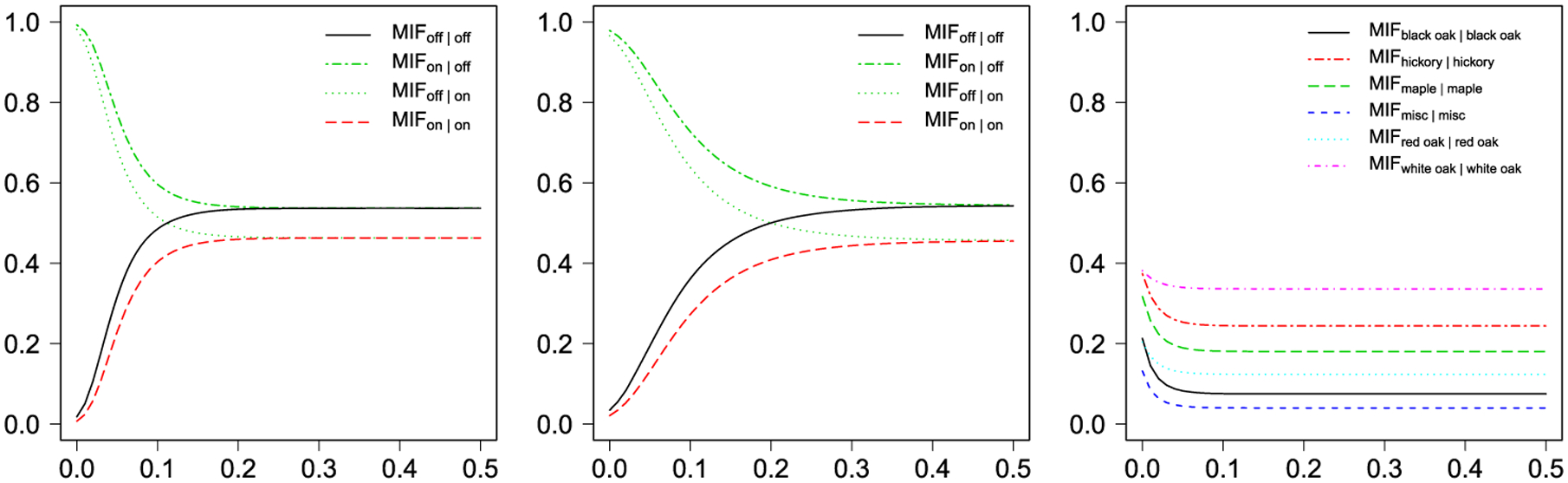
The MIF functions estimated from [left]: amacrine; [middle]: betacells; [right]: lansing (only the MIFs between the same mark are shown here; see Figure S8 for the numerical results of interactions between different marks).

The third dataset in spatstat that was used is the lansing dataset. It contains the locations and botanical classification of trees in a 924 × 924 feet (19.6 acre) area of Lansing Woods, Clinton County, MI, USA. Figure 1 [right] shows the rescaled multitype point pattern that consists of Q = 6 types of trees. The MCF plots are shown in Figure S5 in the Supplementary Material (Li et al. (2019)), which indicate exhibition of clustering among the trees with the same type. With the same hyperparameter, algorithm and convergence diagnostic settings, we applied the proposed model with the choice of c = 0.1. The PSRFs were ranging from 1.003 to 1.022. The estimated model parameters are reported in Figure S8 and the MIFs are summarized in Figure 2 [right]. The pattern reveals that the first five types of trees exhibited clustering, especially for black oak and miscellaneous trees. This means if one species had a clump in an area, then no other species tended to form a clump there. We also found white oak had the least ${\widehat{\varphi }}_{qq}$ value, which suggests its spatial pattern was more likely random. Those findings were also reported in Cox and Lewis (1976) and Cox (1979). In addition, our MIF plots indicates that there was no interaction between the same type trees beyond 90 feet.

5.2. Case study on lung cancer.

Lung cancer is the leading cause of death from cancer in both men and women. Non-small-cell lung cancer (NSCLC) accounts for about 85% of deaths from lung cancer. Current guidelines for diagnosing and treating NSCLC are largely based on pathological examination of H&E-stained tumor tissue section slides. We have developed a ConvPath pipeline (https://qbrc.swmed.edu/projects/cnn/) to determine the locations and types of cells observed in the processed tumor pathology images. Specifically, the classifier, based on a convolutional neural network (CNN), was trained using a large cohort of lung cancer pathology images manually labeled by pathologists, and it can classify each cell by its Q = 3 category: lymphocyte (a type of immune cell), stromal, or tumor cell. The overall classification accuracy is 92.9% and 90.1% in training and independent testing datasets, respectively (Wang et al. (2018)).

In this case study, we used the pathology images from 188 NSCLC patients in the National Lung Screening Trial (NLST). Each patient has one or more tissue slide(s) scanned at 40× magnification. The median size of the slides is 24,244 × 19,261 pixels. A lung cancer pathologist first determined and labeled the region of interest (ROI) within the tumor region(s) from each tissue slide using an annotation tool, ImageScope (Leica Biosystem). ROIs are regions of the slides containing the majority of the malignant tissues and are representative of the whole slide image. Then we randomly chose five square regions, each of which is in a 5000 × 5000 pixel window, per ROI as the sample images. The total number of sample images that we collected was 1585. For each sample image, the ConvPath (illustrated in Figure S9 in the Supplementary Material (Li et al. (2019))) software was used to identify cells from the sample images and classify each cell into one of three types, so that a corresponding spatial map of cells was generated and used as the input of our model. The number of cells in each sample image ranges from n = 2876 to 26,463. Figure 3 shows the examples of two sample images and Figure S10 displays their MCF and multitype K-function plots.

Fig. 3.

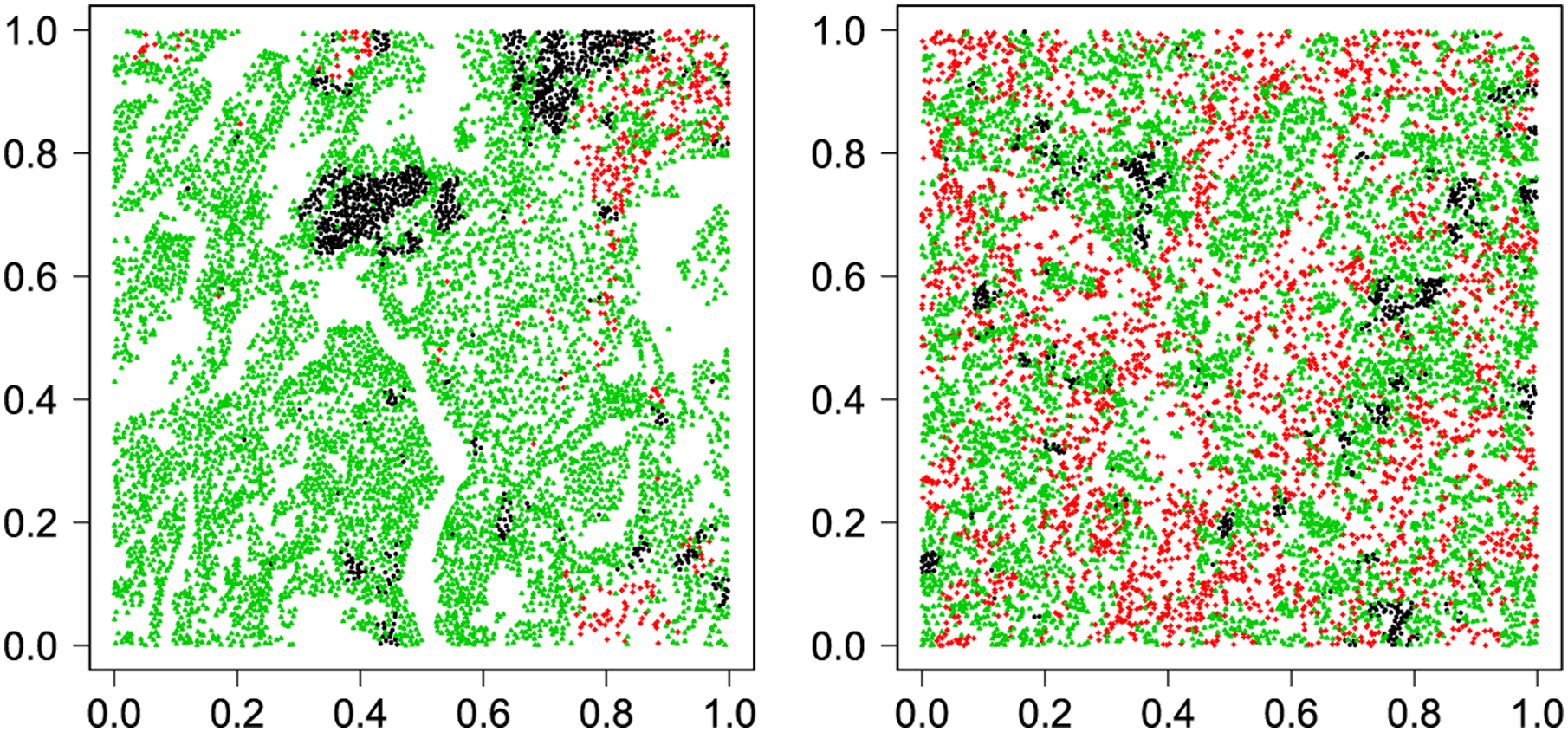
Lung cancer case study: Two examples of the rescaled marked point data from NLST dataset, where black, red and green points represent lymphocyte (○), stromal (+) and tumor (Δ) cells. For the data shown in the left, $\widehat{\lambda }=172.102$, ${\widehat{\pi }}_{\text{lym}}=0.022$, ${\widehat{\pi }}_{\text{str}}=0.173$, ${\widehat{\pi }}_{\text{tum}}=0.805$ and ${\widehat{\varphi }}_{\text{tum},\text{ str}}=0.012$ For the data shown in the right, $\widehat{\lambda }=169.268$, ${\widehat{\pi }}_{\text{lym}}=0.011$, ${\widehat{\pi }}_{\text{str}}=0.603$, ${\widehat{\pi }}_{\text{tum}}=0.386$ and ${\widehat{\varphi }}_{\text{tum},\text{str}}=0.162$.

We applied the proposed model with the same hyperparameter and algorithm settings as described in Section 4 and different choices of c = 0.02, 0.05 and 0.1. We then computed the pairwise Pearson correlation coefficients between the estimated model parameters under different choices of c. These correlations indicated substantial agreement between any pair of settings, with values ranging from 0.967 to 0.997. The estimated parameters (with their summary statistics summarized in Table S5) that we used for the following three downstream analyses were obtained under the most conservative choice of c = 0.1.

5.2.1. Association study.

With the estimated parameters in each sample image, we conducted a downstream analysis to investigate their associations with the other measurements of interest. Specifically, a Cox proportional hazards model (Cox (1992)) was fitted to evaluate the association between the transformed model parameters $\widehat{\mathit{\pi }}$ and $\widehat{\mathbf{\Phi }}$ (in percentile %), and patient survival outcomes, after adjusting for other clinical information, such as age, gender and tobacco history. Multiple sample images from the same patient were modeled as correlated observations in the Cox proportional hazards model to compute a robust variance for each coefficient. The overall p-value for the Cox model was 0.002 (Wald test), and the p-value and coefficient for each individual variable are summarized in Table 2. The results imply that a low interaction between stromal and tumor cells is associated with good prognosis in NSCLC patients (p-value = 0.007). Interestingly, Beck et al. (2011) also discovered that the morphological features of the stroma in the tumor region are associated with patient survival in a systematic analysis of breast cancer. Besides, the abundance of the stromal cells itself (p-value = 0.017) is also a prognostic factor, while the underlying biological mechanism is currently unknown. The positive coefficient of the predictor ϕ_tum,str implies that a higher value may reveal a higher risk of death. Indeed, we obtained ${\widehat{\varphi }}_{\text{tum},\text{str}}=0.012$ for the data shown in Figure 3 [left] and it was from a patient who was still alive over 2615 days after the surgery, while the estimated value of ϕ_tum,str = 0.162 for the data shown in Figure 3 [right] and it was from a patient who died on the 1246th day after the surgery. These two images have distinctive patterns, as the former clearly shows the same type cells tend to clump in the same area, while the latter displays a case where stromal and tumor cells are thoroughly mixed together, indicating the spread of stromal cells into the tumor region. Although the high/low interaction between stromal and tumor cells can be easily seen by eyes in these two images, the patterns are much more subtle for many other images. Therefore, the proposed model can be used to predict the survival time when human visualization does not work.

Table 2.

Lung cancer case study: The p-values of the transformed model parameters (in percentile %) by fitting a Cox proportional hazards model with survival time (defined as the number of days from diagnosis to death for participants who died or last contact for all other participants) and vital status (death or alive) as responses, and model parameters and clinical variables as predictors. The overall p-value (Wald test) is 0.003

Predictor	Coefficient	exp (Coef.)	SE	P-value
${\widehat{\varphi }}_{\text{str},\text{lym}}$	0.147	1.158	0.052	0.106
${\widehat{\varphi }}_{\text{tum},\text{lym}}$	0.030	1.030	0.025	0.546
${\widehat{\varphi }}_{\text{lym},\text{str}}$	−0.009	0.991	0.008	0.543
${\widehat{\varphi }}_{\text{tum},\text{str }}$	0.096	1.100	0.016	0.002
${\widehat{\varphi }}_{\text{lym},\text{tum}}$	−0.002	0.998	0.008	0.896
${\widehat{\varphi }}_{\text{str},\text{tum}}$	−0.059	0.943	0.019	0.128
${\widehat{\pi }}_{\text{lym}}$	0.034	1.035	0.015	0.219
${\widehat{\pi }}_{\text{str}}$	−0.032	0.969	0.007	0.019
$\widehat{\lambda }$	−0.006	0.994	0.003	0.382
Age	0.038	1.039	0.009	0.176
Female/male	−0.138	0.871	0.091	0.631
Smoking/nonsmoking	−0.001	0.999	0.089	0.997

By contrast, we fitted a similar Cox proportional hazards model by using the MCF features as predictors. Specifically, we first used MCF_lym,lym(d), MCF_lym,str(d), MCF_lym,tum(d), MCF_str,str(d) and MCF_str,tum(d), where d = 0.1 for each sample image as covariates. The results are summarized in Table S6 in the Supplementary Material (Li et al. (2019)). As we can see, there was no significant predictor and the overall p-value for the Cox model was 0.60 (Wald test). Next, we tried to vary d from 0 to 0.1. Figure S12(a) shows the p-values of those statistics against d. We repeated this analysis with the features from multitype K-functions and reported the results in Table S7 and Figure S12(b). Again, we were unable to find any association between cell-cell interactions and clinical outcomes. The comparison demonstrates the advantage of modeling the pathology images via the proposed model over the traditional explanatory analysis for characterizing spatial correlation.

5.2.2. Predictive performance by cross-validation.

Lastly, we used leave-one-out cross-validation to evaluate the above Cox proportional hazards model. Specifically, we trained the model by using (N − 1) sample images and then predicted the risk score of the left-out sample. After repeating this step for each of the N sample images, we calculated the average risk score for each patient from all the associated sample images. Based on the average risk score, we divided the patients into two equally sized groups (i.e., low and high-risk). Their corresponding Kaplan-Meier survival curves are shown in Figure 4. The log-rank test shows that there is a significant difference (p-value < 0.0001) between the two curves.

Fig. 4.

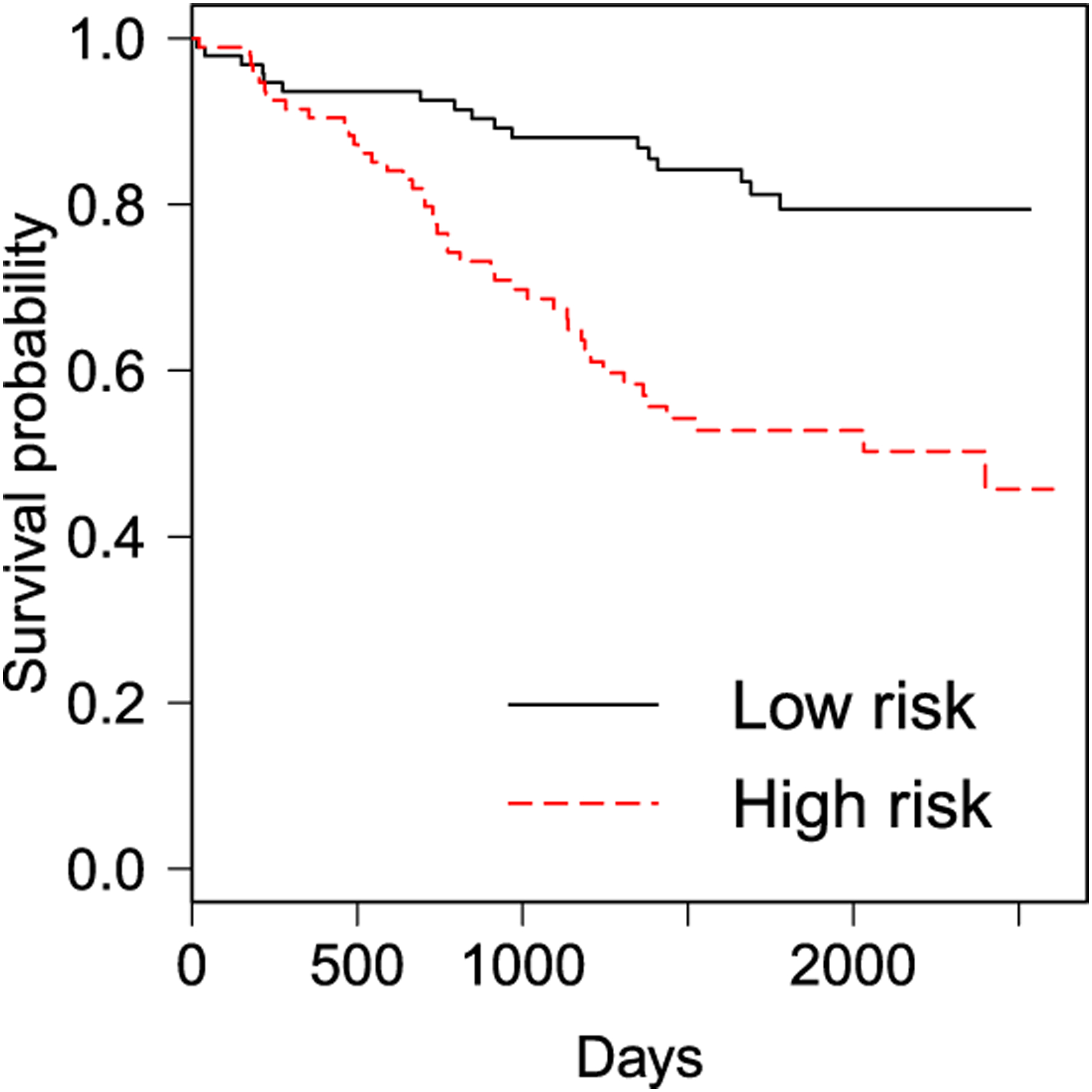
Lung cancer case study: The Kaplan-Meier plot for the low and high-risk groups obtained by leave-one-out cross-validation (log rank test p-value < 0.0001).

5.2.3. Unsupervised clustering analysis.

Furthermore, we performed a model-based clustering analysis on the features extracted by the model. First, each of the eight parameters ${\widehat{\varphi }}_{\text{str},\text{lym }}$, ${\widehat{\varphi }}_{\text{tum },\text{lym }}$, ${\widehat{\varphi }}_{\text{lym},\text{ str}}$, ${\widehat{\varphi }}_{\text{tum },\text{ str}}$, ${\widehat{\varphi }}_{\text{lym },\text{ tum}}$, ${\widehat{\varphi }}_{\text{str},\text{ tum }}$, ${\widehat{\pi }}_{\text{lym }}$, ${\widehat{\pi }}_{\text{str }}$ of multiple sample images from the same patient were averaged. We then used the multivariate Gaussian mixture model (Fraley and Raftery (2002)) to cluster patients using those parameter. To estimate the number of clusters that best represents the data as well as its covariance structure, we plotted the Bayesian information criterion (BIC) values against the number of clusters from 1 to 9, as shown in Figure 5 [left]. It shows that clustering patients into three groups achieves the best fit of the data measured by BIC, where the first, second and third groups have 79, 77 and 32 patients, respectively. Next, we visualized the means of these patient-level parameters for each group, shown as a radar chart in Figure 5 [middle], and plotted the Kaplan-Meier survival curve for each group in Figure 5 [right]. The patients from group 1 had higher survival probabilities, while the patients from the last group had the poor prognosis. The log-rank test shows that there are significant differences (p-value = 0.015) among the survival curves of the three groups. The analysis, again, demonstrates that the proposed mark interaction features can be used as a potential biomarker for patient prognosis.

Fig. 5.

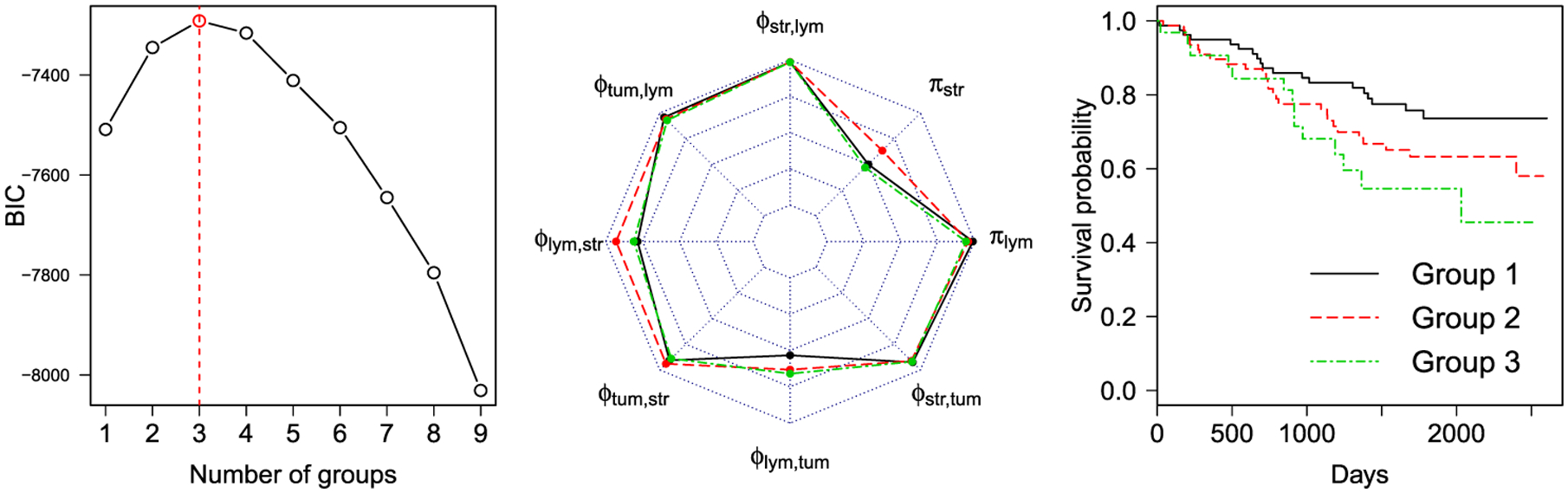
Lung cancer case study: [left] The BIC plot of the model-based clustering on the patient-level parameters; [middle] The radar chart of the averaged patient-level parameters of the three groups (shown in different colors), where the outer ring and the center have the values of 0 and 1, respectively; [right] The Kaplan-Meier plot for the three groups with patient survival (log rank test p-value = 0.015).

6. Conclusion.

The major cell types in a malignant tissue of lung are tumor cells, stromal cells and infiltrating lymphocytes. The distribution of different types of cells and their interactions play a key role in tumor progression and metastasis. For example, stromal cells are connective tissue cells, such as fibroblasts and pericytes, and their interaction with tumor cells is known to play a major role in cancer progression (Wiseman and Werb (2002)). Tumor-infiltrating lymphocytes have been associated with patient prognosis in multiple tumor types previously (Brambilla et al. (2016), Huh, Lee and Kim (2012)). Recent advances in deep learning methods have made possible the automatic identification and classification of cells at large scale. For example, the ConvPath pipeline could determine the location and cell type for thousands of cells. However, it is challenging to utilize the vast amount of information extracted digitally. In this study, we developed a Bayesian statistical method to model the spatial interaction among different types of cells in tumor regions. We focused on modeling the spatial correlation of marks in a spatial pattern that arose from a pathology image study. A Bayesian framework was proposed in order to model how the mark in a pattern might have been formed given the points. The proposed model can utilize the spatial information of thousands of points from any point processes. The output of the model is the parameters that characterize the spatial pattern. After a certain transformation, the parameters are identifiable and interpretable, and most importantly, transferable for conducting an association study with other measurements of interest. Furthermore, this statistical methodology provides new insights into the biological mechanisms of cancer.

For the lung cancer pathology imaging data, our study shows the interaction strength between stromal and tumor cells is associated with patient prognosis. This parameter can be easily measured using the proposed method and used as a potential biomarker for patient prognosis. This biomarker can be translated into real clinical tools at low cost because it is based only on tumor pathology slides, which are available in standard clinical care.

Several extensions of our model are worth investigating. First, the proposed model can be extended to finite mixture models for inhomogeneous mark interactions. Second, the correlation among first- and second-order intensity parameters could be taken into account by modeling them as a multivariate normal distribution. Third, in some scenarios, we may need to consider edge effects in that the marks associated with the points within the observation window may also interact with those marks of points outside the window. Therefore, some edge-correction methods, such as minus sampling, should be employed. Last but not least, the proposed model provides a good chance to investigate the performance of other approximate Bayesian computation methods, such as variational Bayes (Ren et al. (2011)). These could be future research directions.

APPENDIX: MCMC ALGORITHM

Update of ω: We update each of ω_q, q = 1, … , Q − 1 by using the DMH algorithm. We first propose a new ${\omega }_q^{*}$ from $\text{N}\left({\omega }_q,{\tau }_{\omega }^2\right)$. Next, according to equation (2.5), we implement the Gibbs sampler to simulate an auxiliary variable z* starting from z based on the new ω*, where all the elements are the same as ω excluding the qth one. The proposed value ${\omega }_q^{*}$ is then accepted to replace the old value with probability min(1, r). The Hastings ratio r is given as

$$r=\frac{p\left(\mathit{\text{z}}*|\mathit{\omega },\mathbf{\Theta },\lambda \right)}{p(\mathit{\text{z}}|\mathit{\omega },\mathbf{\Theta },\lambda )}\frac{p\left(\mathit{\text{z}}|\mathit{\omega }*,\mathbf{\Theta },\lambda \right)}{p\left(\mathit{\text{z}}*|\mathit{\omega }*,\mathbf{\Theta },\lambda \right)}\frac{\text{N}\left({\omega }_q^{*};{\mu }_{\omega },{\sigma }_{\omega }^2\right)}{\text{N}\left({\omega }_q;{\mu }_{\omega },{\sigma }_{\omega }^2\right)}\frac{J\left({\omega }_q;{\omega }_q^{*}\right)}{J\left({\omega }_q^{*};{\omega }_q\right)},$$

where the form of p(z|ω, Θ, λ) is given by equation (2.4). As a result, the normalizing constant in equation (2.4) can be canceled out. Note that the last fraction term, which is the proposal density ratio, equals 1 for this random walk Metropolis update on ω_q.

Update of Θ: We update each of θ_qq′, q = 1, … , Q − 1, q′ = q, … , Q by using the DMH algorithm. We first propose a new ${\theta }_{q{q}^{\prime }}^{*}$ from $\text{N}\left({\theta }_{q{q}^{\prime }},{\tau }_{\theta }^2\right)$ and set ${\theta }_{q^{\prime }q}^{*}={\theta }_{q{q}^{\prime }}^{*}$ as the matrix is symmetric. Next, according to equation (2.5), an auxiliary variable z* is simulated via the Gibbs sampler with z as the starting point. This simulation should be based on the new Θ*, where all the elements are the same as Θ except the two elements corresponding to θ_qq′ and θ_q′q The proposed value ${\theta }_{q{q}^{\prime }}^{*}$ as well as ${\theta }_{q^{\prime }q}^{*}$ is then accepted to replace the old values with probability min(1, r). The Hastings ratio r is given as

$$r=\frac{p\left(\mathit{\text{z}}*|\mathit{\omega },\mathbf{\Theta },\lambda \right)}{p(\mathit{\text{z}}|\mathit{\omega },\mathbf{\Theta },\lambda )}\frac{p\left(\mathit{\text{z}}|\mathit{\omega },\mathbf{\Theta }*,\lambda \right)}{p\left({\mathit{\text{z}}}^{*}|\mathit{\omega },\mathbf{\Theta }*,\lambda \right)}\frac{\text{N}\left({\theta }_{q{q}^{\prime }}^{*};{\mu }_{\theta },{\sigma }_{\theta }^2\right)}{\text{N}\left({\theta }_{q{q}^{\prime }};{\mu }_{\theta },{\sigma }_{\theta }^2\right)}\frac{J\left({\theta }_{q{q}^{\prime }};{\theta }_{q{q}^{\prime }}^{*}\right)}{J\left({\theta }_{q{q}^{\prime }}^{*};{\theta }_{q{q}^{\prime }}\right)},$$

where the form of Pr(z|θ, λ) is given by equation (2.4). As a result, the normalizing constant in equation (2.4) can be canceled out. Note that the last fraction term, which is the proposal density ratio, equals 1 for this random walk Metropolis update on θ_qq′.

Update of λ: We update the decay parameter λ by using the DMH algorithm. We first propose a new λ* from a gamma distribution Ga(λ²/τ_λ, λ/τ_λ), where the mean is λ and the variance is τ_λ. Next, according to equation (2.5), we implement the Gibbs sampler to simulate an auxiliary variable z* starting from z based on the new λ*. The proposed value λ* is then accepted to replace the old value with probability min(1, r). The Hastings ratio r is given as

$$r=\frac{p\left(\mathit{\text{z}}*|\mathit{\omega },\mathbf{\Theta },\lambda \right)}{p(\mathit{\text{z}}|\mathit{\omega },\mathbf{\Theta },\lambda )}\frac{p\left(\mathit{\text{z}}|\mathit{\omega },\mathbf{\Theta },{\lambda }^{*}\right)}{p\left(\mathit{\text{z}}*|\mathit{\omega },\mathbf{\Theta },{\lambda }^{*}\right)}\frac{\text{Ga}\left(\lambda *;a,b\right)}{\text{Ga}(\lambda ;a,b)}\frac{J\left(\lambda ;\lambda *\right)}{J\left(\lambda *;\lambda \right)},$$

where the form of Pr(z|θ, λ) is given by equation (2.4). As a result, the normalizing constant in equation (2.4) can be canceled out. Note that the last fraction term, which is the proposal density ratio, equals 1 for this random walk Metropolis update on λ.