ABSTRACT
Over the last decade, chemotherapy treatments have dramatically shifted to outpatient services such that nearly 90% of all infusions are now administered outpatient. This shift has challenged oncology clinics to make chemotherapy treatment as widely available as possible while attempting to treat all patients within a fixed period of time. Historical data from a Veterans Affairs chemotherapy clinic in the United States and staff input informed a discrete event simulation model of the clinic. The case study examines the impact of altering the current schedule, where all patients arrive at 8:00 AM, to a schedule that assigns patients to two or three different appointment times based on the expected length of their chemotherapy infusion. The results identify multiple scheduling policies that could be easily implemented with the best solutions reducing both average patient waiting time and average nurse overtime requirements.
KEYWORDS: Discrete event simulation (DES), scheduling, healthcare, chemotherapy
1. Introduction
1.1. Background
In 1930, the United States (U.S.) Congress authorised the President to establish the Veteran’s Administration (VA) in order to provide care for the men and women who served in the U.S. military (Slocum, 2014; U.S. Department of Veterans Affairs, 2018b, 2018c). While the VA provides a wide range of services to veterans nationwide, its healthcare system is arguably the most important and most costly service. Since its creation, the VA healthcare system has expanded from 54 hospitals to 153 hospitals, 909 community based outpatient clinics, and 135 nursing home clinics. VA Medical Centers(VAMCs) provide full spectrum services, ranging from routine outpatient services to emergency care to specialised services such as oncology, neurology, and prosthetics. Often, VA hospitals are located adjacent to medical schools, allowing experienced physicians to provide excellent care to veterans while training the next generation of medical providers.
Our focus is on improving scheduling for the outpatient chemotherapy clinic at the U.S. Veteran’s Affairs Medical Center in Durham, North Carolina, which provides care to over 200,000 veterans across 26 counties in the state of North Carolina (U.S. Department of Veterans Affairs, 2018a). However, since not all VAMCs are capable of providing oncology services, the Durham VAMC treats patients from states in the region, with patients often travelling from northern South Carolina, southern Virginia, and as far east as the North Carolina coastal counties.
The chemotherapy clinic is open 250 days a year and administered more than 3,500 doses of chemotherapy in 2013. The clinic is staffed with five chemotherapy certified nurses that cycle patients through 14 infusion chairs throughout the day. The clinic administers over 80 different chemotherapy regimens (regimens refer to the combination of one or more drugs) and provides ancillary services such as phlebotomies and blood transfusions. While some treatments take 15 minutes, others take upwards of six to eight hours – yet in each case, the patient is told to arrive at 8:00 AM for treatment. This practice has resulted in very long wait times for the patients and significant overtime hours for the nursing staff.
1.2. Clinic overview
The daily process for the chemotherapy clinic consists of three major phases: (1) lab work, (2) pharmacy processing, and (3) chemotherapy infusion. When patients arrive to the clinic, their first stop is the phlebotomy station. The phlebotomy station is staffed with two phlebotomists, one arriving at 6:00 AM and the other arriving at 7:30 AM. Patients are called in to the phlebotomy station on a first come, first served (FCFS) basis. The phlebotomist draws multiple blood samples, which are then escorted to the hospital’s main lab. Lab tests are required because providers must ensure their patients can safely receive chemotherapy. Chemotherapy drugs are fundamentally toxic to the body and typically work by either destroying cells or preventing cell replication. The drugs are unable to differentiate between good cells and cancer cells, which are both affected during chemotherapy treatments, so lab tests are essential for determining whether a patient can withstand their next round of treatment. Once the main lab completes the testing, the patient’s doctor will review the results to ensure the patient can tolerate treatment. If the patient is healthy enough for treatment, the doctor will notify the attending nurse to submit the patient’s chemotherapy order to the pharmacy. If the patient is not a viable candidate for treatment, the doctor will either postpone treatment to a later date or they may supplement the patient with a blood transfusion, platelets, etc.
Unlike many VAMCs, the Durham clinic has a dedicated pharmacy located next to the infusion clinic. The pharmacy is staffed with two pharmacists who rotate between working in the hospital’s main pharmacy and the chemotherapy pharmacy. The pharmacy operates as two single server processes in series. The order starts with one pharmacist entering all of the patient and order information and printing out drug labels. Once data entry is complete, the second pharmacist will gather all of the necessary supplies to mix the drug in the neighbouring clean room under a ventilation hood. Once the drug has been prepared, the pharmacy delivers the chemotherapy drugs to the infusion clinic. The pharmacy processes drug orders on a FCFS basis, unless one of the nurses asks the pharmacists to bump an order to the front of the line (typically for patients with very long infusion times).
While the nurses wait for their patients’ lab results and chemotherapy drugs from the pharmacy, they collect vital signs and administer chemotherapy premedication drugs, which must be taken at least 30 minutes prior to starting an infusion. Once the nurses receive their patients’ chemotherapy drugs, the process is fairly deterministic since they are pumped in to the patients’ blood stream at a predetermined rate. Occasionally patients experience adverse reactions to the chemotherapy drugs, which can delay or prematurely end a treatment, but these instances are very rare.
VAMCs are at a significant disadvantage when it comes to controlling their patient flow. In many cases, patients rely on VA sponsored buses to get to the hospital and unlike most community hospitals, some patients will be travelling over three hours for their appointment. As a result, VAMCs are reluctant to enforce strict adherence to appointment times and will generally do everything in their power to treat patients whenever they arrive. However, by telling every patient to arrive at 8:00 AM the chemotherapy clinic cannot effectively control the order in which patients are treated.
When every patient is scheduled to arrive at 8:00 AM, the clinic ensures the lab, pharmacy, and nursing staff will be fully utilised in the morning and the staff rarely waits on patients to arrive; however, patients spend significantly more time in the system waiting for service. Furthermore, this is not necessarily the most efficient scheduling method as it creates a longer queue at the phlebotomy station, which may delay lab results for certain patients. When patients with short infusions get their lab results ahead of those patients with long infusions, the pharmacy builds a backlog of orders that are tail heavy with long infusions. Now, instead of starting a five-hour infusion at 10 AM, the nurses might not be able to start the infusion until 12 PM.
As a population of patients, veterans with cancer are one of the last demographics that should spend hours waiting for service. The goal of this project was to build a simulation of the clinic to examine how various scheduling heuristics affected the average waiting time in the system (measured from the time a patient checks in until the patient starts their chemotherapy infusion) and the clinic’s annual overtime cost. The first step was to build a simulation that accurately models the current system where every patient was told to arrive at 8 AM. The simulation uses a combination of historical data and anecdotal evidence from the clinic’s staff to model various process times. A collaborative effort from the nursing staff, pharmacy, and doctors verified that the system is modelled correctly, and historical overtime data served to validate the simulation’s construction. Once the base schedule simulation was built, the study examined the impact of each proposed schedule against the current schedule.
The rest of this paper is organised as follows: Section 2 discusses relevant literature, Section 3 presents the simulation model, Section 4 summarises key results from the appointment policies, and Section 5 provides some final thoughts.
2. Literature review
2.1. Discrete event simulation in healthcare
Much of the discrete event simulation (DES) literature in healthcare focuses on emergency departments (ED). These studies often include patient-centric performance measures such as waiting time or length of stay along with provider-focused metrics like resource utilisation and productivity (Abo-Hamad & Arisha, 2013). Several studies present DES-based decision support systems to improve management of emergency departments (Ordu, Demir, & Fofallis, 2019), especially under strained or capacity constrained conditions (Kadri, Chaabane, & Tahon, 2014).
These studies cover geographically diverse clinics of varying scales including high-volume facilities (Oh, Novotny, Carter, Ready, & Campbell, 2016). Gul, Guneri, and Gunal (2019) present a case study for managing a network of EDs from five public hospitals in Istanbul, Turkey, to evaluate preparedness for earthquakes. The interested reader should consult Gul and Guneri (2015) for a recent survey of ED simulation studies for normal and disaster conditions.
DES has also supported analysis and management of optometry clinics (Seminelli, Wilson, & McConnell, 2016) and retinal services (Demir, Southern, Verner, & Amoaku, 2018), as well as specialised cancer treatment clinics administering radiation (Babashov et al., 2017).
In a related study, Rohleder, Lewkonia, Bischak, Duffy, and Hendijani (2011) use DES to improve patient waiting time at an outpatient orthopaedic clinic seeing 50–100 patients per day, most of whom have scheduled appointments throughout the day which differs from our study. Another closely related study is Richardson and Cohn (2018) which uses DES to understand the impact of make-ahead chemotherapy drug policies. Unlike Richardson and Cohn (2018), the case study in this paper centres on appointment block scheduling schemes to shape demand at a VA clinic.
2.2. General scheduling
Nearly 90% of all oncology patients will be treated in an ambulatory (outpatient) setting over the course of their battle with cancer, which is why many professionals in the oncology and haematology field have realised a need for improved efficiency (Williamson, 2008). Although some outpatient clinics operate twenty-four hours a day, most mirror normal business hours, which presents the challenge of treating every patient within a limited period of time. Unlike the inpatient setting, outpatient nurses cannot pass their patient off to the next shift. Most infusion clinics tend to front load all of their appointments in an effort to reduce overtime hours, but this can result in long wait times for patients. Studies show that cancer patients tend to value quality of care above all other factors; excessive waiting times have become the most prevalent source of dissatisfaction (Thomas, Glynne-Jones, & Chait, 1997). However, quality of care and excessive wait times are not a zero sum game, which is why many researchers are attempting to find ways to improve outpatient chemotherapy scheduling techniques.
The primary goal for chemotherapy clinics is to maximise the utilisation of its infusion chairs so that the clinic can treat as many patients as possible in a single day without exceeding normal business hours. The current policy at the Durham VA clinic is an example of the simplest block scheduling technique. In this case, the number of blocks, , equals 1, and the number of patients assigned to that block, , is equal to the total number of patients scheduled on that day. This technique is designed to minimise the service providers’ idle times, but it typically comes at the expense of the patient whom experiences longer waiting times for service (Gupta & Denton, 2008). The other end of the spectrum regarding block scheduling is to set the number of blocks equal to the number of patients, such that , and the length of time allocated to each block is equal to the expected mean service time for each (Welch & Bailey, 1952). This type of schedule has several drawbacks, primarily that it works best for a single server process (which the chemotherapy clinic is not), and its complexity can be very challenging for schedulers to execute.
A common practice for primary care doctors is to use a multiple-block/fixed interval rule (Cayirli & Veral, 2003). Using this rule, clinics assign multiple patients identical appointment times, which are spread out across equal intervals throughout the day. For example, three patients could be assigned appointment times at 8:30 AM, and three more patients would be assigned appointments at 9:00 AM. This works particularly well in primary care or general practice settings because the mean service time is usually small (less than 15 minutes), but the wide range of chemotherapy infusion times may prohibit chemotherapy clinics from using fixed intervals.
2.3. Chemotherapy scheduling
Few outpatient services in the healthcare field are as complex as the delivery of chemotherapy because there are multiple ancillary processes that work together before a patient can start their treatment. Depending on the processing capacity and variability of those ancillary services (phlebotomists, lab technicians, and pharmacists), it can be extremely difficult to develop an accurate appointment system. Some clinics encourage pre-infusion appointments, allowing the providers to review lab results 24–48 hours prior to a patient’s chemotherapy infusion, thereby eliminating the uncertainty of those processes, but this is not practical for VA hospitals since many of their patients travel a great distance for treatment. Much of the reviewed literature focused exclusively on the infusion phase of outpatient chemotherapy clinics, which is a significant simplification because it eliminates the uncertainty, variability, and delays of the lab and pharmacy phases (Chabot & Fox, 2005; Delaney, Jalaludin, Moylan, & Barton, 2002; Hesaraki, Dellaert, & de Kok, 2019; Turkcan, Zeng, & Lawley, 2012).
One of the most significant advances in chemotherapy scheduling was the development of a meaningful patient classification system: Chabot and Fox (2005) develop acuity levels that represent a combination of the total amount of treatment time and the nursing attention each patient would require based on their prescribed chemotherapy regimen, where the acuity value was equal to the total treatment time divided by thirty minutes. Patients were scheduled using a multiple-block/variable interval system, with each nurse treated as a single-server and intervals were blocked off according to patient acuity levels. Chabot and Fox (2005) recognise that acuity levels did not eliminate the complexities involved in scheduling chemotherapy patients, but if clinics included acuity levels during the scheduling process, they would be able to better quantify a nurse’s workload.
Turkcan et al. (2012) builds on Chabot and Fox (2005) by developing algorithms and heuristics in a 2-stage integer program to minimise patient treatment delays and staff overtime, while maximising staff utilisation. In order to balance nurse workloads, the integer program includes each patient’s acuity level and for each nurse, the sum of their patient’s total acuity was required to be less than or equal to a predetermined value. While this study provides the most detailed analysis of chemotherapy operations, yielding one of the best optimisation methodologies in its field, it only examines the infusion phase of the outpatient chemotherapy treatment process. Without addressing the lab and pharmacy phases, this planning and scheduling model cannot be implemented.
There are a number of outpatient chemotherapy DES studies in the literature (Ahmed, ElMekkawy, & Bates, 2011; Alvarado, Cotton, Ntaimo, Pérez, & Carpentier, 2018; Liang, Turkcan, Ceyhan, & Stuart, 2015; Woodall, Gosselin, Boswell, Murr, & Denton, 2013; Yokouchi, Aoki, Sang, Zhao, & Takakuwa, 2012). Liang et al. (2015) use both DES and an optimisation model to improve patient flow and scheduling in an outpatient chemotherapy clinic, but these studies consider a clinic where appointments are spread through the day, with 45% of appointments requiring no chemotherapy at all. While the study considers multiple patient classes and routings in a multi-facility setting, it is not directly applicable to the Durham VAMC. Yokouchi et al. (2012) also suggests an appointment scheduling system based on infusion times but stop short of providing a heuristic scheduling rule. A few studies suggest ordering patients by decreasing infusion time is a good target sequence (Garaix, Rostami, & Xie, 2018; Suss, Bhuiyan, Demirli, & Batist, 2017), though Garaix et al. (2018) is limited by strong assumptions such as “the pharmacy is not a bottleneck and drugs arrive on time,” there is no idle time in an oncologist’s schedule, and all patients arrive on time.
Of the few studies that have reached implementation and tested their algorithms or models, most are too specific to a particular clinic or hospital, thus their findings cannot be replicated elsewhere (Belter et al., 2012; Hendershot et al., 2005; Kallen, Terrell, Lewis-Patterson, & Hwang, 2012). Several clinics have attempted to create fast-tracking programmes that assign a higher priority to patients with shorter infusion times or patients that require minimal nursing attention. These are logical strategies; however, their success is entirely dependent on pharmacy capacity, and neither of the studies discuss how to best schedule these appointments.
Eisenburg (2009) highlights a common issue with many outpatient chemotherapy deliver systems, which is particularly evident at the Durham VAMC: nurses are involved in the scheduling appointments. Instead of focusing solely on providing care, some nurses have an active role establishing appointments and balancing their patient load. But when nurses manage appointments independently, clinics lose the ability to control patient flow through the system.
The volume of existing research regarding outpatient chemotherapy scheduling demonstrates the significant need for improvement, yet the vast majority of the research results cannot be implemented due to either an oversimplification of the problem or the complexity of the model. The few studies that reached implementation were generally designed for a specific subset of patients or the system required a resource capacity that could not be widely replicated. A simple and easy-to-implement heuristic that clinics could use as a guideline for scheduling chemotherapy appointments would be an invaluable tool.
3. Simulation model
3.1. Model definition
Patients move through the Durham VAMC chemotherapy clinic processes according to Figure 1. In the model, the only entities in the system are the patients. The number of patients that enter the clinic varies from day to day, as does the type of chemotherapy regimens administered. The attributes that characterise each unique patient are: (1) Arrival Time and (2) Chemotherapy Regimen. Both of these attributes are sampled from an appropriate distribution, which will be discussed in the sections below. Next, there are several sub-attributes that characterise a patient’s treatment requirements based on his/her chemotherapy regimen: (1) Appointment Time, (2) Infusion Length, (3) Labs required prior to infusion, and (4) Probability of needing labs. Under the current system, every patient’s appointment time was 8:00 AM.
Figure 1.
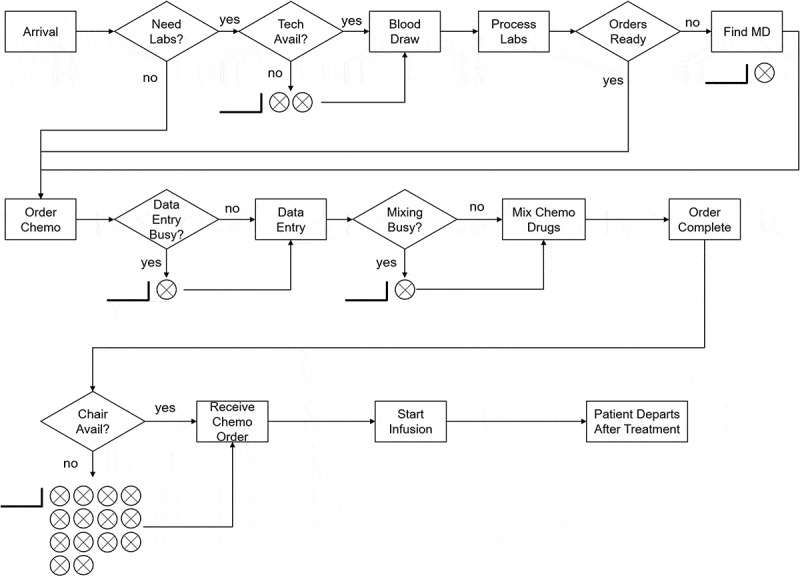
Infusion clinic patient flow diagram (does not include rare events such as unfavourable lab results or adverse reactions to infusions)
The processes for this model are listed below and their corresponding processing times will be discussed in the following sections:
Patient Arrivals,
Blood Draw,
Lab Processing,
Wait on Chemotherapy Orders,
Data Entry,
Mix Chemotherapy Drugs, and
Chemotherapy Infusion.
The resources for this model and their associated capacities are listed in Table 1. Notice that the lab process does not have an assigned resource because the clinic does not have the ability to process labs internally. Instead, lab processing times are modelled purely as a delay rather than a process that seizes a resource during its delay. Similarly, the process of waiting on chemotherapy orders is modelled purely as a delay.
Table 1.
Clinic resources
| Resource Capacity | Capacity |
|---|---|
| Phlebotomist | 1–2 |
| Data Entry Pharmacist | 1 |
| Mixing Pharmacist | 1 |
| Nurse | 3–4 |
3.2. Patient arrivals
Although every patient is scheduled for an 8:00 AM appointment, the daily variance in arrival times is significant. Some patients try to game the system, knowing that if they show up early they can be the first patient in the queue, whereas other patients are indifferent to their arrival time because they know that their infusion will be an all-day event. It is difficult to quantify the impact of these beliefs or to account for them in a simulation, and it is probably unrealistic to assume patients would display the same behaviour if the clinic used a meaningful appointment system. However, without having data to the contrary, all simulations follow the same arrival time distribution, regardless of the appointment time.
To model the patient arrival times, the simulation uses historical check-in times from the patients at the clinic. The earliest arrival time from the sample data is 6:30 AM and the latest is 10:20 AM. However, there are only two patients who arrived after 10:00 AM and occasionally nurses tell their patients with shorter infusions to come later in the morning. Since these two data points are significant outliers (60 minutes greater than the next latest arrival time), it is reasonable to assume that these patients were not instructed to arrive at 8:00 AM, therefore they are excluded from the sample population.
The rest of the data points are scaled by subtracting the sample time from 6:30 AM, where 6:30 AM is the earliest data point in the set. This step converts each data point from a time to the number of minutes it is from the lower bound (6:30 AM).
Based on historical arrival times, we model each patient’s arrival time as an independent and identical sample from a generalised Beta distribution of the form with lowerbound , upperbound , and shape parameters (Kuhl et al., 2010). Our best fit resulted in an arrival time distribution modelled by 6:30 AM + minutes. Goodness of fit tests and sensitivity analysis for this choice (and others in this paper) may be found in Slocum (2014).
3.3. Patient distribution
In looking at the average number of patients that visited the chemotherapy clinic, a strong correlation emerges between the number of nurses scheduled to work on a given day and the number of patients that were treated. As summarized in Table 2, historical data from January- October 2013 revealed that 82.7% of the time there were four nurses on the schedule and 17.3% of the time there were 3 nurses on the schedule. There were three instances when the clinic operated with two nurses; however those days were limited to the 2nd, 3rd, and 4th of January, therefore they were excluded from the sample population.
Table 2.
Patients treated each day based on number of nurses
| Nurses | Probability | Average Number Patients Treated | Standard Deviation |
|---|---|---|---|
| 3 | 17.3% | 12.1 | 2.2 |
| 4 | 82.7% | 14.7 | 2.7 |
The number of patients who received treatment at the clinic when there are 3 nurses on the schedule is significantly different than the number of patients who are treated when there are four nurses on the schedule. Based on historical data which included lower and upper bounds, we model the number of patients treated each day, , according to
| (1) |
where rounds to the nearest integer value.
3.4. Phlebotomy station
The phlebotomy station is the first queue that patients enter when they arrive to the clinic. The clinic has two phelobomists and under the current schedule, one works from 6:00 AM until 2:00 PM and the other works from 7:30 AM until 3:30 PM.
The average amount of time required to draw a patient’s blood is 5 minutes, although some patients' veins are more challenging than others, in which case a phlebotomist could spend up to 10 minutes trying to access a vein. After 10 minutes of trying to find a vein, the phlebotomist typically directs the patient to the infusion room where a specialist will come to draw their blood.
The difficulty in modelling the phlebotomy station is that chemotherapy patients represent less than half of the patients that come through the station each day. Haematology and oncology patients that are scheduled to meet with their doctor also use the clinic’s phlebotomy station, and chemotherapy patients are not given priority. From personal observations, there are rarely two phlebotomists in the office at the same time, as one is either absent, on break, or completing administrative work instead of drawing blood samples.
The simulation assumes a constant service time of 10 minutes throughout the day, which is double the average service time during these periods. Sensitivity analysis shows the results are insensitive to this assumption (Slocum, 2014). By using a service time of double the average service time, the model attempts to account for the impact non-chemotherapy patients would have on the phlebotomy queue length and waiting time.
3.5. Lab results
Each chemotherapy regimen attacks cancer cells differently, but the general concept is that chemotherapy drugs work by killing cells during a specific phase of the cell cycle and are unable to differentiate between good cells and cancer cells. Therefore, doctors require lab tests to determine whether a patient can withstand their next round of chemotherapy. The most common tests prior to receiving chemotherapy are complete blood count (CBC) tests and chemistry (Chem-7) tests. CBC tests measure a patient’s ability to recover from an infection or blood loss, while the Chem-7 tests indicates whether a patient’s metabolism will be able to clear the chemotherapy drugs adequately.
At the VA, over 95% of the regimens required both of these tests. Historically, nurses found the Chem-7 test results generally take longer to receive than the CBC test results. Without access to historical lab result times, the simulation estimated the lab result waiting times with a Beta distribution using the method detailed in Kuhl et al. (2010) and presented below. Define as the time in minutes to receive lab results. Anecdotal evidence from the nursing staff suggests that the fastest they can get both test results is 45 minutes (), the mode () is 70 minutes, and the longest amount of time they have waited is 150 minutes (). The nurses also believe the average time they spend waiting for lab results is 75 minutes (). Using this information, we derive the shape parameters for the generalised Beta distributions below. Let , and minutes; solving
| (2) |
| (3) |
yields and resulting in
| (4) |
3.6. Chemotherapy orders
Occasionally, a patient’s lab results will be ready but the nursing staff does not have chemotherapy orders to give the pharmacy. When this happens, the nurse has to locate the patient’s provider and ask them for chemotherapy orders. VA hospitals have not switched to electronic orders, thus the doctor must provide hard copy orders for every patient. This can be particularly challenging at the Durham VA hospital, because often times its oncologists spend several days each week at the Duke University Hospital.
The frequency of these delays is unclear, therefore the simulation uses anecdotal evidence to capture the process. According to the nursing staff, they have to track down orders for 25% of their patients. The lower bound for this delay is zero minutes, since it is possible for the doctor to deliver orders simultaneously with the lab results. The nurses agreed that the mode is roughly 10 minutes and the upper bound is 120 minutes; however, the most common waiting time is 20 minutes. The time to locate chemotherapy orders is
| (5) |
3.7. Pharmacy process
The pharmacy operates as two single server queues in series, where the first stage is the data entry phase and the second stage is the mixing phase. The chemotherapy clinic does not have two dedicated pharmacists, rather the hospital rotates its 14–16 pharmacists between the main pharmacy and the chemotherapy pharmacy to ensure all of their employees are capable of supporting either assignment and to limit the amount of exposure the pharmacists have to potentially harmful drugs.
Typically, the senior pharmacist in the chemotherapy room is responsible for the data entry portion of the process because it requires significant attention to detail and if the pharmacy makes a mistake, it usually occurs during data entry. For this simulation, the data entry phase refers to the time interval starting when the pharmacy receives the order until the time the mixing pharmacist enters the clean room to mix the drugs. During this phase, the pharmacist reviews the order and dosage calculations, enters the patient information, enters the drug data, and prepares a layout of drugs and mixing solutions. Once all of this is complete, both pharmacists review the layout together to verify that the order is correct – this ends the data entry phase. Typically, this process takes approximately 20 minutes, with a lower bound of 15 minutes and an upper bound of 25 minutes. This process is modelled with the following Beta distribution:
| (6) |
The next phase is the mixing phase, which begins when the mixing pharmacist enters the clean room. The mixing pharmacist carries all of the drugs to the ventilation hood and proceeds to mix all of the drug orders under the hood thereby reducing their exposure to the drugs. While some of the drugs take longer to dissolve in the saline solution than others, this process takes approximately 15 minutes, with a lower bound of 5 minutes and an upper bound of 25 minutes. It is modelled with the Beta distribution below:
| (7) |
3.8. Chemotherapy regimen data
Initially, one may think that the type of cancer, whether it be colon, lung, or pancreatic would be important to the simulation, but it turns out to be largely irrelevant. Instead, knowing which treatment regimen a patient is on provides much more useful information, because the regimen dictates the expected infusion length, probability of needing labs, and determines which labs are required prior to treatment.
One of the ways the simulation attempts to schedule patients is based on the expected length of their infusion. The simulation breaks the various infusions lengths into four categories: Quick, Short, Intermediate, and Long. A quick infusion is one that requires less than 1 hour of chair time. Quick infusions account for 49.3% of all infusions. A short infusion is one that takes between 1 and 2 hours. Short infusions account for 21.4% of all infusions. Intermediate infusions are those that take between 2 and 4 hours, and account for 18% of all infusions. Long infusions are those that take greater than 4 hours to administer and they account for 11.3% of all infusions.
The type of chemotherapy regimen that a patient is prescribed dictates the probability of needing labs when they arrive for treatment. Although labs are required prior to any patient receiving chemotherapy, labs are only required on the first day of treatment for patients receiving multiday infusions. For example, a patient that is on the FCR/FC regimen will have labs drawn on the first day of treatment when they receive FCR, but on days two and three the patient will come straight back to the infusion clinic and the nurses will give the pharmacy their chemotherapy order. In this example, the probability of needing labs for FCR is 1 and the probability of needing labs for FC is 0. Similarly, for a five day treatment such as Decitabine, a patient will only have labs drawn on 20% of their visits. Table 3 summarizes the empirical distribution of infusions and Slocum (2014) provides the probability of labs for all chemotherapy regimens administered in the last year. Table 4 lists the average infusion length for each chemotherapy regimen.
Table 3.
Empirical infusion distribution based on 1829 patient appointments from 1 January – July 1 2013. Note: PMF: probability mass function; CDF: cumulative distribution function
| PMF | CDF | Regimen | Count | PMF | CDF | Regimen | Count | PMF | CDF | Regimen | Count |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.000547 | 0.000547 | 0.45 NSS | 1 | 0.007108 | 0.315473 | CISPLATIN | 13 | 0.000547 | 0.632586 | Magnesium 1 gram | 1 |
| 0.002734 | 0.00328 | 0.9 NSS | 5 | 0.022963 | 0.338436 | CISPLATIN > 75MG/M2 | 42 | 0.011482 | 0.644068 | OXALI/BEVAC | 21 |
| 0.002734 | 0.006014 | 1 UNIT BLOOD | 5 | 0.00328 | 0.341717 | CYCLO/DOXOR | 6 | 0.018589 | 0.662657 | OXALI/BEVAC 1st dose | 34 |
| 0.020776 | 0.026791 | 2 UNITS BLOOD | 38 | 0.014215 | 0.355932 | CYCLO/VELC | 26 | 0.032258 | 0.694915 | OXALIPLATIN | 59 |
| 0.002187 | 0.028978 | 2 UNITS BLOOD + PLATELET | 4 | 0.031711 | 0.387644 | DECITABINE | 58 | 0.004374 | 0.699289 | PACLI/CARBO | 8 |
| 0.00164 | 0.030618 | 5-FU | 3 | 0.002187 | 0.389831 | DOCET/HERCE/PETUZ | 4 | 0.00164 | 0.700929 | PACLITAXEL | 3 |
| 0.015856 | 0.046473 | ABVD | 29 | 0.006561 | 0.396391 | DOCET/ZOMET | 12 | 0.004921 | 0.70585 | PAMIDRONATE > 60 mm | 9 |
| 0.004921 | 0.051394 | ADO-TRASTUZUMAB EMTANSINE | 9 | 0.030618 | 0.427009 | DOCETAXEL | 56 | 0.004921 | 0.710771 | PANIT/IRINO | 9 |
| 0.055768 | 0.107162 | Ancillary Therapy | 102 | 0.00164 | 0.42865 | DOXORUBICIN HCL | 3 | 0.001093 | 0.711864 | PANITUMUMAB | 2 |
| 0.018589 | 0.125752 | AZACITADINE (Vidaza) | 34 | 0.008748 | 0.437397 | EOX | 16 | 0.02515 | 0.737015 | PEMETREXED | 46 |
| 0.008748 | 0.1345 | BENDAMUSTINE HCL | 16 | 0.00328 | 0.440678 | EPIRUBICIN | 6 | 0.002187 | 0.739202 | PLATELET | 4 |
| 0.007108 | 0.141607 | BEP | 13 | 0.066703 | 0.507381 | ETOPOSIDE | 122 | 0.009841 | 0.749043 | R-CHOP | 18 |
| 0.00164 | 0.143248 | BEVAC/CAPEC | 3 | 0.02187 | 0.529251 | FC | 40 | 0.001093 | 0.750137 | R-CVP | 2 |
| 0.009295 | 0.152542 | BEVACIZUMAB | 17 | 0.011482 | 0.540733 | FCR | 21 | 0.002187 | 0.752324 | R-EPOCH | 4 |
| 0.000547 | 0.153089 | BLEOMYCIN | 1 | 0.00164 | 0.542373 | FERRLECIT | 3 | 0.00164 | 0.753964 | R-ESHAP | 3 |
| 0.017496 | 0.170,585 | CARBO/DOCET | 32 | 0.004921 | 0.547294 | FOLFIRI/OX | 9 | 0.002187 | 0.756151 | RICE | 4 |
| 0.010388 | 0.180973 | CARBO/ETOPO | 19 | 0.011482 | 0.558775 | FOLFOX | 21 | 0.021323 | 0.777474 | RITUX/BENDA | 39 |
| 0.009295 | 0.190268 | CARBO/IRINO | 17 | 0.029524 | 0.5883 | GEMCITABINE HCL | 54 | 0.000547 | 0.778021 | RITUX/CYCLOS | 1 |
| 0.04538 | 0.235648 | CARBO/PACLI | 83 | 0.008748 | 0.597048 | HERCEPTIN | 16 | 0.00328 | 0.781301 | RITUX/FLUDA/CYCLO | 6 |
| 0.004921 | 0.240569 | CARBO/PACLI/BEVAC | 9 | 0.00164 | 0.598688 | IFOSF/DOXOR | 3 | 0.000547 | 0.781848 | RITUX/VELC | 1 |
| 0.009295 | 0.249863 | CARBO/PEMET | 17 | 0.005467 | 0.604155 | IRINO/BEVAC | 10 | 0.016402 | 0.79825 | RITUXAN | 30 |
| 0.018589 | 0.268453 | CARFILZOMIB | 34 | 0.000547 | 0.604702 | IRINO/PANIT | 1 | 0.009295 | 0.807545 | VELCA/PAMID | 17 |
| 0.000547 | 0.268999 | CISPL/5-FU | 1 | 0.013122 | 0.617824 | IRINOTECAN HCL | 24 | 0.022417 | 0.829962 | VELCA/ZOMET | 41 |
| 0.018589 | 0.287589 | CISPL/DOCET | 34 | 0.002734 | 0.620558 | IRON DEXTRAN | 5 | 0.045927 | 0.875888 | VELCADE | 84 |
| 0.012575 | 0.300164 | CISPL/ETOPO | 23 | 0.005467 | 0.626025 | IV Medication | 10 | 0.025697 | 0.90159 | VENOFER | 47 |
| 0.003827 | 0.303991 | CISPL/GEMCI | 7 | 0.004374 | 0.630399 | IVIG-GAMMUNEX | 8 | 0.098414 | 1 | ZOMETA | 180 |
| 0.004374 | 0.308365 | CISPL/PEMET | 8 | 0.00164 | 0.632039 | IXABEPLIONE | 3 |
Table 4.
Average infusion length for each chemotherapy regimen (h:mm) based on industry standards and clinic nursing staff input
| Regimen | Infusion Time | Regimen | Infusion Time | Regimen | Infusion Time |
|---|---|---|---|---|---|
| 0.45 NSS | 0:30 | CISPLATIN | 4:00 | Magnesium 1 gram | 1:00 |
| 0.9 NSS | 1:00 | CISPLATIN > 75MG/M2 | 4:00 | OXALI/BEVAC | 3:00 |
| 1 UUNIT BLOOD | 1:30 | CYCLO/DOXOR | 1:20 | OXALI/BEVAC 1st dose | 3:30 |
| 2 UNITS BLOOD | 3:00 | CYCLO/VELC | 1:10 | OXALIPLATIN | 2:00 |
| 2 UNITS BLOOD + PLATELET | 3:30 | DECITABINE | 1:00 | PACLI/CARBO | 3:30 |
| 5-FU | 2:00 | DOCET/HERCE/PETUZ | 3:00 | PACLITAXEL | 3:00 |
| ABVD | 0:55 | DOCET/ZOMET | 1:15 | PAMIDRONATE > 60 mm | 1:30 |
| ADO-TRASTUZUMAB EMTANSINE | 0:30 | DOCETAXEL | 1:00 | PANIT/IRINO | 2:30 |
| Ancillary Therapy | 0:20 | DOXORUBICIN HCL | 0:20 | PANITUMUMAB | 3:00 |
| AZACITADINE (Vidaza) | 0:05 | EOX | 2:20 | PEMETREXED | 0:10 |
| BENDAMUSTINE HCL | 1:00 | EPIRUBICIN | 0:20 | PLATELET | 0:20 |
| BEP | 5:00 | ETOPOSIDE | 1:00 | R-CHOP | 6:00 |
| BEVAC/CAPEC | 1:30 | FC | 1:30 | R-CVP | 6:00 |
| BEVACIZUMAB | 1:30 | FCR | 5:00 | R-EPOCH | 8:00 |
| BLEOMYCIN | 1:05 | FERRLECIT | 1:00 | R-ESHAP | 6:00 |
| CARBO/DOCET | 1:30 | FOLFIRI/OX | 5:40 | RICE | 5:00 |
| CARBO/ETOPO | 1:30 | FOLFOX | 0:10 | RITUX/BENDA | 5:00 |
| CARBO/IRINO | 2:00 | GEMCITABINE HCL | 0:30 | RITUX/CYCLOS | 5:30 |
| CARBO/PACLI | 3:30 | HERCEPTIN | 1:00 | RITUX/FLUDA/CYCLO | 6:30 |
| CARBO/PACLI/BEVAC | 4:30 | IFOSF/DOXOR | 2:00 | RITUX/VELC | 1:10 |
| CARBO/PEMET | 1:10 | IRINO/BEVAC | 2:30 | RITUXAN | 4:00 |
| CARFILZOMIB | 1:40 | IRINO/PANIT | 4:30 | VELCA/PAMID | 1:35 |
| CISPL/5-FU | 4:00 | IRINOTECAN HCL | 1:30 | VELCA/ZOMET | 0:17 |
| CISPL/DOCET | 5:00 | IRON DEXTRAN | 7:40 | VELCADE | 0:05 |
| CISPL/ETOPO | 5:00 | IV Medication | 1:00 | VENOFER | 2:00 |
| CISPL/GEMCI | 4:30 | IVIG-GAMMUNEX | 4:00 | ZOMETA | 0:15 |
| CISPL/PEMET | 4:10 | IXABEPLIONE | 3:00 |
Due to patients with consecutive days of treatment, each day is not independent from the previous day. Since this model only simulates one day at a time, it was important to include the probability of a patient requiring labs in order to account for the impact multiday patients have on the system. These patients are typically the first to have their pharmacy orders placed because they are able to bypass the lab phase and their chemotherapy orders are on hand from the previous day. If the model assumed patients always required labs, the pharmacy would rarely receive orders before 9:00 AM, which is unrealistic.
3.9. Verification and validation
Multiple staff members reviewed the model logic; further, the nurses, pharmacists, and doctors all agreed some rare occurrences should be omitted from the model such as appointment no-shows and adverse reactions to infusions.
We used several statistics to validate the simulation to include number of patients treated, wait time statistics, processing times, and historical overtime data. Using 20 replications of 7,500 iterations, the model treated an average of 13.7 patients per day which matches the historical throughput while the minimum (7) and maximum (21) are consistent with the clinic’s historical records. The processing times for lab results and the pharmacy match the anecdotal times presented by the nursing staff and pharmacists. Personal observations of the clinic confirm the simulation’s backlog of chemotherapy orders at the data entry process is very indicative of true behaviour. Interested readers should see Slocum (2014) for more validation details.
3.10. Approach
After considering several simulation software packages, we chose to implement the simulation in a combination of Microsoft Excel and Visual Basic for Applications (VBA) for several reasons. The most important factor was the administrators’ high comfort level and familiarity with the software. Using software they had experience with in other clinic solutions maximised their ability to manipulate and display simulation results themselves.
The VBA source code comprises four major modules:
Patient Creation,
Base Schedule,
Proposed Schedule, and
Loop Construction/Main Menu.
Slocum (2014, pp. 26–30) develops the model in detail with pseudocode snippets for various processes. The entire source code for each module is available from (Slocum, 2014, App. E). The simulation interface was specifically designed to compare the baseline schedule to a proposed schedule. An example of one MS Excel output is included in the Appendix as Figure A1.
We chose to use 20 replications of 7,500 iteration after pilot simulations of each schedule for 2,500 and 5,000 iterations provided nearly identical results but did not sufficiently capture the tails of the patient distribution. Further, there were concerns over computation time in order to be able to work in near-real time with stakeholders from the Durham VA clinic. Using these settings produced results quickly on their machines as well.
Since the clinic’s current policy (base case) is a trivial block schedule with blocks, we first consider a selection of reasonable two block schedules for simulation and testing. We also assess performance of select three block schedules. VAMC staff assisted with developing the criteria for a “reasonable” policy which emphasised simplicity and ease of implementation – these criteria greatly reduced the possible schedules to be tested. Table 5 summarises the simulation inputs of interest.
Table 5.
Required inputs to simulate proposed schedule. These were the decisions available to the chemotherapy clinic
| Simulation Inputs | Description |
|---|---|
| Number of Schedule Blocks () | Number of appointment slots to use |
| Appointment Times | Example (): 8 AM, 10 AM, 12 PM |
| Patient Population (if ) | Patients to assign to first appointment |
4. Results
Based on VAMC nursing staff inputs, this study examined two scheduling policies that met the ease of implementation criterion. The results below were obtained using the method of synchronised common random numbers such that the patients who would arrive early (late) to the first appointment block arrive equally early (late) to the subsequent appointments tested (Law, 2007). Each schedule was simulated for 7,500 iterations.
The first policy was a fixed-block scheduling approach with two blocks. This would be easiest to implement but potentially challenging to adequately shape patient arrivals into only two appointment slots. The second option tested was a three fixed-block policy which provides the clinic with greater flexibility and control in assigning appointment times.
4.1. Two appointment policies
The two appointment policy categorised patients based on their chemotherapy regimen’s expected infusion length and assigned them to one of two potential appointment times. The first appointment time remained at 8:00 AM. Key performance drivers were the patient population and the appointment time.
The patient population refers to the patients (or chemotherapy regimens) that received an alternate appointment time. For example, if the patient population was 60 minutes, then all patients whose infusions are less than or equal to 60 minutes were given the second appointment time. This second appointment time ranged from 8:00 AM to 4:00 PM. If the second appointment time was too close to 8:00 AM, there is little change from the base schedule; if the appointment time was too late in the afternoon, nurse overtime increases.
The simulation tested patient population cut-offs of 30, 60, 90, and 120 minutes which comprise 32, 49, 61, and 71 percent of the total patient population, respectively. The appointment times evaluated ranged in 30 minute increments from 10:30 AM to 1:00 PM. This results in the schedules that are combinations of Table 6. For example, the (3–2) schedule assigns patients with infusions 90 minutes or shorter an 11:00 AM appointment time (patients with infusions greater than 90 minutes receive the 8:00 AM appointment). Figure 2 illustrates the average performance for these two appointment policies.
Table 6.
Two appointment schedules tested; schedules are named (-) for reference. Empirical distribution of patient population provided (e.g., 67% of patients require an infusion that is 90 minutes or less)
| Patient Population Index () | Patient Population | Percent of Patients | Appointment Index () | Appointment Time |
|---|---|---|---|---|
| 1 | 30 minutes | 32% | 1 | 10:30 AM |
| 2 | 60 minutes | 49% | 2 | 11:00 AM |
| 3 | 90 minutes | 67% | 3 | 11:30 AM |
| 4 | 120 minutes | 71% | 4 | 12:00 PM |
| 5 | 12:30 PM | |||
| 6 | 1:00 PM |
Figure 2.
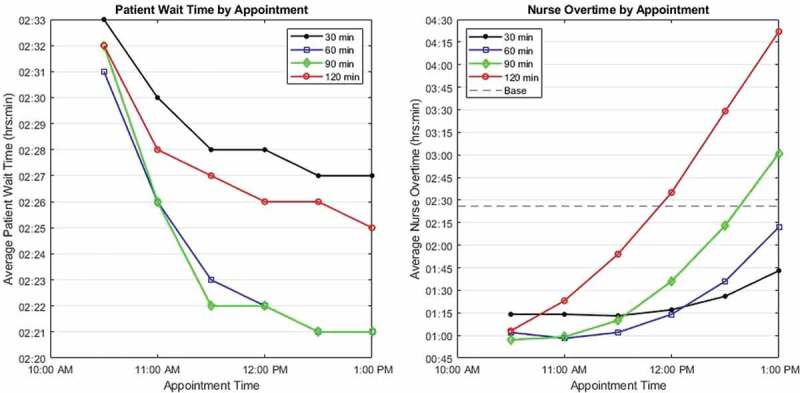
(Colour online) Average performance of proposed two appointment policies. Note the different axis scales for patient waiting time (left) and nurse overtime (right); the base case for patient waiting time is 3:05 (off chart), for nurse overtime, 2:26
From Figure 3 it is clear schedules 2–2 and 3–2 are statistically indistinguishable with 3–1 being the best schedule to minimise overtime and 2–3 best for reducing patient wait times. This illustrates the tradeoff between performance metrics and greatly simplifies the decision space. For reference, all two appointment schedule results are in Appendix B, Table B1.
Figure 3.
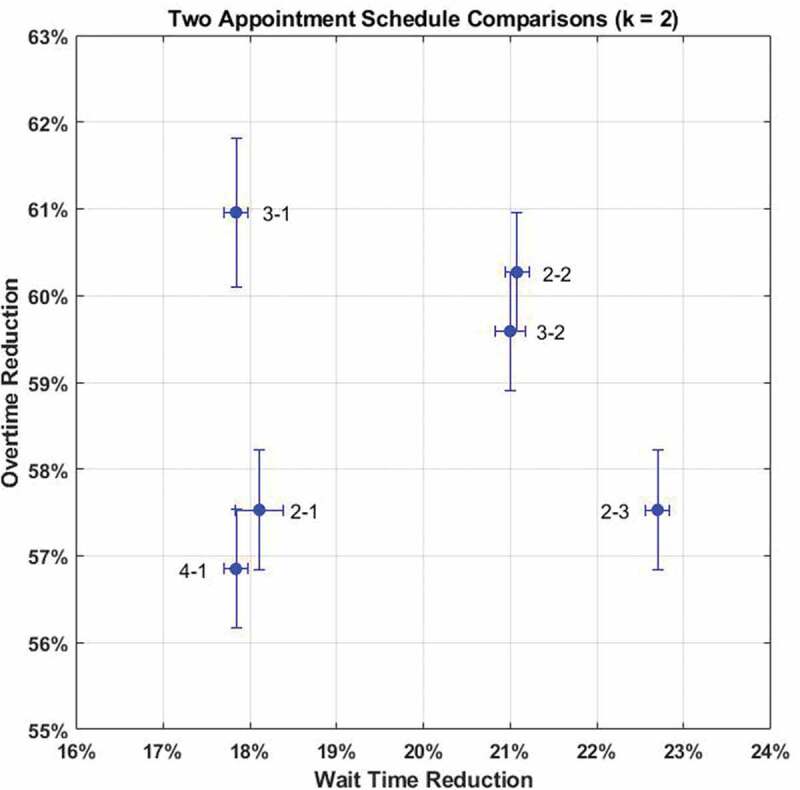
Comparison of best two appointment schedules () with 95% confidence intervals for mean performance
4.2. Three appointment policies
The two appointment policy is the simplest to implement but exploring the impact of a three appointment policy provides insights to understand the tradeoffs between scheduling complexity and key performance metrics. From the results in Section 4.1, the best policies shared two traits: the patient populations were evenly distributed across the appointment times and the fixed intervals were sufficiently spread out. Note that although small fixed intervals continue to reduce overtime, they unnecessarily increase patient waiting times. The interested reader can consult (Slocum, 2014, Ch. 5) for a more detailed discussion of fixed interval selection. We chose to group patients into three groups based on infusion lengths less than or equal to 30 minutes, more than 30 but less than or equal to 120 minutes, and longer than 120 minutes. These three groups account for 32, 36, and 32 percent of the total population respectively. Because Section 4.1 shows that regardless of patient population, appointment times after 12:30 PM increase average overtime in the clinic, we constructed the schedules in Table 7.
Table 7.
Three appointment schedules tested where is the infusion length in minutes
| 1st Appointment | 2nd Appointment | 3rd Appointment | |
|---|---|---|---|
| Schedule Name | min | min | min |
| 1 | 8:00 AM | 9:30 AM | 11:00 AM |
| 2 | 8:00 AM | 9:30 AM | 11:30 AM |
| 3 | 8:00 AM | 10:00 AM | 11:30 AM |
| 4 | 8:00 AM | 10:00 AM | 12:00 PM |
| 5 | 8:00 AM | 10:30 AM | 12:00 PM |
| 6 | 8:00 AM | 10:30 AM | 12:30 PM |
Figure 4 demonstrates schedules 4 and 5 are dominant. Though statistically indistinguishable, schedule 4’s even two hour spacing between appointment times may be more intuitive for nurses, patients, and administrators. Schedule 4 outperforms the best schedule by 6% in overtime and 3% in wait time reduction. All results for three appointment schedules are in Appendix B, Table B2.
Figure 4.
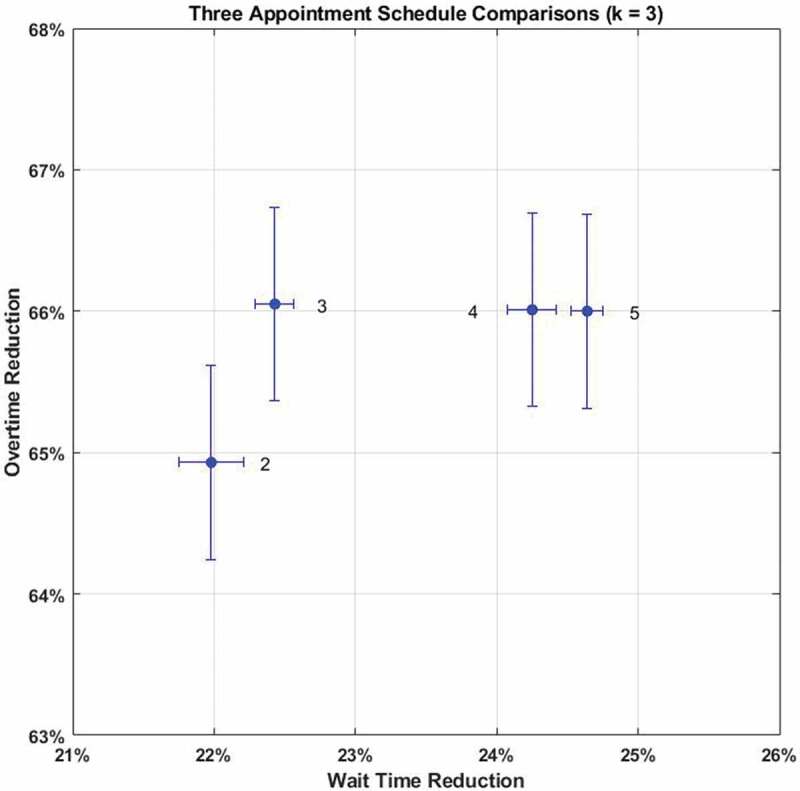
Comparison of best three appointment schedules () with 95% confidence intervals for mean performance
4.3. Discussion
As an example of how these policies affect clinic performance metrics, Figure 5 provides a visual summary of a 17 patient example with their infusion times labelled in minutes. The top example illustrates the clinic’s current policy. Notice the various infusions categories are widely intermixed and the longest treatments were processed 9th, 10th, and 17th. By failing to sequence these longer infusions earlier in the schedule, the clinic worked 3.7 hours of overtime. The best two appointment schedule from Section 4.1 makes a visible difference to the same patient list resulting in a schedule with zero overtime hours and the last patient infusion concluding at 3:59 PM. After applying the best schedule from Section 4.2, the long and intermediate infusions are clearly grouped first. This schedule achieves zero overtime with the final infusion complete at 3:52 PM. Table 8 summarizes performance measures for the example in Figure 5.
Figure 5.
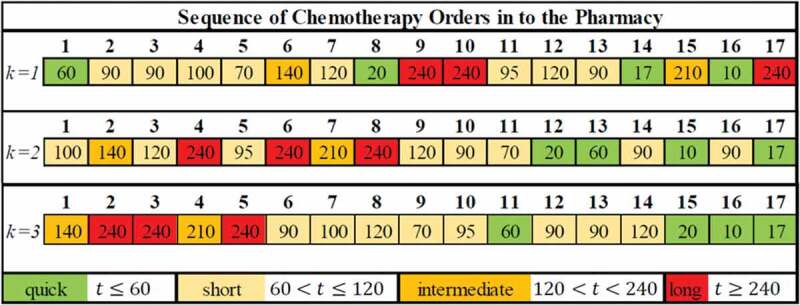
(Colour online) Pharmacy sequences for single appointment (top), two appointments (middle), and three appointments (bottom) with infusion times in minutes
Table 8.
Performance measures from example in Figure 5
| Number of Appointments (k) |
Average Number of Orders in Pharmacy Queue | Average Waiting Time (h:mm) |
|---|---|---|
| 4.6 | 3:28 | |
| 2.2 | 2:26 | |
| 1.4 | 2:13 |
One practical solution to cope with variability in the lab process is to stagger appointment times to break up the massive influx of pharmacy orders between 9:00–10:30 AM. The two and three appointment policies reduce average waiting time in the clinic predominantly by spreading out chemotherapy orders. In the example shown in Figure 5, the average queue length varied greatly between the three policies. As the number of appointment blocks increases, the average number of orders will decrease until a lowerbound. Due to the variability in the lab process, this lowerbound is unlikely to be zero. For a more detailed discussion of model results, the reader is encouraged to consult (Slocum, 2014, Ch. 5–6).
5. Conclusion
This study examined two scheduling policies that can be easily implemented at the Durham VAMC chemotherapy clinic. The best two appointment policy assigns all patients infusions taking less than 1 hour an appointment time of 11:00 AM (recall the rest are scheduled for 8:00 AM). This schedule reduced the average waiting time in the clinic by 21% and reduced average nurse overtime by 60%.
With three appointments, the best policy assigns 12:00 PM appointments for patients with infusion lengths less than or equal to 30 minutes, 10:00 AM appointments for patients with infusion lengths of 31–120 minutes, and 8:00 AM appointments for patients with infusions longer than 120 minutes. This schedule reduced the average waiting time in the clinic by 24% and the average overtime by 66%.
To minimise overtime costs, the optimal scheduling solution appears to prioritise patients according to a Longest Infusion Time (LIT) heuristic. This may not always be practical based on constant appointment changes, additions, and uncertain daily patient volume until the day of treatment. However, chemotherapy clinics can used standardised fixed-block scheduling techniques to shape the patient arrivals such that the longest infusion times arrive first and the shortest infusion times arrive last. Increasing the number of blocks moves the schedule close to the LIT order but at the cost of increased complexity.
VA and community hospitals that treat a high volume of Medicaid or Medicare patients may have little incentive to change their current practices (U.S. Centers for Medicare & Medicaid Services, 2019a, 2019b). Generally speaking, they do not have to compete for business and their monetary compensation for treatment is low, therefore providers may be largely indifferent to patient waiting times. But as the population of veterans from over a decade of war, access to healthcare increases as a result of the Affordable Care Act (U.S. 111th Congress, 2010), and oncology treatment protocols increase patient life expectancies, the demand for chemotherapy services will likely outpace supply. Administrators would be well-served by applying cost-free solutions, like good scheduling, to reduce operating costs and improve patient care.
Acknowledgments
This paper would not have been possible without the nurses at the Durham VAMC infusion clinic whose patience and willingness to share their expertise supported every aspect of this project. The fourth author was supported by a grant from the U.S. Army Research Office (grant # W911NF1910055).
Appendix A. Sample Output
Figure A1.
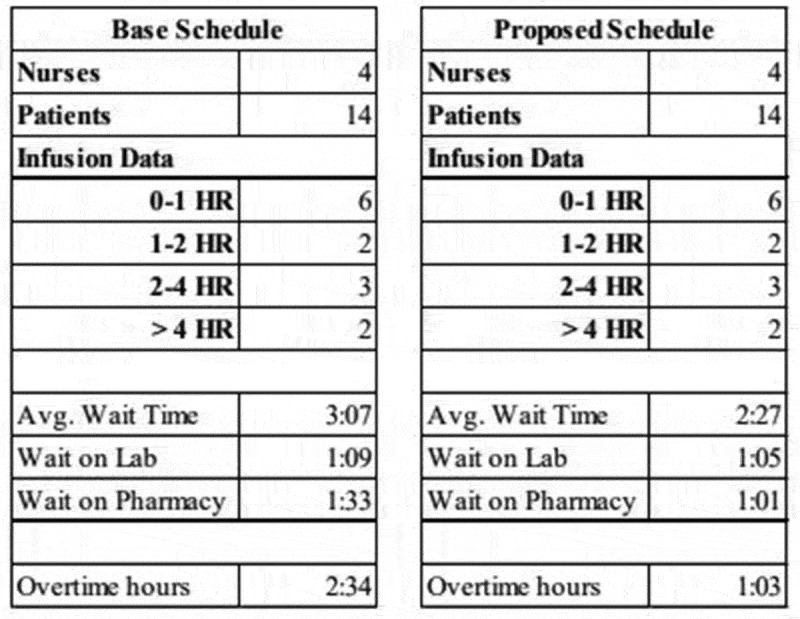
Example of Simulation Output Table for a proposed schedule (right) as compared to the base schedule (left). In this scenario, the number of nurses, patients, and the required infusions are identical for appropriate comparison. Simulation results include average wait time, delays at the lab and pharmacy, and the number of nurse overtime hours
Appendix B. Simulation Results
Table B1.
Simulation results for all two appointment schedules. The mean patient wait times and nurse overtime results reported in “hours:minutes” format. The “% Reduction” column denotes the percent reduction in customer wait time (left) and nurse overtime (right); negative values indicate an increase. Lower and upper endpoints for the 95% confidence interval for the mean also provided in the “hours:minutes” format
| i–j | Patient Pop. (min) | Appt Time | Wait Time | % Reduction | Lower | Upper | Overtime | % Reduction | Lower | Upper |
|---|---|---|---|---|---|---|---|---|---|---|
| Base |
All |
8:00 |
3:05 |
|
|
|
2:26 |
|
|
|
| 1–1 | 30 | 10:30 | 2:33 | 17.30% | 2:32 | 2:33 | 1:14 | 49.32% | 1:12 | 1:17 |
| 1–2 | 30 | 11:00 | 2:30 | 18.40% | 2:29 | 2:30 | 1:14 | 49.32% | 1:12 | 1:17 |
| 1–3 | 30 | 11:30 | 2:28 | 20.00% | 2:28 | 2:29 | 1:13 | 50.00% | 1:11 | 1:16 |
| 1–4 | 30 | 12:00 | 2:28 | 19.53% | 2:27 | 2:28 | 1:17 | 47.26% | 1:14 | 1:19 |
| 1–5 | 30 | 12:30 | 2:27 | 20.54% | 2:27 | 2:28 | 1:26 | 41.10% | 1:24 | 1:29 |
| 1–6 |
30 |
13:00 |
2:27 |
20.54% |
2:27 |
2:28 |
1:43 |
29.45% |
1:41 |
1:45 |
| 2–1 | 60 | 10:30 | 2:31 | 18.11% | 2:30 | 2:32 | 1:02 | 57.53% | 1:00 | 1:04 |
| 2–2 | 60 | 11:00 | 2:26 | 21.08% | 2:26 | 2:27 | 0:58 | 60.27% | 0.56 | 1:00 |
| 2–3 | 60 | 11:30 | 2:23 | 22.70% | 2:22 | 2:23 | 1:02 | 57.53% | 1.00 | 1:04 |
| 2–4 | 60 | 12:00 | 2:22 | 23.24% | 2:21 | 2:22 | 1:14 | 48.88% | 1:12 | 1:16 |
| 2–5 | 60 | 12:30 | 2:21 | 23.78% | 2:21 | 2:21 | 1:36 | 33.80% | 1:33 | 1:38 |
| 2–6 |
60 |
13:00 |
2:21 |
23.78% |
2:21 |
2:22 |
2:12 |
9.59% |
2:10 |
2:14 |
| 3–1 | 90 | 10:30 | 2:32 | 17.84% | 2:31 | 2:32 | 0:57 | 60.96% | 0:54 | 0:59 |
| 3–2 | 90 | 11:00 | 2:26 | 21.00% | 2:25 | 2:26 | 0:59 | 59.59% | 0.57 | 1:01 |
| 3–3 | 90 | 11:30 | 2:22 | 23.24% | 2:22 | 2:23 | 1:10 | 52.05% | 1.08 | 1:12 |
| 3–4 | 90 | 12:00 | 2:22 | 22.80% | 2:21 | 2:22 | 1:36 | 34.25% | 1:34 | 1:38 |
| 3–5 | 90 | 12:30 | 2:21 | 23.78% | 2:21 | 2:22 | 2:13 | 8.90% | 2:11 | 2:15 |
| 3–6 |
90 |
13:00 |
2:21 |
23.78% |
2:21 |
2:22 |
3:01 |
23.97% |
2:58 |
3:03 |
| 4–1 | 120 | 10:30 | 2:32 | 17.84% | 2:32 | 2:33 | 1:03 | 56.85% | 1:01 | 1:05 |
| 4–2 | 120 | 11:00 | 2:28 | 19.67% | 2:28 | 2:29 | 1:23 | 43.15% | 1:21 | 1:25 |
| 4–3 | 120 | 11:30 | 2:27 | 20.54% | 2:26 | 2:27 | 1:54 | 21.92% | 1.52 | 1:56 |
| 4–4 | 120 | 12:00 | 2:26 | 20.86% | 2:25 | 2:26 | 2:35 | 6.16% | 2:33 | 2:38 |
| 4–5 | 120 | 12:30 | 2:26 | 20.80% | 2:26 | 2:26 | 3:29 | 43.15% | 3:26 | 3:31 |
| 4–6 | 120 | 13:00 | 2:25 | 21.62% | 2:25 | 2:26 | 4:22 | 79.45% | 4:19 | 4:24 |
Table B2.
Simulation results for all three appointment schedules. The mean patient wait times and nurse overtime results reported in “hours:minutes” format. The “% Reduction” column denotes the percent reduction in customer wait time (left) and nurse overtime (right); negative values indicate an increase. Lower and upper endpoints for the 95% confidence interval for the mean also provided in the “hours:minutes” format
| 1st Appt | 2nd Appt | 3rd Appt | Wait Time | % Reduction | Lower | Upper | Overtime | % Reduction | Lower | Upper | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Base |
8:00 |
n/a |
n/a |
3:05 |
|
|
|
2:26 |
|
|
|
| 1 | 8:00 | 09:30 | 11:30 | 2:28 | 19.71% | 2:28 | 2:29 | 0:53 | 63.67% | 0:50 | 0:55 |
| 2 | 8:00 | 09:30 | 11:30 | 2:24 | 21.98% | 2:23 | 2:24 | 0:51 | 64.93% | 0:49 | 0:53 |
| 3 | 8:00 | 10:00 | 11:30 | 2:23 | 22.43% | 2:23 | 2:23 | 0:49 | 66.05% | 0:47 | 0:51 |
| 4 | 8:00 | 10:00 | 12:00 | 2:20 | 24.25% | 2:19 | 2:20 | 0:49 | 66.01% | 0:47 | 0:51 |
| 5 | 8:00 | 10:30 | 12:00 | 2:19 | 24.64% | 2:19 | 2:19 | 0:49 | 66.00% | 0:47 | 0:51 |
| 6 | 8:00 | 10:30 | 12:30 | 2:16 | 26.39% | 2:15 | 2:16 | 0:56 | 61.47% | 0:54 | 0:58 |
Funding Statement
This work was supported by the US Army Research Office [W911NF1910055].
Disclaimer
The views expressed in this paper are those of the authors and do not reflect the official policy or position of the United States Army, the Department of Defense, the Department of Veterans Affairs, or the United States Government.
Disclosure statement
No potential conflict of interest was reported by the authors.
References
- Abo-Hamad, W., & Arisha, A. (2013). Simulation-based framework to improve patient ex- perience in an emergency department. European Journal of Operational Research, 224(1), 154–166. [Google Scholar]
- Ahmed, Z., ElMekkawy, T., & Bates, S. (2011). Developing an efficient scheduling template of a chemotherapy treatment unit: A case study. Australasian Medical Journal, 4(10), 575–588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarado, M., Cotton, T., Ntaimo, L., Pérez, E., & Carpentier, W. (2018). Modeling and simulation of oncology clinic operations in discrete event system specification. Simulation, 94(2), 105–121. [Google Scholar]
- Babashov, V., Aivas, I., Begen, M., Cao, J., Rodrigues, G., D’Souza, D., & Lock, M. (2017). Reducing patient waiting times for radiation therapy and improving the treatment planning process: A discrete-event simulation model (radition treatment planning). Clinical Oncology, 29(6), 385–391. [DOI] [PubMed] [Google Scholar]
- Belter, D., Hasley, J., Severtson, H., Fix, A., Michelfelder, L., Michalak, K., & Abella, P. (2012). Evaluation of outpatient oncology services using lean methodology. Oncology Nurs- Ing Forum, 39(2), 136–140. [DOI] [PubMed] [Google Scholar]
- Cayirli, T., & Veral, H. (2003). Outpatient scheduling in health care: A review of literature. Production and Operations Management, 12(4), 519–549. [Google Scholar]
- Chabot, G., & Fox, M. (2005). The creation of a patient-classification system in an outpatient infusion center setting. Oncology Nursing Forum, 32(3), 535–538. [DOI] [PubMed] [Google Scholar]
- Delaney, B., Jalaludin, B., Moylan, E., & Barton, M. (2002). The development of a model of outpatient chemotherapy delivery—chemotherapy basic treatment equivalent (CBTE). Clinical Oncology, 14(5), 406–412. [DOI] [PubMed] [Google Scholar]
- Demir, E., Southern, D., Verner, A., & Amoaku, W. (2018). A simulation tool for better management of retinal services. BMC Health Services Research, 18(1), 759–766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisenburg, S. (2009). Ambulatory oncology clinics: Oncology nurses juggle staffing and scheduling in the outpatient setting. ONS Connect, 24(8), 6–8. [PubMed] [Google Scholar]
- Garaix, T., Rostami, S., & Xie, X. (2018). Daily outpatient chemotherapy appointment scheduling with random deferrals. Flexible Services and Manufacturing Journal, 1–25. (published online 21 Sep 2018). Retrieved from 10.1007/s10696-018-9326-x [DOI] [Google Scholar]
- Gul, M., & Guneri, A. (2015). A comprehensive review of emergency department simulation applications for normal and disaster conditions. Computers & Industrial Engineering, 83, 327–344. [Google Scholar]
- Gul, M., Guneri, A., & Gunal, M. (2019). Emergency department network under disaster conditions: The case of the possible major Instanbul earthquake. Journal of the Operational Research Society, 1–15. Retrieved from 10.1080/01605682.2019.1582588 [DOI] [Google Scholar]
- Gupta, D., & Denton, B. (2008). Appointment scheduling in health care: Challenge and opportunities. IIE Transactions, 40(9), 800–819. [Google Scholar]
- Hendershot, E., Murphy, C., Doyle, S., Van-Clieaf, J., Lowry, J., & Honeyford, L. (2005). Outpatient chemotherapy administration: Decreasing wait times for patients and families. Journal of Pediatric Oncology Nursing, 22(1), 31–37. [DOI] [PubMed] [Google Scholar]
- Hesaraki, A., Dellaert, N., & de Kok, T. (2019). Generating outpatient chemotherapy appointment templates with balanced flowtime and makespan. European Journal of Operational Research, 275(1), 304–318. [Google Scholar]
- Kadri, F., Chaabane, S., & Tahon, C. (2014). A simulation-based decision support system to prevent and predict strain situations in emergency department systems. Simulation Modelling Practice and Theory, 42, 32–52. [Google Scholar]
- Kallen, M., Terrell, J., Lewis-Patterson, P., & Hwang, J. (2012). Improving wait time for chemotherapy in an outpatient clinic at a comprehensive cancer center. Journal of Oncology Practice, 8(1), e1–e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhl, M., Ivy, J., Lada, E., Steiger, N., Wagner, M., & Wilson, J. (2010). Univariate input models for stochastic simulation. Journal of Simulation, 4(2), 81–97. [Google Scholar]
- Law, A. (2007). Simulation modeling and analysis (4th ed., pp. 578–593). Boston, MA: McGraw-Hill. [Google Scholar]
- Liang, B., Turkcan, A., Ceyhan, M., & Stuart, K. (2015). Improvement of chemotherapy patient flow and scheduling in an outpatient oncology clinic. International Journal of Production Research, 53(24), 7177–7190. [Google Scholar]
- Oh, C., Novotny, A., Carter, P., Ready, R., & Campbell, D. (2016). Use of a simulation-based decision support tool to improve emergency department throughput. Operations Research for Health Care, 9, 29–39. [Google Scholar]
- Ordu, M., Demir, E., & Fofallis, C. (2019). A decision support system for demand and capacity modelling of an accident and emergency department. Health Systems, 1–26. (Published online 6 Jan 2019). Retrieved from doi. 10.1080/20476965.2018.1561161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson, D., & Cohn, A. (2018). Modeling the impact of make-ahead chemotherapy drug policies through discrete event simulation. In Rabe M., Juan A., Mustafee N., Skoogh A., & Johansson B. (Eds.), Proceedings of the 2018 Winter Simulation Conference (pp. 2690–2700), Gothenburg, Sweden. [Google Scholar]
- Rohleder, T., Lewkonia, P., Bischak, D., Duffy, P., & Hendijani, R. (2011). Using simulation modeling to improve patient flow at an outpatient orthodpedic clinic. Health Care Management Science, 14(2), 135–145. [DOI] [PubMed] [Google Scholar]
- Seminelli, M., Wilson, J., & McConnell, B. (2016). Implementing discrete event simulation to improve optometry clinic operations. In Roeder T., Frazier P., Szechtman R., Zhou E., Huschka T., & Chick S. (Eds.), Proceedings of the 2016 Winter Simulation Conference (pp. 2157–2168), Washington, D.C., USA. [Google Scholar]
- Slocum, R. (2014). Improving Chemotherapy Infusion Operations through the Simulation of Scheduling Heuristics. Masters thesis, Operations Research Graduate Program, North Carolina State University, http://www.lib.ncsu.edu/resolver/1840.16/9276 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suss, S., Bhuiyan, N., Demirli, K., & Batist, G. (2017). Toward implementing patient flow in a cancer treatment center to reduce patient waiting time and improve efficiency. Journal of Oncology Practice, 13(6), 383, e530–e537. [DOI] [PubMed] [Google Scholar]
- Thomas, S., Glynne-Jones, R., & Chait, I. (1997). Is it worth the wait? a survey of patients’ satisfaction with an oncology outpatient clinic. European Journal of Cancer Care, 6(1), 50–58. [DOI] [PubMed] [Google Scholar]
- Turkcan, A., Zeng, B., & Lawley, M. (2012). Chemotherapy operations planning and scheduling. IIE Transactions on Healthcare Systems Engineering, 2(1), 31–49. [Google Scholar]
- U.S. 111th Congress . (2010). The Patient Protection and Affordable Care Act (H.R. 3590). https://www.govinfo.gov/app/details/BILLS-111hr3590enr.
- U.S. Centers for Medicare & Medicaid Services . (2019a). Medicaid.gov. https://www.medicaid.gov/
- U.S. Centers for Medicare & Medicaid Services . (2019b). Medicare.gov. https://www.medicare.gov
- U.S. Department of Veterans Affairs . (2018a). Durham VA health care system website. https://www.durham.va.gov
- U.S. Department of Veterans Affairs . (2018b). History – Department of Veterans Affairs (VA). https://www.va.gov/aboutva/vahistory.asp
- U.S. Department of Veterans Affairs . (2018c). VA History In Brief. https://www.va.gov/opa/publications/archives/docs/history in brief.pdf, 12
- Welch, J., & Bailey, N. (1952). Appointment systems in hospital outpatient departments. The Lancet, 259(6718), 1105–1108. [DOI] [PubMed] [Google Scholar]
- Williamson, T. (2008). The shift of oncology inpatient care to outpatient care: The challenge of retaining expert oncology nurses. Clinical Journal of Oncology Nursing, 12(2), 186–189. [DOI] [PubMed] [Google Scholar]
- Woodall, J., Gosselin, T., Boswell, A., Murr, M., & Denton, B. (2013). Improving patient access to chemotherapy treatment at Duke Cancer Institute. Interfaces, 43(5), 449–461. [Google Scholar]
- Yokouchi, M., Aoki, S., Sang, H., Zhao, R., & Takakuwa, S. (2012). Operations analysis and appointment scheduling for an outpatient chemotherapy department. In Laroque C., Himmelspach J., Pasupathy R., Rose O., & Uhrmacher A. (Eds.), Proceedings of the 2012 Winter Simulation Conference (pp. 1–12), Berlin, Germany. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- U.S. Centers for Medicare & Medicaid Services . (2019a). Medicaid.gov. https://www.medicaid.gov/


