Abstract
Multilevel random-effects models have become a popular method in the analysis of clustered data. Such analyses enable researchers to quantify within-cluster and between-cluster variations of an outcome and to separate individual-level and cluster-level effects of covariates by taking advantage of the hierarchical structure of clustered data. The tutorial article by Austin and Merlo1 was a timely effort intended to provide a comprehensive and up-to-date review of the tools and approaches. However, we feel that some important ideas and concepts described in this article need clarification.
1 ∣. INDIVIDUAL-LEVEL COVARIATE EFFECTS VS WITHIN-CLUSTER EFFECTS AND COVARIATE CENTERING
The authors stated in their case study that odds ratios estimated from their fitted multilevel logistic models are conditional cluster-specific measures of association or intracluster measures of association, and therefore, they may be interpreted as odds ratios for within-cluster comparisons. This statement can be problematic because, as the authors noted, it leads to difficulty with the interpretation of the effects of cluster-level covariates. Conditional likelihood methods are known to yield estimates of within-cluster effects of individual-level covariates but not of cluster-level covariates because the values of cluster-level covariates do not vary within clusters. Intuitively, one would consider the within-cluster effects of cluster-level covariates to be zero. Before further discussing this, we note that even the estimated effects of individual-level covariates are not necessarily identical with their within-cluster effects.
Consider the illustrative case of estimating the effect of patient age on the probability of hospitalization. For simplicity, we describe multilevel models that include only 1 patient-level covariate, age. The following models can be specified for a patient i within hospital j with a binary outcome yij, death, because of any cause within 1 year of hospital admission,
| (1) |
| (2) |
| (3) |
| (4) |
where α0j is the random hospital effect and is the hospital mean of age.
Models of these forms have been used to examine the potential bias in the estimated effect of an individual-level covariate by Neuhaus and Kalbfleisch,2 Berlin et al,3 Begg and Parides4, and Delong et al.5 They found that models (2) to (4) yielded nearly identical estimates of individual-level effect, α1, which also equaled the estimated within-cluster effect by using the conditional likelihood method, but model (1) yielded a different estimate, which was confounded by the effect of the cluster-level mean. These results are important, particularly in health services research where exposure or intervention rate often varies across hospitals, but were not adequately described in this tutorial.
Because the case study was primarily based on fitted models that included the age covariate centered to its grand mean, we can specify an additional model,
| (5) |
where is the grand mean among all patients. This model and model (1) have the same slope α1 and are different only in the intercept α0. Therefore, the estimated α1 from model (5) can similarly be confounded by the effect of cluster-level mean, and one should be cautious when interpreting it as a within-hospital effect.
Centering the covariates is often thought to be a trivial issue and is typically done for the purpose of facilitating statistical computation or interpretation. Surprisingly, it can lead to substantially different results in multilevel modeling analysis. Strictly speaking, centering a covariate to its grand mean does not provide adjustment for the confounding effect of its cluster-level mean and thus does not yield a within-cluster effect estimate. On the other hand, there are various situations under which the confounding effect of a cluster-level mean becomes inconsequential. It can be easily seen that the estimated age effect from model (1) should be close to its within-cluster effect when the hospital mean effect in model (2) is zero, when the hospital mean varies little in model (3) and is close to the grand mean in model (5), or when the patient age effect equals the hospital mean effect in model (4).
We noted that the authors also fitted a model similar to model (4) in the last section of their illustration. The estimated odds ratio for the within-hospital effect was 1.08 per year increase in age (95% CI: 1.07-1.08), or 2.16 per 10-year increase, very close to the original estimate of 2.12, and the hospital mean effect was of similar magnitude with an odds ratio of 1.11 (95% CI: 1.09-1.13) per year increase in age. Therefore, the estimated odds ratio for the within-hospital effect of age was 2.16 and was slightly underestimated without adjusting for the hospital-level effect of age. Despite a very small difference, it may not be viewed as a negligible difference by a clinician because the estimated effects of patient age and hospital mean of age were both statistically significant.
2 ∣. CLUSTER-LEVEL COVARIATE EFFECTS VS CONTEXTUAL EFFECTS
Now we return to the issue of interpreting cluster-level effects. The study of contextual effects was introduced as an important feature of the multilevel modeling analysis in this article. Indeed, the nature of hierarchically structured data provides a unique opportunity for exploring the influences of organization or environment. The cluster-level covariates are often included in multilevel models for the reason of their potential contextual effects on individual-level outcomes. The authors introduced 3 alternative measures of cluster-level effects, the approximated marginal effects, the interval odds ratio, and the proportion of opposed odds ratios, to get around the difficulty with the within-cluster interpretation of these effects, but did not describe how the contextual effects should be estimated and are related to these alternative measures.
The contextual effects are commonly defined as the cluster-level effects adjusted for individual-level characteristics. To facilitate the estimation of contextual effects, it helps to write a multilevel model in the form of regression models at multiple levels. Taking the model specified by the authors in their case study as an example and for simplicity keeping only 1 individual-level covariate of age and 1 hospital-level covariate of hospital volume (hvolj), we can specify 2 models as follows.
| (6) |
| (7) |
The coefficient α2 for the hospital volume in model (7) indicates the change in the dependent variable, γ0j, the logit-scale average hospital death rate, because of a unit change in the hospital volume. It is straightforward to interpret its estimate as a contextual effect. For example, the authors used the hospital volume covariate in hundreds of patients and obtained an estimated odds ratio of 0.95 (95% CI: 0.92-0.98). This shows a significant contextual effect on the outcome of death among patients of same age and other characteristics, the reduced odds of death by 5% in a hospital with 100 more patients.
Furthermore, we can see that centering the age covariate to the hospital means in the patient-level model as in model (3) will lead to a different interpretation of the hospital volume effect. The coefficient α2 in this case is not usually considered a contextual effect. Following Begg and Parides,4 the contextual effect of the hospital mean of age can be calculated as α2 – α1, or in odds ratios. Because the estimated within-hospital and hospital mean effects of patient age were reported by the authors, we can obtain an estimate of the contextual effect of the hospital mean age covariate as an odds ratio of 1.03 (1.11/1.08) per 1-year increase.
3 ∣. EXPLAINING CLUSTER-LEVEL VARIATION OR “UNEXPLAINED” CONTEXTUAL EFFECTS
Unlike the contextual effects estimated as the cluster-level covariate effects, the authors described the estimation of general contextual effects measured via cluster variances. It is often of substantive interest to researchers to quantify the change in the estimated cluster variances because of the addition of an individual-level or cluster-level covariate in the multilevel models. For example, Rysavy et al6 estimated the proportion of hospital variation in infant survival that could be attributed to hospital-level approaches to care after controlling for infant-level maternal and neonatal characteristics. This parallels the analysis of proportion of the residual variances explained in ordinary linear or logistic regression analysis and probably can be more appropriately termed “explaining the unexplained (or residual) contextual effects.”
While it is well known that the residual variance will generally decrease with the addition of covariates in ordinary linear regression models, it is perhaps much less recognized and not well understood that, to the contrary of expectation, the cluster variance can increase with the addition of covariates in both multilevel logistic models (Snijders and Bosker7) and multilevel linear models (University of Texas at Austin8). The authors stated that the proportional change in cluster variance when outcomes are binary does not behave like an R2-type statistic and the inclusion of additional covariates can result in an increase in the variance of the distribution of the random effects. We conducted an investigation into this issue using both observed and simulated data and found somewhat different results. The usually observed decrease in cluster variance with the addition of covariates in ordinary linear models should still hold true with cluster-level covariates in the multilevel logistic models, but not with individual-level covariates. We present an example to illustrate this in the following.
Data on the survival outcomes of extremely preterm infants born between April 1, 2006 and March 31, 2011 were taken from 24 United States hospitals. We fitted a multilevel logistic regression model with a random intercept only and models that included 1 infant-level covariate, gender, birth weight, gestational age, plurality (multiple vs singleton birth) or exposure to antenatal corticosteroids prior to delivery, or included 1 hospital-level covariate, the hospital proportion or mean of these covariates. These infant characteristics were significantly associated with the survival outcome. Figure 1 plots the estimated hospital variances from our analysis. It can be seen that all 5 models with a hospital-level covariate have a smaller hospital variance than the intercept-only model, but 3 models with an infant-level covariate had a larger cluster variance and 2 have a smaller one. Also, not shown in the figure, including additional hospital-level covariates in these models resulted in further decreases in the estimated hospital variance.
FIGURE 1.
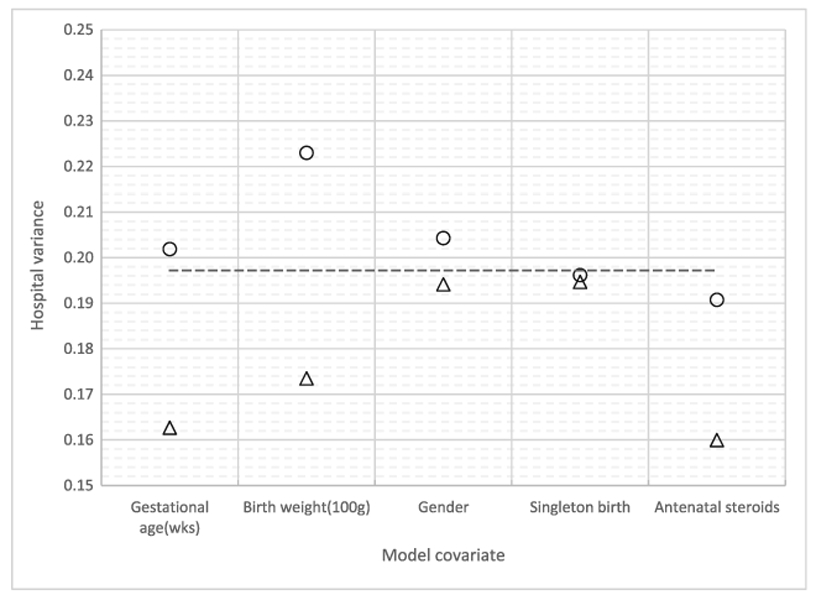
Hospital variance estimates from multilevel logistic models of infant survival. Dashed horizontal line: intercept-only model; circle: models with 1 infant-level covariate; triangle: models with 1 hospital-level covariate of mean or proportion
Clearly, an implication of our findings is that using multilevel logistic models to quantify the proportional change in cluster variance should be conducted only among cluster-level covariates. One may compare an intercept-only model to models with cluster-level covariates or compare a model with both individual-level and cluster-level covariates to a model with the same set of individual-level covariates and additional cluster-level covariates.
It is not surprising that cluster variance usually decreases with the addition of cluster-level covariates. This may be best conceived if we view a multilevel model as a set of models at multiple levels. For example, the random-effect term, α0j, is simply the random error term of a hospital-level linear regression model (7), and its variance should be expected to decrease with the addition of covariates. Furthermore, from the point of view of estimating the contextual effects, one would be interested in the changes because of the effects of cluster-level covariates while having individual-level covariates fixed.
4 ∣. CONCLUSION
In this letter, we have tried to clarify several important issues in this very useful primer for practicing statisticians and epidemiologists: (1) We caution readers that interpreting the effects of individual-level covariates as within-cluster effects could potentially be misleading; (2) we point out that taking the perspective of estimating contextual effects could help avoid the difficulty with the interpretation of cluster-level effects; (3) we demonstrate that while cluster variance may increase with the addition of individual-level covariates, the usual decrease in cluster variance with the addition of covariates observed in ordinary linear models should be similarly expected with cluster-level covariates in multilevel models, and discussed the impact of this result on modeling strategy.
ACKNOWLEDGEMENT
This work was supported in part by The National Institutes of Health and the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) (U10HD036790).
REFERENCES
- 1.Austin PC, Merlo J. Intermediate and advanced topics in multilevel logistic regression analysis. Stat Med. 2017;36(20):3257–3277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Neuhaus J, Kalbfleisch JD. Between- and within-cluster covariate effects in the analysis of clustered data. Biometrics. 1998;54(2):638–645. [PubMed] [Google Scholar]
- 3.Berlin JA, Kimmel SE, Ten Have TR, Sammel MD. An empirical comparison of several clustered data approaches under confounding due to cluster effects in the analysis of complications of coronary angioplasty. Biometrics. 1999;55(2):470–476. [DOI] [PubMed] [Google Scholar]
- 4.Begg MD, Parides MK. Separation of individual-level and cluster-level covariate effects in regression analysis of correlated data. Stat Med. 2003;22(16):2591–2602. [DOI] [PubMed] [Google Scholar]
- 5.DeLong ER, Coombs LP, Ferguson TB, Peterson ED. The evaluation of treatment when center-specific selection criteria vary with respect to patient risk. Biometrics. 2005;61(4):942–949. [DOI] [PubMed] [Google Scholar]
- 6.Rysavy MA, Li L, Bell EF, et al. Between-hospital variation in treatment and outcomes in extremely preterm infants. N Engl J Med 2015; 372: 1801–1811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Snijders TAB, Bosker R. Multilevel analysis: An introduction to basic and advanced multilevel modeling. 2nd ed. SAGE Publications; 2011. [Google Scholar]
- 8.University of Texas at Austin. Multilevel modeling tutorial: Using SAS, Stata, HLM, R, SPSS, and Mplus. The Department of Statistics and Data Sciences; March 2015. (https://stat.utexas.edu/images/SSC/documents/SoftwareTutorials/MultilevelModeling.pdf). [Google Scholar]


