Abstract
Intracellular drug delivery by rapid squeezing is one of the most recent and simple cell membrane disruption-mediated drug encapsulation approaches. In this method, cell membranes are perforated in a microfluidic setup due to rapid cell deformation during squeezing through constricted channels. While squeezing-based drug loading has been successful in loading drug molecules into various cell types, such as immune cells, cancer cells, and other primary cells, there is so far no comprehensive understanding of the pore opening mechanism on the cell membrane and the systematic analysis on how different channel geometries and squeezing speed influence drug loading. This article aims to develop a three-dimensional computational model to study the intracellular delivery for compound cells squeezing through microfluidic channels. The Lattice Boltzmann method, as the flow solver, integrated with a spring-connected network via frictional coupling, is employed to capture compound capsule dynamics over fast squeezing. The pore size is proportional to the local areal strain of triangular patches on the compound cell through mathematical correlations derived from molecular dynamics and coarse-grained molecular dynamics simulations. We quantify the drug concentration inside the cell cytoplasm by introducing a new mathematical model for passive diffusion after squeezing. Compared to the existing models, the proposed model does not have any empirical parameters that depend on operating conditions and device geometry. Since the compound cell model is new, it is validated by simulating a nucleated cell under a simple shear flow at different capillary numbers and comparing the results with other numerical models reported in literature. The cell deformation during squeezing is also compared with the pattern found from our compound cell squeezing experiment. Afterward, compound cell squeezing is modeled for different cell squeezing velocities, constriction lengths, and constriction widths. We reported the instantaneous cell center velocity, variations of axial and vertical cell dimensions, cell porosity, and normalized drug concentration to shed light on the underlying physics in fast squeezing-based drug delivery. Consistent with experimental findings in the literature, the numerical results confirm that constriction width reduction, constriction length enlargement, and average cell velocity promote intracellular drug delivery. The results show that the existence of the nucleus increases cell porosity and loaded drug concentration after squeezing. Given geometrical parameters and cell average velocity, the maximum porosity is achieved at three different locations: constriction entrance, constriction middle part, and outside the constriction. Our numerical results provide reasonable justifications for experimental findings on the influences of constriction geometry and cell velocity on the performance of cell-squeezing delivery. We expect this model can help design and optimize squeezing-based cargo delivery.
I. INTRODUCTION
An ideal drug loading technique needs to meet requirements such as simplicity, efficiency, delivery speed, dosage controllability, non-invasiveness, cell type independency, cargo material independency, and cost. Many strategies have been tested for encapsulating drugs and other bioactive agents into the cells considering these factors. These strategies can be categorized as macro- and micro-approaches.1 In macro-techniques, drugs are delivered to a bulk suspension of cells via conventional setups. The most popular approaches are membrane chemical perturbation2 and mechanical methods.3 Chemical methods rely on stimulating the phospholipid bilayer followed by oxidation or peroxidation of constituent lipids and insertion of amphiphilic peptides or proteins.4 In mechanical methods, different forces are used to disturb the cell membrane.1 Particle bombardment,5 fluid shear,6 osmotic pressure,7 and field-assisted delivery methods such as sonoporation,8 optoporation,9 thermoporation,10 magnetoporation,11 and electroporation12 are all mechanical strategies. Process complexity, cell viability, cytotoxicity, and inconsistent material delivery are major disadvantages of macro-techniques.1
Micro- and nano-encapsulation techniques have been introduced to tackle the shortcomings of macro-techniques. In these approaches, microfabrication and nano-technology are utilized to precisely control the delivery procedure.1 Intracellular delivery is carried out at the single-cell level with a high level of efficiency and throughput.1 Among different micro-techniques, recent studies13–17 show that drug encapsulation methods based on mechanical-membrane-disruption in microfluidic devices might be superior to others due to the simple setup and controllable throughput, and there are significantly lower chances of cells experiencing irreversible damage or death. Furthermore, if treated correctly, as there are no physical or chemical changes outside the cell membrane, there are lower risks of immune reaction. This vector-free microfluidic platform relies on cell membrane mechanical disruption to facilitate the target materials’ cytosolic delivery. This approach hypothesizes that the sudden deformation of the cell as it travels through constriction with a width smaller than its diameter creates transient membrane pores. The size of these pores depends on the shear and compressive forces exerted on the cell during squeezing. Drugs from the surrounding medium can diffuse directly into the cytoplasm throughout the life span of the pores. This approach could theoretically enable the diffusive delivery of any drugs small enough to pass through the pores.
There have been several works on generating pores in the cell membrane by squeezing them through narrow constrictions17,18 and ridges.19 Sharei et al. studied the shear-induced drug loading phenomena using a simple microfluidic device. The device consisted of 45 identical parallel microfluidic channels 30%–80% smaller than cell diameter. The rectangle channels had a width ranging from 4 to 8 μm and length ranging from 10 to 40 μm. Mechanoporation or rapid mechanical deformation of cell shape through microfluidic constrictions has been used to load different sizes of biomolecules, including core–shell (CdSe) quantum dots,20 siRNA,21 antigen,13 recombinant IFN regulatory factor 5,22 fluorescently labeled tRNAs,23 Janus kinase inhibitors,24 fluorescent tris-N-nitrilotriacetic acid probes (≈1 kDa),25 and cascade blue dextran polymer.26 While squeezing-based drug loading has shown success in loading drugs into various cell types, there is so far no systematic analysis on how different channel geometries and squeezing speed influence drug loading. Since the experimental visualization of nano-scale transient pores and their recovery processes in the buffer solution are difficult, a numerical study of this problem is important. To model this phenomenon, proper models for compound cell and damage should be introduced.
There have been few studies on numerical modeling of compound cell dynamics in shear flow and microfluidic channels. Leong et al.27 used the finite difference method (FDM) and the immersed boundary method (IBM) to model a nucleated cell entrance into a micro-channel. To model the compound cell, they introduced a compound droplet model standing for two interfaces called the cortex and the nuclear membrane. The model was made of interfacial tension and elastic modulus for both cortex and nuclear membranes. They showed that cell velocity reduces during entry and rises after it, which was in agreement with their experiments. They also concluded that the nucleus stiffness determines its position during squeezing. While a stiff core is pushed toward the cell front, a viscous (soft) nucleus is moved toward the rear. A two-dimensional compound vesicle behavior in the shear flow was also analyzed using the boundary integral method (BIM) by Veerapaneni et al.28 They showed that the nucleus size and stiffness significantly impacted tank treading and tumbling dynamics of the capsule. In another study, Kaoui et al.29 employed a lattice Boltzmann method (LBM) and the IBM to model a two-dimensional hybrid vesicle in shear flow between two parallel plates. They categorized different dynamic states of the cell based on the internal vesicle size. The front-tracking and droplet model was applied to quantify spherical compound capsule deformation in shear flow by Luo et al.30 Their results showed that compound capsules have smaller deformations as compared to homogenous capsules of the same size. They also analyzed the effect of the inner capsule size and capillary numbers on both outer and inner vesicles’ deformation. Luo and Bai31 also conducted a study similar to Ref. 30 to simulate non-spherical compound cells’ deformation in shear flow. The deformation of a capsule with a stiff nucleus as a model for eukaryotic cells was also investigated by Alizad Banaei et al.32 Neo-Hookean constitutive law was implemented to model the elastic membrane. FDM on the staggered grid was considered as the flow solver coupled with the cell model through an IBM. The effects of the bending stiffness of both cell and nucleus and viscosity ratio of inner and outer fluids on cell deformation were studied in this research. They observed that a compound capsule experiences smaller deformation compared with a simple cell. They showed that the compound vesicle shape is thicker in the middle portion causing it more challenging to pass through narrow passages. Casquero et al.33 studied the two- and three-dimensional rheologies of a nucleated cell as a representative for a white blood cell (WBC) and a circulating tumor cell (CTC) in both shear and parabolic flows in straight and narrowing channels. In this study, the standard finite element (FE) procedure, neo-Hookean constitutive law, and IBM were brought into play for numerical simulations. They showed the dependency of cell dynamics on the core filling fraction and capillary number. Recently, a high-performance computational platform called HARVEY was extended by Gounley et al.34 to study the shape change of a homogenous and compound cell inside constricted channels. This parallel platform uses a finite element method (FEM) for the cell model, the LBM as the flow solver, and the IBM to handle the fluid–structure interaction (FSI). The LBM–IBM–FEM framework results were in agreement with Luo et al.30 in the shear flow. They concluded that the inner membrane engages in two distortion modes: first, parallel with the flow direction in the constriction area and then perpendicular to the flow direction at the narrowing exit. Tan et al.35 simulated the nucleus effect with different stiffnesses on CTC deformation squeezing through a micropore by combining the LBM and a spring-connected network (SN) via an IBM. Their results indicated that a compound CTC translocation time increased concerning the model without the inner core. Rahmat et al.36 developed a three-dimensional Discrete Multi-Physics comprised of a meshless particle-based method that incorporated the smoothed particle hydrodynamics (SPH) and the mass-spring model to replicate a compound cell dynamics under a simple shear flow within a broad range of capillary numbers. The results disclosed that the compound cell deformation is changed when the nucleus size is sufficiently large. Volume-of-fluid (VOF) method, together with the octree-based adaptive mesh refinement algorithm,37 was also utilized to optimize the design of deformability-based microfilters for CTC detection. It was shown that the maximum instantaneous cell velocity always occurs when the nucleus passes through the exit of the microfilter channel. A more detailed review on the compound cell and droplet squeezing in narrow confinements can be found in Ref. 38.
Modeling shear-induced pore formation is complicated since cell damage happens at different scales, including nano-scale membrane pore initialization to microscale cell membrane rupture. Most of the cellular-level simulations for shear-mediated pore formations on the cell membrane are related to the modeling of hemoglobin release (hemolysis) from red blood cells (RBCs) due to high shear stress in either medical or microfluidic devices.39 Arora and co-workers40–42 introduced the first cellular model to quantify the RBC hemolysis in medical devices. In this model, a droplet model was used as the RBC. A tensor with arrays containing functions of strain tensor and vorticity tensor of the flow field over the pathlines was applied on the RBC model for calculating RBC deformation. The model had some ad hoc parameters, which should be determined by trial and error. Afterward, Vitale et al.43 presented a more complete model for pore formation on the RBC membrane under shear flow ranging from 4000 to 42 000 s−1. This model also contained some empirical parameters to compute the index of hemolysis (IH). Choosing the empirical coefficients improperly could even lead to a wrong prediction pore formation trend. Sohrabi and Liu44 presented a multiscale strained-based model that did not have any ad hoc parameters dependent on the device and operating conditions. In this model, the RBC-transient pore was determined based on RBC membrane local strain. Molecular dynamics (MD) and coarse-grained molecular dynamics (CGMD) correlations were applied to compute the pore radius. Instantaneous Hb diffused out of the pores was calculated by introducing a diffusion equation. The results of the model were in agreement with the model by Vitale et al.43 Nikfar et al.39,45 extended and modified the proposed model in Ref. 44 to calculate the hemolysis during microfiltration and different medical devices. The obtained results were in the range of corresponding experimental data. A novel cell damage index (CDI) was suggested by Gusenbauer et al.46 using LBM–SN–IBM to quantify the RBC mechanical hemolysis in a micrometer-sized channel. The proposed CDI embraced the effect of both RBC volume fraction (hematocrit) and channel geometry information. Luo and Bai47 modeled solute delivery from an elastic capsule flowing through microfluidic channel constriction. They combined the front-tracking method and FEM to simulate the two-phase flow field and calculate capsule membrane tension. They found that an increase in constriction length or a reduced constriction width enhanced the cell membrane’s release process during squeezing. A more detailed review on modeling transient pore formation can be found in Refs. 39,45, and 48.
In this article, for the first time, drug loading due to compound cell fast squeezing through a microchannel with sudden constriction is numerically modeled. The simulation is performed by coupling LBM and SN via a frictional-based IBM. To the best knowledge of authors, modeling and validating a hybrid capsule using mentioned tools have not been performed so far. Similar to Refs. 23,28, and 29, we use MD49 and CGMD50 to correlate the local areal strain on cell membrane and transient pore radius. A new mathematical model is introduced to quantify passive cargo diffusion into the cell upon squeezing. The proposed correlation does not have any empirical parameters depending on the flow regime and device geometry. The remainder of the article is structured as follows: after describing the problem, first the numerical algorithm and then the experimental setup are described. Next, the cell model is validated by simulating a compound capsule in a simple shear flow at different capillary numbers. Prior to the parametric study, the velocity and deformation of a compound cell inside a constricted channel are validated by our microfluidic experiment. Finally, the drug encapsulation into compound cell squeezing through a slit is investigated for different average cell velocities, channel constriction lengths, and channel constriction widths. The article is wrapped up by summarizing the findings and suggesting a potential future work.
II. PROBLEM DESCRIPTION
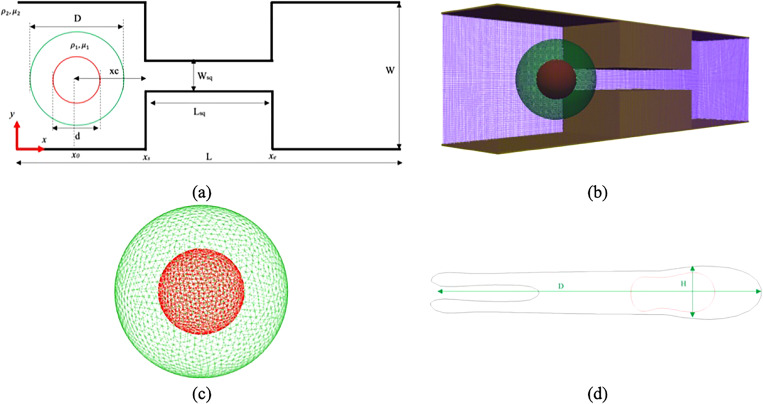
Figure 1(a) schematically illustrates the problem in this article. As the figure shows, the channel is composed of one constricted section and two identical wider sections. The entire channel length is L, while Lsq denotes the constriction length. The constriction width and total width of the setup are named by Wsq and W, respectively. Z stands for the channel depth. As it has been shown in other numerical studies,30,34,36 the nucleus can occupy a different portion of the cell cytosol such that . Here, we keep equal to 0.5. It has also been shown that the shear modulus ratio can vary between 0.01 and 100, i.e., .36 In this article, to make the nucleus stiffer enough compared to the cell, we assumed that is equal to 5.0. The fluid outside and inside the cell is the same, so . The fluid properties are listed in Table II. Consistent with numerical simulation carried out by Sharei et al.,17 the cell membrane diameter is equal to . In order to have a squeezing setup similar to CellSqueeze setup,14,17 the lengths of different parts of the computational domain are set as listed in Table I. Other parameters shown in Fig. 1(a) are set as follows:
| (1) |
FIG. 1.
Problem description: (a) a schematic view, (b) a domain computational grid, (c) a compound cell triangular network, and (d) a schematic view of the deformed cell.
TABLE II.
The values of different parameters used in this study.
| Parameter | Physical value | LB value |
|---|---|---|
| Cell stretching coefficient | 7 × 10−4 Nm−1 | 0.700 |
| Cell local area constraint | 2 × 10−5 Nm−1 | 0.020 |
| Cell global area constraint | 3 × 10−4 Nm−1 | 0.300 |
| Cell bending coefficient | 5 × 10−18 Nm | 0.005 |
| Cell volume constraint | 900 Nm−2 | 0.900 |
| Nucleus stretching coefficient | 7 − 35 × 10−4 Nm−1 | 0.700–3.500 |
| Nucleus local area constraint | 2 × 10−5 Nm−1 | 0.020 |
| Nucleus global area constraint | 3 × 10−4 Nm−1 | 0.300 |
| Nucleus bending coefficient | 5 × 10−18 Nm | 0.005 |
| Nucleus volume constraint | 900 Nm−2 | 0.900 |
| Equilibrium distance (rmin) | 1.0 × 10−6 m | 1.000 |
| Morse cut-off distance (rcut) | 1.0 × 10−6 m | 1.000 |
| Morse energy well width (α) | 2 × 10−6 m−1 | 2.000 |
| Morse energy well depth (ɛ) | 10−14 Nm | 10.00 |
| Fluid viscosity (μ) | 0.001 Pa s | 1.000 |
| Fluid density (ρ) | 1000 kg m−3 | 1.000 |
TABLE I.
Cell position and constrictions specification in different microchannels analyzed in this study.
| Lsq | x0(μm) | xs(μm) | xe(μm) |
|---|---|---|---|
| L1 = 0.15L | 20.3 | 27.50 | 37.50 |
| L2 = 0.30L | 15.3 | 22.50 | 42.50 |
| L3 = 0.45L | 10.3 | 17.50 | 47.50 |
III. NUMERICAL ALGORITHM
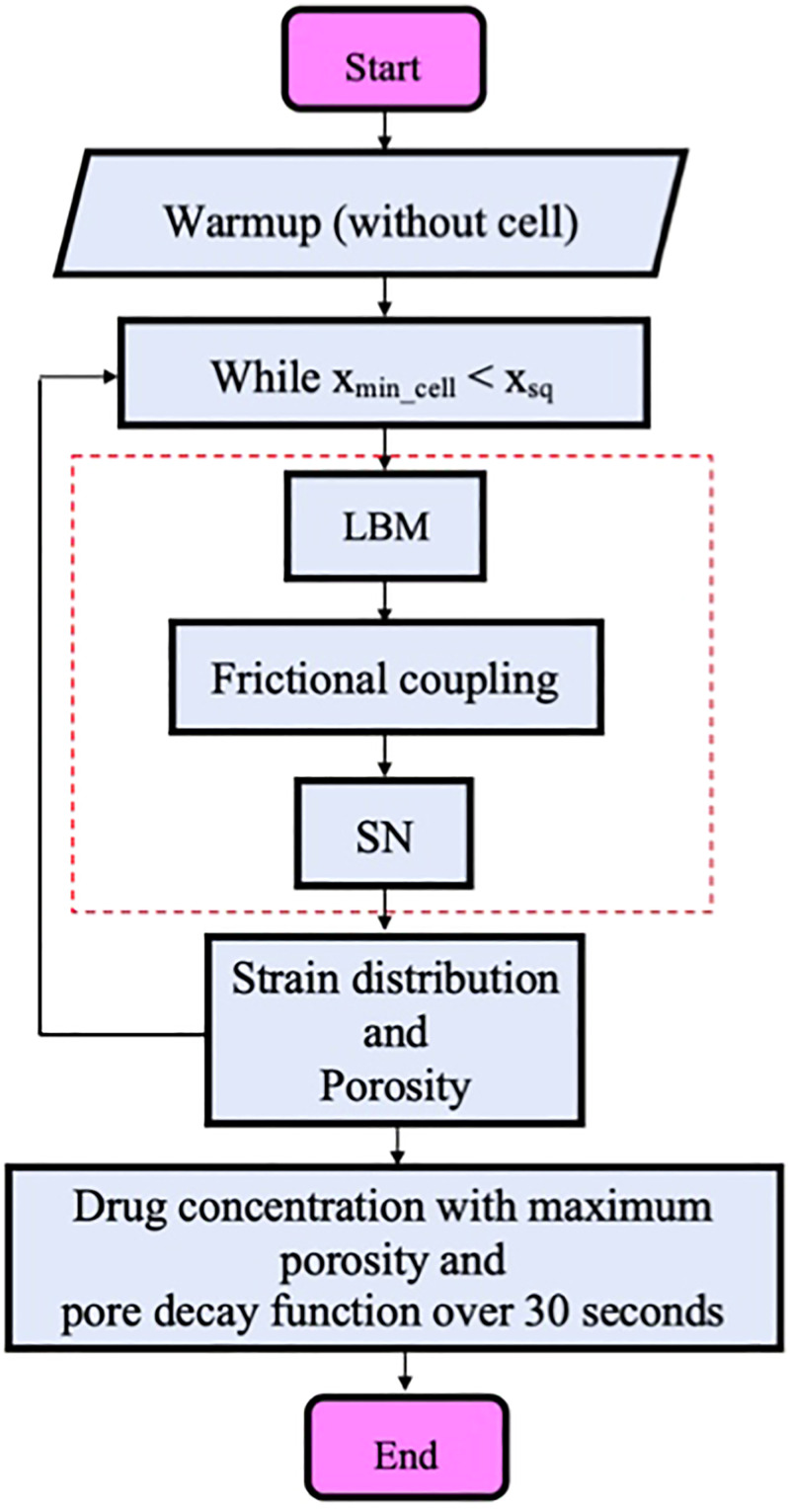
The flow chart of the numerical procedure is displayed in Fig. 2. As the flow chart shows, the numerical simulation is initiated by solving the flow field inside the microchannel without cell as the warmup solution. The warmup solution is continued until the steady-state flow field inside the channel is achieved. The reason for using a warmup solution is to avoid getting sudden unphysical changes on the compound cell membrane and its core due to unconverged flow field forces. The computational platform main loop is then started until the cell minimum horizontal coordinates are inside constriction, i.e., . We do not model the cell recovery process after squeezing because of the small time step in the LBM solver. In the main loop, the flow field is solved by an LBM solver. Flow field variables in terms of forces and velocities are coupled with the cell model through a friction-based IBM. The coupling part is shown inside a dashed rectangle in Fig. 2. In each iteration inside the loop, which stands for a time step, the local areal strain on each triangular patch and corresponding cell porosity are computed by MD and CGMD correlations. At the end of the squeezing process, we calculate the drug concentration with maximum porosity achieved during passage through constriction. The maximum porosity is used to calculate the drug concentration because the effect of compressive forces on pore closure is not very well understood. Our previous study on pore formation due to large deformation48 confirms that pores can remain open for a long time during high-speed stretching. It should be mentioned that using maximum porosity can overestimate the drug concentration. However, pores may remain open longer than 30 s which is used as the drug loading time scale in simulation. Therefore, these two factors can compensate each other and provide the reasonable value for cell drug concentration. Due to the complexity of visualization of drug concertation in the experiment, there is no experimental data on drug concentration inside the cell after squeezing. Based on the cell biology findings for membrane sealing dynamics, membrane repair kinetics occurs at about 30 s after a pore is formed. Also, experimental studies14,17 confirm that 70%–90% of the delivery process happens during first minute after the squeezing process regardless of the device design. It should be mentioned that this time scale can reach several minutes provided that there is no calcium in the buffer.17,18 We hence assume that all the cell membrane pores are circular, and they are decayed in 30 s based on an exponential function. A diffusion-based model is then used to calculate the cargo concentration inside the cytoplasm. We do not consider the effect of the drug molecule size in this study.
FIG. 2.
Numerical algorithm flow chart.
Our model is implemented in the free, open-source package ESPResSo version 4.1.4.51 ESPResSo uses parallelization computations and can be used on desktop machines, clusters, and supercomputers with hundreds of CPUs. All the simulations in this study are performed on a workstation with 3.2 GHz with 12 Intel Core-i7 CPUs and 16.0 GB RAM. ESPResSo has some modules to support GPU acceleration. In this package, C++ source codes are controlled by scripting language Python. For modeling membranes, we use PyOIF52–54 that provides validated computational models for cell flow modeling. The PyOIF module is integrated into ESPResSo with some modifications and is available under the GNU General Public License terms. Like ESPResSo, PyOIF is combined C++ codes in the software core and Python scripting to control the core. It is worth mentioning that implementing and validating the compound cell model have not been carried out in mentioned packages.55 The simulation works with a different set of units based on lattice Boltzmann (LB) units. To convert physical units to LB ones, the following scales are taken into account for time [t], length [L], and force [F], respectively:
| (2) |
For example, in all simulations, the time step is set to 0.01, equal to . In Secs. III A–III D, different components of the numerical approach are explained in detail. The results are visualized by ParaView version 5.8.0-RC1.
A. Flow solver
As it was mentioned, LBM is here used as the flow solver. This method is extensively used in fluid mechanics and computational hemodynamics.52,54,56 In this approach, the Boltzmann kinetic equation is solved instead of Navier–Stokes equations.57 The Boltzmann kinetic equation unknown is the distribution function for fictitious particles. Macroscopic properties can also be computed after finding the distribution function. The lattice is made of cubic cells. The lattice is unalterable during the computational procedure. D3Q19 version of the LBM (three dimensions with 19 discrete velocities) is utilized in this article. A structured grid with constant spacing is also constructed with a set of discretized velocities, . The LBM dynamics in the presence of an external force involve streaming and collision steps can be written as follows:57
| (3) |
where is the time step, is the relaxation time, and is the equilibrium function related to macroscopic variables velocity and density. is the external force applied to the fluid. It should be mentioned that is essential where the existence of the cell domain is replaced through force density. Also, is as follows:
| (4) |
is the lattice speed of sound. Macroscale density and velocity can be calculated as follows:
| (5) |
B. Compound cell model
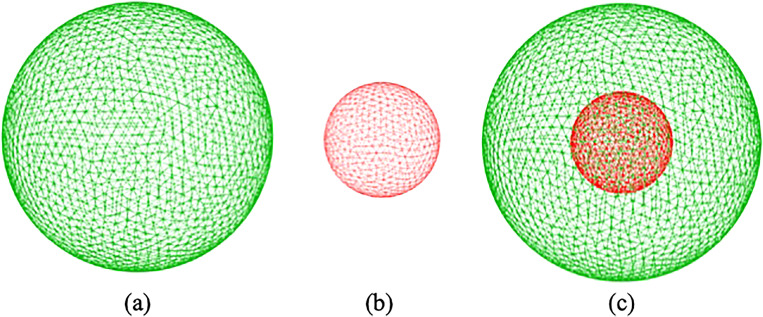
In this study, the compound capsule is made of two concentric spherical membranes immersed in the fluid domain (Fig. 3). The fluid interaction advects the boundaries of the cell and its core. This method is widely used in the modeling of biological problems.45,52,54 The outer and inner vesicles are discretized to triangular meshes, as shown in Fig. 3. Geometrical parameters such as mesh edge, mesh face, and the angle between adjacent faces are implemented using proper mathematical relations to model stretching, bending stiffness, and other cell characteristics. The nodal points on the membrane, which are called immersed boundary (IB) points, are moved by Newton’s equation of motion as follows:
| (6) |
in which is the coordinates vector of IB points. is the IB point acting force that comprises two terms: fluid forces and elastomechanical forces from the compound capsule forces. The fluid-induced forces are described in Sec. III C, and the cell force field is explained here.
FIG. 3.
Spring connected network for (a) cell membrane, (b) nucleus, and (c) compound capsule.
To capture the membrane properties, we use different moduli acting in the spring network. The first one is the stretching modulus. The stretching force is nonlinear and applied between two mesh points A and B symmetrically. This force for point A can be written as follows:52,53
| (7) |
is the stretching coefficient, is the unit vector pointing from A toward B, , and stands for neo-Hookean nonlinearity. is the initial or relaxed length of mesh edge AB, whereas is the present edge AB length. is edge extension or compression. The second class of moduli are area constrain moduli. To implement these restrictions, we compute the surface variations of triangle ABC from resting condition . The area constrain is applied by assigning a shrinking/expanding force for every vertex,52,53
| (8) |
where is the area coefficient and is the unit vector emitting from the centroid of triangle ABC toward vertex A. The same calculations are employed for area forces on vertexes B and C. The area force should be very restrictive; therefore, a global area force is also applied to the cell,52,53
| (9) |
As can be seen, the area force is divided into two parts: local and global parts . The third force is called the bending force. The source of this force is changing the angle between two neighboring triangles. Assuming as the resting angle between two adjacent triangles, the bending force can be related to angle deviation as below:52,53
| (10) |
is the unit normal vector to the triangle ABC. The last force is the volume force to keep the whole volume constant. This force is also a global force. This force is related to triangle ABC and divided into three separate parts and applied at triangle vertices,
| (11) |
where is the volume coefficient. stands for volume change between the current state (V) and initial state . is also the unit normal vector to the plane ABC pointing inside the cell. The physical values and lattice Boltzmann values of the mentioned moduli used in this study for cell and nucleus are listed in Table II. In the table, the cell and nucleus values are differentiated by c and n indices, respectively. In the SN model, different moduli can be related to macroscopic properties as follows:52,53
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
where G, K, Y, and are shear modulus, compression modulus, Young’s modulus, and Poisson’s ratio, respectively. is the macroscopic bending modulus measured by micropipette aspiration. Finally, to complete the compound capsule model and preserve the nucleus inside the cell, a repulsive Morse potential is used between vertices on the cell and nucleus membranes as follows:
| (17) |
Here, r is the distance between cell membrane points and nucleus points, is the equilibrium distance, and is the energy well depth. Also, determines the potential width. For , there is no interaction between cell and nucleus and . The Morse potential parameter values can be found in Table II.
C. Frictional fluid-cell coupling
In this article, the interaction between fluid and IB points in the SN model is handled through dissipative or frictional coupling.57 This approach works based on the drag flow applied on the cell and nucleus mesh points. The drag force is comparable with the velocity difference between lattice points (u) and IB points as follows (v):
| (18) |
Here, ξ is a friction coefficient, and it is expressed in . It should be noticed that linear interpolation is utilized for calculating in the cell points based on neighboring lattice velocities. This technique naturally guarantees the no-slip conditions between fluid and membranes because it enforces minimal velocity difference between fluid and soft membranes. The prevalent friction coefficient role is to convey the drag force of the fluid onto the cell membrane and vice versa. does not depend on any physical quantity and is completely phenomenological. Hence, we should identify its proper value.58 It was shown that the friction coefficient fair value is a function of different parameters.58 It has been shown that for a cell constructed of n mesh points and with the surface area of S, the friction coefficient can be computed as follows:
| (19) |
Reference values can be found in Ref. 59. These values also depend on fluid density and viscosity. For example, is equal to for , , , and . We assume that the inside and outside of the cell are occupied with the same fluid (see Table II for fluid properties). In the simulations, is the same for both inner and outer membranes. To have equal for both membranes, they should have the same . For the coupling of fluid and cell, enters as a part of in Eq. (6). The coupling is mutual, so the opposite force is exerted on the fluid and enters [Eq. (3)].
D. Drug loading model
As the compound capsule squeezes through constriction, it experiences deformation due to fluid-induced forces and geometrical parameters, such as constriction length and constriction width. Pore formation at the molecular level is a statistical phenomenon.48,49,60 There are myriad MD and CGMD simulations to understand the physics of the pore formation in lipid bilayers.50,61–63 Similar to our previous work,39,44,45 the study by Koshiyama and Wada49 is used to compute the pore probability as a function of areal strain,
| (20) |
where and are mean and variance of critical areal strain, respectively.44 To relate the triangular mesh areal strain to the pore radius , the theoretical correlation obtained from CGMD simulations in the study by Tolpekina et al.50 is utilized,
| (21) |
Here, is the intact tensionless membrane area without a pore; is the compressibility modulus of membrane; and is the line tension coefficient. Sharei et al.17 observed that 70%–90% of the loading process happens in the first minute after the treatment process. The reported time scale depends on neither the operating conditions nor system design. Also, McNeil and Steinhardt64 reported that membrane recovery is completed at about 30 s after a transient injury is generated. Our previous work on the pore dynamics under large deformations48 reveals that pores can remain open for a long time during high-speed stretching. Therefore, we assume that the cell reaches the maximum porosity during the squeezing process. This assumption can lead to overestimation of drug concentration. However, there is no experimental data on drug intensity measurement inside the cell after fast squeezing. Based on the experimental observations, we assume that all the pores, regardless of their size, are healed in 30 s with an exponential decay function, i.e., in which is the initial pore area. is the decay rate and can be determined assuming that after 30 s. Drug loading is a diffusion-driven process.17 Therefore, the drug concentration inside the cell cytoplasm can be governed as follows:
| (22) |
where C and are drug concentration inside the cell and the effective diffusion coefficient, respectively. In this study, the effective membrane diffusivity is considered constant throughout the treatment process and equal to 3 × 10−15 m2/s.17 The membrane diffusivity was obtained by simulating the case of a delivery material diffusing into a porated cell that is suspended in a buffer-containing delivery materials.17 They also simulated the case of delivery material diffusing out of a previously delivered cell into a clean buffer (i.e., one with no delivery material). The information that corresponds to the material loss and the loaded material were plotted and used to estimate the corresponding membrane diffusivity. Experiments were performed at 20 °C. However, it was declared that delivery efficiency was minimally affected by temperature.17 Equation (22) is integrated over a control volume constructed on the cell membrane. Using the divergence theorem, the volume integrals are then converted to surface integrals. A surface integral on the cell surface is subsequently approximated as follows:
| (23) |
is equal to 0 since nothing diffuses out from cell cytosol. We also assume that the drug concentration in buffer solution does not change during the process because the cell size is much smaller than the buffer solution volume. Therefore, we can write as follows:
| (24) |
is the cell membrane thickness determined based on the local areal strain . More details on the calculation of can be found in our previous article.44 By substituting Eq. (24) and pore decay function into Eq. (23) and solving the resulting ordinary differential equation (ODE) assuming C = 0 at t = 0, we have
| (25) |
IV. EXPERIMENTAL SETUP
In this research, the numerical results for cell squeezing are validated by our experimental results. In Secs. IV A–IV C, the details of the experimental setup are described.
A. Device fabrication
The microfluidic channels are fabricated using the standard UV lithography method. First, the channel drawings are made using AutoCAD. Chrome masks are fabricated using a direct laser writing tool, DWL 66+ (Quattrone Nanofabrication Facility at the Singh Center for Nanotechnology, University of Pennsylvania). The mask is used to make the master pattern in SU-8 2007 (MicroChem) coated on a silicon wafer. The fabrication process is done at the Center for Photonics and Nanoelectronics (CPN) at Lehigh University. SU8-2007 is spun on a silicon wafer at 1000 rpm. After soft bake, the SU-8 is exposed to UV light using Suss MA6/BA6. After development, the SU-8 patterns are hard baked at 150 °C for 30 min. Sylgard 184 PDMS is mixed with the curing agent at a ratio of 10:1 and poured over the photoresist master. After degassing the PDMS for 2 h, it is left to cure overnight in the oven. The inlets and outlets are punched out of the PDMS channel before attaching it to a large coverslip with oxygen plasma treatment.
B. Cell culture
Human prostate cancer cells, PC-3 (ATCC, USA), are cultured with F-12k media (ATCC, USA) with 10% fetal bovine serum (Sigma Aldrich, USA) and 1% penicillin–streptomycin solution (Sigma Aldrich, USA) at 37 °C with 5% CO2 in the incubator. The morphology of the cells is analyzed under the microscope. To harvest the cells for squeezing experiments, the cells are detached with diluted trypsin solution (Sigma Aldrich, USA) and pelleted at 200 × g. The collected cells are washed with phosphate-buffered saline (PBS) twice before they get resuspended with PBS for the following use.
C. Cell squeezing and imaging
After the PC-3 cells are resuspended in PBS, the sample is loaded into a syringe and placed on a Harvard PHD 2000 syringe pump. The channels are first treated with bovine serum albumin (BSA, Sigma Aldrich, USA) to avoid cell adhesion to the PDMS wall. Then, the syringe is connected to the inlet of the channel, and the syringe pump is used to generate the flow rate. The images are acquired with an Olympus IX70 microscope with a 35× SPlan objective using a XIMEA CB120CG-CM color CMOS camera. The video is analyzed with Fiji.
V. RESULTS AND DISCUSSION
Having shown present algorithm can generate results similar to other numerical approaches30,34,36 for modeling compound cell in the shear flow at different capillary numbers (see the supplementary material), the drug loading process via fast squeezing is modeled in this section. In the corresponding experiment,17 45 identical, parallel microfluidic channels were utilized to squeeze the cells, and the results were reported based on the cell average velocity in each channel. Here, a constant force is applied to the LB points to drive the fluid and create the target cell average velocity over the squeezing process. Target cell average velocity is calculated based on the distance passed by the cell during squeezing time. Periodic inlet/outlet boundary conditions are also employed. To avoid cell collision with channel walls, a repulsive potential called soft-sphere potential is applied between wall and membrane points as follows:51
| (26) |
where r is the inter-particle distance and a is the potential energy. For , is equal to zero. In our simulation, is sufficient to prevent the cell from colliding with the channel wall. It is worth mentioning that a fixed time step is considered for all the simulations (0.01[t] = 10−8 s). Following the procedure explained in the supplementary material, the simulations were performed for 500, 1000, 1500, 2000, and 3000 vertex points on the cell membrane. The results revealed that no remarkable change can be observed beyond meshes with 2000 points. To track cell deformation during squeezing, H and D are calculated as depicted in Fig. 1(d). The simulation continues until the whole cell leaves the constriction.
A. Squeezing validation
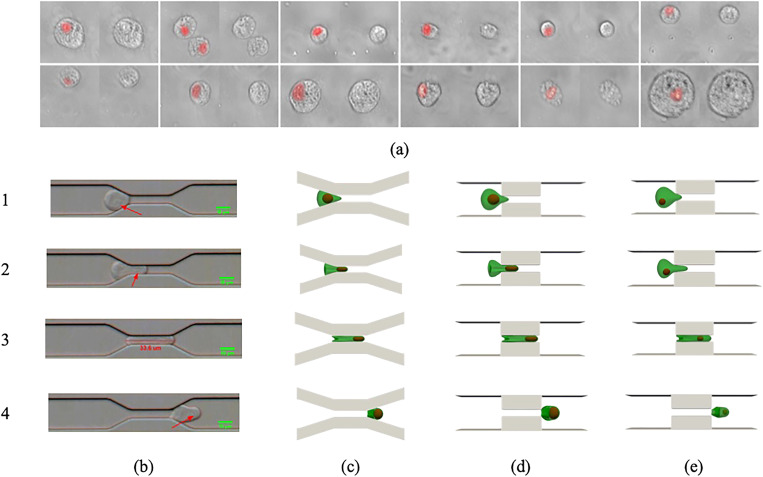
To ensure that our numerical platform can generate physical results, we compare the squeezing of a compound cell with the squeezing of cultured human PC-3 cells with diameter through a slit with length and width as shown in Fig. 4. The nucleus size is nearly half the cell membrane diameter. In the experiment, the average cell velocity reaches in the constriction. The cell squeezing process is recorded in a microfluidic channel with a high-speed camera and is compared with the cell squeezing pattern found from simulation. The nucleus of the PC-3 cells is first analyzed by comparing several images of stained PC-3 cells [Fig. 4(a)]. The identification of the nucleus in bright-field high-speed recording is done with manual observation based on stained images.
FIG. 4.
The numerical snapshots together with experimental ones are displayed in Figs. 4(b) (Multimedia view) and 4(d) (Multimedia view). The nucleus position in experimental snapshots is shown by an arrow. As it can be seen, there is an acceptable agreement between results. However, the constriction angle is different in the simulation and experiment, because the cell is very close to the constriction entry, the constriction profile will not influence the numerical results considerably. As Figure 4(c) depicts, the snapshots of the cell shape in gradual constriction are similar to those in sudden constrictions. It should be mentioned that in the experimental studies,14,17 only the effect of constriction length and width was analyzed. Similarly, in this study, we just focus on the impact of length and width of the constriction. In both experimental and numerical results, because of strong viscous force in the narrow part (high-velocity region), a protrusion is formed at the membrane tip as it is pushed toward the slit section. Given the squeezing velocity, the cell elongation lasts up to a specific point inside the constriction. After that when the cell is almost completely inside the channel, the membrane tail velocity becomes larger than the membrane tip velocity. Therefore, the cell tail moves toward the cell tip. As the cell passes the constriction area, the cell head starts expanding at the other side of the micropore. The dynamics of the nucleus can also be understood from both simulation and experiment. When the cell tip touches the narrow channel, the nucleus first adjusts its shape to enter the slit. Inside the constriction, the nucleus moves faster than the cell because it is closer to the high-speed zone or the channel centerline. As a result, the nucleus moves toward the cell tip as it comes out of constriction. To show the effect of the nucleus size and position on the compound cell deformation, the squeezing of a compound cell with the same size as shown in Figs. 4(c) and 4(d) with smaller nucleus that is not located in the cell center is simulated [Fig. 4(e)]. As it can be seen, the cell and nucleus dynamics are similar to cases shown in Figs. 4(c) and 4(d) except for minor differences in cell diameters. Table III lists the axial (D) and vertical (H) cell diameters corresponding to the snapshots shown in Fig. 4. As it can be observed, good agreement exists between experimental and numerical results regardless of device design and nucleus size and position. Such quantitative comparison for other cell types can be found in other articles.45,65 It is worth mentioning, in all the simulations, that cell volumes remain constant due to large volume forces (Table II).
TABLE III.
Comparison between horizontal (D) and vertical (H) cell diameters in experiment and different numerical simulations shown in Figs. 4(c)–4(e).
| Position | (b) | (c) | (d) | (e) | ||||
|---|---|---|---|---|---|---|---|---|
| D (μm) | H (μm) | D (μm) | H (μm) | D (μm) | H (μm) | D (μm) | H (μm) | |
| 1 | 19.73 | 16.14 | 20.15 | 17.04 | 20.43 | 17.14 | 20.37 | 17.24 |
| 2 | 25.15 | 13.47 | 24.37 | 13.84 | 24.39 | 13.89 | 24.31 | 13.93 |
| 3 | 32.57 | 5.00 | 32.38 | 4.98 | 32.44 | 4.98 | 32.39 | 4.97 |
| 4 | 19.76 | 11.79 | 18.93 | 10.47 | 18.95 | 10.48 | 18.97 | 10.49 |
B. Squeezing velocity
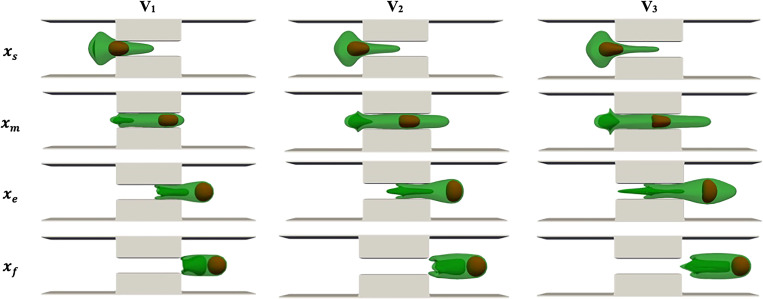
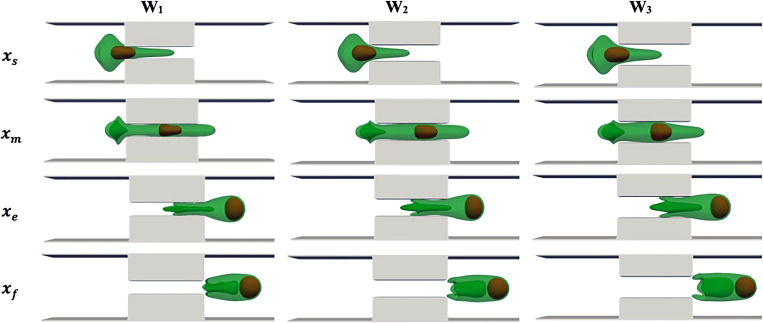
The effect of cell average velocity on drug loading is examined in this section. The results are reported based on squeezing velocity because experiments in Refs. 14 and 17 have used the cell average velocity in multiple individual channels to report the results. We adjust the external force applied on the LB point to generate different average cell velocities, including , and . The range of squeezing velocity is within the range reported in Refs. 14 and 17. Here, the squeezing length and width are fixed at and , respectively. Figure 5 shows the simulation snapshots at different velocities when the cell center is approximately located at constriction beginning , channel center , constriction end , and process end . The cell and nucleus dynamics are similar to what explained in the squeezing validation part. The complicated structure of the cell tail can be related to the velocity difference between the tail center (located in high-speed area) and the tail edge (located near the walls). Increasing the velocity results in a more complicated structure in the cell tail due to higher velocity difference in the center and the edge of the cell tail. As squeezing velocity increases, the cell head expansion at the constriction exit becomes more significant due to a stronger driving force on the cell. The final cell length and width are also larger at higher squeezing velocities. As the squeezing velocity increases, the nucleus deformation increases and reconciles with the micropore width more easily. At lower squeezing velocity, the nucleus is very close to the cell head because of lower cell velocity as compared to the nucleus. Therefore, the nucleus exerts a larger force on the cell head at low velocities due to the cell and nucleus proximity. It should be mentioned that after the cell back leaves the micropore, the cell would start recovering/expanding in the buffer solution. Cell shape recovery is not modeled here due to its larger time scale compared to the simulation time scale.
FIG. 5.
Cell shapes during squeezing at different velocities with Lsq = L2, Wsq = 0.4 D.
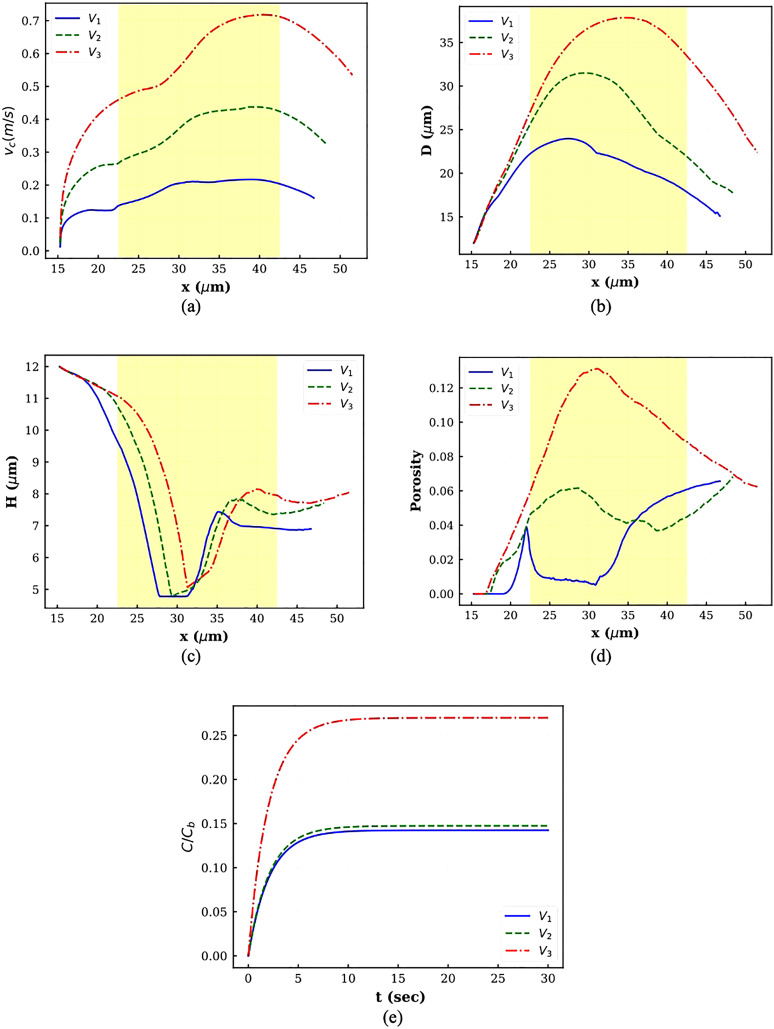
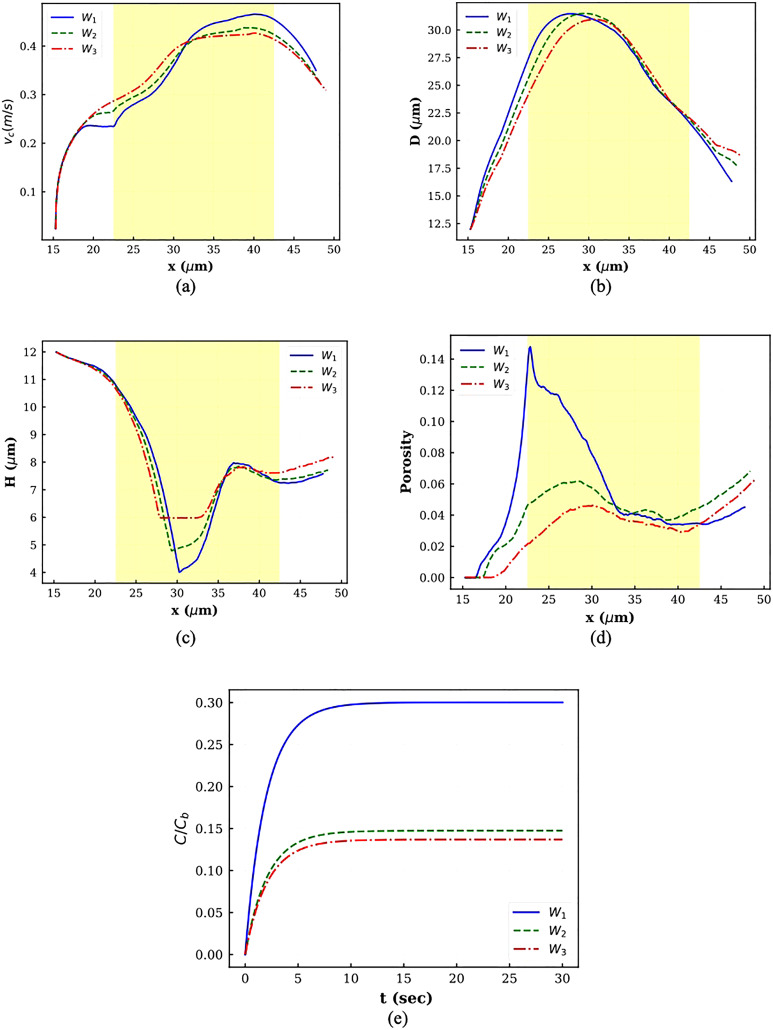
The instantaneous cell center velocity is plotted in Fig. 6(a) for different squeezing velocities. In all the graphs, the constriction zone is shaded. As the figure indicates, the cell starts moving at . For all the cases, the velocity graph has four regions. In the first region, the velocity goes up at a milder rate, while in the second zone, the velocity increase happens at a higher rate. In the third region, the velocity remains almost constant. Finally, the cell center velocity decreases sharply. The first zone happens when the cell is trying to occupy the slit. During this stage, the velocity increases at a lower rate since the cell shape is not consistent with the micropore. As the squeezing velocity increases, this step takes a longer time because the cell tail has a sharper edge in higher squeezing velocity due to sudden deformation (Fig. 5). After shape change occurs thoroughly, the velocity increases faster since there is no objection against the cell movement. The velocity remains constant until the cell head locates nearly at . At this point, the cell center velocity decreases since it enters the high-pressure or low-velocity region.
FIG. 6.
Plots of different parameters for squeezing at different velocities: (a) cell center velocity, (b) horizontal diameter, (c) vertical diameter, (d) porosity, and (e) normalized drug concentration.
The axial and transversal cell diameter variations are depicted in Figs. 6(b) and 6(c), respectively. As Fig. 6(b) shows, in all the cases, first, the axial diameter increases and then decreases. As the velocity goes up, the cell elongation lasts a longer time. The transversal diameter variations have a reverse trend. It decreases during squeezing through constriction and then increases sharply on the other side of constriction. The transversal diameter reduction is slightly smaller in higher velocities because the cell volume should remain constant. The cell deformation results in pore formation and porosity. As Fig. 6(d) shows, at V3, the porosity first rises until the cell center reaches . Afterward, the porosity experiences reduction due to cell shrinkage. At lower velocities, in addition to cell deformation, the nucleus is an important player. At V1, a sharp jump is observed near as a result of strong interaction between inner and outer membranes since both cell and nucleus are trying to go inside a constricted area smaller than their diameter. The porosity then falls and remains nearly constant until the cell center meets the channel center. In this region, there is no considerable interaction between the cell and the nucleus. Afterward, the porosity increases because the cell and nucleus are very close to each other. Therefore, the cell membrane feels a large force from the stiff nucleus, which leads to an increase in porosity. At V2, as cell elongation continues, the porosity increases. Along with cell axial reduction, the porosity also diminishes. However, when the cell head reaches near , due to the enormous interaction between the cell and the nucleus, the porosity starts going up. As it can be observed, at V1 and V2, the cell porosity increases even after the cell leaves the constriction because the velocity difference between the cell and the nucleus is negligible, and they have large interaction with each other. Figure 6(e) contains plots for drug loading variation within 30 s after squeezing. As the corresponding graphs show, the intracellular drug concentration increases with increasing squeezing velocity. Moreover, as the figure shows, as the velocity increases, the cell needs more time to reach a steady drug concentration value. These observations are in agreement with experimental findings in Refs. 14 and 17. Figure 6(e) shows that by increasing velocity from V1 to V2, the loaded drug does not increase significantly, while increasing velocity from V2 to V3 results in around 60% enhancement in drug loading. It is worth mentioning that using average porosity decreases the normalized drug concentration inside the cell. For example, at V3, normalized drug concentration obtained by average porosity reaches to 14% over 30 s.
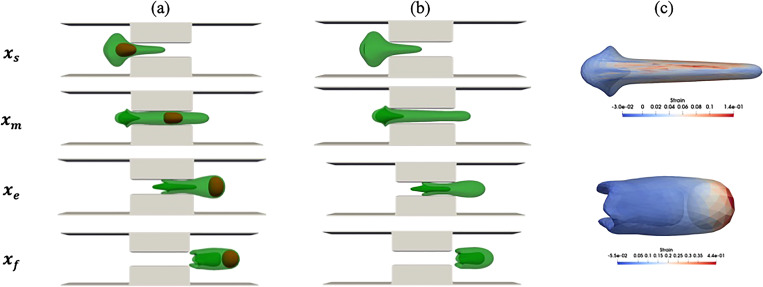
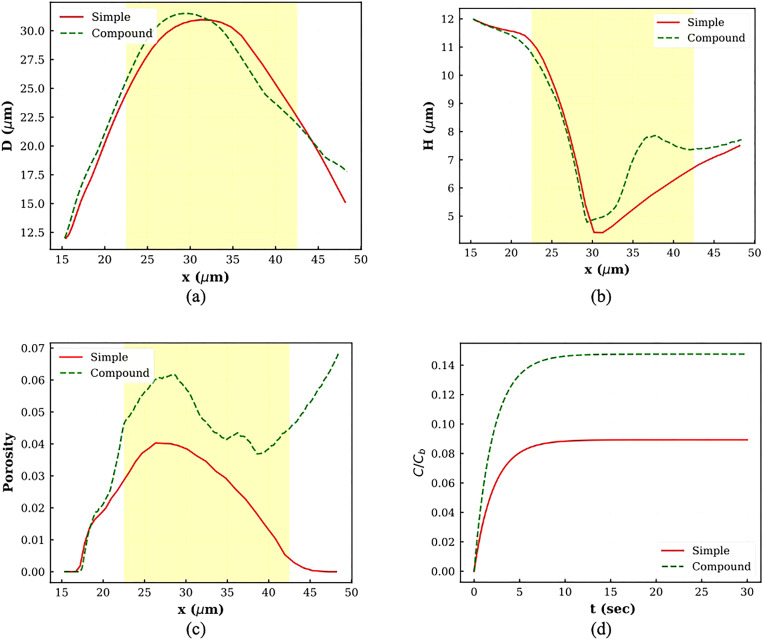
To show the effect of the nucleus on cell squeezing dynamics, the compound cell shapes at V2 are compared with simple cell shapes under the same conditions. As Figs. 7(a) and 7(b) show, the nucleus presence causes the compound cell membrane to have thicker width than simple cell membrane. Also, the compound cell length during squeezing is larger than the simple cell length due to interaction between the nucleus and the cell membrane. As the figure shows, the nucleus does not have a significant effect on cell tail configuration. Different diameters, porosities, and drug concentrations for both compound and simple cell are compared in Fig. 8. Compatible with what were observed in Figs. 7(a) and 7(b), both compound cell length (D) and compound cell width (H) are larger than the simple capsule due to interaction between the cell and the nucleus [Figs. 8(a) and 8(b)]. As Fig. 8(c) shows, the trend of compound cell porosity is completely different from that for the simple cell. As discussed earlier, for a compound cell, the porosity has more complex behavior and increases even after cell leaves the constriction due to interaction between the cell and the nucleus. However, the porosity of the simple capsule first increases because the cell length increases and then decreases as a result of cell length reduction on the other side of constriction. The areal strain distribution at the location of maximum porosity for both simple cell and compound cell is shown in Fig. 7(c). Considering Figs. 7(c) and 8(c), the maximum porosity in the compound cell is due to strong interaction between the cell and the nucleus at the end of the process, while simple cell maximum porosity is observed when the cell has the maximum length in the middle of the channel. Also, maximum porosity of the compound cell is larger than simple one. Figure 8(d) shows that normalized drug intensity inside the compound capsule is about 75% larger than drug concentration inside the simple capsule.
FIG. 7.
Comparison between compound and simple capsule at V = V2, Lsq = L2, and Wsq = 0.4 D: (a) compound cells, (b) a simple cell, and (c) maximum areal strain distribution at the maximum porosity location.
FIG. 8.
Plots of different parameters for comparison between compound and simple cell squeezing: (a) horizontal diameter, (b) vertical diameter, (c) porosity, and (d) normalized drug concentration.
C. Squeezing channel width
To quantify the channel width effect on the drug loading process, we simulate compound capsule squeezing through channels with three different constriction widths, i.e., , , and . D is the cell diameter. In this section, the cell average velocity is kept constant and equal to . The constriction length is also fixed at . The cell shapes at different locations inside the described channels are portrayed in Fig. 9. It can be seen that cell protrusion is more obvious for narrower channels. Since the cell average velocity is identical, a bigger force should be applied to drive the cell through narrower micropores. Therefore, the cell membrane is stretched more in smaller constriction. Cell elongation is observed until the cell can take up the whole constricted area. For narrower constrictions, the cell tail has a sharp edge due to the large driven force. The cell enlarges as its head is sufficiently on the other side of constriction. Cell expansion is more significant for narrower channels due to the area difference after constriction. At the end of the process, the cell dimensions are larger in channels with wider constrictions. Since the cell average velocity is almost constant, the distance between the cell and the nucleus remains the same in all the test cases. However, the nucleus is vertically compressed more in smaller constriction.
FIG. 9.
Cell shapes during squeezing through constrictions with different widths at V = 400 mm/s and Lsq = L2.
The cell center velocity vs the center location is displayed in Fig. 10(a) for different constriction widths. In all the graphs, the constriction zone is shaded. All three graphs have the same trend as discussed in Sec. V B. As the figure shows, for smaller constriction, the center velocity at is less than others because the cell deforms more to enter constriction. However, the cell velocity inside the constriction is higher for smaller constriction. As Fig. 10(b) demonstrates, and consistent with Fig. 9, the axial diameter increases until the cell center is near , and after that, the axial diameter decreases. Figure 10(c) shows that cell transversal diameter decreases up to . The transversal diameter reduction is proportional to constriction width. Porosity graphs for different cases are displayed in Fig. 10(d). As shown in the figure, the porosity increases as the cell tries to adapt to the constriction. Over this time, the cell is stretched, and meanwhile, there is considerable interaction between the cell and the nucleus. The cell–nucleus interaction is larger in narrower channels due to small space between the nucleus and the cell. Similar to Sec. V B, when the cell leaves the constriction, the porosity again increases due to the small distance between the cell and the nucleus. For W2 and W3, the maximum porosity is achieved when the cell is completely outside the constriction, while for W1, maximum porosity happens when the cell is trying to go inside the narrow region. Maximum porosity decreases with increasing squeezing width. The normalized drug concentration obtained using maximum porosity during squeezing for different cases is shown in Fig. 10(e). As the figure shows, the drug concertation is a function of maximum porosity and increases with channel width reduction. The same trend was observed in experimental studies.14,17 It should be mentioned that there is no distinct difference in loaded drug between constriction width of W2 and W3, while the drug concentration is doubled by changing from W2 to W1.
FIG. 10.
Plots of different parameters for squeezing through constrictions with different widths: (a) cell center velocity, (b) horizontal diameter, (c) vertical diameter, (d) porosity, and (e) normalized drug concentration.
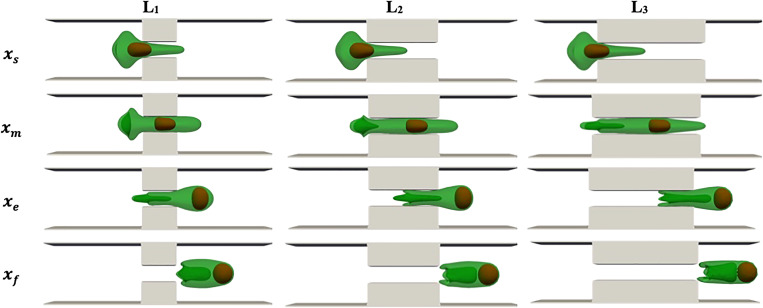
D. Squeezing channel length
Finally, to check the role of squeezing length on the drug loading procedure, we model the squeezing process at a constant flow rate and constriction width for three different constriction lengths, namely, , , and . The simulation snapshots when the cell center is at different locations are shown in Fig. 11. The dynamics of the cell and the nucleus are quite similar to what was seen in Secs. V A–V C. As the figure shows, the cell is stretched more in the channel with a larger constriction length due to higher force to drive the flow inside the channel. For longer constriction lengths, the nucleus has more time to reach the cell front and apply a pushing force to the membrane tip.
FIG. 11.
Cell shapes during squeezing through constrictions with different lengths at V = 400 mm/s and Wsq = 0.4 D.
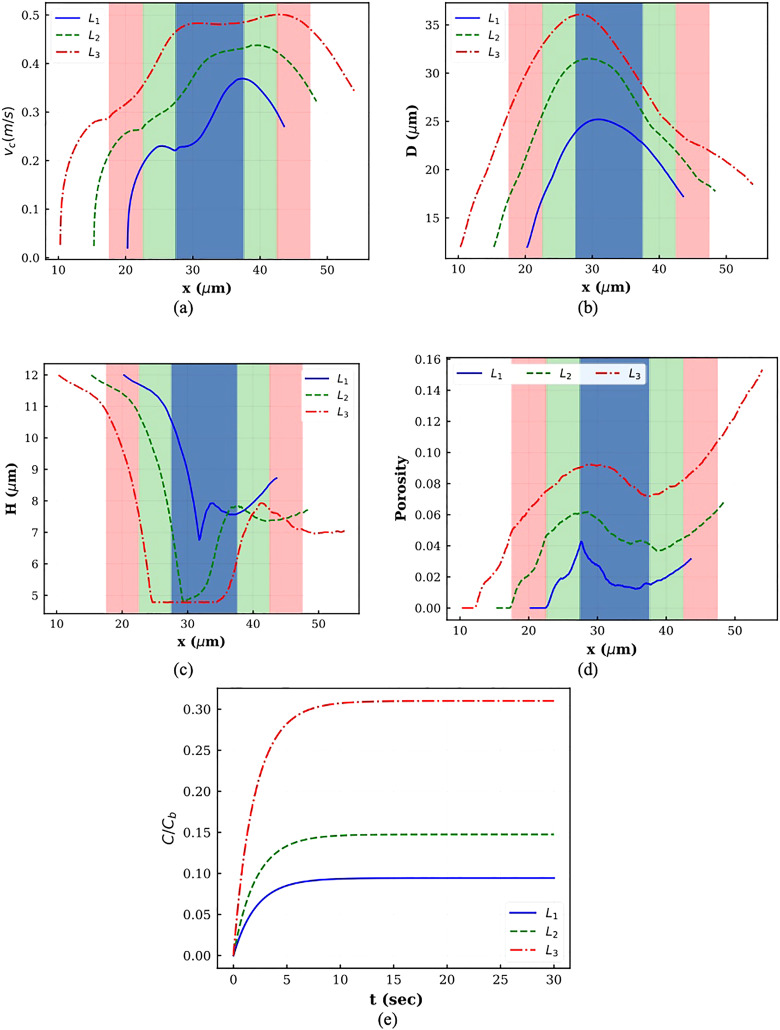
The cell center velocities corresponding to the cases shown in Fig. 11 are displayed in Fig. 12(a). Constriction regions in various channels are shaded by different colors. The trend of all three graphs is identical and similar to what was observed in Secs. V A–V C. As the graphs show, the instantaneous cell velocity increases with increasing constriction length. To have a constant average velocity during the process, the cell should move faster in longer constrictions. As a result of velocity increase, both axial and vertical cell deformations increase with increasing constriction length [Figs. 12(b) and 12(c)]. As Fig. 12(d) indicates, considerably larger deformation and higher cell–nucleus interaction in longer constriction lead to higher porosity. In all the cases, the porosity increases as the cell leaves the constriction due to strong interaction between the cell and the nucleus. For smaller constriction length, the maximum porosity is observed at the beginning of the process, while for larger constriction length, the nucleus has more time to apply forces on the cell tip and the cell porosity keeps increasing until the end of the process. Therefore, consistent with experimental findings,14,17 higher loaded drug concentration can be achieved by increasing the squeezing length.
FIG. 12.
Plots of different parameters for squeezing through constrictions with different lengths: (a) cell center velocity, (b) horizontal diameter, (c) vertical diameter, (d) porosity, and (e) normalized drug concentration.
VI. CONCLUSION
We presented a multiscale model based on LBM, SN, frictional coupling, MD simulations, and CGMD results to model the intracellular drug delivery via fast squeezing. The proposed method does not have any empirical parameters depending on channel geometry and operating conditions. Our results show that the loaded drug concentration increases with increasing squeezing channel length, decreasing squeezing channel width, and increasing squeezing velocity. The numerical results agree with the trend in experimental findings.14,17 Simulating the fast squeezing of a compound capsule inside a narrowing channel is a complicated phenomenon in biophysics, and there are still many unanswered questions for developing comprehensive theoretical models in this area. Squeezing velocity, constriction length and width, interaction between the cell and the nucleus, mechanical properties of the cell and the nucleus, their sizes, shapes, and initial positions are few parameters that can change the results. In this study, we assumed that the nucleated cell is spherical, and the nucleus is located exactly at the center of the cell. However, experimental observations show that cells are not completely spherical, and nucleus can be positioned at different locations in the cytoplasm (Fig. 4). Moreover, in our simulation, the cytoplasm and external fluid were considered the same, while the difference between the two mentioned fluids can change the cell and nucleus dynamics. It was also hypothesized that all the pores are circular and can be sealed in 30 s. However, it has been observed that pores can have different shapes and closure times.48 Calculating drug loading using the maximum porosity during squeezing is another simplification in our model. Compressive force during squeezing can change the pore size during the process, but modeling this effect is still complicated.48 Finally, we did not implement any threshold for cell rupture during squeezing, while in the real application, the cell might be permanently damaged and unable to recover from squeezing. The mentioned shortcomings are under study in our group. It is worth mentioning that using CGMD approaches for modeling the whole process could be another alternative solution that can visualize the topological behavior of the cell and nucleus membranes and pore formation with finer details. This topic is also our target in future studies. Such computational model can be used to explore the optimal squeezing velocity and channel geometry to maximize the drug payload while maintaining cell integrity.
SUPPLEMENTARY MATERIAL
See the supplementary material for the validation of the compound cell model under a shear flow.
AUTHORS' CONTRIBUTIONS
M.N. designed research, performed research, analyzed data, and wrote the paper. M.R. performed research, analyzed data, and wrote the paper. R.P. designed and performed the experiment and wrote the paper. Y.Z. cultured the cells and wrote the paper. Y.L. designed and directed research, performed research, analyzed data, and wrote the paper.
ACKNOWLEDGMENTS
This work was supported by the National Institutes of Health under Grant No. R01HL131750 and the National Science Foundation under Grant No. CBET 2039310. We would also like to thank Dr. Iveta Jancigova from the cell-in-fluid biomedical modeling and computation group at the University of Zilina, Zilina, Slovakia, for her constructive comments on ESPResSo and PyOIF.
DATA AVAILABILITY
The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- 1.Morshedi Rad D., Alsadat Rad M., Razavi Bazaz S., Kashaninejad N., Jin D., and Ebrahimi Warkiani M., “A comprehensive review on intracellular delivery,” Adv. Mater. 33(13), 2005363 (2021). 10.1002/adma.202005363 [DOI] [PubMed] [Google Scholar]
- 2.Kitao T. and Hattori K., “Erythrocyte entrapment of daunomycin by amphotericin B without hemolysis,” Cancer Res. 40(4), 1351–1353 (1980). [PubMed] [Google Scholar]
- 3.Potter H. and Heller R., “Transfection by electroporation,” Curr. Protoc. Mol. Biol. 2018, 9.3.1–9.3.13. 10.1002/cpmb.48 [DOI] [PubMed] [Google Scholar]
- 4.Wang T. Y., Libardo M. D. J., Angeles-Boza A. M., and Pellois J. P., “Membrane oxidation in cell delivery and cell killing applications,” ACS Chem. Biol. 12(5), 1170–1182 (2017). 10.1021/acschembio.7b00237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cheng L., Ziegelhoffer P. R., and Yang N. S., “In vivo promoter activity and transgene expression in mammalian somatic tissues evaluated by using particle bombardment,” Proc. Natl. Acad. Sci. U.S.A. 90(10), 4455–4459 (1993). 10.1073/pnas.90.10.4455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Blackman B. R., Barbee K. A., and Thibault L. E., “In vitro cell shearing device to investigate the dynamic response of cells in a controlled hydrodynamic environment,” Ann. Biomed. Eng. 28(4), 363–372 (2000). 10.1114/1.286 [DOI] [PubMed] [Google Scholar]
- 7.Okada C. Y. and Rechsteiner M., “Introduction of macromolecules into cultured mammalian cells by osmotic lysis of pinocytic vesicles,” Cell 29(1), 33–41 (1982). 10.1016/0092-8674(82)90087-3 [DOI] [PubMed] [Google Scholar]
- 8.Wyber J. A., Andrews J., and D’Emanuele A., “The use of sonication for the efficient delivery of plasmid DNA into cells,” Pharm. Res. 14(6), 750–756 (1997). 10.1023/A:1012198321879 [DOI] [PubMed] [Google Scholar]
- 9.Kurata S. I., Tsukakoshi M., Kasuya T., and Ikawa Y., “The laser method for efficient introduction of foreign DNA into cultured cells,” Exp. Cell Res. 162(2), 372–378 (1986). 10.1016/0014-4827(86)90342-3 [DOI] [PubMed] [Google Scholar]
- 10.Kurosawa O., Oana H., Matsuoka S., Noma A., Kotera H., and Washizu M., “Electroporation through a micro-fabricated orifice and its application to the measurement of cell response to external stimuli,” Meas. Sci. Technol. 17(12), 3127–3133 (2006). 10.1088/0957-0233/17/12/S02 [DOI] [Google Scholar]
- 11.Krötz F. et al. , “Magnetofection—A highly efficient tool for antisense oligonucleotide delivery in vitro and in vivo,” Mol. Ther. 7(5), 700–710 (2003). 10.1016/S1525-0016(03)00065-0 [DOI] [PubMed] [Google Scholar]
- 12.Neumann E., Schaefer-Ridder M., Wang Y., and Hofschneider P. H., “Gene transfer into mouse lyoma cells by electroporation in high electric fields,” EMBO J. 1(7), 841–845 (1982). 10.1002/j.1460-2075.1982.tb01257.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Szeto G. L. et al. , “Microfluidic squeezing for intracellular antigen loading in polyclonal B-cells as cellular vaccines,” Sci. Rep. 5(1), 1–13 (2015). 10.1038/srep10276 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sharei A. et al. , “Cell squeezing as a robust, microfluidic intracellular delivery platform,” J. Vis. Exp. 81, 1 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sierra H., Cordova M., Chen C. S. J., and Rajadhyaksha M., “Confocal imaging-guided laser ablation of basal cell carcinomas: An ex vivo study,” J. Invest. Dermatol. 135(2), 612–615 (2015). 10.1038/jid.2014.371 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yu K. et al. , “Mechanical loading disrupts osteocyte plasma membranes which initiates mechanosensation events in bone,” J. Orthop. Res. 36(2), 653–662 (2018). 10.1002/jor.23665 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sharei A. et al. , “A vector-free microfluidic platform for intracellular delivery,” Proc. Natl. Acad. Sci. U.S.A. 110(6), 2082–2087 (2013). 10.1073/pnas.1218705110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sharei A. et al. , “Plasma membrane recovery kinetics of a microfluidic intracellular delivery platform,” Integr. Biol. 6(4), 470–475 (2014). 10.1039/C3IB40215K [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Liu A. et al. , “Microfluidic generation of transient cell volume exchange for convectively driven intracellular delivery of large macromolecules,” Mater. Today 21(7), 703–712 (2018). 10.1016/j.mattod.2018.03.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lee J. et al. , “Nonendocytic delivery of functional engineered nanoparticles into the cytoplasm of live cells using a novel, high-throughput microfluidic device,” Nano Lett. 12(12), 6322–6327 (2012). 10.1021/nl303421h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sharei A. et al. , “Ex vivo cytosolic delivery of functional macromolecules to immune cells,” PLoS One 10(4), e0118803 (2015). 10.1371/journal.pone.0118803 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Griesbeck M. et al. , “Sex differences in plasmacytoid dendritic cell levels of IRF5 drive higher IFN-production in women,” J. Immunol. 195(11), 5327–5336 (2015). 10.4049/jimmunol.1501684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tu C., Santo L., Mishima Y., Raje N., Smilansky Z., and Zoldan J., “Monitoring protein synthesis in single live cancer cells,” Integr. Biol. 8(5), 645–653 (2016). 10.1039/C5IB00279F [DOI] [PubMed] [Google Scholar]
- 24.Li J. et al. , “Microfluidic-enabled intracellular delivery of membrane impermeable inhibitors to study target engagement in human primary cells,” ACS Chem. Biol. 12(12), 2970–2974 (2017). 10.1021/acschembio.7b00683 [DOI] [PubMed] [Google Scholar]
- 25.Kollmannsperger A. et al. , “Live-cell protein labelling with nanometre precision by cell squeezing,” Nat. Commun. 7(1), 1–7 (2016). 10.1038/ncomms10372 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Saung M. T. et al. , “A size-selective intracellular delivery platform,” Small 12(42), 5873–5881 (2016). 10.1002/smll.201601155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Leong F. Y., Li Q., Lim C. T., and Chiam K. H., “Modeling cell entry into a micro-channel,” Biomech. Model. Mechanobiol. 10(5), 755–766 (2011). 10.1007/s10237-010-0271-1 [DOI] [PubMed] [Google Scholar]
- 28.Veerapaneni S. K., Young Y. N., Vlahovska P. M., and Bławzdziewicz J., “Dynamics of a compound vesicle in shear flow,” Phys. Rev. Lett. 106(15), 158103 (2011). 10.1103/PhysRevLett.106.158103 [DOI] [PubMed] [Google Scholar]
- 29.Kaoui B., Krüger T., and Harting J., “Complex dynamics of a bilamellar vesicle as a simple model for leukocytes,” Soft Matter 9(33), 8057–8061 (2013). 10.1039/c3sm51032h [DOI] [Google Scholar]
- 30.Luo Z. Y., He L., and Bai B. F., “Deformation of spherical compound capsules in simple shear flow,” J. Fluid Mech. 775, 77–104 (2015). 10.1017/jfm.2015.286 [DOI] [Google Scholar]
- 31.Luo Z. Y. and Bai B. F., “Dynamics of nonspherical compound capsules in simple shear flow,” Phys. Fluids 28(10), 101901 (2016). 10.1063/1.4965251 [DOI] [Google Scholar]
- 32.Alizad Banaei A., Loiseau J. C., Lashgari I., and Brandt L., “Numerical simulations of elastic capsules with nucleus in shear flow,” Eur. J. Comput. Mech. 26(1–2), 131–153 (2017). 10.1080/17797179.2017.1294828 [DOI] [Google Scholar]
- 33.Casquero H., Bona-Casas C., and Gomez H., “NURBS-based numerical proxies for red blood cells and circulating tumor cells in microscale blood flow,” Comput. Methods Appl. Mech. Eng. 316, 646–667 (2017). 10.1016/j.cma.2016.09.031 [DOI] [Google Scholar]
- 34.Gounley J., Draeger E. W., and Randles A., “Numerical simulation of a compound capsule in a constricted microchannel,” Procedia Comput. Sci. 108, 175–184 (2017). 10.1016/j.procs.2017.05.209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Tan J., Sohrabi S., He R., and Liu Y., “Numerical simulation of cell squeezing through a micropore by the immersed boundary method,” Proc. Inst. Mech. Eng. Part C 232(3), 502–514 (2018). 10.1177/0954406217730850 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rahmat A., Barigou M., and Alexiadis A., “Deformation and rupture of compound cells under shear: A discrete multiphysics study,” Phys. Fluids 31(5), 051903 (2019). 10.1063/1.5091999 [DOI] [Google Scholar]
- 37.Chang P., Landry C., Chen X., and Tan H., “Compound droplet dynamics of a tumor cell squeezing through conical microfilters,” Theor. Comput. Fluid Dyn. 34(3), 287–300 (2020). 10.1007/s00162-020-00534-y [DOI] [Google Scholar]
- 38.Zhang Z., Xu J., and Drapaca C., “Particle squeezing in narrow confinements,” Microfluid. Nanofluid. 22(10), 120 (2018). 10.1007/s10404-018-2129-2 [DOI] [Google Scholar]
- 39.Nikfar M., Razizadeh M., Zhang J., Paul R., Wu Z. J., and Liu Y., “Prediction of mechanical hemolysis in medical devices via a Lagrangian strain-based multiscale model,” Artif. Organs 44(8), E348–E368 (2020). 10.1111/aor.13663 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Arora D., Computational Hemodynamics Hemolysis and Viscoelasticity (Rice University, 2005). [Google Scholar]
- 41.Arora D., Behr M., and Pasquali M., “A tensor-based measure for estimating blood damage,” Artif. Organs 28(11), 1002–1015 (2004). 10.1111/j.1525-1594.2004.00072.x [DOI] [PubMed] [Google Scholar]
- 42.Arora D., Behr M., and Pasquali M., “Hemolysis estimation in a centrifugal blood pump using a tensor-based measure,” Artif. Organs 30(7), 539–547 (2006). 10.1111/j.1525-1594.2006.00256.x [DOI] [PubMed] [Google Scholar]
- 43.Vitale F. et al. , “A multiscale, biophysical model of flow-induced red blood cell damage,” AIChE J. 60(4), 1509–1516 (Apr. 2014). 10.1002/aic.14318 [DOI] [Google Scholar]
- 44.Sohrabi S. and Liu Y., “A cellular model of shear-induced hemolysis,” Artif. Organs 41(9), 80–91 (2017). 10.1111/aor.12832 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Nikfar M., Razizadeh M., Paul R., and Liu Y., “Multiscale modeling of hemolysis during microfiltration,” Microfluid. Nanofluid. 24(5), 33 (2020). 10.1007/s10404-020-02337-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gusenbauer M. et al. , “Cell damage index as computational indicator for blood cell activation and damage,” Artif. Organs 42(7), 746–755 (2018). 10.1111/aor.13111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Luo Z. Y. and Bai B. F., “Solute release from an elastic capsule flowing through a microfluidic channel constriction,” Phys. Fluids 31(12), 121902 (2019). 10.1063/1.5129413 [DOI] [Google Scholar]
- 48.Razizadeh M., Nikfar M., Paul R., and Liu Y., “Coarse-grained modeling of pore dynamics on the red blood cell membrane under large deformations,” Biophys. J. 119(3), 471–482 (2020). 10.1016/j.bpj.2020.06.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Koshiyama K. and Wada S., “Molecular dynamics simulations of pore formation dynamics during the rupture process of a phospholipid bilayer caused by high-speed equibiaxial stretching,” J. Biomech. 44(11), 2053–2058 (2011). 10.1016/j.jbiomech.2011.05.014 [DOI] [PubMed] [Google Scholar]
- 50.Tolpekina T. V., Den Otter W. K., and Briels W. J., “Simulations of stable pores in membranes: System size dependence and line tension,” J. Chem. Phys. 121(16), 8014–8020 (2004). 10.1063/1.1796254 [DOI] [PubMed] [Google Scholar]
- 51.Weik F. et al. , “ESPResSo 4.0—An extensible software package for simulating soft matter systems,” Eur. Phys. J. Spec. Top. 227(14), 1789–1816 (2019). 10.1140/epjst/e2019-800186-9 [DOI] [Google Scholar]
- 52.Cimrák I., Gusenbauer M., and Schrefl T., “Modelling and simulation of processes in microfluidic devices for biomedical applications,” Comput. Math. Appl. 64(3), 278–288 (2012). 10.1016/j.camwa.2012.01.062 [DOI] [Google Scholar]
- 53.Cimrák I., Gusenbauer M., and Jančigová I., “An ESPResSo implementation of elastic objects immersed in a fluid,” Comput. Phys. Commun. 185(3), 900–907 (2014). 10.1016/j.cpc.2013.12.013 [DOI] [Google Scholar]
- 54.Jančigová I., Kovalčíková K., Weeber R., and Cimrák I., “PyOIF: Computational tool for modelling of multi-cell flows in complex geometries,” PLoS Comput. Biol. 16(10), e1008249 (2020). 10.1371/journal.pcbi.1008249 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Cimrak I. and Jancigova I., Computational Blood Cell Mechanics: Road Towards Models and Biomedical Applications (Taylor & Francis, 2018). [Google Scholar]
- 56.Kushchenko Y. K. and Belyaev A. V., “Effects of hydrophobicity, tethering and size on flow-induced activation of von Willebrand factor multimers,” J. Theor. Biol. 485, 110050 (2020). 10.1016/j.jtbi.2019.110050 [DOI] [PubMed] [Google Scholar]
- 57.Ahlrichs P. and Dünweg B., “Simulation of a single polymer chain in solution by combining lattice Boltzmann and molecular dynamics,” J. Chem. Phys. 111(17), 8225–8239 (1999). 10.1063/1.480156 [DOI] [PubMed] [Google Scholar]
- 58.Cimrák I., “Effect of dissipative coupling parameter in a computational model on the inclination angle of red blood cells in a shear flow,” in ACM International Conference Proceeding Series (ACM, 2018). [Google Scholar]
- 59.Bušík M., Slavík M., and Cimrák I., “Dissipative coupling of fluid and immersed objects for modelling of cells in flow,” Comput. Math. Methods Med. 2018, 1 (2018). 10.1155/2018/7842857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Paul R., Zhou Y., Nikfar M., Razizadeh M., and Liu Y., “Quantitative absorption imaging of red blood cells to determine physical and mechanical properties,” RSC Adv. 10(64), 38923–38936 (2020). 10.1039/D0RA05421F [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Tomasini M. D., Rinaldi C., and Tomassone M. S., “Molecular dynamics simulations of rupture in lipid bilayers,” Exp. Biol. Med. 235(2), 181–188 (2010). 10.1258/ebm.2009.009187 [DOI] [PubMed] [Google Scholar]
- 62.Den Otter W. K., “Free energies of stable and metastable pores in lipid membranes under tension,” J. Chem. Phys. 131(20), 11B614 (2009). 10.1063/1.3266839 [DOI] [PubMed] [Google Scholar]
- 63.Leontiadou H., Mark A. E., and Marrink S. J., “Molecular dynamics simulations of hydrophilic pores in lipid bilayers,” Biophys. J. 86(4), 2156–2164 (2004). 10.1016/S0006-3495(04)74275-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.McNeil P. L. and Steinhardt R. A., “PLasma membrane disruption: Repair, prevention, adaptation,” Annu. Rev. Cell Dev. Biol. 19(1), 697–731 (2003). 10.1146/annurev.cellbio.19.111301.140101 [DOI] [PubMed] [Google Scholar]
- 65.Quinn D. J. et al. , “Combined simulation and experimental study of large deformation of red blood cells in microfluidic systems,” Ann. Biomed. Eng. 39(3), 1041–1050 (2011). 10.1007/s10439-010-0232-y [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See the supplementary material for the validation of the compound cell model under a shear flow.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.