Abstract
RNA molecules play critical roles in cellular functions at the level of gene expression and regulation. The intricate 3D structures and the functional roles of RNAs make RNA molecules ideal targets for therapeutic drugs. The rational design of RNA-targeted drug requires accurate modeling of RNA-ligand interactions. Recently a new computational tool, RLDOCK, was developed to predict ligand binding sites and binding poses. Using an iterative multiscale sampling and search algorithm and a energy-based evaluation of ligand poses, the method enables efficient and accurate predictions for RNA-ligand interactions. Here we present a detailed illustration of the computational procedure for the practical implementation of the RLDOCK method. Using Flavin mononucleotide (FMN) docking to F. nucleatum FMN riboswitch as an example, we illustrate the computational protocol for RLDOCK-based prediction of RNA- ligand interactions. The RLDOCK software is freely accessible at http://https://github.com/Vfold-RNA/RLDOCK.
Keywords: RNA-ligand interaction, flexible docking, scoring function, RNA-targeted ligand
1. Introduction
RNA molecules play essential roles in cellular functions at the level of protein synthesis,1 gene regulation,2 nucleotide modification,3 and functional response to environmental changes.4 In particular, non-coding RNAs directly participate in tumorigenesis and neurological, cardiovascular and many other human diseases.5 For example, RNAs are implicated in a number of diseases such as Huntington’s disease and AIDS.
RNA molecules fold up to form complicated tertiary structures that consist of different motifs at various levels of complexity, such as stem-loop, hairpins, bulges, and pseudoknots. Highly structured regions of RNA with an array of different structural motifs can serve as an ideal receptor and druggable target for small molecules (ligands).8-10 The drugability of RNA is particularly appreciated if the protein target lacks suitable ligand-binding pockets.
The drugability of RNA structures has inspired tremendous efforts to develop RNA-based therapeutic strategies.6, 7 So far, many ligands have been discovered to target RNA through various mechanisms. For example, amino- glycoside antibiotics target bacterial ribosomal RNA with high affinity and specificity to inhibit protein synthesis,11-13 ribocils selectively bind to Flavin mononucleotide (FMN) riboswitch to terminate gene expression and subsequently inhibit further bacterial infection,14 anthraquinone derivatives target HIV transactivation response element to inhibit viral replication.15 Moreover, designed ligand-RNA aptamer complexes can potentially enhance therapeutic applications. For example, experiments indicated that a complex of a modified RNA aptamer and tetramethylrosamine (a fluorescent malachite green analogue) can regulate the cell cycle of S.cerevisiae.16 An accurate computational tool for predicting ligand-RNA interactions can greatly facilitate in vitro selection of RNA aptamers that bind to a specific ligand and ligands that bind to a specific RNA aptamer to optimize intended aptamer structures.17
Over the past decades, various experimental methods, such as X-ray crystallography,18 nuclear magnetic resonance (NMR) spectroscopy,19 and cryo-electron20 microscopy, have been used to determine biologically important RNA-ligand complex structures, As of December 2020, there have been more than 400 experimentally determined RNA-ligand complexes structures deposited in the Protein Data Bank21 (PDB) database, of which more than 75% were discovered over the past decade. These structures have provided much needed data for understanding RNA-ligand interactions and developing structure-based discovery of drugs.
In parallel with the experimental advances in structure determination of RNA-ligand complexes, substantial efforts have been devoted to the computational modeling of RNA-ligand binding. The computational efforts can be mainly classified into two categories: data-driven and physics-based models. Machine learning as a data-driven approach has been extensively applied to the study of RNA-ligand docking. Additionally, other data-driven models, such as DrugScoreRNA22, 23 and LigandRNA,24 predict ligand binding using statistical potentials derived from the structural data of the known RNA-ligand complexes. Physics-based approaches such as DOCK625 and MORDOR,26 however, employ physical energy functions for ligand-RNA interactions and predict the ligand-RNA complex by minimizing the energy. The different approaches have shown significant success for different RNA-ligand systems.27 However, in general, the accuracy for an RNA-ligand model is lower than that of protein-ligand docking models, and the performance cannot meet the requirement for drug design and other applications such as virtual screening and selection of ligands and RNA aptamers for the intended aptamer-ligand complex structures.17 One of the key problems is that, compared with protein-ligand complexes, we have far less known RNA-ligand complex structures.28 The insufficient number and diversity of known RNA-ligand complex structures can directly impact the reliability of both the data-driven and the physical approaches, which rely on the structural data to optimize model parameters. In recent years, as more and more RNA-ligand complexes structures are determined,29 we can realistically expect continuous improvements in the accuracy of computational models for RNA-ligand binding.
Given the limited availability of known structures, physics-based approaches become an attractive alternative. For a physics model, complete sampling and accurate scoring for the binding modes (also referred to as binding poses) are two key bottlenecks.25, 30 To tackle these bottleneck problems, we recently developed the RLDOCK model30 (http://https://github.com/Vfold-RNA/RLDOCK). The RLDOCK model has two key components. First, the model employs a novel multi-tier screening algorithm that enables an iterative exhaustive search for the binding sites and ligand conformations. Second, the scoring of the different binding modes is based on a comprehensive physics-based energy function. In this Methods paper, we focus on the detailed illustration of the computational procedure for the practical implementation of RLDOCK. As an application of the RLDOCK, we show the computational prediction for the binding mode of FMN (ligand) docking to F.nucleatum FMN riboswitch (RNA; PDB21 identifier: 2yie31).
In Fig. 1 we show the pipeline of the RLDOCK method. The main algorithm of RLDOCK has two components: the sampling of the possible ligand binding modes and the scoring of the different binding modes. In RLDOCK, sampling is guided by scoring (energy) function. Therefore, in what follows, we first describe the scoring function then introduce the sampling method.
Figure 1:
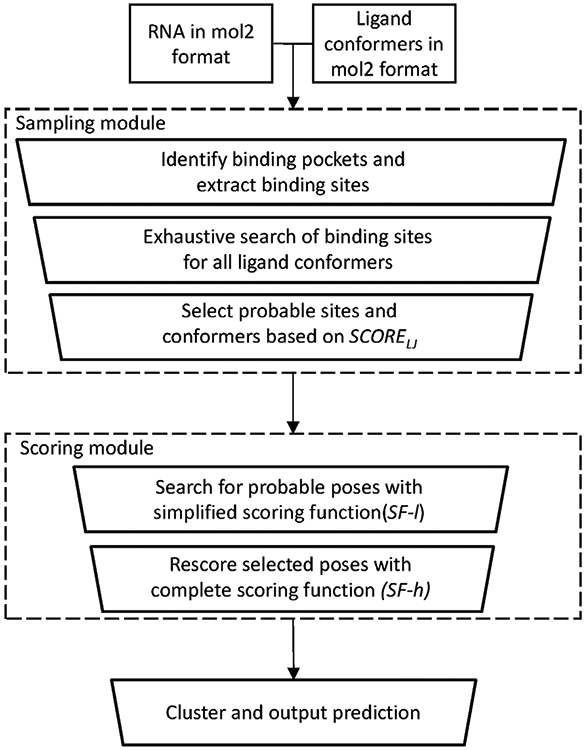
The workflow of the RLDOCK model.
2. Method
2.1. Preparation of the system
The RLDOCK model uses the 3D structure of the RNA and the chemical structure of the ligand as the input information. Depending on the flexibility of the ligand molecule, the model generates an ensemble of 3D conformers for the ligand.
An initial structure of a ligand can be generated from its 2D chemical information using cheminformatics tools such as Open Babel32 and OMEGA TK.33 Staring from the initial ligand structure, we generate diverse 3D conformers for the ligand and group structurally similar ligand conformers into clusters. Here the structural similarity is measured by the root-mean-square deviation (RMSD) of the heavy atoms between the structures. On a workstation powered with an AMD Ryzen Threadripper 1950X 16-Core Processor and 64 GB RAM, we generate an ensemble of 30 diverse conformers for a ligand.
Using UCSF Chimera,34 we prepare the input RNA and ligand structures as mol2 files. The files contain not only the atomic coordinates but also the partial charges carried by the atoms. Unlike proteins, RNAs are highly charged, therefore, electrostatic interaction is critical for ligand-RNA binding and the charge assignments are important for the model.
2.2. Scoring function
The scoring function in RLDOCK is based on the free energy change upon ligand binding to the RNA. The total free energy of the system comprises the following components: (a) the mutual van der Waals (VDW) Ulj and (b) Coulomb Ue interaction energies between ligand and RNA atoms, (c) the polar hydration energy, which is decomposed into self-polarization energy Uself of the RNA and ligand atoms and the mutual polarization energy Upol between the different charged atoms, (d) the nonpolar hydration energy Usa, (e) the hydrogen-bond energy Uh, and (f) the intramolecular VDW interaction energy between ligand atoms Uinternal. The hydration energies are calculated based on the generalized Born approximation with the solvent-accessible surface area (GB/SA model).35-40 For a given RNA-ligand binding mode i, the total energy score is given by the following formula; See Appendix A for a detailed illustration of each energy term.
| ##(1) |
where the weight coefficients41 c are introduced to account for the correlation between the different components, and the superscripts R and L denote the RNA and the ligand, respectively.
The evaluation of the scoring function (energy) for each sampled ligand binding mode is computationally demanding. Therefore, an effective method to speed up energy calculation is a critical ingredient in the RLDOCK model. RLDOCK uses two methods to achieve a fast energy calculation.
2.2.1. Grid-based Lennard-Jones (LJ) energy map
One of the approaches used in RLDOCK is to pre-tabulate the energy values for pairwise interactions, specifically, the VDW interaction energy, which, as shown in Appendix A, is in the form of a Lennard-Jones (LJ) potential. The basic strategy is to discretize the 3D space and pre-compute the LJ interaction energy between all the RNA atoms and a ligand atom placed at a grid site. In practice, we discretized the space with a grid spacing of 0.2Å and place common atom types (C, N, O, P, S, etc) at each grid. The LJ energy values for the different atom types on each grid site gives the grid energy map. For a given binding mode, the mutual VDW energy can be quickly evaluated by summing up the grid energies over the grids occupied by the ligand atoms.
2.2.2. A simplified scoring function
The solvent-accessible surface area (SASA) and the Born radii of the atoms are sensitive to the structure of the RNA-ligand complex and hence need to be computed/updated for each ligand-RNA binding mode generated in the sampling process. Therefore, the time-consuming SASA and Born radii calculations become the most time-demanding steps in the whole computational process. In RLDOCK, the problem is resolved by applying an initial crude screening process where the following simplified and fast calculations for the SASA and Born radii can be used.
The calculation of SASA, which is determined by the molecular shape, is intrinsically a many-body problem. As an approximation, we simply add up the SASA changes of each pair of ligand-RNA atoms and ignore the existence of other atoms in the calculation of each ligand-RNA atom pair.
We neglect the ligand docking-induced changes in the Born radii and the self-polarization energy for RNA.
We use the VDW radii to approximate the Born radii of the bound ligand atoms.
The above approximations can lead to an increase in the computational efficiency of thousands of folds.
2.2.3. Method for parameter optimization
The scoring function contains 8 weight coefficients. We determine the coefficients by minimizing the difference between the predicted and the experimentally determined binding modes for a training set. Our training set contains 30 RNA-ligand complexes deposited in the PDB; See Appendix B. The 30 cases are selected to cover a diverse range of different RNA and ligand types. In the training set, the RNA sizes range from 516 to 2337 heavy atoms and the ligand sizes vary from 10 to 52 heavy atoms, with an average of 1318 and 25 atoms for RNA and ligand, respectively.
For each of the 30 ligand-RNA complexes, a ligand binding mode ensemble is generated. The coordinated descent method42 is applied to optimize the weight coefficients. Repeated application of the coordinate descent method results in multiple sets of putative weight coefficients, and the set that corresponds to the minimum RMSD between the predicted and the experimentally determined ligand pose are selected: clj = 3.30, ce = 1.32, ch = 1.32, csa = 1.26(0.30), cpol = 1.38(0.36), , , . The values in the parentheses refer to the parameter used for the simplified scoring function above.
2.3. Sampling and scoring ligand-RNA binding modes
We use four variables, R, L, A, and O, to describe a ligand pose. Here the ligand atom A (referred to as the anchor atom) is fixed at position R (referred to as the anchor site), and the ligand pose is generated by the 3D rotation O of the ligand conformer L about A. As shown below, RLDOCK uses a multi-tier sieving process to search for the ligand binding pose efficiently.
2.3.1. Global sampling of the anchor sites
We configure the RNA structure in a box whose six boundaries are 3Å away from the outermost atoms of the RNA, and discretize the box space with a simple cubic lattice of grid size 0.5Å.
- We search for all the possible anchor sites that involve no steric clashes with a ligand or an RNA atom and reside inside a pocket of the RNA structure.
- To probe the steric clash, we place a virtual sphere of radius 2 Å the grid sites and let the sphere traverse the RNA surface to detect the atomic overlap. The clash-free grid sites are kept as the viable anchor sites R.
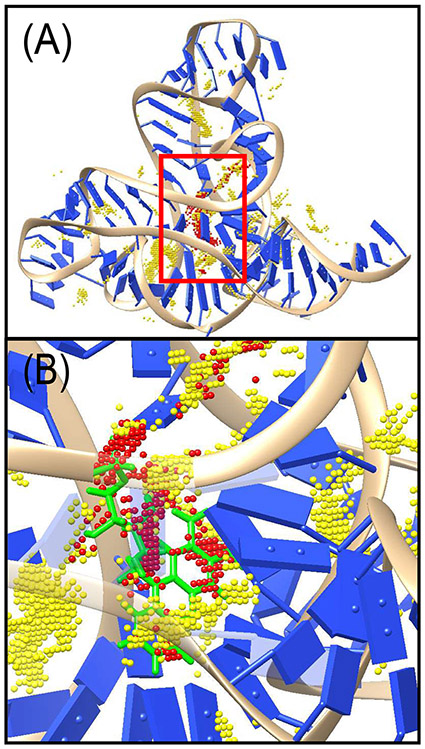
- To identify the RNA pockets, on each anchor site selected above, we move the sphere 6Å along the six directions of the egocentric coordinates: left and right; front and back; up and down. If the test probe meets any RNA atom in at least five directions, the anchor site is considered to be inside a pocket and would be forwarded to the next step; see Fig.2A.
Figure 2:
(A) Visualization of the binding sites for F.nucleatum FMN riboswitch (PDB21 identifier: 2yie31). Dots in yellow denote the possible binding sites based on consideration of steric clash. Dots in red denotes the top-300 selected candidate binding sites based on LJ energy. (B) is an enlarged view of a region surrounded by a red rectangle of (A). The crystal structure of the ligand is displayed with green as a reference.
2.3.2. Sampling binding modes based on the ligand-RNA van der Waals interactions
In this step, we use the RNA-ligand VDW interaction energy (LJ potential) to sample and select plausible poses. We note that this step is primarily a shape-based selection as the LJ potential is a soft potential for the volume exclusion.
For each anchor site R selected in the previous step, we enumerate all the possible L, A, and O, and find the minimum LJ energy LJ1(R). We keep 300 anchor sites R from the top-300 lowest LJ1(R) energies.
For each R site selected above, for each given ligand conformer L, we sample all the possible A and O, and find the minimum LJ energy LJ2(R, L). We keep the 3 ligand conformers L from the top-3 lowest LJ2(R, L) energies.
For each (R, L) pair selected above, for each ligand atom A as the anchor atom, we sample all the possible rotations O about A and find the minimum LJ energy LJ3(R, L, A). We keep the anchor atoms A from the top-3 lowest LJ3(R, L, A).
Here we rotate the ligand around 500 uniformly orientated axes with a 10° increment in the rotation angle. The rotations result in a total of 36×500 = 18000 ligand orientations. In summary, the LJ potential-guided sampling leads to a total of 300 × 3 × 3 × 18000 ~ 5 × 107 binding modes.
2.3.3. Scoring binding modes based on the full ligand-RNA interaction energy.
As shown below, we use a two-step approach to efficiently score the ~ 5 × 107 binding modes.
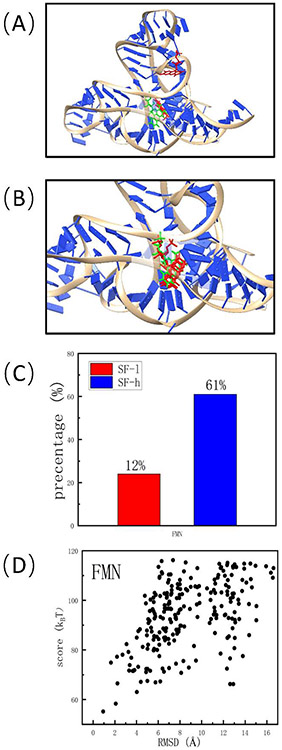
Initial coarse-grained scoring of the ligand orientations. For each of the 300 anchor sites R selected above, using the aforementioned simplified energy function, we quickly select the top-10 poses. This step leads to a pool of 300 × 10 = 3000 potential binding modes; See Fig. 3A.
Further refinement using the rigorous energy function. We re-score the 3000 binding modes using the original rigorous energy function; See Fig. 3B.
Figure 3:
The intermediate results obtained from the scoring module for F.nucleatum FMN riboswitch (PDB21 identifier: 2yie31). (A) The top-3 poses scored by the simplified scoring function. (B) The top-3 poses scored by the complete, rigorous scoring function. (C) The percentage of the near-native poses among the top-100 poses predicted by the simplified and the complete scoring functions, respectively. Here “near-native” means the RMSD is less than 2.0 Å with respect of the experimentally determined pose. (D) The correlation between the final score given by RLDOCK and the RMSD with respect of crystal structure for the predicted poses after clustering.
2.3.4. Clustering of the binding modes.
Starting from the top-ranked binding mode, we cluster the ligand poses according to the structural similarity. We use 2 Å as the RMSD cutoff a cluster. The top-scored pose in each cluster is chosen to represent the cluster. This step leads to a list of ranked binding modes (ligand poses). The top ligand pose is output as a mol2 file for visualization.
3. Application of the RLDOCK model
As an illustration, we apply RLDOCK to predict the FMN (ligand) pose in the FMN-F. nucleatum FMN riboswitch (RNA) complex. The ligand FMN contains 31 heavy atoms. We prepare an input ensemble of 30 conformers for the ligand. The global sampling procedure predicts 2205 anchor sites. Anchoring each of the 31 heavy atoms to the 2205 sites for each of the 30 ligand conformers results in a total of 2205 × 30 × 31 × 18000 ~ 3.7 × 1010 binding modes. Subsequent LJ energy-based sampling and ranking of above binding modes leads to a list of top-300 anchor sites. As shown in Fig. 2, the selected binding sites are indeed in the pocket region.
For each of the 300 selected anchor sites, the simplified scoring function selects the top-10 binding poses from the ~ 5 × 107 candidates; See Fig. 3A. Subsequent re-scoring using the rigorous energy function gives the re-ranked 3000 binding modes. Finally, the clustering procedure leads to the final 527 ranked binding modes; See Fig. 3B. The predicted top-ranked FMN ligand pose is within 2.0Å (RMSD) from the crystal structure; See Fig. 3C and D.
The executable file for RLDOCK is available at https://github.com/Vfold-RNA/RLDOCK. Here are some tips for a successful implementation of RLDOCK.
For a larger RNA (atoms ~ 3 × 104) RLDOCK requires a computing power with larger RAM (≥ 128G) and more CPU threads (≥ 32).
For a large flexible ligand (rotatable bonds > 12), we suggest generating multiple ensembles of ligand conformers instead of a single large ensemble.
4. Conclusion
Using a novel multi-scale method for global sampling and energy-guided search for ligand binding pose, the RLDOCK method can successfully predict RNA-ligand near-native binding modes; See Tables 1 and 2. As shown in Table 1, RLDOCK can successfully predict the binding mode within the top-10 poses with a success rate of 70% for all the three data sets tested. For the training set and Test set 2, the top-ranked binding mode can give successful hits for more than 50% of the cases. For Test set 1, which contains 200 RNA-ligand cases, the success rate of the top-ranked pose is less than 40%, suggesting the need for further refinement of the method.
Table 1:
The success rate of RLDOCK for different data setsa
| Data set | Number of cases | Top 1 | Top 3 | Top 10 |
|---|---|---|---|---|
| Training set30 | 30 | 50.0% | 70.0% | 86.7% |
| Test set 130 | 200 | 39.0% | 56.5% | 72.5% |
| Test set 224b | 38 | 55.3% | 60.5% | 71.0% |
In this table, a prediction is successful if the best RMSD of the top binding modes is less than 2.0Å with respect to the native binding mode.
The four ribosomal RNA cases are excluded from the 42 RNA-ligand complexes.
Table 2:
| Docking model | Top 1 | Top 3 |
|---|---|---|
| RLDOCK30 | 55.3% | 60.5% |
| DOCK625b | 36.8% | 44.7% |
| rDock43c | 28.9% | 47.4% |
| rDock_solv43c | 39.5% | 55.3% |
| AutoDock Vina44d | 31.6% | 44.7% |
A prediction is successful if the best RMSD of the top binding modes is less than 2.0Å with respect to the native binding mode.
The data is obtained from Ref. 24.
For rDock and rDock solv, the cavity is defined using the reference ligand method, the radius of outer sphere is set as 5, and a final 50 runs-per-ligand rDock job is performed.
The centroid of the native ligand binding pose is set as the center of the docking box. The size of the docking box is set as 20Å ×20Å ×20Å
As shown in Table 2, compared with other docking models, RLDOCK has a better performance on a validation set of 38 RNA-ligand complexes. The promising performance of RLDOCK indicates that it may serve as a new valuable tool for predicting RNA-ligand interactions in the discovery of lead compounds as RNA-targeted drugs and the selection of ligand-bound RNA aptamers.
However, the applicability of the RLDOCK method is challenging for large RNAs and ligands. For systems with a large RNA such as the ribosomal RNA (~ 5 × 104 atoms) or a large flexible ligand (rotatable bonds > 12), The time-consuming sampling of the binding modes causes prohibitive low computational efficiency of the method. Further improvement in the computational efficiency is possible. For example, the rDock model applies the genetic algorithm to generate initial ligand conformers and refine the conformer ensemble “on-the-fly” using Monte Carlo simulation.43 Another major challenge for the application of the RLDOCK model stems from RNA conformational flexibility. Unlike a protein, an RNA molecule often folds into multiple conformers with comparable stabilities. RNA conformational multiplicity and the resultant flexibility of RNA binding pockets can affect ligand binding affinity. The conformational heterogeneity can also negatively influence the crystal packing of RNA structures and challenge the structure determination for ligand-RNA complexes. The current version of RLDOCK assumes a rigid RNA structure and cannot treat RNA conformational changes upon ligand binding. The RLDOCK method here, combined with an RNA folding model, however, may provide a promising new method to treat ligand-induced RNA conformational changes.
Highlights.
RLDOCK is a novel computational tool that predicts RNA-ligand interactions using a multiscale sampling method.
A global search algorithm enables the complete sampling of ligand binding sites.
An energy-guided coarse-grained sampling method facilitates a fast search for ligand conformations and orientations.
A physics-based energy function successfully scores and ranks different binding modes.
A two-step scoring approach leads to a substantial speed-up in the computational prediction of the ligand-binding mode.
RLDOCK is a valuable new tool for RNA-targeted drug discovery.
5. Acknowledgments
This work was supported by the National Institutes of Health under Grants R01-GM117059 and R35-GM134919 to S-J.C.
Appendix
Appendix A. Energy terms in the scoring function
(a). VDW interaction energy Ulj
The Lennard-Jones (LJ) potential ΔUlj is applied to represent VDW interaction:
| #(2.) |
Here the subscripts r and l denote the atom of RNA and ligand, respectively. rrl represents the distance between the two atoms and σrl = 0.8(Rr + Rl) is the equilibrium distance, where Rr (Rl) is the radii of RNA (ligand) atom. A cut-off distance rcut = 2.5(Rr + Rl) is applied in the LJ potential calculation.
(b). Coulomb interaction Ue
The electrostatic interaction ΔUe is the Coulomb interaction between RNA and ligand atoms:
| #(3.) |
Here Zr and Zl denote the electric charges of the atoms r in RNA and l in ligand, respectively, rrl is the distance between atoms, e is the electronic charge, εc (=20 in our calculation) is the dielectric constant of the RNA-ligand complex.
(c). Polar hydration energy
Polar hydration interaction is decomposed into the mutual polarization energy Upol and self-polarization energy Uself of the RNA and ligand atoms.
Mutual-polarization energy
The mutual polarization energy change ΔUpol is obtained as below:
| #(4.) |
where , , and are the mutual polarization of the complex, the RNA alone, and the ligand alone, respectively. We estimate the three mutual polarization energies from the GB model:35-40
| #(5.) |
where εw (=78) denotes the dielectric constant of water. The dielectric constant εc is assumed to be the same for the bound and the unbound RNA and ligand. The subscripts i and j (i ≠ j) represent respective molecule (complex, RNA alone, or ligand alone). rij denotes the distance between these two atoms. Bi and Bj are the Born radii of atoms i and j.
For an atom i in the RNA-ligand complex, RNA alone, or ligand alone, its Born radius is calculated as follows:
| #(6.) |
| #(7.) |
| #(8) |
| #(9) |
Here ai and aj denote the VDW radii of atoms i and j, respectively. rij is the distance between atoms i and j. Sj is the structural scaling factor and is equal to 1 if there is no overlap between the atoms. In general, Sj < 1 in the RNA-ligand complex, RNA alone, or ligand alone.
Self-polarization energy
The self-polarization energies of the RNA and of the ligand are calculated as the following:
| #(10.) |
Here and denote the Born radii of atom r(or l) in the RNA (or ligand) before and after the ligand-RNA docking, respectively.
(d). Nonpolar hydration energy Usa
The nonpolar hydration energy ΔUsa is evaluated according to the change in the solvent-accessible surface area (SASA):45-47
| #(11) |
where ΔSA is the total SASA change before and after the ligand docking.
| #(12) |
Here SAcomplex denotes the SASA of the RNA-ligand complex for the given pose (R, L, A, O). SARNA and SAligand are the SASA of the RNA alone and ligand alone, respectively.
In the simplified scoring function, the sum of the SASA change for each ligand-RNA atom pair gives the approximate total SASA change:
| #(13.) |
where ΔSArl denotes the SASA changes of the RNA atom r and the ligand atom l upon binding.
We choose σ = 0.0054 kcal/(mol · Å2) for the empirical atomic solvation parameter σ.48
(e). Hydrogen-bond interaction energy Uh
The hydrogen-bond interaction energy ΔUh between the RNA and ligand is calculated as:
| #(14) |
where uh(rrl) is the hydrogen-bond energy of an RNA-ligand atom pair. We evaluate the hydrogen-bond energy via an empirical formula:49
| #(15.) |
Here rmin = 0.8(Rr + Rl and rmax = 1.3(Rr + Rl).
(f). Ligand intramolecular VDW interaction energy Uinternal
We also use LJ potential to evaluate ligand intramolecular VDW interaction:
| #(16.) |
Here i and j denote a non-bonded heavy atom pair in the ligand, rij is the distance between the two atoms, and σij = 0.8(Ri + Rj) is the equilibrium distance, where Ri and Rj are the radii of atom i and j, respectively. A cut-off distance rcut = 2.5(Ri + Rj) is applied here for the LJ potential.
The VDW radii and the structural scaling factors for various atom types can be obtained from http://www.rbvi.ucsf.edu/chimera/current/docs/UsersGuide/midas/vdwtables.html and Ref. 39, respectively.
Appendix B. List of data sets
List of PDB IDs for RNA-ligand complexes in the data sets
| Training set | |||||
|---|---|---|---|---|---|
| 1AKX | 1ET4 | 1F27 | 1LVJ | 1PBR | 1J8G |
| 1KOC | 1QD3 | 1Y26 | 2ET4 | 2FD0 | 2BE0 |
| 2BEE | 2F4T | 2KTZ | 2O3X | 2XO1 | 3DIX |
| 3FO4 | 3GES | 3SUH | 3SUX | 3SKL | 4LVW |
| 4LW0 | 4FEJ | 4FEO | 4NYB | 4KQY | 5C45 |
| Test set 1 | |||||
| 1AJU | 1AM0 | 1ARJ | 1BYJ | 1DDY | 1EHT |
| 1EI2 | 1EVV | 1F1T | 1FMN | 1FUF | 1FYP |
| 1I7J | 1I9V | 1J7T | 1KOD | 1LC4 | 1MWL |
| 1NBK | 1NEM | 1NTA | 1NTB | 1O15 | 1O9M |
| 1Q8N | 1RAW | 1TN1 | 1TN2 | 1TOB | 1UTS |
| 1UUD | 1UUI | 1XPF | 1YKV | 1YLS | 1YRJ |
| 1ZZ5 | 292D | 2A04 | 2AU4 | 2B57 | 2EES |
| 2EET | 2EEU | 2EEW | 2ESI | 2ESJ | 2ET3 |
| 2ET5 | 2ET8 | 2F4S | 2F4U | 2FCX | 2FCY |
| 2FCZ | 2G5K | 2G5Q | 2G9C | 2GCV | 2GDI |
| 2GIS | 2GQ5 | 2HOP | 2JUK | 2KD4 | 2KGP |
| 2KU0 | 2KX8 | 2KXM | 2L1V | 2L8H | 2MIY |
| 2MXS | 2N0J | 2OE5 | 2OE8 | 2PWT | 2QWY |
| 2TOB | 2W89 | 2XNW | 2XNZ | 2XO0 | 2YDH |
| 2YIE | 3B4B | 3B4C | 3C3Z | 3C44 | 3C5D |
| 3C7R | 3D0U | 3D2X | 3DIG | 3DIL | 3DIM |
| 3DIO | 3DIY | 3DIZ | 3DJ0 | 3DJ2 | 3DS7 |
| 3DVV | 3DVZ | 3DW4 | 3DW6 | 3E5C | 3E5E |
| 3E5F | 3F2Q | 3F2T | 3F4G | 3F4H | 3FO6 |
| 3FU2 | 3G4M | 3GAO | 3GCA | 3GER | 3GOG |
| 3GOT | 3GX2 | 3GX3 | 3GX5 | 3GX6 | 3GX7 |
| 3IQN | 3IQR | 3IRW | 3K1V | 3LA5 | 3NPN |
| 3NPQ | 3OWI | 3OWZ | 3Q3Z | 3Q50 | 3RKF |
| 3S4P | 3SD3 | 3SKI | 3SKR | 3SKT | 3SKW |
| 3SKZ | 3SLM | 3SLQ | 3TD1 | 3TZR | 3WRU |
| 4AOB | 4B5R | 4ERL | 4F8U | 4F8V | 4FE5 |
| 4FEL | 4FEN | 4FEP | 4FRG | 4GPW | 4GPX |
| 4GPY | 4JF2 | 4K32 | 4L81 | 4LVV | 4LVX |
| 4LVY | 4LVZ | 4LX5 | 4LX6 | 4NYA | 4NYC |
| 4NYD | 4NYG | 4OQU | 4P20 | 4PDQ | 4QK8 |
| 4QK9 | 4QKA | 4QLM | 4QLN | 4RZD | 4TS0 |
| 4TS2 | 4TZX | 4TZY | 4WCQ | 4WCR | 4XNR |
| 4YAZ | 4YB0 | 4YB1 | 4ZC7 | 5C7U | 5C7W |
| 5NDH | 5NEF | ||||
| Test set 2 | |||||
| 1AJU | 1AM0 | 1BYJ | 1EHT | 1EI2 | 1F1T |
| 1F27 | 1FMN | 1FYP | 1J7T | 1KOC | 1KOD |
| 1MWL | 1NBK | 1NEM | 1PBR | 1Q8N | 1TOB |
| 1UTS | 1UUD | 1UUI | 1XPF | 1Y26 | 2BE0 |
| 2BEE | 2ET8 | 2F4U | 2FCZ | 2FD0 | 2GDI |
| 2O3X | 2OE5 | 2PWT | 2TOB | 3D2X | 3GX2 |
| 3SUX | 4P20 | ||||
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Nissen P, Hansen J, Ban N. Moore, Peter B, Steitz TA. (2000). The structural basis of ribosome activity in peptide bond synthesis. Science, 289, 920–930. [DOI] [PubMed] [Google Scholar]
- [2].Trapnell C, Hendrickson DG, Sauvageau M, Goff L, Rinn JL, Pachter L. (2013). Differential analysis of gene regulation at transcript resolution with RNA-seq. Nat. Biotechnol, 31, 46–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Watkins NJ, Bohnsack MT. (2012). The box C/D and H/ACA snoRNPs: key players in the modification, processing and the dynamic folding of ribosomal RNA. Wiley Interdiscip. Rev. RNA, 3, 397–414. [DOI] [PubMed] [Google Scholar]
- [4].Johansson J, Mandin P, Renzoni A, Chiaruttini C, Springer M, Cossart P. (2002). An RNA thermosensor controls expression of virulence genes in Listeria monocytogenes. Cell, 110, 551–561. [DOI] [PubMed] [Google Scholar]
- [5].Esteller M (2011). Non-coding RNAs in human disease. Nat. Rev. Genet, 12, 861–874. [DOI] [PubMed] [Google Scholar]
- [6].Crooke ST, Witztum JL, Bennett CF, Baker BF. (2018). RNA-targeted therapeutics. Cell Metab., 27, 714–739. [DOI] [PubMed] [Google Scholar]
- [7].Yin W, Rogge M. (2019). Targeting RNA: a transformative therapeutic strategy. Clin. Transl. Sci, 12, 98–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Hermann T (2016) Small molecules targeting viral RNA. Wiley Interdiscip. Rev. RNA, 7, 726–743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Warner KD, Hajdin CE, Weeks KM. (2018). Principles for targeting RNA with drug-like small molecules. Nat. Rev. Drug Discov, 17, 547–558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Costales MG, Childs-Disney JL, Haniff HS, Disney MD. (2020). How we think about targeting RNA with small molecules. J. Med. Chem, 63, 8880–8900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Fourmy D, Recht MI, Blanchard SC, Puglisi JD. (1996). Structure of the A site of Escherichia coli 16S ribosomal RNA complexed with an aminoglycoside antibiotic. Science, 274, 1367–1371. [DOI] [PubMed] [Google Scholar]
- [12].Lynch SR, Gonzalez RL, Puglisi JD. (2003). Comparison of X-ray crystal structure of the 30S subunit-antibiotic complex with NMR structure of decoding site oligonucleotide-paromomycin complex. Structure, 11, 43–53. [DOI] [PubMed] [Google Scholar]
- [13].Demirci H, Murphy F IV., Murphy E, Gregory ST, Dahlberg AE, Jogl G. (2013). A structural basis for streptomycin-induced misreading of the genetic code. Nat. Commun, 4, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Howe JA, Wang H, Fischmann TO, Balibar CJ, Xiao L, Galgoci AM, Malinverni JC, Mayhood T, Villafania A, Nahvi A, Murgolo N, Barbieri CM, Mann PA, Carr D, Xia E, Zuck P, Riley D, Painter RE, Walker SS, Sherborne B, de Jesus R, Pan W, Plotkin WA, Wu J, Rindgen D, Cummings J, Garlisi CG, Zhang R, Sheth PR, Gill CG, Tang H, Roemer T. (2015). Selective small-molecule inhibition of an RNA structural element. Nature, 526, 672–677. [DOI] [PubMed] [Google Scholar]
- [15].Ganser LR, Lee J, Rangadurai A, Merriman DK, Kelly ML, Kansal AD, Sathyamoorthy B, Al-Hashimi HM. (2018). High-performance virtual screening by targeting a high-resolution RNA dynamic ensemble. Nat. Struct. Mol. Biol, 25, 425–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Grate D, Wilson C. (2001) Inducible regulation of the S. cerevisiae cell cycle mediated by an RNA ap- tamer–ligand complex. Bioorg. Med. Chem, 9, 2565–2570. [DOI] [PubMed] [Google Scholar]
- [17].Panigaj M, Johnson MB, Ke W, McMillan J, Goncharova EA, Chandler M, Afonin KA. (2019) Aptamers as modular components of therapeutic nucleic acid nanotechnology. ACS nano, 13, 12301–12321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Zhang W, Szostak JW, Huang Z. (2016). Nucleic acid crystallization and X-ray crystallography facilitated by single selenium atom. Front Chem. Sci. Eng, 10, 196–202. [Google Scholar]
- [19].Fürtig B, Richter C, Wöhnert J, Schwalbe H. (2003). NMR spectroscopy of RNA. Chem. Bio. Chem, 7, 726–743. [DOI] [PubMed] [Google Scholar]
- [20].Lukavsky PJ. (2009) Structure and function of HCV IRES domains. Virus Res., 139, 166–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. (2000). The protein data bank. Nucleic Acids Res., 28, 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Pfeffer P, Gohlke H. (2007). DrugScoreRNA–knowledge-based scoring function to predict RNA-ligand interactions. J. Chem. Inf. Model, 47, 1868–1876. [DOI] [PubMed] [Google Scholar]
- [23].Krüuger DM, Bergs J, Kazemi S, Gohlke H. (2011). Target flexibility in RNA-ligand docking modeled by elastic potential grids. ACS Med. Chem. Lett, 2, 489–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Philips A, Milanowska K, Łach G, Bujnicki JM. (2013). LigandRNA: computational predictor of RNA-ligand interactions. RNA, 19, 1605–1616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Lang PT, Brozell SR, Mukherjee S, Pettersen EF, Meng EC, Thomas V, Rizzo RC, Case DA, James TL, Kuntz ID. (2009). DOCK 6: combining techniques to model RNA-small molecule complexes. RNA, 15, 1219–1230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Guilbert C, James TL. (2008). Docking to RNA via root-mean-square-deviation-driven energy minimization with flexible ligands and flexible targets. J. Chem. Inf. Model, 48,1257–1268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Sun LZ, Zhang D, Chen SJ. (2017). Theory and Modeling of RNA Structure and Interactions with Metal Ions and Small Molecules. Annu. Rev. Biophys, 46, 227–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Liu T, Lin Y, Wen X, Jorissen RN, Gilson MK. (2007). BindingDB: a web-accessible database of experimentally determined protein–ligand binding affinities. Nucleic Acids Res. 35, D198–D201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Philips A, Łach G, Bujnicki JM. (2015). Computational methods for prediction of RNA interactions with metal ions and small organic ligands. Methods Enzymol., 553, 261–285. [DOI] [PubMed] [Google Scholar]
- [30].Sun LZ, Jiang Y, Zhou Y, Chen SJ. (2020). RLDOCK: A New Method for Predicting RNA-Ligand Interactions. J. Chem. Theory Comput, 16, 7173–7183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Vicens Q, Mondragón E, Batey RT. (2011). Molecular sensing by the aptamer domain of the FMN riboswitch: a general model for ligand binding by conformational selection. Nucleic Acids Res., 39, 8586–8598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Yoshikawa N, Hutchison GR. (2019). Fast, efficient fragment-based coordinate generation for Open Babel. J Cheminform, 11, 49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Hawkins PCD, Skillman AG, Warren GL, Ellingson BA, Stahl MT. (2010). Conformer Generation with OMEGA: Algorithm and Validation Using High Quality Structures from the Protein Databank and Cambridge Structural Database. J. Chem. Inf. Model, 50, 572–584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. (2004). UCSF Chimera- visualization system for exploratory research and analysis. J. Comput. Chem, 25, 1605–1612. [DOI] [PubMed] [Google Scholar]
- [35].Still WC, Tempczyk A, Hawley RC, Hendrickson T. (1990). Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc, 112, 6127–6129. [Google Scholar]
- [36].Hawkins GD, Cramer CJ, Truhlar DG. (1995). Pairwise solute descreening of solute charges from a dielectric medium. Chem. Phys. Lett, 246, 122–129. [Google Scholar]
- [37].Zou X, Sun Y, Kuntz ID. (1999). Inclusion of solvation in ligand binding free energy calculations using the generalized-born model. J. Am. Chem. Soc, 121, 8033–8043. [Google Scholar]
- [38].Nymeyer H, Garcia AE. (2003). Simulation of the folding equilibrium of a helical peptides: a comparison of the generalized Born approximation with explicit solvent. Proc. Natl. Acad. Sci. U.S.A, 100, 13934–13939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Liu HY, Kuntz ID, Zou X. (2004). Pairwise GB/SA scoring function for structure-based drug design. J. Phys. Chem. B, 108, 5453–5462. [Google Scholar]
- [40].Liu HY, Zou X. (2006). Electrostatics of ligand binding: parameterization of the generalized Born model and comparison with the Poisson-Boltzmann approach. J. Phys. Chem. B, 110, 9304–9313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Kang X, Shafer RH, Kuntz ID. (2004). Calculation of ligand-nucleic acid binding free energies with the generalized-born model in DOCK. Biopolymers, 73, 192–204. [DOI] [PubMed] [Google Scholar]
- [42].Wright SJ. (2015). Coordinate descent algorithms. Math. Program, 151, 3–34. [Google Scholar]
- [43].Ruiz-Carmona S, Alvarez-Garcia D, Foloppe N, Garmendia-Doval AB, Juhos S, Schmidtke P, Barril X, Hubbard RE, Morley SD. (2014). rDock: a fast, versatile and open source code for docking ligands to proteins and nucleic acids. PLOS Comput. Biol, 10, e1003571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Trott O, Olson AJ. (2010). AutoDock Vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization and multithreading. J. Comput. Chem, 31, 455–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Simonson T, Brunger AT. (1994). Solvation Free Energies Estimated from Macroscopic Continuum Theory: An Accuracy Assessment. J. Phys. Chem, 98, 4683–4694. [Google Scholar]
- [46].Vallone B, Miele A, Vecchini P, Chiancone E, Brunori M. (1998). Free Energy of Burying Hydrophobic Residues in the Interface Between Protein Subunit. Proc. Natl. Acad. Sci. U.S.A, 95, 6103–6107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Raschke TM, Tsai J, Levitt M. (2001). Quantification of the Hydrophobic Interaction by Simulations of the Aggregation of Small Hydrophobic Solutes in Water. Proc. Natl. Acad. Sci. U.S.A, 98, 5965–5969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Treesuwan W, Wittayanarakul K, Anthony NG, Huchet G, Alniss H, Hannongbua S, Khalaf AI, Suckling CJ, Parkinson JA, Mackay SP. (2009). A Detailed Binding Free Energy Study of 2:1 Ligand-DNA Complex Formation by Experiment and Simulation. Phys. Chem. Chem. Phys, 11, 10682–10693. [DOI] [PubMed] [Google Scholar]
- [49].Morley SD, Afshar M. (2004). Validation of an empirical RNA-ligand scoring function for fast flexible docking using Ribodock. J. Comput. Aided Mol. Des, 18, 189–208. [DOI] [PubMed] [Google Scholar]