Accelerated Computation of Free Energy Profile at Ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semiempirical Reference Potential. 4. Adaptive QM/MM

Abstract

Although quantum mechanical/molecular mechanics (QM/MM) methods are now routinely applied to the studies of chemical reactions in condensed phases and enzymatic reactions, they may experience technical difficulties when the reactive region is varying over time. For instance, when the solvent molecules are directly participating in the reaction, the exchange of water molecules between the QM and MM regions may occur on a time scale comparable to the reaction time. To cope with this situation, several adaptive QM/MM schemes have been proposed. However, these methods either add significantly to the computational cost or introduce artificial restraints to the system. In this work, we developed a novel adaptive QM/MM scheme and applied it to the study of a nucleophilic addition reaction. In this scheme, the configuration sampling was performed with a small QM region (without solvent molecules), and the thermodynamic properties under another potential energy function with a larger QM region (with a certain number of solvent molecules and/or different levels of QM theory) are computed via extrapolation using the reference-potential method. Our simulation results show that this adaptive QM/MM scheme is numerically stable, at least for the case studied in this work. Furthermore, this method also offers an inexpensive way to examine the convergence of the QM/MM calculation with respect to the size of the QM region.

Graphical Abstract

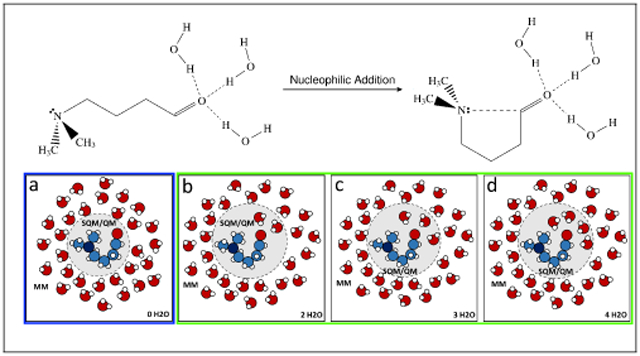
1. Introduction

Hybrid quantum mechanical/molecular mechanical (QM/MM) methods are nowadays well accepted for the simulations of chemical reactions in condensed phases and enzymatic reactions. ^1-10 However, applications of these methods are always hindered by their steep computational expense and complexity in domain partitioning. First, in order to determine the reaction mechanism, a long molecular dynamics simulation at a certain ab initio level is needed, from which statistical properties can be extracted reliably. With a subfemtosecond time step for propagation, 10⁶–10⁹ steps of energy and force evaluations are required to reach a nanosecond to microsecond time scale. Second, the size of the QM region matters. Defining the QM region is often based on chemical intuition and is inevitably a compromise between accuracy and efficiency. A small QM region may lead to systematically biased results.^11-15 Last but not least, the partitioning of the whole system into the QM and the MM regions is nontrivial, especially when solvent molecules are explicitly participating in the reactions. By including some of the solvent molecules near the solute molecule into the QM region, one can capture the quantum mechanical interaction between the solute and the solvent molecules. However, it introduces another technical difficulty in maintaining dynamic continuity when the exchange of solvent molecules between the QM and the MM regions takes place, especially when an abrupt on-the-fly repartitioning scheme of the QM and MM regions is adopted. To surmount this difficulty, various schemes of adaptive QM/MM methods have been proposed,^16-19 which can be categorized broadly into restrained QM/MM schemes^20-22 and adaptive QM/MM schemes.^23-30 In the former class of schemes, solvent exchange between the QM and the MM regions is prevented by applying a restraining potential. However, the evolution of the system under study is no longer under a realistic Hamiltonian due to the introduction of an artificial restraint, and an unbiasing process is necessary. In the adaptive QM/MM scheme, an effective QM/MM potential is adopted by a weighted average of the potentials from multiple means of partitioning of the system with different combinations of the solute and solvent molecules. This may markably increase the computational expense.

Fortunately, if we are interested in equilibrium thermodynamic properties only, for instance the free energy profile, instead of real dynamics, these properties can be calculated indirectly via the reference-potential approach,^31-34 of which the idea has been applied to many studies.^35-59 Specifically, the QM/MM partitioning with a fixed number of solvent molecules in the QM region is the target Hamiltonian state denoted by H₁. The specific water molecules inside the QM region may vary from one snapshot to another, and the exchange of solvent molecules between the QM and MM regions is just a permutation of the state before the exchange takes place. Meanwhile, another partitioning scheme excluding all the solvent molecules from the QM region corresponds to Hamiltonian H₀, which serves as the reference potential. The ensemble average of an operator X under H₁ can be computed from the ensemble of H₀ via reweighting:⁶⁰

$$\langle X{\rangle }_1=\frac{\int X{e}^{-\beta H_1}\mathrm{d}\mathbf{R}}{\int e^{-\beta H_1}\mathrm{d}\mathbf{R}}=\frac{\int X{e}^{\beta (H_0-H_1)}{e}^{-\beta H_0}\mathrm{d}\mathbf{R}}{\int e^{\beta (H_0-H_1)}{e}^{-\beta H_0}\mathrm{d}\mathbf{R}}=\frac{{\langle X{e}^{\beta (H_0-H_1)}\rangle }_0}{\langle e^{\beta (H_0-H_1)}{\rangle }_0},$$

where 〈·〉 denotes the ensemble average or expectation, and the subscript “0” or “1” indicates the Hamiltonian under which the ensemble is calculated. Here, $\frac{e^{\beta (H_0-H_1)}}{{\langle e^{\beta (H_0-H_1)}\rangle }_0}$ can be considered as the weight under H₁ for the configurations sampled with H₀. For a generalized ensemble, the equation can be slightly more complicated, but the idea is the same. Recently, Jia et al proposed a reference-potential method for the free energy calculations at an expensive level of theory using a unique Boltzmann ensemble.⁴³ Li et al extended this method to mixed ensembles from, but not limited to, umbrella sampling (US)⁶⁰ simulations.⁴⁹ In these methods, a long simulation using a less expensive Hamiltonian is performed to explore the phase space, and from this simulation a free energy profile corresponding to this Hamiltonian can be estimated using well-established postprocessing methods such as the multistate Bennett acceptance ratio (MBAR)^61,62 and the weighted histogram analysis method (WHAM).^63-65 Next, a correction in the free energy from this inexpensive Hamiltonian to the Hamiltonian of interest is calculated by using thermodynamic perturbation (TP).⁶⁶ In this way, expensive direct simulations at the high level Hamiltonian can be avoided. When the correction for a mixed ensemble is calculated, weight factors from the MBAR analysis should be used.⁴⁹ Therefore, the TP should be carried out with nonuniform weights for the samples. Thermodynamic expectations of any structural properties can be computed in a similar way.^49,55

In this work, we put forth a new method for the free energy calculations with an adaptive QM domain for the study of the intramolecular nucleophilic addition reaction of Me₂N–(CH₂)₃–CH=O (NCO) molecule (Fig. 1), utilizing the idea of energy reweighting in the reference-potential methods. It has been shown in a previous study that explicit solvation matters for the thermodynamic property calculations along the reaction.⁶⁷ The umbrella sampling simulations are carried out only at the hybrid semiempirical/MM level, specifically PM6⁶⁸/MM level, without a single water molecule in the QM region. After the simulation, the trajectories are postprocessed for semiempirical QM/MM or ab initio QM/MM energy calculations with a certain number of solvent molecules included in the QM region, from which the free energy profiles at these levels are obtained. This paper is organized in the following way. In section 2, the theory behind this method and the simulation setup are explained. The results are presented subsequently with discussion in section 3. Finally, a conclusion for this study is presented in section 4.

Figure 1:

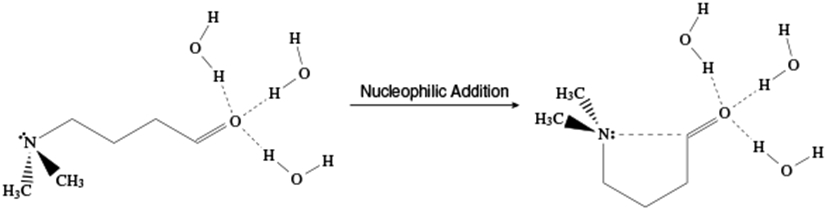
Nucleophilic addition reaction of Me₂N–(CH₂)₃–CH=O (NCO) molecule studied in this work.

2. Method

2.1. Multistate Thermodynamic Perturbation (MsTP) Method

The MsTP method, previously known as MBAR+wTP, was proposed by Li et al.⁴⁹ recently. Derivation of the MsTP method has been fully presented in ref. 49. In this method, enhanced sampling methods such as umbrella sampling simulations are conducted under a reference (and usually inexpensive) Hamiltonian, for instance, semiempirical (SE) QM/MM. Thermodynamics properties under this reference Hamiltonian can be obtained using MBAR analysis, and then they are corrected to the target Hamiltonian using the weighted thermodynamic perturbation. These steps can be integrated into the MBAR formulation as explained in the following.

With trajectories from K simulations using different potential energy functions U_k as is typically done in umbrella sampling, thermodynamic properties, which depend only on coordinates, under another potential energy function U_t can be computed via

$$\langle \mathbf{A}{\rangle }_t=\frac{\sum _{n=1}^N{w}_t({\mathbf{r}}_n)\mathbf{A}({\mathbf{r}}_n)}{\sum _{n=1}^N{w}_t({\mathbf{r}}_n)},$$ (1)

in which N_k is the number of configurations extracted from the kth simulation and

$$w_t({\mathbf{r}}_n)=\frac{\text{exp}[-\beta U_t({\mathbf{r}}_n)]}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-\beta U_k({\mathbf{r}}_n)]}$$ (2)

is the unnormalized weight of configuration r_n under U_k. $N=\sum _k{N}_k$ is the total number of snapshots. Here, f_k is known as the free energy corresponding to U_k and can be obtained by iteratively solving the MBAR equations

$$f_i=-{\beta }^{-1}\text{ln}\sum _{n=1}^N\frac{\text{exp}[-\beta U_i({\mathbf{r}}_n)]}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-\beta U_k({\mathbf{r}}_n)]},\forall i=1,\dots ,K.$$ (3)

In US, the potential energy functions used for configuration sampling are

$$U_k({\mathbf{r}}_n)=U_0({\mathbf{r}}_n)+W_k({\mathbf{r}}_n),$$ (4)

where U₀(r) and W_k(r) are the unbiased potential energy function and the biasing potential for the kth simulation, respectively. Equation 2 can be rewritten as

$$w_t({\mathbf{r}}_n)=\frac{\text{exp}[-\beta \Delta U_t({\mathbf{r}}_n)]}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-\beta W_k({\mathbf{r}}_n)]},$$ (5)

with ΔU_t(r) = U_t(r) – U₀(r). Further defining the free energy f_t corresponding to the potential energy function U_t(r)

$$f_t=-{\beta }^{-1}\text{ln}\sum _{n=1}^N{w}_t({\mathbf{r}}_n),$$ (6)

we obtain the normalized weight for configuration r_n under the potential energy function U_t(r)

$${\tilde{w}}_t({\mathbf{r}}_n)=\frac{\text{exp}[\beta f_t-\beta \Delta U_t({\mathbf{r}}_n)]}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-\beta W_k({\mathbf{r}}_n)]},$$ (7)

and eq. 1 can be simplified as

$$\langle \mathbf{A}{\rangle }_t=\sum _{n=1}^N{\tilde{w}}_t({\mathbf{r}}_n)\mathbf{A}({\mathbf{r}}_n).$$ (8)

It can be easily identified that for a single unbiased simulation with K = 1 and W = 0, eq. 7 can be rewritten as the normal TP equation. Therefore, the idea behind eq. 7 can be seen as multistate thermodynamics perturbation (MsTP). MsTP has been applied to the calculations of free energy profiles for chemical reactions in condensed phase rendered in both one dimensional⁴⁹ and two dimensional⁵⁵ reaction coordinates. The computational expense decreases by 2 orders of magnitude comparing with direct QM/MM calculations while maintaining a high accuracy.

Specifically for this adaptive QM/MM calculation, potential energy function U₀(r) corresponds to the partitioning with a solvent-free QM region described by a semiempirical Hamiltonian PM6. W_k(ξ(r)) is the restraining potential on a predefined collective variable (CV) ξ(r) that may enhance the phase space sampling in a certain region. $U_M^{\prime }(\mathbf{r})$ is the potential energy function for the partitioning with M solvent molecules in the QM region described by either a semiempirical QM or an ab initio QM level of theory. The prime sign here is to emphasize that the QM level of theory can be either the same as or different from the reference Hamiltonian. If A is an indication function δ of some chosen CV ξ(r)

$$\delta ({\xi }_m-\xi (\mathbf{r}))=\{\begin{array}{cc}1,\hfill & \text{if}-\Delta \xi ∕2<{\xi }_m-\xi (\mathbf{r})<\Delta \xi ∕2\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}},$$ (9)

we have the PMF for $U_M^{\prime }(\mathbf{r})$ as

$$F_M({\xi }_m)=-{\beta }^{-1}\text{ln}\sum _{n=1}^N{\omega }_M({\mathbf{r}}_n)\delta ({\xi }_m-\xi ({\mathbf{r}}_n))$$ (10)

defined up to an additive constant, and

$$w_M({\mathbf{r}}_n)=\frac{\text{exp}[-\beta \Delta U_M^{\prime }({\mathbf{r}}_n)]}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-\beta W_k({\mathbf{r}}_n)]}=\frac{\text{exp}[-\beta (U_M^{\prime }({\mathbf{r}}_n)-U_0({\mathbf{r}}_n))]}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-\beta W_k({\mathbf{r}}_n)]}.$$ (11)

Similarly, the potential of mean force (PMF) for U₀(r) is

$$F_0({\xi }_m)=-{\beta }^{-1}\text{ln}\sum _{n=1}^N{\omega }_0({\mathbf{r}}_n)\delta ({\xi }_m-\xi ({\mathbf{r}}_n)),$$ (12)

in which

$${\omega }_0({\mathbf{r}}_n)=\frac{1}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-\beta W_k({\mathbf{r}}_n)]}.$$ (13)

Random noise in the potential of mean force from finite sampling was eliminated by a Gaussian smoothing on the density-of-states of $\Delta U_M^{\prime }(\mathbf{r})$.⁶⁹ Gaussian processes regression (GPR) method⁷⁰ is used to eliminate the statistical noise in the free energy profile from the MsTP calculation.

2.2. Model Setup

Me₂N–(CH₂)₃–CH=O (NCO) was solvated in a TIP3P water⁷¹ sphere with a radius of 20 Å centering at the NCO molecule, which contains 1020 water molecules. The whole system was optimized by 2000 steps of steepest descent algorithm and 3000 steps of conjugate gradient method. The optimized structure was heated up to 300 K in 1 ns and then further relaxed for 10 ns. Periodic boundary condition was not applied, and the water sphere was restrained by a soft half-harmonic potential with a force constant of 10 kcal · mol⁻¹ · Å⁻² to prevent evaporation. The integration time step was set to 2 fs, and the SHAKE algorithm was enabled to constrain all the bonds involving hydrogen atoms. The nonbonded interaction was fully counted without any truncation. The van der Waals (vdW) parameters for the NCO molecule were taken from the general AMBER force field (GAFF)⁷² for the ring-opening structure, and the AM1bcc charges from the reactant configuration were assigned to the NCO molecule. The temperature was regulated to 300 K using the Langevin dynamics with a collision frequency of 1 ps⁻¹.⁷³

2.3. Umbrella Sampling

The phase space exploration was assisted by umbrella sampling.⁶⁰ The distance between the nitrogen and carbonyl carbon atoms of the NCO molecule was chosen as the CV ξ(r), which ranges from 1.50 to 5.00 Å with an increment of 0.05 Å. Overlap matrix proposed by Klimovich et al.⁷⁴ was used to monitor the degree of overlap between adjacent simulation windows. Extra windows were added when the overlap between neighboring windows are insufficient, resulting in 84 windows in total. The setup of the restraint potential in each window simulation can be found in the Supporting Information (SI). The central region contains only the NCO molecule, and PM6 was used for its interaction potential. For each US window, the whole system was optimized by 1000 steepest descent steps and 1000 conjugate gradient steps. The relaxed system was heated to 300 K in 100 ps, followed by a 1-ns production simulation. The temperature was maintained at 300 K by using the Langevin dynamics with a collision frequency of 1 ps⁻¹. The integration time step was set to 1 fs with SHAKE turned on for both the MM and QM regions. The configurations were saved every 1 ps for subsequent free energy analysis. The free energy profile at this level was computed using the MBAR analysis method. After that, single point energies under PM6/MM and ωB97X-D⁷⁵/6-31+G(d,p)/MM levels were obtained for the MsTP calculations. For the single point energy calculations, the QM region was augmented with M = 0, 2, 3, or 4 water molecules that are closest to the oxygen atom in the carbonyl group. These water molecules were chosen on the fly. The propagation of the molecular dynamics simulations and single point energy calculations were carried out using the AMBER 18 package suite.⁷⁶ Interfacing with Gaussian 16 package⁷⁷ was utilized when wB97X-D energy calculations were requested.

3. Results and Discussion

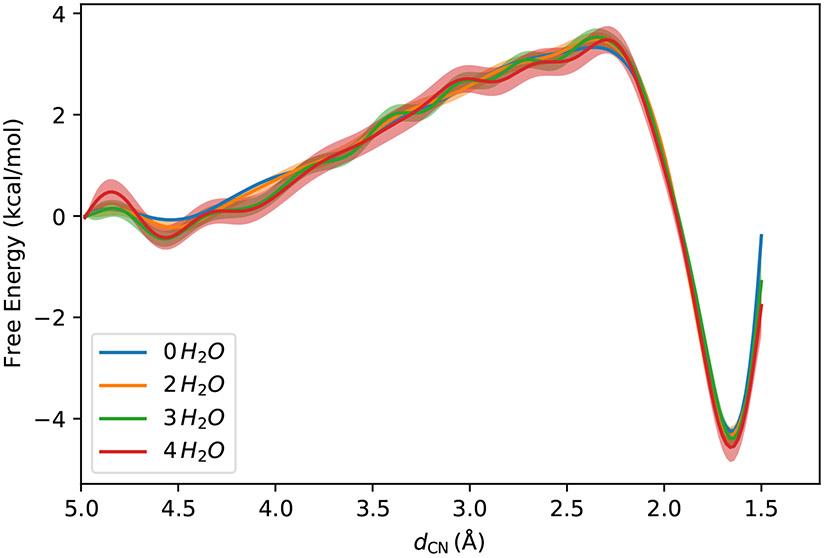
3.1. Potential of Mean Force at the PM6/MM Levels

The free energy profiles at the PM6/MM level are shown in Fig. 2. Since in the US simulations the QM region had no water molecules included, the uncertainty of the free energy profile is very small. The free energy profile shows a shallow well at d_CN = 4.54 Å for the reactant but a deep well at d_CN = 1.66 Å for the product. The barrier for the forward reaction is 3.4 kcal/mol, and the reaction free energy is 4.2 kcal/mol. By including two water molecules in the QM region, the free energy profile shows only a small difference from that with a solvent-free QM region. The locations of the reactant and the product are nearly unchanged, with the new locations being d_CN = 4.52 Å and d_CN = 1.66 Å for the reactant and the product, respectively. The barrier for the forward reaction becomes 3.5 kcal/mol, and the reaction free energy is 4.3 kcal/mol. The PM6 free energy profile with two water molecules in the QM region has already reached convergence by comparing it with those enveloping more water molecules into the QM region. The results indicate that under the PM6/MM level of theory, the solvent molecules mainly play a role as an electrostatic per-turber to the NCO molecule that only weakly tunes the reaction. As shown in Fig. S1, the magnitude of charge transferred from the solute molecule to the solvent is smaller than 0.1e, even when the C-N bond has formed. In order to compare the adaptive simulation proposed in the current work with the restrained simulation method, we performed another round of umbrella sampling simulation, with additional restraints applied to the distances between the oxygen atoms in the NCO molecule and three water molecules nearby. The harmonic restraining potential $W(d)=\frac{1}{2}{k}_d(d-d_0{)}^2$ centers at d₀ = 2.8 Å and the strength k_d is 40 kcal · mol⁻¹ · Å⁻². The results are plotted in Fig. S2, which shows a nice agreement between the adaptive simulation method and the restrained simulation method.

Figure 2:

Free energy profiles at the PM6/MM levels with different numbers of water molecules in the QM region. The shaded areas are the 95% confidence intervals.

3.2. Potential of Mean Force at the DFT/MM Levels

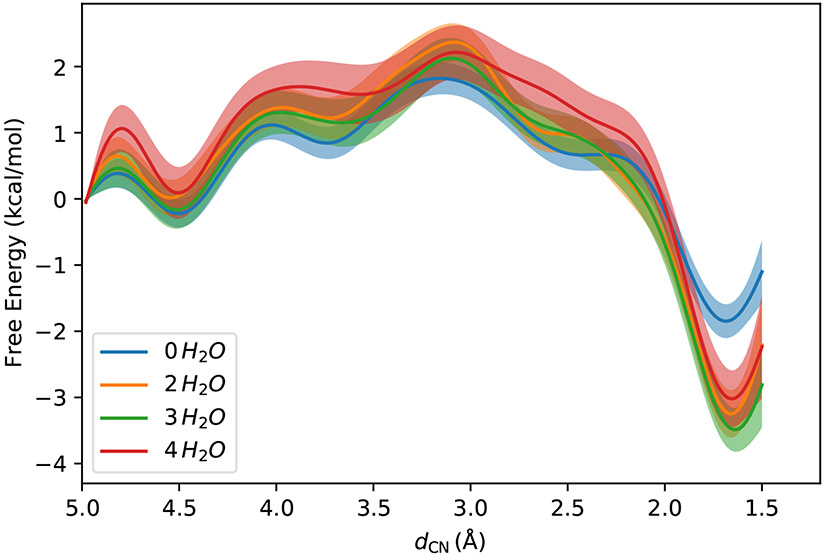
Extrapolation to the DFT/MM level using the US trajectories from the PM6/MM simulations is also possible, and the free energy profiles are shown in Fig. 3. Similar to the results at the PM6/MM level, the locations of the reactant, the products and the transition states are nearly independent of the number of water molecules in the QM region. Without water molecules in the QM region, the free energy barrier for the forward reaction and the reaction free energy are 2.0 kcal/mol and −1.6 kcal/mol, respectively. Both of them are much smaller than those under the PM6/MM level of theory in their absolute values. An early transition state can be observed, which has a longer C–N bond length than that under the PM6/MM level of theory. This is not unexpected, since the basis set in the DFT calculation was much more diffusive than that in the PM6 calculations. When two water molecules are added to the QM region, the free energy profile shows large deviations from the one at the same level of theory but with no solvent molecules in the QM region, especially at the product side. When solvent molecules in the MM region are represented as background charges that polarize the electronic structure of the QM region, charge transfer is not allowed between the QM solute molecule and the MM solvent molecules. When two nearest solvent molecules are bracketed into the QM region, the water molecules can accommodate the extra electrons around the oxygen atom in the carbonyl group, especially after the formation of the C–N bond. Therefore, the product is stabilized by 1.6 kcal/mol, and the reaction free energy becomes −3.3 kcal/mol. The free energy barrier for the forward reaction increases to 2.4 kcal/mol. Adding more water molecules into the QM region does not significantly change the profile. With three water molecules in the QM region, the reactant and the product are located at d_CN = 4.52 Å and 1.64 Å, and the free energy barrier and the reaction free energy are 2.3 kcal/mol and −3.3 kcal/mol. With four water molecules in the QM region, the reactant and the product are located at d_CN = 4.50 Å and 1.66 Å, and the free energy barrier and the reaction free energy are 2.1 kcal/mol and −3.1 kcal/mol. Considering the uncertainties in the free energy profiles, these numbers are statistically identical. Therefore, when two water molecules are included in the QM region, the free energy profile has converged.

Figure 3:

Free energy profiles at the DFT/MM levels with different numbers of water molecules in the QM region. The shaded areas are the 95% confidence intervals.

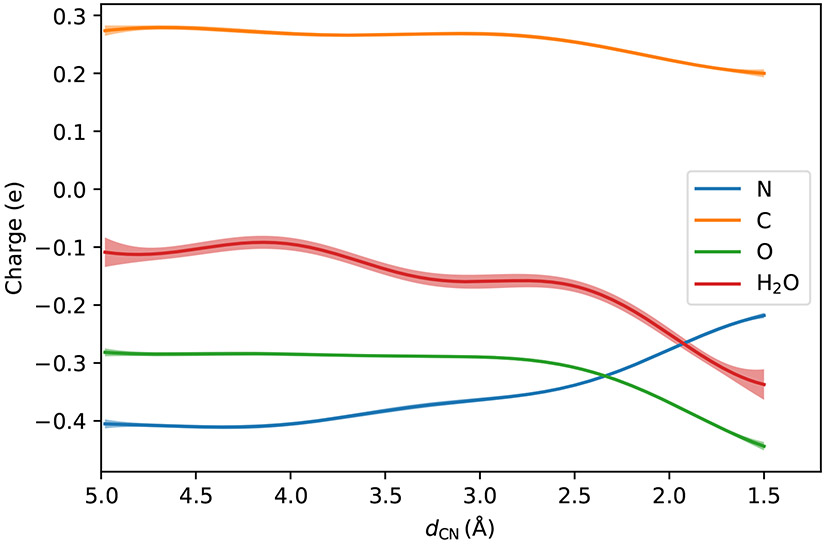
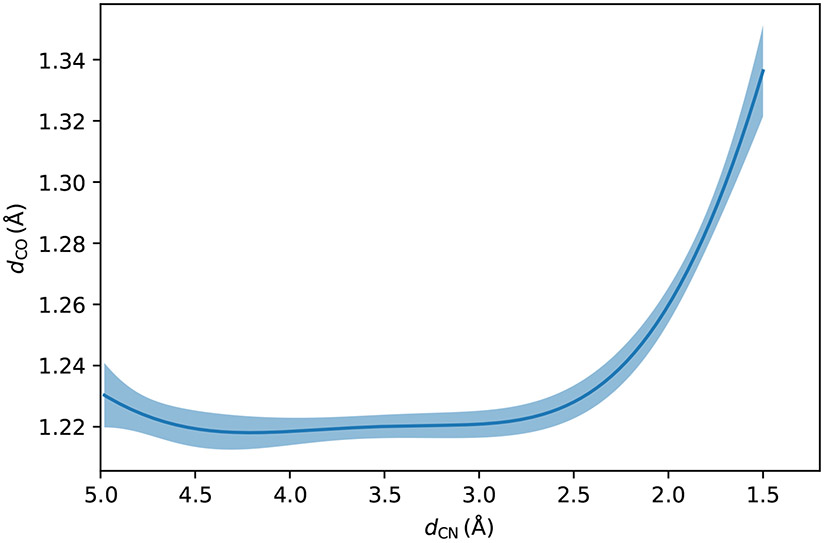
The variations of the CM5 charges⁷⁸ of the polar atoms in the NCO molecule during the reaction are shown in Fig. 4, with the atomic charges of the bonded hydrogen atoms merged into those of the heavy atoms. This shows that when the nitrogen atom approaches the carbon atom in the carbonyl group, the lone pair electrons of the nitrogen atom become shared electrons between the nitrogen atom and the carbon atom, and push the shared electrons in the carbonyl group to the oxygen side. Some portion of the electrons drifts away from oxygen atom in the carbonyl group to the water molecules hydrogen-bonded to the carbonyl group. As a result, the CM5 charge of the nitrogen atom rises (becomes less negative) by about 0.187e, that of the oxygen atom in the carbonyl group declines by about 0.162e, and the four water molecules near the carbonyl oxygen atom accept about 0.228 electron altogether. Since the carbonyl carbon atom accepts electrons from the nitrogen atom but donates electrons to the oxygen atom, its CM5 charge decreases by only 0.074e. This agrees with the previous observation of the N⁺∣C–O⁻ pattern.⁷⁹ Since the bond order between the carbon atom and the oxygen atom in the carbonyl group decreases, the bond length increases during the reaction, as can be seen in Fig. 5. In the reactant region, the CO bond distance remains around 1.22 Å. When the distance between the nitrogen atom and the carbon atom is smaller than 3.0 Å (on the product side), the CO bond length gets elongated quickly.

Figure 4:

Alternations of atomic CM5 charges along the reaction at the DFT/MM level with four water molecules in the QM region. The shaded areas are the 95% confidence intervals.

Figure 5:

Variations of the C=O bond length along the reaction at the DFT/MM level with four water molecules in the QM region. The shaded area is the 95% confidence interval.

If we define a buffer region between the QM and the MM regions, this method can be straightforwardly combined with the permuted adaptive partitioning (PAP) scheme²⁴ by setting the PAP Hamiltonian at a certain QM level of theory as the target Hamiltonian. In spite of its rigor, the PAP partition scheme is computationally very demanding and scales poorly with the size of the buffer region. Therefore, only one permutation is considered in this work, in which the nearest M solvent molecules are bracketed into the QM region. The consequence is the loss of the detailed balance and the continuity of the trajectory because of the introduction of human intervention in picking the water molecules to be included in the QM region. Other partition schemes can be adopted. However, as shown in Fig. S3, the permutation we have used (bracketing the nearest M solvent into the QM region) in this work has the largest impact on the free energy change from the reactant to the product, since it can best relax the extra electron density around the oxygen atom in the NCO molecule once the C–N bond has formed. The other scheme (with the second and third nearest water molecules in the QM region) underestimates the reaction free energy, due to that the magnitude of the electron transfer from the NCO molecule to the solvent is underestimated, especially at the product side.

4. Conclusion

In this work, we proposed a novel method for adaptive QM/MM simulations of chemical reaction in a homogeneous environment, which is based on the reference-potential method and can be easily implemented. With this method, extrapolations to a different level of theory and/or to a different size of the QM region are made possible. The uncertainty increases with the “aggressiveness” of the extrapolation. Increasing the number of water molecules being bracketed into the QM region increases the standard deviation of the potential of mean force. Fortunately, this numerical difficulty can be easily solved by extending the length of the simulation at the low level of theory. This method also offers a convenient way to check the convergence of the QM/MM calculations with respect to the size of the QM region even in a heterogeneous but invariant embedding environment. Semiempirical methods such as PM6 should be used with care, due to the difficulty in handling the charge transfer effect with minimum basis sets.