Cointegration of single-transistor neurons and synapses by nanoscale CMOS fabrication for highly scalable neuromorphic hardware

Cointegration of single-transistor neurons and synapses for highly scalable neuromorphic hardware is demonstrated.

Abstract

Cointegration of multistate single-transistor neurons and synapses was demonstrated for highly scalable neuromorphic hardware, using nanoscale complementary metal-oxide semiconductor (CMOS) fabrication. The neurons and synapses were integrated on the same plane with the same process because they have the same structure of a metal-oxide semiconductor field-effect transistor with different functions such as homotype. By virtue of 100% CMOS compatibility, it was also realized to cointegrate the neurons and synapses with additional CMOS circuits. Such cointegration can enhance packing density, reduce chip cost, and simplify fabrication procedures. The multistate single-transistor neuron that can control neuronal inhibition and the firing threshold voltage was achieved for an energy-efficient and reliable neural network. Spatiotemporal neuronal functionalities are demonstrated with fabricated single-transistor neurons and synapses. Image processing for letter pattern recognition and face image recognition is performed using experimental-based neuromorphic simulation.

INTRODUCTION

Although software-based artificial neural networks (ANNs) have led to breakthroughs in a variety of intelligent tasks, they inevitably have inherent delays and energy consumption because the hardware structure to support the ANNs is still based on the von Neumann architecture (1–3). To overcome these limitations, hardware-based ANNs, known as brain-inspired neuromorphic systems, have been intensively studied (4–6). The human brain consists of neurons for the information encoding and synapses for the memory and learning function, as shown in Fig. 1A. There are about 10¹¹ neurons and 10¹⁵ synapses, and thus, it is important to implement neurons and synapses with high density and low power to mimic the brain in hardware, especially for mobile devices and Internet of Things applications (7, 8).

Fig. 1. Concept of cointegrated single-transistor neurons and synapses.

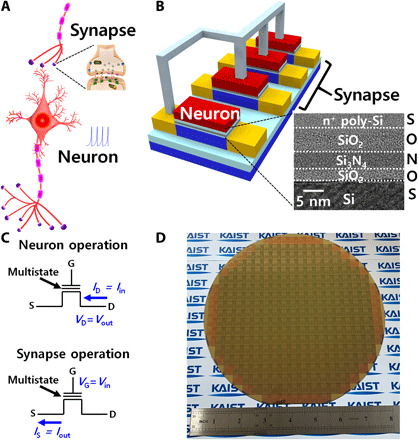
(A) Schematic of biological neuron and synapse. About 10¹¹ neurons and 10¹⁵ synapses are densely interconnected in human brain. (B) Schematic of cointegrated single-transistor neurons and synapses. They have exactly the same SONOS structure, which includes a charge trap layer (Si₃N₄) in the gate dielectrics as shown in the cross-sectional transmission electron microscopy (TEM) image. They are fabricated with the same fabrications and connected through metallization. (C) Operation scheme of the neuron and synapse. The input and output of the neuron are current and voltage, respectively, while those of the synapse are voltage and current. (D) Fabricated 8-inch wafer in which single-transistor neurons, synapses, and additional CMOS circuits were cointegrated. It was fabricated with 100% standard Si CMOS fabrications. Photo Credit: J.-K. Han, Korea Advanced Institute of Science and Technology (KAIST).

Neurons are mainly composed of complementary metal-oxide semiconductor (CMOS)–based circuits, while synapses primarily comprise memristors (9–15). However, circuit-based neurons are problematic for high packing density and power consumption with low cost because they are composed of a capacitor, integrator, and comparator including many transistors (16, 17). To overcome the limitations of circuit-based neurons, few works to cointegrate memristor-based artificial neuron devices and synaptic devices in a single crossbar array for a fully memristive neural network have been reported (18–20). Memristor-based neurons were realized with a single device, diffusive memristor (SiO_x:Ag), or metal-insulator transition materials (NbO_x and VO_x). Meanwhile, neuronal inhibition and tunability of firing threshold voltage are important for an energy-efficient and reliable neural network. The inhibitory function of the neuron related to biological lateral inhibition can improve energy efficiency by firing only specific neurons and enhance learning efficiency by enabling winner-takes-all (WTA) mechanism (21–23). In addition, the tunable firing threshold voltage related to biological homeostasis can allow reliable computation even when some neurons and synapses fail by process variations and endurance problems (24–26). However, the memristor-based neurons could not self-function for control of neuronal inhibition and firing threshold voltage because of the lack of controllability.

On the other hand, it is advantageous that neuron devices and synaptic devices have the same homotypic structures and materials because simultaneous integration of neurons and synapses in a single chip with the same fabrication process is possible. Specific interconnections owing to inherent heterotypic structures and materials can impose constraints on reducing packing density and simplifying process complexity. Also, extra energy consumption cannot be avoided at the interface between the neurons and the synapses. However, there was no work that neuron devices and synapse devices are cointegrated with having exactly the same structures and materials.

The metal-oxide semiconductor field-effect transistor (MOSFET) structure is attractive for commercialization because it has been verified for more than 60 years. In addition, the neuromorphic hardware should contain additional CMOS circuits to support processing units, peripheral interfaces, memory, clocking circuits, and input/output (I/O) for a complete application, as well as neurons and synapses (27–30). Therefore, if both neuron devices and synaptic devices can be realized with the same MOSFET structures, then commercialization of highly scalable neuromorphic system can be boosted by cointegration of neurons, synapses, and additional CMOS circuits on the same plane with commercial CMOS fabrication.

In this work, highly scalable neuromorphic hardware was implemented by simultaneously integrating multistate single-transistor neurons and synapses on the same plane, in which both devices have the same homotypic MOSFET structure. In detail, the MOSFET for a neuron and a synapse encloses a charge trap layer in gate dielectrics with the same manner as a commercial flash memory based on a silicon-oxide-nitride-oxide-silicon (SONOS) structure that comprise a gate polycrystalline Si (S), blocking SiO₂ (O), charge trap Si₃N₄ (N), tunneling SiO₂ (O), and channel single-crystalline Si (S). Because of this CMOS compatibility, they were fabricated and integrated on the same plane using the standard Si CMOS fabrication. It is possible to cointegrate single-transistor neurons and synapses with CMOS circuits for processing units, peripheral interfaces, memory, clocking circuits, and I/O at the same time, and thus, cointegration of the entire neuromorphic system is available. Therefore, a highly scalable neural network can be implemented in a single chip, which can enhance packing density, reduce chip cost, and simplify fabrication procedures. Neuron devices and synaptic devices were fabricated and directly interconnected, and their connection properties were analyzed. The abovementioned charge trap Si₃N₄ in the MOSFET can allow multistates. The multistates according to trapped charges control the excitatory/inhibitory function or change the firing threshold voltage in the neuron, while they regulate synaptic weight in the synapse. Although the applicability of charge trap flash memory as a synapse has already been confirmed by taking advantage of its maturity of device technologies, stable multistate operations, high ratio of on/off conductance, and superior retention characteristics (31, 32), cointegration of a Si-based single-transistor neuron with Si-based synapses has not been reported ever as a homotypic configuration. Homotypic neurons and synapses were directly connected to realize spatiotemporal neural computations. At the same time, CMOS circuits such as a current mirror and inverter, which are key elements for analog and digital circuits, were fabricated on the same plane to show the feasibility of cointegration of the interface and control circuits. In addition to real device fabrication, image recognition was successfully implemented with the aid of experimental-based simulations.

RESULTS

Unit device characteristics of neuron and synapse

N-channel single-transistor neuron and synapse have the same SONOS structure, as shown in Fig. 1B. The intercalated charge trap nitride (Si₃N₄) in the multilayered gate dielectrics allows multistates according to the amount of trapped charges. They can perform two functions: (i) enable excitatory/inhibitory function or tuning the firing threshold voltage (V_T,firing) in the neuron and (ii) control weight update in the synapse. Like the homotype, the neuron and the synapse have the same structure but operate differently, as shown in Fig. 1C. For neuron operation, input current (I_in) collected from the presynapses is applied to a n⁺ drain (or source) electrode, and output voltage (V_out) is produced from the same n⁺ drain (or source) electrode. For synapse operation, the voltage transferred from the preneuron (V_in) is applied to the gate electrode of the synapse, and output current (I_out) is flown from the n⁺ source (or drain) electrode. These neurons and synapses were fabricated on an 8-inch wafer by using the same standard Si CMOS process and were connected to each other through metallization for a monolithically integrated neuromorphic system, as shown in Fig. 1D. The fabrication details are described in fig. S1.

As mentioned earlier, the excitation/inhibition of the neuron is determined by electron trapping in the nitride of the SONOS structure. An inhibitory function that disables the firing of the neuron is necessary, because it can improve the energy efficiency of the neuromorphic system by selectively firing a specific neuron. Hence, it can realize effective learning and inference through the WTA mechanism (21–23). As shown in Fig. 2A, unless the electrons are trapped in the nitride, the neuron is at a low-resistance state. Thus, current flows through the channel when the I_in is applied. As a consequence, charges are not integrated and a leaky integrate-and-fire (LIF) function is inhibited. Otherwise, the neuron is at a high-resistance state (HRS) when trapped electrons in the nitride raise a potential barrier between the n⁺ source and a p-type channel referred to as a p-n built-in potential. Accordingly, charges are integrated until the firing. For the neuron operation, the gate of the neuron transistor is a kind of a pseudo-gate, unlike a conventional actual gate. It is used not for the LIF operation but for charge trapping. For electron trapping in the nitride, a positive voltage pulse is applied to the pseudo-gate. Afterward, it is sustained in a floating state for the neuron operation. Because of nonvolatility of the trapped charges even without gate biasing, energy consumption is much smaller compared to our previous study, which required additional and continuous gate voltage control (33, 34).

Fig. 2. Unit device characteristics of single-transistor neuron and synapse.

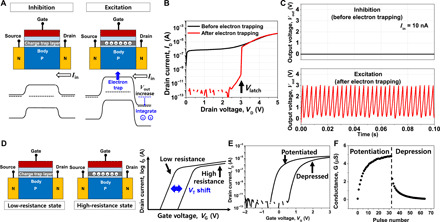
(A) Operation principle of the single-transistor neuron. The excitation/inhibition of the neuron is determined by electron trapping in the nitride. (B) Output characteristic (I_D-V_D) of the fabricated single-transistor neuron. The single-transistor latch (STL) phenomenon that allows threshold switching near V_latch was observed only after electron trapping (excitatory). (C) Spiking characteristics of the fabricated single-transistor neuron. The neuronal spiking by LIF operation was excited after electron trapping, while it was inhibited before electron trapping. (D) Operation principle of the single-transistor synapse. The weight of the synapse can be adjusted by controlling the trapped charge density in the nitride. (E) Transfer characteristic (I_D-V_G) of the fabricated single-transistor synapse after potentiation and depression. Threshold voltage (V_T) was shifted leftward after potentiation and rightward after depression. (F) Potentiation-depression (P-D) characteristic of the fabricated single-transistor synapse. Thirty-two levels of the conductance state were secured (5 bits).

Figure 2B shows output characteristics of the fabricated n-channel single-transistor neuron, which is represented by the drain current versus drain voltage (I_D-V_D). Its gate length (L_G) and channel width (W_CH) are 880 and 280 nm, respectively. Before the electron trapping, I_D flows regardless of V_D. After the electron trapping with a gate voltage (V_G) of 12 V and a pulse time of 100 μs, the I_D does not flow at a low V_D. However, a large amount of I_D abruptly flows beyond a critical V_D; this is called latch-up voltage (V_latch). This is known as a phenomenon of single-transistor latch (STL) and serves as a threshold switch (35, 36).

Figure 2C shows the V_out versus time when a constant I_in was applied to the drain electrode of the single-transistor neuron, before and after the electron trapping. V_G of 12 V was applied for electron trapping (excitatory), and V_G of −12 V was applied for electron detrapping (inhibitory). After trapping and detrapping, the gate was sustained in a floating state for the neuron operation. The V_out was measured at the same drain electrode. Before the electron trapping, the applied I_in directly flowed through the channel toward the source, and charge accumulation (integration) was not allowed. As a result, the inhibitory function was enabled, unlike the two-terminal–based memristor–based neuron. After the electron trapping, the applied I_in did not flow out toward the source, and charges accumulated in a parasitic capacitor (C_par). According to this integration process, V_D equivalent to V_out was increased before the V_T,firing. Simultaneously, iterative impact ionization was induced by the increased V_D, and holes accumulated in the body. When the V_out reaches V_latch, which is the same as the V_T,firing, the accumulated charges in C_par are suddenly discharged by STL. This is a firing process. Therefore, spiking of the neuron was mimicked. Figure S2 shows the energy band diagram during the LIF operation, which was extracted by a technology computer-aided design (TCAD) device simulation. Note that at the moment of the firing, the energy barrier between the n⁺ source and the p-type body is lowered enough to allow the integrated charges to escape toward the source. The measured spiking frequency (f) was increased as the I_in was increased.

In addition to the control of the excitation and inhibition, the V_T,firing was tunable by controlling the trapped charge density in the nitride. This tunable property of the V_T,firing is important to implement a reliable neuromorphic system (23, 24). If the conductivity of the synapse is unsuitably low or high owing to process-induced variability and endurance problems, then the targeted number of firings cannot be achieved. To suppress this instability, a tunable V_T,firing is required. As shown in fig. S3A, the V_latch was increased by the applied program pulse. This is because the number of carriers supplied from the source to the body was reduced owing to the lowered body potential (i.e., the increased built-in potential at the n⁺ source and the p-type body) by the trapped electrons. As a result, V_T,firing of the spiking was increased, as shown in fig. S3 (B and C). In summary, the demonstrated multistate single-transistor neuron harnesses both controllability of the excitatory/inhibitory function and tunability of the V_T,firing.

A leaky characteristic by diffusion of ions through a membrane is important in a biological neuron. This is because if there is no leaky characteristic, then the previous signal below threshold will retain the voltage until another upcoming input induces firing even after a long time. We performed current pulse measurements to confirm the LIF characteristic of the fabricated single-transistor neuron. A square pulse of 1-Hz frequency with a peak of 500 pA and a duty rate of 2% was applied to the drain electrode, and the V_out was measured at the same drain electrode. As shown in fig. S4A, it was confirmed that the V_out was decreased when no input current was applied. This represents the leaky property. On the basis of the measured data, the LIF behavior of the single-transistor neuron was modeled with a simulation program with integrated circuit emphasis (SPICE) simulation using a threshold switch and a parasitic capacitor, as shown in fig. S4B. Note that nodes for voltage sensing and nodes for switching are equal in a voltage-controlled threshold switch. C_par, V_T,firing, and resistance at HRS (R_off) were set as 8 pF, 3 V, and 5 terohms, respectively. As a consequence, there was good agreement between the simulated and the measured spiking characteristic (fig. S4A).

The f of the LIF neuron can be modeled as follows

$$f=\frac{1}{{\displaystyle {\int }_0^{V_{\mathrm{T},\text{firing}}}}\left(\frac{C_{\text{par}}}{I_{\text{in}}-\frac{V_{\text{out}}}{R_{\text{off}}}}\right)d{V}_{\text{out}}}$$

where R_off is an off-state current at HRS during the integration. As the V_T,firing decreases, the f increases because the firing occurs at the lower voltage. It should be noted that the V_T,firing, which corresponds to the V_latch in Fig. 2B, is determined by various parameters such as L_G, body doping concentration (N_body), and energy bandgap (36, 37).

As the L_G increases, the V_latch and V_T,firing are increased because it requires higher drain voltage to enable the latch-up owing to a reduced lateral electric field (E_lateral). Note that the E_lateral can be approximated to (V_D − V_S)/L_G. Figure S5A shows the V_T,firing as a function of the L_G. In addition to the measurements, we performed device simulations to confirm the similar tendency between the V_T,firing and the L_G shorter than the fabricated L_G with the aid of a Synopsys Sentaurus TCAD Transient simulation. As expected, as the L_G was decreased, V_T,firing was decreased by the reduction in V_latch. When the L_G is shortened to 250 nm, the V_T,firing can be decreased to 1.1 V. Figure S5 (B and C) shows the f and the energy per spike (E/spike) as a function of the L_G, respectively. The E/spike for 1 s was calculated by multiplying I_in and the area under one spike in Fig. 2C, which shows measured output voltage (V_out) versus time. Thus, it is extracted as $I_{\text{in}}·{\int }_0^{\frac{1}{f}}{V}_{\text{out}}\mathit{dt}$. As the L_G was decreased, the f was increased and the E/spike was decreased by the reduced V_T,firing. When the L_G is reduced to 250 nm, the f can be increased to 7.6 kHz and the E/spike can be reduced to 1.3 pJ/spike at the I_in of 10 nA. On the other hand, when the L_G is smaller than 250 nm, the STL does not occur owing to the leakage caused by punchthrough current directly flowing via n⁺ drain to n⁺ source. Thus, neuron operation may not be enabled. Further downscaling of L_G will be possible with the aid of junction engineering such as pocket (or halo) implantation via suppression of punchthrough leakage that disables the STL.

As the I_in increases, charging speed becomes faster, and the f tends to be increased. Besides the V_T,firing and I_in, the C_par plays an important role in controlling the f. From the above equation, the f is increased as the C_par is reduced because it takes shorter time to charge the smaller parasitic capacitor. To confirm the effect of the C_par, we measured the f and extracted the E/spike by connecting the external capacitor parallel to the single-transistor neuron. L_G was fixed as 880 nm. Figure S6 (A and B) shows that the f was increased and E/spike was decreased as the C_par was decreased. To confirm the neuron characteristics with a smaller C_par than the measured C_par, we performed device simulations with the aid of Synopsys Sentaurus TCAD. Notably, it is difficult to characterize the capacitance of a sub-picofarad level owing to pad capacitance of the device. Note that a pad size is larger than 100 μm by 100 μm for direct probing compared to a single-transistor neuron size. According to the simulation data, when the C_par was 0.5 pF, the f could be increased to 11.7 kHz and the E/spike could be reduced to 0.7 pJ/spike at an I_in of 10 nA. Therefore, it is better to reduce the C_par of the single-transistor neuron to enhance the computational speed and energy efficiency. This means that miniaturization of the single-transistor neuron is favorable to enhance neuron performance, i.e., they are scalable to each other.

Power consumption was compared between the single-transistor neuron and the memristor-based neuron. The peak power consumption was extracted from the multiplication of peak current and peak V_out (fig. S7). It was found that the single-transistor neuron consumed a peak power of 1.5 μW, which was 7- to 261-fold smaller than memristor-based neurons (18, 20). This low peak power consumption compared to the memristor-based neurons is attributed to a small cross-sectional channel area for current flowing due to the high scalability of the nano-CMOS fabrication. Its fabricated area was extracted from the product of the channel thickness (50 nm, i.e., channel height) and the channel width (280 nm). In addition, power consumption was compared between the single-transistor neuron and a conventional circuit-based neuron. Average power consumption of the circuit-based neuron is in a range of 0.3 to 78.16 μW (9–11). It is well known that average power consumption is much smaller than peak power consumption. Note that the peak power consumption of the single-transistor neuron is comparable to the averaged power consumption of the circuit-based neuron, because power is not consumed during the integration when the spike current does not flow. For example, the average power in one spike was extracted as 15.4 nW, when the I_in was 10 nA. Therefore, the single-transistor neuron can consume low power for neuromorphic computing.

On the other hand, it is noteworthy that the single-transistor neuron has a bidirectional characteristic, in which the spiking operation is possible in both the drain I/O and source I/O (fig. S8). When the current is forced to the drain electrode (drain I/O), the positive charges are integrated in the drain-side parasitic capacitor. Accordingly, the level of the V_out is low at the resting state and high at the integration state, as shown in fig. S8A. On the contrary, when the current is pulled out from the source (source I/O), negative charges are integrated at the source-side parasitic capacitor. In other words, a level of the V_out is high at the resting state and low at the integration state, as shown in fig. S8B. This bidirectional characteristic can provide more degrees of freedom in designing a neuromorphic system. Thus, we used both methods to construct a neuromorphic system.

Because the synapse device has the same SONOS structure as the neuron, the weight of the synapse can be adjusted by controlling the trapped charge density in the nitride. For example, if the electrons are trapped by applying a positive bias to the gate, then the threshold voltage (V_T) is shifted rightward and the channel conductance is decreased at the same read voltage, as depicted in Fig. 2D. This is a kind of depression. Otherwise, V_T is shifted leftward and the channel conductance is increased at the same read voltage. This is a kind of potentiation. Figure 2E shows transfer characteristics of the fabricated n-channel single-transistor synapse, which is represented by the drain current versus gate voltage (I_D-V_G). Its L_G and W_CH are 1880 and 180 nm, respectively. V_T was adjusted by the applied gate voltage that controls the trapped charge density. The potentiation-depression (P-D) curve in Fig. 2F shows the conductance change (weight update) according to the number of applied pulses with an identical amplitude and duty cycle. Both V_G and V_D for the reading operation were set as 1 V. The V_G for potentiation and depression was set as −11 V with a pulse width of 100 ms and 11 V with a pulse width of 10 μs, respectively. As a result, 32 levels (5 bits) of conductance states were secured. It is noteworthy that the V_G for potentiation and depression can be reduced by engineering a thickness of a tunneling oxide and a dielectric constant of a blocking oxide.

Cointegration of neuron and synapse

If a neuron and a synapse are homotypic, then they can be integrated on the same plane at the same time with the same fabrication. Thereafter, they can be connected by metal interconnections. This cointegration is demonstrated for two layers in a neural network. One is a prelayer composed of a presynaptic neuron and a transmitted synapse. The other is a postlayer comprising a transmitting synapse and a postsynaptic neuron. Figure 3 (A to C) shows the cointegrated presynaptic neuron and transmitted synapse as the prelayer. Referring to the circuit schematic of Fig. 3A, a constant input current (I_in,neuron) is applied to the drain electrode of the neuron, and the drain is connected to a gate of the synapse to apply the output voltage from the presynaptic neuron (V_{out,preneuron}). Note that this configuration uses the abovementioned drain I/O scheme. Therefore, when spiking of the neuron occurs, the corresponding drain current (I_D) flows through the channel of the synapse. Its magnitude is modulated by the synaptic weight. Figure 3B shows the fabricated presynaptic neuron and transmitted synapse interconnected through metallization. As shown in Fig. 3C, the spike-shaped output current of the transmitted synapse (I_out,syn) was increased according to the V_{out,preneuron} of the excited presynaptic neuron in order of weight: w₁ < w₂ < w₃. It should be noted that the f of the I_out,syn was determined by the I_in,neuron. Note that stable inference operation is allowed unless the tunneling oxide thickness of the SONOS-based synapse is reduced (fig. S9). This is because the synaptic weight would not be changed by V_{out,preneuron}, which is small compared to the voltage of potentiation/depression (P/D). Therefore, it is suitable for off-chip learning application, where learning is not necessary in the hardware. However, by engineering the V_T,firing of the neuron and the thickness of the tunneling oxide (T_ox) in the synapse, the weight of the transmitted synapse can be changed by the output voltage of the presynaptic neuron without extra pulse modulation circuits. This means that it is also applicable to on-chip learning applications.

Fig. 3. Cointegrated single-transistor neuron and synapse.

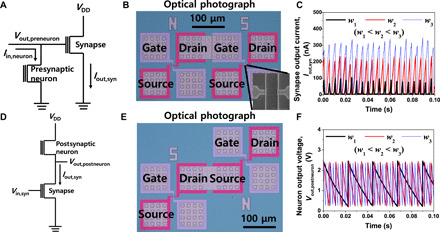
(A) Circuit diagram of presynaptic neuron and transmitted synapse connection in the prelayer of neural network. The output voltage of the presynaptic neuron (V_{out,preneuron}) is transmitted to the gate of the synapse. (B) Fabricated presynaptic neuron and transmitted synapse interconnected through metallization. (C) Measured synapse output current (I_out,syn) as a function of synaptic weight. The level of I_out,syn became higher when the synaptic weight was larger. (D) Circuit diagram of transmitting synapse and postsynaptic neuron in the postlayer of neural network. The current of the transmitting synapse is applied to the source of the postsynaptic neuron. (E) Fabricated transmitting synapse and postsynaptic neuron interconnected through metallization. (F) Measured neuron output voltage (V_{out,postneuron}) as a function of synaptic weight. The spiking frequency (f) of V_{out,postneuron} became higher when the synaptic weight was larger.

To confirm the applicability to on-chip learning, we increased the V_T,firing of the neuron to 5.5 V by increasing the N_body to 1×10¹⁸ cm⁻³ and increasing the L_G to 1.9 μm. At the same time, when the T_ox of the synapse is reduced, the weight of the synapse can be further changed by the lower voltage. As shown in fig. S9A, the hysteresis was increased under the same voltage condition when T_ox of the synapse was reduced from 3 to 2 nm. This implies that a larger threshold voltage (V_T) shift and conductance change can be made under the same P/D voltage. Figure S9B shows that when the T_ox of the synapse was 2 nm, the V_T of the synapse was gradually shifted by the spike of the neuron. On the other hand, when the T_ox is 3 nm, the V_T shift was not significant, as shown in fig. S9C. The depression where the conductance gradually decreases occurred by neuron spiking for the T_ox of 2 nm, as shown in fig. S9D. However, the conductance was not changed significantly for the T_ox of 3 nm. From the viewpoint of retention characteristics, a T_ox of 3 nm was better than a T_ox of 2 nm, as shown in fig. S9E. Therefore, a T_ox of 3 nm is suitable for off-chip learning applications that require good retention characteristics without weight change, and a T_ox of 2 nm is suitable for on-chip learning applications that require a weight change with lower P/D voltage. It should be noted that the formation of various gate oxide thicknesses has already been used for a commercial logic chip. The abovementioned features are readily realized by CMOS fabrications. By the way, only depression was shown in fig. S9D because V_{out,preneuron} is positive when the firing occurs. However, the potentiation can also be achieved when the source I/O is used. When 0 V is applied to the drain of the presynaptic neuron and input current is applied to the source, V_{out,preneuron} is 0 V at the resting state, and it is negative when the firing occurs, which induces potentiation of the transmitted synapse. Therefore, bidirectional characteristic of the single-transistor neuron can allow both depression and potentiation.

Figure 3 (A to C) shows the analysis of one presynaptic neuron and one transmitted synapse connection, when the I_in,neuron to the excited postsynaptic neuron was fixed. To show the effect of I_in,neuron with excitatory/inhibitory function in the single-transistor neuron, we constructed an array structure for cointegration with high density. Figure S10 shows the array structure in which both presynaptic excited and inhibited neurons with different I_in,neuron values and transmitted synapses with different conductance (weight) were connected. As shown in fig. S10A, each neuron was connected to four synapses with different weight, and different I_in,neuron were applied to each neuron. Synapses have four different weights (w₁ < w₂ < w₃ < w₄). As an example, the first neuron to the third neuron were excited in which electrons were trapped in the charge trap layer, and the fourth neuron was inhibited in which electrons were not trapped in the charge trap layer. For each excited neuron, a different I_in,neuron was applied. In more detail, 500 pA, 1 nA, and 5 nA were applied for the first, second, and third neurons, respectively. Last, the I_out,syn of the transmitted synapse was measured in each synapse. Figure S10B shows a color map to represent the f of the I_out,syn of each synapse in the array. The f of the I_out,syn was expressed with brightness. A dark-colored pixel indicates a synapse with a high f, and a white-colored pixel indicates a synapse with a low f. As the I_in,neuron applied to the presynaptic neuron was increased, the spiking frequency of the I_out,syn was increased. Figure S10C shows a color map to represent the peak current of the I_in,neuron of each synapse in the array. The peak current of the I_in,neuron was expressed with brightness. A dark-colored pixel indicates a synapse with high peak current, and a white-colored pixel indicates a synapse with low peak current. As the synaptic weight was increased from w₁ to w₄, the peak current of I_in,neuron was increased. Synapses in the first column did not show firing events regardless of the I_in,neuron of the presynaptic neuron, because the V_T of the synapse was higher than the output voltage of the presynaptic neuron. Synapses in the last row did not show firing events regardless of the synaptic weight, either. It is because the presynaptic neuron was inhibited.

On the other hand, it is curious how many transmitted synapses can be cointegrated with a single presynaptic neuron. Theoretically, it is possible to drive a number of the transmitted synapses that are connected to the single presynaptic neuron. As an example, we simulated the architecture composed of one presynaptic neuron and 100 synapses with the aid of the SPICE circuit simulator. The current flowing from the neuron to the synapses is negligibly small because the gate of the synapse has very high input resistance due to a low level of gate leakage current. It should be noted that the gate leakage current of the fabricated synapses was less than 1 pA. Because there is no direct current flowing from the neuron to the synapses, the number of transmitted synapses that can be driven by the V_{out,preneuron} of the presynaptic neuron is not limited. As a result, V_{out,preneuron} was invariant although 10 synapses were connected to the single presynaptic neuron, as shown in fig. S10D. Furthermore, the V_{out,preneuron} was not varied even when the weight of each synapse was changed. This is an important advantage of cointegration with a MOSFET-based three-terminal synapse such as SONOS compared to cointegration with a resistor-based two-terminal synapse such as a memristor. Because of the loading effect, the number of synapses inevitably affects the neuronal output when two-terminal synapses are connected (38, 39). For example, neuron oscillation was impossible when the number of two-terminal synapses with a conductance (G) of 1 nS was more than 10. This is because the current is flown out to the synapses by increased conductance, as shown in fig. S10E. This problem was exacerbated for the larger G, as shown in fig. S10F, because larger current is flown out to the synapses. Referring to fig. S10F, as the number of the transmitted synapses was increased, the leakage current toward the synapses was increased and the f of the presynaptic neuron was decreased. Then, when the number of synapses exceeded a certain level, spiking did not occur. To solve this problem of two-terminal synapses, a 1T1R configuration composed of an extra transistor (1T) and a memristor (1R) or a buffer circuit is required. However, these configurations sacrifice layout efficiency, worsen fabrication complexity, and increase hardware cost.

Figure 3 (D to F) shows the cointegrated postlayer composed of the transmitting synapse and the postsynaptic neuron. As shown in the circuit schematic of Fig. 3D, a constant gate voltage (V_in,syn) is applied to the transmitting synapse, and the drain of the synapse is connected to the source of the postsynaptic neuron. I_out,syn is thus applied to the postsynaptic neuron. The output voltage is measured at the source of the postsynaptic neuron. In other words, it adopts the source I/O scheme. If the I_out,syn is applied from the source of the transmitting synapse to the drain of the postsynaptic neuron (drain I/O scheme), then the source voltage of the transmitting synapse is varied by the deviation of the output voltage of the postsynaptic neuron (V_{out,postneuron}). Otherwise, if the drain of the transmitting synapse is connected to the source of the postsynaptic neuron (source I/O scheme), then such issue is mitigated. This feature is attributed to saturated drain current that is very insensitive to the change of the V_D in a saturation region. Figure 3E shows the fabricated transmitting synapse and postsynaptic neuron interconnected through metallization. As shown in Fig. 3F, the f of the V_{out,postneuron} is increased according to the increment of I_out,syn from the transmitting synapse in order of weight: w₁ < w₂ < w₃.

Another way to connect the transmitting synapse and the postsynaptic neuron is suggested in fig. S11A, where a current mirror is used. The current mirror is composed of two NMOSFETs and two PMOSFETs. As a channel length of the transmitting synapse is aggressively scaled down, I_out,syn cannot be sufficiently saturated by the short-channel effects, even in the source I/O scheme. In this case, a current mirror between the transmitting synapse and the postsynaptic neuron is necessary that can isolate the sharing node. This configuration is also attractive to modulate the I_out,syn over a wide range. Reduction in I_out,syn is important to realize ultralarge-scale integration of a neuromorphic system where the postsynaptic neuron is connected to numerous synapses. A low level of I_in smaller than 10 μA, which is below the current range where the latch-up occurred in Fig. 2B, is preferred for nominal operation of the single-transistor neuron. When the I_in is higher than 10 μA, the current flows out to the source without charge integration. Therefore, the postsynaptic neuron does not operate when a number of synapses are connected. The aforementioned concerns can be resolved by cointegrating a current mirror between the transmitting synapse and the postsynaptic neuron. Figure S11B shows the cointegrated transmitting synapse, the current mirror, and the postsynaptic neuron interconnected through metallization. Figure S11C shows the measured transfer characteristics of the fabricated PMOSFET, and fig. S11D shows the output current of the output PMOSFET in the current mirror. As a result, spiking of the postsynaptic neuron was achieved when it was excited, as shown in fig. S11E. Otherwise, when it was inhibited, no spiking was observed. In addition to the current mirror that can be used for analog circuitry, an inverter, which is a fundamental block to construct digital logic circuitry that controls the neural network for collecting, processing, and transporting data, was also fabricated on the same plane with cointegration of the neuron and synapse at the same time, as shown in fig. S12. The current mirror and inverter are examples to show the feasibility of cointegration with analog circuits and digital circuits.

Gain modulation and coincidence detection

Using the cointegrated neurons and synapses, we carried out spatiotemporal neural computations such as gain modulation and coincidence detection. In biology, gain modulation is observed in many cortical areas and is thought to play an important role in maintaining stability (40–43). Here, additive operation of gain modulation was realized by cointegration of two transmitting synapses and one postsynaptic neuron, as shown in the circuit diagram of Fig. 4A. Two types of presynaptic inputs are applied to the gate electrodes of two synapses. A driving input (V_G,S1) enables the postsynaptic neuron to fire, and a modulatory input (V_G,S2) tunes the effectiveness of the driving input, as illustrated in Fig. 4B. As shown in Fig. 4C, the f of the postsynaptic neuron was modulated by the V_G,S2 for the fixed V_G,S1. This is because the I_in applied to the postsynaptic neuron was increased as the V_G,S2 was increased. Figure 4D shows a secondary data that the f was increased as the V_G,S2 was increased at various V_G,S1. Figure 4E shows another secondary data of the f as a function of the V_G,S1 at various V_G,S2. Referring to Fig. 4E, a shift along with a vertical direction is similar to the additive operation of output gain modulation (42). It should be noted that such additive operation of output gain modulation underlies sophisticated sensory processing in biology.

Fig. 4. Gain modulation and coincidence detection by cointegrated single-transistor neuron and synapses.

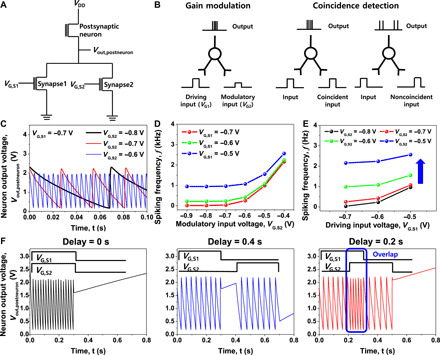
(A) Circuit diagram of connected two transmitting synapses and one postsynaptic neuron for gain modulation and coincidence detection. (B) Schematic diagram of gain modulation and coincidence detection. Neuronal output can be determined by the modulatory input as well as the driving input, and the coincidence of the two inputs can be detected from the neuronal output. (C) Spiking characteristics of the postsynaptic neuron depending on the modulatory input voltage (V_G,S2) when the driving input voltage (V_G,S1) was fixed. The spiking frequency (f) was increased as the V_G,S2 was increased because the input current to the postsynaptic neuron was increased. (D) f as a function of the V_G,S2 at various V_G,S1. (E) f as a function of the V_G,S1 at various V_G,S2. It showed a shift in the vertical direction, which is a typical additive operation of output modulation. (F) Spiking characteristics of the postsynaptic neuron depending on the delay between the two signals. f was larger when two signals became more synchronized. When two signals overlapped for a certain period of time, the f was increased only in the overlap region.

Coincidence detection is another important neural computation that encodes information by detecting the occurrence of temporally close but spatially distributed input signals. It has been found that coincidence detection is significant for highly efficient information processing in auditory and visual systems (44–47). By the cointegration of neuron and synapses, coincidence detection is also possible. When two inputs were applied at the same time, the f was increased because the I_in applied to the postsynaptic neuron was increased, as illustrated in Fig. 4B. Accordingly, it is possible to determine whether two inputs are simultaneously applied. Figure 4F shows the corresponding data. When the two input signals applied at the same time, the f of the neuron was larger than the other cases of the two signals that were not synchronized. In addition, when two input signals overlapped for a certain period of time, the f of the neuron increased only in the overlap region.

Letter recognition with hardware circuit simulation

The neuromorphic system is commonly used to recognize images such as letters, numbers, objects, and faces. Pattern recognition of a letter was demonstrated with the aid of SPICE circuit simulations that were based on the measured neuron-synapse characteristics. As a simple model, the neuron is composed of a threshold switch and a parasitic capacitor connected in parallel. As a result, the simulated electrical properties are similar to the measured characteristics from the fabricated neuron, as shown in fig. S3. The synapse was implemented with a three-terminal MOSFET, and the weight of the synapse was controlled by adjusting the V_T. We implemented two types of neural networks: a classifier based on a single-layer perceptron (SLP) and an autoencoder based on a multilayer perceptron (MLP). First, a neural network for the classifier was constructed to distinguish the letters “n,” “v,” and “z,” which was composed of 3 × 3 black-and-white pixels (Fig. 5A). It was composed of nine input layers labeled with “i₁” to “i₉,” which correspond to each pixel and three output layers labeled with “O_n,” “O_v,” and “O_z” that are corresponding to each letter (Fig. 5B). The circuit diagram for the classifier is shown in fig. S13. Note that the output neurons were connected to each other to enable the lateral inhibition. According to the output voltage of the output neurons, each letter was identified. First spiking occurred in the first neuron for the input of n, the second neuron was for the input of v, and the third neuron was for the input of z. It should be noted that the multistate properties of the single-transistor neuron play an important role in recognizing a pattern. First, it was confirmed that the unwanted spiking was inhibited by the neuronal inhibition before reaching the V_T,firing, which can enhance the energy efficiency of the neural network. Second, it was verified that the pattern was well recognized by appropriately tuning the V_T,firing, even if the synaptic weight was changed abnormally. This feature can enhance the reliability of the neural network.

Fig. 5. Letter recognition with hardware-based circuit simulation by reflecting the measured characteristics of single-transistor neuron and synapse.

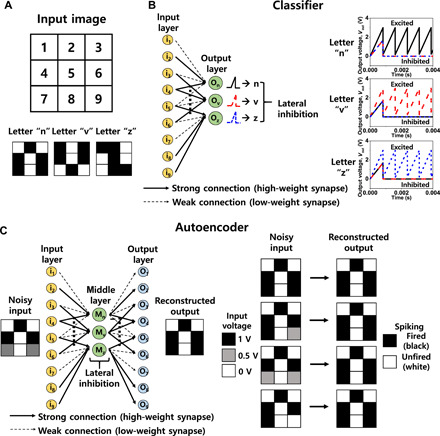
(A) Input image of the 3 × 3 pixel letter pattern. (B) SLP for a classifier and classification results. Each input layer represents each pixel, and each output layer represents each letter. Classification determined by which neuron expressed spiking first was performed. All other neurons except the first spiked output neuron were laterally inhibited. (C) MLP network for an autoencoder and its encoding/decoding results. Each input layer represents each pixel of noisy input, and each output layer represents each pixel of reconstructed output by the autoencoder. The output neuron that was fired could be newly decoded as a black pixel, and the output neuron that was not fired could be newly decoded as a white pixel to reconstruct a clearer image from a blurred noisy pattern.

If the weight of the synapse is unsuitably low or high owing to process-induced variability and endurance problems, then the neuron cannot be fired with the targeted number. For instance, the V_T,firing should be lowered if the current input to the neuron is too small because the weight of the synapse is abnormally low. In the reverse case, if the weight of the synapse is too high, then the V_T,firing must be increased. This allows the number of neuron firings to be stably maintained regardless of the nonideal synapse operations. To show the benefit of the multifiring threshold property, we performed SPICE circuit simulations. Consider a situation where an input pattern is n. The first output neuron should be fired, and other neurons should be inhibited before the firing. However, when the threshold voltage (V_T) of the high-weight synapses connected to the first output neuron was abnormally increased to 0.35 V from 0 V, the current from the synapses to the first output neuron decreased. As a result, the first output neuron could not be fired and instead, another output neuron was fired, as shown in fig. S14A. Therefore, the pattern recognition failed. At this time, normal pattern recognition could be achieved by lowering the V_T,firing of the first neuron to 2.6 V, as shown in fig. S14B. Otherwise, when the V_T of the low-weight synapses connected to the second output neuron was abnormally decreased to −0.1 V from 1 V, the current from the synapses to the second output neuron increased. As a consequence, the second output neuron was fired in advance to the first output neuron and the first output neuron was inhibited, as shown in fig. S14C. Therefore, the pattern recognition failed. At this time, normal pattern recognition could be achieved by increasing the V_T,firing of the second neuron to 3.4 V, as shown in fig. S14D. In summary, reliable pattern recognition was performed by tuning the V_T,firing of the single-transistor neuron when the weight of the synapses was abnormally changed. It should be noted that an additional circuit is needed for the actual implementation of V_T,firing tunable single-transistor neuron, which receives the V_out of the neuron for reading abnormal spiking frequency and transmits voltage pulse to the gate for tuning the V_T,firing.

To improve the recognition rate of an image, an autoencoder is commonly used (48). The autoencoder can remove the effect of noisy input and reconstruct the image by encoding the image and decoding it again. As shown in Fig. 5C, we implemented the autoencoder by use of the MLP network with one middle layer. The input layer and the output layer were composed of nine neurons, and each layer represented each pixel. After encoding three letters in the first perception, the information of each pixel was newly decoded in the second perception. A circuit diagram for the autoencoder is shown in fig. S15. It should be noted that the inhibitory function of the single-transistor neuron allowed the autoencoder operation. In more detail, the middle neurons were connected to each other to enable lateral inhibition, and hence, the noisy signal could be removed. Receiving the signal from the middle neurons, some output neurons were fired, while others were not fired. The fired output neuron was decoded as a black pixel, while the unfired output neuron was decoded as a white pixel, as shown in Fig. 5C. As a result, noisy input images became clearer via the image reconstruction by the autoencoder.

Face recognition with software simulation

Using the hardware-based circuit simulation, we implemented off-chip learning that is applicable to inference operation with fixed weights of the synapses. On the other hand, on-chip learning is also possible by using additional circuits. With the aid of a MATLAB software simulation, a network capable of face recognition through on-chip learning was explored. A fully connected two-layer spiking neural network consisting of 32 × 32 input neurons, 20 neurons in a middle layer, and 3 output neurons was designed, as shown in Fig. 6A. The measured neuron-synapse characteristics were reflected to the simulation based on the circuit diagram of Fig. 6B. From the Yale Face Database, nine training images composed of 32 × 32 pixels were selected (Fig. 6C) (49). After clustering from an unsupervised crossbar, the classification was evaluated by a supervised crossbar. The input neurons generated presynaptic spikes (V_pre) with the timing proportional to the pixel intensity of the training image, as depicted in fig. S16A. Synapses that received presynaptic spikes transmitted current to the postsynaptic neurons according to weight. The current mirror was used as an interface circuit to reduce the current level from the synapses to the postsynaptic neurons. It should be emphasized that these circuits for waveform generation can be cointegrated on the same plane with neurons and synapses by standard CMOS fabrications. The postsynaptic neuron that received the highest current caused postsynaptic spikes to be fired for updating the synaptic weights of the synapses, which were connected with the fired postsynaptic neuron. A proper shape of the postsynaptic spike (V_post) was generated by a waveform generator, which was composed of a pulse voltage with sequential negative and positive polarities. Referring to the pulse scheme illustrated in fig. S16A, when the presynaptic spike was fired earlier than the postsynaptic spike (t_pre − t_post = Δt < 0), positive long-term depression voltage (V_LTD) was applied to the gate of the synapse, which decreased the conductance of the synapse. On the other hand, the conductance of the synapse was increased by negative long-term potentiation voltage (V_LTP) applied to the gate of the synapse, if the presynaptic spike was fired later than the postsynaptic spike (t_pre − t_post = Δt > 0) (23). A simplified spike timing–dependent plasticity learning rule scheme was used for the synaptic weight update (25). The face recognition was evaluated with 24 test set images, containing 8 images of each person (fig. S16B). After the training, the conductance of the synapses was determined, as shown in the visual map diagram of the synapse array (Fig. 6D and fig. S16C). As a result, a recognition rate of 95.8% was achieved for “after training with the lateral inhibition” and that of below 60% was observed for “after training without the lateral inhibition,” as shown in Fig. 6E. Unless the lateral inhibition was applied, a high-level recognition was not performed because the global weight updates were performed via the firing of all engaged neurons. In addition, although the conductance of the synapses were abnormally changed by process-induced variability or endurance problems, the recognition failure was prevented by the V_T,firing modulation. Figure S16D shows the extracted recognition rate by inference operation without the V_T,firing modulation and with the V_T,firing modulation, when the conductance of the synapses (G) was abnormally changed by process-induced variability or endurance problems. For example, it can be assumed that G is randomly and abnormally changed to 2G_min. The recognition rate was decreased as the device failure rate was increased, unless the V_T,firing modulation is applied. Otherwise, the recognition failure would be prevented when the V_T,firing was modulated. These results prove that the efficient and reliable neural network can be implemented by the multistate single-transistor neuron.

Fig. 6. Face recognition with software-based simulation by reflecting the measured characteristics of single-transistor neuron and synapse.

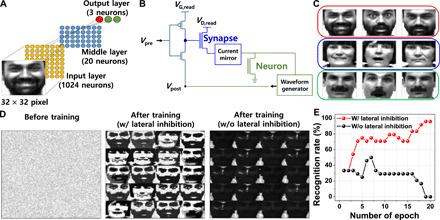
(A) Spiking neural network for face recognition. The input layer is composed of 1024 neurons that represent each pixel, the middle layer is composed of 20 neurons, and the output layer is composed of three neurons that represent each person’s face. (B) Simplified circuit diagram to represent the connection of neuron-synapse. Neuronal output is converted through a waveform generator to make a proper pulse shape applied to the synapse for spike timing–dependent plasticity learning. (C) Nine training images of three people. (D) Visual map of the synapse array to represent the conductance of the synapses, “before training,” “after training with lateral inhibition,” and “after training without lateral inhibition.” (E) Comparison of recognition rate depending on the number of training epochs between “after training with lateral inhibition” and “after training without lateral inhibition.” Higher recognition rate is achieved with the inhibitory function of the neurons. Photo Credit: J.-K. Han, Korea Advanced Institute of Science and Technology (KAIST).

To realize such large-scale neural network, variability should be minimized as much as possible. Therefore, cycle-to-cycle variation and device-to-device variation of the SONOS-based single-transistor neuron and synapse were evaluated, as shown in fig. S17. Blue symbols represent a high-V_T state that more electrons are trapped, and black symbols denote a low-V_T state that less electrons are trapped. Note that the higher V_T induces higher firing threshold voltage for neuron device and lower weight for synaptic device. In contrast, the lower V_T induces lower firing threshold voltage for neuron device and higher weight for synaptic device. For switching in between two states, a programming pulse of 11.5 V with a 500-μs pulse width was used to trap the electrons, and an erasing pulse of −11.5 V with a 50-ms pulse width was used to detrap the electrons. Cumulative distribution of V_T to show cycle-to-cycle variation was plotted after 50 cycles in fig. S17A. Its SDs of the high V_T and low V_T were 0.0103 and 0.0185, respectively. From these data, stable operation can be assured. Other cumulative distribution of V_T to show device-to-device variation was also plotted for 40 different samples in fig. S17B. Its SDs of the high V_T and low V_T were 0.0369 and 0.0428, respectively. From these data, device and process variability cannot be a concern due to well-established CMOS technology. In addition, the endurance performance of the SONOS-based single-transistor neuron and synapse was measured. As shown in fig. S18, a V_T shift by the repetitive trappings in the gate dielectrics was characterized. Such V_T shift should also be minimized as small as possible because the firing threshold voltage of the neuron and the weight of the synapse can be changed. Otherwise, it can provoke degradation of a learning rate and inference error of the neural network. For further improvement of endurance characteristics, various technologies such as high-pressure annealing, Si-rich nitride, and bandgap engineering can be used (50–52).

DISCUSSION

Completely CMOS-based neuromorphic hardware with high scalability was fabricated by the cointegration of single transistor–based neurons and synapses that are homotypic. The charge-trapping layer intercalated in the neurons and synapses allows multistates. They were used to control the excitatory/inhibitory function and to modulate the firing threshold voltage for the neurons, which were not accomplished at memristor-based neurons (table S1). They were also used to determine the weight for the synapses. A footprint area of the single-transistor neuron could be reduced to 6 F², and its power consumption can be smaller than 1.5 μW (table S2). Because the neuron and the synapse have exactly the same structure, they were simultaneously integrated on the same plane at the same time with the same fabrications. This feature permits improvement of packing density, reduction of chip cost, and simplification of the fabrication procedures. In addition, it is possible to cointegrate with additional CMOS circuits for processing units, peripheral interfaces, memory, clocking circuits, and I/O because of the same in situ CMOS fabrications.

MATERIALS AND METHODS

Fabrication

Neurons and synapses with the same SONOS structure, which had a tunneling oxide (SiO₂) of 3 nm, a charge trap nitride (Si₃N₄) of 6 nm, and a blocking oxide (SiO₂) of 8 nm, were fabricated. They were interconnected through metallization (Ti/TiN/Al) using a standard Si CMOS process. See fig. S1 for details of the fabrication process.

Electrical characterization

Electrical characteristics of the cointegrated neurons and synapses were measured using a B1500 semiconductor parameter analyzer (Agilent Technologies). I-V characteristics of the neuron and synapse were measured by voltage source current measurement mode, and the spiking characteristic of the neuron was measured by current source voltage measurement mode. A semiconductor pulse generator unit was used to control the excitation/inhibition and the firing threshold voltage of the neuron, as well as the weight of the synapse. The leaky characteristic of the neuron was measured using a Keithley 6221 current pulse source (Keithley). The source current was measured using a 428 current amplifier (Keithley) and a TDS 744A oscilloscope (Tektronix).

Transmission electron microscopy and scanning electron microscopy analysis

Transmission electron microscopy (TEM) images were taken with a field-emission scanning transmission electron microscope (HD-2300A) by Hitachi High-Technologies Corporation. Scanning electron microscopy (SEM) images were taken with a critical-dimension scanning electron microscope (S-9260A) by Hitachi High-Technologies Corporation.

Device simulation

Device simulations for the analysis of the neuron characteristics were performed using a TCAD Sentaurus simulator (Synopsys). All the device parameters were set as the closest values obtained from the SEM and TEM images.

Hardware-based circuit simulation

Circuit simulations for the letter pattern recognition were performed using LTspice software (Analog Devices). Neurons were modeled with a capacitor and a threshold switch, wherein the parasitic capacitance (C_par) and the firing threshold voltage (V_T,firing) were extracted from the measured spiking characteristics of the neuron. Synapses were modeled with a three-terminal MOSFET, in which the device parameters were set as the closest values obtained from the SEM and TEM images. The weight of the synapses was controlled by changing the threshold voltage (V_T) of the MOSFET.

Software-based simulation

Software simulations for the face image recognition were performed using MATLAB. Spiking characteristics of the neurons and P-D characteristics of the synapses were reflected in the simulation.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/32/eabg8836/DC1