Abstract
Background:
Integrating results from multiple samples is often desirable, but privacy restrictions may preclude full data pooling, and most datasets do not include fully harmonized variable sets. We propose a simulation-based method leveraging partial information across datasets to guide creation of synthetic data, based on explicit assumptions about the underlying causal structure, that permits pooled analyses that adjust for all desired confounders in the context of privacy restrictions.
Methods:
This proof-of-concept project uses data from the Health and Retirement Study (HRS) and Atherosclerosis Risk in Communities (ARIC) study. We specified an estimand of interest and a directed acyclic graph (DAG) summarizing the presumed causal structure for the effect of glycated hemoglobin (HbA1c) on cognitive change. We derived publicly reportable statistics to describe the joint distribution of each variable in our DAG. These summary estimates were used as data-generating rules to create synthetic datasets. After pooling, we imputed missing covariates in the synthetic datasets and used the synthetic data to estimate the pooled effect of HbA1c on cognitive change, adjusting for all desired covariates.
Results:
Distributions of covariates, as well as model coefficients and associated standard errors for our model estimating the effect of HbA1c on cognitive change were similar across cohort-specific original and pre-imputation synthetic data. The estimate from the pooled synthetic incorporates control for confounders measured in either original dataset.
Discussion:
Our approach has advantages over meta-analysis or individual-level pooling/data harmonization when privacy concerns preclude data sharing and key confounders are not uniformly measured across datasets.
Keywords: Simulation, privacy, data pooling, data harmonization
INTRODUCTION
Combining data from multiple studies can enhance research by broadening the diversity of study participants or by improving statistical power. Unfortunately, privacy restrictions often preclude full data pooling. While data from multiple studies can be combined by meta-analysis1, related Bayesian approaches2,3, coordinated analsyes4,5, or aggregate-data based approaches6, analyses may not be perfectly parallel due to differences in covariate sets or parameterizations, and summary measures may remain confounded. Partially or fully synthetic data approaches may permit data sharing and pooled analyses while remaining consistent with data privacy goals.7–12 Most prior work has conceptualized data generation as a statistical problem with the goal of posting synthetic datasets for analyses,7–12 without grounding the data generation in prior knowledge of the causal structure. Although some synthetic data approaches have applied causal discovery algorithms13,14, some controversy about the validity and utility of causal discovery algorithms remains, and epidemiologists typically rely on expert knowledge to generate causal models.15–17 Here, we propose a simulation-based method leveraging partial information across datasets that draws on researchers’ prior understanding of the causal structure to guide creation of synthetic data, permitting pooled analyses in the context of privacy restrictions that adjust for all desired confounders. These synthetic datasets preserve the complexity of the original data sources relevant to estimating the desired estimand and can be used in lieu of formal data pooling of the original datasets to conduct pooled analyses. Imputation of missing covariates in the pooled data also allows for pooled estimates that explicitly account for all desired confounders.
This proof-of-concept paper uses data from the Health and Retirement Study (HRS) and the Atherosclerosis Risk in Communities Study (ARIC) to illustrate this method. We use the motivating example of estimating the effect of glycated hemoglobin (HbA1c) on cognitive change in the domain of memory. This work was a collaborative effort between two separate institutions. After specifying the estimand and the presumed causal structure, we propose a method that uses publicly reportable summary statistics to construct synthetic datasets. Each analyst accessed raw data for only one of the two studies and only publicly reportable information (i.e., summary statistics from regression models) was shared. Here we demonstrate that we are able to generate synthetic datasets from these summary statistics that allow estimation of the pooled effect estimate of interest without direct access to individual-level data. We then demonstrate the opportunity for control of desired confounders measured in at least one contributing data set using the pooled synthetic datasets through imputation of missing covariates.
METHODS
Data Sources
The Health and Retirement Study (HRS) is a nationally representative cohort with a target population of noninstitutionalized adults age 50+ in the contiguous United States.18,19 HRS participants have been invited to study visits every 2 years since 1998; new participants are enrolled at approximately 6-year intervals to maintain a steady-state sample. The subset of HRS participants ages 50+ who participated in blood collection at the 2006 or 2008 HRS interviews and have valid measures of HbA1c were eligible for inclusion (n=12,186). After excluding participants with missing or ambiguous/unknown status on race (n=551), childhood socioeconomic status (CSES) (n=3), education (n=43) and memory assessment at the HRS wave where they completed blood collection (n=80), our final HRS analytic sample included 11,509 participants. All subjects provided informed consent to participate in HRS.
The Atherosclerosis Risk in Communities (ARIC) Study is a multicenter population-based prospective cohort study that enrolled participants in 1987 to 1989, when they were ages 45 to 64. The subset of ARIC participants aged 50+ with valid measures of HbA1c from ARIC Visit 2 (1990–1992) were eligible for inclusion (n=12,533). After excluding participants who were neither Black nor White due to small numbers (n=36), and participants missing data on dietary pattern (n=325), education (n=18) and memory assessment at Visit 2 (n=111), our final ARIC analytic sample included 12,043 participants. The ARIC study was approved by the institutional review boards of all participating institutions. All subjects provided informed consent to participate in ARIC.
Outcome assessment
In both HRS and ARIC, memory was assessed by delayed recall of a 10-word list, scored as the number of correctly recalled nouns.20 In HRS, delayed recall scores are available at each biennial HRS wave from sample baseline (2006 or 2008) through 2012. In ARIC, we use delayed recall scores obtained at Visit 2 (1990–1992), Visit 4 (1996–1998), Visit 5 (2011–2013) and Visit 6 (2016–2018). We standardized the memory scores separately within each cohort by subtracting the cohort-specific mean and dividing by the cohort-specific standard deviation within the subset of participants ages 50–65 years old at the time of HbA1c measurement (2006 or 2008 for HRS, 1990–1992/Visit 2 for ARIC).
Exposure assessment
Glycated hemoglobin (HbA1c) is a measure of blood glucose concentration over the past 2 to 3 months; it is used for diagnosis of diabetes and for disease management among people with diabetes.21 In HRS, HbA1c was measured by dried blood spot in either 2006 or 2008 (year randomly assigned).22 In ARIC, HbA1c was measured in stored whole blood samples from Visit 2.23 For the purpose of these analyses, we anticipated that the effect of HbA1c on cognition may differ for values above 6.5%, the threshold used for diagnosis of diabetes.
Covariates
Age, race (White, Black), gender (male, female), and education (Less than High School, High School, College or more) were self-reported in both HRS and ARIC. For this proof-of-concept analysis, we selected one plausible confounder from each data set that was not measured in the other sample. Information on childhood socioeconomic status (CSES) was available in HRS but not ARIC. In HRS, CSES is a validated continuous composite score based on measures of childhood financial capital (income or wealth), childhood human capital (stock of knowledge and skills, e.g. parental educational attainment) and childhood social capital (quality and number of relationships with household adults).24 Information on diet was available from ARIC, but not HRS. ARIC participants completed a food-frequency questionnaire at Visit 1. We use two indices of dietary patterns derived from principal components analyses, which can be interpreted as the degree of adherence to a “western” (i.e., highest factor loadings for refined grains, processed meat, fried food, and red meat) or “prudent” (i.e. highest factor loadings for cruciferous, carotenoid, or other vegetables, and fruit) dietary pattern.25
Statistical methods
We provide a detailed explanation of how each step was implemented in the eMethods, and provide code on Github (https://github.com/powerepilab/Sim_for_data_pooling). We encourage the reader to reference the eMethods and code as they read through the following sections of the manuscript.
Step 1: Specify the presumed causal structure based on prior knowledge.
We specified, a priori, the estimand and described the presumed, corresponding causal structural model using a directed acyclic graph (DAG). Here, we choose to estimate the marginal effect of HbA1c on cognitive change (Figure 1). HRS included all variables in the DAG except diet, while ARIC included all variables except childhood SES.
Figure 1.
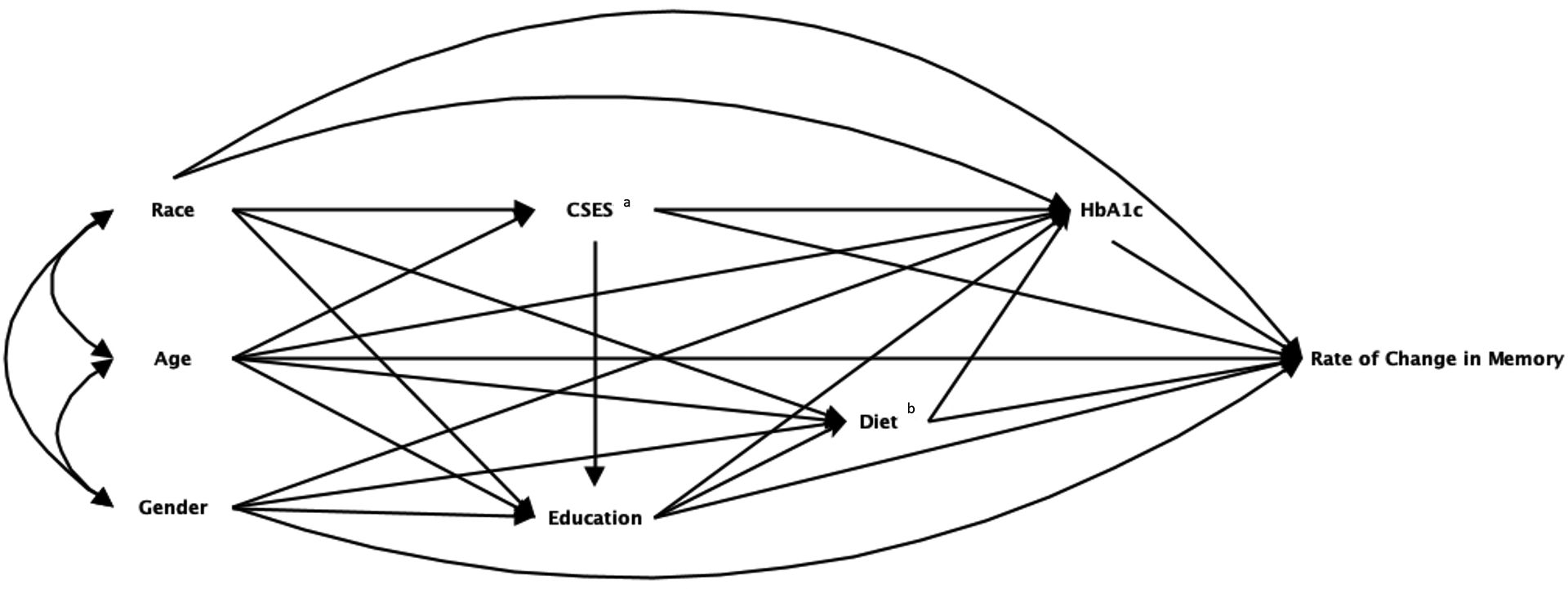
Directed acyclic graph (DAG) depicting the structural causal model for the association between HbA1c and change in memory scores over time
a Variable presents in the HRS dataset and not in the ARIC dataset.
b Variable presents in the ARIC dataset and not in the HRS dataset.
Abbreviations: Health and Retirement Study (HRS) and Atherosclerosis Risk in Communities (ARIC) Study, glycated hemoglobin (HbA1c)
Note: We specified, a-priori, the estimand of interest and described the corresponding causal structural model using a directed acyclic graph (DAG). This DAG, informed by prior analyses and knowledge, includes all exposures, confounders, effect modifiers, and outcomes measured in at least one dataset, that we deem sufficient to allow estimation of the estimand of interest.
Step 2: Estimation of data generating rules in the original datasets.
We estimated the joint distributions of all variables represented in the DAG using individual-level data in each dataset. Decisions about the dependencies used to derive the data generating rules were based on the DAG derived in Step 1 (Figure 1) and are described in Table 1. Decisions about the specific functional form for the approach to estimating the data generating rules was based on consideration of the individual-level data in HRS and recognition that inclusion of higher-level interactions or use of non-parametric approaches may increase the possibility of deductive re-constitution of individual-level data.
Table 1.
Summary of data generating rules with dependencies determined from the causal DAG and appropriate functional form for the modelling based on exploration of individual-level data in HRS
| Variable | Variable Type | Dependency | Functional Form |
|---|---|---|---|
| Age, Gender, Race | Categorical | Exogenous | Sample proportions in categories defined by gender, race, and 5-year age groups; assumes a uniform distribution within 5 years of age |
| CSES (HRS only) | Continuous, approximately normally distributed | CSES | Age, Race | Linear regression model |
| Education | Categorical | Education | Age, Race, Gender, CSES (HRS only) | Multinomial regression model |
| Diet (ARIC only) | Continuous, approximately normally distributed | Diet | Race, Gender, Education, Age | Linear regression model |
| HbA1c | Continuous, not normally distributed | HbA1c | Age, Race, Gender, Education, CSES (HRS only), Diet (ARIC only) | Gamma regression model |
| Rate of Change in Memory | Continuous, repeated measures | Rate of Change in Memory | Age, Race, Gender, Education, CSES (HRS only), Diet (ARIC only), HbA1c | Linear mixed effects model |
Abbreviations: ARIC, Atherosclerosis Risk in Communities Study; CSES, childhood SES; DAG, directed acyclic graph; HbA1C, glycated hemoglobin; HRS, Health and Retirement Study
For age, race, and gender we used non-parametric summaries of the joint distribution for these variables corresponding to the observed distribution in the respective datasets. To estimate the distributions for other variables in the DAG, we used regression models, predicting each variable as a function of its parents. Analyses were conducted first in HRS by one analyst (TF) with access to the raw data. Guided by the decisions made in estimating these quantities in HRS, TF then requested publicly reportable information summarizing the joint distributions and associations for the variables in the DAG in ARIC from a second analyst (XL), who had access to the individual-level ARIC data. Only publicly reportable information was transferred to the primary analyst (TF) for use in synthetic data generation, including regression coefficients and distributional parameters of residuals from each regression model.
It should be noted that the approach itself does not guarantee lack of privacy concerns. The summary information created should adhere to typical data security rules implemented to avoid individual-level identification. Just as one would suppress summary statistics that might be identifying from general publication, similar caution should be taken when creating and releasing the data generating rules. If sufficient precautions are taken, this step generates publicly reportable information that can be easily shared, akin to summaries of the data frequently shared in published papers.
Step 3: Generate and validate the synthetic data.
We generated simulated datasets of identical size to the original HRS (n=11,509) and ARIC (n=12,043) datasets. We generated data for each variable in a stepwise process that preserved the causal structure of the data. We generated data separately for HRS and ARIC based on the data-generating rules derived from each dataset.
To reflect the uncertainty in any single data generation, we iterated the data generation process 5,000 times. Next, we compared the covariate distributions in the original datasets to the average distributions across iterations, as well as effect estimates and standard errors of the observed association of HbA1c and memory decline with the average associations and associated standard errors in the synthetic data, to identify coding errors and gross model misspecification.
Step 4: Pool simulated datasets & impute data for missing variables.
We pooled pairs of HRS and ARIC simulated datasets and conducted a single imputation to impute covariates missing from each dataset using multivariate imputation by chained equations (MICE),26,27 Dietary measures were imputed for synthetic HRS participants, while childhood SES measures were imputed for synthetic ARIC participants. To understand the importance of including the imputed covariates, we computed effect estimates and standard errors of the observed association of HbA1c and memory change in the synthetic data before and after imputation in the individual, simulated HRS and ARIC datasets.
Step 5: Estimate the causal effect of interest.
Finally, we compute effect estimates and standard errors of the observed association of HbA1c and memory decline after imputation in the pooled synthetic HRS and ARIC datasets to derive a pooled effect estimate that includes adjustment for all of the confounding variables, including those structurally missing from one dataset, as well as cohort and the interaction between cohort and all other terms in the model except for the HbA1c by age term.
In sensitivity analyses, we considered pooling and estimating pooled effects omitting CSES and diet as covariates and estimation of a simpler model omitting cohort by covariate terms. We also provide a random effects meta-analysis estimate of the coefficients of interest (age*HbA1c above and below 6.5) based on parallel analyses in each original dataset.
Simulation Study
Finally, we conducted a simulation study to illustrate the impact of using relatively simple, parametric models – which may be misspecified relative to the true data generating process -- to generate our synthetic data while achieving our privacy goals. Details of this simulation study are available in eAppendix A and eAppendix B. We first generated a simulated dataset (i.e. original simulated data). Next we followed the process above to generated synthetic data and effect estimates in the synthentic data under three scenarios. Scenario 1 considers the situation where the data generating process perfectly matches the parametric assumptions detailed above. Scenario 2 explores a misspecification of the data-generating process for our exposure (HbA1c). Scenario 3 explores misspecification of the underlying data-generating process for both exposure and outcome. For each Scenario, we estimate the effect of HbA1c on cognitive change using the model described in equation 7 of the eMethods in the original simulated data. We then compare this to the synthetic, cohort-specific results for the effect of memory on cognitive change generated through repeating steps 1–5 above using our original assumptions about the data-generating mechanism. This provides an assessment of the impact of misspecifying the data generating process through assumption of reasonable, parametric models, on recovering the coefficients that would be estimated in the original data.
RESULTS
The distributions of all variables in the HRS and ARIC synthetic datasets (averaged over 5,000 iterations) were similar to those in the original datasets (Table 2). Overall fits for the model of HbA1c on change in memory scores from the synthetic datasets reflected the original effect estimates, with reasonably similar precision (Table 3). Estimates in the synthetic datasets pre- and post-imputation were also similar (Table 3), suggesting that there was little residual confounding introduced by the omission of diet or childhood SES data. The estimates for the associations between HbA1C and cognitive change in the synthetic, pooled data after imputation of missing covariates and adjustment for cohort fell in between the cohort-specific original estimates (Table 4), and precision was improved for the estimate of the impact of HbA1c under 6.5 on excess cognitive change compared to either of the original datasets (Figure 2). In this case, sensitivity analyses suggested that imputation of missing covariates did not substantially change estimates, but confirmed the necessity of including cohort by confounder interactions, as pooled models omitting these terms produced estimates of slope outside the range of the individual estimates from the original cohorts (Table 4).
Table 2:
Distributions of variables in the original and synthetic (pre-imputation) HRS and ARIC datasets.
| HRS Original | HRS Synthetica | ARIC Original | ARIC Synthetica |
|---|---|---|---|
| N (%) or Mean (SD) | N (%) or Mean (SD) | N (%) or Mean (SD) | N (%) or Mean (SD) |
| 11509 | 11509 | 12043 | 12043 |
| 69 (10) | 70 (11) | 58 (5) | 59 (5) |
| 5.9 (1.0) | 5.9 (0.96) | 5.8 (1.2) | 5.8 (1.2) |
| 5.6 (0.4) | 5.5 (0.7) | 5.5 (0.4) | 5.3 (0.8) |
| 7.7 (1.4) | 7.2 (0.6) | 8.5 (2.0) | 7.4 (0.7) |
| 6810 (59) | 6810 (59) | 6676 (55) | 6675 (55) |
| 4699 (41) | 4699 (41) | 5367 (45) | 5368 (45) |
| 9972 (87) | 9971 (87) | 9265 (77) | 9265 (77) |
| 1537 (13) | 1538 (13) | 2778 (23) | 2778 (23) |
| 2458 (21) | 2551 (22) | 2702 (22) | 2805 (23) |
| 7718 (67) | 7657 (67) | 5032 (42) | 4999 (42) |
| 1333 (12) | 1301 (11) | 4309 (36) | 4239 (35) |
| 0.07 (1.05) | 0.05 (1.06) | NA | NA |
| NA | NA | 0.03 (0.99) | 0.04 (0.99) |
| NA | NA | −0.02 (0.98) | −0.03 (0.98) |
| −0.39 (1.10) | −0.44 (1.19) | −0.04 (1.01) | −0.001 (1.09) |
Synthetic dataset distributions are averaged over 5,000 iterations.
Abbreviations: ARIC, Atherosclerosis Risk in Communities Study, CSES, childhood SES, HRS, Health and Retirement Study, HS, high school
Table 3:
Model results comparing results for the linear mixed model for trajectories in memory z-score across the original and synthetic datasets
| Variable | ARICa Original Beta (95% CI) | ARIC Synthetic Beta (95% CI) | ARIC Synthetic + Imputation Beta (95% CI) | HRS Original Beta (95% CI) | HRS Synthetic Beta (95% CI) | HRS Synthetic + Imputation Beta (95% CI) |
|---|---|---|---|---|---|---|
| (Intercept) | 0.36 (0.31, 0.41) | 0.36 (0.32, 0.39) | 0.32 (0.29, 0.36) | 0.67 (0.6, 0.75) | 0.67 (0.6, 0.75) | 0.67 (0.59, 0.74) |
| HbA1ca (Below 6.5) | −0.04 (−0.08, −0.01) | −0.04 (−0.06, −0.03) | −0.04 (−0.06, −0.03) | 0.01 (−0.03, 0.06) | 0.01 (−0.02, 0.04) | 0.01 (−0.02, 0.05) |
| HbA1ca (Above 6.5) | −0.05 (−0.06, −0.03) | −0.05 (−0.07, −0.02) | −0.04 (−0.07, −0.02) | −0.07 (−0.1, −0.04) | −0.07 (−0.13, −0.02) | −0.07 (−0.13, −0.02) |
| Age | −0.59 (−0.64, −0.55) | −0.59 (−0.65, −0.54) | −0.57 (−0.63, −0.52) | −0.53 (−0.58, −0.48) | −0.53 (−0.58, −0.49) | −0.53 (−0.58, −0.49) |
| Black | −0.43 (−0.47, −0.39) | −0.43 (−0.47, −0.4) | −0.42 (−0.46, −0.39) | −0.48 (−0.54, −0.42) | −0.48 (−0.53, −0.42) | −0.48 (−0.54, −0.42) |
| Greater than HS | 0 (ref) | 0 (ref) | 0 (ref) | 0 (ref) | 0 (ref) | 0 (ref) |
| HS Education | −0.17 (−0.2, −0.13) | −0.17 (−0.2, −0.14) | −0.15 (−0.18, −0.11) | −0.39 (−0.45, −0.33) | −0.39 (−0.45, −0.33) | −0.39 (−0.45, −0.32) |
| Less than HS | −0.46 (−0.51, −0.42) | −0.46 (−0.5, −0.43) | −0.41 (−0.46, −0.37) | −0.84 (−0.92, −0.76) | −0.84 (−0.92, −0.76) | −0.83 (−0.91, −0.75) |
| Male | −0.4 (−0.43, −0.37) | −0.4 (−0.43, −0.37) | −0.4 (−0.43, −0.37) | −0.35 (−0.39, −0.31) | −0.35 (−0.39, −0.31) | −0.34 (−0.38, −0.29) |
| CSES | NA | NA | 0.04 (0.02, 0.06) | 0.05 (0.03, 0.07) | 0.05 (0.03, 0.07) | 0.05 (0.03, 0.07) |
| Prudent Diet Score | −0.01 (−0.03, 0.002) | −0.01 (−0.03, 0.0005) | −0.01 (−0.03, 0.001) | NA | NA | −0.01 (−0.04, 0.02) |
| Western Diet Score | −0.03 (−0.05, −0.02) | −0.03 (−0.05, −0.02) | −0.03 (−0.05, −0.02) | NA | NA | −0.02 (−0.05, 0.004) |
| Age*Black | 0.051 (0.016, 0.086) | 0.051 (0.0001, 0.102) | 0.046 (−0.005, 0.097) | 0.054 (0.013, 0.096) | 0.054 (0.018, 0.091) | 0.054 (0.018, 0.091) |
| Age*Greater than HS | 0 (ref) | 0 (ref) | 0 (ref) | 0 (ref) | 0 (ref) | 0 (ref) |
| Age*HS Education | −0.003 (−0.032, 0.026) | −0.003 (−0.05, 0.044) | −0.014 (−0.063, 0.034) | 0.035 (−0.009, 0.079) | 0.035 (−0.005, 0.075) | 0.034 (−0.006, 0.075) |
| Age*Less than HS | 0.019 (−0.021, 0.06) | 0.019 (−0.036, 0.074) | −0.009 (−0.071, 0.053) | 0.044 (−0.011, 0.098) | 0.043 (−0.005, 0.092) | 0.042 (−0.006, 0.091) |
| Age*Male | −0.014 (−0.043, 0.014) | −0.014 (−0.057, 0.028) | −0.015 (−0.057, 0.028) | 0.037 (0.009, 0.065) | 0.037 (0.012, 0.061) | 0.035 (0.01, 0.061) |
| Age*CSES | NA | NA | −0.02 (−0.043, 0.002) | 0.015 (0.001, 0.03) | 0.015 (0.003, 0.028) | 0.015 (0.003, 0.028) |
| Age*Prudent Diet Score | −0.006 (−0.02, 0.008) | −0.006 (−0.027, 0.015) | −0.006 (−0.027, 0.015) | NA | NA | 0.001 (−0.011, 0.013) |
| Age*Western Diet Score | 0.008 (−0.006, 0.023) | 0.008 (−0.013, 0.029) | 0.008 (−0.013, 0.029) | NA | NA | 0.003 (−0.01, 0.015) |
| Age*HbA1c (Below 6.5)a | −0.055 (−0.089, −0.022) | −0.055 (−0.082, −0.029) | −0.056 (−0.083, −0.03) | −0.047 (−0.076, −0.017) | −0.047 (−0.065, −0.028) | −0.047 (−0.065, −0.029) |
| Age*HbA1c (Above 6.5)a | 0.007 (−0.015, 0.028) | 0.007 (−0.036, 0.049) | 0.006 (−0.037, 0.048) | 0.013 (−0.012, 0.038) | 0.013 (−0.02, 0.046) | 0.013 (−0.02, 0.046) |
Abbreviations: ARIC, Atherosclerosis Risk in Communities; HRS, Health and Retirement Study; CI, Confidence Interval; HbA1c, Glycated Hemoglobin; CSES, Childhood Socioeconomic Status
HbA1c modelled as a linear spline. HbA1c (below 6.5) refers to the linear association with memory scores observed for a one unit change in HbA1c values below 6.5, the threshold for diabetes, while HbA1c (above 6.5) refers to the linear association with memory scores observed for a one unit change in HbA1c values above 6.5.
Table 4:
Model results of linear mixed model for trajectories of memory z-score across original and pooled synthetic data
| Variable | ARIC Original Beta (95% CI) | HRS Original Beta (95% CI) | Pooled Synthetic Data with Imputation Beta (95% CI) | Sensitivity: Pooled Synthetic Data (No Imputation) Beta (95% CI) | Sensitivity: Pooled Synthetic Data with Imputation (No Adjustment for Cohort) Beta (95% CI) |
|---|---|---|---|---|---|
| (Intercept) | 0.36 (0.31, 0.41) | 0.67 (0.6, 0.75) | 0.32 (0.28, 0.36) | 0.37 (0.33, 0.4) | 0.39 (0.35, 0.42) |
| Cohorta | NA | NA | 0.35 (0.27, 0.42) | 0.36 (0.29, 0.43) | NA |
| HbA1c (Below 6.5)b | −0.04 (−0.08, −0.01) | 0.01 (−0.03, 0.06) | −0.04 (−0.06, −0.03) | −0.05 (−0.06, −0.03) | −0.02 (−0.04, −0.01) |
| HbA1c (Above 6.5)b | −0.05 (−0.06, −0.03) | −0.07 (−0.1, −0.04) | −0.05 (−0.07, −0.02) | −0.05 (−0.08, −0.02) | −0.06 (−0.08, −0.03) |
| Age | −0.59 (−0.64, −0.55) | −0.53 (−0.58, −0.48) | −0.57 (−0.62, −0.51) | −0.59 (−0.64, −0.55) | −0.49 (−0.52, −0.46) |
| Black | −0.43 (−0.47, −0.39) | −0.48 (−0.54, −0.42) | −0.42 (−0.46, −0.39) | −0.43 (−0.46, −0.4) | −0.44 (−0.47, −0.41) |
| HS Education | −0.17 (−0.2, −0.13) | −0.39 (−0.45, −0.33) | −0.15 (−0.18, −0.11) | −0.17 (−0.2, −0.14) | −0.16 (−0.19, −0.13) |
| Less than HS | −0.46 (−0.51, −0.42) | −0.84 (−0.92, −0.76) | −0.41 (−0.46, −0.37) | −0.47 (−0.51, −0.43) | −0.49 (−0.53, −0.45) |
| Male | −0.4 (−0.43, −0.37) | −0.35 (−0.39, −0.31) | −0.4 (−0.43, −0.37) | −0.42 (−0.44, −0.39) | −0.38 (−0.41, −0.36) |
| CSES | NA | 0.05 (0.03, 0.07) | 0.04 (0.02, 0.06) | NA | 0.04 (0.03, 0.06) |
| Prudent Diet Score | −0.01 (−0.03, 0.002) | NA | −0.01 (−0.03, 0.001) | NA | −0.01 (−0.03, 0.002) |
| Western Diet Score | −0.03 (−0.05, −0.02) | NA | −0.03 (−0.05, −0.02) | NA | −0.03 (−0.05, −0.01) |
| Cohort*HbA1c (Below 6.5)a,b | NA | NA | 0.061 (0.029, 0.093) | 0.06 (0.028, 0.092) | NA |
| Cohort*HbA1c (Above 6.5)a,b | NA | NA | −0.023 (−0.079, 0.032) | −0.025 (−0.08, 0.03) | NA |
| Cohort*Agea | NA | NA | 0.033 (−0.030, 0.096) | 0.062 (0.005, 0.118) | NA |
| Cohort*Black Racea | NA | NA | −0.058 (−0.123, 0.008) | −0.063 (−0.128, 0.002) | NA |
| Cohort*HS Educationa | NA | NA | −0.24 (−0.31, −0.17) | −0.25 (−0.32, −0.18) | NA |
| Cohort*Less than HSa | NA | NA | −0.42 (−0.51, −0.33) | −0.44 (−0.52, −0.35) | NA |
| Cohort*Malea | NA | NA | 0.058 (0.006, 0.109) | 0.062 (0.013, 0.111) | NA |
| Cohort*CSESa | NA | NA | 0.015 (−0.009, 0.04) | NA | NA |
| Cohort*Prudent Diet Scorea | NA | NA | 0.004 (−0.021, 0.029) | NA | NA |
| Cohort*Western Diet Scorea | NA | NA | 0.01 (−0.017, 0.036) | NA | NA |
| Age*Black | 0.051 (0.016, 0.086) | 0.054 (0.013, 0.096) | 0.042 (−0.008, 0.092) | 0.049 (−0.001, 0.098) | 0.026 (0.001, 0.052) |
| Age*HS Education | −0.003 (−0.032, 0.026) | 0.035 (−0.009, 0.079) | −0.015 (−0.064, 0.034) | −0.001 (−0.048, 0.046) | 0.002 (−0.024, 0.028) |
| Age*Less than HS | 0.019 (−0.021, 0.06) | 0.044 (−0.011, 0.098) | −0.01 (−0.073, 0.052) | 0.022 (−0.031, 0.076) | −0.032 (−0.064, 0.0001) |
| Age*Male | −0.014 (−0.043, 0.014) | 0.037 (0.009, 0.065) | −0.015 (−0.058, 0.028) | −0.008 (−0.048, 0.033) | 0.043 (0.024, 0.062) |
| Age*CSES | NA | 0.015 (0.001, 0.03) | −0.02 (−0.042, 0.003) | NA | 0.008 (−0.002, 0.018) |
| Age*Prudent Diet Score | −0.006 (−0.02, 0.008) | NA | −0.006 (−0.027, 0.015) | NA | 0.005 (−0.004, 0.014) |
| Age*Western Diet Score | 0.008 (−0.006, 0.023) | NA | 0.008 (−0.013, 0.029) | NA | 0.001 (−0.008, 0.01) |
| Age*HbA1c (Below 6.5)b | −0.055 (−0.089, −0.022) | −0.047 (−0.076, −0.017) | −0.05 (−0.065, −0.035) | −0.05 (−0.065, −0.035) | −0.032 (−0.045, −0.019) |
| Age*HbA1c (Above 6.5)b | 0.007 (−0.015, 0.028) | 0.013 (−0.012, 0.038) | 0.01 (−0.016, 0.036) | 0.01 (−0.016, 0.036) | −0.002 (−0.025, 0.02) |
| Cohort*Age*Black Racea | NA | NA | 0.013 (−0.048, 0.075) | 0.004 (−0.057, 0.065) | NA |
| Cohort*Age*High School Educationa | NA | NA | 0.05 (−0.013, 0.113) | 0.028 (−0.033, 0.089) | NA |
| Cohort*Age*Less than HSa | NA | NA | 0.054 (−0.025, 0.132) | 0.0002 (−0.069, 0.07) | NA |
| Cohort*Age*Malea | NA | NA | 0.05 (0.001, 0.1) | 0.045 (−0.002, 0.092) | NA |
| Cohort*Age*CSESa | NA | NA | 0.035 (0.01, 0.06) | NA | NA |
| Cohort*Age*Prudent Diet Scorea | NA | NA | 0.007 (−0.016, 0.031) | NA | NA |
| Cohort*Age*Western Diet Scorea | NA | NA | −0.005 (−0.03, 0.019) | NA | NA |
Abbreviations: ARIC, Atherosclerosis Risk in Communities; HRS, Health and Retirement Study; CI, Confidence Interval; HbA1c, Glycated Hemoglobin; HS, High School; CSES, Childhood Socioeconomic Status
ARIC considered to be the reference group. This term refers to the difference attributable to being a member of HRS rather than ARIC.
HbA1c modelled as a linear spline. HbA1c (below 6.5) refers to the linear association with memory scores observed for a one unit change in HbA1c values below 6.5, the threshold for diabetes, while HbA1c (above 6.5) refers to the linear association with memory scores observed for a one unit change in HbA1c values above 6.5.
Figure 2. Effect estimates and confidence intervals for the association between HbA1c and cognitive change across the original, synthetic, and pooled data.
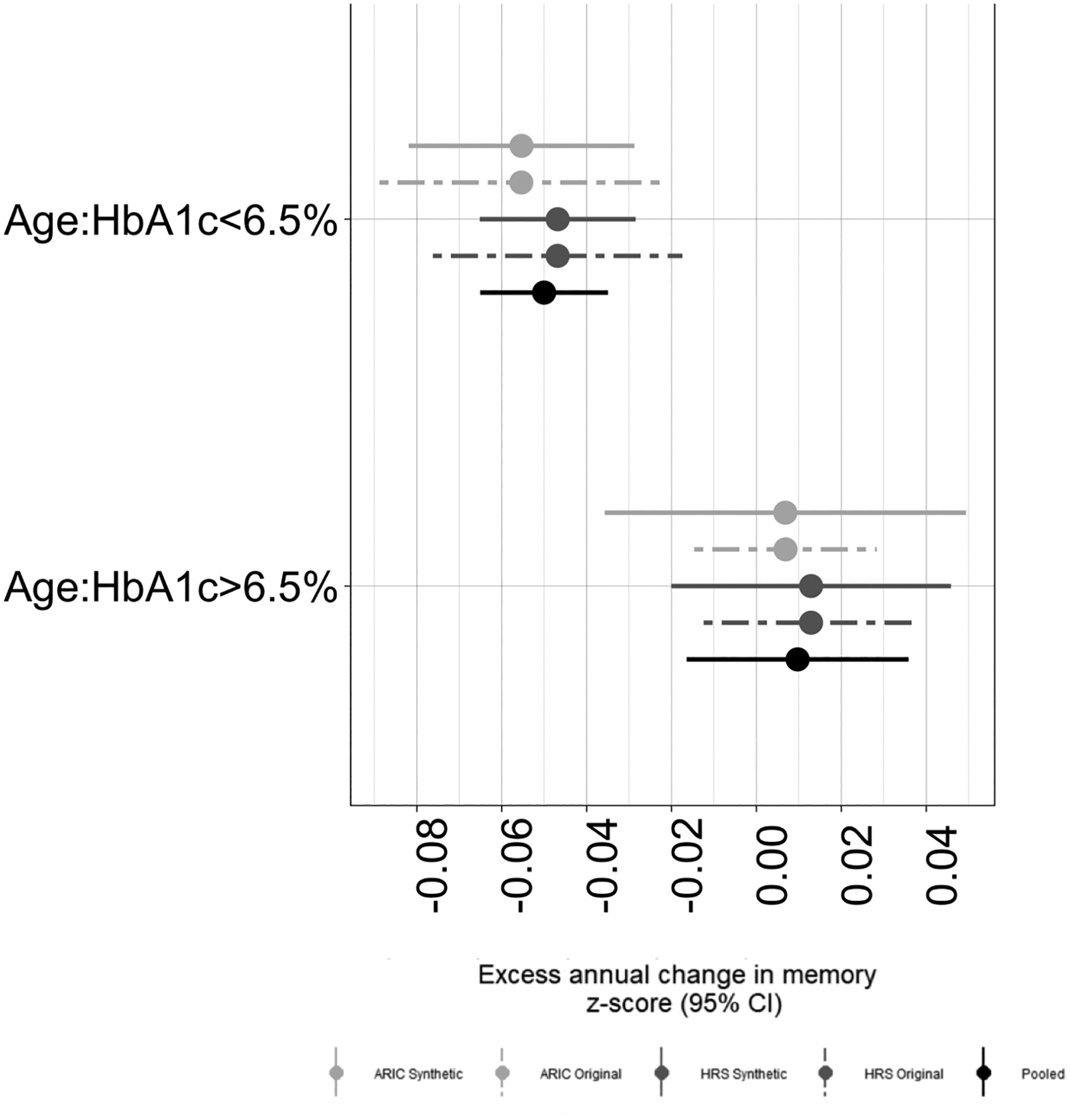
Dashed lines denote estimates and 95% confidence intervals for the effect of HbA1c on rate of memory decline for models fit using the original HRS and ARIC original data. Solid lines denote the average of 5000 effect estimates with 95% confidence bands for the effect of HbA1c on rate of memory decline for models fit with HRS, ARIC and Pooled synthetic data. Estimates of difference in HbA1c were estimated separately for those with HbA1c above and below 6.5%.
As expected given little evidence of residual confounding by CSES or diet, pooled estimates for the interaction of age*HbA1c below and above 6.5 were similar to the meta-analysis estimates (Below 6.5: −0.05, 95%CI: −0.073, −0.028; above 6.5: 0.010, 95%CI: −0.007, 0.026). Our simulation study illustrates that once we assume a model to estimate the causal effect of HbA1c on cognitive change, misspecification of the data generating rules used to generate the synthetic data did not lead to substantial differences between the synthetic, cohort-specific effect estimates and the equivalent effect estimates in the original (simulated, so as to have known data generating mechanisms) data (see eAppendix).
DISCUSSION
We demonstrated that we can use publicly reportable summary statistics to create synthetic datasets that allow estimation of the pooled effect estimate of interest by a single analyst without direct access to all of the relevant individual-level data. Use of the causal inference framework makes our assumptions explicit and provides a guide for generation of synthetic data. Moreover, use of imputation provides an opportunity to allow better control for confounding by covariates not uniformly found in individual datasets. Our sensitivity analyses also suggest that it is important to recognize that confounders may have different impact in different samples, and that this heterogeneity is important to recognize when estimating summary effects in pooled, individual-level data.
Combining data from multiple sources to address a specific question has many benefits, including the potential for increased statistical power and increased diversity in sample composition. While pooling and harmonization of individual-level data remains the gold-standard approach, this approach is often impractical or inefficient given the effort needed to obtain required legal agreements and fulfill associated contractual obligations, as well as other barriers related to provider willingness for data sharing. While the approach outlined here represents one solution to overcoming these barriers, others have been proposed as well. Meta-analysis1 of published statistics is common and creates no privacy concerns, but requires published analyses to have parallel designs and analyses. Bayesian approaches allowing generalized synthesis of the evidence are more flexible, but ultimately similar in their requirement for availability of published analyses.2,3 Coordinated analyses, such as those facilitated by the Integrative Analysis of Longitudinal Studies of Aging and Dementia (IALSA) research network4,5, overcome some of the limitations of meta-analyses by ensuring each contributing sample produces parallel analyses, which are then meta-analyzed, but cannot overcome issues of missing covariate data in individual datasets. Sharing of aggregate-level data (e.g. risk-set data sharing, summary table data-sharing), using varying approaches for confounding control, has been shown to allow statistical inference akin to what is achievable with access to individual-level data.6 However, depending on the level of aggregation and confounder control method, a subset of the aggregated data may remain close to or equivalent to individual-level data, which may not be permissible, and differences in availability of data on potential confounders remains an issue.
In comparison to these approaches, the approach we outline has some advantages. As with other approaches sharing aggregate-level data, our approach can be used to avoid sharing of individual-level data, given sufficient attention to the specification of the models. However, unlike these aggregate level approaches, the data generating rules can be used to simulate individual-level data by the recipient, allowing imputation and control for structurally missing covariates. Moreover, our approach easily incorporates consideration of effect modifiers, and because data pooling will increase the sample size of small groups, will support better evaluation of subgroup effects. Finally, as the presented approach is closely aligned with the process used for applications of the parametric g-formula28–31, this approach may form the basis for simulations to answer related questions.
The idea of synthetic data generation to address issues of data sharing and privacy concerns is not new. Generation of fully or partially synthetic data for the purpose of minimizing disclosure risk was initially proposed by Rubin7 and Little8 in 1993, who proposed multiple imputation of synthetic data as an alternative to other approaches, including perturbation, masking, and cell suppression. More recently, others have proposed use of machine learning algorithms to synthesize data (e.g.,9–12). To date, there has been less work adopting a causal framework, though Bayesian network approaches which involve both a causal discovery stage (to estimate the relevant causal structure) and regression-based or machine learning methods to generate synthetic data have been proposed.13,14
Our approach is similar to other synthetic data generating processes in that it creates data generating rules using parametric or non-parametric descriptions of the data distribution.32,33 However, most prior work conceptualizes synthetic data generation as a purely statistical problem, without reference to the underlying causal structure. Our approach specifies that these structures can be used to guide the data synthesis method just as they guide data analysis. If our goal was to publicly release fully imputed datasets for broad use, other methods allowing use of a smaller number of synthesized datasets might be more appropriate.34–36
As our approach generates a fully synthetic dataset, there is no 1:1 correspondence between the observed and synthetic data, and many argue that this eliminates identification disclosure risk.36–39 However, fully synthetic data such as ours remain susceptible to attribution or inferential disclosure risk.39,40 For settings in which there is a clearly defined concern about a potential attribution risk, formal methods to quantify attribution risk can be applied.37,39
This study has several strengths. Most importantly we provide a detailed, rigorous approach for creating complex synthetic datasets. We generated data based on the DAG, simulating each variable as a function of its parents. This simulation process is akin to application of the parametric G- formula to create the data28–31, differing in the fact that we do not impose treatment, thus the joint distributions implied by the causal structure of the DAG are built into the synthetic samples. The imputation of the missing covariates can be conceptualized as a convenient approach to bias correction, assuming that the joint distribution of the covariate found in a data set in which it was measured also applies in a data set in which it was not.
This study also has limitations. Although we chose childhood SES and diet a priori, as theoretically important confounders this was not borne out in the data. By using multiple imputation, we were able to derive pooled estimates controlling for confounders measured in at least one of the datasets. The success of this approach will depend, in general, on whether the missing covariate values in one sample can be appropriately imputed based on the distributions in another data set and whether there are interactive effects between covariates missing from different datasets in determining the exposure or outcome. For example, if childhood SES had modified the effect of diet on cognition, we could not plausibly recover this. Whether use of multiple imputation is appropriate should be considered on a case-by-case basis and merits further exploration in both real and simulated datasets. Despite these caveats, results obtained when imperfectly imputing a structurally missing covariate is unlikely to be more systematically biased than results obtained from analyses which simply omit the variable if the missing variable is an important confounder. Our approach relies on assumptions to simulate the joint distribution of variables within each data set (i.e., adequate specification of the data generating rules) as well as assumptions to justify pooling the data and estimating a single coefficient. With respect to the joint distribution, our process includes checks to identify gross misspecification, but as with any model for an unknown data generating process, our models are undoubtedly misspecified, especially given constraints on the degree to which we could use interactions or non-parametric approaches given privacy concerns. However, our simulation study provides some assurance that misspecification of the data generating process through use of reasonable parametric models does not lead to estimates that differ substantially from those that would be obtained using the original data. The assumptions to justify pooling the two datasets are distinct and mirror the assumptions necessary for any efforts to estimate a single parameter in pooled data. Similarly, as with any attempt at causal inference, we assume that our DAG is correct, that the covariates considered are sufficient to ensure exchangeability, and that our statistical estimand represents the causal quantity of interest. If this is not true, then the estimates from the original data and the pooled synthetic data will be biased. Our approach is designed to overcome specific hurdles to conducting pooled analyses, namely the need for access to individual-level data and lack of overlap in covariates; as such, all the limitations and challenges one would encounter if individual-level data pooling of the original data were possible still apply. In addition, as with other similar approaches to creating synthetic data36, our synthetic data can only capture relationships inherent in the joint distribution of the variables considered; if developed to address one research question, it cannot necessarily be repurposed for a second question with a different causal structure. Finally, imputation of missing variables using multiple imputations by chained equations (MICE) may not be the best approach. Other imputation methods or methods may be more appropriate. We acknowledge that this was a proof-of-concept study. While this approach is broadly generalizable, the implementation of the steps will need to be tailored to the presumed causal structure generating the data and the causal quantity of interest. Studies like this can only be successful with a strong and open communication between the analysts for each cohort. Though not necessary, common coding of variables and models provides a much cleaner and streamlined analysis. Incorporating additional cohorts into this study (and possibly more analysts) would require a structured communication plan at project inception.
Though we demonstrate this procedure with two datasets, the approach itself can be used for multiple datasets and provides a backbone for more complex extensions necessary to address substantive questions of interest. Potential extensions include incorporating time-varying exposures and accounting for selection bias due to death or drop-out when creating our synthetic datasets. Other potential extensions include extension to more complex causal scenarios incorporating mediators and confounders; extensions dealing with missing data within the variables measured in the original cohort; creation of synthetic, nationally representative samples based on data from less representative samples; and pre-implementation evaluation of randomized controlled trial study designs.
Supplementary Material
Acknowledgements:
The authors thank the staff and participants of the ARIC and HRS studies for their important contributions.
Funding:
The results reported herein correspond to specific aims of grant R01AG057869 to investigators Melinda C. Power and M. Maria Glymour from NIH/NIA.
The Atherosclerosis Risk in Communities Study is carried out as a collaborative study supported by National Heart, Lung, and Blood Institute contracts (HHSN268201700001I, HHSN268201700002I, HHSN268201700003I, HHSN268201700005I, HHSN268201700004I). Neurocognitive data is collected by U01 2U01HL096812, 2U01HL096814, 2U01HL096899, 2U01HL096902, 2U01HL096917 from the NIH (NHLBI, NINDS, NIA and NIDCD), and with previous brain MRI examinations funded by R01-HL70825 from the NHLBI. The authors thank the staff and participants of the ARIC study for their important contributions. The Health and Retirement Study data is sponsored by the National Institute on Aging (grant number U01AG009740) and was conducted by the University of Michigan. Neither NHLBI nor NIA had any role in design and conduct of the study; management, analysis, and interpretation of the data; preparation, review, or approval of the manuscript; or decision to submit the manuscript for publication.
Footnotes
Reproducibility: The HRS data used in this study are available on the Health and Retirement Study website (http://hrsonline.isr.umich.edu/). ARIC data can be made available to interested researchers through established study protocols (https://sites.cscc.unc.edu/aric/). We have posted our code on Github (https://github.com/powerepilab/Sim_for_data_pooling) and encourage the reader to reference the code as they read through the following sections of the manuscript.
Conflicts of Interest: All authors declare no conflicts of interest.
References:
- 1.DerSimonian R, Laird N. Meta-analysis in clinical trials. Control Clin Trials 1986;7(3):177–88. [DOI] [PubMed] [Google Scholar]
- 2.Ades AE, Sutton AJ. Multiparameter evidence synthesis in epidemiology and medical decision-making: current approaches. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2006;169(1):5–35. [Google Scholar]
- 3.Spiegelhalter DJ, Best NG. Bayesian approaches to multiple sources of evidence and uncertainty in complex cost-effectiveness modelling. Stat Med 2003;22(23):3687–709. [DOI] [PubMed] [Google Scholar]
- 4.Zammit AR, Piccinin AM, Duggan EC, Koval A, Clouston S, Robitaille A, Brown CL, Handschuh P, Wu C, Jarry V, Finkel D, Graham RB, Muniz-Terrera G, Bjork MP, Bennett D, Deeg DJ, Johansson B, Katz MJ, Kaye J, Lipton RB, Martin M, Pederson NL, Spiro A, Zimprich D, Hofer SM. A coordinated multi-study analysis of the longitudinal association between handgrip strength and cognitive function in older adults. J Gerontol B Psychol Sci Soc Sci 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hofer SM, Piccinin AM. Integrative data analysis through coordination of measurement and analysis protocol across independent longitudinal studies. Psychol Methods 2009;14(2):150–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Li X, Fireman BH, Curtis JR, Arterburn DE, Fisher DP, Moyneur E, Gallagher M, Raebel MA, Nowell WB, Lagreid L, Toh S. Validity of Privacy-Protecting Analytical Methods That Use Only Aggregate-Level Information to Conduct Multivariable-Adjusted Analysis in Distributed Data Networks. Am J Epidemiol 2019;188(4):709–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rubin DB. Statistical disclosure limitation. J. Off. Stat 1993;9(2):461–468. [Google Scholar]
- 8.Little R Statistical analysis of masked data. J. Off. Stat 1993;9(2):407–426. [Google Scholar]
- 9.Reiter JP. Using CART to Generate Partially Synthetic Public Use Microdata. Journal of Official Statistics 2005;21(2):441. [Google Scholar]
- 10.Drechsler J Using Support Vector Machines for Generating Synthetic Datasets. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010;148–161. [Google Scholar]
- 11.Caiola G, Reiter JP. Random Forests for Generating Partially Synthetic, Categorical Data. Trans. Data Privacy 2010;3(1):27–42. [Google Scholar]
- 12.Dandekar A, Zen RAM, Bressan S. A Comparative Study of Synthetic Dataset Generation Techniques. Cham: Springer International Publishing, 2018;387–395. [Google Scholar]
- 13.Young J, Graham P, Penny R. Using Bayesian networks to create synthetic data. Journal of Official Statistics 2009;25(4):549. [Google Scholar]
- 14.Goncalves A, Ray P, Soper B, Stevens J, Coyle L, Sales AP. Generation and evaluation of synthetic patient data. BMC Med Res Methodol 2020;20(1):108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hernán MA, Hsu J, Healy B. A Second Chance to Get Causal Inference Right: A Classification of Data Science Tasks. CHANCE 2019;32(1):42–49. [Google Scholar]
- 16.Hernán MA, Hernández-Díaz S, Werler MM, Mitchell AA. Causal Knowledge as a Prerequisite for Confounding Evaluation: An Application to Birth Defects Epidemiology. American Journal of Epidemiology 2002;155(2):176–184. [DOI] [PubMed] [Google Scholar]
- 17.Freedman D, Humphreys P. Are There Algorithms That Discover Causal Structure? Synthese 1999;121(1):29–54. [Google Scholar]
- 18.Juster FT, Suzman R. An Overview of the Health and Retirement Study. The Journal of Human Resources 1995;30:S7–S56. [Google Scholar]
- 19.Fisher GG, Ryan LH. Overview of the Health and Retirement Study and Introduction to the Special Issue. Work, Aging and Retirement 2017;4(1):1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Knopman DS, Ryberg S. A verbal memory test with high predictive accuracy for dementia of the Alzheimer type. Arch Neurol 1989;46(2):141–5. [DOI] [PubMed] [Google Scholar]
- 21.Standards of Medical Care in Diabetes—2014. Diabetes Care 2014;37(Supplement 1):S14–S80. [DOI] [PubMed] [Google Scholar]
- 22.Crimmins EM, Faul JD, Kim JK, Guyer H, Langa KM, Ofstedal MB, Sonnega A, Wallace RB, Weir DR. Documentation of Biomarkers in the 2006 and 2008 Health and Retirement Study. Ann Arbor, Michigan: Institute for Social Research, University of Michigan, 2013. [Google Scholar]
- 23.Selvin E, Ning Y, Steffes MW, Bash LD, Klein R, Wong TY, Astor BC, Sharrett AR, Brancati FL, Coresh J. Glycated hemoglobin and the risk of kidney disease and retinopathy in adults with and without diabetes. Diabetes 2011;60(1):298–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Vable AM, Gilsanz P, Nguyen TT, Kawachi I, Glymour MM. Validation of a theoretically motivated approach to measuring childhood socioeconomic circumstances in the Health and Retirement Study. PLoS One 2017;12(10):e0185898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lutsey PL, Steffen LM, Stevens J. Dietary intake and the development of the metabolic syndrome: the Atherosclerosis Risk in Communities study. Circulation 2008;117(6):754–61. [DOI] [PubMed] [Google Scholar]
- 26.Azur MJ, Stuart EA, Frangakis C, Leaf PJ. Multiple imputation by chained equations: what is it and how does it work? Int J Methods Psychiatr Res 2011;20(1):40–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.White IR, Royston P, Wood AM. Multiple imputation using chained equations: Issues and guidance for practice. Statistics in Medicine 2011;30(4):377–399. [DOI] [PubMed] [Google Scholar]
- 28.Hernan MA, Robins JM. Causal Inference: What If. Boca Raton: Chapman & Hall/CRC, 2020. [Google Scholar]
- 29.Taubman SL, Robins JM, Mittleman MA, Hernan MA. Intervening on risk factors for coronary heart disease: an application of the parametric g-formula. Int J Epidemiol 2009;38(6):1599–611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Westreich D, Cole SR, Young JG, Palella F, Tien PC, Kingsley L, Gange SJ, Hernan MA. The parametric g-formula to estimate the effect of highly active antiretroviral therapy on incident AIDS or death. Stat Med 2012;31(18):2000–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Keil AP, Edwards JK, Richardson DB, Naimi AI, Cole SR. The parametric g-formula for time-to-event data: intuition and a worked example. Epidemiology 2014;25(6):889–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mohan HS. A Review Of Synthetic Data Generation Methods For Privacy Preserving Data Publishing. International Journal of Scientific & Technology Research, 2017;6(3). [Google Scholar]
- 33.Lin PJ, Samadi B, Cipolone A, Jeske D, Cox S, Rendon C, Holt D, Xiao R. Development of a Synthetic Data Set Generator for Building and Testing Information Discovery Systems. Vol. 0, 2006. [Google Scholar]
- 34.Raghunathan TE, Reiter JP, Rubin DB. Multiple imputation for statistical disclosure limitation. Journal of Official Statistics 2003;19(1):1–16. [Google Scholar]
- 35.Drechsler J, Reiter JP. Sampling With Synthesis: A New Approach for Releasing Public Use Census Microdata. Journal of the American Statistical Association 2010;105(492):1347–1357. [Google Scholar]
- 36.Reiter JP. Releasing multiply imputed, synthetic public use microdata: an illustration and empirical study. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2005;168(1):185–205. [Google Scholar]
- 37.Hu J, Reiter JP, Wang Q. Disclosure Risk Evaluation for Fully Synthetic Categorical Data. Cham: Springer International Publishing, 2014;185–199. [Google Scholar]
- 38.Wei L, Reiter JP. Releasing synthetic magnitude microdata constrained to fixed marginal totals. Statistical Journal of the IAOS 2016;32:93–108. [Google Scholar]
- 39.Hu J Bayesian Estimation of Attribute and Identification Disclosure Risks in Synthetic Data. arXiv. Vol. 14 December 2018. 2019. [Google Scholar]
- 40.Karr AF, Kohnen CN, Oganian A, Reiter JP, Sanil AP. A Framework for Evaluating the Utility of Data Altered to Protect Confidentiality. The American Statistician 2006;60(3):224–232. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


