Predicting Hospital Resource Use During COVID-19 Surges: A Simple but Flexible Discretely Integrated Condition Event Simulation of Individual Patient-Hospital Trajectories

Abstract

Objectives

To assist with planning hospital resources, including critical care (CC) beds, for managing patients with COVID-19.

Methods

An individual simulation was implemented in Microsoft Excel using a discretely integrated condition event simulation. Expected daily cases presented to the emergency department were modeled in terms of transitions to and from ward and CC and to discharge or death. The duration of stay in each location was selected from trajectory-specific distributions. Daily ward and CC bed occupancy and the number of discharges according to care needs were forecast for the period of interest. Face validity was ascertained by local experts and, for the case study, by comparing forecasts with actual data.

Results

To illustrate the use of the model, a case study was developed for Guy’s and St Thomas’ Trust. They provided inputs for January 2020 to early April 2020, and local observed case numbers were fit to provide estimates of emergency department arrivals. A peak demand of 467 ward and 135 CC beds was forecast, with diminishing numbers through July. The model tended to predict higher occupancy in Level 1 than what was eventually observed, but the timing of peaks was quite close, especially for CC, where the model predicted at least 120 beds would be occupied from April 9, 2020, to April 17, 2020, compared with April 7, 2020, to April 19, 2020, in reality. The care needs on discharge varied greatly from day to day.

Conclusions

The DICE simulation of hospital trajectories of patients with COVID-19 provides forecasts of resources needed with only a few local inputs. This should help planners understand their expected resource needs.

Introduction

Faced with the potential for many admissions for COVID-19, hospitals worldwide have sought to anticipate their needs for critical care (CC) beds, related equipment, and staffing. Given the lack of knowledge of this disease,1, 2, 3, 4, 5 it was deemed necessary early in the pandemic to resort to the use of some form of predictive model,^{6 , 7} formal or informal, capable of forecasting the demand for resources as the epidemic evolved.⁸ Although various epidemiologic models have been developed,9, 10, 11, 12 these address the likely course of the epidemic at a national or regional level13, 14, 15, 16, 17, 18, 19, 20—a level of aggregation that is not helpful for individual hospitals. Even when the predictions were for a city,^{15 , 21 , 22} these remained too broad to reflect the needs of an individual institution. In a particular center, the pattern of arrivals and the mix of the population from its catchment population might not reflect that of the larger area.²³ Nosocomial infections and tertiary referrals may add further to a hospital’s case load.

Apart from the possible differences in the epidemic between a hospital’s catchment area and the broader region, specialty services may vary locally, and these will affect the demand for resources. To anticipate bottlenecks in delivery, any predictive modeling has to sufficiently adjust to each center’s circumstances. This requires a model capable of simulating in detail the course of patients according to a particular hospital’s practices. Because most centers do not have the capability to develop these simulations on their own, a tool that may be used by many hospitals to model patient flow during the COVID-19 pandemic can be of benefit. Such a tool must allow the customization of inputs to produce suitable estimates that hospital teams can reliably use to make decisions regarding expanding capacity, providing care for patients with other illnesses, requests for external support, and so on. Given the substantial uncertainty surrounding a novel virus epidemic, the model must allow for consideration of many scenarios. Because the epidemic changes as it progresses and is modified by imposition and withdrawal of mitigation measures, the model must be capable of incorporating new data as they become available and its structure must remain flexible and adaptable.

In this article, we describe the development of a model that meets these requirements. It was created at the request of an English National Health Service (NHS) Foundation Trust (Guy’s and St Thomas’ Trust [GSTT]). As is common for individual hospitals, they faced extreme time constraints that required a model able to produce results within days. The intent was to make the model available to other hospitals nationally and internationally, and thus, it had to be constructed using widely available spreadsheet software and be capable of simulating the trajectories at an adequate level of detail; it needed to be extremely flexible and easily and quickly adaptable because the data and needs were rapidly changing. This article focuses on the design and structuring of the simulation of hospital resource use, from arrival in the emergency department (ED) to discharge or death. A separate article, which deals with the local epidemiologic predictions, is in development. These details, though important to the full implementation of the forecasts, are not covered here because the simulation of hospital trajectories is not bound to any specific way of deriving the epidemiologic estimates and users can incorporate to the model what seems logical for their own context by replacing the existing estimates. To illustrate how the simulation works, a case study was presented using the inputs provided by GSTT in early April 2020.

Methods

Discretely Integrated Condition Event Simulation

The model was designed and implemented using a discretely integrated condition event (DICE) simulation.²² This allowed the model to be entirely specified and run in Microsoft Excel (Microsoft Corporation, Redmond, WA), a widely available and familiar spreadsheet application, with no need for specialized software.²⁴ By the same token, DICE models are easily understood and readily modified.²⁵ Using DICE allowed us to develop the model in less than 1 week and to modify the model on a daily basis as understanding of the pandemic and the hospital’s circumstances changed.

DICE simulation has been described in detail elsewhere—additional information, templates, training materials, and the DICE engine are freely available at https://dice.impact-hta.eu/. DICE is an approach to designing and structuring a simulation by separating the information to be processed from the changes that are forecast to happen. The information is stored in a table of uniquely named Conditions (names italicized here), and the changes are specified in Events (named with no spaces, capitalized, and bolded here). Each change is expressed in text that respects Excel syntax but without the “=” sign. A small macro reads the tables and processes them row by row, successively inserting an “=” sign to activate each expression in turn. Because all elements of the model are tabulated with no programming or hidden parts, a DICE model is very transparent, readily understood, and easily modified by editing the text expressions or adding or deleting rows in the tables. DICE has been used by health technology assessment agencies, including the English National Institute for Health and Care Excellence²⁶ and the French Haute Autorité de Santé,²⁷ and further developed as part of the Impact HTA Horizon 2020 project (https://www.impact-hta.eu/).

Model Design

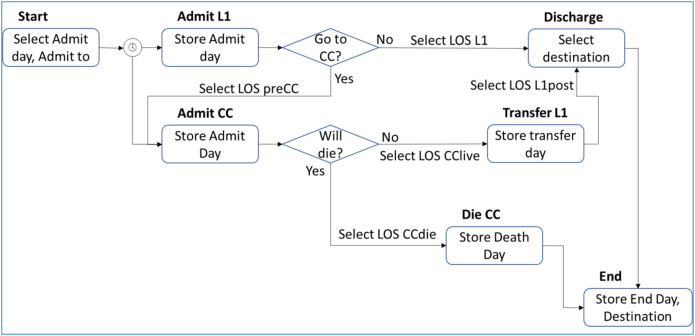
To address the complexities of the hospital trajectories, the model was specified as an individual simulation,²⁸ where the movements between wards and into and out of hospital were considered as events that happened on particular days (Fig. 1 ). Although the pathways were not particular to patients with COVID-19, the model focused on COVID-19–related admissions and not arrivals to the ED for other indications.

Figure 1.

Schematic of the DICE COVID-19 hospital management model. Events are represented by the boxes and arrows indicate possible pathways.

CC indicates critical care; COVID-19, coronavirus disease 2019; DICE, discretely integrated condition event; L1, Level 1; LOS, length of stay.

For each individual patient, the simulation assigned a calendar day on which that patient presented to the ED based on the distribution of arrival times that was obtained from the fits to local data (for the GSTT case study, the data and fits are provided in Appendix 1 in Supplemental Materials found at https://doi.org/10.1016/j.jval.2021.05.023). This arrival happened at the Start event, and the patient was then admitted either to the ward (at event AdmitL1) or to CC (AdmitCC). While in CC, a patient may have had a tracheostomy (Trach), required renal replacement therapy (RRT), or died (DieCC). Survivors were transferred to the ward (TransferL1) and then may be discharged or died in the ward (Discharge). On DieCC, Discharge, or end of the specified calendar period of predictions, End was triggered. This terminated the replication and reported those results.

Admission to either Level 1 (L1) or CC was determined in Start by applying a probability (stored in condition pEDtoL1) using a random number. Depending on the decision, the corresponding event was triggered. In the same way, it was determined in AdmitL1 whether the patient would be transferred to CC. If transferred, the timing of transfer was assigned based on a draw from a distribution describing the length of stay (LOS) on the ward before transfer. If no transfer would occur, the time until discharge or death was drawn from the corresponding LOS distribution. On admission to CC, the model determined whether the patient would die in CC and if so when. If not, then the day of transfer to L1 was selected from the relevant distribution. A tracheostomy may be performed if the LOS in CC met local standards. The need for RRT was determined based on its frequency (stored in pRRT). On TransferL1, the remaining LOS was assigned from the corresponding distribution. At Discharge, the destination (home, home with care, community care, nursing home) was chosen according to the proportions observed locally. At every event, its calendar time of occurrence was recorded.

All information processed by the model was contained in 47 conditions (Table 1 ), 9 event times, and 8 outputs (Table 2 ). Among the conditions, 4 were dynamic (values could change during simulation) and track what was happening to the patient. These were processed during the execution. Of the remainder, 21 were static (values did not change during simulation) and reflected user inputs that covered the time horizon and start date for the simulation, the parameters of the various equations that controlled model flow, and the probabilities that operated at junctures; 6 pertained to model control and the rest were random numbers that helped individualize the course of each patient.

Table 1.

Conditions in the COVID-19 DICE simulation.

Name	Initial level for GSTT	Description
Dynamic
Date	StartDate	Current date in simulation
StartDay	changing	Starting day selected for each patient
AdmitTo	changing	Admission location (1 = CC, 2 = L1) for each patient
DischDest	changing	Destination for each live discharge
Static
TimeHorizon	100	User-specified number of days to run simulation
StartDate	March 23, 2020	User-specified calendar date for start of simulation
pEDtoL1	0.96∗	Probability of transfer from ED to L
pL1toCC	0.22∗	Probability of transfer from L1 to CC
pDieCC	0.3∗	Fraction of patients who will die in CC
pSurvL1	0.85∗	Fraction of patients who will die in L1
pRRT	0.3∗	Fraction of patients in CC who require RRT
pHome	0.15∗	Cumulative proportion of discharges home
pHomewCare	0.575∗	Cumulative proportion of discharges home with care
pCommBed	0.9575∗	Cumulative proportion of discharges to community care bed
pCareHome	0.9915∗	Cumulative proportion of discharges to care home
BetaWillGoCC	1	Beta parameter for Weibull LOS in L1 before transfer to CC
LambdaWillGoCC	0.69314718	Lambda parameter for Weibull LOS in L1 before transfer to CC
BetaL1	1.4150375	Beta parameter for Weibull LOS in L1 only
LambdaL1	0.31889391	Lambda parameter for Weibull LOS in L1 only
BetaDieCC	1	Beta parameter for Weibull LOS before death in CC
LambdaDieCC	0.11552453	Lambda parameter for Weibull LOS before death in CC
BetaLiveCC	1	Beta parameter for Weibull LOS in CC before transfer to L1
LambdaLiveCC	0.1732868	Lambda parameter for Weibull LOS in CC before transfer to L1
BetaL1post	0.77760758	Beta parameter for Weibull LOS in L1 after transfer from CC
LambdaL1post	0.05675878	Lambda parameter for Weibull LOS in L1 after transfer from CC
Model control
NextEventTime	0	System, stores the time of the next event
NextEvent	1	System, stores the index number of the next event
Time	0	System, the current model time, in days
WillGoCC	Changing	Flag indicating whether patient will transfer from L1 to CC
WillDieCC	Changing	Flag indicating whether patient will die in CC
DieInL1	Changing	Flag indicating whether patient will die in L1

Dynamic conditions may change value during the simulation; static conditions retain their initial value during an iteration, but these may change for scenarios and uncertainty analyses (random number conditions not listed).

CC indicates critical care; COVID-19, coronavirus disease 2019; DICE, discretely integrated condition event; ED, emergency department; GSTT, Guy’s and St Thomas’ Trust; L1, Level 1; LOS, length of stay.

^∗Source: GSTT provided the initial values for their location.

Table 2.

Events in the COVID-19 DICE simulation and outputs recorded.

Name	Initial time	Description
Start	Changing	Specific to each patient
DieCC	Changing	When patient will die, if death occurs in CC
AdmitCC	Changing	Depends on the start date for each patient and admission destination
AdmitL1	Changing	Depends on the start date for each patient and admission destination
TransferL1	Changing	Depends on survival in CC
Tracheostomy	Changing	At least 14 days into CC stay
RRT	Changing	Depends on risk and LOS in CC
Discharge	Changing	Selected from LOS distribution
End	TimeHorizon	Duration of simulation set by analyst

Output	Recorded at	Description
rAdmitL1	AdmitL1	Date of first admission to ward for each patient
rAdmitCC	AdmitCC	Date of first admission to CC for each patient
rTransferL1	TransferL1	Date of transfer to ward from CC for each patient
rRRT	RRT	Date of initiating RRT for each patient
rTrach	Trach	Date of performing tracheostomy for each patient
rDischarge	Discharge	Date of discharge or death from L1 for each patient
rDischDest	Discharge	Location of care upon discharge
RepNum	System	Replication number if model rerun multiple times

CC indicates critical care; COVID-19, coronavirus disease 2019; DICE, discretely integrated condition event; L1, Level 1; LOS, length of stay; RRT, renal replacement therapy.

The distributions of LOS at various points according to the pathway could be specified using various distributions (exponential, Weibull, log-logistic) based on the observed local data. If a user did not have the data or expertise to fit their own LOS distributions, they needed to only specify the median and interquartile range of their local LOS, and the model would automatically refit the distributions on an empirical basis.

The model recorded the dates of all changes in location of care and reported these for each patient. The output was then processed to accumulate the numbers of patients in each location of care on any given day, and these were compared with the capacity limits for each location as set by the user to determine whether they were exceeded. If exceeded, the date and amount beyond capacity were recorded. This approach was implemented because the hospital team believed that all hospitals have means to expand their capacity and implementing queues was less useful and not realistic. The impact of expanding had repercussions on the ability of a hospital to deliver elective hospital care. Knowing when reserve capacities would be required also allowed the hospital to cancel appointments, cancel surgeries, and otherwise prepare.

Validation

The model was validated as far as possible in accordance with published guidelines.²⁹ Face validity of the model was established by the expert clinicians on the team, who ensured that the modeled pathways corresponded to the clinical reality. Verification of the implementation was performed by an independent modeler following a standard protocol. Predictive validity was more difficult to establish because of a lack of data. Forecasts were provided to the hospital team, and anecdotally, they reported back that these were reasonably accurate, but no detailed data were provided back to the modeling team. Given the continued pandemic pressures, even to this date, the data required for detailed predictive validation have not been made available to us. Nevertheless, it was possible to compare predictions of the timing and duration of peak resource requirements.

Uncertainty

A model such as this one bears 3 types of uncertainty.³⁰ The use of random numbers to select values from distributions and to determine trajectories creates stochastic uncertainty. This can be addressed in DICE by setting the number of replications to be done based on stability analyses. To do so, one or more outputs must be designated as the ones for which stability will be measured. The time until the peak CC demand and the level of the peak were of most interest for this model. The assumptions made in the model implementation create structural uncertainty. In DICE, this is handled by specifying alternative scenarios. For this model, scenarios could be specified covering any of the inputs or combinations. Finally, parameter uncertainty arises from the statistical uncertainty surrounding many of the inputs. The uncertainty table in a DICE model allows the analyst to specify the parameters that bear statistical uncertainty and their distributions. Both deterministic and probabilistic analyses can be run on these parameters. In this model, uncertainty analyses could be specified for the probabilities that control the trajectories and for the LOSs in each ward. Other parameters such as those pertaining to mortality can also be included.

Case Study

This work was undertaken by the team at the London School of Economics and Political Science in collaboration with GSTT to assist with planning resource allocation during the initial pandemic surge of COVID-19. This NHS Foundation Trust has a bed capacity of 1277 beds, including 1090 general and acute beds, 75 maternity beds, and 112 CC ICU beds (see https://www.cqc.org.uk/sites/default/files/new_reports/AAAE1480.pdf) and, annually, deals with approximately 2.6 million patient contacts of varying case mix, 95 000 of whom are treated as inpatients (see https://www.guysandstthomas.nhs.uk/about-us/who-we-are/facts-figures.aspx). The Emergency Department and Urgent Care Centre at GSTT is one of the busiest in the NHS, with 240 000 patient encounters per annum, predominately drawn from South London and of widely varying individual characteristics. GSTT was able to expand bed capacity based on surge principles for a conventional response where a hospital’s CC resources should expand immediately by 20% above baseline, followed by capacity expansion of at least 200% above baseline to meet demands using local, regional, national, and international resources.³¹

The GSTT team made several specifications on Thursday, March 26, 2020, defining a model to characterize their own setting (Table 3 ). To meet these specifications in the time allowed and with the data provided, the initial design for the model considered the wards as compartments and simulated the transfers among them. This cohort model was functional the following Wednesday, April 1, 2020. Eventually, this early cohort model was found to be insufficient to handle the heterogeneity in management, dependencies of transfer probabilities on LOSs, and more complex pathways. Therefore, it was converted to the individual simulation reported here.

Table 3.

Specifications for the model.

•Patients present to the ED at a given rate, which may change over time. •From ED, patients may go home (with or without care), to L1 care (general ward), to L2 or L3 CC, or may die. •No patients remain in ED overnight. •From L1 care, patients may go home (with or without care), to CC, or die. •From CC, patients may go to L1 care or die (no direct discharges). • At each level of care, there are capacity constraints: ○ Capacity in CC increases in 6 phases. Each phase is activated when previous capacity is reached. ○ Activation of next phase capacity occurs overnight. ○ Discharges requiring additional care at home or in a facility also face capacity constraints. •Staffing requirements are by level of care and per bed or patient. • A particular Trust is defined by: ○ Case influx from its catchment population and possible transfers ○ Its capacities at each level and phase ○ Its clinical practices ○ The occupancies at the start of the simulation

CC indicates critical care; ED, emergency department; L1, Level 1; L2, Level 2; L3, Level 3.

The case load data for the case study were obtained for Lambeth and Southwark, the primary catchment populations for the GSTT hospitals. These are inner London boroughs with a population of 644 864, approximately 43% of them in the black, Asian, and minority ethnic category of racial identification and toward the poorest in the United Kingdom. Lambeth is categorized as the 22nd most deprived and Southwark as the 44th most deprived of 326 local English authorities.

The daily cases presenting to the ED in the Lambeth and Southwark catchment area for GSTT were obtained from Public Health England (tabulated in Appendix 1 in Supplemental Materials found at https://doi.org/10.1016/j.jval.2021.05.023). Given the time constraints, flexible fractional polynomials were fit to the data (statistics in Appendix 1 in Supplemental Materials found at https://doi.org/10.1016/j.jval.2021.05.023), and a quadratic distribution was chosen as the simplest reasonable fit. Much later, a full dynamic transmission compartmental epidemiologic model was developed and fit to the data for many locations worldwide. Those fits (not reported here) can also be implemented in the DICE simulation using a separate module to generate the cases. Indeed, the DICE simulator can accept any user-defined way of generating the cases provided that the user’s equations produce estimates of the daily number of cases expected during the period of interest. The DICE model reported here uses these estimates for its purpose of predicting hospital flows once a patient arrives at hospital.

For the LOS distributions, the GSTT team provided the median and interquartile range for each ward, by pathway (eg, separately for patients going to a ward first then to CC from those going directly to CC). The model estimates the corresponding Weibull parameters. A Weibull distribution was chosen because it allows for the longer tail expected by the hospital and encompasses the simpler exponential distribution as a special case. Indeed, in some cases, the fitted shape parameter was 1, indicating that the distribution reduced to exponential.

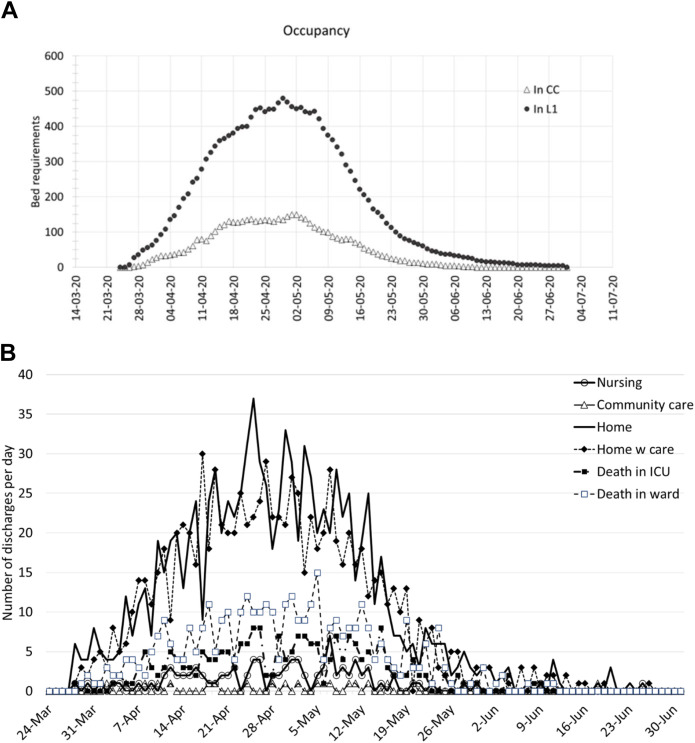
Analyses for the GSTT case study involved 80 replications (peak CC demand stabilized after 71 replications), with the average across replications taken as the estimate. For GSTT, the local data showed a steady rise in cases with a peak occurring between March 30, 2020, and April 1, 2020. The peak in the fits to these data coincided with those days with a 7-day moving average in this catchment area of 12.7 new COVID-19 cases per 100 000 people, whereas the quadratic fit predicted a rate of 12.4. Based on the fits to the observed data and GSTT’s LOS distributions and probabilities at particular junctures, the DICE model estimated GSTT’s expected daily bed occupancy in L1 and CC (Fig. 2 A). The model tended to predict higher occupancy than what was eventually observed (eg, for the first 7 days of April, the model predicted average ward daily occupancy of 344.9 than an actual average of 325.1). The timing of peaks was quite close, however. For CC, for example, the model predicted more than 120 beds would be needed between April 9, 2020, and April 17, 2020, than from April 7, 2020, to April 19, 2020 in reality. Bed occupancy was forecast to persist long after the case influx diminished to near 0 because of the longer tails in the LOS projections. The predicted number of deaths varied considerably from day to day, as did live discharges by destination (Fig. 2B), but the curves roughly followed those of bed occupancy.

Figure 2.

Daily bed occupancy and predicted discharges predicted by the model.

CC indicates critical care; ICU, intensive care unit; L1, Level 1.

Discussion

This model simulates the within-hospital course of patients with COVID-19 presenting to a hospital ED. It was created in close collaboration with clinical and operational leaders at the hospital level for GSTT and is functional to support local planning during any further surges. The objective was to aid bed utilization capacity planning under circumstances where it was unclear given original informal projections, whether capacity would be sufficient to meet demand.

The model developed was specified entirely in a small set of Excel tables that characterized complex patient flows in a simple yet accurate manner. It was executed by a standard, freely available DICE macro (downloadable from https://www.impact-hta.eu/), which can be used with any DICE model. DICE eases exposition of local circumstances by using readily accessed software and simplifying the expertise required to undertake the modeling by specifying complex patient flows through tabulated conditions and events. These only require the user to add local data to an input template. Additional complexity of patient flows (eg, to a step-down unit) or of resource use (eg, extracorporeal membrane oxygenation) can be incorporated through further specification of conditions and events where data exist.

The model can be downloaded and adapted by any user to their local hospital by modifying any of the small set of inputs. Local practices can be accommodated by changing the probabilities that control movement between wards, RRT, and tracheostomy. These can be obtained from the locally observed frequencies. Other resource use can be added to each ward, including staff requirements, by incorporating additional rows in the corresponding event tables. If the user has access to an epidemiologic forecasting model for new cases per day, this can be coupled to the hospital resource use module. Alternatively, forecasts can be made by fitting local observed case data.

The model itself has a few limitations. At the time the model was constructed, heterogeneity in hospital trajectories according to patient characteristics was not well understood and is, thus, not incorporated. As the determinants of course and outcome become clearer, they can be included in the model by adding patient profiles with these characteristics (a built-in feature of DICE) and deriving the affected condition values based on these. For example, if age and comorbidities affect the probability of going to CC and the case-fatality rates, then profiles covering the local age range and comorbidity distributions can be specified. These would be used to adjust the CC probability and the lambda parameter of the death equation.

The version of the model reported here does not include interventions such as extracorporeal membrane oxygenation or medications used to treat COVID-19 or its complications. As these emerge and their effects become clearer, they can be added to the care in the appropriate wards. Although it was not the purpose of the model to compare treatments for COVID-19, the simulation can accommodate these comparisons if a user provides information on the effects of a treatment on LOS or the various probabilities. DICE automatically reruns the model for each specified intervention, changing only those conditions that are affected by treatment. Incorporating the costs requires adding the relevant inputs (eg, cost of treatment, per diem costs in ward and CC) and specifying corresponding outputs (eg, treatment cost, hospital cost, total cost), which are accrued at the appropriate events. Estimating quality-adjusted life-years would require adding utilities to the inputs and projecting the course of patients after discharge—including consideration of any long-term consequences of COVID-19 infection and their impact on quality-adjusted life-years.

Although the model includes occupancy of beds by patients with other non-COVID diagnoses, these were not actively modeled (kept static) because the clinical team was unable to specify their trajectories during the pandemic. Given its flexibility, the model can incorporate their dynamic management if this information becomes available.

The application of this model to a specific hospital may be constrained by the availability and quality of data for that hospital. At GSTT, they could access electronic patient records. Even with these tools, however, it was difficult to obtain accurate data on ward occupancy. Across the United Kingdom, electronic recording varies, with many hospitals still using paper records. The predictive distribution of arrival dates for new cases and their cumulative volume were obtained by fitting local data for the catchment population of GSTT. The in-hospital trajectories were simulated based on the experience at GSTT. Ideally, the user has estimates of the median LOS and interquartile range in their ward and CC to model local flows. If lacking local data, a hospital wishing to use the model can run plausible scenarios using the default inputs and calibrate these to the specific information available (eg, death rate, range of LOS).

The COVID-19 pandemic has prompted a profusion of mathematical modeling,^{14 ,} 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45 but the vast majority of these models focus on the epidemiology46, 47, 48, 49, 50, 51, 52, 53, 54, 55 and the impact of mitigation measures.^{11 ,} 56, 57, 58, 59, 60, 61, 62, 63, 64 A few models have sought to inform hospital resource use planning,^{9 ,} 65, 66, 67, 68 but these also largely focus on the impact on the capacity of mitigation scenarios at a regional or national level69, 70, 71—they do not attempt to model the actual patient trajectories. Despite some attempts to localize projections to specific hospitals,^{72 , 73} many of the inputs were obtained from the early publications addressing the epidemics in China and Italy, and they model patient flow in relatively simple terms. The simulation reported here was based on fully local inputs and models the trajectories in detail. Moreover, it is very flexible and can be modified to accommodate other institutions’ practices and data.

Conclusion

It is possible to simulate the hospital and discharge course of patients with COVID-19 using a DICE simulation defined by conditions and event specified in Excel tables and executed by a simple macro. Additional details of the patient flows and resource use can be incorporated through additional conditions and events if local data and expertise allow. The predictions are useful for resource capacity planning and preparedness. A health authority needs to only rely on a small amount of local data to specify a few inputs to adapt the model to their context and aid their understanding of how their own patient flows will affect their ability to match uncertain demands being placed on their capacity. This modeling will be increasingly valuable as the pandemic progresses and should be considered as new waves emerge to ensure appropriate planning of in-hospital resources to deliver safe, timely, and resilient healthcare services.

Article and Author Information

Author Contributions:Concept and design: Caro, Möller, V. Santhirapala, Gill, Johnston, El-Boghdadly, R. Santhirapala, Kelly, McGuire

Acquisition of data: V. Santhirapala, Gill, Johnston, El-Boghdadly, R. Santhirapala, Kelly

Analysis and interpretation of data: Caro, Möller

Drafting of the manuscript: Caro

Critical revision of the paper for important intellectual content: Caro, Möller, V. Santhirapala, Gill, Johnston, El-Boghdadly, R. Santhirapala, Kelly, McGuire

Statistical analysis: Caro, Möller

Obtainingfunding: McGuire

Supervision: El-Boghdadly, McGuire

Other: Construction of Model: Caro, Möller

Conflict of Interest Disclosures: Dr Caro reported receiving grants from the European Union’s Horizon 2020 research and innovation program under grant agreement no. 779312 during the conduct of the study. Drs Caro and Möller are employed by Evidera. No other disclosures were reported.

Funding/Support: This project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement no. 779312. The views expressed in this article are those of the authors and not necessarily those of the European Commission.

Role of the Funder/Sponsor: The funder had no role in the work or the content of this paper, or in the decision to submit the manuscript for publication.