Computer simulation of the effectiveness of novel cardiac arrest response systems

Abstract

Aims

To use a computer simulation model to predict the response time and survival impact of a sample of novel cardiac arrest response systems, such as those that use cellphone apps to dispatch citizen mobile responders and those that use drones to deliver an AED to the cardiac arrest location.

Methods

We developed a model which applies a Monte Carlo approach to simulate the response time and predicted survival for cardiac arrest events within a specific region. We used the model to compare the performance of 4 different novel response systems, along with simulated EMS performance, in Bellevue, Washington. We estimated the 10 year cost for each system, which was utilized together with the system performance predictions in a cost-benefit analysis.

Results

The best performing systems in the simulation were a mobile responder system capable of providing both CPR and defibrillation, similar to the PulsePoint verified responder program, as well as a drone AED delivery system with bystander application. Both systems showed an incremental improvement in survival of 10% over the simulated EMS survival. The systems that provided the best cost-benefit ratio were the mobile responder system providing only CPR (PulsePoint Respond) and drone systems with bystander application.

Conclusions

Our simulation results suggest that these novel response systems have the potential to substantially improve survival at an efficient cost.

Introduction

Over 350,000 out-of-hospital sudden cardiac arrests occur each year in the United States.¹ Out-of-hospital sudden cardiac arrest survival remains stubbornly low at around 10%,² due in part to the difficulty of achieving early defibrillation through the response provided by emergency medical service (EMS). EMS response times are often minutes longer than that necessary to achieve high survival rates.³ Automated External Defibrillators (AEDs) have put the tools for early treatment into the hands of bystanders and other responders who do not have medical training. Although there are a number of successful applications of Public Access Defibrillation (PAD) strategies with AEDs, only 2–5% of out-of-hospital cardiac arrests are treated with an AED prior to EMS arrival.[2], [4], [5] In many cases, even when an AED is in the vicinity of a cardiac arrest, it is not used due to difficulty in locating or retrieving it by a bystander.⁵ Additionally, about 70% of cardiac arrests occur in private residences,² although few AEDs are located in homes. New response system concepts are being proposed, tested, and implemented to augment the EMS response to cardiac arrests with citizen responders to provide early CPR and defibrillation treatment. These response systems share the objective of bringing the AED and treatment to the cardiac arrest location, rather than relying on a bystander to initiate the retrieval of a nearby AED.

One approach is the use of smart phone apps to dispatch citizen mobile responders within a close radius of the cardiac arrest location, employing a type of “crowdsourcing” of the initial cardiac arrest treatment response. One prominent system, PulsePoint,⁶ is active in 3992 communities, primarily throughout the United States. Their volunteer citizen responder network provides CPR to public location cardiac arrests but relies on EMS to provide defibrillation. PulsePoint recently introduced a professional version of their response system, which has verified responders. These are off-duty first responder professionals, who are dispatched by the app to both public and private locations, and these may carry an AED to provide both defibrillation and CPR until EMS arrives. Other mobile responder systems include GoodSAM in the United Kingdom,⁷ which is similar to PulsePoint, “AED on wheels” in Singapore,⁸ which equips taxi cabs with AEDs for a dispatched response, and HartslagNu (Heartsafe Now) in the Netherlands,⁹ which directs citizen mobile responders both directly to the arrest location as well as to nearby PAD AEDs, then to the arrest location. A second approach is to use drones to deliver an AED to the cardiac arrest location. These systems dispatch a drone with an AED in its payload at the same time as EMS dispatch. The drone’s ability to fly above buildings and take a direct route can result in significantly shorter response times. A bystander or dispatched mobile responder then applies the AED.

These systems, many of which are still in their infancy, have been used only in a small number of studies and simulated rescues.[10], [11], [12] Although these new response systems have had sporadic successes, their effectiveness remains largely unknown. Modelling and simulation can be used to predict the performance of new systems prior to implementation. Although real-world studies may take months or years to generate sufficient data, modelling and simulation can provide predictions under many operational strategies and conditions in relatively short time.

Modelling and simulation of cardiac arrest response

Modelling and simulation methods have been employed since the 1970s to evaluate and improve operational strategies for emergency response systems. Much of the focus has been on optimizing EMS systems by optimizing ambulance base locations[13], [14], [15], [16] and evaluating strategies to improve availability and response time.[17], [18], [19]

A limited body of modelling and simulation work has been published for the emerging systems that augment EMS, and we are not aware of any studies that have systematically compared emerging systems. Pulver et al. solved a coverage problem to determine drone locations in Salt Lake City, Utah,²⁰ while Boutillier et al. optimized drone locations in Toronto using a Markov Chain queueing model to predict a 3 minute improvement over EMS response.²¹ Claesson et al. modeled drone locations around Stockholm, Sweden, and predicted that a drone would arrive before EMS in 32% of urban cases and 93% of rural cases.²² Marshall et al. used Monte Carlo simulation to predict response times of dispatched mobile responders in Belfast, Ireland.²³ The model predicted arrival before EMS in 19% of cases, while a corresponding trial found 15% of cases were treated before EMS.

This paper describes a simulation study that we conducted to estimate the potential effectiveness of these emerging response systems. Our simulation model predicts the response times and incorporates the geographical attributes of the region under simulation, including the locations of existing ambulance bases, the type of road network in the region, and the effects of weather on the drone response capability. Our model has the flexibility to simulate a large diversity of systems and any geographic region. The model also evaluates the effect of response times on cardiac arrest survival. The intended purpose of the model is to inform decision-makers on the potential response time and survival improvements of different response system concepts. We applied the model to simulate response times and predicted survival of four novel response systems, along with a simulated EMS response. Together with a cost estimate for each system, we provide a cost-benefit analysis, from which public health decision-makers could find the most efficient and beneficial option that meets both budgets and community preferences.

Methods

Study setting

To demonstrate the use of our model to compare the effectiveness of different systems within a single region, we simulated a region within the city of Bellevue, Washington, covering 40 sq. km of the city’s 83 sq. km. Bellevue is a city in King County, Washington, lying just east of Seattle, with a population of 147,000. The city of Bellevue had 85 out of hospital cardiac arrests in 2019, about 20% of which were witnessed and had an initial rhythm of ventricular fibrillation (VF). It is primarily a suburban city, with a downtown area with a few high-rise buildings.

Model construction

Our model was constructed to capture the complex sequence of both transit time and non-transit times which constitute the overall response time from the 911 call until treatment. A detailed discussion of the model inputs, data sources, construction, logic, and calculations can be found in a previous work.[24], [25] A brief overview is provided here.

For driving responses, we used an empirically derived Minkowski distance metric to approximate the actual road network distances (the Minkowski distance is a generalized distance metric, which in 2 dimensions uses the formula $d=({\left(x_1-x_2\right)}^p+{\left(y_1-y_2\right)}^p$)^1/p.[26], [27] The Euclidean distance, p = 2, and the Manhattan distance, p = 1, are specific cases of the Minkowski distance). We assumed a Euclidean distance, (straight line route), for drone responses, and a near Euclidean distance for walking responses, allowing for obstacle navigation. Our model includes additional non-transit factors for the time from 911 call to dispatch, from dispatch until start of transit, and from arrival until start of treatment. Other stochastic factors, such as the availability of ambulances, mobile responders, and drones, are applied as well. Table 1 provides a list of these factors and their nominal values. The data used to identify the inputs for the model was sourced from published literature, data provided by the King County public health department, manufacturers’ drone specifications, and where necessary, elicited from experts in emergency response systems as well as drone operations.

Table 1.

Description of system factors used in simulation model, with nominal simulation values.

Description of System Factor	Nominal value
Time from 911 call to EMS dispatch (minutes)	0.5
Time from EMS dispatch to start of ambulance transit (minutes)	3
Ambulance velocity (km/h)	70
Ambulance availability (due to other calls, maintenance, etc.)	76%
Time from EMS arrival until start of treatment (minutes)	1
Mobile responder density (responders per sq km in system)	5
Mobile responder dispatch time from 911 call (minutes)	1
Mobile responder time from alert to begin walk transit (minutes)	0.75
Mobile responder time from alert to begin driving transit (minutes)	1
Mobile responder walking velocity (km/h)	7
Mobile responder driving velocity (km/h)	32
Mobile responder reliability (likelihood of acting upon alert)	0.3
AED reliability (likelihood AED is in a fully functional state)	0.99
Time from mobile responder arrival until start of treatment (minutes)	1
Time from 911 call to drone dispatch (minutes)	1
Drone vertical flight time (minutes)	0.5
Drone velocity (km/h)	80
Drone descent and AED deployment time (minutes)	1
Drone operational availability (due to other calls, maintenance, etc.)	96%
Drone weather availability	90%
Time from drone arrival until start of treatment (minutes)	1

Model structure and logic

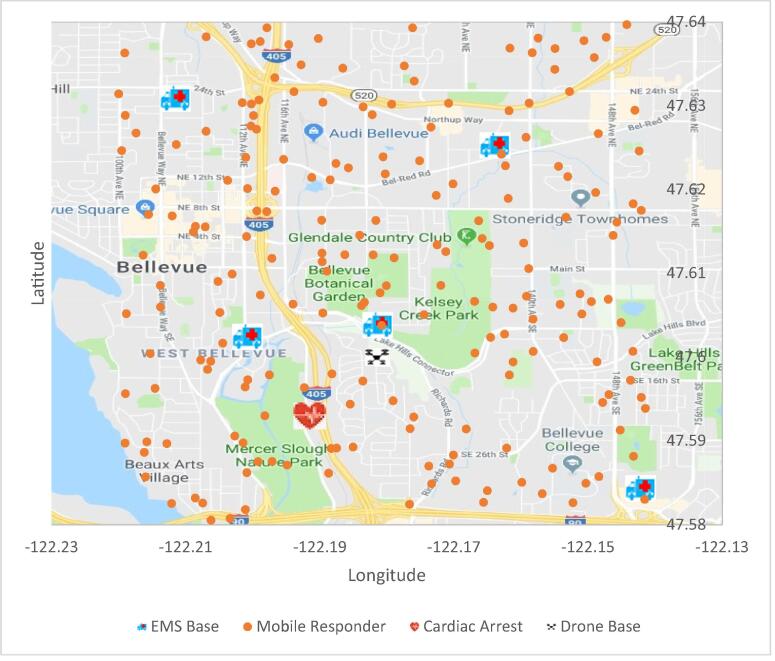
We used this data to construct simulation models of multiple systems. For each system, the model fixed certain values, including the actual Bellevue EMS locations, and assumed drone locations at existing Bellevue fire stations. Each run of the model simulated the system’s response to one cardiac arrest event. This included random sampling to determine the cardiac arrest location, the locations of the mobile responders (if any), and the availability of the responders for that event (Fig. 1). The model then calculated, for each available responder, the distance from the responder to the cardiac arrest event and the corresponding response time. The travel distance depends upon whether the responder is flying, driving, or walking. All response times included travel time (based on the travel distance and the responder’s speed) and non-transit delays. For example, the EMS response time included both transit time as well as dispatch time, chute time, and time from arrival until treatment. Our model does not distinguish between cardiac arrests in public locations and private residences, and is limited to witnessed arrests with shockable arrhythmias.

Fig. 1.

Simulation region of Bellevue, Washington, with the randomly sampled locations of cardiac arrests and mobile responders and the fixed locations of EMS and drone bases.

The primary objective of the model was to estimate response times, i.e. t_CPR, the elapsed time (minutes) at which CPR would begin, and t_defib, the elapsed time at which defibrillation would begin. To provide context to the response times, our model also estimated a survival probability for each event. Cardiac arrest survival rates have been correlated with many factors, including the time from collapse to CPR and the time to defibrillation.² In analyzing witnessed arrests with an initial rhythm of VF, Valenzuela et al. performed regression analysis on a number of factors but concluded that a simple model with these two factors provides nearly the same predictive capability as the complex model.²⁸ We employed their logistic regression model to predict P_s, the survival probability for each simulated cardiac arrest case, whereby:

$$logit\left(P_s\right)=0.26-0.106t_{\mathit{CPR}}-0.139t_{\mathit{defib}}$$ (1)

To apply this survival prediction model, we limited the simulation to only witnessed cases with VF, without quantifying the survival gains for other cardiac arrests.

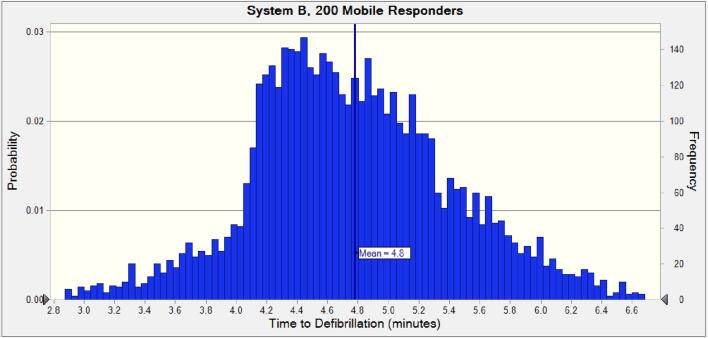
As each cardiac arrest simulation includes many stochastic factors (cardiac arrest location, mobile responder locations, responder availability), we used Monte Carlo simulation (a method utilizing many simulation runs with random factors sampled independently for each run) to perform thousands of simulated events, which yielded a distribution of response times and survival predictions (Fig. 2). System performance was characterized as the mean of these distributions.

Fig. 2.

Monte Carlo simulation results for time-to-defibrillation for a mobile responder system with a responder density of 5/sq. km.

Our model was implemented using Excel 2016 (Microsoft) with Crystal Ball (Oracle). Statistical analysis was performed using Minitab Version 18 (Minitab). The model validation process was described in a previous work.²⁵

Application of simulation model

We simulated one established mobile responder system and three emerging novel systems:

• A.A mobile responder system which provides CPR therapy only; similar to the PulsePoint Respond system.
• B.A mobile responder system which provides both CPR and defibrillation; a verified responder system, in which all responders are provided AEDs to keep near them e.g. in their cars.
• C.A drone AED delivery system which relies upon bystanders to apply and operate the AED, as well as provide CPR when coached by the AED, similar to the Flirtey trial in Reno, Nevada.¹²
• D.A drone AED delivery system which relies upon dispatched mobile responders to apply and operate the AED; a currently untested system concept.

The intent of this paper is not to compare all possible systems, but to demonstrate a robust modeling method for comparing the cost effectiveness of different systems.

For each modelled system, we evaluated multiple operating conditions. For the mobile responder systems, we ran simulations with responder densities of 2/sq. km, 5/sq. km, 8/sq. km. The drone systems simulated 1, 2, and 5 drones, based at the existing fire stations within the region. System D, which utilizes both drone delivery and mobile responders, was simulated at all 9 combination of conditions.

Each system was simulated as working in conjunction with the existing EMS system. As a baseline for comparison, we also simulated response time and survival with only the existing EMS system. Our study was focused on the response time improvements provided by these novel systems, and we did not include the potential for bystander CPR and PAD defibrillation as alternative means of response. We ran 5000 Monte Carlo simulations for each system under each condition.

Cost estimates of system

We estimated the cost to implement and operate each of these systems over a period of 10 years. We also considered a fifth alternative, as a point of comparison, which is the addition of a basic life support (BLS) ambulance to the Bellevue EMS fleet. Our cost estimates came from retail and catalog costs, or published literature, where available. Otherwise, we elicited estimates from experts in the fields of EMS and drone operations. Although the systems costs are uncertain and change over time, we believe the relative costs of each system are reasonably accurate, as these systems employ many of the same cost components. We created a cost model for each system, considering capital costs, consumable costs, and recurring expenses. Our models calculated a Net Present Value over 10 years of operation assuming a 5% discount rate. Our cost models assumed 100 cardiac arrest responses per year, accounting for increased events with population growth. For the EMS fleet with one additional BLS ambulance, we allocated 20% of the ambulance’s cost to the response to cardiac arrests, as the ambulance would provide additional utility in non-cardiac medical responses. An example cost model for system D with 5 drones and a density of 2 responders per sq. km is shown in Table 2.

Table 2.

Example 10-year NPV cost model for system D with 5 drones and a density of 2 responders per sq. km.

Capital costs
Drone	$119,048
Telemetry hardware	$4,762
Ground control station/EMS dispatch	$14,286
Drone nest	$47,619
AED	$9,714
Consumables costs
Payload drop mechanism	$772
Drone Battery	$1,604
AED Pads	$46,330
AED Battery	$15,752
Recurring costs
Drone pilot (subscription)	$23,165
Drone/Nest Maintenance	$57,913
Administration	$193,043
Total 10 year NPV Cost	$534,009

Results

The mean response times and survival predictions of the simulations are shown in Table 3. Response times showed improvements in mean time-to-defibrillation from 0.1 minutes (decimal time) for System D (1 drone with 2 verified responders/sq. km) to 2.3 minutes for System B (8 verified responders/sq. km). The predicted incremental improvement in survival rate for patients with witnessed VF ranges from 3% to 10%. These survival rate improvements would result in 4–17 additional lives saved over the 10-year period.

Table 3.

Predicted Mean Time-to-Defibrillation and Mean Survival Probability results of simulations of 4 systems (A: mobile responders providing CPR only; B: mobile responders provisioned with AEDs; C: drone AED delivery with bystander application; D: drone AED delivery with mobile responder application).

System	Mobile Responder Density (per sq. km)	Drones	Mean Time to Defib (decimal minutes)	Mean Time to CPR (decimal minutes)	Mean Survival Probability
A	2	N/A	6.8*	5.4	0.22
A	5	N/A	6.8*	4.8	0.24
A	8	N/A	6.8*	4.5	0.24
B	2	N/A	5.4	5.4	0.26
B	5	N/A	4.8	4.8	0.29
B	8	N/A	4.5	4.5	0.30
C	N/A	1	5.6	5.6	0.27
C	N/A	2	5.2	5.2	0.28
C	N/A	5	4.7	4.7	0.30
D	2	1	6.7	6.7	0.22
D	2	2	6.7	6.7	0.22
D	2	5	6.6	6.6	0.23
D	5	1	6.0	6.0	0.26
D	5	2	5.8	5.8	0.26
D	5	5	5.6	5.6	0.27
D	8	1	5.8	5.8	0.26
D	8	2	5.5	5.5	0.27
D	8	5	5.3	5.3	0.28
EMS	N/A	N/A	6.8	6.8	0.20

*System A does not provide defibrillation, thus time to defibrillation is equivalent to the simulated EMS time.

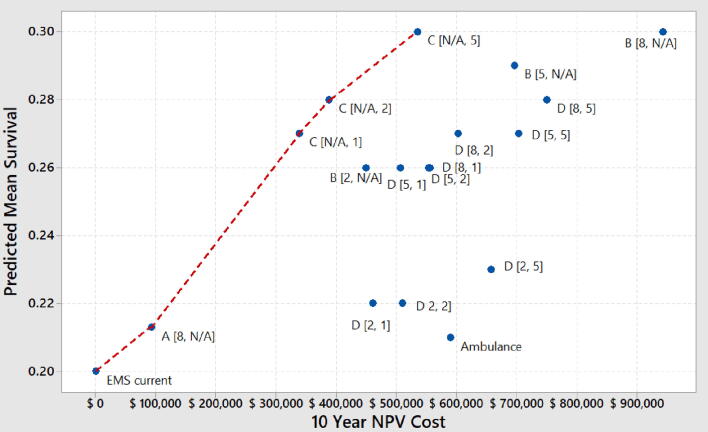
The estimated mean survival is plotted against the 10-year NPV cost for each combination of system and operating conditions (Fig. 3). The systems along the red line represent the efficient (non-dominated) solutions that have lower cost and better survival rates than the systems that are below and to the right of that line. Thus, these results suggest that, in this region, the most efficient systems can expect to save approximately 3 lives per $100,000 spent over ten years.

Fig. 3.

Cost-benefit analysis of system options, showing 10 year system cost estimate and predicted mean survival (for witnessed VF cases) for each system. The system conditions [density of responders, number of drones] are shown in the brackets by each system designator (systems with no mobile responders or no drones have N/A). The red line connects the systems that provide the maximum benefit for a given cost.

Discussion

The simulation results show that the novel response systems are expected to reduce the response times for CPR and defibrillation and increased the survival rates from the benchmark (the existing EMS system). Although improvements were expected, because these systems are expansions of the current EMS system and should not perform worse than the benchmark, the simulation results estimate the magnitude of improvements that can be obtained and identify the conditions required to achieve these improvements. System A (mobile responder providing only CPR) provides the smallest improvement to predicted survival because it reduces time to CPR but not time to defibrillation. Because response time decreases with increased responder density, the mobile responder systems require a significant density of responders (8/sq. km) to achieve a substantial improvement in response time. Although systems like PulsePoint advertise large citizen responder networks, the activation acceptance rate of the responders is low,²⁹ and thus high densities of responders are necessary for system effectiveness.

Unlike System A, Systems B (mobile responders with AED) and C (drone AED delivery) provide both CPR and defibrillation. These systems can reduce average response times by 2.3 minutes and can improve predicted survival rate by up to 10%. Although the verified responders likely have higher reliability than the citizen network, significant densities of responders are still required to achieve the largest survival improvements. Although the technology costs (i.e. cell phone app integration with 911 dispatch system) of such a system are minimal, the cost of equipping each responder with an AED is substantial. System C provided the best predicted survival with minimal operational costs. Although the drones are the largest cost of these systems, the small number of drones is less expensive than the large number of AEDs required by System B. In System C, however, bystanders may be unwilling to apply the AED to the cardiac arrest victim.[30], [31] As these systems are untested, it is not currently known how prevalent this bystander apprehension may be.

System D (drone delivery with mobile responder activation) avoids potential problems with bystander use by utilizing trained mobile responders to apply the AED. This increases response time, however, because both the drone and the mobile responder must arrive at the arrest location to start the treatment. The fact that the mobile responders do not carry AEDs in this system may provide advantages over system B, such as improved responder activation acceptance rate, as well as reduced costs due to fewer AEDs required.

There are some limitations to our modeling and simulation approach and our results. These results are from a simulation of a single region, using specific attributes of the locale (EMS stations, road network, and weather). Modelling of other regions could reveal differences in response time improvements or survival. The model assumed no bystander CPR and deployment of PAD AEDs in a community, and it does not consider the redirection of en route ambulances. Our model does not distinguish between cardiac arrests in public locations and private residences, and assumes all cardiac arrests are recognized by the 911 system. Our model evaluates the aleatory variation, or natural randomness of factors in the response to cardiac arrest. This study does not evaluate the epistemic uncertainty in the factor inputs that were used, including the logistic survival model. These limitations would affect the accuracy of the survival prediction. Additionally, our model does not quantify the survival improvement for patients who are not witnessed VF arrests. We acknowledge that estimating costs of systems, some of which are not yet implemented, has considerable uncertainty. Data from real world trials and simulations of the untested systems are needed to better understand assumptions within the model, such as bystander willingness to apply an AED retrieved from a drone.

Conclusions

Novel cardiac arrest response systems have the potential to improve response times and survival, but previous studies have not systematically compared their cost and effectiveness. The results from our simulation study suggest that these systems can incrementally improve the survival rate as much as 10%, at efficient costs, compared with a high performing EMS system in Bellevue, Washington. The benefits of these systems could be even greater in communities or regions with typical or poor EMS response times.

CRediT authorship contribution statement

Greg Lancaster: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing - original draft, Visualization, Project administration. Jeffrey W. Herrmann: Methodology, Validation, Writing - review & editing, Visualization, Supervision, Project administration.

Declaration of Competing Interest

Dr. Greg Lancaster, the corresponding author, is an employee of Philips Healthcare.

Dr. Jeffrey Hermann has no conflicts of interest.