Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2021 Jul 21;6(30):19822–19835. doi: 10.1021/acsomega.1c02528

Temperature-Dependent Properties of Molten Li2BeF4 Salt Using Ab Initio Molecular Dynamics

Khagendra Baral †, Saro San †, Ridwan Sakidja ‡, Adrien Couet §, Kumar Sridharan §, Wai-Yim Ching †,*
PMCID: PMC8340400  PMID: 34368569

Abstract

graphic file with name ao1c02528_0013.jpg

Molten lithium tetrafluoroberyllate (Li2BeF4) salt, also known as FLiBe, with a 2:1 mixture of LiF and BeF2 is being proposed as a coolant and solvent in advanced nuclear reactor designs, such as the molten salt reactor or the fluoride salt cooled high-temperature reactor. We present the results on the structure and properties of FLiBe over a wide range of temperatures, 0–2000 K, from high-throughput ab initio molecular dynamics simulation using a supercell model of 504 atoms. The variations in the local structures of solid and liquid FLiBe with temperature are discussed in terms of a pair distribution function, coordination number, and bond angle distribution. The temperature-dependent electronic structure and optical and mechanical properties of FLiBe are calculated. The optical and mechanical property results are reported for the first time. The results above and below the melting temperature (∼732 K) are compared with the experimental data and with data for crystalline FLiBe. The electronic structure and interatomic bonding results are discussed in correlation with the mechanical strength. A novel concept of total bond order density (TBOD), an important quantum mechanical parameter, is used to characterize the internal cohesion and strength in the simulated models. The results show a variation in the rate of change in properties in solid and liquid phases with anomalous behavior across the melting region. The observed trend is the decrease in mechanical strength, band gap, and TBOD in a nonlinear fashion as a function of temperature. The refractive index shows a surprising minimum at 850 K, among the tested temperatures, which lies above the melting point. These findings provide a new platform to understand the interplay between the temperature-dependent structures and properties of FLiBe salt.

1. Introduction

Molten salts (MSs) are a special class of ionic liquids with specific properties and a diverse range of applications.1,2 In recent years, they have received tremendous interest along with the relatively rapid development of advanced nuclear energy technologies. The most common MSs are nitrates, for use at relatively low temperatures below 560 °C, and alkali fluorides, chlorides, and hydroxides and their mixed combinations, for use at higher temperatures. They have a variety of important applications such as in thermal energy storage,3,4 advanced nuclear reactor technologies,5−9 concentrated solar power and battery industry,10−14and so forth. Relatively recently, there has been a resurgence of interest in advanced nuclear technologies with the development of several high-temperature reactor designs using molten salt as a coolant or a fuel, which have the potential to change the landscape of carbon-free energy generation with much reduced cost.15 A fundamental understanding of the structure and properties of MSs and their interaction with the surroundings and contents is necessary to accelerate their applications in the current and emerging advanced nuclear technologies.16,17 However, there are still many aspects of scientific issues on MS that are not well-understood.

Next-generation nuclear reactors are drawing considerable attention worldwide. Among the leading candidate is the molten salt reactor (MSR) where molten fluoride salts are being considered both as a primary coolant and as a solvent for nuclear fuel. Lithium tetrafluoroberyllate (FLiBe) is one of the fluoride salts that have been extensively used in the MSR experiment(s) as a coolant and solvent for fissile material due to its advantageous thermophysical properties.1,2,18−27 Properties such as small absorption cross section for thermal neutrons, high thermal efficiency, low spent fuel per unit energy, high degree of passive safety, high heat capacity, atmospheric pressure operation, chemical stability at high temperature, low melting point, and high boiling point make FLiBe a primary candidate for application in MSRs.9,22,28−31 FLiBe has a melting and boiling point of ∼732 and ∼1703 K, respectively.31 The liquid salt is a good solvent for nuclear fuel as it can dissolve high concentrations of Th + U fuel.24 FLiBe can also be used as a tritium breeding material in fusion reactors because of its high chemical stability.8,19,21,32 Thus, complete information regarding the temperature-dependent atomic structure and macroscopic properties is crucial for the further advancement of FLiBe in nuclear applications.

Although the experimental efforts have been accumulating27,33−42 in parallel with simulation,26,43−50 the lack of fundamental understanding at the atomistic level has been an issue in the required application of FLiBe for the MSR. Recently available specialized facilities and instrumentation have enhanced the state-of-the-art experimental research on molten salts.31,51−54 However, an understanding of the connectivity between atomistic properties with experimental characterization results is crucially important especially given that FLiBe is toxic and corrosive at high temperatures which precludes cost-effective experimental research over a wide range of temperatures.55 The profound effect of trace impurities in molten salt on its corrosivity and contamination from corrosion products further makes experimental work extremely challenging particularly at higher temperatures.16 Hence, the implications on the corrosion effect of FLiBe such as the formation of oxides by the reaction with water and with reactor container metallic alloys must be addressed.31,51,56 To limit the extent of the corrosion, molten salt redox potential control has been proposed with either the addition of a metallic buffer, a soluble redox couple buffer, or overhead gas control. In addition to the redox potential, fluoroacidity, which describes the coordination of the solvent, is also an important parameter of the salt. FLiBe is a fluoroacid salt since BeF2 can accept electrons from fluoride ions and form complexes with fluorides. As an example, the atomic interaction and change in properties from the amorphous solid to liquid state need to be fully elucidated to reveal the implications on the reaction 2LiF + BeF2 → 2Li+ + BeF42– at high temperature and estimation of redox potential52,57 since control of redox potential is essential to mitigate the corrosion by FLiBe in MSR. The formation of these monomeric fluoro complexes helps in minimizing the fluorine potential of the melt and reduces corrosion. To address these challenges, a comprehensive understanding of the structure and properties of FLiBe over a wide range of temperatures is necessary.

Experimental studies on FLiBe salt are still limited due to the high costs for such work associated with its toxicity and corrosivity. Accurate and effective computer simulation is a viable alternative to complement the experiments and provide new insights to guide the experiments. There are relatively few such studies on FLiBe and they are limited to a structure at a particular or a narrow range of temperatures. Even where classical and first-principles molecular dynamics (MD) have been used to some extent to study crystalline,58 solid, and liquid FLiBe26,43,44,47−50,59 using different methods and potentials, they are mostly focused on the structure, dynamical features, thermodynamic and vibrational properties, thermal neutron scattering cross section data, and so forth, whereas information on electronic, optical, and mechanical properties of FLiBe over a wide range of temperatures is still not covered.

This paper expounds the temperature-dependent structural, physical, and electronic properties of FLiBe salt at an atomistic level based on ab initio molecular dynamics (AIMD). Our motivation is to use accurate large-scale modeling to unravel some of the missing links discussed above and to provide future directions in the study of this salt. We start with a detailed investigation of the crystalline FLiBe. Then, the structures and properties of FLiBe as a function of temperature are systematically studied covering both the amorphous and the liquid phases at 10 different temperatures (0, 300, 450, 700, 730, 750, 850, 1000, 1500, and 2000 K). With the melting point being ∼732 K, these temperatures cover the solid and liquid state. The structure at 2000 K is above the boiling point of FLiBe (∼1703 K) and is treated as a superheated liquid. In this paper, we first provide a description of the computational methods and approaches and then results with detailed descriptions starting with the crystalline model followed by amorphous and liquid phases. These results are further discussed in connection with experimental findings.

2. Methods and Models

The accuracy of results in any atomistic simulation depends mainly on the accuracy of interactions between atoms in the system. The use of empirical force field potential in many classical MD simulations lacks sufficient accuracy compared to AIMD. It cannot, for example, predict the relevant electronic structure properties when the structure changes with temperature. Each new condition requires the fitting of a set of potential parameters which is limited in some cases due to inevitable indeterminacy. Moreover, such a potential cannot reproduce the temperature-dependent physical properties. In this context, the use of density functional theory (DFT)-based AIMD is the more accurate route to simulate the electronic structure and properties. Hence, AIMD is necessary to capture the critical details for the crystalline, amorphous, and liquid phases of FLiBe at different temperatures. Although the AIMD provides highly reliable results, it has a limitation in the case of a large system with several thousands of atoms and for long-time calculation. For such a simulation, an MD study using machine learning-based interatomic potential is shown to be more efficient with comparable accuracy to DFT.60−63

In this study, we use two DFT-based methods: Vienna Ab initio Simulation Package (VASP)64,65 and orthogonalized linear combination of atomic orbitals (OLCAO).66 VASP is used for AIMD simulation, geometry optimization, and calculation of mechanical properties. We use the projector augmented wave (PAW) method67,68 and describe the exchange–correlation energy by Perdew–Burke–Ernzerhoff (PBE) generalized gradient approximation (GGA).69 The Brillouin zone is sampled at Γ-point only for supercell models and k-point mesh (5 × 5 × 7) for the crystalline system. A high cutoff energy of 500 eV is set for the plane-wave basis expansion, and the electronic convergence criterion is chosen to be 10–5 eV. For the ionic relaxation, forces are converged to 10–3 eV/Å at zero pressure. The VASP relaxed structures are used as input to the OLCAO package for electronic structure and optical property evaluation. Details about the OLCAO method are presented in Supporting Information.

The initial crystal structure of FLiBe is taken from X-ray diffraction data.70 It has a rhombohedral symmetry hexagonal lattice defined by cell lengths “a” and “c”. The amorphous and liquid FLiBe models are simulated using the melt-quenching technique using AIMD similar to our previous studies.71−73 All simulations are carried out under NVT ensemble where the number of atoms (N), volume (V), and temperature (T) are held constant. The heat bath temperature is controlled using a Nose thermostat.74,75 A time step of 1 fs is chosen for the ionic motion integration. Based on the unit cell crystal structure with 126 atoms (Li = 36, Be = 18, and F = 72), we construct a cubic supercell containing 504 atoms (Li = 144, Be = 72, and F = 288), with periodic boundary conditions. The initial cubic supercell is heated to 2000 K within just 2 ps. The melt is further heated for 10 ps at this elevated temperature to fully eliminate the memory effect of the initial configuration. After this, the temperature of the system is lowered to 1500, 1000, 850, 750, 730, 700, 450, and finally to 300 K. At each temperature, the system is well-equilibrated for 10 ps to ensure it overcomes the diffusive stage and losses memory of atomic position and velocity history configuration from the previous structure. The velocity autocorrelation function (VACF) (see Supporting Information, Figure S1) ensures the loss of initial velocity from the previous configuration in the simulated model. It provides information on the dynamic motion of atoms with time. It shows that in the liquid model, the VACF dies out fast implying that the ions can leave the cage made up of surrounding ions more quickly. In a solid model, the VACF has more features and they die out much more slowly compared to melt which is due to the presence of more BeF4– tetrahedrons and the ordered structure of solid FLiBe. Out of 10 ps equilibration time, the pressure and temperature fluctuations are minimized through 8 ps, and an averaged structure is taken from the last 2 ps run. A nominal cooling rate of 20 K/ps is used to anneal the structures, which is reasonable in an accurate AIMD simulation.76 The equilibrium volume at each temperature is determined from the AIMD run of the system in the NPT ensemble at atmospheric pressure. The NPT ensemble uses a Parrinello–Rahman method77,78 with a Langevin thermostat79 as implemented in VASP. In the Langevin thermostat, the temperature of the system is maintained through a modification of Newton’s equation of motion by introducing a friction coefficient and random force. The friction coefficients for all atomic and lattice degrees of freedom are taken to be 20 ps–1 which are system-dependent and can only be optimized with enough testing. In the NPT ensemble, pressure (P) is kept constant along with N and T. The final structure at 0 K is obtained from the structure at 300 K by optimizing the atomic position and cell volume to converge the force and energy to a local minimum state at 0 K. Table 1 lists the cell parameters of the simulated model at different temperatures. The same naming of models used in Table 1 will be applied to all figures, results, and discussion sections.

Table 1. Structural Parameters for the FLiBe Model at Different Temperaturesa.

models a (Å) b (Å) c (Å) αo βo γo density volume
crystal-exp* 13.281 13.281 08.888 90.00 90.00 120.00 2.180 1357.700
crystal-sim 13.447 13.447 08.995 90.00 90.00 120.00 2.144 1408.729
T0 18.405 18.405 18.405 90.00 90.00 90.00 1.908 6234.582
T300 18.538 18.538 18.538 90.00 90.00 90.00 1.866 6370.928
T450 18.625 18.625 18.625 90.00 90.00 90.00 1.840 6460.838
T700 18.760 18.760 18.760 90.00 90.00 90.00 1.800 6602.824
T730 18.801 18.801 18.801 90.00 90.00 90.00 1.788, 1.97–2.08† 6645.732
T750 18.915 18.915 18.915 90.00 90.00 90.00 1.757, 1.95–2.05† 6767.367
T850 19.009 19.009 19.009 90.00 90.00 90.00 1.731, 1.90–2.02† 6868.752
T1000 19.214 19.214 19.214 90.00 90.00 90.00 1.675, 1.80–1.95† 7093.522
T1500 19.519 19.519 19.519 90.00 90.00 90.00 1.597 7437.105
T2000 19.597 19.597 19.597 90.00 90.00 90.00 1.571 7525.745
Open in a new tab
a

Volume in Å3, density in gm/cm3, Crystal-exp = experimental structure, and Crystal-sim = simulated structure. *Ref (70), †The experimental range of density is taken based on the values reported in refs (80)–85.

3. Results

3.1. Crystalline FLiBe

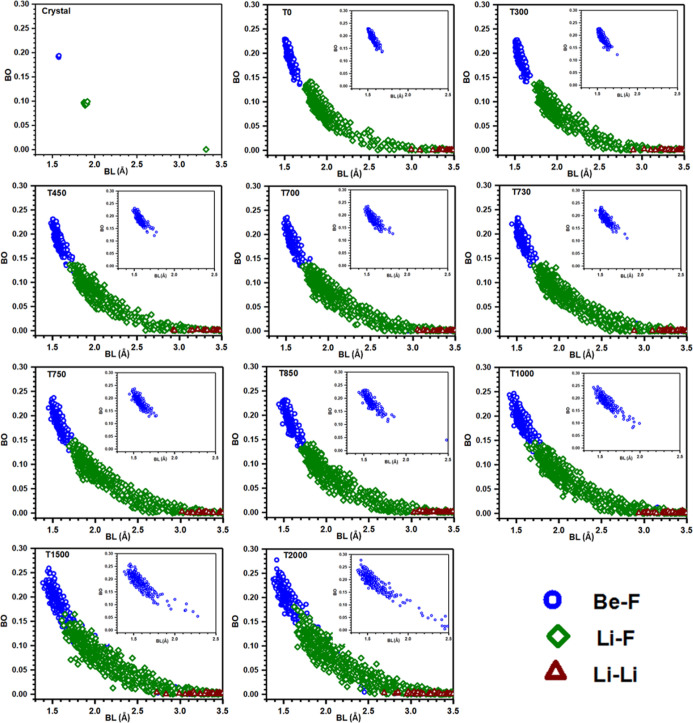
Crystalline FLiBe has been well-studied in the past.58,70,86−92 It has a rhombohedral symmetry of space group R3̅ (148) with a hexagonal setting. The initial cell parameters and atom position data, taken from X-ray diffraction work by Seiler,70 are relaxed using VASP (see Section 2). The lattice parameters, density, and volume of the original and final relaxed crystal are presented in Table 1. Compared to experimental values, our calculated cell volume is increased by 3.75% and hence the density is underestimated by 1.65%. The ball and stick representations of this crystal in two different orientations are shown in Figure 1. Each Li+ and Be2+ ions form tetrahedrons with F– ions. Each F– ion shares one Be and two Li as the nearest neighbors. These tetrahedra are interconnected along the c-axis in the hexagonal cell. The Be–F bond length (BL) in BeF42– varies from 1.568 to 1.578 Å and the averaged value is 1.573 Å. There exist two different types of LiF43– tetrahedra, so the Li–F bonds are distributed over a wider range from 1.874 to 1.913 Å, than Be–F bonds. These observed BLs are in close agreement with the experimental result, although slightly overestimated, which are in the range of 1.550–1.561 and 1.846–1.889 Å for Be–F and Li–F pairs, respectively.70 The variation of BL between different types of bonds with the corresponding bond order (BO) values is presented in Figure 9 to be discussed later. It is observed that the Be–F bonds are congregated with overlapped BO values, while the Li–F bonds are more scattered with slightly different BO values. Hence, the key difference between Be–F and Li–F bonds is that Be–F bonds are nearly identical with high BO values, whereas Li–F bonds spread in a certain range and have low BO values. The next nearest neighbor Li–F pairs are at 3.315 Å with almost zero BO.

Figure 1.

Figure 1

Open in a new tab

Ball and stick structures of relaxed crystalline FLiBe in two different orientations (Li = green, Be = blue, and F = orange).

Figure 9.

Figure 9

Open in a new tab

Bond order vs bond length plot for FLiBe at different temperatures. The inset shows the distribution of Be–F bonds up to the cutoff distance of 2.5 Å.

Even though numerous studies explore the geometry of the FLiBe crystal, the complete electronic structure results at the atomic level are rarely reported.27,70,87 The calculated density of states (DOS) for this crystal is shown in Figure 2a. The zero of the energy is set at the top of the valence band (VB). The VB DOS has two parts: the upper and lower. The lower part lies below −19 eV and spreads in the 1 eV energy range. The F’s 2s orbital is the main contributor for the DOS in this region, while a small contribution comes from Be and Li’s 2s and 2p orbitals. The upper part which spreads over the 3.6 eV range can be divided into three segments A, B, and C separated by a small energy gap. B and C have one sharp peak, while A has one major peak followed by two minor peaks. The atom-resolved partial DOS (PDOS) shows the orbitals of Be contribute to the segments B and C only, while those of Li and F contribute to all three segments. Therefore, a distinctive feature of DOS is that Be does not have any contribution for the upper VB. The DOS spectrum in the conduction band (CB) region is rather rough with many pronounced peaks of varying intensities which is the consequence of different types of Be–F and Li–F bond pairs. The PDOS shows that F mainly contributes to the VB, while Li and Be contribute to the CB. An important feature is that the DOS for crystalline FLiBe is completely different from the amorphous model at 0 K (T0) (see Figure 7 to be discussed later). The calculated band structure for the FLiBe crystal is shown in Figure 2b. This material is an insulator with a direct large band gap of 7.172 eV at the Γ zone. This value could be slightly smaller than the real band gap value as the local density approximation adopted in this calculation has been well-known to underestimate the band gap in an insulator.93−95 A similar band structure result is reported in a DFT calculation applying GGA87 with a band gap value of 7.599 eV, a little larger than our value. The top of bulk VB is quite flat implying a large hole effective mass. The band gap of crystalline FLiBe is 1.02 eV larger than that of the amorphous model T0.

Figure 2.

Figure 2

Open in a new tab

Calculated (a) total and atom-resolved partial density of states and (b) band structure for crystalline FLiBe.

Figure 7.

Figure 7

Open in a new tab

Calculated total and atom-resolved partial density of states for the simulated FLiBe model at 0, 730, and 1500 K.

The calculated total bond order density (TBOD), pair-resolved partial BOD (PBOD), and partial charge (PC) for each atom in the crystalline model are listed in Table 2. The TBOD for crystalline FLiBe is higher than that of T0 and other models shown in the same table. The higher TBOD value for the crystal indicates that it is internally stronger than the corresponding amorphous and liquid models. The PBOD is higher for the Be–F pair which implies that this bond is stronger than Li–F. The PC is positive for Li and Be and negative for F, so both Li and Be lose charge to F atoms as expected.

Table 2. Calculated TBOD, PBOD, Averaged Partial Charge of Ions, Band Gap (E), Refractive Index (n), and Plasma Frequency (ωp) in the Simulated FLiBe Salt.

    PBOD (e/Å3)
 partial charge (in e)
      
models TBOD (e/Å3) Li–F Be–F Li–Li Li Be F E (eV) n ωp (eV)
crystal 0.01959 0.00978 0.00981 0.00000 0.568 0.866 –0.501 7.172 1.264 19.71
T0 0.01718 0.00841 0.00877 0.00000 0.569 0.880 –0.504 6.152 1.211 17.34
T300 0.01662 0.00809 0.00853 0.00000 0.570 0.883 –0.506 6.047 1.208 17.25
T450 0.01617 0.00782 0.00834 0.00001 0.575 0.885 –0.509 5.875 1.207 17.38
T700 0.01559 0.00748 0.00810 0.00001 0.578 0.890 –0.510 5.788 1.206 17.23
T730 0.01552 0.00746 0.00805 0.00001 0.579 0.891 –0.511 5.636 1.203 17.02
T750 0.01516 0.00727 0.00789 0.00001 0.580 0.892 –0.513 5.612 1.201 16.42
T850 0.01489 0.00708 0.00780 0.00001 0.585 0.894 –0.514 5.598 1.199 16.62
T1000 0.01408 0.00669 0.00738 0.00001 0.587 0.898 –0.518 5.033 1.203 16.37
T1500 0.01315 0.00625 0.00688 0.00001 0.591 0.905 –0.522 4.797 1.205 16.21
T2000 0.01284 0.00619 0.00663 0.00001 0.585 0.922 –0.523 3.982 1.210 15.42
Open in a new tab

The calculated optical properties for the FLiBe crystal in the form of frequency-dependent complex dielectric functions are shown in Figure 3a. The imaginary dielectric function ε2 has many absorption peaks with different intensities with the onset energy at 7.17 eV. The major absorption peaks denoted by P1–P6 occur at 10.48, 12.9, 14.52, 16.34, 18.50, and 21.77 eV, respectively. These peaks in ε2 are consistent with the sharp peaks in CB and VB DOS spectra. The real part ε1 is obtained from imaginary part ε2 using Kramer-Kroning transformation96 and it shows features similar to that of ε2. The refractive index is calculated from the square root of ε1(0) to be 1.264 which is higher than that for T0 and other models (see Table 2). The energy loss function (ELF) for this crystal calculated from the inverse of the complex dielectric function is shown in Figure 3b. The ELF spectrum has one sharp peak followed by minor peaks on both sides. This spectrum is asymmetric with a long plateau on the right side above 30 eV. The plasmon peak identified by the peak position of the spectrum with frequency ωp lies at 19.71 eV which defines the frequency of collective excitation of valence electrons in the system. This value in the crystal is higher than that for the amorphous and liquid model listed in Table 2.

Figure 3.

Figure 3

Open in a new tab

Calculated (a) optical dielectric functions and (b) energy loss function for the FLiBe crystal.

The mechanical property of a crystal depends on its symmetry. In a hexagonal setting, the elastic properties are defined by five independent elastic constants C11, C12, C13, C33, and C44, whose values in the FLiBe crystal are 75.581, 38.512, 32.115, 98.142, and 18.529 GPa, respectively. From the elastic coefficients Cij and related compliance ratio Sij, the mechanical parameters can be calculated (see Supporting Information). The Young’s modulus (E), bulk modulus (K), and shear modulus (G) derived from these elastic constants are 54.091, 50.359, and 20.474 GPa, respectively. The elastic moduli for the crystal are larger than those of the T0 model (see Table 4) which implies that the internal forces and strength are higher in a crystal than in the amorphous model. The calculated Poisson’s ratio (η) and Pugh’s modulus ratio (G/K) for this crystal are 0.321 and 0.406, respectively. The G/K is an important criterion defined by Pugh to separate the brittleness (G/K > 0.57) and ductility (G/K < 0.57) of a material.97 It follows a trend just opposite to η. The higher Poisson’s ratio (or G/K < 0.57) in the crystalline model indicates that it is more ductile or less brittle as compared to amorphous and liquid models.

Table 4. Calculated Elastic Constants and Elastic Moduli (in Gpa) for Amorphous and Liquid FLiBe at Different Temperaturesa.

models C11 C12 C44 C44′ E K G η G/K
T0 52.063 21.041 17.803 15.511 42.955 31.382 16.886 0.272 0.538
T300 49.757 19.257 17.303 15.250 41.666 29.423 16.482 0.264 0.560
T450 38.561 12.956 12.477 12.803 31.628 21.511 12.601 0.255 0.586
T700 35.773 10.254 12.413 12.760 30.789 18.760 12.552 0.226 0.669
T730 40.152 11.274 14.326 14.439 35.075 20.900 14.371 0.220 0.688
T750 30.459 10.610 13.409 09.924 29.247 17.226 12.015 0.217 0.698
T850 29.806 09.079 12.044 10.364 27.577 15.988 11.372 0.213 0.711
T1000 33.827 11.195 11.483 11.316 28.468 18.739 11.416 0.246 0.609
T1500 37.800 12.027 12.303 12.887 31.272 20.618 12.537 0.247 0.608
T2000 28.483 08.697 12.173 09.893 27.126 15.292 11.261 0.204 0.736
Open in a new tab
a

C44′= (C11 – C12)/2 (see Supporting Information).

3.2. Amorphous and Liquid FLiBe

We discuss our results dividing them mainly into two regions according to different phases of the system: liquid structures above the melting point (>732 K) and amorphous structures below the melting point (<732 K) including the structure T730 close to the melting point. The final equilibrated structures, in the ball and stick form, at each temperature are shown in Figure S2.

3.2.1. Structural Information

The structure of noncrystalline FLiBe becomes more disordered with the increase in temperature. This is illustrated in Figure 4 for models T0, T730, and T1500, respectively. The different cell sizes used here are proportional to their volume at different temperatures. Be2+ and F– ions form a tetrahedral linkage of BeF42–, while the Li+ ions interact with these tetrahedra and balance the charge. With the increase in temperature, a number of these tetrahedrons decreases due to the elongation of Be–F bonds and they become more scattered than that in T = 0 K. In the section for bonding analysis, we will provide more detailed information on these structures rather than the discussion made here based on merely a geometric sketch. The volume increases and the density decreases when we move from T0 to the T2000 model as anticipated. The reported experimental density for T730, T750, T850, and T1000 models is in the range of 1.97–2.08, 1.95–2.05, 1.90–2.02, and 1.8–1.95 gm/cm3, respectively.80−85 Our calculated density for T730, T750, T850, and T1000 (see Table 1) is underestimated by 9.2, 9.9, 8.9, and 6.9%, respectively, of the reported values as the application of GGA overestimates the cell volume98 in addition to the rapid cooling rate normally associated with the AIMD simulations.

Figure 4.

Figure 4

Open in a new tab

Ball and stick and polyhedral structures of final relaxed FLiBe at three different temperatures 0, 730, and 1500 K.

3.2.2. Pair Distribution Function

The pair distribution function (PDF) defined as 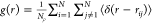Inline graphic, where N is the total number of atoms and ρ is the number density, gives the probability of finding a particle at a distance r from another particle. The calculated PDFs for the simulated model at different temperatures are shown in Figure 5. It depicts the local structural information and distribution of ions in the presence of neighboring ions. The inset on the top panel of the figure shows a magnified portion of the first peak. The Be–F pair has a very sharp symmetric peak followed by a deep minimum implying stable and compact BeF42– clusters and a relatively well-defined first coordinated cell. The intensity of the peak decreases from T0 to T700 with a sharp decrease on moving from T0 to T300. After 700 K, the intensity slightly increases and remains almost constant throughout 850–2000 K. The peak position shifts slightly right with the increase in temperature. For the Li–F pair, the peak is broader as compared to Be–F and the distribution is somewhat asymmetric with its minimum being above zero implying a possible exchange between F– and Li+ ions. The intensity of the Li–F peak decreases with an increase in temperature. The peak position shifts slightly to the right from T0 to T450, but after that, the BL decreases slightly (by 0.01 Å), and hence, the peak position also shifts left and then remains almost constant in the 700–2000 K range. For the F–F pair, the intensity decreases, peak width increases, and the peak position shifts to the right with the increase in temperature. The average BL for Be–F, Li–F, and F–F pairs in T0 is 1.567, 1.887, and 2.572 Å, respectively. A similar result (1.564 Å) is reported for the Be–F pair in a computational study of FLiBe at 32 K.44 From X-ray diffraction data, Vaslow and Narten38 found that the Be–F, Li–F, and F–F pairs have relatively similar BLs 1.58, 1.85, and 2.563–3.020 Å, respectively, at 828 and 1023 K. Our calculated BLs for Be–F, Li–F, and F–F pairs at 850 and 1000 K are 1.575, 1.893, and 2.588 Å, respectively, which are consistent with the experimental finding of Vaslow and Narten.38 In a computational study of FLiBe at 973 K, Nam et al.(47) found the Be–F, Li–F, and F–F BLs to be at 1.55, 1.88, and 2.58 Å, respectively. The Be–F, Li–F, and F–F BLs reported by Salanne et al. in a theoretical study of FLiBe at 873 K are 1.58, 1.81, and 2.61 Å, respectively.48 The finding of a decrease in intensity and increase in width of distribution for both Be–F and Li–F pairs indicate that Be and Li solvation shells become loose with the increase in temperature. The averaged BL calculated based on the first peak of the PDF follows the order of Be–F < Li–F < F–F. The PDFs for cations pairs Li–Li, Li–Be, and Be–Be are rather spiky showing the different possible distribution of these ions. The change in peak positions in these pairs is irregular.

Figure 5.

Figure 5

Open in a new tab

Pair distribution function for the simulated model at different temperatures. The insets in figures (a–c) show the magnified image of the first peak.

3.2.3. Coordination Number and Bond Angle Analysis

The first shell coordination number (CN) of Li and Be ions with the surrounding F ions is calculated by the numerical integration of PDF defined as 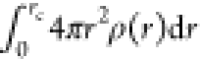Inline graphic where rc is the cutoff distance estimated from the first minimum of the corresponding PDF. The calculated CNs for Li and Be with two different cutoff distances are presented in Table 3. The CN value is large with a longer cutoff distance as expected. In the T0 model, Be maintains tetrahedral coordination, while the CN for Li is slightly higher than 4. Even if both Li and Be ions retain close coordination with the F atom, their local structure reflected by PDF are totally different as explained above. The average CN of Be remains constant up to 450 K and then decreases when the temperature is increased from 0 to 2000 K as the interatomic separation with F increases with the increase in temperature. In the case of Li, the CN decreases for shorter cutoff distance and increases for longer cutoff distance with the increase in temperature. However, in both cases, the decrease or increase is not regular. In an X-ray diffraction study of FLiBe, Vaslow and Narten determined the tetrahedral coordination for both Be and Li ions at 828 and 1023 K.38 In a theoretical study of FLiBe, Nam et al.(47) calculated the CN for Be and Li to be 4 and 4.7, respectively (at 973 K), while Salanne et al.(48) calculated a CN of 4 (at 873 K) for both Be and Li ions.

Table 3. Coordination Number Distribution for Li and Be Atoms in the Simulated FLiBe Model with Two Different Cutoff Distances (CDs).
    coordination number (CN)
atoms CD (Å) crystal T0 T300 T450 T700 T730 T750 T850 T1000 T1500 T2000
Li 2.80 4.00 4.24 4.31 4.24 4.26 4.33 4.19 4.30 4.10 4.08 4.14
  3.40 4.00 4.46 4.67 4.66 4.85 4.91 4.86 4.87 4.96 4.90 5.12
Be 1.80 4.00 4.00 4.00 4.00 3.98 3.97 3.96 3.94 3.79 3.60 3.32
  2.40 4.00 4.00 4.00 4.00 3.99 3.99 3.99 3.99 3.90 3.75 3.58
Open in a new tab

The distributions of bond angles F–Be–F and F–Li–F in the simulated model are shown in Figure 6. The F–Be–F angle for T0 is symmetric with a sharp peak centered at ∼109.5°, a perfect tetrahedral angle. The peak becomes broader, and the intensity decreases on moving from T0 to T2000. The distribution becomes wider and asymmetric and the peak position shifts to the right, on the higher angle side, with an increase in temperature. This shows systematic changes in bond angles in BeF42– tetrahedra toward lower CN consistent with increasing PC (see Section 3.2.5) with the increase in temperature. The F–Li–F angle spreads over a wider range with a broader peak than the F–Be–F angle. The intensity decreases, the peak becomes broader, and the distribution becomes wider with the increase in temperature. Compared to F–Be–F, the shift of the peak position is small for F–Li–F, but the intensity drops significantly. The difference in bond angle distribution in F–Be–F and F–Li–F is due to different charges, CNs, and arrangements of Li and Be ions.

Figure 6.

Figure 6

Open in a new tab

Distribution of (a) F–Be–F and (b) F–Li–F bond angles in FLiBe at different temperatures.

3.2.4. Electronic Structure

The electronic structure is the fundamental property of a material that assists to explore many physical properties. In particular, the evaluation of interatomic bonding facilitates the understanding of mechanical properties in a substance and its implication on the corrosion of materials. A thorough understanding of the electronic structure is only possible through exhaustive atomic-level quantum mechanical calculation rather than simply inferring from structural parameters. It is surprising to note that, like crystalline FLiBe, the published literature still lacks a complete result regarding the electronic structure in amorphous and liquid FLiBe. Our study fills this gap through rigorous DFT calculation using OLCAO.

The calculated total DOS data for FLiBe at different temperatures are shown in Figure S3. Overall, the DOS spectra look similar in the studied model at different temperatures. Like the crystalline model, the VB DOS is divided into two parts: lower and upper. The lower part DOS lies below −18 eV and it has one major peak. The upper part VB DOS spreads within the 0–7.5 eV energy range and it has one major and one minor peak. The minor peak becomes less prominent and starts to merge with the body of spectra from T1500. Compared to the crystalline model, the VB DOS has a fewer sharp peak, and it spreads over a wider energy range. The CB DOS is flatter and almost similar in all models. One of the striking features observed in the DOS spectra is their intensity decreases with the increase in temperature and the peak of spectra in the VB region becomes less sharp. We provide details on DOS spectra and their origination from constituent atoms by plotting the atom-resolved PDOS, shown in Figure 7, at 0, 730, and 1500 K to represent the three different temperature stages of the FLiBe. The PDOS shows that the deep lower VB DOS spectrum mainly comes from the F atom. It also shows that the upper VB DOS spectrum is mostly dominated by orbitals of F with an admixture of Li and Be orbitals. The Li and Be atoms mainly contribute to the CB DOS. When we move from T0 to the T2000 model, the band gap decreases continuously, which is reflected in the CB region of Figure S3. The calculated band gap values are presented in Table 2 and their variation with temperature is shown in Figure 8. It is seen that the decrease in band gap is not linear, and it has a different slope in the solid and liquid regions. The vertical dashed line represents the melting point of the FLiBe. Most importantly above 850 K, where the structure is in the liquid phase, the band gap decreases sharply implying that in the melt, more ions are free and conductive.

Figure 8.

Figure 8

Open in a new tab

Variation of TBOD and band gap as a function of temperature in FLiBe. The hollow symbols are data for the T2000 model.

3.2.5. Interatomic Bonding and Charge Transfer

The interatomic bonding is the most important part of the electronic structure calculation which helps to understand the internal cohesion and strength of the material. The calculated values of TBOD and PBOD are listed in Table 2. Like crystalline FLiBe, the Be–F pairs have a higher BOD value than Li–F which implies that Be–F bonds are stronger than Li–F. The variation of TBOD with temperature in the FLiBe system is displayed in Figure 8. The TBOD decreases with an increase in temperature but in a nonlinear fashion with a change in slope around the melting point. The most interesting result found is that the TBOD decreases sharply after 850 K, implying that liquid FLiBe is internally weaker than the solid phase.

We dig into the electronic structure results further by calculating the BO values for all possible bonded pairs and provide details of bonding analysis. The use of the BO value derived accurately from electronic structure calculation based on a real bond provides more information to characterize the interatomic strength rather than just using a geometrical distribution of an atom pair in a specified distance as in the PDF. The characteristics of bonding topology are vividly displayed in Figure 9 in the form of the BO versus BL plot. It is observed that the crystalline, amorphous, and liquid FLiBe have a broad range of bonding patterns varying from very strong to weak bonds. The details of bonding in the crystalline model are discussed earlier in the paper, so in this section, we focus our discussion on the remaining models. In all models, the Be–F bonds are much stronger than Li–F bonds with a high BO value due to the presence of some partial covalent character. Collins et al. in a deformation density study of FLiBe has also shown that Be–F has high bonding density than Li–F, implying the partial covalent character of Be–F bonds.92 In T0 and T300 models, the Be–F bonds are clustered in a narrow BL region, but as the temperature increases, they start to spread up from the T450 model. The figure in the inset displays the distribution of Be–F bonds in the range of 1.30–2.50 Å BL. It is seen that with an increase in temperature, more elongated Be–F bonds exist. The scattered BO values with varying BL at higher temperatures imply the different possibility of Be–F coordination than at lower temperatures where CN is 4. Also, for T0 and T300 models, the BO values for Be–F and Li–F pairs are separated by a narrow gap, but from the T450 model, they start to mix up and overlap each other, which increase as a function of temperature. Both Be–F and Li–F pairs spread in a wide region and become more random with the increase in temperature; however, the expansion for Be–F bonds is more systematic than Li–F. Near or beyond 3 Å, some Li–Li pairs, with a nearly zero BO value, exist which indicates that Li–Li covalent bonding is strictly prohibited in both amorphous and liquid FLiBe systems.

The calculated PC for each atom, presented in Figure S4, provides further insights into the mechanism of charge transfer between the ions in the studied system. The distribution becomes more scattered with the increase in temperature. The averaged PC values calculated for each atom in all models are plotted in Figure S5 and listed in Table 2. Like the crystalline model, the PC is positive for Li and Be ions and negative for F ions. Hence, the net charge transfer in the system is from Li and Be to F ions. With the increase in temperature from 0 to 2000 K, the PC increases for Be and decreases for F. The PC for Li increases from T0 to T1500 model but slightly decreases for T2000. In most of the MD calculations, the predefined same PC values are used for the simulation at different temperatures. The variation of PC with temperature in our result shows that only quantum calculation can account for such an effect precisely in the atomic interaction.

3.2.6. Optical Properties

The calculated real and imaginary parts of dielectric functions for the simulated models are shown in Figure S6. Compared to the crystalline model, the absorption curve ε2 in the amorphous and liquid models has entirely different features. The ε2 curve for the crystal is spiky with many peaks, while amorphous and melted models have one prominent peak, and the curve is flatter. However, for both cases, the peaks in ε2 are consistent with the corresponding peaks in DOS spectra in their CB region. An important observation is that when we move from T0 to the T2000 model, even if the feature of ε2 is almost similar, the absorption edge shifts at the lower energy end. The real part ε1 follows the same trend as ε2. The calculated refractive indices (n) for all models are listed in Table 2. The variation of n with temperature is shown in Figure 10. The value of n decreases first, reaches a minimum at 850 K, and then increases with temperature. Although the n value decreases from T0 to the T850 model, interestingly, the slope in the solid region below 700 K and across the melting point, in the region between 700 and 850 K, is different. The refractive index increases sharply from the T1500 to T2000 model. The calculated ELFs at different temperatures are presented in Figure S7. The ELF spectrum has one major peak followed by a minor peak with a long plateau on the right side. The calculated plasma frequencies (ωp) are listed in Table 2. It is observed that the ωp and intensity of the spectrum decrease with the increase in temperature from 0 to 2000 K.

Figure 10.

Figure 10

Open in a new tab

Variation of the refractive index in the simulated model at different temperatures. The hollow square is the refractive index for the T2000 model.

3.2.7. Mechanical Properties

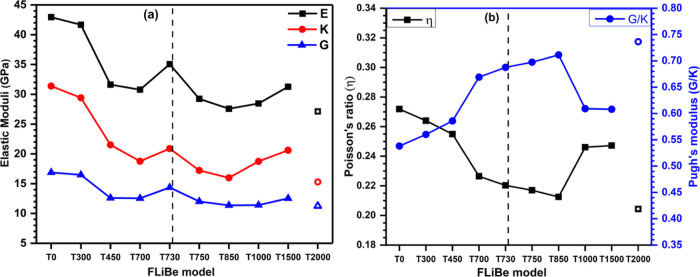
The understanding of temperature-dependent mechanical strength in FLiBe salt is important in the viewpoint of its application at high temperatures. In this study, we present the results on elastic and mechanical properties of FLiBe obtained using ab initio calculations. A set of linear elastic coefficients Cij and the mechanical properties derived from them at various temperatures are listed in Table 4. In the cubic cell, the independent elastic constants can be defined by three components C11, C12, and C44 which are listed in the table. In general, the amorphous and liquid structures are isotropic; however, due to the small cell size effect, some degree of anisotropy is unavoidable as indicated by slightly different values of C44 and C44′. The values of E, K, G, η, and G/K as a function of temperatures in the simulated model are shown in Figure 11. Overall, the values of E, K, and G decrease on moving from the T0 to T2000 model but irregularly. Noticeably, a different trend in decrease is observed in the solid and liquid region. From T300 to T700, the elastic moduli decrease sharply but from T730 to T850, the rate in decrease is slow. The elastic moduli increase on moving from T850 to T1500. An irregular change in elastic moduli values in the series on moving through T700 → T730 → T750 shows that this salt exhibits some unusual mechanical behavior across the melting point. The values of E, K, and G decrease sharply for the superheated liquid at 2000 K when the temperature is increased beyond 1500 K. The value of η decreases from T0 to T850 and increases from T850 to T1500 when the temperature is increased from 0 to 1500 K. η decreases sharply from T1500 to T2000. The G/K follows exactly the opposite nature of η.

Figure 11.

Figure 11

Open in a new tab

Calculated (a) elastic moduli and (b) Poisson’s and Pugh’s modulus ratio at different temperatures for FLiBe salt. The hollow symbols disconnected from the curves are data for the T2000 model.

4. Discussion

Finally, we discuss our results presented above and highlight some exciting new findings in this study of FLiBe salt. Our results obtained from AIMD simulation provide a wealth of information on the electronic structure of crystalline, amorphous, and liquid FLiBe in a wide range of temperatures and reveal their interconnectivity with physical properties. This will facilitate the understanding of the temperature-dependent structure and properties of FLiBe which is necessary in the application of this salt to energy systems. Such data providing the information at the atomic level cannot be obtained directly by experimental means.

The crystalline FLiBe has substantially distinct structural and physical characteristics compared to amorphous and liquid models. This crystal is an insulator with a large direct band gap than the amorphous and liquid model. Even if Be and Li ions in the crystal and amorphous model at 0 K have the same (for Be) or close (for Li) CN value, their bonding pattern is entirely different. In the crystal, Be–F and Li–F bonds are concentrated in a limited range with almost overlapped BO values, but in the amorphous model, they are spread over a wide range with varying BO values. Another different result in the crystalline FLiBe is the existence of the nearest neighbor of Li–F pairs which do not exist in the amorphous and liquid model, rather these latter phases have Li–Li pairs. Additionally, the higher TBOD and elastic moduli in the crystal imply that it is internally stronger than amorphous and liquid FLiBe.

The amorphous and liquid phases of FLiBe also have distinct local structures. The PDF and bond angle distribution show that the melted structures are more random than the amorphous structures. Be mainly forms the BeF42– tetrahedra at the lower temperature; however, with the increase in temperature, the abundance of perfect tetrahedra decreases as indicated by a continuous decrease in CN of Be. The decrease in CN of Be is consistent with the increase in PC of Be with the increase in temperature. The CN values presented with two different cutoff distances show that they are higher with longer cutoff distances. It is consistent with the inclusion of more bonded pairs with the increase in BL, as shown in Figure 9. The CN of Be decreases for both cutoff distances, while the CN of Li decreases for shorter cutoff distance and increases for longer cutoff distance with the increase in temperature.

In MD calculations, the bonding is interpreted based on the PDF which is a purely geometric parameter. Our results provide a more comprehensive picture of the chemical bonding using the BO value derived from the quantum calculation which more accurately represents the internal strength of the studied material. The BO–BL plot in Figure 9 provides a rich display of bonding distributions within these complex structures and allows us to gain a more complete picture of the internal distribution of the bond strengths. The Be–F bonds spread in a narrow range compared to Li–F and they have a higher BOD value, as listed in Table 2, implying that Be–F bonds have an ionic character as well as a partial covalent character, while Li–F bonds are mostly ionic. Calculation of PBOD reveals that Be–F bonds have a higher contribution to the overall bonding of the system than Li–F. For T0 and T300 models, Be–F and Li–F bonds have distinguishable BO values, but from T450, they start to mix up and overlap. This implies the elongation of BL in some Be–F pairs, as shown in the inset of Figure 9, and more randomness in the distribution of Be–F bonds with the increase in temperature. The shortening of BL in some Li–F pairs can also be seen in the same figure. However, the average BL follows the order of Be–F < Li–F, and the order of BO is just the opposite.

As emphasized above, the internal strength of the FLiBe salt is characterized by introducing the TBOD and its interconnectivity with mechanical properties is revealed. The highest TBOD for T0 indicates that this model is internally strong which is reflected in the calculated mechanical properties that T0 has high E, K, and G values. The TBOD decreases from T0 to T2000 and similarly, overall, a decrease in elastic moduli is observed on moving from T0 to T2000. However, since the elastic moduli do not depend merely on the TBOD, they do not follow the same trend as TBOD. The PC discussed in our study is another informative quantity obtained from ab initio calculation which is missing in many previous MD studies. We show that the PC of atoms in FLiBe strongly depends on the temperature. Our result shows that the PC increases for Li and Be, while it decreases for the F atom with the increase in temperature. Most of the MD simulations use the same PC value to study the temperature-dependent properties. In this context, our calculation provides more accurate results with detailed information of charge on each atom as compared to other studies.

The calculated refractive index for amorphous and liquid FLiBe is smaller than that of the crystalline model. In a rather old study,89 the refractive index of the FLiBe crystal is reported to be ≪1.331, and there have been no recent and detailed studies in this area. In our study, the refractive index decreases first from 0 to 850 K and then increases with the increase in temperature. An interesting result found is that the refractive index is minimum in the liquid phase at 850 K. It is noteworthy that there are no existing theoretical and experimental studies on the optical properties of amorphous and liquid FLiBe. Our results can be a pathway for the exploration of the refractive index by experimental or other means. Our results show an abrupt change in the properties of FLiBe such as a sharp decrease in TBOD and band gap and an increase in elastic moduli, Poisson’s ratio, and refractive index at 850 K which indicates that there will be some structural changes in FLiBe melt at this temperature. This observation is also supported by a sharp decrease in the first shell CN for both Li and Be ions above 850 K. Overall, our study reveals a clear demarcation that separates the bonding and optical and mechanical properties of crystalline, amorphous, and liquid FLiBe. These findings may pave a new way to diagnose and distinguish these structures by experimental means.

5. Conclusions

This AIMD simulation performed over a wide range of temperatures enhances the knowledge of the structure and properties of FLiBe salt. One of our findings is that the crystalline and amorphous FLiBe at the same temperature (0 K) have different local structures and bonding. Crystalline FLiBe has a comparatively higher density, band gap, TBOD, refractive index, and elastic moduli than that of the corresponding amorphous and liquid models. The FLiBe crystal appears to be more ductile than its amorphous and liquid counterparts. We show the effective use of the concept of BO to analyze the internal bonding in the FLiBe system. The association between Be and F ions is stronger than that for Li and F as characterized by a higher BO value for the Be–F pair in all models. Overall, the density, band gap, TBOD, and mechanical strength decrease with the increase in temperature from 0 to 2000 K. Another significant finding is that solid and liquid phases of FLiBe have a different rate of change in properties with some anomalous behavior across the melting point. The most important discovery is that the refractive index has a minimum value near 850 K where the FLiBe is in the liquid state. To the best of our knowledge, the optical and mechanical properties of FLiBe salt over the wide temperature range are reported for the first time and we anticipate that our results will motivate future experimental works in this direction.

Acknowledgments

This research used the resources of the National Energy Research Scientific Computing Center supported by DOE under contract no. DE-AC03-76SF00098 and the Research Computing Support Services (RCSS) of the University of Missouri system. K.B. has been supported in part by a research grant from the School of Graduate Studies at UMKC.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c02528.

  • Details of computational methods; velocity autocorrelation function in the simulated model; structural models of simulated FLiBe; density of states of the simulated FLiBe model; partial charge distribution of Li, Be, and F atoms; averaged partial charge of Li, Be, and F atoms; dielectric functions of the simulated model; energy loss function of the simulated model; and references (PDF)

Author Contributions

W.-Y.C. and R.S. initiated the project. W.-Y.C. and K.B. did the calculations. S.S., A.C., and K.S. provided insights. All the authors participated in the discussion and interpretation of the results. W.-Y.C. and K.B. wrote the paper. All authors edited and proofread the final manuscript.

The authors declare no competing financial interest.

Supplementary Material

ao1c02528_si_001.pdf (1.8MB, pdf)

References

  1. Guo S.; Zhang J.; Wu W.; Zhou W. Corrosion in the molten fluoride and chloride salts and materials development for nuclear applications. Prog. Mater. Sci. 2018, 97, 448–487. 10.1016/j.pmatsci.2018.05.003. [DOI] [Google Scholar]
  2. Grimes W. R. Molten-salt reactor chemistry. Nucl. Appl. Technol. 1970, 8, 137–155. 10.13182/nt70-a28621. [DOI] [Google Scholar]
  3. An X.-H.; Cheng J.-H.; Su T.; Zhang P. In Determination of thermal physical properties of alkali fluoride/carbonate eutectic molten salt. AIP Conf. Proc. 2017, 1850, 070001. 10.1063/1.4984415. [DOI] [Google Scholar]
  4. Misra A. K.; Whittenberger J. D.. Fluoride salts and container materials for thermal energy storage applications in the temperature range 973–1400 K. 22nd Intersociety Energy Conversion Engineering Conference; AIAA, 1987; p 9226.
  5. Ying D.; Yang H.; Lyu H.; Tan Y.; Jing F.; Li L.; Xiao F.; Liu J.; Zhang H.; Yang J.; He T. Activation of FLiBe coolant in the molten salt reactor. Ann. Nucl. Energy 2019, 129, 62–66. 10.1016/j.anucene.2019.01.038. [DOI] [Google Scholar]
  6. Cadwallader L. C.; Longhurst G. R.. Flibe Use in Fusion Reactors-An Initial Safety Assessment; Idaho National Laboratory (INL): Idaho Falls, ID (US), 1999.
  7. Sun K.; Wilson J.; Hauptman S.; Ji R.; Dave A. J.; Zou Y.; Hu L.-w. Neutronics modeling and analysis of the TMSR-SF1 fuel lattice and full core with explicit fuel particle distribution and random pebble loadings. Prog. Nucl. Energy 2018, 109, 171–179. 10.1016/j.pnucene.2018.08.005. [DOI] [Google Scholar]
  8. Suzuki A.; Terai T.; Tanaka S. Tritium release behavior from Li2BeF4 molten salt by permeation through structural materials. Fusion Eng. Des. 2000, 51–52, 863–868. 10.1016/s0920-3796(00)00233-7. [DOI] [Google Scholar]
  9. Delpech S.; Cabet C.; Slim C.; Picard G. S. Molten fluorides for nuclear applications. Mater. Today 2010, 13, 34–41. 10.1016/s1369-7021(10)70222-4. [DOI] [Google Scholar]
  10. Forsberg C.; Zheng G.; Ballinger R. G.; Lam S. T. Fusion Blankets and Fluoride-Salt-Cooled High-Temperature Reactors with Flibe Salt Coolant: Common Challenges, Tritium Control, and Opportunities for Synergistic Development Strategies Between Fission, Fusion, and Solar Salt Technologies. Nucl. Tech. 2020, 206, 1778–1801. 10.1080/00295450.2019.1691400. [DOI] [Google Scholar]
  11. Gaune-Escard M.Molten Salts: From Fundamentals to Applications; Springer Science & Business Media, 2002; Vol. 52. [Google Scholar]
  12. Kim J.; Shin D.; Jung Y.; Hwang S. M.; Song T.; Kim Y.; Paik U. LiCl-LiI molten salt electrolyte with bismuth-lead positive electrode for liquid metal battery. J. Power Sources 2018, 377, 87–92. 10.1016/j.jpowsour.2017.11.081. [DOI] [Google Scholar]
  13. Nitta K.; Inazawa S.; Sakai S.; Fukunaga A.; Itani E.; Numata K.; Hagiwara R.; Nohira T. Development of molten salt electrolyte battery. SEI Tech. Rev. 2013, 76, 33–39. [Google Scholar]
  14. Wang X.; Rincon J. D.; Li P.; Zhao Y.; Vidal J. Thermophysical Properties Experimentally Tested for NaCl-KCl-MgCl2 Eutectic Molten Salt as a Next-Generation High-Temperature Heat Transfer Fluids in Concentrated Solar Power Systems. J. Sol. Energy Eng. 2021, 143, 041005. 10.1115/1.4049253. [DOI] [Google Scholar]
  15. Cho A. The little reactors that could. Am. Assoc. Adv. Sci. 2019, 363, 806–809. 10.1126/science.363.6429.806. [DOI] [PubMed] [Google Scholar]
  16. Serp J.; Allibert M.; Beneš O.; Delpech S.; Feynberg O.; Ghetta V.; Heuer D.; Holcomb D.; Ignatiev V.; Kloosterman J. L.; Luzzi L.; Merle-Lucotte E.; Uhlíř J.; Yoshioka R.; Zhimin D. The molten salt reactor (MSR) in generation IV: overview and perspectives. Prog. Nucl. Energy 2014, 77, 308–319. 10.1016/j.pnucene.2014.02.014. [DOI] [Google Scholar]
  17. Delpech S.; Merle-Lucotte E.; Heuer D.; Allibert M.; Ghetta V.; Le-Brun C.; Doligez X.; Picard G. Reactor physic and reprocessing scheme for innovative molten salt reactor system. J. Fluor. Chem. 2009, 130, 11–17. 10.1016/j.jfluchem.2008.07.009. [DOI] [Google Scholar]
  18. Bahri C. N. A. C. Z.; Al-Areqi W. a. M.; Ruf M. I. F. M.; Majid A. A. Characteristic of molten fluoride salt system LiF-BeF2 (Flibe) and LiF-NaF-KF (Flinak) as coolant and fuel carrier in molten salt reactor (MSR). AIP Conf. Proc. 2017, 1799, 040008. 10.1063/1.4972932. [DOI] [Google Scholar]
  19. Nishimura H.; Terai T.; Yamawaki M.; Tanaka S.; Sagara A.; Motojima O. Compatibility of ferritic steels with Li2BeF4 molten salt breeder. J. Nucl. Mater. 2002, 307–311, 1355–1359. 10.1016/s0022-3115(02)01123-6. [DOI] [Google Scholar]
  20. Wu H.; Carotti F.; Gakhar R.; Patel N.; Scarlat R. O. Fluorination of nuclear graphite IG-110 in molten 2LiF-BeF2 (FLiBe) salt at 700 °C. J. Fluor. Chem. 2018, 211, 159–170. 10.1016/j.jfluchem.2018.04.001. [DOI] [Google Scholar]
  21. Suzuki A.; Terai T.; Tanaka S. In-situ HT release behavior from molten Li2BeF4 salt. Fusion Eng. Des. 1998, 39–40, 781–785. 10.1016/s0920-3796(98)00381-0. [DOI] [Google Scholar]
  22. Suzuki A.; Terai T.; Tanaka S. Change of tritium species in Li2BeF4 molten salt breeder under neutron irradiation at elevated temperature. J. Nucl. Mater. 1998, 258–263, 519–524. 10.1016/s0022-3115(98)00423-1. [DOI] [Google Scholar]
  23. Romatoski R. R.; Hu L. W. Fluoride salt coolant properties for nuclear reactor applications: A review. Ann. Nucl. Energy 2017, 109, 635–647. 10.1016/j.anucene.2017.05.036. [DOI] [Google Scholar]
  24. Fukada S. Flibe-tritium research for fission or fusion reactors at Kyushu University. J. Plasma Fusion Res. 2013, 10, 22–26. [Google Scholar]
  25. Sohal M. S.; Ebner M. A.; Sabharwall P.; Sharpe P.. Engineering Database of Liquid Salt Thermophysical and Thermochemical Properties; Idaho National Laboratory (INL): ID (US), 2010. [Google Scholar]
  26. Jabes B. S.; Agarwal M.; Chakravarty C. Structure and transport properties of LiF-BeF2 mixtures: Comparison of rigid and polarizable ion potentials#. J. Chem. Sci. 2012, 124, 261–269. 10.1007/s12039-012-0225-5. [DOI] [Google Scholar]
  27. Li Y.; Liu X.; Wang B.; Wang C. Raman and theoretical studies on structural evolution of Li2BeF4 and binary LiF-BeF2 melts. J. Mol. Liq. 2021, 325, 115208. 10.1016/j.molliq.2020.115208. [DOI] [Google Scholar]
  28. Flanagan G. F.; Holcomb D. E.; Cetiner S. M.. FHR Generic Design Criteria; Oak Ridge National Lab.(ORNL): Oak Ridge, TN (US), 2012. [Google Scholar]
  29. Khokhlov V.; Ignatiev V.; Afonichkin V. Evaluating physical properties of molten salt reactor fluoride mixtures. J. Fluor. Chem. 2009, 130, 30–37. 10.1016/j.jfluchem.2008.07.018. [DOI] [Google Scholar]
  30. Williams D. F.; Clarno K. T. Evaluation of salt coolants for reactor applications. Nucl. Tech. 2008, 163, 330–343. 10.13182/nt08-a3992. [DOI] [Google Scholar]
  31. Zheng G.; He L.; Carpenter D.; Sridharan K. Corrosion-induced microstructural developments in 316 stainless steel during exposure to molten Li2BeF4(FLiBe) salt. J. Nucl. Mater. 2016, 482, 147–155. 10.1016/j.jnucmat.2016.10.023. [DOI] [Google Scholar]
  32. Nishimura H.; Suzuki A.; Terai T.; Yamawaki M.; Tanaka S.; Sagara A.; Motojima O. Chemical behavior of Li2BeF4 molten salt as a liquid tritium breeder. Fusion Eng. Des. 2001, 58–59, 667–672. 10.1016/s0920-3796(01)00581-6. [DOI] [Google Scholar]
  33. Briggs R.Molten-Salt Reactor Program Semiannual Progress Report for Period Ending January 31, 1964; Oak Ridge National Lab.: TN (US), 1964.
  34. Ignat’ev V. V.; Merzlyakov A. V.; Subbotin V. G.; Panov A. V.; Golovatov Y. V. Experimental investigation of the physical properties of salt melts containing sodium and lithium fluorides and beryllium difluoride. Atom. Energy 2006, 101, 822–829. 10.1007/s10512-006-0175-4. [DOI] [Google Scholar]
  35. Yajima K.; Moriyama H.; Oishi J.; Tominaga Y. Surface tension of lithium fluoride and beryllium fluoride binary melt. J. Phys. Chem. 1982, 86, 4193–4196. 10.1021/j100218a021. [DOI] [Google Scholar]
  36. Williams D.Assessment of Candidate Molten Salt Coolants for the NGNP/NHI Heat-Transfer Loop; Oak Ridge National Lab.(ORNL): Oak Ridge, TN (US), 2006. [Google Scholar]
  37. Kondo M.; Nagasaka T.; Sagara A.; Noda N.; Muroga T.; Xu Q.; Nagura M.; Suzuki A.; Terai T. Metallurgical study on corrosion of austenitic steels in molten salt LiF-BeF2 (Flibe). J. Nucl. Mater. 2009, 386–388, 685–688. 10.1016/j.jnucmat.2008.12.317. [DOI] [Google Scholar]
  38. Vaslow F.; Narten A. H. Diffraction pattern and structure of molten BeF2-LiF solutions. J. Chem. Phys. 1973, 59, 4949–4954. 10.1063/1.1680711. [DOI] [Google Scholar]
  39. Kelleher B. C.; Dolan K. P.; Brooks P.; Anderson M. H.; Sridharan K. Batch-Scale Hydrofluorination of Li27BeF4 to Support Molten Salt Reactor Development. J. Nucl. Eng. Radiat. Sci. 2015, 1, 041010. 10.1115/1.4030963. [DOI] [Google Scholar]
  40. Doniger W. H.; Falconer C.; Elbakhshwan M.; Britsch K.; Couet A.; Sridharan K. Investigation of impurity driven corrosion behavior in molten 2LiF-BeF2 salt. Corrosion Sci. 2020, 174, 108823. 10.1016/j.corsci.2020.108823. [DOI] [Google Scholar]
  41. Lam S. T.; Li Q.-J.; Mailoa J.; Forsberg C.; Ballinger R.; Li J. The impact of hydrogen valence on its bonding and transport in molten fluoride salts. J. Mater. Chem. A 2021, 9, 1784–1794. 10.1039/d0ta10576g. [DOI] [Google Scholar]
  42. Carotti F.; Liu E.; Macdonald D. D.; Scarlat R. O. An electrochemical study of hydrogen in molten 2LiF-BeF2 (FLiBe) with addition of LiH. Electrochim. Acta 2021, 367, 137114. 10.1016/j.electacta.2020.137114. [DOI] [Google Scholar]
  43. Liu S.; Su T.; Cheng J.; An X.; Zhang P.; Liu H.; Yao S.; Xie L.; Hou H. Investigation on molecular structure of molten Li 2 BeF 4 (FLiBe) salt by infrared absorption spectra and density functional theory (DFT). J. Mol. Liq. 2017, 242, 1052–1057. 10.1016/j.molliq.2017.07.051. [DOI] [Google Scholar]
  44. Dai J.; Han H.; Li Q.; Huai P. First-principle investigation of the structure and vibrational spectra of the local structures in LiF-BeF2 Molten Salts. J. Mol. Liq. 2016, 213, 17–22. 10.1016/j.molliq.2015.10.053. [DOI] [Google Scholar]
  45. Klix A.; Suzuki A.; Terai T. Study of tritium migration in liquid Li2BeF4 with ab initio molecular dynamics. Fusion Eng. Des. 2006, 81, 713–717. 10.1016/j.fusengdes.2005.09.034. [DOI] [Google Scholar]
  46. Nam H. O.; Morgan D. Redox condition in molten salts and solute behavior: A first-principles molecular dynamics study. J. Nucl. Mater. 2015, 465, 224–235. 10.1016/j.jnucmat.2015.05.028. [DOI] [Google Scholar]
  47. Nam H. O.; Bengtson A.; Vörtler K.; Saha S.; Sakidja R.; Morgan D. First-principles molecular dynamics modeling of the molten fluoride salt with Cr solute. J. Nucl. Mater. 2014, 449, 148–157. 10.1016/j.jnucmat.2014.03.014. [DOI] [Google Scholar]
  48. Salanne M.; Simon C.; Turq P.; Heaton R. J.; Madden P. A. A First-Principles Description of Liquid BeF2and Its Mixtures with LiF: 2. Network Formation in LiF–BeF2. J. Phys. Chem. B 2006, 110, 11461–11467. 10.1021/jp061002u. [DOI] [PubMed] [Google Scholar]
  49. Heaton R. J.; Brookes R.; Madden P. A.; Salanne M.; Simon C.; Turq P. A First-Principles Description of Liquid BeF2and Its Mixtures with LiF: 1. Potential Development and Pure BeF2. J. Phys. Chem. B 2006, 110, 11454–11460. 10.1021/jp061000+. [DOI] [PubMed] [Google Scholar]
  50. Zhu Y.; Hawari A. I. Thermal neutron scattering cross section of liquid FLiBe. Prog. Nucl. Energy 2017, 101, 468–475. 10.1016/j.pnucene.2017.03.028. [DOI] [Google Scholar]
  51. Zheng G.; Kelleher B.; Cao G.; Anderson M.; Allen T.; Sridharan K. Corrosion of 316 stainless steel in high temperature molten Li2BeF4 (FLiBe) salt. J. Nucl. Mater. 2015, 461, 143–150. 10.1016/j.jnucmat.2015.03.004. [DOI] [Google Scholar]
  52. Kelleher B.; Dolan K.; Anderson M.; Sridharan K. Observed Redox Potential Range of Li2BeF4Using a Dynamic Reference Electrode. Nucl. Tech. 2016, 195, 239–252. 10.13182/nt15-140. [DOI] [Google Scholar]
  53. Zheng G.; Sridharan K. Corrosion of structural alloys in high-temperature molten fluoride salts for applications in molten salt reactors. Jom 2018, 70, 1535–1541. 10.1007/s11837-018-2981-2. [DOI] [Google Scholar]
  54. Britsch K.; Anderson M.; Brooks P.; Sridharan K. Natural circulation FLiBe loop overview. Int. J. Heat Mass Tran. 2019, 134, 970–983. 10.1016/j.ijheatmasstransfer.2018.12.180. [DOI] [Google Scholar]
  55. Zheng G.; Kelleher B.; He L.; Cao G.; Anderson M.; Allen T.; Sridharan K. High-Temperature Corrosion of UNS N10003 in Molten Li2BeF4(FLiBe) Salt. Corrosion 2015, 71, 1257–1266. 10.5006/1657. [DOI] [Google Scholar]
  56. Zheng G.; Carpenter D.; Hu L.-W.; Sridharan K., High Temperature Corrosion of Structural Alloys in Molten Li2BeF4 (FLiBe) Salt. Advances in Materials Science for Environmental and Energy Technologies V: Ceramic Transactions; American Ceramic Society, 2016; Vol. 260, pp 93–101. [Google Scholar]
  57. Stempien J. D.; Ballinger R. G.; Forsberg C. W. An integrated model of tritium transport and corrosion in Fluoride Salt-Cooled High-Temperature Reactors (FHRs) - Part I: Theory and benchmarking. Nucl. Eng. Des. 2016, 310, 258–272. 10.1016/j.nucengdes.2016.10.051. [DOI] [Google Scholar]
  58. Busing W. R. Interpretation of the Crystal Structure of Li2BeF4 in Terms of the Born-Mayer-Huggins Model. J. Chem. Phys. 1972, 57, 3008–3010. 10.1063/1.1678699. [DOI] [Google Scholar]
  59. Wang J.; Song H.; Bai Y.; Sun W.. Thermal neutron scattering data for liquid molten salt LiF-BeF2. EPJ Web of Conferences; EDP Science, 2020; Vol. 239, p 14004.
  60. Pan G.; Chen P.; Yan H.; Lu Y. A DFT accurate machine learning description of molten ZnCl2 and its mixtures: 1. Potential development and properties prediction of molten ZnCl2. Comput. Mater. Sci. 2020, 185, 109955. 10.1016/j.commatsci.2020.109955. [DOI] [Google Scholar]
  61. Liang W.; Lu G.; Yu J. Theoretical prediction on the local structure and transport properties of molten alkali chlorides by deep potentials. J. Mater. Sci. Technol. 2021, 75, 78–85. 10.1016/j.jmst.2020.09.040. [DOI] [Google Scholar]
  62. Liang W.; Lu G.; Yu J. Machine-Learning-Driven Simulations on Microstructure and Thermophysical Properties of MgCl2-KCl Eutectic. ACS Appl. Mater. Interfaces 2021, 13, 4034–4042. 10.1021/acsami.0c20665. [DOI] [PubMed] [Google Scholar]
  63. Li Q.-J.; Küçükbenli E.; Lam S.; Khaykovich B.; Kaxiras E.; Li J. Development of robust neural-network interatomic potential for molten salt. Cell Rep. Phys. Sci. 2021, 2, 100359. 10.1016/j.xcrp.2021.100359. [DOI] [Google Scholar]
  64. Kresse G.; Furthmuller J.. Vienna Ab-initio Simulation Package (VASP): The guide; Universität Wien, VASP-Guide, 2002. [Google Scholar]
  65. Kresse G.; Furthmuller J. Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169. 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
  66. Ching W.-Y.; Rulis P.. Electronic Structure Methods for Complex Materials: The Orthogonalized Linear Combination of Atomic Orbitals; Oxford University Press: Great Clarendon Street, Oxford, United Kingdom, 2012. [Google Scholar]
  67. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953. 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
  68. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758. 10.1103/physrevb.59.1758. [DOI] [Google Scholar]
  69. Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
  70. Seiler P. Estimation of ionicity coefficients in Li2BeF4 crystals by X-ray diffraction. Acta Crystallogr., Sect. B: Struct. Sci. 1993, 49, 223–235. 10.1107/s0108768192009510. [DOI] [Google Scholar]
  71. Baral K.; Li A.; Ching W.-Y. Ab initio modeling of structure and properties of single and mixed alkali silicate glasses. J. Phys. Chem. A 2017, 121, 7697–7708. 10.1021/acs.jpca.7b06530. [DOI] [PubMed] [Google Scholar]
  72. Baral K.; Li A.; Ching W.-Y. Ab initio molecular dynamics simulation of Na-doped aluminosilicate glasses and glass-water interaction. AIP Adv. 2019, 9, 075218. 10.1063/1.5092617. [DOI] [Google Scholar]
  73. Baral K.; Li A.; Ching W.-Y. Ab Initio Study of Hydrolysis Effects in Single and Ion-Exchanged Alkali Aluminosilicate Glasses. J. Phys. Chem. B 2020, 124, 8418–8433. 10.1021/acs.jpcb.0c05875. [DOI] [PubMed] [Google Scholar]
  74. Nosé S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. 10.1063/1.447334. [DOI] [Google Scholar]
  75. Nosé S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. 10.1080/00268978400101201. [DOI] [Google Scholar]
  76. Hafner J. Ab-initiosimulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. 10.1002/jcc.21057. [DOI] [PubMed] [Google Scholar]
  77. Parrinello M.; Rahman A. Crystal structure and pair potentials: A molecular-dynamics study. Phys. Rev. Lett. 1980, 45, 1196. 10.1103/physrevlett.45.1196. [DOI] [Google Scholar]
  78. Parrinello M.; Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
  79. Allen M. P.; Tildesley D. J.. Computer Simulation of Lquids; Oxford University Press: Great Clarendon Street, Oxford, United Kingdom, 2017. [Google Scholar]
  80. Blanke B.; Bousquet E.; Curtis M.; Murphy E.. Density and Viscosity of Fused Mixtures of Lithium, Beryllium, and Uranium Fluorides; Mound Lab.: Miamisburg, Ohio, 1956. [Google Scholar]
  81. Cantor S.Physical Properties of Molten-Salt Reactor Fuel, Coolant, And Flush SaltS; Oak Ridge National Lab.: TN (US), 1968. [Google Scholar]
  82. Cantor S.; Ward W. T.; Moynihan C. T. Viscosity and Density in Molten BeF2-LiF Solutions. J. Chem. Phys. 1969, 50, 2874–2879. 10.1063/1.1671478. [DOI] [Google Scholar]
  83. Janz G. J.; Gardner G. L.; Krebs U.; Tomkins R. P. T. Molten salts: volume 4, Part 1, fluorides and mixtures electrical conductance, density, viscosity, and surface tension data. J. Phys. Chem. Ref. Data 1974, 3, 1–115. 10.1063/1.3253134. [DOI] [Google Scholar]
  84. Rosenthal M.Molten-Salt Reactor Program Semiannual Progress Report: For Period Ending August 31, 1969; Oak Ridge National Laboratory: TN (US), 1970.
  85. Janz G. J. Thermodynamic and transport properties for molten salts: correlation equations for critically evaluated density, surface tension, electrical conductance, and viscosity data. J. Phys. Chem. Ref. Data 1988, 17, 311. [Google Scholar]
  86. Burns J. H.; Gordon E. K. Refinement of the crystal structure of Li2BeF4. Acta Crystallogr. 1966, 20, 135–138. 10.1107/s0365110x66000240. [DOI] [Google Scholar]
  87. https://materialsproject.org/materials/mp-4622/ (accessed 02/11/2021).
  88. McGinnety J. A. Crystal forces in lithium tetrafluoroberyllate. J. Chem. Phys. 1973, 59, 3442–3443. 10.1063/1.1680499. [DOI] [Google Scholar]
  89. Roy D. M.; Roy R.; Osborn E. F. Fluoride Model Systems: IV, The Systems LiF-BeF2 and PbF2-BeF2. J. Am. Ceram. Soc. 1954, 37, 300–305. 10.1111/j.1151-2916.1954.tb14042.x. [DOI] [Google Scholar]
  90. Roy D. M.; Roy R.; Osborn E. F. Phase Relations and Structural Phenomena in the Fluoride-Model Systems LiF-BeF2 and NaF-BeF2. J. Am. Ceram. Soc. 1950, 33, 85–90. 10.1111/j.1151-2916.1950.tb12766.x. [DOI] [Google Scholar]
  91. Seiler P.; Dunitz J. D. Are ionic solids really built of ions? New evidence from x-ray diffraction. Helv. Chim. Acta 1986, 69, 1107–1112. 10.1002/hlca.19860690518. [DOI] [Google Scholar]
  92. Collins D. M.; Mahar M. C.; Whitehurst F. W. Bonding in lithium tetrafluoroberyllate(II). Acta Crystallogr., Sect. B: Struct. Sci. 1983, 39, 303–306. 10.1107/s010876818300244x. [DOI] [Google Scholar]
  93. Godby R. W.; Schlüter M.; Sham L. J. Self-energy operators and exchange-correlation potentials in semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 10159. 10.1103/physrevb.37.10159. [DOI] [PubMed] [Google Scholar]
  94. Perdew J. P. Density functional theory and the band gap problem. Int. J. Quantum Chem. 1985, 28, 497–523. 10.1002/qua.560280846. [DOI] [Google Scholar]
  95. Grüning M.; Marini A.; Rubio A. Density functionals from many-body perturbation theory: The band gap for semiconductors and insulators. J. Chem. Phys. 2006, 124, 154108. 10.1063/1.2189226. [DOI] [PubMed] [Google Scholar]
  96. Martin P. C. Sum rules, Kramers-Kronig relations, and transport coefficients in charged systems. Phys. Rev. 1967, 161, 143. 10.1103/physrev.161.143. [DOI] [Google Scholar]
  97. Pugh S. F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. London, Edinburgh Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. 10.1080/14786440808520496. [DOI] [Google Scholar]
  98. Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. 10.1103/physrevlett.100.136406. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao1c02528_si_001.pdf (1.8MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES