Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2021 Jul 23;6(30):19629–19641. doi: 10.1021/acsomega.1c02257

Metallaborazines: To Be or Not To Be Delocalized

Rafael Islas †,*, David Arias-Olivares †,‡, Andrés Becerra-Buitrago §, Luis Carlos García-Sánchez §, Lya Neftaly Méndez-Ayón ∥, Bernardo Zuniga-Gutierrez ∥
PMCID: PMC8340438  PMID: 34368550

Abstract

graphic file with name ao1c02257_0017.jpg

In the current work, the analysis of the electronic delocalization of some metallacycles, based on borazine, was realized by employing magnetic criteria, such as the induced magnetic field and magnetically induced current densities, and electronic criteria, such as adaptative natural density partitioning and the analysis of molecular orbitals. The current metallaborazines were generated from isoelectronic substitutions. The main question is whether the electronic delocalization increases or decreases. The results showed that metal–N bonded borazines could be cataloged as delocalized compounds. On the other hand, the metal–B bonded borazines could be cataloged as nonaromatic (or weak aromatic) compounds based on the results of this analysis.

1. Introduction

The history of borazine begins in 1926 when Stock and Pohland synthesized this molecule from the reaction of ammonia and diborane.1 It was Wiberg, in 1948, who proposed the pseudonym “inorganic benzene”.2 Chemically, borazine is more susceptible to addition reactions, but some groups have reported some electrophilic reactions.3,4 Borazine’s electronic delocalization has been widely studied employing different methodologies based on the energetic, magnetic, and structural criteria.5−19 Borazine has been cataloged as benzene’s inorganic analogue because both molecules present hexagonal planar rings, bond length equalization, and 6π electrons (the criteria for aromatic compounds), and one conclusion of these analyses is that the π electrons in borazine are not delocalized as the π electrons in benzene due to the electronegativity difference between the nitrogen and boron atoms. Some authors extended the analysis of the electronic delocalization in other boro-azo compounds. For example, in 2015, Srivastava and Misra reported the analysis of the electronic delocalization in a “carborazine” ring and its derivates that are six-membered ring analogues to borazine but with two carbons replacing one boron atom and one nitrogen atom (positions 1 and 4). This incorporation increases the electronic delocalization compared with borazine.20 In 2020, Anstöter et al. modeled the aromatization of (BN)nHn azabora-annulenes. In particular, they found that “borazocine”, [B4N4H8]2–, has a diatropic character (compared with benzene), and it could form coordinated compounds such as sandwich complexes.21 An interesting analysis about the nature of the chemical bond of borazine was realized by Kalemos. In that work, the author analyzed the excited states of the fragments BH and NH to form the ground state of borazine (the author also analyzed boraxine and carborazine with the same methodology).22 The author also established the importance of the resonance structures that differ in the way the 6π electrons are initially placed on the parental centers.22

On the other hand, metallabenzenes are benzenes with a CH unit substituted by a metal fragment,23,24 both units are chemical analogues, in agreement with “isolobal analogy” proposed by Hoffmann.25 This theory establishes that one chemical unit can be replaced by another one with a similar shape and similar energy of their respective frontier molecular orbitals. In metallabenzenes, the d atomic orbitals of the metal atom participate in the electronic delocalization.23 The existence of these compounds was theoretically predicted by Thorn and Hoffmann in 1979.26 In their work, they proposed that electronic delocalization is the mechanism that stabilizes the metallacycles. Three years later, in 1982, the first metallabenzene was synthesized by Roper et al. and its planarity (associated with aromatic compounds) was confirmed by X-ray diffraction.27

In the current work, the electronic delocalization of hypothetical systems proposed in silico, generated by the combination of metallabenzenes and borazines, metallaborazines, was studied. These compounds are formed by the borazine ring with a metal fragment in the ring (vide infra). The question is: Can the incorporation of a metal fragment (bonded to N or B) increase the electron delocalization of weakly delocalized borazine?

The idea of metallaborazines is not fully new, some of them have been already synthesized. In 1992, Koch et al. tried to synthesize a titanium borazine, but the compound obtained was not a planar ring and included two Ti atoms replacing two boron atoms (molecular formula: PhB(MeN)3(TiCl2)2). The structure obtained was described by the authors as a “geometrical body whose surface consists of four, bent, irregular squares or as a tetrahedron...”. And the reason for the nonplanar structure is the strong intramolecular Ti–N interactions.28 One year later, in 1993, Koch et al. synthesized and reported the X-ray structure of a tellurium-substituted borazine, with the molecular formula MeN[PhBN(Me)]2TeCl2. The structure shows that the tellurium atom is bonded to the borazine’s nitrogen atoms and it is a nonplanar ring (close to the “boat” geometry).29 It was in 2018 when Less et al. reported the synthesis of an aluminum-substituted borazine. The ring is a planar structure, and the metal atom is bonded to borazine’s nitrogen atoms. They also reported a low aromatic behavior.30

2. Results

2.1. Structural Results

2.1.1. Geometrical Analysis

Two types of borazines were optimized: M–B type (with the metal atom bonded to boron atoms) and M–N type (with the metal atom bonded to nitrogen atoms); see Section 5 for more information. In Figure 1, the geometries of the optimized cycles are depicted with the complete metallic fragment (metal and ligands). Osmium cycles were not planar after the optimization and they were not studied as aromatic compounds. Planar or quasi-planar rings are related to delocalized systems. Rhenium and platinum cycles were planar cycles. Iridium cycles were quasi-planar, especially the IrB cycle that presented a 13° dihedral; but despite this, they were analyzed with magnetic methodologies (vide infra). Some dihedral angles of all of the cycles are condensed in Table 1. In Figure 2, the metallic centers were simplified for a better interpretation, and the bond lengths of the (quasi)planar cycles are depicted (osmium cycles were not considered). All of the B–N bond distances were in the range of 1.426 Å, and the bond length was computed in borazine at the same level of theory. The values in the Ir cycle varied due to the orientation of PH3 and CO linked to Ir metal; also, this spatial orientation decreased the symmetry of the ring. For this reason, four B–N bond distances were reported in IrB and IrN systems. As a reference system, borazine is also depicted.

Figure 1.

Figure 1

Open in a new tab

Optimized structures studied in the current work.

Table 1. Selected Dihedral Anglesa.

2.1.1.

Open in a new tab
a

The measures are the absolute values of the angles. Here, Os = Os(PH3)2Cl2, Re = Re(CO)4, Ir = Ir(PH3)2CO, and Pt = Pt(C5H5).

Figure 2.

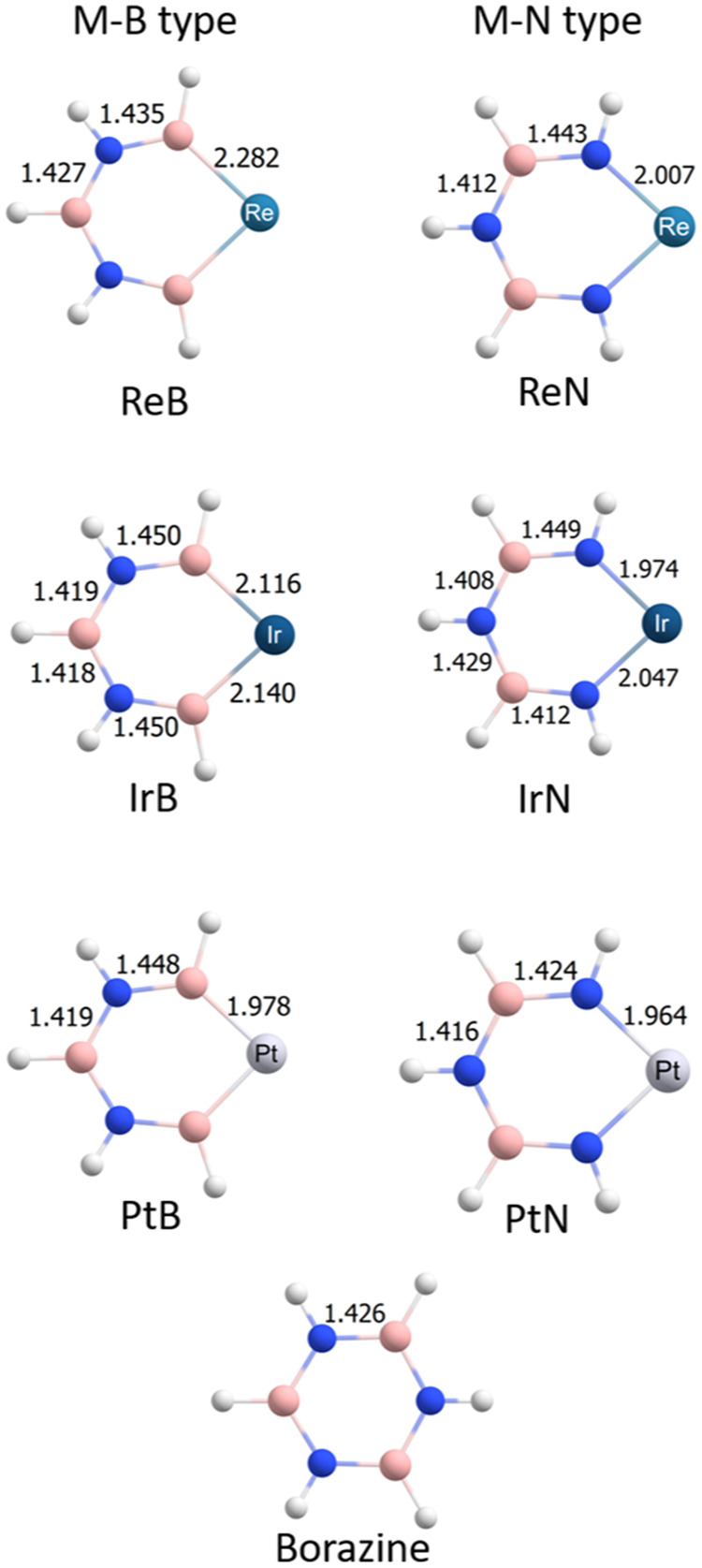
Figure 2

Open in a new tab

Selected bond lengths of the rings are depicted. The units are in Å. In this image, Re = Re(CO)4, Ir = Ir(PH3)2CO, and Pt = Pt(C5H5), and only the (quasi)planar structures are depicted. Borazine is incorporated for reference.

It is easier to see the difference between the planarity of all of the rings if they are superposed. In Figure 3, the overlayed geometries of the metallaborazines are depicted, and it was clear that there was no significant structural difference in the selected rings.

Figure 3.

Figure 3

Open in a new tab

Superposed structures. All of the rings proposed in the current work were overlayed for better appreciation of their planarity.

In some calculations (vide infra), the metallaborazines proposed in the current work were compared with the computational models of the synthesized aluminum–borazine (Al–N) and tellurium–borazine (Te–N). The geometries analyzed are depicted in Figure 4, and they were optimized at the same level of theory as the other rings.

Figure 4.

Figure 4

Open in a new tab

Computational models of the synthesized metallaborazines.

2.1.2. Electron Structure Details

The electron structure analysis was tackled by three different and complementary methodologies: the adaptative natural density partitioning (AdNDP)31 and the molecular orbital construction with two closed-shell fragments: the metal ligand (ML) in the singlet state and the ring in its singlet state. These fragments were used to calculate the energy decomposition analysis combined with the extended transition state theory with the natural orbitals of chemical valence (ETS–NOCV).32 Besides the electron structure details, another electron density-based descriptor was used, i.e., the electron density of delocalized bonds (EDDB).33,34

Figure 5 shows the MO analysis for rhenaborazine in its two possible configurations Re–B type and Re–N type. The Re–B molecule presents only two doubly occupied molecular orbitals with π symmetry (H-5 and H-7), which come from the ring fragment. On the other hand, the Re–N molecule presents three doubly occupied molecular orbitals as a combination of occupied MOs from the ring and the LUMO from the ML fragment; this LUMO is a linear combination of 24.5% of py and 19% of dz2. These three molecular orbitals of Re–N resembled those from the classical aromatic system, following Hückel’s rule for 4n + 2 π electrons.

Figure 5.

Figure 5

Open in a new tab

Qualitative molecular orbital analysis for Re–B-type (left) and Re–N-type (right) cycles. Only the MOs of interest are depicted.

This trend was followed in all of the systems studied (see MOs in the Supporting Information), and it was found that all M–B-type molecules have 4nπ electrons, while M–N-type molecules have (4n + 2)π electrons. For the M–B-type molecules, the 4nπ electrons were associated with Hückel antiaromatic topology due to the almost inexistent participation of the metals’ d atomic orbitals. Furthermore, in the M–N-type molecules, the contribution from the occupied orbitals came from a linear combination of py and d orbitals adapted by symmetry from the metal. Also, for the previously synthesized system (Al and Te borazines) of M–N type, the trend of (4n + 2)π electrons is also depicted (with n = 2), as predicted by the in silico M–N-type models.

The orbitals adapted by symmetry from the metal give insights into the possible Möbius nature of the systems. The Mauksch and Tsogoeva relationship was used,35 and not only the HOMO but also the whole π space was observed. ReB and IrB have no contribution of d orbitals from the metal to the π-type MOs. In contrast to the other M–B-type metallaborazine, PtB presents the first contribution of d orbitals from the metal to the π-MO structure. The dyz AO from the metal contributes, in phase, to the LUMO structure of the metallaborazine, meaning a Hückel conjugation.

On the other hand, the M–N type presents an important contribution from the metal d AOs. For ReN, the contribution of metal to the π-type molecular orbitals mainly comes from the LUMO fragment of ML. This LUMO fragment is composed of dyz-type AO, which is in phase with the ring, giving rise to a pure Hückel conjugation.

For IrN, in all of the MO of interest, the dyz and dxz contribution was observed. The H-2 of Irida-N-borazine also has a contribution from pz AO of the metal. The higher contribution always comes from dyz rather than dxz. This linear combination of atomic orbitals, according to their weights, has more Hückel characteristics than Möbius characteristics.

For PtN, this is the first molecule of the set under study that presents a pure Möbius conjugation but is not large enough to be considered a Möbius aromatic molecule. While all of the structure has the contribution of dyz AO from Pt, the HOMO has a higher contribution of dxz AO from Pt. This dxz AO has a phase inversion, giving rise to a d-conjugation Möbius MO with a contribution of 20% but 80% Hückel characteristics. Despite this d-conjugation Möbius MO, the other two MOs have Hückel conjugation.

Notwithstanding the presence of d-conjugation Möbius MO in Ir and Pt–N borazine, all M–N borazines could be characterized as Hückel aromatic systems. In contrast to the synthesized TeN, there is no important participation of d molecular orbitals in the π molecular orbital analysis.

The AdNDP calculation allows the analysis of the bonding pattern in molecules. Also, the π space was observed with the AdNDP analysis, once again; the Re systems are depicted in Figure 6, while the other plots are given in the Supporting Information. Figure 6 shows the AdNDP analysis for Re systems; for ReB (bottom), the σ space suggested that there was not a σ bond between Re and the ring. It was found that it had only four σ bonds instead of six, as shown in ReN (top). The 3c–2e is shown for both molecules in Figure 6, and ReB did not contain the metal contribution in their orbitals, whereas ReN did. While there was only one 4c–2e for ReB, there were five of them for ReN, suggesting a delocalized system. Finally, there was not a 6c–2e orbital for ReB, while there were two of them for the ReN system, showing a higher π-delocalized nature on the system. The last two orbitals from ReB (three in the ReN system) resemble those molecular orbitals observed in Figure 5.

Figure 6.

Figure 6

Open in a new tab

Adaptive natural density partitioning (AdNDP) analysis for ReN and ReB systems; ON: occupation number.

In contrast to ReB, all of the M–B-type molecules presented 6σ × 2c–2e with ON = 1.9. The nature of the orbitals for M–B-type molecules did not contain the metal contribution, while the M–N-type molecules always contained the metal contribution in their AdNDP orbitals in the 3c–, 4c–, 5c–, and 6c–2e search. Thus, the AdnDP analysis provided the π nature of the systems, suggesting a completely delocalized structure for the M–N-type molecules, while the M–B-type molecules did not due to the lack of metal orbital participation in the π orbital contributions.

A part of contribution of the ML to the ring was observed through the MO analysis and the AdNDP analysis. A quantitative approximation of these interactions was depicted by energy decomposition analysis (EDA calculation) combined with the ETS–NOCV. Table 2 reports all EDA data, where the percentages of ΔE for electrostatic and orbital interactions are depicted in kcal/mol. All M–B-type systems had a bigger electrostatic interaction contribution (above 60%) compared with the M–N-type molecules, which had larger values for the orbital interaction contribution (above 50%). A low dispersive contribution to the energy interaction was observed for all systems analyzed. Thus, high σ and π contributions to the orbital energy in the M–N-type molecules are expected as well as the formation of stronger covalent interactions between the metal and the N ring. The percentages of energies involved for electrostatic and orbital contributions for the M–N type in silico proposed systems are in agreement with those exposed by the synthesized ones.

Table 2. EDA for All Moleculesa.
metal net charge ML charge ring charge ΔEPau ΔEEle ΔEOrb ΔEDis ΔEInt
ReB –1 1 –2 513.82 –629.97 –373.98 –5.06 –495.19
          62.75% 37.25%    
ReN 1 1 0 400.66 –284.74 –370.3 –4.37 –258.75
          43.48% 56.52%    
IrB –1 1 –2 571.55 –657.11 –377.20 –5.75 –468.28
          63.54% 36.46%    
IrN 1 1 0 267.49 –196.42 –305.21 –5.75 –239.66
          39.15% 60.85%    
PtB –1 1 –2 566.95 –753.94 –334.42 –3.45 –525.09
          69.27% 30.73%    
PtN 1 1 0 343.16 –263.12 –299.69 –4.37 –224.25
          46.76% 53.24%    
AlN 0 0 0 648.55 –308.53 –550.12 –3.17 –213.26
          35.93% 64.07%    
TeN 0 0 0 573.37 –327.11 –484.25 –5.18 –243.17
          40.32% 59.68%    
Open in a new tab
a

Energy is presented in kcal/mol. The charge of each fragment (ML = metal and its ligands) is depicted as well as the total (net) charge.

To analyze the symmetry and the deformation density of ΔEorb, which helps to understand the chemical bonds between the fragments, the NOCV was carried out. In the NOCV scheme, the deformation density flux (charge density flux) goes from red zones to blue zones. As predicted by AdNDP analysis, there was no evidence of the σ bond between Re and the B ring (Figure 7, left), there was only charge transfer from the ring to the ML fragment, in σ as well as in the π space without the concentration (blue zones) of electron density in the bonding zone. On the other hand, the Re–N molecule presented that charge flows from pz orbitals in the nitrogen zones and from the dyz orbitals from the metal to the bonding zone. These dyz orbitals are in phase with the ring, giving rise to a Hückel conjugation instead of Möbius-like aromaticity. This charge flow also indicates the σ bond (Figure 7, right). In the π space, a clear contribution from the rings (pz nitrogen) goes to the metal (dxz) but this does not mean a dxz contribution from the metal.

Figure 7.

Figure 7

Open in a new tab

NOCV analysis for ReB (left) and ReN (right). Charge flows from red zones to blue zones. Isovalue = 0.003 au. The fragments selected are C5H5 and ML+.

For the other molecules, NOCV is presented in the Supporting Information; for Ir and Pt borazines, a σ bond is present in the M–B-type as well as M–N-type molecules as a blue zone between the fragments. The σ bond is a result of symmetry-adapted linear combinations of the p orbitals from nitrogen or boron, and the d orbitals from the metal in the ring. While the σ space shows a clear ring formation of Ir and Pt borazines, the π space shows a flow from the π orbitals in the ring to the metal, increasing the concentration of charge density around the metal atom. Furthermore, in the M–N type, the σ symmetry of the deformation density has greater values (or is stronger) than the π symmetry, which explains the formation of the ring followed by the delocalized π interaction of the molecules in the M–N-type systems as well as in the experimental AlN and TeN molecules. Furthermore, the symmetry of the deformation density around the metal resembles a dyz-like orbital, avoiding a phase inversion in the π symmetry of the ring, while in the M–B type, the π–δ interaction is more important than σ stabilization, giving rise to a greater electrostatic interaction in these systems than the orbital one.

For completeness, the EDDB as a DFT-based descriptor is shown in Figure 8. As expected, and previously reported,33,36 benzene presents a fully chemical resonance over the system. This is also observed for borazine, which presents a low aromatic behavior but a delocalized electron density. In contrast, ReB does not present a delocalized electron density over the ring as expected according to the herein descriptors. Nevertheless, Re–N presents a low, but still, delocalized electron density over the ring. This pattern is extended to all M–B-type molecules, with a nondelocalized electron density, while M–N-type molecules present the delocalized pattern in different magnitudes; the less but still delocalized is Ir–N (see all figures in the Supporting Information). The models of the already synthesized Al–N and Te–N borazines do not present this electron density delocalization; instead, the electron density is localized over the nitrogen but it still presents a low diatropic current density, suggesting a very low aromatic behavior, which is in full agreement with Bzind (see Section 2.2.2). This response could be associated with the higher electronegativity of nitrogen atoms.

Figure 8.

Figure 8

Open in a new tab

EDDBs for benzene, borazine, ReB, and ReN. Isovalue = 0.015.

2.2. Electronic Delocalization Analysis

2.2.1. Magnetically Induced Current Densities (MICDs)

The MICD37 was computed using the four-component Dirac Hamiltonian where the induced current is related to the aromatic character of a system38 (see Section 5). The current density plots were extracted at the molecular plane, 1a0, and 2a0 from the molecular plane. In all cases, at the molecular plane, an external diatropic flux was observed, a paratropic flux in the inner part of the ring, and diatropic currents around each atom. This behavior was consistent with the borazine current density (see the Supporting Information).

At 1a0 from the molecular plane, for all M–N-type systems, a ring current flowing above the ring was observed; this diatropic current was still present and easier to visualize at 2a0 from the molecular plane. On the other hand, for all M–B-type systems, the total ring current above the ring was not present. However, local diatropic ring currents were exhibited over the metal center as well as nitrogen atoms, while in the inner part of the ring, a paratropic current was exposed. Figure 9 shows, as an example, the total MICD for (A) borazine, (B) ReB, and (C) ReN molecules at 2a0 from the molecular plane.

Figure 9.

Figure 9

Open in a new tab

2D plot of the MICD at 2a0 from the molecular plane in different systems: (A) borazine, (B) ReB, and (C) ReN. Blue circles in (A) belong to N atoms, while those in (B) and (C) represent the metal atom. Line color is proportional to the intensity of the vector.

Borazine exhibited a clear diamagnetic current density over the ring as well as the ReN molecule. The ReB molecule did not exhibit a ring current density; instead, a localized diatropic response over Re and N was observed. All molecules studied here exhibited the same behavior, i.e., for the metal–B systems, there was not ring current density but a localized diatropic response over the metal and nitrogen atoms. For the metal–N systems, a ring current density was depicted. In all cases, the diatropic response was higher in the metal atom, followed by nitrogen and boron, as expected.

According to the MICD 2D plots, the M–N-type systems presented a total diatropic current over the ring. They did exhibit a delocalized nature in the electron density, while the M–B-type systems did not. To quantify the strength of the ring current, a 15a0 x 15a0 plane was conveniently placed bisecting the bond between atoms 3 and 4 in the ring (where the metal represents atom number 1). It is important to recall that the strength current density is plane-dependent and was computed through the two-dimensional Gauss–Lobatto quadrature. It means that it is convenient to avoid nuclei as well as to place the plane close to metal atoms due to the diatropic behavior. Thus, the further plane is that that bisects the bond between atoms 3 and 4 (if metal is 1).

Figure 10 presents the integration values through the path over the selected plane. As usual, borazine presented a low diatropic strength current. Around borazine, the M–B-type metallaborazines are shown. The values of the total strength current (Table 3) are diatropic, as the total diatropic values corresponded to the high values associated with diatropic currents around each atom in the ring. For the M–N-type delocalized cases, the values for Re, Ir, and Pt were close for the benzene system with a reference value of 13.09 nA/T (Table 3) for the same plane used in the metallaborazines, while for a symmetric bisected C–C bond, the value corresponded to 9.55 nA/T at the same level of theory. Thus, the electronic delocalization for M–N-type metallaborazines increases, while the atomic weight of the metal decreases. As observed in EDDBs, the already synthesized Al and Te–N borazines do not present a clear delocalized electron density pattern, and as a consequence, a low diatropic current density is depicted and a low strength current density is computed. These magnetic results of the experimental borazines are in full agreement with Bzind, i.e., the magnetic response is more alike borazine than in silico M–N borazines here presented.

Figure 10.

Figure 10

Open in a new tab

Strength current path of each molecule studied. Borazine and benzene were incorporated as references of aromatic and weak aromatic molecules, respectively.

Table 3. Total Strength Current Density in nA/T for All Molecules Studieda.
molecule Bz Pt–N Ir–N Re–N Re–B Pt–B Al–N borazine Te–N Ir–B
nA/T 13.09 10.61 10.31 8.81 7.02 5.89 4.68 3.95 2.78 2.36
Open in a new tab
a

Bz corresponds to benzene and is sorted from more to less delocalized.

2.2.2. Induced Magnetic Field (Bind)

The isosurfaces of the z-component of the induced magnetic field, also known as Bzind,39 are depicted in Figure 11. The blue and red regions are related to the diatropic and paratropic responses, respectively. All of the systems proposed in the current work were analyzed with this methodology, except for the osmium rings, which were not planar structures, and as consequence, they were not considered as possible aromatic compounds. Also, benzene, the archetype of the aromatic compounds, was analyzed as the reference of delocalized molecules. In Figure 11, the isosurface associated with benzene’s response was homogeneous around the molecular ring. In the same lines, borazine was analyzed as a reference, and it was clear that the electronegativity difference between the nitrogen and boron atoms generated “diatropic islands” around the nitrogen atoms, denoting that electronic delocalization in this inorganic ring is not so homogeneous as benzene’s response. The M–B-type molecules presented, in their respective Bz isosurfaces, the same diatropic islands around their nitrogen atoms, denoting that electronic delocalization was similar to the borazine isosurface. The presence of the metal fragment did not impact the M–B-type molecules’ magnetic response. At the center of the M–B rings, it was possible to recognize small paratropic regions. On the other hand, the M–N-type molecules presented a more homogeneous response around the ring skeleton. The diatropic response was better distributed if they were compared with borazine and M–B-type molecules. But this magnetic response was not comparable in extension and shape with benzene’s response. In the M–N-type molecules, the boron atoms were found out of the diatropic regions, as a consequence of the electronegative difference between nitrogen and boron atoms. The shape and distribution of the diatropic regions were indicative that M–N-type molecules were slightly more delocalized.

Figure 11.

Figure 11

Open in a new tab

Isosurfaces of the z-component of the induced magnetic field, or Bzind, computed in benzene and borazine, the M–B-type and M–N-type molecules proposed in this work. The value of the isosurface is |Bz| = 13.8 ppm. The blue and the red regions are associated with the diatropic and paratropic regions, respectively. The pink spheres represent the boron atoms.

Also, the profiles of Bzind and nucleus-independent chemical shifts (NICS)40 were plotted and are depicted in Figure 12. Computational models of the synthesized aluminum–borazine and tellurium–borazine were included in the profiles’ plots for comparison with the in silico metallaborazines. The values of Bz show a high difference between the aromatic benzene and the in silico and in vitro metallaborazines. All of the metallaborazines and borazine could be considered as low aromatic compounds. The M–N-type molecules were slightly more diatropic compared with the M–B-type. The paratropic values observed in both plots were generated by more localized σ electrons. This increase in the values of Bzind and NICS was also observed in benzene for the same reason.41

Figure 12.

Figure 12

Open in a new tab

Profiles of the (a) z-component of the induced magnetic field and (b) nucleus-independent chemical shifts. The units are in ppm.

3. Discussion

The analysis of the electronic delocalization in the two subsets of metallaborazines was carried out by complementary theoretical methodologies.

In the molecules labeled as M–B-type borazines, the computed Bzind generated three diatropic islands over the more electronegative regions, i.e., N and M atoms, denoting nonhomogeneous electronic delocalization (comparable with borazine’s response), associated with low aromatic compounds. The MICD results supported the low aromatic response of the M–B-type borazines. The bond length difference in the analyzed rings was negligible, in agreement with the nonaromatic character. Also, the EDDB analysis of M–B-type molecules showed a low delocalized response similar to borazine. But the electronic analysis (MO’s and AdNDP) supported the idea that M–B-type borazines were antiaromatic systems following the Hückel’s rule of 4nπ electrons. Thus, it is possible that the magnetic response gave a false positive for the nonaromatic response due to the higher concentration of the diatropic response in some regions, giving rise to a total diatropic response (negative values of Bz and positive strengths for MICD). This set of molecules were categorized as antiaromatic systems as the electron analysis indicated as well as the reinterpretation of the magnetic response.

Nevertheless, in the M–N-type borazines, the electronic delocalization was more homogeneous. The response of these systems was slightly more diatropic than borazine’s Bzind and MICD analysis. This aromatic magnetic response was supported by the electron structure analysis, where all molecules followed Hückel’s rule of (4n + 2) π electrons. But all of the M–N-type molecules were not comparable with benzene’s response.

It is important to mention that the accumulation of electron density around nitrogen atoms could generate a cyclic electron delocalization through the boron atoms.5

4. Conclusions

It was observed that the inclusion of a metallic fragment did not increase the electronic delocalization significantly when they were compared with borazine.

Finally, if electronic delocalization is the mechanism that stabilizes metallabenzenes, this phenomenon is favored when the metal is bonded to the nitrogen atoms (M–N-type borazines) according to the results, in agreement with the experimentally reported aluminum–borazine and tellurium–borazine systems.

5. Methodology and Computational Details

Two types of cycles were proposed: one was the M–N-type and the other one was the M–B-type. The M–N-type nomenclature indicates the metal fragment, M, was bonded to the nitrogen atoms, and the M–B-type was the boron analogue. In the current work, M = Os(PH3)2Cl2, Re(CO2)4, Ir(PH3)2CO, and Pt(C5H5).

The in silico construction of the metallaborazines was realized following the next methodology

  • Some metallabenzenes were selected (see Table 4).

  • The general formula of the metallabenzenes is MC5H5. In the ring, the five carbon atoms (C5 fragment) have 20 valence electrons.

  • The M–B-type rings were formed replacing the five carbons with two nitrogen atoms and three boron atoms, completing the 19 valence electron fragment B3N2. Hence, it was necessary to include an extra electron to fulfill the 20 valence electrons. Thus, the B3N2–1 fragment was generated, which was isoelectronic to C5 and allowed the isoelectronic substitution in MC5H5.

  • The M–N-type rings were formed by replacing the five carbon atoms with three nitrogen atoms and two boron atoms, building the B2N3 fragment, which had 21 valence electrons; consequently, it was necessary to remove one valence electron. The result was the 20 valence electron fragment B2N3+1, which was isoelectronic to C5 (see Scheme 1).

Table 4. Inorganic Rings Proposed after the Isoelectronic Substitution.

5.

Open in a new tab

Scheme 1. Isolobal Substitution Employed in Metallabenzenes is Depicted.

Scheme 1

Open in a new tab

The organic ring C5 was replaced with its inorganic (boro-azo) versions.

Eight inorganic compounds were proposed following this isoelectronic substitution scheme and are summarized in Table 4.

All of the structures were optimized employing the M06-L functional42 and the all-electron TZVP basis of Slater-type orbitals for the metal atom, and the TZVP basis set for the non-metal atoms.43 The inclusion of the dispersion correction (Grimme D3)44 was done. All these calculations were produced in ADF-2014.45 All of the geometries were minima in their respective potential energy surfaces (PESs).

These optimized models were used as basis to construct the molecular orbital (MO) diagram, to explain Hückel’s rule for aromatic compounds based on the relativistic wave function at the M06-L functional using the Kohn–Sham formalism.46 Also, the zero-order regular approximation (ZORA)47 was employed to take into account scalar relativistic effects. This MO construction was based on the ML fragments (metal with its ligands) and the rings, which helps to understand the interaction between the fragments through an analysis of bonding energies, combining a fragmented approach to the molecular structure with the decomposition of the interaction energy between fragments according to the Morokuma–Ziegler analysis (EDA decomposition scheme). This interaction between fragments was decomposed as follows

5.

where ΔEPau, ΔEEle, ΔEOrb, and ΔEDis represent the Pauli repulsion, electrostatic interaction, orbital-mixing terms, and dispersion correction, respectively.48,49

This Morokuma–Ziegler analysis was combined with the extended transition state theory with the natural orbitals of chemical valence (ETS–NOCV)32 to have a better description of ΔEOrb, to set up the interaction between the metal and the ring(s). In this work, the density charge flows from the red zones (Δρ < 0) to the blue zones (Δρ > 0). For a complete description of the ETS–NOCV methodology, please read the Supporting Information file.

The induced magnetic field, or Bind, was computed with the following formula

5.

where σ represents the shielding tensor and Bext represents the external magnetic field applied perpendicular to the xy plane and its module is equal to 1 T (|Bext | = 1 T).39 The shielding tensors for the isosurfaces were computed with deMon2k50 employing the PBE functional51,52 in conjunction with the Jorge-atzp basis53 and the GEN-A2 auxiliary functions.54 Isosurfaces of the z-component of the induced magnetic field, Bzind, were employed as a measure of the magnetic response and it is equivalent to the z-component of the NICS40 (also known as NICSzz). Bz and Bzind have been employed in several kinds of molecules such as borazine5 and other metallacycles.55−58 Also, the profiles of Bz (and NICS) were computed for a numerical comparison between the molecules. The profiles’ tensors were computed with the Gaussian 09 program59 with the PBE0 functional51,52,60 and the Jorge-atzp basis.53 For all of the cases, the rings were placed perpendicular to the z-axis of the Cartesian coordinate system and Bext was oriented parallel to the same axis.

Adaptative natural density partitioning (AdNDP)31 analysis was performed employing the M06-L functional and the LANDL2Z basis set61 to obtain the respective wave functions as implemented in the Gaussian 09 program. These wave functions were used in the AdNDP 2.0 program developed by Boldyrev and co-workers.62 The AdNDP method analyzes the first-order reduced density matrix and it represents the electronic structure in terms of n-center–two electron (nc–2e) bonds to recover both Lewis bonding element lone pairs (1c–2e), or chemical bonds (2c–2e), and delocalized bonding elements, which can be associated to electronic delocalization. For a complete view of the delocalized nature of the electron density, the electron density for delocalized bond (EDDB) function has been used with the same level of theory as AdNDP. This wave function produces the EDDB function for the electrons delocalized through all chemical bonds in the molecule, and the visualization was implemented with isovalues of 0.015.

The magnetically induced current density (MICD),37 which is related to the aromatic behavior, was calculated using the linear response function63 and the perturbing operator for the magnetic field. The MICD was plotted in the streamline representation of the current density using PyNGL64 and was computed in DIRAC 1765 at the DFT level of theory with the B3LYP functional.66−68 The four-component Dirac–Coloumb Hamiltonian has been used alongside the unrestricted kinetic balance.69 The cc-pVDZ basis set was employed for all atoms, except for metal atoms.70,71 For the latter, the uncontracted and special Dyall double-zeta basis set was employed.72

Acknowledgments

R.I. and D.A.-O. are grateful to Fondecyt Regular 1201436 for the financial support. L.C.G.-S. and A.B.-B. acknowledge CECAD for the Computing Facility and CIDC for the financial support under project 4-50-598-19.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c02257.

  • Strength current densities; MICD plots; MO’s diagrams; first and second NOCV plots; EDDBs for all of the molecules proposed; and ETS–NOCV complete description (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao1c02257_si_001.pdf (2.4MB, pdf)

References

  1. Stock A.; Pohland E. Borwasserstoffe, IX.: B3N3H6. Ber. Dtsch. Chem. Ges. 1926, 59, 2215–2223. 10.1002/cber.19260590907. [DOI] [Google Scholar]
  2. Wiberg E. Das “anorganische Benzol” B3N3H6 und seine Methylhomologen. Naturwissenschaften 1948, 35, 212–218. 10.1007/BF00597606. [DOI] [Google Scholar]
  3. Chiavarino B.; Crestoni M. E.; Fornarini S. Electrophilic Substitution of Gaseous Borazine. J. Am. Chem. Soc. 1999, 121, 2619–2620. 10.1021/ja983799b. [DOI] [Google Scholar]
  4. Chiavarino B.; Crestoni M. E.; Marzio A. D.; Fornarini S.; Rosi M. Gas-Phase Ion Chemistry of Borazine, an Inorganic Analogue of Benzene. J. Am. Chem. Soc. 1999, 121, 11204–11210. 10.1021/ja992220m. [DOI] [Google Scholar]
  5. Islas R.; Chamorro E.; Robles J.; Heine T.; Santos J. C.; Merino G. Borazine: to be or not to be aromatic. Struct. Chem. 2007, 18, 833–839. 10.1007/s11224-007-9229-z. [DOI] [Google Scholar]
  6. Timoshkin A. Y.; Frenking G. “True” Inorganic Heterocycles: Structures and Stability of Group 13–15 Analogues of Benzene and Their Dimers. Inorg. Chem. 2003, 42, 60–69. 10.1021/ic020361a. [DOI] [PubMed] [Google Scholar]
  7. Cyrański M. K. Energetic Aspects of Cyclic Pi-Electron Delocalization: Evaluation of the Methods of Estimating Aromatic Stabilization Energies. Chem. Rev. 2005, 105, 3773–3811. 10.1021/cr0300845. [DOI] [PubMed] [Google Scholar]
  8. Schleyer P. vR.; Jiao H.; Hommes N. J. R. vE.; Malkin V. G.; Malkina O. L. An Evaluation of the Aromaticity of Inorganic Rings: Refined Evidence from Magnetic Properties. J. Am. Chem. Soc. 1997, 119, 12669–12670. 10.1021/ja9719135. [DOI] [Google Scholar]
  9. Fink W. H.; Richards J. C. Relative aromaticity in heteropolar inorganic analogs of benzene. J. Am. Chem. Soc. 1991, 113, 3393–3398. 10.1021/ja00009a026. [DOI] [Google Scholar]
  10. Fowler P. W.; Steiner E. Ring Currents and Aromaticity of Monocyclic π-Electron Systems C6H6, B3N3H6, B3O3H3, C3N3H3, C5H5-, C7H7+, C3N3F3, C6H3F3, and C6F6. J. Phys. Chem. A 1997, 101, 1409–1413. 10.1021/jp9637946. [DOI] [Google Scholar]
  11. Pelloni S.; Monaco G.; Lazzeretti P.; Zanasi R. Beyond NICS: estimation of the magnetotropicity of inorganic unsaturated planar rings. Phys. Chem. Chem. Phys. 2011, 13, 20666–20672. 10.1039/c1cp21952a. [DOI] [PubMed] [Google Scholar]
  12. Steinmann S. N.; Jana D. F.; Wu J. I.-C.; Schleyer P. R.; Mo Y.; Corminboeuf C. Direct Assessment of Electron Delocalization Using NMR Chemical Shifts. Angew. Chem., Int. Ed. 2009, 48, 9828–9833. 10.1002/anie.200905390. [DOI] [PubMed] [Google Scholar]
  13. Baranac-Stojanović M. New insight into the anisotropic effects in solution-state NMR spectroscopy. RSC Adv. 2014, 4, 308–321. 10.1039/C3RA45512B. [DOI] [Google Scholar]
  14. Charistos N. D.; Papadopoulos A. G.; Sigalas M. P. Interpretation of electron delocalization in benzene, cyclobutadiene, and borazine based on visualization of individual molecular orbital contributions to the induced magnetic field. J. Phys. Chem. A 2014, 118, 1113–1122. 10.1021/jp411410r. [DOI] [PubMed] [Google Scholar]
  15. Phukan A. K.; Guha A. K.; Silvi B. Is delocalization a prerequisite for stability of ring systems? A case study of some inorganic rings. Dalton Trans. 2010, 39, 4126–4137. 10.1039/b920161k. [DOI] [PubMed] [Google Scholar]
  16. Tsipis A. C.; Depastas I. G.; Tsipis C. A. Diagnosis of the σ-, π-and (σ+ π)-Aromaticity by the Shape of the NICSzz-Scan Curves and Symmetry-Based Selection Rules. Symmetry 2010, 2, 284–319. 10.3390/sym2010284. [DOI] [Google Scholar]
  17. Müller M.; Maichle-Mössmer C.; Sirsch P.; Bettinger H. F. Is There B.-N. Bond-Length Alternation in 1, 2: 3, 4: 5, 6-Tris (biphenylylene) borazines?. ChemPlusChem 2013, 78, 988–994. 10.1002/cplu.201300110. [DOI] [PubMed] [Google Scholar]
  18. Fowler P. W.; Bean D. E.; Seed M. Investigating the Threshold of Aromaticity and Antiaromaticity by Variation of Nuclear Charge. J. Phys. Chem. A 2010, 114, 10742–10749. 10.1021/jp106697j. [DOI] [PubMed] [Google Scholar]
  19. Monaco G.; Zanasi R. The making of ring currents. Phys. Chem. Chem. Phys. 2016, 18, 11800–11812. 10.1039/C5CP07250F. [DOI] [PubMed] [Google Scholar]
  20. Srivastava A. K.; Misra N. Introducing “carborazine” as a novel heterocyclic aromatic species. New J. Chem. 2015, 39, 2483–2488. 10.1039/C4NJ02089H. [DOI] [Google Scholar]
  21. Anstöter C. S.; Gibson C. M.; Fowler P. W. Modelling aromatisation of (BN)nH2n azabora-annulenes. Phys. Chem. Chem. Phys. 2020, 22, 15919–15925. 10.1039/D0CP02284E. [DOI] [PubMed] [Google Scholar]
  22. Kalemos A. The nature of the chemical bond in borazine (B3N3H6), boroxine (B3O3H3), carborazine (B2N2C2H6), and related species. Int. J. Quantum Chem 2018, 118, e25650 10.1002/qua.25650. [DOI] [Google Scholar]
  23. Bleeke J. R. Metallabenzenes. Chem. Rev. 2001, 101, 1205–1228. 10.1021/cr990337n. [DOI] [PubMed] [Google Scholar]
  24. Fernández I.; Frenking G.; Merino G. Aromaticity of metallabenzenes and related compounds. Chem. Soc. Rev. 2015, 44, 6452–6463. 10.1039/C5CS00004A. [DOI] [PubMed] [Google Scholar]
  25. Hoffmann R. Building Bridges Between Inorganic and Organic Chemistry (Nobel Lecture). Angew. Chem., Int. Ed. 1982, 21, 711–724. 10.1002/anie.198207113. [DOI] [Google Scholar]
  26. Thorn D. L.; Hoffmann R. Delocalization in metallocycles. Nouv. J. Chim. 1979, 3, 39–45. [Google Scholar]
  27. Elliott G. P.; Roper W. R.; Waters J. M. Metallacyclohexatrienes or ‘metallabenzenes.’ Synthesis of osmabenzene derivatives and X-ray crystal structure of [Os(CSCHCHCHCH)(CO)(PPh3)2]. J. Chem. Soc., Chem. Commun. 1982, 14, 811–813. 10.1039/C39820000811. [DOI] [Google Scholar]
  28. Koch H.-J.; Roesky H. W.; Bohra R.; Noltemeyer M.; Schmidt H.-G. Cyclometallaborazines: Borazines with Metal Atoms as Ring Building Blocks: PhB(MeN)3(TiCl2)2. Angew. Chem., Int. Ed. 1992, 31, 598–599. 10.1002/anie.199205981. [DOI] [Google Scholar]
  29. Koch H.-J.; Roesky H. W.; Besser S.; Herbst-Irmer R. Synthese und Struktur des ersten Tellur-haltigen Borazin-Derivats und einer Tellur-haltigen Bor – Stickstoff-Spiro-Verbindung. Chem. Ber. 1993, 126, 571–574. 10.1002/cber.19931260304. [DOI] [Google Scholar]
  30. Less R. J.; Hanf S.; García-Rodríguez R.; Bond A. D.; Wright D. S. A [HN(BH=NH)2]2– Dianion, Isoelectronic with a β-Diketiminate. Organometallics 2018, 37, 628–631. 10.1021/acs.organomet.7b00436. [DOI] [Google Scholar]
  31. Zubarev D. Y.; Boldyrev A. I. Developing paradigms of chemical bonding: adaptive natural density partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. 10.1039/b804083d. [DOI] [PubMed] [Google Scholar]
  32. Mitoraj M. P.; Michalak A.; Ziegler T. On the Nature of the Agostic Bond between Metal Centers and β-Hydrogen Atoms in Alkyl Complexes. An Analysis Based on the Extended Transition State Method and the Natural Orbitals for Chemical Valence Scheme (ETS-NOCV). Organometallics 2009, 28, 3727–3733. 10.1021/om900203m. [DOI] [Google Scholar]
  33. Szczepanik D. W.; Żak E.; Dyduch K.; Mrozek J. Electron delocalization index based on bond order orbitals. Chem. Phys. Lett. 2014, 593, 154–159. 10.1016/j.cplett.2014.01.006. [DOI] [Google Scholar]
  34. Szczepanik D. W.; Andrzejak M.; Dyduch K.; Żak E.; Makowski M.; Mazur G.; Mrozek J. A uniform approach to the description of multicenter bonding. Phys. Chem. Chem. Phys. 2014, 16, 20514–20523. 10.1039/C4CP02932A. [DOI] [PubMed] [Google Scholar]
  35. Mauksch M.; Tsogoeva S. B. Strict Correlation of HOMO Topology and Magnetic Aromaticity Indices in d-Block Metalloaromatics. Chem. – Eur. J. 2018, 24, 10059–10063. 10.1002/chem.201802270. [DOI] [PubMed] [Google Scholar]
  36. Szczepanik D. W.; Andrzejak M.; Dominikowska J.; Pawełek B.; Krygowski T. M.; Szatylowicz H.; Solà M. The electron density of delocalized bonds (EDDB) applied for quantifying aromaticity. Phys. Chem. Chem. Phys. 2017, 19, 28970–28981. 10.1039/C7CP06114E. [DOI] [PubMed] [Google Scholar]
  37. Elvidge J.; Jackman L. 181. Studies of aromaticity by nuclear magnetic resonance spectroscopy. Part I. 2-Pyridones and related systems. J. Chem. Soc. 1961, 859–866. 10.1039/jr9610000859. [DOI] [Google Scholar]
  38. Sundholm D.; Fliegl H.; Berger R. J. F. Calculations of magnetically induced current densities: theory and applications. WIREs Comput. Mol. Sci. 2016, 6, 639–678. 10.1002/wcms.1270. [DOI] [Google Scholar]
  39. Islas R.; Heine T.; Merino G. The Induced Magnetic Field. Acc. Chem. Res. 2012, 45, 215–228. 10.1021/ar200117a. [DOI] [PubMed] [Google Scholar]
  40. Schleyer P. vR.; Maerker C.; Dransfeld A.; Jiao H. J.; Hommes N. Nucleus-independent chemical shifts: A simple and efficient aromaticity probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. 10.1021/ja960582d. [DOI] [PubMed] [Google Scholar]
  41. Heine T.; Islas R.; Merino G. σ and π contributions to the induced magnetic field: Indicators for the mobility of electrons in molecules. J. Comput. Chem. 2007, 28, 302–309. 10.1002/jcc.20548. [DOI] [PubMed] [Google Scholar]
  42. Zhao Y.; Truhlar D. G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101 10.1063/1.2370993. [DOI] [PubMed] [Google Scholar]
  43. Van Lenthe E.; Baerends E. J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. 10.1002/jcc.10255. [DOI] [PubMed] [Google Scholar]
  44. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  45. te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Fonseca Guerra C.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. 10.1002/jcc.1056. [DOI] [Google Scholar]
  46. Kohn W.; Sham L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  47. van Lenthe E.; Snijders J. G.; Baerends E. J. The zero-order regular approximation for relativistic effects: The effect of spin–orbit coupling in closed shell molecules. J. Chem. Phys. 1996, 105, 6505–6516. 10.1063/1.472460. [DOI] [Google Scholar]
  48. Michalak A.; DeKock R. L.; Ziegler T. Bond Multiplicity in Transition-Metal Complexes: Applications of Two-Electron Valence Indices. J. Phys. Chem. A 2008, 112, 7256–7263. 10.1021/jp800139g. [DOI] [PubMed] [Google Scholar]
  49. Mitoraj M. P.; Michalak A.; Ziegler T. A Combined Charge and Energy Decomposition Scheme for Bond Analysis. J. Chem. Theory Comput. 2009, 5, 962–975. 10.1021/ct800503d. [DOI] [PubMed] [Google Scholar]
  50. Geudtner G.; Calaminici P.; Carmona-Espíndola J.; del Campo J. M.; Domínguez-Soria V. D.; Moreno R. F.; Gamboa G. U.; Goursot A.; Köster A. M.; Reveles J. U.; Mineva T.; Vásquez-Pérez J. M.; Vela A.; Zúñinga-Gutierrez B.; Salahub D. R. deMon2k. WIREs Comput. Mol. Sci. 2012, 2, 548–555. 10.1002/wcms.98. [DOI] [Google Scholar]
  51. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  52. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)]. Phys. Rev. Lett. 1997, 78, 1396 10.1103/PhysRevLett.78.1396. [DOI] [PubMed] [Google Scholar]
  53. Canal Neto A.; Jorge F. E. All-electron double zeta basis sets for the most fifth-row atoms: Application in DFT spectroscopic constant calculations. Chem. Phys. Lett. 2013, 582, 158–162. 10.1016/j.cplett.2013.07.045. [DOI] [Google Scholar]
  54. Calaminici P.; Janetzko F.; Köster A. M.; Mejia-Olvera R.; Zuniga-Gutierrez B. Density functional theory optimized basis sets for gradient corrected functionals: 3d transition metal systems. J. Chem. Phys. 2007, 126, 044108 10.1063/1.2431643. [DOI] [PubMed] [Google Scholar]
  55. Vásquez-Espinal A.; Poater J.; Solà M.; Tiznado W.; Islas R. Testing the effectiveness of the isoelectronic substitution principle through the transformation of aromatic osmathiophene derivatives into their inorganic analogues. New J. Chem. 2017, 41, 1168–1178. 10.1039/C6NJ02972H. [DOI] [Google Scholar]
  56. Islas R.; Poater J.; Solà M. Analysis of the Aromaticity of Five-Membered Heterometallacycles Containing Os, Ru, Rh, and Ir. Organometallics 2014, 33, 1762–1773. 10.1021/om500119c. [DOI] [Google Scholar]
  57. Arias-Olivares D.; Becerra-Buitrago A.; García-Sánchez L. C.; Islas R. In Silico Analysis of the Electronic Delocalization in Some Double Fused-Ring Metallabenzenes. ACS Omega 2021, 6, 9887–9897. 10.1021/acsomega.1c00632. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Arias-Olivares D.; Becerra-Buitrago A.; García-Sánchez L. C.; Islas R. Correction to “In Silico Analysis of the Electronic Delocalization in Some Double Fused-Ring Metallabenzenes”. ACS Omega 2021, 6, 16251–16252. 10.1021/acsomega.1c02718. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; J A Montgomery J.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Keith T.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas O.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 09, revision D.01, Gaussian Inc.: Walllingford, CT, 2013.
  60. Adamo C.; Barone V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. 10.1063/1.478522. [DOI] [Google Scholar]
  61. Hay P. J.; Wadt W. R. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J. Chem. Phys. 1985, 82, 270–283. 10.1063/1.448799. [DOI] [Google Scholar]
  62. Tkachenko N. V.; Boldyrev A. I. Chemical bonding analysis of excited states using the adaptive natural density partitioning method. Phys. Chem. Chem. Phys. 2019, 21, 9590–9596. 10.1039/C9CP00379G. [DOI] [PubMed] [Google Scholar]
  63. Saue T.; Jensen H. A. Linear response at the 4-component relativistic level: Application to the frequency-dependent dipole polarizabilities of the coinage metal dimers. J. Chem. Phys. 2003, 118, 522–536. 10.1063/1.1522407. [DOI] [Google Scholar]
  64. PyNGL, Developed at the National Center for Atmospheric Research, 2019. http://www.pyngl.ucar.edu/.
  65. Visscher L.; Jensen H. J. A.; Bast R.; Saue T.. et al. DIRAC, a relativistic ab initio electronic structure program, Release DIRAC17, 2017. http://www.diracprogram.org.
  66. Becke A. D.; Edgecombe K. E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. 10.1063/1.458517. [DOI] [Google Scholar]
  67. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  68. Vosko S. H.; Wilk L.; Nusair M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis. Can. J. Phys. 1980, 58, 1200–1211. 10.1139/p80-159. [DOI] [Google Scholar]
  69. Bast R.; Jusélius J.; Saue T. 4-Component relativistic calculation of the magnetically induced current density in the group 15 heteroaromatic compounds. Chem. Phys. 2009, 356, 187–194. 10.1016/j.chemphys.2008.10.040. [DOI] [Google Scholar]
  70. Dunning T. H. Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  71. Pritchard B. P.; Altarawy D.; Didier B.; Gibson T. D.; Windus T. L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. 10.1021/acs.jcim.9b00725. [DOI] [PubMed] [Google Scholar]
  72. Dyall K. G.; Gomes A. S. Revised relativistic basis sets for the 5d elements Hf–Hg. Theor. Chem. Acc. 2010, 125, 97. 10.1007/s00214-009-0717-7. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao1c02257_si_001.pdf (2.4MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES