The Inflation Response of the Human Lamina Cribrosa and Sclera: Analysis of Deformation and Interaction

Abstract

This study investigated the inflation response of the lamina cribrosa (LC) and adjacent peripapillary sclera (PPS) in post-mortem human eyes with no history of glaucoma. The posterior sclera of 13 human eyes from 7 donors was subjected to controlled pressurization between 5-45 mmHg. A laser-scanning microscope (LSM) was used to image the second harmonic generation (SHG) response of collagen and the two-photon fluorescent (TPF) response of elastin within the volume of the LC and PPS at each pressure. Image volumes were analyzed using digital volume correlation (DVC) to calculate the three-dimensional (3D) deformation field between pressures. The LC exhibited larger radial strain, E_rr, and maximum principal strain, E_max, (p < 0.0001) and greater posterior displacement (p = 0.0007) compared to the PPS between 5-45 mmHg, but had similar average circumferential strain, E_θθ, and maximum shear strain, Γ_max. The E_max and Γ_max were highest near the LC-PPS interface and lowest in the nasal quadrant of both tissues. Larger LC area was associated with smaller E_max in the peripheral LC and larger E_max in the central LC (p ≤ 0.01). The E_max, Γ_max, and E_θθ in the inner PPS increased with increasing strain in adjacent LC regions (p ≤ 0.001). Smaller strains in the PPS were associated with a larger difference in the posterior displacement between the PPS and central LC (p < 0.0001 for E_max and E_rr), indicating that a stiffer pressure-strain response of the PPS is associated with greater posterior bowing of the LC.

1. Introduction

The optic nerve head (ONH) is a structure in the back of the eye that supports the axons of the retinal ganglion cells (RGC) as they exit the eye. The RGC axons in the ONH traverse a connective tissue structure called the lamina cribrosa (LC) [1-4], composed of a stack of cribiform plates [5] containing mostly collagen and elastin [6, 7] that form a beam and pore network structure when viewed en face. Elastin and collagen fibers from the LC beams insert circumferentially into a 1-2 mm wide [8] annular region of the sclera called the peripapillary sclera (PPS) [9]. The LC is thinner [10, 11] and less dense in collagen and elastin than the surrounding PPS [9]. Thus, mechanically the ONH can be considered a composite structure composed of an inner more compliant shell supported by a stiffer outer ring. The mismatch in material stiffness causes the hoop stresses induced by the intraocular pressure (IOP) to concentrate in the PPS. To minimize changes to the scleral canal opening from IOP fluctuations, the scleral thickness is maximum at the PPS and the PPS is mechanically reinforced by a highly aligned, circumferential arrangement of collagen and elastin fibers [8, 9].

The biomechanical behavior of the ONH is widely considered to play an important role in RGC dysfunction and death in glaucoma [12-16]. Excessive strains in the ONH induced by changes in either intraocular or intracranial pressure may alter the nutritional capability of capillaries supporting ONH axons. Larger tensile strains within the LC, PPS, and their junction may promote stretch activation of resident astrocytes and lamina cribrocytes. This may alter the physiological support for the axons passing through the LC and lead to detrimental remodeling of the ONH connective tissues. Glaucoma is characterized by significant ONH remodeling, in which the LC progressively thins, develops a more bowed shape, and assumes a more posterior position relative to the PPS [17-22].

Experimental studies have investigated the pressure-induced deformation response of the ONH of post-mortem human [23-25], porcine [26, 27], and mouse [28, 29] eyes. These studies have generally reported a heterogeneous strain field within the LC, with regions of large strains exceeding 10%. We developed an ex vivo inflation test method that used second harmonic generation (SHG) imaging and digital volume correlation (DVC) to measure the 3D deformational field resulting from an increase in IOP with micrometer-scale resolution [24]. We found that the in-plane strains were larger in the peripheral than central region of the LC. Moreover, both the largest in-plane tensile and shear strains were concentrated at the boundary between the LC and PPS. Strains were also consistently higher in the inferior, superior, and temporal regions compared to the nasal region. The larger strains in the peripheral LC were associated with a larger pore area fraction and lower connectivity [30]. These experimental findings agree with recent specimen-specific modeling studies of ovine eyes by Voorhees et al. [31], which predicted strain heterogeneity with higher stretch of LC pores near the PPS interface. In this model, material properties influenced the level of strain within the ONH, but patterns of strain variation were primarily determined by LC microstructure and pore geometry. The higher strains in the peripheral LC may also be caused by the mismatch in the curvature, thickness, collagen/elastin fiber orientation, and mismatch in material properties of the LC and PPS. Jan et al. [32] studied the variation in collagen fiber crimp within the LC and PPS with IOP in ovine eyes and found that collagen fiber crimp decreased with IOP and that fiber waviness and recruitment fraction was higher in the PPS compared to the LC as IOP increased. These findings suggest a significant difference in the nonlinear pressure-strain response of the two tissues.

Computational modeling studies have demonstrated that the ONH deformation and stress states are strongly influenced by the intraocular pressure (IOP) and mechanical properties of the LC and surrounding sclera [33-37]. Sigal et al. [38, 39] showed that the stiffness and thickness of the LC and PPS had the largest influence on IOP-induced deformation response. The IOP-induced deflection of the LC is most sensitive to the elastic modulus and thickness of the LC [40] and that this displacement can be anterior or posterior relative to the surrounding PPS. Scleral canal expansion was most sensitive to the elastic modulus and thickness of the sclera [36]. Coudrillier et al. [27] investigated the pressure-induced strain response of the sclera using stereoscopic imaging and 3D-DIC [41], and of the LC using micro-CT imaging and DVC [26] in two different groups of porcine eyes. They observed that stiffening the sclera by collagen cross-linking using local application of glutaraldehyde caused strains in the sclera and LC to decrease, with tensile strains decreasing more in the LC than in the sclera. This shows that the stiffness of the sclera significantly affects deformation of the ONH; however, the authors did not measure strains in both the sclera and LC of the same eye.

Previous inflation tests of the sclera using 3D digital image correlation (DIC) did not have sufficient resolution to determine strains in the ONH [35, 41, 42]. Pavlatos et al. [43, 44] developed an ultrasound scanning method with 3D ultrasound speckle tracking simultaneously to measure the strains in the PPS and LC of porcine and human eyes; however, the ultrasound imaging method does not have sufficient resolution to measure regional variation in the strain response at the level of LC structural features. In this study, we present a method to measure simultaneously the 3D deformation in the LC and PPS volume, which was implemented in 13 post mortem, normal human eyes under controlled pressurization with micrometer resolution. Regional strain variation in the LC and PPS was investigated and strains were analyzed for differences and associations with age, LC area, LC strain magnitude, and LC posterior displacement relative to the PPS.

2. Methods

2.1. Specimen preparation and inflation test

Thirteen human eyes from 4 male and 3 female donors between the ages of 61-100 years (mean 74±12 years) with no history of glaucoma were obtained from the National Disease Research Interchange and Eversight Eye Bank ( Table 1). Donor eyes were shipped on ice wrapped in wet gauze within 24-48 hours post-mortem.

Table 1:

The demographics of the human donor eyes used for inflation testing.

Eye ID	Sex	Age (yr)	Race	Right/Left Eye
Specimen 1*	Female	90+	Caucasian	Right
Specimen 2*	Female	90+	Caucasian	Left
Specimen 3*	Female	64	Caucasian	Right
Specimen 4*	Female	64	Caucasian	Left
Specimen 5*	Male	79	Caucasian	Right
Specimen 6*	Male	79	Caucasian	Left
Specimen 7*	Male	61	Caucasian	Right
Specimen 8*	Male	61	Caucasian	Left
Specimen 9*	Male	61	African American	Right
Specimen 10*	Male	61	African American	Left
Specimen 11	Male	76	Caucasian	Right
Specimen 12*	Female	83	Caucasian	Right

^*Indicates a left and right eye pair.

Posterior scleral specimens were prepared and imaged within 72 hours post-mortem at 18°C and at ocular pressures of 5, 10, and 45 mmHg. Images taken at 5 mmHg represented the baseline (unloaded) ONH state, as this was approximately the lowest pressure at which the average eye would hold its shape based [24]. The optic nerve was cut flush with the sclera to expose the LC (Fig. 1a), and the cornea, anterior sclera, choroid, and retina were removed. The posterior scleral cup was glued to a polycarbonate ring (Fig. 1b), which was mounted on a custom inflation holder (Fig. 1c). Scleral specimens were imaged following a protocol similar to our previous studies [24, 25], but with several changes. The posterior surface of the LC for each specimen was aligned with a 10x Apochromat, 0.45 NA, water-immersion, inverted imaging objective for a Zeiss, laser-scanning microscope (LSM 710 NLO, Oberkochen, Germany) used in 2P imaging mode (Fig. 1d). Specimens were imaged using a coherent Chameleon Ultra II laser with an excitation wavelength of 780 nm and a laser power of 12-17%. The SHG of collagen (Fig. 1e) was collected using a bandpass filter of 390-410 nm, and the two photon fluorescence (TPF) of elastin (Fig. 1f) was collected using another bandpass filter of 470-550 nm . In SHG, specimens are imaged with two-photon excitation near 800 nm. At this wavelength, collagen will absorb the two photons and emit one higher energy photon at half the wavelength, allowing for imaging of the structure of collagen in 3D [45]. Elastin fibers will also autofluoresce under SHG excitation in the range of 470-550 nm.

Figure 1:

Experimental setup for the inflation test of the human LC and PPS of the same eye showing the a) ONH cut flush to the sclera; b) ring-mounted posterior scleral cup; c) custom inflation holder; d) Zeiss LSM 710; e) the maximum intensity projection of the SHG image volume and f) of the TPF image volume for specimen Specimen 2; and g) the imaging setup with components labeled.

The gain for the TPF and the SHG channels was tuned separately (Zeiss 2015, Oberkochen, Germany) to balance the brightness of the images within the LC from SHG and TPF and prevent the acquisition of oversaturated pixels. For the TPF channel, we used a master gain of 500-570, a digital gain of 1.0, and a digital offset of 4. For the SHG channel, we used a master gain of 630-700, a digital gain of 1.0-1.1, and a digital offset of 8. The TPF signal was also found to be more sensitive to the presence of surface debris from the removal of the post-LC myelinated optic nerve. We found that tissue debris could appear in the TPF images around the LC pores and at the cut LC surface after the first pressurization to 45 mmHg. To solve this issue we first pressurized the specimen to 45 mmHg and equilibrated for 10 minutes. The surface of the LC and PPS was then cleaned of any debris by rinsing the sample surface with PBS before the pressure was lowered back to the baseline pressure of the experiment. This resulted in a more stable TPF signal over the course of the inflation experiment.

The pressure was set to 5, 10, and 45 mmHg for each specimen using an external water column . Each sample was equilibrated for at least 25 minutes at each pressure before imaging , and imaging speed was maximized so as to minimize the effects of creep. For 4 specimens we imaged at additional intermediate pressures of 7.5 mmHg and 25 mmHg to characterize the nonlinear pressure-strain response. The X and Y directions within each image were aligned with the nasal-temporal (N-T) and inferior-superior (I-S) axes of the LC respectively, and the out-of-plane (anterior-posterior) direction was designated as Z (Fig. 1f). Two duplicate Z-stacks containing 2x2 tiled images of 512x512 pixels, with a 15% overlap were acquired at each pressure, starting at the lowest visible depth in the LC and PPS with images taken sequentially every 3 or 5 μm up to the posterior LC and PPS surface. 2x2 tiled images were required because the 10x lens did not have a wide enough field of view to image the entire LC. We were able to image 200-300 μm deep into the LC from the cut surface and 25 μm deep into the PPS, and total image depth varied between 250-400 μm for all specimens. The image acquisition time varied between 4-6 minutes for each 2x2 tiled Z-stack depending on the imaging depth. In some early specimens imaged with 3 μm Z-spacing, the imaging time exceeded 5 minutes, which could result in baseline positional errors ≥ 1 μm due to creep (Supplemental Table S2). We increased the Z-spacing to 5 μm and decreased the zoom factor to 0.6x for later specimens to reduce the effects of creep and to image a larger PPS region. This change in Z-spacing was found to result in smaller displacement and strain errors in the pilot eye Specimen 8 (Supplemental Sec. S2.4). The X and Y resolution within the images was either 2.55 or 2.77 μm/pixel for a zoom factor of 0.65x or 0.60x respectively (Supplemental Table S1).

2.2. Image post-processing

The SHG and TPF Z-stacks were imported into FIJI [46], and the image channels were split into two files containing the TPF and SHG signals. The SHG and TPF Z-stacks were post-processed by deconvolution using a theoretical point spread function using the iterative deconvolution function in Huygens Essentials (SVI, Hilversum, NL), a background value of 10 and a signal to noise ratio of 3. This step significantly reduced the image noise, blur, and average background intensity from the images. The contrast of the SHG and TPF image volumes were enhanced using piecewise contrast limited adaptive histogram equalization (CLAHE) within FIJI [46].

2.3. Division of the LC and PPS

The maximum intensity projection of the SHG image volume was created in FIJI [46] and used to separate the LC and PPS. The sclera appeared in the maximum intensity projection as an oversaturated region that was significantly brighter compared to the LC. The boundary between the LC and PPS was defined by manually picking points on the maximum intensity projection using FIJI (Fig. 1e). An ellipse was fit to the points using the Matlab function fit_ellipse (Ohad Gal, 2003), and used to segment the displacement field corresponding to the LC from the PPS. The LC area was approximated as the area of the ellipse, A = πab. A second ellipse 200 μm larger in radius was used to segment the inner PPS from the rest of the PPS. The center of the central retinal artery and vein (CRAV) was manually marked and a circle of radius r = 200 μm was used to segment the central LC from the CRAV, which was excluded from the regional strain analyses because of the CRAV’s stiffer strain response and poorer correlation. A circle of r = 200 μm was sufficient to fully encircle the visible CRAV for all specimens [24]. The central and peripheral regions of the LC were divided by calculating the mid-radial distance between the points marked on the LC opening and the CRAV circle. The central LC (1), peripheral LC (2), and inner PPS (3) were further divided into the superior (S), inferior (I), temporal (T) and nasal (N) quadrants using 45° and 135° bisectors centered on the CRAV. The inner PPS and peripheral LC quadrants were also divided using 0° and 90° bisectors centered on the CRAV. These divisions resulted in 8 regions in the PPS, 8 regions in the peripheral LC, and 4 regions in the central LC within which displacement and strain results were averaged and compared (Fig. 2).

Figure 2:

The segmentation of the central LC (1), peripheral LC (2), and PPS (3) and circumferential divisions within the LC and PPS for specimen Specimen 12.

2.4. Digital volume correlation

The Fast Fourier DVC (FIDVC) algorithm developed by Bar Kochba et al. [47] was used to analyze the SHG and TPF volumes in order to calculate the 3D displacement components U_X, U_Y, and U_Z between the reference pressure of 5 mmHg and the test pressures. In DVC, the images are divided into subvolumes surrounding points defined in the reference image at baseline pressure. These are compared to subvolumes at subsequent pressures for displacement tracking. FIDVC refines the resolution of the displacement field through successive iterations where the subvolume size is reduced and the spacing between displacement calculations is halved. This protocol used a starting subvolume size of 128x128x64 pixels and a coarse calculation spacing of 32x32x16 pixels, which was refined through 4 iterations to a final subvolume size of 64x64x16 pixels and calculation spacing of 4x4x2 pixels [24]. Volumes were correlated incrementally between each pressure step to avoid decorrelation errors from large deformations. The cumulative displacement fields for inflation from 5-25 and 5-45 mmHg were obtained from the sum of the incremental displacement fields from 5-10 mmHg and 10-25 mmHg and from 5-10 and 10-45 mmHg. FIDVC correlation and strain calculation was conducted using a 2013 Macbook Pro (16 GB RAM, 2.8 GHz Intel Core i7 processor). Correlation took 7 hours and displacement post-processing and strain calculation took 1 hour per pressure increment. The cross-correlation coefficients and components of the displacement field in microns were exported for subsequent analysis of DVC error and uncertainty. Volumes were correlated incrementally between each pressure step to avoid decorrelation errors from large deformations.

2.5. Displacement post-processing

The baseline positional error, which includes the effects of creep during image acquisition, was estimated for all specimens by correlating the 2 duplicate image volumes acquired at 5 mmHg using DVC as described previously [24]. The DVC correlation errors were estimated by numerically applying a rigid body displacement and a uniform triaxial strain state that was 2% tension in X and Y and 5% compression in Z, applying DVC to calculate the displacement field, and calculating the difference between the numerically applied displacements and the DVC displacements at each point to define a displacement error field. Likewise, the strain error field was calculated as the difference between the numerically applied strains and the DVC displacements at each point. The baseline and DVC correlation displacement and strain errors were summarized using 4 metrics: bias (average of the error field), uncertainty (standard deviation of the error field), average absolute error (average of the absolute value of the error field), and absolute uncertainty (standard deviation of the absolute value of the error field), as shown in Supplemental Sections S1.3-S1.4. Error analysis was performed separately for the SHG and TPF image volumes and averaged within the LC and PPS (Supplemental Sec. S2.2).

We developed the following sequence of filters to remove regions with poor DVC correlation, high displacement errors, and displacement outliers. The specifications of the displacement filters, such as the threshold and subset size, and the settings used for image post-processing (Section 2.2), were selected from a study that varied the settings one by one for a specimen with poor contrast to determine their effects on the error metrics. The settings selected reduced the average bias in the X and Y displacement error to less than 0.32 pixel (< 0.8 μm) and the average absolute X and Y displacement errors to less than 0.4 pixel (< 0.9 μm).

We first applied a DVC correlation coefficient filter, which removed regions with a DVC correlation coefficient ≤ 0.001 within the LC and ≤ 0.01 within the PPS. Regions with cross-correlation coefficients below these values corresponded to dark or oversaturated areas with low contrast. We were only able to image the more superficial 25 μm of the PPS, as deeper features appeared out of focus and shadowed by the overlying tissue. The shadowed areas had lower contrast; thus, we used a larger DVC correlation coefficient threshold of 0.01 for the PPS to remove shadowed areas. The displacements were masked by the DVC displacement error fields to remove points with an absolute error exceeding 2 μm (Supplemental Sec. S1.4). Displacement calculations within 40 pixels (110 μm) of the edges of the image volumes in the X − Y plane were also removed because pressurization to 45 mmHg caused these points to displace outside of the imaging region. We further removed displacement outliers that deviated by more than 10 μm from the average displacement of the surrounding 15x15 grid point (77x77 μm) neighborhood (Supplemental Sec. S1.2). A 3D Gaussian filter was applied to smooth the remaining displacements and to interpolate within small holes in the displacement field within the X − Y plane (Supplemental Sec. S1.2). The effects of the post-processing steps are illustrated for Specimen 10 at 3 Z depths in Supplemental Section S2.3.

The visible surface of the PPS region appeared planar (flat) in the TPF volumes because of specimen preparation, which progressively shaved the ONH with a scalpel to expose the connective tissue beams of the LC as described in Midgett et al. [24]. The imaged depth of 25 μm was also too small to accurately calculate the displacement gradient in Z. Thus, the displacement components, U_X, U_Y, and U_Z of the PPS regions were averaged through Z and smoothed using a 2D Gaussian filter prior to strain calculation (Supplemental Sec. S1.2). DVC analysis within the LC was fully 3D with accurate displacement calculations through 200 μm of depth, but DVC within the PPS was similar to 3D-DIC, with accurate 3D displacement calculations only on the surface of the PPS.

2.6. Strain calculation

The components of the Green-Lagrange strain tensor within the LC were calculated from the displacement gradients of the smoothed displacement field (Supplemental Sec. S1.1). The displacement components U_X, U_Y, and U_Z were smoothed globally in the LC; however, a local smoothing scheme was used for the PPS surface because it was simpler to apply to the irregular shape. For the LC, the displacement components were fit to a 6th-order polynomial in the X and Y directions and a 1st-order polynomial in the Z direction. A linear fit was used in Z because of the poorer resolution and because the dimension in Z was significantly smaller than in X and Y [24]. For the PPS, the Z-averaged displacement components I = X, Y, Z in the 23x23 (250x250 μm), X-Y neighborhood around each grid point were fit to a plane as, U_I = aX + bY + c. The displacement gradients in the LC and PPS were evaluated from the smoothed displacement fields at each grid point and used to calculate the Green-Lagrange strain components E_XX, E_YY, and E_XY in the Cartesian coordinate system as,

$$\begin{gathered} E_{XX}=\frac{\partial U_X}{\partial X}+\frac{1}{2}\left[{\left(\frac{\partial U_X}{\partial X}\right)}^2+{\left(\frac{\partial U_Z}{\partial X}\right)}^2+{\left(\frac{\partial U_Z}{\partial X}\right)}^2\right], \\ {E}_{YY}=\frac{\partial U_Y}{\partial Y}+\frac{1}{2}\left[{\left(\frac{\partial U_X}{\partial Y}\right)}^2+{\left(\frac{\partial U_Y}{\partial Y}\right)}^2+{\left(\frac{\partial U_Z}{\partial Y}\right)}^2\right], \\ {E}_{XY}=\frac{1}{2}\left[\frac{\partial U_X}{\partial Y}+\frac{\partial U_Y}{\partial X}+\frac{\partial U_X}{\partial X}\frac{\partial U_X}{\partial Y}+\frac{\partial U_Y}{\partial X}\frac{\partial U_Y}{\partial Y}+\frac{\partial U_Z}{\partial X}\frac{\partial U_Z}{\partial Y}\right]. \end{gathered}$$ (1)

For the LC, we also calculated the strains E_ZZ, E_XZ, and E_YZ as,

$$\begin{gathered} E_{ZZ}=\frac{\partial U_Z}{\partial Z}+\frac{1}{2}\left[{\left(\frac{\partial U_X}{\partial Z}\right)}^2+{\left(\frac{\partial U_Y}{\partial Z}\right)}^2+{\left(\frac{\partial U_Z}{\partial Z}\right)}^2\right], \\ {E}_{XZ}=\frac{1}{2}\left[\frac{\partial U_X}{\partial Z}+\frac{\partial U_Z}{\partial X}+\frac{\partial U_X}{\partial X}\frac{\partial U_X}{\partial Z}+\frac{\partial U_Y}{\partial X}\frac{\partial U_Y}{\partial Z}+\frac{\partial U_Z}{\partial X}\frac{\partial U_Z}{\partial Z}\right], \\ {E}_{YZ}=\frac{1}{2}\left[\frac{\partial U_Y}{\partial Z}+\frac{\partial U_Z}{\partial Y}+\frac{\partial U_X}{\partial Y}\frac{\partial U_X}{\partial Z}+\frac{\partial U_Y}{\partial Y}\frac{\partial U_Y}{\partial Z}+\frac{\partial U_Z}{\partial Y}\frac{\partial U_Z}{\partial Z}\right]. \end{gathered}$$ (2)

To prevent calculation of strains in areas of poor correlation, displacement gradients were only evaluated at grid points if 80% or more of the points in the surrounding 5x5 neighborhood had displacement correlation.

The in-plane strain components E_XX, E_YY, and E_XY were used to calculate the maximum principal strain E_max and the maximum shear strain Γ_max in the X-Y plane at each grid point in the LC and PPS as,

$$\begin{gathered} E_{max}=\frac{E_{XX}+E_{YY}}{2}+\sqrt{{\left(\frac{E_{XX}-E_{YY}}{2}\right)}^2+{E_{XY}}^2}, \\ {\Gamma }_{max}=\sqrt{{\left(\frac{E_{XX}-E_{YY}}{2}\right)}^2+{E_{XY}}^2}. \end{gathered}$$ (3)

To calculate the strain components in the cylindrical coordinate system, the angular position θ was determined for each grid point by calculating the angle between a line connecting the center of the CRAV region, defined in Sec. 2.3, and the X axis, aligned with the nasal-temporal direction. The radial strain E_rr, the circumferential (hoop) strain E_θθ, and the radial-circumferential shear strain E_rθ were calculated using coordinate transformation as,

$$\begin{gathered} E_{rr}=E_{XX}{\cos }^2\theta +2E_{XY}\cos \theta \sin \theta +E_{YY}{\sin }^2\theta , \\ {E}_{\theta \theta }=E_{XX}{\sin }^2\theta -2E_{XY}\cos \theta \sin \theta +E_{YY}{\cos }^2\theta , \\ {E}_{r\theta }=(E_{YY}-E_{XX})\cos \theta \sin \theta -E_{XY}({\sin }^2\theta -{\cos }^2\theta ), \end{gathered}$$ (4)

2.7. Statistics

The strain measures E_rr, E_θθ, E_max, and Γ_max between 5-10, 10-45, and 5-45 mmHg were averaged both overall and for each region of the LC and PPS. The anterior-posterior displacement U_Z between 5-10, 10-45, and 5-45 mmHg was averaged in the full LC, central LC, peripheral LC, and inner PPS. Linear models were used to test for: 1) differences in U_Z and the strain outcomes in the central LC, peripheral LC, and inner PPS; 2) differences in the strain outcomes between the nasal, superior, temporal, and inferior quadrants of the central LC, peripheral LC, and inner PPS; 3) differences in the relative magnitude of E_θθ and E_rr within the full LC and PPS; 4) associations between the strain outcomes and the donor age, LC area, and difference in U_Z between the central LC and PPS, which indicates bowing; 5) associations between regionally-averaged strains within the peripheral LC and adjacent PPS; and 6) differences in strain between 5-10 mmHg and 10-45 mmHg. In 5 of the eyes (Specimens 1, 4, 7, 11, and 13), one out of eight of the inner PPS regions was mostly dark and failed to correlate (< 40% correlation). These regions were omitted from the analysis, leaving 99 regional strain measures for comparison of strain in the peripheral LC and inner PPS.

For analysis of data with one measurement per eye, all estimates and p-values are from general linear models, which take into account the correlation in outcome between the 2 eyes of a single donor. For all outcomes, the normal distribution function and the link identity function were used with the general linear models. For analysis of data with more than one measurement per eye, all estimates and p-values are from linear mixed models, which take into account the donor as a random effect as well as correlations among the repeated measurements from one eye. The explanatory variables in the models, such as region or quadrant, were fixed effects. Measurements from different regions of the LC and PPS of a single eye were assumed to have a compound symmetry correlation structure, in which the measurements from any 2 of the 20 regions have the same correlation. For both types of models, least squares means were used to estimate mean outcome. The Tukey-Kramer method was used to adjust significance levels for multiple pairwise comparisons. An estimate or a comparison was considered significant if the corresponding p-value from the model was 0.05 or less. All analyses were performed using SAS 9.2 (SAS Institute, Cary, NC).

3. Results

3.1. Displacement and strain errors

3.1.1. Baseline positional and DVC correlation errors

The baseline positional errors and DVC displacement and strain errors are summarized in each eye in Supplemental Section S2.2. Within TPF images of the LC and PPS, the U_X and U_Y bias was less than or equal to 0.70 μm (0.27 pixel), uncertainty was less than or equal to 0.47 μm (0.18 pixel), and average absolute error was less than or equal to 0.81 μm (0.30 pixel). U_Z bias, uncertainty, and absolute average error was less than or equal to 3.6 μm (0.72 pixel), indicating poorer resolution in the Z direction. The E_XX, E_YY, E_XY bias was less than or equal to 0.0006, uncertainty was less than or equal to 0.0023, and average absolute error was less than or equal to 0.0017. Bias estimates average DVC accuracy over a large area, whereas absolute average error estimates average DVC accuracy at a single point. Average absolute displacement and strain errors in the LC and PPS were similar, demonstrating that DVC correlation and strain calculation in each tissue had similar accuracy (Supplemental Tabs. S2-S4). For DVC analysis of the SHG images of the LC, average absolute displacement errors were 2%-9% higher and average absolute strain errors were 20%-27% higher than determined for the TPF volumes of the LC. The higher DVC errors in the SHG images were localized at the LC-PPS boundary, where the DVC correlation was poor because of the poor contrast of the PPS (Table S3, Supplemental Figs. S5-S30).

E_ZZ absolute average error within TPF images of the LC was less than or equal to 0.028, an order of magnitude larger than the in-plane strain errors. E_ZZ could not be calculated in the PPS because the imaged depth of 25 μm was too small. For these reasons, E_ZZ strain was not compared in this study.

3.1.2. Comparison of strain from SHG and TPF image volumes

The difference between the LC strains measured by DVC for inflation from 5 to 45 mmHg from the SHG volumes and the LC strains measured from the TPF volumes was calculated at each grid point for the in-plane strains E_rr, E_θθ, E_rθ, E_max, and Γ_max in all 13 eyes and then averaged in the LC. The average absolute strain differences between the TPF and SHG image volumes were small, varying from 0.00046-0.00133 (Supplemental Table S6), which were less than the average absolute DVC errors measured for the in-plane strain components (Supplemental Table S3). This indicated that the elastin and collagen structures deformed together at the resolution of the DVC correlation. Further analyses in the sections below were performed using the displacements and strains obtained from the TPF image volumes.

3.2. Deformation of the LC and PPS

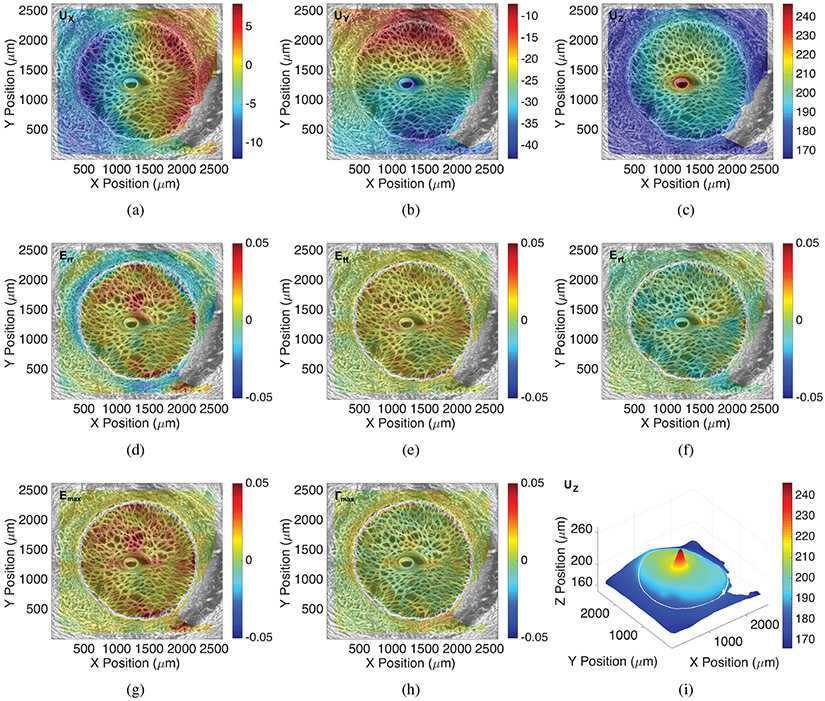
All 13 eyes exhibited significant posterior deflection of the LC and PPS between 190-600 μm for inflation from 5 to 45 mmHg. The posterior deformation varied by up to 50 μm across the LC and PPS surface, resulting in a variety of deformed LC shapes at 45 mmHg (Fig. 3). The LC displaced posteriorly relative to the PPS by 0.6-21.0 μm on average for each specimen (p = 0.0007, n = 13, Table 2). Strains within the LC and PPS increased nonlinearly with pressure showing a J-shaped curve typical of soft, collagenous tissues (Fig. 4). Within the LC, E_rr and E_θθ were predominantly tensile and the average shear strain E_rθ was an order of magnitude smaller than E_rr and E_θθ. Within the PPS, E_θθ was predominantly tensile, but E_rr varied significantly between specimens (Figs. 4-5 and Supplemental Figures S7-S32). Four specimens had an average compressive E_rr in the range of −0.4% to −2.2%, two had E_rr that was less than 0.3%, and seven had an average tensile E_rr in the range of 0.5% to −2.9%. Among the 13 specimens, the average E_rr (1.9 ±0.5%) was larger than E_θθ (1.5 ±0.5%) in the LC (p = 0.05, n = 13, Fig. 8), while E_θθ (1.5 ± 0.5%) was significantly larger than E_rr (0.3 ± 1.3%) in the PPS (p = 0.002, n = 13, Fig. 8) because the PPS region of nearly half of the specimens had an average E_rr that was negative or near zero.

Figure 3:

The U_Z displacement contours (μm) for inflation from 5-45 mmHg, the sum of the pressure increments 5-10 and 10-45 mmHg, within the LC and PPS for specimens a) 1, b) 2, c) 3, d) 4, e) 5, f) 6, g) 7, h) 8 i) 9, j) 10, k) 11, l) 12, and m) 13. The LC displaced more posteriorly than the PPS on average, and the deformed shape varied significantly between different specimens.

Table 2:

Comparison of the posterior displacement U_Z in the LC and PPS for inflation from 5-45 mmHg, the sum of the pressure increments 5-10 and 10-45 mmHg. The posterior displacement was significantly larger in the LC compared to the PPS (p = 0.0007, n = 13).

Outcome, 5-45 mmHg (n = 13)	Average in LC	Average in Inner PPS	Estimated Mean Difference (95% CI)	p-value
UZ (μm)	366.56±105.93	359.21±109.93	7.81 (3.29, 12.33)	0.0007

Figure 4:

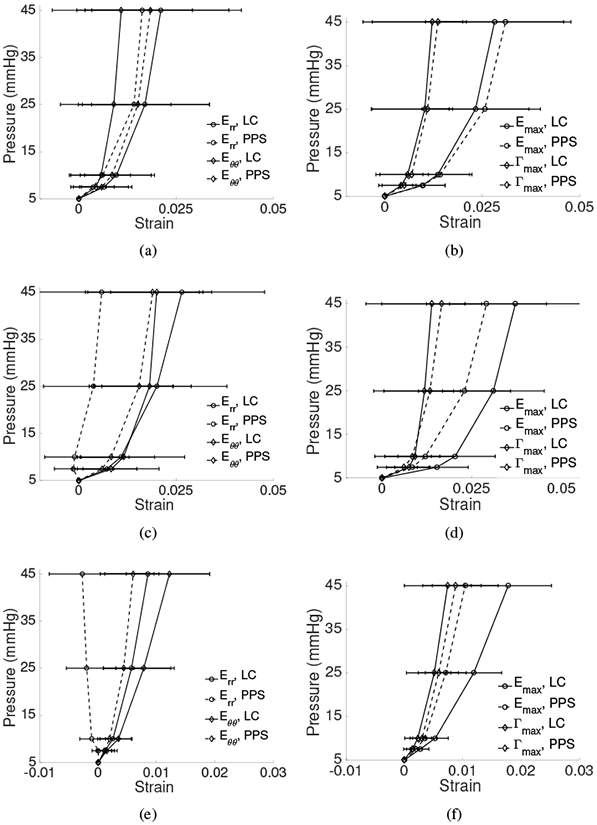
The specimen-averaged pressure-strain response for inflation from 5-45 mmHg, the sum of the pressure increments 5-10 and 10-45 mmHg, in the LC (—) and PPS (- -) for E_rr, E_θθ (left column) and E_max, Γ_max (right column) for: a-b) Specimen 1, c-d) Specimen 2, and e-f) Specimen 13. Deformation within the LC was predominantly tensile with small Γ_max. E_rr was smaller in the PPS compared to the LC and could be (a) tensile, (c) near-zero, or (e) compressive on average. Error bars indicate ±1 standard deviation.

Figure 5:

Colored contour maps for the thickness-averaged full-field displacement (μm) and strain response for inflation from 5-45 mmHg, the sum of the pressure increments 5-10 and 10-45 mmHg, calculated by DVC from the TPF volume for Specimen 11, showing the displacement components a) U_X, b) U_Y, c) U_Z, and strain components d) E_rr, e) E_θθ, f) E_rθ, g) E_max, h) Γ_max. i) The 3D plot of the posterior displacement U_Z displacement showing the deformed shape. This LC exhibited large posterior bowing relative to the PPS. In the LC, E_rr and E_θθ were tensile. For this specimen, E_θθ was tensile and E_rr was compressive in the PPS. The Γ_max was largest at the LC-PPS interface. The maximum intensity projection of the TPF images are overlaid for illustrative purposes.

Figure 8:

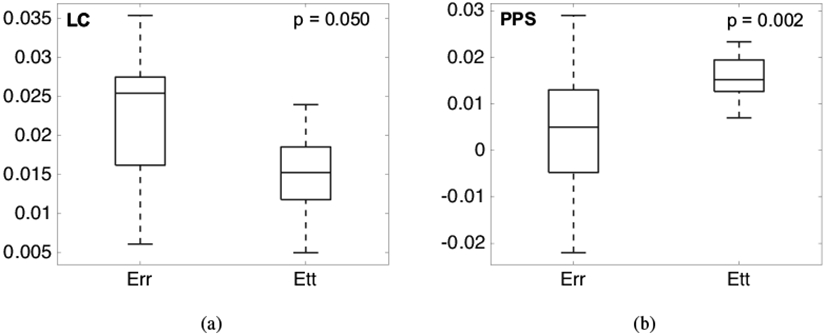
Comparison of average E_rr and E_θθ (n = 13) for inflation from 5-45 mmHg, the sum of the pressure increments 5-10 and 10-45 mmHg: a) within the LC, where E_rr was larger than E_θθ and b) within the PPS, where E_θθ is larger than E_rr.

3.2.1. Effects of age

In the narrow age range (61-100 years) of the 13 specimens, the strain outcomes were not significantly associated with age in the LC or PPS (p ≥ 0.3, Fig. S5, Supplemental Table S7).

3.2.2. Effects of LC area

The average LC strains were not significantly associated with the area of the LC. However, strains in the central LC increased significantly with increasing LC area (E_θθ: p = 0.01, E_max: p = 0.01, n = 13, Fig. 6a, Table S8), while strains in the peripheral LC decreased significantly with increasing LC area (E_rr: p = 0.01, E_max: p = 0.01, n = 13, Fig. 6b, Table S8). Strains in the inner PPS decreased with increasing LC area (E_θθ: p = 0.02, E_max: p = 0.07, n = 13, Fig. 6c, Table S8)

Figure 6:

Variation in the average strains E_rr, E_θθ, E_max, Γ_max for inflation from 5-45 mmHg, the sum of the pressure increments 5-10 and 10-45 mmHg, with LC area in the a) central LC, b) peripheral LC, and c) inner PPS. Increasing LC area was associated with increased central LC strains and decreased peripheral LC and PPS strains.

3.2.3. Regional strain variations in the LC and PPS

The E_max, E_rr, and Γ_max were significantly higher in the peripheral LC regions than in the central LC regions (p ≤ 0.002, Fig. 7a,c-d, Table S9), and E_max and E_rr were significantly higher in the peripheral LC regions than in the inner PPS regions (p < 0.0001, Fig. 7a,c, Tab S9). However, Γ_max was significantly higher (p < 0.0001, Fig. 7d, Tab S9) and E_rr was significantly lower (p = 0.001, Fig. 7a, Tab S9) in the inner PPS compared to the central LC. The circumferential strain E_θθ was similar in all 3 regions (p > 0.5, Fig. 7b, Tab S9).

Figure 7:

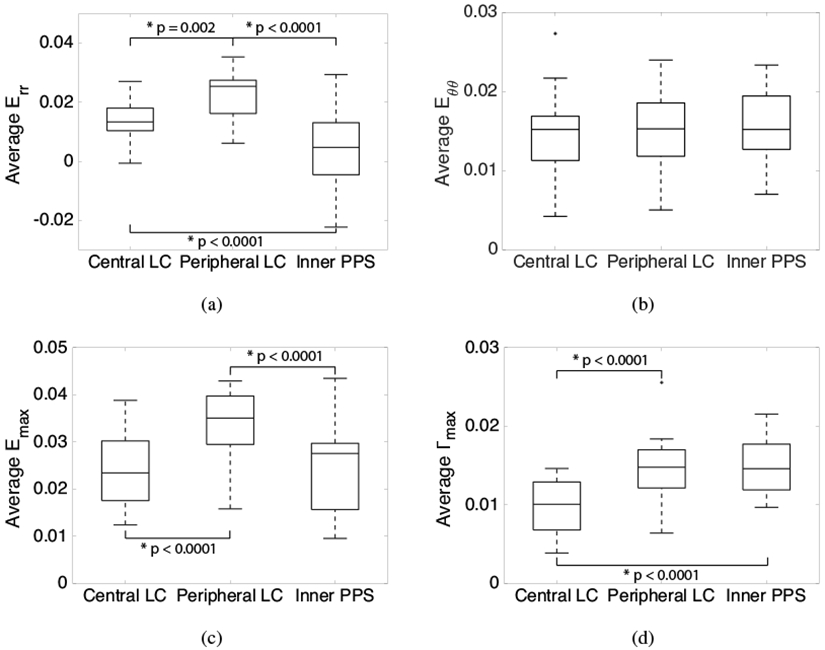
Comparison of average strain in the central LC, peripheral LC, and inner PPS (n = 13) for inflation from 5-45 mmHg, the sum of the pressure increments 5-10 and 10-45 mmHg: a) E_rr is largest in the peripheral LC, b) E_θθ is similar in all 3 regions, c) E_max is largest in the peripheral LC, and d) Γ_max is smallest in the central LC. Box plots were generated using the Matlab function boxplot where the central line within each box represents the median of the group, the top and bottom edges of each box represent the 25th and 75th percentiles respectively, the whisker lengths extend to the most extreme values not considered outliers, and the outliers (+’s) are the values outside of the ±2.7σ range.

The maximum principal strain E_max and maximum shear strain Γ_max varied significantly between the quadrants in the central LC, peripheral LC, and inner PPS (Fig. 9, Table S10). For all 3 regions, E_max was smallest in the nasal quadrant and highest in the inferior or temporal quadrants and Γ_max was smallest in the nasal and superior quadrant and highest in the inferior and temporal quadrants. The full comparison of each strain measure between the quadrants is shown in Supplemental Table S10.

Figure 9:

Comparison of average Γ_max for an inflation from 5-45 mmHg, the sum of the pressure increments 5-10 and 10-45 mmHg, in the superior (S), inferior (I), nasal (N), and temporal (T) quadrants (n = 13): a) Γ_max was smallest in the nasal and superior quadrants within the central LC, b) Γ_max was smallest in the nasal quadrant within the peripheral LC, and c) Γ_max was smallest in the nasal and superior quadrants within the inner PPS.

3.2.4. Relationship between LC and PPS strains

We next compared the average strain in the LC and PPS and examined for associations between strains in the 8 peripheral LC regions (Fig. 2) and in the adjacent 8 inner PPS regions (Fig. 10, Table 4). In general, the strain outcomes in the inner PPS increased with increasing strain in the adjacent LC regions (E_θθ: p < 0.0001, E_max: p = 0.001, Γ_max: p < 0.0001, n = 99, Fig. 10a-b,d). The highest correlation coefficient was calculated for the circumferential strain, E_θθ, which was not statistically significantly different between the inner PPS and peripheral LC. The circumferential strain E_θθ in the inner PPS also increased with increasing radial strain E_rr in the peripheral LC (p < 0.0001, n = 99, Fig. 10e, Table 4). In contrast, E_rr in the inner PPS decreased with increasing E_θθ in the peripheral LC (p = 0.08, n = 99), though the trend was not statistically significant because of large variations in E_rr (Fig. 10f, Table 4).

Figure 10:

Variations in the strain response of the inner PPS with variations in the adjacent, peripheral LC strain response for inflation from 5-45 mmHg, the sum of the pressure increments 5-10 and 10-45 mmHg, showing a) the E_max in the PPS increased with E_max in the LC, b) the Γ_max in the PPS increased with Γ_max in the LC, c) the E_rr in the PPS did not vary significantly with E_rr in the LC, d) the E_θθ in the PPS increased with E_θθ in the LC, e) the E_θθ in the PPS increased significantly with E_rr in the LC, and f) the E_rr in the PPS decreased with E_θθ in the LC.

Table 4:

Associations between the regionally-averaged strains in the peripheral LC and inner PPS (n = 99) for inflation from 5-45 mmHg, the sum of the pressure increments 5-10 and 10-45 mmHg. The E_max, E_θθ, and Γ_max in PPS regions increased with the same strain components in adjacent LC regions (p ≤ 0.001, n = 99). In addition, E_θθ in PPS regions increased significantly with E_rr in adjacent LC regions (p < 0.0001, n = 99), and E_rr in PPS regions decreased with E_θθ in adjacent LC regions (p = 0.08, n = 99).

Regional Strain Peripheral LC	Associations (n=99) Inner PPS	Mean Change in PPS Strain with unit increase in adjacent LC Strain (95% CI)	p-value
Err	Err	−0.1818 (−0.4138, 0.0502)	0.12
Eθθ	Eθθ	0.4847 (0.3583, 0.6111)	< 0.0001
Emax	Emax	0.2916 (0.1294, 0.4538)	0.001
Γmax	Γmax	0.5624 (0.4116, 0.7131)	< 0.0001
Err	Eθθ	0.2455 (0.1638, 0.3273)	< 0.0001
Eθθ	Err	−0.3796 (−0.8059, 0.0468)	0.08

To investigate the influence of the PPS on LC deformation, we compared the ratio of E_θθ for inflation from 10-45 mmHg and 5-10 mmHg $(E_{\theta \theta }^{10-45}∕E_{\theta \theta }^{5-10})$ in the LC and PPS. The ratio $E_{\theta \theta }^{10-45}∕E_{\theta \theta }^{5-10}$ was significantly smaller in the inner PPS (1.6 ± 0.4) than in the full LC (2.0 ± 0.7) (p = 0.02, Fig. 11a), which suggests that the pressure-strain response of the inner PPS exhibited greater stiffening at higher strains than the LC. The ratio $E_{\theta \theta }^{10-45}∕E_{\theta \theta }^{5-10}$ was also smaller in the peripheral LC (1.8 ± 0.7) compared to the central LC (2.8 ± 1.9), but the comparison was not significant because of large variations in the central LC (p = 0.08, Fig. 11b).

Figure 11:

Comparison of the ratio of E_θθ for inflation from 10-45 mmHg and from 5-10 mmHg $(E_{\theta \theta }^{10-45}∕E_{\theta \theta }^{5-10})$ a) in the full LC and inner PPS and b) in the central and peripheral LC. The ratio $E_{\theta \theta }^{10-45}∕E_{\theta \theta }^{5-10}$ was significantly larger in the LC compared to the PPS (p = 0.02, n = 13) and trended larger in the central LC compared to the peripheral LC (p = 0.08, n = 13).

To investigate the effect of the inflation response from 5-45 mmHg of the PPS on the posterior bowing of the LC, we calculated the difference in the average posterior displacement U_Z in the inner PPS and the central LC, which we will refer to as the posterior bowing of the LC. The posterior bowing of the LC decreased significantly with increasing E_max (p < 0.0001, n = 13, Fig. 12a) and with decreasing E_rr (p < 0.0001, n = 13, Fig. 12b) in the inner PPS. The LC posterior bowing also tended to decrease with increasing circumferential strain E_θθ (p = 0.31, n = 13, Fig. 12c) and maximum shear strain Γ_max (p = 0.10, n = 13, Fig. 12d) in the inner PPS. The E_rr in the inner PPS also decreased with increasing U_Z difference between the central and peripheral LC (p < 0.0001, n = 13,Fig. 12e, Table S11).

Figure 12:

The association of relative U_Z displacement between the central LC, peripheral LC, and the inner PPS and E_rr and E_max strain for inflation from 5-45 mmHg, the sum of the pressure increments 5-10 and 10-45 mmHg, in the inner PPS (n = 13): a) the E_max in the PPS decreased significantly with increased posterior bowing of the LC, b) the E_rr in the PPS decreased significantly with increased posterior bowing of the LC, c) the Γ_max in the PPS decreased with increased posterior bowing of the LC, d) the E_θθ in the PPS decreased with increased posterior bowing of the LC, and e) the E_rr in the PPS decreased significantly with increased U_Z difference between the central and peripheral LC. Compressive E_rr strain in the inner PPS was associated with larger posterior LC bowing relative to the PPS and increased U_Z difference between the central and peripheral LC.

4. Discussion

We developed an improved inflation test method to measure the 3D deformation response of the human ONH using DVC by replacing SHG [24] with TPF. Using the TPF images dramatically improved the accuracy of the DVC displacement correlation in the PPS and in the LC at the LC-PPS boundary, which reduced the average absolute strain errors in the LC by 25% and made the displacement and strain errors within the PPS and LC comparable. The average absolute difference in the pointwise strains calculated from DVC correlation of the TPF and SHG images in the LC was 0.046-0.133%, which was less than the average absolute DVC strain errors in the LC. This suggested that the imaged elastin and collagen structures were colocalized and deformed together at the resolution of the DVC correlation. This is not surprising as the elastin and collagen fibers are known to course linearly across the LC within the connective tissue beams in histological preparations [48] ; however, their interfiber connections are not well understood. Differences in the strain response of the collagen and elastin within the LC could indicate a lower amount of interfiber connections or regional heterogeneity in the elastin and collagen content, but a finer spatial resolution is needed to further investigate for these differences.

The magnitude of strains measured in the LC and PPS were within the expected ranges based on past inflation studies. The average maximum principal strains of approximately 3% for inflation from 5-45 mmHg, the sum of the pressure increments 5-10 and 10-45 mmHg,, with local strains as large as 10%, were similar to those reported by Sigal et al. [23] and by our prior studies for the same pressure range and age range [24, 25]. Within the LC, the radial and circumferential strains were predominantly tensile, while the shear strains were on average an order of magnitude smaller than the tensile strains. However, there were localized regions, particularly in the peripheral LC, where the shear strains were comparable in magnitude to the tensile strains. As expected, the circumferential strain in the PPS was predominantly tensile. In contrast, the average radial strain in the PPS was either compressive or tensile depending on the specimen. The pressure-strain relationship for both tissue structures became steeper at higher pressure (J-shaped) and the effect was greater for the PPS than LC. The greater compliance of the LC at higher pressure may expose the ONH axons and cells to injurious levels of strain that over time can lead to glaucoma damage.

Both the LC and PPS structures displaced posteriorly, up to 600 μm, for inflation from 5 to 45 mmHg. The posterior displacement varied by as much as 50 μm across the LC and PPS surfaces. The average LC displacement was greater (more posterior) than that of the PPS, but only by as much as 21 μm, which was on average less than 10% of the total displacement of the PPS. The average posterior displacement of the LC relative to the PPS (LC posterior bowing) was greater in eyes with lower maximum principal strains in the PPS (from 5-45 mmHg). Greater LC bowing was also associated with greater compressive radial Err strain within the inner PPS. The higher tensile strains that would result in the central LC from greater bowing and the higher compressive radial strains in the PPS can have detrimental effects on the physiological function of the glial and neural tissues of the LC and on vascular nutrition for RGC axons by vessels entering the LC through the PPS, as well as those within LC beams. These findings corroborate computational modeling studies suggesting that a stiffer sclera relative to the LC leads to greater LC bowing [36, 37, 40], as well as the finding by Coudrillier et al. of greater pressure-induced LC strains in porcine eyes with sclera stiffened by glutaraldehyde exposure [27].

Clinical OCT imaging studies of the LC anterior border displacement have shown that in early glaucoma eyes, the anterior LC can move anteriorly or posteriorly relative to Bruch’s membrane at higher IOP [49, 50]. The work of Fazio et al. [51] suggested racial differences in this displacement, with patients of European descent more likely to exhibit anterior displacement of the anterior LC border after large IOP increases, while patients of African descent were more likely to exhibit posterior displacement. The recent work of Behkam et al. [52] suggests there may also be racioethnic differences in the regional heterogeneity of the pressure-strain response of post-mortem human eyes. However, there appears to be no significant movement of the anterior LC border in eyes with advanced glaucoma damage [49, 53, 54]. Significant collagen accumulation with axonal damage in advanced glaucoma eyes may stiffen the ONH relative to the sclera and reduce the relative displacement of LC [7]. Several recent studies have also measured ONH strain distribution in vivo due to IOP changes from clinical OCT images [50, 55]; however, there are many differences between the clinical OCT imaging studies and the present ex vivo inflation study that prevent a direct comparison of the respective displacement and strain response. The clinical studies involved glaucoma subjects, who may have experienced significant remodeling of the connective tissues of the ONH and not older patients with normal eyes. The ex vivo tests probed the deformation response of the posterior LC volume and relative displacements were reported with respect to the posterior scleral surface, while the clinical studies measured the displacement of the anterior LC border relative to Bruch’s membrane. In the ex vivo inflation tests, the optic nerve was removed, which eliminated the physical constraints of the optic nerve on LC deformation, as well as the effects of blood flow and optic nerve tissue pressure. Moreover, a larger pressure increase was applied from a significantly lower baseline pressure of 5 mmHg, and the applied pressure was held for 30 minutes to an hour to remove the effects of creep. IOP changes in the clinical studies were applied on top of the physiological IOP and optic nerve tissue pressure, and the tissues were imaged shortly after to measure deformation. Thus, the resulting LC deformation measured in clinical studies described transient perturbations from a preloaded state, while the ex vivo studies measured the equilibrium response of the ONH specifically to pressure elevation from a nearly unloaded state.

We found significant differences in the average strain response of the central LC, peripheral LC, and inner PPS. The maximum principal strain and radial strain were largest in the peripheral LC. The maximum shear strain was smallest in the central LC and comparable in the peripheral LC and inner PPS and concentrated at the LC-PPS border. Circumferential strain was similar in all three regions, suggesting uniform circumferential expansion of the PPS and LC components of the ONH. Strains within the inner PPS and peripheral LC exhibited the same quadrant variations. The maximum principal and maximum shear strains were smallest nasally and highest inferiorotemporally. As a result, there were significant correlations in the circumferential, maximum principal, and maximum shear strains between the inner PPS regions and the adjacent peripheral LC regions. These findings agree with the studies of Yanhui et al. [44], who investigated the strain response of the LC and PPS in human donor eyes using high frequency ultrasound. They found that the ONH displaced more posteriorly after acute IOP increase than the sclera and that this was correlated with scleral canal expansion. While this method did not have sufficient resolution to probe LC strains in regions as small as this study, they similarly found that shear strains were higher in the peripheral ONH and inner sclera and concentrated near the vicinity of the LC-PPS interface. In addition, they found that out of plane compressive strains were concentrated in the anterior portion of the ONH. Coudrillier et al. similarly found higher compressive strains in the anterior LC in porcine eyes [26].

We found no significant relationships between the LC area and the overall pressure-induced LC strains, yet regionally, larger LC area was associated with larger strains in the central LC (E_max and E_θθ) and smaller strains in the peripheral LC (E_max and E_rr) and inner PPS (E_max and E_θθ). The radial strains E_rr were either compressive or tensile in the inner PPS, and the 2 specimens with greatest LC area (> 4 mm²) exhibited compressive radial strains. Consider a simple model of the LC as a circular plate clamped to a thicker and stiffer PPS [56]. The LC is loaded by an internal pressure and by the scleral hoop stresses generated by the pressure. The internal pressure causes the LC to bow posteriorly relative to the PPS, producing bending stresses that in the posterior volume are tensile in the central LC and compressive in the peripheral LC near the LC-PPS junction [56, 57]. The scleral hoop stresses generate tensile membrane stresses that are uniform in the LC; thus the stresses in the posterior volume of the peripheral LC and possibly the radial stress in the inner PPS can be negative or positive depending on the relative magnitude of the bending and membrane stresses. The bending stresses scale with the LC area, and a larger area would produce higher tensile strains in the central LC and smaller tensile to compressive strains in the peripheral LC and inner PPS. This simple plate model neglects the initial curvature of the LC, the complicated structure of the LC-PPS junction, the regionally varying anisotropy of the sclera, and its compliance. These factors can affect the strain state in the LC and PPS. A more detailed computational modeling study is needed to investigate the origins of the ring of compressive E_rr in the PPS and the effects of these features on the deformation response of the PPS to pressure elevation. Our previous study by Midgett et al. [24] with a wider age range did not find a significant relationship between LC area and average LC strain, but a more recent study with more specimens by Ling et al. [30] showed that strains in general increased with LC area. Neither study was able to accurately measure strains at the junction between the LC and PPS.

Several limitations should be considered when interpreting the results of this study. While the correlations between larger LC area and increased central LC bowing and strain make sense mechanically, it should be noted that this study had only two eyes from one donor with large LC areas (> 4mm²). Ten of the donor eyes had similar LC areas between 2.75-3.25 mm². Further studies that include a larger range of LC areas are needed to determine the relationship between strains and area of the LC. Preliminary analysis, showed no significant differences in average LC and PPS strains with sex; however, we do not have enough donors to adequately investigate for sex differences. We could image at most 300 μm deep below the posterior cut surface of the LC and obtained accurate DVC correlation in the central 200 μm of this region. For the denser PPS, we could image and obtain accurate DVC correlation reliably only 25 μm below the posterior surface. The displacements in the PPS were averaged through the thickness of the image volume and used to approximate the 3D displacements of the PPS surface. Thus, we cannot yet characterize the strain response through the full thickness of the PPS. DVC accuracy was also poorer in the out-of-plane Z direction. While the average absolute DVC displacement and strain errors in the imaging (X − Y) plane were less than 1/4 of a pixel (< 0.9 μm) and less than < 0.17% strain, the average absolute displacement error for the out of plane displacement U_Z and out of plane strain E_ZZ were an order of magnitude higher. Higher error in Z is caused by greater blurring of the TPF and SHG signal in Z and shadowing from the more posterior features. For this reason, we chose to analyze the components of strains in the X − Y plane in the posterior 200 μm of the LC volume. However, the in-plane strain components were evaluated using all three components of displacements, U_X, U_Y, and U_Z. Thus the posterior displacement U_Z, from bowing, contributes to E_XX and E_YY. While we determined that the PPS surface was planar on average at the high level of magnification used for TPF imaging, we noted height variation on the order of 300 μm from blood vessel insertion sites and other features. Thus, the choice to project the PPS surface displacements to a plane in order to calculate strains may have influenced strain accuracy. Further, the area of the PPS that correlated with DVC varied widely between specimens. We chose to analyze the inner 200 μm of the PPS, which generally correlated well; however, five out of thirteen eyes did not have sufficient correlation (< 40%) to analyze strains within 1 of the 8 inner PPS regions. Our limited age range for subjects, while typical for those with glaucoma, did not permit a full analysis of the effect of age on strains. We recognize that the behavior of post mortem eyes may differ from that of the living ONH.

5. Conclusions

We improved a method to measure the pressure-induced deformation of the LC and PPS by enabling DVC correlation of both the LC and PPS simultaneously. The main findings were:

1. In eyes with larger LC area, the maximum principal strain and radial strain decreased in the peripheral LC and the maximum principal strain and circumferential strain increased in the central LC.

2. The radial, maximum principal, and maximum shear strains were significantly higher in the peripheral LC compared to the central LC, and smallest in the nasal quadrant. The radial and maximum principal strains were also larger in the peripheral LC compared to the inner PPS.

3. The LC displaced more posteriorly than the PPS over all pressures and exhibited less strain stiffening for inflation from 10-45 mmHg relative to inflation from 5-10 mmHg.

4. The maximum principal strain and radial strain in the inner PPS decreased with increased posterior LC bowing relative to the PPS, and the PPS radial strain became compressive for the 3 eyes with the largest posterior LC bowing (> 16μm). Two of these 3 eyes also had the largest LC area (4mm²).

These findings suggest that a larger LC area and stiffer sclera promote greater posterior bowing of the LC to IOP elevation. This method provides quantitative characterization of the biomechanical interaction of the PPS and LC during inflation. The findings may be useful for validating computation modeling studies of the LC and PPS tissue system [36, 37] and for mechanobiological studies of the mechanism of axonal dysfunction in glaucoma.

Table 3:

Comparison of the average E_rr and E_θθ for inflation from 5-45 mmHg, the sum of the pressure increments 5-10 and 10-45 mmHg, in the full LC and inner PPS. The E_rr was greater than E_θθ in the LC (p = 0.05, n = 13), with the exception of the 2 LC with largest area. The E_rr was significantly smaller than E_θθ in the PPS (p = 0.002, n = 13), and could be compressive.

Region	Strain Outcomes 5-45 mmHg	Estimated Mean Strain (95% CI)	p-value
Full LC (n = 13)	Err	0.0188 (0.0156, 0.0220)	0.05
	Eθθ	0.0149 (0.0117, 0.0181)
Inner PPS (n = 13)	Err	0.0032 (−0.0044, 0.0108)	0.002
	Eθθ	0.0148 (0.0073, 0.0224)

Table 5:

Comparison of the ratio of E_θθ for inflation from 10-45 mmHg and from 5-10 mmHg $(E_{\theta \theta }^{10-45}∕E_{\theta \theta }^{5-10})$. The ratio $E_{\theta \theta }^{10-45}∕E_{\theta \theta }^{5-10}$ was larger in the full LC than in the inner PPS (p = 0.02, n = 13) and also larger in the central LC than in the peripheral LC (p = 0.08, n = 13).

Outcome 1 (n = 13)	Outcome 2 (n = 13)	Estimated Mean Difference in Outcomes 1 and 2 (95% CI)	p-value
$E_{\theta \theta }^{10-45}∕E_{\theta \theta }^{5-10}$, LC Full	$E_{\theta \theta }^{10-45}∕E_{\theta \theta }^{5-10}$, Inner PPS	0.3831 (0.0624, 0.7038)	0.02
$E_{\theta \theta }^{10-45}∕E_{\theta \theta }^{5-10}$, Central LC	$E_{\theta \theta }^{10-45}∕E_{\theta \theta }^{5-10}$, Peripheral LC	0.9690 (−0.1015, 2.0396)	0.08