Ion Pairing and the Structure of Gel Coacervates

Abstract

A scaling model for the structure of coacervates is presented for mixtures of oppositely-charged polyelectrolytes of both symmetric and asymmetric charge-densities for different degrees of electrostatic strength and levels of added salt. At low electrostatic strengths, weak coacervates, with the energy of electrostatic interactions between charges less than the thermal energy, k_BT, are liquid. At higher electrostatic strengths, strong coacervates are gels with crosslinks formed by ion pairs of opposite charges bound to each other with energy higher than k_BT. Charge-symmetric coacervates are formed for mixtures of oppositely-charged polyelectrolytes with equal and opposite charge-densities. While charge-symmetric weak coacervates form a semidilute polymer solution with a correlation length equal to the electrostatic blob size, charge-symmetric strong coacervates form reversible gels with a correlation length on the order of the distance between bound ion pairs. Charge-asymmetric coacervates are formed from mixtures of oppositely-charged polyelectrolytes with different charge-densities. While charge-asymmetric weak coacervates form double solutions with two correlation lengths and qualitatively different chain conformations of polycations and polyanions, charge-asymmetric strong coacervates form bottlebrush and star-like gels. Unlike liquid coacervates, for which an increase in the concentration of added salt screens electrostatic interactions, causing structural rearrangement and eventually leads to their dissolution, the salt does not affect the structure of strong coacervates until ion pairs dissociate and the gel disperses.

Graphical Abstract

1. Introduction

Coacervation is an electrostatically-induced phase separation of mixtures of oppositely-charged polyelectrolytes into a polymer-rich phase, coacervate, and a coexisting dilute phase. This dilute phase contains isolated chains and/or small complexes of oppositely-charged chains in low, but non-negligible, concentrations.^1–5 Coacervates are ubiquitous in biological systems^6–16 and have found numerous technological applications as coatings,^17–20 encapsulants,^21–24 and responsive materials^25–32 in the food,^33–35 pharmaceutical,^36–38 and other industries.^39,40 Such a diverse array of applications became possible as a result of variations in the molecular details of the charged species (e.g., biological or synthetic macromolecules, charge-density, sequence, salt, and solvent conditions, etc.) and a theoretical description of these features should initiate further development of their design and applications.

Despite significant progress in the development of theoretical descriptions of coacervation from the original Voorn–Overbeek (VO) model^41,42 to present day, there is still no unifying description of the coacervate structure at the molecular level.^43–45 In particular, most models successfully distinguish between different physical behaviors in different association regimes, depending on the strength of electrostatic interactions per charge relative to the thermal energy, k_BT, but have yet to unify the behavior across the full range of association strengths.

Most of the theoretical efforts have focused on weak or liquid coacervates with electrostatic interaction energy lower than k_BT per charge. The phase behavior and structure of weak coacervates have been successfully predicted by molecular dynamics (MD)^46,47 and field-theoretic simulations (FTS)^{2–4,48–50} of coarse-grained molecular models incorporating chain connectivity, excluded-volume repulsions with a slightly-positive excluded-volume parameter, and calculation of the long-range Coulombic correlations of the electrostatic interactions. However, coarse-grained numerical simulations can be too complicated and expensive to obtain accurate structure and phase coexistence conditions across the high dimensionality of parameter space, particularly near the critical point due to large fluctuations and finite simulation-cell-size effects.

In contrast, analytical theories, such as the random phase approximation (RPA),^{2–4,48–58} are more amenable for understanding coacervation behavior as a function of many different molecular features. In the RPA formalism, the free energy is obtained by calculating the one-loop corrections to the mean-field solution of the Hamiltonian of the system. Although at high concentrations the results are quantitatively consistent with field-theoretic simulations, at low concentrations this approximation fails catastrophically.^2–4 The RPA misses in predicting the concentration of the dilute phase by several orders of magnitude due to an overestimation of the charge-charge correlations in the Debye–Hückel approximation and the assumption of Gaussian chain statistics.^3,59,60 The renormalized Gaussian fluctuation (RGF) theory^59,60 partially compensates for this deficiency by self-consistently renormalizing the chain statistics, but relies on a number of approximations.

However, many experiments with synthetic polyelectrolytes in which gel coacervates are observed are in the strong association regime with electrostatic interactions stronger than k_BT per charge.^61–66 Transfer-matrix (TM) theory and associated numerical simulations have become robust methods to describe such strong coacervates, particularly in the prediction of phase behavior.^67–74 However, the TM theoretical description depends on an underlying adsorption model, where nearly all charges along a polyelectrolyte are paired with either a counter-ion or a site on an oppositely-charged chain, which limits applicability of the theory to strongly-charged polyelectrolytes in the strong association regime.

Integral equation formalisms, in particular, liquid-state theories or PRISM, should in principle cover both weak and strong association regimes, but they are restricted by obtuse closure approximations necessary for their analytical and numerical implementation, which do not allow their systematic improvement.^75–78 Similarly, analytical extensions of the Voorn–Overbeek model to account for chain connectivity, electrostatic fluctuations, and ion binding rely on an underlying mean-field approximation and an assumption of homogeneous structure, which limit predictions for highly-correlated or inhomogeneous structures.^79–84

Scaling models, however, offer a versatile approach to predicting phase behavior and structures of coacervates depending on many molecular features, without the numerical complications of other models. A combination of such analytical theories and molecular simulations will enable progress in understanding coacervation phenomena. Thus far, scaling arguments have accounted for the effects of molecular architecture,^58,85–88 solvent conditions,^5,89 chain rigidity asymmetry,⁹⁰ and charge-density asymmetry,⁵ but have not yet taken into account ion binding at strong association strengths. The focus of the present work is to span the weak and strong association regimes to describe the structure of the coacervate phase formed from solution mixtures of polyions with both symmetric and asymmetric charge-densities as a function of electrostatic strength and ionic content.

Here we extend a scaling theory of coacervates formed from mixtures of oppositely-charged polyelectrolytes^2,5,86,89 to include ion binding in the strong association regime. The focus of the current work is not predicting phase equilibria conditions, but on predicting the structure of coacervates spanning different charge-asymmetry regimes across a range of association strengths. In section 2, we review the scaling results for mixtures of polyanions and polycations with symmetric charge-densities along their contours in the weak association regime and extend these results to include formation of ionic bonds between these chains. In section 3, we review weak coacervates formed by charge-asymmetric polyelectrolytes, develop scaling predictions for the structure of bottlebrush gels in the strong association regime, and discuss the effects of salt on the structure of the strong coacervates. While salt screens electrostatic interactions, leading to swelling and ultimately to dissolution of the weak coacervates, it does not affect strong coacervates until the bound ion pairs dissociate. The main results are summarized and discussed in section 4.

2. Charge-Symmetric Coacervates

We consider a coacervate formed by the complexation of mixtures of polycations and polyanions (formed in equilibrium with a dilute supernatant). The structure and thermodynamics of such coacervates are similar to block polyampholytes, and differ only in constraining the stoichiometry of opposite charges occurring within the coacervate, as well as in the small difference in free energies of the order of 1/N occurring from a decrease in the ideal gas entropy due to pairing of equivalent oppositely-charged polyelectrolytes with degrees of polymerization N.^2,86,91

The strength of electrostatic interactions depends on the Bjerrum length l_B, the distance at which two elementary charges in a solvent with dielectric constant ϵ interact with thermal energy k_BT. We introduce a dimensionless Bjerrum length

$$u=\frac{l_{\text{B}}}{b}=\frac{e^2}{k_{\text{B}}Tϵb}$$ (2.1)

where e is the elementary charge and b is the statistical segment size or Kuhn length.⁹² For simplicity, we assume that both polyanions and polycations have the same segment length, b₊ = b₋ ≡ b, and therefore, dimensionless ratios of Bjerrum to segment lengths are also the same, u₊ = u₋ = l_B/b ≡ u. We relax this assumption and the assumption of a θ-solvent for the uncharged backbone in Appendix D. For salt-free aqueous (with l_B ≈ 0.7 nm) solutions of flexible polyelectrolytes (with b ≈ 1 nm), u is of order unity.

First, we consider charge-symmetric coacervates, formed from mixtures of charge-symmetric polycations and polyanions without added salt in a θ-solvent for the neutral backbones (Figure 1). By charge-symmetric, we mean polyions having the same electrostatic blob size, D_e+ = D_e− ≡ D_e. Electrostatic blobs are sections of a chain with the energy of electrostatic interaction with an adjacent section of comparable size and charge on the order of thermal energy kBT:^93,94

$$l_{\text{B}}\frac{{\left(f{g}_{\text{e}}\right)}^2}{D_{\text{e}}}\simeq 1,$$ (2.2)

where f is the fraction of charged monomers. In a θ-solvent, an electrostatic blob with an average number of monomers g_e ≃ u^−2/3f^−4/3 and charge efg_e has the size

$$D_{\text{e}}\simeq b{g}_{\text{e}}^{1/2}\simeq b{u}^{-1/3}{f}^{-2/3}.$$ (2.3)

Note that in scaling analysis, numerical coefficients on the order of unity are omitted and small higher-order corrections to the leading term are ignored; “≃” denotes equality within such a level of accuracy.^92,95 Since we have assumed equal segment sizes b₊ = b₋ ≡ b and thus equal dimensionless Bjerrum lengths u₊ = u₋ = l_B/b ≡ u, charge-symmetric coacervates consist of polyelectrolytes with the same linear number density of charges γ along the array of electrostatic blobs of polycations and polyanions,

$${\gamma }_{+}={\gamma }_{-}\equiv \gamma \simeq \frac{f{g}_{\text{e}}}{D_{\text{e}}}\simeq {\left(D_{\text{e}}{l}_{\text{B}}\right)}^{-1/2}\simeq \frac{1}{b}{\left(\frac{f}{u}\right)}^{1/3}$$ (2.4)

and therefore with equal degrees of ionization f₊ = f₋ ≡ f. However, the polyelectrolytes do not necessarily have the same degrees of polymerization N₊ and N₋ or number of polymeric charges per chain N₊f₊ and N₋f₋.

Figure 1:

Symmetric coacervates formed by mixing oppositely-charged polyelectrolytes with symmetric electrostatic blobs. Increasing the electrostatic interaction strength results in the formation of bound pairs of positive and negative charges and the formation of a reversible network.

2.1. Charge-Symmetric Weak (Liquid) Coacervates

Salt-free charge-symmetric weak coacervates are semidilute solutions formed from mixtures of charge-symmetric oppositely-charged polyelectrolytes and are characterized by a single correlation length. The composition of the coacervate is 1:1 in terms of charges in solution. If polycations and polyanions are mixed in salt-free solutions in off-stoichiometric proportions, the coacervate will remain neutral, and the excess charge will be expelled to the supernatant in the form of complexes or free chains.^5,78 At the optimal distance D_e from each other, the electrostatic blobs repel the same-sign neighboring blobs and attract the oppositely-charged blobs of the same size and charge magnitude with an energy k_BT. Oppositely-charged blobs are more likely to be close to each other because of lower electrostatic energy and higher statistical weight of these configurations, even though the coacervate is electroneutral with the same number density of positive and negative charges and the same number of positive and negative blobs.^2–5,86

The electrostatic attractions are balanced by the short-range repulsion (three-body in a θ-solvent or two-body in a good solvent). Therefore, the coacervate structure is similar to that of a semidilute polymer solution for whatever solvent conditions we are considering with the free energy of repulsive short-range interactions k_BT per “blob”, which is a section of polyions with pervaded volume of ∼ ξ³. The correlation length ξ, defined as the average distance between the nearest monomers on neighboring chains, in a charge-symmetric weak coacervate is equal to the electrostatic blob size (eq. 2.3) and can be written as^2,5,86

$$\xi \simeq D_{\text{e}}\simeq b{u}^{-1/3}{f}^{-2/3},$$ (2.5)

in a θ-solvent. The correlation length ξ decreases with increasing electrostatic strength u. Accordingly, the equilibrium polyion monomer concentration $\overline{c}$ of a coacervate,⁵ which is a close packing of electrostatic blobs, increases with increasing electrostatic strength u as

$$\overline{c}\simeq \frac{g_{\text{e}}}{D_{\text{e}}^3}\simeq \frac{u^{1/3}{f}^{2/3}}{b^3}.$$ (2.6)

This concentration (also eqs. 2.8 and 3.6) is the optimal concentration of the coacervate phase in equilibrium with a polymer-poor supernatant phase. Note that we did not calculate the entire free energy of the coacervate but described the coacervate structure on different scales by a balance of forces on those scales. This scaling description is valid at electrostatic strengths u up to f^−1/2, the upper boundary of weak coacervates. For this electrostatic strength u ≃ f^−1/2, the correlation length and electrostatic blob size are reduced to the Gaussian size between charges, b/f^1/2, at which there is on average only one charge in each electrostatic blob with a size on the order of the Bjerrum length,

$${\xi }^{\min }\simeq D_{\text{e}}^{\min }\simeq b/f^{1/2}\simeq l_{\text{B}},$$ (2.7)

and the coacervate concentration saturates at

$$\overline{c}\simeq f^{1/2}/b^3.$$ (2.8)

At this crossover electrostatic interaction strength u ≃ f^−1/2, the counter-ions would condense onto the polyelectrolytes and reduce their effective line density of charges to one charge per Bjerrum length:^96,97

$$l_{\text{B}}{\gamma }^{\text{eff}}\simeq \{\begin{array}{ll}{u}^{2/3}{f}^{1/3}\hfill & \text{for}u<f^{-1/2}\hfill \\ 1\hfill & \text{for}u>f^{-1/2}\hfill \end{array}$$ (2.9)

for the dilute pure solutions of polycations and polyanions (prior to mixing the solutions and forming a coacervate). If the polyelectrolytes with condensed counter-ions are mixed in solution, however, the polymeric charges are compensated by the oppositely-charged polyelectrolytes, releasing condensed counter-ions and thus minimizing the solution free energy.

2.2. Ion Pairing: Transition from Weak to Strong Coacervates

The strength of electrostatic interactions can be increased, for example, by decreasing the dielectric constant of the solvent, and thus increasing the ratio of the Bjerrum length l_B to ionic bond length l. If this ratio l_B/l significantly exceeds unity, the electrostatic attraction results in binding of positive and negative charges into ion pairs. The binding starts as soon as the electrostatic gain −k_BTl_B/l exceeds the entropic loss due to localizing a positive polymeric charge next to a negative polymeric charge, k_BT ln $\left(f\overline{c}{l}^3\right)$,

$$\Delta F_{\text{ionic}\text{bond}}\simeq -k_{\text{B}}T\left[\ln \left(f\overline{c}{l}^3\right)+l_{\text{B}}/l\right]\approx -k_{\text{B}}T\left[\ln \left(f\overline{c}{b}^3{\lambda }^3\right)+u/\lambda \right],$$ (2.10)

where $\overline{c}$ is the polyion monomer concentration in the coacervate and we introduced a dimensionless bond length,

$$\lambda \equiv l/b.$$ (2.11)

The bond length l is approximately equal to the size of two ions bonded together, which is typically on the order of 1 − 5 Å, and therefore a typical value of λ is less than unity.

It should be noted that this ionic binding energy (eq. 2.10) invokes continuum dielectric response concepts, while the ionic bond length l (and λ) arises from a more detailed microscopic picture, which is likely chemistry dependent, but is effective in capturing the degree of local dielectric mismatch.^82,98,99 Further, this ionic binding energy neglects cooperativity or other concentration-dependent effects beyond the localization entropy. Finally, it is important to impress that the correlated-charge interaction that forms an ion pair or ionic bond, is important for description of the equilibrium structure, but also for describing the long-lived reversible or “sticky” interactions between heterotypic associative polymers (e.g., between polycations and polyanions discussed here) that are crucial for describing the dynamics of these reversible gels. Such consequences of the sticky nature of these associations on their rheology, will be explored in future work.

Thus, ionic binding is favorable (−ΔF_{ionic bond} > 0) for electrostatic interaction strengths above the crossover,

$$u^{*}\simeq \lambda \ln \left(\frac{1}{f^{3/2}{\lambda }^3}\right)$$ (2.12)

where for simplicity we have assumed that the concentration of the coacervate saturates at $\overline{c}\simeq f^{1/2}/b^3$ (eq. 2.8) prior to ion binding. This assumption corresponds to u^∗ > f^−1/2 and fails for the cases of very weakly-charged polyelectrolytes (f ≪ 1) or strongly-charged polyelectrolytes (f ∼ 1). Even if the assumption of the coacervate concentration saturating at $\overline{c}\simeq f^{1/2}/b^3$ fails, a complete solution of the transcendental inequality (−ΔF_{ionic bond} > 0, eq. 2.10) affects principally the numerical prefactor of u^∗, but only slightly affects the logarithmic functional form. In a scaling analysis, we proceed with u^∗ as estimated in eq. 2.12.

Treating the ionic bonding as a chemical equilibrium between free and bound ions,⁸² the number density of bound ions can be approximated

$${\overline{c}}_{\text{bound}\text{ions}}\simeq {(\tilde{f}\overline{c})}^2{b}^3{\lambda }^3\exp \left(-\Delta F_{\text{ionic}\text{bond}}/k_{\text{B}}T\right)$$ (2.13)

where the capture volume is approximated as V_c ≈ l³ ≃ b³λ³ and $\tilde{f}$ is the effective fraction of charged monomers which decreases from f to 0 as bound ion pairs are formed. The number density of free ions (i.e., polyelectrolyte charges not bound into ion pairs) is

$${\overline{c}}_{\text{free}\text{ions}}\simeq \tilde{f}\overline{c}\simeq f\overline{c}-{\overline{c}}_{\text{bound}\text{ions}}.$$ (2.14)

For weak coacervates discussed in Section 2.1, nearly all the ions are free and the effective fraction of charged monomers is almost unperturbed, $\tilde{f}\simeq f$. The formation of ion pairs leads to a decrease in the effective fraction of free charges $\tilde{f}$. The electrostatic blob size

$$D_{\text{e}}\simeq b{u}^{-1/3}{\tilde{f}}^{-2/3}$$ (2.15)

remains effectively constant, but weakly increases with a decrease in the number density of free ions ${\overline{c}}_{\text{free}\text{ions}}$. At intermediate strength of electrostatic interactions (u^∗ < u < u_x, where u^∗ is given by eq. 2.12 and u_x is defined below, in eq. 2.17), there are several electrostatic blobs of size D_e between ion pairs separated by the distance

$$d_{\text{ion}\text{pairs}}\simeq D_{\text{e}}{\left(\frac{1/(f-\tilde{f})}{g_{\text{e}}}\right)}^{1/2}\simeq \frac{b}{{(f-\tilde{f})}^{1/2}},$$ (2.16)

which is the Gaussian size of the chain section between cross-links of the reversible network. As the electrostatic interaction strength is increased and more ion pairs are formed, d_{ion pairs} decreases and D_e increases. If the number density of bound ion pairs is equal to the number density of free charges along the polyelectrolytes in the coacervate, ${\overline{c}}_{\text{bound}\text{ions}}\simeq {\overline{c}}_{\text{free}\text{ions}}\approx {(f/2)}^{3/2}/b^3$, and $\tilde{f}\simeq f/2$. This crossover occurs at

$$u_{\text{x}}\simeq \lambda \ln \left(\frac{1}{f^3{\lambda }^6}\right),$$ (2.17)

for which the average distance between bound ions is comparable to the average distance between free charges and is on the order of the Bjerrum length,

$$d_{\text{ion}\text{pairs}}\simeq D_{\text{e}}\simeq l_{\text{B}}\simeq b/f^{1/2}.$$ (2.18)

At higher electrostatic strengths for large u ≳ u_x, the probability that the charges will be bound into ion pairs is higher than the probability that they remain in the form of isolated charges; the distance between ion pairs continues to decrease with increasing strength of electrostatic interactions until all charges are bound into reversible cross-links.

Gelation occurs if there is more than one cross-link per chain for electrostatic interaction strengths, u^∗ < u < u_x. However, it is important to recognize that within a scaling analysis,

$$u_{\text{gel}}\simeq u^{*}\simeq u_{\text{x}}\simeq \lambda \ln \left(\frac{1}{f\lambda }\right)\approx \lambda ;$$ (2.19)

the transition between weak and strong coacervates occurs in a relatively narrow range of electrostatic strengths (Figure 2). The electrostatic strength u^∗ ≃ u_x at this crossover is on the order of unity for f ≈ 1 and l ≈ b and is shifted to lower electrostatic interaction strengths for shorter ionic bond lengths. Importantly, this implies that ionic binding occurs if the Bjerrum length exceeds the ionic bond length, l_B > l, consistent with the molecular dynamics simulations of block polyampholytes, which showed a transition from free to bound ions at l_B ≈ l ln(1/f).⁹¹

Figure 2:

The dependence of (a) important length scales and (b) the concentrations of charge-symmetric θ-coacervates on the dimensionless electrostatic interaction strength u = l_B/b for both weak and strong association regimes. (a) Blue line: the electrostatic blob size D_e (eqs. 2.3, 2.15). Thick green line: the average distance d_{ion pairs} between bound ion pairs (eqs. 2.16, 2.20). (b) Purple line: the equilibrium concentration $\overline{c}$ of the charge-symmetric θ-coacervate (eqs. 2.6, 2.8). Orange line: the number density of free ions ${\overline{c}}_{\text{free}\text{ions}}$ (eq. 2.14). Thick red line: the number density of bound ions ${\overline{c}}_{\text{bound}\text{ions}}$ (eq. 2.13). Logarithmic axes.

2.3. Charge-Symmetric Strong (Gel) Coacervates

At high strength of electrostatic interactions (u > u_x), all ions are paired into bound ion pairs and there are no free charges. These bound ion pairs form reversible cross-links corresponding to a special case of a gel formed by A–B associative polymers. For such charge-symmetric strong coacervates, the correlation length in a θ-solvent is

$$\xi \simeq d_{\text{ion}\text{pairs}}\simeq b/f^{1/2}$$ (2.20)

and is equivalent to the Gaussian size of the chain section between cross-links. The correlation volumes are close-packed, with number density of monomers $\overline{c}\simeq f^{1/2}/b^3$ (value of purple line at high u, Figure 2b). Inside the blob, the chain conformations are almost Gaussian in θ-solvents and swollen in good solvents.⁹⁵

In accordance with the affine or phantom network models for unentangled flexible polymers, the plateau shear modulus of this strong coacervate is G = υk_BT, where the density of strands is υ ≃ f^3/2/b³ provided that most network strands are elastically effective, and is approximately,

$$G\simeq \frac{f^{3/2}}{b^3}{k}_{\text{B}}T.$$ (2.21)

It should be noted that highly cross-linked coacervates (high f, with many cross-links per chain) are likely brittle unless plasticized by water and/or salt, perhaps consistent with observed glassy behavior and solid-like precipitates for dense coacervates at low-salt.^61,100–102 Predictions for the dynamics and mechanics of strong coacervates are the subject of future work.

In the present scaling theory, we have focused thus far on the description of charge-symmetric coacervates formed from mixtures of polyelectrolytes with less than one charge per Kuhn segment. In the case of multiple charges per Kuhn length, f > 1, the binding of the opposite charges is effectively the binding of f charges within a segment with ionic binding energy −k_BTfu/λ, which occurs at an electrostatic strength u ≳ λ/f. The concentration of bound ions can be determined in the same way as in eq. 2.13 using the ionic binding energy of multivalent segments. It should also be noted that in the strong association regime, both the distribution of the charges and the asymmetry of charge valence between polyanions and polycations should be of consequence. Here, our results focus on the generic case of fN monovalent charges uniformly distributed along a polymer of polymerization index N, separated by on the order of 1/f uncharged monomers. In the current model, strongly non-uniform distribution of charges along the chains and asymmetric valence of oppositely-charged chains are not considered.

2.4. Salt Effects on Charge-Symmetric Coacervates

The addition of salt screens the electrostatic interaction on a Debye screening length scale

$$r_{\text{D}}={\left(8\pi l_{\text{B}}{c}_{\text{s}}\right)}^{-1/2}\simeq {\left(bu{c}_{\text{s}}\right)}^{-1/2}$$ (2.22)

where $c_{\text{s}}=c_{\text{s}}^{+}=c_{\text{s}}^{-}$ is the concentration of monovalent salt. At low salt concentrations, corresponding to a large Debye length r_D > D_e, salt ions practically do not affect the properties of the coacervate.^4,5,89 In the case of charge-symmetric weak coacervates, this low-salt regime corresponds to the salt concentrations (teal line, Figure 3a):

$$c_{\text{s}}<c_{\text{s},\text{h}}\simeq \frac{{\tilde{f}}^{4/3}}{b^3{u}^{1/3}},$$ (2.23)

above which the Debye length is smaller than the electrostatic blob size. Note that in the case of charge-symmetric weak coacervates, the ions brought into solution with polyelectrolytes as counter-ions are no longer needed for charge compensation in the charge neutral coacervate and act as salt ions. The presence of salt due to counter-ions from the polyelectrolytes, with a concentration much lower than the concentration of polymeric charges $f\overline{c}\simeq f^{3/2}/b^3<c_{\text{s},\text{h}}$, hardly affects the coacervate in the absence of added salt. At added salt concentrations exceeding c_s,h, the chain segments in neighboring blobs interact via the screened Coulomb potential. Therefore, the interaction between oppositely-charged polyions can be described as the effective two-body attraction between elementary charges of number density $\tilde{f}\overline{c}$ with an effective negative second virial coefficient $-l_{\text{B}}{r}_{\text{D}}^2$.^5,89 The corresponding free energy density is

$$-k_{\text{B}}T{l}_{\text{B}}{r}_{\text{D}}^2{(\tilde{f}\overline{c})}^2$$ (2.24)

and is balanced by the short-range excluded volume interactions on the order of thermal energy k_BT between sections of chains with size

$${\xi }^{\text{s}}\simeq \frac{b^4{c}_{\text{s}}}{{\tilde{f}}^2},\text{for}{c}_{\text{s}}>c_{\text{s},\text{h}}\text{and}u<u_{\text{x}}$$ (2.25)

which is insensitive to u, since an increase in the electrostatic interaction strength is compensated by a decrease in the Debye length.^5,89 Pure solutions of polyelectrolytes with single sign of charge with added salt consist of swollen chains of thermal blobs of size ξ^s.^94,103 Oppositely-charged polyelectrolytes in the coacervate are organized as a dense packing of these blobs (Figure 3). In the case of a θ-solvent, the polyion monomer concentration, $\overline{c}\simeq 1/\left(b^2{\xi }^{\text{s}}\right)$, is determined by the size, ξ^s ≃ bg^1/2, of the Gaussian correlation blob containing g monomers and the close packing condition of these correlation blobs, $\overline{c}\simeq g/{\left({\xi }^{\text{s}}\right)}^3$. Thus, the concentration of polyions in the coacervate

$$\overline{c}\simeq {\tilde{f}}^2{b}^{-6}{c}_{\text{s}}^{-1},\text{for}{c}_{\text{s}}>c_{\text{s},\text{h}}\text{and}u<u_{\text{x}}$$ (2.26)

decreases hyperbolically⁸⁹ with the salt concentration in the high-salt regime. Note that we have assumed adding salt to a coacervate with 1:1 macromolecular charges. (Recall that if the polycations and polyanions are mixed in salt-free solutions in off-stoichiometric proportions, the excess charge will be expelled to the supernatant.) However, in the presence of added salt, the coacervate is no longer constrained to be 1:1 stoichiometric of polymeric charges, as small ions can partition into the coacervate in non-stoichiometric ratios to satisfy the overall charge neutrality. If the concentration asymmetry is too large, the coacervate will no longer form. Such effects have been systematically explored in the literature.^1,4,5,78

Figure 3:

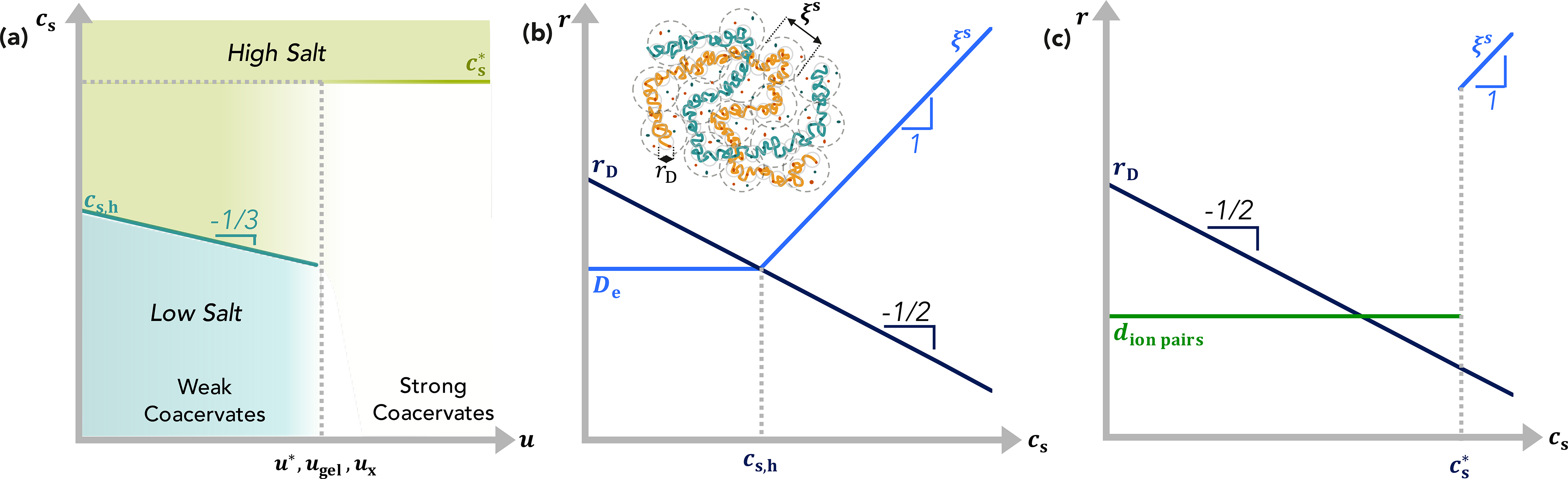
(a) Crossover salt concentrations of charge-symmetric θ-coacervates as a function of the strength of electrostatic interactions. (b-c) Important length scales of charge-symmetric θ-coacervates at electrostatic strengths (b) u < u_x for weak coacervates and (c) u > u_x for strong coacervates as a function of salt concentration. (b, inset) Schematic of structure of charge-symmetric weak θ-coacervates at high-salt conditions. Logarithmic axes.

At the crossover between weak and strong coacervates with both free and bound charges, at electrostatic interaction strengths u ≈ u_x, the electrostatic blobs are screened upon the addition of salt but the ion pairs are unaffected for salt concentrations, $c_{\text{s},\text{h}}<c_{\text{s}}<c_{\text{s}}^{*}$. For strong coacervates (u > u_x) with many bound ion pairs, the structure of the reversibly-cross-linked gel is almost unchanged (Figure 3c) with increasing salt concentration until the bound ion pairs begin to dissociate at $c_{\text{s}}=c_{\text{s}}^{*}$. As the ion pairs dissociate, the coacervate returns to the weak coacervate in the high-salt regime (inset, Figure 3b).

For simplicity, in Figure 3, we have assumed that all ion pairs dissociate at a critical salt concentration $c_{\text{s}}^{*}$, rather than within a certain range of salt concentrations, and that this critical dissociation salt concentration is in the high-salt regime. This is in agreement with experiments of gel coacervates by Schlenoff and coworkers,^61–63,101 which show a transition from rubbery to liquid-like behavior at a monovalent salt concentration [KBr] ≈ 1.4 M or c_s ≈ 0.84 nm⁻³. It should be noted that the (formation and) dissociation of ion pairs is a cross-linking process, a transition related to changes in the connectivity of polymeric charges, similar to geometric percolation and other sol–gel transitions, and thus important for the dynamics of the material.

However, it is challenging and beyond the scope of the present scaling analysis to estimate a universal prediction for $c_{\text{s}}^{*}$. In fact, $c_{\text{s}}^{*}$ may not be experimentally accessible for all systems.¹⁰⁴ At first approximation, it might be assumed that ion pairs dissociate as the Debye length becomes comparable to the length of the ionic bond, r_D ≈ l, which is reasonable for the r_D ≈ 2.6 Å corresponding to the experimental transition from gel to liquid coacervates discussed above, but the definition of screening lengths and the continuum description of the medium already breaks down at larger length scales ∼ 3−5 Å. A more sophisticated estimate would need to account for the specific structure of the solvent, molecular polarizabilities of all species, and the effects of ions on solvent quality. Due to ion-specific effects and local solvation shell differences, the strength of the ion pairs and the ability to dissociate probably also depends on the specific chemistry of the ionic species.^104,105 Finally, at such high salt concentrations, the dimensionless electrostatic interaction strength u also changes with salt concentration since the local dielectric environment non-monotonically depends on both salt and polymer concentrations.

3. Charge-Asymmetric Coacervates

Oppositely-charged polyelectrolytes with electrostatic blobs of different sizes form charge-asymmetric coacervates with different number densities of charges along the arrays of electrostatic blobs of polycations and polyanions, γ₊ ≠ γ₋. In the case of equal Kuhn lengths, b₊ = b₋ ≡ b, this condition implies different fractions of charged monomers on the chains, f₊ ≠ f₋. More precisely, charge-asymmetric coacervates consist of oppositely-charged polyelectrolytes with different sizes of chain sections between adjacent charges, $b_{+}/f_{+}^{\nu }\ne b_{-}/f_{-}^{\nu }$, where general scaling exponent ν describing the solvent condition quality is 1/2 for θ-solvents and 0.588 for athermal solvents.

3.1. Charge-Asymmetric Weak (Liquid) Coacervates

With electrostatic interaction energy per charge less than the thermal energy, u < 1, weak coacervates are liquid and resemble two interpenetrating polymeric solutions, characterized by two corresponding correlation lengths: ξ₊ for polycations and ξ₋ for polyanions.⁵ A polyelectrolyte with higher linear charge number density along the array of their electrostatic blobs (for definiteness assumed to be the polyanion, γ₋ > γ₊) creates a higher electric field that attracts oppositely-charged polyelectrolytes of lower charge-density. In the case of salt-free, charge-asymmetric θ-coacervates, the polycations absorb on the polyanion, forming a charge-compensating coat with a correlation length, defined as the average distance between the nearest monomers on neighboring polycations,

$${\xi }_{+}\simeq \frac{1}{{\overline{c}}_{+}{b}^2}\simeq \frac{b}{u^{1/3}{f}_{+}^{1/2}{f}_{-}^{1/6}}$$ (3.1)

determined by the local balance of electrostatic attraction of polycations to polyanions and short-range repulsion between polycations.⁵ The average distance between sections of adjacent polyanions determines the correlation length,

$${\xi }_{-}\simeq \{\begin{array}{ll}b\frac{f_{-1}^{1/12}}{f_{+}^{3/4}{u}^{1/3}}\hfill & \text{for}{L}_{-}>{\xi }_{-}\hfill \\ b{\left(\frac{f_{-}{N}_{-}}{f_{+}^{3}u}\right)}^{1/5}\hfill & \text{for}{L}_{-}<{\xi }_{-}\hfill \end{array}$$ (3.2)

and corresponds to the thickness of the polycation coat at which the electroneutrality of the coacervate is established.⁵ Depending on the ratio of the length $L_{-}\simeq N_{-}b{\left(u{f}_{-}^2\right)}^{1/3}$ of the array of the electrostatic blobs of the polyanion (with degree of polymerization N₋) and their correlation length ξ₋, charge-asymmetric coacervates can have either cylindrical or spherical symmetry of the compensating polycation coat on larger length scales. Charge-asymmetric coacervates of cylindrical symmetry with L₋ > ξ₋ and, thus, overlapping highly-charged polyanions are called double-semidilute. Charge-asymmetric coacervates of spherical symmetry with L₋ < ξ₋ and, thus, non-overlapping (dilute) highly-charged polyanions within the background of the lower charge-density polycations are called dilute–semidilute.⁵

Thus, salt-free charge-asymmetric weak coacervates consist of two interpenetrating polymer solutions, each with its own correlation length and qualitatively different chain conformations. These conformations are similar to those of pure polycationic and polyanionic solutions of corresponding polymer concentrations.⁵ Polycations with a lower charge-density are almost unperturbed by the electrostatic interactions, with a size $R_{+}\simeq b{N}_{+}^{1/2}$, while polyanions with a higher charge-density adopt conformations similar to semidilute polyelectrolytes in a θ-solvent, with a size

$$R_{-}\simeq {\xi }_{-}{\left(\frac{N_{-}}{g_{-}}\right)}^{1/2}\simeq b{N}_{-}^{1/2}{\left(\frac{f_{-}}{f_{+}}\right)}^{3/8}\text{for}{L}_{-}>{\xi }_{-}$$ (3.3)

and g₋ monomers in the correlation blob of size ξ₋.⁵ Note that the polyanion chain in charge-asymmetric θ-coacervates with f₊ = f₋ corresponds to a random walk with size $R_{-}\approx b{N}_{-}^{1/2}$, as discussed in Section 2, but its size increases in salt-free charge-asymmetric θ-coacervates by the three-eighths power of the asymmetry factor, f₋/f₊.

3.2. Double-Semidilute: Bottlebrush Gel

In the weak association regime, an increase in the strength of the electrostatic attractions (increase in u) results in a thinner coat of polycations around the polyanion (eqs. 3.1–3.2). At low salt, the concentrations of polycations and polyanions increase proportionally to each other with an increase in u. However, in the strong association regime, with a further increase in the strength of electrostatic interactions u, electrostatic attraction results in the binding of positive and negative charges and a cascade of structural transitions. At even higher electrostatic strength (u > u_x, Section 3.2.2) all opposite charges become paired, resulting in a fully-cross-linked reversible network (Figure 4).

Figure 4:

Conformational changes of the double-semidilute coacervate with increasing dimensionless electrostatic interaction strength u = l_B/b due to an increase in the fraction of bound ions resulting in the formation of bottlebrush gels when all charges are bound in ion pairs. The mixed bottlebrush/double-semidilute coacervate regime (u^∗ < u < u_x) is narrow, but increases with asymmetry of charge fraction f₋/f₊ between the polyanions and polycations.

The free energy of an ionic bond is the sum of the electrostatic gain and entropic loss, as for charge-symmetric coacervates, discussed in detail in Section 2.2. For charge-asymmetric coacervates, we write the binding energy, analogously to charge-symmetric coacervates (eq. 2.10), as

$$\begin{gathered} \Delta F_{\text{ionic}\text{bond}}\simeq -k_{\text{B}}T\left[\ln \left(f_{+}{\overline{c}}_{+}{l}^3\right)+\ln \left(f_{-}{\overline{c}}_{-}{l}^3\right)+l_{\text{B}}/l\right] \\ \approx -k_{\text{B}}T\left[\ln \left(f_{+}{\overline{c}}_{+}{b}^3{\lambda }^3\right)+u/\lambda \right]\simeq -k_{\text{B}}T\left[\ln \left(f_{-}{\overline{c}}_{-}{b}^3{\lambda }^3\right)+u/\lambda \right], \end{gathered}$$ (3.4)

where we have recalled that the salt-free optimal coacervate is electroneutral with equal number density of positive and negative charges $f_{+}{\overline{c}}_{+}=f_{-}{\overline{c}}_{-}$ and the ratio of the ionic bond length to the Kuhn length is λ = l/b. Thus, ionic binding is favorable (−ΔF_{ionic bond} > 0) for electrostatic interaction strengths above the crossover,

$$u^{*}\simeq \lambda \ln \left(\frac{1}{f_{+}^{3/2}{\lambda }^3}\right)$$ (3.5)

where for simplicity we have assumed that the concentration of charges in the coacervate has saturated at

$$f_{+}{\overline{c}}_{+}=f_{-}{\overline{c}}_{-}\simeq \frac{f_{+}^{3/2}}{b^3}$$ (3.6)

prior to ion binding. ${\overline{c}}_{+}$ and ${\overline{c}}_{-}$ are the optimal monomer concentrations of polycations and polyanions

Even in the cases where this assumption $u^{*}>f_{-}^{-1/2}$ fails, u^∗ predicted in eq. 3.5 is an acceptable estimate, as discussed in Section 2.2 for charge-symmetric coacervates below eq. 2.12. It is important to note that the onset of binding is dictated by the charge fraction of the lower-charged polycations and is insensitive to the charge on the polyanions.

3.2.1. Mixed Regime

As the polycations bind to the polyanion, the attraction of polycations to the polyanions with binding energy ΔF_{ionic bond} (eq. 3.4) is balanced by the short-range repulsion between the polycations (two-body in a good solvent and three-body in a θ-solution). Repulsion between these polycations results in their extension away from the polyanion backbone, forming a brush of side loops, tails, and bridges of the charge-asymmetric coacervate (Figure 5).

Figure 5:

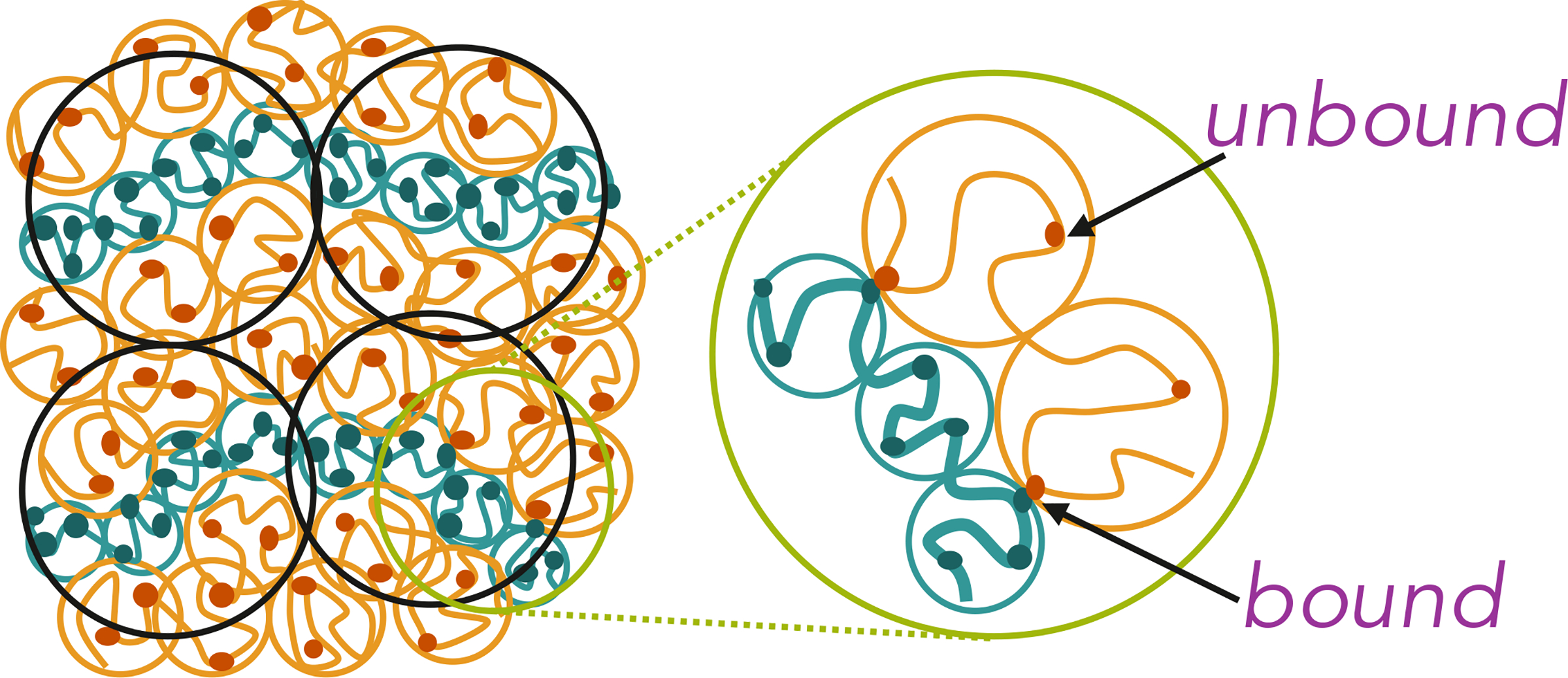
Formation of side loops, tails, and bridges in charge-asymmetric coacervates due to ionic bonds, bound pairs of positive and negative charges. A side loop is formed by a section of a polycation connected to the same polyanion by two ion pairs (cross-links). A bridge is a section of a polycation connected by ion pairs (cross-links) to two different polyanions.

Consider a bottlebrush-like configuration with a polyanion backbone and N₋/n_a side loops. Here n_a is the average number of monomers along the polyanion backbone between neighboring bound pairs of positive and negative charges. These bound pairs act as cross-links connecting polycation side loops to the polyanion backbone of the bottlebrush. The free energy of the bottlebrush per polyanion chain is

$$F=\frac{N_{-}}{n_{\text{a}}}\left(F_{\text{a}}+F_{\text{c}}+\Delta F_{\text{ionic}\text{bond}}\right)$$ (3.7)

where F_a is the free energy of the polyanion spacer containing n_a monomers, and F_c is the free energy of an extended side loop section of a polycation bound to the polyanion.

The free energy of a polyanion spacer of size r_a between neighboring ionic bonds consists of elastic and Coulombic parts

$$F_{\text{a}}\simeq k_{\text{B}}T\left[\frac{r_{\text{a}}^2}{b^2{n}_{\text{a}}}+l_{\text{B}}\frac{{\left(f_{-}{n}_{\text{a}}\right)}^2}{r_{\text{a}}}\right].$$ (3.8)

At low electrostatic strengths with low fraction of bound ions, F_a ≫ F_c, the tension in the polyanion spacer is controlled by the balance of electrostatic repulsion and the elastic free energy cost of stretching the polyanion backbone (eq. 3.8), and is not significantly influenced by the repulsion between polycation side loops. In this case, the size of the polyanion section containing n_a monomers is almost the same as in the absence of any binding (the fraction n_a/N₋ of the total length L₋ ≃ b²N₋/D_e− of the array of electrostatic blobs) with an average size

$$r_{\text{a}}\simeq b^2{n}_{\text{a}}/D_{\text{e}-}.$$ (3.9)

The free energy per one bottlebrush side loop in a θ-solvent at fixed spacer length r_a between neighboring side loops is the sum of elastic stretching and three-body repulsion free energy of n_c monomers in the pervaded volume of a side loop ~ $r_{\text{a}}{r}_{\text{c}}^2$

$$F_{\text{c}}\simeq k_{\text{B}}T\left[\frac{r_{\text{c}}^2}{b^2{n}_{\text{c}}}+b^6\frac{n_{\text{c}}^3}{{\left(r_{\text{a}}{r}_{\text{c}}^2\right)}^2}\right]$$ (3.10)

where r_c is the size of a side loop. The minimization of this free energy gives the optimal side loop size (the first section of the red line in Figure 6 and eq. 3.16 below)

$$r_{\text{c}}\simeq \frac{b^{4/3}{n}_{\text{c}}^{2/3}}{r_{\text{a}}^{1/3}}\approx r_{\text{c},0}{\left(\frac{r_{\text{c},0}}{r_{\text{a}}}\right)}^{1/3}$$ (3.11)

which is extended by the factor (r_c,0/r_a)^1/3 from the root-mean-square Gaussian size of the side loop,

$$r_{\text{c},0}\simeq n_{\text{c}}^{1/2}b\simeq b/f_{+}^{1/2}.$$ (3.12)

Thus, the corresponding free energy of repulsion between side loops is

$$F_{\text{c}}\approx k_{\text{B}}T{\left(\frac{r_{\text{c},0}}{r_{\text{a}}}\right)}^{2/3}$$ (3.13)

Figure 6:

Schematic illustrations and the dependence of the length scales on the dimensionless electrostatic interaction strength u for bottlebrush complexes of polyanion backbone and polycation loops and tails for the cases with (a) a self-similar carpet up to the polycation correlation length ξ₊ and (b) no self-similar carpet for u > u_cut−off. Teal line: polyanion correlation length ξ₋ (eq. 3.2). Orange line: polycation correlation length ξ₊ (eqs. 3.1, 3.26). Red line: size r_c of the smallest polycation side loop (eqs. 3.11, 3.16, 3.34). Blue line: optimal distance r_a between neighboring ionic bonds (eqs. 3.15, 3.33). Green line: average separation d₋ between neighboring negative charges (bound to or unbound from a charge on a polycation) along the polyanion backbone (eqs. 3.18, 3.20). Logarithmic axes.

An increase in the number of ionic bonds (and the corresponding decrease of the distance r_a between neighboring bonds) with increasing strength of electrostatic interactions u lowers the binding free energy per polyanion, but increases the free energy F_c of repulsion between side loops (eq. 3.13). At a high grafting density, the minimization of the free energy of the bottlebrush, eq. 3.7, with respect to n_a with a fixed backbone extension, corresponds to the balance of the ionic bond energy ΔF_{ionic bond} and the repulsion free energy F_c per shortest side loops (eq. 3.13 with r_c,0 from eq. 3.12)

$$F_{\text{c}}\simeq k_{\text{B}}T{\left(\frac{b}{r_{\text{a}}}\right)}^{2/3}{f}_{+}^{-1/3}\simeq \Delta F_{\text{ionic}\text{bond}}\simeq k_{\text{B}}T\left[\ln \left(f_{+}^{3/2}{\lambda }^3\right)+\frac{u}{\lambda }\right].$$ (3.14)

This balance leads to an optimal distance between neighboring ionic bonds—neighboring grafting points of the bottlebrush (first section of the blue line, Figure 6)

$$r_{\text{a}}\simeq \frac{b}{f_{+}^{1/2}}{\left[\ln \left(f_{+}^{3/2}{\lambda }^3\right)+\frac{u}{\lambda }\right]}^{-3/2}\approx r_{\text{c},0}{\left(\frac{\lambda }{u}\right)}^{3/2}\text{for}{u}^{*}<u\le u_{\text{x}}.$$ (3.15)

decreasing with increasing strength u of electrostatic interactions.

Since the average spacing between negative charges along the polyanion is smaller than the average distance r_c,0 ≃ b/f^1/2 between positive charges, in order to localize positive charges near negative charges densely distributed along the polyanion, the adsorbed polycations are stretched orthogonally away from the polyanion contour. Repulsion between densely-adsorbed polycations (three-body repulsion in a θ-solvent and two-body repulsion in a good solvent) forces them to extend away from the adsorbing backbone, forming a brush layer. The height of the brush is determined by the size of the linking segment, the average size of the polycation containing 1/f₊ monomers between the positive charges, which is the smallest loop between the polyanion adsorption sites. The brush thickness in the mixed bottlebrush/double-semidilute solution regime can then be obtained from eqs. 3.11, 3.12, 3.15 as

$$r_{\text{c}}\approx r_{\text{c},0}{\left(\frac{r_{\text{c},0}}{r_{\text{a}}}\right)}^{1/3}\simeq \frac{b}{f_{+}^{1/2}}{\left(\frac{u}{\lambda }\right)}^{1/2}\text{mixed}\text{regime}\text{for}{u}^{*}<u\le u_{\text{x}}$$ (3.16)

and corresponds to a polycation spacer extended by the factor (u/λ)^1/2 from its original size $r_{\text{c},0}\simeq b/f_{+}^{1/2}$ as the distance between neighboring ionic bonds decreases (first section of the red line, Figure 6). The extension of the chains relative to the unperturbed size of the isolated random coils $\left(R_{+}\simeq b{N}_{+}^{1/2}\right)$ reduces the conformational entropy of polycations in the adsorption layer. The repulsion energy between the polycation segments is on the order of k_BT per correlation blob of size ξ_brush and is balanced by the entropic elasticity. The resulting smallest correlation length of the polycations in the brush of loops (i.e., the correlation length of a blob closest to the polyanion inside the brush) is approximately the spacing between grafting points along the polyanion, r_a. The brush correlation length increases radially as ∼ r^1/2 in a brush with cylindrical symmetry,

$${\xi }_{\text{brush}}\simeq \sqrt{r{r}_{\text{a}}}\simeq \frac{b^{1/2}}{f_{+}^{1/4}}{\left(\frac{\lambda }{u}\right)}^{3/4}{r}^{1/2}$$ (3.17)

and as ∼ r in a brush with spherical symmetry (star-like gel coacervates, Appendix C). This brush correlation length decreases by a factor (λ/u)^3/4 with increased strength of electrostatic interactions. Thus, the bottlebrush complex of a strongly-charged polyanion, partially compensated by the weakly-charged bound polycations, consists of sections of polycation chains forming strongly-stretched minimal-size loops, extended in the cylindrical brush conformation.

The average spacing between the neighboring charges along a polyanion with an electrostatically-extended backbone is

$$d_{-}\simeq \frac{D_{\text{e}-}}{f_{-}{g}_{\text{e}-}}\simeq \frac{b{u}^{1/3}}{f_{-}^{1/3}}\text{for}u<u_{\text{t}}$$ (3.18)

This spacing d₋ increases with the strength of electrostatic interactions u, as depicted by the first section of the green line in Figure 6. At higher binding strength u > u_t, the tension in the polyanion bottlebrush backbone is controlled by repulsion between polycation side loops. At a crossover binding energy ΔF_{ionic bond} ≈ F_a ≈ F_c, the steric repulsion between polycation side loops is on the order of Coulomb repulsion between the charges along the polyanion. This crossover binding strength is on the order of thermal energy k_BT times the number of the polyanion electrostatic blobs along the spacer of size r_a (eq. 3.15) between neighboring ion pairs: (l_B/l)_t ≃ u_t/λ ≃ r_a/D_e−. The corresponding crossover electrostatic strength is

$$u_{\text{t}}\simeq \lambda \frac{r_{\text{a}}}{D_{\text{e}-}}\simeq \frac{f_{-}^{4/13}{\lambda }^{15/13}}{f_{+}^{3/13}}.$$ (3.19)

The average separation between neighboring charges along the sterically-extended backbone is

$$d_{-}\simeq \frac{r_{\text{a}}}{f_{-}{n}_{\text{a}}}\simeq b\frac{f_{+}^{1/2}}{f_{-}}{\left[\frac{u}{\lambda }+\ln \left(f_{+}^{3/2}{\lambda }^3\right)\right]}^{5/2}\approx \frac{b{f}_{+}^{1/2}{u}^{5/2}}{f_{-}{\lambda }^{5/2}}\text{for}{u}_{\text{t}}<u<u_{\text{x}}$$ (3.20)

where n_a is the number of monomers in a strand of size r_a (eq. 3.15) between two neighboring ionic bonds along the polyanion backbone and u_x will be defined below (eq. 3.25). This dependence of the separation between neighboring charges d₋ on the strength of electrostatic interactions u is shown by the second section of green line in Figure 6. Balancing the elastic energy of this strand and the binding energy of an ionic bond,

$$k_{\text{B}}T\frac{r_{\text{a}}^2}{b^2{n}_{\text{a}}}\simeq \Delta F_{\text{ionic}\text{bond}}$$ (3.21)

gives

$$n_{\text{a}}\simeq \frac{r_{\text{a}}^2}{b^2\left[\frac{u}{\lambda }+\ln \left(f_{+}^{3/2}{\lambda }^3\right)\right]}\approx \frac{{\lambda }^4}{f_{+}{u}^4}\text{for}{u}_{\text{t}}<u<u_{\text{x}}.$$ (3.22)

If the average distance d₋ between neighboring charges along the polyanion backbone is shorter than the optimal distance r_a between neighboring grafting points (eq. 3.15), there will be uncompensated charges along the polyanion with effective linear-charge-density

$${\gamma }_{-}^{\text{eff}}\approx 1/d_{-}-1/r_{\text{a}}>{\gamma }_{+}^{\text{eff}}.$$ (3.23)

The fraction d₋/r_a of polycation charges are bound to polyanions, while the rest remain as unbound charges along polycation chains within the charge-compensating coats around the polyanions. This case corresponds to a mixed regime with polycation charges disproportionated into two populations.

The number of uncompensated charges per spacer, using eq. 3.22,

$$f_{-}{n}_{\text{a}}-1\simeq \frac{f_{-}{\lambda }^4}{f_{+}{u}^4}-1$$ (3.24)

approaches zero (i.e., full compensation) at

$$u_{\text{x}}\simeq \lambda {\left(f_{-}/f_{+}\right)}^{1/4},$$ (3.25)

which increases as the one-fourth power of the asymmetry parameter f₋/f₊.

A polycation chain can be completely embedded in the brush with a series of extended linking segments along the polycation, each of which is connecting two polyanion adsorption sites. In this way, all the positive charges along the chain can be adsorbed onto the polyanion. However, some polycations in this conformation can unfold some of their extended linking segments and release associated negatively charged adsorption sites on the polyanion. These liberated negatively charged sites can form ion pairs with other adsorbed polycations without changing the adsorption energy. A few of the polycation side chains extend further away from the bottlebrush backbone into the next layer, forming a self-similar carpet^95,106,107 laying on top of a cylindrical brush formed by extended minimal loops of thickness r_c. As a result, the adsorbed polycations bind to the polyanion through loops of different sizes. Allowing the variation of polycation loop size reduces the entropic part of the free energy, making the adsorption layer thermodynamically more favorable than an adsorption layer consisting of only extended minimal polycation loops. Among the polycation segments (loops, tails, or bridges) of various sizes along the polyanion, the smallest loops formed by the linking segments are entirely located in the brush layer. In contrast, only the portions near the ends of a larger loop dwell in the brush, while the rest of the loop is located above the brush (e.g., green loop in Figure 7).

Figure 7:

Schematic illustrations in radial and axial projections of the bottlebrush under self-similar carpet structure. Polycation loops and tails (orange) are bound to the polyanion backbone (teal). The minimal loops of polycations without free charges are extended and form a brush layer with brush thickness r_c and the minimum brush correlation length ξ_brush. Several typical polycation chains are shown, with minimal loops in blue and extended linking segments entering the self-similar carpet in green. Sections outside the brush layer contain free charges and form a self-similar carpet with the first layer of size r_c,0 on the order of the size of the unperturbed Gaussian chain section between neighboring polycation charges.

For polymers above the brush, the first correlation blob of the self-similar carpet is of the optimal Gaussian size $r_{\text{c},0}\simeq b/f_{+}^{1/2}$, and contains 1/f₊ monomers of polycation chains. Several linking segments unfold into the next layer of the carpet and so forth. The self-similar carpet of polycations around the complex brush has a correlation length ξ_carpet increasing linearly with the distance r − r_c. The 3D number density of positive charges ${\left(\left(r-r_{\text{c}}\right)r_{\text{c},0}^2\right)}^{-1}$ decreases hyperbolically, while the line density of positive charges increases linearly $(r-r_{\text{c}})/r_{\text{c},0}^2$ with radial distance r. Thus, polycations form a two-layer structure, including a brush layer and a self-similar carpet on top of it on length scales up to the correlation length ξ₊ of the semidilute polycation coat.

The polycation correlation length ξ₊ is the cut-off distance of the concentration decay of the polycation two-layer coat (i.e., the polycation concentration levels off at a distance ξ₊ from the polyanion), which sets an upper limit for the size of the self-similar carpet. If the charges along the polyanion backbone are not significantly compensated and their line density is still on the order of γ₋, the cut-off correlation length of the carpet is the same as in a weak (liquid) coacervate⁵ (eq. 3.1, orange line in Figure 6):

$${\xi }_{+}\simeq \frac{b}{u^{1/3}{f}_{+}^{1/2}{f}_{-}^{1/6}}.$$ (3.26)

For strongly-charged polyanions with a high fraction of charged monomers,

$$f_{-}\gtrsim u^{-2},$$ (3.27)

the cut-off correlation length ξ₊ of the semidilute polycation coat saturates at a minimum size on the order of the ideal size $r_{\text{c},0}\simeq b/f_{+}^{1/2}$ of the linking segment, which is the size of the first layer in the self-similar carpet. Since the self-similar carpet is cut-off by the polycation correlation length ξ₊ and the size of the first correlation blob of the self-similar carpet is also the Gaussian size of a polycation linker r_c,0, no self-similar carpet exists for very strongly-charged polyanions (eq. 3.27). (Figure 9c)

Figure 9:

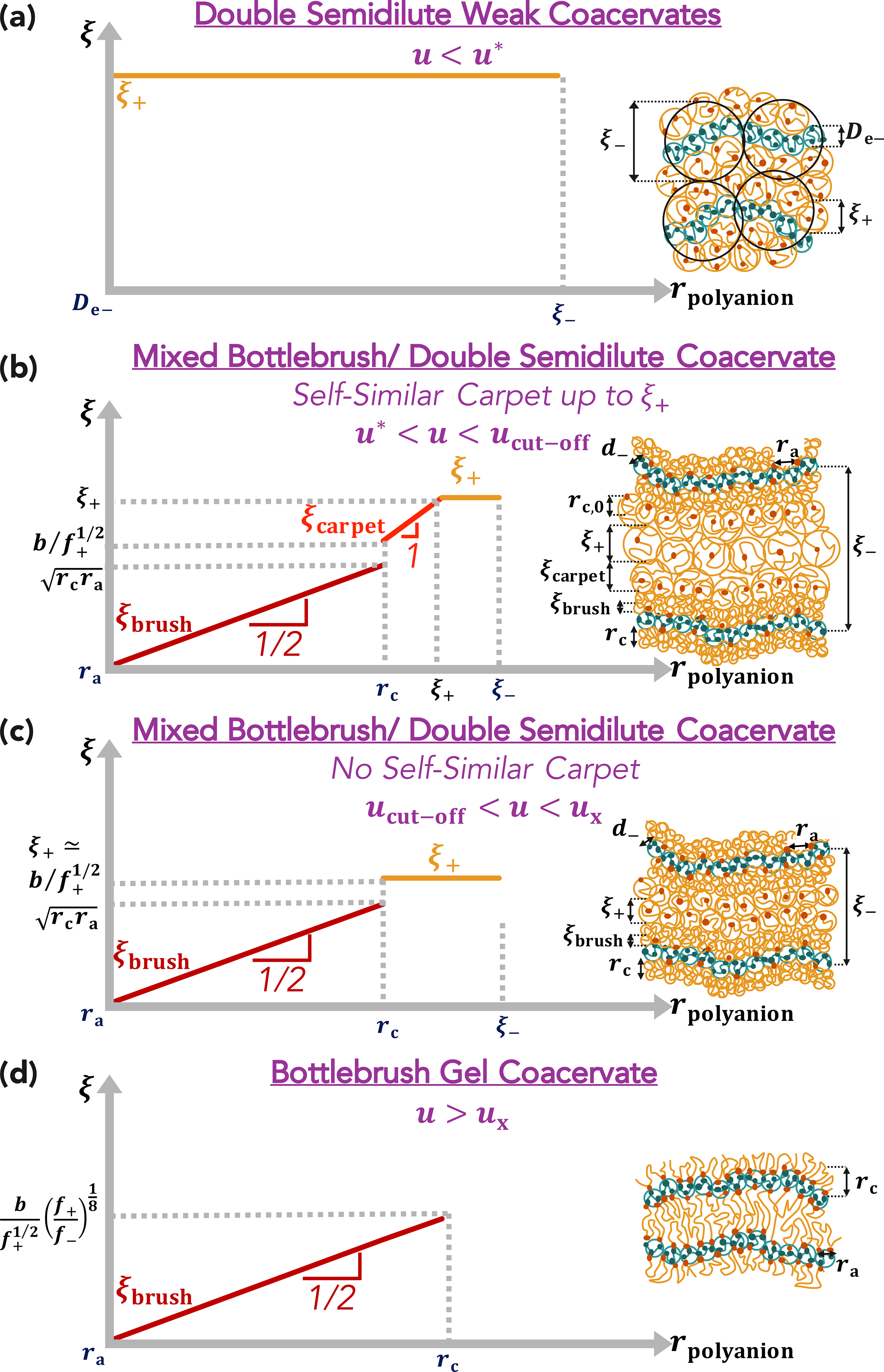
Schematic illustrations and the dependence of the correlation length of the polycation coat on the distance from the polyanion backbone (r_polyanion) for (a) double-semidilute weak coacervates (u < u^∗), (b) mixed bottlebrush/double-semidilute coacervates with self-similar carpet (u^∗ < u < u_cut−off), (c) mixed bottlebrush/double-semidilute coacervates without self-similar carpet (u_cut−off < u < u_x), and (d) bottlebrush gel coacervates u > u_x. Logarithmic axes.

However, the self-similar carpet can also be completely cut-off for ξ₊ > r_c,0, if the polycation correlation length is smaller than the extended brush size r_c > ξ₊ (Figure 8). This occurs for electrostatic strengths above the cut-off electrostatic strength,

$$u>u_{\text{cut-off}}\simeq {\left({\lambda }^3/f_{-}\right)}^{1/5}$$ (3.28)

This minimum cut-off correlation length is achieved in the mixed regime (i.e., prior to complete ion binding and gel formation at u_x, eq. 3.25), for strongly-charged polyanions,

$$f_{-}\gtrsim f_{+}^{5/9}/{\lambda }^{8/9}.$$ (3.29)

In this case, with f₋ satisfying inequality 3.29, the electric field of the higher charge-density polyanion is strong enough for the correlation length ξ₊ of the polycation coat to be smaller than the brush width r_c for u < u_x, resulting in no self-similar carpet around the bottlebrush complex for u_x > u > u_cut−off (Figure 6b). For lower f₋ the electric field attracting polycations to polyanions is weak, and the self-similar carpet forms around the brush layer up to the cut-off distance ξ₊ (Figures 6a and 9b).

Figure 8:

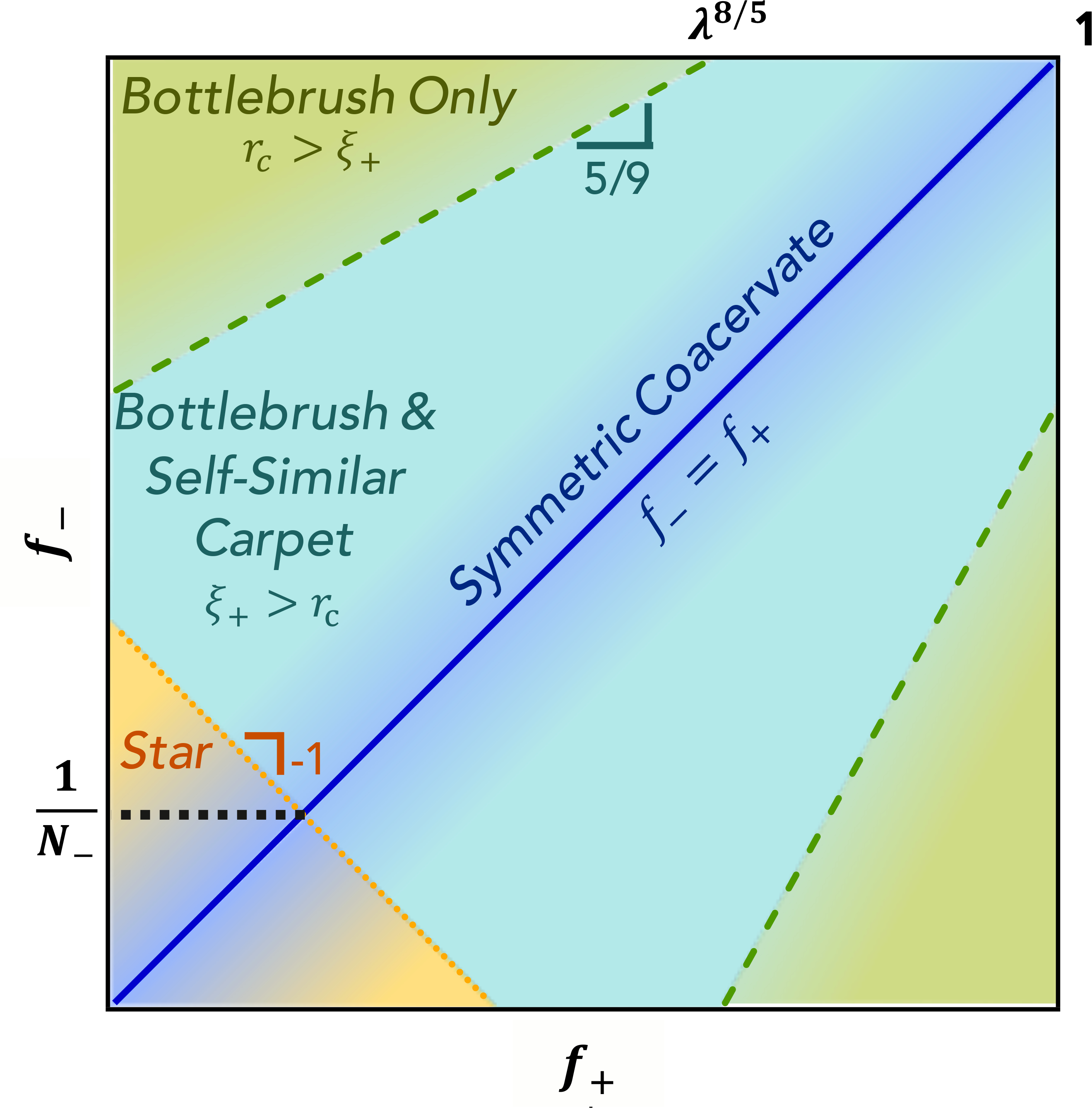
The relative values of the fraction of charged monomers of the polycations, f₊, and the polyanions, f₋, dictate the structure of the coacervate complex. Strong coacervates can be charge-symmetric (blue shaded region, blue line indicating f₊ = f₋) or chargeasymmetric. Charge-asymmetric coacervates can be bottlebrush-like with cylindrical symmetry or star-like (orange shaded region, Appendix C) for short polyanions or polycations with long linking segments. Bottlebrush complexes can be surrounded by self-similar carpets for small electric fields attracting the polycations to the polyanions (teal shaded region, ξ₊ > r_c) or without self-similar carpets for stronger charge asymmetries (green shaded region, ξ₊ < r_c. Note: We have assumed polyanions of higher charge-density than polycations (γ₋ > γ₊ or f₋ > f₊) in the text for definiteness; this corresponds to the upper left region of the figure, with the lower right showing the mirrored regions for γ₊ > γ₋. Logarithmic axes.

Thus, the mixed regime corresponds to two cases: a bottlebrush complex surrounded by a self-similar carpet on length scales smaller than the cut-off correlation length of the polycations ξ₊, and a bottlebrush complex without a self-similar carpet for ξ₊ < r_c. At the onset of the mixed regime, a self-similar carpet will form along with the brush. However, for higher electrostatic strengths (u_cut−off < u < u_x) the self-similar carpet would be completely cut-off and will not exist. Figure 9 shows the variation of the correlation length of the polycation coat with the distance from the polyanion backbone (r_polyanion). Weak coacervates have a nearly uniform correlation length within a scaling approach, neglecting logarithmic corrections,⁵ as shown in Figure 9a. Gel coacervates have a correlation blob size ξ_brush that increases radially with the brush thickness according to eq. 3.17 until the brush thickness r_c (Figure 9b,c,d). If the bulk polycation correlation length ξ₊ > r_c, a self-similar carpet forms with correlation blob size ξ_carpet increasing linearly with distance from the polyanion up to distance ξ₊ from the polyanion. The polycation concentration profile is almost uniform at larger distances r_polyanion from the polyanion (Figure 9b). If ξ₊ < r_c, there is no self-similar carpet on top of the brush layer and the polycation correlation length at distances from the polyanion r_polyanion larger than the size of the brush r_c is nearly uniform (Figure 9c). At higher strengths of electrostatic interactions u > u_x, there are no unbound charges; the separation between polyanions is on the order of the polycation brush thickness r_c, and the correlation blob size of those polycations ξ_brush increase radially with the distance r_polyanion from the polyanion according to eq. 3.17 (Figure 9d).

3.2.2. Bottlebrush Regime

The coacervate forms a gel if there is on the order of one bridging polycation per polyanion. This requires more than one grafting site per polyanion, that is, r_a < L₋:

$$N_{-}\gtrsim n_{\text{a}}\simeq \frac{{\lambda }^4}{f_{+}{u}^4}.$$ (3.30)

and for polyanions to be separated by less than the chain size of the polycations ξ₋ < R₊:

$$N_{+}\ge \frac{f_{-}^{1/6}}{f_{+}^{3/2}{u}^{2/3}}.$$ (3.31)

Equivalently, these conditions set an electrostatic strength necessary for gelation,

$$u_{\text{gel}}\simeq \{\begin{array}{ll}\frac{\lambda }{f_{+}^{1/4}{N}_{-}^{1/4}}\hfill & \text{for}\lambda >\frac{f_{-}^{1/4}{N}_{-}^{1/4}}{f_{+}^2{N}_{+}^{3/2}}\hfill \\ \frac{f_{-}^{1/4}}{f_{+}^{9/4}{N}_{+}^{3/2}}\hfill & \text{for}\lambda <\frac{f_{-}^{1/4}{N}_{-}^{1/4}}{f_{+}^2{N}_{+}^{3/2}}\hfill \end{array}.$$ (3.32)

At and above u_gel, there are bridges between neighboring polyanions, forming a cross-linked reversible network.

With a further increase in the strength of the electrostatic interactions above u_x, all charges bind into ionic bonds, and the coacervate consists entirely of the bottlebrush gel (Figures 4 and 9d). In this case, the polycation spacers are either in an extended loop configurations, with both end charges bound to charges of the same polyanion, or in the extended bridge conformation connecting different polyanions. The distance between neighboring polyanions is controlled by the size r_c of these bridges containing 1/f₊ polycation monomers. In this bottlebrush gel regime, the conformations of the polyanion backbone and of side loops and bridges (uncharged spacers of polycations) are independent of the strength of electrostatic interactions (as long as u > u_x) and depend only on the balance of the elastic free energies of backbone and side chains (the right sections of horizontal lines for u > u_x in Figure 6). Assuming Gaussian chain statistics on length scales smaller than the chain sections between the ionic bonds, the free energy of the backbone is $k_{\text{B}}T{r}_{\text{a}}^2/r_{\text{a},0}^2$ per spacer containing 1/f₋ monomers with mean square unperturbed Gaussian size $r_{\text{a},0}^2\simeq b^2/f_{-}$, while the free energy per side chain section is given by eq. 3.13 with $r_{\text{c},0}\simeq b/f_{+}^{1/2}$ defined in eq. 3.12. Minimizing the free energy in eq. 3.7 with n_a = 1/f₋ with respect to r_a at the optimal value u_x (eq. 3.25) and above it, we obtain the size of the polyanion spacer (Figure 6)

$$r_{\text{a}}\simeq \frac{b}{f_{+}^{1/8}{f}_{-}^{3/8}}\simeq \frac{b}{f_{-}^{1/2}}{\left(\frac{f_{-}}{f_{+}}\right)}^{1/8}\text{bottlebrush}\text{gel}\text{regime}\text{for}u\ge u_{\text{x}}$$ (3.33)

and the size of the side chain sections (Figures 6)

$$r_{\text{c}}\simeq \frac{b{f}_{-}^{1/8}}{f_{+}^{5/8}}\simeq \frac{b}{f_{+}^{1/2}}{\left(\frac{f_{-}}{f_{+}}\right)}^{1/8}\text{bottlebrush}\text{gel}\text{regime}\text{for}u\ge u_{\text{x}}$$ (3.34)

which is the spacing between polyanion backbones. The ionic binding stretches both polycations and polyanions by the factor

$${\left(f_{-}/f_{+}\right)}^{1/8}\simeq {\left(u_{\text{x}}/\lambda \right)}^{1/2}$$ (3.35)

with respect to the Gaussian size of the corresponding spacer. This degree of stretching relative to the Gaussian strands between crosslinks is reduced to unity in the charge-symmetric limit, as predicted for strong θ-coacervates (eq. 2.20), and increases as the one-eighth power of the asymmetry factor f₋/f₊.

Our scaling predictions for the brush layer are thus far based on a scaling model^108–113 assuming that all polycations uniformly stretch to a height r_c. There is a higher entropy state in which there is a distribution of side chain sizes of polycations.^114–118 Some polycation side chains in this distribution do not reach the outermost blob of the brush while others extend further beyond r_c. The side chains of neighboring bottlebrush complexes mix in an interpenetration zone with a size δ, larger than the size ${\xi }_{\text{brush}}\left(r_{\text{c}}\right)\simeq \sqrt{r_{\text{c}}{r}_{\text{a}}}$ (eq. 3.17) of the terminal blob of our simplified model with identical side chain sizes. The side chains that do not reach the interpenetration layer can only form loops or tails, while the side chains that reach the interpenetration layer can form loops, tails, or bridges between neighboring bottlebrushes. If one assumes a parabolic potential acting on brush segments in the outer shell of the bottlebrush structure,^{116,119–121} the thickness of the interpenetration layer is estimated to be

$$\delta \simeq \frac{b^{4/3}}{f_{+}^{2/3}{r}_{\text{c}}^{1/3}}\simeq \frac{b}{f_{+}^{1/2}}{\left(\frac{f_{+}}{f_{-}}\right)}^{1/24}.$$ (3.36)

Neighboring cylindrical bottlebrush complexes have volume of contact

$$V\simeq r_{\text{a}}{r}_{\text{c}}^{3/2}{\delta }^{1/2}\simeq \frac{b^3}{f_{+}^{3/2}}{\left(\frac{f_{+}}{f_{-}}\right)}^{5/24},$$ (3.37)

per length r_a along the contour of the bottlebrush. The attraction energy between two bottlebrushes per length r_a is k_BT per blob within the contact volume,

$$\Delta F^{*}\simeq \frac{V}{{\delta }^3}{k}_{\text{B}}T\simeq \frac{r_{\text{a}}{r}_{\text{c}}^{3/2}}{{\delta }^{5/2}}{k}_{\text{B}}T\simeq {\left(\frac{f_{+}}{f_{-}}\right)}^{1/12}{k}_{\text{B}}T.$$ (3.38)

The number density of bottlebrush sections of length r_a is equal to the number density of polycation linking segments,

$$v\simeq f_{+}{\overline{c}}_{+}\simeq \frac{1}{r_{\text{a}}{r}_{\text{c}}^2}\simeq \frac{f_{+}^{3/2}}{b^3}{\left(\frac{f_{-}}{f_{+}}\right)}^{1/8}.$$ (3.39)

A small shear deformation strain on the order of ϵ changes the typical distance between neighboring bottlebrushes by distance ϵr_c. The strain induced by such a deformation in the interpenetration layer (ϵr_c/δ) is amplified by the factor r_c/δ due to the lower energetic cost of stretching the nearly ideal interpenetration layer relative to the strongly stretched and therefore much stiffer parts of the brush. The energy of deformation is proportional to the square of the strain amplification factor, and thus, the plateau shear elastic modulus G of the bottlebrush gel coacervate is

$$G\simeq v\Delta F^{*}\frac{r_{\text{c}}^2}{{\delta }^2}\simeq \frac{1}{{\delta }^3}{\left(\frac{r_{\text{c}}}{\delta }\right)}^{3/2}{k}_{\text{B}}T\simeq f_{+}^{3/2}{\left(\frac{f_{-}}{f_{+}}\right)}^{3/8}\frac{k_{\text{B}}T}{b^3},$$ (3.40)

which reduces in the charge-symmetric case f₊ = f₋ to the prediction of eq. 2.21 for charge-symmetric strong θ-coacervates. For electrostatic strengths above u_x, the network structure and its modulus are u-independent, until attractive dipolar interactions between the bound ion pairs form quadrupoles and higher-order multiplets, as discussed in Section A.

3.3. Salt Effects on Charge-Asymmetric Coacervates

The addition of salt leads to the screening of the electrostatic interactions, modifying the structure of the coacervate as the Debye length (eq. 2.22) becomes comparable to the hierarchy of length scales present in charge-asymmetric coacervates (Figure 10). At low salt concentrations with Debye screening length r_D > ξ₋, there is no effect of added salt on the coacervate. This low-salt regime corresponds to salt concentrations,

$$c_{\text{s}}<c_{\text{s},1}\simeq \frac{f_{+}^{3/2}{f}_{-}^{-1/6}}{b^3{u}^{1/3}}\text{for}u<u_{\text{x}}$$ (3.41)

For weak double-semidilute coacervates, u < u^∗, and for mixed double-semidilute/bottlebrush coacervates with some unpaired charges of polycations and polyanions, u^∗ < u < u_x, salt affects the structure of the coacervate in the intermediate regime with Debye length ξ₊ < r_D < ξ₋. In this salt regime with salt concentrations

$$c_{\text{s},1}<c_{\text{s}}<c_{\text{s},\text{h}}\simeq \frac{f_{+}{f}_{-}^{1/3}}{b^3{u}^{1/3}}\simeq {\left(\frac{f_{-}}{f_{+}}\right)}^{1/2}{c}_{\text{s},1}\text{for}u<u_{\text{x}}$$ (3.42)

salt ions screen the electrostatic repulsion between polyanions on scales larger than the Debye radius, but attraction between oppositely-charged polyelectrolytes predominates on smaller length scales r < r_D. The thickness of the polycation coat decreases with increasing salt concentration from its salt-free value ξ₋ to the Debye length r_D (Figure 10b–e):

$${\xi }_{-}^{\text{s}}\simeq r_{\text{D}}\approx {\left(bu{c}_{\text{s}}\right)}^{-1/2}\text{for}u<u_{\text{x}}$$ (3.43)

releasing some of the unbound polycations. However, in the mixed regime with both bound and unbound polycations, the Coulomb attraction of charges within the brush layer and the self-similar carpet is weaker than the binding energy, short range repulsion, and stretching free energies between adsorbed polycations. Therefore, these layers are unaffected by salt, as long as the salt does not dissociate the ion pairs.

Figure 10:

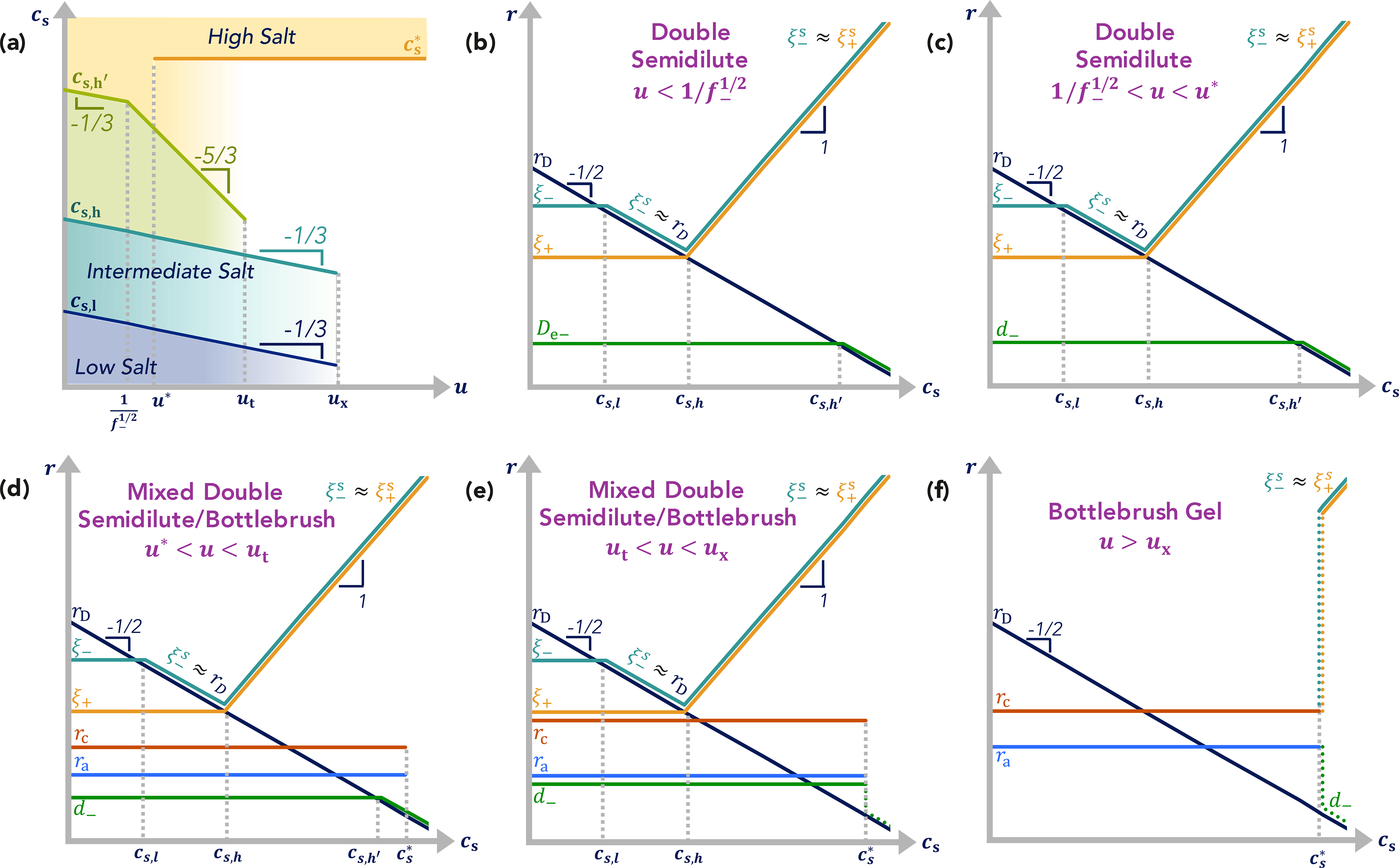
(a) Crossover salt concentrations of double-semidilute/bottlebrush gel θ-coacervates as a function of electrostatic interaction strength. (b-c) Important length scales of charge-asymmetric θ-coacervates at electrostatic strengths (b) $u<1/f_{-}^{1/2}$, (c) $1/f_{-}^{1/2}<u<u^{*}$, (d) u^∗ < u < u_t, (e) u_t < u < u_x, and (f) u > u_x as a function of salt concentration. Logarithmic axes.

In the high-salt regime with r_a < r_D < ξ₊, corresponding to salt concentrations c_s > c_s,h, the interaction between oppositely-charged polyions can be described as an effective two-body attraction (as discussed in detail for charge-symmetric coacervates in Section 2.2) in a solution of elementary charges of number densities $f_{+}{\overline{c}}_{+}$ and $f_{-}{\overline{c}}_{-}$, represented by the effective negative second virial coefficient $-l_{\text{B}}{r}_{\text{D}}^2$ and the effective free energy density

$$-k_{\text{B}}T{l}_{\text{B}}{r}_{\text{D}}^2\left(f_{+}{\overline{c}}_{+}\right)\left(f_{-}{\overline{c}}_{-}\right)\simeq -k_{\text{B}}T\frac{f_{+}^{9/2}{f}_{-}^{3/2}}{b^{12}{c}_{\text{s}}^3}$$ (3.44)

where the polycation concentration is ${\overline{c}}_{+}\simeq {\left(f_{+}^3{f}_{-}\right)}^{1/2}{b}^{-6}{c}_{\text{s}}^{-1}$ and the polyanion concentration is ${\overline{c}}_{-}\simeq f_{+}^2{b}^{-6}{c}_{\text{s}}^{-1}$. The total charge on the polyanions in the coacervate is higher than the total charge on the polycations, $f_{-}{\overline{c}}_{-}/f_{+}{\overline{c}}_{+}~{\left(f_{-}/f_{+}\right)}^{1/2}$.⁵ Attraction between polycations and polyanions is stabilized by short-range repulsion on the order of k_BT at the correlation length (Figure 10b–e):

$${\xi }^{\text{s}}\simeq {\xi }_{+}^{\text{s}}\simeq {\xi }_{-}^{\text{s}}\simeq \frac{b^4{c}_{\text{s}}}{f_{+}^{3/2}{f}_{-}^{1/2}}\text{for}{c}_{\text{s}}>c_{\text{s},\text{h}},$$ (3.45)

which is larger than in the case of charge-symmetric θ-coacervates by the three-halves power of the asymmetry factor, (f₋/f₊)^3/2. The structure of this coacervate in the high salt regime c_s > c_s,h is similar to the “scrambled egg” symmetric coacervate,^5,86 a dense packing of correlation blobs of size ξ^s with half of the blobs containing polyanion sections and half containing polycation sections. In the mixed regime, u^∗ < u < u_x, all polycations with unpaired charges have been released from the coacervate, and the only unpaired charges are on polyanions or on polycations in the self-similar carpet. The salt does not affect the structure of the bottlebrush gel (u ≥ u_x) in the high-salt regime for the Debye screening length l < r_D < ξ₊ (l is the ionic bond length), since the distance between the polyanions is equal to the loop size, ξ₋ ≈ r_c (Figure 10d).

In both the weak coacervate and in the mixed regime, for electrostatic interaction strengths u < u_t, and at still higher salt concentrations,

$$c_{\text{s}}>c_{\text{s},{\text{h}}^{\prime }}\simeq \{\begin{array}{ll}\frac{f_{-}^{4/3}}{b^3{u}^{1/3}}\hfill & \text{for}u<1/f_{-}^{1/2}\hfill \\ \frac{f_{-}^{2/3}}{b^3{u}^{5/3}}\hfill & \text{for}1/f_{-}^{1/2}<u<u_{\text{t}}\hfill \end{array}$$ (3.46)

the electrostatic repulsion of like-charges is screened, reducing the stretching of polyanion backbone, so that for $u<1/f_{-}^{1/2}$ electrostatic blobs containing multiple charges are separated by a distance of the Debye length, D_e− ≈ r_D (Figure 10b) and for $1/f_{-}^{1/2}<u<u_{\text{t}}$ adjacent charges are separated by a distance of the Debye length, d₋ ≈ r_D (Figure 10c,d). The crossover between the two scaling regimes occurs at $u\simeq 1/f_{-}^{1/2}$ where there is on average one charge per electrostatic blob. Recall that, for higher electrostatic interaction strengths, u > u_t, the stretching of the polyanion occurs due to steric repulsion of the polycation side loops (eq. 3.20) and is unaffected by an increase in the salt concentrations above $c_{\text{s},{\text{h}}^{\prime }}$ (Figure 10e,f).

As discussed in Section 2.4 for charge-symmetric strong coacervates, the bound ion pairs will begin to dissociate above a critical salt concentration, $c_{\text{s}}^{*}$. Depending on the range of salt concentrations over which all bound charges dissociate, the structure of a strong coacervate will revert to either a mixed double-semidilute/bottlebrush coacervate or a weak double-semidilute coacervate at the same salt concentrations (Figure 10). Ultimately, at high enough salt, all ion pairs will be dissociated, and the structure will be almost the same as that of a weak double-semidilute coacervate at high-salt conditions. At these high-salt conditions, the chain conformations of the polycations are Gaussian in both charge-symmetric and charge-asymmetric θ-coacervates. In contrast to charge-symmetric θ-coacervates with Gaussian conformations of all polymers, in charge-asymmetric θ-coacervates the conformations of polyanions are substantially non-Gaussian and are similar to conformations of the same chains in a polyelectrolyte solution at the same salt and polymer concentration. The conformations of polyanions in high-salt charge-asymmetric coacervates can be described as linear arrays of electrostatic blobs of size D_e,− up to the Debye length r_D, self-avoiding walks on length scales between r_D and ξ^s, and random walks of correlation volumes on length scales exceeding ξ^s.⁵ For even higher salt concentrations ($c_{\text{s}}>c_{\text{s},{\text{h}}^{\prime }}$, eq. 3.46) with Debye radius smaller than polyanion electrostatic blob size, r_D < D_e,−, polyanions are ideal on larger scales than the correlation blob ξ^s (eq. 3.45) as well as on length scales smaller than the thermal blob size ${\xi }_{\text{T}}\simeq D_{\text{e},-}^3/r_{\text{D}}^2$, which both increase proportionally to the salt concentration. In symmetric coacervates, with $f_{+}=f_{-},{\xi }^{\text{s}}\simeq {\xi }_{\text{T}}$, but the range of self-avoiding behavior increases with the three-halves power of the asymmetry parameter ξ^s/ξ_T ≃ (f₋/f₊)^3/2.⁵

4. Conclusions

We have extended a scaling theory of coacervates formed from mixtures of oppositely-charged polyelectrolytes to the strong association regime with electrostatic interaction energy between two elementary charges greater than the thermal energy k_BT, at which the formation of pairs of bound ions occurs. The structure of the coacervate is determined by the balance of electrostatic attraction between oppositely-charged polyelectrolytes, electrostatic repulsion between like-charged polyelectrolytes, short-range repulsion, and chain elasticity.

The structure of the coacervate is a semidilute polymer solution, and as such, is molecular-weight independent. Molecular weight effects on phase equilibria, however, have been observed in experiments and simulations and are due primarily to the stability of the isolated chains and globular complexes in dilute solution and resultant shifts of the critical point and equilibrium concentration of the supernatant. Further, chemical incompatibility as described by the Flory–Huggins χ parameter have been assumed to be negligible in this model. Such effects could be included in the description in the future — the balance of chemical incompatibility with ionic binding strength can lead to microphase separation⁷⁴ or the absence of coacervation.

For salt-free, charge-symmetric θ-coacervates with D_e− = D_e+ = D_e, the weak coacervate is a liquid with a dense packing of these electrostatic blobs with neighboring oppositely-charged blobs of size D_e attracting each other with energy on order of k_BT. This attraction is stabilized by short-range non-electrostatic repulsion with an energy on the order of k_BT between chain sections of size D_e. As the strength of electrostatic interactions is increased, the correlation length ξ = D_e decreases to a Gaussian size of a strand between neighboring charges b/f^1/2, and the concentration of the charge-symmetric coacervate saturates at f^1/2/b³. Further increase in the electrostatic interaction strength results in the formation of bound ion pairs. These charge-symmetric strong coacervates form isotropic randomly crosslinked networks with a correlation length of Gaussian size between the bound ion pairs. At even higher electrostatic strengths, the bound ion pairs can aggregate into higher order ionic clusters, which are balanced by chain elasticity and short-range repulsion, and resemble ionomers or micelles with dense ionic cores and coronas of neutral chain segments.

The addition of salt screens the electrostatic interactions in the coacervates on the scale of the Debye length r_D. At low salt concentrations with Debye length larger than the electrostatic blob size, r_D > D_e, the structure of the charge-symmetric weak coacervate is unperturbed by the salt. At higher salt concentrations, r_D < D_e, the unpaired ions interact through screened Coulomb potentials resulting in an effective two-body attraction of oppositely-charged polyions balanced by short-ranged excluded volume interactions at a distance of the electrostatic correlation length, ξ^s. The weak coacervate in the high salt regime is a dense packing of blobs of size ξ^s. For strong coacervates with many ion pairs, the structure of the coacervate is unperturbed by the addition of salt until the ion pairs dissociate and the gel is dispersed.

In the charge-asymmetric case with stronger polyanion intramolecular repulsion D_e− < D_e+, the weak coacervate is a mixture of two interpenetrating polyelectrolyte solutions characterized by two correlation lengths, ξ₊ < ξ₋. The chain conformations of both polycations and polyanions in the coacervates are similar to their conformations in the corresponding pure polyelectrolyte solutions of the same corresponding concentrations. The weaker-charged polycations are adsorbed on the stronger-charged polyanions, forming charge-compensating coats around them. This electrostatic attraction of polycations to polyanions is balanced by a short-ranged repulsion between polycations (three-body in a θ-solvent and two-body in a good solvent). The thickness of the polycation coat is the interpolyanion correlation length ξ₋, and in salt-free mixtures it is determined by the length scale at which the polycation coat compensates the polyanion charge. With an increase in the strength of electrostatic interactions, the polyanion chains extend, and the polycation coat is drawn tighter to the polyanion. At higher electrostatic interaction strengths, opposite charges form bound ion pairs, resulting in the formation of a mixed ionic/screening coat coacervate and, ultimately, at an even higher electrostatic strength, an ionic network of bottlebrush-like polyanion backbones with polycation side loops and bridges. For polycations with very long spacers between positively charges or very short polyanions, the gel coacervates are star-like (Appendix C).

In the mixed regime of charge-asymmetric coacervates, the salt screens the electrostatic interactions, characterized by a hierarchy of scales, on the scale of the Debye length. At low salt concentrations, with Debye length longer than the polyanion correlation length (for r_D > ξ₋), the structure of the coacervate is almost the same as in the salt-free case. For intermediate salt concentrations with a Debye length between the two correlation lengths, ξ₊ < r_D < ξ₋, unbound polycations are released and the thickness of the polycation coat decreases to the order of the Debye radius r_D. At higher salt conditions with the Debye length smaller than the polycation side loops ξ₊ > r_D, all unbound polycations are released from the screening coat, since all the unpaired charges along the polyanion backbone are screened from the ionic content. The bound ion pairs do not dissociate until an even higher salt concentration, which is ion-specific and chemistry dependent. In the bottlebrush regime of charge-asymmetric coacervates, the presence of many bound ion pairs in the coacervate prevents structural rearrangement due to salt screening up to their dissociation.

The scaling model predictions outlined above are expected to be useful in the design and development of new coacervate materials. These results are the first comprehensive description of the structure of coacervates formed from oppositely-charged polyelectrolytes as a function of charge-density asymmetry, added ionic content, and electrostatic interaction strength. In the low charge-density limit, the results are consistent with previous scaling models, molecular dynamics simulations, the random phase approximation, and field-theoretic simulations. In the high charge-density limit, the results for charge-symmetric strong coacervates are consistent with predictions from transfer-matrix theory.

The transition from weak to strong coacervates can be systematically tested by preparing a coacervate of hydrophilic polyelectrolytes with symmetric or asymmetric charge-density (such as quaternized poly(diallyl dimethyl ammonium) and neutralized poly(acrylic acid) or polymeric ionic liquids based on poly(allyl glycidyl ether)¹²² of different charge fractions) in a salt-free aqueous solution. Isotropic, charge-symmetric coacervates correspond to f₋/f₊ ≈ 1, while, bottlebrush gel coacervates are accessible for charge asymmetries f₋/f₊ ≳ 10, and star-like gel coacervates (Appendix C for f₋/f₊ ≃ (f₋N₋)², i.e., on the order of f₋ ≈ 1 and f₊ ≈ 0.01 for a short polyanion with degree of polymerization N₋ ≈ 10).

The strength of electrostatic interactions can be increased by changing the solvent through dialysis from water (or higher dielectric constant solvents such as formamide) to lower dielectric constant solvents such as acetonitrile or methanol, possibly without significantly affecting the solvent quality. Exchanging the solvent from water to methanol increases u by a factor of 2−3, while dialyzing to lower dielectric constant solvents could expand the range of u further, solubility permitting. Tetrahydrofuran–water mixtures are another option for maintaining similar solvent quality while altering the dielectric constant of the medium. The polymer concentration in the complexes can be measured by weighing dried complexes. Free salt or counter-ions content can be measured by solution conductivity measurements. The formation of ion pairs can be detected by an increase in the elastic modulus. The structural predictions can be tested by scattering experiments; X-ray or neutron scattering can be used to determine the overall polymeric structure and neutron scattering using isotopically-labeled polyions can be used to selectively visualize the structural correlations of polycations or polyanions individually. Future work seeks to develop theoretical models to predict the mechanics and dynamics of gel coacervates.

E Nomenclature

Charge-Symmetric Coacervates

k_BT

thermal energy

N

polyelectrolyte degree of polymerization

l_B

Bjerrum length

ϵ

solvent dielectric constant

e

elementary charge

b

Kuhn length

u ≡ l_B/b

dimensionless Bjerrum length (eq. 2.1)

D_e

electrostatic blob size (eq. 2.3, 2.15)

f

fraction of charged monomers

g_e

number of monomers in an electrostatic blob

γ

linear number density of charges (eq. 2.4)

ξ

correlation length (eq. 2.5, 2.20)

$\overline{c}$

polyion monomer concentration in the coacervate (eq. 2.6, 2.8, 2.26)

γ^eff

effective line density of charges (eq. 2.9)

l

ionic bond length

ΔFionic bond

ionic bond ionic binding energy (eq. 2.10)

λ ≡ l/b

dimensionless ionic bond length (eq. 2.11)

u^∗

crossover electrostatic strength to form ion pairs (eq. 2.12)

${\overline{c}}_{\text{bound}\text{ions}}$

number density of bound ions in the coacervate (eq. 2.13)

V_c

capture volume

$\tilde{f}$

effective fraction of charged monomers

${\overline{c}}_{\text{free}\text{ions}}$

number density of free charges in the coacervate (eq. 2.14)

d_{ion pairs}

average distance between ion pairs (eq. 2.16, 2.18, 2.20)

u_x

crossover electrostatic strength for fully-crosslinked network (eq. 2.17)

u_gel

crossover electrostatic strength for gelation (eq. 2.19)

G

shear modulus (eq. 2.21)

υ

number density of network strands

r_D

Debye length (eq. 2.22)

c_s

salt concentration

c_s,h

high-salt concentration (eq. 2.23)

ξ^s

electrostatic correlation length in coacervates with added salt (eq. 2.25)

g

number of monomers in a correlation blob

$c_{\text{s}}^{*}$

critical dissociation salt concentration

Charge-Asymmetric Coacervates

ν

general scaling exponent, = 1/2 for θ-solvents and = 0.588 for good solvents

ξ₊,ξ₋

correlation length of polycations (eq. 3.1), polyanions (eq. 3.2)

L₋

length of the array of electrostatic blobs of the polyanion

R₊,R₋

end-to-end distance of polycations, polyanions (eq. 3.3)

ΔF_{ionic bond}

ionic binding energy (eq. 3.4)

u^∗

crossover electrostatic strength to form ion pairs (eq. 3.5)

n

size of a chain segment

f₋/f₊

asymmetry factor

r_c

optimal size of a side loop (eq. 3.11, 3.16, 3.34)

rc,0

root-mean-square Gaussian size of a side loop (eq. 3.12)

r_a

optimal distance between neighboring ionic bonds (eq. 3.15, 3.33)

ξ_brush

correlation length in the brush layer (eq. 3.17)

d₋

average spacing of neighboring charges (eq. 3.26, 3.28)

u_t

crossover electrostatic strength to sterically-extend polyanion backbone (eq 3.27)

ξ_carpet

correlation length in the carpet layer

${\gamma }_{-}^{\text{eff}},{\gamma }_{+}^{\text{eff}}$

effective linear number-density of charges along polyanion, polycation

u_x

crossover electrostatic strength for fully-crosslinked network (eq. 3.21)

u_cut−off

crossover electrostatic strength for cut-off of self-similar carpet (eq. 3.24)

u_gel

crossover electrostatic strength for gelation (eq. 3.32)

δ

thickness of the interpenetration layer (eq. 3.36)

V

contact volume (eq. 3.37)

ΔF^∗

bridging attraction energy (eq. 3.38)

υ

number density of polycation linking segments (eq. 3.39)

G

shear modulus (eq. 3.40)

u_cond,+,u_cond,−

crossover electrostatic strength to condense counter-ions on polycations, polyanions

c_s,l

low-salt concentration (eq. 3.41)

c_s,h

high-salt concentration (eq. 3.42)

c₊,c₋

monomer concentration of polycations, polyanions

ξ_s

electrostatic correlation length in coacervates with added salt (eq. 3.45)

$c_{\text{s},{\text{h}}^{\prime }}$

higher salt concentration (eq. 3.46)

$c_{\text{s}}^{*}$

critical dissociation salt concentration

A. Strong Coacervates with Ionic Aggregates

At higher values of the electrostatic strength, u, there is a cascade of transitions as ion pairs in the strong coacervate, which can be approximated as permanent dipoles, aggregate into higher-order multiplets, such as quadrupoles, hexapoles, and octapoles, lowering their Coulomb energy. Analogously to micelles, each multiplet is surrounded by a corona formed by neutral chain sections linking charged monomers.^123,124 These ionic aggregates are stabilized by interchain repulsion and chain elasticity of the neutral segments.⁹¹

The formation of the higher-order multiplets in charge-symmetric coacervates can be treated similarly to the formation of ion pairs, since bound ions with an aggregation number s − 2 (e.g., s = 2 for ion pairs and s = 4 for quadrupoles) are in chemical equilibrium with ionic aggregates with an aggregation number s. The formation energy is

$$\Delta F_{\text{multiplet},s}\simeq -k_{\text{B}}T\left[\ln \left(l^3{f}^{3/2}/b^3\right)+l_{\text{B}}/(sl)\right]\approx u/(s\lambda ),$$ (A.1)

which is analogous to the binding energy of ion pairs (eq. 2.10), with k_BT l_B/l electrostatic energy per charge in the multiplet. This attraction energy overcomes the free energy cost due to the increase of the number of chains in the corona as long as the electrostatic interaction strengths

$$u>u_s\simeq s\lambda \ln \left(\frac{1}{f^{3/2}{\lambda }^{3/2}}\right)\approx s\lambda ,$$ (A.2)

resulting in the formation of multiplets with aggregation number s.

Thus, it is expected that for charge-symmetric strong coacervates at high electrostatic strengths, there is a cascade of ion binding conditions, as observed in simulations of block polyampholytes⁹¹ and similar to that observed in ionic aggregates of ionomers.¹²⁵ Depending on the number density of ionic aggregates relative to the concentration of uncharged monomers, which is determined by the fraction of charged monomers f and ion size,^126–128 these multiplets may form inclusions of spherical, cylindrical, planar, or bicontinuous symmetries^129,130 analagous to microphase formation in block copolymers.¹³¹ In charge-asymmetric bottlebrush coacervates, however, this multiplet cascade is unfavorable, since the attractive dipolar interactions must overcome elastic brush resistance for further stretching or bending, and can be observed only at very high electrostatic strengths, u ≫ u_x.

B. Highly-Charged Polyelectrolytes and Counter-ion Condensation

In the case of isolated solutions of pure polyelectrolytes, before mixing and forming a coacervate, the counter-ions condense on the stronger-charged polyanion at $u_{\text{cond,}-}>f_{-}^{-1/2}$ and in some cases on the weaker-charged polycations at $u_{\text{cond},+}>f_{+}^{-1/2}$. Counter-ion condensation on the polyanions occurs at the same electrostatic interaction strength at which the concentration of the coacervate saturates (${\overline{c}}_{+}\simeq f_{+}^{1/2}/b^3$ and ${\overline{c}}_{-}\simeq f_{+}^{3/2}/\left(f_{-}{b}^3\right)$). As discussed in Section 2.1 for charge-symmetric coacervates, the release of these condensed counter-ions provides an additional driving force for the formation of a coacervate, with an entropic gain of k_BT per released small ion. Except for f ≪ 1 and f ≳ 1, the polyions in the charge-symmetric coacervate bind at electrostatic strengths higher than the electrostatic strength at which counter-ions condense on the isolated polyelectrolytes in pure solutions. This was a consequence of the entropic penalty for localizing a pair of opposite charges, which vanishes for f ∼ 1 and becomes asymptotically smaller (ln f ≪ f^−1/2) than the electrostatic gain of condensing a counter-ion for f ≪ 1. For charge-asymmetric coacervates, the binding of polycations and polyanions in the coacervate proceeds at electrostatic strengths higher than the electrostatic strength at which counter-ions condense on isolated polyanions (but may occur at lower u than counter-ion condensation on the lower-charge-density polycations in the pure solution). This is a consequence of the fact that the electric field of the highly-charged polyanion attracts the polycations, which leads to complexation. For both charge-symmetric and charge-asymmetric coacervates, the entropic gain of releasing condensed counter-ions increases with the fraction of charged ions.

C. Dilute–Semidilute: Star-like Gel

Mixed bottlebrush/double-semidilute, as well as bottlebrush gel regimes, are expected for relatively long polyanions with an end-to-end distance larger than the corresponding correlation length ξ₋ of double-semidilute solutions or side loops/bridges size r_c of bottlebrush gels. However, shorter, highly-charged polyanions with the contour length L₋ of the linear array of electrostatic blobs smaller than the correlation length ξ₋ do not overlap with each other. The symmetry of the electric field attracting the polycations to the polyanion still remains cylindrical at short distances from the polyanion, r < L₋; the structure of the polycation coat around the polyanion at these smaller length scales is similar to the double-semidilute case, discussed in Sections 3.1–3.2. Nonetheless, these shorter polyanions have spherical symmetry of their polycation coats on length scales between L₋ and ξ₋, forming dilute/semidilute double solutions and multi-arm star-like gels (Figure C.1).

Figure C.1:

Star-like gels are formed by increasing the electrostatic interaction strength of dilute semidilute weak coacervates. Examples of the chain conformations of polycation bridges and loops in the star-like gel are shown in blue.

For weak coacervates, polyanions were dilute in a semidilute polycation solution for the case of polyanions with length L₋ shorter than the correlation length ξ₋, while for the case of L₋ > ξ₋, a double-semidilute solution of polyanions and polycations was formed.⁵ In the strong association regime, ion pairs are stabilized by interchain repulsion and chain elasticity of the entire brush layer. Star-like gels have cylindrical symmetry of the brush around the polyanion at short distances r < L₋, but have spherical symmetry on larger length scales r > L₋. For such a side-chain brush layer, the correlation length of the brush in the uniform stretching approximation is

$${\xi }_{\text{brush}}(r)\simeq \{\begin{array}{ll}\sqrt{r_{\text{a},\text{sph}}r}\hfill & \text{for}{r}_{\text{a},\text{sph}}<r<L_{-}\hfill \\ \frac{r}{\sqrt{f_{-}{N}_{-}}}\hfill & \text{for}{L}_{-}<r<r_{\text{c},\text{sph}}\hfill \end{array}$$ (C1)

increasing radially as ∼ r^1/2 in the cylindrical zone close to the polyanion and increasing radially as ∼ r till a brush height, r_c,sph. Conservation of mass results in a side chain size,

$$r_{\text{c},\text{sph}}\simeq \frac{b}{f_{+}^{1/2}}{\left(f_{-}{N}_{-}\right)}^{1/4}$$ (C2)

which is the radius of the star-like complexes. The distance between ionic bonds on the polyanion is

$$r_{\text{a},\text{sph}}\simeq \frac{b}{f_{-}^{1/2}}{\left(f_{-}{N}_{-}\right)}^{1/4}$$ (C3)

and is determined by the balance of the entropic elasticity of the polyanion and the steric repulsion of the polycation segments.

It is important, however, that in the gel regime, the spacing between the polyanions is on the order of the size of the side chain loops and bridges. Thus, for the formation of star-like gels (Figure C.1), with spherical symmetry at large length scales and cylindrical symmetry at small length scales, the length $L_{-}\simeq r_{\text{a},\text{sph}}{f}_{-}{N}_{-}\simeq b{f}_{-}^{-1/2}{\left(f_{-}{N}_{-}\right)}^{5/4}$ of the stretched polyanion must be smaller than the side chain brush layer r_c,sph, limiting the star-like gels to polyanions with

$$f_{-}{N}_{-}\lesssim {\left(\frac{f_{-}}{f_{+}}\right)}^{1/2}.$$ (C.4)

Star-like gels are then only possible for very short polyanions and very weakly-charged polycations with long spacers between positive charges. For longer polyanions, dilute–semidilute weak coacervates transition to cylindrical bottlebrush gels, as the polyanions overlap upon increasing the electrostatic strength.

Similar to the calculation of the modulus for bottlebrush gel coacervates in Section 3.2.2, we assume a parabolic potential acting on brush segments in the outer shell of the spherical brush^{116,119–121} and estimate the thickness of the interpenetration layer as

$$\delta \simeq \frac{b}{f_{+}^{1/2}}{\left(f_{-}{N}_{-}\right)}^{-1/12},$$ (C.5)

which contains $g\simeq f_{+}^{-1}{\left(f_{-}{N}_{-}\right)}^{-1/6}$ monomers. Neighboring star-like complexes have volume of contact

$$V\simeq r_{\text{c},\text{sph}}^{5/2}{\delta }^{1/2}\simeq \frac{b^3}{f_{+}^{3/2}}{\left(f_{-}{N}_{-}\right)}^{7/12}$$ (C.6)

with k_BT attraction energy per blob within the contact volume between two stars:

$$\Delta F^{*}\simeq \frac{V}{{\delta }^3}{k}_{\text{B}}T\simeq {\left(\frac{r_{\text{c},\text{sph}}}{\delta }\right)}^{5/2}{k}_{\text{B}}T\simeq {\left(f_{-}{N}_{-}\right)}^{5/6}{k}_{\text{B}}T$$ (C.7)

The number density of star-like complexes is

$$v\simeq \frac{1}{r_{\text{c},\text{sph}}^3}\simeq \frac{f_{+}^{3/2}}{b^3}{\left(f_{-}{N}_{-}\right)}^{-3/4}$$ (C.8)

which contains f₋N₋ polycation strands. The plateau shear elastic modulus G of the star-like gel coacervate is

$$G\simeq v\Delta F^{*}{\left(\frac{r_{\text{c},\text{sph}}}{\delta }\right)}^2\simeq \frac{1}{{\delta }^3}{\left(\frac{r_{\text{c},\text{sph}}}{\delta }\right)}^{3/2}{k}_{\text{B}}T\simeq f_{+}^{3/2}{\left(f_{-}{N}_{-}\right)}^{3/4}\frac{k_{\text{B}}T}{b^3},$$ (C.9)

which reduces at the crossover of star-like to bottlebrush coacervates (N₋ ≲ (f₋f₊)^−1/2, eq. C.4) to the prediction of eq. 3.40 for bottlebrush gel θ-coacervates.

D. Coacervates from Polyelectrolytes with Unequal Kuhn Lengths in a General Solvent

Below we present the main results obtained for the general scaling exponent ν, describing different solvent conditions for an uncharged backbone of unequal Kuhn lengths, b₊ for polycations and b₋ for polyanions. The case ν = 1/2 describes a θ-solvent, which was discussed in detail in the main text for b ≡ b₊ = b₋, and the case ν = 0.588 describes the corresponding athermal solvent.

Charge-Symmetric Coacervates

Charge-symmetric coacervates have the same electrostatic blob size D_e, which interact with an energy on the order of k_BT.

$$l_{\text{B}}\frac{{\left(f_{+}{g}_{\text{e}+}\right)}^2}{D_{\text{e}}}\simeq l_{\text{B}}\frac{\left(f_{+}{g}_{\text{e}+}\right)\left(e{f}_{-}{g}_{\text{e}-}\right)}{D_{\text{e}}}\simeq l_{\text{B}}\frac{{\left(f_{-}{g}_{\text{e}-}\right)}^2}{D_{\text{e}}}\simeq 1$$ (D.2.2)

Note that charge-symmetric coacervates formed from polyelectrolytes with unequal Kuhn lengths do not have the same degree of ionization, but rather, they have degrees of ionization associated with the asymmetry of their Kuhn lengths, (f₋/f₊)^ν = b₋/b₊, since the polyions have equal linear-charge-densities:

$$\frac{f_{+}{g}_{\text{e}+}}{D_{\text{e}}}\simeq f_{+}^{\frac{\nu }{2-\nu }}{l}_{\text{B}}^{\frac{\nu -1}{2-\nu }}{b}_{+}^{\frac{-1}{2-\nu }}\simeq {\gamma }_{+}\equiv \gamma \equiv {\gamma }_{-}\simeq \frac{f_{-}{g}_{\text{e}-}}{D_{\text{e}}}\simeq f_{-}^{\frac{\nu }{2-\nu }}{l}_{\text{B}}^{\frac{\nu -1}{2-\nu }}{b}_{-}^{\frac{-1}{2-\nu }}$$ (D.2.4)

The correlation length ξ within the charge-symmetric coacervate is equal to the electrostatic blob size.

$$\xi \simeq D_{\text{e}}\simeq b_{+}^{\frac{2}{2-\nu }}{l}_{\text{B}}^{\frac{-\nu }{2-\nu }}{f}_{+}^{\frac{-2\nu }{2-\nu }}\simeq b_{-}^{\frac{2}{2-\nu }}{l}_{\text{B}}^{\frac{-\nu }{2-\nu }}{f}_{-}^{\frac{-2\nu }{2-\nu }}$$ (D.2.5)

Charge-symmetric coacervates have the same electrostatic blob size with the same number of charges per blob. The overall coacervate is composed of half positively-charged blobs and half negatively-charged blobs, but differences in the Kuhn lengths result in different numbers of monomers in the positively-charged and negatively-charged electrostatic blobs. Accordingly, charge-symmetric coacervates can have different polyelectrolyte monomer concentrations, ${\overline{c}}_{+}$ and ${\overline{c}}_{-}$,

$${\overline{c}}_{+}\simeq \frac{g_{\text{e}+}}{D_{\text{e}+}^3}\simeq \frac{{\left(l_{\text{B}}{f}_{+}^2\right)}^{\frac{3\nu -1}{2-\nu }}}{b_{+}^{\frac{5}{2-\nu }}},{\overline{c}}_{-}\simeq \frac{g_{\text{e}-}}{D_{\text{e}-}^3}\simeq \frac{{\left(l_{\text{B}}{f}_{-}^2\right)}^{\frac{3\nu -1}{2-\nu }}}{b_{-}^{\frac{5}{2-\nu }}}$$ (D.2.6)

As the electrostatic interaction strength is increased, the electrostatic blob decreases and saturates to a size on the order of the Bjerrum length,

$$b_{+}{f}_{+}^{-\nu }\simeq l_{\text{B}}\simeq b_{-}{f}_{-}^{-\nu }$$ (D.2.7)

at which there is on average only one charge per electrostatic blob. The coacervate concentrations saturate at

$${\overline{c}}_{+}\simeq f_{+}^{3\nu -1}/b_{+}^3,{\overline{c}}_{-}\simeq f_{-}^{3\nu -1}/b_{-}^3$$ (D.2.8)

for Bjerrum lengths larger than eq. D.2.7, above which, counter-ions would condense around the pure polyelectrolytes and reduce their effective line density of charges to one charge per Bjerrum length:

$${\gamma }^{\text{eff}}\simeq \{\begin{array}{ll}{l}_{\text{B}}^{\frac{\nu -1}{2-\nu }}{\left(\frac{f_{+}^{\nu }}{b_{+}}\right)}^{\frac{1}{2-\nu }}\simeq l_{\text{B}}^{\frac{\nu -1}{2-\nu }}{\left(\frac{f_{-}^{\nu }}{b_{-}}\right)}^{\frac{1}{2-\nu }}\hfill & \text{for}{l}_{\text{B}}<\frac{f_{+}^{-\nu }}{b_{+}}\simeq \frac{f_{-}^{-\nu }}{b_{-}}\hfill \\ 1/l_{\text{B}}\hfill & \text{for}{l}_{\text{B}}>\frac{f_{+}^{-\nu }}{b_{+}}\simeq \frac{f_{-}^{-\nu }}{b_{-}}\hfill \end{array}$$ (D.2.9)

In the coacervate, the polymeric charges are instead compensated by the oppositely-charged polyelectrolytes, corresponding to ionic binding with energy per bond,

$$\Delta F_{\text{ionic}\text{bond}}\simeq -k_{\text{B}}T\left[\ln \left(f_{+}{\overline{c}}_{+}{l}^3\right)+\ln \left(f_{-}{\overline{c}}_{-}{l}^3\right)+l_{\text{B}}/l\right]$$ (D.2.10)

The binding begins at a crossover Bjerrum length:

$$l_{\text{B}}^{*}\simeq l\ln \left(\frac{1}{f_{+}^{3\nu }}\right)\simeq l\ln \left(\frac{1}{f_{-}^{3\nu }}\right).$$

The concentration of bound ions can be calculated as:

$${\overline{c}}_{\text{bound}\text{ions}}\simeq \left({\tilde{f}}_{+}{\overline{c}}_{+}\right)\left({\tilde{f}}_{-}{\overline{c}}_{-}\right)l^3\exp \left(-\Delta F_{\text{ionic}\text{bond}}/k_{\text{B}}T\right)$$

The concentrations of bound and unbound ions are equal, on the order of $f_{+}^{3\nu }/b_{+}^3\simeq f_{-}^{3\nu }/b_{-}^3$ when the electrostatic blob size and the distance between ion pairs are approximately equal on the order of the Bjerrum length:

$$d_{\text{ion}\text{pairs}}\simeq D_{\text{e}}\simeq l_{\text{B}}\simeq b_{+}{f}_{+}^{-\nu }\simeq b_{-}{f}_{-}^{-\nu }$$ (D.2.18)

After most ions are paired, the distance between ion pairs in the charge-symmetric coacervate saturates at the size of the chain section between crosslinks

$$\xi \simeq d_{\text{ion}\text{pairs}}\simeq b_{+}{f}_{+}^{-\nu }\simeq b_{-}{f}_{-}^{-\nu }.$$ (D.2.20)

The shear modulus of the charge-symmetric coacervate is

$$G\simeq {\left(\frac{f_{+}^{\nu }}{b_{+}}\right)}^3{k}_{\text{B}}T\simeq {\left(\frac{f_{-}^{\nu }}{b_{-}}\right)}^3{k}_{\text{B}}T.$$ (D.2.21)

Charge-Asymmetric Coacervates

In the case of salt-free, charge-asymmetric coacervates, the lower-charge-density polycations absorb on the polyanion, forming a charge-compensating coat with a correlation length

$${\xi }_{+}\simeq \frac{1}{{\overline{c}}_{+}{b}_{+}^2}\simeq \frac{b_{+}{b}_{-}^{\frac{1}{4-2\nu }}}{f_{+}^{1/2}{f}_{-}^{\frac{\nu }{4-2\nu }}{l}_{\text{B}}^{\frac{1}{4-2\nu }}}.$$ (D.3.1)

The distance between sections of polyanions determines the second correlation length,

$$\underset{\_}{-}\simeq \{\begin{array}{ll}\frac{b_{+}^{3/2}{f}_{-}^{\frac{\nu (2-3\nu )}{4-2\nu }}}{b_{-}^{\frac{2-3\nu }{4-2\nu }}{f}_{+}^{\frac{3\nu }{2}}{l}_{\text{B}}^{2-\nu }}\hfill & \text{for}{L}_{-}>{\xi }_{-}\hfill \\ \frac{{\frac{3}{4_{+}}}^{4-3\nu }{\left(f_{-}{N}_{-}\right)}^{\frac{2-3\nu }{4-3\nu }}}{l_{\text{B}}^{\frac{3\nu -1}{4-3\nu }}{f}_{+}^{\frac{3\nu }{4-3\nu }}}\hfill & \text{for}{L}_{-}<{\xi }_{-}\hfill \end{array}$$ (D.3.2)

the thickness of the polycation coat at which the electroneutrality of the coacervate is established. Polycations of lower charge-density are almost unperturbed by the electrostatic interactions, with a size $R_{+}\simeq b_{+}{N}_{+}^{\nu }$, while polyanions with a higher charge-density have a size

$$R_{-}\simeq {\xi }_{-}{\left(\frac{N_{-}}{g_{-}}\right)}^{1/2}\simeq b_{-}{N}_{-}^{1/2}{\left(\frac{b_{+}/f_{+}^{\nu }}{b_{-}/f_{-}^{\nu }}\right)}^{3/4}\text{for}{L}_{-}>{\xi }_{-}$$ (D.3.3)

In the spherical-symmetry case (Appendix C), polyanions have an almost unperturbed polyelectrolyte size R₋ ≃ L₋ as in a dilute polyelectrolyte solution.

The ionic binding energy is approximated as

$$\begin{gathered} \Delta F_{\text{ionic}\text{bond}}\simeq -k_{\text{B}}T\left[\ln \left(f_{+}{\overline{c}}_{+}{l}^3\right)+\ln \left(f_{-}{\overline{c}}_{-}{l}^3\right)+l_{\text{B}}/l\right] \\ \approx -k_{\text{B}}T\left[\ln \left(f_{+}{\overline{c}}_{+}{l}^3\right)+l_{\text{B}}/l\right]\simeq -k_{\text{B}}T\left[\ln \left(f_{-}{\overline{c}}_{-}{l}^3\right)+l_{\text{B}}/l\right] \end{gathered}$$ (D.3.4)

with concentration of charges saturated at $\text{to}\text{address}\text{social}\text{determinants}\text{of}\text{refugee}\text{mental}\text{health}$. Thus, ionic binding is favorable for electrostatic interaction strengths greater than a crossover Bjerrum length,

$$l_{\text{B}}^{*}\simeq l\ln \left(\frac{b_{+}^3}{f_{+}^{3\nu }{l}^3}\right).$$ (D.3.5)

Minimization of the total free energy (eq. 3.7) results in an optimal distance between neighboring ionic bonds

$$r_{\text{a}}\simeq \frac{b_{+}}{f_{+}^{3/2-2\nu }}{\left[\ln \left(\frac{f_{+}^{3\nu }{l}^3}{b_{+}^3}\right)+\frac{l_{\text{B}}}{l}\right]}^{2\nu -5/2}\simeq \frac{b_{+}}{f_{+}^{3/2-2\nu }}{\left(\frac{l}{l_{\text{B}}}\right)}^{5/2-2\nu }\text{mixed}\text{regime}\text{for}{l}_{\text{B}}^{*}<l_{\text{B}}\le l_{\text{B},\text{x}}$$

which corresponds to a polycation spacer extended in a cylindrical brush with thickness

$$r_{\text{c}}\simeq \frac{b_{+}}{f_{+}^{\nu }}{\left(\frac{l_{\text{B}}}{l}\right)}^{1-\nu }\text{mixed}\text{regime}\text{for}{l}_{\text{B}}^{*}<l_{\text{B}}\le l_{\text{B},\text{x}}$$ (D.3.16)

in the mixed regime. The correlation length of polycation side loops and bridges in the brush increases radially in a cylindrical bottlebrush geometry as

$${\xi }_{\text{brush}}\simeq \sqrt{r{r}_{\text{a}}}\simeq \frac{b_{+}^{1/2}}{f_{+}^{3/4-\nu }}{\left(\frac{l}{l_{\text{B}}}\right)}^{5/4-\nu }{r}^{1/2}.$$ (D.3.17)

In an electrostatically-extended backbone, the average distance between neighboring charges is

$$d_{-}\simeq \frac{D_{\text{e}-}}{f_{-}{g}_{\text{e}-}}\simeq \frac{b_{-}^{\frac{1}{2-\nu }}{l}_{\text{B}}^{\frac{1-\nu }{2-\nu }}}{f_{-}^{\frac{\nu }{2-\nu }}}\text{for}{l}_{\text{B}}<l_{\text{B},\text{t}}$$ (D.3.18)

Above a crossover electrostatic strength

$$l_{\text{B},\text{t}}\simeq l^{\frac{(7-4\nu )(2-\nu )}{14-17\nu +4{\nu }^2}}\frac{b_{+}^{\frac{2(2-\nu )}{14-17\nu +4{\nu }^2}}{f}_{-}^{\frac{4\nu }{14-17\nu +4{\nu }^2}}}{b_{-}^{\frac{4}{14-17\nu +4{\nu }^2}}{f}_{+}^{\frac{(2-\nu )(3-4\nu )}{14-17\nu +4{\nu }^2}}}$$ (D.3.19)

the binding of polycation side loops results in a sterically-extended backbone with the average separation between neighboring charges

$$d_{-}\simeq \frac{r_{\text{a}}}{f_{-}{n}_{\text{a}}}\approx \frac{b_{-}^{\frac{1}{\nu }}{f}_{+}^{(1-\nu )(3-4\nu )}2\nu l_{\text{B}}^{(1-\nu )(7-4\nu )}2v}{b_{+}^{\frac{1-\nu }{\nu }}{f}_{-}{l}^{(1-\nu )(7-4\nu )}2\nu }\text{for}{l}_{\text{B},\text{t}}<l_{\text{B}}<l_{\text{B},\text{x}}$$ (D3.20)

where n_a is the number of monomers of size r_a,

$$n_{\text{a}}\simeq \frac{r_{\text{a}}^{1/\nu }{l}^{\frac{1-\nu }{\nu }}}{b_{-}^{1/\nu }{l}_{\text{B}}^{\frac{1-\nu }{\nu }}}\simeq {\left(\frac{b_{+}}{b_{-}}\right)}^{1/\nu }{f}_{+}^{\frac{4\nu -3}{2\nu }}{\left(\frac{l_{\text{B}}}{l}\right)}^{\frac{6\nu -7}{2\nu }}\text{for}{l}_{\text{B},\text{t}}<l_{\text{B}}<l_{\text{B},\text{x}}$$ (D.3.22)

The number of uncompensated charges per spacer is

$$f_{-}{n}_{\text{a}}-1\simeq {\left(\frac{b_{+}}{b_{-}}\right)}^{1/\nu }{f}_{-}{f}_{+}^{\frac{4\nu -3}{2\nu }}{\left(\frac{l_{\text{B}}}{l}\right)}^{\frac{6\nu \nu }{2\nu }}-1$$ (D.3.24)

and reaches full compensation at

$$l_{\text{B},\text{x}}\simeq l{\left[{\left(\frac{b_{+}}{b_{-}}\right)}^2\frac{f_{-}^{2\nu }}{f_{+}^{3-4\nu }}\right]}^{1/(7-6\nu )}$$ (D.3.25)

The resulting bottlebrush complex has size

$$r_{\text{a}}\simeq \frac{b_{-}^{\frac{5-4\nu }{7-6\nu }}{b}_{+}^{\frac{2(1-\nu )}{7-6\nu }}}{f_{-}^{\frac{\nu (5-4\nu )}{7-6\nu }}{f}_{+}^{\frac{(1-\nu )(3-4\nu )}{7-6\nu }}}\text{bottlebrush}\text{gel}\text{regime}$$ (D.3.33)

between grafted side chains of length

$$r_{\text{c}}\simeq \frac{b_{+}^{\frac{9-8\nu }{7-6\nu }}{f}_{-}^{\frac{2\nu (1-\nu )}{7-6\nu }}}{b_{-}^{\frac{2(1-\nu )}{7-6\nu }}{f}_{+}^{\frac{3-2{\nu }^2}{7-6\nu }}}\text{bottlebrush}\text{gel}\text{regime}$$ (D.3.34)

For a parabolic potential acting on brush segments in the outer shell of the bottlebrush structure, the thickness of the interpenetration layer is estimated to be

$$\delta \simeq \frac{f_{+}^{\frac{22{\nu }^2-21\nu -6}{6(7-6\nu )}}{f}_{-}^{\frac{\nu (2\nu -3)}{6(7-6\nu )}}}{b_{+}^{\frac{34\nu -39}{6(7-6\nu )}}{b}_{-}^{\frac{2\nu -3}{6(7-6\nu )}}}$$ (D.3.36)

Neighboring cylindrical bottlebrush complexes have volume of contact

$$V\simeq r_{\text{a}}{r}_{\text{c}}^{3/2}{\delta }^{1/2}\simeq \frac{b_{+}^{\frac{225-202\nu }{12(7-6\nu )}}{b}_{-}^{\frac{27-14\nu }{12(7-6\nu )}}}{f_{+}^{\frac{\nu (27-14\nu )}{12(7-6\nu )}}{f}_{-}^{\frac{96-63\nu -10\nu 2}{12(7-6\nu )}}}$$ (D.3.37)

per length r_a along the contour of the bottlebrush. The attraction energy per length r_a between two bottlebrushes is k_BT per blob within the contact volume,

$$\Delta F^{*}\simeq \frac{V}{{\delta }^3}{k}_{\text{B}}T\simeq \frac{r_{\text{a}}{r}_{\text{c}}^{3/2}}{{\delta }^{5/2}}{k}_{\text{B}}T\simeq {\left(\frac{b_{-}}{b_{+}}\right)}^{\frac{9-2\nu }{12(7-6\nu )}}\frac{f_{+}^{\frac{189\nu -122{\nu }^2-60}{12(7-6\nu )}}}{f_{-}^{\frac{\nu (9-2\nu )}{12(7-6\nu )}}}{k}_{\text{B}}T.$$ (D.3.38)

The number density of bottlebrush sections of length r_a is

$$v\simeq \frac{1}{r_{\text{a}}{r}_{\text{c}}^2}\simeq \frac{f_{+}^{\frac{9-7\nu }{7-6\nu }}{f}_{-}^{\frac{\nu }{7-6\nu }}}{b_{+}^{\frac{2(10-9\nu )}{7-6\nu }}{b}_{-}^{\frac{1}{7-6\nu }}}.$$ (D.3.39)

The plateau shear elastic modulus G of the bottlebrush gel coacervate is

$$G\simeq v\Delta F^{*}\frac{r_{\text{c}}^2}{{\delta }^2}\simeq \frac{1}{{\delta }^3}{\left(\frac{r_{\text{c}}}{\delta }\right)}^{3/2}{k}_{\text{B}}T\simeq {\left(\frac{f_{+}^{\nu }}{b_{+}}\right)}^{9/4}{\left(\frac{f_{-}^{\nu }}{b_{-}}\right)}^{3/4}{k}_{\text{B}}T.$$ (D.3.40)