Abstract
Quantum mechanics/molecular mechanics (QM/MM) simulations are a popular approach to study various features of large systems. A common application of QM/MM calculations is in the investigation of reaction mechanisms in condensed-phase and biological systems. The combination of QM and MM methods to represent a system gives rise to several challenges that need to be addressed. The increase in computational speed has allowed the expanded use of more complicated and accurate methods for both QM and MM simulations. Here, we review some approaches that address several common challenges encountered in QM/MM simulations with advanced polarizable potentials, from methods to account for boundary across covalent bonds and long-range effects, to polarization and advanced embedding potentials.
Keywords: long-range effects, polarizable force fields, pseudobond, QM/MM
1 |. INTRODUCTION
The simulation of reaction processes in complex biological systems such as enzymes, or condensed-phase systems, requires the description of changes in electronic and nuclear degrees of freedom. Although quantum methods can adequately describe electronic effects, the modeling of the systems of interest is limited by the size and the time scale that can be carried out in reasonable computational times. By contrast, molecular mechanics methods allow the study of systems with millions atoms but are limited to the type of system for which the force field was designed, and most force fields used for these simulations are nonreactive.1
Quantum mechanics/molecular mechanics (QM/MM) methods emerged in the mid-1970s as a proposal to study enzymatic reactions.2 Since then, QM/MM methods have been widely applied to study various chemical and biochemical systems.3–9 QM/MM methods aim to leverage the advantages of both quantum and classical approaches by combining two levels of theory. The quantum model focuses on the region of the system where the reactive processes of interest take place, while the classical model describes the rest of the system. For example, if the process involves a reaction in the active site of an enzyme (see Figure 1), the residues and any other molecules (or fragments) involved in the reaction will be assigned as the QM subsystem, and the rest of the enzyme, solvent, counterions, and so forth will be represented by the MM force field.
FIGURE 1.
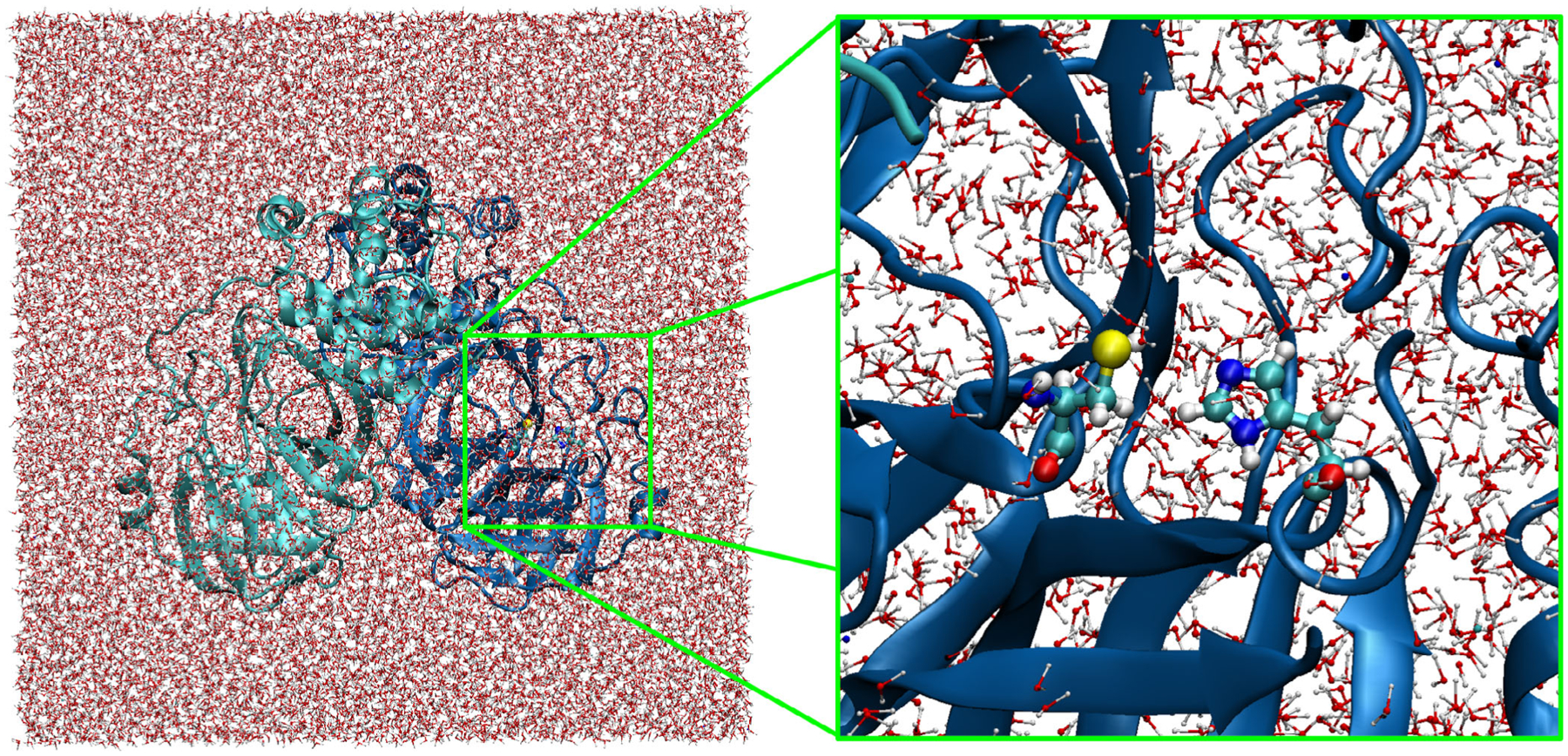
Main protease of SARS-CoV2 in a box of water.10 The whole protein (left) and a close-up in the active site (right) are shown. Histidine 41 and cysteine 145 amino acid residues are represented by balls and cylinders. PDB: 6LU711
There are a wide variety of combinations for the treatment of the QM and MM subsystem. The QM subsystem may be represented by empirical valence bond (EVB),12–14 semiempirical,15,16 or ab initio Hamiltonians.17–20 For the MM environment many QM/MM simulations employ nonpolarizable point-charge force fields (npFFs).21–23 More recently, increase in computational speed and algorithmic developments have allowed the use of more accurate potentials which may include explicit representation of electronic polarization, more elaborate electrostatics, and in some cases, explicit inclusion of other quantum effects.24–27
The coupling of QM and MM methods to represent a system gives rise to several challenges such as how to couple these two levels of theory across covalent boundaries, how to treat long-range effects in the context of QM subsystems, coupling of the quantum and classical Hamiltonians and how to treat the explicit couplings, among others. In this review, we present approaches that tackle several of these issues.
This article is organized as follows. Section 2 provides an overview of the QM/MM approach. It describes what force fields are, the different types of embedding, as well as some methods to include polarization. Section 3 describes the challenges involved in separating the QM and MM regions across covalent bonds, and solutions that have been proposed. The differences between the link atom, double link atom, as well as localized self-consistent field (LSCF) and generalized hybrid orbital (GHO) methods will be described. In Section 3.2 the role played by long-range interactions and methods that have been developed to include them efficiently will be described. In Section 4, we will describe some recent development for QM/MM simulations using advanced polarizable force fields. Finally, in Section 5, we will show some of the methods implemented in layered interacting CHEmical models (LICHEM), a code developed in the group to perform QM/MM simulations, followed by concluding remarks.
2 |. CLASSICAL MM ENVIRONMENTS IN QM/MM
Many QM/MM simulations rely on the combination of QM methods with the use of potential-energy functions, called force fields.28 Many force fields approximate the energy and forces of the system by separating the contributions into bonded and nonbonded interactions. In several cases, the nonbonded interactions are approximated by Coulomb and Van der Waals interactions. Some examples are: AMBER,23 CHARMM,21 GROMOS,29 MMFF,30 MM3,31 MM4,32 OPLS,22 and UFF.33
A common expression for fixed-charge, nonpolarizable force fields is show in Equation (1)
| (1) |
where the first three terms are the bonded contributions and the last two represent nonbonded interactions. Kb, Kθ, and Kϕ are force constants for bonds, angles, and dihedral terms; b0 and θ0 are equilibrium values for bond length and angles between atoms; n is the dihedral multiplicity; δ is the dihedral angle phase; q are partial (generally atomic) charges; ε are the well depths; and σ are the van der Waals radii. In the above equation, and throughout the rest of the review all equations use atomic units.
Given the functional form of the potential, the total energy for a QM/MM system can be separated in three contributions: the contribution from the QM subsystem, the contribution from the MM environment, and the interaction between both regions. The first two contributions are straightforward to evaluate. In principle, any combination of QM and MM methods can be chosen. The interaction between the QM and MM regions poses some challenges as mentioned above. The combination of the levels of theory can be achieved by two main approaches termed the subtractive and additive coupling schemes.
In the subtractive method, the QM/MM energy is obtained by:
| (2) |
that is, first the energy of the complete system (QM and MM regions) is evaluated at the MM level, then the energy of the QM region calculated in the QM level is added, and finally, the energy of the QM region evaluated at the MM level is subtracted. This method is straightforward but has the disadvantage that it requires several calculations at different levels of theory of the same set of atoms.
In the additive scheme, the QM/MM energy is calculated by:
| (3) |
that is, the energy QM/MM is the sum of the contributions QM and MM regions evaluated at its own level plus the contribution due to coupling. The complexity of the QM/MM methods depends on how the coupling term is expressed.
The last term in Equation (3) can be further subdivided depending on the individual terms of the classical force field. If the force field uses a functional form as in Equation (1), the QM/MM interaction can be divided as:
| (4) |
In both substractive and attractive schemes, it is possible to further subdivide the approaches depending on how each of the terms in the QM/MM interaction is calculated. In the mechanical embedding approach, the interaction between the QM and MM regions are handled at the force field level. The QM subsystem is thus kept in place by MM interactions. Similarly to Equation (1), all bonded terms involving QM atoms are represented with the respective MM functions, and all nonbonded interactions involving QM and MM atoms are represented by point charges and Lennard-Jones potential energy terms. In this approach, the calculation of the QM system is performed isolated from the MM region, and therefore, the wave function is not explicitly polarized by the external field from the MM environment.
In the electrostatic embedding scheme, the electrostatic interactions between the two regions, , are included in the QM calculation. In this case, the MM atoms polarize the electrons in the QM subsystem via an effective Hamiltonian,
| (5) |
where HQM is the electronic Hamiltonian for the QM subsystem, M is the number of MM atoms that have a partial charge qj, and ri and Rj are the positions of electron i and MM atom j. In this approach, the QM subsystem interacts with the MM region as a set of external point charges (or higher order multipoles). However, mutual polarization effects or other nonelectrostatic interactions are not taken into account.
2.1 |. Polarizable QM/MM
The force fields mentioned so far are extremely efficient and provide a convenient approach to investigate myriad systems. These force fields in some cases can exhibit limited accuracy in the reproduction of certain regions of the potential energy surface. One major reason for the reduced accuracy involves the approximations employed to represent the bonded and nonbonded interactions. In many cases, the nonbonded interactions are represented by two separate terms assuming pair-wise additivity. These terms aim to represent the underlying physical interactions, however there are several approximations that are employed, which lead to the neglect of some physical interactions. In general, the electrostatic interactions between particles are approximated by fixed atomic partial charges. Dispersion and repulsion effects are approximated by a Lennard-Jones (or similar) function.34–36
The use of fixed atomic point charges may be unable to capture or accurately represent several important effects such as charge density anisotropy, and charge penetration. In addition, the approximation of the charge density by fixed point charges neglects certain many-body effects such as explicitly accounting for electronic polarization or charge-transfer. Polarization effects can be included by explicitly taking into account the effect of the electric field on the charge distribution of the constituent molecules. Several polarizable force fields have been developed including AMOEBA,37 CHARMM,38 EFP,39,40 GEM,41,42 GROMOS,43 NEMO44 and SIBFA,45 which employ one of the methods below to describe polarization effects.
In the case where the force field has an explicit term to represent the electronic polarization of the classical environment, it is necessary to account for the interaction between this effect in the MM and the QM subsystem. In this case, the polarization embedding scheme is such that the QM and MM regions are mutually polarized. Thus, not only the QM region is polarized by the QM charges, but also the MM region responds to the chemical environment in the QM region. Three basic types of polarizable models have been developed: fluctuating charge model,46,47 Drude oscillator model,48,49 and induced dipole model.50,51
The fluctuating charge (FQ) model is one of the most straightforward polarizable models. It is based on the principle of electronegativity equalization. That is, a charge oscillates between the atoms until the electronegativities of the atoms are equalized. This method allows the modification of the value of the partial charges in response to the electric field, thus altering molecular polarization. This can be done by coupling the charges to the environment using electronegativity or chemical potential equalization schemes.52,53 The FQ method uses a Taylor expansion truncated up to second-order terms of the atomic chemical potential to express the energy required to create a charge, Q,
| (6) |
The energies required to create +1 and −1 charges on an atom, obtained from Equation (6)
| (7) |
| (8) |
using the definition of ionization potential as IP = E(+1) − E(0) and electron affinity as EA = E(0) − E(−1) we obtain:
| (9) |
| (10) |
where the χ0 is the electronegativity and η0 is the chemical hardness. Equation (6) can be rewritten as:
| (11) |
The previous equation can be generalized for a set of N atoms
| (12) |
The optimal charge distribution is achieved by minimizing the energy with respect to the charges on each atom:
| (13) |
The constraints used in solving the previous equation include total charge conservation:
| (14) |
and electronegativity equalization at convergence:
| (15) |
The FQ method has been used in the CHARMM force field54 and in the universal force field.33 The atom-bond electronegativity equalization method (ABEEM) is based in the principle of electronegativity equalization.55–57 The ABEEM method divides the molecular electron density as a sum of the electron density located on atoms and the electron density around bonds. The total energy of a molecule, Emol, can then be expressed as58:
| (16) |
where and χa − b* are the valence-state electronegativities of atom a and bond a − b in the molecule, respectively, is the valence-state energy of atom a, , ηa − b* are the valence-state hardness of atom a, bond a − b, respectively, qa and qa − b are the partial charges of atom a and bond a − b, respectively, Ci,a.b are considered as adjustable parameters, R is the distance between charge sites and k is an overall correction coefficient. The ABEEM/MM model has been used to describe the solvation of OH− ion59 and water clusters.60,61
The Drude oscillator model incorporates electronic polarizability by representing an atom as a two-particle system: a charged core with charge q0 and a charged shell, also called a Drude particle, with charge qD. The core and shell are linked by a harmonic spring. In the absence of an electric field, the Drude particle is located at the atomic core. Otherwise, the Drude particle will be at a distance d from the atomic core in the presence of an electric field:
| (17) |
The atomic induced dipole then is treated as:
| (18) |
The atomic polarizability, α, is related to the force constant k of the harmonic spring connecting the core and shell and is determined by
| (19) |
In principle, the Drude oscillator, qD, the force constant of the harmonic spring, kD, or both can be tuned to achieve an appropriate polarization response. The Drude particle method has been used for various systems such as DNA,62 gold63 and germanium nanoparticles,64 and halogen-containing compounds.65
In the induced dipole model the polarization response is represented by a set of inducible dipoles that arise due to the external permanent and induced electric field. The induced dipole moment at the site i is:
| (20) |
where Tij is the dipole–dipole interaction tensor defined by:
| (21) |
where I is the identity matrix and x, y, and z are Cartesian components along the vector between atoms i and j at distance rij.
When polarizable potentials are employed in QM/MM calculations, an additional energy term arises in the QM/MM interaction: , which is added to the total energy:
| (22) |
where describes the explicit polarization, in the case of dipolar force fields, arising from the dipolar interaction between the induced dipoles and the permanent and induced electric field. This term is calculated via the following formula:
| (23) |
where represents the electrostatic field on atom i arising from the permanent charges, and higher permanent moments (if present), and Ei represents the sum of and the electrostatic field on atom i due to the induced dipoles on other sites.
AMOEBA is an example of a polarizable force field that employs the induced dipole formalism and has been implemented for QM/MM simulations.66–71 AMOEBA uses the following functional form:
Given that the induced dipoles depend on the electric fields, Equation (23) can be rewritten as:
| (24) |
where the first term corresponds to the induced dipole interaction, and the second corresponds to the interaction of the induced dipoles at site i with the electric field at site I arising from the and subsystems.
It is important to note that the equations for the induced dipoles and the QM wave function are coupled. These equations can be solved iteratively using an SCF approach by computing the induced dipoles at each SCF cycle, resulting in a fully self-consistent (fsc) approach.50 Alternatively, it is possible to decouple the solution of the iterative dipoles by approximating the MM external field interacting with the QM wavefunction by only including the permanent field arising from the MM environment,66 resulting in a partially self-consistent (psc) QM/MM polarization approach.
Force fields that explicitly consider polarization changes in response to the chemical environment offer a more accurate description of electrostatic interactions. In fact, it is known that polarization effects become more relevant in highly charged systems.72 The dipole moment in a molecule is known to change significantly according to the state of aggregation. A polarizable force field has the versatility to reproduce both gas phase and liquid phase properties simultaneously. For example, the nonpolarizable TIP3P73 additive model calculates a hydrogen bond energy for a water dimer greater than the accepted value. In contrast, polarizable models produce energy closer to the values calculated with ab initio methods.74 In addition, distributed multipoles introduce charge density anisotropy that is lost in isotropic point charge distributions. Table 1 shows the interaction energy of the internal five waters in a cluster of 21 water molecules, where five molecules were treated quantum mechanically, while the remaining molecules were modeled with TIP3P or AMOEBA.66 The results show that including polarization is important to reduce the error with respect to the reference values.
TABLE 1.
Quantum mechanics (QM)/molecular mechanics (MM) solvation energy for the (H2O)5(H2O)16 → (H2O) + (H2O)4(H2O)16 system
| QM | MM | Esolv (eV) | % error | |
|---|---|---|---|---|
| B97D | – | −1.5239 | 0.00 | (3.12) |
| B97D | AMOEBA | −1.4663 | 3.78 | (6.78) |
| B97D | TIP3P | −1.2817 | 15.89 | (18.52) |
| B97D | AMOEBAa | −1.2387 | 18.71 | (21.25) |
| B3LYP | – | −1.3901 | 0.00 | (11.63) |
| B3LYP | AMOEBA | −1.4835 | 6.72 | (5.69) |
| B3LYP | TIP3P | −1.2977 | 6.65 | (17.50) |
| B3LYP | AMOEBAa | −1.2560 | 9.65 | (20.15) |
| PBE0 | – | −1.5156 | 0.00 | (3.65) |
| PBE0 | AMOEBA | −1.5814 | 4.34 | (0.53) |
| PBE0 | TIP3P | −1.3999 | 7.64 | (11.00) |
| PBE0 | AMOEBAa | −1.3575 | 10.43 | (13.70) |
| MP2 | – | −1.5730 | – | – |
| – | AMOEBA | −1.5419 | – | – |
| – | AMOEBAa | −0.5091 | – | – |
Source: Adapted with permission from E.G. Kratz, (A). R. Walker, L. Lagardère, F. Lipparini, (J).-P. Piquemal, (G). Andrés Cisneros, J. Comput. Chem. 2016, 37, 1019–1029. Copyright 2016 American Chemical SocietyNotes: Errors relative to MP2 are given in parentheses. The calculations were performed with the AMOEBA optimized structure, the 6–311++G(d,p) basis set, and do not include BSSE corrections.
Without MM polarization.
Another recent example of the importance of polarizable environments in QM/MM is shown in the work of Loco et al.75 In this work the QM/AMOEBA method, which interfaces the GAUSSIAN76 and TINKER/TINKER-HP77 packages has been used to compute excitations properties on the Thiazole Orange dye (TO) intercalated in DNA solvated in water (Figure 2). Several different types of QM/MM molecular dynamics (MD) simulations have been conducted, here we will focus on two of them. First, the QM subsystem is only composed of the TO dye (denoted QM/MM) as previously done by Loco et al.78 Second, the QM subsystem is composed of the TO dye and two pairs of nucleobases (denoted QM/MM[PB]). The calculated results indicate charge-transfer intruder states for the larger QM subsystem (QM/MM [PB]), leading to the delocalization of the TO π—π* transition on the QM nucleobases. Though, we observe a small difference of the excitation energy value between QM/MM and QM/MM(PB) when using the AMOEBA polarizable force field. However, complementary studies, using the nonpolarizable AMBER99sb force field79 and the TIP3P water model, have shown a non-negligible difference of the excitation energy between QM/MM and QM/MM(PB). Therefore, computed excitation energies from polarizable QM/MM are less sensitive to the choice of the QM subsystem than classical QM/MM simulations. Embedding polarization effects are a key factor not only for QM/MM calculations but also to compute gas and condensed phase properties.
FIGURE 2.
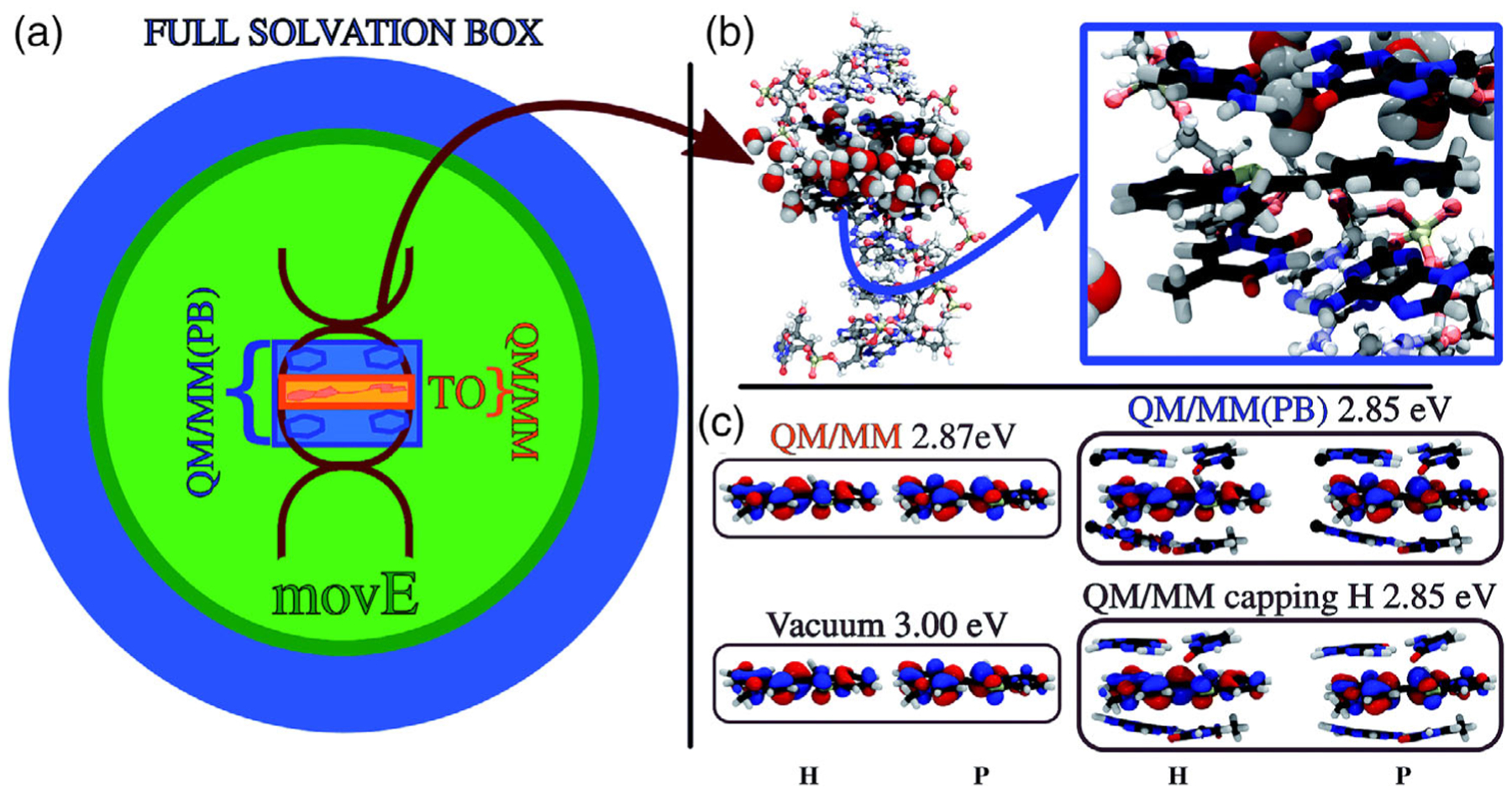
(a) Pictorial representation of the TO dye buried in the DNA double helix, embedded in a sphere of water (16,500 atoms). The different colors represent the differences for each of the QM/MM partition schemes employed. (b) The DNA structure is highlighted in a ball-and-stick representation, leaving the first water solvation shell around the TO dye. The QM subsystem defined in this work, tagged as QM/MM(PB) and made up of the TO dye and the four closest nucleobases (NBs) is zoomed out and represented in licorice style in the blue square. (c) NTOs and excitation energies relative to the ππ* bright excitation of the TO dye embedded in different environments, from vacuum to the QM/MM(PB) partition scheme. H and P denote the hole and particle, respectively
Source: Reproduction from D. Loco, L. Lagardère, G. A. Cisneros, G. Scalmani, M. Frisch, F. Lipparini, B. Mennucci, J.P. Piquemal, Chem. Sci., 2019, 10, 7200—Published by The Royal Society of Chemistry75
3 |. QM/MM BOUNDARY CONSIDERATIONS
The combination of quantum and classical methods results in short- and long-range boundaries that require special consideration. In the short-range regime, the junction between the QM subsystem and the MM environment requires care in cases where covalent bonds are present across the QM/MM boundary. There are scenarios where, even if no chemical bonds are cut, it is necessary to pay special attention to this boundary, for example if molecular exchange between the QM and MM regions is possible or likely. For long-range interactions, it is necessary to consider the role of these effects on the QM/MM energies and forces. In this section, we provide a brief review of approaches that have been developed to address both types of scenarios.
3.1 |. Boundary between QM and MM subsystems
One of the challenges in QM/MM is the description of atoms at the boundary between QM and MM subsystems involving covalent bonds. In general, atoms that are important in the reactive process are described at the QM level of theory, while the remaining atoms are described at the MM level of theory. In the case where only noncovalent interactions are involved, the separation between the QM and MM subsystems is straightforward. In the cases where a covalent bond (or more) need to be cut to create the two subsystems, the atoms involved in the covalent bond, and atoms near the boundary, need then to be treated with care. Indeed, the two different levels of theories used in QM/MM must be coupled to describe atoms and accurately compute the energy of the system. The challenging description of QM/MM boundary atoms have been addressed in different manners leading to the development of various approaches, some of which are mentioned below.
The link atom is the most commonly used method due to its simplicity and ease of implementation.80,81 The idea is to add a supplementary atom (i.e., link atom), generally an hydrogen atom, to fill the empty valence in the QM subsystem arising for each cut covalent bond (Figure 3a). The link atom is then only described at the QM level, resulting in the addition of three extra degrees of freedom. This can result in modifications of the electronic structure and the chemical properties of the QM subsystem. Moreover, the closeness between the link atom and the charge of the MM atoms may induce an overpolarization from the MM toward the QM subsystem. In order to overcome those issues, improvements have been suggested, such as the double link atom (DLA)82 among others. In the DLA method, two supplementary atoms, usually hydrogen atoms, are linked to both atoms of the broken bond to create the QM and MM subsystems. The idea here is to overlap both QM and MM link atoms (QMH and MMH) to ensure an overall neutral net charge, avoiding then an overpolarization from the MM toward the QM (Figure 3a). Also, it is possible to use the double link-atom method with a point charge or a single s-type Gaussian function on the boundary atoms. In the latter, the charges are delocalized, providing a better description of the charge density distribution of the MM boundary atoms.
FIGURE 3.
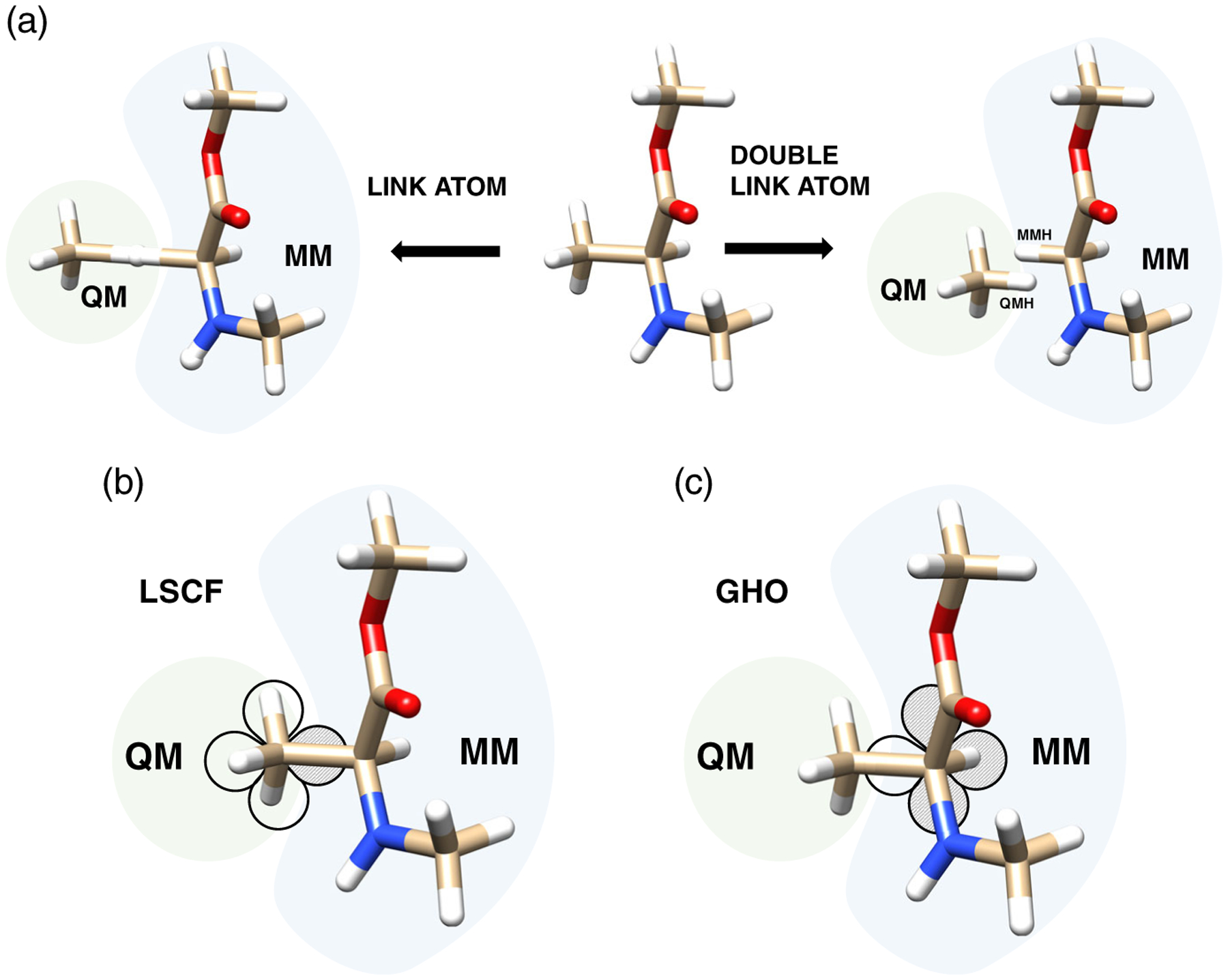
Representation of (a) link atom approaches: Simple link atom80, 81 (left) and double link atom (right),82 and frozen localized orbitals where gray orbitals are kept frozen while plain white orbitals are optimized during QM optimization: (b) LSCF,83–88 (c) GHO methods89,90
Methods using frozen localized, hybrid orbitals have been developed to describe QM/MM boundary atoms, following pioneering work from Warshel and Levitt.2 Later, Rivail and coworkers83–88 have developed the LSCF method. The idea is to describe the QM atom of the broken bond using a set of hybrid orbitals. The orbital pointing toward the MM atom (shaded gray orbital in Figure 3b) is kept frozen during the QM SCF optimization, while other orbitals (plain white orbitals in Figure 3b) are optimized with all QM orbitals. In a related approach, the GHO method developed by Gao et al.,89,90 the set of orbitals is placed on the MM atom of the broken bond. In this case, the hybrid orbital pointing toward the QM atom is optimized with all the QM orbitals (plain white orbital in Figure 3c) while the other orbitals on the MM atom are kept frozen during the SCF optimization procedure. Overall, the use of frozen orbitals does not alter the electronic and chemical properties of the system. However, it requires additional parametrization steps of the orbitals depending on the nature of the bond to be cut.
The pseudobond approach involves the use of “taylor-made” pseudopotentials. In this method the QM atom of the broken bond is described using effective core potentials (ECP) specifically parametrized to reproduce the environment of the covalent bond. The QM atom is denoted as Cps and is located in the QM region (Figure 4a). Pseudobonds should mimic the original chemical and structural properties of the broken bond between the QM and MM subsystems. Following Zhang et al. previous works,91,92 Parks et al.93 have developed new parameters for pseudobonds for common bonds found in biological systems such as: Cps(sp3)-C(sp3), Cps(sp3)-C(sp2,carbonyl), and Cps(sp3)-N(sp3). The parametrization of the ECPs are independent of the force fields and the latest pseudobonds also include a minimal basis-set, which overcomes previous dependence of the pseudobond to specific basis sets. In parallel, Dilabio et al.94 have developed quantum capping potentials, which include additional terms compare to ECP as spherical screening and Pauli repulsion, which contribute then to the refinement of pseudobonds.
FIGURE 4.
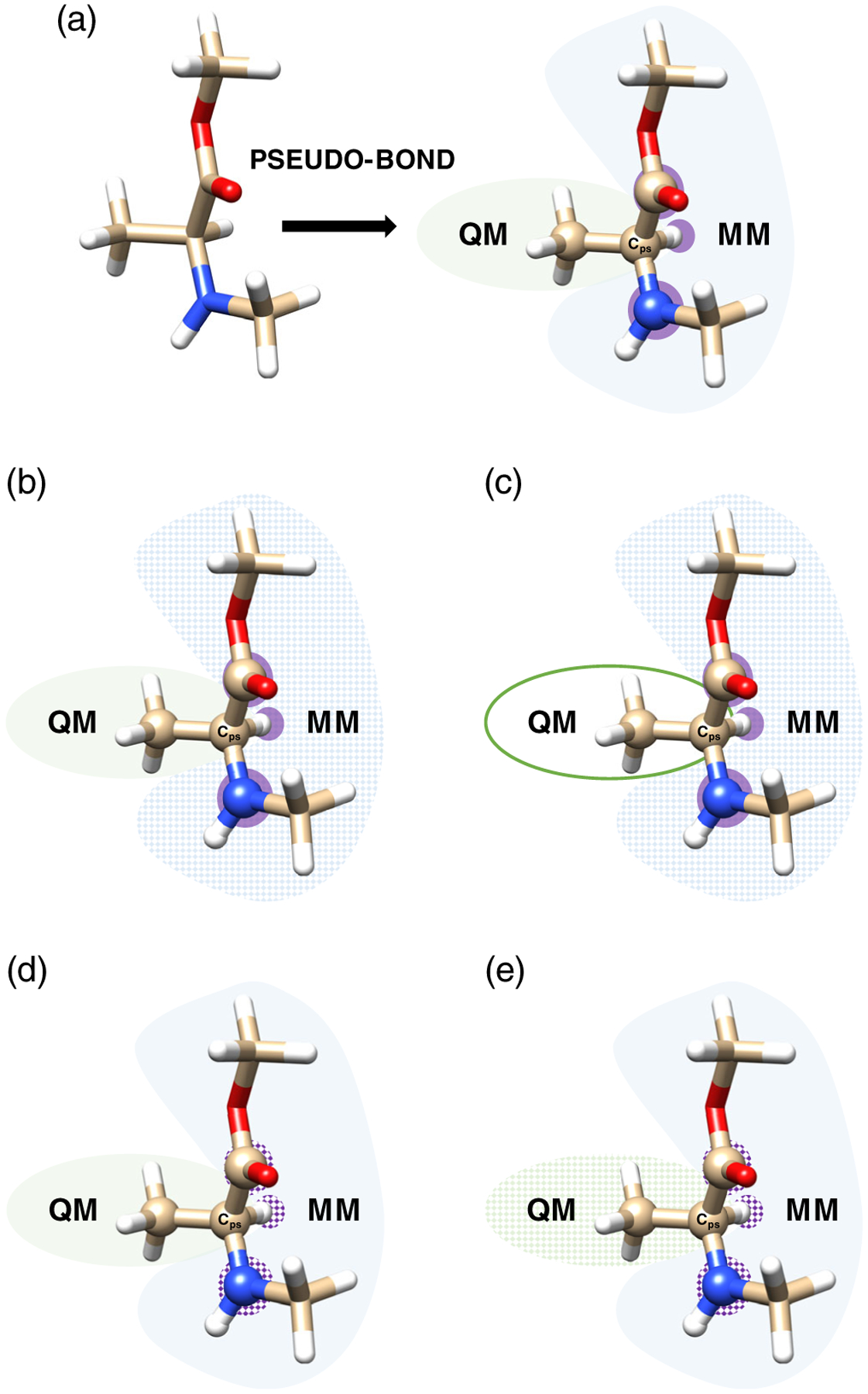
(a) Molecular schematic representation of the pseudobond approach for polarizable QM/MM optimization, with QM (MM) atoms in the green(blue) shaded regions, and boundary atoms shaded in purple. In this approach, a polarizable QM/MM involves four calculations: (b) QM polarized by the static MM field (blue shaded region), (c) MM without charges on QM (green circle) or boundary atoms (purple shaded atoms), (d) MM polarization including static (approximate) QM field (green and purple shaded regions), (e) MM optimization with static field from QM and boundary atoms (green and purple shaded regions)66
In the case of polarizable QM/MM, special care needs to be taken to address the polarization interaction across the QM/MM boundary. The pseudobond approach has been extended to encompass polarization effects.66 In addition to using pseudobonds, boundary atoms (purple shaded surface in Figure 4) need to be considered to compute a QM/MM optimization, which is performed by means of four energy calculations such as: QM energy in the MM static field (Figure 4b), MM energy with no charge on the QM atoms and boundary atoms (Figure 4c), MM polarization energy with charges on the QM atoms (Figure 4d), MM optimization with no polarization from the QM subsystem, pseudobond and boundary atoms (Figure 4e). This approach avoids the overpolarization from the MM toward the QM, Kratz et al.66 have demonstrated the accuracy of using it on oligopeptide chains in the gas phase with LICHEM.
In another recent example, Das et al.95 studied the polarization effect of uracil DNA glycosylase (UDG) on substrates leading to a “tautomeric strain” phenomena. UDG belongs to the excision repair enzyme family which its role is to cleave the N1–C1′ to remove mutagenic uracil from DNA. The activation of the N1–C1′ bond has been investigated actively both the focus of experimental and computational studies because uracil is not considered as the best of leaving group, giving rise to questions about the reaction mechanism.
Das et al. performed QM calculations on a cluster model based on the active site as well as QM/MM calculations on the full UDG system including eight pseudobonds to investigate the effect of the environment on the aromaticity of uracil, and how this affects the reactivity.95 Based on the results from both approaches, a step-wise dissociative mechanism for UDG was proposed (Figure 5). Interestingly, the active site of UDG includes several nearby residues interacting with UDG by means of hydrogen bonds. Calculated aromaticity indicators (NICS and HOMED) for uracil in the cluster model suggest that the uracil experiences an increase in aromaticity compared with uracil in the gas phase, to values similar to higher energy uracil tautomers. Including the full polarized protein environment increases the aromaticity of uracil even more. This “tautomeric strain” enables the reduction of the activation barrier to cleave uracil from UDG thanks to the polarization effects.95
FIGURE 5.
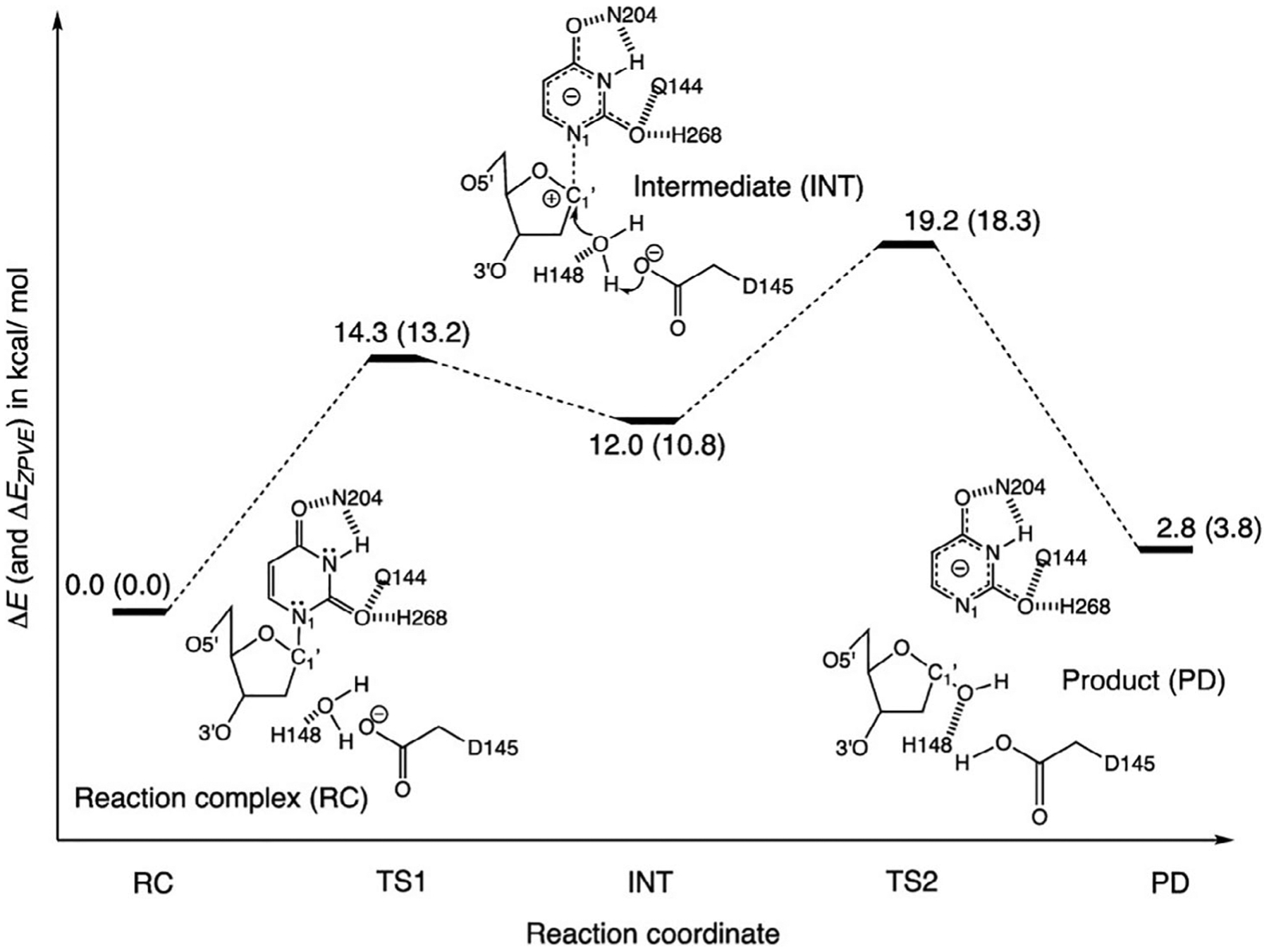
Relative energies (ΔE, in kcal/mol) of computed stationary points along the stepwise dissociative pathway of UDG, based on a constrained and truncated QM model of the UDG active site. Values corrected for zero-point energy vibration (ZPVE) are shown in parentheses (ΔEZPVE, in kcal/mol). Geometries of all stationary points were optimized at the ωB97X-D/6–31+G(d) level
Source: Reprinted with permission from J. Am. Chem. Soc. 2019, 141, 35, 13739–13743. Copyright 2019 American Chemical Society95
3.2 |. Long-range electrostatics in QM/MM
Long-range interactions in biomolecular and condensed-phase simulations play an important role that needs to be accounted for in order to properly represent a bulk system. One approach to simulate a bulk system is by the use of periodic boundary conditions (PBC). A popular approach to include long-range effects under PBC in classical simulations is the smooth particle mesh Ewald (sPME) approach.96 The sPME approach relies on an approximation of the Ewald summation method97 that uses the fast Fourier transform approach, resulting in scaling.
Briefly, for a system with N point charges, the electrostatic energy of a system under PBC is given by:
| (25) |
where the asterisk over the sum denotes that the terms with n = 0 and either j = i are omitted.
The direct calculation of the electrostatic energy in Equation (25) is and additionally, is only conditionally convergent. The Ewald method97 divides the electrostatic interaction into a sum of three contributions: direct, reciprocal, and correction terms,
| (26) |
The direct term is given by
| (27) |
where β is the Ewald splitting parameter. The reciprocal term is defined as
| (28) |
where V = a1 ·a2 × a3 is the volume of the box, is the lattice in reciprocal space and S(m) is the structure factor defined by
| (29) |
The correction term in Equation (26) is composed by the self-energy (Eself).
| (30) |
The above expressions for the correction can be modified to take into account other corrections such as non-neutral unit cells, polarization response, surface terms, and so forth.98
The Ewald method avoids the conditional convergence in Equation (25), albeit the algorithm is . The sPME and related approaches approximate the reciprocal sum by using a discrete convolution on an interpolating grid, resulting in a algorithm. This approach is extremely efficient when a discrete representation, that is, point charges or point multipoles, is employed, because the discrete charge distribution can be interpolated on a grid in a relatively straightforward fashion.98
The interpolation on a regular grid (or set of grids) of the continuous charge density, such as that from the QM subsystem in QM/MM calculations, presents a challenge. One way to overcome this challenge is to approximate the continuous QM charge density by a discrete representation (e.g. point charges) as was originally proposed by Nam et al.99 for QM/MM-Ewald, and by Walker et al.100 Giese and York developed the ambient potential composite Ewald approach, which avoids the use of dense Fourier grids for the QM electronic density, and performs a direct interaction of the QM charge density with the reciprocal potential.101 The use of an accurate approach to interact the continuous charge density of the QM subsystem with the charges of the MM environment was shown to avoid SCF instabilities and artifacts in PMF calculations.101
Long-range effects can also be approximated by boundary potential models. In the case of QM/MM calculations several methods have been proposed, including the EVB (EVB/MM) framework,12 the spherical solvent boundary potential (SSBP),102 the generalized solvent boundary potential (GSBP),103 the solvated macromolecule boundary potential (SMBP).104 One more approach to approximate long-range effects is to use a cutoff method coupled with switching or shifting functions, without taking the long-range effects explicitly into account.105–107
Another method that has been developed for both point-charge, and multipolar/polarizable QM/MM calculations is the QM/MM Long-Range Electrostatic Correction (QM/MM-LREC). The QM/MM-LREC scheme uses a minimum image convention and a switching and smoothing function to avoid edge effects and incorporate long-range electrostatic interactions, while at the same time matching the energies and forces with sPME levels of accuracy.66,108
The minimum image convention method considers the interactions between each particle i with all particles j within a cutoff radius Rcut. If the distance rij between the particles i and j is less than half the length of the primary unit cell then the same image is considered, on the other hand, if the distance between the particles i and j is larger, the neighboring image is used.
In the QM/MM-LREC scheme, each particle i interacts with every particle j within a certain cutoff distance rij. This leads to a modified Coulomb interaction such that
| (31) |
where
| (32) |
and
| (33) |
Here s is an adjustable integer exponent controlling the decay of the damping function (see Figure 6). The LREC scheme avoids the need to approximate the QM charge density for reciprocal space by considering only the first replicas around the primary cell. It also has the advantage that Hessians can be calculated analytically, and the switching function can be employed for any discrete embedding field including monopoles and higher order multipoles. This approach has been recently extended to a hybrid approach allowing a reduction in the cutoff distance.109
FIGURE 6.
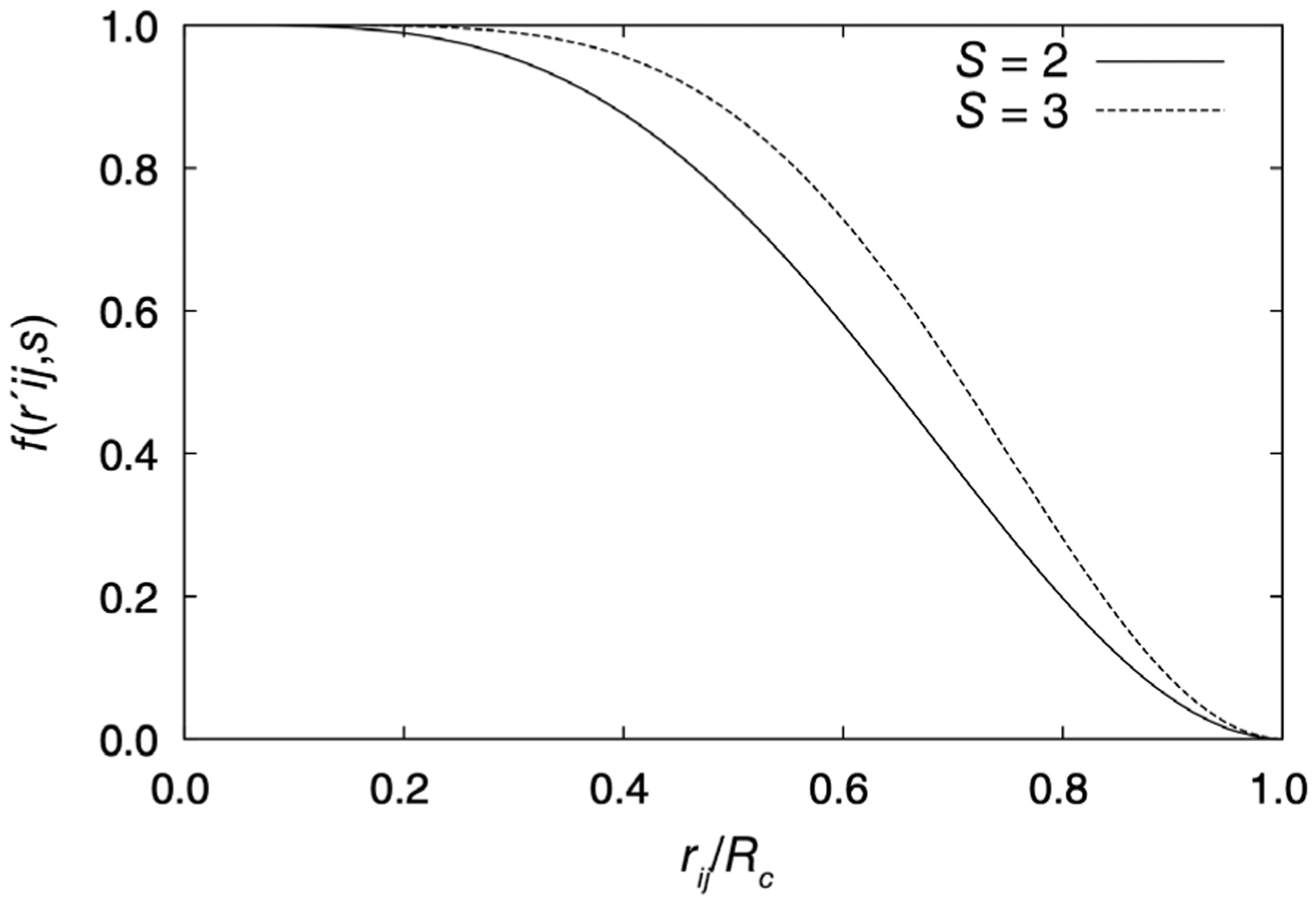
LREC damping function with s = 2 and s = 3. Increasing the exponent moves the inflection point of the LREC function closer to the cutoff radius
Source: Reprinted with permission from E.G. Kratz, R.E. Duke, G.A. Cisneros, Long-range electrostatic corrections in multipolar/polarizable QM/MM simulations. Theor. Chem. Acc. 2016, 135, 166
4 |. QM/MM WITH ADVANCED POTENTIALS
The QM/MM approaches described so far only involve electrostatic and polarization embedding of the QM wavefunction (23). The inclusion of explicit polarization improves the description of the MM environment, however, other effects are approximated by calculating them via the classical terms, e.g. Van der Waals,110 or are neglected altogether, e.g. charge transfer.
Several approaches have been developed to include a more accurate description of the MM environment. One recently proposed approach is to employ potentials based on the many body decomposition. One such family of potentials is the MB-pol and MB-DFT potentials.111 We have recently described a new QM/MM implementation involving MB-pol and MB-DFT within LICHEM and within Gaussian to compare partially self-consistent (psc) and fully self-consistent (fsc) polarizable QM/MM approaches.112 These implementations include explicit Coulomb and polarization embedding of the QM wavefunction and a many-body potential representation of the MM environment. The use of MB-pol and MB-DFT allows for a very accurate representation of the environment. This results in various advantages such as no longer needing additional functions or approximations to ensure continuous energy and forces in adaptive QM/MM calculations.113,114
Another approach to improve the description of the environment in QM/MM simulations is to use advanced potentials that explicitly include one or more of the missing components in the embedding environment. One approach that allows an explicit term-by-term embedding is by employing potentials that include separate terms for each physical interaction, such as the effective fragment potential (EFP) which can include exchange and charge transfer115 and using the induced dipole model as in the polarizable embedding model by Mennucci et al.,51 the fragment exchange potential,116 the QMFF,117 Exchange fragment potential,118 among others. See the recent review of QM:MM and QM: QM embedding approaches by Jones et al. for a thorough review.119
We have developed a QM/MM implementation within LICHEM that interfaces PSI4 with GEM where the MM subsystem is represented by GEM and thus all MM and QM/MM interactions are calculated using the GEM interaction terms. The Gaussian electrostatic model (GEM) is a polarizable potential that uses Gaussian auxiliary basis sets (ABSs) to build the molecular electron density.41 The philosophy for GEM is to have a density-based force field with errors below 0.2 kcal/mol for total energy and forces compared with high level QM reference. This is achieved by using separate contributions for each of the terms obtained from QM energy decomposition analysis (EDA): Coulomb, Exchange, polarization, charge transfer and dispersion. The GEM densities are obtained by fitting QM relaxed densities to a set of auxiliary Hermite Gaussian basis sets.
Two procedures can be used to perform the adjustment of molecular electron densities through Hermite Gaussians: the conventional analytical variational Coulomb adjustment or the numerical adjustment of the molecular electrostatic potential. The analytical density fitting method relies on the use of Gaussian auxiliary bas functions to expand molecular electron density
| (34) |
where is the approximate density and K(r) are Hermite Gaussians. The expansion coefficients ck can be obtained by minimizing the self-energy of the error in the density according to some metric
| (35) |
Different operators can be used, including the the coulomb operator or the damped Coulomb operator .120 The minimization of Equation (35) with respect to the expansion coefficients ck give rise to a linear system of equations:
| (36) |
where Pμν is the density matrix. The solution of Equation (36) requires the inversion of a the ABS matrix . Although in principle G must be positive definite and symmetric, in practice, it is almost singular and, therefore, the diagonalization to obtain its inverse must be done carefully. To this end, both analytical and numerical approaches have been developed to perform the fitting of the molecular densities.121, 122
The latest GEM water model has been fitted to match the total energy of the dimer surface and hexamer clusters reported by Paesani et al.,123 as well as the individual GEM terms (Coulomb, exchange, polarization, and Van der Waals) to reference symmetry adapted perturbation theory (SAPT) with aug-cc-pVTZ.124 The fitted density for GEM was calculated at the CCSD(T)/aug-cc-pVTZ level.124, 125 The ABSs employed involve 70 primitives, resulting in approximately 280,000 functions for a system of 512 waters. The integrals required for the calculation of the GEM terms are evaluated using an extension of the sPME approach for Gaussian functions,124, 125 which has been implemented in the gem.pmemd program, which is available with the AmberTools release.126
The first implementation of the QM/GEM approach involved only the Coulomb embedding term.127 The use of GEM provides an accurate polarization environment for the QM wavefunction and avoids penetration error effects because of the description of the MM environment with explicit (frozen) densities compared with conventional point charge force fields as shown in Figure 7.
FIGURE 7.
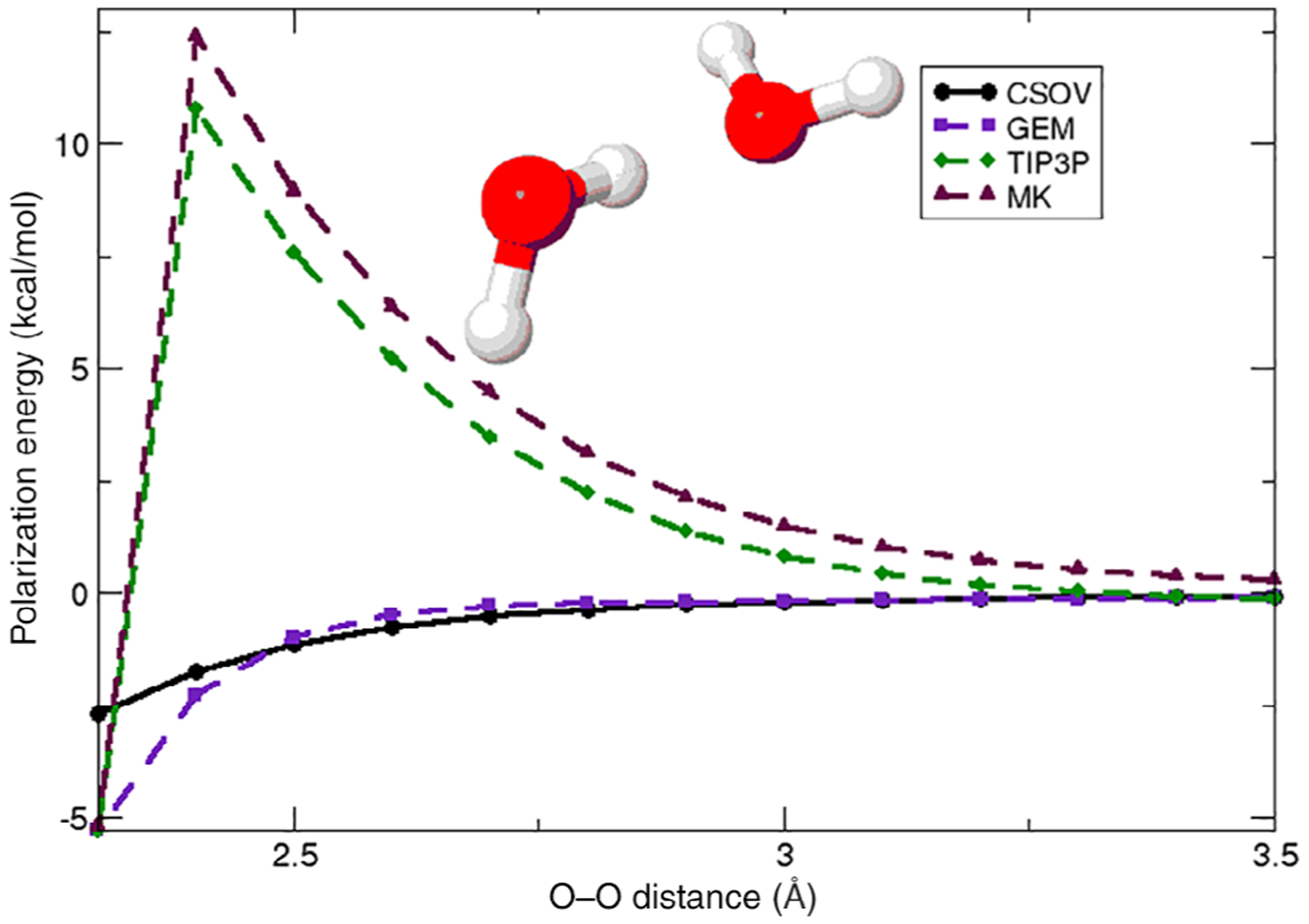
Polarization of the QM subsystem for one QM water by one GEM water
Source: Adapted with permission from J. Phys. Chem. B 2006, 110, 28, 13682–13684. Copyright 2006 American Chemical Society
For the current implementation, the total QM/MM interaction energy between the subsystems, EQM/GEM, involves four terms: Coulomb, Exchange-repulsion, polarization, and dispersion: .70
The Coulomb and exchange-repulsion terms involve three-center integrals between the QM density and the fitted GEM density:
| (37) |
and
| (38) |
where Kexch is a proportionality constant.42,121,128 The polarization interaction is calculated using the same approximation described above for LICHEM with AMOEBA. The dispersion term is approximated by a multipolar expansion taking the 6, 8, and 12 terms into consideration. The exchange proportionality parameter, as well as the coefficients for the dispersion term have been parametrized by linear least squares to match the SAPT2+ 3/aug-cc-pVTZ components for the 10 water dimers.129
In this implementation we considered two approaches for the calculation of the total interaction depending on the calculation of the QM/GEM exchange-repulsion term. In both cases the QM/GEM dispersion terms are added a posteriori to the total energy (and forces). The Coulomb term is calculated by including the GEM density in the core Hamiltonian in both alternative approaches. Thus, the difference in the two approaches involves only the exchange-repulsion component. In one approach, the exchange-repulsion intermolecular interaction is calculated after the SCF has completed The second approach involves the inclusion of the exchange-repulsion term explicitly in the SCF, that is, explicit exchange-repulsion embedding. This is achieved by including the GEM density in the core Hamiltonian:
| (39) |
in which VGEM involves the introduction of the three-center integrals of the QM MOs with the GEM density in the core Hamiltonian by:
| (40) |
where the first term corresponds to the Coulomb integrals and the second term to the overlap integrals multiplied by the exchange-repulsion proportionality constant. In this second case the exchange-repulsion proportionality constant is different than the former case since the QM wavefunction experiences a different external potential (see below). In all cases the required integrals have been programmed into a modified version of Psi4.130
The QM/GEM implementation in LICHEM was assessed by comparing the total intermolecular interaction Energies, as well as the individual interaction terms for a subset of the water dimer potential reported by Babin et al.123 as described in Ref. 70 The maximum unsigned error (MUE), and root mean squared error (RMSE) for the clustered dimers is shown in Figure 8. In the original comparison, the term-by-term comparison was done with respect to SAPT2+3/aug-cc-pVTZ, which does not provide a straightforward separation of the induction and polarization components. Therefore, the dispersion + polarization terms were analyzed together. As can be seen from Figure 8, the use of GEM for the Coulomb, polarization and exchange-repulsion embedding provides an accurate environment for the hybrid calculation.
FIGURE 8.
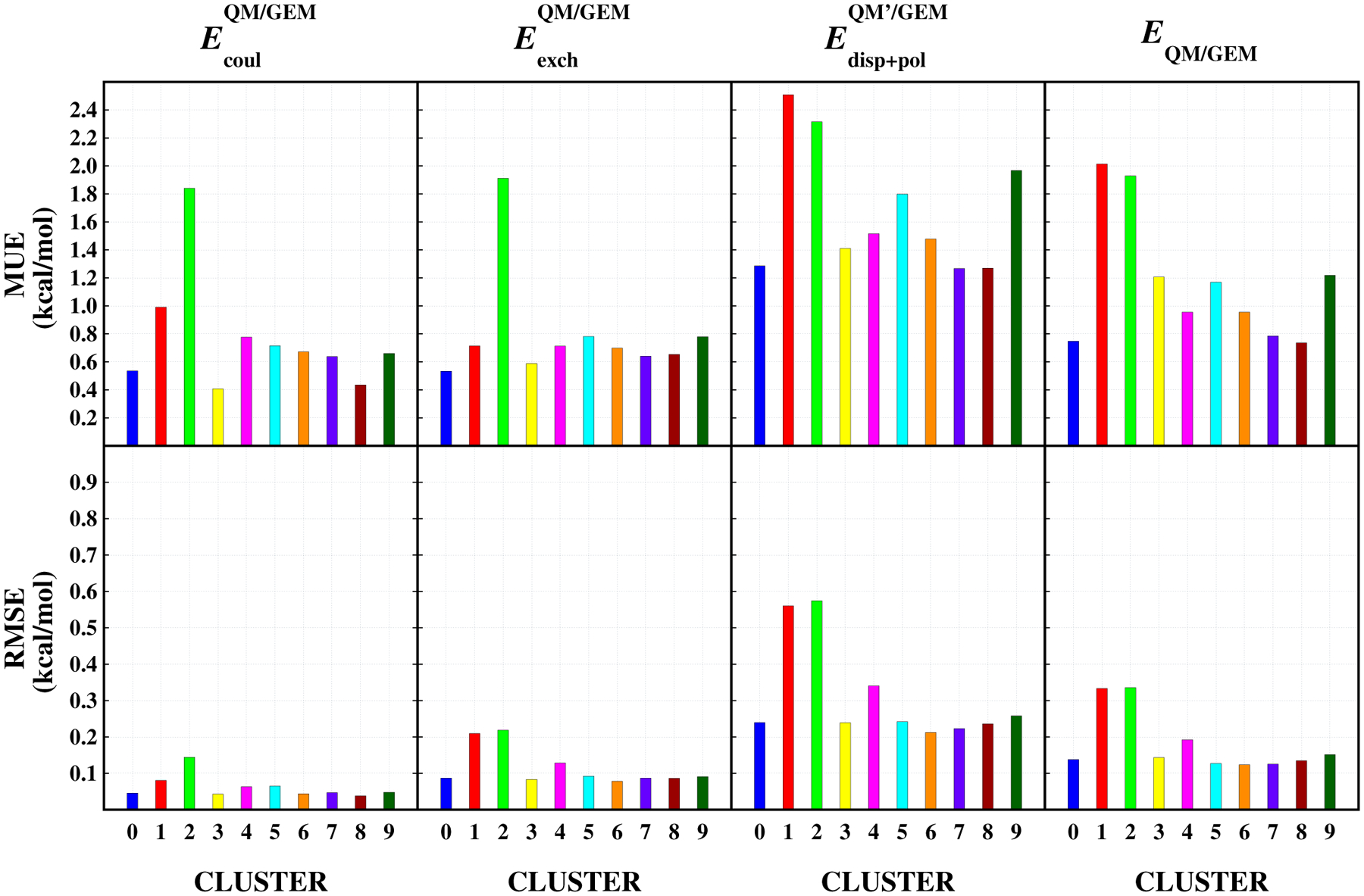
Errors per cluster with respect to SAPT. The errors corresponding to the coulomb interaction energy are depicted on the first column, and the errors corresponding to the exchange interaction energy are given on the second column. The computed errors for the sum of dispersion and polarization energies are depicted on the third, while the error for total energy is given on the fourth column
Source: Reprinted with permission from J. Phys. Chem. Lett. 2018, 9 (11), 3062–3067. Copyright 2018 American Chemical Society
5 |. LICHEM
Various methods described above including the pseudobond, and QM/MM-LREC, have been implemented in the LICHEM software (Layered Interacting CHEmical Models) package in the context of both nonpolarizable and polarizable potentials including AMOEBA, GEM, and MB-Pol.70,131,132 At its core, LICHEM is an interface that can couple QM codes such as Gaussian,76 NWChem133 and Psi4130 and MM codes such as TINKER,134 TINKER-HP,77 and LAMMPS.135
When AMOEBA (or another multipolar force field) is employed, LICHEM uses an approximation for the classical multipolar environment to allow the seamless integration with multiple QM codes66,136 LICHEM provides a variety of approaches for nonpolarizable and polarizable QM/MM simulations including single point energies, Monte Carlo (Grand Canonical and Isothermal-Isobaric ensembles), and path integral Monte Carlo. Geometry optimizations can be performed in an iterative procedure, where QM and MM atoms are optimized separately. QM atoms are optimized including MM charges or multipoles. Then, MM atoms are optimized including point charges comes from electron density from QM atoms. This procedure continues until convergence criteria are met.
Geometry optimization algorithms for single structures are limited to critical points along a surface. In many cases, it is useful to determine the entire reaction path that connects two, or several critical points to investigate a reaction mechanism. An entire reaction path can be optimized by performing an optimization with multiple replicas between the reactant and product states. Several algorithms have been developed for this end. One such family is called the chain-of-replica methods. These methods represent a path as a string of beads connected to each other. LICHEM has two chain-of-replica algorithms for path optimization, the Nudged Elastic Band (NEB),137, 138 and the quadratic string method (QSM).139
The nudged elastic band (NEB) method137 is an efficient method for finding the minimum energy path (MEP) between a given initial and final state of a transition. To sample regions between stationary points (minima or transition states), spring forces can be added to ensure continuity of the path. In the NEB method, the modified forces (F′) of the elastic band on the bead p and the step n are given by:
| (41) |
where K is the spring constant and ΔR is the displacement between replicas defined as:
| (42) |
Spring forces contribute to the elastic band method in locating the MEP. However, to prevent the beads from slipping to the minimum, it is necessary to eliminate the forces parallel to the reaction. The forces are then given by
| (43) |
where τ is a tangent unit vector indicating the direction of the reaction path.
The climbing image (CI) NEB method is a modification to the NEB method. The IC travels upward along the tangent to find an approximate transition state structure. The transition state forces in the IC (replica c) are expressed as:
where the forces are inverted along the tangent.138
The QSM139 does not require a predetermined step size and eliminates the need for an artificial spring constant. Instead, the approximate Hessian confidence radius and surface are updated at the end of each iteration. First, the QSM algorithm calculates the energy and gradients of all user-defined beads. The approximate Hessians (Hk) constructed from the gradients in the initial step are updated with the damped Broyden–Fletcher–Goldfarb–Shanno (DBFGS) algorithm.140
| (44) |
where i indicates to the iteration number and
| (45) |
| (46) |
with
| (47) |
| (48) |
The update of Hk is followed by the update of the trust radii using the energy as a merit function;
| (49) |
Both NEB and QSM require optimized structures for the end-points (e.g. reactant and product) as well as an initial guess of the intermediate images (beads). One approach to generate this initial guess is to use a linear interpolation between the end-point coordinates. In QM/MM simulations this is usually accomplished using only the coordinates of the QM subsystem, and use the MM environment from one of the ends for all the beads. However, this can lead to issues during the path optimization such as discontinuities along the trajectory. One approach to avoid this is to employ a restraint MM optimization approach.141, 142
In this case, the initial stages of the iterative QM/MM path optimization are performed with restraints on the MM atoms during the MM part of the optimization. These restraints are reduced at each subsequent iteration. Figure 9 shows a flowchart that describes these approaches in LICHEM.
FIGURE 9.
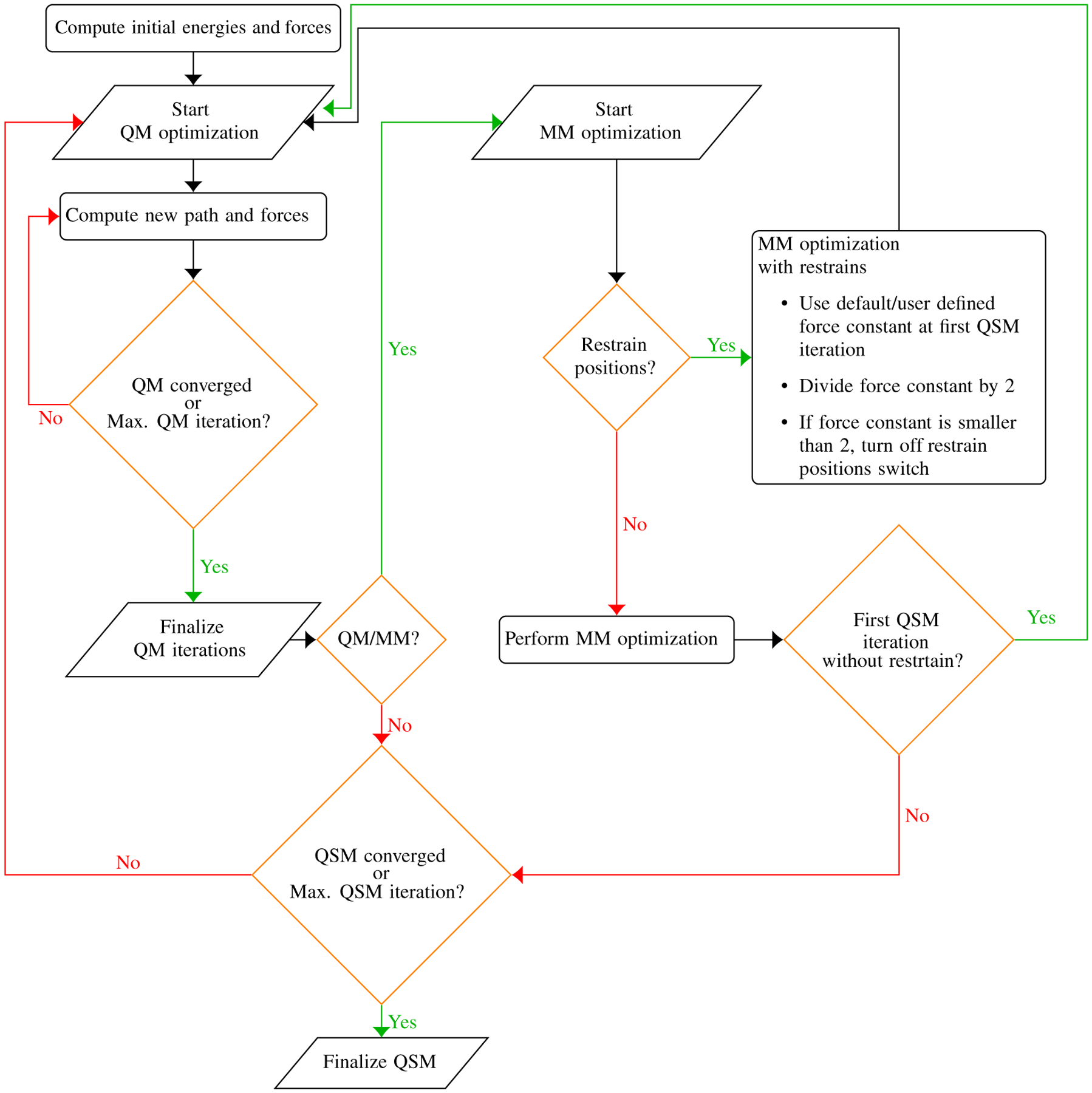
Flowchart of QSM algorithm implemented within LICHEM
Source: Reprinted with permission from H. Gökcan, E. Antonio Vázquez-Montelongo, G. Andrés Cisneros, J. Chem. Theory Comput. 2019, 15 (5), 3056–3065. Copyright (2020) American Chemical Society
One more algorithmic advantage that can be applied in the case of “chain-of-replica” approaches is the fact that each bead can be calculated independently. Therefore, it is possible to employ hybrid-parallelization paradigms such that the QM or MM parts of the calculation employ the parallelism inherent in the respective codes (i.e., MPI, OpenMP, cuda, etc.) and the path optimizer used MPI to run all beads in parallel. This approach has been implemented in LICHEM for QSM.143 Figure 10 shows performance metrics for a test reaction comparing NEB, QSM and QSM with restrained MM optimization.
FIGURE 10.
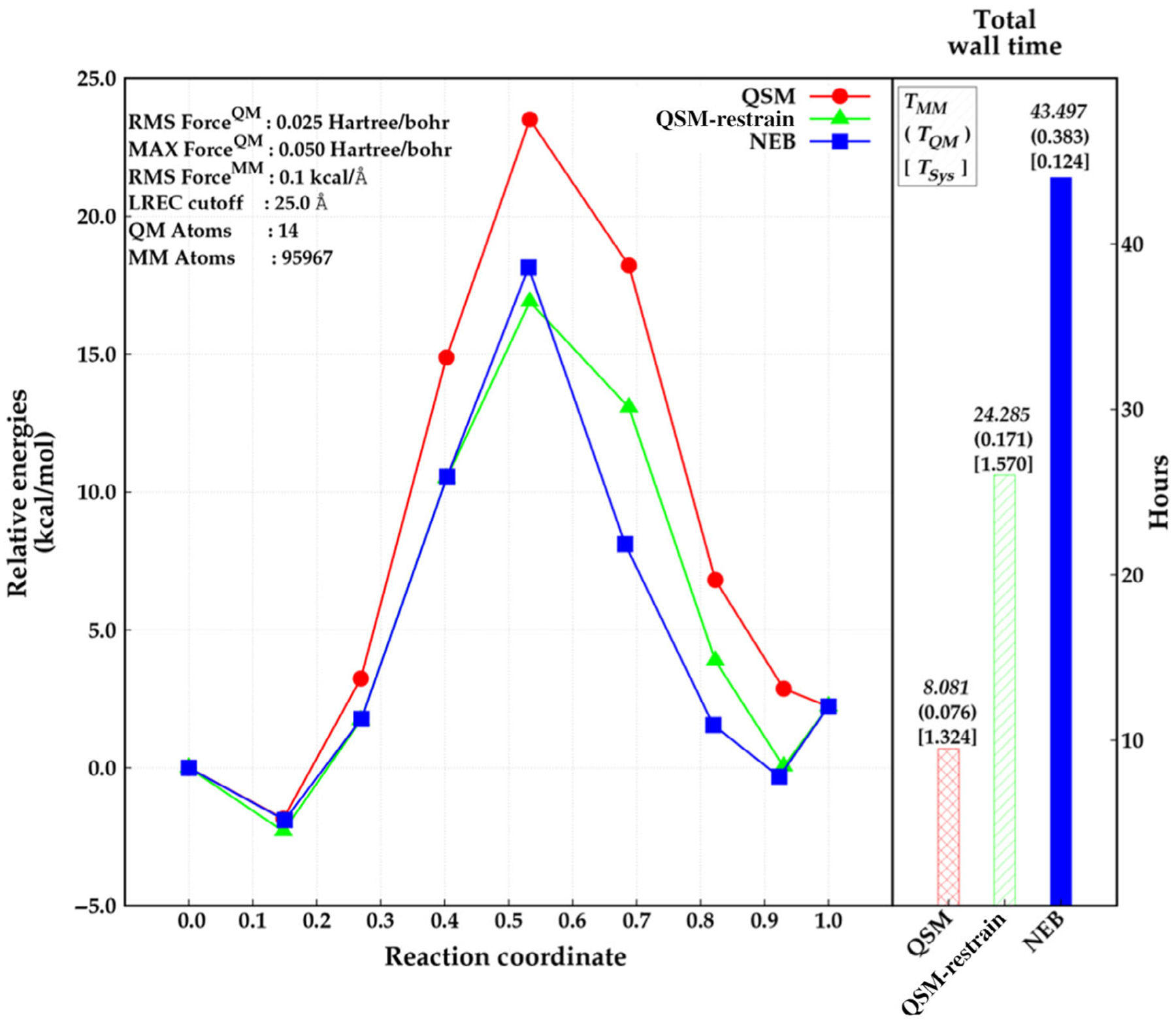
Relative energies obtained by NEB (blue, square) and QSM (red, circle), and QSM using the restrained-MM method (green, triangle) along the reaction coordinate (left), and total wall time required for the optimization in hours (right). The wall time for MM calculations, QM calculations, and for system calls are depicted above the wall time bars (right)
Source: Reprinted with permission from H. Gökcan, E. Antonio Vázquez-Montelongo, G. Andrés Cisneros, J. Chem. Theory Comput. 2019, 15 (5), 3056–3065. Copyright (2019) American Chemical Society
One example of the use of the methods mentioned above for a QM/MM calculation with AMOEBA was reported by Vázquez-Montelongo et al.,25 who performed polarizable QM/MM simulations to investigate the N-tert-butyloxycarbonylation (Boc) of aniline in ionic liquid mixture composed of water/[EMIm][BF4]. Boc is a common group used to protect molecules in organic synthesis.144
Vázquez-Montelongo et al. have assessed the role of the solvent in four different possible reaction mechanisms of N-tert-Boc protection of aniline using LICHEM. Two of them require an activation of the Boc group by a water molecule or a cation ([EMIm]+), while the other two do not (denoted configuration C2). Here we will focus on the two possible mechanisms of configuration C2 which are shown in Figure 11a,d. Reaction (1) (Figure 11a, denoted Scheme 1c in the original study) represents a sequential mechanism: first, the nucleophic attack of the aniline to the carbonyl of one of the Boc groups occurs, followed by the formation of CO2. Reaction (2) corresponds to the concerted mechanism (Figure 11d, denoted Scheme 1d in the original study) where the nucleophic attack of the aniline to the carbonyl of one of the Boc groups and the formation of CO2 occur concurrently.
FIGURE 11.
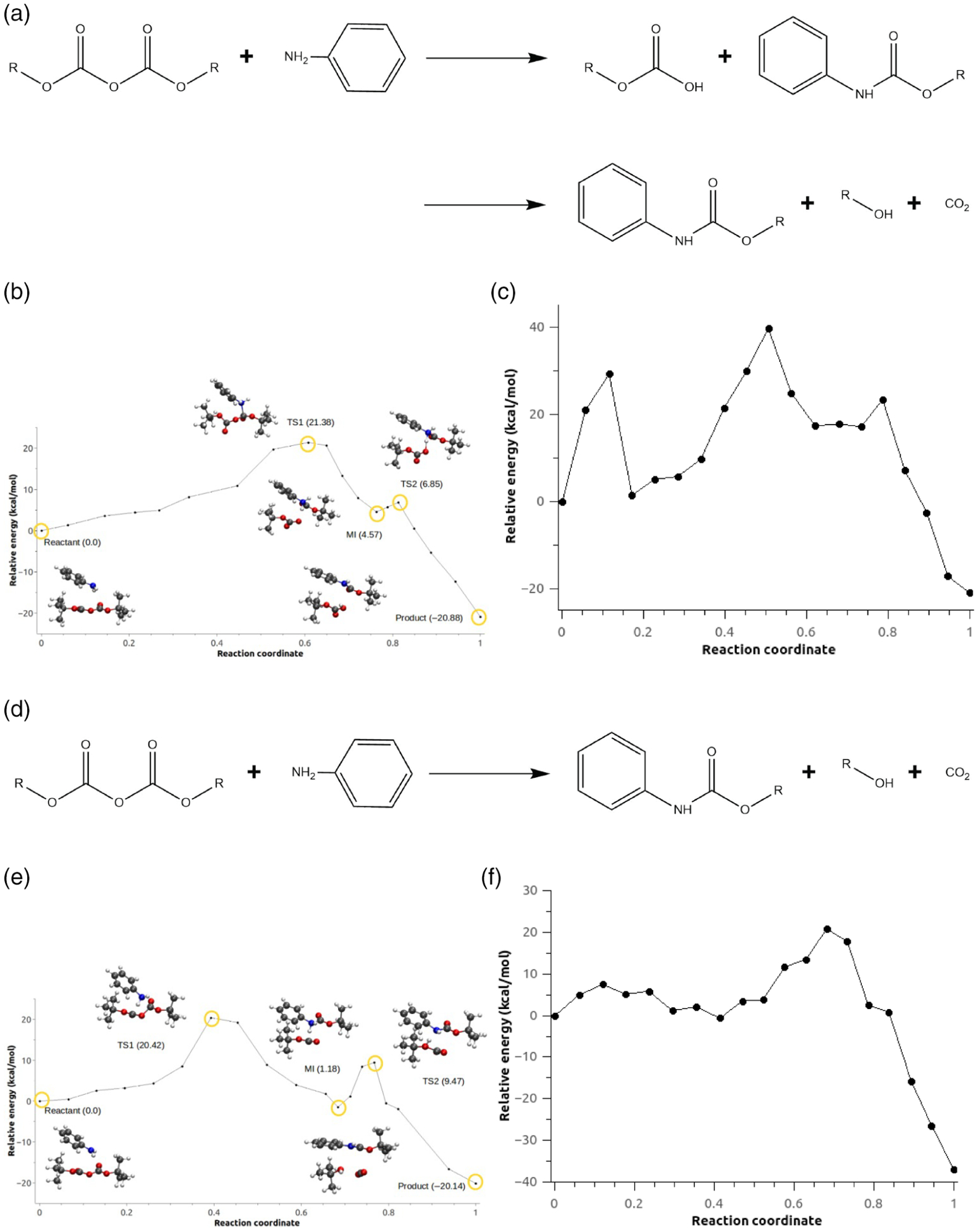
(a) Reaction scheme for the N-tert-butoxycarbonylation of aniline for the step-wise mechanism. (b) Minimum energy path for configuration C2, Scheme 1c. (c) Minimum energy path for Scheme c for configuration C2 without the AMOEBA polarization term. (d) Reaction scheme for the N-tert-butoxycarbonylation of aniline for the concerted mechanism. (e) Minimum energy path for configuration C2, Scheme 1d. (f) Minimum energy path for Scheme d for configuration C2 without the AMOEBA polarization term
Source: Adapted from E.A. Vazquez-Montelongo, J.E. Vazquez-Cervantes, G.A. Cisneros, Polarizable ab initio QM/MM study of the reaction mechanism of N-tert-butyloxycarbonylation of aniline in [EMIm][BF4]. Molecules 2018, 23, 283025
The path optimization methods described above have been applied to obtain MEPs for both reaction schemes (Figure 11b,e). The calculated rate-limiting barrier for reaction (1) is 21.38 kcal/mol compared with 20.42 kcal/mol for reaction (2). In order to assess the effect of polarization on reaction paths, the MEPs were recomputed with the AMOEBA polarization term set to zero during the calculation (Figure 11c,f). In this case, MEP with or without the polarization terms give similar barriers for reaction (1), although the shape of the reaction path without polarization is drastically altered, and the intermediate and TS2 observed in the original path are no longer observed. In the case of reaction (2), the differences between the calculated paths with and without polarization are more significant. The energy barrier computed between the reactant and product increases significantly when the polarization is not taken into account, and the shape of the path is also affected. This example illustrates the necessity to include explicit polarization within QM/MM calculations in highly charged environments.
6 |. CONCLUSIONS
The computational study of reactions in biological and condensed-phase systems has been advanced by the combination of QM and MM methods. Here, we have reported recent advances in the development of QM/MM including polarizable force fields. The use of polarizable potentials such as AMOEBA, gives rise to novel issues that need to be considered, including challenges at the internal and external boundaries (long-range effects) and coupling to the QM software. This review focused on the methods and approaches that have been developed and implemented in LICHEM to address these, and other challenges, such as the extension of the pseudobond approach, the development and implementation of QM/MM-LREC, the implementation of restrained MM path optimizations coupled with the QSM, implementation of advanced force fields for QM/MM such as MB-Pol and GEM, and so forth. Several examples have been provided to underscore the utility of polarizable potentials and their usefulness in the study of complex biological and condensed phase systems.
ACKNOWLEDGMENTS
This work was supported by R01GM108583 and NSF-CHEM/CLP 1856162. Computational time was provided by the University of North Texas CASCaM’s CRUNTCh3 high-performance cluster partially supported by NSF grant CHE-1531468.
Footnotes
CONFLICT OF INTEREST
The authors have declared no conflicts of interest for this article.
REFERENCES
- 1.Xiao G, Ren M, Hong H. 50 million atoms scale molecular dynamics modelling on a single consumer graphics card. Adv Eng Softw. 2018;124:66–72. http://www.sciencedirect.com/science/article/pii/S0965997818306811. Accessed 24 Aug 2020. [Google Scholar]
- 2.Warshel A, Levitt M. Theoretical studies of enzymic reactions: dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J Mol Biol. 1976;103(2):227–49. http://www.sciencedirect.com/science/article/pii/0022283676903119. Accessed 31 Jul 2020. [DOI] [PubMed] [Google Scholar]
- 3.Lin H, Truhlar DG. QM/MM: what have we learned, where are we, and where do we go from here? Theor Chem Accounts. 2006;117(2): 185. 10.1007/s00214-006-0143-z. [DOI] [Google Scholar]
- 4.Senn HM, Thiel W. QM/MM methods for biomolecular systems. Angew Chem Int Ed. 2009;48(7):1198–229. 10.1002/anie.200802019. [DOI] [PubMed] [Google Scholar]
- 5.van der Kamp MW, Mulholland AJ. Combined quantum mechanics/molecular mechanics (QM/MM) methods in computational enzymology. Biochemistry. 2013;52(16):2708–28. 10.1021/bi400215w. [DOI] [PubMed] [Google Scholar]
- 6.Brunk E, Rothlisberger U. Mixed quantum mechanical/molecular mechanical molecular dynamics simulations of biological systems in ground and electronically excited states. Chem Rev. 2015;115(12):6217–63. 10.1021/cr500628b. [DOI] [PubMed] [Google Scholar]
- 7.Duarte F, Amrein BA, Blaha-Nelson D, Kamerlin SCL. Recent advances in QM/MM free energy calculations using reference potentials. Biochim Biophys Acta. 2015;1850(5):954–65. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4547088/. Accessed 24 Oct 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ahmadi S, Barrios Herrera L, Chehelamirani M, Hostaš J, Jalife S, Salahub DR. Multiscale modeling of enzymes: QM-cluster, QM/MM, and QM/MM/MD: a tutorial review. Int J Quantum Chem. 2018;118(9):e25558. 10.1002/qua.25558. [DOI] [Google Scholar]
- 9.Magalĥaes RP, Fernandes HS, Sousa SF. Modelling enzymatic mechanisms with QM/MM approaches: current status and future challenges. Israel J Chem. 2020;60(7):655–66. 10.1002/ijch.202000014. [DOI] [Google Scholar]
- 10.Komatsu TS, Koyama Y, Okimoto N, Morimoto G, Ohno Y, Taiji M. COVID-19 related trajectory data of 10 microseconds all atom molecular dynamics simulation of SARS-CoV-2 dimeric main protease. 2020. https://data.mendeley.com/datasets/vpps4vhryg/2. Accessed 04 Jun 2020. [DOI] [PMC free article] [PubMed]
- 11.Jin Z, Du X, Xu Y, Deng Y, Liu M, Zhao Y, et al. Structure of Mpro from SARS-CoV-2 and discovery of its inhibitors. Nature. 2020;582 (7811):289–93. 10.1038/s41586-020-2223-y. [DOI] [PubMed] [Google Scholar]
- 12.Warshel A, Weiss RM. An empirical valence bond approach for comparing reactions in solutions and in enzymes. J Am Chem Soc. 1980;102(20):6218–26. 10.1021/ja00540a008. [DOI] [Google Scholar]
- 13.Åqvist J, Warshel A. Simulation of enzyme reactions using valence bond force fields and other hybrid quantum/classical approaches. Chem Rev. 1993;93(7):2523–44. 10.1021/cr00023a010. [DOI] [Google Scholar]
- 14.Kamerlin SCL, Warshel A. The EVB as a quantitative tool for formulating simulations and analyzing biological and chemical reactions. Faraday Discuss. 2010;145(0):71–106. 10.1039/B907354J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Govender K, Gao J, Naidoo KJ. AM1/d-CB1: a semiempirical model for QM/MM simulations of chemical glycobiology systems. J Chem Theory Comput. 2014;10:4694–707. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4478602/. Accessed 24 Oct 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ojeda-May P, Nam K. Acceleration of semiempirical QM/MM methods through message passage interface (MPI), hybrid MPI/open multiprocessing, and self-consistent field accelerator implementations. J Chem Theory Comput. 2017;13(8):3525–36. 10.1021/acs.jctc.7b00322. [DOI] [PubMed] [Google Scholar]
- 17.Štrajbl M, Hong G, Warshel A. Ab initio QM/MM simulation with proper sampling: “first principle” calculations of the free energy of the autodissociation of water in aqueous solution. J Phys Chem B. 2002;106(51):13333–43. 10.1021/jp021625h. [DOI] [Google Scholar]
- 18.Intharathep P, Tongraar A, Sagarik K. Ab initio QM/MM dynamics of H3O+ in water. J Comput Chem. 2006;27(14):1723–32. 10.1002/jcc.20503. [DOI] [PubMed] [Google Scholar]
- 19.Hu H, Yang W. Development and application of ab initio QM/MM methods for mechanistic simulation of reactions in solution and in enzymes. Theochem. 2009;898(1–3):17–30. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3800091/. Accessed 24 Oct 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fang D, Lord RL, Cisneros GA. Ab initio QM/MM calculations show an intersystem crossing in the hydrogen abstraction step in Dealkylation catalyzed by AlkB. J Phys Chem B. 2013;117(21):6410–20. 10.1021/jp403116e. [DOI] [PubMed] [Google Scholar]
- 21.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J Comput Chem. 1983;4(2):187–217. 10.1002/jcc.540040211. [DOI] [Google Scholar]
- 22.Jorgensen WL, Maxwell DS, Tirado-Rives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J Am Chem Soc. 1996;118(45):11225–36. 10.1021/ja9621760. [DOI] [Google Scholar]
- 23.Case DA, Cheatham TE III, Darden T, Gohlke H, Luo R, Merz KM Jr, et al. The Amber biomolecular simulation programs. J Comput Chem. 2005;26(16):1668–88. 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hagras MA, Glover WJ. Polarizable embedding for excited-state reactions: dynamically weighted polarizable QM/MM. J Chem Theory Comput. 2018;14(4):2137–44. 10.1021/acs.jctc.8b00064. [DOI] [PubMed] [Google Scholar]
- 25.Vázquez-Montelongo E, Vázquez-Cervantes J, Cisneros G. Polarizable ab initio QM/MM study of the reaction mechanism of N-tert-butyloxycarbonylation of aniline in [EMIm][BF4]. Molecules. 2018;23(11):2830 http://www.mdpi.com/1420-3049/23/11/2830. Accessed 24 Sep 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Giovannini T, Puglisi A, Ambrosetti M, Cappelli C. Polarizable QM/MM approach with fluctuating charges and fluctuating dipoles: the QM/FQFμ model. J Chem Theory Comput. 2019;15(4):2233–45. 10.1021/acs.jctc.8b01149. [DOI] [PubMed] [Google Scholar]
- 27.Giovannini T, Riso RR, Ambrosetti M, Puglisi A, Cappelli C. Electronic transitions for a fully polarizable QM/MM approach based on fluctuating charges and fluctuating dipoles: linear and corrected linear response regimes. J Chem Phys. 2019;151(17):174104. 10.1063/1.5121396. [DOI] [PubMed] [Google Scholar]
- 28.Notman R, Anwar J. Breaching the skin barrier—insights from molecular simulation of model membranes. Adv Drug Deliv Rev. 2013; 65(2):237–50. http://www.sciencedirect.com/science/article/pii/S0169409X12000907. Accessed 24 Aug 2020. [DOI] [PubMed] [Google Scholar]
- 29.Scott WRP, Hünenberger PH, Tironi IG, Mark AE, Billeter SR, Fennen J, et al. The GROMOS biomolecular simulation program package. J Phys Chem A. 1999;103(19):3596–607. 10.1021/jp984217f. [DOI] [Google Scholar]
- 30.Halgren TA. MMFF VI. MMFF94s option for energy minimization studies. J Comput Chem. 1999;20(7):720–9. . [DOI] [PubMed] [Google Scholar]
- 31.Allinger NL, Yuh YH, Lii JH. Molecular mechanics. The MM3 force field for hydrocarbons. 1. J Am Chem Soc. 1989;111(23):8551–66. 10.1021/ja00205a001. [DOI] [Google Scholar]
- 32.Allinger NL, Chen K, Lii JH. An improved force field (MM4) for saturated hydrocarbons. J Comput Chem 1996;17(5–6):642–668. . [DOI] [Google Scholar]
- 33.Rappe AK, Casewit CJ, Colwell KS, Goddard WA, Skiff WM. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J Am Chem Soc. 1992;114(25):10024–35. 10.1021/ja00051a040. [DOI] [Google Scholar]
- 34.Muñoz-Muñoz YM, Guevara-Carrion G, Llano-Restrepo M, Vrabec J. Lennard-Jones force field parameters for cyclic alkanes from cyclopropane to cyclohexane. Fluid Phase Equilib. 2015;404:150–60. http://www.sciencedirect.com/science/article/pii/S0378381215300029. Accessed 24 Oct 2020. [Google Scholar]
- 35.Van Vleet MJ, Misquitta AJ, Stone AJ, Schmidt JR. Beyond Born–Mayer: improved models for short-range repulsion in ab initio force fields. J Chem Theory Comput. 2016;12(8):3851–70. 10.1021/acs.jctc.6b00209. [DOI] [PubMed] [Google Scholar]
- 36.Boulanger E, Huang L, Rupakheti C, MacKerell AD Jr, Roux B. Optimized Lennard-Jones parameters for druglike small molecules. J Chem Theory Comput. 2018;14(6):3121–31. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5997559/. Accessed 24 Oct 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ponder JW, Wu C, Ren P, Pande VS, Chodera JD, Schnieders MJ, et al. Current status of the AMOEBA polarizable force field. J Phys Chem B. 2010;114(8):2549–64. 10.1021/jp910674d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lopes PEM, Lamoureux G, Mackerell AD Jr. Polarizable empirical force field for nitrogen-containing heteroaromatic compounds based on the classical Drude oscillator. J Comput Chem. 2009;30(12):1821–38. 10.1002/jcc.21183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Gordon MS, Fedorov DG, Pruitt SR, Slipchenko LV. Fragmentation methods: a route to accurate calculations on large systems. Chem Rev. 2012;112(1):632–72. 10.1021/cr200093j. [DOI] [PubMed] [Google Scholar]
- 40.Gurunathan PK, Acharya A, Ghosh D, Kosenkov D, Kaliman I, Shao Y, et al. Extension of the effective fragment potential method to macromolecules. J Phys Chem B. 2016;120(27):6562–74. 10.1021/acs.jpcb.6b04166. [DOI] [PubMed] [Google Scholar]
- 41.Cisneros GA, Piquemal JP, Darden TA. Intermolecular electrostatic energies using density fitting. J Chem Phys. 2005;123(4):44109. 10.1063/1.1947192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Piquemal JP, Cisneros GA, Reinhardt P, Gresh N, Darden TA. Towards a force field based on density fitting. J Chem Phys. 2006;124(10):104101. 10.1063/1.2173256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Geerke DP, van Gunsteren WF. On the calculation of atomic forces in classical simulation using the charge-on-spring method to explicitly treat electronic polarization. J Chem Theory Comput. 2007;3(6):2128–37. 10.1021/ct700164k. [DOI] [PubMed] [Google Scholar]
- 44.Holt A, Karlström G. Improvement of the NEMO potential by inclusion of intramolecular polarization. Int J Quantum Chem. 2009;109(6):1255–66. 10.1002/qua.21950. [DOI] [Google Scholar]
- 45.Gresh N, Cisneros GA, Darden TA, Piquemal JP. Anisotropic, polarizable molecular mechanics studies of inter- and intramolecular interactions and ligand-macromolecule complexes. A bottom-up strategy. J Chem Theory Comput. 2007;3(6):1960–86. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2367138/. Accessed 24 Aug 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Rick SW, Stuart SJ, Berne BJ. Dynamical fluctuating charge force fields: application to liquid water. J Chem Phys. 1994;101(7):6141–56. 10.1063/1.468398. [DOI] [Google Scholar]
- 47.Lipparini F, Barone V. Polarizable force fields and polarizable continuum model: a fluctuating charges/PCM approach. 1. Theory and implementation. J Chem Theory Comput. 2011;7(11):3711–24. 10.1021/ct200376z. [DOI] [PubMed] [Google Scholar]
- 48.Lu Z, Zhang Y. Interfacing ab initio quantum mechanical method with classical Drude osillator polarizable model for molecular dynamics simulation of chemical reactions. J Chem Theory Comput. 2008;4(8):1237–48. 10.1021/ct800116e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Boulanger E, Thiel W. Solvent boundary potentials for hybrid QM/MM computations using classical Drude oscillators: a fully polarizable model. J Chem Theory Comput. 2012;8(11):4527–38. 10.1021/ct300722e. [DOI] [PubMed] [Google Scholar]
- 50.Loco D, Polack É, Caprasecca S, Lagardère L, Lipparini F, Piquemal JP, et al. A QM/MM approach using the AMOEBA polarizable embedding: from ground state energies to electronic excitations. J Chem Theory Comput. 2016;12(8):3654–61. 10.1021/acs.jctc.6b00385. [DOI] [PubMed] [Google Scholar]
- 51.Bondanza M, Nottoli M, Cupellini L, Lipparini F, Mennucci B. Polarizable embedding QM/MM: the future gold standard for complex (bio)systems? Phys Chem Chem Phys. 2020;22(26):14433–48. 10.1039/D0CP02119A. [DOI] [PubMed] [Google Scholar]
- 52.Cieplak P, Dupradeau FY, Duan Y, Wang J. Polarization effects in molecular mechanical force fields. J Phys Condens Matter. 2009;21(33):333102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Li P, Merz KM. Metal ion modeling using classical mechanics. Chem Rev. 2017;117(3):1564–686. 10.1021/acs.chemrev.6b00440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Patel S, Mackerell AD Jr, Brooks CL III. CHARMM fluctuating charge force field for proteins: II. Protein/solvent properties from molecular dynamics simulations using a nonadditive electrostatic model. J Comput Chem. 2004;25(12):1504–14. 10.1002/jcc.20077. [DOI] [PubMed] [Google Scholar]
- 55.Yang ZZ, Wang CS. Atom-bond electronegativity equalization method. 1. Calculation of the charge distribution in large molecules. Chem A Eur J. 1997;101(35):6315–21. 10.1021/jp9711048. [DOI] [Google Scholar]
- 56.Wang CS, Shen-Min L, Yang ZZ. Calculation of molecular energies by atom-bond electronegativity equalization method. J Mol Struct THEOCHEM. 1998;430:191–9. http://www.sciencedirect.com/science/article/pii/S0166128098902391. Accessed 15 Dec 2020. [Google Scholar]
- 57.Wang CS, Yang ZZ. Atom-bond electronegativity equalization method. II. Lone-pair electron model. J Chem Phys. 1999;110(13):6189–97. 10.1063/1.478524. [DOI] [Google Scholar]
- 58.Yang ZZ, Wang CS. Atom-bond electronegativity equalization method and its applications based on density functional theory. J Theor Comput Chem. 2003;02(02):273–99. 10.1142/S0219633603000434. [DOI] [Google Scholar]
- 59.Shi H, Gong LD, Liu C, Lu LN, Yang ZZ. ABEEM/MM OH− models for OH−(H2O)n clusters and aqueous OH−: structures, charge distributions, and binding energies. Chem A Eur J. 2020;124(28):5963–78. 10.1021/acs.jpca.0c03941. [DOI] [PubMed] [Google Scholar]
- 60.Zhao CL, Zhao DX, Jiang QY, Zhang HX, Li S, Yang ZZ. Polarizable TIP7P water model with perturbation charges evaluated from ABEEM. J Phys Chem B. 2020;124(12):2450–64. 10.1021/acs.jpcb.9b11775. [DOI] [PubMed] [Google Scholar]
- 61.Qian P, Yang Z. Application of the ABEEM/MM model in studying the properties of the water clusters (H2O)n (n = 7–10). Sci China Ser B Chem. 2007;50(2):190–204. 10.1007/s11426-007-0003-2. [DOI] [Google Scholar]
- 62.Savelyev A, MacKerell AD Jr. All-atom polarizable force field for DNA based on the classical Drude oscillator model. J Comput Chem. 2014;35(16):1219–39. 10.1002/jcc.23611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Asef K, Nasser SJ, Hosein M. Modified Drude model for small gold nanoparticles surface plasmon resonance based on the role of classical confinement. Sci Rep. 2020;10(1):6517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Daun KJ, Menser J, Asif M, Musikhin S, Dreier T, Schulz C. Evaluation of Drude parameters for liquid germanium nanoparticles through aerosol-based line-of-sight attenuation measurements. J Quant Spectrosc Radiat Transf. 2019;226:146–56. http://www.sciencedirect.com/science/article/pii/S0022407318309178. Accessed 15 Dec 2020. [Google Scholar]
- 65.Lin FY, MacKerell AD. Polarizable empirical force field for halogen-containing compounds based on the classical Drude oscillator. J Chem Theory Comput. 2018;14(2):1083–98. 10.1021/acs.jctc.7b01086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Kratz EG, Duke RE, Cisneros GA. Long-range electrostatic corrections in multipolar/polarizable QM/MM simulations. Theor Chem Accounts. 2016;135(7):166. 10.1007/s00214-016-1923-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Dziedzic J, Mao Y, Shao Y, Ponder J, Head-Gordon T, Head-Gordon M, et al. TINKTEP: a fully self-consistent, mutually polarizable QM/MM approach based on the AMOEBA force field. J Chem Phys. 2016;145(12):124106. 10.1063/1.4962909. [DOI] [PubMed] [Google Scholar]
- 68.Mao Y, Shao Y, Dziedzic J, Skylaris CK, Head-Gordon T, Head-Gordon M. Performance of the AMOEBA water model in the vicinity of QM solutes: a diagnosis using energy decomposition analysis. J Chem Theory Comput. 2017;13(5):1963–79. [DOI] [PubMed] [Google Scholar]
- 69.Loco D, Lagardère L, Caprasecca S, Lipparini F, Mennucci B, Piquemal JP. Hybrid QM/MM molecular dynamics with AMOEBA polarizable embedding. J Chem Theory Comput. 2017;13(9):4025–33. 10.1021/acs.jctc.7b00572. [DOI] [PubMed] [Google Scholar]
- 70.Gökcan H, Vázquez-Montelongo EA, Cisneros GA. LICHEM 1.1: recent improvements and new capabilities. J Chem Theory Comput. 2019;15(5):3056–65. 10.1021/acs.jctc.9b00028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Dziedzic J, Head-Gordon T, Head-Gordon M, Skylaris CK. Mutually polarizable QM/MM model with in situ optimized localized basis functions. J Chem Phys. 2019;150(7):074103. 10.1063/1.5080384. [DOI] [PubMed] [Google Scholar]
- 72.Li P, Song LF, Merz KM. Parameterization of highly charged metal ions using the 12–6-4 LJ-type nonbonded model in explicit water. J Phys Chem B. 2015;119(3):883–95. 10.1021/jp505875v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79(2):926–35. 10.1063/1.445869. [DOI] [Google Scholar]
- 74.Lopes PEM, Roux B, MacKerell AD. Molecular modeling and dynamics studies with explicit inclusion of electronic polarizability: theory and applications. Theor Chem Accounts. 2009;124(1):11–28. 10.1007/s00214-009-0617-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Loco D, Lagardère L, Cisneros GA, Scalmani G, Frisch M, Lipparini F, et al. Towards large scale hybrid QM/MM dynamics of complex systems with advanced point dipole polarizable embeddings. Chem Sci. 2019;10(30):7200–11. http://xlink.rsc.org/?DOI=C9SC01745C. Accessed 31 Jul 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, et al. Gaussian 16 Revision C.01 Wallingford, CT: Gaussian Inc; 2016. [Google Scholar]
- 77.Lagardère L, Jolly LH, Lipparini F, Aviat F, Stamm B, Jing ZF, et al. Tinker-HP: a massively parallel molecular dynamics package for multiscale simulations of large complex systems with advanced point dipole polarizable force fields. Chem Sci. 2018;9(4):956–72. 10.1039/C7SC04531J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Loco D, Jurinovich S, Cupellini L, Menger MFSJ, Mennucci B. The modeling of the absorption lineshape for embedded molecules through a polarizable QM/MM approach. Photochem Photobiol Sci. 2018;17(5):552–60. http://xlink.rsc.org/?DOI=C8PP00033F. Accessed 28 Sep 2020. [DOI] [PubMed] [Google Scholar]
- 79.Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins Struct Funct Bioinformatics. 2006;65(3):712–25. 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Field MJ, Bash PA, Karplus M. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. J Comput Chem. 1990;11(6):700–33. 10.1002/jcc.540110605. [DOI] [Google Scholar]
- 81.Singh UC, Kollman PA. A combined ab initio quantum mechanical and molecular mechanical method for carrying out simulations on complex molecular systems: applications to the CH3Cl + Cl− exchange reaction and gas phase protonation of polyethers. J Comput Chem. 1986;7(6):718–30. 10.1002/jcc.540070604. [DOI] [Google Scholar]
- 82.Das D, Eurenius KP, Billings EM, Sherwood P, Chatfield DC, Hodošček M, et al. Optimization of quantum mechanical molecular mechanical partitioning schemes: Gaussian delocalization of molecular mechanical charges and the double link atom method. J Chem Phys. 2002;117(23):10534–47. 10.1063/1.1520134. [DOI] [Google Scholar]
- 83.Monard G, Loos M, Théry V, Baka K, Rivail JL. Hybrid classical quantum force field for modeling very large molecules. Int J Quantum Chem. 1996;58(2):153–9. . [DOI] [Google Scholar]
- 84.Ferenczy GG, Rivail JL, Surján PR, Náray-Szabó G. NDDO fragment self-consistent field approximation for large electronic systems. J Comput Chem. 1992;13(7):830–7. 10.1002/jcc.540130706. [DOI] [Google Scholar]
- 85.Théry V, Rinaldi D, Rivail JL, Maigret B, Ferenczy GG. Quantum mechanical computations on very large molecular systems: the local self-consistent field method. J Comput Chem. 1994;15(3):269–82. 10.1002/jcc.540150303. [DOI] [Google Scholar]
- 86.Assfeld X, Rivail JL. Quantum chemical computations on parts of large molecules: the ab initio local self consistent field method. Chem Phys Lett. 1996;263(1–2):100–6. https://www.sciencedirect.com/science/article/abs/pii/S0009261496011657. Accessed 17 Sep 2020. [Google Scholar]
- 87.Monari A, Rivail JL, Assfeld X. Theoretical modeling of large molecular systems. Advances in the local self consistent field method for mixed quantum mechanics/molecular mechanics calculations. Acc Chem Res. 2013;46(2):596–603. 10.1021/ar300278j. [DOI] [PubMed] [Google Scholar]
- 88.Ferré N, Assfeld X, Rivail JL. Specific force field parameters determination for the hybrid ab initio QM/MM LSCF method. J Comput Chem. 2002;23(6):610–24. 10.1002/jcc.10058. [DOI] [PubMed] [Google Scholar]
- 89.Gao J, Amara P, Alhambra C, Field MJA. Generalized hybrid orbital (GHO) method for the treatment of boundary atoms in combined QM/MM calculations. Chem A Eur J. 1998;102(24):4714–4721. 10.1021/jp9809890. [DOI] [Google Scholar]
- 90.Amara P, Field MJ, Alhambra C, Gao J. The generalized hybrid orbital method for combined quantum mechanical/molecular mechanical calculations: formulation and tests of the analytical derivatives. Theor Chem Acc Theory Comput Model. 2000;104(5):336–43. 10.1007/s002140000153. [DOI] [Google Scholar]
- 91.Zhang Y, Lee TS, Yang W. A pseudobond approach to combining quantum mechanical and molecular mechanical methods. J Chem Phys. 1999;110(1):46–54. 10.1063/1.478083. [DOI] [Google Scholar]
- 92.Zhang Y Improved pseudobonds for combined ab initio quantum mechanical/molecular mechanical methods. J Chem Phys. 2005;122(2):024114. 10.1063/1.1834899. [DOI] [PubMed] [Google Scholar]
- 93.Parks JM, Hu H, Cohen AJ, Yang W. A pseudobond parametrization for improved electrostatics in quantum mechanical/molecular mechanical simulations of enzymes. J Chem Phys. 2008;129(15):154106. 10.1063/1.2994288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.DiLabio GA, Hurley MM, Christiansen PA. Simple one-electron quantum capping potentials for use in hybrid QM/MM studies of biological molecules. J Chem Phys. 2002;116(22):9578–84. 10.1063/1.1477182. [DOI] [Google Scholar]
- 95.Das R, Vázquezvázquez-Montelongo EA, Andrés G, Cisneros A, Wu JI. Ground state destabilization in uracil DNA glycosylase: let’s not forget “tautomeric strain” in substrates. J Am Chem Soc. 2019;141(35):13739–13743. https://pubs.acs.org/sharingguidelines. Accessed 24 Sep 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A smooth particle mesh Ewald method. J Chem Phys. 1995;103(19):8577–93. 10.1063/1.470117. [DOI] [Google Scholar]
- 97.Ewald PP. Die Berechnung optischer und elektrostatischer Gitterpotentiale. Ann Phys. 1921;369(3):253–87. 10.1002/andp.19213690304. [DOI] [Google Scholar]
- 98.Darden TA. Extensions of the Ewald method for Coulomb interactions in crystals. International tables for crystallography. Atlanta, GA: American Cancer Society; 2010. p. 458–81. 10.1107/97809553602060000772. [DOI] [Google Scholar]
- 99.Nam K, Gao J, York DM. An efficient linear-scaling Ewald method for long-range electrostatic interactions in combined QM/MM calculations. J Chem Theory Comput. 2005;1(1):2–13. 10.1021/ct049941i. [DOI] [PubMed] [Google Scholar]
- 100.Walker RC, Crowley MF, Case DA. The implementation of a fast and accurate QM/MM potential method in Amber. J Comput Chem. 2008;29(7):1019–31. [DOI] [PubMed] [Google Scholar]
- 101.Giese TJ, York DM. Ambient-potential composite Ewald method for ab initio quantum mechanical/molecular mechanical molecular dynamics simulation. J Chem Theory Comput. 2016;12(6):2611–32. 10.1021/acs.jctc.6b00198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Beglov D, Roux B. Finite representation of an infinite bulk system: solvent boundary potential for computer simulations. J Chem Phys. 1994;100(12):9050–63. 10.1063/1.466711. [DOI] [Google Scholar]
- 103.Im W, Berneche S, Roux B. Generalized solvent boundary potential for computer simulations. J Chem Phys. 2001;114(7):2924–37. 10.1063/1.1336570. [DOI] [Google Scholar]
- 104.Benighaus T, Thiel W. Long-range electrostatic effects in QM/MM studies of enzymatic reactions: application of the solvated macromolecule boundary potential. J Chem Theory Comput. 2011;7(1):238–49. 10.1021/ct1005455. [DOI] [PubMed] [Google Scholar]
- 105.McCann BW, Acevedo O. Pairwise alternatives to Ewald summation for calculating long-range electrostatics in ionic liquids. J Chem Theory Comput. 2013;9(2):944–50. [DOI] [PubMed] [Google Scholar]
- 106.Acevedo O Simulating chemical reactions in ionic liquids using QM/MM methodology. Chem A Eur J. 2014;118(50):11653–66. 10.1021/jp507967z. [DOI] [PubMed] [Google Scholar]
- 107.Acevedo O, Jorgensen WL. Quantum and molecular mechanical Monte Carlo techniques for modeling condensed-phase reactions. WIREs Comput Mol Sci. 2014;4(5):422–35. 10.1002/wcms.1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Fang D, Duke RE, Cisneros GA. A new smoothing function to introduce long-range electrostatic effects in QM/MM calculations. J Chem Phys. 2015;143(4):44103. 10.1063/1.4926652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Pan X, Rosta E, Shao Y. Representation of the QM subsystem for long-range electrostatic interaction in non-periodic ab initio QM/MM calculations. Molecules. 2018;23(10):2500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Riccardi D, Li G, Cui Q. Importance of van der Waals interactions in QM/MM simulations. J Phys Chem B. 2004;108(20):6467–78. 10.1021/jp037992q. [DOI] [PubMed] [Google Scholar]
- 111.Reddy SK, Straight SC, Bajaj P, Huy Pham C, Riera M, Moberg DR, et al. On the accuracy of the MB-pol many-body potential for water: interaction energies, vibrational frequencies, and classical thermodynamic and dynamical properties from clusters to liquid water and ice. J Chem Phys. 2016;145(19):194504. [DOI] [PubMed] [Google Scholar]
- 112.Lambros E, Lipparini F, Cisneros GA, Paesani F. A many-body, fully polarizable approach to QM/MM simulations. J. Chem. Theo. Comput 2020;16 12:7462–7472. https://pubs.acs.org/doi/10.1021/acs.jctc.0c00932. Accessed 17 Sep 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Duster A, Wang CH, Lin H. Adaptive QM/MM for molecular dynamics simulations: 5. On the energy-conserved permuted adaptive-partitioning schemes. Molecules. 2018;23(9):2170. 10.3390/molecules23092170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Watanabe HC, Cui Q. Quantitative analysis of QM/MM boundary artifacts and correction in adaptive QM/MM simulations. J Chem Theory Comput. 2019;15(7):3917–28. 10.1021/acs.jctc.9b00180. [DOI] [PubMed] [Google Scholar]
- 115.Viquez Rojas CI, Slipchenko LV. Exchange-repulsion in QM/EFP excitation energies—beyond polarizable embedding. J Chem Theory Comput. 2020;16(10):6408–6417. 10.1021/acs.jctc.9b01156. [DOI] [PubMed] [Google Scholar]
- 116.Chen X, Qu Z, Suo B, Gao J. A self-consistent coulomb bath model using density fitting. J Comput Chem. 2020;41(18):1698–708. 10.1002/jcc.26211. [DOI] [PubMed] [Google Scholar]
- 117.Giese TJ, York DM. Quantum mechanical force fields for condensed phase molecular simulations. J Phys Condens Matter. 2017;29(38):383002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Chen X, Gao J. Fragment exchange potential for realizing Pauli deformation of Interfragment interactions. J PhysChemLett. 2020;11(10):4008–16. 10.1021/acs.jpclett.0c00933. [DOI] [PubMed] [Google Scholar]
- 119.Jones LO, Mosquera MA, Schatz GC, Ratner MA. Embedding methods for quantum chemistry: applications from materials to life sciences. J Am Chem Soc. 2020;142(7):3281–95. 10.1021/jacs.9b10780. [DOI] [PubMed] [Google Scholar]
- 120.Jung Y, Sodt A, Gill PMW, Head-Gordon M. Auxiliary basis expansions for large-scale electronic structure calculations. Proc Natl Acad Sci. 2005;102(19):6692–7. https://www.pnas.org/content/102/19/6692. Accessed 09 Sep 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Cisneros GA, Piquemal JP, Darden TA. Generalization of the Gaussian electrostatic model: extension to arbitrary angular momentum, distributed multipoles, and speedup with reciprocal space methods. J Chem Phys. 2006;125(18):184101. 10.1063/1.2363374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Cisneros GA, Elking D, Piquemal JP, Darden TA. Numerical fitting of molecular properties to Hermite Gaussians. Chem A Eur J. 2007;111(47):12049–56. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2366033/. Accessed 03 Nov 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Babin V, Leforestier C, Paesani F. Development of a “first principles” water potential with flexible monomers: dimer potential energy surface, VRT spectrum, and second virial coefficient. J Chem Theory Comput. 2013;9(12):5395–403. 10.1021/ct400863t. [DOI] [PubMed] [Google Scholar]
- 124.Duke RE, Starovoytov ON, Piquemal JP, Cisneros GA. GEM*: a molecular electronic density-based force field for molecular dynamics simulations. J Chem Theory Comput. 2014;10(4):1361–5. 10.1021/ct500050p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Duke RE, Cisneros GA. Ewald-based methods for Gaussian integral evaluation: application to a new parameterization of GEM. J Mol Model. 2019;25(10):307 https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6741781/. Accessed 03 Nov 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Case DA, Belfon K, Ben-Shalom IY, Brozell SR, Cerutti DS, Cheatham TE, et al. AMBER 2020. San Francisco: University of California; 2020. [Google Scholar]
- 127.Cisneros GA, Piquemal JP, Darden TA. Quantum mechanics/molecular mechanics electrostatic embedding with continuous and discrete functions. J Phys Chem B. 2006;110(28):13682–4. 10.1021/jp062768x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Wheatley RJ, Price SL. An overlap model for estimating the anisotropy of repulsion. Mol Phys. 1990;69(3):507–33. 10.1080/00268979000100371. [DOI] [Google Scholar]
- 129.Tschumper GS, Leininger ML, Hoffman BC, Valeev EF, Schaefer HF, Quack M. Anchoring the water dimer potential energy surface with explicitly correlated computations and focal point analyses. J Chem Phys. 2002;116(2):690–701. 10.1063/1.1408302. [DOI] [Google Scholar]
- 130.Parrish RM, Burns LA, Smith DGA, Simmonett AC, DePrince AE, Hohenstein EG, et al. Psi4 1.1: an open-source electronic structure program emphasizing automation, advanced libraries, and interoperability. J Chem Theory Comput. 2017;13(7):3185–97. 10.1021/acs.jctc.7b00174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Kratz EG, Walker AR, Lagardère L, Lipparini F, Piquemal JP, Andrés Cisneros G. LICHEM: a QM/MM program for simulations with multipolar and polarizable force fields. J Comput Chem. 2016;37(11):1019–29. 10.1002/jcc.24295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Kratz EG, Walker AR, Lagardere L, Lipparini F, Piquemal JP, Gokcan H. LICHEM: Layered Interacting CHEmical models. University of North Texas: The Cisneros Research Group; 2020. https://github.com/CisnerosResearch/LICHEM. Accessed 30 Nov 2020. [Google Scholar]
- 133.Valiev M, Bylaska EJ, Govind N, Kowalski K, Straatsma TP, Van Dam HJJ, et al. NWChem: a comprehensive and scalable open-source solution for large scale molecular simulations. Comput Phys Commun. 2010;181(9):1477–89. http://www.sciencedirect.com/science/article/pii/S0010465510001438. Accessed 03 Nov 2020. [Google Scholar]
- 134.Rackers JA, Wang Z, Lu C, Laury ML, Lagardère L, Schnieders MJ, et al. Tinker 8: software tools for molecular design. J Chem Theory Comput. 2018;14(10):5273–89. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6335969/. Accessed 03 Nov 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Plimpton S Fast parallel algorithms for short-range molecular dynamics. J Comput Phys. 1995;117(1):1–19. http://www.sciencedirect.com/science/article/pii/S002199918571039X. Accessed 03 Nov 2020. [Google Scholar]
- 136.Devereux M, Raghunathan S, Fedorov DG, Meuwly M. A novel, computationally efficient multipolar model employing distributed charges for molecular dynamics simulations. J Chem Theory Comput. 2014;10(10):4229–41. 10.1021/ct500511t. [DOI] [PubMed] [Google Scholar]
- 137.Jónsson H, Mills G, Jacobsen KW. Nudged elastic band method for finding minimum energy paths of transitions. Classical and quantum dynamics in condensed phase simulations. Singapore: World Scientific; 1998. p. 385–404. 10.1142/9789812839664_0016. [DOI] [Google Scholar]
- 138.Henkelman G, Uberuaga BP, Jónsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J Chem Phys. 2000;113(22):9901–4. 10.1063/1.1329672. [DOI] [Google Scholar]
- 139.Burger SK, Yang W. Quadratic string method for determining the minimum-energy path based on multiobjective optimization. J Chem Phys. 2006;124(5):54109. 10.1063/1.2163875. [DOI] [PubMed] [Google Scholar]
- 140.Fletcher R Practical methods of optimization. 2nd ed. USA: Wiley-Interscience; 1987. [Google Scholar]
- 141.Xie L, Liu H, Yang W. Adapting the nudged elastic band method for determining minimum-energy paths of chemical reactions in enzymes. J Chem Phys. 2004;120(17):8039–52. 10.1063/1.1691404. [DOI] [PubMed] [Google Scholar]
- 142.Cisneros GA, Liu H, Lu Z, Yang W. Reaction path determination for quantum mechanical/molecular mechanical modeling of enzyme reactions by combining first order and second order “chain-of-replicas” methods. J Chem Phys. 2005;122(11):114502. [DOI] [PubMed] [Google Scholar]
- 143.Gökcan H, Kratz E, Darden TA, Piquemal JP, Cisneros GA. QM/MM simulations with the Gaussian electrostatic model: a density-based polarizable potential. J PhysChemLett. 2018;9(11):3062–7. 10.1021/acs.jpclett.8b01412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Sarkar A, Roy SR, Parikh N, Chakraborti AK. Nonsolvent application of ionic liquids: organo-catalysis by 1-alkyl-3-methylimidazolium cation based room-temperature ionic liquids for chemoselective N-tert-butyloxycarbonylation of amines and the influence of the C-2 hydrogen on cataly. J Org Chem. 2011;76(17):7132–40. 10.1021/jo201102q. [DOI] [PubMed] [Google Scholar]
RELATED WIREs ARTICLES
- NCIPLOT and the analysis of noncovalent interactions using the reduced density gradient.


