A High-Fidelity 3D Micromechanical Model of Ventricular Myocardium

Abstract

Pulmonary arterial hypertension (PAH) imposes a pressure overload on the right ventricle (RV), leading to myofiber hypertrophy and remodeling of the extracellular collagen fiber network. While the macroscopic behavior of healthy and post-PAH RV free wall (RVFW) tissue has been studied previously, the mechanical microenvironment that drives remodeling events in the myofibers and the extracellular matrix (ECM) remains largely unexplored. We hypothesize that multiscale computational modeling of the heart, linking cellular-scale events to tissue-scale behavior, can improve our understanding of cardiac remodeling and better identify therapeutic targets. We have developed a high-fidelity microanatomically realistic model of ventricular myocardium, combining confocal microscopy techniques, soft tissue mechanics, and finite element modeling. We match our microanatomical model to the tissue-scale mechanical response of previous studies on biaxial properties of RVFW and examine the local myofiber-ECM interactions to study fiber-specific mechanics at the scale of individual myofibers. Through this approach, we determine that the interactions occurring at the tissue scale can be accounted for by accurately representing the geometry of the myofiber-collagen arrangement at the micro scale. Ultimately, models such as these can be used to link cellular-level adaptations with organ-level adaptations to lead to the development of patient-specific treatments for PAH.

1. Introduction

Cardiac diseases like pulmonary arterial hypertension (PAH) lead to substantial adaptations in cardiac tissue structure and mechanical behavior. PAH imposes a chronic pressure overload on the right ventricle (RV) of the heart, which can cause the RV to initially thicken via hypertrophy of the myofibers to mitigate increased wall stress, but later dilate and lose contractile function, leading to RV failure. Previous work characterizing the complex changes in PAH has identified that the amount of RV remodeling resulting from pressure overload is one of the major predictors of poor prognosis in RV function [1,2]. As such, there is a need to quantify the mechanical state of the RV in order to better understand the factors influencing the onset, progression, and potential reversibility of remodeling in response to PAH through the development of computational models.

While the tissue-scale (~1-cm) structure and mechanics of RV myocardial tissue have been studied previously [3], knowledge of the mechanical contributions of and interactions between myofibers and the surrounding extracellular matrix (ECM) remains incomplete. Avazmohammadi et al. highlighted the importance of accounting for myofiber-collagen interactions in order to capture the full anisotropic mechanical behavior of the tissue [4]. This was accomplished through the addition of a myofiber-collagen interaction term in the strain energy density function based on the joint extension of myofibers and collagen fibers. Despite this important finding, the precise form of this coupling has yet to be characterized at the scale of individual myofibers, requiring more advanced histological approaches focused on the specific arrangement of myofibers and collagen in the myocardium.

To this end, multiscale computational modeling, particularly the development of models that are faithful to the microstructure of the myocardium, is important in order to gain insight into the cellular-level mechanical environment. Our specific objective was to determine to what extent the coupling behavior observed at the tissue scale could be accounted for by recapitulating the cellular-scale geometric arrangement of myofibers and ECM in the myocardium. For this first study, we based our model on a high-resolution 3D imaging dataset from rabbit myocardium, with the aim to match the results of our previous tissue-level model in planar biaxial deformations [4]. Then, based on the matched stress-strain responses, we quantify myofiber and ECM strain profiles under applied biaxial strain and further investigate the influence of myofiber-collagen mechanical interactions derived from the micro-scale deformations of myofibers and extracellular matrix.

2. Methods

2.1. Finite Element Mesh Construction

A high-fidelity representation of the myocardial tissue structure is essential in understanding cell-scale adaptations and linking them with remodeling events at the tissue and organ level. To achieve this, we developed a model using previously acquired 3D imaging datasets of ventricular myocardium from New Zealand white rabbits. Harvesting of the heart, sectioning, labeling, and imaging were performed at the University of Utah using previously developed methods [5, 6]. Briefly, myocardium samples of 5-mm diameter were obtained from the left ventricle and were then cryosectioned into slices with thickness of 100 μm. Slices were labeled and mounted compression-free by sealing within Fluoromount-G (Electron Microscopy Science, PA, USA). 3D image stacks were acquired via laser scanning confocal microscopy, with a tissue volume of 204×204×60 μm imaged. The segmentation and reconstruction of the 3D tissue geometry was performed using a semi-automatic approach based on watershed methods and histogram-based thresholding [5]. This method was used to segment myocytes, fibroblasts, coronary blood vessels, and extracellular space (Fig. 1). Manual smoothing and feature separation was performed using Seg3D (sci.utah.edu).

Fig. 1.

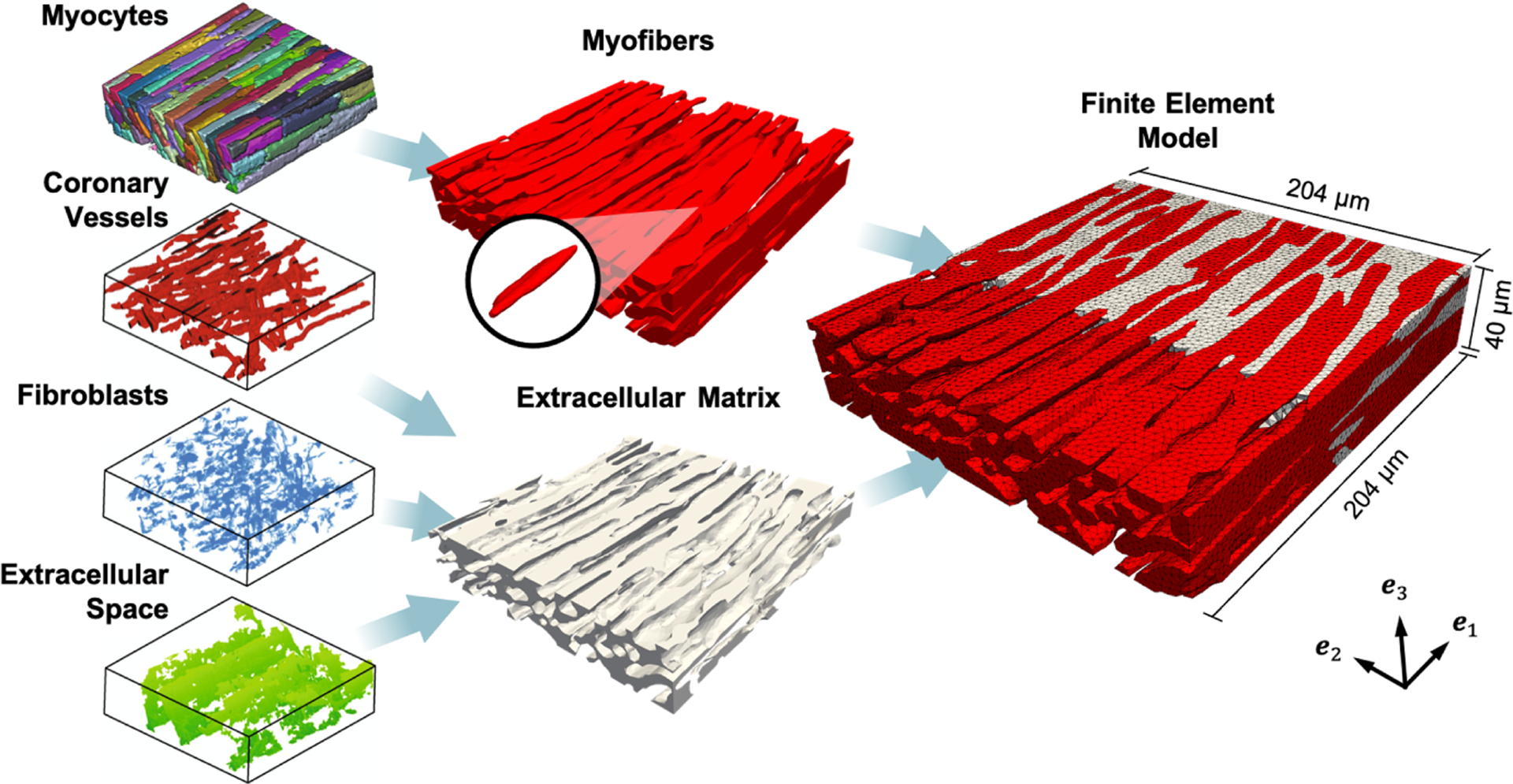
Finite element model developed from 3D geometry. Left: Geometry of myocytes, coronary vessels, fibroblasts, and extracellular space [6]. Center: Myocytes joined into the myofiber phase (red), with representative myocyte highlighted. Coronary vessels, fibroblasts, and extracellular space joined into the extracellular matrix phase (gray). Right: Cross-section of FE model showing myofiber elements embedded in ECM elements. Coordinate axes {e₁, e₂, e₃} indicate the image and laboratory axes.

For simplicity in the development of the initial finite element (FE) model, myocytes were connected and combined into a “myofiber” phase, rather than individual myocytes, according to knowledge of the interconnected arrangement of myocytes in the myocardium. Coronary vessels, fibroblasts, and extracellular space were combined into an “extracellular matrix” or “collagen” phase in order to eliminate cavities within the model domain. This two-phase segmentation was cleaned with island removal and Gaussian smoothing and was then used to generate a volumetric mesh consisting of ~1.1 million linear tetrahedral elements within Simpleware ScanIP (Synopsys, CA, USA) (Fig. 1), with final dimensions of 204×204×40 μm. Image processing was performed such that the orientation of myocytes was aligned with the e₁ axis in the image, and the cross-fiber direction with the e₂ axis.

2.2. Constitutive Modeling

We focused this study on passive myocardial mechanics at the cell and tissue scales. Thus, the mechanical properties of the myofiber and ECM phases were characterized with hyperelastic, nonlinear, anisotropic, incompressible material models adapted from our previous studies [3,4]. Deformations were described with the deformation gradient tensor F, given by

$$F_{ij}=\frac{\partial x_i}{\partial X_j}=\left[\begin{array}{lll}\frac{\partial x_1}{\partial X_1}\hfill & \frac{\partial x_1}{\partial X_2}\hfill & \frac{\partial x_1}{\partial X_3}\hfill \\ \frac{\partial x_2}{\partial X_1}\hfill & \frac{\partial x_2}{\partial X_2}\hfill & \frac{\partial x_2}{\partial X_3}\hfill \\ \frac{\partial x_3}{\partial X_1}\hfill & \frac{\partial x_3}{\partial X_2}\hfill & \frac{\partial x_3}{\partial X_3}\hfill \end{array}\right],$$ (1)

where X is a material point in the reference configuration moving to a new point x in the deformed configuration. From this we defined the right Cauchy-Green tensor C = F^TF and the Green-Lagrange strain tensor E = (C − I)/2, where I is the identity tensor.

Myofibers.

Since individual myofiber orientations could be directly obtained from the imaging dataset, we defined the myofiber direction f as the predominant direction of the long axes of myofibers in the mesh (e₁), which was fairly constant throughout the geometry with a splay of 2.5°. We defined the cross-fiber (or sheet) direction s as the direction normal to the myofibers within the plane of the mesh, aligned with e₂ (Fig. 1).

The myofiber strain energy ψ_myo was modeled using a modification of a well-established orthotropic constitutive form from Holzapfel and Ogden [7]. In particular, this form consisted of an isotropic matrix stiffened by mutually orthogonal fiber families along f and s within the layer, given by

$${\psi }_{\text{myo}}=\frac{{\mu }_{\text{myo}}}{2}\left(I_1-3\right)+\frac{a_{\text{f}}}{2b_{\text{f}}}\left\{\text{exp}\left[b_{\text{f}}{\left(I_{4\text{f}}-1\right)}^2\right]-1\right\}+\frac{a_{\text{s}}}{2b_{\text{s}}}\left\{\text{exp}\left[b_{\text{s}}{\left(I_{4\text{s}}-1\right)}^2\right]-1\right\},$$ (2)

where I₁ = tr C is related to the isotropic stretch, and I_4f = f · Cf and I_4s = s · Cs are analogous to square of the stretch along the f and s directions, respectively.{μ_myo, a_f, b_f, a_s, b_s} are the material parameters. Here, the exponential ground matrix term in [7] was replaced with a Neo-Hookean form, and the fiber-sheet interaction term was omitted with the aim of recovering this behavior instead from the interaction of discrete myofiber and ECM phases in the model geometry.

Extracellular Matrix.

Individual collagen fibers, having diameters at the scale of less than 1 μm, were not visible in the image. In light of this, the ECM/collagen phase was modeled as an isotropic matrix reinforced by a distribution of undulated, linearly stiffening collagen fibers described by the orientation distribution function (ODF) Γ_θ and recruitment function Γ_s. The collagen fiber splay was represented with a von Mises distribution, given by

$${\Gamma }_{\theta }(\theta )=\frac{\text{exp}\left(\kappa \text{ cos}\left(\theta -{\mu }^{\text{c}}\right)\right)}{2\pi I_0(\kappa )},$$ (3)

where $\theta \in \left[-\frac{\pi }{2},\frac{\pi }{2}\right]$ is the in-plane angle used to define the collagen fiber orientation n, I₀(κ) is the modified Bessel function of order 0, and μ^c and 1/κ are related to μ and ${\sigma }_{\theta }^2$ in the normal distribution, respectively, with σ_θ being the fiber splay. The recruitment function was given by the half-normal distribution

$${\Gamma }_s\left({\lambda }_s\right)=\{\begin{array}{ll}\frac{\text{exp}\left(-\frac{{\left(\lambda \text{ub}-{\lambda }_s\right)}^2}{2{\sigma }_s^2}\right)}{{\sigma }_s\sqrt{2\pi }\text{ erf}\left(\frac{\left({\lambda }_{\text{ub}}-1\right)}{\sqrt{2}{\sigma }_s}\right)}\hfill & \text{ for }{\lambda }_s\in \left(1,{\lambda }_{\text{ub}}\right]\hfill \\ 0\hfill & \text{ otherwise }\hfill \end{array},$$ (4)

where λ_s is the fiber slack stretch at which collagen fibers begin contributing to the ECM stress, λ_ub is the upper-bound slack stretch of maximum recruitment, and σ_s controls the rate of recruitment. The final expression for the ECM constitutive form ψ_ECM was thus given by

$${\psi }_{\text{ECM}}=\frac{{\mu }_{\text{col}}}{2}\left(I_1-3\right)+\frac{{\eta }_{\text{col}}}{2}{\int }_{-\pi /2}^{\pi /2}{\Gamma }_{\theta }(\theta ){\int }_1^{{\lambda }_{\theta }}{\Gamma }_s\left({\lambda }_s\right){\left(\frac{{\lambda }_{\theta }}{{\lambda }_s}-1\right)}^{2}d{\lambda }_{s}d\theta ,$$ (5)

where ${\lambda }_{\theta }=\sqrt{n\cdot Cn}$ is the component of the fiber stretch in the n direction. {μ_col, η_col, μ^c, σ_θ, λ_ub, σ_s} are the material parameters. In order to match the tissue-scale collagen fiber recruitment, the fiber slack stretch was determined based on previous modeling results [4], which also indicated the collagen fiber distribution was aligned with the myofibers (f) in the model (μ^c = 0°).

2.3. FE Simulations

Single Layer Simulation.

The structure-based model was originally developed to capture tissue-scale myofiber/collagen/interaction stresses with more dispersed fiber distributions. Thus, as a fitting target for the microanatomical model, we simulated a stress-strain response using the structure-based model (Eq. 27 in [4]) guided by the highly aligned structure of the microanatomical finite element geometry. Myofiber and ECM elements were assigned their corresponding fitted material models (Eqs. 2 and 5) in the FE geometry and assumed to be perfectly bonded. Deformations were applied to the boundary surfaces of the model in varying biaxial strain configurations E₁₁:E₂₂ = 0.30:0.30, 0.30:0.15, and 0.15:0.30. The microanatomical constitutive parameters were then calibrated such that the second Piola-Kirchhoff stress response of both models matched. All simulations were performed on the Stampede2 supercomputer at the Texas Advanced Computing Center using the open-source software FEniCS (fenicsproject.org).

Linking to the Tissue Scale.

In order to reproduce the fiber ensemble response associated with the higher-splay myofiber and collagen fiber structure of the full-thickness RVFW, rather than the highly aligned structure of the confocal microscopy dataset, the microanatomical results required a homogenization routine to link the cell-scale and tissue-scale mechanics. Using the histologically measured myofiber and collagen orientation distribution functions of previous studies (Fig. 7 in [4]), the micro-scale FE model stress-strain response was integrated over the tissue-scale orientation distribution to compute an effective dispersed stress as a function of transmural depth (from endo- to epicardium). The effective stress was then integrated over the transmural depth to predict the tissue-level stress.

3. Results

The stress-strain response of the microanatomical constitutive models successfully reproduced the tissue-scale structural model predictions (Fig. 2). Fitted parameters are listed in Table 1. Since the micro-level structure involved highly aligned myofibers oriented in the e₁ direction, the model exhibited exponentially stiffening myofiber stress along e₁ with negligible stress along e₂. The ECM exhibited nonlinear stiffening during collagen fiber recruitment (0.17 < E < 0.20), after which fibers were fully recruited and the ECM response became linear, as demonstrated previously [4]. The overall response was governed by myofiber behavior in the low-strain regime (E < 0.17), whereas at higher strains, the ECM became the major contributor to the RVFW stress. This behavior was primarily observed in loading paths that stretched the collagen (along e₁) beyond the slack stretch, as opposed to the E₁₁:E₂₂ = 0.15:0.30 in which collagen recruitment was not significant.

Fig. 2.

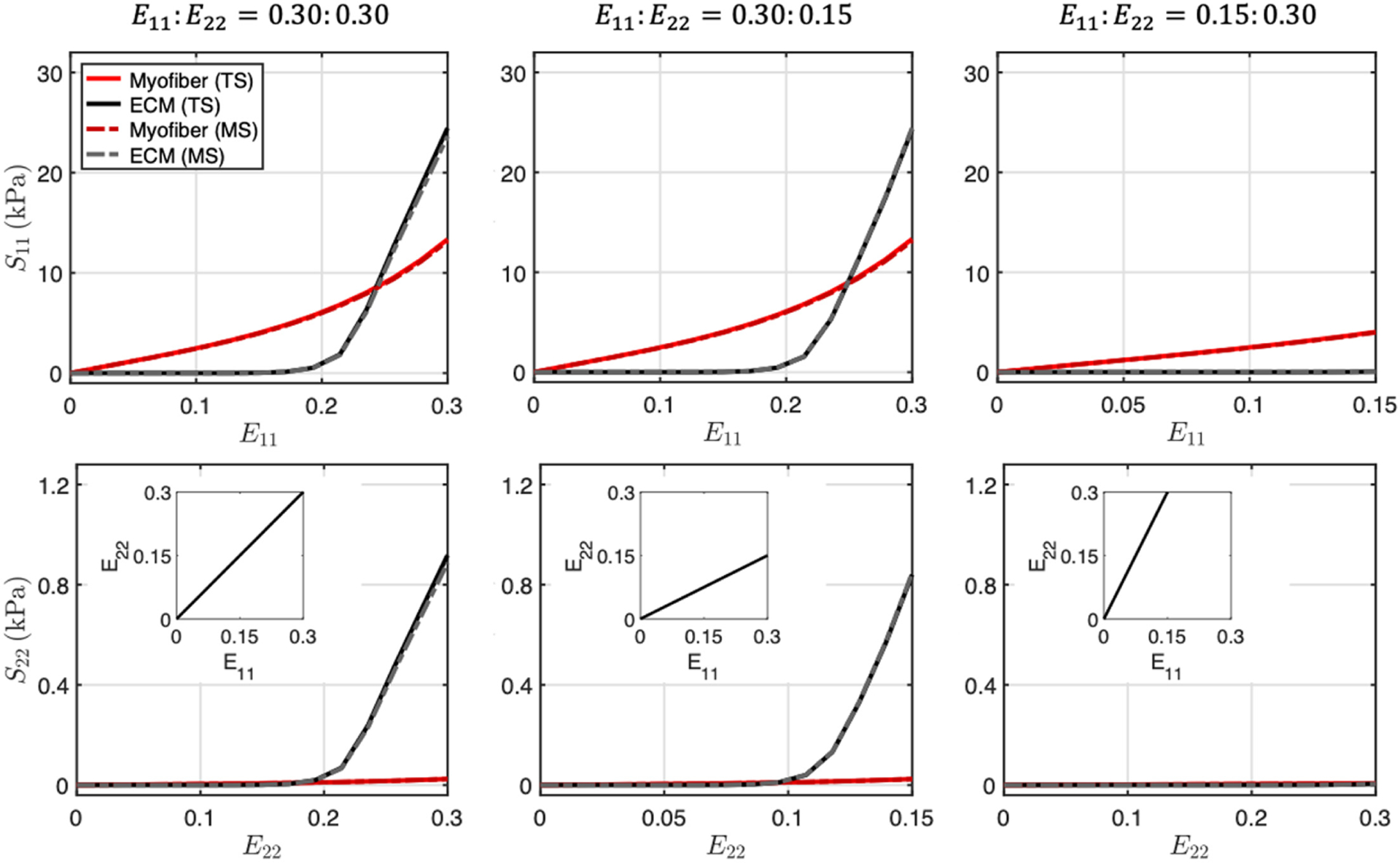
Myofiber (red) and extracellular matrix fiber (black) stresses in response to biaxial strain deformations: E₁₁:E₂₂ = 0.30:0.30, 0.30:0.15, 0.15:0.30. Solid lines: predictions from tissue-scale structural model. Dotted lines: fitted response of microanatomical model. Abbreviations: tissue scale (TS), micro scale (MS).

Table 1.

Constitutive parameters for micro-scale myofiber and ECM models fitted to tissue-scale structure-based model prediction [4].

Myofiber					ECM
μmyo (Pa)	af (kPa)	bf	as (kPa)	bs	μcol (Pa)	ηcol (MPa)	μc (deg)	σθ (deg)	λub	σs
0.059	8.94	1.59	0.0813	1.29	0.050	1.91	0.0	11.0	1.205	0.022

At maximum deformation, the strain fields within the myofiber and ECM phases (Fig. 3) showed that although the distribution of myofiber and ECM strains along e₁ and e₂ followed the applied boundary strains in an average sense, there was a high level of heterogeneity throughout the volume (Fig. 4). Along e₁, regions of ECM at the tips of myofibers exhibited decreases in E₁₁, but increases in areas between adjacent myofibers. An opposite trend was observed along e₂, where significant regions of ECM located between the tips of adjacent myofibers showed pronounced increases in E₂₂. This was observed for all biaxial loading paths, although the amount of increase was not as prominent when collagen fibers were not being recruited (e.g., E₁₁:E₂₂ = 0.15:0.30). Substantial shear strains also developed in the model.

Fig. 3.

Midplane cross-sections of E₁₁ and E₂₂ at maximum deformation for the myofiber and ECM phases. Myofibers and ECM are shown separately for clarity.

Fig. 4.

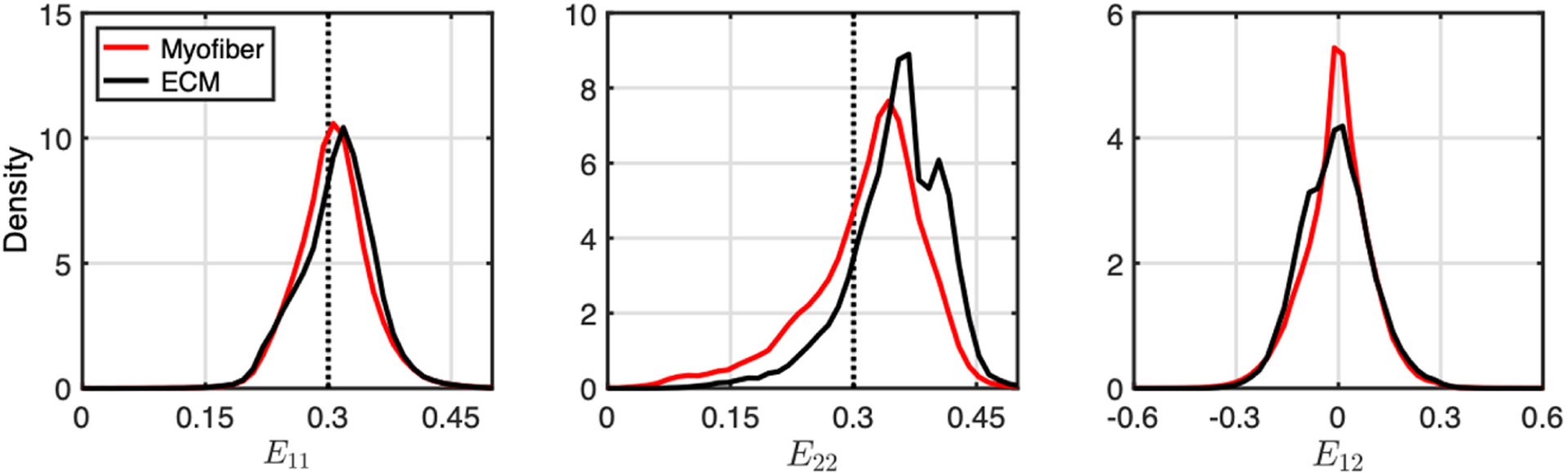
Normalized histograms of E₁₁ E₂₂, and E₁₂ in myofiber (red) and ECM (black) elements at maximum applied strain for the equibiaxial loading path. Dotted lines indicate applied strain.

Using the structure-based model, the mechanical response of a single tissue-scale layer of RV myocardium was modeled by applying the histologically measured fiber splays for myofibers and collagen fibers rather than the attributes of the confocal microscopy dataset. The micro-scale model was homogenized over the orientation distribution function and offered a very close match (Fig. 5a). The full transmural homogenization also demonstrated the effect of transmurally varying fiber orientation through the generation of significant cross-fiber stress in both the myofiber and ECM phases (Fig. 5b). Homogenization over the fiber angle θ microanatomical model response was also found to generate this effect, though to a lesser extent. The combination of both increased splay at a given level along with transmural variation in preferred direction resulted in stress-strain behavior showing qualitative similarity to tissue-level studies [4].

Fig. 5.

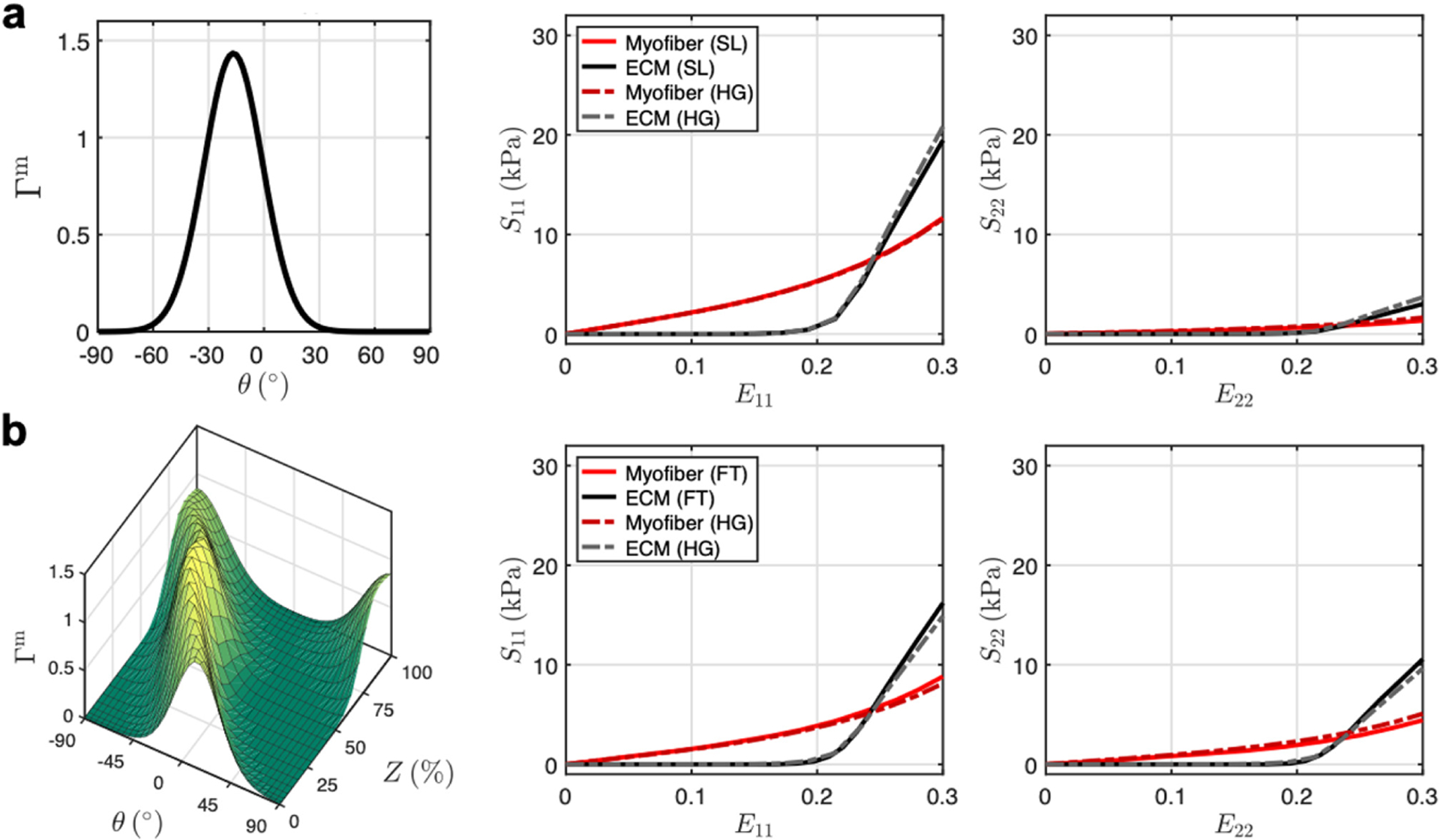
(a) Homogenization of micro-scale stress-strain response using fiber orientation distribution (Γ^m) of a single RV layer. (b) Homogenization to full-thickness RVFW fiber structure over transmural depth Z. Solid lines: tissue-level model. Dotted lines: micro-level model homogenized with tissue-scale fiber splay and transmural variation. Abbreviations: single layer (SL), full-thickness (FT), homogenization (HG).

4. Discussion

In this study, we developed a finite element model of ventricular myocardium based on a high resolution imaging dataset of a representative tissue element volume. We then used structurally motivated constitutive modeling approaches to both quantify the micro-scale strain and stress fields in the tissue as well as link the micro-scale mechanical response to previously established tissue-scale modeling studies. To the best knowledge of the authors, this study constitutes a major first step in the development of microanatomically-based computational models of cardiac tissue. Use of FE techniques to represent individual myofibers reveals the complexity of the cellar-scale mechanical environment under biaxial deformation, requiring the present approach.

The direction-dependent effects on local strain profiles found in the microanatomical simulation (Figs. 3 and 4) suggest that the complex cellular-scale arrangement of myofibers and collagen fibers in the myocardium indeed contribute to interactions that manifest at the tissue scale. As an example to highlight the localized effects brought on by accounting for discrete myofiber geometry, we conducted simulations of a simplified geometry based on an isolated myofiber from the microanatomical simulation in Fig. 6. At the myofiber-ECM interface, there are increased strains along the e₁ direction in the myofibers paired with decreased strains in the ECM (compared to the applied boundary strain). Further away from the myofiber, the strain in the ECM returns to the applied strain. In contrast, in the e₂ direction, the presence of the myofiber produces a band of increased strain along its long axis, and strains in the ECM are slightly below the applied strain further away from the myofiber. We theorize that these alterations in the local strain fields contribute to myofiber-collagen coupling stresses.

Fig. 6.

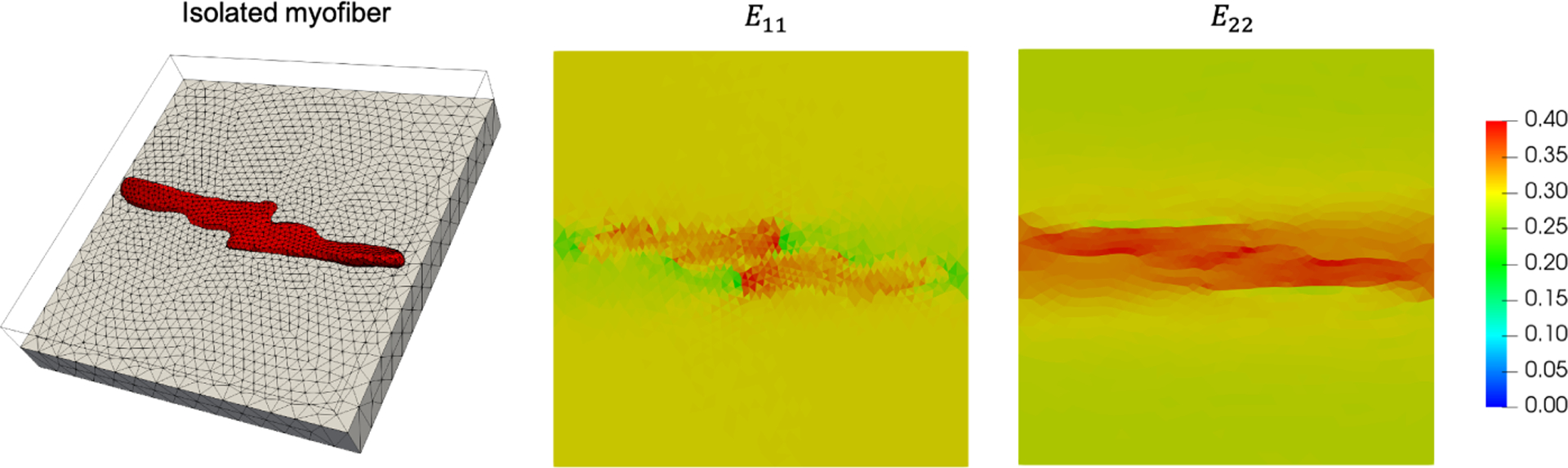
Left: FE mesh of isolated myofiber (red) embedded in ECM (gray). Right: Midplane cross-sections of E₁₁ and E₂₂ at maximum equibiaxial deformation.

Additionally, successful prediction of the tissue-scale stress-strain response based on the homogenization of the microanatomical model, for both a single layer and for the transmural thickness, provides another possible mechanism for the coupling interactions proposed in previous tissue-scale work. Accounting for discrete myofibers embedded in extracellular matrix, while very appearing highly aligned at the scale of individual myofibers, still gives rise to the dispersed stress-strain response observed at greater length scales. For the full-thickness homogenization, the transmural variation in orientation also contributes significantly to the overall stress response. It is clear that both effects are needed to account for the experimental observations; however, it must be noted that the transmural variation in fiber orientation is likely the dominant factor determining the mechanical anisotropy of the full-thickness tissue.

In summary, this model establishes a baseline set of mechanical identifiers at the micro scale that undergo alterations in PAH. Future work will be focused on construction of a microanatomical representation of post-PAH RVFW in order to perform direct comparisons in the local mechanics under biaxial deformation. Through this microanatomical approach, exploration of cellular-scale stress transfer between myocytes and their surroundings can be integrated into larger-scale models and used to further probe the effect of micro-level events on organ-level function. Ultimately, our microanatomical model will allow us to investigate fiber-specific remodeling of the cardiac microstructure in response to structural heart disease.