Dynamics of flow in trapezoidal enclosure having a heated inner circular cylinder containing Casson nanofluid

Abstract

In this article, simulation of the two-dimensional flow of natural convective transport in the partially heated lid-driven trapezoidal cavity was presented with finite element method using software called COMSOL Multiphysics®. Inside the cavity a stationary circular cylinder with a high temperature has been placed. The enclosure was filled with $Cu-H_{2}O$ nanofluid. The flow is assumed to be two-dimensional and has been examined when the parallel sides of the cavity are adiabatic. The temperature on non-parallel sides is assumed to be cold. The top wall of the cavity moves with a velocity ${\eta }_0$ in the positive x-direction, and the considered fluid is a non-Newtonian Casson nanofluid. Computation has been done for the Rayleigh numbers ${10}^4,{10}^5$ and 10⁶, the Casson fluid parameter $0.1,0.5$, and 1, and the nanofluid solid volume fraction 0 and 0.15. Prandtl number is kept fixed at $Pr=6.2$ throughout the calculations. Isotherms and streamlines were sketched to visualize the distribution of temperature and flow field in the cavity. The impacts of governing parameters such as Casson parameter, solid volume fraction, Rayleigh number on heat transfer, and flow field were numerically computed and analyzed. Average Nusselt number also exhibited in a tabular and graphical form to signify the rate of heat transfer in the cavity. It was found that the centers of the two larger circulations were observed to migrate towards the top wall of the cavity as the Rayleigh number increased. Furthermore, heat transport was enhanced as the concentration of nanoparticles increased.

Finite element analysis; Inner heated circular cylinder; Trapezoidal cavity; Casson nanofluid

1. Introduction

The analysis of lid-driven cavity in fluid dynamics has essential applications in different industrial and engineering areas to understand the distribution of heat and the flow velocity. Many studies have been carried out about the lid-driven cavity by previous researchers taking into consideration the geometry of the cavity, imposing different forces, applying different thermal conditions. The pioneering work on lid-driven cavities was presented by Shanker and Deshpande [1]. Following them, Chamkha [2] has presented the analysis on the lid-driven cavity flow of the square region with internal heat source or drain. Also, Wang et al. [3] have computed the lid-driven cavity with fin of porous surface exposed to mixed convection. Furthermore, Oztop and Geridonmez [4] investigated a square cavity utilizing magnetic body force to better understand flow streamlines and temperature distribution in the cavity as the lid travels back and forth. They found that moving the lid forward causes greater convection than moving it backward. Also, Farsani et al. [5] analyzed the lid-driven rectangular cavity to simulate the flow analysis in the liquid-solid interface dynamics. Moreover, Dahani et al. [6] have computed the sinusoidal temperature variation function on one side of the rectangular cavity with the combined effect of magnetic field and convection in the cavity. Selimefendigil and Oztop [7] also, examined the characteristics of modeling and optimization of flow of nanofluid in the trapezoidal cavity under the influence of magnetic field. Further, Al-Rashed et al. [8] have discussed the influences of magnetic field on the flow of nanofluid in the three-dimensional cavity. Linearly heated mixed convection in a lid-driven square cavity using numerical simulation with the method of Lattice Boltzmann was reported by Kefayati et al. [9].

Chatterjee and Halder [10] have computed the transport of magnetic fluid with the heat transfer and mixed convection inside the square cavity when two cylinders were rotating differently. Also, Chatterjee and Mishra [11] have investigated the cavity flow with a pair of heated cylinders under unsteady flow of magnetic fluid. Furthermore, Karimi et al. [12] have studied the flow dynamics of Newtonian fluid in a lid-driven square cavity when two cylinders were placed inside the cavity and arranged horizontally. The analysis of lid-driven when filled is nanofluid has attracted the attention of many researchers by considering varieties of geometries like square, rectangle, and trapezium. Accordingly, Snoussi et al. [13] have considered the cavity in the form of u-shaped filled with water-based nanofluid. Also, Yigit et al. [14] have computed the heat transfer of nanofluid in cylindrical shape when its wall is rotating. Further, the examination of heat transfer and flow of fluid inside the trapezoidal cavity filled with Casson fluid has been presented by Hamid et al. [15] and Kefayati and Huilgol [16] analyzed the mixed convection flow of non-Newtonian fluid using Lattice Boltzmann Method simulation. Mohammed et al. [17] investigated the properties of mixed convection flow in a square cavity with a solid barrier and magnetic field influence computationally. They discovered that increasing the Reynolds number with the Casson fluid parameter increases heat transport, but increasing the Hartmann number has the reverse effect. Recently, Mohammed [18] discussed the numerical simulation of Mixed convection of Casson fluid in a lid-driven trapezoidal enclosure via the finite element method. In the study, the isotherms get progressively distorted and convection takes over when the Richardson number is high. The analysis of three dimensional cavity flow filled with non-Newtonian micropolar fluid has been examined by Manaa et al. [19]. They presented the numerical simulation for natural convection of two diffusivities in a three-dimensional lid-driven cavity. The analysis of the combined effect of mixed convection and magnetic field on the lid-driven cavity of the rectangular region which is partially heated by Colak et al. [20], double-lid-driven rectangular cavity by Louaraychi et al. [21], lid-driven cavity with double layers with porosity by Astanina et al. [22]. Moreover, Wang et al. [23] has focused on the transport of mass and heat in an oscillatory lid-driven square cavity. Gowda et al. [24] have studied the convection of a cavity with discreetly heated walls of the trapezoidal enclosure under different values of Rayleigh. Furthermore, Wubshet and Mohammed [25] have recently published a paper on a lid-driven trapezoidal cavity with a non-uniform temperature at the bottom wall. The examination of cavity flow of hybrid-nanofluid was also presented by [26] very recently.

The current study aims to present a detailed analysis of natural convection in a trapezoidal enclosure consisting of an inner circular cylinder filled with Casson nanofluid using the finite element method. The effects of governing parameters such as the Casson parameter, solid volume fraction, and Rayleigh number on heat transfer and flow field are numerically investigated. The nature of average Nusselt numbers is also investigated for numerous parameters. According to the above-mentioned previous research studies and to the authors' knowledge, there is no other study in the literature that uses the finite element method to characterize natural convection in a trapezoidal enclosure consisting of an inner circular cylinder filled with Casson nanofluid.

2. Basic mathematical equations

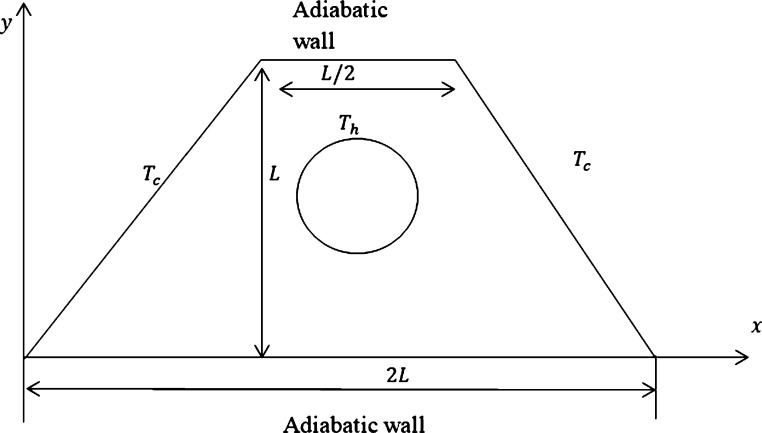
Fig. 1 represents the flow domain of the trapezoidal region with inner hot circular cylinder associated with thermal boundary conditions considered for this study. L is the height of the trapezoidal region, 2L is the length of the bottom and the top wall is $\frac{L}{2}$ length. The radius $r=0.2$ of the circular cylinder is positioned inside a trapezoidal enclosure and Cu-water nanofluid of Casson fluid is filled the space between them. The cylinder is kept at a uniform high temperature while the non-parallel sidewalls of the trapezoidal enclosure are sustained at cooled isothermal temperature. Such heating condition has resulted in the buoyancy-driven convection flow. Moreover, the trapezoidal enclosure has adiabatic temperature on walls at the bottom and top. The heat transfer scenario and flow field of the current study assumed the conditions of laminar, incompressible, and steady. Also, the shape and size of the nanoparticles are taken to be uniform. The fundamental equation of state for incompressible flow of Casson fluid and an isotropic is given as

$${\tau }_{ij}=\{\begin{array}{c}\hfill 2(\frac{{\tau }_0}{\sqrt{2\pi }}+k_c)e_{ij}\mathit{\text{if}}\pi >{\pi }_c\\ \hfill 2(\frac{{\tau }_0}{\sqrt{2{\pi }_c}}+k_c)e_{ij}\mathit{\text{if}}\pi <{\pi }_c,\end{array}$$

where $e_{ij}=\frac{1}{2}(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i})$ is the strain tensor rate, $\pi =e_{ij}{e}_{ij}$ is the multiplication of the strain tensor rate with itself, ${\tau }_{ij}$ is the component of the strain tensor, $k_c$ is the Casson coefficient of viscosity, $u_i$ is the velocity components and ${\tau }_0$ is the fluid yield stress. Assuming the steady-state condition the equations governing the flow of fluid and transfer of heat of the Casson nanofluid confined in the enclosure are given by [10], [15]:

$$\frac{\partial v}{\partial y}+\frac{\partial u}{\partial x}=0,$$ (1)

$$v\frac{\partial u}{\partial y}+u\frac{\partial u}{\partial x}=-\frac{1}{{\rho }_{nf}}\frac{\partial p}{\partial x}+\frac{{\mu }_{nf}}{{\rho }_{nf}}(1+\frac{1}{\gamma })(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}),$$ (2)

$$v\frac{\partial v}{\partial y}+u\frac{\partial v}{\partial x}=-\frac{1}{{\rho }_{nf}}\frac{\partial p}{\partial y}+\frac{{\mu }_{nf}}{{\rho }_{nf}}(1+\frac{1}{\gamma })(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2})+g{\beta }_{nf}(T-T_c),$$ (3)

$$v\frac{\partial T}{\partial y}+u\frac{\partial T}{\partial x}={\alpha }_{nf}(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}),$$ (4)

where, $u,v,p$, and T are the fluid velocity components of in the x− and y− directions, the pressure, and the temperature, respectively. $\beta ,g,\sigma ,\mu$, and ρ are the fluid thermal expansion coefficient, the acceleration due to gravity, the electrical conductivity, the dynamic viscosity, and the density, respectively. $\alpha =\frac{\kappa }{\rho c}$ is the thermal diffusivity, κ is the thermal conductivity, c is the specific heat capacity.

Figure 1.

Schematic diagram.

The following coupled system of equations shows nanofluid thermophysical properties

$${\rho }_{nf}=(1-\varphi ){\rho }_f+\varphi {\rho }_s,$$ (5)

$${(\rho c_p)}_{nf}=(1-\varphi ){(\rho c_p)}_f+\varphi {(\rho c_p)}_s,$$ (6)

$${(\rho \beta )}_{nf}=(1-\varphi ){(\rho \beta )}_f+\varphi {(\rho \beta )}_s$$ (7)

$$k_{nf}=k_f\frac{k_s+2k_f-2\varphi (k_f-k_s)}{k_s+2k_f+\varphi (k_f-k_s)},$$ (8)

$${\alpha }_{nf}=\frac{k_{nf}}{{(\rho c_p)}_{nf}},$$ (9)

$${\mu }_{nf}=\frac{{\mu }_f}{{(1-\varphi )}^{2.5}},$$ (10)

ϕ is nanoparticles volume fraction. The following Table 1 lists properties, base fluid, and nanoparticles under the study.

Table 1.

Thermo-physical properties of nanoparticles and base fluid.

Properties	Base fluid (water)	Nanoparticles (Cu)
μ (Pa s)	8.55 × 10−4	–
cp (J/kgK)	4.179 × 103	3.85 × 102
ρ (kg/m3)	9.971 × 102	8.933 × 103
k (W/mK)	0.613	401
β (k−1)	2.761 × 10−4	1.67 × 10−5
α (m2 s−1)	1.47 × 107	1.17 × 10−4

The dimensionless variables are

$$X=\frac{x}{L},Y=\frac{y}{L},\eta =\frac{uL}{{\alpha }_f},\zeta =\frac{vL}{{\alpha }_f},P=\frac{p{L}^2}{{\rho }_{nf}{\alpha }_f^2},\theta =\frac{T-T_c}{T_h-T_c},$$ (11)

Substituting the dimensionless variables (11) into the governing equations (1)-(4), the following dimensionless equations obtained:

$$\frac{\partial \eta }{\partial X}+\frac{\partial \zeta }{\partial Y}=0,$$ (12)

$$\eta \frac{\partial \eta }{\partial X}+\zeta \frac{\partial \eta }{\partial Y}=-\frac{\partial P}{\partial X}+\frac{{\mu }_{nf}}{{\alpha }_f{\rho }_{nf}}(1+\frac{1}{\gamma })(\frac{{\partial }^2\eta }{\partial X^2}+\frac{{\partial }^2\eta }{\partial Y^2}),$$ (13)

$$\eta \frac{\partial \zeta }{\partial X}+\zeta \frac{\partial }{\zeta }\partial Y=-\frac{\partial P}{\partial Y}+\frac{{\mu }_{nf}}{{\alpha }_f{\rho }_{nf}}(1+\frac{1}{\gamma })(\frac{{\partial }^2\zeta }{\partial X^2}+\frac{{\partial }^2\zeta }{\partial Y^2})+\frac{{(\rho \beta )}_{nf}}{{\beta }_f{\rho }_{nf}}RaPr\theta ,$$ (14)

$$\eta \frac{\partial \theta }{\partial X}+\zeta \frac{\partial \theta }{\partial Y}=\frac{{\alpha }_{nf}}{{\alpha }_f}(\frac{{\partial }^2\zeta }{\partial X^2}+\frac{{\partial }^2\zeta }{\partial Y^2})$$ (15)

where Pr and Ra denote Prandtl number and Rayleigh number which are formulated as:

$$Pr=\frac{{\nu }_f}{{\alpha }_f},Ra=\frac{g{\rho }_f{\beta }_f(T_h-T_c)L^3}{{\mu }_f{\alpha }_f}.$$

The boundary conditions for the equations ((12) - (15)) are stated as:

On the non-parallel walls: $\eta =\zeta =\theta =0$.

On the inner circular cylinder: $\eta =\zeta =0,\theta =1$.

On the bottom wall: $\eta =\zeta =\frac{\partial \theta }{\partial x}=0$.

On the top wall: $\eta =1,\zeta =\frac{\partial \theta }{\partial x}=0$.

The equation of local heat transfer rate on the surface of a cylinder in terms of Nusselt number is formulated as,

$$N{u}_L=-\frac{k_{nf}}{k_f}{\left(\frac{\partial \theta }{\partial Y}\right)}_{Y=0}.$$

The average Nusselt number, formulated as,

$$N{u}_{avg}=-\frac{k_{nf}}{k_f}\frac{1}{L}\underset{0}{\overset{L}{\int }}\frac{\partial \theta }{\partial Y}dX.$$

3. Numerical computation

With the help of the finite element method, the governing dimensionless equations (12)–(15) were computed to get the streamlines and heat distribution in the cavity. To find the solution we need to eliminate the pressure term occurring in the equation of momentum. In order to do so penalty method is employed with the help of the equation of continuity by introducing the penalty parameter φ as:

$$P=-\phi (\frac{\partial \eta }{\partial X}+\frac{\partial \zeta }{\partial Y}).$$ (16)

The equation of continuity (12) is exactly fits for huge values of φ. The distinctive values of φ that resulted in a consistent solution is 10⁷.

By means of equation (16), the equations of momentum (13) and (14) are condensed to:

$$\eta \frac{\partial \eta }{\partial X}+\zeta \frac{\partial \eta }{\partial Y}=\phi \frac{\partial }{\partial X}(\frac{\partial \eta }{\partial X}+\frac{\partial \zeta }{\partial Y})+\frac{{\mu }_{nf}}{{\alpha }_f{\rho }_{nf}}(1+\frac{1}{\gamma })(\frac{{\partial }^2\eta }{\partial X^2}+\frac{{\partial }^2\eta }{\partial Y^2}),$$ (17)

$$\eta \frac{\partial \zeta }{\partial X}+\zeta \frac{\partial }{\zeta }\partial Y=\phi \frac{\partial }{\partial Y}(\frac{\partial \eta }{\partial X}+\frac{\partial \zeta }{\partial Y})+\frac{{\mu }_{nf}}{{\alpha }_f{\rho }_{nf}}(1+\frac{1}{\gamma })(\frac{{\partial }^2\zeta }{\partial X^2}+\frac{{\partial }^2\zeta }{\partial Y^2})+\frac{{(\rho \beta )}_{nf}}{{\beta }_f{\rho }_{nf}}RaPr\theta .$$ (18)

The rest detailed mathematical calculation is found in the paper by Wubshet and Mohammed [25]. The grid independence test was ensured by considering mesh size, the elements number, and elements on the boundary was given as shown in Table 2. It was tested by calculating the percentage error of the variation of non-dimensional average Nusselt number $(N{u}_{avg})$ on the heated circular cylinder. The less percentage error 0.0017 at an extremely fine mesh with a number of elements equals $33,540$ and boundary elements equal to 936 is selected to find the desired accuracy to the problem. The recommended grid structure for this work is given in Fig. 2.

Table 2.

Grid independence study at Ra = 10⁶,γ = 0.5, and ϕ = 0.15.

Mesh size	Mesh elements	Boundary elements	Nuavg	Percentage error $(\text{\%})$
Normal	1944	180	5.8347
Fine	3064	228	5.8398	0.087
Finer	9375	481	5.8566	0.29
Extra fine	25720	936	5.8718	0.26
Extremely fine	33540	936	5.8719	0.0017

Figure 2.

Mesh of the trapezoidal cavity.

The current numerical approach is further confirmed by comparing the findings of the current code for $Pr=0.7$ and $Ra={10}^3$ to the Salam and Ahmed [27] investigation. As demonstrated in Fig. 3, the current code is in good accord with the previous work of Salam and Ahmed [27] shown in Fig 5a of their article.

Figure 3.

Graphs showing the comparison of the findings of the current code for Pr = 0.7 and Ra = 10³ to the Salam and Ahmed [27] results.

The solutions of the velocity components are expressed in terms of $\eta ,\zeta$ and ψ is stream function are expressed as $\eta =\frac{\partial \psi }{\partial Y}$ and $\zeta =\frac{\partial \psi }{\partial X}$.

4. Results and discussion

Under this subtopic, the numerically computed results were presented and discussed for the flow in a trapezoidal enclosure consisting of an inner circular cylinder filled with Casson nanofluid. The impacts of the Casson fluid parameter (γ), Rayleigh number (Ra), and the volume fraction (ϕ) on the flow dynamics, heat distribution, and heat transfer rate are examined. For Rayleigh numbers ${10}^4,{10}^5$ and 10⁶, Casson fluid parameter $0.1,0.5$, and 1, and nanofluid solid volume fraction were 0 and 0.15 the computation were performed. Also, $Pr=6.2$ is maintained throughout calculations.

The effect of the Rayleigh number on isotherms and streamlines for numerous values of Casson fluid parameter and solid volume fraction of nanofluid the current configuration are depicted in Fig. 4. The temperature change between the hot around the circular cylinder situated inside the cavity and side walls with cold temperature resulted in the flow field inside the trapezoidal enclosure. Hence, the vortices of the flow start from the hot inner circular cylinder due to its high temperature and move due to the effect of buoyancy force to the insulated bottom and top walls of the trapezoidal cavity. After that, they change their orientation from the insulated bottom to the top wall after being influenced by the cold sidewalls. This cyclic movement resulted in the convection vortices inside the enclosure. Fig. 4 (a), Fig. 4 (c) and Fig. 4 (e) were sketched to analyze the effects of Rayleigh number on streamline in the trapezoidal enclosure. Two major revolving vortices surrounding the interior hot cylinder demonstrated flow dynamics and heat transmission characteristics. Density and temperature disparities between the cold trapezoidal enclosure walls and the hot cylinder body create vortices that resemble natural convection currents. Fig. 4 (a) and Fig. 4 (b) were sketched for Rayleigh number $Ra={10}^4$. For this particular case, the circulation is weak inside the trapezoidal enclosure because of the minor influence of natural convection. The contours of the temperature distribution appear as horizontal lines at low values of the Rayleigh number ($Ra={10}^4$) because the heat transmission mechanism of conduction is the dominant one. It has also been seen that the thickness of the thermal boundary layer for $Ra={10}^4$ is quite thin. As Rayleigh number amounted to $Ra={10}^6$, the streamlines and contours of temperature distribution were fully transformed from uniform to non-uniform as seen in Fig. 4 (e) and Fig. 4 (f). The convection effect is enhanced in this scenario, and the thickness of the thermal boundary layer expands. The influence of convective heat transfer becomes more important when the Rayleigh number is increased, and separate boundary layers emerge along the cavity's active walls. Higher velocities and strong convection are shown by the streamlines and isotherms in the boundary layers along with the active circular cylinder. The shape of isotherms and streamlines and heat transfer rate were controlled by Rayleigh number.

Figure 4.

Rayleigh number effect on streamlines and isotherms respectively on the left and right with γ = 0.5 and ϕ = 0.15.

Fig. 5 displays the isotherms and streamlines for various values of solid volume fraction and Rayleigh numbers. The isotherms and streamlines for base fluid and nanofluid were sketched in diverse colors to describe the effect of nanofluid on the fluid flow and thermal fields. The blue color represents the nanofluid while the base fluid is given in red color. It can be seen from the graphs that there is a minor difference in the stream function values between the nanofluid and the base fluid. In addition, both the base fluid and the nanofluid have a similar flow field pattern consisting of two spinning vortices around the inner cylinder. It can be noted that using nanofluid increases the fluid flow strength. The reason for this is because when thermal energy increases, the stream function and fluid velocity increase as well.

Figure 5.

Variation of streamlines and isotherms respectively on the left and right with γ = 0.5.

The Casson fluid parameter γ impacts on isotherms and streamlines on the inner heated circular cylinder are depicted in Fig. 6. Effective viscosity of the fluid decreases as a result of an increment in the Casson parameter. So, the lower value of γ shows an adverse influence on viscosity. The pattern of isotherms reflects important interaction between thermal boundary layers for high values of Casson fluid parameter. It is observed that the temperature variation towards the top wall of the cavity was enhanced as the values of γ increased. This is due to the diffusion of thermal energy from the heated inner circular cylinder.

Figure 6.

Casson parameter effect on streamlines and isotherms respectively on the left and right with ϕ = 0.15 and Ra = 10⁶.

The patterns of the velocities η and ζ due to γ and Ra are displayed in Fig. 7 and Fig. 8 respectively. From the graphs, it can be observed that the streamline for the velocities was changing rapidly as the amount of Casson parameter and Rayleigh number were enhanced for both η and ζ. Also, the graphs reveal that more variation in the velocity was observed along the y-axis than the velocity along the x-axis. The variation of velocity along the y-axis has symmetric property and it is high when compared with the velocity along the x-axis with the same change in the Casson parameter. Furthermore, the velocity around the inner circular cylinder is higher than the y-axis velocity as shown in Fig. 7(b,d,f). Physically, an increment in the velocities due to a reduction in the viscosity of Casson fluid resulted in an increment in the buoyancy force. Similar behavior was observed when the Rayleigh number changes from low to high values as seen from Fig. 8.

Figure 7.

Casson parameter effect on velocities η and ζ respectively, on the left and right) with ϕ = 0.15 and Ra = 10⁵.

Figure 8.

Rayleigh number effect on velocities η (on the left) and ζ (on the right) with ϕ = 0.15 and γ = 0.5.

$N{u}_{avg}$ variation with Ra on inner heated circular cylinder for different values of γ is shown in Table 3 and drawn in Fig. 9. The figure and table depict that for lesser values of Rayleigh number, $N{u}_{avg}$ is not affected much by varying γ but the variation in the value of Ra results in a significant change in the value of $N{u}_{avg}$. Moreover, the graph and table reflect that the effect of γ will increase the average Nusselt number which enhances the heat transfer rate.

Table 3.

Table of values showing Nu_avg with Ra on the heated inner circular cylinder for different values γ.

γ	Ra	Nuavg	γ	Ra	Nuavg
0.1	103	3.6119	0.5	105	3.7752
0.1	104	3.6120	0.5	106	5.8719
0.1	105	3.6269	1	103	3.6119
0.1	106	4.2623	1	104	3.6165
0.5	103	3.6119	1	105	3.9160
0.5	104	3.6139	1	106	6.6635

Figure 9.

The impact of Rayleigh number for different values of γ on average Nusselt number.

5. Conclusions

This study presents the numerical simulation of a lid-driven trapezoidal cavity filled with Casson nanofluid with a heated circular cylinder inside the cavity. The impact of the governing parameters was discussed and the numerical results were presented in graphs and tables to describe the variations of velocities and temperature fields. The main findings are summarized as follows:

• •As Rayleigh number Ra increases the centers of the two bigger circulations move towards the top wall of the cavity.
• •Both γ and Ra enhanced the average Nusselt number.
• •An increment in nanoparticle concentration resulted in an increment in heat transfer rate on the inner circular cylinder.
• •As the Rayleigh number increase, the transfer of heat on the circular cylinder getting high.
• •The strength of streamline velocity increases with Rayleigh number Ra on both non-parallels sides of the cavity.

Declarations

Author contribution statement

Mohammed Hirpho & Wubshet Ibrahim: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data included in article/supp. material/referenced in article

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.