Abstract
COVID-19 poses many challenges for hospitals around the world. Each country attempts to solve the problems in its hospitals using different methods. In Turkey, two pandemic hospitals were built in İstanbul, the most crowded province. In addition, some hospitals were designated as pandemic hospitals. This study focuses on the methods used for site selection for a pandemic hospital in Atakum, a district of Samsun City, Turkey. As a solution to the problem, initially, spatial analysis was performed using GIS to produce maps based on seven criteria obtained from the insight of an expert team. Analytic hierarchy process (AHP) augmented by interval-valued Pythagorean fuzzy numbers (PFNs) was then used to determine weights for the criteria. Distance to transportation network was the most important criterion influencing the selection process and the least significant one was the distance to fire stations. Based on the criteria weights, and five rules specified by the expert team, 13 suitable locations for a pandemic hospital were determined using GIS. The technique for order preference by similarity to ideal solution (TOPSIS) method was used to determine the final ranking of 13 alternative locations (A1–A13). A10 was identified as the most appropriate site and A11 as the least appropriate site for a pandemic hospital. Finally, sensitivity analysis was performed to investigate how changes in weight values of the criteria affect the ranking of the alternatives.
Keywords: COVID-19, Pandemic hospital, Site selection, Pythagorean fuzzy AHP, TOPSIS
Introduction
The novel coronavirus (COVID-19) has spread to many countries since its discovery at the end of 2019 in Wuhan, China, and World Health Organization (WHO) officially declared COVID-19 an unprecedented health crisis and a worldwide pandemic. The COVID-19 pandemic has changed daily lives deeply, put social life and public health under unprecedented pressure, and economies have fallen into recession (WHO 2020; Rostami-Tabar and Rendon-Sanchez 2021; Aslan et al. 2021).
The COVID-19 pandemic has caused numerous ripple effects (Ivanov and Dolgui 2021). The ripple effect (also known as risk propagation) is described as a sudden disruption at a few nodes in a supply chain network (Li and Zobel 2020; Yılmaz et al. 2021). When considered in terms of the health sector, despite the increasing demand for essential medical supplies and equipment, limited access to them reveals the whiplash effect in the supply chain. COVID-19 has also posed many challenges for hospitals around the world, including supplies, equipment, human resources, and space, in addition to putting pressure on the overall healthcare system (Yağma et al. 2020; Bragazzi et al. 2020). Each country has tried to solve the problems in its hospitals by using different methods. Countries such as China and Turkey have built emergency hospitals during the pandemic, whereas others such as Spain, the USA, Brazil, and India have turned venues such as stadiums, dormitories, and hostels into temporary pandemic hospitals (Yağma et al. 2020). Hospitals, which play a critical role in the national and local response to emergencies such as communicable disease epidemics, have revamped their procedures in order to distinguish patients with COVID-19 from non-COVID-19 (WHO 2014; Alban et al. 2020). In Turkey, two pandemic hospitals were built in Istanbul, the most crowded province. In addition, hospitals with specialist physicians in infectious diseases and clinical microbiology, chest diseases, and internal diseases and having a tertiary level adult intensive care unit were accepted as pandemic hospitals (Yağma et al. 2020; Ministry of Health 2020).
Hospital site selection can be considered as a multi-criteria decision-making (MCDM) problem since it includes issues belonging to different fields and there are several and sometimes conflicting stakeholders to take into account (Dell’Ovo et al. 2018). This study investigates the selection of a site for a pandemic hospital to be built in Atakum, a district of Samsun with a population of 221.082 in 2020. The 5-year average annual population growth rate of Atakum district is 5.4%, which is the highest rate in Samsun Province (TSI 2020).
This paper develops an analytical tool that combines three techniques, geographic information systems (GIS), Pythagorean fuzzy analytic hierarchy process (PFAHP), and technique for order preference by similarity to ideal solution (TOPSIS) to obtain suitable sites for a pandemic hospital in Atakum. In several areas of use, GIS is an effective method of analyzing spatial data (Rızvanoğlu et al. 2020). An integrated GIS-MCDM method provides a practical approach that can manage time and costs, while reducing errors and increasing the efficiency of the decision-making process (Eghtesadifard et al. 2020). Moreover, a more accurate and systematic evaluation is ensured by integrating MCDM methods and fuzzy sets (Çalış Boyacı et al. 2021). Pythagorean fuzzy sets (PFSs) allow users to assess uncertainties in the real world more accurately and reliably, while helping to eliminate uncertainties (Ak and Gul 2019; Garg 2018). The integrated approach of combining PFSs, AHP, and TOPSIS has been effectively applied in various fields in the literature, such as risk assessment (Ak and Gul 2019; Bakioglu and Atahan 2021), ATM site selection (Yildiz et al. 2020), wind power farm location selection (Otay and Jaller 2020), hospital service quality evaluation (Yucesan and Gul 2020), green supplier selection (Çalık 2020), and transportation company selection (Sarkar and Biswas 2021). From the limited number of studies in the literature related to the selection of the site for a pandemic hospital, it is seen that the criteria to be considered are similar to the selection criteria for a hospital site (Hashemkhani Zolfani et al. 2020; Aydin and Seker 2021). However, criteria weights may differ. A review of studies on hospital site selection and criteria used in these studies are given in Table 1. Table 1 shows that GIS and MCDM are the most commonly used methods and research for hospital site selection problems. According to the authors’ best knowledge, there are no studies that combine GIS, PFSs, and MCDM methods. This study aims to fill this gap.
Table 1.
Review of hospital site selection studies
| Author(s) | Year | Method(s) used | Application region | Criteria |
|---|---|---|---|---|
| Vahidnia et al. | 2009 | GIS, FAHP | Iran | (1) Distance from arterial routes, (2) travel time, (3) contamination, (4) land cost, (5) population density |
| Soltani and Marandi | 2011 | GIS, FAHP, FANP | Iran | (1) Distance to arterial roads, (2) distance to existing hospitals, (3) parcel area, (4) population density |
| Chatterjee and Mukherjee | 2013 | AHP | India | (1) Cost of land, (2) land topography, (3) land ownership, (4) running/maintenance cost, (5) population density, (6) education, (7) economic condition, (8) proximity to public transport, (9) space for future construction, (10) availability of existing infrastructure, (11) proximity to market |
| Rahimi et al. | 2017 | GIS, AHP | Iran | (1) Population density, (2) fair distribution of hospitals all over the city, (3) fast and easy accessibility, (4) proximity to the main roads, (5) being far from airport, (6) not being located on the river path, (7) being far from industrial centers, (8) proximity to fire stations, (9) land area |
| Dell’Ovo et al. | 2018 | GIS, AHP | Italy | (1) Center of Urban redevelopment, (2) flexibility, (3) building density, (4) accessibility, (5) services, (6) green area, (7) network infrastructures, (8) noise pollution, (9) air pollution, (10) unhealthy industries, (11) value of the area, (12) land ownership, (13) land suitability |
| Soltani et al. | 2019 | GIS, AHP | Iran | (1) Transportation network, (2) existing healthcare centers, (3) land use, (4) population density, (5) distance from industrial centers, (6) distance from existing fire stations, (7) distance from urban green spaces |
| Şahin et al. | 2019 | AHP | Turkey | (1) Medical technology, (2) number of total beds, (3) units, (4) total hospitals, (5) population, (6) possibility of population change, (7) population age structure, (8) income, (9) air pollution, (10) access to water resources, (11) inner-city, (12) upstate, (13) medical industry, (14) medicine industry, (15) labor market, (16) incentive, (17) legislation, (18) policies, (19) tax |
| Nsaif et al. | 2020 | GIS, MCA | Iraq | (1) Existing hospitals and medical centers, (2) distance to roads, (3) river, (4) slope, (5) population |
| Kahev et al. | 2020 | GIS, AHP, Improved Genetic Algorithm | Iran | (1) Distance from existing hospitals, (2) distance from population centers, (3) distance from fire stations, (4) distance from strong power lines, (5) distance from road network, (6) distance from fault, (7) distance from parks |
| Rezayee | 2020 | GIS, MCA | Malaysia | (1) Existing hospital, (2) residential area, (3) main road, (4) river, (5) ferry route, (6) ferry terminal |
Methodology
A methodology that combines three techniques, GIS, PFAHP, and TOPSIS, for a pandemic hospital site selection is proposed in this study. This section explains these methods.
Geographic information systems (GIS)
GIS is a computer-based tool that is used in many areas, such as land management, emergency management, environmental sciences, and public health. The ability to ask complex questions about the environment, analyze features together, and then show multiple aspects of the results on a map makes GIS a powerful tool. GIS allows the investigation of many factors based on spatial data, including monitoring, evaluation of risk factors, development of control strategies, and the management of the process (Sisman 2013). The spatial and non-spatial data are combined in separate layers and can be queried and analyzed together in GIS (see Fig. 1).
Fig. 1.
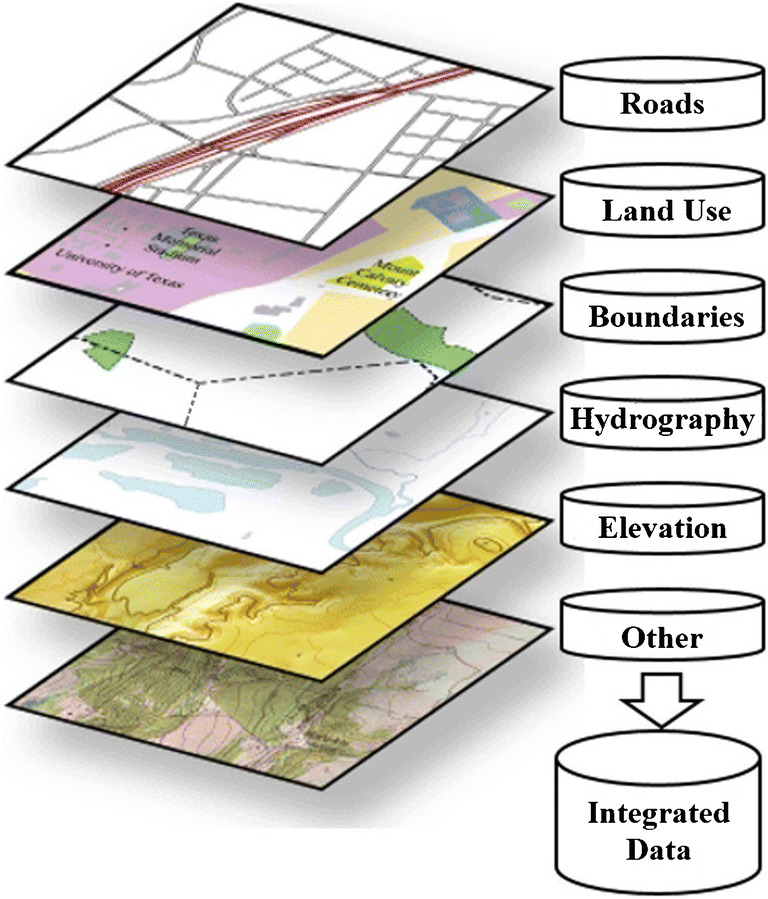
GIS data in different layers (Artz 2014).
PFAHP
Preliminaries of PFSs
PFSs, which are an extension of intuitionistic fuzzy sets, were first proposed by Yager (2014) and have been applied to a variety of problems respecting uncertainty such as interval type-2 fuzzy sets, hesitant fuzzy sets, and intuitionistic fuzzy sets (Ak and Gul 2019). PFSs are more efficient and flexible to solve problems that include uncertainty (Ilbahar et al. 2018; Ak and Gul 2019; Gul 2020). In PFSs, unlike intuitionistic fuzzy sets, the sum of membership and non-membership degrees can exceed 1, but their sum of squares cannot (Zhang and Xu 2014; Zeng et al. 2016; Ilbahar et al. 2018; Ak and Gul 2019; Gul 2020). This is expressed in Eqs. (1) and (2).
Definition 1
Let a set X be a universe of discourse. A PFS P is an object having the form (Zhang and Xu 2014; Zeng et al. 2016; Ilbahar et al. 2018; Ak and Gul 2019; Gul 2020):
| 1 |
where the function μP : X → [0, 1] defines the degree of membership and vP : X → [0, 1] defines the degree of non-membership of the element x ∈ X to P, respectively, and for every x ∈ X, it holds:
| 2 |
For any PFS P and x ∈ X, is called the degree of indeterminacy of x to P.
Definition 2
Let β = P(μβ, vβ), , and be three Pythagorean fuzzy numbers (PFNs), and λ> 0, then the operations on these three PFNs are defined as Eqs. (3) to (6) (Zhang and Xu 2014; Zeng et al. 2016):
| 3 |
| 4 |
| 5 |
| 6 |
Definition 3
Let and be two Pythagorean fuzzy numbers, a nature quasi-ordering on the Pythagorean fuzzy numbers is defined as follows (Zhang and Xu 2014; Zeng et al. 2016; Yucesan and Gul 2020):
To compare the PFSs, a score function is proposed (Zhang and Xu 2014). For a PFN β = P(μβ, vβ), the score function of β can be defined as Eq. (7) (Zhang and Xu 2014; Zeng et al. 2016):
| 7 |
On the basis of score function of PFNs, the following laws are defined to compare two PFNs (Zhang and Xu 2014).
Definition 4
Let be two PFNs, s(β1) and s(β2) be the scores of β1 and β2, then
If s(β1) < s(β2), then β1 ≺ β2
If s(β1) > s(β2), then β1 ≻ β2
If s(β1) = s(β2), then β1~β2
Steps of the PFAHP
The steps of interval-valued PFAHP are as follows (Ilbahar et al. 2018):
Step 1. Construct the compromised pairwise comparison matrix R = (rik)m × m based on linguistic evaluations of experts using the scale proposed by Ilbahar et al. (Ilbahar et al. 2018).
Step 2. Calculate the differences matrix D = (dik)m × m between the lower and upper values of the membership and non-membership functions using Eqs. (8) and (9):
| 8 |
| 9 |
| 10 |
| 11 |
Step 4. Calculate the determinacy value τ = (τik)m × m using Eq. (12):
| 12 |
Step 5. Multiply the determinacy degrees with S = (sik)m × m matrix to obtain the matrix of weights T = (tik)m × m before normalization using Eq. (13):
| 13 |
Step 6. Compute each normalized priority weight wi using Eq. (14):
| 14 |
TOPSIS
The TOPSIS method was presented by Hwang and Yoon (1981). The basic principle of the TOPSIS method is that the chosen alternative has the shortest distance to the ideal solution and the furthest distance to the negative ideal solution. The stages to be followed in the TOPSIS method can be summarized as follows:
Step 1. Calculate the normalized decision matrix.
Step 2. Form the weighted normalized decision matrix.
Step 3. Determine the ideal and negative-ideal solutions.
Step 4. Calculate the separation of each alternative from the ideal solution and the separation from the negative-ideal solution.
Step 5. Calculate the relative closeness to the perfect solution.
Step 6. Rank the preference order.
Details of the TOPSIS method are found in numerous papers (Hwang and Yoon 1981; Opricovic and Tzeng 2004; Mousavi-Nasab and Sotoudeh-Anvari 2017; Ramya and Devadas 2019; Adalı and Tuş 2021).
Implementation of the proposed methodology
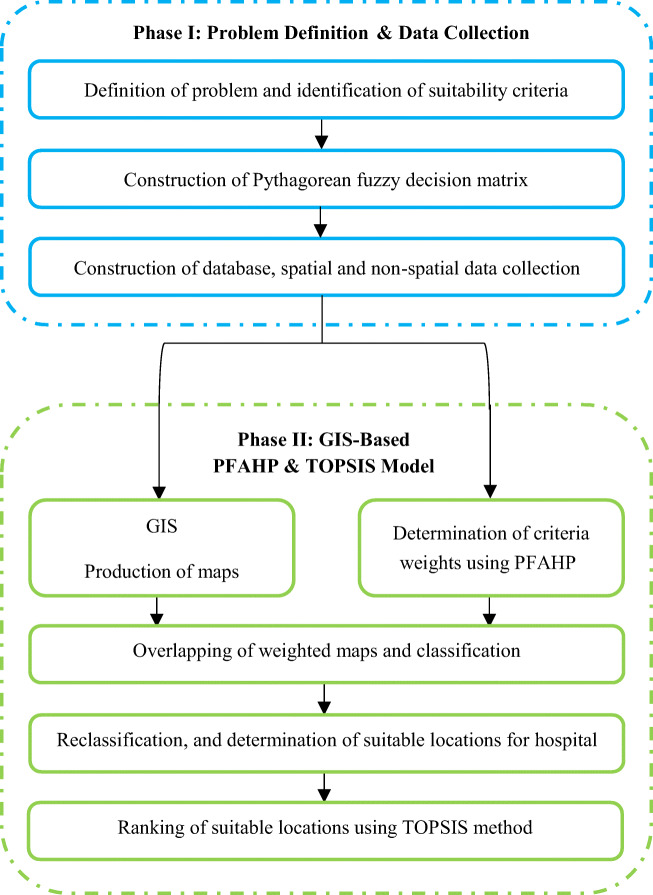
The implementation of the proposed methodology is described in this section. The flow chart of the proposed method adopted for a pandemic hospital site selection problem is given in Fig. 2. There are two phases for the proposed method: problem definition and data collection and the GIS-based PFAHP and TOPSIS model (Fig. 2).
Fig. 2.
The flow chart of the proposed method
Problem definition and data collection
This study focuses on the selection of the site for a pandemic hospital in Atakum district using GIS-based PFAHP and TOPSIS methods. Atakum has a total area of 355 km2 but with varying population density. The eastern coastal part is the most densely populated region of the district. The study area is shown in Fig. 3.
Fig. 3.
The study area (Google Earth image ©).
In this study, criteria influencing the site selection process were determined by eliciting opinion from an expert team of five members and by considering previous studies given in Table 1, as follows. The criteria are represented by Cj, where C1, C3, and C7 are to be maximized and C2, C4, C5, and C6 are to be minimized. The detailed information about the expert team is listed in Table 2.
C1: Population density
C2: Distance to transportation network
C3: Distance to existing hospitals
C4: Distance to fire stations
C5: Land value
C6: Slope
C7: Distance to industrial areas
Table 2.
Information about the expert team
| Expert ID | Title | Education | Experience (years) |
|---|---|---|---|
| Expert 1 | Urban planner | Ph.D. | 23 |
| Expert 2 | Urban planner | M.Sc. | 24 |
| Expert 3 | Urban planner | B.Sc. | 10 |
| Expert 4 | Medical doctor | M.D. | 28 |
| Expert 5 | Medical doctor | M.D. | 23 |
Production of maps
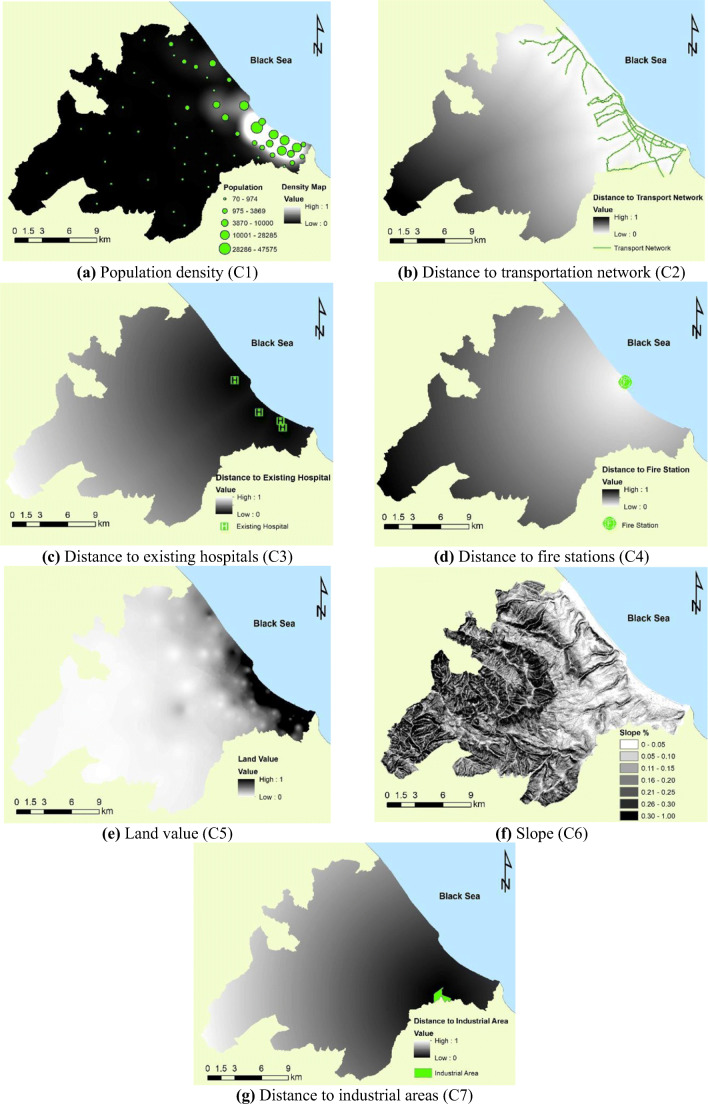
In this study, seven criteria were used to determine the most suitable alternative locations for a pandemic hospital. Data used in the study were obtained from several sources. Population density maps for 2020 of the 57 neighborhoods in Atakum District (TSI 2020) were obtained. The industrial area map was based on the Atakum zoning plan. The location of existing hospitals, fire stations, and transport network including main roads and the tramway system was obtained using a handheld receiver and satellite images. Land value data was based on sale prices present on web pages; 93 sales data were used to produce a value map of the study area. The topographic gradient map was produced based on the Shuttle Radar Topography Mission (SRTM) digital elevation model (USGS 2021).
In this study, several types of spatial analysis were used, and the maps of the seven criteria given in Fig. 4a to g were produced using ArcGIS software. Euclidean distance analysis was used to produce the distance maps of the transport network, existing hospitals, fire stations, and industrial areas. The population density map was produced using kernel density analysis based on the population of neighborhoods, and the value map was produced based on the location of real estate for sale, using inverse distance weighted (IDW) analysis, which is an interpolation method.
Fig. 4.
GIS layer of each criterion. a Population density (C1). b Distance to transportation network (C2). c Distance to existing hospitals (C3). d Distance to fire stations (C4). e Land value (C5). f Slope (C6). g Distance to industrial areas (C7)
Results and discussion
PFAHP method for determining the criteria weights
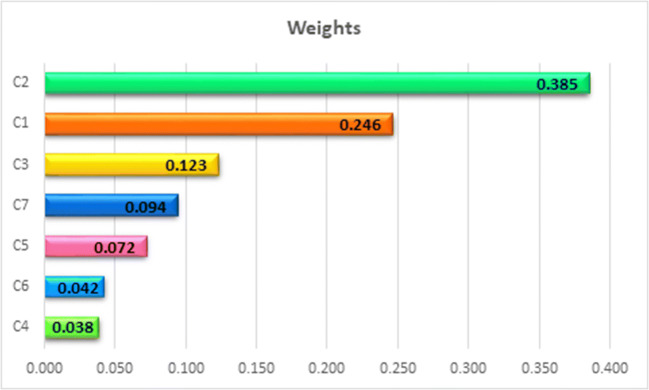
The weights for the criteria were obtained using interval-valued PFAHP. The weighting scale of interval-valued PFAHP is given in Table 3. The linguistic terms presented in Table 3 are used by the expert team to evaluate the relative importance of the seven criteria (Table 4). Table 5 is obtained using lower and upper values of membership degree (μL, μU) and lower and upper values of non-membership degree (vL, vU).The difference matrix (D) and interval multiplicative matrix (S) are given in Tables 6 and 7, respectively. The determinacy value matrix (τ) and weights before normalization (T) are given in Tables 8 and 9, respectively. Finally, weights of the criteria determined by using PFAHP method are given in Fig. 5. As shown in Fig. 5, C2 “distance to transportation network” is the most important criterion influencing the selection process, with a weight of 0.385; and the least significant one is the C4 “distance to fire stations” with a weight of 0.038. Distance to transportation network is a critical criterion for the selection of a hospital site. Studies by Dell’Ovo et al. (2018) and Rahimi et al. (2017) determined a similar finding. The results further indicate that C1 “population density” is the second most important criterion.
Table 3.
The weighting scale of interval-valued PFAHP
| Linguistic terms | Interval-valued PFNs | |||
|---|---|---|---|---|
| μL | μU | vL | vU | |
| Certainly low importance (CLI) | 0.00 | 0.00 | 0.90 | 1.00 |
| Very low importance (VLI) | 0.10 | 0.20 | 0.80 | 0.90 |
| Low importance (LI) | 0.20 | 0.35 | 0.65 | 0.80 |
| Below average importance (BAI) | 0.35 | 0.45 | 0.55 | 0.65 |
| Average importance (AI) | 0.45 | 0.55 | 0.45 | 0.55 |
| Above average importance (AAI) | 0.55 | 0.65 | 0.35 | 0.45 |
| High importance (HI) | 0.65 | 0.80 | 0.20 | 0.35 |
| Very high importance (VHI) | 0.80 | 0.90 | 0.10 | 0.20 |
| Certainly high importance (CHI) | 0.90 | 0.10 | 0.00 | 0.00 |
| Exactly equal (EE) | 0.1965 | 0.1965 | 0.1965 | 0.1965 |
Table 4.
Pairwise linguistic evaluations of the expert team for the criteria
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | |
|---|---|---|---|---|---|---|---|
| C1 | EE | BAI | AAI | VHI | AAI | HI | AAI |
| C2 | AAI | EE | AAI | VHI | HI | VHI | HI |
| C3 | BAI | BAI | EE | HI | AAI | AAI | AI |
| C4 | VLI | VLI | LI | EE | BAI | AI | BAI |
| C5 | BAI | LI | BAI | AAI | EE | AAI | BAI |
| C6 | LI | VLI | BAI | AI | BAI | EE | BAI |
| C7 | BAI | LI | AI | AAI | AAI | AAI | EE |
Table 5.
Pairwise comparison of the criteria obtained by using PFNs
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | |
|---|---|---|---|---|---|---|---|
| C1 | ([0.1965, 0.1965], [0.1965, 0.1965]) | ([0.35, 0.45], [0.55, 0.65]) | ([0.55, 0.65], [0.35, 0.45]) | ([0.80, 0.90], [0.10, 0.20]) | ([0.55, 0.65], [0.35, 0.45]) | ([0.65, 0.80], [0.20, 0.35]) | ([0.55, 0.65], [0.35, 0.45]) |
| C2 | ([0.55, 0.65], [0.35, 0.45]) | ([0.1965, 0.1965], [0.1965, 0.1965]) | ([0.55, 0.65], [0.35, 0.45]) | ([0.80, 0.90], [0.10, 0.20]) | ([0.65, 0.80], [0.20, 0.35]) | ([0.80, 0.90], [0.10, 0.20]) | ([0.65, 0.80], [0.20, 0.35]) |
| C3 | ([0.35, 0.45], [0.55, 0.65]) | ([0.35, 0.45], [0.55, 0.65]) | ([0.1965, 0.1965], [0.1965, 0.1965]) | ([0.65, 0.80], [0.20, 0.35]) | ([0.55, 0.65], [0.35, 0.45]) | ([0.55, 0.65], [0.35, 0.45]) | ([0.45, 0.55], [0.45, 0.55]) |
| C4 | ([0.10, 0.20], [0.80, 0.90]) | ([0.10, 0.20], [0.80, 0.90]) | ([0.20, 0.35], [0.65, 0.80]) | ([0.1965, 0.1965], [0.1965, 0.1965]) | ([0.35, 0.45], [0.55, 0.65]) | ([0.45, 0.55], [0.45, 0.55]) | ([0.35, 0.45], [0.55, 0.65]) |
| C5 | ([0.35, 0.45], [0.55, 0.65]) | ([0.20, 0.35], [0.65, 0.80]) | ([0.35, 0.45], [0.55, 0.65]) | ([0.55, 0.65], [0.35, 0.45]) | ([0.1965, 0.1965], [0.1965, 0.1965]) | ([0.55, 0.65], [0.35, 0.45]) | ([0.35, 0.45], [0.55, 0.65]) |
| C6 | ([0.20, 0.35], [0.65, 0.80]) | ([0.10, 0.20], [0.80, 0.90]) | ([0.35, 0.45], [0.55, 0.65]) | ([0.45, 0.55], [0.45, 0.55]) | ([0.35, 0.45], [0.55, 0.65]) | ([0.1965, 0.1965], [0.1965, 0.1965]) | ([0.35, 0.45], [0.55, 0.65]) |
| C7 | ([0.35, 0.45], [0.55, 0.65]) | ([0.20, 0.35], [0.65, 0.80]) | ([0.45, 0.55], [0.45, 0.55]) | ([0.55, 0.65], [0.35, 0.45]) | ([0.55, 0.65], [0.35, 0.45]) | ([0.55, 0.65], [0.35, 0.45]) | ([0.1965, 0.1965], [0.1965, 0.1965]) |
Table 6.
The difference matrix
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | |
|---|---|---|---|---|---|---|---|
| C1 | ([0.00, 0.00]) | ([−0.30, −0.10]) | ([0.10, 0.30]) | ([0.60, 0.80]) | ([0.10, 0.30]) | ([0.30, 0.60]) | ([0.10, 0.30]) |
| C2 | ([0.10, 0.30]) | ([0.00, 0.00]) | ([0.10, 0.30]) | ([0.60, 0.80]) | ([0.30, 0.60]) | ([0.60, 0.80]) | ([0.30, 0.60]) |
| C3 | ([−0.30, −0.10]) | ([−0.30, −0.10]) | ([0.00, 0.00]) | ([0.30, 0.60]) | ([0.10, 0.30]) | ([0.10, 0.30]) | ([−0.10, 0.10]) |
| C4 | ([−0.80, −0.60]) | ([−0.80, −0.60]) | ([−0.60, −0.30]) | ([0.00, 0.00]) | ([−0.30, −0.10]) | ([−0.10, 0.10]) | ([−0.30, −0.10]) |
| C5 | ([−0.30, −0.10]) | ([−0.60, −0.30]) | ([−0.30, −0.10]) | ([0.10, 0.30]) | ([0.00, 0.00]) | ([0.10, 0.30]) | ([−0.30, −0.10]) |
| C6 | ([−0.60, −0.30]) | ([−0.80, −0.60]) | ([−0.30, −0.10]) | ([−0.10, 0.10]) | ([−0.30, −0.10]) | ([0.00, 0.00]) | ([−0.30, −0.10]) |
| C7 | ([−0.30, −0.10]) | ([−0.60, −0.30]) | ([−0.10, 0.10]) | ([0.10, 0.30]) | ([0.10, 0.30]) | ([0.10, 0.30]) | ([0.00, 0.00]) |
Table 7.
The interval multiplicative matrix
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | |
|---|---|---|---|---|---|---|---|
| C1 | ([1.000, 1.000]) | ([0.355, 0.708]) | ([1.413, 2.818]) | ([7.943, 15.849]) | ([1.413, 2.818]) | ([2.818, 7.943]) | ([1.413, 2.818]) |
| C2 | ([1.413, 2.818]) | ([1.000, 1.000]) | ([1.413, 2.818]) | ([7.943, 15.849]) | ([2.818, 7.943]) | ([7.943, 15.849]) | ([2.818, 7.943]) |
| C3 | ([0.355, 0.708]) | ([0.355, 0.708]) | ([1.000, 1.000]) | ([2.818, 7.943]) | ([1.413, 2.818]) | ([1.413, 2.818]) | ([0.708, 1.413]) |
| C4 | ([0.063, 0.126]) | ([0.063, 0.126]) | ([0.126, 0.355]) | ([1.000, 1.000]) | ([0.355, 0.708]) | ([0.708, 1.413]) | ([0.355, 0.708]) |
| C5 | ([0.355, 0.708]) | ([0.126, 0.355]) | ([0.355, 0.708]) | ([1.413, 2.818]) | ([1.000, 1.000]) | ([1.413, 2.818]) | ([0.355, 0.708]) |
| C6 | ([0.126, 0.355]) | ([0.063, 0.126]) | ([0.355, 0.708]) | ([0.708, 1.413]) | ([0.355, 0.708]) | ([1.000, 1.000]) | ([0.355, 0.708]) |
| C7 | ([0.355, 0.708]) | ([0.126, 0.355]) | ([0.708, 1.413]) | ([1.413, 2.818]) | ([1.413, 2.818]) | ([1.413, 2.818]) | ([1.000, 1.000]) |
Table 8.
The determinacy values
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | |
|---|---|---|---|---|---|---|---|
| C1 | 1.00 | 0.80 | 0.80 | 0.80 | 0.80 | 0.70 | 0.80 |
| C2 | 0.80 | 1.00 | 0.80 | 0.80 | 0.70 | 0.80 | 0.70 |
| C3 | 0.80 | 0.80 | 1.00 | 0.70 | 0.80 | 0.80 | 0.80 |
| C4 | 0.80 | 0.80 | 0.70 | 1.00 | 0.80 | 0.80 | 0.80 |
| C5 | 0.80 | 0.70 | 0.80 | 0.80 | 1.00 | 0.80 | 0.80 |
| C6 | 0.70 | 0.80 | 0.80 | 0.80 | 0.80 | 1.00 | 0.80 |
| C7 | 0.80 | 0.70 | 0.80 | 0.80 | 0.80 | 0.80 | 1.00 |
Table 9.
Weights before normalization
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | |
|---|---|---|---|---|---|---|---|
| C1 | 1.000 | 0.425 | 1.692 | 9.517 | 1.692 | 3.767 | 1.692 |
| C2 | 1.692 | 1.000 | 1.692 | 9.517 | 3.767 | 9.517 | 3.767 |
| C3 | 0.425 | 0.425 | 1.000 | 3.767 | 1.692 | 1.692 | 0.848 |
| C4 | 0.076 | 0.076 | 0.168 | 1.000 | 0.425 | 0.848 | 0.425 |
| C5 | 0.425 | 0.168 | 0.425 | 1.692 | 1.000 | 1.692 | 0.425 |
| C6 | 0.168 | 0.076 | 0.425 | 0.848 | 0.425 | 1.000 | 0.425 |
| C7 | 0.425 | 0.168 | 0.848 | 1.692 | 1.692 | 1.692 | 1.000 |
Fig. 5.
Weights for the criteria
Identification of suitable locations using GIS
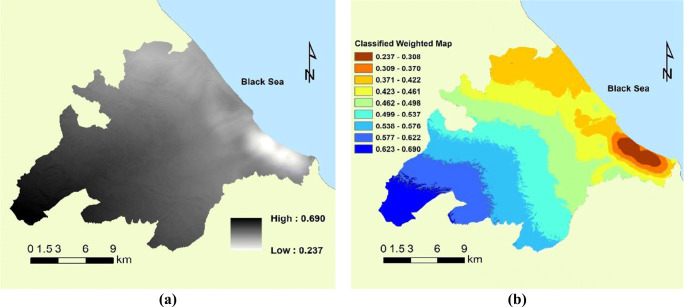
This subsection presents maps for the seven criteria (Fig. 4), which were normalized and combined according to their weight to form a single weighted map (Fig. 6a) and classified weighted map (Fig. 6b).
Fig. 6.
a Weighted map; b classified weighted map
The classified weighted map (Fig. 6b) identifies the regions most suitable for the location of a pandemic hospital. To determine the most suitable locations, further conditions must be considered:
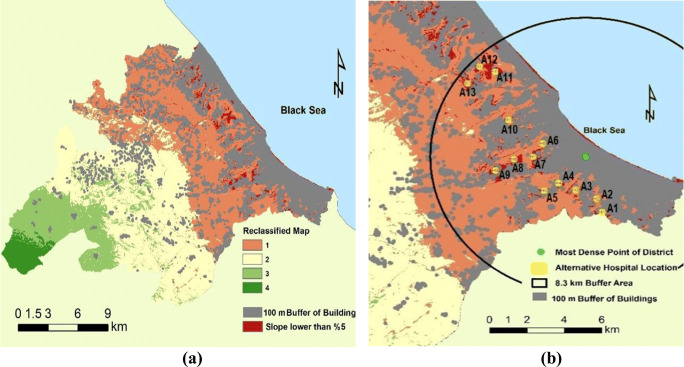
Nsaif et al. (2020) used a topographic gradient of less than 10% for the immediate vicinity in their hospital site selection study. The area of the current study is relatively flat, and so the gradient has been set as less than 5%.
Some studies specify that an ambulance should reach the hospital within 8 min (Pell et al. 2001; Pons and Markovchick 2002; Zègre-Hemsey et al. 2011; Terzi et al. 2013). The current study has applied an 8-min time limit and 50 km/h average speed (Terzi et al. 2013). This sets an 8.3-km radius from the point of densest population within which the location of the pandemic hospital must lie.
The Regulation of Spatial Plans Production in Turkey and the Regulation of Investment Principles of Ministry of Health Hospitals specify 25 hospital beds per 10K population with an area of 130 m2 per bed. Given a population of 221K, a hospital in Atakum would require an area at least 50.000 m2 for a suitable location (Regulation of Spatial Planning 2014; Regulation of Investment Principles of Ministry of Health Hospitals 2003).
Any suitable location must be at least 100 m from existing buildings.
Every selected location must be at least 500 m from all other selected locations.
According to the reclassified map (Fig. 7a), redrawn to include the supplementary conditions, 13 suitable locations were identified for a pandemic hospital (Fig. 7b).
Fig. 7.
a Reclassified weighted map; b alternative hospital locations
Ranking the alternatives using TOPSIS method
The TOPSIS method was used to rank the locations (A1−A13). In Table 10, the normalized values obtained from the ArcGIS software are used to construct the decision matrix, and then TOPSIS was applied to obtain the ranking of the locations. According to Table 10, A10 is identified as the most appropriate site and A11 as the least appropriate site for a pandemic hospital in Atakum.
Table 10.
Ranking of the alternative locations
| Site | Normalized value | TOPSIS rank | ||||||
|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | ||
| A1 | 0.120 | 0.004 | 0.082 | 0.255 | 0.194 | 0.000 | 0.037 | 2 |
| A2 | 0.244 | 0.018 | 0.067 | 0.225 | 0.182 | 0.035 | 0.041 | 4 |
| A3 | 0.153 | 0.031 | 0.084 | 0.198 | 0.142 | 0.027 | 0.018 | 11 |
| A4 | 0.125 | 0.005 | 0.076 | 0.180 | 0.121 | 0.040 | 0.027 | 3 |
| A5 | 0.037 | 0.005 | 0.105 | 0.197 | 0.075 | 0.017 | 0.029 | 5 |
| A6 | 0.274 | 0.030 | 0.068 | 0.101 | 0.192 | 0.031 | 0.122 | 6 |
| A7 | 0.071 | 0.028 | 0.084 | 0.133 | 0.172 | 0.035 | 0.107 | 12 |
| A8 | 0.040 | 0.022 | 0.122 | 0.153 | 0.110 | 0.017 | 0.124 | 9 |
| A9 | 0.006 | 0.019 | 0.164 | 0.193 | 0.023 | 0.016 | 0.134 | 8 |
| A10 | 0.177 | 0.003 | 0.068 | 0.102 | 0.141 | 0.035 | 0.203 | 1 |
| A11 | 0.033 | 0.044 | 0.078 | 0.128 | 0.122 | 0.025 | 0.312 | 13 |
| A12 | 0.022 | 0.014 | 0.109 | 0.158 | 0.083 | 0.012 | 0.337 | 7 |
| A13 | 0.038 | 0.024 | 0.118 | 0.170 | 0.051 | 0.038 | 0.320 | 10 |
In terms of mathematical simplicity and flexibility, the TOPSIS approach has advantages. It is also excellent at solving large, complicated decision-making problems (Adalı and Tuş 2021). TOPSIS is implemented effectively for site selection problems (Yal and Akgün 2014; Çetinkaya et al. 2016; Jozaghi et al. 2018; Luo et al. 2020; Adalı and Tuş 2021).
Sensitivity analysis
Sensitivity analysis was performed to investigate how changes in weight values of the criteria affect the ranking of the alternatives. For this reason, the weight values of the criteria are adjusted for two separate situations, and the alternative locations are re-evaluated. Table 11 shows the results of the proposed model, Scenario 1 (S1), in which all criteria were given equal weight, and Scenario 2 (S2), in which the weight value of the most important criterion (C2) and the weight value of the least important criterion (C4) were swapped. It can be seen from Table 11 that A10 is the first alternative according to the proposed model and S1; A6 is the first alternative according to S2. In addition, it is possible to say that the rankings of A8 and A10 have not changed significantly. The sensitivity analysis results show that the criteria weights are very important in the pandemic hospital site selection.
Table 11.
Sensitivity analysis results
| Site | Rank | ||
|---|---|---|---|
| Proposed model | S1 | S2 | |
| A1 | 2 | 5 | 11 |
| A2 | 4 | 8 | 3 |
| A3 | 11 | 12 | 4 |
| A4 | 3 | 9 | 5 |
| A5 | 5 | 7 | 13 |
| A6 | 6 | 4 | 1 |
| A7 | 12 | 13 | 6 |
| A8 | 9 | 10 | 10 |
| A9 | 8 | 6 | 12 |
| A10 | 1 | 1 | 2 |
| A11 | 13 | 11 | 7 |
| A12 | 7 | 2 | 8 |
| A13 | 10 | 3 | 9 |
Conclusion
Hospitals play a critical role in the national and local response to emergencies such as pandemics. This paper describes a scientific framework that combines GIS, PFAHP, and TOPSIS that is used to determine the optimum location for a pandemic hospital in Atakum. As the first step, spatial analysis is performed using GIS to produce maps for the criteria elicited from the insight of the expert team. AHP strengthened by interval-valued PFNs was then used to obtain the criteria weights. Distance to transportation network was the most important criterion, and the least significant one was the distance to fire stations. Based on the criteria weights, and the five rules determined from the expert team, 13 suitable locations for a pandemic hospital were identified using GIS. The TOPSIS method was then used to determine the ranking of the 13 alternative locations (A1−A13). Finally, a sensitivity analysis was performed to show the robustness of the framework.
The proposed method has the advantage of encouraging decision-makers to address complex decision-making problems with a highly methodological basis for decision support. Use of linguistic term sets is another functional benefit of the proposed approach since decision-makers often prefer linguistic evaluations to construct the decision matrix. In addition, use of PFSs manages the uncertainty and vagueness of the perceptions of the expert team during the subjective judgment process.
This study may be expanded to other crowded cities in Turkey for future work. Criteria and the number may be amended based on the characteristics of the study area. Furthermore, other fuzzy MCDM methods can be compared to the proposed method.
Author contribution
Aslı Çalış Boyacı: conceptualization, methodology, validation, formal analysis, data curation, writing (original draft), writing (review and editing), and visualization
Aziz Şişman: software, methodology, formal analysis, data curation, writing (original draft), writing (review and editing), and visualization
Data availability
Not applicable.
Declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Adalı EA, Tuş A. Hospital site selection with distance-based multi-criteria decision-making methods. Int J Healthc Manag. 2021;14(2):534–544. [Google Scholar]
- Ak MF, Gul M. AHP–TOPSIS integration extended with Pythagorean fuzzy sets for information security risk analysis. Complex Intell Syst. 2019;5:113–126. [Google Scholar]
- Alban A, Chick SE, Dongelmans DA, Vlaar APJ, Sent D. ICU capacity management during the COVID-19 pandemic using a process simulation. Intensive Care Med. 2020;46:1624–1626. doi: 10.1007/s00134-020-06066-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Artz M (2014) What is GIS? https://gisandscience.com/2014/05/27/what-is-gis/ (Retrieved 10 February 2021)
- Aslan MF, Unlersen MF, Sabanci K, Durdu A. CNN-based transfer learning–BiLSTM network: A novel approach for COVID-19 infection detection. Appl Soft Comput. 2021;98:106912. doi: 10.1016/j.asoc.2020.106912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aydin N, Seker S. Determining the location of isolation hospitals for COVID-19 via Delphi-based MCDM method. Int J Intell Syst. 2021;36:3011–3034. doi: 10.1002/int.22410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakioglu G, Atahan AO. AHP integrated TOPSIS and VIKOR methods with Pythagorean fuzzy sets to prioritize risks in self-driving vehicles. Appl Soft Comput. 2021;99:106948. [Google Scholar]
- Bragazzi NL, Mansour M, Bonsignore A, Ciliberti R. The role of hospital and community pharmacists in the management of COVID-19: towards an expanded definition of the roles, responsibilities, and duties of the pharmacist. Pharmacy. 2020;8(3):2–15. doi: 10.3390/pharmacy8030140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Çalık A. A novel Pythagorean fuzzy AHP and fuzzy TOPSIS methodology for green supplier selection in the Industry 4.0 era. Soft Comput. 2020;25:2253–2265. doi: 10.1007/s00500-020-05294-9. [DOI] [Google Scholar]
- Çalış Boyacı A, Şişman A, Sarıcaoğlu K. Site selection for waste vegetable oil and waste battery collection boxes: a GIS-based hybrid hesitant fuzzy decision-making approach. Environ Sci Pollut Res. 2021;28:17431–17444. doi: 10.1007/s11356-020-12080-5. [DOI] [PubMed] [Google Scholar]
- Çetinkaya C, Özceylan E, Erbaş M, Kabak M. GIS-based fuzzy MCDA approach for siting refugee camp: A case study for southeastern Turkey. Int J Disaster Risk Reduct. 2016;18:218–231. [Google Scholar]
- Chatterjee D, Mukherjee B. Potential hospital location selection using AHP: A study in rural India. Int J Comput Appl. 2013;71(17):1–7. [Google Scholar]
- Dell’Ovo M, Capolongo S, Oppio A. Combining spatial analysis with MCDA for the siting of healthcare facilities. Land Use Policy. 2018;76:634–644. [Google Scholar]
- Eghtesadifard M, Afkhami P, Bazyar A. An integrated approach to the selection of municipal solid waste landfills through GIS, K-Means and multi-criteria decision analysis. Environ Res. 2020;185:109348. doi: 10.1016/j.envres.2020.109348. [DOI] [PubMed] [Google Scholar]
- Garg H. Some methods for strategic decision-making problems with immediate probabilities in Pythagorean fuzzy environment. Int J Intell Syst. 2018;33(4):687–712. [Google Scholar]
- Gul M. Application of Pythagorean fuzzy AHP and VIKOR methods in occupational health and safety risk assessment: the case of a gun and rifle barrel external surface oxidation and colouring unit. Int J Occup Saf Ergon. 2020;26(4):705–718. doi: 10.1080/10803548.2018.1492251. [DOI] [PubMed] [Google Scholar]
- Hashemkhani Zolfani S, Yazdani M, Ebadi Torkayesh A, Derakhti A. Application of a gray-based decision support framework for location selection of a temporary hospital during COVID-19 pandemic. Symmetry. 2020;12:886. [Google Scholar]
- Hwang CL, Yoon K. Multiple attribute decision making. Lecture notes in economics and mathematical systems. Berlin: Springer-Verlag; 1981. [Google Scholar]
- Ilbahar E, Karaşan A, Cebi S, Kahraman C. A novel approach to risk assessment for occupational health and safety using Pythagorean fuzzy AHP & fuzzy inference system. Saf Sci. 2018;103:124–136. [Google Scholar]
- Ivanov D, Dolgui A. OR-methods for coping with the ripple effect in supply chains during COVID-19 pandemic: Managerial insights and research implications. Int J Prod Econ. 2021;232:107921. doi: 10.1016/j.ijpe.2020.107921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jozaghi A, Alizadeh B, Hatami M, Flood I, Khorrami M, Khodaei N, Tousi EG. A comparative study of the AHP and TOPSIS techniques for dam site selection using GIS: A case study of Sistan and Baluchestan province, Iran. Geosciences. 2018;8(12):494–517. [Google Scholar]
- Kaveh M, Kaveh M, Mesgari MS, Paland RS. Multiple criteria decision-making for hospital location-allocation based on improved genetic algorithm. Appl Geomatics. 2020;12:291–306. [Google Scholar]
- Li Y, Zobel CW. Exploring supply chain network resilience in the presence of the ripple effect. Int J Prod Econ. 2020;228:107693. [Google Scholar]
- Luo C, Ju Y, Santibanez-Gonzalez EDR, Dong P, Wang A. The waste-to-energy incineration plant site selection based on hesitant fuzzy linguistic Best-Worst method ANP and double parameters TOPSIS approach: A case study in China. Energy. 2020;211:118564. [Google Scholar]
- Ministry of Health. Pandemic Hospitals (2020) https://hasta.saglik.gov.tr/Eklenti/36907/0/pandemi-hastaneleripdf.pdf. (Retrieved 2 January 2021)
- Mousavi-Nasab SH, Sotoudeh-Anvari A. A comprehensive MCDM-based approach using TOPSIS, COPRAS and DEA as an auxiliary tool for material selection problems. Mater Des. 2017;121:237–253. [Google Scholar]
- Nsaif QA, Khaleel SM, Khateeb AH. Integration of GIS and remote sensing technique for hospital site selection in Baquba district. J Eng Sci Technol. 2020;15(3):1492–1505. [Google Scholar]
- Opricovic S, Tzeng GH. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur J Oper Res. 2004;156:445–455. [Google Scholar]
- Otay I, Jaller M. A novel Pythagorean fuzzy AHP and TOPSIS method for the wind power farm location selection problem. J Intell Fuzzy Syst. 2020;38(1):835–852. [Google Scholar]
- Pell JP, Sirel JM, Marsden AK, Ford I, Cobbe SM. Effect of reducing ambulance response times on deaths from out of hospital cardiac arrest: cohort study. BMJ. 2001;322:1385–1388. doi: 10.1136/bmj.322.7299.1385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pons PT, Markovchick VJ. Eight minutes or less: does the ambulance response time guideline impact trauma patient outcome? J Emerg Med. 2002;23(1):43–48. doi: 10.1016/s0736-4679(02)00460-2. [DOI] [PubMed] [Google Scholar]
- Rahimi F, Goli A, Rezaee R. Hospital location-allocation in Shiraz using geographical information system (GIS) Shiraz E-Med J. 2017;18(8):e57572. [Google Scholar]
- Ramya S, Devadas V. Integration of GIS, AHP and TOPSIS in evaluating suitable locations for industrial development: A case of Tehri Garhwal district, Uttarakhand, India. J Clean Prod. 2019;238:117872. [Google Scholar]
- Regulation of Investment Principles of Ministry of Health Hospitals (2003) https://planlamadb.saglik.gov.tr/Eklenti/3163/0/saglik-bakanligina-ait-hastanelerin yatirim-esaslarinin-belirlenmesine-dair-yonergepdf.pdf (Retrieved 3 February 2021)
- Regulation of Spatial Planning (2014) https://www.mevzuat.gov.tr/mevzuat?MevzuatNo=19788&MevzuatTur=7&MevzuatTertip=5 (Retrieved 3 February 2021)
- Rezayee M. Hospital site selection in Iskandar Malaysia using GIS-multi criteria analysis. Int J Basic Sci Appl Comput. 2020;2(10):8–15. [Google Scholar]
- Rızvanoğlu O, Kaya S, Ulukavak M, Yeşilnacar Mİ (2020) Optimization of municipal solid waste collection and transportation routes, through linear programming and geographic information system: a case study from Şanlıurfa, Turkey. Environ Monit Assess 192(9). 10.1007/s10661-019-7975-1 [DOI] [PubMed]
- Rostami-Tabar B, Rendon-Sanchez JF. Forecasting COVID-19 daily cases using phone call data. Appl Soft Comput. 2021;100:106932. doi: 10.1016/j.asoc.2020.106932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Şahin T, Ocak S, Top M. Analytic hierarchy process for hospital site selection. Health Policy Technol. 2019;8:42–50. [Google Scholar]
- Sarkar B, Biswas A. Pythagorean fuzzy AHP-TOPSIS integrated approach for transportation management through a new distance measure. Soft Comput. 2021;25:4073–4089. doi: 10.1007/s00500-020-05433-2. [DOI] [Google Scholar]
- Sisman A. Epidemiologic features and risk factors of Crimean–Congo hemorrhagic fever in Samsun province, Turkey. J Epidemiol. 2013;23(2):95–102. doi: 10.2188/jea.JE20120097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soltani A, Marandi EZ. Hospital site selection using two-stage fuzzy multi-criteria decision making process. J Urban Environ Eng. 2011;5(1):32–43. [Google Scholar]
- Soltani A, Inaloo RB, Rezaei M, Shaer F, Riyabi MA. Spatial analysis and urban land use planning emphasising hospital site selection: a case study of Isfahan city. Bull Geogr Socio-Econ Ser. 2019;43:71–89. [Google Scholar]
- Terzi O, Sisman A, Canbaz S, Dündar C, Peksen Y. A geographic information system-based analysis of ambulance station coverage area in Samsun, Turkey. Singap Med J. 2013;54(11):653–658. doi: 10.11622/smedj.2013228. [DOI] [PubMed] [Google Scholar]
- TSI. Turkish Statistical Institute (2020) https://biruni.tuik.gov.tr/medas/?kn=95&locale=tr (Retrieved 20 February 2021)
- USGS (2021) Earth explorer. https://earthexplorer.usgs.gov (Retrieved 15 January 2021)
- Vahidnia MH, Alesheikh AA, Alimohammadi A. Hospital site selection using fuzzy AHP and its derivatives. J Environ Manag. 2009;90:3048–3056. doi: 10.1016/j.jenvman.2009.04.010. [DOI] [PubMed] [Google Scholar]
- World Health Organization (WHO) (2014) Hospital preparedness for epidemics. http://apps.who.int/iris/bitstream/handle/10665/151281/9;jsessionid=C7E947D70C7BDC6C6FA2D0C1D8F10487?sequence=1. Accessed 20 Feb 2021
- World Health Organization (WHO) (2020) COVID-19 Strategy Update. https://www.who.int/publications/i/item/covid-19-strategy-update---14-april-2020. Accessed 25 Feb 2021
- Yager RR. Pythagorean membership grades in multicriteria decision making. IEEE Trans Fuzzy Syst. 2014;22(4):958–965. [Google Scholar]
- Yağma NM, Donkor AG, Gökler ME. Management of hospitals during COVID-19 pandemic. Med Res Rep. 2020;3:155–161. [Google Scholar]
- Yal GP, Akgün H. Landfill site selection utilizing TOPSIS methodology and clay liner geotechnical characterization: a case study for Ankara, Turkey. Bull Eng Geol Environ. 2014;73:369–388. [Google Scholar]
- Yildiz A, Ayyildiz E, Gümüş AT, Özkan C. A modified balanced scorecard based hybrid Pythagorean fuzzy AHP-TOPSIS methodology for ATM site selection problem. Int J Inf Technol Decis Mak. 2020;19(2):365–384. [Google Scholar]
- Yılmaz ÖF, Özçelik G, Yeni FB. Ensuring sustainability in the reverse supply chain in case of the ripple effect: A two-stage stochastic optimization model. J Clean Prod. 2021;282:124548. doi: 10.1016/j.jclepro.2020.124548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yucesan M, Gul M. Hospital service quality evaluation: an integrated model based on Pythagorean fuzzy AHP and fuzzy TOPSIS. Soft Comput. 2020;24:3237–3255. [Google Scholar]
- Zègre-Hemsey J, Sommargren CE, Drew BJ. Initial ECG acquisition within 10 minutes of arrival at the emergency department in persons with chest pain: time and gender differences. J Emerg Nurs. 2011;37(1):109–112. doi: 10.1016/j.jen.2009.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng S, Chen J, Li X. A hybrid method for Pythagorean fuzzy multiple-criteria decision making. Int J Inf Technol Decis Mak. 2016;15(2):403–422. [Google Scholar]
- Zhang X, Xu Z. Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int J Intell Syst. 2014;29(12):1061–1078. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Not applicable.