Large-scale functional coactivation patterns reflect the structural connectivity of the medial prefrontal cortex

Abstract

The medial prefrontal cortex (MPFC) is among the most consistently implicated brain regions in social and affective neuroscience. Yet, this region is also highly functionally heterogeneous across many domains and has diverse patterns of connectivity. The extent to which the communication of functional networks in this area is facilitated by its underlying structural connectivity fingerprint is critical for understanding how psychological phenomena are represented within this region. In the current study, we combined diffusion magnetic resonance imaging and probabilistic tractography with large-scale meta-analysis to investigate the degree to which the functional coactivation patterns of the MPFC are reflected in its underlying structural connectivity. Using unsupervised machine learning techniques, we compared parcellations between the two modalities and found congruence between parcellations at multiple spatial scales. Additionally, using connectivity and coactivation similarity analyses, we found high correspondence in voxel-to-voxel similarity between each modality across most, but not all, subregions of the MPFC. These results provide evidence that meta-analytic functional coactivation patterns are meaningfully constrained by underlying neuroanatomical connectivity and provide convergent evidence of distinct subregions within the MPFC involved in affective processing and social cognition.

A central premise in modern neuroscience is that function follows structure: structural connections constrain the possible configurations of functional communication, placing restrictions on the functional repertoires of particular brain regions. Indeed, decades of work, from early neuroscientists such as Karl Lashley through contemporary primate neurophysiology and neuroimaging studies, has challenged the dominant view of strictly localized cortical functions for many behavioral and cognitive tasks (Passingham et al., 2001) (Miller and Cohen, 2001). As such, to understand the functional description of any particular brain region, it is critical to identify the other regions with which it communicates and describe their underlying anatomical connectivity. These issues will be particularly magnified in parts of the brain with diverse connectivity patterns and heterogeneous functional profiles. One such region that is broadly implicated in studies of social cognition and affective processes is the medial prefrontal cortex (MPFC).

The prefrontal cortex, including the MPFC, is a richly connected system thought to maintain activity by integrating information and directing information flow across distributed cortical areas (Miller and Cohen, 2001). Essential for the integration of this information is both the intrinsic connectivity between columnar layers of the cortical regions and extrinsic connectivity to other cortical and subcortical regions (Passingham et al., 2002). Though less is known about how intrinsic connectivity serves higher-order behavioral phenomena, there has been a marked increase in our understanding of how extrinsic connectivity supports these processes both within humans and across species.

Using a combination of structural and functional connectivity measures, researchers have found a large degree of correspondence between human and macaque connectivity within prefrontal cortical regions, with a notably strong similarity between species in the MPFC (Sallet et al., 2013). More recent work further divided these regions and demonstrated that human and macaque brains show some key differences but largely similar functional connectivity profiles of subregions within the lateral prefrontal cortex between species (Neubert et al., 2014). For example, posterior ventrolateral prefrontal cortex areas supporting cognitive control are relatively consistent between species, but more frontopolar cortex involved in abstract planning and social cognition shows a relatively distinct functional connectivity in humans. Similarly, subregions within the MPFC involved in decision-making and reward-related processes have shown a strong connectivity profile similarity between human and macaques, with notable divergence between species in dorsal MPFC regions (Chavez and Heatherton, 2015) which are broadly implicated in social cognition (Denny et al., 2012; Wagner et al., 2012).

Moreover, other comparative analyses of human and primate neuroanatomy have suggested that the phylogenetic expansion of the prefrontal cortex may have been driven by disproportionately greater white matter volume (Schoenemann et al., 2005). This may reflect a greater degree of connectivity of the MPFC to other cortical regions that support higher-order human cognitive functions such as those supporting social cognition and affective regulation.

In the human neuroimaging literature, the MPFC, broadly construed, has been implicated in a variety of social and affective processes including mentalizing, person perception, self-reference, reward and regulation (see Wagner et al., 2012; 2019 for review). Indeed, there is a fair degree of debate surrounding the functional role of even its subdivisions, such as the ventral MPFC. For example, some researchers have argued that portions of the MPFC primarily serve social cognitive functions, whereas others have argued that they serve response inhibition and other reward and decision-making functions (Delgado et al., 2016). However, to understand what the activation of a particular brain region means, we also need to understand the activity of portions of the MPFC with their ‘neural context’ (Neubert et al., 2014)—what other regions activate with it and the anatomical connections that facilitate this communication. To the degree that brain activity in portions of the MPFC is serving diverse forms of social and affective processes, one way to disentangle the unique representation of each process is to examine the coactivation patterns, particularly across a large volume of studies and extant work in each of these domains.

A popular method for automating meta-analyses of functional magnetic resonance imaging (fMRI) at a large scale is Neurosynth (Yarkoni et al., 2011). In brief, Neurosynth is based on a text mining procedure that captures counts of terms (e.g. ‘memory’, ‘emotion’) within the published literature. These term metrics are then wedded with the activation coordinates in standard space listed in the tables of the same papers to create a database of large-scale activation patterns per term. This automated procedure produces results that are consistent with other meta-analytic results generated manually. Moreover, in addition to providing meta-analyses of particular terms, the database generated by this procedure can also estimate the degree to which a brain region shares coactivation with any other region of the brain across the same collection of studies.

Meta-analytic coactivation patterns are a useful way of informing cortical specialization based on fMRI data at large scale. Indeed, these approaches have been useful for parcellating the functional specialization of targeted regions of the brain. For example, Chang et al. (2013) combined Neurosynth and resting state connectivity to segment different subsections of the insular cortex. More recently, De La Vega et al. (2016) used Neurosynth to identify a tripartite clustering solution of a broadly defined portion of the medial frontal cortex, including the MPFC. These researchers identified three major parcels of the MPFC, along with subsections within each parcel. These studies provided evidence that large-scale coactivation patterns may help identify functional subsections of the brain. However, anatomical connectivity information is not considered in these studies, and thus, they cannot speak to the degree to which the structural connectivity of these regions may inform or constrain these interpretations.

Within a neuroimaging context, diffusion magnetic resonance imaging (dMRI) is the primary method to assay the structural connectivity across the brain. Moreover, researchers have also demonstrated the functional significance of structural connectivity based on dMRI methods. For example, Saygin et al. (2012) were able to accurately predict the location of the fusiform face area (FFA) within individuals based only on their structural connectivity as measured by dMRI. In this study, dMRI outperformed fMRI group-level FFA mapping within the same sample of subjects. This provides evidence that distinctions in function are underpinned by fine-grained differences in structural connectivity. Moreover, given that most interpretations of coactivation patterns rest on assumptions of their underlying structural connectivity, functional parcellation based on meta-analytic coactivation may be reflected in the dMRI structural connectivity patterns of the MPFC.

To this end, in the current study, we examined the correspondence between structural connectivity and meta-analytic coactivation in the MPFC by deploying a multimodal unsupervised machine learning approach. Using k-means clustering within each modality, we compared the clustering solutions of patterns of functional coactivation to those derived from patterns of structural connectivity within the MPFC. We tested the corresponding mutual information of the clustering solution between the two modalities at multiple numbers of cluster solutions. To the degree that each clustering solution accurately reflects one another, this would provide evidence that large-scale coactivation patterns are supported by the underlying anatomical connectivity of the MPFC. Furthermore, we related connectivity and coactivation similarity measures across all voxel-to-voxel pairs within the MPFC to investigate unclustered voxelwise correspondence between modalities. These analyses provide a complimentary approach to relating structural connectivity data to meta-analytic coactivation.

Methods

Anatomical and dMRI images of 103 healthy volunteers (mean age 43 ± 19 years; 43 males and 60 females) from the NKI Rockland sample were acquired from the 1000 functional connectomes project (Nooner et al., 2012). Access and analysis of these data was approved by the Institutional Review Board at the University of Oregon. The dMRI scans were acquired on a Siemens TrioTim 3T scanner with 137 diffusion directions, and data were analyzed using the FSL Diffusion Toolbox (Behrens et al., 2003). Standard preprocessing included brain extraction, eddy current correction and motion correction. To model the underlying white matter architecture, a dual-fiber model was implemented using the Bayesian Estimation of Diffusion Parameters Obtained using Sampling Techniques method (BEDPOSTx; Behrens et al., 2007) to account for crossing fiber uncertainty in the diffusion imaging signal. Probabilistic tractography was used to generate a distance-corrected connectivity matrix between our a priori MPFC mask and the whole brain. The dimensions of the matrix are MPFC-by-the-rest-of-the-brain (∼5000 × ∼230 000) with each row of the matrix representing the connections from a given MPFC voxel to the whole brain. From our seed mask, 5000 distance-corrected probabilistic tract streamlines were taken at each voxel. These results were then normalized to Montreal Neurological Institute (MNI) standard space using non-linear registration warps from each subject’s diffusion-weighted image in functional magnetic resonance of the brain nonlinear image registration tool (FNIRT). To create a group-level matrix, we summed the matrices of each of the subjects together before submitting them to the clustering solution.

To compare the structural and functional organization of MPFC, we studied two datasets: a sample of dMRI images from 103 participants and version 0.7 of the Neurosynth database (Yarkoni et al., 2011). We performed k-means clustering on both datasets. The analysis code for the dMRI data is publicly available in the form of a Jupyter Notebook (https://github.com/chavezlab/parcellation-tutorial). All Neurosynth data were analyzed using Neurosynth core-tools in Python tools (https://github.com/neurosynth/neurosynth). We used the scikit-learn Python package implementations of all machine learning algorithms used. All statistical analyses of brain data take place in 2 mm isotropic MNI152 standard space.

A challenge for any segmentation analysis is defining the area of interest. Often there is no non-arbitrary way of deciding which voxels to include (Eickhoff et al., 2016). This is especially difficult for a brain area as amorphous as MPFC. As such, we selected our MPFC mask based on the MFC clustering analysis from De La Vega et al. (2016). This mask is representative of what is broadly considered MPFC in the literature, and it excludes voxels that lack sufficient data within the Neurosynth framework.

We clustered each of the voxels inside our MPFC mask based on similarity of connectivity to the whole brain. To perform the clustering analysis, we took the Pearson correlation between every pair of rows in the group matrix, resulting in an MPFC-by-MPFC correlation matrix. We then used the k-means algorithm on this matrix four times to find clustering solutions at k = 2 through k = 5. We chose k-means because of its computational efficiency, goodness-of-fit characteristics and good performance for small numbers of clusters (Thirion et al., 2014). We used scikit-learn’s default k-means behavior which involved using the k-means++ initialization procedure, running the algorithm 10 times on different centroid seeds and selecting the best solution based on the lowest inertia to avoid local minima.

The k-means algorithm works by selecting k points and iteratively clustering nearby points using some distance metric, most often Euclidean distance. The correlation matrix is used to specify the locations of each of the MPFC voxels in a correlational similarity vector space. The algorithm repeats a specified number of times to find the best solution. The best choice of k depends in large part on the goals of the analyst. Given a range of values of k, however, there are standard practices for picking the best value, a common one being the silhouette score. For our purposes, to evaluate at which number of clusters the different modalities best reflect one another, we compared the dMRI-derived clustering solutions with the Neurosynth-generated solutions using the adjusted mutual information score. This metric measures the degree of similarity between two labelings of the same data. Since the measure is symmetric and independent of label permutations, it is useful for capturing the similarity between two clustering solutions when the ground-truth solution is unknown.

The Neurosynth database is a repository of fMRI activations scraped from published studies (Yarkoni et al., 2011). We analyzed the most recent version (version 0.7), which contains activation and text data from 14 371 fMRI studies. The studies in the database span the full range of the published neuroimaging literature, include data from males and females, span a wide age range and cover multiple ethnicities. For each study in the database, the peak activations for all of the contrasts reported in the activation tables are collected along with the text from the article’s abstract.

Using the activation data from Neurosynth, we clustered voxels in our MPFC mask based on similarity of whole-brain coactivation to compare to our structure-based parcellation. We first created a binary matrix for the voxels inside MPFC with each row corresponding to an MPFC voxel and every column representing a study. A 1 in the matrix indicates that the study reported activation within 10 mm of that voxel, while a 0 means no activation was reported near that voxel. We created a similar activation matrix for the entire brain. To reduce dimensionality, we applied principal component analysis (PCA) to this whole-brain matrix and reduced it to 100 PCA components. PCA, by way of the singular value decomposition of the data matrix A, gives the optimal rank r approximation of A. High-dimensional datasets often exhibit low-rank structure, and often, noise in the data increases the rank of the data and makes columns that would be linearly dependent on one another independent. For this reason, PCA can help to filter noise. After applying PCA, we then calculated the Pearson pairwise distances between the two matrices, resulting in an MPFC-by-whole-brain (PCA reduced) distance matrix. We then used the k-means algorithm on this matrix to generate clustering solutions between k = 2 and k = 5 clusters.

To further clarify the relationship between structure and function in the MPFC, we compared the similarity structure of each of the modalities. For the dMRI data, we used the same MPFC-by-MPFC correlation matrix that we used for clustering. Each row vector of the matrix measures the similarity between the connectivity of a given voxel with the connectivity of every other voxel in MPFC. For the Neurosynth data, we took the MPFC-by-whole-brain (PCA) matrix that we used for clustering and correlated each of the rows with all of the other rows, which resulted in an MPFC-by-MPFC matrix. Although the initial matrix represented the coactivation similarity between each MPFC voxel and the voxels in the rest of the brain, this new matrix represents the relationships among MPFC voxels. To compare this matrix with the dMRI matrix, we simply correlated the two matrices. Since both matrices are symmetric, we took the correlation between the bottom, off-diagonal triangle of each of the matrices.

Results

We identified multiple spatial scales where dMRI-based structural connectivity and Neurosynth-based functional coactivation converge to a similar clustering solution of the MPFC. The divergence between clustering solutions at k > 5 prohibited direct comparison as it was unclear which parcels were analogous across both modalities. The successive increase of k reveals a hierarchical structuring of MPFC. Hierarchy is not enforced by the clustering algorithm itself as each fitting of k-means is independent of the other model fits. Other clustering methods, like Ward’s hierarchical clustering, enforce hierarchy between clustering solutions. Within the scope of k = 2 through k = 5, all solutions but k = 3 showed a strong relationship based on the adjusted mutual information score, as is shown in Figure 1. Final clustering parcellation solutions are shown in Figure 2. At the broadest spatial scale of k = 2, the two parcellations divided the MPFC along the inferior/posterior axis into dorsal and ventral areas. The divide between ventral and dorsal in both parcellations occurs at the anterior tip of the corpus callosum. The drawn distinction between ventral and dorsal MPFC for both clustering techniques reflects previously described differences in functional behavior between these two areas of cortex (see Denny et al., 2012; Wagner et al., 2012).

Fig. 1.

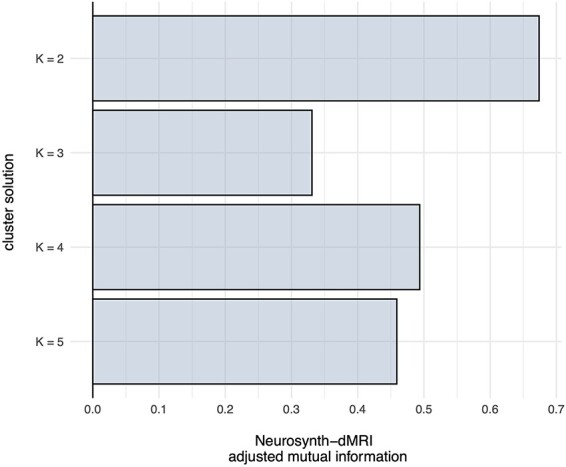
The adjusted mutual information between the clustering solutions of both meta-analytic coactivation and structural connectivity modalities. Higher mutual information indicates more congruence between clustering solutions. The k = 2 and k = 4 mutual information scores show that there is a notable similarity between the Neurosynth-based clusters and the dMRI-based clusters.

Fig. 2.

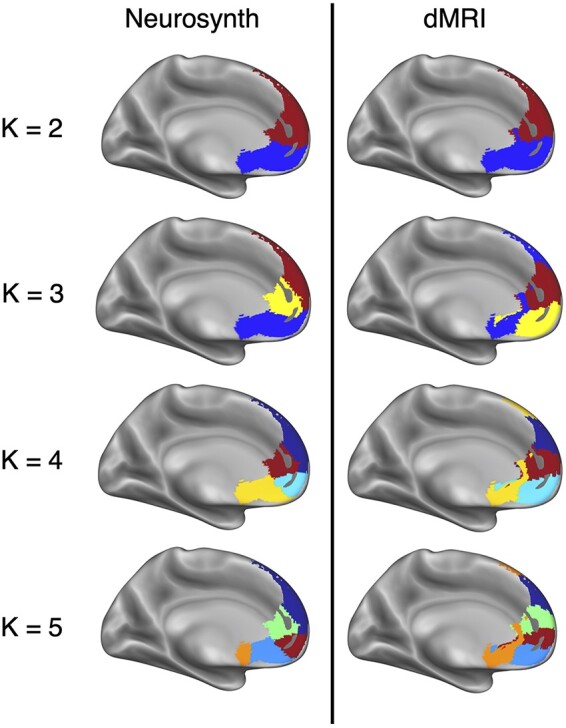
K-means clustering solutions for meta-analytic coactivation and dMRI modalities. Colors indicate analogous clusters that were identified between modalities. The greatest correspondence between the two modalities was at a cluster resolution of k = 2 followed by k = 4.

The k = 3 clustering solutions showed the weakest correspondence as the dMRI-based clustering divided the ventral portions of MPFC into subgenual cortex and vMPFC while largely grouping the rest of the mask into a large dorsal MPFC cluster. The Neurosynth-based subdivision kept subgenual cortex and ventral MPFC together but divided the dorsal area into a rostral cingulate area and a dorsal MPFC area. Aside from the k = 2 solutions, k = 4 showed the best congruence between modalities, measured by the adjusted mutual information score. Both clustering solutions found clusters corresponding to rostral anterior cingulate cortex (rACC), dorsal MPFC, ventral anterior cingulate cortex (vACC) and ventral MPFC.

Across all clustering solutions, two major features stand out. First, the dMRI-based parcellations consistently draw a distinction between vACC and ventral MPFC. This division first appears in the k = 3 solution. The k = 4 and k = 5 solutions feature almost the exact same clusters for these two brain areas, indicating that the distinction is robust across different fittings of the model. Second, for k = 3 through k = 5, the dorsal MPFC cluster remains consistent across both modalities and numbers of clusters. While the boundaries created by the clustering algorithm should be interpreted with caution, the fact that this cluster is robust to modality and separate fittings of k-means is notable.

To more directly test the relationship between structure and function, we correlated the bottom triangle of the MPFC-by-MPFC similarity matrices of each modality. This allowed us to ask whether a pair of voxels that show a high degree of similarity within a modality also shows a high degree of similarity in the other modality. The results of this analysis are summarized in the hexbin plot (used to help visualize scatter plot points when large amounts of data are over-plotted like the voxel-by-voxel pairwise relationships here) in Figure 3A. For the lower-triangle, off-diagonal comparisons, we found that there is a positive relationship (Pearson R = 0.77; Spearman ρ = 0.74, all P-values < 0.0001) between connectivity similarity and coactivation similarity across all voxel-to-voxel pairwise relationships.

Fig. 3.

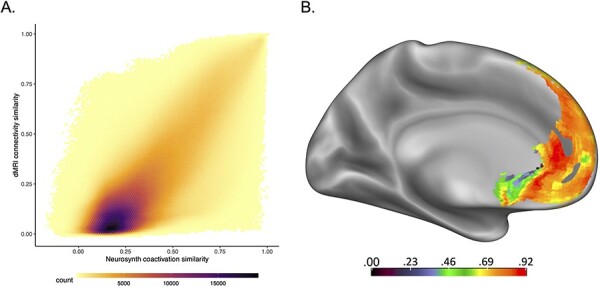
The results of the connectivity and coactivation similarity analyses. (A) Hexbin plot showing the relationship between connectivity similarity from the dMRI data and coactivation similarity from the Neurosynth data for all unique pairwise voxel-to-voxel combinations to the rest of the MPFC. Overall, there was a positive relationship between connectivity and coactivation similarity between each voxel pair (Pearson R = 0.77; Spearman ρ = 0.74, all P-values < 0.0001), such that when the connectivity similarity between two voxels was high, the coactivation similarity was also high and vice versa. (B) Displayed here are the voxelwise correlations between structural connectivity similarity and meta-analytic coactivation similarity, showing relatively good correspondence in portions of the rostral anterior cingulate cortex and dorsal MPFC and less correspondence in the subgenual anterior cingulate cortex, parts of the rostral MPFC and medial orbitofrontal cortex. Note: though the relative comparisons of modality correspondence between regions can be inferred from these analyses, the raw correlation values indicated in the key are likely inflated due to the sparsity of each modality’s similarity matrix.

Next, for each off-diagonal row of the MPFC × MPFC similarity matrix in each modality (corresponding to an individual voxel’s similarity to the rest of the MPFC), we correlated these similarity values to the corresponding row of the other modality to calculate voxelwise correspondence between the two measures. These results are displayed in Figure 3B. We found that relative to the other parts of the MPFC, the subgenual ACC, medial OFC and rostral MPFC show relatively weaker correspondence between the two modalities, but most other regions tend to be better. Regions of poorer correspondence largely mirrored the areas of inconsistent overlap between the modalities in the clustering analysis. Note, however, that the strength of these relationships may be difficult to interpret, given that the raw correlation values in these analyses are likely inflated due to the sparsity of each matrix.

Discussion

In this study, we took a multimodal unsupervised machine learning approach to examine the correspondence in cortical parcellation of the MPFC based on fMRI-based meta-analytic coactivation and dMRI-based structural connectivity. For both analyses, we used correlation-based measures to generate similarity matrices, which were then used in iterative applications of the k-means algorithm. These results also showed similar solutions between the two methods across multiple cluster resolutions. We found that the two modalities found the best agreement at a two-cluster resolution, separating the dorsal and ventral MPFC. Beyond the two-cluster solution, the next best correspondence was the four-cluster solution. This solution identified regions of the rostral cingulate, subgenual anterior cingulate, ventral frontal pole and dorsal MPFC. Taken together, these analyses suggest that regions defined through meta-analytic coactivation parcellation are largely, though not perfectly, reflected in underlying patterns of structural connectivity within the MPFC. Furthermore, using connectivity and coactivation similarity measures, we found a relatively large correspondence between structural connectivity profiles and coactivation profiles across much of the MPFC. Together, our results suggest that meta-analytic coactivation patterns—used to define functionally homogeneous regions (see De La Vega et al., 2016)—reflect empirically derived structural connectivity patterns.

The MPFC is one of the major portions of the default mode network, which is broadly implicated in processing information related to internally focused tasks, autobiographical memory, thinking about the future, self-representation and mentalizing (Buckner et al., 2008). As such, there is a high degree of functional heterogeneity within this region, and researchers have turned to methods such as resting-state functional connectivity (Andrews-Hanna et al., 2010) and multivariate methods (Chavez and Heatherton, 2015) to better understand how psychological processes are represented within this area and how they are communicated to the rest of the brain. Moreover, there have also been efforts to parcellate portions of the frontal cortex, including the MPFC, based on coactivation patterns based on meta-analytic coactivation in a large-scale collection of studies (De La Vega et al., 2016). Underlying each of these methods is the assumption that the distributed functional profile of the MPFC is supported by its anatomical connectivity via local and long-rage white matter pathways. To the best of our knowledge, this study is the first to directly relate cortical parcellations based on structural connectivity to those based on meta-analytic coactivation. Given the high degree of correspondence between the two modalities, our results provide evidence that these two modalities, despite being generated from quite different sources of data, identify similar organizational boundaries within the MPFC. Nonetheless, there remain some caveats and limitations of the current approach.

Although different clustering solutions aligned more or less well, the question of the ‘correct’ number of clusters is often considered a red herring. As Eickhoff et al. (2015) have pointed out, connectivity-based parcellation does not address the question of a ground-truth parcellation. Certain parcellations will be more optimal than others that given some criteria and the data, but these parcellations are best seen as broad heuristics. For example, the k = 4 solutions showed close alignment, suggesting real similarities in the patterns of structural connectivity and functional coactivation patterns in the dorsal MPFC, rACC, vACC and the ventral MPFC. Though clustering algorithms draw hard boundaries, the boundaries themselves should not be overinterpreted. Aside from the constraints of the algorithm, the effects of registration error should give further pause in overinterpreting the boundaries, as well as limitations related to the spatial resolution and indirect measurement of underlying brain measurements for both fMRI and dMRI data. These results do, however, show that at multiple cluster resolution levels, the functional patterns of coactivity are closely related to the underlying patterns of structural connectivity as measured by these methods.

Using voxelwise similarity analyses, we also showed that structural connectivity and meta-analytic coactivation showed highly related voxel-to-voxel similarity between each modality. Put differently, when two voxels showed a high degree of connectivity similarity, they also showed a high degree of coactivation similarity. Moreover, we also found that the direct connectivity to coactivation similarity reflected one another across most regions of the MPFC, with the exception of areas of subgenual cortex. Although convergent clustering solutions are important for establishing relatively homogeneous regions of shared topological organization of the cortex that can be detected with each measure, they can be greatly influenced by the exact clustering algorithm being used, and there is not always a principled reason for choosing one over another. The connectivity and coactivation similarity analyses provide additional evidence of correspondence between structural connectivity and meta-analytic coactivation and complement the clustering analyses to highlight areas where clustering solutions are more likely to be unstable or otherwise less informative.

In conclusion, the results of the current study suggest that there is a general agreement between parcellation schemes based on meta-analytic coactivation patterns and structural connectivity with the MPFC that are supported by voxelwise similarities between each modality. These results help us to further understand and characterize the organization of the MPFC which is broadly implicated in brain imaging studies of social psychological and affective phenomena. Moreover, these results provide evidence that, in part, confirms the assumption that structural connectivity within this region may constrain its functional profile. There is a dearth of studies comparing the results of parcellations between different modalities, making it unclear as to how well connectivity-based parcellation methods reproduce and under what circumstances (Eickhoff et al., 2015). Nonetheless, our results offer a direct comparison of two of these approaches, showing that meta-analytic coactivation and dMRI-based parcellations are not only consistent with one another but also reflect known functional differences of the MPFC.

Tutorial and Open Science Practices

A walk-through and code to perform the k-mean clustering analysis has been made available via GitHub: https://github.com/chavezlab/parcellation-tutorial. The dMRI data used in this study are open and freely available through the Nathan Kline Institute: http://fcon_1000.projects.nitrc.org/indi/enhanced/. Neurosynth core-tools is an open-source, freely available Python package and data resource available on GitHub: https://github.com/neurosynth/neurosynth.

Conflicts of Interests

None declared.