Gone but not lost: implications for estimating HIV care outcomes when loss to clinic is not loss to care

Abstract

Background:

In some time-to-event analyses, it is unclear whether loss to follow-up should be treated as a censoring event or a competing event. Such ambiguity is particularly common in HIV research that uses routinely collected clinical data to report the timing of key milestones along the HIV care continuum. In this setting, loss to follow-up may be viewed as a censoring event, under the assumption that patients who are “lost” from a study clinic immediately enroll in care elsewhere, or a competing event, under the assumption that people “lost” are out of care all together.

Methods:

We illustrate an approach to address this ambiguity when estimating the 2-year risk of antiretroviral treatment initiation among 19,506 people living with HIV who enrolled in the IeDEA Central Africa cohort between 2006 and 2017, along with published estimates from tracing studies in Africa. We also assessed the finite sample properties of the proposed approach using simulation experiments.

Results:

The estimated 2-year risk of treatment initiation was 69% if patients were censored at loss to follow-up or 59% if losses to follow-up were treated as competing events. Using the proposed approach, we estimated that the 2-year risk of ART initiation was 62% (95% confidence interval: 61, 62). The proposed approach had little bias and appropriate confidence interval coverage under scenarios examined in the simulation experiments.

Conclusions:

The proposed approach relaxes the assumptions inherent in treating loss to follow-up as a censoring or competing event in clinical HIV cohort studies.

Introduction

Early HIV diagnosis and linkage to care, rapid antiretroviral therapy (ART) initiation, and sustained viral suppression improve survival among people living with HIV and prevent onward transmission to their HIV-uninfected partners ^1,2. Along the entire HIV care and treatment continuum, routinely collected clinical data (such as data from electronic health records) offer the potential to estimate the timing and persistence of key milestones, including initiation of ART and viral suppression. However, clinical data from routine service delivery settings are plagued by loss to follow-up. In contrast to interval cohort studies, where loss to follow-up simply masks observation of the outcome of interest, loss to follow-up in clinical cohort studies is a mixture of true loss to clinical care and loss to observation in that cohort. ³

Loss to clinical care is important because it can itself affect important health outcomes. For example, a patient with newly diagnosed HIV who has been lost early from clinical care may have no opportunity to initiate ART for the period that he is out of care. On the other hand, loss to observation from a specific clinical cohort does not always imply being lost from clinical care altogether. Patients may be lost to follow-up at a specific facility yet remain in clinical care by transferring to another facility. When such “transfers out” are not captured by records maintained at the first facility, this phenomenon is known as a “silent transfer.” In this scenario, patients may continue to experience outcomes along a continuum of care after being lost to follow-up in a specific clinical cohort ⁴. Such silent transfers are common, particularly in settings with decentralized health care systems and mobile populations, and may occur prior to treatment initiation.⁵ When monitoring the timing of treatment initiation using records from the first facility alone, silent transfers can lead to erroneous conclusions regarding the probability of treatment initiation over time.

The disposition of patients lost to follow-up in clinical cohorts has important implications for data analysis. For example, when estimating the cumulative incidence of ART initiation after entry into care, some patients are likely to become lost to follow-up at a study site before initiating ART. Traditional analyses of these data would proceed in one of two ways: 1) censor patients at loss to follow-up, which would yield a valid estimate of the cumulative incidence of ART initiation under the assumption that patients who are lost to follow-up at this facility initiate ART (presumably at a different facility) with the same probability at each time point as participants remaining in the study ⁶; or 2) treat loss to follow-up as a competing event that precludes ART initiation, which yields a valid estimate under the assumption that patients who are lost to follow-up from this facility are permanently lost to clinical care and do not initiate ART before the end of the study period.

Neither assumption is likely to hold for all patients. It is likely that some patients who are lost to follow-up at a specific facility are re-engaged in care elsewhere while others are truly out of care or have died. If these outcomes were known, patients who were lost to follow-up at a study site but engaged in care elsewhere would be censored, and death and complete disengagement from care would be treated as competing events. However, the disposition of patients lost to follow-up is usually unknown. Tracing studies have been conducted to understand what happens to these patients^7,8. These studies provide estimates of the proportions of patients classified as lost to follow-up who have engaged in care elsewhere or died that can be used to adjust our analyses to account for the ambiguity in patient outcomes.

Here, we present an approach to use information from tracing studies or expert knowledge to account for what happens after loss to follow-up when estimating the cumulative incidence of key milestones along the HIV care continuum. We illustrate this approach to estimate cumulative incidence of ART initiation over time among eligible patients in the International epidemiology Databases to Evaluate AIDS (IeDEA) Central Africa cohort, and we evaluate the finite sample properties of the proposed approach using simulation experiments.

METHODS

Motivating example

The parameter of interest in the motivating example is the risk ⁹, or cumulative incidence, of ART initiation over 2 years since entry into HIV care among patients who enrolled in care at one of 15 clinical care sites in Central Africa. Moreover, we compare the timing of ART initiation between participants enrolling in three calendar time periods roughly corresponding to three treatment eras: 1) 2006 – 2009 (when WHO guidelines recommended treatment initiation when CD4<200); 2) 2010 – 2015 (when WHO guidelines recommended treatment initiation when CD4<350); 3) 2016 – 2017 (when WHO guidelines recommended immediate treatment). During the first 2 years in care, many patients become lost to follow-up at the study sites before they have the opportunity to start ART, which may impede our ability to estimate the probability of ART initiation. We applied the proposed approach to account for the fact that it was unclear if these patients should be censored, under the assumption that they enrolled in care elsewhere, or if these losses to follow-up should be treated as competing events, under the assumption that these patients were permanently out of care or had died.

Study sample

The Central Africa IeDEA cohort has been described in detail elsewhere ^10,11. Briefly, the Central Africa IeDEA cohort is a multi-country collaboration that compiles clinical data from patients receiving HIV care and treatment at participating health facilities in the Central African region. We included 19,506 participants living with HIV who 1) had a first documented clinic visit in a participating facility in Rwanda, Democratic Republic of Congo, or Burundi between 1 January 2006 and 31 December 2017; 2) had at least one follow-up clinic visit or laboratory test in the 6 months after enrollment (to restrict to those truly enrolled in care); and 3) were not known to have started ART prior to their first visit at a participating facility.

Outcome definitions

Patients were followed from entry into HIV care at a study site until documented ART initiation, death, transfer to another facility, loss to follow-up, or administrative censoring at 2 years after enrollment or on 31 December 2017. ART initiation was defined as documentation of having been prescribed a regimen of three or more antiretroviral drugs, and patients were considered to have died if there was a documented death in the clinic database; information on death was collected by clinic staff. Patients were considered lost to follow-up on their last visit date prior to a 6 month-gap in documented clinic visits or laboratory records ^12–14 and were not allowed to re-enter the cohort for this analysis.

Approach

In settings with no loss to follow-up, one may estimate the risk of ART initiation using the Aalen–Johansen estimator ¹⁵. The Aalen–Johansen estimator is used rather than the Kaplan–Meier estimator to account for the unavoidable competing event of death and allow loss to clinical care to be treated as a competing event, when appropriate. When loss to follow-up is present, the analyst has traditionally been faced with 2 options: 1) to censor patients at loss to follow-up under an assumption that the hazard of starting ART at time t is identical for patients lost to follow-up and those under observation; or 2) to treat loss to follow-up as a competing event under the assumption that patients have zero probability of initiating ART after loss to follow-up.

In time-to-event analyses, the decision to treat a specific endpoint as a censoring event or a competing event can have a dramatic impact on results. In particular, when calculating risk using the Kaplan–Meier or Aalen–Johansen estimators ¹⁵, censored individuals’ person–mass is redistributed onto persons who continue under follow-up, such that events that occur after a participant is censored carry more ‘weight’ than events before that participant was censored, reflecting the implicit assumption that censored participants experienced the same hazard of the event of interest as participants remaining under observation ¹⁶. This assumption is often labeled “no informative censoring” ^17,18. In contrast, when a participant experiences a competing event, his unobserved event is not redistributed to future event times, under the implicit assumption that a competing event precludes the event of interest from occurring ¹⁹. Accordingly, if any participants are lost to follow-up, censoring them at loss to follow-up will yield a higher risk of an outcome of interest than treating loss to follow-up as a competing event ²⁰.

We first estimate the risk of ART initiation under the two standard approaches to illustrate a likely best case scenario for ART initiation, in which patients are censored at loss to follow-up under the assumption that they are in care elsewhere and have the same probability of ART initiation as people remaining in the study, and worst case scenario, in which we treat loss to follow-up as a competing event that precludes ART initiation.

Next, we accounted for loss to follow-up using tracing weights according to the following algorithm implemented in a dataset with one record per person:

1. For participants not lost to follow-up (i.e., those who had documented ART initiation, death, or transfer, or were administratively censored prior to [or without ever] meeting the definition of loss to follow-up or experiencing any of the above events): Assign a weight of 1.

2. For participants lost to follow-up:

   1. Create a second, duplicate, record.
   2. Censor the first record at loss to follow-up and assign a weight of ρ_i, where ρ_i is the probability that the patient is enrolled in care elsewhere.
   3. Treat the second record as though the patient experienced a competing event at the time of loss to follow-up and assign a weight of 1-ρ_i.

3. Apply desired estimator in the expanded and weighted data.

Under each approach (i.e., censoring at loss to follow-up, treating loss to follow-up as a competing event, and accounting for loss to follow-up using the proposed approach), we report the risk functions for ART initiation, the risk of ART initiation at 2 years after care enrollment, and subdistribution hazard ratios comparing ART initiation over the three calendar time periods. Risks were estimated by applying a weighted Aalen–Johansen estimator in the extended dataset outlined above, and hazard ratios were estimated using a weighted subdistribution Cox proportional hazards model²¹ in the extended dataset. Details on the statistical approach can be found in eAppendix 1, sample SAS and R code to implement the approach can be found in eAppendix 2, and an R package to implement the proposed approach can be found at https://github.com/edwardsjk/mccc.

Using external information about ρ_i

The true probability that a patient is engaged in care at another clinical site, ρ_i, is unknown and must be estimated. While, ideally, one would conduct a tracing study in the population of interest by ascertaining the status of a random sample of patients lost to follow-up at the study sites, often additional data collection at a study site is not feasible. In this setting, one may inform the proposed approach using information from tracing studies conducted in similar settings. For example, tracing studies were conducted among patients in ART programs lost to follow-up at types of health facilities similar to those in our study in East Africa, western Africa, and southern Africa. These studies are summarized in a systematic review by Zurcher et al. ²² and several other recent publications ^23,24. A subset of these studies reported both the number of patients successfully traced and the number found to be enrolled in care elsewhere (i.e., undocumented, or silent, transfers). This proportion ranged from 2% to 54%. Because ART programs were rapidly expanding during the study time period, calendar year was likely an important predictor of whether a patient lost from a facility included in the study enrolled in care elsewhere. To account for this trend in the proportion of silent transfers, we modeled this proportion as a function of calendar year when patient tracing occurred and used the results to predict the proportion of patients lost from study sites who had silently transferred at the time that each patient in the main study (i.e., our dataset) was lost to follow-up. We let this predicted proportion stand in for the probability that a specific patient lost to follow-up was actually in care elsewhere, ${\widehat{\rho }}_i$.

Specifically, we gathered published estimates into a dataset along with the year of data collection for each estimate. Then, we fit the logistic regression model

$$logit\left\{p_s\right\}={\beta }_0+{\beta }_1{Z}_{\mathrm{s}}+{\beta }_2{Z}_s^2$$

where p_s was the proportion of patients who appeared lost in study s who were later found to be in care, and Z_swas the year that study s was conducted (or the study midpoint). In the logistic model, each study s was weighted by the total number of patients successfully traced.

We next used estimates of ${\widehat{\beta }}_0,{\widehat{\beta }}_1,{\widehat{\beta }}_2$ to predict $\widehat{p_s}$ for hypothetical studies conducted at the time that each patient in the study was lost to follow-up. Under the assumption that individuals lost to follow-up in a given year in the study were exchangeable with participants in the tracing studies conducted in those years, ${\widehat{\rho }}_i$ was estimated as the predicted value

$${\widehat{\rho }}_i=\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{i}\mathrm{t}\left\{{\widehat{\beta }}_0+{\widehat{\beta }}_1{X}_{\mathrm{i}}+{\widehat{\beta }}_2{X}_i^2\right\}$$

where X_i was the year in which patient i became lost from the study and $\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{i}\mathrm{t}\left(v\right)=\exp \left(v\right)/[1+\exp \left(v\right)]$. Because year was included in the models, all patients lost in the same year had the same estimated probability of being in care elsewhere.

In eAppendix 1, we show how ρ_i could be informed by prior knowledge rather than estimated from external data. We also conducted a sensitivity analysis (shown in eAppendix 4) in which we varied ρ_i for all participants from 0.02 to 0.54, to reflect results from tracing studies with the lowest and highest proportion of patients found to be in care elsewhere.

Incorporating uncertainty about ρ_i

Uncertainty in the final point estimates should reflect both sampling error in the main study and uncertainty about ρ_i. Uncertainty about ρ_i is represented in this analysis by the estimated standard errors around the predicted proportions in care. Standard errors for the risks and subdistribution hazard ratios were estimated as the standard deviations of the point estimates from 1000 bootstrap samples of the study data. To propagate uncertainty about ρ_i through the analysis, we set the probability that an individual was in care in each bootstrap sample k as ${\widehat{\rho }}_i^k=\mathrm{expit}\left\{{\widehat{\gamma }}_i^k\right\}$, where ${\widehat{\gamma }}_i^k$ was a random draw from the normal distribution $N\left(\mathrm{logit}\left\{{\widehat{\rho }}_i\right\},\widehat{V}\left[\mathrm{logit}\left\{{\rho }_i\right\}\right]\right).$

Simulations

We explored the finite sample properties of the proposed approach using a series of simulation experiments. Simulation experiments and results are described in eAppendix 3.

All analyses were conducted in R 3.6.0 and SAS 9.4.

This study was approved by Institutional Review Boards at the Albert Einstein College of Medicine and the University of North Carolina at Chapel Hill.

RESULTS

Example

Of the 19,506 participants, 63% were female and the majority (52%) were between the ages of 21 and 40 (Table 1). The rate of participant enrollment was similar across the three calendar time periods, resulting in similar numbers of participants enrolled in each of the first two periods and slightly under half that number enrolled in the third period. Of participants who became lost to follow-up before starting ART, over half entered care during the first period. In the second period, a greater proportion of new patients were, by definition, eligible for ART at the time of enrollment. By the third period, when guidelines stipulated early treatment, very few patients were lost prior to initiating ART. Participant characteristics by calendar period are described in eAppendix 5.

Table 1.

Demographic and clinical characteristics of 19,506 patients who entered HIV care between 1 January 2006 and 31 December 2017 at 15 Central Africa IeDEA clinical sites and were followed for ART initiation up to 2 years.

Characteristics	Overall (N = 19,506)		Patients lost to follow-up (Nlost = 4387)
	n	%	n	%
Male sex	7257	37	1645	38
Country of health facility
Burundi	4387	22	997	23
Democratic Republic of Congo	3268	17	293	7
Rwanda	11,851	61	3097	71
Age at enrollment (in years)
10 or under	1442	7	294	7
11 – 20	1196	6	283	5
21 – 30	5717	29	1485	34
31 – 40	6429	33	1380	31
41 – 50	3336	17	696	16
51+	1386	7	249	6
Calendar year of enrollment
2006 – 2009	7929	41	2765	63
2010 – 2014	8325	43	1478	34
2015 – 2017	3252	17	144	3

ART: antiretroviral therapy

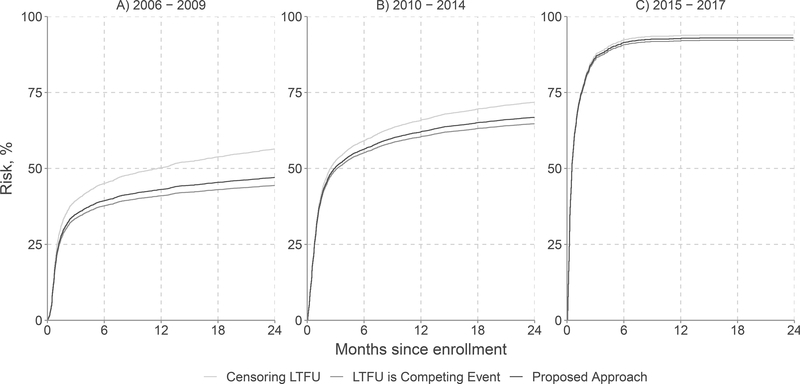
Overall, 63% of patients (n=12,253) started ART and 23% (n=4387) were lost to follow-up within 2 years after entry into care (Table 2). The proportion lost to follow-up prior to ART initiation was highest for enrollees from 2006 – 2009 (35%) and dropped to 4% by enrollees in the 2015 – 2017 period. Under an approach that censored participants at loss to follow-up, the overall 2-year risk of ART initiation was 69% (95% CI: 67.8, 69.3), ranging from 56% in the earliest calendar time period to 94% in the most recent period (Table 3). If losses to follow-up were treated as competing events, the overall 2-year risk of ART initiation was 59% (95% CI: 58.6, 60.0), ranging from 44% in the earliest period to 92% in the most recent period. Figure 1 presents the entire 2-year risk functions estimated using all three approaches in each period.

Table 2.

Outcomes at 2 years since entry into care among 19,506 patients who entered HIV care at one of 15 Central Africa IeDEA sites between 1 January 2006 and 31 December 2017

Outcome	Overall n = 19,506		Patients entering care between 2006 – 2009 n = 7929		Patients entering care between 2010 – 2014 n = 8325		Patients entering care between 2015 – 2017 n = 3252
	n	%	n	%	n	%	n	%
Started ART	12,253	63	3942	50	5438	65	2873	88
Recorded deaths a	192	1.0	79	1.0	98	1.2	15	0.51
Documented transfer to another facility	88	0.54	50	0.63	34	0.43	4	0.12
Lost to follow-up prior to ART	4387	23	2765	35	1478	18	144	4.4
Administratively censored	2586	13	1093	14	1277	15	216	6.6

^aThe reported number of deaths is known to underestimated, as there is likely misclassification between loss to follow-up prior to ART and death.

Table 3.

Risk of ART initiation by 2 years, and subdistribution hazard ratios comparing ART initiation between calendar time periods, among 19,506 patients who entered HIV care at one of 15 Central Africa IeDEA sites between 1 January 2006 and 31 December 2017

Approach	2-year risk, %	95% CI	Subdistribution hazard ratio	95% CI
Censoring at loss to follow-up
Overall	68	68, 69
2006 – 2009	56	55, 58	1
2010 – 2014	72	71, 73	1.4	1.4, 1.5
2015 – 2017	94	93, 95	4.1	3.9, 4.4
Treating loss to follow-up as a competing event
Overall	59	59, 60.0
2006 – 2009	44	43, 45	1
2010 – 2014	65	64, 66	1.8	1.6, 1.7
2015 – 2017	92	91, 93	4.8	4.5, 5.1
Accounting for loss to follow-up using the proposed approach
Overall	62	61, 62
2006 – 2009	47	46, 48	1
2010 – 2014	67	66, 68	1.6	1.5, 1.7
2015 – 2017	93	92, 94	4.8	4.5, 5.1

CI: Confidence interval

Figure 1.

Risk of antiretroviral therapy initiation over 2 years since entry into care among 19,506 patients who entered HIV care at one of 15 Central Africa IeDEA sites between 1 January 2006 and 31 December 2017 after censoring patients lost to follow-up (LTFU; light grey curves), treating loss to follow-up as a competing event (dark grey curves), and accounting for loss to follow-up using the proposed approach (black curves)

Applying the individual values of ${\widehat{\rho }}_i$, the estimated overall 2-year risk of ART initiation was 62% (95% CI: 61.0, 62.3), ranging from 47% in the earliest period to 93% in the most recent period. Under all approaches, subdistribution hazard ratios illustrated the acceleration in ART initiation in later periods. Subdistribution hazard ratios were similar under all approaches considered. Details regarding values of ${\widehat{\rho }}_i$ may be found in eAppendix 2.

In the simulation experiments, handling loss to follow-up using the proposed tracing weights yielded results with smaller bias and root mean squared error than treating loss to follow-up as a censoring or competing event. Moreover, the proposed approach yielded near 95% CI coverage in most scenarios while approaches that treated loss to follow-up as a censoring or competing event produced coverage that was below the nominal level in all scenarios examined. Poor confidence interval coverage among the standard approaches was due primarily to bias; standard errors were similar between the approaches, though the proposed approach yielded standard errors that were slightly larger than the standard approaches, on average.

DISCUSSION

Weighting participants who were lost to follow-up from clinical HIV programs using the proposed approach leverages information from published tracing studies and allows investigators to relax the dubious assumptions inherent in treating loss to follow-up as a censoring event or a competing event. In all calendar time periods examined, applying the tracing weights yielded an estimated probability of ART initiation above that estimated by treating loss to follow-up as a competing event, but below that estimated by censoring patients at loss to follow-up. Simulation experiments confirmed that the proposed approach yields results with little bias and appropriate CI coverage in settings similar to the example.

The proposed approach offers a formal method for incorporating knowledge about the probability of being in care after loss to follow-up into the estimated risk and its confidence interval. This knowledge was encoded in results from tracing studies of people lost to HIV care at specific study sites in Africa. While tracing studies have been used to reduce bias in mortality estimates ^25,26 and estimates of retention in care ^24,27, they have not been widely used to estimate the risk of other outcomes along the continuum of HIV care. Unlike approaches that use external validation data to account for misclassification of the outcome of interest (e.g., ^28,29), here, we propose using these external validation data to account for “misclassification” between a competing event and a censoring event.

In this example, the high proportion of patients experiencing the outcome (here, ART initiation) in each calendar period prior to loss to follow-up limited the difference between results obtained using the proposed approach and other candidate approaches (e.g., treating loss to follow-up as a censoring or competing event). However, as demonstrated in the simulation experiments, when investigating outcomes with substantial loss to follow-up prior to the outcome of interest, the choice of how to handle losses to follow-up will have a more profound impact on the results.

A primary assumption underlying the proposed approach is that the probability of being engaged in care, given that a participant appears to be lost, is the same between the main study sample and the data provided in the tracing studies. This assumption may be relaxed to be conditional on a set of measured variables by including these variables in the model for ${\widehat{p}}_i$. In our example, because the final analysis was stratified by calendar time, we included calendar year in the model for $\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}\left\{p\right\}$ to allow ${\widehat{\rho }}_i$ to vary by person based on her date of loss to follow-up. In general, the model for ${\widehat{\rho }}_i$ should include any variable later stratified upon or used as an exposure, in addition to any factors that are likely to affect the probability of silent transfer and whose distribution varies between the tracing data and the main study data ³⁰. However, the richness of the model for ${\widehat{\rho }}_i$ is limited by the coarseness of the tracing data; in many settings tracing data are available only in aggregate form without individual-level covariates; for example, published tracing data are likely to include only calendar year and geographic setting rather than rich data on participant characteristics. When possible, tracing studies should be designed to collect the individual- and facility-level covariates believed to be associated with the probability of silent transfer to allow quantitative transportability of the findings to other settings. However, in settings where a variable thought to both predict ${\widehat{\rho }}_i$ and differ between the main study and tracing data is not included in the tracing data, one could include that variable in the model for ${\widehat{\rho }}_i$ and place an informative prior distribution on the regression coefficient corresponding to that variable using Markov Chain Monte Carlo or data augmentation. ³¹ Alternatively, one could conduct a sensitivity analysis under presumed values of ${\widehat{\rho }}_i$ within strata of covariates measured in the main study.

The standard approaches ignored the uncertainty in the probability of silent transfer, either treating ${\widehat{\rho }}_i$ as fixed at 0 (i.e., treating loss to follow-up as a competing event) or as fixed at 1 (i.e., censoring at loss to follow-up). In the proposed approach, uncertainty in the estimation of ${\widehat{\rho }}_i$ is propagated through to the final CIs around the estimated risk using the two-stage bootstrap approach defined above, resulting in wider CIs than the standard approaches, in general. However, in the example described in this paper, the widths of the CIs obtained using the proposed approach were not substantially wider than CIs obtained other approaches considered, likely due to the small proportion of patients lost to follow-up prior to ART and the large numbers of participants included in the tracing studies (resulting in low variability around ${\widehat{\rho }}_i$). In eAppendix 3, we illustrated that standard errors estimated under the proposed approach increased as the size of the tracing study decreased, resulting in wider confidence intervals.

Estimates of ${\widehat{\rho }}_i$ are subject to systematic error in addition to random error. In particular, the tracing studies used to estimate ${\widehat{\rho }}_i$ likely suffer from selection bias due to logistical challenges in tracing all participants lost from a specific facility. Methods for addressing systematic error when using estimates from tracing studies is an important area of future research. Simple approaches that could be employed when using the proposed methods include reweighting the relative importance of various tracing studies according to perceived study quality, or calculating bounds ³² on the proportion of silent transfers from tracing studies as part of a sensitivity analysis.

In our example, we presented a descriptive analysis comparing the cumulative incidence of ART initiation in selected Central Africa facilities among three calendar time periods roughly corresponding to eras with different treatment guidelines. Had we wished to estimate a causal effect in a setting with confounding, or generalize or transport results to a different target population, we could have combined the proposed approach with inverse probability of treatment ³³ or sampling ^30,34 weights.

While we focused on an example specific to research in clinical cohorts of people in care for HIV, the proposed approach is relevant beyond HIV. For example, this approach could be used to account for the ambiguity brought about by loss to follow-up from datasets produced by pharmaceutical claims, substance use treatment facilities, school records, employment records, or antenatal care records, among others.

Formal approaches to incorporate external sources of knowledge to address bias in epidemiologic studies are critical to improving inference. With increasing access to clinical data for epidemiologic research, handling inevitable losses to follow-up will be a growing challenge faced by analysts that must be considered carefully in order to minimize bias. The tracing weights proposed here add a weapon to the epidemiologist’s arsenal available for combatting systematic bias in estimates of outcome incidence and associations by integrating external information.