Constructing and adjusting estimates for household transmission of SARS-CoV-2 from prior studies, widespread-testing and contact-tracing data

Abstract

Background

With reduced community mobility, household infections may become increasingly important in SARS-CoV-2 transmission dynamics.

Methods

We investigate the intra-household transmission of COVID-19 through the secondary-attack rate (SAR) and household reproduction number (R_h). We estimate these using (i) data from 29 prior studies (February–August 2020), (ii) epidemiologically linked confirmed cases from Singapore (January–April 2020) and (iii) widespread-testing data from Vo’ (February–March 2020). For (i), we use a Bayesian random-effects model that corrects for reverse transcription–polymerase chain reaction (RT–PCR) test sensitivity and asymptomatic cases. We investigate the robustness of R_h with respect to community transmission rates and mobility patterns.

Results

The corrected pooled estimates from prior studies for SAR and R_h are 24% (20–28%) and 0.34 (0.30–0.38), respectively. Without corrections, the pooled estimates are: SAR = 18% (14–21%) and R_h = 0.28 (0.25–0.32). The corrected estimates line up with direct estimates from contact-tracing data from Singapore [R_h = 0.32 (0.22–0.42)] and population testing data from Vo’ [SAR = 31% (28–34%) and R_h = 0.37 (0.34–0.40)]. The analysis of Singapore data further suggests that the value of R_h (0.22–0.42) is robust to community-spread dynamics; our estimate of R_h stays constant whereas the fraction of infections attributable to household transmission (R_h/R_eff) is lowest during outbreaks (5–7%) and highest during lockdowns and periods of low community spread (25–30%).

Conclusions

The three data-source types yield broadly consistent estimates for SAR and R_h. Our study suggests that household infections are responsible for a large fraction of infections and so household transmission may be an effective target for intervention.

Key Messages

• With reduced mobility, household infections are becoming increasingly important in the transmission of SARS-CoV-2.

• We study two separate quantities that track household transmission: household secondary-attack rate and intra-household reproduction number.

• We pool estimates for both quantities from household-infection studies and add (upwards) corrections for low test sensitivity and lack of asymptomatic testing.

• These corrected estimates line up with central estimates from two disjointed data sources: blanket-testing data from Italy and contact-tracing data from Singapore.

• Our analysis suggests that interventions targeted towards reducing household transmission (e.g. early isolation, encouraging household hygiene, etc.) may be effective at reducing the spread of the virus.

Background

Social distancing and lockdowns reduce community transmission of SARS-CoV-2 but do not directly address household transmission. When social restrictions are in peak use, household infections become increasingly important in percentage terms of virus transmission. Prior studies^1–13 find that household members have a higher risk of infection compared with other contacts, with spouses being most likely and children being least likely to get infected. Existing meta-estimates of the secondary-attack rate (SAR) for COVID-19 fall in the 15–19% range.¹⁴ In comparison, estimates of SAR for the MERS-CoV and SARS-CoV-1 epidemics were 3–3.5× and 2–2.5× smaller, respectively.¹⁴ In addition, estimates of SAR for COVID-19 do not account for selective testing of (symptomatic) household members and test sensitivity, and can thus underestimate viral spread.

Methods

The dynamics of disease spread are described via the effective reproduction number R, which measures the average number of new infections caused by each infected person i. To quantify household transmission, we decompose R into two components: R = R_c + R_h. The community (respectively, intra-household) reproduction number R_c (respectively, R_h) is the average number of infections caused by an infected individual outside (respectively, inside) their household. The ratio R_h/R measures the fraction of transmission occurring within households. In addition to R_h, we consider household SAR: the probability that an infected person i infects a specific household member j. SAR measures the prevalence of infection among susceptible individuals, whereas R_h measures the growth of infection within households.

Estimation methodology

Estimating these metrics requires household-level data. Specifically, we need:

• Test results (positive and negative) for all household members.

• Properly attributed household-infection data, i.e. identifying primary cases and constructing household-transmission chains.

• End-of-study outcomes—if there are still active cases at termination, the data may undercount the number of infections attributed to the case.

Assuming these are available, SAR can be estimated as the ratio of secondary household cases to susceptible household members, and R_h can be estimated as the ratio of secondary household infections to total household cases (unlike household SAR, R_h does not require negative case counts).

Challenges in estimation

In practice, estimating R_h and SAR is made difficult by (i) asymptomatic infections (asymptomatic cases may constitute 18–43% of all infections,^15–19 yet studies predominantly test symptomatic individuals) and (ii) the low sensitivity of standard tests [reverse transcription–polymerase chain reaction (RT–PCR) tests have near-perfect specificity,²⁰ but low and time-varying sensitivity—average sensitivity in the 10 days following symptom onset is estimated as 83% by²¹ and 70% by²²]. Sensitivity also varies between different swab types²¹ and testing facilities.²²

Many recent studies of household transmission do not adjust estimates of SAR for low test sensitivity and asymptomatic cases. To address this, we adjust all our estimates based on literature-inferred priors for sensitivity and asymptomatic rates.

Data sources and estimation procedure

We propose two approaches for estimating R_h and SAR while accounting for asymptomatic cases and test sensitivity: (i) adjusting and aggregating estimates from prior work and (ii) constructing (corrected) direct estimates from COVID case data. For the former, we use a random-effects model to pool estimates from previous studies, correcting for sensitivity and asymptomatic cases. For the latter, we estimate R_h and SAR using a blanket-testing data set from Vo’, Italy,¹⁵ and estimate R_h using a data set of epidemiologically linked cases based on scraping publicly available contact-tracing data from Singapore.^23,24 As estimates from these distinct data sources (previous studies, blanket testing and contact tracing) rely on different assumptions, general agreement between them supports the robustness of our conclusions.

Estimates from previous studies

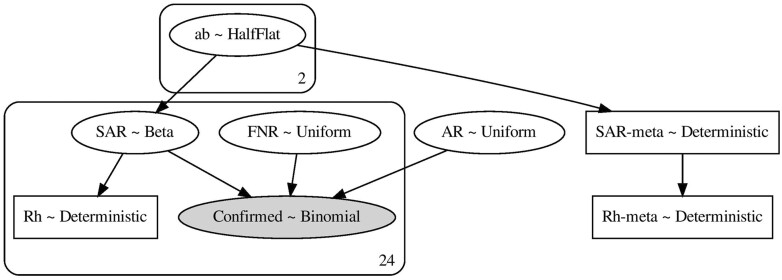
We found 29 household-transmission studies^{1–9,11–13,25–41} satisfying our selection criteria (see Supplementary Figure S1, available as Supplementary data at IJE online, for PRISMA⁴² diagram). Of these studies, nine tested all household contacts multiple times over the observation period. The remaining 21 performed single testing and require adjustments to correct for the undercounting of secondary cases due to RT–PCR false negatives. Out of them, eight tested only symptomatic contacts and thus require corrections that account for the selective testing. We use a Bayesian random-effects model with a per-study false-negative rate (FNR, equal to 1-sensitivity) and a global asymptomatic rate (AR): both are sampled from study-informed weak priors. We model the probability of the i^th study with I_i index cases and N_i household contacts observing P_i positive tests as Binomial[n = N_i, p = SAR_i · (1 – FNR_i) · (1 – AR)]. By fitting the random-effects model, we obtain a posterior distribution for SAR_i conditioned on the data. We compute corrected counts of secondary cases $\stackrel{-}{P_i}$ as the product of $\stackrel{-}{SA{R}_i}$ and N_i, where $\stackrel{-}{SA{R}_i}$ is a random sample from the posterior probability of SAR from the i^th study. Using these corrected counts$\stackrel{-}{P_i}$, we can estimate the corrected household reproduction number for the i^th study, (R_h)_i, as $\frac{{\stackrel{-}{P}}_i}{{\stackrel{-}{P}}_i+I_i}.$ See Figure 1 for a graphical representation of the model (a textual description is given in the Supplementary Material, available as Supplementary data at IJE online).

Figure 1.

A schematic of the Bayesian graphical model for computing the pooled estimates of SAR and R_h. Inference was performed via MCMC sampling using PyMC 3.4 with the built-in NUTS sampler. The sampler used eight chains with 2000 iterations each. The burn-in period is 2000. MCMC, Markov Chain Monte Carlo; NUTS, No U-Turn Sampler; PyMC, Python package for Bayesian statistical modelling.

Assumptions/limitations

The model assumes that all infections among household contacts are attributed to the index case. This assumption might inflate the SAR estimate (it treats tertiary transmissions as secondary) but is inevitable, since studies do not distinguish between secondary and tertiary cases. Another limitation is that most studies do not stratify based on household sizes and thus the model treats infection probability as independent of household size.

Direct estimate from contact-tracing data

We scraped a dashboard²⁴ of Singapore’s contact-tracing data²³ and extracted metadata for each positive case, including an undirected 6588-patient graph providing information about epidemiologically linked cases. Confirmation dates for cases ranged from 23 January to 19 April 2020.

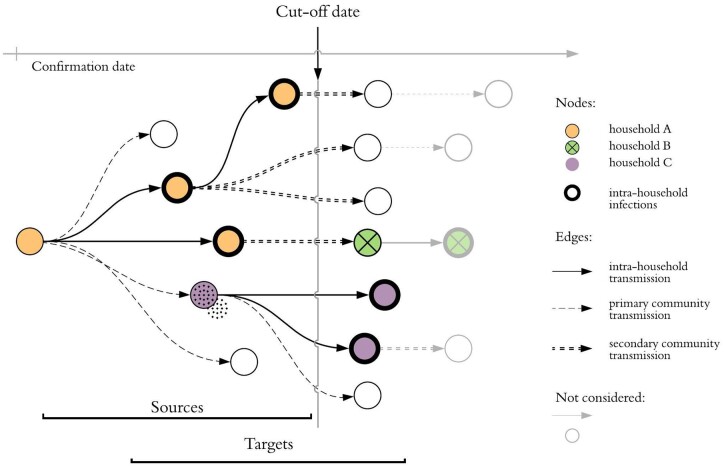
We consider two cases epidemiologically linked if there is a direct edge between them (Case i—Case j) or if they are connected via a cluster (Case i—Cluster A—Case j). We then label each case as a ‘source’ case, a ‘target’ case or both. A source case is any case with a confirmation date before a given cut-off date t. For each source, the corresponding target cases are the epidemiologically linked cases that have a confirmation date between 0 and 14 days after that of the source. Target cases with confirmation date ≤t (i.e. before the cut-off date) are thus labelled as both source and target. A schematic of the labelling procedure is shown in Figure 2.

Figure 2.

Schematic infection graph: nodes represent positive cases and their horizontal position indicates confirmation date. We consider the subset of the graph containing cases with confirmation date prior to the cut-off date: target nodes are infected by sources. R can be estimated as R = (number of targets)/(number of sources) and hence R = 13/7 for this cluster. There are three distinct households in the cluster and thick borders denote secondary household infections. The household reproductive number is R_h = 5/7. R, reproduction number; R_h, intra-household reproduction number.

We selected a cut-off date t of 27 March 2020 based on two criteria: (i) t should pre-date the large worker dormitory outbreaks in Singapore, which made accurate contact tracing difficult;⁴³ and (ii) t should be more than 2 weeks prior to the last confirmation date in the data set, to avoid undercounting target cases due to end-of-study truncation bias. The resulting subset of the infection graph contains 710 cases: 417 sources and 599 targets (306 nodes are labelled as both source and target).

The average effective reproduction rate R_eff can be estimated as the ratio of target cases to source cases. When there is a direct edge between two cases, the edge annotation reflects the relationship between them. R_h can be thus estimated as the ratio of the total number of household targets to the total number of source cases. Since there is no annotation for ‘household’, we use the annotation ‘family member’ as a proxy. This assumption may inflate or deflate R_h: we do not observe partners and roommates, but we do observe family members not residing in the same household. We obtain upper and lower reproduction number central estimates by varying how the untraced cases (singletons) are labelled.

Assumptions/limitations

Just as for the prior studies, the Singapore contact-tracing data cannot be used to distinguish between secondary and tertiary cases in a household, as infected household members are typically interconnected with an undirected edge in the graph. However, unlike the prior study data, the Singapore data set does not contain information about household sizes of confirmed cases, making the estimation of SAR impossible. Asymptomatic transmission is not a substantial issue for counting the number of household infections, as all household members of confirmed cases are typically tested. We do, however, correct for test sensitivity assuming an FNR of 20%.

Direct estimates from blanket-testing data. Most of the population in the town of Vo’, Italy, was tested both at the start of a lockdown and 14 days later.¹⁵ The two phases of testing covered 86% (2812 subjects) and 72% (2343 subjects) of the population in Vo’, respectively. After filtering for truncation bias (cf. Appendix), there are 53 primary cases, 23 secondary cases and 84 susceptible individuals.

The household SAR is again estimated as the ratio of secondary cases to total susceptible individuals, and R_h as the ratio of targets to sources (as was done for Singapore). We label the cases that are confirmed during the first round of testing (73 cases) as sources and the secondary cases attributed to one of the source cases (23 cases) as targets. The second testing date thus acts as a cut-off date for labelling cases as sources and targets.

We adjust our estimates for test sensitivity by using point estimates of sensitivity and AR derived from the data. Asymptomatic cases were 41% of the confirmed cases and, out of subjects residing in households with at least one confirmed case, four have experienced symptoms but have tested negative. This yields 5.7 [4 × (1 + 0.41)] expected false negatives, which corresponds to a test sensitivity of 78%.

Results

Estimates from previous studies

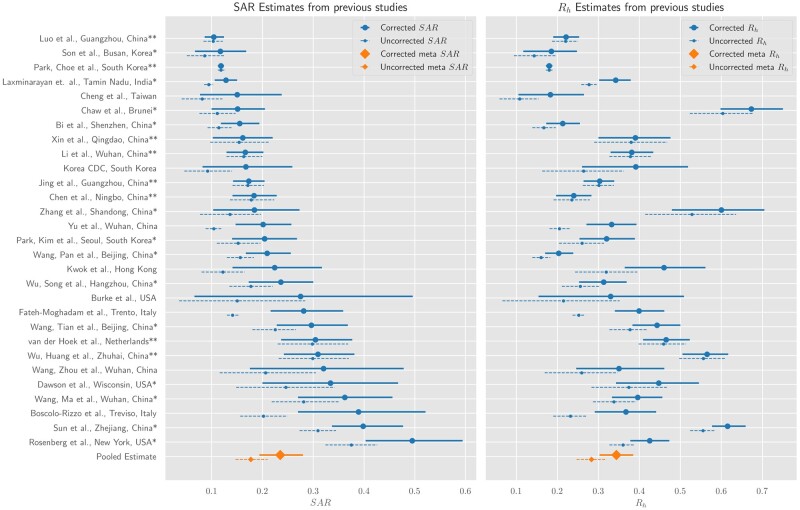
Fitting a random-effects model to the data from the 29 studies yields a pooled corrected SAR estimate of 24% (95% confidence interval: 20–28%) and an R_h estimate of 0.34 (0.3–0.38). Without corrections for asymptomatic cases and test sensitivity, the pooled estimates for SAR and R_h are 18% (14–21%) and 0.28 (0.25–0.32). Study-level SAR and R_h are shown in Figure 3 and Table 1, and precise counts and estimates in Table 2. We find substantial heterogeneity in the SAR and R_h estimates across studies. Moreover, the relative orderings of studies by SAR and R_h are considerably different. To gain further insight, we stratify the studies based on location (see Supplementary Figures S2 and S3, available as Supplementary data at IJE online), average household size (see Supplementary Figure S4, available as Supplementary data at IJE online) and stringency of the mitigation strategy (see Supplementary Figure S5, available as Supplementary data at IJE online). Both metrics are smaller in East Asian countries [22 studies, SAR: 21% (17–25%), R_h: 0.30 (0.26–0.34)] compared with other countries [7 studies: SAR: 33% (20–46%), R_h: 0.48 (0.38–0.57)] (see Table 1). More stringent preventative measures correspond to decreases in both metrics: for 13 studies that placed contacts in quarantine, SAR and R_h were 21% (16–28%) and 0.30 (0.24–0.36) compared with 26% (20–32%) and 0.43 (0.37–0.49) for 16 studies that did not (see Table 1). A subgroup analysis based on average household size partially explains why the relative ordering of studies varies when ranking by SAR and by R_h: the 10 studies with small average household sizes (<2.9 members) had higher SAR: 29% (19–40%), but lower R_h: 0.34 (0.25–0.41) than the 9 studies with large average household size (>4) where SAR: 22% (15–30%) and R_h: 0.48 (0.40–0.57) (see Table 1). Other potential causes contributing to heterogeneity include both intrinsic demographic variation (e.g. age distributions) and extrinsic factors (e.g. ventilation and hygiene). Graphical illustrations of all subgroup analyses are given in the Supplementary data at IJE online.

Figure 3.

Adjusted literature estimates for SAR and R_h. Dashed lines show estimates from the original studies. Solid lines show 95% credible intervals from a Bayesian hierarchical model, which adjusts estimates for false negatives and asymptomatics where appropriate. The meta-estimates refer to the pooled estimate for SAR and R_h. In the left plot, the meta-estimate (orange) are the model’s credible intervals for the pooled SAR. If a study has a single asterisk, this means it was unnecessary to adjust for asymptomatics (only false negatives). The double asterisk means no adjustment was necessary. R_h, intra-household reproduction number; SAR, household secondary-attack rate.

Table 1.

Literature estimates: this table contains study-level data for the number of index cases, secondary cases and total household contacts

Name	Index cases	Secondary infections	Household contacts	Average household	SAR (corrected)	SAR (uncorrected)	Rh (corrected)	Rh (uncorrected)	Correction	Contacts quarantined
Bi et al., Shenzhen, China*	391	77	686	2.75	16% (12–20%)	11% (9–14%)	0.21 (0.17––0.26)	0.17 (0.14–0.20)	FNR	False
Boscolo-Rizzo et al., Treviso, Italy	179	54	269	2.5	36% (25–48%)	20% (15–24%)	0.35 (0.28–0.42)	0.23 (0.19–0.27)	AR/FNR	True
Burke et al., USA	10	2	19	2.9	22% (7–40%)	14% (4–25%)	0.29 (0.14–0.44)	0.21 (0.09–0.33)	AR/FNR	True
Chaw et al., Brunei*	19	28	264	14.89	15% (10–21%)	11% (8–15%)	0.67 (0.59–0.75)	0.60 (0.52–0.68)	FNR	True
Chen et al., Ningbo, China**	157	49	272	2.73	18% (14–23%)	18% (14–22%)	0.24 (0.20–0.28)	0.24 (0.19–0.28)	–	False
Cheng et al., Taiwan	100	10	151	2.51	15% (8–23%)	8% (4–12%)	0.18 (0.10–0.26)	0.11 (0.06–0.15)	AR/FNR	True
Dawson et al., Wisconsin, USA*	26	16	64	3.46	31% (19–43%)	23% (15–32%)	0.43 (0.33–0.52)	0.36 (0.27–0.45)	FNR	False
Fateh-Moghadam et al., Trento, Italy	1489	500	3546	3.38	27% (21–34%)	14% (13–15%)	0.39 (0.33–0.45)	0.25 (0.24–0.27)	AR/FNR	True
Jing et al., Guangzhou, China**	215	93	542	3.52	17% (14–20%)	17% (14–20%)	0.30 (0.27–0.34)	0.30 (0.26–0.34)	–	False
Korea CDC, South Korea	30	9	119	4.96	17% (8–26%)	9% (5–14%)	0.39 (0.27–0.53)	0.26 (0.16–0.36)	AR/FNR	False
Kwok et al., Hong Kong	53	24	206	4.88	23% (14–32%)	12% (8–16%)	0.47 (0.36–0.56)	0.32 (0.25–0.40)	AR/FNR	True
Laxminarayan et. al., Tamin Nadu, India*	997	380	4066	5.07	13% (11–15%)	9% (8–10%)	0.34 (0.30–0.38)	0.28 (0.26–0.29)	FNR	False
Li et al., Wuhan, China**	105	64	392	4.73	17% (13–20%)	16% (13–20%)	0.38 (0.33–0.43)	0.38 (0.33–0.43)	–	True
Luo et al., Guangzhou, China**	347	96	946	3.72	10% (9–12%)	10% (8–12%)	0.22 (0.19–0.25)	0.22 (0.19–0.25)	–	True
Park, Choe et al., South Korea**	5706	1250	10 592	2.85	12% (11–12%)	12% (11–12%)	0.18 (0.17–0.19)	0.18 (0.17–0.19)	–	True
Park, Kim et al., Seoul, South Korea*	97	34	225	3.31	21% (14–27%)	15% (11–20%)	0.32 (0.25–0.39)	0.26 (0.21–0.32)	FNR	True
Rosenberg et al., New York, USA*	229	131	343	2.49	47% (39–56%)	37% (32–42%)	0.41 (0.37–0.46)	0.36 (0.33–0.39)	FNR	False
Son et al., Busan, Korea*	108	16	212	2.96	12% (7–17%)	8% (5–12%)	0.18 (0.12–0.25)	0.14 (0.09–0.20)	FNR	False
Sun et al., Zhejiang, China*	148	189	598	5.04	41% (34–48%)	31% (28–35%)	0.62 (0.58–0.66)	0.56 (0.53–0.58)	FNR	False
Wang, Ma et al., Wuhan, China*	85	47	155	2.82	38% (28–48%)	29% (22–36%)	0.41 (0.34–0.47)	0.34 (0.29–0.40)	FNR	True
Wang, Pan et al., Beijing, China*	585	111	714	2.22	21% (17–26%)	16% (13–18%)	0.20 (0.17–0.24)	0.16 (0.14–0.18)	FNR	True
Wang, Tian et al., Beijing, China*	124	77	335	3.7	30% (23–38%)	23% (18–27%)	0.45 (0.39–0.51)	0.38 (0.33–0.42)	FNR	False
Wang, Zhou et al., Wuhan, China	25	10	43	2.72	35% (18–52%)	21% (12–31%)	0.37 (0.25–0.48)	0.27 (0.17–0.36)	AR/FNR	False
Wu, Huang et al., Zhuhai, China**	35	48	148	5.22	32% (24–38%)	30% (24–38%)	0.57 (0.51–0.62)	0.56 (0.50–0.61)	–	False
Wu, Song et al., Hangzhou, China*	144	50	280	2.94	24% (17–31%)	18% (14–22%)	0.32 (0.26–0.38)	0.26 (0.21–0.30)	FNR	False
Xin et al., Qingdao, China**	31	19	125	5.03	16% (10–23%)	16% (10–21%)	0.39 (0.30–0.48)	0.38 (0.29–0.47)	–	False
Yu et al., Wuhan, China	560	143	1396	3.49	20% (14–26%)	10% (9–12%)	0.33 (0.27–0.39)	0.20 (0.18–0.23)	AR/FNR	True
Zhang et al., Shandong, China*	11	12	93	9.45	19% (10–28%)	14% (7–20%)	0.60 (0.48–0.71)	0.53 (0.42–0.64)	FNR	False
van der Hoek et al., Netherlands**	54	47	155	3.87	30% (23–37%)	29% (22–35%)	0.46 (0.40–0.52)	0.45 (0.39–0.50)	–	False
Global meta-estimate	12060	3586	26 956	3.23	24% (20–28%)	18% (14–21%)	0.34 (0.30–0.38)	0.28 (0.25–0.32)
China	2963	1085	6725	3.27	24% (19–30%)	19% (15–24%)	0.35 (0.30–0.41)	0.30 (0.26–0.35)
Not China	9097	2501	20 231	3.22	24% (17–32%)	17% (12–22%)	0.35 (0.28–0.42)	0.27 (0.21–0.33)
East Asia	9076	2456	18 494	3.04	21% (17–26%)	16% (13–20%)	0.30 (0.26–0.34)	0.25 (0.21–0.29)
Not East Asia	2984	1130	8462	3.83	33% (21–46%)	23% (14–34%)	0.48 (0.39–0.57)	0.39 (0.29–0.50)
Small household	7467	1741	13 244	2.77	29% (19–40%)	20% (13–27%)	0.34 (0.25–0.41)	0.26 (0.20–0.33)
Medium households	3164	1072	7701	3.43	23% (16–30%)	18% (12–23%)	0.35 (0.29–0.42)	0.30 (0.24–0.36)
Large households	1429	773	6011	5.21	22% (15–30%)	18% (12–25%)	0.48 (0.40–0.57)	0.42 (0.33–0.52)
Contacts quarantined	9335	2363	18 875	3.02	21% (16–28%)	14% (11–18%)	0.30 (0.24–0.36)	0.23 (0.19–0.27)
Contacts not quarantined	2725	1223	8081	3.97	26% (20–32%)	21% (15–26%)	0.43 (0.37–0.49)	0.38 (0.32–0.44)

It includes estimates and 95% confidence intervals of study-level SAR and R_h (with and without AR/FNR adjustments). The weight columns contain the contribution of each study towards the meta-estimate. A high SAR value does not always imply a high R_h value, or vice versa. SAR measures the prevalence of infection among susceptible individuals, whereas R_h measures the growth of infection within households. The relationship between the two measures is described by the equation: SAR = R_h × (#total infected)/(#susceptible). Assuming a fixed ratio of primary to secondary infections, SAR is inversely proportional to the relative number of susceptible individuals. Studies that have larger numbers of susceptible members (larger average household size) tend to have smaller SAR values. Conversely, studies that have smaller household sizes tend to have larger SAR values.

Table 2.

Estimates for effective reproductive number R_eff and household reproductive number R_h, computed for different values of cut-off date: for each cut-off date, we count the number of cases assigned as sources and targets

Cut-off date	Sources	Targets	Household targets	Untraced	Reff	R h	Ratio
Jan-26	4	16	3	0	4.00 [4.00–4.00]	0.94 (0.64–1.23)	0.23
Jan-27	7	16	3	0	2.29 [2.29–2.29]	0.54 (0.34–0.73)	0.23
Jan-28	8	22	4	0	2.75 [2.75–2.75]	0.62 (0.43–0.82)	0.23
Jan-29	12	22	4	0	1.83 [1.83–1.83]	0.42 (0.26–0.57)	0.23
Jan-30	16	27	4	0	1.69 [1.69–1.69]	0.31 (0.18–0.45)	0.19
Jan-31	17	27	4	0	1.59 [1.59–1.59]	0.29 (0.17–0.42)	0.19
Feb-1	18	27	4	0	1.50 [1.50–1.50]	0.28 (0.16–0.40)	0.19
Feb-2	18	27	4	0	1.50 [1.50–1.50]	0.28 (0.16–0.40)	0.19
Feb-3	22	35	7	0	1.59 [1.59–1.59]	0.40 (0.26–0.54)	0.25
Feb-4	26	35	7	0	1.35 [1.35–1.35]	0.34 (0.21–0.46)	0.25
Feb-5	28	35	7	1	1.25 [1.21–1.29]	0.31 (0.17–0.46)	0.25
Feb-6	31	37	7	2	1.19 [1.12–1.26]	0.28 (0.15–0.42)	0.24
Feb-7	33	37	7	4	1.12 [1.00–1.24]	0.27 (0.14–0.39)	0.24
Feb-8	38	42	8	5	1.11 [0.98–1.24]	0.26 (0.15–0.38)	0.24
Feb-9	39	42	8	5	1.08 [0.95–1.21]	0.26 (0.14–0.37)	0.24
Feb-10	41	42	8	6	1.02 [0.89–1.17]	0.24 (0.13–0.35)	0.24
Feb-11	43	64	11	6	1.49 [1.31–1.63]	0.32 (0.21–0.43)	0.21
Feb-12	47	67	13	6	1.43 [1.26–1.55]	0.35 (0.24–0.45)	0.24
Feb-13	56	68	13	6	1.21 [1.10–1.32]	0.29 (0.19–0.39)	0.24
Feb-14	61	71	14	7	1.16 [1.04–1.28]	0.29 (0.18–0.39)	0.25
Feb-15	67	72	15	7	1.07 [0.97–1.18]	0.28 (0.18–0.38)	0.26
Feb-16	69	73	15	7	1.06 [0.96–1.16]	0.27 (0.17–0.37)	0.26
Feb-17	72	73	15	7	1.01 [0.92–1.11]	0.26 (0.17–0.36)	0.26
Feb-18	75	74	15	7	0.99 [0.90–1.08]	0.25 (0.16–0.34)	0.25
Feb-19	77	74	15	7	0.96 [0.88–1.05]	0.24 (0.15–0.34)	0.25
Feb-20	78	74	15	8	0.95 [0.86–1.05]	0.24 (0.15–0.33)	0.25
Feb-21	80	74	15	8	0.93 [0.84–1.02]	0.23 (0.14–0.32)	0.25
Feb-22	81	74	15	9	0.91 [0.82–1.02]	0.23 (0.14–0.32)	0.25
Feb-23	82	74	15	9	0.90 [0.81–1.01]	0.23 (0.14–0.32)	0.25
Feb-24	82	74	15	9	0.90 [0.81–1.01]	0.23 (0.14–0.32)	0.25
Feb-25	82	74	15	9	0.90 [0.81–1.01]	0.23 (0.14–0.32)	0.25
Feb-26	84	130	24	10	1.55 [1.38–1.67]	0.36 (0.27–0.45)	0.23
Feb-27	87	131	24	10	1.51 [1.35–1.62]	0.34 (0.26–0.43)	0.23
Feb-28	90	131	24	10	1.46 [1.31–1.57]	0.33 (0.25–0.42)	0.23
Feb-29	92	132	24	10	1.43 [1.29–1.54]	0.33 (0.24–0.41)	0.23
Mar-1	97	133	24	10	1.37 [1.24–1.47]	0.31 (0.23–0.39)	0.23
Mar-2	100	134	24	10	1.34 [1.22–1.44]	0.30 (0.22–0.38)	0.22
Mar-3	100	134	24	11	1.34 [1.21–1.45]	0.30 (0.22–0.38)	0.22
Mar-4	102	134	24	12	1.31 [1.18–1.43]	0.29 (0.22–0.37)	0.22
Mar-5	110	134	24	14	1.22 [1.08–1.35]	0.27 (0.20–0.35)	0.22
Mar-6	121	136	25	17	1.12 [0.99–1.26]	0.26 (0.19–0.33)	0.23
Mar-7	126	148	26	18	1.17 [1.03–1.32]	0.26 (0.18–0.33)	0.22
Mar-8	133	149	27	20	1.12 [0.97–1.27]	0.25 (0.18–0.32)	0.23
Mar-9	142	149	27	21	1.05 [0.91–1.20]	0.24 (0.17–0.31)	0.23
Mar-10	148	155	29	22	1.05 [0.91–1.20]	0.24 (0.18–0.31)	0.23
Mar-11	155	158	29	24	1.02 [0.88–1.17]	0.23 (0.17–0.30)	0.23
Mar-12	163	167	31	26	1.02 [0.88–1.18]	0.24 (0.18–0.30)	0.23
Mar-13	174	178	32	30	1.02 [0.87–1.20]	0.23 (0.17–0.29)	0.22
Mar-14	181	183	34	38	1.01 [0.84–1.22]	0.23 (0.18–0.29)	0.23
Mar-15	190	199	43	42	1.05 [0.86–1.27]	0.28 (0.22–0.35)	0.27
Mar-16	201	203	44	46	1.01 [0.82–1.24]	0.27 (0.21–0.33)	0.27
Mar-17	220	216	51	67	0.98 [0.75–1.29]	0.29 (0.23–0.35)	0.3
Mar-18	237	222	53	87	0.94 [0.69–1.30]	0.28 (0.23–0.33)	0.3
Mar-19	253	228	57	110	0.90 [0.63–1.34]	0.28 (0.22–0.34)	0.31
Mar-20	269	242	62	140	0.90 [0.59–1.42]	0.29 (0.23–0.34)	0.32
Mar-21	282	256	64	168	0.91 [0.57–1.50]	0.28 (0.23–0.34)	0.31
Mar-22	294	265	67	209	0.90 [0.53–1.61]	0.28 (0.23–0.34)	0.32
Mar-23	306	300	79	224	0.98 [0.57–1.71]	0.32 (0.26–0.38)	0.33
Mar-24	338	337	86	265	1.00 [0.56–1.78]	0.32 (0.23–0.41)	0.32
Mar-25	368	572	94	292	1.55 [0.87–2.35]	0.32 (0.23–0.41)	0.21
Mar-26	395	585	102	319	1.48 [0.82–2.29]	0.32 (0.22–0.42)	0.22
Mar-27	417	599	108	366	1.44 [0.77–2.31]	0.32 (0.22–0.42)	0.23
Mar-28	444	2105	109	387	4.74 [2.53–5.61]	0.31 (0.21–0.40)	0.06
Mar-29	465	2120	117	402	4.56 [2.45–5.42]	0.31 (0.22–0.40)	0.07
Mar-30	489	2333	127	419	4.77 [2.57–5.63]	0.32 (0.24–0.41)	0.07
Mar-31	520	2566	134	446	4.93 [2.66–5.79]	0.32 (0.24–0.40)	0.07
Apr-1	565	2658	137	461	4.70 [2.59–5.52]	0.30 (0.22–0.38)	0.06
Apr-2	608	3228	142	473	5.31 [2.99–6.09]	0.29 (0.22–0.37)	0.05
Apr-3	669	3274	147	498	4.89 [2.81–5.64]	0.27 (0.20–0.34)	0.06
Apr-4	688	3276	147	501	4.76 [2.76–5.49]	0.27 (0.20–0.34)	0.06
Apr-5	783	3293	157	526	4.21 [2.52–4.88]	0.25 (0.19–0.31)	0.06
Apr-6	839	3298	159	537	3.93 [2.40–4.57]	0.24 (0.18–0.29)	0.06
Apr-7	975	3835	163	595	3.93 [2.44–4.54]	0.21 (0.16–0.26)	0.05

Among the targets, we identify cases that are linked to infected household members. The ‘Untraced’ column contains the number of cases in the data with a confirmation date prior to the cut-off date that are not linked to any other cases. In the case of R_eff, the square brackets are not confidence intervals, but rather upper and lower bounds on R_eff, depending on how the untraced cases are labelled (labelling as sources yields a lower bound and labelling as targets yields an upper bound on the central estimate for R_eff).

Estimates from Singapore contact-tracing data

Our estimate for the reproduction number R (see ‘Methods’) is (number of target nodes)/(number of source nodes) = 599/417 = 1.44 (0.77–2.31). There are 108 household infections in the graph, yielding an uncorrected estimate of R_h and binomial confidence intervals of 108/417 = 0.26 (0.23–0.29). After correcting for test sensitivities, the resulting corrected estimate for R_h is 0.36 (0.24–0.48).

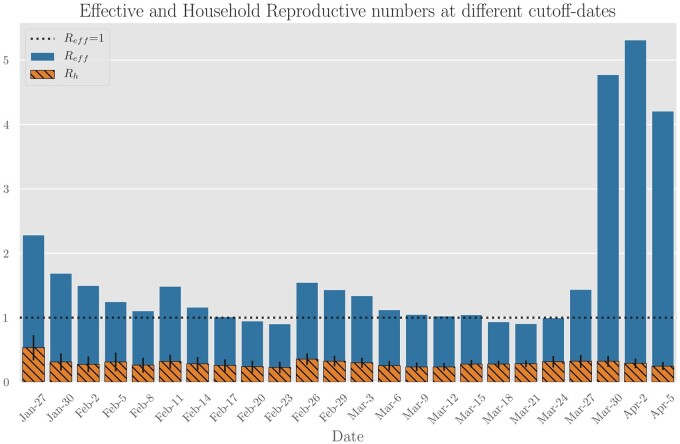
We repeated the calculations for various values of cut-off date t to ensure that our estimates are robust to the choice of t. Figure 4 contains estimates for cut-off dates other than 27 March; estimates for R_eff range between 0.90 and 4.93, and estimates of corrected R_h ranges from 0.19 to 0.34. The fraction of cases attributable to household infection (R_h/R) ranges from 0.20 to 0.30.

Figure 4.

Aggregate estimates of effective and household reproduction numbers in Singapore based on contact-tracing data while varying the cut-off date (i.e. the date after which source infections are ignored). Household transmission appears to stay constant, with the intra-household reproduction number in the 0.2–0.3 range. The ratio of infections attributable to households decreases sharply at the end of March due to large outbreaks in migrant-worker dormitories. Even though their infections are not annotated as households, this suggests that cohabitation and proximity play a large role in transmission dynamics.

Estimates from Vo’s blanket-testing data

Our estimation procedure yields an uncorrected estimate for SAR of 27% (24–30%) and R_h of 0.32 (0.28–0.36). With the FNR and AR correction described in ‘Methods’, the corrected estimates are SAR = 31% (28–34%) and R_h = 0.37 (0.34–0.40).

A subgroup analysis suggests that testing did not decrease the household transmission due to early isolation. The SAR associated with 10 households where the first household member had symptoms a week prior to the test date is essentially unchanged at 26%. Our analysis may overestimate the SAR in Vo’ due to violations of single index case assumptions and the presence of additional household infections attributable to community spread. However, due to smaller-than-typical household sizes of 2.1, we expect that such violations are infrequent. We expect Vo’s SAR and R_h estimates to be larger than those of other locations due to an older population, lack of risk awareness and insufficient protective measures in early February.

The contribution of household transmission to R

Central estimates for R_h based on literature estimates, contact-tracing data and blanket-testing data varied from 0.36–0.39. We now estimate how much household transmission contributes to overall transmission levels, i.e. the ratio of the effective household reproductive number R_h to the total effective reproductive number R.

For Singapore, we estimate that R_h is 19–34% of R, meaning that household infections account for 19–34% of total disease transmission.

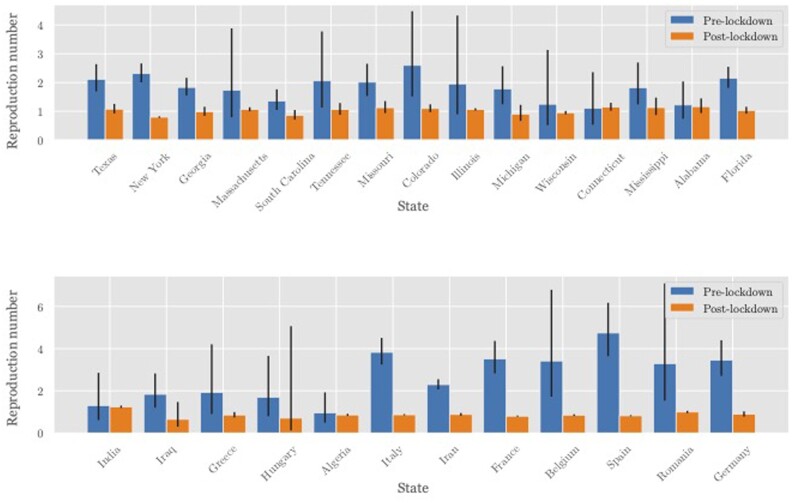
For other geographic regions, we model R_h = 0.3 pre lockdown (based on the previous section) and R_h = 0.3 · M post lockdown, where M is the time spent at home relative to pre lockdown (e.g. M = 1.11 for the USA⁴⁴). We estimate the pre- and post-lockdown R from death-count data across regions where enough data were available for both time periods (Figure 5).

Figure 5.

Estimated values of the reproduction number R pre and post lockdown in a subset of US states (top) and other countries (bottom). The growth rate was estimated from daily death statistics to avoid testing bias. This was translated into a reproduction number R via the generation time distribution;³ 95% confidence intervals are shown. R, reproduction number; US, United States of America.

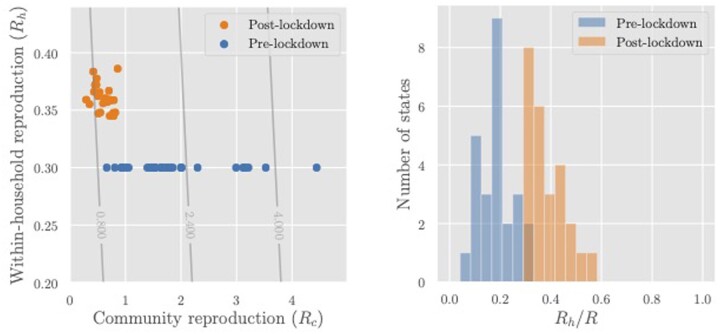
Figure 6 (left) plots the community reproduction number (R – R_h) against R_h for each region both pre and post lockdown. Figure 6 (right) shows a histogram of the estimated contribution of household transmission to the total reproduction number (R_h/R) pre and post lockdown. The share of R attributed to household transmission increased to 25–50% post lockdown, indicating that there may be meaningful benefits (in terms of overall transmission) from interventions that reduce R_h.

Figure 6.

Left: Reproduction numbers for community transmission (R_c) and intra-household transmission (R_h) for the regions whose R values are shown in Figure 4. The overlaid contour plot shows level sets of the overall reproduction number R = R_h + R_c. Right: Estimated share of transmission attributable to household infections (Rh/R). In both graphs, Rh = 0.3 pre lockdown is assumed. Post-lockdown R_h of an area is calculated by multiplying the pre-lockdown value with a mobility factor M obtained from Google’s estimates of the average time spent in residential areas. R_c, community reproduction number; R_h, intra-household reproduction number; R, reproduction number; M, mobility factor (increase in mobility post lockdown).

Discussion

Should non-pharmaceutical interventions (NPIs) target household transmission?

In order for households to be a fruitful target for policy interventions, household transmissions should (i) play a role in disease spread, (ii) be amenable to intervention (i.e. preventable in practice) and (iii) have potential for downstream community transmissions. Our estimates in the previous sections suggest that, for SARS-CoV-2, condition (i) is satisfied. We now turn our attention to the other two conditions.

(ii) Is household transmission inevitable? The data suggest that household transmission is not inevitable in the strictest sense—SAR is lower than 100%, even after adjustments.

There is also evidence that SAR can be reduced by behavioural interventions. Wang et al. al.³⁵ found that the SAR was lower in households where people wore masks at home, cleaned regularly with disinfectant and avoided close contact with the primary cases. Li et al.³² found that the SAR was 0% for households where the primary case was isolated on symptom onset compared with 16.9% (uncorrected) without isolation. Our subgroup analysis of quarantine status also suggests that isolation of cases and quarantine can be effective for reducing household transmission.

(iii) Is household transmission contained? Interventions targeting household transmission would also have little effect if secondary cases resulted in no downstream community infections. Since we cannot reliably attribute community infections to primary vs secondary household cases in our data, we instead discuss the key factors distinguishing secondary cases from primary cases in terms of downstream effects:

1. Demographic variability, e.g. household infections may skew towards children, whose transmission dynamics differ from those of adults.^45,46

2. Community exposure, e.g. household infections are more likely to be from high- to low-exposure individual(s), who may have a lesser effect on community transmission. Contact patterns⁴⁷ and the large number of essential workers⁴⁸ suggest that this will dampen but not nullify the effect of household transmission.

3. Early isolation : household members may notice the source’s symptoms and self-isolate early, preventing downstream community transmission. However, this is in fact a household NPI, and thus its success actually supports rather than detracts from the effectiveness of household interventions.

Overall, our results suggest that households may indeed be a worthwhile intervention point and motivate further study into quantifying containment.

Implications for modelling

Our estimates can also inform simulated models of SARS-CoV-2 dynamics (e.g.^46,49–51). These models often inform policy^17,52,53 but common estimates of average transmission risk are often in the 0.5–0.8 range.⁵⁴ Our estimates of household SAR suggest that these estimates are likely implausible, as households present, on average, one of the highest risks of infection among contacts (high duration indoors); household SAR is thus a likely upper bound on the average transmission risk.

Limitations and conclusions

Being an observational study, the primary limitation of our work lays in the gathered data and, more specifically, the assumptions that we must put on the data to facilitate valid estimation of R_h and SAR. We have outlined these assumptions and their associated drawbacks explicitly throughout Sections 2 and 3. Conversely, an advantage of our work is that we obtain three separate—yet broadly agreeing—estimates based on rather orthogonal modelling assumptions.

Another limitation stems from heterogeneity in the global response to the COVID-19 pandemic; each data source that we consider is inevitably influenced by health policy at the time and place where the data were collected. However, we are able to partially explain this heterogeneity in terms of geography and household policy. Also, the stability of our estimates over time (cf. Figure 4 and related discussion) and the data source lends them some credence.

Our work has presented a set of data sources and corresponding methods for estimating household transmission of SARS-CoV-2. Specifically, we estimate the intra-household reproduction number (R_h) and the household SAR using contact-tracing data from Singapore, widespread-testing data from Vo’ and aggregated data from prior studies, applying the necessary corrections for test sensitivity and asymptomatic cases. Our estimates suggest that household transmission constitutes a stable and significant component of overall transmission and is also not inevitable, making it a promising target for further research and intervention design. Relatedly, our results encourage further study into understanding and explaining the observed heterogeneity in household transmission.

Supplementary data

Supplementary data are available at IJE online.

Ethics approval

Not applicable (no human subjects used), as we performed the study from publicly available observational data.

Funding

None.

Data availability

Outside of what was directly downloaded from cited works, the data for this work (namely formatted contact-tracing data from Singapore) and scripts for reproducing the results are available at https://github.com/Andrewilyas/covid-household-transmission. The data were scraped and processed from the following web dashboard: https://www.againstcovid19.com/singapore/dashboard.

Conflict of interest

None declared.