Abstract
We propose a new methodological framework for studying status exchange in marriage. As shown in recent debates on status-race or status-beauty exchange, the conventional loglinear modeling approach is prone to controversial specifications and alternative interpretations. In this study, we develop a simple method – the Exchange Index – with cohort-and-gender-specific relative status measures, statistical distribution balancing, and nonparametric matching. While allowing for multiple covariate controls, our Exchange Index measures the average difference in spouse’s status between intermarriages and matched ingroup marriages. To demonstrate the new framework, we use two analytical examples of status-race and status-age exchange, based on the IPUMS 2000 US Census 5% microdata sample. To verify our new method, we also conduct replication and simulation studies. Our approach reduces model dependency, improves flexibility to account for confounders, allows for examination of heterogeneous patterns, speaks to fundamental concepts in status exchange theory, and takes advantage of increasingly available large-scale microdata.
Status exchange in marriage refers to a marriage pattern in which one spouse compensates for his or her disadvantage – relative to the other spouse – in one status dimension with an advantage in another status dimension. Statistically speaking, status exchange is an exception rather than a rule, since most marriages in modern societies tend to form between spouses with similar statuses or characteristics, which is called “homogamy.” However, status exchange is sociologically meaningful because it reveals status stratification across groups.
One prominent example is the potential status-race exchange in black-white intermarriages in the US, which has captured sociological attention for seven decades now (Davis 1941; Merton 1941).1 That individuals exchange social status to marry across racial boundaries is indicative of racial stratification and inequality. Despite a dramatic improvement in whites’ racial attitudes towards blacks (Schuman et al. 1997) and increases in racial intermarriages since the 1960s, the presence and the persistence of status exchange, if true, would reveal a racial hierarchy in which whites are preferred to blacks as marriage partners in American society (Schoen and Wooldrege 1989; Kalmijn 1993; Qian 1997; Gullickson 2006a; Torche and Rich 2016). In addition to this classic question of status-race exchange in black-white intermarriages, there has also been growing research interest in intermarriages involving races other than blacks and whites and intermarriages of ethnic groups (e.g., Qian 1997; Fu 2001; Rosenfeld 2001), as well as potential exchanges of individual traits and characteristics other than race and social status (e.g., England and McClintock 2009; McClintock 2014; Schwartz et al. 2016; Qian and Lichter 2018). Researchers are also interested in documenting similarities and differences across societies (e.g., Kalmijn and van Tubergen 2006; Hou and Myles 2013; Gullickson and Torche 2014). While many of these studies recognize the importance of status exchange as a substantive phenomenon, inconsistencies and disputes arise, even when all the researchers study the same subject using the same data for the same society at the same time. We propose that one reason for the current disarray in the literature lies in the difficulty with the methodology – loglinear model analysis – that has hitherto been the standard method of choice in studying status exchange.
Two recent debates published in the American Journal of Sociology (AJS) (Rosenfeld 2005, 2010; Gullickson and Fu 2010; Kalmijn 2010) and the American Sociological Review (ASR) (McClintock 2014, 2017; Gullickson 2017) exemplified the controversial nature of the conventional loglinear modeling framework for studying status exchange in marriage. Scholars in the two debates all built their studies on the established theories and prior findings of assortative mating and status exchange in marriage (Davis 1941; Merton 1941; for reviews, see Kalmijn 1998; Schwartz 2013; Lichter and Qian 2019). They all aimed at understanding whether and to what extent a socioeconomic advantage of one spouse is associated with marrying a spouse with an advantage in an ascribed characteristic, i.e., race (the AJS debate on status-race exchange) or physical attractiveness (the ASR debate on status-beauty exchange). In the AJS debate, Rosenfeld (2005, 2010) disagreed with Gullickson and Fu (2010) and Kalmijn (2010), as well as a number of previous studies that find supportive empirical evidence of status exchange in racial intermarriages (Kalmijn 1993; Qian 1997; Fu 2001; Gullickson 2006b), largely over specification of high-order interaction terms between husband’s and wife’s race and education, and parameterization for exchange.2 Similarly, the divergence of opinions between McClintock (2014, 2017) and Gullickson (2017) in the ASR debate over the evidence of exchange between status and physical attractiveness is mainly around model assumptions about marginal distributions of key variables, and interpretation of certain high-order interaction terms so as to identify exchange.
While the debates were methodological, surprisingly, all the studies accepted and applied sophisticated loglinear models to control for the confounding of marginal distributions and other factors. In the loglinear modeling approach, identification of status exchange hinges on whether the observed frequencies of couples with combinations of characteristics of interest are different from the “expected” ones if status exchange is absent. Due to different loglinear model specifications, the expected frequencies are defined differently, yielding different empirical findings and supporting different interpretations.
Borrowing the machinery of causal inference methodology, we propose a new methodological framework for studying status exchange in marriage. The new framework is simple in being model-free and meeting the demands for balancing and identification in studying status exchange marriages. Interpretation of results is easy, straightforward, and unambigious. Moreover, it gives researchers the flexibility to account for multiple confounders simultaneously and to examine heterogeneity in the degree of status exchange by subgroups.
Why Loglinear Model?
Limitations of the loglinear model are well known. For example, the model only considers married couples and thus ignores the dyamics of marriage to the exclusion of non-married persons in the analysis (Schoen 1986). Another limitation is that status attributes can only be categorical. Why, then, has the loglinear model been unquestioningly accepted as the method of choice for studying status exchange? The reason is that the loglinear model has long been thought to meet two methodological needs for studying status exchange: balancing distribution and identifying exchange.
“Balancing distribution” refers to the need to statistically adjust for unequal distributions of key characteristics under consideration not only between husbands and wives but also between intermarriages and ingroup marriages. For simplicity, let us consider two characteristics, group membership (denoted as G) and social status (denoted as S). “Group” refers to any characteristic that can be used for exchange. Following the past literature, we are mainly concerned with an ascribed attribute by which an intermarriage is defined (e.g., race). “Status” refers to achieved socioeconomic status characteristics (e.g., education) that can be used in exchange for a spouse’s desirable group membership. We use the following notations: GH for husband’s group membership, GW for wife’s group membership, SH for husband’s social status, and SW for wife’s social status. Moreover, let SH(GH) denote husband’s social status when the husband belongs to group G, and SW(GW) denote wife’s social status when the wife belongs to group G.
Not only do distributions of S differ by gender and group membership, i.e.,
they also differ by marriage type, i.e., intermarriage vs ingroup marriage. Such unequal distributions by gender and marriage type confound the study of status exchange in marriage. Let us take studying status-race exchange in the US as an example, with S proxied by educational attainment and G being race. We know that blacks on average had lower educational attainment than whites. We also know that in the past, white men attained higher average education than white women, while black men attained lower average education than black women. Given such unequal distributions of education specific to gender and race, we would like to determine, under the model of no exchange, the statistical distributions of SH(GH) and SW(GW) across four types of marriages:
This is balancing, a difficult task. Traditionally, the loglinear modeling approach has been chosen to accomplish it. Let us assume that the data being analyzed are in the form of a four-way cross-classified table, indexed by i, j, k, and l, denoting GH, SH, GW, and SW respectively. A loglinear model decomposes the observed frequency, typically into hierarchical components in the following form:
| (1) |
In this expression, μ1 … μ4 in line 1 represent the marginal distributions of the four variables, GH, SH, GW, and SW; μ12 and μ34 in line 2 represent the marginal association between G and S for husbands and wives respectively; μ13 and μ24 in line 3 represent the marginal association between husbands and wives in G and S respectively. Sociologically speaking, μ12 and μ34 capture gender-specific status differences by group membership, i.e., educational disparity by race in our example, or the so-called “within-person correlation” between status and group membership (Schwartz, Zeng and Xie 2016); μ13 and μ24 capture homogamy in G and S, i.e., racial homogamy and education homogamy in our example. While scholars may debate over what else should be controlled for in line 4, they tend to agree that these terms in lines 1 through 3 should all be controlled for in studies of status exchange. Status exchange parameters in line 5 are either implicitly or explicitly specified in the loglinear model, which we will discuss later.
As has been evident in the recent debates, disagreement on how to specify the extra control parameters in line 4 results in inconsistent findings and contradicting conclusions. These extra control parameters are usually specified as constrained or unconstrained versions of three-way interaction terms between the four key variables GH, SH, GW, and SW. They serve to control for noteworthy patterns of couples with specific characteristics that may confound the identification of status exchange, especially regarding those conditional patterns of intermarriages. In the debate on the status-race exchange, for example, Rosenfeld (2005, 2010) argues that all two- and three-way interactions should be included as controls in the loglinear models, because status exchange is “a four-way interaction between the education and race of both spouses” (Rosenfeld 2005:1309). However, Gullickson and Fu (2010) and Kalmijn (2010) argue that some three-way interaction terms also capture the effects of status exchange and, therefore, should be omitted or specified in particular ways. Kalmijn (2010) further differs from Gullickson and Fu (2010) in allowing racial homogamy to vary by a couple’s average education, and educational homogamy to vary by a couple’s race while forcing the degree of educational homogamy of intermarriages into being the average between black and white ingroup marriages. Similarly, in the debate on the status-beauty exchange, the disagreement over how to specify and interpret multiple-way interactions is also consequential. In sum, differences in the specification of extra control parameters reflect scholars’ prior understanding of expected status association patterns in intermarriages if status exchange should be absent, or in other words, the null model of no exchange.3
Status exchange is widely conceived as deviation from general marriage patterns allowing for status and group homogamy but no exchange. Once the null model of no exchange is defined as a loglinear model specification, extra parameters can be entered in equation 1 (line 5) to capture status exchange. A status exchange intermarriage means that the spouse from a disadvantaged group has an advantaged status relative to the other spouse from an advantaged group; these parameters all involve multi-way interaction involving four variables, GH, GW, SH, and SW.
More specifically, exchange may be represented by the interaction between a couple’s status difference and group difference: (GH-GW)(SH-SW), a particular, highly constrained form of the general GH*GW*SH*SW four-way interaction. This point has not previously been fully explicated in the literature, causing confusion among researchers in comparing and interpreting results. Some scholars treat status exchange parameters as four-way interation terms (e.g., Rosenfeld 2005, 2010), while others consider certain three-way interaction terms to be adequate (e.g., Gullickson and Fu 2010). Sometimes, status exchange parameters are specified to be asymmetric by gender. In all loglinear approaches, models are very complicated, often to the point of confusing both researchers and readers, because four-way interaction parameters are needed to identify status exchange.
An alternative yet similar identification strategy with loglinear models is not to use parameters to represent status exchange, but to compare observed marriage frequencies to predicted frequencies under a model of no status exchange (Kalmijn 1993, 2010; Qian 1997; Schwartz et al. 2016). Underprediction (i.e., higher observed than predicted frequency) and overprediction (i.e., lower observed than predicted frequency) for different combinations of GH, GW, SH, and SW can inform us of the presence or absence of status exchange. In Kalmijn (2010: 1259), for example, the observed ratio of male-dominant (in education) marriages (i.e., SH>SW) as opposed to female-dominant marriages (i.e., SH<SW) among couples of a black husband with a white wife (i.e., GH< GW) is 1.33 times the expected ratio, higher than comparable ratios among white-white and black-black marriages and thus constitutes evidence of status exchange. This identification strategy shares almost all the promises and pitfalls with the first strategy.
In addition, the loglinear modeling approach relies on model selection. In theory, the goodness-of-fit indices, such as the Bayesian Information Criterion (BIC) and likelihood ratio test (G2), help researchers decide whether to reject one model in favor of another (Powers and Xie 2008). In practice, researchers often compare a set of loglinear models that may not always follow a nested structure. The selection of the best fitting model for the observed data, not uncommonly, hinges on the researcher’s judgment call. As shown in both the ASR and AJS debates, inconsistent findings have emerged from different studies, as evidence for status exchange is sensitive to model specification.
We do not believe that the methodological conundrum for studying status exchange can be resolved with improvements of loglinear models. Otherwise, the past several decades of active research on the topic would have yielded a set of well tested models accepted by all. Studies in the ASR and AJS debates, among others, testify to the need for better methodology, ideally with minimal model dependency, parsimonious specification, robust identification, and intuitive interpretation. To meet this challenge, we go beyond the loglinear approach that models marriage frequencies to identify status exchage indirectly and propose a new methodological framework for studying and quantifiying status exchange directly.
We utilize covariate balancing techniques in the causal inference literature to estimate the effect of the treatment of intermarriage. The word “treatment” requires further explanation. In the causal inference literature, it is an exogenous cause that produces the causal effect on the outcome variable. For intermarriage, it is possible that marriage partners take each other’s multiple attributes, including both G and S, into consideration when forming a marriage. Therefore, it is implausible to claim that intermarriage is a true treatment that causes the spouse’s social attributes. However, as long as we are interested in the statistical association between intermarriage and spousal attributes, we can borrow covariate balancing methods in causal inference to derive an estimator to quantify this interest, indicating the statistical association between intermarriage and spousal attributes, be it causal or not. Although we do not necessarily treat intermarriage as a true treatment, we can still apply the following statistical methods and interpret the results as informative descriptions.
Redefining Status Exchange as a Treatment Effect
Our new methodological framework treats the two genders separately, focusing on one gender at a time and asking what kind of spouse he/she would marry. Such separate treatment of the two genders seems unusual, considering that a marriage affects both the husband and the wife simultaneously. However, behaviorally, marriage is best understood as a two-sided match between a potential husband and a potential wife in a marriage market (Logan, Hoff, and Newton 2008; Xie, Cheng and Zhou 2015). Seen this way, the causal effect of intermarriage should be defined separately for husbands and wives. Moreover, gender asymmetry has been well recognized in the literature of status exchange. In the case of racial intermarriages, intermarriages between black men and white women in the United States are much more common than those between black women and white men, with supportive evidence of status exchange found more often for the former than for the latter. Similarly, the case of status-beauty exchange is also gender-specific, with beauty likely to be a woman’s trait trading for men’s status. While in loglinear models, gender-asymmetry is often accounted for with high-order gender-specific interactions, our new approach allows for separate treatments by gender with gender-specific reference groups for comparison.
We first analyze men and then analyze women analogously. Suppose we have a sample of n couples in a population. Let i (i=1…n) represent the ith man with fixed group and status attributes (GHi, SHi), to be married to a wife characterized by (GWi, SWi). Theoretically, our framework can easily handle high dimensions of both G and S. For exposition simplicity and consistency with the literature, we will treat G and S as one-dimensional for now. Further, we assume, again for simplicity, that G is dichotomous and S is continuous. Let G=1 denote the higher group, and G=0 denote the lower group. For our status-race exchange example, G=1 for whites, and G=0 for blacks.
We now define status exchange as a counterfactual question in a standard potential outcome casual analysis (Holland 1986; Morgan and Winship 2015). Starting from the husband’s perspective, for agent i, his attributes (GHi, SHi) are fixed, but he may marry a wife in either the same group or a different group. For simplicity, we call intermarriage “treatment,” and ingroup marriage “control,” although this labelling is arbitrary and can be reversed. We borrow the language of treatment and control from the causal inference literature to devise a method to balance out differences in covariates between intermarriage couples and ingroup marriage couples. Let treatment variable D be defined as:
Associated with the two counterfactual conditions are two potential outcomes of wife’s status:
| (2) |
The individual-level causal effect of intermarriage for the husband is thus:
| (3) |
Of course, quantity (3) is not estimable because we only observe one of the two potential outcomes of a given man, either if the man is intermarried, or if he is not. Although we cannot estimate the individual-level effect of intermarriage as in (3), we hope to estimate the group-level average treatment effect. For example, at the population level, we define the Average Treatment Effect (ATE) as:
| (4) |
We may also limit the average to subpopulations, say , changing expression (4) to ATE(δW|).
Of course, it would be incorrect to estimate (4) with the so-called “naïve” estimator – the observed average difference in between husbands who intermarry and those who do not, i.e., by
| (5) |
where the first summation is with respect to all () intermarriages, and the second summation is with respect to all () ingroup marriages. We know that formula (5) is a biased estimator of (4) due to selection: men who intermarry are systematically different from men who do not. This selection bias is well documented in the literature and easy to show empirically. For example, as shown later in the paper, black men who intermarry (i.e., marry white women) have on average higher social status (in ) than black men who do not intermarry (i.e., marry black women). The past literature on status exchange, exemplified by the AJS and ASR debates, can be characterized as being mainly concerned with the following research question: between intermarriages (D=1) and ingroup marriages (D=0), if we statistically control for observed differences in the social status of one spouse (e.g., ), do we still observe a difference between the two marriage types in the other spouse’s social status (e.g., )?
Fortunately, with the status exchange question redefined this way, we can now resort to using methodological tools in causal inference (e.g., Morgan and Winship 2015) to address it. The situation in which we are concerned only with observed differences (in ) between intermarried husbands and non-intermarried husbands is called “ignorability.” Under the ignorability assumption, there is no unobserved confounding in the outcome variable (i.e., ) by treatment status, i.e., between intermarriages (D=1) versus ingroup marriages (D=0). One common methodological solution for causal inference in this case is to conduct matching across treatment status so as to achieve balance in covariate by treatment status (D=1 versus D=0) (Morgan and Winship 2015). In our case, this is relatively simple. Since we have only one covariate (i.e., ) to balance, we can just match a control case (D=0) to a treated case (D=1) directly, using covariate . If is a vector with many covariates, we can either match it exactly or reduce its dimensionality by first estimating the propensity score of treatment as a function of and then matching on the propensity score. When we conduct one-to-one matches with treated cases (intermarriages) as units, the resulting average difference in between matched intermarriages and ingroup marriages is an estimator of the treatment effect on the treated (ATT). Moreover, considering that intermarriages are usually much fewer than comparable ingroup marriages in a population, we may also conduct many-to-one matches to take better advantage of additional control cases to improve efficiency. In that case, while keeping each treated case at a full weight of 1, we can inversely weight the matched control cases (ingroup marriages) in proportion to the number of corresponding treated cases. The resulting weighted average difference in between the treated and control groups is an efficient ATT estimator of intermarriage. This is indeed what we did for the analytical examples, as will be discussed later.
What further makes the study of status exchange challenging is the complication that, given balanced , the distribution of wives’ social status (i.e., ) may also differ systematically between those who intermarry and those who do not, simply reflecting the overall differences in by group, as noted earlier, Dist(SW) ≠ Dist(SW(GW)). For example, regardless of marital partner, white women on average tend to have higher educational attainment than black women. When this is the case, the potential outcomes become dependent on treatment D in spite of balanced . In loglinear models, a common solution is to control the marginal distributions of and and their marginal association, i.e., μ3, μ4, and μ34 in eq. (1). In our new framework, as is redefined as the outcome variable, we can instead address this issue before matching by equalizing the marginal distributions of wives’ status between the treated and control marriages, using weighting or resampling techniques. Intuitively, this distribution balancing procedure ensures that the husband’s decision to intermarry or not will not lead to finding a wife from different candidate pools by social status.
We now easily shift our attention to the perspective of wife as the focal spouse and develop an analogous methodology to estimate, with balanced wives’ social status (i.e., ), the effect of intermarriage on the social status of husbands (i.e., ). In addition, we know that the meaning of status exchange depends on group status (G). For a husband in the lower group, say a black husband, (), exchange means that his white wife would have a lower status than a black wife otherwise, i.e., . By symmetry, for a white wife in the higher group (), exchange means that she would marry a higher-status black husband than a white husband, i.e.,
Our new methodological framework is theory-driven, requiring the researcher to choose a substantive focus on the effects of a particular type of intermarriage. In other words, what we propose is not a simple canned statistical tool but an approach that should be integrated with substantive questions and accordingly defined treatment and control groups. To illustrate, suppose we are interested in status-race exchange. The literature has mostly been concerned with black-husband and white-wife () intermarriages, which account for the majority of black-white marriages in the US. For ease of exposition and consistency with the literature, here we also focus on this type of () intermarriage and will estimate the intermarriage effects for black husbands and white wives in such marriages, respectively. For husbands involved in () intermarriages, we estimate their treatment effect on the treated (ATT) as follows:
| (6a) |
Analogously, we define and then estimate the ATT of intermarriage for wives involved in () intermarriages:
| (6b) |
Conceptually we can also define analogous ATT estimands for the other type of intermarriages in which . Indeed, when such situations arise, the researcher should do so.
In the above setup, we take an observed ingroup marriage as the counterfactual to an intermarriage. Our new methodological framework can also easily incorporate a hypothetical marriage as the counterfactual to meet varying research needs. An issue is what alternative marriages the researcher wishes to compare intermarriages to. For example, Qian and Lichter (2018) are interested in the local marriage market opportunities and constraints. Hence, they define the pool of alternative spouses for first-married couples as those who, at the time of observed marriages, are unmarried, within a particular age range, and living in the same metropolitan area. Nevertheless, no matter what criteria the researcher uses for selecting the counterfactual, once the criteria are defined, procedures of our methodological framework can all be implemented, as summarized in the next section.
Implementing the New Methodology
The loglinear model has been widely used in previous studies, mostly because it has the capacity to separate out unequal marginal distributions (Powers and Xie 2008), called “balancing” earlier in this paper. With our new methodological framework, we can achieve balancing through three steps: First, before we perform any statistical analysis, we transform an observed social status measure to make it relative, within a birth cohort and a gender; second, when necessary, we resample ingroup marriages, counterfactual cases, to achieve equivalence in the non-focal spouse’s status distribution between intermarriages and ingroup marriages; third, we match ingroup marriages with intermarriages by the social status of the focal spouse. Then, as the final step, we identify status exchange by estimating the intermarriage effect on the social status of the non-focal spouse.4
Step 1: Converting Status to Percentile Ranking
We construct a relative measure of socioeconomic status so that its distribution is fixed. Using external data, such as census data, we can convert an observed status measure into the percentile rank for a given birth cohort and gender combination. The person’s percentile rank in a subpopulation is a well-defined and easily interpretable relative measure of social status. For continuous status variables such as income, we can calculate individual percentile ranks through sorting individuals in the sample or population. For categorical variables, especially those with an ordinal structure such as education, with assumptions of an underlying continuous distribution, we can also convert discrete status levels into conceptually continuous percentile ranks. Recent studies have demonstrated the advantages of relative measures and their feasibility in studying social inequality and mobility (Chetty et al. 2016; Song et al. 2020; Dong and Xie 2018).
Step 2: Equalizing the Non-focal Spouse’s Status Distributions between Controls and Treated Cases
When the treated and control groups differ greatly in the distribution of the non-focal spouse’s status, we have the option to resample the controls randomly so as to equalize the marginal distribution of the non-focal spouse’s status (i.e., the outcome) among the controls to that among the treated cases. This is an optional step, analogous to the controlling for the joint distribution of the non-focal spouse’s status and group on top of their marginal distributions in the loglinear approach, i.e., μ3, μ4, and μ34 in Equation (1). We devised this step to accomplish a common practice in removing non-focal spouse’s status differences between intermarriages and ingroup marriages as a potential confounding factor in the identification of status exchange. However, this step may appear somewhat counterintuitive to some methodologically sophisticated readers, as the distribution of potential outcomes is commonly assumed to be independent of treatment assignment and therefore needs not to be balanced between treated and control groups. Clearly, whether to carry out this optional resampling step hinges on the researcher’s null model of no status exchange. In our procedure described here, we follow the past literature on status exchange in assuming the balance in the potential outcome between intermarriages and ingroup marriages as a part of the null model. However, making different assumptions about the null model of no exchange, researchers may skip this step and proceed to step 3 directly.5
For () intermarriages, we equalize either Dist(SW(GW=0)) to Dist(SW(GW=1)) when studying the intermarriage effect on the husband, or Dist(SH(GH=1)) to Dist(SH(GH=0)) when studying the intermarriage effect on the wife. This resampling methodology can be used even when status is measured with multiple dimensions (i.e., by multiple variables). In operation, we randomly draw a sample of controls at each nominal level of the non-focal spouse’s education so that the distribution of the resampled controls is the same between the controls and the treated cases. For example, when studying the intermarriage effect from the husband’s perspective, the sampling proportion of controls at level k of wife’s status is
| (7) |
As used in our analytical examples later, to best preserve the sample size and minimize the number of control cases lost to the resampling method, we choose to be over all possible k. can be any smaller positive value, too, resulting in a smaller sampling proportion of controls at each k. As an alternative, weighting controls with weights in eq. (7) also achieves the same objective. When studying the intermarriage effect from the wife’s perspective, we instead use a formula similar to eq. (7) to calculate the random sampling proportion of controls at level k of husband’s status.
Step 3: Matching Controls to Treated Cases by the Focal Spouse’s Status and Other Covariates
To estimate the ATT of intermarriage, we match ingroup couples to intermarriage couples from either the husband’s or the wife’s perspective. For () intermarriages, we either match on when examining the effect of intermarriage on wife’s status (i.e., from the husband’s perspective), as in (6a), or match on when examining the effect of intermarriage on husband’s status (i.e., from the wife’s perspective), as in (6b).
We prefer matching over regression adjustment. Intermarriages are selective, constituting a small proportion of all marriages. Many individuals who marry within their groups share no common characteristics and experiences with those who intermarry. A whole-population/whole-sample analysis with regression adjustment is prone to over-extrapolation due to potential lack of common support between the two types of marriages. The matching approach, albeit at the cost of reducing sample size, guarantees comparability in observed characteristics between intermarriages and comparable ingroup marriages. It also facilitates straightforward estimation of the ATT, a quantity that directly relates to our interest in understanding the treatment effect of intermarriage on those who are intermarried.
Matching is also attractive because it is nonparametric (Morgan and Winship 2015). While in general we may want to consider the benefit versus the cost of propensity-score matching (Rosenbaum and Rubin 1984) as opposed to full covariate matching, the choice is inconsequential in our setting. So long as we are concerned with only one covariate, full covariate matching is equivalent to propensity-score matching. Moreover, with matching, it is straightforward to account for multiple confounders, a task very challenging if not impossible for a loglinear model. Considerations in marital selection could be multidimensional (e.g., McClintock 2014; Qian and Lichter 2018). In the setting of multidimensional S, suppose that we are interested in status exchange specific to one dimension (covariate) of S but would like to control for the confounding of other observed dimensions of S, we can include the other dimensions through stratification, full covariate matching, or propensity-score matching. To illustrate this point, in our analytical example on status-race exchange detailed later, we control for the confounding of age homogamy by including husband’s and wife’s (coarsened) ages as full matching covariates. Similarly, in our second analytical example on status-age exchange, we control for racial homogamy by stratification on husband’s and wife’s race.
Step 4: Exchange Index (EI) Estimator
In the resulting matched sample, intermarriages and ingroup marriages are balanced on observed characteristics of the focal spouse. Through Steps 1 through 3, we have accomplished the first methodological task for studying status exchange in marriage, balancing. Under the ignorability assumption that the non-focal spouse’s status difference only differs systematically in the covariates observed and matched, matched ingroup marriages are counterfactual cases for observed intermarriages. The average difference in the non-focal spouse’s relative status (as measured in percentile rank) between intermarriages and matched ingroup marriages is the estimated ATT of intermarriage. Hereafter, we call this nonparametric estimator the “Exchange Index” (EI). For (), for example, we can estimate ) for husbands as:
| (8a) |
where is the weighted average value of wife’s S for matched control cases (i.e., ingroup marriages) for the ith intermarriage, is the number of intermarriages of the type (), and the summation sign is with respect to all such intermarriages. Similarly, we can estimate for wives as
| (8b) |
where is the weighted average value of husbands’ S for matched control cases (i.e., ingroup marriages) for the ith intermarriage. We use observed in eq. (8a) and observed in eq. (8b) from the same observed intermarried couples. However, we construct their counterfactuals from different ingroup marriages for comparison: in eq. (8a) from () ingroup married couples, and in eq. (8b) from () ingroup married couples. For the status-race exchange example, in eq. (8a) is drawn from black-black marriages, and from white-white marriages. With this design, reveals, for “the same” black husbands, whether and to what extent their wives would have lower social status on average when they intermarry. Similarly, indicates whether and to what extent on average white wives would marry husbands of higher status when they intermarry. Hence, and serve to meet the second methodological need in studies of status exchange, identification, by directly measuring status exchange that is gender-specific.
To extend this methodology to the situation in which group membership G is continuous, we can define intermarriages and ingroup marriages by categorizing couple’s group difference, i.e., (), with thresholds. Let us take studying status-age exchange as an example, where age conceptually constitutes the G variable. Based on the observed distribution of marriages by couple’s age difference or prior substantive knowledge, we may define marriages in which α as age-homogamous “ingroup” marriages, as older-husband and younger-wife “intermarriages,” and α as younger-husband and older-wife “intermarriages,” with . After categorizing marriage types, we can define the treatment and control marriage types, conduct resampling – if deemed necessary – and matching, and estimate and in a way similar to the above situation in which G is categorical.6
Comparative Advantages of the New Framework over Loglinear Models
Our new methodology, while simple and easy to implement, adequately meets the methodological needs of research on status exchange. It provides a superior alternative to loglinear modelling. While loglinear models require the inclusion of many parameters for high-order interactions (shown in eq. 1), our new approach yields a single, simple, nonparametric summary measure. The results from the new approach are also straightforward to interpret, because the estimated quantity directly reveals average percentile points of status that have been exchanged for intermarrying.
Loglinear models are suited only for data in cross-classified tables and thus cannot incorporate many covariates, especially continuous covariates. In contrast, the new approach provides much more flexibility and can easily accommodate other control variables as well as multiple dimensions of status measures. In addition, matching estimation implicitly allows for heterogeneous treatment effects, or interactions between treatments and other covariates (Morgan and Winship 2015). One could also examine heterogeneity in the strength of status exchange along other dimensions, a task almost impossible to accomplish with loglinear models. This is true because matching is nonparametric and can be applied to any subgroup defined by pre-treatment covariates. We demonstrate the usefulness of our approach in studying heterogeneous treatment effects of intermarriage by stratifying data on one’s own social status (S). Given that S predicts the propensity of intermarriage, this approach is tantamount to the heterogeneous treatment effect model (Brand and Xie 2010; Xie, Brand and Jann 2012).
Our new methodological approach removes ambiguity in defining status exchange parameters and specification of other control variables in loglinear models. As summarized in our previous discussion and Table 1, while past researchers all agreed about the use of loglinear models, they differed greatly in how to specify parameters to identify status exchange and other control variables. Disagreement over model specification has led to different substantive conclusions. Our new approach is model-free and thus is not subject to disputes over model specifications.
Table 1.
Comparison between approaches: Selected recent studies on status-race exchange in the US
| Conventional loglinear modeling framework | New covariate balancing framework | |||||||
|---|---|---|---|---|---|---|---|---|
| Rosenfeld (2005) Model 5 | Gullickson and Fu (2010) Model 2 | Kalmijn (2010) Model 2 | (Example 1) | |||||
| Evidence for status-race exchange | Null | Supportive | Supportive | Heterogenous by gender, group, and status | ||||
| Outcome variable | Marriage frequency | Marriage frequency | Marriage frequency | Spouse’s status | ||||
| Status Exchange Estimator | Odds ratio of status exchange between intermarriages and ingroup marriages | Odds ratio of status exchange between intermarriages and ingroup marriages | Hypergamy Ratio (between observed and predicted ratios of intermarriages with status exchange) | Exchange Index (average difference in the spouse’s status between matched intermarriages and ingroup marriages) | ||||
| Explicitly specified in the model estimation with statistical test? | Yes | Yes | No | Yes | ||||
| Marginal distribution controls | SH, GH, SW, GW | SH, GH, SW, GW | SH and SW as cohort- and gender-specific relative percentile ranks | |||||
| Two-way marginal association controls | SH * GH, SW * GW, (GH = GW), (GH = GW = black), ((GH =black, GW = white) or (GH = white, GW = black)), (GH=black, GW=white), | SH * GH, SW * GW, SH * SW, GH * GW | SH * GH, SW * GW, SH * SW, (GH = GW) | Equalizing the distribution ingroup marriages (D=0) to intermarriages (D=1) and on SW or SW, specific to the type of intermarriage and perspective of the husband or wife under study. Matching ingroup marriages (D=0) to intermarriages (D=1) on SH or SW, specific to the type of intermarriage and perspective of the husband or wife under study. |
||||
| Extra Control Parameters | SH * SW * GH, SH * SW * GW, (GH=GW) * SH * SW, ((GH =black, GW = white) or (GH = white, GW = black)) * (SH(GH=black) or SW(GW=black)) |
1/2(GH+GW)* (SH≠SW), 1/2(SH+SW)* (GH = GW) |
||||||
| Flexibility for controlling confounders? | Limited | Limited | Limited | Large | ||||
| Ability to examine heterogeneity? | Difficult | Difficult | Difficult | Easy | ||||
What is perhaps the greatest advantage of our new approach, in comparison with the loglinear approach taken in the past, is that the Exchange Index approach directly speaks to classical theories on status exchange (Merton 1941; Davis 1941) while accommodating newly developed theoretical discussions separating out two different forces driving mate selection, “dyadic exchange” and “market exchange” (Gullickson and Torche 2014; Torche and Rick 2017). First, ever since Merton (1941) and Davis (1941), a couple’s status gap and group differences are fundamental in defining and understanding status exchange. According to theory, status gaps should be much larger in intermarriages than in ingroup marriages if the spouse from the disadvantaged group compensates the other spouse from the advantaged group with excess status. In our approach, as one spouse’s status is held constant by matching, we directly measure the average status difference in the non-focal spouse between intermarriages and ingroup marriages. In other words, unlike the focus of loglinear models on the odds ratio of intermarriages with and without status exchange, our approach enables us to directly quantify status in exchange, and link empirical findings to theoretical discussion on status gap differences between intermarriages and ingroup marriages.
Second, recent research has distinguished two separate social forces that shape or constrain the formation of intermarriage: the classic exchange discussed earlier, called “dyadic exchange” and “market exchange” (Gullickson and Torche 2014; Torche and Rich 2017). The notion of market exchange is supported by a long and well established sociological understanding that inter-group interaction (marriage in this case) results first from contextual (structural) exposure and only secondarily from individuals’ choices (e.g., Zeng and Xie 2008). Given a strong norm of educational homogamy, for pure reasons of structural exposure high education should increase intermarriage chances for those from disadvantaged groups and decrease intermarriage chances for those from advantaged groups (e.g., Fu 2001; Gullickson 2006b; Gullickson and Torche 2014; Torche and Rich 2017). In other words, intermarriage may trend upwards over time due to changes in market exchange without changes in individual-level preferences for intermarriage, i.e., dyadic exchange. With loglinear models, distinguishing dyadic exchange from market exchange is difficult, because both fit the same observed overall intermarriage patterns. In contrast, stratifying on race-specific spouse’s status (or even other balancing covariates), our approach can easily identify heterogenous status exchange effects, net of market exchange. We are therefore able to compare dyadic exchange across status boundaries in a non-parametric way to check whether status exchange in marriage is status-dependent. For illustration, we will apply our new methodological framework to study not just overall patterns of status exchange in intermarriages but also heterogeneity by husband’s and wife’s status.
Two Analytical Examples
We demonstrate our approach with two analytical examples. The first examines the education-race exchange among US black and white marriages in 2000, which responds to the AJS debate (Rosenfeld 2005, 2010; Gullickson and Fu 2010; Kalmijn 2010). The second examines the education-age exchange among all US marriages in 2000 so that we can illustrate the method when the group variable (G) in exchange is continuous.
Data, Ranking, and Measures
For both examples, we make use of the IPUMS 5 percent microdata sample of the 2000 US census. We focus on prevailing marriages in which the wife is 25–49 years old, and both spouses can be identified with no missing information on their educational attainment, age, and race. For simplicity, husband’s and wife’s social status, SH and SW, are measured one-dimensionally as relative educational status in percentile ranks. Specifically, individuals in the population – regardless of marital status – are ranked by their educational attainment relative to others of the same gender and the same birth cohort. To smooth data, we make moving intervals for 11-year birth cohorts, centered on the birthyear of the indexed individual.7 While educational attainment is by nature categorical, we take advantage of the 11 categories for the highest attained education in the 2000 census. Individuals with the same educational attainment are assigned to the mid-point percentile rank of all members belonging to their cohort- and gender-specific educational attainment group.
As discussed earlier, the treatment variable is constructed as a dichotomous indicator that distinguishes intermarriages from ingroup marriages. For simplicity, we focus only on status exchange in the dominant type of intermarriages in each example, that is, black-husband and white-wife marriages for the first example and older-husband younger-wife marriages for the second example. Consequently, in the first example, the treatment variable D is coded 1 for () intermarriages and 0 for () or () ingroup marriages. In the second example, the treatment variable D is coded as 1 for marriages in which the husband is over 4 years older than the wife, i.e., , and 0 for marriages of which the husband’s minus wife’s age is between 4 and −3 years, i.e., .
Resampling
In the first example on black-husband and white-wife marriages, based on the proportions calculated in eq. (7), we randomly sample () ingroup marriages to match the proportion of () intermarriages at each level of wife’s education. Similarly, we randomly sample () ingroup marriages to match the proportion of the treated () intermarriages at each level of husband’s education. In the second example on old-husband and young-wife marriages, we randomly sample ingroup marriages according to the distribution of () intermarriages by either when studying the intermarriage effect from the husband’s perspective, or when studying the effect from the wife’s perspective.
Matching and Identification
In contrast to a naïve comparison between intermarriages and all observed ingroup marriages, we use matching to produce a refined counterfactual sample that only includes ingroup marriages of comparable characteristics. Matching is performed using the resampled controls, resulting from the previous step. Depending on studying from the perspective of the husband or that of the wife, we conduct full exact matching on or . Note that the matched ingroup marriages often differ in number from corresponding intermarriages. Unmatched observations are given zero weight; matched intermarriages are given a full (one) weight, with matched ingroup marriages weighted proportionally in each matching pair in order to make weighted control cases equal in number to treated cases.8
In the first example on status-race exchange, the research interest is on the effect of black-husband and white-wife intermarriage either from the husband’s perspective or from that of the wife. In the former, we estimate by matching () ingroup marriages to () intermarriages on . In the latter, we estimate the by matching () ingroup marriages to () intermarriages on . At the same time, to control for the effect of age homogamy, we also include both husband’s and wife’s age as covariates for coarsened exact matching in producing two matched samples from the perspective of either the husband or the wife.
Similarly, in the second example of education-age exchange, we are interested in the effect of age heterogamous marriage of husbands over 4 years older than wives from either the husband’s or the wife’s perspective. In the former, we estimate by matching age homogamous marriages to older-husband and younger-wife () intermarriages on and . In the latter, we estimate from the wife’s perspective by matching age homogamous marriages and older-husband and younger-wife () intermarriages on and . Also, we include husband’s and wife’s race as additional matching covariates in producing both matched samples to account for the confounding effect of racial homogamy. For illustration of how matching facilitates balancing the unequal distributions and estimating status exchange, in both examples and from each perspective, we also report the naïve EI based on the average difference in the non-focal spouse’s social status between all observed intermarriages and ingroup marriages.
Status-Race Exchange
We analyze the data to shed new light on status exchange in intermarriages between black men and white women, a main focus in the past literature. With a few exceptions (e.g., Rosenfeld 2005, 2010), most of the earlier studies have provided supportive evidence of status-race exchange in racial intermarriages in the United States, especially between black men and white women (Kalmijn 1993; Qian 1997; Gullickson 2006a; Torche and Rich 2016). This pattern has been found with data from the 1970s to 2010s, despite increasing rates of racial intermarriages, reaffirming saliency of racial stratification in the US. In addition, we are also interested in how status-race exchange patterns may vary by husband’s and wife’s education. Due to market exchange, higher education, or socioeconomic status in general, may facilitate black men to intermarry while hindering white women from intermarrying (e.g., Fu 2001; Gullickson 2006b; Torche and Rich 2016).
We identify 1,288,738 prevailing marriages in which the wife is 25–49 years old among the black and non-Hispanic white population in the 2000 US census 5 percent microdata sample, with non-missing percentile ranks of the couple’s educational attainment. Prevalence of the four racial marriage types differs substantially. Of all these marriages, intermarriages account for 0.6 percent, intermarriages 0.2 percent, ingroup marriages 7.5 percent, and 91.7 percent.
We choose to focus on status exchange for the dominant type of intermarriages. If status exchange exists, we expect black husbands to marry white wives of lower status on average than black wives, i.e., , or white wives to marry black husbands of higher status than white husbands on average, i.e., .
The simple descriptive statistics, as reported under the “observed” columns in Table 2, do not reveal substantive patterns of education-race exchange. For intermarriages, i.e., D = 1, the average educational ranks of the husbands and wives are very similar, at 51.28th and 50.69th percentiles respectively. In comparison, husbands and wives of ingroup marriages have on average lower ranks at 46.12th and 47.84th percentiles, respectively, while those of ingroup marriages have higher average ranks at 54.21th and 53.33th percentiles.
Table 2.
Status-race exchange in black-husband and white-wife intermarriages in the US, 2000
|
From the husband’s perspective:
black-husband and white-wife intermarriages (D=1) vs. black marriages (D=0), i.e., |
From the wife’s perspective:
black-husband and white-wife intermarriages (D=1) vs. white marriages (D=0), i.e., |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Observed | Resampled for Dist()) Matched on |
Observed | Resampled for Dist()) Matched on |
||||||||
| D=1 | D=0 | D=1 | D=0 | D=1 | D=0 | D=1 | D=0 | ||||
| Husband’s social status () | 51.28 | 46.12 | 51.55 | 51.55 | 51.28 | 54.21 | 51.31 | 50.27 | |||
| Wife’s social status () | 50.59 | 47.84 | 50.71 | 52.15 | 50.59 | 53.33 | 50.64 | 50.64 | |||
| Exchange Index | 2.75*** [naïve] | −1.44*** | −2.93*** [naïve] | 1.04*** | |||||||
| N | 7513 | 96861 | 7342 | 66424 | 7513 | 1181505 | 7495 | 562007 | |||
Notes:
p < 0.001, based on robust standard errors.
A reexamination of the data with our new methodological framework, as reported in Table 2, reveals supportive evidence of status exchange from both the husband’s and wife’s perspectives. First, from the husband’s perspective, whereas the naïve as observed is greater than 0, the matching-based is negative and statistically significant. An of −1.44 suggests that wives of black husbands who intermarry rank on average 1.44 points lower in terms of education percentile than those of comparable black husbands who marry black wives. This finding is in line with the expectation of status exchange, i.e., . Furthermore, from the perspective of the wife, the naïve is −2.93, but the matching-based is 1.04. The latter estimate suggests that intermarriage for white wives results in an increase of 1.04 percentile points in their husband’s status, consistent with the expectation of status exchange, i.e., .
How should we understand the effect size substantively? One way to interpret the estimates is to compare them to the observed status difference between the focal spouses who intermarry and those who do not. That is, we may gauge the loss/gain in the non-focal spouse’s status against the focal spouse’s observed status advantage/disadvantage. Here, from the husband’s perspective, the observed status advantage of black husbands who intermarry over black husbands who do not is 5.16 percentile point (51.28−46.12 as reported in the “observed” columns of Table 2). Thus, an of −1.44 means that intermarrying white women would cost a black husband in wife’s status at an average amount equivalent to 27.9 percent of their own status advantage. From the wife’s perspective, interpreted in a similar fashion, an of 1.04 suggests that intermarrying a black man compensates a white woman’s status disadvantage relative to white women married to white men by 38.0 percent (i.e., 1.04/(50.59–53.33)) on average.
We now go beyond a simple analysis of an overall exchange effect by gender, as our approach allows for the examination of heterogeneity in status exchange across social status. Figure 1 presents the matching-based and across own status quintile groups of the black husbands (on the left) and white wives (on the right). From the husband’s perspective, we find supportive evidence of status exchange in all but the bottom quintile groups. Except for black husbands from the bottom status group, ranges between −0.85 and −2.94 among those in other higher status quintiles, statistically different from 0 in the middle three quintiles. From the wife’s perspective, is statistically significant and positive among those white wives who rank in the bottom 40 percent by relative status, 5.38 and 1.33 on average in the first and second bottom quintiles, respectively. This suggests that status-race exchange is heterogeneous by gender, race, and status. Exchange is particularly pronounced among white women of relatively low status who intermarry black husbands. We also report detailed results in Appendix A.
Figure 1.
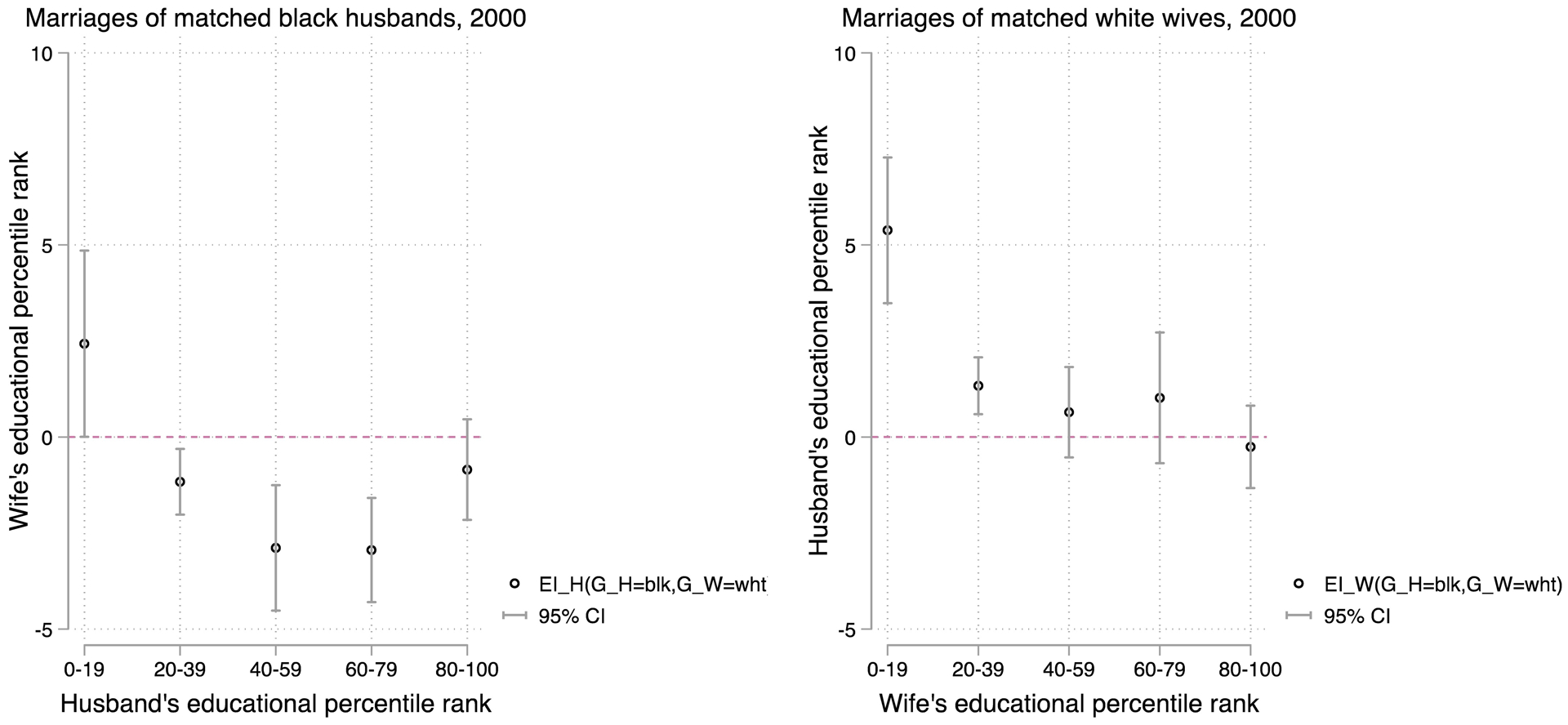
Heterogeneous status-race exchange by own status in black-husband and white-wife intermarriages in the US, 2000
Status-Age Exchange
Motivated by the past literature, we similarly focus on status-age exchange and how the exchange may differ between husband’s and wife’s perspectives. England and McClintock (2009), for example, attribute gender asymmetry to the “double standard of aging in the marriage market,” because physical appearance weighs more in the preference of men choosing women than that of women choosing men. They also find weak evidence suggesting a variation in status-age exchange by husband’s and wife’s education. Several other studies of status-age exchange did not systematically study the variation by husband’s or wife’s education (e.g., McClintock 2014; Qian and Lichter 2018). As a result, there is a need for understanding the heterogeneity in status-age exchange by gender and own status, a task well suited for our new methodological framework.
With the US 2000 Census IPUMS 5 percent microdata sample, we identify 1,603,075 prevailing marriages of which the wife ages 25–49 and both spouses’ percentile ranks of educational attainment are non-missing. Of all such marriages, 25.7 percent are older-husband and younger-wife ( age-hypergamous marriages, 5.98 percent are younger-husband and older-wife age-hypogamous marriages, and 68.3 percent are age homogamous marriages.
Our analysis focuses on the dominant type, older-husband and younger-wife ( age-hypergamous marriages. If status-age exchange exists in such marriages, others being equal, we expect husbands to marry younger wives of lower average status than similar-age wives, i.e., , or wives to marry older husbands of higher average status than similar-age husbands, i.e., .
According to simple descriptive statistics, as reported under the “observed” columns in Table 3, couples of age-homogamous marriages attain higher educational status on average = 53.13, = 52.16) than their counterparts in age-hypergamous marriages = 49.37, = 47.67). That is, there is status disadvantage for both husbands and wives in age-hypergamous marriages relative to their peers. In both marriage types, it is also noteworthy that the average social status of husbands tends to be higher than that of wives.
Table 3.
Status-age exchange in older-husband and younger-wife marriages in the US, 2000
|
From the husband’s perspective:
older-husband and younger-wife age-hypergamous marriages (D=1) vs. age-homogamous marriages (D=0), i.e., |
From the wife’s perspective:
older-husband and younger-wife age-hypergamous marriages (D=1) vs. age-homogamous marriages (D=0), i.e., |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Observed | Resampled for Dist()) Matched on |
Observed | Resampled for Dist()) Matched on |
||||||||
| D=1 | D=0 | D=1 | D=0 | D=1 | D=0 | D=1 | D=0 | ||||
| Husband’s status () | 49.37 | 53.13 | 49.61 | 49.61 | 49.37 | 53.13 | 49.38 | 48.76 | |||
| Wife’s status () | 47.67 | 52.16 | 47.73 | 46.76 | 47.67 | 52.16 | 47.73 | 47.73 | |||
| Exchange Index | −4.49*** [naïve] | 0.96*** | −3.76*** [naïve] | 0.62*** | |||||||
| N | 412274 | 1094932 | 337452 | 605036 | 412274 | 1094932 | 409864 | 543690 | |||
Notes:
p < 0.001, based on robust standard errors.
With our new methodology, we find supportive evidence for status-age exchange as a general pattern among wives, but not among husbands, in age-hypergamous marriages. From the husband’s perspective, the naïve is −4.49. However, the matching-based is 0.96, statistically significant from zero. This means that for husbands, marrying younger wives rather than similar-age wives increases their wives’ relative status by 0.91 percentile points on average. It is inconsistent with the expectation of status exchange, i.e., < 0. However, from the wife’s perspective, with the matching-based being 0.62 and statistically significant, there is evidence for status-age exchange. Compared with those marrying husbands of similar ages, wives marrying older husbands have higher husbands’ educational ranks on average. With the average gap in education percentiles between the two types of marriages as a scale, marrying more than 4 years older husbands compensates for the observed status disadvantage of those women by 13.8 percent (i.e., 0.62/(47.67–52.16)) on average. In other words, we find gender asymmetry in status-age exchange.
This result of an overall effect, however, is misleading. After examining heterogeneity, we uncover status-age exchange as a monotonical function of one’s own status so that it is present only for high-status old husbands and low-status young wives. As presented in Figure 2, from the husband’s perspective (left part of Figure 2), separately by husband’s quintile status groups, status-age exchange is present for those ranking in the top 20 percent, indeed, with a loss of 1.71 percentile points in wife’s status by marrying a younger as opposed to a similar-aged wife. In contrast, from the wife’s perspective (right part of Figure 2), status-age exchange is present for those wives ranking from the bottom to the 60th percentile. For a wife in the bottom quintile status group, marrying an older husband on average increases 3.78 percentile points in husband’s status. However, this benefit decreases to 2.07 and 0.50 percentile points for those from the 20–40 and 40–60 quintile status groups, respectively, and disappears altogether for those wives with higher status. See Appendix A for details of the estimated results.
Figure 2.
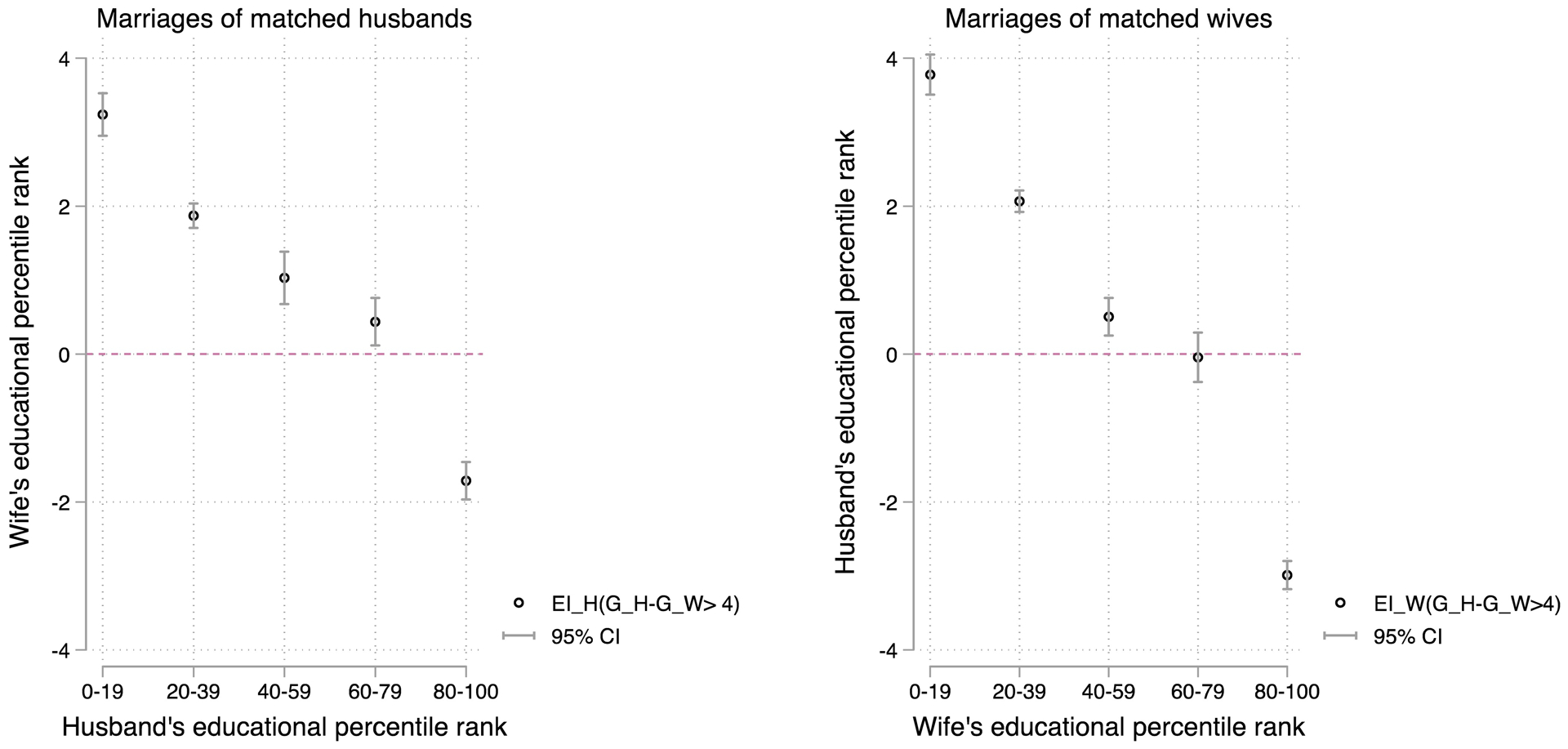
Heterogeneous status-age exchange by own status in older-husband and younger-wife age-hypergamous marriages in the US, 2000
Replication and Simulation Results
To further verify our new methodological approach, we answer two questions in this section: First, how would results differ if we instead used conventional loglinear models to analyze the same empirical data? Second, in a simulation setting, can our approach successfully identify exchange when we specify this and yield null evidence when we specify no exchange? For simplicity, we focus on the case of status-race exchange in the AJS debate.
To answer the first question, we replicate loglinear models of Rosenfeld (2005), Gullickson and Fu (2010), and Kalmijn (2010) with the 2000 census data used in our first analytical example.9 Here, we only focus on the overall evidence of status exchange, because the loglinear models used in these studies are not designed to estimate gender-specific effects or heterogeneous effects by husbands’ and wives’ education. As reported in Appendix B, the loglinear models produced results similar to those reported in the three studies originally using the 1980 census data. The results using Gullickson and Fu’s loglinear model show evidence of status exchange. So does the hypergamy ratio calculated based on Kalmijn’s model: the ratio of observed intermarriage frequency in which a black husband has higher education than his white wife (i.e., “male dominance” in Kalmijn’s term) over intermarriage frequency in which a black husband has less education than his white wife (i.e., “female dominance”), is greater than the same ratio according to random pairing after controlling for selected marginal and joint distributions of education and race of the couple. In contrast, similar to the position taken in the AJS debate, our replication of Rosenfeld’s model fails to support status exchange. In sum, evidence on the overall evidence of status exchange using loglinear models is mixed, as in the previous studies, depending on model specification.
To answer the second question, we conduct two simulation experiments. One specifies the presence of status-race exchange in black-husband and white-wife marriages, with the gender-specific exchange effects resembling the empirical pattern reported for our first analytical example. By design, the other experiment assumes no status exchange in black-husband and white-wife marriages. To save space, details of our data generating process, simulation procedures, and detailed results are reported in Appendix C. In sum, our first experiment confirms that our approach successfully identifies status exchange, as well as its gender-specific difference in effects, when we specify this. In the second experiment, our approach reveals no false positive evidence of exchange when status exchange is specified as non-existent.
One reflection from the simulation experiments is also noteworthy. In our approach, we first standardize education (or any other measure of social status) using relative percentile ranks. This transformation from original interval scales to relative percentile ranks, however, is not linear (but monotonic). Aggregation from the individual level to a group level is at the percentile rank scale, as specified in equation 8. We can no longer convert the magnitude of estimated effects in relative percentile points back to that in the original interval level, due to the loss of scale in the non-linear transformation.10 A useful lesson is that while our approach can conveniently identify status exchange and estimate its effects measured in percentile points, we cannot convert the estimated effects in percentile ranks back to the original status scale. Users of our method should be aware of this tradeoff.
Discussion and Conclusion
In this paper, we present a new and simple methodological framework for studying status exchange in marriages. Our approach has three key features. First, we use relative measures of social status, defined as a relative position in a given gender and cohort. Second, we use a potential outcomes approach in quantifying the impact of intermarriage, separately for husbands and wives who are involved in such marriages. Third, we use a nonparametric matching method to estimate the consequence of intermarriage and thus derive the Exchange Index as a measure of status exchange.
The setup of our conceptual framework requires the ignorability assumption, i.e., no unmeasured confounders between intermarriages and ingroup marriages except for husbands’ and wives’ observed characteristics. The ignorability assumption is necessary if we wish to interpret the Exchange Index as the causal effect of intermarriage. However, it is always possible to use the matching method to compute the Exchange Index even when the researcher suspects that the ignorability is unlikely to hold true. In this case, the researcher may interpret the Exchange Index as a descriptive measure of status exchange to know the presence or absence of status exchange. More information or a different assumption is needed for the researcher to determine if, and to what extent, the “effect” of status exchange is causal.
Our new methodological approach has a number of desirable properties, as compared to traditional loglinear models. First, it is simple and easy to implement. Second, it is flexible in allowing additional covariates and examination of heterogeneity by covariates. Third, as a nonparametric method, it removes ambiguity and disagreement over model specifications. Finally, it yields quantities that are directly relevant to long-standing theoretical propositions about status exchange.
While our proposed method offers several advantages relative to the loglinear model, the two approaches share one key limitation. The EI only summarizes a static pattern among married couples but fails to capture the dynamic process of marriage formation (Schoen 1986). As a result, along with loglinear models, our approach does not address the two-sex problem -- the mating dynamics between males and females (Pollak 1986; Logan, Hoff, and Newton 2008; Xie, Cheng and Zhou 2015). Earlier work on two-sex mating models either focuses on a single dimension of assortative mating, e.g., age (Schoen 1981), or evaluates the consequences of observed mating outcomes for the growth of populations (Pollard 1975; Song and Mare 2017). None of these works, however, answers the question regarding individuals’ preferences for intermarriage, the main research question in the status-exchange literature. More future work is needed on this subject.
We applied our new methodological framework to two empirical settings taking advantage of the IPUMS US 2000 Census 5% microdata sample, one on status-race exchange and the other on status-age exchange. Our first analytical example, while analyzing data of a more recent period than 1980, directly corresponds to the AJS debate on status-race exchange. With our new methodological framework, we find supportive evidence for status exchange as a general pattern for black-husband and white-wife intermarriages from the perspectives of both husband and wife. What is more interesting, however, is that our new approach reveals heterogeneous effects of intermarriage: evidence of status-race exchange is especially pronounced for black husbands whose status ranks above the bottom 20 percent and for white wives whose status ranks in the bottom 40 percent relative to their peers of the same gender, respectively. This gender-, group-, and status-specific heterogeneity of status-race exchange likely accounts for inconsistent findings in previous studies, since they specify multiple high-order interaction terms between gender, group, and status in their loglinear models differently. Our second analytical example focuses on status-age exchange. From studying age-hypergamous marriages, we find overall supportive evidence for status-age exchange from the wife’s perspective but not from that of the husband. However, our further analysis reveals heterogenous effects: status-age exchange exists among wives ranking in the bottom 60 percent and among husbands who rank in the top 20 percent in relative status.
In our exposition and examples, we only considered the situation in which the status variable (S) is a one-dimensional covariate. However, our approach can easily be extended to situations in which S is multi-dimensional and/or there are multiple confounders. When S is multi-dimensional, we would treat S differently both as bases for matching (for individual’s own status) and as outcomes (for spouse’s status). Similarly, multiple potential confounders can be accounted for as bases for matching. As bases for matching extend to many covariates, the researcher is likely to encounter the sparseness problem, as there are few comparable cases for matching in a multi-dimensional space. However, the researcher can summarize multi-dimensional S and confounders with the estimated propensity score so that matching is sufficient on the basis of the estimated propensity score (Rosenbaum and Rubin 1984; Morgan and Winship 2015). As outcomes for spouse’s status, the researcher can examine multiple dimensions of S separately.
Beyond its usefulness for studying status-exchange in marriage, the same methodological framework can also be extended to describe other similarly patterned social phenomena where comparisons are difficult to operationalize. One potential example is immigration and intergenerational mobility, where research interest centers on the difference in intergenerational mobility between immigrants in a destination country from an origin country and their peers who stay in the origin country (Borjas 1993). Since social status, be it measured by occupation, education, or earnings, is typically not comparable between the origin country and the destination country, traditional models of intergenerational mobility (such as loglinear models) cannot be applied. One possibility is to use our method: transforming social status into percentile ranks, with immigrants ranked in the destination country and stayers ranked in the origin country, then matching immigrants with stayers by parental social status. In this way, we can straightforwardly answer the question of how immigration affects the relative social status of the next generation either on average or by parental social status.
Our use of relative measures also makes our proposed approach suitable for temporal and international comparisons, especially in the presence of structural changes. Relative status measures make it possible to utilize different socioeconomic status measures that are otherwise incommensurate. Both different coding schemes of the same socioeconomic status measure and different status measures can be translated into comparable scales of relative percentile ranks. This is especially useful when facing structural shifts in a society that render the same status measure to have different meanings over time. For example, because of the expansion of higher education, a college degree has become less selective and prestigious than before. Also, when some status measures are incommensurate in absolute levels due to institutional differences across societies, relative measures help standardize them for comparison so long as they maintain validity in differentiating individual socioeconomic standings within each society.
In summary, we have proposed a new methodological framework for studying status exchange to overcome shortcomings of the conventional loglinear modeling approach. Through the use of relative ranks of social status, statistical distribution balancing, and non-parametric matching, our method yields the Exchange Index that directly measures the average difference in spouse’s status between intermarriages and matched ingroup marriages. In this paper, we illustrated the new method with two empirical examples, replicated loglinear models used in the prior literature, and conducted a simulation study. We showed that our approach reduces model dependency, improves flexibility to account for confounders, allows for examination of heterogeneous patterns, and speaks to fundamental concepts in status exchange theory. We expect that future research on status exchange in marriage will increasingly use our proposed method in replacement of the conventional loglinear approach.
Acknowledgments
We thank the anonymous reviewers, Arron Gullickson, Zhenchao Qian, Christine Schwartz, Xi Song, and the audience of our presentations at the PAA 2019 Annual Meeting and RC28 2019 Summer Meeting for helpful comments on earlier versions of this paper, and Matthijs Kalmijn for help on replication of his earlier work. The research was supported by the National Institutes of Health (grant R01-HD-074603-01), the Office of Population Research at Princeton University, and by the National Natural Science Foundation of China (grant no. 72003006). The ideas expressed herein are those of the authors.
Appendix A. Detailed results of the heterogeneous status exchange in two analytical examples, as plotted in Figure 1 and 2
Table A1.
Estimated Exchange Indexes by the focal spouse’s status quintile groups in the two analytical examples of status-race and status-age exchange in marriage
| Analytical Example 1: Status-race exchange | Analytical Example 2: Status-age exchange | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Husband’s status quintiles | Coef. | s.e. | CI(lower) | CI(upper) | N | Coef. | s.e. | CI(lower) | CI(upper) | N |
| 80–100 | −0.850 | 0.667 | −2.158 | 0.457 | 12693 | −1.714 | 0.129 | −1.967 | −1.461 | 212654 |
| 60–79 | −2.944 | 0.691 | −4.299 | −1.589 | 12371 | 0.436 | 0.164 | 0.115 | 0.757 | 145162 |
| 40–59 | −2.888 | 0.834 | −4.523 | −1.253 | 9578 | 1.030 | 0.181 | 0.676 | 1.384 | 106643 |
| 20–39 | −1.166 | 0.436 | −2.021 | −0.311 | 36085 | 1.870 | 0.085 | 1.704 | 2.036 | 369655 |
| 0–19 | 2.427 | 1.236 | 0.003 | 4.851 | 3039 | 3.238 | 0.147 | 2.950 | 3.526 | 108374 |
| Wife’s status quintiles | Coef. | s.e. | CI(lower) | CI(upper) | N | Coef. | s.e. | CI(lower) | CI(upper) | N |
| 80–100 | −0.259 | 0.547 | −1.332 | 0.813 | 151353 | −2.990 | 0.097 | −3.181 | −2.800 | 249858 |
| 60–79 | 1.018 | 0.869 | −0.685 | 2.720 | 57611 | −0.044 | 0.171 | −0.379 | 0.290 | 86487 |
| 40–59 | 0.645 | 0.600 | −0.532 | 1.821 | 95590 | 0.504 | 0.130 | 0.250 | 0.759 | 141238 |
| 20–39 | 1.334 | 0.378 | 0.594 | 2.074 | 252415 | 2.065 | 0.074 | 1.920 | 2.210 | 375627 |
| 0–19 | 5.381 | 0.968 | 3.484 | 7.278 | 12533 | 3.778 | 0.138 | 3.507 | 4.049 | 100344 |
Appendix B. Comparison of results from the EI approach and selected loglinear models, based on the first analytical example of status-race exchange.
Table B1.
Comparison of results from different approaches studying status-race exchange in black husband and white wife marriages, based on US 2000 Census IPUMS 5% microdata sample
| Study | Approach | Key finding | Evidence of exchange |
|---|---|---|---|
| Rosenfeld (2005): Model 5 | Loglinear modelling | log-odds (exchange parameter) = −0.1109*** | No |
| Gullickson and Fu (2010) Model 2 | Loglinear modelling | log-odds (exchange parameter) = 0.1067*** | Yes |
| Kalmijn (2010) Model 1-Hypergamy Ratio | Loglinear modelling | observed/expected ratio (black-white) = 1.36 | Yes |
| Exchange Index (EI) | Covariate balancing | = −1.44*** ; = 1.04*** | Yes |
Notes:
p<0.001. Loglinear models replicated here are specified in the original papers. Data introduction can be found in the section of the first analytical example. Full details of model statistics and estimated coefficients of other parameters are available upon request.
Appendix C. Two simulation experiments
Consider four types of marriages in a hypothetical population as follows:
| Husband is Black | Husband is White | |
|---|---|---|
| Wife is Black | Type 1 | Type 3 |
| Wife is White | Type 2 (the treated) | Type 4 |
Let us index the husband’s latent status score by , and the wife’s latent status score by . We then decompose and to , a shared component between the couple, and and respectively the husband’s and the wife’s deviations from the shared component. Further, let represent white-white marriage’s status advantage over black-black marriages, with intermarriages’ status advantage assumed to be half of it (per the assumption made in Kalmijn 1993 and 2010); and are gender-specific status exchange terms that are allowed to be heterogenous across couples. With these notations, we write the following model of status decomposition for the four types of marriages.
Type 1 black-black marriages
| (C1.1) |
| (C1.2) |
Type 2 black-white marriages
| (C2.1) |
| (C2.2) |
Type 3 white-black marriages
| (C3.1) |
| (C3.2) |
Type 4 white-white marriages
| (C4.1) |
| (C4.2) |
In our simulation, we assume
To estimate EI, we first need to convert and in the original interval scale into percentile ranks, and . We focus only on estimating EI for Type 2 intermarriages. Our simulated sample consists of 10,000 marriages in total, including 2,000 Type 1 (Control group for estimating ), 700 Type 2 (Treated); 300 Type 3, and 7,000 Type 4 (Control group for estimating ).
Substantively, indicates the structural gap in average status between whites and blacks due to racial stratification. In our simulation, it accounts for about 10–13 percent of the full range of or . The magnitude of relative to and captures status homogamy, resulting in a correlation of 0.6 between and in our simulation. Although heterogenous across couples in Type 2 intermarriages, black husbands have 4 latent status points higher on average than those matched under homogamy, and white wives 2 points lower on average. In other words, the treatment effect of Type 2 intermarriage from the wife’s perspective (i.e., , that is, gain in ) is larger in magnitude than that from the husband’s perspective (i.e., , that is, loss in ).
Due to nonlinear transformation from latent continuous scores to percentile ranks in the first step for calculating EI, we cannot analytically derive the precise true effects in percentile ranks. This is true even though we know from the simulation setup the true treatment effects in latent status scores (i.e., 4 and −2). To verify the consistency of our EI estimates, we resort to a computational method that derives the true values of treatment effects in percentile ranks based on a population-level simulation of 1 million marriages.
Figure C1 reports estimated and , each based on 1000 simulations, as specified above with gender-specific status exchange. The results suggest that our EI approach successfully and consistently identify gender-specific status exchange patterns. As a falsification test, Figure C2 reports another set of and estimates, each also based on 1000 simulations specified as above, except that and are now both set to zero. In this scenario of no status exchange in generating the data, racial status gap and status homogamy are the only forces shaping and . In this case, our EI approach yields null evidence for status exchange.
Figure C1.
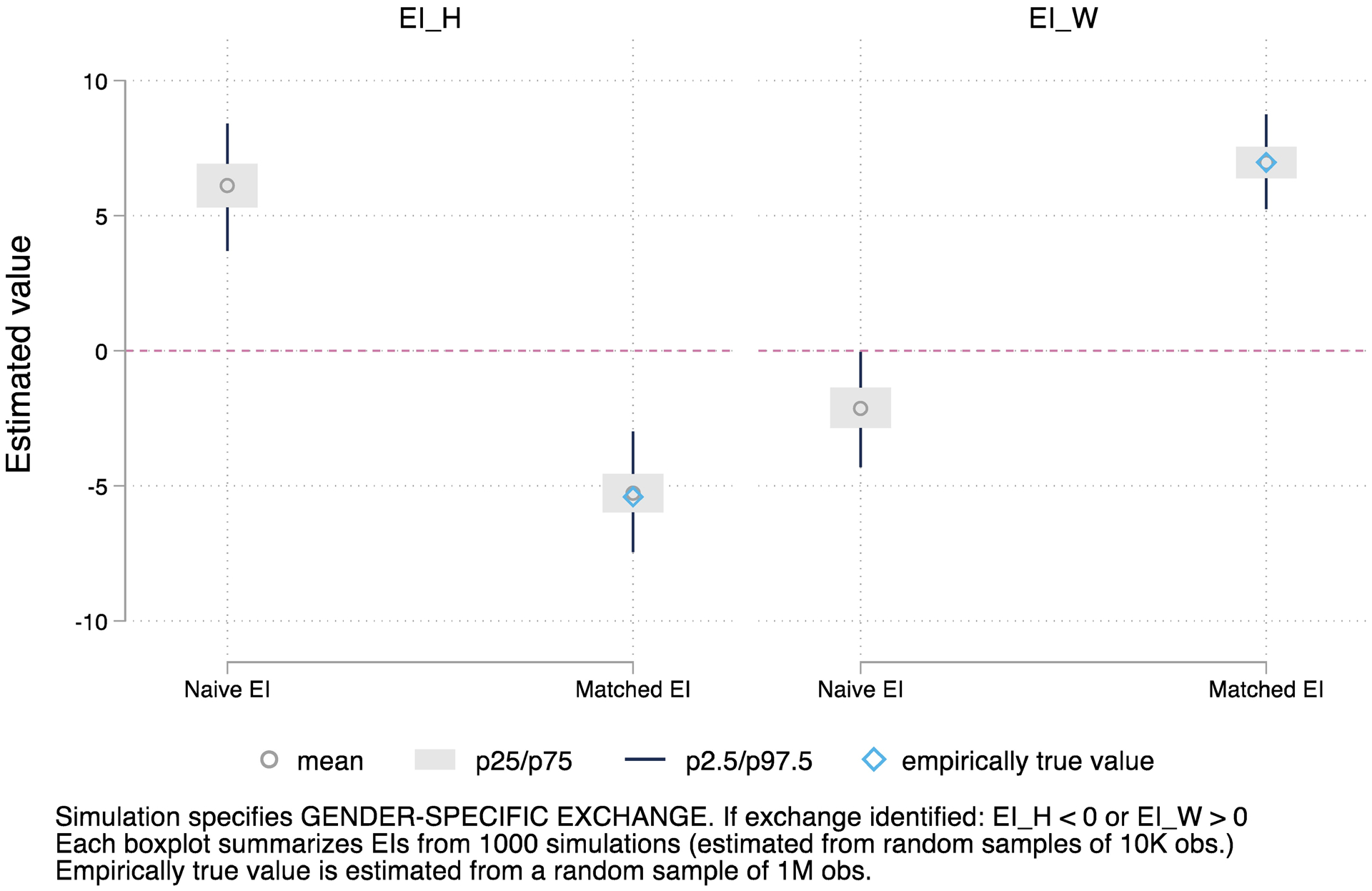
Estimated EIs in Simulation Experiment 1: Gender-specific status exchange specified
Figure C2.
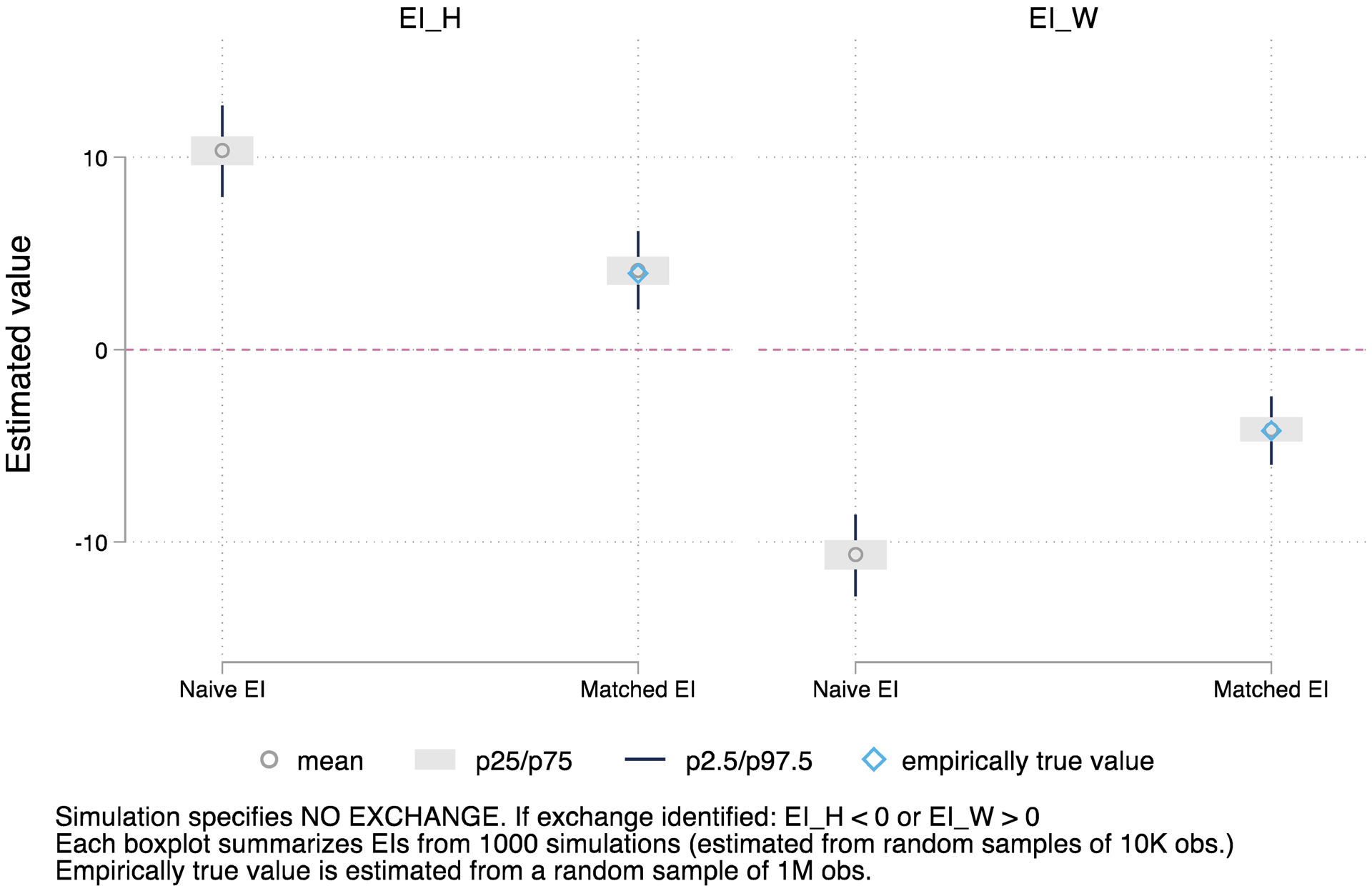
Estimated EIs in Simulation Experiment 2: No status exchange specified
Footnotes
Following the literature on status exchange in marriage, by marriage we refer to a heterosexual marriage throughout the article, although our proposed method is applicable to other types of marriages.
Hou and Myles (2013) and Schwartz, Zeng and Xie (2016) also provide summaries and comments about the debate.
Another technical, minor disagreement is over the distribution assumption of the outcome variable, marriage frequency. As noted by both Rosenfeld (2005) and Gullickson (2017), estimated results of status exchange from loglinear models may differ between assuming a Poisson or assuming a negative binomial distribution.
For detailed illustration of the implementation procedures, we also include our STATA program of the status-race analytical example as an online appendix.
Indeed, we did not have this step in earlier versions of this paper. We added this step in response to Christine Schwartz’s comments on an earlier version of this paper. We thank her for raising the issue.
It is also possible to keep G as continuous and estimate in the matched sample the correlation between and the outcome S as a summary measure of status exchange. This measure indicates the “marginal effect” of a one-unit difference in couple’s group difference on the social status of the spouse.
To avoid including individuals too young to have completed education or too old as being influenced by survival selection by education, we restrict the analysis to the 2000 population aged 25–60. This means that for spouses aged 25–29 in our analytical sample, their percentile ranks are in fact calculated based on 6 to 10-year moving birth cohort intervals. Also, recall that wife’s age in our analytical sample ranges between 25 and 49. Marriages of husbands younger than 25 or older than 60 are excluded from our analytical sample given that the husband’s percentile rank is missing by design here. Previously, we also constructed percentile ranks based on birth cohorts fixed on each decade, combining different waves of census microdata and taking averages for each cohort. The results from our alternative analytical examples are very similar to the ones reported in this version of the paper. We chose the current design to show that our approach can be applied simply with a single cross-sectional data source.
We use the STATA -cem- package and follow Blackwell et al. (2009) to weight each observation.
There are, of course, other models and methods in a broadly similar loglinear modeling framework developed before and after the two debates (e.g., Qian 1997; Fu 2001; Gullickson 2006b; Hou and Myles 2013; Schwartz et al. 2016). Here, we chose these three models as examples, mainly considering their direct involvement in and correspondence to the AJS debate.
We thank an anonymous AJS reviewer for pushing us to think about this.
Contributor Information
Yu Xie, Princeton University and Peking University.
Hao Dong, Peking University.
References
- Blackwell Matthew, Iacus Stefano, King Gary and Porro Giuseppe. 2009. “CEM: Coarsened Exact Matching in Stata.” The Stata Journal, 9(4): 524–546. [Google Scholar]
- Borjas George J. 1993. “The Intergenerational Mobility of Immigrants.” Journal of Labor Economics 11(1):113–135. [Google Scholar]
- Brand Jennie E and Yu Xie. 2010. “Who Benefits Most from College? Evidence for Negative Selection in Heterogeneous Economic Returns to Higher Education.” American Sociological Review, 75(2): 273–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chetty Raj, Grusky David, Hell Maximilian, Hendren Nathaniel, Manduca Robert and Narang Jimmy. 2016. “The Fading American Dream: Trends in Absolute Income Mobility since 1940.” Science, 356 (6336): 398–406 [DOI] [PubMed] [Google Scholar]
- Davis Kingsley. 1941. “Intermarriage in Caste Societies.” American Anthropologist, 43(3): 376–395. [Google Scholar]
- Dong Hao and Xie Yu. 2018. “Eight Decades of Educational Assortative Marriages in China.” Paper presented at the annual meeting of the Population Association of America, Denver, CO. [Google Scholar]
- England Paula and McClintock Elizabeth Aura. 2009. “The Gendered Double Standard of Aging in US Marriage Markets.” Population and Development Review, 35(4):797–816. [Google Scholar]
- Fu Vincent Kang. 2001. “Racial Intermarriage Pairings.” Demography, 38(2): 147–159. [DOI] [PubMed] [Google Scholar]
- Gullickson Aaron. 2006a. “Black/white Interracial Marriage Trends, 1850–2000.” Journal of Family History, 31(3): 289–312. [Google Scholar]
- Gullickson Aaron. 2006b. “Education and Black/white Interracial Marriage.” Demography, 43(4): 673–689. [DOI] [PubMed] [Google Scholar]
- Gullickson Aaron. 2017. “Comments on Conceptualizing and Measuring the Exchange of Beauty and Status.” American Sociological Review, 82(5): 1093–1099. [Google Scholar]
- Gullickson Aaron and Fu Vincent Kang. 2010. “Comment: An Endorsement of Exchange Theory in Mate Selection.” American Journal of Sociology, 115(4): 1243–1251. [Google Scholar]
- Gullickson Aaron, and Torche Florencia. 2014. “Patterns of Racial and Educational Assortative Mating in Brazil.” Demography 51(3): 835–56 [DOI] [PubMed] [Google Scholar]
- Holland Paul. 1986. “Statistics and Causal Inference.” Journal of the American Statistical Association, 81(396): 945−−970. [Google Scholar]
- Hou Feng and Myles John. 2013. “Interracial Marriage and Status-caste Exchange in Canada and the United States.” Ethnic and Racial Studies, 36(1): 75–96. [Google Scholar]
- Kalmijn Matthijs. 1993. “Trends in Black/White Intermarriage.” Social Forces, 72(1): 119–146. [Google Scholar]
- Kalmijn Matthijs. 1998. “Intermarriage and Homogamy: Causes, Patterns, Trends.” Annual Review of Sociology, 24(1): 395–421. [DOI] [PubMed] [Google Scholar]
- Kalmijn Matthijs. 2010. “Educational Inequality, Homogamy, and Status Exchange in Black‐White Intermarriage: A Comment on Rosenfeld.” American Journal of Sociology, 115(4): 1252–1263. [Google Scholar]
- Kalmijn Matthijs, and Fran van Tubergen. 2006. “Ethnic Intermarriage in the Netherlands: Confirmations and Refutations of Accepted Insights.” European Journal of Population 22: 371–397. [Google Scholar]
- Lichter Daniel T. and Qian Zhenchao. 2019. “The Study of Assortative Mating: Theory, Data, and Analysis.” Pp. 303–337 in Analytical Family Demography, edited by Schoen Robert. Cham, Switzerland: Springer. [Google Scholar]
- Logan John Allen, Hoff Peter D. and Newton Michael A.. 2008. “Two-Sided Estimation of Mate Preferences for Similarities in Age, Education, and Religion.” Journal of the American Statistical Association, 103(482): 559–569. [Google Scholar]
- McClintock Elizabeth Aura. 2014. “Beauty and Status: The Illusion of Exchange in Partner Selection?” American Sociological Review, 79(4): 575–604. [Google Scholar]
- McClintock Elizabeth Aura. 2017. “Support for Beauty-Status Exchange Remains Illusory.” American Sociological Review, 82(5): 1100–1110. [Google Scholar]
- Merton Robert K. 1941. “Intermarriage and the Social Structure.” Psychiatry, 4(3): 361–374. [Google Scholar]
- Morgan Steven L. and Winship Christopher. 2015. “Counterfactuals and Causal Inference: Methods and Principles for Social Research.” Second Edition. New York, NY: Cambridge University Press. [Google Scholar]
- Pollard John Hurlstone. 1975. Mathematical Models for the Growth of Human Populations. Cambridge: Cambridge University Press. [Google Scholar]
- Pollak Robert A. 1986. “A Reformulation of the Two-sex Problem.” Demography, 23(2): 247–259. [PubMed] [Google Scholar]
- Powers Daniel and Xie Yu. 2008. Statistical Methods for Categorical Data Analysis. Second edition. Bingley, UK: Emerald Group Publishing. [Google Scholar]
- Qian Zhenchao. 1997. “Breaking the Racial Barriers: Variations in Interracial Marriage Between 1980 and 1990.” Demography, 34(2): 263–276. [PubMed] [Google Scholar]
- Qian Zhenchao and Lichter Daniel T.. 2018. “Marriage Markets and Intermarriage: Exchange in First Marriages and Marriages.” Demography, 55(3): 849–875. [DOI] [PubMed] [Google Scholar]
- Rosenbaum Paul R. and Rubin Donald B.. 1984. “Reducing Bias in Observational Studies Using Subclassification on the Propensity Score.” Journal of the American Statistical Association, 79(387): 516–524. [Google Scholar]
- Rosenfeld Michael J. 2001. “The Salience of Pan-national Hispanic and Asian Identities in U.S. Marriage Markets.” Demography 38(2): 161–75. [DOI] [PubMed] [Google Scholar]
- Rosenfeld Michael J. 2005. “A Critique of Exchange Theory in Mate Selection.” American Journal of Sociology, 110(5): 1284–1325. [Google Scholar]
- Rosenfeld Michael J. 2010. “Still Weak Support for Status-caste Exchange: A Reply to Critics.” American Journal of Sociology, 115(4): 1264–1276. [Google Scholar]
- Schoen Robert. 1981. “The Harmonic Mean as the Basis of a Realistic Two-sex Marriage Model.” Demography 18: 201–216. [PubMed] [Google Scholar]
- Schoen Robert. 1986. “A Methodological Analysis of Intergroup Marriage.” Sociological Methodology 16: 49–78. [Google Scholar]
- Schoen Robert, and Wooldredge John. 1989. “Marriage Choices in North Carolina and Virginia, 1969–71 and 1979–81.” Journal of Marriage and Family, 51(2): 465–81. [Google Scholar]
- Schwartz Christine R. 2013. “Trends and Variation in Assortative Mating: Causes and Consequences.” Annual Review of Sociology, 39: 451–70. [Google Scholar]
- Schwartz Christine R., Zeng Zhen and Xie Yu. 2016. “Marrying Up by Marrying Down: Status Exchange between Social Origin and Education in the United States.” Sociological Science 3: 1003–1027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuman Howard, Steeh Charlotte, Bobo Lawrence, and Krysan Maria. 1997. Racial Attitudes in America: Trends and Interpretations. Rev. ed. Cambridge, MA: Harvard University Press. [Google Scholar]
- Song Xi, Massey Catherine G, Rolf Karen A, Ferrie Joseph P, Rothbaum Jonathan L, and Xie Yu. 2020. “Long-term Decline in Intergenerational Mobility in the United States since the 1850s.” Proceedings of the National Academy of Sciences (PNAS) 116(39): 19392–19397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song Xi, and Mare Robert D.. “Short-term and Long-term Educational Mobility of Families: A Two-sex Approach.” Demography 54, no. 1 (2017): 145–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torche Florencia and Rich Peter. 2016. “Declining Racial Stratification in Marriage Choices? Trends in Black/White Status Exchange in the United States, 1980 to 2010.” Sociology of Race and Ethnicity, 3(1): 31–49. [Google Scholar]
- Xie Yu, Brand Jennie E. and Jann Ben. 2012. “Estimating Heterogeneous Treatment Effects with Observational Data.” Sociological Methodology, 42(1): 314–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie Yu, Cheng Siwei and Zhou Xiang. 2015. “Assortative Mating without Assortative Preference.” Proceedings of the National Academy of Sciences, USA 112 (19): 5974–5978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng Zhen and Xie Yu. 2008. “A Preference-Opportunity-Choice Framework with Applications to Intergroup Friendship.” American Journal of Sociology 114: 615–648. [DOI] [PMC free article] [PubMed] [Google Scholar]


