Dynamic distortion in resonant galvanometric optical scanners

Abstract

High-speed optical systems are revolutionizing biomedical imaging in microscopy, DNA sequencing, and flow cytometry, as well as numerous other applications, including data storage, display technologies, printing, and autonomous vehicles. These systems often achieve the necessary imaging or sensing speed through the use of resonant galvanometric optical scanners. Here, we show that the optical performance of these devices suffers due to the dynamic mirror distortion that arises from the variation in torque with angular displacement. In one of two scanners tested, these distortions result in a variation of signal-to-noise (Strehl) ratio by an order of magnitude across the field of view, degrading transverse resolution by more than a factor of 2. This mirror distortion could be mitigated through the use of stiffer materials, such as beryllium or silicon carbide, at the expense of surface roughness, as these cannot be polished to the same degree of smoothness as common optical glasses. The repeatability of the dynamic distortion indicates that computational and optical corrective methods are also possible.

1. INTRODUCTION

Resonant galvanometric optical scanners [1–3] are used in numerous applications, including intraoperative imaging [4–6], microscopy [7–9], retinal imaging [10–12], optical coherence tomography [13–15], underwater imaging [16], DNA sequencing [17], flow cytometry [18], data storage [19], virtual reality and high-resolution display technology [20–22], high-resolution printing [23,24], data recognition [25], quality control [26], and autonomous vehicles [27–29]. The mirrors in these devices deflect a beam of light while oscillating sinusoidally at the resonant frequency of the galvanometer, allowing them to operate at high frequencies with low power demands, low vibrations, small footprints, and even in harsh environments [16,27–33]. Due to the sinusoidal nature of the oscillation, their angular acceleration is proportional to their angular displacement (beam deflection). As a result, the torque changes dynamically throughout the scan proportionally to the angular displacement [34], and therefore, so does the resulting induced wavefront aberration. While the maximum acceptable wavefront aberration varies with application, a widely used criterion is that the wavefront root-mean-squared (RMS) should be smaller than one-fourteenth of the wavelength of the light used, or equivalently, a Strehl ratio equal to or greater than 0.8 (Maréchal’s criterion) [35]. High-resolution imaging techniques such as structured illumination microscopy [36] or stimulated emission depletion microscopy [37] could have even more stringent requirements.

Brosens’s formula [34,38], derived for a rectangular mirror oscillating sinusoidally around its central axis, shows the dependence of the mirror deformation δ (see Fig. 1 left diagram) due to the dynamic torque in terms of the mirror substrate thickness t, density ρ, modulus of elasticity E, the Poisson’s ratio ν and diameter D, as well as the sinusoid amplitude θ and frequency f :

$$\delta \alpha \frac{\rho f^2{D}^5\theta }{E{t}^2}\left(1-v^2\right).$$ (1)

Fig. 1.

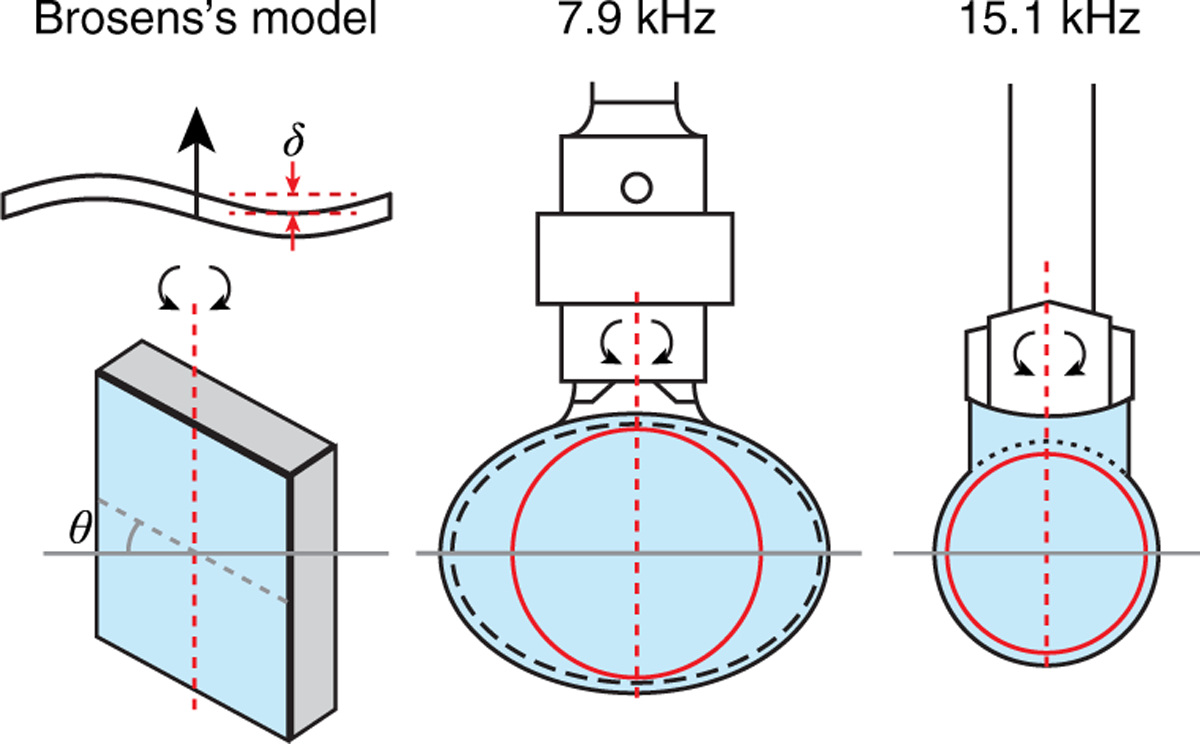
Brosens’s model [34,38] assumes an axle along the center of a rectangular scanner and the tested 7.9 kHz and 15.1 kHz scanners were held by a single hinge.

Irrespective of the departure of a scanner deformation from Brosens’s mechanical model, this proportionality informs us of the relative impact of the relevant physical parameters and can therefore be used to compare mirror substrates and/or resonant scanners. While building custom scanners is rare, at least one manufacturer, Electro-optical Products Corporation (EOPC; Ridgewood, NY, USA), allows the use of customer-provided mirrors. Surprisingly, the shape and amplitude of the dynamic wavefront distortions of commercial resonant galvanometric optical scanners are not known, or least reported [39] and as a result the real-world performance of these systems is not well documented. A custom Shack–Hartmann wavefront sensor (SHWS) was used to characterize the mirror distortion in two widely used resonant scanners depicted in Fig. 1-a 7.9 kHz CRS scanner by GSI Lumonics (now Cambridge Technology, Bedford, MA, USA) [8,40–50] and a 15.1 kHz SC-30 by EOPC [9,11,12,51–69] utilizing a custom mirror. The Shack–Hartmann wavefront sensor was selected both for convenience, as it was available to us, and because of our extensive experience with this type of sensor. We first present measurements of mirror distortions as a function of angular displacement, then we discuss the implications of these distortions for imaging, and finally, we propose two corrective methods, one computational and one optical.

2. METHODS

A. Experimental Setup

A custom SHWS [70] that accounts for focal shift [71] due to the low Fresnel number of its lenslets (geometrical focal length, f_l = 9.35 mm, and lenslet pitch, D_l = 203 μm) was used to measure resonant scanner mirror distortions. In the optical setup, depicted in Fig. 2, collimated light from a 680 nm superluminescent diode from Superlum (Carrigtwohill, Co. Cork, Ireland) is focused onto a piece of paper after reflection on the resonant scanner mirror. The scanner deflection moves the focused spot across the paper, effectively erasing the phase (wavefront) information of the first pass of the light through the optical system [72]. In this way, the SHWS, which is optically conjugate to the resonant scanner mirror surface sees a de-scanned wavefront generated by the light focused on the paper. This de-scanning is desirable because the tip and tilt that would be seen by the wavefront sensor in a single-pass setup would be orders of magnitude larger than the mirror distortions to be measured.

Fig. 2.

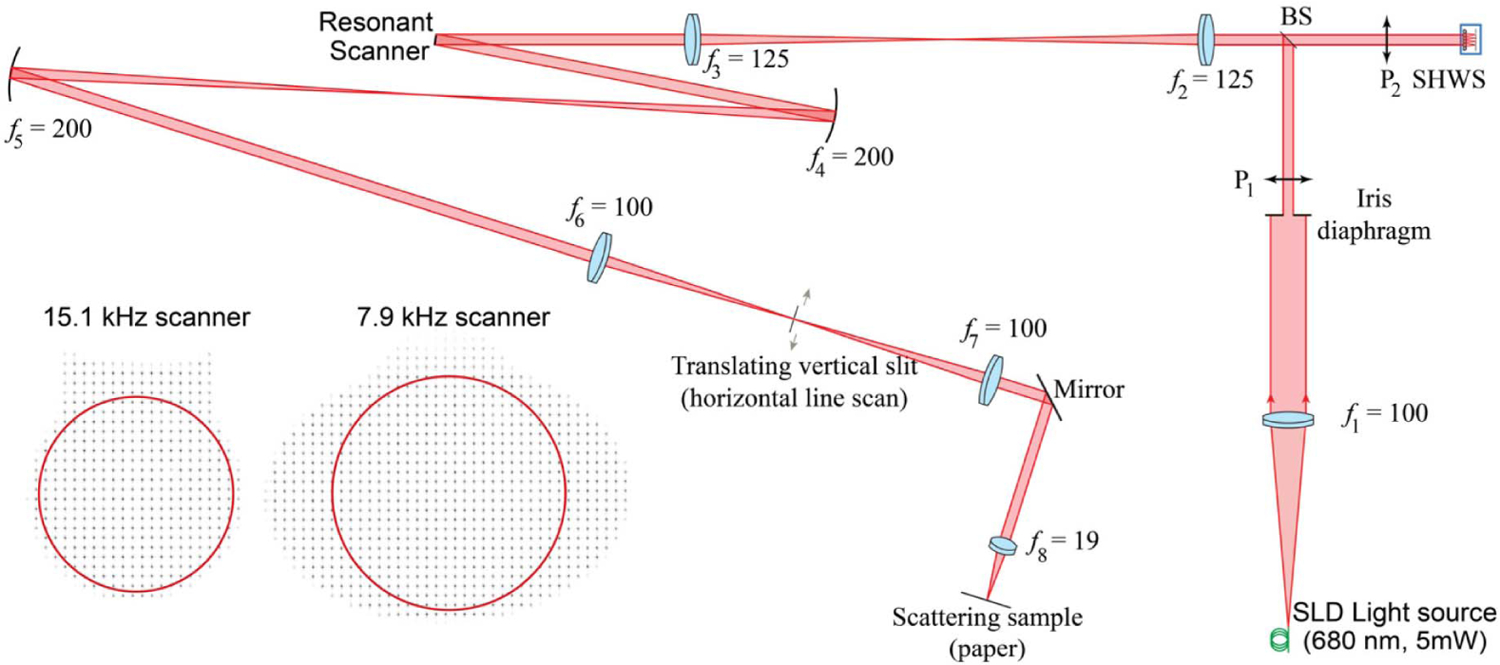
Experimental setup diagram for measuring the dynamic wavefront distortions of resonant scanners.

The dynamic wavefront aberrations were measured at different portions of the scan by collecting light passing through a slit approximately 400 μm in width and optically conjugate to the image plane. To mitigate undesired reflections from the slit edges, the light source was electronically modulated to turn on only when the focused beam is within the slit. In this way, the slit allowed us to confirm that the data was indeed captured at the desired scanner mirror orientation. An alternate single-pass strategy by Brown et al. [39] that used a pulsed laser diode synchronized with a torsion bar scanner showed non-diffraction-limited wavefront distortions.

B. Data Collection

The angular orientations at which the dynamic wavefront distortion was measured were determined by first capturing SHWS images while the slit was moved across the entire motor range and recording the total image intensity. The images are brighter at the edges of the resonant scanner field of view, due to the lower angular velocity. By measuring the location and separation of the intensity peaks after averaging five measurements, we found these to be repeatable with a 3σ-error lower than 0.1°.

Background-subtracted SHWS images were captured at 13 uniformly spaced slit locations within the central 90% of the scanner field of view, first with the scanning moving clockwise, and counterclockwise later. The resulting wavefront aberration maps captured both the dynamic distortion of the resonant scanner mirror and the static wavefront aberrations from both elements in the optical setup and the resonant scanner mirror itself.

The static aberrations were measured by capturing additional measurement with the resonant scanner motor rotated around the mirror rotation axis, and its amplitude set to its minimum value (~0.2°). This small amplitude is needed for the wavefront phase information of the beam reaching the paper to be erased by the moving of the focused spot across the rough surface of the paper.

C. Wavefront Estimation

Reference search boxes for centroiding were determined using lattice vectors evaluated from an average of all SHWS images captured at different positions of the scan. An iterative fractional centroid finding algorithm [73–75] was used to determine the centroids of each SHWS lenslet image. In the first iteration, the center of a pixel that contained the peak intensity value was chosen as the initial centroid and in subsequent iterations, the centroid was evaluated with a search box of width equal to the diffraction-limited spot width (2λf_l/D_l), which is re-centered on the centroid estimated in the previous iteration. The displacement of the centroids along the x and y dimensions due to dynamic distortions of the resonant scanner at each normalized half-scan angle position were obtained by subtracting the centroids of the images capturing the static aberrations from those of the dynamic plus static SHWS aberrations. Assuming that the lenslets were uniformly illuminated [76], the local wavefront slopes were calculated as the ratio of the centroid displacements and the lenslet focal length. Circles were fitted to the SHWS images and 90% of the mirror area was used as the pupil for wavefront estimation, as shown by the red circles in Fig. 2 above. This resulted in pupil diameters of 4 mm (311 lenslets) and 5 mm (480 lenslets) for 15.1 kHz and 7.9 kHz scanners, respectively. We then evaluated the averaged Zernike polynomial gradients up to the 15th order over square lenslets [77] and used these to least squares fit the estimated local wavefront slopes. The calculations were validated against zonal reconstruction based on Southwell’s slope geometry [78] and optometric trial lenses. We note that the wavefront RMS reproducibility error is 5.3 nm, which is close to the oblique trefoil and vertical astigmatism values reported for the 7.9 kHz resonant scanner. The point spread function (PSF) was evaluated using the discrete Fourier transform of the complex amplitude distribution of the field incident at the pupil of the SHWS [79] and the Strehl ratio was then estimated from the normalized on-axis intensity.

3. RESULTS

The dynamic wavefront distortion of the 7.9 kHz resonant scanner measured within the central 90% of a 6.1° scanning angle over a circular pupil, 5 mm in diameter, is shown in Fig. 3. The distortion reaches a maximum wavefront RMS error of 28 nm. When decomposed into Zernike polynomials using the axis of rotation as the y-coordinate axis, and the x axis passing through the mirror center, oblique astigmatism dominates the distortion comprising 74% of the wavefront RMS, as can be seen in the top row of wavefronts in Fig. 3(b). Oblique trefoil (5%) and vertical astigmatism (3%) are the two next most substantial aberrations. The strong anti-symmetric components of the wavefront relative to the x axis might appear unexpected given the mirror symmetry, but it can be explained by the fact that the mirror is attached to the scanner axle at only one end. The attached end of the mirror “follows” the axle rotation, while the opposite end lags, effectively twisting the mirror surface. The magnitude of the dynamic distortion, and in particular the magnitudes of oblique astigmatism and trefoil are linear with angular displacement (correlation coefficient ≥0.98 for oblique astigmatism), repeatable across trials to within 27% (5.8 nm), and repeatable between the clockwise and counterclockwise rotations to within 1% (0.2 nm). For scanning amplitudes equal to or smaller than the one tested here, the mirror dynamic distortion in this scanner is below Maréchal’s criterion for the 680 nm light used in our measurements as well as Strehl ratio and PSF calculations, shown in Figs. 3(f) and 3(g). Here it is important to note that although the angular displacement and the angular acceleration change sinusoidally with time, the angular acceleration varies linearly with angular displacement, and thus, the linear relationship between aberration amplitude and total wavefront RMS and angular displacements is expected.

Fig. 3.

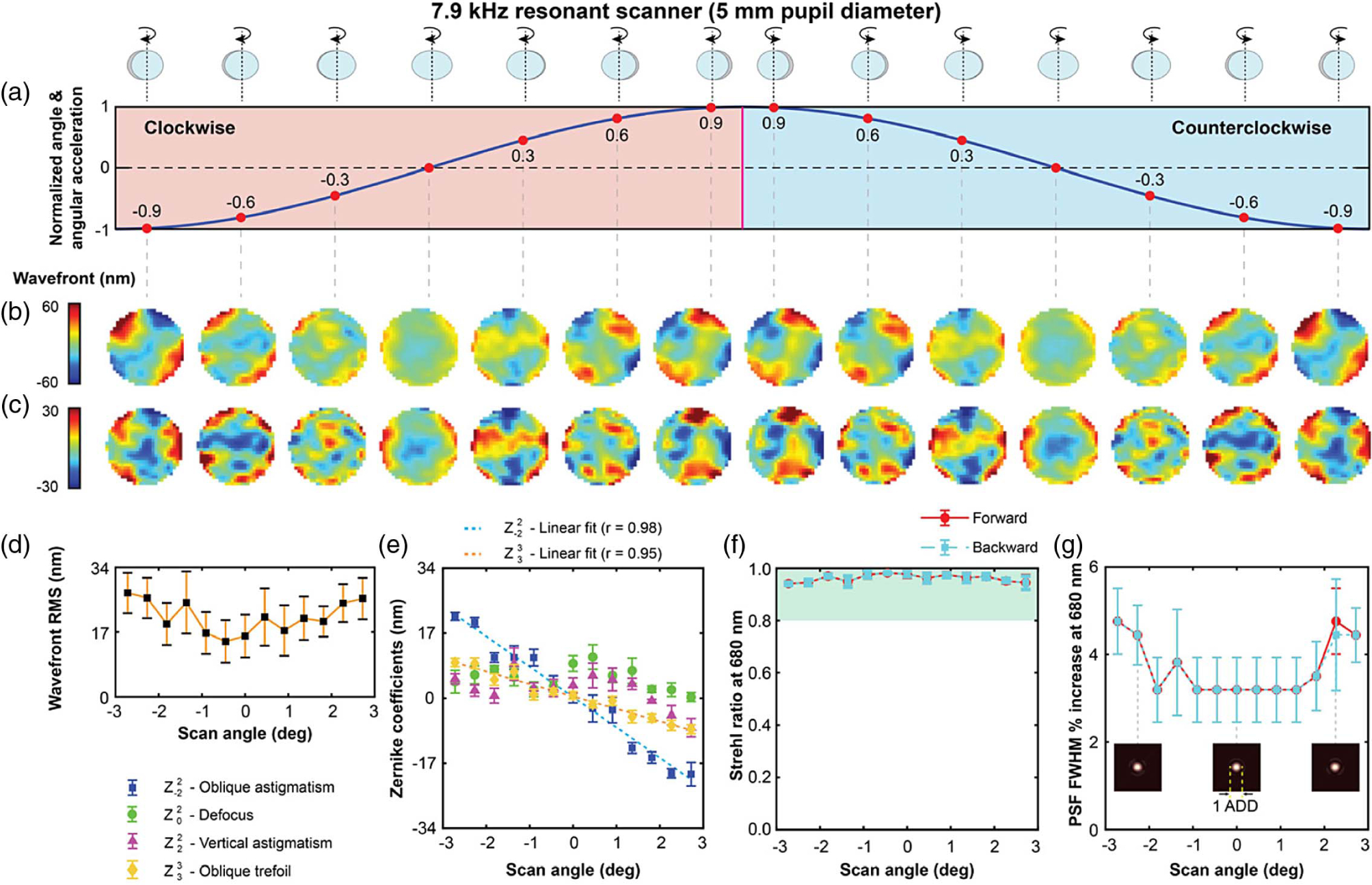
Dynamic wavefront distortions over a 5 mm pupil diameter in the 7.9 kHz resonant scanner operating at 6.1° across the sinusoidal oscillation are shown in (a). The total wavefront distortions are shown in (b), and oblique astigmatism subtracted wavefronts in (c). The plots of the variation of wavefront RMS, Zernike coefficients, Strehl ratio (at 680 nm) and increase in the FWHM of the PSF (at 680 nm), across the field of view, are shown in (d)–(g). The green shaded region in (f) satisfies the Maréchal criterion. The inset diagrams in (g) show PSFs at three different scanner mirror orientations.

The dynamic wavefront distortion of the 15.1 kHz resonant scanner, measured over the central 90% of a 4.9° field of view and a 4 mm circular pupil, is about 7 times larger, as it can be seen in Fig. 4. As expected from Eq. (1), the mirror distortion in this scanner is larger than the 7.9 kHz scanner, due to the thinner mirror substrate and the higher resonant frequency, despite the smaller diameter and field of view. The maximum wavefront RMS near the edge of the scan is 186 nm, dominated by oblique astigmatism (88%) and oblique trefoil (4.5%), both being linear with angular displacement (0.99 correlation coefficients). These wavefront aberrations are repeatable across measurements to within 3.5% (4.6 nm) and between clockwise and counterclockwise rotation within 3.3% (1.5 nm). When evaluating the Strehl ratio and full width at half-maximum of the radially averaged PSF at the test wavelength, we find that the mirror distortion results in a 10-fold reduction of the Strehl ratio, when compared to that at the center of the scanning range. Also, the radially averaged width of the PSF, often used as a measure of image resolution, broadens by more than a factor of 2. The dashed curves in Figs. 4(f) and 4(g) also show how the optical performance would improve to better than Maréchal’s criterion with the correction of oblique astigmatism alone.

Fig. 4.

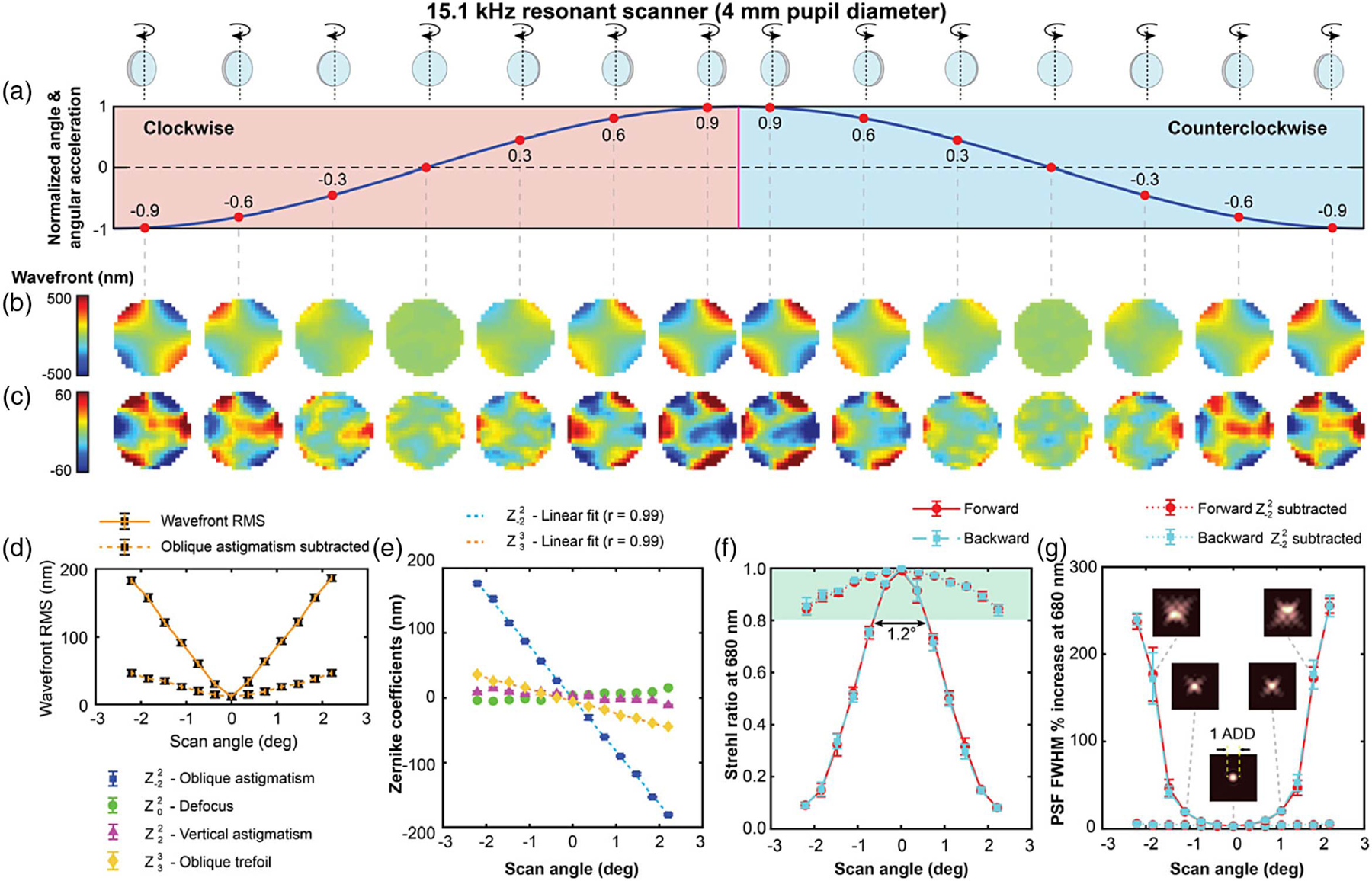
Dynamic wavefront distortions over a 4 mm pupil diameter in the 15.1 kHz resonant scanner operating at 4.9° across the sinusoidal wave are shown in (a). The total wavefront distortions are shown in (b), and oblique astigmatism subtracted wavefronts in (c). The plots of the variation of wavefront RMS, Zernike coefficients, Strehl ratio (at 680 nm) and increase in the FWHM of the PSF (at 680 nm), across the field of view, are shown in (d)–(g). Additional curves in (f) and (g) using dashed lines show the theoretical Strehl ratio and PSF FWHM predicted if oblique astigmatism was corrected. The green shaded region in (f) satisfies the Maréchal criterion. The inset diagrams in (g) show PSFs at three different scanner mirror orientations.

Measurement of the dynamic wavefront RMS across four different fields of view (see Fig. 5) show that the mirror distortion is independent of the amplitude of the resonant scanner oscillation, only depending on the mirror angular displacement from its central position.

Fig. 5.

Wavefront RMS of the dynamic wavefront distortions for different maximum scan amplitudes of the 15.1 kHz resonant scanner, illustrating how the mirror distortion depends on the angular displacement, and not on the oscillation amplitude.

To illustrate how the resonant scanning mirror’s dynamic distortion affects an imaging system, we captured an image of a flat piece of paper in a custom adaptive optics confocal scanning ophthalmoscope [12], which for all practical purposes can be thought of as a reflectance confocal microscope with a piece of paper as sample. This instrument uses a 15.1 kHz EOPC scanner with a mirror identical to the one tested with the SHWS and was operated at ~5° field of view with a 4 mm circular pupil. Paper was selected as a target due to its intricate structure when seen at high magnification. A raw image was captured using light from a 790 nm superluminescent diode from Superlum (Carrigtwohill, Co. Cork, Ireland) with pixels uniformly spaced across the paper with 1:1 aspect ratio. This raw image shows an ~70% intensity reduction toward the left and right edges (see top left panels of Fig. 6), where the resonant scanner mirror is most distorted. This is consistent with the calculated reduction in Strehl ratio shown in Fig. 4, considering that the confocal detector is 1.0 Airy disk in diameter, as opposed to a point detector. The variation in intensity across image columns can be approximated as a sinusoidal curve, as the cyan line shows. A second image with uniform intensity across columns was created by normalizing the intensity of each column (see bottom left panel in Fig. 6). Then, the power spectrum of each column was calculated (bottom center panel in Fig. 6). The spectra show the attenuation of spatial frequency contrast at both the left and right edges of the image, within the optical bandwidth of the system (bottom right panel in Fig. 6). The spatial frequencies between 1 and 30 cycles/deg, which correspond to the lowest 50% of the optical bandwidth are attenuated by ~70%, while the 30–60 cycles/deg vary smoothly between a reduction of 70% and 0%, with the latter reached at the end of the optical band, where noise dominates. The attenuation of effectively all spatial frequencies after accounting for the lower photon count at the confocal detector means that image contrast of objects of any scale will be attenuated, and thus harder to resolve due to the dynamic distortion of the resonant scanner mirror.

Fig. 6.

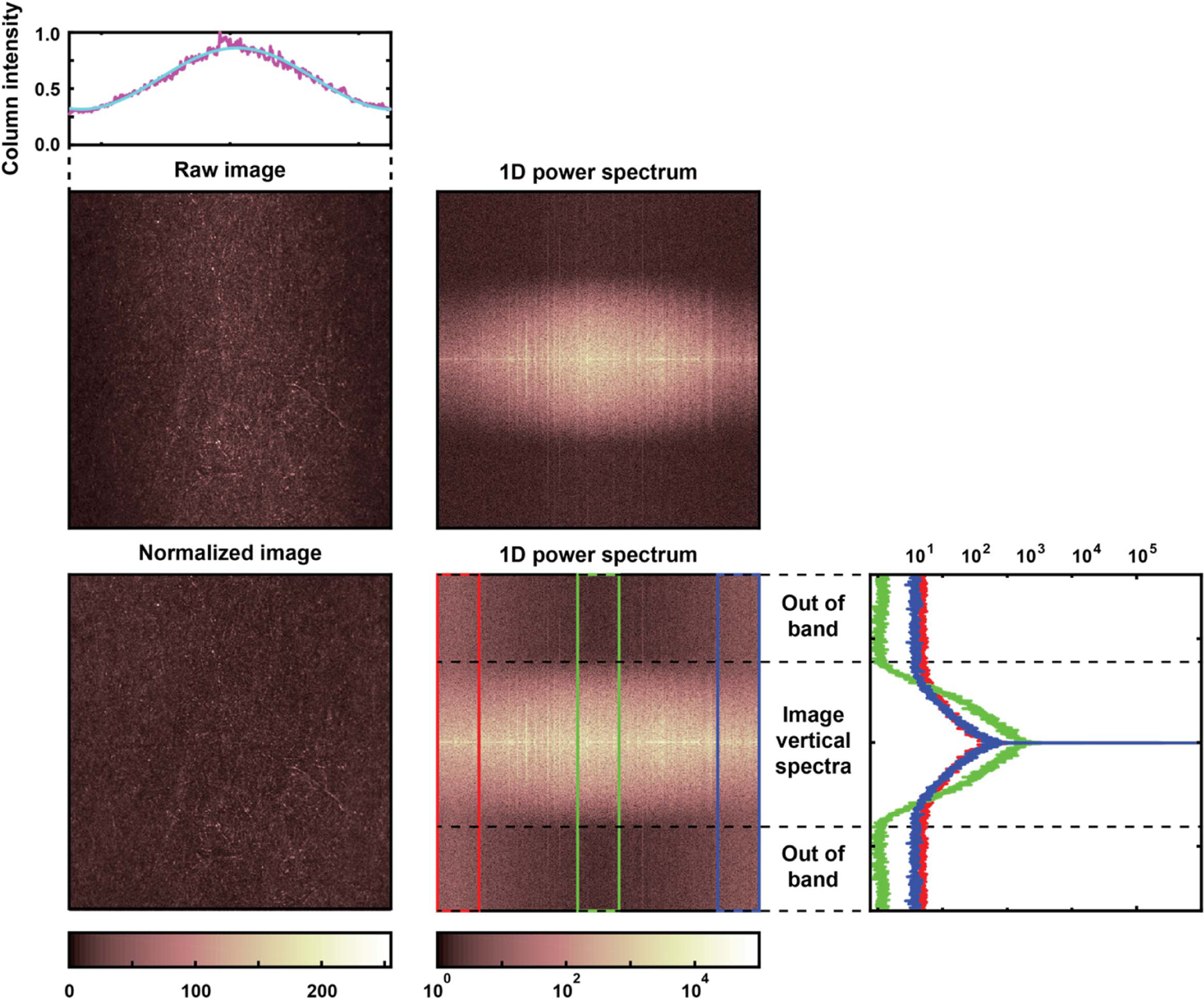
Images of the paper before and after column-wise intensity normalization (top) captured with a custom reflectance confocal microscope with a 15.1 kHz resonant scanner and 5° field of view, and their corresponding column-wise power spectra (bottom). Note the dark left and right edges indicating the lower Strehl ratio due to the resonant scanner mirror distortion and the attenuation of higher spatial frequencies in the same areas (arrows).

4. DISCUSSION AND SUMMARY

The dynamic distortion in two widely used resonant galvanometric optical scanners was measured and found to be dominated by oblique astigmatism that is linear with angular displacement. According to Maréchal’s resolution criterion, the distortion in the 7.9 kHz scanner was found to be negligible for 680 nm light, although according to Brosens’s mechanical modeling, its 12 kHz version (not tested) would not be so. Despite the small distortion, these scanners are often avoided in research and clinical settings due to the audible, and very uncomfortable, sound they generate when operating and that is not easily mitigated even with well-engineered casing. This means that the high-frequency scanners, similar to the 15.1 kHz scanner, are often preferred both because of the higher imaging speeds and higher resonant frequency, which although still audible by younger individuals is substantially more tolerable [80]. Our data shows that this higher scanning rate comes at the considerable price of almost an order of magnitude larger mirror distortion, at least when using a mirror 4.5 mm in diameter. According to Brosens’s formula, an ~30% reduction in mirror size would suffice to mitigate aberrations below Maréchal’s criterion. This pupil reduction would come at the expense of sacrificing resolution or having to change the optical magnification, which would increase static aberrations or optical system complexity.

The repeatable nature of these distortions and their proportionality to angular displacement (see Fig. 5) suggest that corrective methods other than redesigned galvanometer mirrors using harder and/or lighter materials, such as beryllium or silicon carbide, or beam diameter reduction are possible. For example, a computational solution could be implemented as image deconvolution with a field-varying point spread function [81–83]. Although computationally demanding and likely to introduce image artifacts, this approach can correct for oblique astigmatism, oblique trefoil as well as other dynamic, and even static, aberrations. This approach is appealing because it can be used in existing instruments without any hardware modification. When the optical system can be modified, however, an optical correction could be applied by intentional tilting of optical elements with power. Nodal aberration theory [84–86] indicates, the tilting of elements with power can be used to introduce linear astigmatism, that is astigmatism with amplitude that is linear with the field coordinate and also linear coma, that is, the aberrations that dominate the mirror distortion in resonant galvanometric scanners [85,87]. This approach is appealing because it is a permanent solution that does not require data manipulation and could even be customized to account for differences in individual units. Importantly, and irrespective of the correction methods, and as illustrated by the curves in Figs. 4(f) and 4(g), the correction of oblique astigmatism alone will in most cases be sufficient to restore diffraction-limited imaging performance in scanners held by a single hinge.

In summary, dynamic wavefront aberrations and their correction must be considered when using resonant galvanometric scanners for applications in which optical performance is critical, both in terms of transverse resolution and signal-to-noise ratio.