Mechanoelectric coupling and arrhythmogenesis in cardiomyocytes contracting under mechanical afterload in a 3D viscoelastic hydrogel

Significance

The heart autoregulates its contractile strength to maintain cardiac output when pumping blood against the mechanical afterload from vascular resistance. Increased afterload in cardiovascular diseases is associated with cardiac arrhythmias. However, the underlying mechanisms remain elusive. Here, we studied the afterload effect on electrophysiology by embedding single cardiomyocytes in a three-dimensional viscoelastic hydrogel to apply afterload during cell contraction. We found that afterload is acutely transduced via nitric oxide synthase 1 (NOS1) signaling to modulate multiple ion channels to prolong action potential, increase Ca²⁺ transient, and enhance contractility. However, higher afterload causes a discordant alternans that is arrhythmogenic. Hence, our findings reveal an afterload-induced mechano-chemo-electro-transduction pathway that closes feedback loops in cardiac excitation–contraction coupling to enable autoregulation of contractility.

Abstract

The heart pumps blood against the mechanical afterload from arterial resistance, and increased afterload may alter cardiac electrophysiology and contribute to life-threatening arrhythmias. However, the cellular and molecular mechanisms underlying mechanoelectric coupling in cardiomyocytes remain unclear. We developed an innovative patch-clamp-in-gel technology to embed cardiomyocytes in a three-dimensional (3D) viscoelastic hydrogel that imposes an afterload during regular myocyte contraction. Here, we investigated how afterload affects action potentials, ionic currents, intracellular Ca²⁺ transients, and cell contraction of adult rabbit ventricular cardiomyocytes. We found that afterload prolonged action potential duration (APD), increased transient outward K⁺ current, decreased inward rectifier K⁺ current, and increased L-type Ca²⁺ current. Increased Ca²⁺ entry caused enhanced Ca²⁺ transients and contractility. Moreover, elevated afterload led to discordant alternans in APD and Ca²⁺ transient. Ca²⁺ alternans persisted under action potential clamp, indicating that the alternans was Ca²⁺ dependent. Furthermore, all these afterload effects were significantly attenuated by inhibiting nitric oxide synthase 1 (NOS1). Taken together, our data reveal a mechano-chemo-electrotransduction (MCET) mechanism that acutely transduces afterload through NOS1–nitric oxide signaling to modulate the action potential, Ca²⁺ transient, and contractility. The MCET pathway provides a feedback loop in excitation–Ca²⁺ signaling–contraction coupling, enabling autoregulation of contractility in cardiomyocytes in response to afterload. This MCET mechanism is integral to the individual cardiomyocyte (and thus the heart) to intrinsically enhance its contractility in response to the load against which it has to do work. While this MCET is largely compensatory for physiological load changes, it may also increase susceptibility to arrhythmias under excessive pathological loading.

Biological cells are capable of sensing and responding to mechanical forces. In every heartbeat, cardiomyocytes experience large dynamic changes in mechanical forces during diastolic filling (preload, which exerts mechanical strain or stretch on the cell) and systolic contraction against resistance (afterload, which exerts mechanical stress on the cell). In addition to neurohormonal regulation, the heart has intrinsic abilities to regulate the contractile force in response to preload [via the Frank–Starling mechanism (1–3)] or afterload [via the Anrep effect (4, 5)] in order to maintain cardiac output. Changes in mechanical load also regulate electrical activity, referred to as mechano-electric coupling [MEC (6, 7)], which may contribute to cardiac arrhythmias (8, 9). Several ion channels have been found directly mechano-gated or modulated by the mechanical load–induced signaling pathways (10). However, more than 100 y after Bainbridge’s discovery of MEC (11), the exact ionic mechanisms by which mechanical load modulates the electrical activity of the cardiomyocyte remain elusive.

We recently developed a patch-clamp-in-gel technique (12) based on our cell-in-gel system in which isolated cardiomyocytes are embedded in a three-dimensional (3D) viscoelastic hydrogel polymer matrix to apply afterload during cell contraction and investigate the cellular and molecular consequences of increased afterload (13, 14). This approach to apply afterload (mechanical stress) on the cardiomyocyte is profoundly different from previous studies using osmotic swelling, inflation, or uniaxial stretch to apply preload (mechanical strain) on the cardiomyocyte (15). Moreover, the cell-in-gel system imposes afterload during cyclic cardiomyocyte contraction as opposed to a static preload stretch used in most previous studies, with a few exceptions (16). To our knowledge, no data has been available on the ionic mechanisms of MEC under any kind of cyclic mechanical load during cardiomyocyte contraction. Hence, we aimed to study the afterload effects on regulating ion channels and action potential (AP) in cardiomyocytes during contraction in the beat-by-beat cardiac cycle.

Our previous study showed that mouse ventricular cardiomyocytes contracting in a 3D viscoelastic hydrogel exhibited increased intracellular Ca²⁺ transients and increased diastolic Ca²⁺ sparks, with both dependent on localized nitric oxide synthase 1 (NOS1) and Ca²⁺/calmodulin-dependent protein kinase II (CaMKII) signaling (13). In addition to mechanical loading, pathological changes in Ca²⁺ handling and nitric oxide (NO) signaling have also been linked to cardiac arrhythmias (17, 18). Therefore, we investigated the ionic mechanisms of afterload-induced MEC in rabbit (rather than mouse) ventricular myocytes in which the electrophysiology and Ca²⁺ handling properties resemble that of the human heart. We tested the hypothesis that mechanical afterload affects ion channels and Ca²⁺-handling molecules to regulate the AP, Ca²⁺ transient, and contractility in cardiomyocytes. Here, we used the patch-clamp-in-gel methodology to perform current-clamp, voltage-clamp, and AP-clamp experiments while the cardiomyocyte is contracting under afterload in a 3D viscoelastic hydrogel. We found that the afterload on a contracting cardiomyocyte regulated multiple ionic currents, including L-type Ca²⁺ current (I_Ca,L), transient outward K⁺ current (I_to), inward rectifier K⁺ current (I_K1), and a mechanosensitive current inhibited by GsMTx-4 (19), leading to prolonged AP duration (APD) and enhanced Ca²⁺ transient and contractility. However, this afterload also promoted discordant alternans in APD and Ca²⁺ transient, increasing the susceptibility to cardiac arrhythmias. Furthermore, we found that the afterload effects were critically mediated by the localized NOS1–NO signaling.

Results

Mechanical Afterload–Induced Changes in AP.

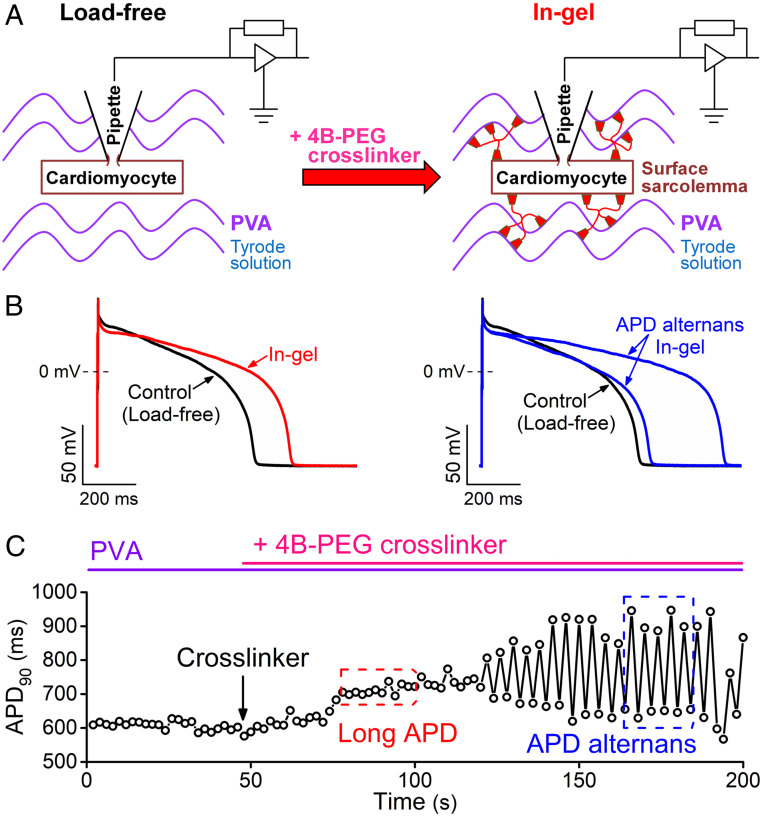
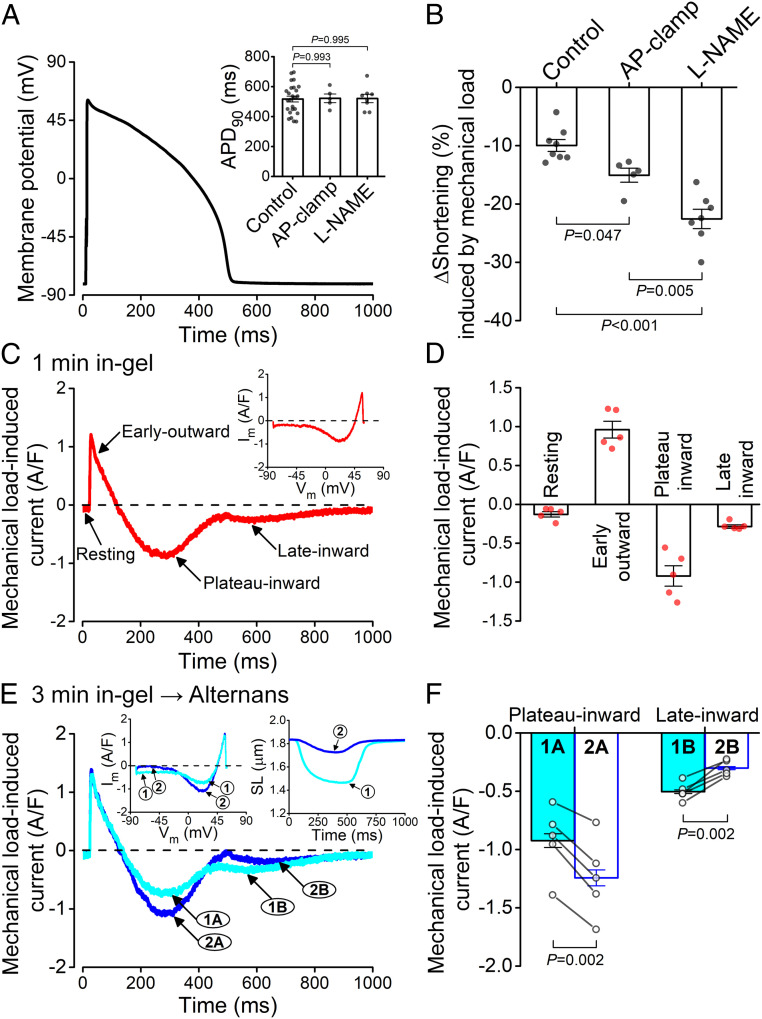
First, we examined how mechanical afterload acutely alters the AP morphology in single rabbit ventricular myocytes contracting in a 3D viscoelastic hydrogel. Fig. 1 shows a schematic of the patch-clamp-in-gel technique and a representative experiment. The patch-clamp experiment was performed in cardiomyocytes embedded in Tyrode’s solution containing polyvinyl alcohol (PVA; Fig. 1 A, Left). After achieving the whole-cell current-clamp configuration, steady-state APs were recorded at 0.5 Hz pacing frequency at room temperature (referred to as “load-free” control; Fig. 1B). Next, adding cross-linker tetraboronate-polyethylene glycol (4B-PEG, 7.5 wt%) to PVA (10 wt%) caused formation of the 3D viscoelastic hydrogel polymer matrix (for details, see Materials and Methods) surrounding the myocyte–electrode assembly (referred to as “in-gel” condition; Fig. 1 A, Right). As the gel stiffens over 2 to 3 min, there is an initial relatively stable prolongation of the APD (Fig. 1 B and C) followed by development of APD alternans (characterized by alternating beats that exhibit long and short APD).

Fig. 1.

Experimental approach to study mechanoelectric coupling. (A) Whole-cell patch-clamp experiments were performed in isolated rabbit ventricular cardiomyocytes embedded in PVA and perfused with Tyrode’s solution (load-free control). Then, 4B-PEG cross-linker was added to form a 3D viscoelastic hydrogel around the cell, which applies mechanical load during contraction. (B) Representative APs before gel formation (control, black) and after formation the gel (in-gel, red) showing APD prolongation and changes in AP morphology under mechanical load. Later, a significant APD alternans (two subsequent APs are shown, blue) developed within 3 min of steady-state pacing (0.5 Hz, room temperature) in gel. (C) Time course of changes in APD₉₀ before and after application of the cross-linker, which forms the gel within seconds.

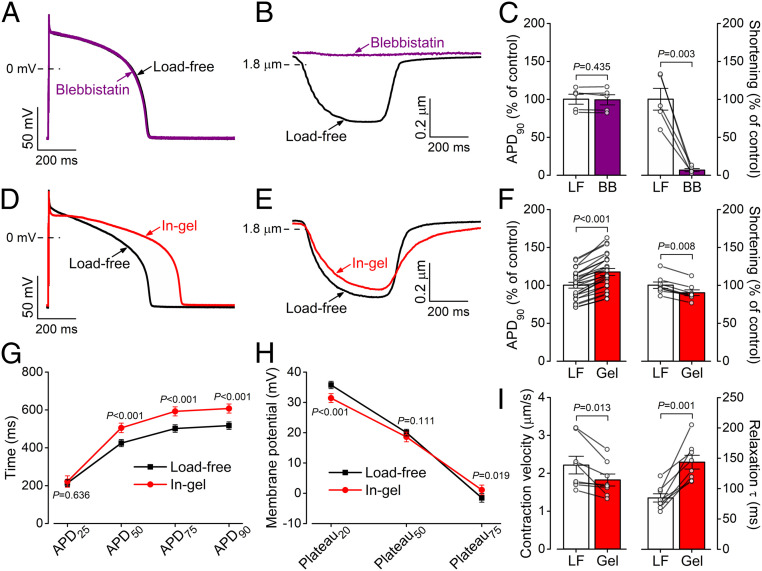
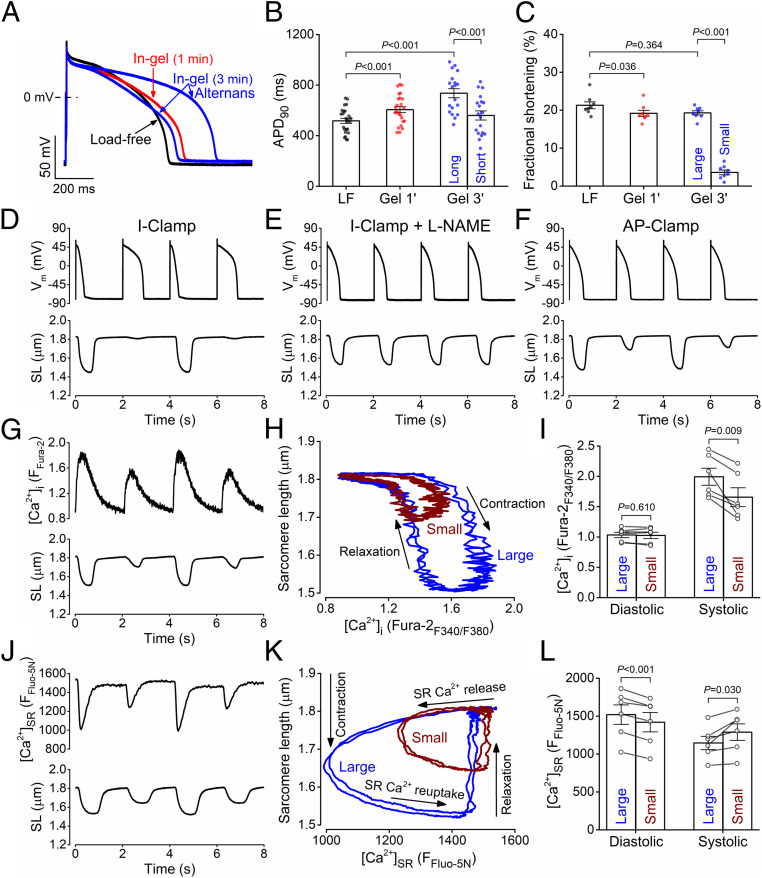
To investigate whether cell contraction by itself influences AP morphology, we measured the AP under load-free conditions in the presence of the myofilament contraction uncoupler blebbistatin (myosin II ATPase inhibitor, 10 μmol/L). As expected, blebbistatin stopped the contraction and relaxed the cardiomyocyte (Fig. 2 A and C), but preventing contraction in the absence of afterload (load-free) had no effect on AP shape or APD. This also agrees with a previous study showing that blebbistatin did not alter APs in Langendorff-perfused rabbit hearts (20). Therefore, the myocyte shortening per se, in the absence of afterload, had no significant acute effect on the electrical activity. This further supports the notion that the electrophysiological changes in Figs. 1 and 2 are the consequences of afterload during cell contraction rather than by sarcomere length changes.

Fig. 2.

Mechanical load affects the AP of ventricular cardiomyocytes. (A–C) Load-free (LF) contraction had no effect on ventricular AP in the rabbit when contraction was stopped using blebbistatin (BB, 10 µmol/L). Cardiomyocytes (n = 5 cells from three animals) were paced at 0.5 Hz frequency steady-state at room temperature. (D–F) Contraction in a 3D viscoelastic hydrogel (Gel, 1 min after crosslinking) significantly prolonged APD in cardiomyocytes (n = 25 cells from seven animals), while the amplitude of the sarcomere shortening slightly decreased (n = 8 cells from four animals). (G) APD prolongation at different phases of the AP in gel (n = 25 cells from seven animals). (H) Decreased early plateau potential (Plateau₂₀) and slightly increased late plateau potential (Plateau₇₅) in gel (n = 25 cells from seven animals). (I) Decreased contraction velocity and markedly increased relaxation time constant in gel (n = 8 cells from four animals). Paired, two-tailed Student’s t test.

Fig. 2 D–I shows APs and contractions of cardiomyocytes under afterload during contraction in the hydrogel (1 min after adding the cross-linker). The AP morphology showed characteristic changes under afterload (Fig. 2D): the AP duration measured at 90% repolarization (APD₉₀) increased from the load-free 517 ± 20 ms to 606 ± 23 ms in gel (Fig. 2 D, F, and G). The AP in gel also exhibited a slightly depolarized resting membrane potential and a more negative early plateau potential (Plateau₂₀) but more positive late plateau potential (Plateau₇₅; Fig. 2 G and H). This corresponds to faster phase-1 and slower phase-3 repolarization of the AP, indicating altered kinetics of the underlying ionic currents. The plateau potential at which the in-gel AP crossed the membrane potential of the load-free AP was 28.9 ± 1.6 mV. As expected, the sarcomere shortening was slightly smaller under mechanical load with fractional shortening decreased from 21.3 ± 0.9% in load-free to 19.2 ± 0.8% in-gel (Fig. 2 E and F). The maximal velocity of sarcomere shortening was slightly decreased in cardiomyocytes contracting under mechanical load, and the relaxation velocity was significantly reduced (τ of relaxation increased from 84.4 ± 6.8 ms load-free to 143.3 ± 11.4 ms in-gel; Fig. 2I). All mechanical load effects on AP were fully reversible upon blebbistatin application (SI Appendix, Fig. S1).

NOS1 Signaling Mediates Mechanoelectric Coupling.

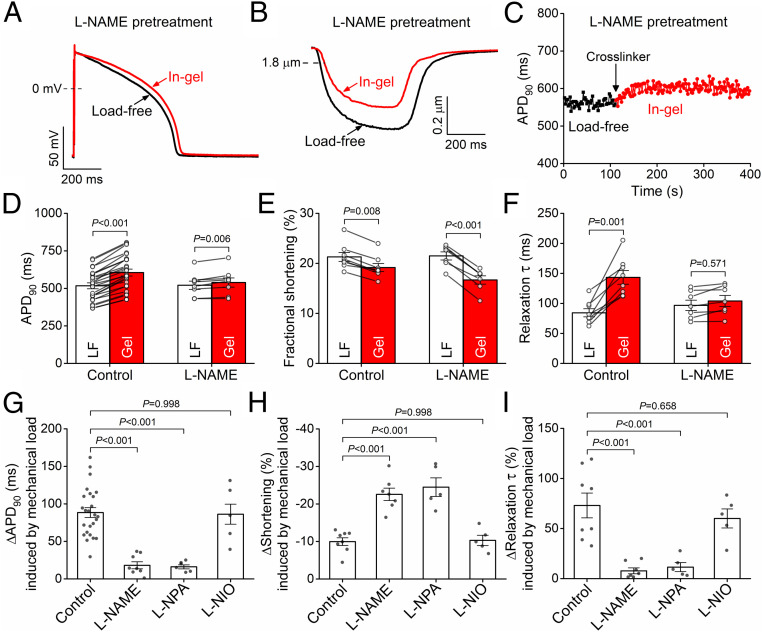
We previously found that nitric oxide synthase (NOS) mediates the mechano-chemo-transduction effect on Ca²⁺ handling under afterload (13). Here, we further tested whether the NOS pathway is also involved in the electrophysiological response of the myocyte to mechanical afterload. Under the load-free condition, pretreating the cells with the NOS inhibitor N^G-nitro-L-arginine methyl ester (L-NAME, 1 mmol/L) had no significant effect on any AP parameters (APD₉₀ was 521 ± 28 ms in L-NAME–pretreated cells versus 517 ± 20 ms in control; Fig. 3 A and D, white bars). Similarly, both fractional shortening and relaxation kinetics during load-free contraction were unchanged in L-NAME (21.5 ± 0.8% versus 21.3 ± 0.9% in L-NAME treatment and control, respectively; Fig. 3 B, E, and F, white bars).

Fig. 3.

Mechanoelectric coupling is predominantly mediated by NOS1 signaling. (A and B) Representative AP and sarcomere shortening traces in cardiomyocyte pretreated with the nonsubtype selective NOS inhibitor L-NAME (1 mmol/L) in load-free (LF) and in-gel (Gel) conditions. (C) Time course of APD change under mechanical load. (D–F) L-NAME pretreatment significantly attenuated APD prolongation (n = 8 cells from four animals), reduced fractional shortening, and attenuated the slowing of relaxation (n = 7 cells from four animals) in gel compared to control (n = 25 cells from seven animals and n = 8 cells from four animals for APD and shortening, respectively). (G–I) The mechanical load–induced APD prolongation was markedly attenuated by the selective NOS1 inhibitor L-NPA (5 μmol/L, n = 6 cells from three animals), whereas the NOS3 inhibitor L-NIO (10 μmol/L, n = 5 cells from three animals) had no effect. The sarcomere shortening under mechanical load was markedly reduced in L-NPA (n = 5 cells from three animals) but not in L-NIO (n = 5 cells from three animals). ANOVA with Dunnett’s post hoc test.

In sharp contrast to the lack of L-NAME effects on load-free cardiomyocyte results, L-NAME pretreatment nearly abolished the afterload-induced changes in APD and AP morphology (Fig. 3 A and D), albeit a slight APD₉₀ prolongation was still observed (by 18.1 ± 4.7 ms; Fig. 3 C and D). In L-NAME–pretreated ventricular myocytes, the afterload produced by the gel caused substantially less fractional shortening than in control (Fig. 3 B and E), and the mechanical load–induced increase in the relaxation decay was prevented (Fig. 3F).

Fig. 3 G–I compares L-NAME with isoform-selective NOS inhibitor effects in which the afterload-induced changes in APD₉₀, shortening, and relaxation velocity are compared to the control without NOS inhibition. The selective NOS1 inhibitor N^ω-propyl-L-arginine (L-NPA, 5 μmol/L) prevented the afterload-induced APD prolongation, further depressed shortening amplitude, and prevented the slowing of relaxation, like the L-NAME effects. In contrast, the NOS3 inhibitor N⁵-(1-Iminoethyl)-L-ornithine (L-NIO, 10 μmol/L) had no effect on any of these parameters when compared to control (Fig. 3 G–I). These results indicate that MEC is mediated predominantly by NOS1 signaling in rabbit ventricular myocytes contracting in a 3D viscoelastic hydrogel.

Mechanical Load–Induced Changes in I_to and AP Phase 1.

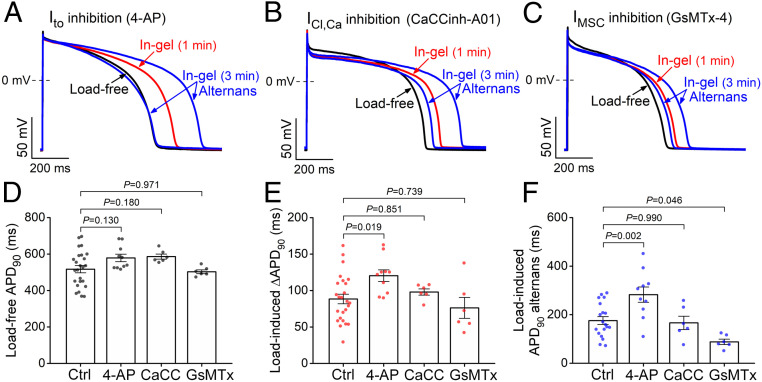
Next, we investigated which ion channels might mediate the afterload-induced increased early AP repolarization (phase 1). Cardiomyocytes were pretreated with selective ion channel inhibitors prior to subjecting them to mechanical load (Fig. 4 A–C). I_to was inhibited using 4-aminopyridine (4-AP, 3 mmol/L), which markedly reduced early repolarization and slightly prolonged load-free APD₉₀ (Fig. 4 A and D). Importantly, under mechanical load, the enhanced phase-1 repolarization was abolished in 4-AP–pretreated cells (Fig. 4A). Moreover, the mechanical load–induced APD₉₀ prolongation and alternans were enhanced in 4-AP–pretreated cells (Fig. 4 E and F). We conclude that an afterload-induced increase in I_to is likely a main contributor to the afterload-induced enhancement of early AP repolarization, an effect that may limit larger afterload-induced increases in APD₉₀ and alternans.

Fig. 4.

Transient outward K⁺ current and a mechanosensitive current contribute to AP changes under mechanical load. (A–C) Representative APs following inhibition of I_to by 4-AP (3 mmol/L), I_Cl,Ca by CaCCinh-A01 (30 µmol/L), and I_MSC by GsMTx-4 (5 µmol/L). (D) Load-free APD in control (Ctrl; n = 25 cells from seven animals) and following pretreatment with 4-AP (n = 10 cells from five animals), CaCCinh-A01 (CaCC; n = 6 cells from three animals), and GsMTx-4 (GsMTx; n = 6 cells from three animals). (E) Mechanical load–induced APD prolongation was more pronounced following 4-AP treatment. (F) Magnitude of mechanical load–induced APD alternans (difference between long and short APDs) was increased by 4-AP (n = 10 cells from five animals), unaltered by CaCCinh-A01 (n = 6 cells from three animals), and reduced by GsMTx-4 (n = 6 cells from three animals) compared to control (n = 19 cells from seven animals). ANOVA with Dunnett’s post hoc test.

Ca²⁺-activated Cl⁻ current (I_Cl,Ca), which has also been implicated in early repolarization (21), was inhibited using CaCCinh-A01 (30 μmol/L). CaCCinh-A01 slightly prolonged load-free APD₉₀ but failed to alter the afterload-induced effects on early repolarization or ΔAPD₉₀ versus control (Fig. 4 B, D, and E). We also tested the potential role of mechanosensitive nonspecific cation current (I_MSC) that can be inhibited using GsMTx-4 (5 μmol/L). GsMTx-4 had no effect on APD₉₀ in load-free cells in solution. In the cells in gel, GsMTx-4 did not change the afterload effects on the early repolarization and APD₉₀, although it did reduce the magnitude of APD alternans (Fig. 4 C–F). Hence, neither I_Cl,Ca nor I_MSC plays a major role in the afterload-induced early repolarization or APD₉₀ prolongation, but I_MSC plays a role in APD alternans.

Profile of Mechanical Load–Induced Membrane Current under AP Clamp.

Next, we investigated the changes in ionic currents that underlie the APD prolongation under afterload. A challenge in measuring individual ionic currents in our cell-in-gel system arises from our emphasis on maintaining physiological intracellular Ca²⁺ cycling during the excitation-contraction coupling under afterload. That precludes the conventional voltage-clamp experiments that typically use exogenous Ca²⁺ buffers to eliminate intracellular Ca²⁺ transient and cell contraction. Therefore, we used our physiological ^selfAP-clamp technique (22) to preserve Ca²⁺ transient and contraction and recorded the total membrane current induced by afterload. First, we recorded the cell’s own steady-state AP under the load-free condition and then used it as the voltage command in ^selfAP clamp (Fig. 5A). The load-free APD₉₀ in ^selfAP-clamp experiments was similar to the APD₉₀ measured in conventional current-clamp experiments (Fig. 5A, Inset). Without ^selfAP clamp, afterload induced a ∼10% decrease in sarcomere shortening (as in Fig. 3H), in which the APD was prolonged by ∼90 ms (Fig. 5B, control). However, in the ^selfAP clamp in which the APD is held constant, the afterload-induced reduction in shortening was even larger (∼15%). If NOS is additionally inhibited in ^selfAP clamp, the afterload-induced reduction in sarcomere shortening was even more severe (∼23% reduction; Fig. 5B). Notably, that suppression of contraction in ^selfAP clamp is similar to L-NAME alone (without AP clamp; Fig. 3H), but that makes sense because L-NAME also suppressed APD prolongation in that case (Fig. 3G). We conclude that the afterload-induced NOS1-mediated effects require APD prolongation to produce their full 57% protection of the myocyte’s ability to shorten, despite the imposed afterload that suppresses shortening (and ejection) by ∼23% without NOS1 (i.e., decreasing shortening by only 10% versus 23%; Fig. 5B). Indeed, the APD prolongation is expected to allow greater myocyte Ca²⁺ loading (more influx and less time for efflux) and, consequently, larger Ca²⁺ transient amplitudes.

Fig. 5.

AP clamp to measure membrane current under mechanical load. (A) AP waveform used in a representative ^selfAP-clamp experiment. Inset shows no difference in APD₉₀ between load-free control (n = 25 cells from seven animals), AP-clamped (n = 5 cells from three animals), and L-NAME (1 mmol/L; n = 8 cells from four animals) pretreated cells. (B) AP clamp (i.e., switching off the feedback of APD prolongation; n = 5 cells from three animals) led to a more pronounced decrease in the amplitude of sarcomere shortening versus control (n = 8 cells from four animals), but it was still larger than that measured in L-NAME (n = 7 cells from four animals). ANOVA with Tukey’s post hoc test. (C) Representative mechanical load–induced current measured in ^selfAP clamp. Inset shows the dynamic current–voltage relationship under AP clamp. (D) Peak current densities of the mechanical load–induced current components (n = 5 cells from three animals). (E) Representative alternating membrane currents during contraction alternans in ^selfAP clamp. Insets show the dynamic current–voltage relationship (Left) and the sarcomere length (SL, Right) under AP clamp. (F) During larger contraction (1), the inward current at the plateau phase was smaller (1A), and the late inward current was larger (1B). Conversely, during the smaller contraction (2), the plateau inward current was larger (2A), and late inward current (2B) was smaller (n = 5 cells from three animals). Paired, two-tailed Student’s t test.

We obtained afterload-induced change in the membrane current by subtracting the ^selfAP-clamp current trace recorded in gel from that in the load-free condition (Fig. 5C). This afterload-induced membrane current shows four distinctive phases: 1) a small (−0.13 ± 0.03 ampere/farad [A/F]) inward current during the resting membrane potential, which is consistent with slightly depolarized resting V_m measured in current clamp; 2) a rapidly declining early outward current (0.96 ± 0.11 A/F peak density), which is consistent with the afterload-induced I_to increase inferred from Fig. 4A; 3) an inward AP plateau current (−0.92 ± 0.13 A/F peak density); and 4) a late slowly declining inward current (−0.28 ± 0.02 A/F) following AP terminal repolarization (Fig. 5 C and D), which is consistent with the larger inward Na/Ca exchange current driven by larger Ca²⁺ transients (23). Characterizing the current–voltage relationship of this net membrane current (Fig. 5C, Inset) revealed that the early outward current reached its peak current density near the AP peak V_m, which is expected for I_to. The inward plateau current reached its peak at ∼+20 mV but was small at membrane potentials below −35 mV, which is similar to the V_m dependence of I_Ca,L.

Notably, the membrane currents under ^selfAP clamp also developed alternans in the later phase of gel formation (Fig. 5E). The early outward current did not alternate, which fits with it being largely I_to, which recovers rapidly and is largely Ca²⁺ independent. The beat with the larger Ca²⁺ transient and contraction would have greater sarcoplasmic reticulum (SR) Ca²⁺ release, which would enhance Ca²⁺-dependent I_Ca,L inactivation and cause less plateau inward I_Ca,L, as observed. Conversely, the larger Ca²⁺ transient would drive a larger inward Na⁺/Ca²⁺ exchange current that is most apparent in late repolarization and at diastole, as observed (Fig. 5 E and F).

These data show that mechanical afterload affects multiple ion channels at different phases of the AP and that the dominant inward currents are regulated by intracellular Ca²⁺ (based on alternans data). Afterload-induced APD prolongation also promotes larger Ca²⁺ transients. The tentative ionic current assignments in the previous two paragraphs make clear sense for the afterload-induced and alternans-related ^selfAP-clamp current changes. Taken together, these data show that the mechanoelectrical coupling provides feedback regulation on excitation–Ca²⁺ signaling–contraction in cardiomyocytes. The afterload-induced membrane currents under ^selfAP clamp provide an overview of the total changes in ionic currents in cardiomyocytes during the AP cycle, which also provide clues on the specific ion channels that might be mechanosensitive.

Mechanical Load Increases I_Ca,L and Decreases I_K1 under Voltage Clamp.

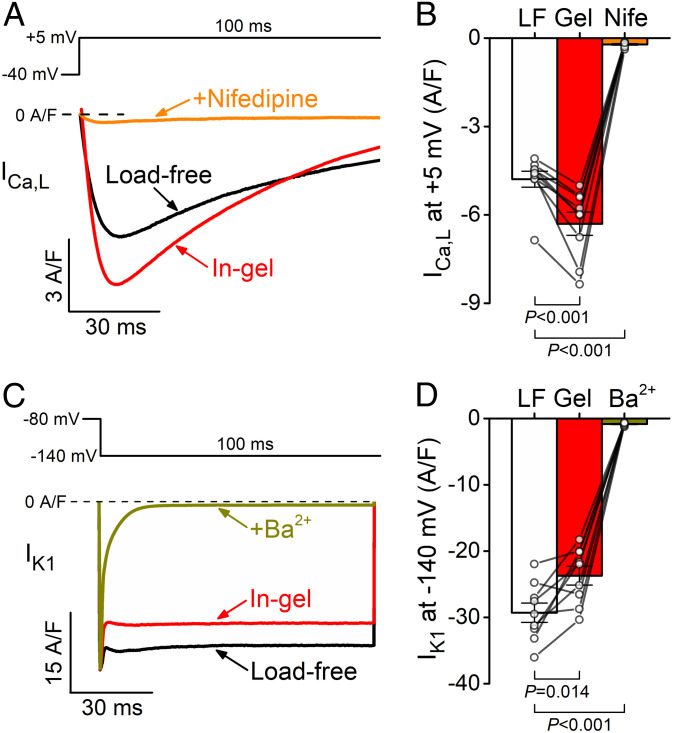
Prompted by the AP-clamp data suggesting mechanosensitive I_Ca,L, we directly tested for afterload-induced change of I_Ca,L. We measured I_Ca,L using conventional voltage-clamp protocol while preserving the Ca²⁺ transients and cell contractions by titrating the Ca²⁺ buffer in the pipette solution (see Materials and Methods). The I_Ca,L was measured during depolarizing pulses to +5 mV from a holding potential of −40 mV (to inactivate Na⁺ channels) and calculated by subtracting the nifedipine-sensitive background current. Mechanical load increased the peak I_Ca,L density from load-free −4.8 ± 0.3 A/F to −6.3 ± 0.4 A/F in gel (Fig. 6 A and B), confirming that afterload induced a significant increase in the I_Ca,L current density.

Fig. 6.

Mechanical load increases I_Ca,L and reduces I_K1 under voltage clamp. (A) Representative I_Ca,L traces during a depolarization pulse to +5 mV in load-free (LF) and in-gel (Gel) conditions. The step current was inhibited by 10 µmol/L nifedipine (Nife). (B) Mechanical load increased I_Ca,L peak density (n = 9 cells from five animals). (C) Representative I_K1 traces during a hyperpolarizing pulse to −140 mV. The current was inhibited by 300 µmol/L Ba²⁺. (D) I_K1 was significantly decreased under mechanical load (n = 9 cells from five animals). ANOVA with Dunnett’s post hoc test.

Next, because I_K1 is known to be important in stabilizing the negative resting V_m in ventricular myocytes, we measured I_K1 using conventional voltage-clamp protocol with a hyperpolarizing pulse to −140 mV. I_K1 was slightly decreased under mechanical load (−23.7 ± 1.4 A/F in gel versus −29.3 ± 1.5 A/F load free; Fig. 6 C and D). These data indicate that an afterload-induced reduction in I_K1 may underly the small depolarization in resting V_m. This reduction in I_K1 is expected to make the diastolic V_m less stable during events like delayed afterdepolarizations (24), which increases the risk of arrhythmias.

Mechanical Afterload Induces Alternans in APD, [Ca²⁺]_SR, [Ca²⁺]_i, and Contraction.

We have observed that some rabbit ventricular myocytes (19 out of 25 cells) not only exhibited APD prolongation but also progressively developed APD alternans after 3 min into gel formation (Fig. 7 A–C). The observed alternans was always discordant; that is, the longer APD occurred during the smaller contraction, while the shorter APD occurred with the larger contraction (Fig. 7D). This load-induced alternans dissipated by either dissolving the gel (SI Appendix, Fig. S2A) or using contraction uncoupler blebbistatin (SI Appendix, Fig. S2B) to relieve the afterload on cardiomyocytes. In comparison, similar discordant alternans occurred in load-free cells following high-dose (1 μmol/L) angiotensin II treatment and higher pacing rate (SI Appendix, Fig. S3) or following treatment with the L-type Ca²⁺ channel activator Bay K8644 (100 nmol/L) (SI Appendix, Fig. S4), suggesting a Ca²⁺-driven mechanism for discordant alternans.

Fig. 7.

AP, contraction, and calcium alternans under mechanical load. (A) APD alternans in cardiomyocytes contracting under mechanical load. (B) APD in load-free (LF) and in-gel conditions (Gel, 1 min; n = 25 cells from seven animals) and during the alternans (Gel, 3 min; short-long-short-long APD; n = 19 cells from seven animals). (C) Fractional shortening of the sarcomere length in load-free and in-gel conditions and during alternans (large-small-large-small contraction; n = 8 cells from four animals). ANOVA with Tukey’s post hoc test. (D–F) Representative AP and contraction alternans in I clamp, AP clamp, and in I clamp following L-NAME pretreatment. (G) Representative intracellular Ca²⁺ concentration ([Ca²⁺]_i) transient and contraction alternans. (H) Trajectories between sarcomere length and [Ca²⁺]_i. (I) Diastolic and peak systolic [Ca²⁺]_i levels during small and large beats during alternans (n = 6 cells from three animals). (J) Representative sarcoplasmic reticulum Ca²⁺ concentration ([Ca²⁺]_SR) transient and contraction alternans. (K) Trajectories between sarcomere length and [Ca²⁺]_SR. (L) Diastolic and peak systolic [Ca²⁺]_SR levels during small and large beats during alternans (n = 6 cells from three animals). Paired, two-tailed Student’s t test.

Importantly, afterload-induced APD alternans was not observed in any of the L-NAME–pretreated cells contracting in gel (Fig. 7E). In contrast, afterload-induced contraction alternans was robust even under ^selfAP clamp (constant AP waveform; Fig. 7F), in which the mechanoelectrical feedback is absent but mechano-Ca²⁺ feedback is present (although the contraction alternans were smaller under ^selfAP clamp). These data indicate that the afterload-induced Ca²⁺ handling changes are responsible for alternans, and the associated APD prolongation may further amplify contraction alternans. Moreover, simultaneous recording of sarcomere shortening and intracellular Ca²⁺ concentration ([Ca²⁺]_i, using Fura-2 fluorescence ratio) showed alternans in systolic [Ca²⁺]_i. There were no beat-to-beat changes in diastolic [Ca²⁺]_i or myofilament Ca²⁺ sensitivity, as evidenced by the overlapping [Ca²⁺]_i versus sarcomere length curves during relaxation (Fig. 7 G–I).

To examine whether the alternans arises from SR Ca²⁺ overload, we directly measured intra-SR [Ca²⁺] ([Ca²⁺]_SR) using Fluo-5N loaded into the SR lumen (25). We found afterload-induced alternating small-large SR Ca²⁺ releases that were paralleled by fluctuations of diastolic [Ca²⁺]_SR levels (Fig. 7 J–L). Notably, tachypacing-induced alternans is usually concordant and starts without variation in diastolic [Ca²⁺]_SR but can progress to diastolic [Ca²⁺]_SR alternans (26, 27), which is consistent with lowered diastolic [Ca²⁺]_SR after the large Ca²⁺ transient in the previous beat drives more Ca²⁺ efflux via Na⁺/Ca²⁺ exchange and less Ca²⁺ influx due to stronger Ca²⁺-dependent inactivation of I_Ca,L.

Discussion

Patch-Clamp-in-Gel Method to Study Afterload Effects on Cardiac Electrophysiology.

This is our first study on how the mechanical afterload on cardiomyocyte during beat-to-beat contraction regulates the AP and ionic currents. We explored the newly developed patch-clamp-in-gel methodology to perform various patch-clamp experiments (i.e., current clamp, voltage clamp, and AP clamp) while the cell was embedded in a 3D viscoelastic hydrogel and contracting under afterload. Here, we discuss our findings in the context of the previous literature but also keep in mind that the patch-clamp-in-gel setting applies 3D mechanical stress on the cell, which differs significantly from most previous studies of MEC by stretching the cell membrane to apply mechanical strain (i.e., uniaxial stretch, osmotic swelling, pipette suction, inflation, etc.). Given that different stress and strain fields on the rod-shaped cell architecture may activate different mechanosensors, the data from different experimental settings may not be directly comparable. Our intention here is to piece together information from relevant studies to gain more comprehensive understanding of the mechano-transduction mechanisms in cardiomyocytes.

Afterload Effects Are Mediated by NOS1–NO Signaling.

Our previous studies using the cell-in-gel system show that the mechano-chemo-transduction is mediated by localized NOS1 signaling that increases the systolic Ca²⁺ transient and contractility in compensatory response to increased afterload (13), but the diastolic spontaneous Ca²⁺ spark rate was also significantly increased under afterload, which could increase the susceptibility to arrhythmias (28). However, little was known about how afterload affects APs and ion channels in cardiomyocytes and how the mechanoelectric coupling relates to Ca²⁺ handling and cell contraction.

Furthermore, the near abolition of afterload-induced AP changes by inhibition of NOS1 indicates that this signaling pathway is critical to the electrophysiological effects of afterload, just as we have reported for the afterload-induced effects on myocyte Ca²⁺ handling (13). Thus, afterload-induced NOS1–NO signaling affects multiple ion channels and Ca²⁺ handling molecules. Future studies are needed to elucidate whether afterload-induced NO signaling directly alters the gating of these channels or indirectly by activating other signaling pathways, such as CaMKII and protein kinase G (PKG), among others. CaMKII has been shown to be activated by S-nitrosylation at serine 290 (29) and modulate sarcolemmal ion channel activities and intracellular Ca²⁺ handling in a very similar way, as observed here (30, 31). In contrast, PKG tends to inhibit I_Ca,L by phosphorylating serine 496 in the β_2a subunit of the L-type Ca²⁺ channel (32); however, details are still debated. Interestingly, NOS1 inhibition (without mechanical load) prolonged APD and increased I_Ca,L in guinea-pig cardiomyocytes (33). Thus, the precise molecular mechanisms by which mechanical afterload and NOS1–NO signaling affect each ion conductance require further investigation. Importantly, this afterload-induced NOS1–NO signaling pathway differs from the (stretch) preload-induced effects on cardiomyocyte Ca²⁺ handling reported by the Prosser and Lederer groups (16, 34), which involved stretch-induced rapid mechano-transduction mediated by microtubular deformation and NADPH oxidase 2 activation. Cell structural elements that sense and transduce mechanical afterload may include the costameres formed by the dystrophin–glycoprotein complex and the vinculin–talin–integrin system and require further investigation (15). These preload and afterload induced mechano-transduction pathways should combine in the working heart where both afterload and preload are present.

Our data using specific inhibitors of NOS1 (Fig. 3) indicates that NOS1 but not NOS3 is critical—almost entirely—for the main afterload effects on AP. However, the GsMTx-4–sensitive I_MSC (Fig. 4) also contributes to the APD alternans. Afterload also affects the major cardiac voltage-gated ion channels I_to, I_Ca,L, and I_K1, which contribute to remodeling the AP at various phases (Figs. 4–6). These ion channels have been reported to be mechanosensitive (7, 10) and are known to be regulated by NOS signaling (17). These data support the notion that afterload-induced NOS1–NO signaling modulates all these ion channels. The differential effect of NOS1 versus NOS3 indicates localized NOS1–NO signaling to these ion channels.

Afterload Effects on Regulating Ion Channels and AP.

Remodeling of AP morphology under mechanical stretch was demonstrated previously in both single-cell (10) and whole-heart (8) levels. Stretching the cardiomyocytes (preload) caused accelerated early AP repolarization and slowed terminal repolarization, which are similar to our finding of the afterload effects (Fig. 2). However, the reversal potential (∼+30 mV) of the afterload-induced current under ^selfAP clamp (Fig. 5C) is far more positive than that reported for stretch-activated currents (between 0 and −20 mV) (35). Moreover, in contrast to the stretch-induced currents with a typical linear current–voltage relationship (35), the afterload-induced membrane current under ^selfAP clamp clearly showed a composite current that changed dynamically during the AP time course (Fig. 5C). Several factors may account for the differences between the afterload effects here and the preload effects in previous studies: the different types of mechanical stimuli applied on cardiomyocytes (mechanical stress under afterload versus mechanical strain under preload), different dimensionality of the forces (3D-resistive afterload versus one-dimensional uniaxial prestretch), cyclic beat-by-beat afterload versus static prestretch, AP clamp versus rectangular-pulse voltage clamp, and preserved Ca²⁺ transient and contraction versus buffered [Ca²⁺]_i and no contraction.

Our finding of the slight depolarization of resting V_m under afterload can be readily explained by the decrease of I_K1 observed in voltage-clamp experiments here (Fig. 6C) and in a previous report using stylus pressure on a mouse myocyte (36). The accelerated phase-1 early repolarization (Fig. 2) is in line with the early outward current enhancement observed in ^selfAP clamp (Fig. 5C), and it was prevented by the I_to inhibitor 4-AP (Fig. 4A). The I_Cl,Ca could also be increased because of the increased Ca²⁺ transients under afterload (37). However, a role for I_Cl,Ca seems unlikely because the afterload-induced early repolarization was not affected by selective I_Cl,Ca inhibition (Fig. 4B) and the early outward current in ^selfAP clamp did not change during Ca²⁺ alternans (Fig. 5E). It merits mention here that the I_to-dependent enhanced early repolarization also enhances the early Ca²⁺ entry through I_Ca,L and the efficacy in triggering SR Ca²⁺ release (38) and therefore may contribute to the afterload-induced contraction enhancement. Hence, physiological changes in blood pressure during daily activities is expected to alter the afterload encountered by the heart, which is expected to finetune the AP and Ca²⁺ signaling to autoregulate contractility in compensatory response to load changes (39).

The APD prolongation and elevation of plateau potentials under afterload are likely to be a consequence of increased I_Ca,L, as tested directly using the conventional voltage-clamp protocol under afterload (Fig. 6A) and in line with previous reports on mechanosensitive I_Ca,L (40, 41). The current–voltage relationship of the afterload-induced inward plateau current (Fig. 5C, Inset) also resembled the profile of I_Ca,L under AP clamp (42, 43). The alternans data in ^selfAP clamp (Figs. 5E and 7F) showed that a larger contraction and larger [Ca²⁺]_i coincided with a decreased inward plateau current and shortened APD in line with the enhanced Ca²⁺-dependent inactivation of I_Ca,L during larger Ca²⁺ release from the SR (44). The late inward current was increased during the larger contraction and larger Ca²⁺ transient, and the current showed a slow decay even after terminal AP repolarization (Fig. 5E), a feature most consistent with an inward Na⁺/Ca²⁺ exchange current elicited by the larger Ca²⁺ transient.

Afterload-Induced Arrhythmogenic Alternans.

The afterload-induced changes in ionic currents led to significant APD prolongation (Fig. 2) and, later, the development of APD alternans (Fig. 7), which increases susceptibility to arrhythmias (45). The discordant alternans was predominantly Ca²⁺ driven (Fig. 7F) and critically dependent on SR Ca²⁺ load (Fig. 7K), as previously demonstrated (26, 27, 46). In line with our data on alternans and its attenuation with GsMTx-4 (Fig. 4), a computer modeling study also predicted that an increase in I_MSC current promotes electromechanically discordant alternans when the alternans is Ca²⁺ driven with negative-voltage Ca²⁺ coupling (47). Ca²⁺-dependent ionic currents and alternans in [Ca²⁺]_i transient are known to significantly impact the beat-to-beat APD variability (48–50). Hence, the prior knowledge on cardiac alternans is consistent with our findings that the afterload on the cardiomyocyte during contraction against resistance causes activation of NOS1–NO signaling, which regulates multiple voltage-gated Ca²⁺ and K⁺ channels leading to enhanced phase-1 AP repolarization, APD prolongation, and enhanced intracellular Ca²⁺ transient and contractility. However, excessive afterload causes SR Ca²⁺ overload and fluctuation leading to discordant [Ca²⁺]_i and APD alternans. APD prolongation and discordant APD alternans are known to provide vulnerable substrates for arrhythmias in the intact heart (45), suggesting that high mechanical load can markedly increase arrhythmia susceptibility in vivo. In line with this, abrupt high mechanical impact on the heart (“commotio cordis”) is strongly associated with cardiac arrhythmias and sudden cardiac death (51). Chronic conditions with increased mechanical load include hypertension (increased afterload), dilated cardiomyopathy (increased wall stress), and myocardial infarction (stiffening of the myocardium and nonuniform mechanical stresses), all of which are associated with increased risk of arrythmias and heart failure (7). QT interval prolongation on the electrocardiogram and alternans (either T wave or pulsus alternans) can be found in a significant fraction of these patients and are associated with poor prognoses (52). At the cell level, remodeling of electrophysiology (APD prolongation, alternans, and increased Ca²⁺ influx) and Ca²⁺ homeodynamics (Ca²⁺ overload and elevated diastolic Ca²⁺) have been shown in cardiomyocytes in many studies of cardiomyopathies (reviewed in ref. 53). Our present study provides insights on how mechanical load also causes electrophysiology and Ca²⁺ remodeling that contribute to arrhythmogenic activities.

Limitation and Perspective.

The patch-clamp-in-gel methodology provides an informative experimental tool for studying the afterload effects on ion channels and APs while the cardiomyocyte is contracting in a 3D viscoelastic hydrogel. The cardiomyocyte is adhered to the hydrogel via binding of the cell-surface glycans to boronated-PEG cross-linked PVA polymer matrix. This experimental setting resembles the binding of cell-surface glycosylated molecules to the extracellular matrix in the 3D viscoelastic myocardium. However, in relating single-cell electrophysiology to arrhythmogenesis in the heart, one must also consider other important factors including the electrical coupling between cells, mechanosensitive properties of noncardiomyocytes, nonuniform anatomical distribution of the mechanical field, and the presence of both preload and afterload in the beating heart. The cell-in-gel methodology is well suited for studying the afterload effect in separation from preload (without prestretch), which is complementary to the various stretching methods for studying the preload effects. Hence, our study of the afterload effects on ion channels and action potentials complements the studies of the preload effects. It is necessary to combine the knowledge obtained from using all these methods to gain a comprehensive understanding of the heart’s intrinsic responses to mechanical loading.

Materials and Methods

Detailed methods can be found in SI Appendix.

Cell-in-Gel System.

The 3D viscoelastic gel matrix was made of a hydrogel system composed of underivatized PVA (10 wt%, 89 to 98 kDa, hydrolyzed, Sigma-Aldrich) and a 4B-PEG cross-linker (7.5 wt%) as previously described (13). The tetravalent boronate group cross-links the PVA hydrogel, embedding the cell in a 3D gel matrix. Based on rheology measurements, mechanical analysis using a viscoelastic model estimated the elastic shear modulus of the hydrogel to be 4.7 kPa, which is comparable to the elasticity in infarcted hearts (54); for further details, see ref. 55. Importantly, the boronate group of 4B-PEG also cross-links the cis-diols of the cell surface glycans to PVA, thereby tethering the cell surface to the gel (13).

Animal Model and Cell Isolation.

Ventricular cardiomyocytes were isolated from 20 young adult (3- to 4-mo-old, male, 2.5 to 3 kg) New Zealand White rabbits (Charles River Laboratories) using a standard enzymatic technique as previously described (56). All animal handling and laboratory procedures were in accordance with the approved protocols of the local Institutional Animal Care and Use Committee at University of California, Davis, conforming to the Guide for the Care and Use of Laboratory Animals published by the US NIH (57).

Patch-Clamp-in-Gel Technique.

Freshly isolated cardiomyocytes were first suspended in PVA and then perfused with Tyrode’s solution. APs and ionic currents were recorded using whole-cell patch clamp with physiological solutions (for ionic composition, see SI Appendix). The cardiomyocytes were continuously stimulated in current-clamp experiments with suprathreshold depolarizing pulses delivered via the patch pipette at 0.5 Hz frequency. To measure the net membrane current induced by mechanical load under physiological conditions, ^selfAP-clamp experiments were conducted as previously described (42). Formation of 3D viscoelastic hydrogel around the contracting cardiomyocyte was then achieved by applying the 4B-PEG cross-linker. All experiments were conducted at room temperature (22 ± 1 °C).

Ca²⁺ Concentration and Cardiomyocyte Contraction.

Parallel cardiomyocyte contraction and intracellular (cytosolic) Ca²⁺ concentration, [Ca²⁺]_i, or intra-SR Ca²⁺ concentration, [Ca²⁺]_SR, were assessed by sarcomere length measurements, Fura-2 fluorescence ratio (F340/F380), and Fluo-5N fluorescence in field-stimulated cardiomyocytes (at 22 °C and 0.5 Hz pacing) using an IonOptix system as previously described (13).

Statistical Analysis.

Data are expressed as the mean ± SEM. The statistical significance of differences was evaluated using a two-tailed Student’s t test (paired or unpaired) to compare two groups and ANOVA to compare multiple groups with Dunnett’s or Tukey’s post hoc tests. Origin 2016 and GraphPad Prism 9 software were used for data plotting and analysis. P < 0.05 was considered statistically significant.

Data Availability

All study data are included in the article and/or SI Appendix.