Significance
The effects of plastic pollution on living organisms is a highly debated subject. There is no direct evidence of high toxicity of microplastic abundantly present in the environment. Nevertheless, microplastic particles can cross many biological barriers and come in direct contact with lipid membranes, which is the last cell protective barrier from the environment. This study demonstrates that microplastic beads ranging from 1 to 10 μm attach to lipid membranes. This attachment leads to significant stretching of the lipid bilayer without requiring any oxidative, or biological, e.g., inflammatory, reactions. This mechanical stretching can potentially lead to serious dysfunction of the cell machinery.
Keywords: microplastic, mechanical stress, destabilization, model cell membrane
Abstract
Estimated millions of tons of plastic are dumped annually into oceans. Plastic has been produced only for 70 y, but the exponential rise of mass production leads to its widespread proliferation in all environments. As a consequence of their large abundance globally, microplastics are also found in many living organisms including humans. While the health impact of digested microplastics on living organisms is debatable, we reveal a physical mechanism of mechanical stretching of model cell lipid membranes induced by adsorbed micrometer-sized microplastic particles most commonly found in oceans. Combining experimental and theoretical approaches, we demonstrate that microplastic particles adsorbed on lipid membranes considerably increase membrane tension even at low particle concentrations. Each particle adsorbed at the membrane consumes surface area that is proportional to the contact area between particle and the membrane. Although lipid membranes are liquid and able to accommodate mechanical stress, the relaxation time is much slower than the rate of adsorption; thus, the cumulative effect from arriving microplastic particles to the membrane leads to the global reduction of the membrane area and increase of membrane tension. This, in turn, leads to a strong reduction of membrane lifetime. The effect of mechanical stretching of microplastics on living cells membranes was demonstrated by using the aspiration micropipette technique on red blood cells. The described mechanical stretching mechanism on lipid bilayers may provide better understanding of the impact of microplastic particles in living systems.
Microplastic is present in sea water (1, 2), abyssal seafloor (3), rain droplets (4), breathable air (5, 6), and even on top of the mountains far from sources of pollution (7). Only in the ocean, several million metric tons of plastic materials enter into water every year (8–10), before being transferred to agricultural fields, rivers, and cities (11, 12) with rainfalls throughout the year (4). Microplastic has an impact on both terrestrial and aquatic ecosystems (12). This plastic contamination negatively affects the soil biophysical properties (12–14) and aquatic ecosystems (15–17).
It was shown recently that microplastic can cross various barriers and enter blood and lymphatic systems, accumulating in organs such as kidney, liver, and brain (18). These findings suggest that the study of interaction between microplastic and lipid bilayers is an important problem. One of the main concerns is the unknown interactions of microplastic with living systems (19–22). Nanoplastic and microplastic particles are rarely directly responsible for death of animals (16); however, they may have impacts at the cellular and subcellular levels (23, 24). As an example, microplastic particles can change the secondary structure of proteins (25) and induce cellular toxicity through oxidative stress, membrane damage, immune response, and genotoxicity (26). Considering the possible microplastic role in the stress or inflammation, only biological pathways or oxidative stress seem to be discussed (26, 27). However, purely physical mechanisms such as mechanical stretching may also induce considerable stress or inflammation for cells or tissues (28, 29).
Since specific interactions between microplastics and cells depend on their size and chemical composition (30), we focus our discussion on the types of microplastics that are, predominantly, present in oceans. The average microplastic size distribution is estimated around 0.1 m to 5 mm (31, 32). Their chemical composition is polypropylene (PP), polyethylene (PE), polystyrene (PS), polyamide, and acrylics (PA) (32, 33). Fundamental studies about the physicochemical interactions of such microplastics with model cell membranes were very limited along the past decades (34–37).
In this article, we offer an insight into the mechanical action of micron-sized microplastic particles with model cell membranes, combining experimental and theoretical approaches. We focus our study on microplastics composed of PE, PS, and polymethylmethacrylate (PMMA) as a member of PA family since these plastics are the most abundant in aquatic environments (32, 38). Although microplastics in oceans have nonuniform sizes and present a wide variety of three-dimensional (3D) shapes (39, 40), for the sake of simplicity we will limit our study to spherical microplastics of sizes 1 to 10 m. In general, mechanical interactions of microparticles and nanoparticles on biological membranes are vaguely studied, despite their importance for biological systems (29, 41). Hereby, we will demonstrate that these microplastics induce a mechanical stress of model cell membrane without the need of indirect assumptions about biological pathways (26, 27).
Results and Discussion
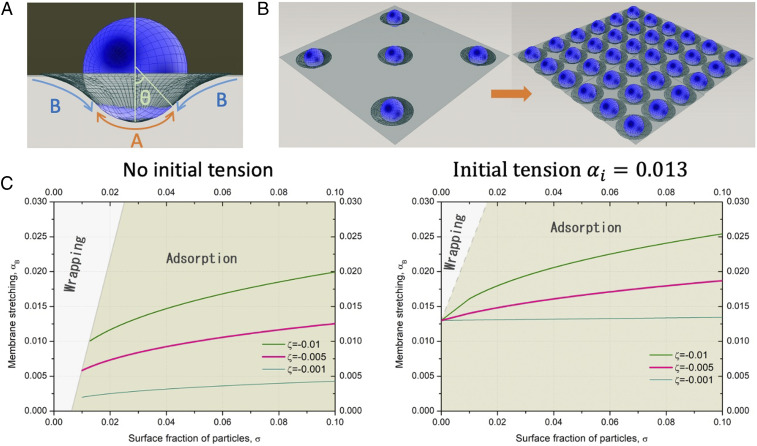
Although the size distribution of microplastics is very broad, their average sizes stay in the range of microns. This is significantly larger than the characteristic thickness of lipid bilayers, 10 nm. The best theoretical description for such scales would be mesoscale simulations that discretize the particles and surfaces in Voronoi polygons and meshes or continuum mean field elastic models within Helfrich Hamiltonian approximation (42). Such big scales would also imply that microscopic details of lipid structure, interactions, and chemical nature of particles may be neglected at least as a first approximation. Thus, at the mesoscale, these particles can be regarded as spheres of micrometer diameter attaching to a lipid bilayer, which is represented as a continuum elastic layer with a fixed compressibility constant (Fig. 1A), thus bringing universality to this model. The interaction between a microplastic particle and the lipid bilayer can be described by a phenomenological interaction parameter , which is negative for the attraction and positive for the repulsion. Similar approach was adopted for the evaluation of a single colloidal particle adsorption to the lipid membrane (43). In case of many microplastics adsorbed at the membrane, instead of an infinite membrane, it is convenient to consider a fixed area of the membrane available per microplastic in the approach similar to Wigner–Seitz cells in solid state physics resulting from Voronoi decomposition of a crystal lattice (Fig. 1B). This approach of fixed area was used to study membrane adsorbed on periodic pillars (44) and recently used for the description of the adsorption of clusters of gold nanoparticles to lipid bilayers (29).
Fig. 1.
(A) A bead adsorbed at the bilayer: part A is in contact with the bilayer, and part B is detached. (B) Schematic of a mechanical stretching effect due to increased surface density of adsorbed beads. (C) Stretching of initially tensionless bilayer induced by the adsorption of 1 and 10 m beads at the lipid bilayer with and without initial tension for different interaction parameters . Wrapping regime corresponds to wrapping of more than half of the area of the bead. Surface fraction is defined as a number of particles per surface area multiplied by excluded area, e.g., 1 for 1 m particle and 100 for 10 m particles. Thus, the plots are independent on the size of the particles.
We believe that the mechanism of stretching and deformation of the membrane due to adsorbed particles is a general phenomenon, and thus, a simple phenomenological model which lacks microscopic details and is general enough would be the most suitable for the description of this phenomenon. Thus, we use the same model that was applied to nanopillars stretching the cell membrane (44) and gold nanoparticles deforming bacteria (29) for microplastic particles at the lipid bilayer with the same notations. Within this model described in detail in ref. 44, we divide the area available per microplastic particle into two parts: the suspended part of the layer A and the adsorbed part B (Fig. 1A). Division in two parts rather than considering smooth transition between the adsorbed and suspended region leads to some inaccuracy in the vicinity of the detachment region between A and B, which is negligible on larger scales. The free energy of the layer per particle is then given by the balance of the stretching/compression of layers A and B and attraction to the microplastics in contact region A. Due to adsorption of the microplastic particle to the bilayer, the area per microplastic at the position would change from the initial value of area of unperturbed bilayer . Stretching of the bilayer is described by the compressibility constant and corresponding parabolic profile for small deformations. The dimensionless parameter that characterizes the local stretching is , and the energy associated with the area change is proportional to . This term is balanced by the attraction to the surface of the microplastics, characterized by the energy of interaction . Another parameter that can characterize the interaction strength is the density of the adsorption points at the surface at a given position , which deviates from the initial uniform distribution due to area change. This parameter allows for generalization of the model to the cases when the adsorption is localized in adsorption points rather than continuously distributed along the surface and it can be expressed in terms of local stretching as . With this the free energy associated with the adsorption of a microplastic can be written as a sum of two terms,
| [1] |
Here is the infinite-small area element, which is used as an integration variable over area of region A for interaction with microplastic and A + B for stretching/compression. For spherical microplastics, and , where is the radius of the microplastic, is the average distance between microplastics, and is the angle between the central axis and the detachment point (44). These expressions are valid for weak adsorption, , which is the case for most practical situations. The free energy is then minimized with respect to local stretching subject to the constraint of the initial area conservation (equivalent to fixing the total number of lipids), . Rewriting Eq. 1 and assuming homogeneous stretching for parts A and B as well as for the initial unperturbed membrane, labeled ,
| [2] |
where is the Lagrange multiplier associated with the area constraint. The minimization of this expression numerically gives equilibrium values for the stretching in A and B as a function of interaction parameters and the diameter of the particles. The microplastic particle concentration appears in the expression as the surface particle density, which is inversely proportional to the average area per particle.
The effect of mechanical stretching depends on the ratio between the adsorption strength, expressed in the attractive interaction energy per area and the compressibility constant of the bilayer, (44, 45), such that
| [3] |
is the only control parameter in the model (Eq. 1). If the adsorption is very strong, for example, in the case of biotin–streptavidin bonds, the adsorption of a single particle on a lipid vesicle may provoke a considerable deformation of the vesicle (46). However, for Van der Waals interactions, the interactions are weaker, and the range of adhesion energy between lipid bilayer and inorganic materials can vary between 1 mJ/ to mJ/ (47). Adhesion energies for polystyrene beads, with a lipid bilayer, were measured to be of the order of 1 mJ/ (45, 48). Thus, considering the compressibility constant of a bilayer k 100 to 300 mN/m, the dimensionless interaction parameter should be in the range 0.003 to 0.01 for polystyrene beads and similar microplastics.
The results of the minimization of the free energy in Eq. 3 for spherical particles with different diameters and interaction parameters are shown in Fig. 1C. Small particles induce less stretching since they have less surface area. At low initial stretching of the bilayer there is a regime of wrapping when more than half of the surface of the particle is in contact with the bilayer. In this regime, stretching increases rapidly with the surface density of adsorbed particles. This regime disappears with increasing size of the particles and with increasing initial tension of the bilayer.
In this model each adsorbed particle consumes an area of the bilayer such that the total area of the bilayer is reduced. Collective effect of accumulation of particles arriving to the membrane leads a global reduction of membrane area and the increase of the membrane tension. Although lipid membranes are in liquid state and lipids can freely move laterally and thus should release mechanical stress, this model assumes that the stress relaxation is a slow process compared to the adsorption of particles from the solution, and the adsorbed particles act as needles. However, the characteristic stress relaxation time is difficult to evaluate. Let us consider, as a very basic simplification, that the water/bilayer interface is similar to a water/oil interface. As the bilayer core is hydrophobic and fluid (49), Young’s law predicts that a colloidal sphere at equilibrium with a liquid interface will straddle the two fluids, its height above the interface defined by an equilibrium contact angle (50). Notably, it was shown that the adsorption of PS microbeads to a water/oil interface is characterized by an unexpectedly slow relaxation, where the complete equilibration may take months (51, 52). By analogy, if the wetting is replacing the partial wrapping, one can expect that the PS microplastics adsorbed at the bilayer have also very slow stress relaxation. However, there could be other factors that may affect the particle relaxation time.
To determine the effect of microplastic particles on the tension of a model cell membrane and also experimentally estimate the relaxation time, a free-standing bilayer, mimicking a mammalian cell composition, was formed in a microfluidic chip in the absence of microplastics (Materials and Methods) (53). The lipidic composition of the free-standing bilayer is chosen to be close to that of plasma membrane (54).
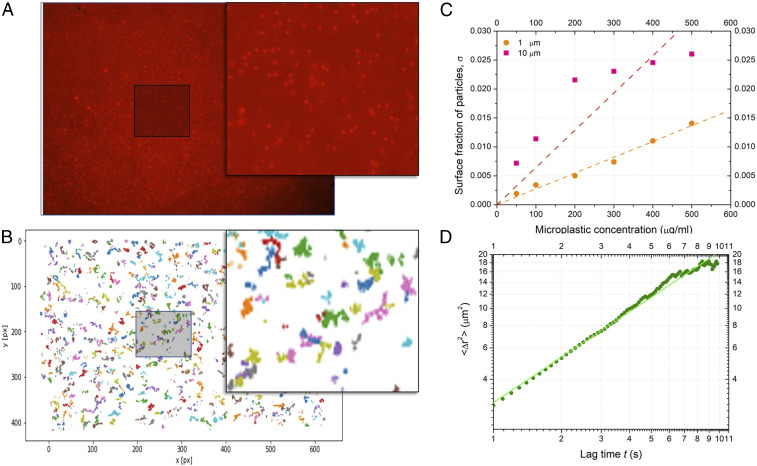
We dispersed 1 m fluorescent PS particles near the lipid bilayer and tracked their motion on the bilayer surface as function of time (Fig. 2). It appears that the PS beads diffuse freely on the bilayer surface with a diffusion coefficient (Fig. 2D). Even after 1 to 2 h, we observed that individual PS beads continued their diffusive motion and never stopped. This observation is also valid for 10 m microplastics. We also observed that the free-standing bilayer can spontaneously move in the z direction, as previously described in ref. 54. As a consequence, it may be possible that the particle diffusion, microfluidic drift, and bilayer motion prevent a rapid stress relaxation, confirming the assumption of the model of slow stress relaxation.
Fig. 2.
(A) An image of red fluorescent 1 m PS microplastics adsorbed on a free-standing lipid bilayer (SI Appendix, Movie S1). (B) Visualization of Brownian trajectories of 1 m PS microplastics after drift removal (SI Appendix, Movie S2). (C) The adsorption isotherm of 1 m PS (orange circles) and 10 m PMMA (pink squares) microplastics adsorbed on a free-standing lipid bilayer with the corresponding linear fits (dashed lines). (D) The extracted mean square displacement () as a function of time in log-log scale. The measured average microplastic diffusion coefficient , which is slightly weaker than the diffusion coefficient of a 1 m microplastic particle in bulk.
Since the surface tension at the oil–water interface is known (Materials and Methods), measuring the contact angle directly from optical inspection (Fig. 3A), one can calculate the bilayer tension from the Young–Dupré equation (55) as mN/m. This tension of the membrane is related to the dimensionless stretching parameter of a suspended part of the membrane as
| [4] |
Thus, assuming the compressibility constant of the bilayer mN/m, the experimental initial stretching of the lipid bilayer in the absence of particles corresponds to . This makes consistent the theoretical values in Fig. 1C with experimental measurements of the lipid bilayer under tension ( mN/m) without microplastics (Fig. 3).
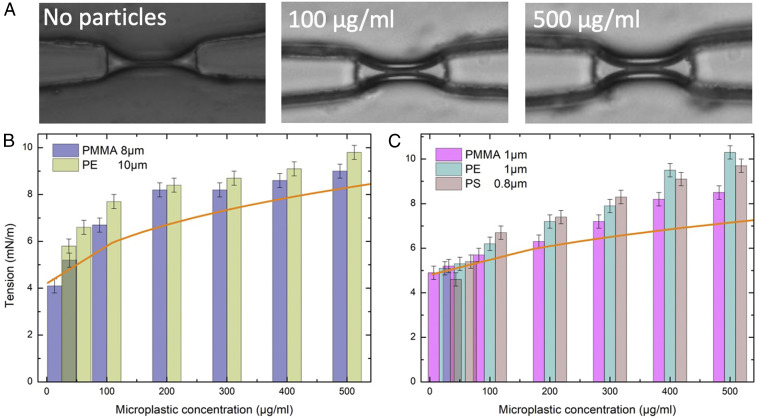
Fig. 3.
(A) Microphotographs of a lipid bilayer in a microfluidic chip, and in contact different microplastic concentration (PE, 1 m/). (B) Membrane tension of a model cell membrane as function of the bulk concentration of 8 m PMMA and 10 m PE. (C) Membrane tension of a model cell membrane as function of concentration of 1 m PMMA and PE and 0.8 m PS. Orange curves are the corresponding theoretical membrane tensions calculated on the basis of the surface fractions (Fig. 2C) and obtained without adjustable parameters.
The bilayer tension as a function of the microplastic concentration was measured for two different sizes. Microplastic particles (PE, or PMMA) of to m diameter and different concentrations (25 to 500 g/mL) were dispersed near the bilayer. At low microplastic concentration (g/mL), the change of the bilayer tension is not significant (Fig. 3B) for all types of microplastic used. However, we observed the increase of bilayer tension with the increase of bulk concentration (Fig. 3B). In the concentration range of to g/mL, the bilayer tension increases quickly from to mN/m. Then, the bilayer tension reaches a plateau at 8 to 10 mN/m, with a maximum tension value g/mL. The other two types of microplastic (PMMA and PE) show similar behavior, while PE microplastics induce a slightly higher bilayer tension than PMMA microplastics (Fig. 3B). Interestingly, this microfluidic setup allows us to perform electrophysiological measurements after the bilayer formation. No significant conductive signals could be measured on a bilayer in the presence of microplastics. Thus, although the microplastics are stretching the bilayer, adsorbed microplastics do not create pores in the bilayer. Since the measured values are already close to lysis tension (49), we have not tested higher microplastic concentrations that would lead to even higher tensions up to break up of the bilayer.
The same set of experiments was repeated for PE, PS, and PMMA microplastics with smaller diameters (m) (Fig. 3C). At low microplastic concentration (g/mL), no significant change of the bilayer tension (Fig. 3C) was detected for all tested microplastic types. In the concentration range to g/mL, the increase of tension is close to linear, from to 8 to 9 mN/m (Fig. 3C). The bilayer tension shows a similar behavior for the three types of microplastic (PMMA, PS, and PE). The maximum measured bilayer tension to 10 mN/m corresponds to microplastics concentration c 400 to 500 g/mL (Fig. 3C).
Since all parameters of the bilayer and the microplastic particles are known, the experimental results can be directly compared with the theoretical estimates without fitting and adjustable parameters. The adsorption curves shown in Fig. 2C for two diameters relate the microplastic concentration in the bulk with the surface fraction . In turn, Eq. 4 relates the measured bilayer tension with the stretching of the free part of the bilayer , thus permitting a direct comparison with stretching curves similar to Fig. 1C. Theoretical tensions are plotted in Fig. 3 B and C with the corresponding orange curves for direct comparison with the experiment. The initial tensions were taken from the experiment, 4 and 5.9 mN/m, correspondingly. The interaction parameter was estimated as for both diameters, and the compressibility coefficient of the bilayer was taken as . Although the correspondence is good qualitatively, the measured tension is slightly higher than that obtained from this simple mechanical stretching model. If we assume that each 1 m particle consumes 1 area, the maximal stretching would be , which corresponds to an experimental tension of 6 to 7 mN/m. It may be possible that there is an additional contribution to stretching from noncoherent dynamic movement of the particles on the surface of the bilayer, which is not considered in the model.
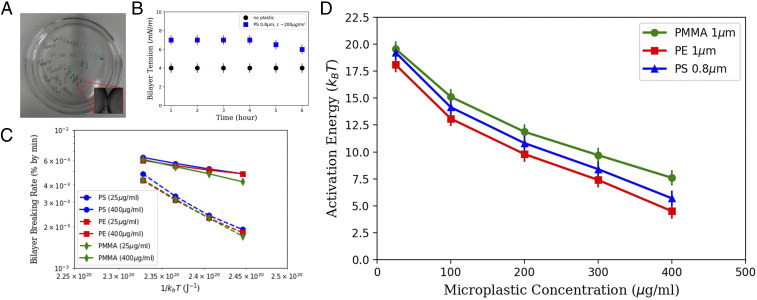
Furthermore, this microfluidic technique allows us to explore the influence of the bilayer stretching on the bilayer stability. Free-standing bilayers, produced in a microfluidic chip, are very suitable when performing electrophysiological measurements. However, they are exposed to microfluidic slight perturbations that may disturb the bilayer lifetime. Thus, to measure the stability, we produced a free-standing bilayer with a different technique, the droplet interface bilayer (DiB; Fig. 4A) method (56). It is more suitable to use the DiB method where bilayers are completely immobile (Materials and Methods). Noteworthy, the measured bilayer tensions formed by DiB method are similar to the bilayer tensions measured in a microfluidic chip for all of the range of used plastic concentration. Interestingly, it also confirms that the stress relaxation of the bilayer in presence of microplastics is pretty slow, as assumed in the theoretical model (Fig. 4B). Then, we produced several free-standing bilayers with the DiB methods and measured the bilayer breaking rate (e.g., droplet coalescence rate; Fig. 4C) as a function of temperature . We observed a shortening of the lifetime as a function of the microplastics concentration. The corresponding bilayer breaking rate enabled us to extract the coalescence energy landscape from the Kramer relation (Fig. 4D). Here is a normalization constant, is the Boltzmann constant, and is the activation energy (57, 58). The simultaneous production of several DiBs allowed us to measure enough statistics of bilayer ruptures within short time. The corresponding extracted energy landscape exhibits a strong reduction of the activation barrier as a function of the microplastic concentration from to . The energy barrier varies quasi-linearly with the bilayer tension, which is controlled by the microplastic concentration. We can compare the reduction of the activation barriers as a function of the type of microplastic. This allows us to classify the microplastics according to their destabilization activity: PE > PS > PMMA.
Fig. 4.
(A) Picture of several DiBs formed in a cylindrical hydrophobic chamber (of 7 cm in diameter) filled with an oil–lipid mixture. The water droplets are colored because they contain g/mL of green PS beads (Materials and Methods). (Inset) Micrograph presenting a bilayer contacting two droplets. (B) Bilayer tension versus time with and without PS microparticles. (C) The droplet coalescence rate (in % per minute) in semilog scale as a function of the thermal energy () and for different types of microplastics. Each point is obtained on an average of 100 events. (D) Extracted energy of activation (expressed in ) as a function of microplastic concentration and composition.
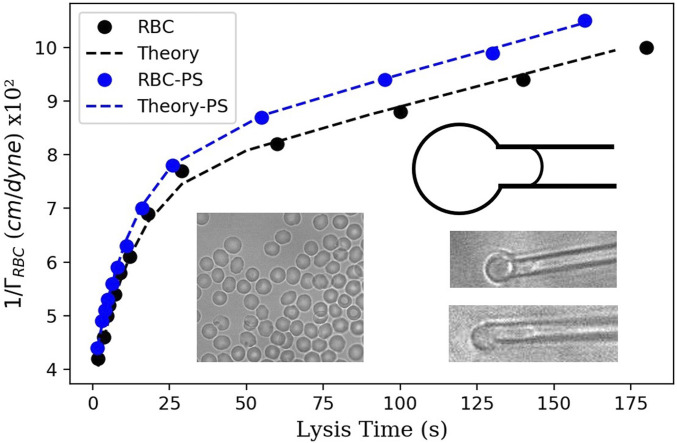
To explore whether our findings for model lipid bilayers are applicable for living cells, we chose the simplest example of living cells: the red blood cells (RBCs). For that purpose, we deposited an RBC solution on a treated glass slide and performed the micropipette aspiration experiment (59, 60) on a single RBC (Materials and Methods). This technique allows an accurate quantification of the effect of membrane stretching in the presence of microplastics. A single RBC was first immobilized on the tip of a micropipette, and a tiny suction was applied to insert a portion of the RBC inside the pipette tip. Gradually increasing aspiration pressure forced the cell to move inside the micropipette (Fig. 5). The RBCs used in the experiment were preswelled (with excess of inner pressure), such that they do not have excess area for a long tongue moving into the pipette. Thus, when they are stressed for sufficient time, they hemolyze and disappear in the micropipette (59, 60). This method allows the measurement of the cell lysis time as a function of the RBC isotropic membrane tension. This RBC isotropic membrane tension is determined from the RBC geometry inside and outside the micropipette for a constant aspiration pressure from Eq. 6 (Materials and Methods). We found that the RBC lysis time as function of the RBC isotropic tension followed a characteristic behavior reported by Evans et al. (60). In order to test a possible effect of microplastics on RBCs, the RBC suspension was washed and replaced by a suspension of RBCs incubated with 0.5 m PS microplastics at g/mL (Materials and Methods). The size of microplastics has been chosen in such a way that it allows for a good coverage of the membrane of RBCs despite its small area. We repeat the time lysis experiments by using the same micropipette as for the experiments without microplastics to achieve a good comparison. It appears the presence of the microplastics reduces significantly the lysis time for all of the range of tested isotropic tensions (Fig. 5). These measurements demonstrated that microplastics not only destabilize model cell membranes but also destabilize RBCs by mechanical stretching.
Fig. 5.
Plot of the reciprocal of the isotropic RBC tension versus the RBC lysis time. Filled black circles indicate experimental results for RBCs in the absence of microplastics; filled blue circles indicate experimental results for RBCs in the 0.5 m PS microplastics solution. Each point corresponds to an average of 10 to 20 single measurements. The corresponding dashed lines are theoretical curves obtained with Eq. 7. (Left Inset) A microscopic image of RBC with no microplastics (on the right) and with microplastics attached to the membrane (on the left). (Right Inset) A schematic and two images of a single RBC partially aspired into a micropipette tip for different applied pressures. A preswell picture of RBCs is also presented.
Conclusions
The effect of microplastics on model cell membranes was studied experimentally and theoretically. For this purpose, we produced free-standing bilayers with two different techniques (microfluidic and DiB methods). Using a microfluidic chip, we measured the increase of the bilayer tension as a function of the microplastic concentration. The increase of tension is more pronounced for 10 m beads than for 1 m beads for the same concentration, which is explained by the difference in particle surface areas. The calculated tension increased is in good agreement with experimental measured values. The observed bilayer stretching does not lead to reversible (or transient) pores, as demonstrated by the electrophysiological measurements inside our microfluidic chip. Using DiBs, we explore the bilayer breaking rate with time and as a function of the microplastic material and concentration. The corresponding bilayer breaking rate reveals that microplastics influence strongly the energy landscape needed to rupture the bilayer. We explain the origin of this bilayer destabilization by the fact that the microplastic particles adsorbed on the bilayer considerably increase the membrane tension even at a low particle concentration since each adsorbed particle consumes a surface area that is proportional to the contact area between each particle and the membrane. While the particle-induced deformation is longer to equilibrate than the characteristic stress relaxation time, the cumulative effect from microplastic particles arriving at the membrane leads to the global reduction of the membrane area and the increase of membrane tension. This study demonstrates that microplastics destabilize the bilayer via mechanical stretching.
We also showed that the microplastics destabilization is not limited only to model cell membranes, but cell membranes can also be stretched due to microplastic adsorption. Although negative effects of microplastics and potential toxicological effects on living cells were reported in literature, such as decrease of metabolic activity, reduction of cell proliferation, and significant changes in morphology of cells (61), it is difficult to indicate the exact mechanism. Most mammalian cells have very complex cell machinery that may hinder the mechanisms of microplastics influence. To reveal the effect of microplastics on cell membranes, we chose human RBCs since these cells have simple membranes, lack of endocytosis, or active processes in cytoskeleton that may interfere with the observed mechanical stretching. Using micropipette aspiration experiments, we observed and quantified the reduction of RBC lysis time in presence of microplastics as a function of the applied pressure. These results are in accordance with the results on model lipid membrane.
The reported effect may have implications in different fields. Mechanical stress may alter the function of membrane proteins or ion channels. The mechanical effects induced by adsorbed microplastics may be noticeable in gravitropism (62) and mechanosensitivity of plant cells, where mechanical pressure of sedimenting particles (amyloplasts) triggers the release of auxin in the direction of the mechanical stimulus, while stretching of the cell membrane by foreign microplastics may alter such processes. The reported bilayer stretching may activate proteins that trigger microplastic internalization (24), and thus, it may give a hint for the unsolved mechanism of microplastic cellular uptake. Finally, the calculation provided in this article, may be used as a method to extract adhesion energies of microparticles, or nanoparticles, with model membranes.
Materials and Methods
Lipid Bilayer Formation with Microfluidics.
Vertical bilayers were made in microchannels with a rectangular cross section and were fabricated using typical soft lithography protocols. Channel dimensions were 300 m in width and 140 m in height. The device was molded with an SU-8 photoresist on a silicon wafer using Sylgard 184 (Dow Corning). The surface of the Sylgard 184 devices was exposed to nitrogen plasma (Diener Electronic GmbH) and sealed with a plasma-treated glass cover slide. The sealed device was rendered hydrophobic by heating it to C overnight. The liquids were dispensed from syringes (Hamilton Bonaduz AG), which were connected to the microfluidic device by Teflon tubing. Computer-controlled syringe pumps were used to control the injection of the water and oil phases. Experiments were performed at room temperature to have the lipids in a fluid phase. Using a volume-controlled system with syringe pumps, two water droplets were injected face to face into microchannels to produce a free-standing lipid bilayer. After a few seconds, the water–oil interface of each finger is covered with a monolayer of lipids molecules. Once the two liquid fingers are brought into contact, the two lipid monolayers interact and form a lipid bilayer within a short time. The system is then stable and can be analyzed, simultaneously, with optical microscopy and by electrophysiological inspection (53, 63).
The horizontal free-standing lipid bilayer use in Fig. 2 is performed using the method describe in refs. 41, 54. Once this bilayer is formed, we could inject the microplastic from the microchannel above the bilayer and/or from the microchannel below the bilayer. We injected the microplastic beads, only, via the bottom channel to avoid sedimentation issues and to visualize easily the bilayer position. As a consequence, we counted the microplastics only on one bilayer side (in Fig. 2C). However, the microplastics are present on both sides of the bilayer while measuring the tension with the vertical bilayer (Figs. 3 A and 4 A). Thus, a factor of 2 is applied to the measured surface coverage, before using these numbers in the theory in Fig. 1 and Eq. 4.
Lipid Bilayer Formation with the DiB Method.
Lipids were dissolved in squalene oil at the molar ratio mentioned in the following text and with a total mass concentration of 5 mg/mL. The lipids were left for 24 h at 50 C under magnetic stirring. The OTS-coated glass container, which has a cylinder shape that is 1 cm in height and a diameter of 7 cm, is filled with the oil–lipid mixture. This device is placed on a hot plate and disposed at desired temperature. A large area of the cylinder can be observed by reflection using a Leica Z16 Microscope connected to a PCO1600 camera. The optical quality is reduced using this technique. However, it is enough to distinguish DiBs that have merged from others. For formation and manipulation of an aqueous microdroplet, a micropipette with a desired tip, having a typical diameter in the range 1 mm, was formed using a micropipette puller SUTTER, model P-97. By this method, two water droplets of nearly equal size are produce manually in this container and left at rest for 30 min. They are brought, gently, into contact via a needle. After a few minutes, a bilayer appears spontaneously at the contact area between the droplets (56, 64). The buffer composition of each droplet could be determined before droplet production. Thus, a controlled amount of microplastics could be dissolved into buffer prior to droplet production.
Lipids.
Lipid mixture mimicking the composition of human plasma cell membrane (54, 65) was achieved by mixing DOPC:DOPE:DOPS:Chol with a molar ratio of 60:30:10 and adding 40% of total molar ratio of cholesterol. DOPC is the abbreviation of 1,2-dioleoyl-sn-glycero-3-phosphocholine, DOPE is 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine, DOPS is 1,2-dioleoyl-sn-glycero-3-phospho-L-serine (sodium salt), and Chol is cholesterol. All of the lipids were purchased from Avanti Polar Lipids.
Surface Tension Measurements.
Surface tension of various lipid monolayers at the oil–water interface was obtained by the pendant drop method using a commercial measurement device (OCA 20, DataPhysics Instruments GmbH). An oil solution containing 5 mg/mL lipids was produced by introducing a droplet from a steel needle into the surrounding oil phase. The interfacial tension was obtained from fitting of the shapes of the droplets by the Young–Laplace equation (55, 66).
| [5] |
Microplastic Beads.
Three different types of microplastic beads were used: PS (m), PE (1 and 10 m), and PMMA (1 and 8 m). PS microbeads were from Bangs Laboratory (0.798 m, Shamrock Green uniformly dyed, Catalog no. DSSG005). PE microbeads were from Cospheric (Catalog no. CPMS-0.96) from diameter 1 to 10 m (sorted to 1 m by a standard microfluidic filter). PMMA microbeads, as an alternate to PA, were from Sigma-Aldrich (Catalog nos. 90875 and 90515) with diameter of 1 and 8 m, respectively. Red fluorescent microplastic (PS) beads were purchased from Thermo-Fisher (R0100), with a diameter of 1 m.
Fluorescence and Image Analysis.
For tracking these beads on the lipid bilayer surface, we used the 3D microfluidic setup described in refs. 41, 54. The fluorescent movies are recorded on Axio Z7 observer microscope (Zeiss) with colibri 7 LED illumination. The tracking particles analysis is performed using Python and TrackPy libraries (67).
RBC Suspension Preparation.
The RBCs were prepared following the protocol by Li et al. (68). RBCs were obtained from 120 L of blood from a fingertip of one of the authors and added to 10 mL of PBS solution (PBS, Sigma) containing 0.5 (in weight) of Bovine Serum Albumin (BSA, Sigma). This solution was centrifuged at 3,500 rpm for 10 min and washed with PBS (this step was repeated three times). Then 6 mL of these washed RBCs was diluted in 200 mL PBS, and a quantity of 10 L PBS 100 M calcein-AM (Abcam) was added at final concentration of 5 M. Calcein-AM was employed as a sensor for membrane integrity as described by Li et al. (68). After 45-min incubation at C, RBC solution was ready for use, and it was applied immediately for experiments. Finally, the RBCs are resuspended in a PBS solution (pH 7.4) at 135 mosM to preswell the cells before the experiments are realized with 0.5 BSA (in weight). Experiments were performed at room temperature ( C). A part of this RBC suspension was incubated with 0.5 m PS microplatics (B500, Thermo-Fisher) at 200 g/mL during 20 min, before being immediately used for experiments.
Micropipette Aspiration Technique.
A small rectangular micropipette chamber was glued on top of a coverslip (0.17 mm thickness), and a PDMS layer was spin coated on the slide surface. Then this slide was heated at C for 30 min in an oven. The slide was mounted on a homemade temperature controller. The glass micropipette was fabricated with a pipette puller (SUTTER, model P-97). With appropriate settings of the puller, the micropipettes were made with the inner radius ranging 1 to 3 m. The micropipettes were approached to the glass slide with an angle of using a motorized micromanipulator (MPC-385, WPI). The pipette was directly connected to pressure pumps (MFCS-EZ, Fluigent) that allow us to apply a controlled and constant negative pressure in the range of 0.1 and 6 kPa (59, 60, 69). After waiting until some RBCs were diffusing around the pipette tip, a slight aspiration was applied that attracted and maintained a selected RBC on the pipette tip. Then, the applied pressure was slowly raised up step by step to increase the volume of RBCs inside the pipette tip. The RBC was then released until RBC lysis was observed (59, 60). The experiment was monitored on a Zeiss Z1 Axio Observer with a 63× magnification objective and recorded with a PCO camera (Imager Pro X 2M). Finally, the RBC membrane integrity was tested by fluorescence technique, as the RBCs were loaded with calcein-AM (68). RBCs that showed poration before aspiration were not considered (68). RBCs in microplastics solution were inspected with a fluorescence to verify the presence of fluorescent PS particles (B500, Thermo-Fischer) on the RBC membranes, as described in ref. 70. This was possible because these fluorescent PS particles are visible at different wavelength excitations in contrast to calcein-AM sensor.
RBC Isotropic Tension and Viscoelastic Model.
Upon constant pipette aspiration, the RBC membrane isotropic tension was calculated using the following equation (60, 69):
| [6] |
where is the inner diameter of the micropipettes, is the diameter of the spherical portion of the RBC outside the pipette, and is the aspiration pressure (59, 60, 69).
A viscoelastic model of RBC has been introduced by Rand (60), and it was used to describe the kinetics of the membrane breakdown. This model relates the lysis time to the isotropic membrane tension such as
| [7] |
where and are the Young’s moduli in two directions, and are viscosities in two directions, is the critical strain, and is the membrane thickness. These parameters were estimated following the discussion in ref. 60.
The theoretical curves in Fig. 5 were calculated from Eq. 7. For the black dashed line (in the absence of microplastics), × cm/dyne, × cm/dyne, , and × cm/dyne. For the blue dashed line (in presence of PS microplastics), × cm/dyne, × , , and × cm/dyne.
Supplementary Material
Acknowledgments
V.A.B. acknowledges financial assistance from the Ministerio de Ciencia, Innovación y Universidades of the Spanish Government (grant CTQ2017-84998-P). J.-B.F. acknowledges funding from SFB1027, subproject B4 (Deutsche Forschungsgemeinschaft [DFG]).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2104610118/-/DCSupplemental.
Data Availability
All study data are included in the article and/or SI Appendix.
References
- 1.Thompson R. C., et al. , Lost at sea: Where is all the plastic? Science 304, 838 (2004). [DOI] [PubMed] [Google Scholar]
- 2.Avio C. G., Gorbi S., Regoli F., Plastics and microplastics in the oceans: From emerging pollutants to emerged threat. Mar. Environ. Res. 128, 2–11 (2017). [DOI] [PubMed] [Google Scholar]
- 3.Krause S., et al. , Persistence of plastic debris and its colonization by bacterial communities after two decades on the abyssal seafloor. Sci. Rep. 10, 9484 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Xia W., Rao Q., Deng X., Chen J., Xie P., Rainfall is a significant environmental factor of microplastic pollution in inland waters. Sci. Total Environ. 732, 139065 (2020). [DOI] [PubMed] [Google Scholar]
- 5.Gasperi J., et al. , Microplastics in air: Are we breathing it in? Curr. Opinion Environ. Sci. Health 1, 1–5 (2018). [Google Scholar]
- 6.Li L., Zhao X., Li Z., Song K., COVID-19: Performance study of microplastic inhalation risk posed by wearing masks. J. Hazard Mater. 411, 124955 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Allen S., et al. , Atmospheric transport and deposition of microplastics in a remote mountain catchment. Nat. Geosci. 12, 339–344 (2019). [Google Scholar]
- 8.Brandon J. A., Jones W., Ohman M. D., Multidecadal increase in plastic particles in coastal ocean sediments. Sci. Adv. 5, eaax0587 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pabortsava K., Lampitt R. S., High concentrations of plastic hidden beneath the surface of the Atlantic Ocean. Nat. Commun. 11, 4073 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Morét-Ferguson S., et al. , The size, mass, and composition of plastic debris in the western North Atlantic Ocean. Mar. Pollut. Bull. 60, 1873–1878 (2010). [DOI] [PubMed] [Google Scholar]
- 11.Rillig M. C., Microplastic in terrestrial ecosystems and the soil? Environ. Sci. Technol. 46, 6453–6454 (2012). [DOI] [PubMed] [Google Scholar]
- 12.Rillig M. C., Lehmann A., Machado A. A. S., Yang G., Microplastic effects on plants. New Phytol. 223, 1066–1070 (2019). [DOI] [PubMed] [Google Scholar]
- 13.Wan Y., Wu C., Xue Q., Hui X., Effects of plastic contamination on water evaporation and desiccation cracking in soil. Sci. Total Environ. 654, 576–582 (2019). [DOI] [PubMed] [Google Scholar]
- 14.De Souza Machado A. A., et al. , Impacts of microplastics on the soil biophysical environment. Environ. Sci. Technol. 52, 9656–9665 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ma H., et al. , Microplastics in aquatic environments: Toxicity to trigger ecological consequences. Environ. Pollut. 261, 114089 (2020). [DOI] [PubMed] [Google Scholar]
- 16.Galloway T. S., Cole M., Lewis C., Interactions of microplastic debris throughout the marine ecosystem. Nat. Ecol. Evol. 1, 1–8 (2017). [DOI] [PubMed] [Google Scholar]
- 17.Cole M., Lindeque P., Halsband C., Galloway T. S., Microplastics as contaminants in the marine environment: A review. Mar. Pollut. Bull. 62, 2588–2597 (2011). [DOI] [PubMed] [Google Scholar]
- 18.Vethaak A. D., Legler J., Microplastics and human health. Science 371, 672–674 (2021). [DOI] [PubMed] [Google Scholar]
- 19.Wright S. L., Kelly F. J., Plastic and human health: A micro issue? Environ. Sci. Technol. 51, 6634–6647 (2017). [DOI] [PubMed] [Google Scholar]
- 20.Li B., et al. , Microplastics in fishes and their living environments surrounding a plastic production area. Sci. Total Environ. 727, 138662 (2020). [DOI] [PubMed] [Google Scholar]
- 21.Gil-Delgado J. A., et al. , Presence of plastic particles in waterbirds faeces collected in Spanish lakes. Environ. Pollut. 220, 732–736 (2017). [DOI] [PubMed] [Google Scholar]
- 22.Wagner S., Reemtsma T., Things we know and don’t know about nanoplastic in the environment. Nat. Nanotechnol. 14, 300–301 (2019). [DOI] [PubMed] [Google Scholar]
- 23.Hwang J., et al. , Potential toxicity of polystyrene microplastic particles. Sci. Rep. 10, 7391 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ramsperger A. F. R. M., et al. , Environmental exposure enhances the internalization of microplastic particles into cells. Sci. Adv. 6, eabd1211 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hollóczki O., Gehrke S., Nanoplastics can change the secondary structure of proteins. Sci. Rep. 9, 16013 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Banerjee A., Shelver W. L., Micro- and nanoplastic induced cellular toxicity in mammals: A review. Sci. Total Environ. 755, 142518 (2021). [DOI] [PubMed] [Google Scholar]
- 27.Hu M., Palić D., Micro- and nano-plastics activation of oxidative and inflammatory adverse outcome pathways. Redox Biol. 37, 101620 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lin Y. M., Li F., Shi X. Z., Mechanical stress is a pro-inflammatory stimulus in the gut: In vitro, in vivo and ex vivo evidence. PloS One 9, e106242 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Linklater D. P., et al. , Mechano-bactericidal actions of nanostructured surfaces. Nat. Rev. Microbiol. 19, 8–22 (2021). [DOI] [PubMed] [Google Scholar]
- 30.Yong C. Q. Y., Valiyaveetill S., Tang B. L., Toxicity of microplastics and nanoplastics in mammalian systems. Int. J. Environ. Res. Publ. Health 17, 1509 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Haegerbaeumer A., Mueller M. T., Fueser H., Traunspurger W., Impacts of micro- and nano-sized plastic particles on benthic invertebrates: A literature review and gap analysis. Front. Environ. Sci. 7, 10.3389/fenvs.2019.00017 (2019). [DOI] [Google Scholar]
- 32.Erni-Cassola G., Zadjelovic V., Gibson M. I., Christie-Oleza J. A., Distribution of plastic polymer types in the marine environment; A meta-analysis. J. Hazard Mater. 369, 691–698 (2019). [DOI] [PubMed] [Google Scholar]
- 33.Desforges J. P. W., Galbraith M., Dangerfield N., Ross P. S., Widespread distribution of microplastics in subsurface seawater in the NE Pacific Ocean. Mar. Pollut. Bull. 79, 94–99 (2014). [DOI] [PubMed] [Google Scholar]
- 34.Rossi G., Barnoud J., Monticelli L., Polystyrene nanoparticles perturb lipid membranes. J. Phys. Chem. Lett. 5, 241–246 (2014). [DOI] [PubMed] [Google Scholar]
- 35.Hollóczki O., Gehrke S., Can nanoplastics alter cell membranes? ChemPhysChem 21, 9–12 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Spanke H. T., et al. , Wrapping of microparticles by floppy lipid vesicles. Phys. Rev. Lett. 125, 198102 (2020). [DOI] [PubMed] [Google Scholar]
- 37.Morandi M. I., et al. , Accumulation of styrene oligomers alters lipid membrane phase order and miscibility. Proc. Natl. Acad. Sci. U.S.A. 118, e2016037118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Muez D. L., et al. , Primer muestreo de microplásticos en arroyos y ríos de la España peninsular. ECOS 29, 2087 (2020). [Google Scholar]
- 39.de Haan W. P., Sanchez-Vidal A., Canals M., Floating microplastics and aggregate formation in the Western Mediterranean Sea. Mar. Pollut. Bull. 140, 523–535 (2019). [DOI] [PubMed] [Google Scholar]
- 40.Shim W. J., Hong S. H., Eo S., “Marine microplastics: Abundance, distribution, and composition” in Microplastic Contamination in Aquatic Environments, Zeng E. Y., Ed. (Elsevier, 2018), chap. 1, pp. 1–26. [Google Scholar]
- 41.Linklater D. P., et al. , Antibacterial action of nanoparticles by lethal stretching of bacterial cell membranes. Adv. Mater. 32, 2005679 (2020). [DOI] [PubMed] [Google Scholar]
- 42.Fedosov D. A., Caswell B., Karniadakis G. E., Systematic coarse-graining of spectrin-level red blood cell models. Comput. Methods Appl. Mech. Eng. 199, 1937–1948 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Deserno M., Elastic deformation of a fluid membrane upon colloid binding. Phys. Rev. E 69, 031903 (2004). [DOI] [PubMed] [Google Scholar]
- 44.Pogodin S., et al. , Biophysical model of bacterial cell interactions with nanopatterned cicada wing surfaces. Biophys. J. 104, 835–840 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Deserno M., Gelbart W. M., Adhesion and wrapping in colloid-vesicle complexes. J. Phys. Chem. B 106, 5543–5552 (2002). [Google Scholar]
- 46.Koltover I., Rädler J. O., Safinya C. R., Membrane mediated attraction and ordered aggregation of colloidal particles bound to giant phospholipid vesicles. Phys. Rev. Lett. 82, 1991–1994 (1999). [Google Scholar]
- 47.Agudo-Canalejo J., Lipowsky R., Critical particle sizes for the engulfment of nanoparticles by membranes and vesicles with bilayer asymmetry. ACS Nano 9, 3704–3720 (2015). [DOI] [PubMed] [Google Scholar]
- 48.Dietrich C., Angelova M., Pouligny B., Adhesion of latex spheres to giant phospholipid vesicles: Statics and dynamics. J. Phys. II France 7, 1651–1682 (1997). [Google Scholar]
- 49.Dimova R., Marques C., Marques C., The Giant Vesicle Book (CRC Press, 2019). [Google Scholar]
- 50.T. Young, III, An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 95, 65–87 (1805). [Google Scholar]
- 51.Kaz D. M., McGorty R., Mani M., Brenner M. P., Manoharan V. N., Physical ageing of the contact line on colloidal particles at liquid interfaces. Nat. Mater. 11, 138–142 (2012). [DOI] [PubMed] [Google Scholar]
- 52.Pagonabarraga I., Adsorbed colloids relax slowly. Nat. Mater. 11, 99–100 (2012). [DOI] [PubMed] [Google Scholar]
- 53.Porret E., et al. , Hydrophobicity of gold nanoclusters influences their interactions with biological barriers. Chem. Mater. 29, 7497–7506 (2017). [Google Scholar]
- 54.Heo P., et al. , Highly reproducible physiological asymmetric membrane with freely diffusing embedded proteins in a 3D-printed microfluidic setup. Small 15, 1900725 (2019). [DOI] [PubMed] [Google Scholar]
- 55.Bibette J., Calderon F. L., Poulin P., Emulsions: Basic principles. Rep. Prog. Phys. 62, 969–1033 (1999). [Google Scholar]
- 56.Bayley H., et al. , Droplet interface bilayers. Mol. Biosyst. 4, 1191–1208 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kramers H. A., Brownian motion in a field of force and the diffusion model of chemical reactions. Physica 7, 284–304 (1940). [Google Scholar]
- 58.Hänggi P., Talkner P., Borkovec M., Reaction-rate theory: Fifty years after kramers. Rev. Mod. Phys. 62, 251–341 (1990). [Google Scholar]
- 59.Evans E., Waugh R., Melnik L., Elastic area compressibility modulus of red cell membrane. Biophys. J. 16, 585–595 (1976). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Rand R. P., Burton A. C., Mechanical properties of the red cell membrane. Biophys. J. 4, 115–135 (1964). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Goodman K. E., Hare J. T., Khamis Z. I., Hua T., Sang Q. X. A., Exposure of human lung cells to polystyrene microplastics significantly retards cell proliferation and triggers morphological changes. Chem. Res. Toxicol. 34, 1069–1081 (2021). [DOI] [PubMed] [Google Scholar]
- 62.Moulia B., Fournier M., The power and control of gravitropic movements in plants: A biomechanical and systems biology view. J. Exp. Bot. 60, 461–486 (2009). [DOI] [PubMed] [Google Scholar]
- 63.Guo Y., Werner M., Fleury J. B., Baulin V. A., Unexpected cholesterol-induced destabilization of lipid membranes near transmembrane carbon nanotubes. Phys. Rev. Lett. 124, 038001 (2020). [DOI] [PubMed] [Google Scholar]
- 64.Fleury J. B., Enhanced water permeability across a physiological droplet interface bilayer doped with fullerenes. RSC Adv. 10, 19686–19692 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.van Meer G., Voelker D. R., Feigenson G. W., Membrane lipids: Where they are and how they behave. Nat. Rev. Mol. Cell Biol. 9, 112–124 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Guo Y., Werner M., Seemann R., Baulin V. A., Fleury J. B., Tension-induced translocation of an ultrashort carbon nanotube through a phospholipid bilayer. ACS Nano 12, 12042–12049 (2018). [DOI] [PubMed] [Google Scholar]
- 67.Allan D., et al. , soft-matter/trackpy: Trackpy (v0.4.2, 2019). Zenodo. https://zenodo.org/record/4682814. Accessed 21 July 2021.
- 68.Li F., Chan C., Ohl C., Yield strength of human erythrocyte membranes to impulsive stretching. Biophys. J. 105, 872–879 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Artmann G. M., et al. , Micropipette aspiration of human erythrocytes induces echinocytes via membrane phospholipid translocation. Biophys. J. 72, 1434–1441 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Dias A., Werner M., Ward K. R., Fleury J. B., Baulin V. A., High-throughput 3D visualization of nanoparticles attached to the surface of red blood cells. Nanoscale 11, 2282–2288 (2018). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or SI Appendix.