Alternating the population and control neural networks to solve high-dimensional stochastic mean-field games

Significance

Mean-field games (MFGs) is an emerging field that models large populations of agents. They play a central role in many disciplines, such as economics, data science, and engineering. Since many applications come in the form of high-dimensional stochastic MFGs, numerical methods that use spatial grids are prone to the curse of dimensionality. To this end, we exploit the variational structure of potential MFGs and reformulate it as a generative adversarial network (GAN) training problem. This reformulation allays a bit the curse of dimensionality when solving high-dimensional MFGs in the stochastic setting, by avoiding spatial grids or uniform sampling in high dimensions, and instead utilizes the structure of the MFG and its connection with GANs.

Abstract

We present APAC-Net, an alternating population and agent control neural network for solving stochastic mean-field games (MFGs). Our algorithm is geared toward high-dimensional instances of MFGs that are not approachable with existing solution methods. We achieve this in two steps. First, we take advantage of the underlying variational primal-dual structure that MFGs exhibit and phrase it as a convex–concave saddle-point problem. Second, we parameterize the value and density functions by two neural networks, respectively. By phrasing the problem in this manner, solving the MFG can be interpreted as a special case of training a generative adversarial network (GAN). We show the potential of our method on up to 100-dimensional MFG problems.

Mean field games (MFGs) are a class of problems that model large populations of interacting agents. They have been widely used in economics (1–4), finance (2, 5–7), industrial engineering (8–10), swarm robotics (11, 12), epidemic modeling (13, 14), and data science (15–17). In MFGs, a continuum population of small rational agents play a noncooperative differential game on a time horizon $\left[0,T\right]$. At the optimum, the agents reach a Nash equilibrium, where they can no longer unilaterally improve their objectives. Given the initial distribution of agents ${\rho }_0\in \mathcal{P}\left({\mathbb{R}}^n\right)$, where $\mathcal{P}\left({\mathbb{R}}^n\right)$ is the space of all probability densities, the solution to MFGs are obtained by solving the system of partial differential equations (PDEs),

$$\begin{array}{cc}\hfill & -{\partial }_t\varphi -\nu \mathrm{\Delta }\varphi +H\left(x,\nabla \varphi \right)=f\left(x,\rho \right)\hspace{1em}\left(\text{HJB}\right)\hfill \\ \hfill & {\partial }_t\rho -\nu \mathrm{\Delta }\rho -\text{div}\left(\rho {\nabla }_{p}H\left(x,\nabla \varphi \right)\right)=0\hspace{1em}\left(\text{FP}\right)\hfill \\ \hfill & \rho \left(x,0\right)={\rho }_0,\hspace{1em}\varphi \left(x,T\right)=g\left(x,\rho \left(\cdot ,T\right)\right),\hfill \end{array}$$ [1.1]

which couples a Hamilton–Jacobi–Bellman (HJB) equation and a Fokker–Planck (FP) equation. Here, $\varphi :{\mathbb{R}}^n\times \left[0,T\right]\to \mathbb{R}$ is the value function, i.e., the policy that guides the agents; $H:{\mathbb{R}}^n\times {\mathbb{R}}^n\to \mathbb{R}$ is the Hamiltonian, which describes the physics of the environment; $\rho \left(\cdot ,t\right)\in \mathcal{P}\left({\mathbb{R}}^n\right)$ is the distribution of agents at time $t$; $f:{\mathbb{R}}^n\times \mathcal{P}\left({\mathbb{R}}^n\right)\to \mathbb{R}$ denotes the interaction between the agents and the population; and $g:{\mathbb{R}}^n\times \mathcal{P}\left({\mathbb{R}}^n\right)\to \mathbb{R}$ is the terminal condition, which guides the agents to the final distribution. Under standard assumptions, i.e., convexity of $H$ in the second variable, and monotonicity of $f$ and $g$—namely, that

$${\int }_{{\mathbb{R}}^n}\left(f\left(y,{\rho }_1\right)-f\left(y,{\rho }_2\right)\right)d\left({\rho }_1-{\rho }_2\right)\left(y\right)>0\hspace{0.17em}\text{for all}\hspace{0.17em}{\rho }_1\ne {\rho }_2,$$

and similarly for $g$—then the solution to Eq. 1.1 exists and is unique. See refs. 18–20 for more details. Although there are a plethora of fast solvers for the solution of Eq. 1.1 in two and three dimensions (20–25), numerical methods for solving Eq. 1.1 in high dimensions are practically nonexistent due to the need for grid-based spatial discretization. These grid-based methods are prone to the curse of dimensionality, i.e., their computational complexity grows exponentially with spatial dimension (26). Thus, grid-based methods cannot be tractably used on, e.g., modeling an energy-efficient heating, ventilation, and air-conditioning system in a complex building, where the dimensions can be as high as 1,000 (27).

Our Contribution.

We present APAC-Net, an alternating population and agent control neural network approach geared toward high-dimensional MFGs in the deterministic and stochastic case. To this end, we phrase the MFG problem as a saddle-point problem (19, 22, 28) and parameterize the value function and the density function. This formulation provides some alleviation to the curse of dimensionality by avoiding the use of spatial grids or uniformly sampling in high dimensions. While spatial grids for MFGs are also avoided in ref. 29, their work is limited to the deterministic setting $\left(\nu =0\right)$. APAC-Net models high-dimensional MFGs in the stochastic setting $\left(\nu >0\right)$. It does this by drawing from a natural connection between MFGs and generative adversarial neural networks (GANs) (30) (Section 3), a powerful class of generative models that have shown remarkable success on various types of datasets (30–35).

1. Variational Primal-Dual Formulation of MFGs

We derive the mathematical formulation of MFGs for our framework; in particular, we arrive at a primal-dual convex–concave formulation tailored for our alternating networks approach. An MFG system Eq. 1.1 is called potential, if there exist functionals $\mathcal{F},\mathcal{G}$ such that

$${\delta }_{\rho }\mathcal{F}=f\left(x,\rho \right)\hspace{1em}\text{and}\hspace{1em}{\delta }_{\rho }\mathcal{G}=g\left(x,\rho \right),$$ [2.1]

where

$$\begin{array}{cc}\hfill & \langle {\delta }_{\rho }\mathcal{F}\left(\rho \right),\mu \rangle =\underset{h\to 0}{lim}\frac{\mathcal{F}\left(\rho +h\mu \right)-\mathcal{F}\left(\rho \right)}{h},\forall \mu ,\hfill \\ \hfill & \langle {\delta }_{\rho }\mathcal{G}\left(\rho \right),\mu \rangle =\underset{h\to 0}{lim}\frac{\mathcal{G}\left(\rho +h\mu \right)-\mathcal{G}\left(\rho \right)}{h},\forall \mu .\hfill \end{array}$$ [2.2]

That is, there exist functionals $\mathcal{F},\mathcal{G}$ such that their variational derivatives with respect to $\rho$ are the interaction and terminal costs $f$ and $g$ from Eq. 1.1. A critical feature of potential MFGs is that the solution to Eq. 1.1 can be formulated as the solution to a convex–concave saddle-point optimization problem. To this end, we begin by stating Eq. 1.1 as a variational problem (19, 22) akin to the Benamou–Brenier formulation for the Optimal Transport (OT) problem:

$$\begin{array}{cc}\hfill & \underset{\rho ,v}{inf}{\int }_0^T\left\{{\int }_{\mathrm{\Omega }}\rho \left(x,t\right)L\left(x,v\left(x,t\right)\right)dx+\mathcal{F}\left(\rho \left(\cdot ,t\right)\right)\right\}\hspace{0.17em}dt+\mathcal{G}\left(\rho \left(\cdot ,T\right)\right)\hfill \\ \hfill & \text{s.t.}{\partial }_t\rho -\nu \mathrm{\Delta }\rho +\nabla \cdot \left(\rho v\right)=0,\hspace{1em}\rho \left(x,0\right)={\rho }_0\left(x\right),\hfill \end{array}$$ [2.3]

where $L:{\mathbb{R}}^n\times {\mathbb{R}}^n\to \mathbb{R}$ is the Lagrangian function corresponding to the Legendre transform of the Hamiltonian $H$, $\mathcal{F},\mathcal{G}:\mathcal{P}\left({\mathbb{R}}^n\right)\to \mathbb{R}$ are mean-field interaction terms, and $v:{\mathbb{R}}^n\times \left[0,T\right]\to {\mathbb{R}}^n$ is the velocity field. Next, setting $\varphi$ as a Lagrange multiplier, we insert the PDE constraint into the objective to get

$$\begin{array}{cc}\hfill & \underset{\varphi }{sup}\underset{\rho \left(x,0\right)={\rho }_0\left(x\right),v}{inf}\hfill \\ \hfill & {\int }_0^T\left\{{\int }_{\mathrm{\Omega }}\rho \left(x,t\right)L\left(x,v\left(x,t\right)\right)dx+\mathcal{F}\left(\rho \left(\cdot ,t\right)\right)\right\}dt+\mathcal{G}\left(\rho \left(\cdot ,T\right)\right)\hfill \\ \hfill & -{\int }_0^T{\int }_{\mathrm{\Omega }}\varphi \left(x,t\right)\left({\partial }_t\rho -\nu \mathrm{\Delta }\right.\rho +\nabla \cdot \left(\rho \left(x,t\right)v\left(x,t\right)\right)\hspace{0.17em}dx\hspace{0.17em}dt.\hfill \end{array}$$ [2.4]

Finally, integrating by parts and minimizing with respect to $v$ to obtain the Hamiltonian via $H\left(x,p\right)=\underset{v}{inf}\left\{-p\cdot v+L\left(x,v\right)\right\}$, we obtain

$$\begin{array}{cc}\hfill & \underset{\rho \left(x,0\right)={\rho }_0\left(x\right)}{inf}\underset{\varphi }{sup}\hfill \\ \hfill & {\int }_0^T\left\{{\int }_{\mathrm{\Omega }}\left({\partial }_t\varphi +\nu \mathrm{\Delta }\varphi -H\left(x,\nabla \varphi \right)\right)\rho \left(x,t\right)\hspace{0.17em}dx+\mathcal{F}\left(\rho \left(\cdot ,t\right)\right)\right\}\hspace{0.17em}dt\hfill \\ \hfill & +{\int }_{\mathrm{\Omega }}\varphi \left(x,0\right){\rho }_0\left(x\right)dx-{\int }_{\mathrm{\Omega }}\varphi \left(x,T\right)\rho \left(x,T\right)dx+\mathcal{G}\left(\rho \left(\cdot ,T\right)\right).\hfill \end{array}$$ [2.5]

Here, our approach follows that of refs. 22, 36, and 37. This formula can also be obtained in the context of HJB equations in density spaces (23) or by integrating the HJB and the FP equations in Eq. 1.1 with respect to $\rho$ and $\varphi$, respectively (28). In ref. 28, it was observed that all MFG systems admit an infinite-dimensional two-player general-sum game formulation, and the potential MFGs are the ones that correspond to zero-sum games. In this interpretation, Player 1 represents the mean field or the population as a whole, and their strategy is the population density $\rho$. Furthermore, Player 2 represents the generic agent, and their strategy is the value function $\varphi$. The aim of Player 2 is to provide a strategy that yields the best response of a generic agent against the population. This interpretation is in accord with the intuition behind GANs, as the key observation is that under mild assumptions on $\mathcal{F}$ and $\mathcal{G}$, each spatial integral is really an expectation from $\rho$. The formulation Eq. 2.5 is the cornerstone of our method.

2. Connections to GANs

GANs.

In GANs (30), we have a discriminator and generator, and the goal is to obtain a generator that is able to produce samples from a desired distribution. The generator does this by taking samples from a known distribution $\mathcal{N}$ and transforming them into samples from the desired distribution. Meanwhile, the purpose of the discriminator is to aid the optimization of the generator. Given a generator network $G_{\theta }$ and a discriminator network $D_{\omega }$, the original GAN objective is to find an equilibrium to the minimax problem

$$\underset{G_{\theta }}{inf}\hspace{0.17em}\underset{D_{\omega }}{sup}{\mathbb{E}}_{x\sim {\rho }_0}\left[\log D_{\omega }\left(x\right)\right]+{\mathbb{E}}_{z\sim \mathcal{N}}\left[\log \left(1-D_{\omega }\left(G_{\theta }\left(z\right)\right)\right)\right].$$ [3.1]

Here, the discriminator acts as a classifier that attempts to distinguish real images from fake/generated images, and the goal of the generator is to produce samples that “fool” the discriminator.

Wasserstein GANs.

In Wasserstein GANs (31), the motivation is drawn from OT theory, where now the objective function is changed to the Wasserstein-1 (W1) distance in the Kantorovich–Rubenstein dual formulation

$$\underset{G_{\theta }}{inf}\hspace{0.17em}\underset{D_{\omega }}{sup}{\mathbb{E}}_{x\sim {\rho }_0}\left[D_{\omega }\left(x\right)\right]-{\mathbb{E}}_{z\sim \mathcal{N}}\left[D_{\omega }\left(G_{\theta }\left(z\right)\right)\right],\text{s.t.}\Vert \nabla D_{\omega }\Vert \le 1,$$ [3.2]

and the discriminator is required to be 1-Lipschitz. In this setting, the goal of the discriminator is to compute the W1 distance between the distribution of ${\rho }_0$ and $G_{\theta }\left(z\right)$. In practice, using the W1 distance helps prevent the generator from suffering “mode collapse,” a situation where the generator produces samples from only one mode of the distribution ${\rho }_0$; for instance, if ${\rho }_0$ is the distribution of images of handwritten digits, then mode collapse entails producing only, say, the 0 digit. Originally, weight-clipping was to enforce the Lipschitz condition of the discriminator network (31), but an improved method using a penalty on the gradient was used in ref. 32.

GANs $\leftrightarrow$ MFGs.

A Wasserstein GAN can be seen as a particular instance of a deterministic MFG (19, 22, 38). Specifically, consider the MFG Eq. 2.5 in the following setting. Let $\nu =0$, $\mathcal{G}$ be a hard constraint with target measure ${\rho }_T$ (as in OT), let $\mathcal{F}$ = 0, and let $H$ be the Hamiltonian defined by

$$H\left(x,p\right)={\mathbb{1}}_{\Vert p\Vert \le 1}=\left\{\begin{array}{cc}0\hspace{1em}\hfill & \Vert p\Vert \le 1\hfill \\ \infty \hspace{1em}\hfill & \text{otherwise}\hfill \end{array}\right.,$$ [3.3]

where we note that this Hamiltonian arises when the Lagrangian is given by $L\left(x,v\right)=\Vert {v\Vert }_2$. Then, Eq. 2.5 reduces to,

$$\begin{array}{cc}\hfill & \underset{\varphi }{sup}{\int }_{\mathrm{\Omega }}\varphi \left(x\right){\rho }_0\left(x\right)\hspace{0.17em}dx-{\int }_{\mathrm{\Omega }}\varphi \left(x\right){\rho }_T\left(x\right)\hspace{0.17em}dx\hfill \\ \hfill & \hspace{1em}\text{s.t.}\Vert \nabla \varphi \left(x\right)\Vert \le 1,\hfill \end{array}$$ [3.4]

where we note that the optimization in $\rho$ leads to ${\partial }_t\varphi -H\left(x,\nabla \varphi \right)=0$. And since $H\left(p\right)={\mathbb{1}}_{\Vert p\Vert \le 1}$, we have that ${\partial }_t\varphi =0$, and $\varphi \left(x,t\right)=\varphi \left(x\right)$ for all $t$. We observe that the above is precisely the W1 distance in the Kantorovich–Rubenstein duality (39).

3. APAC-Net

Rather than discretizing the domain and solving for the function values at grid-points, APAC-Net avoids them by parameterizing the function and solving for the function itself. We make a small commentary that this rhymes with history, in moving from the Riemann to the Lebesgue integral: The former focused on grid-points of the domain, whereas the latter focused on the function values.

The training process for our MFG is similar to that of GANs. We initialize the neural networks $N_{\omega }\left(x,t\right)$ and $N_{\theta }\left(z,t\right)$. We then let

$$\begin{array}{ll}\hfill {\varphi }_{\omega }\left(x,t\right)& =\left(1-t\right)N_{\omega }\left(x,t\right)+tg\left(x\right),\hfill \\ \hfill G_{\theta }\left(z,t\right)& =\left(1-t\right)z+t{N}_{\theta }\left(z,t\right),\hfill \end{array}$$ [4.1]

where $z\sim {\rho }_0$ are samples drawn from the initial distribution. Thus, we set $\rho \left(\cdot ,t\right)=G_{\theta }\left(\cdot ,t\right)\#{\rho }_0$, i.e., the push-forward of ${\rho }_0$. We make a small comment that this idea of sampling to solve a PDE is similar in spirit to that of the Feynman–Kac approach. In this setting, we train $G_{\theta }\left(\cdot ,t\right)$ to produce samples from $\rho \left(\cdot ,t\right)$. We note that ${\varphi }_{\omega }$ and $G_{\theta }$ automatically satisfy the terminal and initial condition, respectively. In particular, $G_{\theta }$ produces samples from ${\rho }_0$ at $t=0$.

Our strategy for training consists of alternately training $G_{\theta }$ (the population) and ${\varphi }_{\omega }$ (the value function for an individual agent). Intuitively, this means we are alternating the population and agent control neural networks (APAC-Net) in order to find the equilibrium. Specifically, we train ${\varphi }_{\omega }$ by first sampling a batch ${\left\{z_b\right\}}_{b=1}^B$ from the given initial density ${\rho }_0$ and ${\left\{t_b\right\}}_{b=1}^B$ uniformly from $\left[\mathrm{0,1}\right]$; so, we are really sampling from the products of the densities ${\rho }_0$ and $\text{Unif}\left(\left[\mathrm{0,1}\right]\right)$. Next, we compute the push-forward $x_b=G_{\theta }\left(z_b,t_b\right)$ for $b=1,\dots ,B$. We then compute the loss,

$$\begin{array}{cc}\hfill {\text{loss}}_{\varphi }=& \frac{1}{B}\sum _{b=1}^B{\varphi }_{\omega }\left(x_b,0\right)+\frac{1}{B}\sum _{b=1}^B{\partial }_t{\varphi }_{\omega }\left(x_b,t_b\right)\hfill \\ \hfill & \hspace{1em}+\nu \mathrm{\Delta }{\varphi }_{\omega }\left(x_b,t_b\right)-H\left({\nabla }_x{\varphi }_{\omega }\left(x_b,t_b\right)\right),\hfill \end{array}$$ [4.2]

where we can optionally add a regularization term

$$\begin{array}{cc}\hfill \text{penalty}=\lambda \frac{1}{B}\sum _{b=1}^B& ∥{\partial }_t{\varphi }_{\omega }\left(x_b,t_b\right)+\nu \mathrm{\Delta }{\varphi }_{\omega }\left(x_b,t_b\right)\hfill \\ \hfill & \hspace{1em}-H\left({\nabla }_x{\varphi }_{\omega }\left(x_b,t_b\right)\right)+f\left(x_b,t_b\right)∥,\hfill \end{array}$$ [4.3]

to penalize deviations from the HJB equations (29, 40). This extra regularization term has also been found effective in, e.g., Wasserstein GANs (3), where the norm of the gradient (i.e., the HJB equations) is penalized. Finally, we back-propagate the loss to the weights of ${\varphi }_w$. To train the generator, we again sample ${\left\{z_b\right\}}_{b=1}^B$ and ${\left\{t_b\right\}}_{b=1}^B$ as before and compute

$$\begin{array}{cc}\hfill {\text{loss}}_G=& \frac{1}{B}\sum _{b=1}^B{\partial }_t{\varphi }_{\omega }\left(G_{\theta }\left(z_b\right),t_b\right)+\nu \mathrm{\Delta }{\varphi }_{\omega }\left(G_{\theta }\left(z_b\right),t_b\right)\hfill \\ \hfill & \hspace{1em}-H\left({\nabla }_x{\varphi }_{\omega }\left(G_{\theta }\left(z_b\right),t_b\right)\right)+f\left(G_{\theta }\left(z_b\right),t_b\right).\hfill \end{array}$$ [4.4]

Finally, we back-propagate this loss with respect to the weights of $G_{\theta }$ (see Algorithm [Alg.] 1).

Algorithm 1: APAC-Net

Require: $\nu$ diffusion parameter, $G$ terminal cost, $H$ Hamiltonian, $f$ interaction term.

Require: Initialize neural networks $N_{\omega }$ and $N_{\theta }$, batch size $B$

Require: Set ${\varphi }_{\omega }$ and $G_{\theta }$ as in Eq. 4.1

while not converged do

train ${\varphi }_{\omega }$:

Sample batch ${\left\{\left(z_b,t_b\right)\right\}}_{b=1}^B$ where $z_b\sim {\rho }_0$ and $t_b\sim \text{Unif}\left(0,T\right)$

$x_b\leftarrow G_{\theta }\left(z_b,t_b\right)$ for $b=1,\dots ,B$.

${\ell }_0\leftarrow \frac{1}{B}{\sum }_{b=1}^B{\varphi }_{\omega }\left(x_b,0\right)$

${\ell }_t\leftarrow \frac{1}{B}{\sum }_{b=1}^B{\partial }_t{\varphi }_{\omega }\left(x_b,t_b\right)+\nu \mathrm{\Delta }{\varphi }_{\omega }\left(x_b,t_b\right)-H\left({\nabla }_x{\varphi }_{\omega }\left(x_b,t_b\right)\right)$

${\ell }_{\text{HJB}}\leftarrow \lambda \frac{1}{B}{\sum }_{b=1}^B\Vert {\partial }_t{\varphi }_{\omega }\left(x_b,t_b\right)+\nu \mathrm{\Delta }{\varphi }_{\omega }\left(x_b,t_b\right)-H\left({\nabla }_x{\varphi }_{\omega }\left(x_b,t_b\right)\right)+f\left(x_b,t_b\right)\Vert$

Back-propagate the loss ${\ell }_{\text{total}}={\ell }_0+{\ell }_t+{\ell }_{\text{HJB}}$ to $\omega$ weights.

train $G_{\theta }$:

Sample batch ${\left\{\left(z_b,t_b\right)\right\}}_{b=1}^B$ where $z_b\sim {\rho }_0$ and $t_b\sim \text{Unif}\left(0,T\right)$

${\ell }_t\leftarrow \frac{1}{B}{\sum }_{b=1}^B{\partial }_t{\varphi }_{\omega }\left(G_{\theta }\left(z_b,t_b\right),t_b\right)+\nu \mathrm{\Delta }{\varphi }_{\omega }\left(G_{\theta }\left(z_b,t_b\right),t_b\right)-H\left({\nabla }_x{\varphi }_{\omega }\left(G_{\theta }\left(z_b,t_b\right),t_b\right)\right)+f\left(G_{\theta }\left(z_b,t_b\right),t_b\right)$

Back-propagate the loss ${\ell }_{\text{total}}={\ell }_t$ to $\theta$ weights.

4. Related Works

High-Dimensional MFGs and Optimal Control.

To the best of our knowledge, the first work to solve MFGs efficiently in high dimensions ($d=100$) was done in ref. 29. Their work consisted of using Lagrangian coordinates and parameterizing the value function using a neural network. Finally, to estimate the densities, the instantaneous change of variables formula (41). This combination allowed them to successfully avoid using spatial grids when solving deterministic MFG problems $\left(\nu =0\right)$ with quadratic Hamiltonians. Besides only computing MFGs with $\nu =0$, another limitation is that for nonquadratic Hamiltonians, the instantaneous change of variables formula may lead to high computational costs when estimating the density. APAC-Net circumvents this limitation by rephrasing the MFG as a saddle-point problem Eq. 2.5 and using a GAN-based approach to train two neural networks instead. For problems involving high-dimensional optimal control and differential games, spatial grids were also avoided (20, 23, 24, 42, 43). However, these methods are based on generating individual trajectories per agent and cannot be directly applied to MFGs without spatial discretization of the density, thus limiting their use in high dimensions.

Reinforcement Learning.

Our work bears connections with multiagent reinforcement learning (RL), where neither the Lagrangian $L$ nor the dynamics (constraint) in Eq. 2.3 are known. Here, a key difference is that multiagent RL generally considers a finite number of players. Ref. 44 proposes a primal-dual distributed method for multiagent RL. Refs. 16 and 45 propose a Q-Learning approach to solve these multiagent RL problems. Ref. 17 studies the convergence of policy gradient methods on mean-field RL problems, i.e., problems where the agents try instead to learn the control, which is socially optimal for the entire population. Ref. 46 uses an inverse RL approach to learn the MFG model along with its reward function. Ref. 47 proposes an actor–critic method for finding the Nash equilibrium in linear-quadratic MFGs and establishing linear convergence.

Generative Modeling with OT.

There is a class of works that focus on using OT, a class of MFGs, to solve problems arising in data science and, in particular, GANs. Ref. 48 presents a tractable method to train large-scale generative models using the Sinkhorn distance, which consist of loss functions that interpolate between Wasserstein (OT) distance and Maximum Mean Discrepancy (MMD). Ref. 49 proposes a mini-batch MMD-based distance to improve training GANs. Ref. 50 proposes a class of regularized Wasserstein GAN problems with theoretical guarantees. Ref. 51 uses a trained discriminator from GANs to further improve the quality of generated samples. Ref. 52 phrases the adversarial problem as a matching problem in order to avoid solving a minimax problem. Finally, ref. 53 provides an excellent survey on recent numerical methods for OT and their applications to GANs.

GAN-Based Approach for MFGs.

Our work is most similar to ref. 38, where a connection between MFGs and GANs is also made. However, APAC-Net differs from ref. 38 in two fundamental ways. First, instead of choosing the value function to be the generator, we set the density function as the generator. This choice is motivated by the fact that the generator outputs samples from a desired distribution. It is also aligned with other generative modeling techniques arising in continuous normalizing flows (40, 54–56). Second, rather than setting the generator/discriminator losses as the residual errors of Eq. 1.1, we follow the works of refs. 19, 22, 23, and 28 and utilize the underlying variational primal-dual structure of MFGs (see Eq. 2.5); this allows us to arrive at the Kantorovich–Rubenstein dual formulation of Wasserstein GANs (39).

5. Numerical Experiments

We demonstrate the potential of APAC-Net on a series of high-dimensional MFG problems. We note that the below examples would not have been possible with previous grid-based methods, as the number of grid-points required to even start the problem grows exponentially with the dimension. We also illustrate the behavior of the MFG solutions for different values of $\nu$ and use an analytical solution to illustrate the accuracy of APAC-Net. We also provide additional high-dimensional results in Appendix B.

Experimental Setup.

We assume without loss of generality $T=1$, unless otherwise stated. In all experiments, our neural networks have three hidden layers, with 100 hidden units per layer. We use a residual neural network (ResNet) for both networks, with skip connection weight 0.5. For ${\varphi }_{\omega }$, we use the Tanh activation function, and for $G_{\theta }$, we use the ReLU activation function. For training, we use ADAM with $\beta =\left(0.5,0.9\right)$, learning rate $4\times 10^{-4}$ for ${\varphi }_{\omega }$, learning rate $1\times 10^{-4}$ for $G_{\theta }$, weight decay of $10^{-4}$ for both networks, batch size 50, and $\lambda =1$ (the HJB penalty parameter) in Alg. 1.

The Hamiltonians in our experiments have the form

$$H\left(x,p,t\right)=c\Vert {p\Vert }_2+f\left(x,\rho \left(x,t\right)\right),$$ [6.1]

where $f\left(x,\rho \left(x,t\right)\right)$ varies with the environment (either avoiding obstacles or avoiding congestion, etc.), and $c$ is a constant (that represents maximal speed). Furthermore, we choose as terminal cost

$$\mathcal{G}\left(\rho \left(\cdot ,T\right)\right)={\int }_{\mathrm{\Omega }}\Vert x-{xT\Vert }_2\rho \left(x,T\right)dx,$$ [6.2]

which is the distance between the population and a target destination. To allow for verification of the high-dimensional solutions, we set the obstacle and congestion costs to only affect the first two dimensions. In Figs. 1–4 and 6, time is represented by color. Specifically, blue denotes starting time, red denotes final time, and the intermediate colors denote intermediate times. We also plot the HJB residual error—that is, ${\ell }_{\mathrm{H}\mathrm{J}\mathrm{B}}$ in Alg. 1—on 4,096 fixed sampled points, which helps us monitor the convergence of APAC-Net. As in standard machine-learning methods, all of the plots in this section are generated by using validation data—i.e., data not used in training—in order to gauge generalizability of APAC-Net. Further details, as well as additional experiments, can be found in the appendix.

Fig. 1.

Comparison of 2D solutions for different values of $\nu$. The agents start at the blue points $\left(t=0\right)$ and end at the red points $\left(t=1\right)$.

Fig. 4.

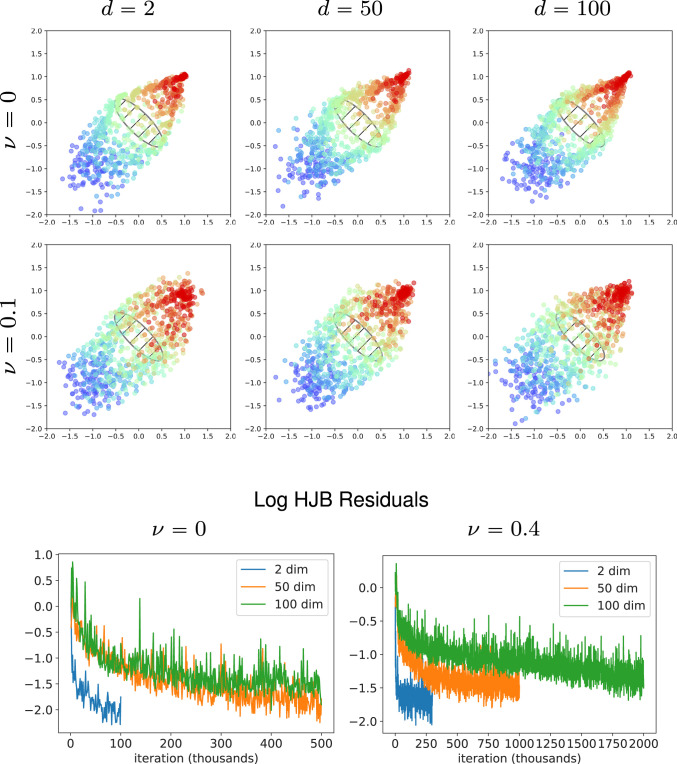
Computation of the congestion problem with a bottleneck in dimensions (dim) 2, 50, and 100 with stochasticity parameter $\nu =0$ and 0.1. For dimensions 50 and 100, we plot the first two dimensions.

Fig. 6.

Computation of the control of the fully nonlinear multiagent quadcopter (12 dimensions). This experiment represents a real-world example of control, where we move the agents from one point to another, with the constraint of having a velocity of zero at the destination. We compute examples with and without noise ($\sigma >0$) and with and without congestion. The HJB residuals (Eq. 4.3) are plotted in the graph.

Effect of Stochasticity Parameter $\nu$.

We investigate the effect of the stochasticity parameter $\nu$ on the behavior of the MFG solutions. In Fig. 1, we show the solutions for two-dimensional (2D) MFGs using $\nu =\mathrm{0,0.2},0.4$, and 0.6. As $\nu$ increases, the density of agents widens along the paths due to the added diffusion term in the HJB and FP equations in Eq. 1.1. The hatched markings are obstacles and are described in Eqs. 6.4 and 6.5. These results are consistent with those in ref. 57.

Obstacles.

We compute the solution to an MFG where the agents are required to avoid obstacles. In this case, we let

$$\begin{array}{cc}\hfill f\left(x_1,x_2,\dots ,x_d\right)=& \hspace{0.17em}{\gamma }_{\text{obst}}\left(max\left\{f_1\left(x_1,x_2\right),0\right\}\right.\hfill \\ \hfill & +\left.max\left\{f_2\left(x_1,x_2\right),0\right\}\right),\hfill \end{array}$$ [6.3]

with ${\gamma }_{\text{obst}}=5$, and denoting $R=\left(\begin{array}{cc}\cos \left(\theta \right)\hfill & -\sin \left(\theta \right)\hfill \\ \sin \left(\theta \right)\hfill & \cos \left(\theta \right)\hfill \end{array}\right)$ with $\theta =\pi /5$, $Q=\left(\begin{array}{cc}5\hfill & 0\hfill \\ 0\hfill & 0\hfill \end{array}\right)$, and $b=\left(\mathrm{0,2}\right)$, then

$$\begin{array}{cc}\hfill f_1\left(x_1,x_2\right)& =-v^{\top }Qv-b\cdot v-1,\hfill \\ \hfill \text{with}\hspace{0.17em}v& =\left(\left(x_1,x_2\right)-\left(-\mathrm{2,0.5}\right)\right)R.\hfill \end{array}$$ [6.4]

Similarly, we let

$$\begin{array}{cc}\hfill f_2\left(x_1,x_2\right)& =-w^{\top }Qw+b\cdot w-1,\hfill \\ \hfill \text{with}\hspace{0.17em}w& =\left(\left(x_1,x_2\right)-\left(2,-0.5\right)\right)R.\hfill \end{array}$$ [6.5]

The obstacles $f_1$ and $f_2$ are shown in hatched markings in Fig. 2. Our initial density ${\rho }_0$ is a Gaussian centered at $\left(-2,-\mathrm{2,0},\dots ,0\right)$ with SD $1/\sqrt{10}\approx 0.32$, and the terminal function is $g\left(x\right)=\Vert \left(x_1,x_2\right)-{\left(\mathrm{2,2}\right)\Vert }_2$. We chose $c=8$ in Eq. 6.1. The numerical results are shown in Fig. 2. Observe that results are similar across dimensions, verifying our high-dimensional computation. We run the 2D problem for 200,000 (200 k) iterations and the 50- and 100-dimensional problems for 300 k iterations.

Fig. 2.

Computation of the obstacle problem in dimensions (dim) 2, 50, and 100 with stochasticity parameter $\nu =0$ and 0.4. For dimensions 50 and 100, we plot the first two dimensions.

Congestion.

We choose the interaction term to penalize congestion, so that the agents are encouraged to spread out. In particular, we have

$$\mathcal{F}\left(\rho \left(\cdot ,t\right)\right)={\int }_{\mathrm{\Omega }}{\int }_{\mathrm{\Omega }}\frac{1}{\Vert \left(x_1,x_2\right)-{\left(y_1,y_2\right)\Vert }^2+1}\hspace{0.17em}d\rho \left(x,t\right)\hspace{0.17em}d\rho \left(y,t\right),$$ [6.6]

which is the (bounded) inverse squared distance, averaged over pairs of agents. Computationally, we sample from $\rho$ twice and then calculate the integrand. Here, our initial density ${\rho }_0$ is a Gaussian centered at $\left(-\mathrm{2,0},-2,\dots ,-2\right)$ with SD $1/\sqrt{10}\approx 0.32$, the terminal function is $\mathcal{G}\left(x\right)=\Vert \left(x_1,x_2\right)-{\left(\mathrm{2,0}\right)\Vert }_2$, and we chose $c=5$ in Eq. 6.1. Results are shown in Fig. 3, where we see qualitatively similar results across dimensions. We run the 2D problem for 100 k iterations and the 50- and 100-dimensional problems for 500 k iterations.

Fig. 3.

Computation of the congestion problem in dimensions (dim) 2, 50, and 100 with stochasticity parameter $\nu =0$ and 0.4. For dimensions 50 and 100, we plot the first two dimensions.

Congestion with Bottleneck Obstacle.

We combine the congestion problem with a bottleneck obstacle. The congestion penalization is the same as Eq. 6.6, and the obstacle represents a bottleneck—thus, agents are encouraged to spread out, but must squeeze together to avoid the obstacle. The initial density, terminal functions, $c$ in Eq. 6.1, and the expression penalizing congestion are the same as in the congestion experiment above. The obstacle is chosen to be

$$\begin{array}{cc}\hfill & f\left(v\right)={\gamma }_{\text{obst}}max\left\{-v^{\top }\left(\begin{array}{cc}5\hfill & 0\hfill \\ 0\hfill & -1\hfill \end{array}\right)v-0.1,0\right\},\hfill \\ \hfill & \hspace{1em}\text{with}\hspace{0.17em}v=\left(x_1,x_2\right)\hfill \end{array}$$ [6.7]

with ${\gamma }_{\text{obst}}=5$. As intuitively expected, the agents spread out before and after the bottleneck, but squeeze together in order to avoid the obstacle (Fig. 4). We run the 2D problem for 100 k iterations and the 50- and 100-dimensional problems for 500 k iterations. We observe similar results across dimensions.

Analytic Comparison.

We verify our method by comparing it to an analytic solution for dimensions 2, 50, and 100 with congestion $\left(\gamma =0.1\right)$ and without congestion $\left(\gamma =0\right)$. For

$$\begin{array}{cc}\hfill f& =\gamma \ln \left(\rho \right),\hspace{1em}H\left(x,p\right)=\frac{\Vert {p\Vert }^2}{2}-\frac{\beta \Vert {x\Vert }^2}{2},\hfill \\ \hfill g\left(x\right)& =\frac{\alpha |x{|}^2}{2}-\left(\nu d\alpha +\frac{\gamma d}{2}\ln \frac{\alpha }{2\pi \nu }\right),\hfill \end{array}$$ [6.8]

and $\nu =\beta =1$ in Eq. 1.1, the explicit formula for $\varphi$ is given by

$$\begin{array}{cc}\hfill \varphi \left(x,t\right)& =\frac{\alpha |x{|}^2}{2}-\left(d\alpha +\frac{\gamma d}{2}\ln \frac{\alpha }{2\pi }\right)t,\hfill \\ \hfill \rho \left(x,t\right)& ={\left(\frac{\alpha }{2\pi }\right)}^{\frac{d}{2}}{e}^{-\frac{\alpha |x{|}^2}{2}},\hfill \end{array}$$ [6.9]

where $\alpha =\frac{-\gamma +\sqrt{{\gamma }^2+4}}{2}$. For the $\gamma =0.1$ case, we use Kernel Density Estimation (58, 59) to estimate $\rho$ from samples of the generator. The derivation of the analytic solution can be found in Appendix A.

For $d=2$, we compute the relative error on a grid of size $32\times 32\times 16$, where we discretize the spatial domain $\mathrm{\Omega }={\left[-\mathrm{2,2}\right]}^2$ with $32\times 32$ points and the time domain $\left[\mathrm{0,1}\right]$ with 16 points. Note here that the grid-points are validation points—i.e., points that were not used in training. For $d=50$ and $d=100$, we use 4,096 sampled points for validation since we cannot build a grid. We run a total of 30 k and 60 k iterations for $\gamma =0$ and $\gamma =0.1$, respectively. We validate every 1 k iterations. Fig. 5 shows that our learned model approaches the true solution across all dimensions for both values of $\gamma$, indicating that APAC-Net generalizes well.

Fig. 5.

Log relative errors in 2, 50, and 100 dimensions (dim) and for $\gamma =\mathrm{0,0.1}$. Here, $\gamma =0$ means no interaction. For the $d=2$ case, we compute the validation on a $32\times 32$ grid over 16 uniformly spaced timesteps with the true $\varphi$ from Eq. 6.9. For the $d=50$ and 100 cases, we compute on a sample of 4,096 sample points, sampled from the initial density.

A Realistic Example: The Quadcopter.

In this experiment, we examine a realistic scenario where the dynamics are that of a Quadcopter (also known as Quadrotor craft), which is an aerial vehicle with four rotary wings (similar to many of the consumer drones seen today). The dynamics of the quadrotor craft are given as,

$$\left\{\begin{array}{cc}\ddot{x}\hfill & \hspace{1em}=\frac{u}{m}l\left(\sin \left(\varphi \right)\sin \left(\psi \right)+\cos \left(\varphi \right)\cos \left(\psi \right)\sin \left(\theta \right)\rho \right)\hfill \\ ÿ\hfill & \hspace{1em}=\frac{u}{m}l\left(-\cos \left(\psi \right)\sin \left(\varphi \right)+\cos \left(\varphi \right)\sin \left(\theta \right)\sin \left(\psi \right)\rho \right)\hfill \\ \ddot{z}\hfill & \hspace{1em}=\frac{u}{m}\cos \left(\theta \right)\cos \left(\varphi \right)-g\hfill \\ \ddot{\psi }\hfill & \hspace{1em}={\tilde{\tau }}_{\psi }\hfill \\ \ddot{\theta }\hfill & \hspace{1em}={\tilde{\tau }}_{\theta }\hfill \\ \ddot{\varphi }\hfill & \hspace{1em}={\tilde{\tau }}_{\varphi }\hfill \end{array}\right.,$$

where $x$, $y$, and $z$ are the usual Euclidean spatial coordinates, and $\varphi$, $\theta$, and $\psi$ are the angular coordinates of roll, pitch, and yaw, respectively. The constant $m$ is the mass, to which we put 0.5 (kilogram), and $g$ is the gravitation acceleration constant on Earth, to which we put 9.81 (meters per second squared). The variables $u$, ${\tilde{\tau }}_{\psi }$, ${\tilde{\tau }}_{\theta }$, ${\tilde{\tau }}_{\varphi }$ are the controls representing thrust and angular acceleration. In order to fit a control framework, the above second-order system is turned into a first-order system:

$$\left\{\begin{array}{cc}{\dot{x}}_1\hfill & \hspace{1em}=x_2\hfill \\ {\dot{x}}_2\hfill & \hspace{1em}=\frac{u}{m}l\left(\sin \left({\varphi }_1\right)\sin \left({\psi }_1\right)+\cos \left({\varphi }_1\right)\cos \left({\psi }_1\right)\sin \left({\theta }_1\right)\rho \right)\hfill \\ {\dot{y}}_1\hfill & \hspace{1em}=y_2\hfill \\ {\dot{y}}_2\hfill & \hspace{1em}=\frac{u}{m}l\left(-\cos \left({\psi }_1\right)\sin \left({\varphi }_1\right)+\cos \left({\varphi }_1\right)\sin \left({\theta }_1\right)\sin \left({\psi }_1\right)\rho \right)\hfill \\ {ż}_1\hfill & \hspace{1em}=z_2\hfill \\ {ż}_2\hfill & \hspace{1em}=\frac{u}{m}\cos \left({\theta }_1\right)\cos \left({\varphi }_1\right)-g\hfill \\ {\dot{\psi }}_1\hfill & \hspace{1em}={\psi }_2\hfill \\ {\dot{\psi }}_2\hfill & \hspace{1em}={\tilde{\tau }}_{\psi }\hfill \\ {\dot{\theta }}_1\hfill & \hspace{1em}={\theta }_2\hfill \\ {\dot{\theta }}_2\hfill & \hspace{1em}={\tilde{\tau }}_{\theta }\hfill \\ {\dot{\varphi }}_1\hfill & \hspace{1em}={\varphi }_2\hfill \\ {\dot{\varphi }}_2\hfill & \hspace{1em}={\tilde{\tau }}_{\varphi }\hfill \end{array}\right.,$$

which we will compactly denote as $\dot{\mathbf{x}}=\mathbf{h}\left(\mathbf{x},\mathbf{u}\right)$, where $\mathbf{h}$ is the right-hand side, $\mathbf{x}$ is the state, and $\mathbf{u}$ is the control. As can be observed, the above is a 12-dimensional system that is highly nonlinear and high-dimensional. In the stochastic case, we add a noise term to the dynamics: $d\mathbf{x}=\mathbf{h}\left(\mathbf{x},\mathbf{u}\right)\hspace{0.17em}dt+\sigma \hspace{0.17em}d{\mathbf{W}}_t$, where $\mathbf{W}$ denotes a Wiener process (standard Brownian motion). The interpretation here is that we are modeling the situation when the quadcopter suffers from noisy measurements.

In our experiments, we set our Lagrangian cost function to be $L\left(\mathbf{u}\right)=\frac{1}{2}\Vert {\mathbf{u}\Vert }_2^2$, and, thus, our Hamiltonian becomes $H\left(\mathbf{p}\right)=\frac{1}{2}\Vert {\mathbf{p}\Vert }_2^2$. Our initial density ${\rho }_0$ is a Gaussian in the spatial coordinates $\left(x,y,z\right)$ centered at $\left(-2,-2,-2\right)$ with SD 0.5, and we set all other initial coordinates to zero (i.e., initial velocity, initial angular position, and initial angular velocity are all set to zero). We set our terminal cost to be a simple norm difference between the agent’s current position and the position $\left(\mathrm{2,2,2}\right)$, and we also want the agents to have zero velocity, i.e.,

$$\mathcal{G}\left(\rho \left(\cdot ,T\right)\right)={\int }_{\mathrm{\Omega }}\Vert \left(x,y,z,\dot{x},\dot{y},ż\right)-{\left(\mathrm{2,2,2,0,0,0}\right)\Vert }_2\rho \left(x,T\right)dx.$$

In our experiments, we set the final time to be $T=4$.

We also add a congestion term to our experiments where the congestion is in the spatial positions, so as to encourage agents to spread out (and thus making midair collisions less likely):

$$\begin{array}{cc}\hfill & \mathcal{F}\left(\rho \left(x,y,z\right)\right)\hfill \\ \hfill & ={\gamma }_{\text{cong}}\frac{1}{{\left(2\pi \right)}^{\frac{3}{2}}}{\int }_{\mathrm{\Omega }}{\int }_{\mathrm{\Omega }}{e}^{\left(-\frac{1}{2}\Vert \left(x,y,z\right)-{\left(\widehat{x},ŷ,\widehat{z}\right)\Vert }_2^2\right)}\hfill \\ \hfill & \hspace{1em}d\rho \left(x,y,z\right)\times d\rho \left(\widehat{x},ŷ,\widehat{z}\right),\hfill \end{array}$$

where in our experiments we put ${\gamma }_{\text{cong}}=20$.

For hyperparameters, we use the same setup as before, except we raise the batch size to 150. Our results are shown in Fig. 6. We see that with congestion, the agents spread out more as expected. Furthermore, in the presence of noise, the agents’ sensors are noisy, and so at terminal time, the agents do not get as close to the terminal point of $\left(\mathrm{2,2,2}\right)$. This noise also adds an envelope of uncertainty, so we do see that the agents are not as streamlined as in the noiseless cases.

We note that most previous attempts at modeling the behavior of quadcopters relied on linearization techniques, but here, we solve the fully nonlinear problem with neural networks. And our approach solves the quadcopter problem in a deterministic and stochastic MFGs context, where we consider many quadcopters and their interactions with each other. This multiagent modeling of the quadcopter would be practically infeasible for grid-based methods, as such a grid would need to discretize a high-dimensional space.

6. Conclusion

We present APAC-Net, an alternating population-agent control neural network approach for tackling high-dimensional stochastic MFGs. To this end, our algorithm avoids the use of spatial grids by parameterizing the controls, $\varphi$ and $\rho$, using two neural networks, respectively. Consequently, our method is geared toward high-dimensional instances of these problems that are beyond reach with existing grid-based methods. APAC-Net therefore sets the stage for solving realistic high-dimensional MFGs arising in, e.g., economics (1–4), swarm robotics (11, 12), and, perhaps most important/relevant, epidemic modeling (13, 14). Our method also has natural connections with Wasserstein GANs, where $\rho$ acts as a generative network and $\varphi$ acts as a discriminative network. Unlike GANs, however, APAC-Net incorporates the structure of MFGs via Eqs. 2.5 and 4.1, which absolves the network from learning an entire MFG solution from the ground up. Our experiments show that our method is able to solve 100-dimensional MFGs.

Since our method was presented solely in the setting of potential MFGs, a natural extension is the nonpotential MFG setting, where the MFG can no longer be written in a variational form. Instead, one would have to formulate the MFG as a monotone inclusion problem (60). Moreover, convergence properties of the training process of APAC-Net may be investigated following the techniques presented in, e.g., ref. 61. Finally, a practical direction involves examining guidelines on the design of more effective network architectures, e.g., PDE-based networks (62, 63), neural ordinary differential equations (41), or sorting networks (64).

Appendix A. Derivation of Analytic Solution

We derive explicit formulas used to test our approximate solutions in Section 6. Assume that $\nu ,\beta >0,\gamma \ge 0$ and

$$H\left(x,p,t\right)=\frac{|p{|}^2}{2}-\frac{\beta |x{|}^2}{2},\hspace{1em}f\left(x,\rho \right)=\gamma \ln \rho .$$ [A.1]

Then, Eq. 1.1 becomes

$$\begin{array}{c}\hfill -{\partial }_t\varphi -\nu \mathrm{\Delta }\varphi +\frac{|\nabla \varphi {|}^2}{2}-\frac{\beta |x{|}^2}{2}=\gamma \ln \rho ,\\ \hfill {\partial }_t\rho -\nu \mathrm{\Delta }\rho -\text{div}\left(\rho \nabla \varphi \right)=0,\\ \hfill \rho \left(x,0\right)={\rho }_0,\hspace{1em}\varphi \left(x,T\right)=\mathrm{\Psi }\left(x\right).\end{array}$$ [A.2]

We find solutions to this system by searching for stationary solutions first:

$$\begin{array}{c}\hfill -\nu \mathrm{\Delta }\varphi +\frac{|\nabla \varphi {|}^2}{2}-\frac{\beta |x{|}^2}{2}=\gamma \ln \rho +\overline{H},\\ \hfill -\nu \mathrm{\Delta }\rho -\text{div}\left(\rho \nabla \varphi \right)=0,\end{array}$$ [A.3]

and then writing

$$\varphi \left(x,t\right)=\varphi \left(x\right)-t\overline{H},\hspace{1em}\rho \left(x,t\right)=\rho \left(x\right).$$ [A.4]

The second equation in Eq. A.3 yields $\rho =c{e}^{-\frac{\varphi }{\nu }}$, where $c$ is chosen so that $\int \rho =1$. Plugging this in the first equation in Eq. A.3, we obtain

$$-\nu \mathrm{\Delta }\varphi +\frac{|\nabla \varphi {|}^2}{2}-\frac{\beta |x{|}^2}{2}=\gamma \ln c-\frac{\gamma }{\nu }\varphi +\overline{H}.$$ [A.5]

Now, we make an ansatz that $\varphi \left(x\right)=\frac{\alpha |x{|}^2}{2}$. Then, we have that $\mathrm{\Delta }\varphi =d\alpha ,\nabla \varphi =\alpha x$, and obtain

$$-\nu d\alpha +\frac{{\alpha }^2|x{|}^2}{2}-\frac{\beta |x{|}^2}{2}=\gamma \ln c-\frac{\gamma \alpha |x{|}^2}{2\nu }+\overline{H}.$$ [A.6]

Therefore, we have that

$${\alpha }^2+\frac{\gamma \alpha }{\nu }=\beta ,\hspace{1em}\overline{H}=-\nu d\alpha -\gamma \ln c.$$ [A.7]

From the first equation, we obtain that

$$\alpha =\frac{-\gamma +\sqrt{{\gamma }^2+4{\nu }^2\beta }}{2\nu }.$$ [A.8]

On the other hand, we have that

$$\int \rho =c\int e^{-\frac{\alpha |x{|}^2}{2\nu }}dx=c{\left(\frac{2\pi \nu }{\alpha }\right)}^{\frac{d}{2}}=1,$$ [A.9]

so

$$c={\left(\frac{\alpha }{2\pi \nu }\right)}^{\frac{d}{2}}\hspace{1em}\text{and}\hspace{1em}\overline{H}=-\nu d\alpha -\frac{\gamma d}{2}\ln \frac{\alpha }{2\pi \nu }.$$ [A.10]

Summarizing, we get that for any $\nu ,\beta >0,\gamma \ge 0$, the following is a solution for Eq. A.2:

$$\begin{array}{cc}\hfill \varphi \left(x,t\right)& =\frac{\alpha |x{|}^2}{2}-\left(\nu d\alpha +\frac{\gamma d}{2}\ln \frac{\alpha }{2\pi \nu }\right)t,\hfill \\ \hfill \rho \left(x,t\right)& ={\left(\frac{\alpha }{2\pi \nu }\right)}^{\frac{d}{2}}{e}^{-\frac{\alpha |x{|}^2}{2\nu }},\hfill \end{array}$$ [A.11]

where $\alpha$ is given by Eq. A.8, and

$$\begin{array}{cc}\hfill g\left(x\right)& =\frac{\alpha |x{|}^2}{2}-\left(\nu d\alpha +\frac{\gamma d}{2}\ln \frac{\alpha }{2\pi \nu }\right)T,\hfill \\ \hfill {\rho }_0\left(x\right)& ={\left(\frac{\alpha }{2\pi \nu }\right)}^{\frac{d}{2}}{e}^{-\frac{\alpha |x{|}^2}{2\nu }}.\hfill \end{array}$$ [A.12]

Choosing $\beta =\nu =1$, Eq. A.11 gives the analytic solution used in Section 6.

Appendix B: Details on Numerical Results and More Experiments

Congestion.

Here, we elaborate on how we compute the congestion term,

$$\mathcal{F}\left(\rho \left(x,t\right)\right)={\int }_{\mathrm{\Omega }}{\int }_{\mathrm{\Omega }}\frac{1}{\Vert \left(x_1,x_2\right)-{\left(y_1,y_2\right)\Vert }^2+1}\hspace{0.17em}d\rho \left(x,t\right)\hspace{0.17em}d\rho \left(y,t\right).$$ [B.1]

We do this by first using the batch ${\left\{z_b\right\}}_{b=1}^B$, which was used for training (and sampled from ${\rho }_0$), and then compute another batch ${\left\{y_b\right\}}_{b=1}^B$, again sampled from ${\rho }_0$. Letting ${\left\{t_b\right\}}_{b=1}^B$ be a batch of time points uniformly sampled in $\left[\mathrm{0,1}\right]$, we estimate the interaction cost with,

$$\mathcal{F}\left(\rho \left(x,t\right)\right)\approx \sum _{i=1}^B\frac{1}{\Vert G_{\theta }\left(z_b,t_b\right)-G_{\theta }{\left(y_b,t_b\right)\Vert }^2+1}.$$ [B.2]

Congestion with Bottleneck Obstacle and Higher Stochasticity.

When choosing a stochasticity parameter $\nu >0.1$, the stochasticity dominates the dynamics, and the obstacles do not interact as much with the obstacle. We plot these results in Fig. 7, where for two dimensions, we trained for 150 k iterations, and for 50 and 100 dimensions, we trained for 800 k iterations. All environment and training parameters are the same as in the Congestion with Bottleneck Obstacle, except that now $\nu =0.4$.

Fig. 7.

Computation of the congestion problem with a bottleneck in dimensions (dim) 2, 50, and 100 with stochasticity parameter $\nu =0.4$. For dimensions 50 and 100, we plot the first two dimensions.

Analytic Comparison.

Here, we mention specifically how we performed Kernel Density Estimation. Namely, in order to estimate the density $\rho$, we take a batch of samples ${\left\{z_b\right\}}_{b=1}^B$ (during training, this is the training batch). Then, at uniformly spaced time points ${\left\{t_b\right\}}_{b=1}\subseteq \left[\mathrm{0,1}\right]$, we estimate the density with the formula,

$$\rho \left(z_b,t_b\right)\approx \frac{1}{B}\frac{1}{{\left(\sigma h\sqrt{2\pi }\right)}^d}{\sum }_{i=1}^B{\sum }_{j=1}^B\text{exp}\left(\frac{{\Vert z_i-z_j\Vert }^2}{{\left(h\sigma \right)}^2}\right),$$ [B.3]

where we choose $\sigma =\sqrt{\frac{\gamma }{\nu }}$, $d$ is the dimension, and $h=B^{-\frac{1}{d+4}}$, in accordance with Scott’s rule for multivariate Kernel Density Estimation (65).

Density Splitting Via Symmetric Obstacle.

Here, we compute an example where we have a symmetric obstacle, and, thus, the generator will learn to split the density. Agents will go left or right of the obstacle, depending on their starting position. Here, we chose the obstacle as,

$$\begin{array}{cc}\hfill & f\left(x_1,x_2,\dots ,x_d\right)={\alpha }_{\text{obst}}max\left\{-v^{\top }Qv+0.1,0\right\},\hfill \\ \hfill & Q=\left(\begin{array}{cc}1\hfill & 0.8\hfill \\ 0.8\hfill & 1\hfill \end{array}\right),v=\left(x_1,x_2\right),\hfill \end{array}$$ [B.4]

and we choose ${\gamma }_{\text{obst}}=20$. The environment and training parameters are the same as in the obstacles example in the main text, except that we choose the HJB penalty $\lambda$ in Alg. 1 to be 0.1. Qualitatively, we see that the solution agrees with our intuition: The agents will go left or right depending on their starting position. Note that the results are similar across dimensions, verifying our computation. For the $2d$, $\nu =0$ case, we trained for 100 k iterations; for the $2d$, $\nu =0.1$ case, we trained for 300 k iterations; for the $50d$ and $100d$, $\nu =0$ case, we trained for 500 k iterations; for the $50d\hspace{0.17em}\nu =0.1$ case, we trained for 1,000 k iterations; and the for the $100d$, $\nu =0.1$ case, we trained for 2,000 k iterations. In Fig. 8, we plot the agents moving through the symmetric obstacles, as well as the HJB residuals.

Fig. 8.

Computation of the obstacle problem where the obstacle is symmetric. We plot the results for dimensions (dim) 2 and 100, and for $\nu =0$ and $\nu =0.1$.

Data Availability

To promote access and progress, we provide our PyTorch implementation at GitHub (https://github.com/atlin23/apac-net).