Review on Applications of ¹⁷O in Hydrological Cycle

Abstract

The triple oxygen isotopes (¹⁶O, ¹⁷O, and ¹⁸O) are very useful in hydrological and climatological studies because of their sensitivity to environmental conditions. This review presents an overview of the published literature on the potential applications of ¹⁷O in hydrological studies. Dual-inlet isotope ratio mass spectrometry and laser absorption spectroscopy have been used to measure ¹⁷O, which provides information on atmospheric conditions at the moisture source and isotopic fractionations during transport and deposition processes. The variations of δ¹⁷O from the developed global meteoric water line, with a slope of 0.528, indicate the importance of regional or local effects on the ¹⁷O distribution. In polar regions, factors such as the supersaturation effect, intrusion of stratospheric vapor, post-depositional processes (local moisture recycling through sublimation), regional circulation patterns, sea ice concentration and local meteorological conditions determine the distribution of ¹⁷O-excess. Numerous studies have used these isotopes to detect the changes in the moisture source, mixing of different water vapor, evaporative loss in dry regions, re-evaporation of rain drops during warm precipitation and convective storms in low and mid-latitude waters. Owing to the large variation of the spatial scale of hydrological processes with their extent (i.e., whether the processes are local or regional), more studies based on isotopic composition of surface and subsurface water, convective precipitation, and water vapor, are required. In particular, in situ measurements are important for accurate simulations of atmospheric hydrological cycles by isotope-enabled general circulation models.

1. Introduction

Two elements-oxygen and hydrogen, in water molecule with their stable isotopes (¹⁶O, ¹⁷O, ¹⁸O, ¹H, and ²H or D) and their ratios (most commonly D/H or ¹⁸O/¹⁶O) have been widely used as hydrological or climatological tracers because of their sensitivity to environmental conditions during the evaporation, condensation, melting, and freezing of water [1,2,3,4,5,6]. Generally, lighter isotopes (¹H, ¹⁶O, and ¹⁷O) are more likely to evaporate into the gas phase, while heavier isotopes (D and ¹⁸O) tend to condense into the liquid or solid phase. Furthermore, the oxygen (expressed as δ¹⁸O) and hydrogen (expressed as δD) isotopic ratios in precipitation are linearly correlated and this relationship is expressed by the Global Meteoric Water line (GMWL) [7]. Changes in the isotopic compositions generally represent the dependence of spatial factors (latitudinal, continental, altitude, and seasonal effects), and deviations from the GMWL at a specific location indicate the climate and environmental conditions [2,8].

Isotopic values have been extensively used in many studies to investigate moisture transport, air mass circulation, precipitation patterns [3,9,10,11], snow hydrology, water movement and balance [12,13,14,15] and the atmospheric water cycle through simulations based on isotope-enabled models [16]. The most depleted isotopic values are observed in polar precipitation, which is formed from cold air masses, and seasonal high and low values are observed, especially in coastal regions [2,4,5]. Thus, isotopic records of polar precipitation (accumulated layers of snow) are used for ice core age dating and as an important indicator of past climate and environmental changes [4,5,7,16,17,18,19,20]. Moreover, in temperate regions, isotopic signals in permafrost (ice wedges) are considered as a paleoclimate tracer [21,22].

In the triple oxygen isotope system, ¹⁷O is the one of the naturally occurring stable isotopes of oxygen with the lowest abundance (0.038%) [23,24], and the enrichment of H₂¹⁷O in water is about half that of H₂¹⁸O [1]. With the growing interest and recent developments in analytical instruments, it has become possible to measure small variations of ¹⁷O in meteoric waters, terrestrial rocks, and minerals [25,26,27]. A mass-dependent between the ratio of ¹⁷O/¹⁶O and ¹⁸O/¹⁶O is less sensitive to temperature, and hence, it is a useful indicator of the kinetic fractionation process. Many studies have used ¹⁷O as a proxy for certain conditions (relative humidity and wind speed) in the moisture source region [10,11]. The relative abundance of ¹⁷O in meteoric water is preferentially reported in terms of ¹⁷O-excess [¹⁷O-excess = ln(δ¹⁷O + 1) − 0.528×ln(δ¹⁸O + 1)][26]. ¹⁷O-excess is an effective parameter for investigating the global hydrological cycle, especially for studying the changes in the relative humidity in the oceanic source region and diffusion-induced kinetic fractionation process [9,10]. Compared with the relative excess of deuterium, which is termed d-excess (d-excess = δD − 8 × δ¹⁸O) and which is widely used as an indicator of kinetic fractionation processes [28,29,30,31,32], ¹⁷O is less dependent on the temperature at evaporation and condensation sites [33]. Thus, the use of ¹⁷O-excess in combination with δ¹⁸O and d-excess provides a potential means to unravel the effect of kinetic fractionation during evaporation at the moisture source, along the transport path, and during the condensation of precipitation [8,10,28,33]. Moreover, supersaturation conditions and cloud ice crystal formation in polar regions are influential in the ¹⁷O composition [30,34].

Although there have been numerous studies on the use of this rare isotope for investigating the water cycle, the processes controlling the spatiotemporal distributions of ¹⁷O in the fundamental hydrological cycle are still not well understood [35,36] and more data is required, particularly on less evaporated water bodies (river, precipitation) [36,37]. Aron et al. [36] proposed the introduction of multiple meteoric water lines in the expression for the variation of ¹⁷O-excess to indicate the importance of regional or local effects on the ¹⁷O pattern. Tian et al. [37] also provided evidence that the ¹⁷O-excess distribution indicated local climatic and geographical conditions rather than general large-scale spatial patterns. Surma et al. [38] mentioned the need to broaden the spatial coverage and long-term observations for refining the global monitoring network and to enable better prediction by the general circulation model. In this review, we introduce the potential applications of ¹⁷O into the hydrological cycle by summarizing the published literature on ¹⁷O-based studies of the hydrological cycle. This paper is organized as following. Section 2 introduces the general definition and isotopic fractionation of ¹⁷O and analytical methods (dual-inlet isotope ratio mass spectrometry and laser absorption spectroscopy) for measuring the ¹⁷O. Section 3 summarizes the published ¹⁷O isotopic values for different sample types and describes the main findings of previous studies. Finally, on the basis of the implications of previous studies, future research needs are highlighted.

2. ¹⁷O Isotope Measurement in Water

2.1. ¹⁷O Definition and Isotopic Fractionation

¹⁷O is the one of the naturally occurring stable isotopes of oxygen, and also it has the lowest abundance, 0.038% [23] (Table 1). The distribution of isotopes in hydrological systems is controlled by isotope fractionation processes. Oxygen isotopes fractionate through mass-dependent isotopic fractionation, which includes kinetic processes, isotopic exchange reactions, and physicochemical phenomena (diffusion, condensation, and evaporation) [1,28]. Moreover, non-mass-dependent fractionation can be induced by chemical effects [39].

Table 1.

Oxygen isotopes, abundances (relative %), δ notation, and δ values of standard materials.

Isotope	Abundance	δ Notation	δ Value of VSMOW2	δ Value of SLAP2	δ Value of GISP
16O	99.76%	–
17O	0.038%	δ17O	0	−29.6986‰ 1	−13.16 ± 0.05 1
18O	0.20%	δ18O	0	−55.5‰ 2	−24.82 ± 0.08 1

¹ Schoenemann et al. [44]. ² IAEA.

Small variations in the ratio of a rare isotope to an abundant isotope, such as ¹⁷O/¹⁶O and ¹⁸O/¹⁶O, due to the mass-dependent fraction, are observed during equilibrium isotope exchange and diffusion of water vapor [1]. Isotopic fractionation is expressed in terms of the fractionation factor (α). For example, the fractionation factor between a liquid (l) and a vapor (v) is defined as

*α_l/v = (*O/¹⁶O)_l/(*O/¹⁶O)_v (1)

where * denotes 17 (¹⁷O) or 18 (¹⁸O). Barkan and Luz [40] reported the liquid-vapor equilibrium fractionation factors for ¹⁷α_l/v and ¹⁸α_l/v to be 1.00496 and 1.00940 at 25.3 °C, respectively, and highlighted their insensitivity to temperature (in the range 11–42 °C). The fractionation factors of ¹⁷α_l/v and ¹⁸α_l/v are related by an exponent θ [40]:

¹⁷α_l/v = (¹⁸α_l/v)^θ  or   θ = (ln¹⁷α_l/v)/(ln¹⁸α_l/v) (2)

The liquid-vapor equilibrium fractionation exponent (θ_eq) was first estimated to be 0.528 by Meijer and Li [41], and later, Barkan and Luz [40] obtained an estimate of 0.529 ± 0.001; it is independent of temperature [40]. Furthermore, the kinetic fractionation effect of the diffusion (θ_diff) of water vapor through air was reported as 0.5184 ± 0.0003, with ¹⁷α_diff and ¹⁸α_diff being 1.0146 ± 0.0002 and 1.0283 ± 0.0003, respectively [29]. Later, ¹⁸α_diff (H₂¹⁸O and H₂¹⁶O diffusion in air above the ocean) was reported to be 1.008 by Uemura et al. [42]. However, for diffusive fractionation, a slight temperature dependence (0.00002/15 °C decreasing trend if the trend is linear) are considered and still uncertain [43]. On the basis of the small difference between θ_eq and θ_diff, equilibrium and kinetic fractionation processes can be distinguished.

The isotopic composition is expressed using the delta notation (δ), which is the ratio of *O/¹⁶O in a sample to that in a standard material multiplied by 1000:

δ*O = (*O/¹⁶O)_sample/((*O/¹⁶O)_VSMOW2 − 1)*1000 (3)

where VSMOW2 (or VSMOW, which stands for Vienna Standard Mean Ocean Water) is the water standard prepared by the International Atomic Energy Agency (IAEA). Thus, a sample’s δ*O is the relative ratio of ¹⁸O/¹⁶O or ¹⁷O/¹⁶O in the sample to that in the VSMOW2 standard, and it is presented in units of permil (%). Moreover, Standard Light Antarctic Precipitation (SLAP2 or SLAP) and Greenland Ice Sheet Precipitation (GISP) are also used as calibration materials. Schoenemann et al. [44] proposed the following VSMOW-SLAP normalization, which improves the accuracy of measurements and universalizes the data expression obtained from different laboratories.

$$\delta {\delta }^{17}{O}_{sample}^{normalized}={\delta }^{17}{O}_{sample}^{measured} \times ({\delta }^{17}{O}_{SLAP2}^{assigned}/{\delta }^{17}{O}_{SLAP2}^{measured})$$ (4)

Here, ${\delta }^{17}{O}_{SLAP2}^{assigned}$ is −29.6986‰, the value defined by Schoenemann et al. [44] as an accepted value for the SLAP2 standard (Table 1) and have been commonly used [30,36,37,38,45,46,47].

The reference lines for the relationship between δ¹⁸O and δ¹⁷O are very useful for interpreting triple oxygen isotope data, and the deviation from the reference lines are expressed by parameter ¹⁷O-excess [26], which is also reported as multiple terms including ¹⁷O_excess [48]_, and Δ¹⁷O [49]. Throughout the manuscript, we used the term ¹⁷O-excess and it is expressed as [29]:

¹⁷O-excess = δ′¹⁷O − λ_ref δ′¹⁸O or ¹⁷O-excess = ln(δ¹⁷O + 1) − λ_ref ln(δ¹⁸O + 1) (5)

Here, λ_ref is the slope of the δ′¹⁷O–δ′¹⁸O line. ¹⁷O-excess indicates the relative excess of ¹⁷O in meteoric waters compared with ocean water. In the equation, δ′ is the logarithmic term of δ and is expressed as δ′ = ln(δ + 1); it linearizes the exponential relationship between isotopic compositions [50]. The parameter ¹⁷O-excess is very small, and it is multiplied by 10⁶ and expressed in units of per meg (1 per meg = 0.001%). The magnitude variation in the line δ′¹⁷O–δ′¹⁸O is very small (the difference between θ_eq and θ_diff corresponds to very small magnitudes of δ′¹⁷O and δ′¹⁸O, and it is commonly described by the ¹⁷O-excess-δ′¹⁸O line) [36]. ¹⁷O-excess represents the mass-dependent deviation from the reference relationship [51]. Luz and Barkan [26] reported the reference relationship as a meteoric water line that was plotted with a slope of 0.528. Thus, ¹⁷O-excess indicates the magnitude of deviation from this reference line.

2.2. ¹⁷O Measurement

An isotope ratio mass spectrometry (IRMS) with fluorination reaction, for converting water to O₂ with CoF₃, was developed by Baker et al. [52]. In the earliest studies, water was converted to O₂ gas, based on electrolysis using CuSO₄ [41] and fluorination using BrF₅ [53]. Baker et al.’s [52] method was modified by Barkan and Luz [40], and it is commonly used for the measurement of water isotopes with high precision [26,42,46,49,54]. Affek et al. [55] modified and proposed an approach to measure oxygen isotopes of CO₂ equilibrated with water, based on the isotopic exchange at steady state between O₂ and CO₂ [56]. Recently, laser absorption spectroscopy has been developed, and it allows less laborious, simultaneous and direct measurements of water isotopologues [36,57].

2.2.1. Dual-Inlet Isotope Ratio Mass Spectrometry

Continuous flow and dual-inlet IRMS have been used for the measurement of δ¹⁸O and δ¹⁷O on the basis of different ion currents corresponding to different isotopologues of water. Meijer and Li [41] reported accuracies of 0.10% for δ¹⁸O and 0.07% for δ¹⁷O and obtained the value of λ_ref as 0.5281 + 0.0015. Barkan and Luz [40] modified the IRMS method with fluorination reaction (Equation 6), which was first developed by Baker et al. [52] and used in many studies.

2H₂O + 4CoF₃ = O₂ + 4CoF₂ +4HF (6)

According to the method described by Barkan and Luz [29], a water sample (2 µL) is injected into a heated nickel tube and converted by fluorination into O₂ gas using CoF₃ reagent. The O₂ gas is then adsorbed on 5 Å molecular sieves contained in a coiled trap at −196 °C. He gas is used as a carrier gas, and after trapping the entire amount of O₂ gas, the He flow is diverted and the residual He in the trap is pumped away. The gaseous O₂ is then trapped in a stainless-steel manifold, which is immersed in a liquid helium tank. The manifold is connected to a dual-inlet mass spectrometer, and δ¹⁷O and δ¹⁸O are measured simultaneously. Sample processing, including the fluorination step (≈30 min) and IRMS measurement, takes around 2.2 h for each sample. The IRMS measurement involves three runs, with each run comprising 30 measurements. The three runs (n = 90) are averaged, and δ¹⁷O and δ¹⁸O are determined with analytical errors of 0.006% and 0.003%, respectively. Atmospheric O₂ was measured for use as the working standard, with an accuracy of 0.005% for δ¹⁷O and 0.004% for δ¹⁸O [40]. The root mean square error of the isotope analysis, performed with a Nu Perspective IRMS instrument, was 0.3% for δ¹⁷O and 0.9% for δ¹⁸O [36]. Schoenemann et al. [44] reported isotopic measurements with a reproducibility of 0.002% for δ¹⁷O and 0.004% for δ¹⁸O for this fluorination method; they used Thermo Finnigan 253. The two-point VSMOV2-SLAP2 normalization and drift corrections are applied, refining the accuracy of the measurements [44]. Wassenaar et al. [58] suggested the importance of calibration by primary working standards which can be altered by improper storage and handling and importance of lab standards for frequent monitoring of the instrument.

2.2.2. Laser Absorption Spectroscopy

Laser absorption spectroscopy can be used for the continuous and direct measurement of water vapor with high precision and accuracy, and cavity ring-down spectroscopy (CRDS) is used for measuring the rate of decay of a laser beam by the beam-absorbing water molecules [59]. The off-axis integrated cavity output spectroscopy (OA-ICOS) laser absorption spectrometer, developed by Los Gatos Research, is based on near-infrared tunable diode laser absorption, with the laser coupled off-axis to a high-finesse optical cavity [60].

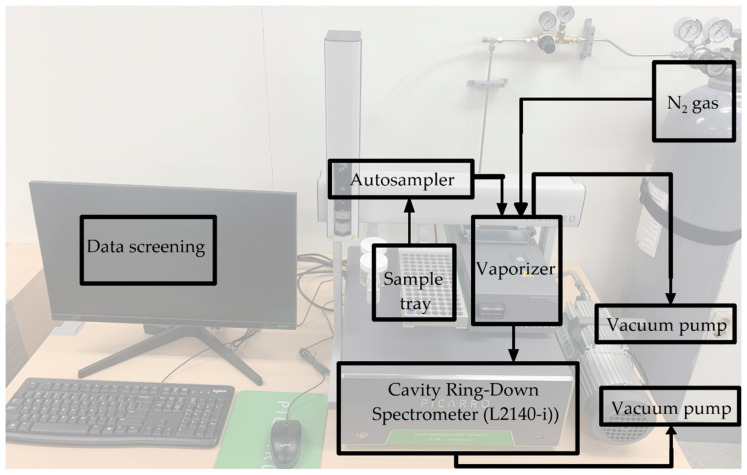
Berman et al. [60] measured the GISP standard by OA-ICOS and reported an δ¹⁷O of −13.12 ± 0.05‰ and a ¹⁷O-excess of 23 ± 10 per meg; Steig et al. [61] reported a measurement with a precision below 8 per meg for δ¹⁷O by a modified version of CRDS (L2130-i-C by Picarro Inc., Santa Clara, CA, USA), which detects strong absorption of H₂¹⁷O and H₂¹⁸O in a wavelength region centered at 7193 cm⁻¹. Currently, Picarro Inc.’s water isotope analyzer model L2140-i is commercially available for the measurement of δ¹⁷O. Liquid water samples (≈1.8 µL) are introduced into an automated vaporization system by an autosampler. Water samples evaporate and they are transported by a diaphragm vacuum pump into the optical cavity of L2140-i (Figure 1). The vapor pressure in the cavity is recommended to be in the range of 17,000–23,000 ppm by the manufacturer, because the isotopic ratios are strongly dependent on the water mixing ratio of the air [62]. The sample volume, sampling speed, measurement repetition, and sampling sequences can be controlled through the autosampler [59]. Sturm and Knohl [62] mentioned less fluctuated temperature conditions to prevent changes in cavity temperature. Pierchala et al. [59] reported the short-term precision of δ¹⁷O and ¹⁷O-excess as 0.028% and 11 per meg, respectively. A memory effect between consecutive samples and the selection of a calibration standard having isotopic values closest to those of the sample were identified as important factors for improving the precision of δ¹⁷O and ¹⁷O-excess [59]. For the improvement of the accuracy and precision of the measurement in laboratories, in-house control standards have been suggested [63]. Berman et al. [60] suggested the memory effect from mixing by syringe and water adhesion to internal surfaces of the instrument. Schauer et al. [57] suggested the syringe actuation which may weaken with large injection numbers, thus fewer injection numbers were recommended. Moreover, data-processing approaches for memory correction and sample sequence avoiding the large difference of isotopic values were also recommended. Salt liners (mesh inserts in the vaporizer unit) and salt-specific corrections are required if water samples contain high minerals and dissolved organic components. The use of a saline water sample could result in an incomplete evaporation of the sample [64]. In laser absorption instruments, organic compounds (ex. methanol) affect spectral interference and thereby cause the isotopic values to diverge from the actual values [65].

Figure 1.

Schematic of the Picarro cavity ring-down spectrometer (L2140-i) installed at the Environmental Geochemistry Laboratory of Ewha Womans University.

3. Use in Hydrological Studies

Small variations in the ¹⁷O/¹⁸O relationship can result from mass-dependent equilibrium (fractionation caused by different saturation vapor pressures) and kinetic fractionation processes (fractionation induced by different diffusivities of water vapor isotopologues) [33]. The parameter ¹⁷O-excess provides information about moisture transport and conditions (relative humidity and wind speed) in the moisture source region [7,35], and it is known to be primarily sensitive to relative humidity and less sensitive to temperature and Rayleigh distillation during moisture transport and precipitation. There are several controlling factors for the ¹⁷O-excess pattern, including the moisture source, mixing of water vapor, rain re-evaporation (mostly in low and mid-latitudes) and supersaturation (at low condensation temperatures) [66]. Although the ¹⁷O-excess in precipitation is primarily interpreted as indicating variations in the relative humidity in the moisture source regions, precipitation in polar and dry regions suggests the importance of fractionation by snow formation and raindrop re-evaporation processes.

Pioneering measurements of δ¹⁷O and δ¹⁸O were performed by Barkan and Luz [40] by using two international water isotope standards, SLAP and VSMOW. Later, the relationship between δ′¹⁷O and δ′¹⁸O was obtained by Luz and Barkan [26] as the GMWL (Equation 7 below). This line is based on the measurements of the GISP, SLAP, polar snow samples [28], and a set of meteoric waters, including precipitation, surface water, cave water, and snow, mostly from Europe and Asia.

δ′¹⁷O = 0.528 * δ′¹⁸O + 0.033   or   ln(δ¹⁷O + 1) = 0.528 * ln(δ¹⁸O + 1) + 0.033 (7)

However, freshwater samples are not covered in this meteoric water line, and the line has been recently refined and discussed by Aron et al. [36]. The observed slopes (λ_obs) in the study of Aron et al. [36] appeared to decrease in the order of snow and ice (0.5285) > ocean (0.5278) > precipitation (0.5273) > surface and subsurface water (0.5261) > plant water (0.5188). This indicates the dominance of kinetic processes at low slopes (close to θ_diff = 0.5184 ± 0.0003) and equilibrium fractionation at higher slopes (close to θ_eq = 0.529 ± 0.001).

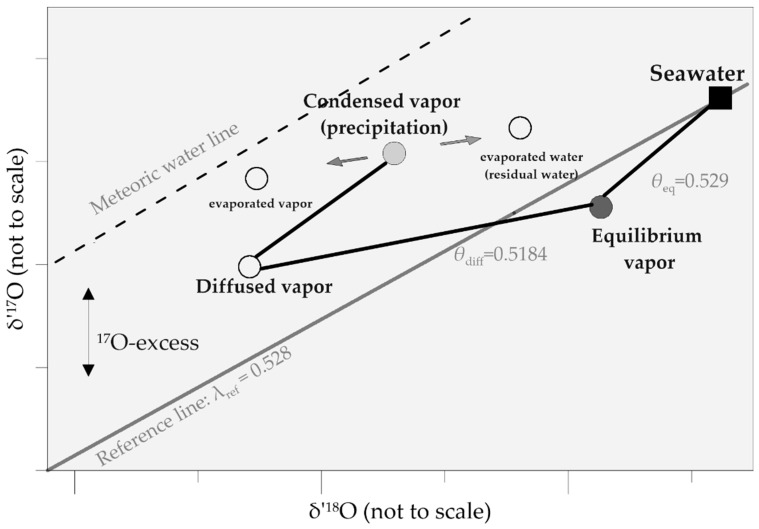
For water vapor, ¹⁷O-excess increases with kinetic fractionation [28]. Kinetic fractionation during the condensation of water vapor to ice in high-latitude precipitation can also be described by the ¹⁷O-excess together with the d-excess [33]. A schematic of δ′¹⁷O and δ′¹⁸O behavior is shown in Figure 2. Evaporated vapor from seawater diffuses through an unsaturated atmosphere, increasing the partition of ¹⁷O. ¹⁷O-excess decrease in condensed vapor (precipitation). Post-condensation evaporation will increase ¹⁷O-excess in evaporated vapor and decrease ¹⁷O-excess in residual evaporated water.

Figure 2.

Schematic of δ′¹⁷O and δ′¹⁸O fractionation in the hydrological cycle. This figure is a simplified modification of the descriptions from Luz and Barkan [26] and Aron et al. [36].

Average ¹⁷O-excess values have been reported in various ranges from −144.4 per meg (Pond in Iran) to 49.7 per meg (Firn core, Greenland) (Table 2). Evaporated water samples (e.g., leaf water, pond, and lake) show negative ¹⁷O-excess values, indicating the presence of kinetic effects [36]. While tap water and precipitation values show positive ¹⁷O-excess, snow and ice core samples show higher positive values.

Table 2.

Summary of published δ¹⁸O, λ_ref and ¹⁷O-excess in different samples. All values are averaged from published values. We note that the sampling location, period, and sampling numbers are distinct depending on the studies; thus, values are representative of local scale variations.

Sample Type	δ18O Range	17O-Excess Mean or Range (Per meg)	λref	Analytical Method	Time Scale	Reference
Low- and mid-latitude Precipitation
Vapor (Mt.Zugspitze, Germany)	(−34.4 to –20.4)	(30 to 82)	0.5265	IRMS	2016 (Feb to May)	[38]
Cave water (Canada and USA)	−9.69 (−17.67 to −6.39)	0.05 (0.03 to 0.07)	0.530	IRMS	2005 (Feb, Jul)	[26]
Cave drip waters (Northwest Switzerland)	−8.7	19	–	Picarro CRDS	2010 (Nov) to 2014 (Jun)	[69]
Fluid inclusions (Northwest Switzerland)	−8.3	10		Picarro CRDS	2012 (Mar) to 2014 (Jun)	[69]
Leaf water (Mpala central Kenya)	7.84 (−0.27 to 16.14)	−0.06 (−0.16 to 0.04)		IRMS	2012 (Jun–Jul)	[47]
Stem water (Mpala central Kenya)	−2.46 (−4.71 to 0.59)	0.02 (0.01 to 0.03)		IRMS	2012 (Jun–Jul)	[47]
Pond (Sistan Oasis, Iran)	25.83 (13.81 to 29.07)	−144.4 (−172 to –56)		IRMS	–	[54]
Lake and pond	−8.06 (−16.03 to 4.19)	0.02 (−0.02 to 0.04)	0.528	IRMS	2002, 2008	[26]
Surface water	−8.88 (−20.31 to 9.56)	−46.4 to 55.67 (mostly 14 to 33)	0.528	IRMS	Global scale	[36]
River, terminal lakes, well, spring, irrigation channel (Sistan Oasis, Iran)	−1.69 (−6.84 to 14.03)	−3.91 (−59 to 25)	–	IRMS	–	[54]
Lake and river (western USA)	−9.58 (−19.11 to −0.34)	5.28 (−39 to 46)		IRMS		[49]
Dam water (Mpala central Kenya)	−1.08 (−3.98 to 2.26)	0.01 (−0.004 to 0.02)		IRMS	2012 (Jun–Jul)	[47]
Tap, spring water (Israel)	−4.99 (−5.74 to –4.24)	0.04 (0.03 to 0.05)	0.515	IRMS	2008	[26]
Tap water (continental USA)	−8 ± 4.7 (−20.7 to −0.7)	17 ± 11 (−6 to 43)	0.526 to 0.527	IRMS	2006 to 2011	[46]
Tap and puddle water (Mpala central Kenya)	3.36 (2.33 to 4.39)	−0.01 (−0.01 to −0.003)	–	IRMS	2012 (Jun–Jul)	[47]
Precipitation (Northwest Switzerland)	−9.9	18		Picarro CRDS	2012 (Mar) to 2014 (Jun)	[69]
Precipitation (Okinawa Island, Japan)	−4.81 (−9.88 to −1.05)	25.26 (4 to 54)		Picarro CRDS	2011 (Jan) to 2012 (Dec)	[71]
Precipitation (central USA)	−6.25	31	0.5275	OA-ICOS	2014 (Jun) to 2018 (May)	[80]
Rain (Indonesia, India, and Israel)	−5.45 (−9.03 to –2.53)	0.04 (0.02 to 0.06)	0.522	IRMS	2005 (Mar to Nov) 2001 to 2008 2008 (Feb to Aug)	[26]
Water vapor (south Indian and Southern Ocean)	−15.45 (−23.41 to −11.65)	13.51 (−6 to 46)	0.532	IRMS	2005 (Dec) to 2006 (Jan)	[42]
Seawater (Atlantic, Pacific Ocean, Mediterranean, and Northern Red Sea)	0.42 (−0.42 to 2.43)	−0.0045 (−0.01 to 0.0038)	0.528	IRMS	–	[26]
Snow (Mt.Zugspitze, Germany)	(−21.7 to −8.3)	(17 to 62)	–	IRMS		[38]
Snow, ice (Canada, Montenegro)	−17.34 (−26.11 to −5.44)	0.02 (−0.01 to 0.04)	0.529	IRMS	2009, 2010	[26]
High-latitude precipitation
Vapor (NEEM, Greenland)	−41.77 (−44.63 to −38.33)	32.33 (15 to 48)	0.528	IRMS	2008 (Aug)	[48]
Snow precipitation (NEEM, Greenland)	−29.60 (−35.53 to −24.33)	35.67 (23 to 43)		IRMS	2008 (Aug)	[48]
Firn core (NEEM, Greenland)	−32.17 (−38.80 to −26.70)	49.70 (30 to 73)	–	IRMS	2003 (Jan) to 2005 (Aug)	[48]
Snow pit (Vostok)	−57.13 (−61.20 to −51.39)	7.43 (−36 to 42)		IRMS	1949 to 2008	[74]
Surface snow (traverse from Zhongshan station to Dome A)	−34.30 (−58.69 to −17.60)	34.95 (9 to 51)		IRMS	2009 (Dec) to 2010 (Jan)	[45]
Snow (transect from Syowa to Dome Fuji)	−47.26 (−56.69 to −30.20)	24.82 (6.1 to 43.8)	–	IRMS	–	[77]
Ice core (Vostok)	−58 (−50.74 to −62.05)	24.31 (−6 to 54)		IRMS	150ka years	[28]
Surface snow (Vostok, Antarctica)	−41.27 (−28.23 to −51.03)	44.5 (25 to 62)	0.528	IRMS	–	[28]
Snow or ice (Dome F, Antarctica)	−58.42	−0.006	–	IRMS		[26]
Ice core (Talos Dome, Antarctica)	−41.67 to −36.52	–	0.5278	IRMS	9.15 to 33.78 ka age	[76]
Ice core (WAIS, Antarctica)	−35.44 (−42.68 to −31.61)	25.22 (2.9 to 38.46)	–	IRMS	25 ka	[30]
Ice core (Taylor Dome, Antarctica)	−39.56 (−42.92 to −37.36)	14.28 (−1 to 28)	0.5313	IRMS	–	[30]
Ice core (Siple Dome Antarctica)	−31.31 (−36.21 to −24.02)	19 (8 to 27)	–	IRMS		[30]
Snow precipitation (Vostok, Antarctica)	−68.47 to −50.51	−27 to 29	0.5308	IRMS	2000 (Feb–Oct)	[34]
Snow precipitation (Vostok, Antarctica)	−58.5 to −52.6	–	0.5269	IRMS	1999 (Dec) to 2000 (Jun)	[77]
Ice core (Dome C, Antarctica)	−56.48 to −46.639		0.5294	IRMS	7.61–24.8 ka age	[76]
Snow precipitation (Dome C, Antarctica)	−55.58 (−69.63 to –38.89)	18.43 (−11 to 47)	0.5282	IRMS	2010 (Sep–Nov)	[77]
Snow (Dome C, Antarctica)	−54.25 (−61.35 to −48.19)	31.64 (14 to 47)	0.5287	IRMS	2010 (Dec) to 2011 (Dec)	[77]
Snow pit (Dome C, Antarctica)	−51.14 (−55.31 to −46.06)	31.68 (17 to 51)	0.528	IRMS	–	[77]

However, the spatial pattern is not globally consistent due to the lack of sufficient observations, as well as large variations in the local-to-regional scale [36]. Globally, δ′¹⁷O and δ′¹⁸O values do not conform to a single meteoric water line, indicating the existence of large spatial differences (regional hydrological processes) in the samples included [36]. Moreover, biases have been suggested on the basis of the water type, sampling bias, and sampling duration. Aron et al. [36] suggested that the δ′¹⁷O-δ′¹⁸O relationship should be refined by using unevaporated waters (flowing surface water and monthly precipitation data). Meteoric water’s ¹⁷O-excess shows significant variation in the compilation of Aron et al. [36], and a single line cannot express the variation.

3.1. Low- and Mid-Latitude Hydrology

Meteoric waters are generally in agreement with the slope of 0.528 [39,67], which is close to the equilibrium fractionation exponent (θ_eq = 0.529) [40]. Re-evaporation of rain drops during warm precipitation and convective storms, and mixture of moisture are considered as the main processes behind the ¹⁷O-excess variation in low- and mid-latitude precipitation [66].

Marine water vapor (southern Indian and Southern Ocean), which can be assumed to be less affected by precipitation and snow formation processes, was first studied by Uemura et al. [42]. For marine vapor (15 m above ocean surface), ¹⁷O-excess ranged between −6 and 46 per meg (mean: −13.5 per meg), and it negatively correlated (slope: −0.64 per meg/%) with the normalized relative humidity (Rh_n, which is the ratio of the water vapor concentration in air to the saturated vapor concentration at the ocean surface temperature). The average impact of the sea surface temperature (SST) on ¹⁷O-excess was insignificant, amounting to about 0.1 per meg/°C, and the observed positive correlation between the SST and ¹⁷O-excess was explained as a consequence of changes in relative humidity at the local scale. The study suggested a small contribution of the air mass mixing from high elevations into the atmospheric boundary layer to ¹⁷O-excess.

In this context, a study found that ¹⁷O-excess measurements in tap waters across continental US (mid-latitudes), which is a proxy for precipitation, ranged from −6 to +43 per meg, with a mean of 17 ± 11 per meg [46]. This study reported the importance of the effect of continental recycling of moisture on the ¹⁷O-excess distribution (large range of 40 per meg) rather than changes in relative humidity (low variation of <5%) at the ocean source. Furthermore, it was found that ¹⁷O-excess in precipitation can be lowered by re-evaporation and mixing processes, and the slopes ranged between 0.526 and 0.527, close to equilibrium fractionation (steady-state evaporation). It was also suggested that atmospheric turbulence and moisture mixing during convective processes (non-steady) should be considered in the interpretation of ¹⁷O-excess patterns. This study revealed the latitudinal difference in the distribution of ¹⁷O-excess, which has low values in southern locations because of the re-evaporation of precipitation and convective processes, and which disappears in the northern location (cold and snowy). This continental-scale data showing differences in local climate is very useful for global circulation models and hydrological studies that incorporate ¹⁷O-excess.

Tap water (as precipitation proxy) across China was studied by Tian et al. [37]. Most water samples indicated the equilibrium fractionation effect, except for the north-west region, where the kinetic effect dominates (re-evaporation effect). No significant seasonal dependence was observed in ¹⁷O-excess. Furthermore, this study mentioned that the ¹⁷O-excess distribution is more relevant to precipitation formation mechanisms under local climatic and geographical conditions compared with consistent large-scale spatial patterns.

The effect of extreme evaporation, which decreases ¹⁷O-excess in residual water, was studied by Surma et al. [54]. Natural waters (Helmand River, shallow wells, artificial freshwater reservoirs, irrigation channels from a delta plain, ephemeral terminal lakes, and residual ponds) from the arid and semiarid environment of the Sistan Oasis, Iran, were investigated in this study. The isolated (un-recharging water bodies) and heavily evaporated (progressive evaporation in this arid and semiarid environment) water bodies showed very low ¹⁷O-excess, reaching −167 per meg, and a distinct ¹⁷O-excess-δ′¹⁸O curve that indicated the region’s relative humidity.

To understand the evaporation dynamics from natural water samples, a study examined dew and precipitation samples from dry (Gobabeb, Namibia), Mediterranean (Nice, France), and humid continental climates (Indianapolis, IN, USA) [68]. This study confirmed that the low ¹⁷O-excess of dew in dry areas (Gobabeb and areas in Indianapolis with a temperature over 14.7 °C) was related to kinetic fractionation with evaporation, while the humid continental area (Nice, France) showed no significant evaporation effect. They also mentioned that the local relative humidity was important for the equilibrium or kinetic fractionation of dew formation.

Triple isotopic measurements in precipitation, drip water and speleothem fluid inclusions from Milandre Cave (Boncourt, North West Switzerland) have been found to be potentially useful for the reconstruction of paleotemperature and moisture variations, particularly for Western Central Europe [69] Both precipitation and drip water measurements were around 18 per meg, while the speleothem fluid inclusions showed ¹⁷O-excess values, similar to those of surface precipitation. This study proposed that the speleothem fluid inclusions may have recorded information about past moisture sources.

The ¹⁷O-excess in precipitation in a tropical region during convective activity was studied in Landais et al. [70]. It was agreeable that the rain re-evaporation process explained the increase in ¹⁷O-excess. However, other factors (changes in the evaporative source, convection, and recycling along trajectories) also influenced convective precipitation. This study highlighted the need to focus on water vapor isotopic composition, isotopic fractionation associated with rain re-evaporation and the re-evaporation rate, and large-scale controls on ¹⁷O-excess variation in future research.

In a tropical region (Mpala in Kenya), Li et al. [47] found that the variation of ¹⁷O-excess in leaf water correlated with the relative humidity. This study mentioned the strong influence of the isotopic composition of ambient vapor with high relative humidity on the slope λ_{transpiration}. Moreover, δ¹⁷O values in leaf water showed a very large variation, and this was likely to indicate the response of δ¹⁷O to the variation in the materials linked to leaf water (e.g., atmospheric CO₂, plant tissue, biomaterials that record animal body water).

Two-year monitoring of ¹⁷O-excess in precipitation in a subtropical region (southern part of Okinawa Island, Japan) was reported in Uechi et al. [71]. For this location, the effect of diffusional fractionation during evaporation in the source region could be reconstructed from the ¹⁷O-excess in the precipitation. Thus, this study suggested that ¹⁷O-excess in precipitation in subtropical and tropical regions allows for the reconstruction of changes in the relative humidity in the moisture source region. Moreover, this study also emphasized that analyzing ¹⁷O in fluid inclusions in speleothem and calcite would be useful for understanding paleoclimate variations.

Surma et al. [38] studied atmospheric and snow from high altitude in Mt. Zugstpitze, Germany and indicated the dominate influence of synoptic processes (e.g., Rayleigh distillation and potential continental recycling) on the atmospheric vapor in mid-latitudes. This study also mentioned that there could be input from deep stratospheric intrusion in this location, however the potential influence was small due to the relatively high vapor content in the local vapor compared to the stratospheric vapor. Moreover, this study comprehensively synthesized and explained the distribution of ¹⁷O-excess and the crucial processes affecting it in more detail. The extension of spatiotemporal observations was noted as important for refining the global monitoring network and for better prediction by the general circulation model.

Recent measurements in stream waters across the Pacific Northwest in the US also show a link between relative humidity and ¹⁷O-excess. The effect of evaporation in the rain shadow of the Cascado Mountain on the ¹⁷O-excess of stream waters was large (higher ¹⁷O-excess corresponded to lower relative humidity) [72]. Later, Passey and Li [49] studied the evaporation effect on triple oxygen isotopes in a river, basin lake (terminal) and freshwater lakes by using an isotope mass balance model. A larger ¹⁷O-excess was observed in unevaporated water (river) compared with evaporated water (basin lake and freshwater lake). This study also reported that ¹⁷O-excess measurements in lacustrine carbonates were representative of precipitation and that their values were similar to those of catchment precipitation.

3.2. High-Latitude Hydrology

The influence of Rh_n changes in the moisture source region and a supersaturation-controlled kinetic isotope effect during in-cloud ice formation (below −20 °C) are mainly considered in ¹⁷O-excess variation of Antarctic precipitation and ice cores [73,74]. Snow formation (clear-sky precipitation or diamond dust) under supersaturation was likely to result in low ¹⁷O-excess in high latitudes and it differed from precipitation formed from cloud-derived and synoptic snowfall [28,30,34]. Moreover, changes in temperature and relative humidity at the source and site, changes in sea ice concentration and descending stratospheric water vapor influenced the ¹⁷O-excess variation [75]. Particularly, the stratospheric air inflow, which was mostly induced by polar vortex to polar troposphere, is more significant in high-latitudes than the low- and mid-latitudes where water content is high enough compared to the stratospheric inflow [38].

Pioneering research by Landais et al. [28] showed spatially (from coast to continent) constant ¹⁷O-excess values (~45 per meg) in surface snow from Antarctica, revealing the low sensitivity of ¹⁷O-excess to the temperature decreasing toward inland Antarctica. Moreover, the ¹⁷O-excess in a Vostok ice core was indicative of changes in oceanic conditions (humidity and wind speed) during the last 150,000 years. An increase in about 20 per meg was observed in ¹⁷O-excess, and it was related to the lower Rh_n and wind speeds in the interglacial period compared to the steady values in the glacial period. Although there could be intrusion from the recirculation of cold Antarctic air and vapor input from the tropical ocean, the surrounding oceanic vapor (source) was proposed as the major factor controlling the ¹⁷O-excess in Antarctic snow. This study suggested the future studies should combine d-excess with ¹⁷O-excess and vapor measurements for tropical areas.

However, the interglacial increase in ¹⁷O-excess corresponding to a lowering of Rh_n observed by Landais et al. [28] was debated in later studies. Winkler et al. [76] suggested that ¹⁷O-excess measurements in coastal sites are more reliable in reconstructing changes in normalized relative humidity compared with remote inland sites such as Vostok [28], where the local effects may be strong. They reported distinct ¹⁷O-excess values in Dome C and the Talos Dome site and suggested that the site conditions at each site (e.g., wind pattern), and different glacial-interglacial changes in the normalized relative humidity, were important.

Winkler et al. [76] studied ¹⁷O-excess changes from 1948 to 2008 in a snow pit near Vostok, by combining the model output from Laboratoire de Meteorologie Dynamique-Zoom (LMDZ) and a simpler Rayleigh-type model Mixed Cloud Isotopic Model (MCIM). This study suggested the complexity of influencing factors (in interannual scale) at sites, such as Vostok, with very low snow accumulation. Touzeau et al. [77] also mentioned that post-deposition effects are expected to have a significant effect on low-accumulation sites. The precipitation type was tropospheric snowfall, and the majority of precipitation events were a type of hoar-frost deposition and diamond dust; the surface humidity was very low in inland sites such as Vostok. Thus, although the water vapor amount in the stratosphere is low, it can change ¹⁷O-excess in remote inland sites.

The kinetic effect of strongly supersaturated conditions at low temperatures on the ¹⁷O-excess (¹⁷O-excess is positively correlated with δ¹⁸O) variation was reported for Dome C site in [77]. Furthermore, Miller [73] suggested the importance of the precipitation regime, whether diamond dust (decrease in ¹⁷O-excess or water vapor supersaturation) or cloud-derived precipitation (increase in ¹⁷O-excess), for the ¹⁷O-excess over the Antarctic ice sheet. Moreover, isotopic fractionation, which increased the ¹⁷O-excess values, was observed to result from moisture recycling processes (sublimation of surface snow) in summer precipitation over East Antarctica [78].

In contrast to the steady values toward the inland region in the study of Landais et al. [28], surface snow samples from Zhongshan station to the Dome A site showed a decrease in ¹⁷O-excess [45]. These lower ¹⁷O-excess values were explained by the kinetic fractionation induced by the supersaturation on ice crystals at low temperatures. This study suggested that differences in moisture sources and supersaturation conditions influenced the variability of ¹⁷O-excess and pointed out the need for more measurements from different sites in Antarctica.

On a broader scale, ¹⁷O-excess was reported to be low in the central East Antarctic Plateau and higher in the coastal marine-influence regions in Schoenemann et al. [30]. This work reported the spatial distribution of ¹⁷O-excess by combining the records for the West Antarctic Ice Sheet (WAIS) divide with those from Vostok [28], EPICA DOME C, and the TALDICE site [76]. Temporally, the variation of ¹⁷O-excess was large in inland sites over the last glaciation. These results remarkably highlighted the importance of the supersaturation of water vapor over ice, and also that ¹⁷O-excess was not solely dependent on changes in relative humidity over the moisture source region during glacial-interglacial variations. This indicates the effect of the temperature gradient in the moisture source, and at the precipitation site, on the ¹⁷O-excess distribution. The change in the boundary of the sea ice extent is another factor that should be considered when referring to the temperature gradient. The expansion of sea ice (or colder conditions) results in the supersaturation conditions appearing earlier, which would decrease ¹⁷O-excess. Moreover, the contribution of relatively enriched moist air evaporated from the sea surface would be restricted for a large sea ice extension. This study highlighted the possibility of reconstructing glacial-interglacial scale changes in climatic conditions (temperature and sea ice extent).

Risi et al. [66] simulated ¹⁷O-excess by using an isotope general circulation model and explained the main controlling processes. Convective processes and re-evaporation were important in the tropical region, while the effect of distillation, mixing of different air masses, and supersaturation were crucial at mid- and high-latitudes. The model requires the tuning of supersaturation, which is the main effect in Antarctica.

Schoenemann and Steig [75] simulated seasonal and spatial variations in ¹⁷O-excess and d-excess in Antarctic precipitation by using the Intermediate Circulation Model. A smaller variation (≈3 to 8 per meg) in seasonal ¹⁷O-excess was simulated over the Southern Ocean compared with a large variation of about 50 and 60 per meg for ice sheet and snowfall. Moreover, changes in the ocean surface relative humidity induced a small variation, the average variation being −1.3 per meg/%. This study suggested that the source region Rh_n and sea surface temperature partially contributed, while the effects from the surface temperature and water content of precipitable vapor were more important to the isotopic variability within the annual cycle.

The use of ¹⁷O-excess as a marker of the source of relative humidity was confirmed in water vapor, surface snow, and shallow ice core from the NEEM site, Greenland in Landais et al. [48]. The study in [43] experimentally reported and confirmed the relationship between the solid-vapor fractionation coefficients for δ¹⁷O and δ¹⁸O (0.528 = (ln¹⁷α_v/s)/(ln¹⁸α_v/s)). An increased ¹⁷O-excess was observed in the winter season, while lower values were observed in summer, indicating the seasonality of the air temperature and relative humidity in the evaporative source region.

Stratospheric air inflow, which has a high ¹⁷O-excess (of the order of 3000 per meg) [38,79] compared with the tropospheric vapor, causes a significant increase in ¹⁷O-excess in high-latitudes [28]. The contribution of evaporative conditions to ¹⁷O-excess is underestimated by the LMDZ model, suggesting that shortcomings in the simulation of ¹⁷O-excess by the GCM should be overcome [66].

4. Summary and Future Direction

With the recent analytical developments for measuring small variations in ¹⁷O in the triple oxygen isotope system, ¹⁷O has been used as a new tracer in studies on regional hydrology and surface hydrology, climate, and paleoclimatology. Dual-inlet isotope ratio mass spectrometry and laser absorption spectroscopy have been developed and commonly used to measure ¹⁷O. The reference relationship, with a slope of 0.528, was developed and, together with d-excess, it allows the separation of the effects of temperature and relative humidity in meteoric waters. ¹⁷O-excess is commonly used as a tracer for examining changes in relative humidity in the moisture source region, while the other influential processes are still being debated. While ¹⁷O-excess may be mainly influenced by the relative humidity in subtropical regions, in polar regions, especially in continental Antarctic sites, this influence is replaced by supersaturation effect, intrusion of stratospheric vapor input, post-depositional processes (local moisture recycling by sublimation), regional circulation patterns, sea ice concentration, and local meteorological conditions. At low and mid-latitudes, the ¹⁷O-excess pattern is mainly affected by changes in the moisture source, mixing of water vapor, re-evaporation of rain drops during warm precipitation, and convective storms. Thus, the spatiotemporal variation of ¹⁷O-excess is large and yet uncertain, indicating multiple meteoric water lines corresponding to the geographical location. Moreover, since the isotopic fractionation is complex in nature and since there is a lack of measurements compared to spatially large variations, more studies on isotopic composition of surface and subsurface samples, precipitation (convective), and water vapor are required. It is also necessary to provide isotope-enabled models with in situ measurements to perform accurate and robust simulations.

Author Contributions

Conceptualization and constructive comments, J.L., Y.H. and D.K.; data collection, Y.N. and M.K.; writing—original draft preparation, Y.N.; writing—review and editing, Y.N. and J.L. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by a Korea Polar Research Institute (KOPRI) research grant (PE21100) and by the R&D Program for Oceans and Polar Regions of the National Research Foundation (NRF) funded by the Ministry of Science and ICT (2020M1A5A1110607). This research was also partially supported by a National Research Council of Science and Technology grant from the Korean government (CAP-17-05-KIGAM).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.