Abstract
Genetic variations have a multitude of effects on proteins. A substantial number of variations affect protein–solvent interactions, either aggregation or solubility. Aggregation is often related to structural alterations, whereas solubilizable proteins in the solid phase can be made again soluble by dilution. Solubility is a central protein property and when reduced can lead to diseases. We developed a prediction method, PON-Sol2, to identify amino acid substitutions that increase, decrease, or have no effect on the protein solubility. The method is a machine learning tool utilizing gradient boosting algorithm and was trained on a large dataset of variants with different outcomes after the selection of features among a large number of tested properties. The method is fast and has high performance. The normalized correct prediction rate for three states is 0.656, and the normalized GC2 score is 0.312 in 10-fold cross-validation. The corresponding numbers in the blind test were 0.545 and 0.157. The performance was superior in comparison to previous methods. The PON-Sol2 predictor is freely available. It can be used to predict the solubility effects of variants for any organism, even in large-scale projects.
Keywords: protein solubility prediction, prediction, machine learning, variation interpretation, artificial intelligence, variation, mutation, PON-Sol2
1. Introduction
Genetic variations have numerous effects. The largest portion of known disease-causing and disease-related variations is in protein-coding regions. In variation interpretation, the goal is to detect the harmful variants. There are numerous prediction methods available for this purpose, e.g., [1,2,3,4]. These tools are useful; however, they do not reveal any details about the causative mechanism and thereby of possible countermeasures, such as drugs and others. Other types of tools have been released for predicting alterations to protein properties, such as solubility.
Solubility of a protein is one of its fundamental characteristics [5]. Solubilities vary widely among proteins and protein forms. Proteome-wide analysis of solubility in Caenorhabditis elegans indicated that about 75% of proteins appear in cells in abundances close to their solubility limits [6]. There has not been evolutionary pressure to make the proteins more soluble.
Two concepts are related to protein–solvent interactions. Solubility is usually defined as the concentration in which intact protein is in equilibrium with solid phase [7,8,9,10]. Precipitated solubilizable protein in solid phase can be made again soluble by dilution. The other phenomenon is aggregation. When proteins aggregate, they bind together, which is often accompanied by irreversible alteration to conformation, leading to the formation of insoluble high-molecular-weight forms [5].
Protein solubility depends on many factors. Intrinsic properties of the protein, solvent, and additives are important along with physical conditions. Relevant protein factors include the amino acid sequence and its composition, three-dimensional structure, accessibility, and intramolecular interactions within the protein as well as protonation status. Salt bridges, electrostatic and hydrophobic interactions, and weak hydrogen bonds all affect solubility. Whether a protein is monomeric or multimeric has also an effect. Important solvent properties include polarity, its bond and interaction-forming ability, density and included additives and constituents, such as excipients, salts, and organic solvents. Concentrations of these compounds have significant contributions to protein solubility. Of the environmental parameters, pH and temperature can affect both the protein and solvent.
Alterations to proteins can affect their properties. Single amino acid alterations can profoundly alter protein solubility and lead to diseases. Severe complex V deficiency [11] and cataract [12] are examples.
To address the effects of protein variants, some prediction methods have been released. These include CamSol [13], OptSolMut [14], PON-Sol [9], SODA [15], and SolubiS [16] and have been reviewed in [10]. CamSol uses a residue-specific solubility profile. Only the algorithm has been described; no method has been made available. OptSolMut was trained with 137 single and multiple variants affecting solubility or aggregation. Weights were optimized for a scoring function with linear programming. PON-Sol, a random forest-based method, was trained this far on the largest dataset of 406 single amino acid substitutions. It grouped variants into three classes: solubility decreasing and increasing variants and those not affecting solubility. SODA has been recommended to predict variants decreasing solubility [15]. It was developed with PON-Sol data. It can predict in addition to substitutions also effects of insertions and deletions. SoluBis is a tool for the optimization of multiple variants to increase protein solubility [16]. It is based on the detection of aggregation prone segments to modify them. The prediction is a combination of interaction analysis with FoldX [17], aggregation prediction with TANGO [18], and structural analysis with YASARA [19].
We have previously developed several high-performance prediction methods for variation effects, mainly based on machine learning (ML) algorithms. These include pathogenicity/tolerance prediction methods PON-P (Olatubosun et al. 2012) and PON-P2 (Niroula et al. 2015) for filtering harmful variants from sequencing datasets. We developed the first generic variation phenotype severity predictor (Niroula and Vihinen, 2017). To investigate the mechanisms and effects of amino acid substitutions, there are PON-Diso (Ali et al. 2014) for protein disorder, PON-Tstab for protein stability (Yang et al. 2018), PROlocalizer (Laurila and Vihinen, 2011) for protein localization, and PON-Sol (Yang et al. 2016) for protein solubility affecting variants.
Since the publication of PON-Sol, a substantial amount of new cases has been published and warranted the development of an entirely new predictor, PON-Sol2, which has superior performance in comparison to the previous tools. We collected by far the largest set of experimentally verified variants and used them to train an ML predictor and tested it in an independent test dataset. The developed tool can be used for variation interpretation and analysis of the mechanisms in disease-related variants and to design variants for protein engineering, protein crystallization, and other applications.
2. Results
We developed a novel machine learning-based predictor for effects of single AASs on protein solubility. We collected a large dataset of over 10,000 cases, which was reduced to 6328 variations to due to class imbalance. There was still imbalance, which was mitigated in the method performance assessment.
The dataset included variants from altogether 77 proteins and represented all substitution types. The distribution of the AASs (Table 1) indicates that leucine (659), alanine (564), and isoleucine (506) are the most common original residues. The most common substitution is by proline (420). The most common amino acid substitutions are L > S (59), L > T (49), L > A (47), and L > E (44) alterations. There were up to 43 variants of a certain substitution type.
Table 1.
Distribution of amino acid residues in the dataset. The original amino acids are in rows and variant residues are in columns.
| A | C | D | E | F | G | H | I | K | L | M | N | P | Q | R | S | T | V | W | Y | Total | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 20 | 37 | 30 | 27 | 32 | 29 | 35 | 25 | 34 | 11 | 30 | 43 | 35 | 40 | 29 | 28 | 35 | 17 | 27 | 564 |
| C | 16 | 0 | 2 | 5 | 1 | 1 | 5 | 5 | 6 | 5 | 4 | 4 | 6 | 3 | 2 | 11 | 2 | 1 | 1 | 3 | 83 |
| D | 23 | 22 | 0 | 28 | 26 | 19 | 16 | 25 | 23 | 30 | 10 | 29 | 33 | 20 | 33 | 29 | 27 | 14 | 18 | 13 | 438 |
| E | 29 | 21 | 29 | 0 | 18 | 25 | 10 | 20 | 22 | 25 | 13 | 18 | 24 | 18 | 19 | 23 | 21 | 19 | 22 | 17 | 393 |
| F | 30 | 11 | 16 | 9 | 0 | 17 | 15 | 6 | 10 | 6 | 2 | 13 | 20 | 14 | 18 | 7 | 18 | 6 | 11 | 8 | 237 |
| G | 29 | 16 | 25 | 23 | 22 | 0 | 27 | 27 | 16 | 33 | 9 | 18 | 38 | 17 | 31 | 23 | 30 | 12 | 20 | 22 | 438 |
| H | 13 | 5 | 7 | 3 | 8 | 8 | 0 | 11 | 6 | 6 | 5 | 7 | 10 | 10 | 6 | 11 | 11 | 10 | 6 | 10 | 153 |
| I | 38 | 19 | 35 | 29 | 11 | 33 | 31 | 0 | 27 | 17 | 15 | 20 | 39 | 30 | 36 | 36 | 22 | 26 | 19 | 23 | 506 |
| K | 26 | 8 | 18 | 29 | 12 | 18 | 18 | 10 | 0 | 15 | 9 | 14 | 24 | 18 | 23 | 18 | 14 | 17 | 6 | 8 | 305 |
| L | 47 | 33 | 35 | 44 | 21 | 41 | 36 | 26 | 41 | 0 | 30 | 37 | 25 | 23 | 34 | 59 | 49 | 28 | 21 | 29 | 659 |
| M | 15 | 13 | 13 | 11 | 9 | 12 | 14 | 14 | 8 | 21 | 0 | 16 | 15 | 17 | 10 | 12 | 5 | 10 | 9 | 9 | 233 |
| N | 10 | 11 | 13 | 14 | 9 | 14 | 9 | 7 | 9 | 10 | 6 | 0 | 16 | 8 | 9 | 7 | 10 | 10 | 7 | 6 | 185 |
| P | 14 | 11 | 12 | 14 | 7 | 17 | 21 | 10 | 7 | 11 | 7 | 6 | 0 | 8 | 11 | 14 | 9 | 21 | 8 | 8 | 216 |
| Q | 14 | 12 | 14 | 11 | 9 | 12 | 12 | 8 | 14 | 12 | 4 | 11 | 15 | 0 | 14 | 18 | 15 | 14 | 5 | 11 | 225 |
| R | 26 | 21 | 25 | 21 | 22 | 22 | 27 | 18 | 17 | 23 | 11 | 21 | 26 | 29 | 0 | 28 | 28 | 28 | 17 | 14 | 424 |
| S | 18 | 8 | 13 | 9 | 11 | 15 | 7 | 6 | 6 | 9 | 4 | 11 | 8 | 9 | 16 | 0 | 15 | 10 | 9 | 11 | 195 |
| T | 26 | 13 | 17 | 20 | 15 | 25 | 17 | 12 | 12 | 22 | 21 | 24 | 25 | 17 | 22 | 32 | 0 | 20 | 11 | 13 | 364 |
| V | 17 | 19 | 21 | 18 | 13 | 19 | 25 | 25 | 24 | 23 | 15 | 22 | 32 | 19 | 33 | 42 | 26 | 0 | 14 | 15 | 422 |
| W | 9 | 5 | 3 | 9 | 6 | 4 | 1 | 2 | 7 | 4 | 3 | 2 | 6 | 4 | 5 | 6 | 5 | 5 | 0 | 2 | 88 |
| Y | 14 | 7 | 11 | 13 | 13 | 15 | 11 | 9 | 11 | 14 | 6 | 6 | 15 | 7 | 15 | 9 | 10 | 12 | 2 | 0 | 200 |
| total | 414 | 275 | 346 | 340 | 260 | 349 | 331 | 276 | 291 | 320 | 185 | 309 | 420 | 306 | 377 | 414 | 345 | 298 | 223 | 249 | 6328 |
2.1. Feature Selection and Method Training
We started with 1081 features in the categories of amino acid propensities and characteristics, conservation, variation type, neighborhood features, and chain length. RFE was applied in feature selection. GOSS down samples the instances on the basis of gradients [20]. Instances with small gradients are well trained and have a small training error, while those with large gradients are undertrained. GOSS retains instances with large gradients while performing random sampling on instances with small gradients. EFB reduces the number of features by regrouping mutually exclusive features into bundles and then treating them as a single feature [20]. This is beneficial especially in sparse feature space where many features are (almost) exclusive and very seldom have non-zero values simultaneously. Thus, these kinds of features can be safely bundled.
An initial comparison of random forest, XGBoost, and LightGBM indicated that the gradient boosting algorithms had better performance. LightGBM was chosen due to its speed to train and run; the performance was almost identical with XGBoost. Results for predictors with all features, 100, 50, and 20 features were very similar; however, they were somewhat better when using a smaller number of features.
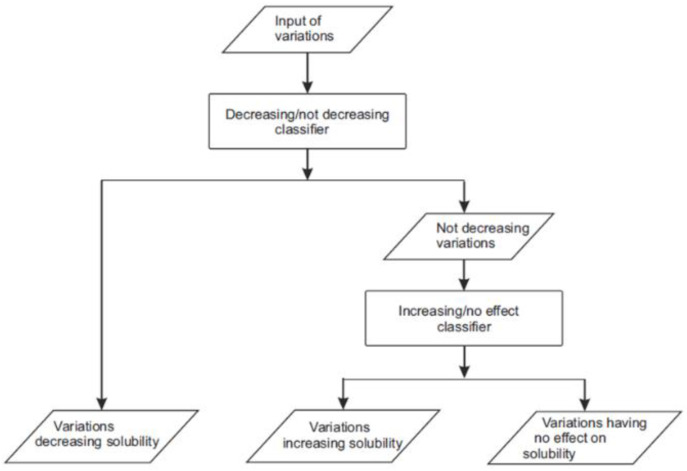
We tested two architectures for the predictor implementation. In one of them, single predictor distributes the cases to three categories. The other one is combination of two two-layer predictors. The reasoning for testing the two-layer predictor was our earlier experience with variant severity predictor PON-PS [21], and variant stability predictor PON-Stab [22] indicated that a combination of two-layer predictions could be beneficial. For the two-layer three-class classifier we generated binary classifiers for both the layers (Figure 1). For the first layer, we marked the variations increasing or having no effect on solubility as “not-decreasing” and trained a “decreasing/not-decreasing” classifier. The second layer only used the variations increasing and having no effect to train an “increasing/no effect” classifier. We chose to use 20 features per predictor in the two-layer predictor and 30 in the single-layer predictor to have as small a set of features as possible and thereby covering the space of feature distribution better.
Figure 1.
Scheme for two-layer three-class classifier.
When we trained the two-layer three-class LightGBM classifier, RFE was used to select 20 features for each layer. As the predictors shared six features, 34 different features were selected (Table 2 and Table 3). Among them there are 22 amino acid features, 11 neighborhood features, and the length of protein sequence. This method was finally chosen as it showed somewhat better performance than the single three-class predictor, its CPR in 10-fold CV was 0.747 (Table 4 and Table 5).
Table 2.
Features selected by RFE for two-layer three-class LightGBM decreasing/not decreasing classifier sorted by importance. Features shared by to the two predictors are underlined.
| Rank | Name | Feature | Description |
|---|---|---|---|
| 1 | FUKS010101 | Amino acid feature | Surface composition of amino acids in intracellular proteins of thermophiles (percent) [25] |
| 2 | JOND920102 | Amino acid feature | Relative mutability [26] |
| 3 | PONP800107 | Amino acid feature | Accessibility reduction ratio [27] |
| 4 | NonPolarAA | Neighborhood feature | Number of nonpolar residues in the neighborhood window |
| 5 | PolarAA | Neighborhood feature | Number of polar residues in the neighborhood window |
| 6 | QIAN880134 | Amino acid feature | Weights for coil at the window position of [28] |
| 7 | AA20D.T | Neighborhood feature | Number of threonine residues in the neighborhood window |
| 8 | PosAA | Neighborhood feature | Number of positively charged residues in the neighborhood window |
| 9 | AA20D.L | Neighborhood feature | Number of leucine residues in the neighborhood window |
| 10 | GEOR030102 | Amino acid feature | Linker propensity from 1-linker dataset [29] |
| 11 | OOBM850102 | Amino acid feature | Optimized propensity to form reverse turn [30] |
| 12 | length | Protein type feature | Number of amino acids in the protein sequence |
| 13 | AA20D.I | Neighborhood feature | Number of isoleucine residues in the neighborhood window |
| 14 | AA20D.P | Neighborhood feature | Number of proline residues in the neighborhood window |
| 15 | KOSJ950115 | Amino acid feature | Context-dependent optimal substitution matrices for all residues [31] |
| 16 | ARGP820102 | Amino acid feature | Signal sequence helical potential [32] |
| 17 | PRAM820103 | Amino acid feature | Correlation coefficient in regression analysis [33] |
| 18 | AA20D.V | Neighborhood feature | Number of valine residues in the neighborhood window |
| 19 | ZIMJ680104 | Amino acid feature | Isoelectric point [34] |
| 20 | CHOP780209 | Amino acid feature | Normalized frequency of C-terminal beta-sheet [35] |
Table 3.
Features selected by RFE for two-layer three-class LightGBM increasing/no effect classifier sorted by importance. Features shared by to the two predictors are underlined.
| Rank | Name | Feature | Description |
|---|---|---|---|
| 1 | VASM830102 | Amino acid feature | Relative population of conformational state C [36] |
| 2 | PRAM820103 | Amino acid feature | Correlation coefficient in regression analysis [33] |
| 3 | DAYM780201 | Amino acid feature | Relative mutability [37] |
| 4 | ChargedAA | Neighborhood feature | Number of charged residues in the neighborhood window |
| 5 | DOSZ010102 | Amino acid feature | Normalized version of SM_SAUSAGE [38] |
| 6 | NonPolarAA | Neighborhood feature | Number of nonpolar residues in the neighborhood window |
| 7 | PRAM820101 | Amino acid feature | Intercept in regression analysis [33] |
| 8 | BROC820102 | Amino acid feature | Retention coefficient in HFBA [39] |
| 9 | PolarAA | Neighborhood feature | Number of polar residues in the neighborhood window |
| 10 | MIRL960101 | Amino acid feature | Statistical potential derived by the maximization of the harmonic mean of Z scores [40] |
| 11 | AA20D.D | Neighborhood feature | Number of aspartic acid residues in the neighborhood window |
| 12 | VASM830101 | Amino acid feature | Relative population of conformational state A [36] |
| 13 | SUYM030101 | Amino acid feature | Linker propensity index [41] |
| 14 | length | Protein type feature | Number of amino acids in the protein sequence |
| 15 | FASG760103 | Amino acid feature | Optical rotation [42] |
| 16 | CHOP780213 | Amino acid feature | Frequency of the 2nd residue in turn [35] |
| 17 | AA20D.L | Neighborhood feature | Number of leucine residues in the neighborhood window |
| 18 | LIFS790102 | Amino acid feature | Conformational preference for parallel beta-strands [43] |
| 19 | PosAA | Neighborhood feature | Number of positively charged residues in the neighborhood window |
| 20 | AA20D.G | Neighborhood feature | Number of glycine residues in the neighborhood window |
Table 4.
Comparison of different three-class LightGBM classifier designs on 10-fold cross-validation.
| Performance Measure | Predictor | ||||
|---|---|---|---|---|---|
| Single Three-Class Classifier | Two-Layer Three-Class Classifier | ||||
| All Features | 30 Features Selected by RFE | All Features | 34 Features Selected by RFE | ||
| TP | − | 257.1/177.2 | 253.6/174.8 | 249.6/172.1 | 249.2/171.8 |
| no | 135.3/135.3 | 138.4/138.4 | 139.7/139.7 | 142.4/142.4 | |
| + | 30.9/63.5 | 30.6/62.9 | 31.6/64.9 | 31.9/65.5 | |
| TN | − | 238.4/323.8 | 236.6/320.7 | 250.9/340.5 | 249.0/337.3 |
| no | 303.3/268.9 | 301.5/268.9 | 293.2/257.4 | 296.1/261.5 | |
| + | 448.2/362.0 | 451.1/365.2 | 443.4/357.5 | 445.0/359.6 | |
| FP | − | 48.4/62.0 | 50.2/65.1 | 35.9/45.3 | 37.8/48.5 |
| no | 70.4/116.9 | 72.2/116.9 | 80.5/128.4 | 77.6/124.3 | |
| + | 24.5/23.8 | 21.6/20.6 | 29.3/28.3 | 27.7/26.2 | |
| FN | − | 22.7/15.7 | 26.2/18.1 | 30.2/20.8 | 30.6/21.1 |
| no | 57.6/57.6 | 54.5/54.5 | 53.2/53.2 | 50.5/50.5 | |
| + | 63.0/129.4 | 63.3/130.0 | 62.3/128.0 | 62.0/127.4 | |
| PPV | − | 0.842/0.742 | 0.835/0.729 | 0.875/0.793 | 0.869/0.781 |
| no | 0.657/0.536 | 0.658/0.543 | 0.635/0.521 | 0.647/0.534 | |
| + | 0.563/0.730 | 0.586/0.752 | 0.520/0.696 | 0.538/0.714 | |
| NPV | − | 0.913/0.954 | 0.901/0.947 | 0.893/0.942 | 0.891/0.941 |
| no | 0.841/0.824 | 0.847/0.832 | 0.847/0.829 | 0.855/0.838 | |
| + | 0.877/0.737 | 0.877/0.738 | 0.877/0.736 | 0.878/0.739 | |
| Sensitivity | − | 0.919/0.919 | 0.906/0.906 | 0.892/0.892 | 0.891/0.891 |
| no | 0.701/0.701 | 0.717/0.717 | 0.724/0.724 | 0.738/0.738 | |
| + | 0.329/0.329 | 0.326/0.326 | 0.336/0.336 | 0.340/0.340 | |
| Specificity | − | 0.831/0.839 | 0.825/0.831 | 0.875/0.883 | 0.868/0.874 |
| no | 0.812/0.697 | 0.807/0.697 | 0.785/0.667 | 0.792/0.678 | |
| + | 0.948/0.938 | 0.954/0.947 | 0.938/0.927 | 0.941/0.932 | |
| CPR | 0.747/0.650 | 0.746/0.650 | 0.743/0.651 | 0.747/0.656 | |
| GC2 | 0.317/0.298 | 0.309/0.289 | 0.322/0.313 | 0.323/0.312 | |
Table 5.
Comparison of different three-class LightGBM classifier designs on blind test dataset.
| Performance Measure | Predictor | ||||
|---|---|---|---|---|---|
| Direct Three-Class Classifier | Two-Layer Three-Class Classifier | ||||
| All Features | 30 Features Selected by RFE | All Features | 34 Features Selected by RFE | ||
| TP | − | 288.0/201.9 | 282.0/197.7 | 272.0/190.7 | 271.0/190.0 |
| no | 154.0/154.0 | 151.0/151.0 | 160.0/160.0 | 159.0/159.0 | |
| + | 11.0/30.0 | 7.0/19.1 | 10.0/27.2 | 14.0/38.1 | |
| TN | − | 235.0/341.9 | 238.0/343.2 | 247.0/355.6 | 258.0/368.3 |
| no | 329.0/303.5 | 323.0/293.2 | 313.0/288.3 | 319.0/298.5 | |
| + | 551.0/451.5 | 541.0/442.4 | 544.0/445.1 | 529.0/431.3 | |
| FP | − | 89.0/132.1 | 86.0/130.8 | 77.0/118.4 | 66.0/105.7 |
| no | 96.0/170.5 | 102.0/180.8 | 112.0/185.7 | 106.0/175.5 | |
| + | 24.0/22.5 | 34.0/31.6 | 31.0/28.9 | 46.0/42.7 | |
| FN | − | 50.0/35.1 | 56.0/39.3 | 66.0/46.3 | 67.0/47.0 |
| no | 83.0/83.0 | 86.0/86.0 | 77.0/77.0 | 78.0/78.0 | |
| + | 76.0/207.0 | 80.0/217.9 | 77.0/209.8 | 73.0/198.9 | |
| PPV | − | 0.764/0.605 | 0.766/0.602 | 0.779/0.617 | 0.804/0.643 |
| no | 0.616/0.475 | 0.597/0.455 | 0.588/0.463 | 0.600/0.475 | |
| + | 0.314/0.571 | 0.171/0.376 | 0.244/0.485 | 0.233/0.472 | |
| NPV | − | 0.825/0.907 | 0.810/0.897 | 0.789/0.885 | 0.794/0.887 |
| no | 0.799/0.785 | 0.790/0.773 | 0.803/0.789 | 0.804/0.793 | |
| + | 0.879/0.686 | 0.871/0.670 | 0.876/0.680 | 0.879/0.684 | |
| Sensitivity | − | 0.852/0.852 | 0.834/0.834 | 0.805/0.805 | 0.802/0.802 |
| no | 0.650/0.650 | 0.637/0.637 | 0.675/0.675 | 0.671/0.671 | |
| + | 0.126/0.126 | 0.080/0.080 | 0.115/0.115 | 0.161/0.161 | |
| Specificity | − | 0.725/0.721 | 0.735/0.724 | 0.762/0.750 | 0.796/0.777 |
| no | 0.774/0.640 | 0.760/0.619 | 0.736/0.608 | 0.751/0.630 | |
| + | 0.958/0.953 | 0.941/0.933 | 0.946/0.939 | 0.920/0.910 | |
| CPR | 0.684/0.543 | 0.665/0.517 | 0.668/0.532 | 0.671/0.545 | |
| GC2 | 0.173/0.150 | 0.165/0.141 | 0.162/0.141 | 0.181/0.157 | |
2.2. Performance Assessment
The method performance was assessed according to published guidelines [23,24]; also, the other items of the guidelines were followed. Due to the uneven distribution of cases in the three solubility categories, we normalized the calculated results in Table 4, Table 5 and Table 6. The first figure indicates the number of cases, the second one is for normalized values for cases in categories TP to FN. For performance measures, the first one is without normalization, the latter one is with normalization, and these are the numbers that we compared. Table 4 lists the 10-fold cross-validation (CV) performance for four classifiers. As the scores were equal or better for predictors with smaller feature sets, we chose the 34-feature two-layer three-class classifier and call it PON-Sol2. The two-layer predictor is marginally better than the single-layer one. Its normalized CPR is 0.656, which is significantly improved compared with 0.491 for the original PON-Sol.
Table 6.
Comparison of the prediction performance of PON-Sol2 with SODA and PON-Sol2.
| Performance Measure | |||||||
|---|---|---|---|---|---|---|---|
| PON-Sol | SODA | SODA (5 as Threshold) | SODA (10 as Threshold) | SODA (17 as Threshold) | PON-Sol2 | ||
| TP | − | 89.0/62.4 | 165.0/115.7 | 66.0bb/46.3 | 33.0/23.1 | 23.0/16.1 | 271.0/190.0 |
| no | 108.0/108.0 | 0.0/0.0 | 180.0/180.0 | 210.0/210.0 | 226.0/226.0 | 159.0/159.0 | |
| + | 39.0/106.2 | 22.0/59.9 | 6.0/16.3 | 5.0/13.6 | 4.0/10.9 | 14.0/38.1 | |
| TN | − | 263.0/390.6 | 103.0/140.9 | 281.0/412.0 | 308.0/447.7 | 316.0/462.6 | 258.0/368.3 |
| no | 280.0/301.5 | 425.0/474.0 | 181.0/161.3 | 106.0/96.6 | 61.0/54.9 | 319.0/298.5 | |
| + | 355.0/295.5 | 321.0/271.7 | 452.0/380.3 | 496.0/413.5 | 538.0/446.6 | 529.0/431.3 | |
| FP | − | 61.0/83.4 | 221.0/333.1 | 43.0/62.0 | 16.0/26.3 | 8.0/11.4 | 66.0/105.7 |
| no | 145.0/172.5 | 0.0/0.0 | 244.0/312.7 | 319.0/377.4 | 364.0/419.1 | 106.0/175.5 | |
| + | 220.0/178.5 | 254.0/202.3 | 123.0/93.7 | 79.0/60.5 | 37.0/27.4 | 46.0/42.7 | |
| FN | − | 249.0/174.6 | 173.0/121.3 | 272.0/190.7 | 305.0/213.9 | 315.0/220.9 | 67.0/47.0 |
| no | 129.0/129.0 | 237.0/237.0 | 57.0/57.0 | 27.0/27.0 | 11.0/11.0 | 78.0/78.0 | |
| + | 48.0/130.8 | 65.0/177.1 | 81.0/220.7 | 82.0/223.4 | 83.0/226.1 | 73.0/198.9 | |
| PPV | − | 0.593/0.428 | 0.427/0.258 | 0.606/0.428 | 0.673/0.468 | 0.742/0.585 | 0.804/0.643 |
| no | 0.427/0.385 | nan/nan | 0.425/0.365 | 0.397/0.357 | 0.383/0.350 | 0.600/0.475 | |
| + | 0.151/0.373 | 0.080/0.229 | 0.047/0.149 | 0.060/0.184 | 0.098/0.284 | 0.233/0.472 | |
| NPV | − | 0.514/0.691 | 0.373/0.537 | 0.508/0.684 | 0.502/0.677 | 0.501/0.677 | 0.794/0.887 |
| no | 0.685/0.700 | 0.642/0.667 | 0.761/0.739 | 0.797/0.782 | 0.847/0.833 | 0.804/0.793 | |
| + | 0.881/0.693 | 0.832/0.605 | 0.848/0.633 | 0.858/0.649 | 0.866/0.664 | 0.879/0.684 | |
| Sensitivity | − | 0.263/0.263 | 0.488/0.488 | 0.195/0.195 | 0.098/0.098 | 0.068/0.068 | 0.802/0.802 |
| no | 0.456/0.456 | 0.000/0.000 | 0.759/0.759 | 0.886/0.886 | 0.954/0.954 | 0.671/0.671 | |
| + | 0.448/0.448 | 0.253/0.253 | 0.069/0.069 | 0.057/0.057 | 0.046/0.046 | 0.161/0.161 | |
| Specificity | − | 0.812/0.824 | 0.318/0.297 | 0.867/0.869 | 0.951/0.944 | 0.975/0.976 | 0.796/0.777 |
| no | 0.659/0.636 | 1.000/1.000 | 0.426/0.340 | 0.249/0.204 | 0.144/0.116 | 0.751/0.630 | |
| + | 0.617/0.623 | 0.558/0.573 | 0.786/0.802 | 0.863/0.872 | 0.936/0.942 | 0.920/0.910 | |
| CPR | 0.356/0.389 | 0.282/0.247 | 0.381/0.341 | 0.375/0.347 | 0.382/0.356 | 0.671/0.545 | |
| GCC | 0.010/0.011 | nan/nan | 0.041/0.045 | 0.022/0.022 | 0.016/0.016 | 0.181/0.157 | |
The performance figures are shown separately for the three categories, and there are clear differences between them. Normalized positive predictive value is the best for solubility decreasing cases (0.781) followed by solubility increasing variants (0.714), while those having no effect have the lowest score (0.534). In the case of normalized NPV, the three categories are predicted almost equally well (0.855 to 0.891). Sensitivity again shows big differences; this time, the solubility decreasing cases have the lowest score. Specificity values, although variable, are closer to each other than those for sensitivity. Normalized CPR of 0.656 shows good performance. Note that a random three-class predictor would have a score of 0.333. The normalized GC2 score is 0.312.
2.3. Performance on Blind Test Set
The obtained cases were initially partitioned to generate a blind test set. This dataset was tested only after the training phase was finished. In the generation of these data, we took into account that in the levoglucosan kinase and β-lactamase, there were several variants that changed the same original residue. To avoid bias in testing, data partition was made so that all substitutions within a position were either in the training or test set.
The blind test set contained 662 variants, of which 338 decreased solubility, 237 increased, and 87 had no effect on solubility. The results in Table 5 are well in line with those for CV in Table 4. The overall scores are somewhat smaller, but otherwise, the results are very similar to CV results. Normalized CPR was 0.545 and normalized CG2 0.157. The differences in individual measures for the three solubility categories are very similar to CV data, indicating that e.g., the PPV and sensitivity of solubility increasing cases are more difficult to predict than the two other classes.
2.4. Comparison to Other Tools
Of the previous methods, only SODA and the original PON-Sol could be compared with PON-Sol2. SODA is designed to predict in addition to AASs also insertions and deletions. It is a binary classifier that predicts variations increasing solubility or decreasing solubility. The score of SODA is calculated from the weighted sum of five score differences.
In an effort to test whether SODA could be used in three-state prediction, we applied different thresholds at 5, 10, and 17 to include a class for variants with no effect on solubility. The threshold at 17 gave the best result (Table 6); however, the normalized CPR is only 0.356, and the normalized GC2 is 0.016. The corresponding scores are 0.389 and 0.011 for PON-Sol. PON-Sol2 is significantly better, the scores being 0.545 and 0.157, respectively. Furthermore, PON-Sol2 is clearly a more balanced predictor, the two other tools showing larger differences for the scores of the different types of solubility effects.
2.5. Large-Scale Variant Prediction
As PON-Sol2 is a fast predictor, it allows large-scale analyses of solubility effects, such as protein-wide effects. Figure 2 shows predictions for all possible single amino acid substitutions in the Bruton tyrosine kinase (BTK) kinase domain [44]. Loss of function variations in BTK cause X-linked agammaglobulinemia (XLA), which is a primary immunodeficiency due to a block in the B cell maturation pathway. BTK is a central signaling molecule during B cell development, and its activity is crucial for maturation of the cells. Gain of function variants in the B cell receptor signaling pathway, where BTK is involved, appear in B cell malignancies, such as chronic lymphocytic leukaemia and Waldenström macroglobulinemia. XLA-causing variants are collected to BTKbase [45]; there are currently over 1800 variants, amino acid substitutions being among the most common alterations. However, the effects of the variants on solubility are not known, apart from some individual cases.
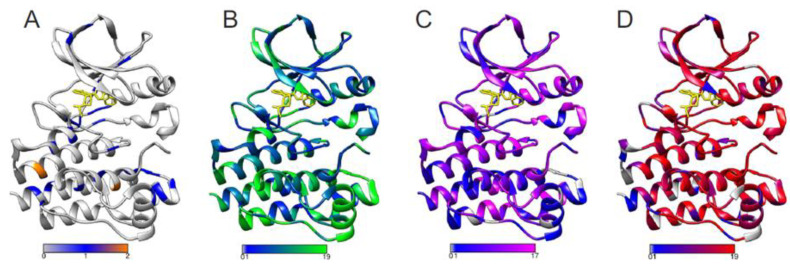
Figure 2.
Predicted solubility and disease-related variations in BTK kinase domain (PDB id 5p9j (69), covalent inhibitor at the ATP binding site is in yellow. (A) Numbers of variations increasing solubility, (B) numbers of variations having no effect on solubility, (C) numbers of variants decreasing solubility, and (D) numbers of XLA-causing variants. Predictions were made for all 19 single amino acid substitutions at every position. bPathogenicity-related variants were predicted with PON-P2. Keys in the bottom show the numbers of variants predicted to have the effect.
Figure 2A–C shows predictions for alterations that increase, decrease, or have no effect on solubility. In addition, the tolerance/pathogenicity predictions were obtained for all substitutions with a reliable PON-P2 predictor [4]. The method classifies variants in three categories: pathogenic, benign, and unclassified variants. Colour coding was used to indicate the numbers for predicted disease-causing variants, which are shown in Figure 2D. The numbers of predicted solubility decreasing alterations in Figure 2C imply certain correlation with 2D. Since many effects lead to XLA, we cannot even expect to see a 1:1 correlation with one effect. Solubility is just one of the effects of variations that lead to XLA. There are substantially more solubility-affecting variants in many positions where there are many disease-related variants.
2.6. PON-Sol2 Web Application
PON-Sol2 web application is freely available at http://structure.bmc.lu.se/PON-Sol2/ (accessed on 26 July 2021) and http://139.196.42.166:8010/ (accessed on 26 July 2021). There is a user-friendly web interface. It accepts variations in two formats: sequence and identifier formats. Sequence submission is for FASTA format amino acid sequence(s) and amino acid substitutions in it (them). Identifier submission requires amino acid substitutions and one of UniProtKB/Swiss-Prot accession ID, Entrez gene ID, or Ensemble ID. For these submissions, PON-Sol2 makes predictions only for variations leading to amino acid substitutions. Batch submission including all variants and proteins of interest is accepted and recommended. PON-Sol2 provides a complete report, which is sent to the user by email when ready.
3. Discussion
Amino acid substitutions can have widely differing effects; for a recent discussion of protein function affecting effects and mechanisms, see [46]. Solubility is one factor that can contribute to changes to function. Some single amino acid changes are responsible for substantially decreased or improved solubility. Many proteins are expressed in concentrations close to their maximal solubility [6]. Predictions of solubility effects have several applications. They can be used in variation interpretation in diseases. Protein engineering could benefit from reliable predictions of solubility alterations due to variations. Knowing which residue to change and how the properties could be changed can be used to design proteins that could be expressed in large quantities in various host organisms and expression systems.
Protein crystallization is another application area for more soluble proteins. X-ray crystallography is based on highly ordered crystals. Despite extensive trials, all proteins are not amenable for crystallization. There are many reasons; one of the common ones is that the protein is not soluble in the required concentrations. This could be improved by modifying the protein to increase its solubility. Even Nuclear Magnetic Resonance (NMR) studies of protein structures in solution require high protein concentrations and would thus benefit from solubility-increasing variants.
PON-Sol2 shows clearly improved performance in comparison to the original PON-Sol. This is expected from much larger training data, 5666 vs. 406 cases. Despite the substantial growth of data, it would still be possible to increase the performance with even bigger sets of experimental cases originating from larger number of proteins. We would need data for variations in different types of proteins and in different structural and sequence contexts.
The single and two-layer implementations did not show marked differences in prediction performance. When training the method, the selected features had relatively small significance scores, unlike in the pathogenicity/tolerance predictor PON-P2 [4]. It was possible to reduce the number of features to 34 in the two-layer predictor. The performance improvement in comparison to a predictor with all the features was not very high. The major benefit comes from the fact that with the limited set of features, representativeness of the variant space may be significantly better. The method is fast and reliable and facilitates predictions even for large numbers of variants.
4. Materials and Methods
4.1. Data
The dataset contains all the original PON-Sol cases of 443 single amino acid substitutions in 71 proteins [9]. In addition, we collected based on an extensive literature search 10,758 variants in six additional proteins: 10 amino acid substitutions (AASs) in ThreeFoil [47], 76 in Escherichia coli cytotoxin [48], 6 in aminoacyl-tRNA synthetase [49], 3 in α-spectrin SH3 domain [50], 6298 in levoglucosan kinase [51], and 4365 inTEM-1 β-lactamase [51]. Altogether, there were 11,201 AASs in 77 proteins. We paid special attention to detect cases affecting (or not) solubility. The literature for aggregation-related variants is substantially larger.
The variants were grouped into three categories: solubility increasing and decreasing cases and those having no effect on solubility. The classifications were obtained from original publications, except for the last two proteins. For those, solubility scores of yeast surface display (YSD) and twin-arginine translocation (Tat) were considered. In the end, only YSD data were used, since the Tat data contained lots of false negatives. As the threshold, we used 0.15 in YSD data to define the three types of variations [51]. Since the dataset was heavily biased toward solubility-decreasing cases, we randomly excluded solubility decreasing cases in levoglucosan kinase and TEM-1 β-lactamase data, so that we finally had 6328 variations, 3136 of which decreased solubility, 1026 increased solubility, and 2166 had no effect, with the ratio of 1:0.69:0.34.
The variants were randomly partitioned into training and test sets. In the case of levoglucosan kinase and TEM-1 β-lactamase, the division was made position wise; i.e., all variations in a certain position were used either for training or testing. In total, 5666 variants (2798 solubility decreasing, 1929 increasing, and 939 without effect on solubility) were used for training. The blind test contained 662 variants, of which 338 decreased solubility, 237 increased solubility, and 87 had no effect.
The datasets are freely available in VariBench database [52,53] at http://structure.bmc.lu.se/VariBench/ponsol2.php (accessed on 26 July 2021).
4.2. Features
We collected as large a set of features as possible, since it is not possible to know beforehand which features and their combinations are useful for predictions. We started with 1081 features of which 617 were amino acid features, 2 were conservation features, 436 were variation type features, 25 were neighborhood features, and 1 was a protein-type feature.
Amino acid features were from the AAindex database (accessed on 2 March 2020) [54] and selected as previously described for PON-P2 [4] and PON-MMR2 [55] predictors. Conservation features included the SIFT score and the number of hits. Protein sequences were used as queries in a DIAMOND v0.9.29 [56] search against the NCBI (accessed on 2 March 2020) bnon-redundant database to find homologous sequences. Then, the sequences with percentage of identical matches greater than 90% were aligned by BLAST [57] and used to calculate the SIFT score (v6.2.1) [58] for each variation.
Variation-type features contained a 20 × 20 matrix for substitutions. Another 6 × 6 matrix was built according to amino acid grouping to hydrophobic (V, I, L, F, M, W, Y, and C), negatively charged (D, E), positively charged (R, K, H), conformational (G, P), polar (N, Q, S), and others (A, T), as previously described [59].
Neighborhood features were defined with a 20-dimensional vector of neighboring residues that counts the occurrences of each amino acid type within a window of 23 positions; the variant position was in the middle. Features for NonPolarAA, PolarAA, ChargedAA, PosAA, and NegAA denote the numbers of nonpolar, polar, charged, positively charged, and negatively charged neighborhood residues [60], respectively. The protein-type feature is for the length of the protein sequence.
4.3. Algorithms
Three machine learning algorithms were initially tested—random forests [61], XGBoost [62], and LigthGBM [20]. All the algorithms were implemented in Python in the standard scikit-learn package [63].
Random forests is an ensemble algorithm. It applies several decision trees on the subset of the dataset and uses the average accuracy of each decision tree to improve the performance and to reduce overfitting. The gradient boosting model evaluates the output features based on the combination output result of weak prediction learner models. It minimizes a loss function to optimize the model. Sequential models are constructed using the decision trees until maximum accuracy is achieved.
XGBoost and LigthGBM are implementations of gradient boosting and based on decision trees. Initial results for LightGBM and XGBoost were similar and better than for random forests. As a result of similar performance, we chose LightGBM, which is faster due to utilizing Gradient-based One-Side Sampling (GOSS) and Exclusive Feature Bundling (EFB).
4.4. Feature Selection
Features were chosen with Recursive Feature Elimination (RFE) [64]. In the beginning of feature selection, RFE was used to train a classifier with all features and to define the importance of all features. Then, the least important feature was eliminated. This was repeated recursively to reduce the features until the specified number was reached. The numbers of features tested were all features, 100, 50, and 20 features. Then, predictors were trained with the selected features and tested. As the results were very similar for different numbers of features, we chose the predictor with the smallest number of features to avoid the curse of dimensionality.
4.5. Performance Evaluation
For single group classification of solubility, measures were determined as previously suggested [23,24]. We included positive predictive value (PPV), negative predictive value (NPV), sensitivity, and specificity. Of the recommended measures, accuracy and Matthews correlation coefficient were not used, as the tool predicts three classes. TP, TN, FP, and FN represent the numbers of true positives, true negatives, false positives, and false negatives, respectively. The standard performance measures were computed by using the following Equations (1)–(7):
| (1) |
| (2) |
| (3) |
| (4) |
To evaluate the overall performance, the correct prediction ratio (CPR) and the generalized squared correlation (GC2) were used, the latter has been suggested for K-class classification [65]. CPR is the percentage of correct predictions. GC2 represents the correlation coefficient of the classification ranging from 0 to 1; larger values show better performance. CPR and GC2 are defined as
| (5) |
| (6) |
where K is the number of classes and N is the number of cases. zij represents the number of cases of class i to class j, xi = ∑jzij represents the number of the inputs associated with class I, and yi = ∑jzij represents the number of inputs predicted to be in class i. The expected number of cases in cell i, j of the confusion matrix can be defined as
| (7) |
As the numbers of variants were not balanced in the three solubility categories, the values were normalized to allow the calculation of reliable performance measures.
Author Contributions
Conceptualization, M.V.; methodology, all authors.; software, Y.Y. and L.Z.; validation, M.V.; investigation, all authors; resources, Y.Y. and M.V.; writing—original draft preparation, M.V.; writing—review and editing, all authors; visualization, L.Z. and M.V.; supervision, Y.Y. and M.V.; project administration, Y.Y. and M.V.; funding acquisition, Y.Y. and M.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Key project of the Natural Science Foundation of the Jiangsu Higher Education Institutions of China grant number 20KJA520010, Collaborative Innovation Center of Novel Software Technology and Industrialization at Soochow University, sVetenskapsrådet grant number 2019-01403, and the Swedish Cancer Society grant numbers CAN 2017/699 and CAN 20 1350. The APC was funded by Vetenskapsrådet.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
PON-Sol2 predictor is available at available at http://structure.bmc.lu.se/PON-Sol2/ (accessed on 26 July 2021) and http://139.196.42.166:8010/ (accessed on 26 July 2021). The program is available at https://github.com/XDcat/PON-Sol2 (accessed on 26 July 2021). Data used for training and testing the method are at VariBench at http://structure.bmc.lu.se/VariBench/ponsol2.php (accessed on 26 July 2021).
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Shihab H.A., Gough J., Cooper D.N., Stenson P.D., Barker G., Edwards K.J., Day I.N.M., Gaunt T.R. Predicting the Functional, Molecular, and Phenotypic Consequences of Amino Acid Substitutions using Hidden Markov Models. Hum. Mutat. 2012;34:57–65. doi: 10.1002/humu.22225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dong C., Wei P., Jian X., Gibbs R., Boerwinkle E., Wang K., Liu X. Comparison and integration of deleteriousness prediction methods for nonsynonymous SNVs in whole exome sequencing studies. Hum. Mol. Genet. 2015;24:2125–2137. doi: 10.1093/hmg/ddu733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Carter H., Douville C., Stenson P.D., Cooper D.N., Karchin R. Identifying Mendelian disease genes with the Variant Effect Scoring Tool. BMC Genom. 2013;14:S3. doi: 10.1186/1471-2164-14-S3-S3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Niroula A., Urolagin S., Vihinen M. PON-P2: Prediction Method for Fast and Reliable Identification of Harmful Variants. PLoS ONE. 2015;10:e0117380. doi: 10.1371/journal.pone.0117380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chiti F., Dobson C.M. Protein Misfolding, Amyloid Formation, and Human Disease: A Summary of Progress over the Last Decade. Annu. Rev. Biochem. 2017;86:27–68. doi: 10.1146/annurev-biochem-061516-045115. [DOI] [PubMed] [Google Scholar]
- 6.Vecchi G., Sormanni P., Mannini B., Vandelli A., Tartaglia G.G., Dobson C.M., Hartl F.U., Vendruscolo M. Proteome-wide observation of the phenomenon of life on the edge of solubility. Proc. Natl. Acad. Sci. USA. 2020;117:1015–1020. doi: 10.1073/pnas.1910444117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Arakawa T., Timasheff S.N. [3]Theory of protein solubility. Methods Enzymol. 1985;114:49–77. doi: 10.1016/0076-6879(85)14005-x. [DOI] [PubMed] [Google Scholar]
- 8.Garidel P. Protein solubility from biochemical, physicochmical and colloidal perspective. [(accessed on 11 June 2021)];Am. Pharm. Rev. 2013 Available online: https://www.americanpharmaceuticalreview.com/Featured-Articles/152568-Protein-Solubility-from-a-Biochemical-Physicochemical-and-Colloidal-Perspective/ [Google Scholar]
- 9.Yang Y., Niroula A., Shen B., Vihinen M. PON-Sol: Prediction of effects of amino acid substitutions on protein solubility. Bioinformatics. 2016;32:2032–2034. doi: 10.1093/bioinformatics/btw066. [DOI] [PubMed] [Google Scholar]
- 10.Vihinen M. Solubility of proteins. ADMET DMPK. 2020;8:391–399. doi: 10.5599/admet.831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Meulemans A., Seneca S., Pribyl T., Smet J., Alderweirldt V., Waeytens A., Lissens W., Van Coster R., De Meirleir L., di Rago J.-P., et al. Defining the Pathogenesis of the Human Atp12p W94R Mutation Using a Saccharomyces cerevisiae Yeast Model. J. Biol. Chem. 2010;285:4099–4109. doi: 10.1074/jbc.M109.046920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Andley U.P., Reilly M. In vivo lens deficiency of the R49C αA-crystallin mutant. Exp. Eye Res. 2010;90:699–702. doi: 10.1016/j.exer.2010.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sormanni P., Aprile F.A., Vendruscolo M. The CamSol Method of Rational Design of Protein Mutants with Enhanced Solubility. J. Mol. Biol. 2015;427:478–490. doi: 10.1016/j.jmb.2014.09.026. [DOI] [PubMed] [Google Scholar]
- 14.Tian Y., Deutsch C., Krishnamoorthy B. Scoring function to predict solubility mutagenesis. Algorithms Mol. Biol. 2010;5:33. doi: 10.1186/1748-7188-5-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Paladin L., Piovesan D., Tosatto S.C.E. SODA: Prediction of protein solubility from disorder and aggregation propensity. Nucleic Acids Res. 2017;45:W236–W240. doi: 10.1093/nar/gkx412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Van Durme J., De Baets G., van der Kant R., Ramakers M., Ganesan A., Wilkinson H., Gallardo R., Rousseau F., Schymkowitz J. Solubis: A webserver to reduce protein aggregation through mutation. Protein Eng. Des. Sel. 2016;29:285–289. doi: 10.1093/protein/gzw019. [DOI] [PubMed] [Google Scholar]
- 17.Guerois R., Nielsen J.E., Serrano L. Predicting Changes in the Stability of Proteins and Protein Complexes: A Study of More Than 1000 Mutations. J. Mol. Biol. 2002;320:369–387. doi: 10.1016/S0022-2836(02)00442-4. [DOI] [PubMed] [Google Scholar]
- 18.Fernandez-Escamilla A.M., Rousseau F., Schymkowitz J., Serrano L. Prediction of sequence-dependent and mutational effects on the aggregation of peptides and proteins. Nat. Biotechnol. 2004;22:1302–1306. doi: 10.1038/nbt1012. [DOI] [PubMed] [Google Scholar]
- 19.Land H., Humble M.S. YASARA: A Tool to Obtain Structural Guidance in Biocatalytic Investigations. Methods Mol. Biol. 2018;1685:43–67. doi: 10.1007/978-1-4939-7366-8_4. [DOI] [PubMed] [Google Scholar]
- 20.Ke G., Meng Q., Finley T., Wang T., Chen W., Ma W., Ye Q., Liu T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. Neural Information Processing Systems; La Jolla, CA, USA: 2017. [Google Scholar]
- 21.Niroula A., Vihinen M. Predicting Severity of Disease-Causing Variants. Hum. Mutat. 2017;38:357–364. doi: 10.1002/humu.23173. [DOI] [PubMed] [Google Scholar]
- 22.Yang Y., Urolagin S., Niroula A., Ding X., Shen B., Vihinen M. PON-tstab: Protein Variant Stability Predictor. Importance of Training Data Quality. Int. J. Mol. Sci. 2018;19:1009. doi: 10.3390/ijms19041009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Vihinen M. How to evaluate performance of prediction methods? Measures and their interpretation in variation effect analysis. BMC Genom. 2012;13:S2. doi: 10.1186/1471-2164-13-S4-S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Vihinen M. Guidelines for Reporting and Using Prediction Tools for Genetic Variation Analysis. Hum. Mutat. 2013;34:275–282. doi: 10.1002/humu.22253. [DOI] [PubMed] [Google Scholar]
- 25.Fukuchi S., Nishikawa K. Protein surface amino acid compositions distinctively differ between thermophilic and mesophilic bacteria. J. Mol. Biol. 2001;309:835–843. doi: 10.1006/jmbi.2001.4718. [DOI] [PubMed] [Google Scholar]
- 26.Jones D.T., Taylor W.R., Thornton J.M. The rapid generation of mutation data matrices from protein sequences. Bioinformatics. 1992;8:275–282. doi: 10.1093/bioinformatics/8.3.275. [DOI] [PubMed] [Google Scholar]
- 27.Ponnuswamy P., Prabhakaran M., Manavalan P. Hydrophobic packing and spatial arrangement of amino acid residues in globular proteins. Biochim. Biophys. Acta BBA Protein Struct. 1980;623:301–316. doi: 10.1016/0005-2795(80)90258-5. [DOI] [PubMed] [Google Scholar]
- 28.Qian N., Sejnowski T.J. Predicting the secondary structure of globular proteins using neural network models. J. Mol. Biol. 1988;202:865–884. doi: 10.1016/0022-2836(88)90564-5. [DOI] [PubMed] [Google Scholar]
- 29.George R.A., Heringa J. An analysis of protein domain linkers: Their classification and role in protein folding. Protein Eng. Des. Sel. 2002;15:871–879. doi: 10.1093/protein/15.11.871. [DOI] [PubMed] [Google Scholar]
- 30.Oobatake M., Kubota Y., Ooi T. Optimization of amino acid parameters for correspondence of sequence to tertiary structures of proteuins. Bull. Inst. Chem. Res. Kyoto Univ. 1985;63:82–94. [Google Scholar]
- 31.Koshi J.M., Goldstein R.A. Context-dependent optimal substitution matrices. Protein Eng. Des. Sel. 1995;8:641–645. doi: 10.1093/protein/8.7.641. [DOI] [PubMed] [Google Scholar]
- 32.Argos P., Rao J.K.M., Hargrave P.A. Structural Prediction of Membrane-Bound Proteins. JBIC J. Biol. Inorg. Chem. 2005;128:565–575. doi: 10.1111/j.1432-1033.1982.tb07002.x. [DOI] [PubMed] [Google Scholar]
- 33.Prabhakaran M., Ponnuswamy P.K. Shape and surface features of globular proteins. Macromolecules. 1982;15:314–320. doi: 10.1021/ma00230a022. [DOI] [Google Scholar]
- 34.Zimmerman J., Eliezer N., Simha R. The characterization of amino acid sequences in proteins by statistical methods. J. Theor. Biol. 1968;21:170–201. doi: 10.1016/0022-5193(68)90069-6. [DOI] [PubMed] [Google Scholar]
- 35.Chou P.Y., Fasman G.D. Prediction of the Secondary Structure of Proteins from their Amino Acid Sequence. Adv. Enzymol. Relat. Areas Mol. Biol. 2006;47:45–148. doi: 10.1002/9780470122921.ch2. [DOI] [PubMed] [Google Scholar]
- 36.Vasquez M., Nemethy G., Scheraga H.A. Computed conformational states of the 20 naturally occurring amino acid residues and of the prototype residue α-aminobutyric acid. Macromolecules. 1983;16:1043–1049. doi: 10.1021/ma00241a004. [DOI] [Google Scholar]
- 37.Dayhoff M.O., Schwartz R.M., Orcutt B.C. A model of evolutionary change in proteins. In: Dayhoff M.O., editor. Atlas of Protein Sequence and Structure. Volume 5. National Biomedical Research Foundation; Washington, DC, USA: 1978. pp. 345–352. [Google Scholar]
- 38.Dosztányi Z., Torda A.E. Amino acid similarity matrices based on force fields. Bioinformatics. 2001;17:686–699. doi: 10.1093/bioinformatics/17.8.686. [DOI] [PubMed] [Google Scholar]
- 39.Browne C., Bennett H., Solomon S. The isolation of peptides by high-performance liquid chromatography using predicted elution positions. Anal. Biochem. 1982;124:201–208. doi: 10.1016/0003-2697(82)90238-X. [DOI] [PubMed] [Google Scholar]
- 40.Mirny L.A., Shakhnovich E.I. How to Derive a Protein Folding Potential? A New Approach to an Old Problem. J. Mol. Biol. 1996;264:1164–1179. doi: 10.1006/jmbi.1996.0704. [DOI] [PubMed] [Google Scholar]
- 41.Suyama M., Ohara O. DomCut: Prediction of inter-domain linker regions in amino acid sequences. Bioinformatics. 2003;19:673–674. doi: 10.1093/bioinformatics/btg031. [DOI] [PubMed] [Google Scholar]
- 42.Fasman G.D. In: Handbook of Biochemistry and Molecular Biology. 3rd ed. Fasman G.D., editor. Volume 1 CRC Press; Cleveland, OH, USA: 1976. [Google Scholar]
- 43.Lifson S., Sander C. Antiparallel and parallel β-strands differ in amino acid residue preferences. Nat. Cell Biol. 1979;282:109–111. doi: 10.1038/282109a0. [DOI] [PubMed] [Google Scholar]
- 44.Vetrie D., Vořechovský I., Sideras P., Holland J., Davies A., Flinter F.A., Hammarström L., Kinnon C., Levinsky R.J., Bobrow M., et al. The gene involved in X-linked agammaglobulinaemia is a member of the src family of protein-tyrosine kinases. Nat. Cell Biol. 1993;361:226–233. doi: 10.1038/361226a0. [DOI] [PubMed] [Google Scholar]
- 45.Väliaho J., Smith C.I.E., Vihinen M. BTKbase: The mutation database for X-linked agammaglobulinemia. Hum. Mutat. 2006;27:1209–1217. doi: 10.1002/humu.20410. [DOI] [PubMed] [Google Scholar]
- 46.Vihinen M. Functional effects of protein variants. Biochimie. 2021;180:104–120. doi: 10.1016/j.biochi.2020.10.009. [DOI] [PubMed] [Google Scholar]
- 47.Broom A., Jacobi Z., Trainor K., Meiering E.M. Computational tools help improve protein stability but with a solubility tradeoff. J. Biol. Chem. 2017;292:14349–14361. doi: 10.1074/jbc.M117.784165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Tripathi A., Gupta K., Khare S., Jain P.C., Patel S., Kumar P., Pulianmackal A.J., Aghera N., Varadarajan R. Molecular Determinants of Mutant Phenotypes, Inferred from Saturation Mutagenesis Data. Mol. Biol. Evol. 2016;33:2960–2975. doi: 10.1093/molbev/msw182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sauter C., Lorber B., Gaudry A., Karim L., Schwenzer H., Wien F., Roblin P., Florentz C., Sissler M. Neurodegenerative disease-associated mutants of a human mitochondrial aminoacyl-tRNA synthetase present individual molecular signatures. Sci. Rep. 2015;5:17332. doi: 10.1038/srep17332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Espargaró A., Castillo V., De Groot N.S., Ventura S. The in Vivo and in Vitro Aggregation Properties of Globular Proteins Correlate With Their Conformational Stability: The SH3 Case. J. Mol. Biol. 2008;378:1116–1131. doi: 10.1016/j.jmb.2008.03.020. [DOI] [PubMed] [Google Scholar]
- 51.Klesmith J.R., Bacik J.-P., Wrenbeck E.E., Michalczyk R., Whitehead T.A. Trade-offs between enzyme fitness and solubility illuminated by deep mutational scanning. Proc. Natl. Acad. Sci. USA. 2017;114:2265–2270. doi: 10.1073/pnas.1614437114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sarkar A., Yang Y., Vihinen M. Variation benchmark datasets: Update, criteria, quality and applications. Database. 2020;2020 doi: 10.1093/database/baz117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Nair P.S., Vihinen M. VariBench: A Benchmark Database for Variations. Hum. Mutat. 2013;34:42–49. doi: 10.1002/humu.22204. [DOI] [PubMed] [Google Scholar]
- 54.Kawashima S. AAindex: Amino Acid index database. Nucleic Acids Res. 2000;28:374. doi: 10.1093/nar/28.1.374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Niroula A., Vihinen M. Classification of Amino Acid Substitutions in Mismatch Repair Proteins Using PON-MMR2. Hum. Mutat. 2015;36:1128–1134. doi: 10.1002/humu.22900. [DOI] [PubMed] [Google Scholar]
- 56.Buchfink B., Xie C., Huson D.H. Fast and sensitive protein alignment using DIAMOND. Nat. Methods. 2015;12:59–60. doi: 10.1038/nmeth.3176. [DOI] [PubMed] [Google Scholar]
- 57.Boratyn G.M., Camacho C., Cooper P., Coulouris G., Fong A., Ma N., Madden T.L., Matten W.T., McGinnis S.D., Merezhuk Y., et al. BLAST: A more efficient report with usability improvements. Nucleic Acids Res. 2013;41:W29–W33. doi: 10.1093/nar/gkt282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sim N.-L., Kumar P., Hu J., Henikoff S., Schneider G., Ng P.C. SIFT web server: Predicting effects of amino acid substitutions on proteins. Nucleic Acids Res. 2012;40:W452–W457. doi: 10.1093/nar/gks539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Shen B., Vihinen M. Conservation and covariance in PH domain sequences: Physicochemical profile and information theoretical analysis of XLA-causing mutations in the Btk PH domain. Protein Eng. Des. Sel. 2004;17:267–276. doi: 10.1093/protein/gzh030. [DOI] [PubMed] [Google Scholar]
- 60.Lockwood S., Krishnamoorthy B., Ye P. Neighborhood Properties Are Important Determinants of Temperature Sensitive Mutations. PLoS ONE. 2011;6:e28507. doi: 10.1371/journal.pone.0028507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Breiman L. Random Forests. Mach. Learn. 2001;45:5–32. doi: 10.1023/A:1010933404324. [DOI] [Google Scholar]
- 62.Chen T., Guestrin C. XGBoost: A Scalable Tree Boosting System; Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery; San Francisco, CA, USA. 13–17 August 2016; pp. 785–794. [Google Scholar]
- 63.Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011;12:2825–2830. [Google Scholar]
- 64.Guyon I., Weston J., Barnhill S., Vapnik V. Gene Selection for Cancer Classification using Support Vector Machines. Mach. Learn. 2002;46:389–422. doi: 10.1023/A:1012487302797. [DOI] [Google Scholar]
- 65.Baldi P., Brunak S., Chauvin Y., Andersen C.A.F., Nielsen H. REVIEW Assessing the Accuracy of Prediction Algorithms for Classification: An Overview. Bioinformatics. 2000;16:412–424. doi: 10.1093/bioinformatics/16.5.412. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
PON-Sol2 predictor is available at available at http://structure.bmc.lu.se/PON-Sol2/ (accessed on 26 July 2021) and http://139.196.42.166:8010/ (accessed on 26 July 2021). The program is available at https://github.com/XDcat/PON-Sol2 (accessed on 26 July 2021). Data used for training and testing the method are at VariBench at http://structure.bmc.lu.se/VariBench/ponsol2.php (accessed on 26 July 2021).