Predicting the epidemic curve of the coronavirus (SARS-CoV-2) disease (COVID-19) using artificial intelligence: An application on the first and second waves

Abstract

Objectives

The COVID-19 pandemic is considered a major threat to global public health. The aim of our study was to use the official epidemiological data to forecast the epidemic curves (daily new cases) of the COVID-19 using Artificial Intelligence (AI)-based Recurrent Neural Networks (RNNs), then to compare and validate the predicted models with the observed data.

Methods

We used publicly available datasets from the World Health Organization and Johns Hopkins University to create a training dataset, then we employed RNNs with gated recurring units (Long Short-Term Memory - LSTM units) to create two prediction models. Our proposed approach considers an ensemble-based system, which is realized by interconnecting several neural networks. To achieve the appropriate diversity, we froze some network layers that control the way how the model parameters are updated. In addition, we could provide country-specific predictions by transfer learning, and with extra feature injections from governmental constraints, better predictions in the longer term are achieved. We have calculated the Root Mean Squared Logarithmic Error (RMSLE), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE) to thoroughly compare our model predictions with the observed data.

Results

We reported the predicted curves for France, Germany, Hungary, Italy, Spain, the United Kingdom, and the United States of America. The result of our study underscores that the COVID-19 pandemic is a propagated source epidemic, therefore repeated peaks on the epidemic curve are to be anticipated. Besides, the errors between the predicted and validated data and trends seem to be low.

Conclusion

Our proposed model has shown satisfactory accuracy in predicting the new cases of COVID-19 in certain contexts. The influence of this pandemic is significant worldwide and has already impacted most life domains. Decision-makers must be aware, that even if strict public health measures are executed and sustained, future peaks of infections are possible. The AI-based models are useful tools for forecasting epidemics as these models can be recalculated according to the newly observed data to get a more precise forecasting.

1. Introduction

1.1. Coronavirus disease – 2019 (COVID-19)

The current form of the severe acute respiratory syndrome noted as COVID-19, is caused by a new variant of formerly known highly pathogenic Coronaviridae. The infection allegedly began to spread from Wuhan, the capital of Hubei province, China, at the end of 2019 [1,2]. On March 11, 2020, the World Health Organization (WHO) has characterized the COVID-19 as a global pandemic. Early genome sequencing has found that the new virus, which was named SARS-CoV-2 by the International Committee on Taxonomy of Viruses, showed a 79.6% homology with SARS-CoV, and has 96% sequence identity with bat coronavirus, suggesting a common origin from SARSr-CoV (severe acute respiratory syndrome-related Coronavirus). Also, the suspected host was thought to be a bat species, Rhinolophus affinis (a horseshoe bat), but the SARS-COV-2 probably needs an intermediate host [2,3].

Symptoms associated with the COVID-19 may include fever, cough, shortness of breath, muscle aches, confusion, headache, sore throat, runny nose, chest pain, diarrhea, nausea, and vomiting [4]. The incubation period of the virus was estimated to be between 1 and 14 days (5 days on average) [5]. Several transmission routes have been identified including respiratory droplets/aerosols, direct contact with virally contaminated objects, and possibly fecal-oral transmission [6]. It seems probable that those with a fulminant disease are most infectious, but reports have identified asymptomatic and pre-symptomatic virus shedding as well. There was also a lack of definite data regarding tertiary and quaternary spreading among humans, but it seems probable that the person who has been exposed to the infection has acquired some (at least temporary) immunity [7].

1.2. The daily number of newly diagnosed infections - epidemic curves

The initial epidemic curves of the COVID-19 outbreak from Hubei, China showed a mixed pattern, indicating that early cases were likely from a continuous common source e.g., from several zoonotic events in Wuhan, followed by secondary and tertiary transmission providing a propagated source for the later cases [8].

The propagated (or progressive source) epidemic curve visualizes the spread of an infectious agent that may be transmitted from human to human starting from with a single index case, that continues to further infect other individuals. This shows up as a series of peaks on the epidemic curve that starts with the index case, followed by successive waves of the infection set apart with respect to the incubation period of the pathogen. The waves continue to follow each other until appropriate mitigation measures, prevention, or treatment are implemented, or the pool of the susceptible population becomes infected. This is a theoretic curve, that is generally influenced by lots of other factors [8].

Several studies investigated the impact of different interventions concerning minimizing contact rates in the population to retard the infection spread, minimize COVID-19 mortality rates and health care utilization, or suppress the epidemic per se. Flattening the curve by reducing peak incidence may limit overall case fatality rates. Nevertheless, most of the early forecasts and simulations started from Bell-shaped curves, that fail to account for the progressive nature of the current outbreak given the known secondary, tertiary even quaternary transmissibility of the virus. Taking this into account, it is suggested that the number of cases might rise once again after pandemic control measures are no longer in effect [9]. It is also possible that the dynamics and the characteristics of the pandemic might be connected to the new variants of the virus [10].

1.3. Insights into predicting the COVID-19 transmission using AI

Various mathematical models may demonstrate and predict the dynamics of different infectious diseases [11]. These models, used to simulate the dynamics of infectious diseases, may be based on statistical, mathematical, empirical, or machine-learning methods [12]. The first attempts to use Artificial Intelligence (AI) in medicine were made in the 1970s. Initially, AI was used to implement programs to help clinical decision-making, but to date, its use is gaining more and more widespread acceptance in biomedical sciences [13]. One class of AI, a form of artificial neural networks, the Recurrent Neural Networks (RNNs) with Long Short-Term Memory (LSTM) were previously used to model and forecast the influenza epidemic, with strong competitiveness and reliable results [14,15].

During the COVID-19 pandemic, various simulation studies reported the use of different AI-based methods to forecast the projections of the COVID-19. Concerning the use of LSTM, Ghany et al. (2021) reported using the LSTM algorithm with ten hidden units to predict the spread of the COVID-19 in terms of confirmed cases and deaths in six gulf countries [16]. In India, a data-driven model based on LSTM was used to predict cases and recoveries, considering the imposed governmental preventive measures like lockdown and isolation [17]. Additionally, Chimmula and Zhang (2020) reported one of the early studies that utilized LSTM networks to simulate the trends of COVID-19 transmission in Canada in order to help public health decision-makers and healthcare workers by building a fully automated, real-time forecasting model for COVID-19 [18]. Furthermore, Kırbaş et al. (2020) discussed in their article the prediction of new cases of COVID-19 in several European countries using three approaches, namely, Auto-Regressive Integrated Moving Average (ARIMA), Nonlinear Autoregression Neural Network (NARNN), and Long-Short Term Memory (LSTM) [19]. Interestingly, Kırbaş and colleagues found that the LSTM model was the most accurate one. In Saudi Arabia, a deep learning model using LSTM was also used for predicting COVID-19 trends in the country [20]. The forecasting accuracy of the LSTM model used in the Saudi study was also compared with predictions obtained by ARIMA and Nonlinear Autoregressive Artificial Neural Networks (NARANN). The LSTM model has revealed a better accuracy in forecasting the total number of COVID-19 cases for one week ahead in comparison with NARANN and ARIMA models [20].

1.4. Rationale and aim of the study

The use of AI-based approaches in forecasting the projections of COVID-19 has been a remark of the pandemic crisis. Various mitigation strategies were imposed by public health authorities in different countries worldwide, and these measures may vary in their intensity, duration, and application. Therefore, reaching a robust and reliable AI-based model for COVID-19 forecasting is considered a challenging mission, especially at the early stages of the pandemic when no enough data can be found. Our present study aimed to use the publicly available official COVID-19 data during the early stage of the pandemic crisis as a training dataset, to predict the possible outcomes of the COVID-19 pandemic (epidemic curve of new cases) using AI-based RNNs, and further, to compare the predictions with the observed data. The model proposed in this study has been applied to forecast the epidemic curves of the first and second pandemic waves in six countries.

2. Materials and methods

2.1. Data

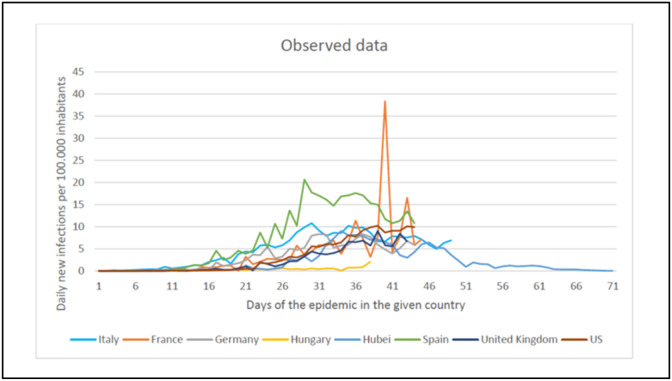
We used the publicly available datasets from the WHO and Johns Hopkins University for the following countries to create the training dataset: Austria, Belgium, China (Hubei), Czech Republic, France, Germany, Hungary, Iran, Italy, Netherlands, Norway, Portugal, Slovenia, Spain, Switzerland, United Kingdom (UK) and the United States of America (USA) [7,21]. Given that most infected people in China were from Hubei province, only data from that province was included. For each country, the date of the first reported infection was set as Day 1 for the disease time scale. (Fig. 1 ).

Fig. 1.

The historical datasets of different countries from first pandemic wave.

When determining the date of the first illness (first identified case), point-source outbreaks were omitted (e.g., those cases where single verified cases were isolated, and no further transmission has occurred). This was important to avoid distortion of the propagated epidemic curves. In Belgium, for example, the first illness occurred on February 02, 2020, and there were no further cases reported for up to 26 days. The next illness occurred on March 01, 2020. The inclusion of the early case from February would contribute to a false learning rule for the AI, hence corrupting the results. As for Hubei Province, the first officially available data was on January 22, 2020. This cannot be considered as the first day of the illness, thus the first infection was arbitrarily defined to occur on January 01, 2020. To account for the extreme variability of daily incident cases reported which probably reflects delays in reporting procedures, a moving average was used (covering 3 days) for the Hubei dataset.

Accordingly, an epidemic curve was obtained for each country with a time series where the first day denotes the day of the first confirmed case, and each successive day indicating the number of newly confirmed cases that day. To account for the country-specific differences in the size of the population, the number of daily new cases was normalized for 100.000 inhabitants in each country. The observation period varies for each country, given the difference of time elapsed since the disease initiation in that country. Accordingly, the longest time series covers the observation period of 90 days. e.g., in Hubei, with the first 22 days lacking valid data and the next 68 days having data. The shortest observation period was in Slovenia with only 30 days.

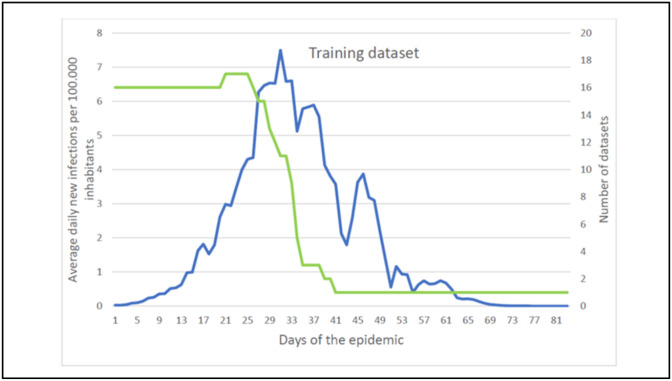
The training data set was obtained by averaging the daily incidence rates per 100 000 inhabitants across the 17 countries included, for each day in the time series. When calculating the average, missing data was left blank, i.e., NULL, e.g., countries that did not contain data for a specific day were excluded from the calculation of average. The resulting training data set is shown in Fig. 2 . It should be noted that the first part of the data set (up to the initial 30 days since Day 1 of the epidemic) contains data for almost all the countries listed, whereas the end of the data set contains only data from Hubei (Fig. 2).

Fig. 2.

The training dataset. Average daily new infections per 100.000 inhabitants (line ) and the Number of datasets (line ).

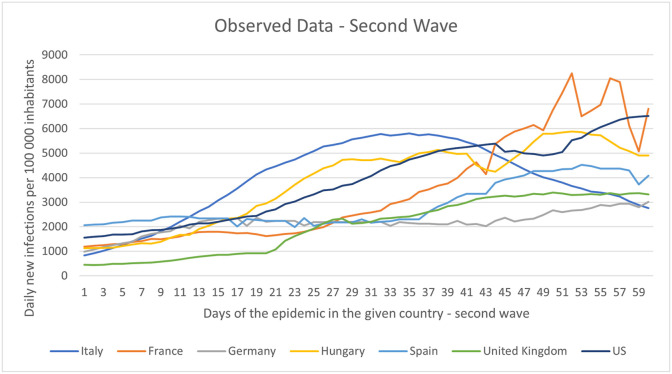
In order to test our model more accurately, we also examined the second waves’ data. To obtain more accurate results for the second wave, we have created an interconnected neural network model, whose first part is the base RNN trained on the first wave data. The second part of the extended model is the neural network component trained on the second wave dataset. The second wave data for each country under study consisted of 85 days. Of these, the first 60 days were used for retraining and the next 25 days for prediction. The training datasets used per country for the second wave are presented in Fig. 3 . However, for each country, the course of the pandemic is different, so the first day of the second wave is determined by country. The first day of the second wave in each country is shown in Table 1 .

Fig. 3.

The observed datasets of different countries from second pandemic wave.

Table 1.

The day 1. of the second wave.

Country	Day 1
France	2020.09.13
Germany	2020.10.23
Italy	2020.10.13
Spain	2020.09.13
Hungary	2020.10.13
UK	2020.09.13
USA	2020.10.13

2.2. RNNs-based models for prediction

The state-of-the-art for time series analysis is AI-based analytic tools, which have the best prediction performance. Recurrent Neural Networks (RNNs) are specifically designed to cope with sequential input, characteristic of textual or temporal data. This architecture is a neural network-based architecture, that contains hidden layers chained according to the time step, with a possibility to predict the next sequence element(s). A time series has a special temporal form, where the input to the i-th hidden layer is at the i-th time-step that has a corresponding x(i) observation. In its original form, a simple RNN tries to predict the next sequence element, however, for the purpose of the current analysis, an encoder-decoder variant is a more natural choice, similarly, to machine translation [22].

For our specific scenario this means that during the encoder phase including time steps 1, …,t the RNN is fed with the already known time series data (the average of the number of new cases normalized to 100 000 inhabitants for day 1…t, respectively), followed by prediction in the decoder phase for the future time steps t+1, …,T. In our analysis, T = t+1 = 90 days is the longest known (Hubei) time interval. Since this covers quite a long data sequence, we have used gated recurring units (namely Long Short-Term Memory – LSTM units) [15]. Fig. 4 depicts our RNN architecture showing how unknown time series elements are predicted. Fig. 4 also shows how the information collected in the first t time-steps are aggregated with a fully connected (dense) neural network layer and a consequent regression output layer to determine a predicted number of new patients as x(t+1).

Fig. 4.

The Recurrent Neural Network (RNN) Architecture used for Prediction.

We used our own approach to design the architecture and build the encoder-decoder process according to the problem. The construction of the network begins with a Sequence Layer, followed by the LSTM blocks shown in Fig. 4, which have a memory capability for the previous state. With this feedback process, the prediction can get much closer to the real one. Dropout layers were added to the LSTM layers of the network to control overfitting. Dropout is a regularization method where input and recurrent connections to LSTM units are probabilistically excluded from activation and weight updates while training a network. It has the effect of reducing overfitting and improving model performance.

We experimented by gradually increasing the epoch number from 50 to 300. The best results were obtained after 150 epochs. In later epochs, there was an inconsistency in both machine capability and the accuracy score. To save training time, we have implemented mini-batch gradient descent in the training process, and the batch size we used was 8. To optimize the training process, we took advantage of the ADAM optimizer by setting the learning rate at 1e-4 and reduced it by 1e-6 for each subsequent epoch.

As for adjusting the hyperparameters (number and components of LSTM layers, dropout probability, optimizer, mini-batch size, learning rate) of our neural model we have applied the Bayesian algorithm, which is well suited for optimizing hyperparameters of classification and regression models. During the evaluation of the results, we have used this trained basic model, but for each country, the state of the basic model was updated with the help of the training data set of that country.

In predicting the second wave, we had much more metadata available, such as viral replication rates, mortality data, numbers indicating the extent of restrictions imposed by governments. Adding these extra features to the system we have developed a solution that takes better account of the circumstances in the prediction, so we can get a more accurate prediction of the number of new cases per day. For the second wave prediction, we have created an interconnected neural network model, whose first part is the base RNN trained on the first wave data. The second part of the extended model is the neural network component trained on the second wave dataset and augmented with the metadata mentioned above. After these two components were connected following their training, they have undergone a state update, which consisted of a retraining step regarding the specific country data to be predicted. The essence of the connected model is that the states of the two sub-networks are updated simultaneously for a given country and the final decision is reached as the weighted sum of the outputs of the two networks. These weight parameters are also embedded in the interconnected neural architecture so adjusted automatically during the training process.

To assess the possible specificities regarding the countries, two approaches were used for prediction as follows:

• •Prediction 1: An algorithm to update the training step and subsequent prediction was formulated. This updating step is based on the general recommendations of transfer learning that considers the already known time interval for the given country and re-training is done in small increments of the RNN network accordingly [22]. Thus, we start predicting the first unknown element x(t+1) from the last 5% of the known data, and the same principle is applied to each subsequent element. Moreover, after each prediction steps our RNN architecture was re-trained, and the subsequent elements were predicted with this updated RNN.
• •Prediction 2: We start predicting the first unknown element x(t+1) from the last known x(t), and all the subsequent elements are predicted only from the preceding ones. Here the rules depicted from the training data set are used, not retraining occurs.

The intuitive interpretations of the difference between Prediction 1 and Prediction 2 are as follows. Prediction 2 makes its predictions utilizing the information derived from the training data set, reflective of the trends in the average time series. It follows those predictions will comply primarily with the Hubei time series, especially in the far future. Therefore Prediction 2 shows the highest fidelity to the country-specific future scenario if the approach to mitigate the epidemic is similar to that in Hubei. Accordingly, this scenario is also reflective of a country-specific future state given the practices of Hubei were followed in said country. On the other hand, Prediction 1 is yielded after the neural network is retrained after any prediction, providing more valid insight into what is expected if the country goes on with the mitigation practices seen during the observation period. This intuition can be also used for the evaluation of the second wave of the pandemic because in this case, the prediction architecture includes the neural network which was trained during the first wave.

2.3. Validation

For the learning dataset, we used the data from the first pandemic wave. That is, we took the available factual data from the first case reported in a country until April 10, 2020. Based on that, we have made the above-mentioned two predictions (1 and 2). Moreover, for the validation process, we used the factual data of the first wave. By country, we considered 85–90 days from the first case reported. Thus, the number of days predicted varied from country to country in the same way as for the learning dataset. The amount of Root Mean Squared Logarithmic Errors (RMSLE) was used for validation. In our analysis, the possible bias regarding the different ratios between the observed and predicted values are interpreted using the RMSLE. Let n be the number of days used for validation. Let p_1i and p_2i be the number of new cases per day obtained using the two prediction methods in the examined time interval and let a_i be the actual data for the given days. Err1 and Err2 will be RMSLE for Prediction 1 and Prediction 2, respectively, where:

$$Er{r}_1=\sqrt{\frac{1}{n}\sum _{i=1}^n{(\log \left(p_{1i}+1\right)-\log \left(a_i+1\right))}^2}$$

$$Er{r}_2=\sqrt{\frac{1}{n}\sum _{i=1}^n{(\log \left(p_{2i}+1\right)-\log \left(a_i+1\right))}^2}$$

We have calculated also the Root Mean Square Error (RMSE) and the Mean Absolute Percentage Error (MAPE), as follows:

$$RMS{E}_1=\sqrt{\frac{1}{n}\sum _{i=1}^n{(p_{1i}-a_i)}^2}$$

$$RMS{E}_2=\sqrt{\frac{1}{n}\sum _{i=1}^n{(p_{2i}-a_i)}^2}$$

$$MAP{E}_1=\frac{100}{n}\sum _{i=1}^n\left|\frac{p_{1i}-a_i}{a_i}\right|$$

$$MAP{E}_2=\frac{100}{n}\sum _{i=1}^n\left|\frac{p_{2i}-a_i}{a_i}\right|$$

2.4. Comparison with other models

In Luo et al. (2021), a simple LSTM model and the XGBoost algorithm were compared on US COVID-19 data [23]. The training set contains data between April 2020 and September 2020, while the prediction is given for 30 days. It is shown that the predicted number of new cases has a high correlation with the previous week's cases. The key features used by the model are the mean and the number of new confirmed cases per day over the previous 7 days. In addition, the day of the week is also a major contributor to the model. This indicates that the number of new confirmed cases is strongly correlated with whether the given day was a working one or not. In contrast to our model, neither Wuhan data were included nor metadata from other restriction measures were used. The model forecasting for the first week shows similar accuracy to our model, but over longer periods, our approach is much closer to the real behavior [23].

Also, Bhimala et al. (2021) [24] have used LSTM-based models to predict the epidemic situation in India. The authors were looking for a relationship between weather conditions and virus spread, so they added additional metadata such as temperature and humidity to the basic model. It has been found that the basic LSTM model gave good approximations with relatively small errors only for a 1–2-day forecast, while when weather data were included, the prediction reliability improved significantly over a weekly time scale. We did not include weather data in the training of our model because we have found that for European countries this information is not so relevant. However, after including other metadata (e.g., mortality rates, virus spread rates, quantified data from government restrictions), our model has also improved significantly compared to the model developed in the first wave. Nevertheless, it was not sufficient to make small modifications to the model architecture as in Bhimala et al.’s study, because it still does not solve the issue of long-term forecasting. Therefore, we have re-designed our model to contain several subnetworks, so that we could obtain a good prediction for the longer term by achieving sufficient diversity.

Additionally, In Kafieh et al. (2021) [25], the main objective was to predict outbreaks in nine countries - Iran, Germany, Italy, Japan, Japan, Korea, Switzerland, Spain, China, and the United States of America. Data between 22 January and 30 July 2020 were used for training and the period 1–31 August 2020 for testing. A multivariate LSTM model is used for prediction by considering the number of occurrences in each class (confirmed/advanced/cured) as input and predicting the values of all three-time series for the next time step (multiple-input multiple-output (MIMO) format). Although good results were obtained on the test dataset, the behavior of the predicted epidemic curve for the following months deviated significantly from the real trend. Specifically, a smoothed curve is the model output, which is typical for LSTM models that attempt to predict over the long term from an incomplete learning data set. We have also experienced this phenomenon in our work hence the combination of several models and the injection of extra features have been applied to overcome it. In this way, we have reached a more realistic behavior.

3. Results

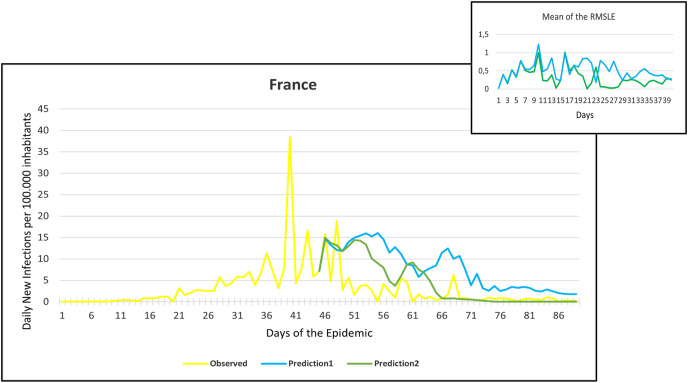
This section shows the outcomes for Prediction 1 and Prediction 2 of the individual country-level data for France, Germany, Hungary, Italy, Spain, the United Kingdom (UK), and the United States of America (USA) (Fig. 5, Fig. 6, Fig. 7, Fig. 8, Fig. 9, Fig. 10, Fig. 11, Fig. 12, Fig. 13, Fig. 14, Fig. 15, Fig. 16, Fig. 17, Fig. 18 ). In each graph, the first day represents the first illness/case of each country. The yellow line represents the factual data of the first wave for 85–91 days from the first illness/case. For each country, the learning database was provided by the data available up to 10 April 2020. The values obtained by the two prediction methods for each country are represented by blue and green lines. The blue line shows Prediction 1, and the green line shows Prediction 2.

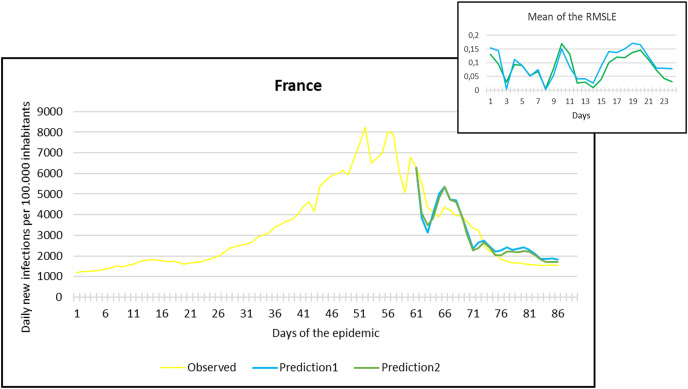
Fig. 5.

Observation and predictions for France During the First Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

Fig. 6.

Observation and predictions for France During the Second Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

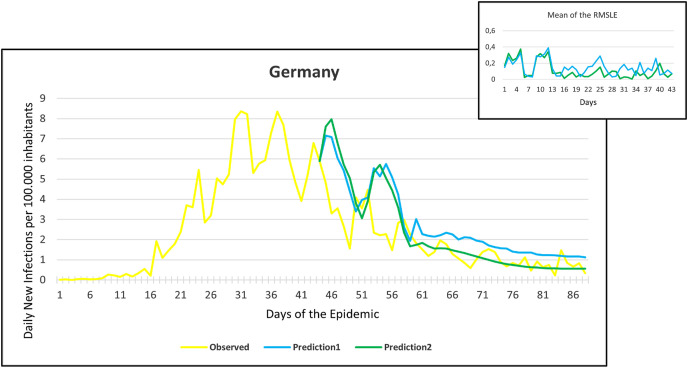
Fig. 7.

Observation and predictions for Germany During the First Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

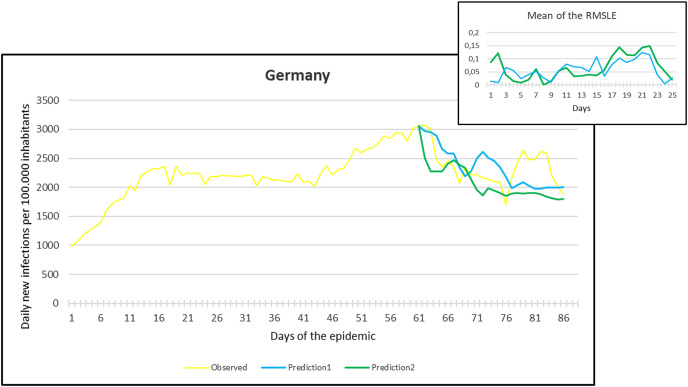
Fig. 8.

Observation and predictions for Germany During the Second Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

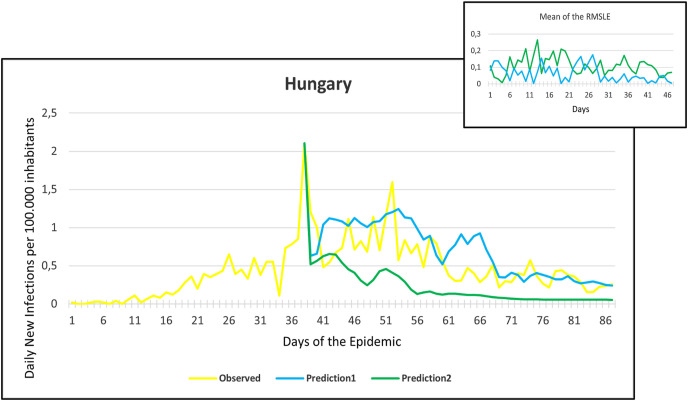
Fig. 9.

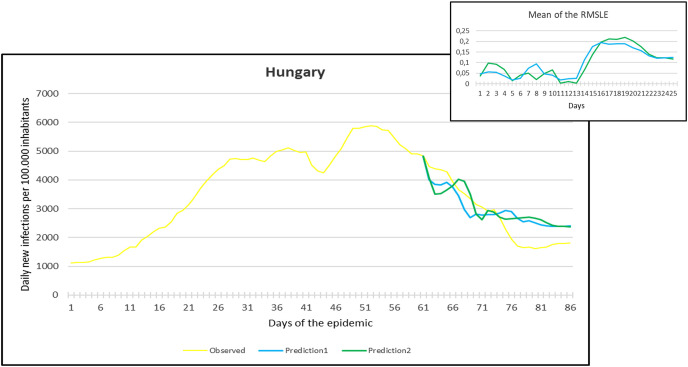
Observation and predictions for Hungary During the First Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

Fig. 10.

Observation and predictions for Hungary During the Second Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

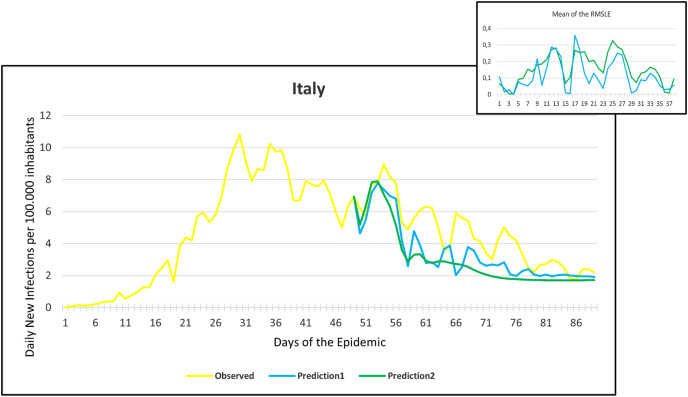
Fig. 11.

Observation and predictions for Italy During the First Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

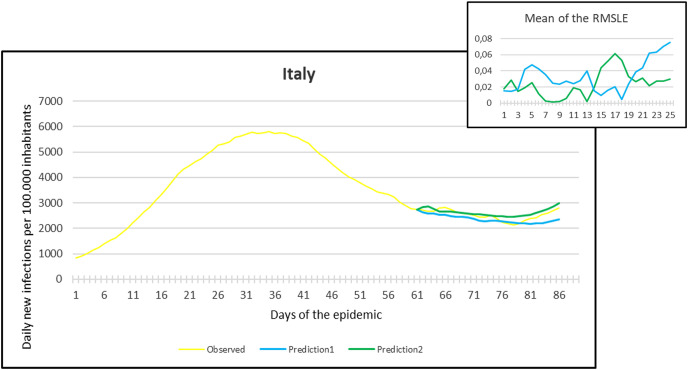
Fig. 12.

Observation and predictions for Italy During the Second Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

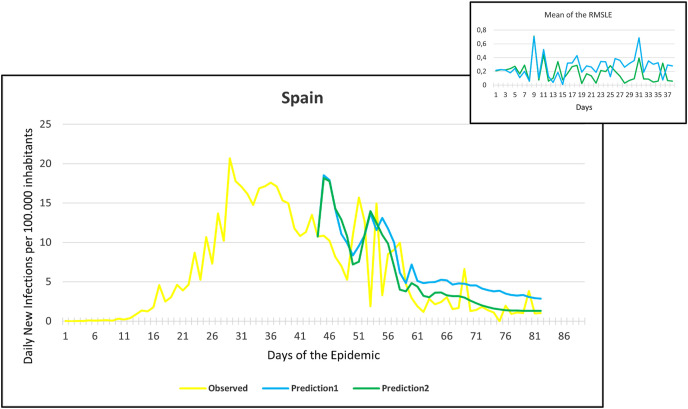
Fig. 13.

Observation and predictions for Spain During the First Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

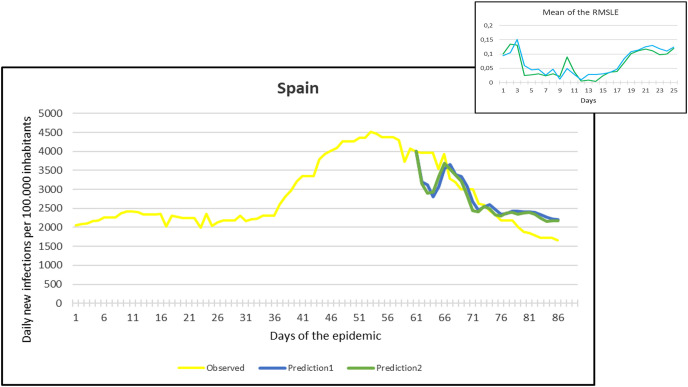
Fig. 14.

Observation and predictions for Spain During the Second Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

Fig. 15.

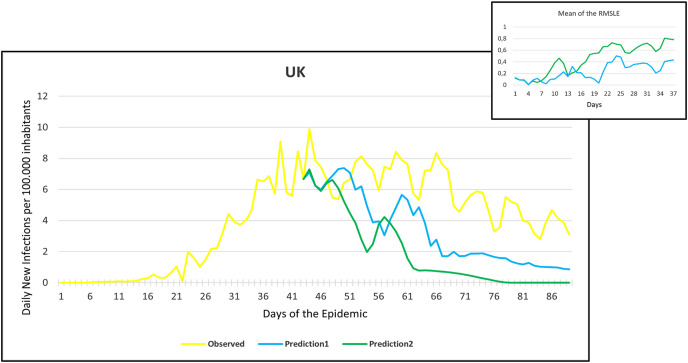
Observation and predictions for the United Kingdom (UK) During the First Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

Fig. 16.

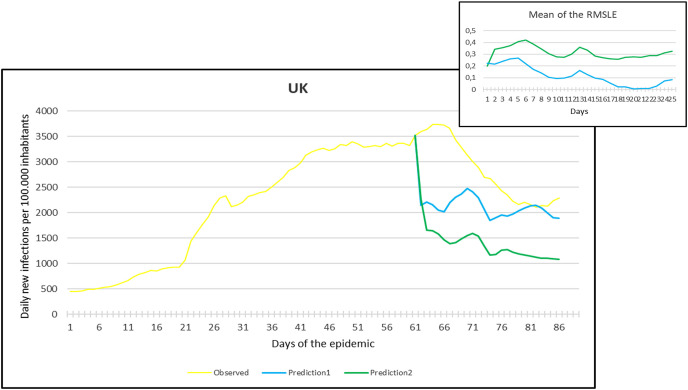
Observation and predictions for the United Kingdom (UK) During the Second Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

Fig. 17.

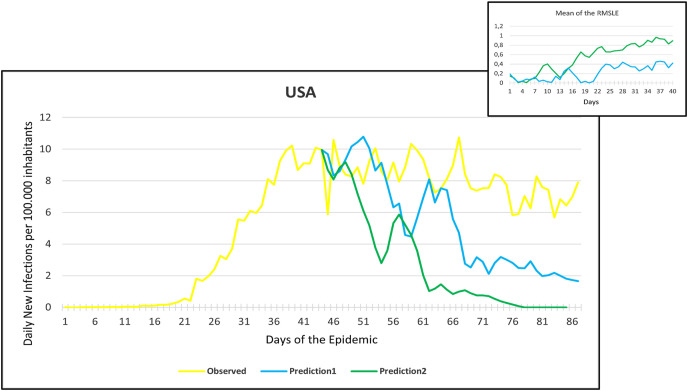
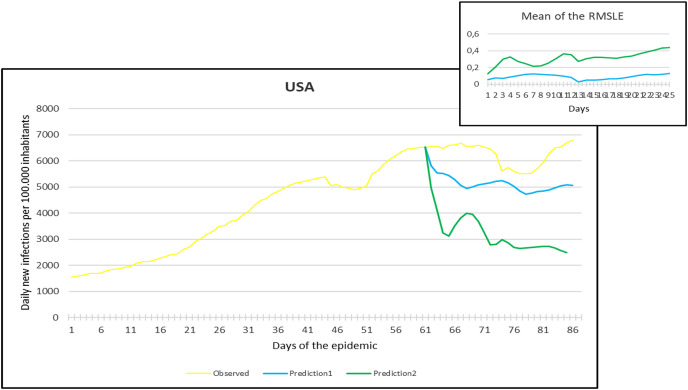
Observation and predictions for the United States of America (USA) During the First Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

Fig. 18.

Observation and predictions for the United States of America (USA) During the Second Pandemic Wave. The small graph in the upper right corner shows the daily error values (RMSLE) calculated for the predictions.

For each main graph, the small graph in the upper right corner contains the daily error values calculated for the predictions. The more accurate the prediction, the smaller the RMSLE error. It should be noted that if the error function is parallel to the x-axis, it means that the trend of the prediction is the same as the real trend, only at a lower or higher scale. Also, total Root Mean Square Error (RMSE), Root Mean Squared Logarithmic Errors (RMSLE), and the Mean Absolute Percentage Error (MAPE) by country are shown in Table 2, Table 3 .

Table 2.

Total Root Mean Square Error (RMSE), Root Mean Squared Logarithmic Errors (RMSLE), and the Mean Absolute Percentage Error (MAPE) for the first wave.

Country	RMSE of Prediction 1	RMSE of Prediction 2	Mean of RMSLE of Prediction 1	Mean of RMSLE of Prediction 2	MAPE of Prediction 1	MAPE of Prediction 2
Hungary	0.31	0.42	0.06	0.107	51.9	66.5
UK	3.12	4.56	0.234	0.455	43.35	65.75
Italy	1.56	1.83	0.114	0.155	20.89	28.5
Spain	4.23	3.96	0.266	0.181	137.41	74.65
Germany	1.51	1.49	0.147	0.108	94.18	52.39
France	8.34	5.54	0.513	0.307	585.07	189.7
USA	3.48	5.78	0.216	0.528	35.52	63.86

Table 3.

Total Root Mean Square Error (RMSE), Root Mean Squared Logarithmic Errors (RMSLE), and the Mean Absolute Percentage Error (MAPE) for the second wave.

Country	RMSE of Prediction 1	RMSE of Prediction 2	Mean of RMSLE of Prediction 1	Mean of RMSLE of Prediction 2	MAPE of Prediction 1	MAPE of Prediction 2
Hungary	597.47	640.46	0.097	0.099	24.94	25.62
UK	897.02	1511.89	0.117	0.311	22.34	50.87
Italy	216.64	162	0.033	0.024	7.24	5.65
Spain	488.98	467.48	0.07	0.064	17.05	15.24
Germany	349.79	409.15	0.057	0.064	13.07	13.45
France	698.1	621.62	0.094	0.081	23.18	19.32
USA	1216.21	3188.18	0.088	0.308	18.13	50.11

4. Discussion

The COVID-19 pandemic has impacted most life sectors including healthcare services provision, economy, politics, education, and social life [[26], [27], [28], [29]]. Additionally, the pandemic sheds the light on challenges of countries’ preparedness and crisis management [30]. Consequently, this global crisis has opened avenues for more effective and efficient application of AI in various aspects of fighting and tackling infectious diseases, which will help various authorities for better preparedness to meet the predicted repercussions of the disease spread, based on AI models. At the early stage of the COVID-19 outbreak when little data were available regarding the nature and transmissibility of SARS-CoV-2, modeling studies have attempted to predict the epidemic outcomes using the Susceptible-Exposed-Infectious-Recovered (SEIR) model, based on data from Wuhan, China; the starting point of the outbreak [31]. Besides, forecasting and predicting the COVID-19 trajectories was not the only application of AI during the current pandemic. AI has been adopted in contact tracing, tracking public health behaviors, and currently in COVID-19 case detection and vaccination [[32], [33], [34]]. Moreover, various AI-based approaches have been reported in the literature and were used to forecast the COVID-19 outcomes. For example, the adaptive neuro-fuzzy inference system hybrid model (ANFIS) that was used to predict the confirmed cases in China [35], and the Modified Auto-Encoder for Modeling Time Series that was proposed to model the transmission dynamics of the COVID-19 and evaluating the interventions [36].

Since March 2020, we have had the opportunity in our present study to use the declared numbers of daily new cases of COVID-19 to predict our models and to compare the predicted trajectories with the observed data. Our proposed model could be considered for describing the curve in most of the situations similar to that at the beginning of the pandemic (scarce knowledge on the virus, limited ability to track cases, molecular tests available but with low rates of processability, strict lockdown as a major countermeasure). To better assess the applicability of our models in further pandemic stages, forecasting the trajectories of new cases of COVID-19 were reported for six countries during the first pandemic wave and second pandemic wave as well. During the first pandemic wave, we can notice in the models that Prediction 1 is more accurate for some countries (Hungary, Italy, UK, USA), while Prediction 2 is more accurate for others (France, Germany, Spain). In countries that imposed strict measures (e.g., strict lockdown), for example, France, Hungary, Italy, and Spain, the predicted models and observed data were closely similar with better accuracy, however, this was not the case in the UK and the USA. The reason behind this could be linked to the fact that the learning dataset was based mainly on data from Hubei province where a strict total lockdown was imposed there, unlike the UK and the USA. Besides. this is likely because the countermeasures differed from those applied in Wuhan and then Europe, and because at the very beginning, tests were not available (or were too expensive). This corroborates the hypothesis that our proposed model works better in specific conditions/contexts.

On the other hand, projections of the second pandemic waves using prediction 1 and prediction 2 models in France, Hungary, Italy, and Spain revealed closely similar trends of both prediction models. Nevertheless, the prediction models seem to be not working well with UK and USA data. This could be caused by the same reasons explained above during the first pandemic wave or might be influenced by the emergence of the new variants (mutations) of the virus [10].

The findings of our study underscore that the COVID-19 pandemic is a propagated source outbreak, therefore repeated peaks on the epidemic curve (rise of the daily number of newly diagnosed infections) are to be anticipated. Predictions that were made using AI-based RNNs further implicate that albeit the majority of investigated countries are near or over the peak of the curve, they should prepare for a series of successively high peaks in the near future, until all susceptible people will be infected by the SARS-CoV-2, or effective preventive (e.g., vaccination) or treatment options will become available and utilized effectively. These scenarios are similar to other known propagated source epidemics, e.g., SARS and measles [37].

Albeit suppression and mitigation measures can reduce the incidence of infection, COVID-19 disease, given its relatively high transmissibility reflected by average R0 values of 3.28, will continue to spread, most likely [38]. Accordingly, public health measures must be implemented as the incubation period of the virus may be long (1–14 days, but there are some opinions, that this can be 21 days), during which time asymptomatic or pre-symptomatic spreading may ensue. Moreover, currently, it is uncertain whether those who were diagnosed with COVID-19 infection will acquire sufficient immunity or not [5]. Finally, data from countries with warm climates suggest that summer is unlikely to stop the pandemic, as the virus was already spreading in Australia and South Africa as well [7,9]. This is why the recurrence of another peak is very likely, and the end of the pandemic cannot be accurately predicted at this time.

Nevertheless, recent publications showed that the earlier the mitigation attempts are in place (e.g., border closure, closing schools, the lockdown of the country, curfew), the more effective is the reduction of the spread of the epidemic [9]. In fact, analyzing the effects of a suppression strategy concerning the COVID-19, it was shown that early implementation of suppression at 0.2 deaths per 100 000 population per week could save 30.7 million lives compared to late implementation of these measures at 1.6 deaths per 100 000 population per week [39]. This seems to be the case in the countries, which had prior knowledge regarding coronavirus infections (e.g., China, Singapore, Hong Kong), as they were more prepared to implement public health measures, and had more equipment as well as health care personnel in place to mitigate the spread of infections. Those countries, that failed to implement efficient and strict mitigation policies in a timely manner, were facing difficulty in controlling the spread of the disease, as is the case of Italy, the UK and the USA [38]. There are some new research data denoting that the lockdown measures are not as effective as the vaccination of the population, but these need more investigations and time to establish [40].

To the best of our knowledge, our study is among the scarce literature that modeled the predicted evolution of the newly diagnosed infections using AI-based Recurrent Neural Networks, during the early period of the first pandemic wave. Most studies to the date of conducting our study on the first wave expected a single peak of the epidemic curve, but some fear the emergence of future peaks when mitigation-suppression measures will be discontinued. According to our model, this can even happen, if strict measures are sustained.

Nevertheless, the are some limitations to our study. As the nature of SARS-COV-2 is relatively unknown or dynamic, and it is prone to mutations, the prediction of the spread of the pandemic is not an easy mission. Factors that influenced the reported new cases per day, for example, the efficiency of reporting, the different quality and timing of public health measures, country-specific age-pyramid, and chronic disease burden of the population were not included in our training data set due to lack of reliable data. We did not investigate the number of deaths and recoveries, as we found no reliable data at that time (during early stages of the pandemic). Similarly, the data regarding diagnostic tests performed per country, or death rates were omitted, given they are highly influenced by the countries’ economic wellbeing, health care systems, facilities and capacities, and other factors [41,42]. There are lots of unforeseen uncertainties and coincidences which could not be implemented in our model, for example, there were days when a large number of people have been diagnosed with COVID-19 on one day (for example in care homes in France or Hungary) that caused a large increase in the number of the daily new cases [38]. The effect of vaccination against COVID-19 seems to be ground-breaking, but this has to be proven for a longer period of time, as the vaccine rollouts have been only started at the end of 2020 [40,43].

5. Conclusion

The approach we have proposed provides a much more realistic prediction over a longer period. By optimizing classical recurrent neural network models, adding extra features, and combining transfer learning with a complex architecture of interconnected subnetworks, we can predict the entire epidemic curve of a given wave of an epidemic with good approximation accuracy based on a few weeks of data from the outbreak.

However, the emergence of different viral mutations also changes the behavior of the epidemic curve, for which the presented neural network model is not fully prepared yet. This is because the behavior of the training dataset strongly influences the prediction behavior. Our plans include improving this shortcoming of our model. Since the parameters of the mathematical models describing epidemic spread are easily updatable, we can use different mathematical approaches (e.g., SEIR) to simulate the epidemic spread process by considering the occurrence of multiple mutations. The outputs of these simulations are then used as a training data set to further develop the neural network model. The validation process will be based on the effects of currently available COVID-19 virus variants (e.g., the British or the Indian mutations). Thus, the overall future goal is to develop a much more flexible prediction model. The influence of this global epidemic has dug deep into the day-to-day conduct of everyone, with unforeseen challenges still pending for governments and policymakers. Starting from this, everyone, especially decision-makers must be aware, that the current situation might be just the beginning, and even if strict public health measures are executed and sustained, future peaks of infections are possible. The findings of our study underscore that the COVID-19 pandemic is a propagated source epidemic, therefore repeated peaks of the rise of the daily number of newly diagnosed infections are to be anticipated. In countries where strict control measures were imposed, the predicted models were closely similar to the observed data. The AI-based predictions might be useful tools and can be recalculated according to the newly observed data to get a more precise forecast of the pandemic, taking into account the new variants of the virus and the effect of the available vaccination possibilities. AI-based predictions, which include the wider knowledge about the virus and the prevention, are expected to provide public health practitioners and decision-makers with sufficient data that would be useful in improving countries’ preparedness to the next stage of a pandemic.

Author contributions

Conceptualization, LRK, TB, JZ, AH; methodology, the methodology was discussed by all co-authors; Data curation: AH, ABA, TB, AT, IV led the data curation and formal analysis; TB, ABA, and GJS made the data extraction and updating. The AI-based analysis and validation were made by AT, TB, IV, AH. Visualizations were made by AT, TB, IV, GJS, AH, ABA, and LRK. Writing—original draft preparation, all authors; Writing—review and editing, all authors; funding acquisition, JZ, and AH. The literature search was done by LRK, ABA, AH, SH, GJS, SG, JZ, RG. The interpretation and review of the literature, methods, results were made in close collaboration by all co-authors. All authors have read and agreed to the submitted version of the manuscript.

Funding

This study was supported by the European Union, co-financed by the European Social Fund and European Regional Development Fund [Grant No. EFOP-3.6.1-16-2016-00022 Debrecen Venture Catapult Program (providing support for SH, LRK), by the European Union [EFOP-3.6.2-16-2017-00009 Establishing Thematic Scientific and Cooperation Network for Clinical Research (providing support for RG), by the Janos Bolyai Research Fellowship of the Hungarian Academy of Sciences (providing support for JZ), by the Hungarian Brain Research Program 2.0 under grant number 2017–1.2.1-NKP-2017-00002 and the ED_18-1-2019-0028 (providing support for LRK, TB, AT). The research was also supported by the UNKP-19-3-I. New National Excellence Program of the Ministry for Innovation and Technology (providing support for AT). The research was supported in part by the project EFOP-3.6.2-16-2017-00015 supported by the European Union, co-financed by the European Social Fund. This work was also supported in part by the project EFOP-3.6.3-VEKOP-16-2017-00002, supported by the European Union, co-financed by the European Social Fund (providing support for IV). The funders had no role in the writing of the manuscript or the decision to submit it for publication, no involvement in data collection, analysis, or interpretation; trial design; patient recruitment; or any aspect pertinent to the study.

Institutional review board statement

Not Applicable.

Informed consent statement

Not Applicable.

Data availability statement

All data sources are publicly available and were described and cited in the methods section.

Consent for publication

Not Applicable.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.