Abstract
Background and Objective
The COVID-19 pandemic results in an intense flow of patients to hospitals especially to the intensive care units (ICUs) to be treated. The ICUs will therefore be confronted with a massive influx of patients (e.g. Spain and Italy). However, if the number of patients is higher than the resources available in ICUs, rationing decisions such as determining and evaluating the criteria for ICU admission becomes essential. In this case, the decision of which patients will be admitted to the ICUs may put significant pressure on healthcare personnel. The goal of this paper is to determine the criteria to be used in the decision of admission of COVID-19 patients to the ICUs.
Methods
A three-step methodology is applied. In the first step, the evaluation criteria are determined, and then the criteria are prioritized using a fuzzy analytical hierarchy process (AHP) in an uncertain and multiple-criteria environment choice. Finally, COVID-19 patients are ranked using the Multi-Objective Optimization Method by Ratio Analysis to find out which patient is more urgent.
Results
According to experts’ evaluation of ICU admission criteria, “increment of >2 in SOFA score” seems the most dominant factor among others. The proposed methodology is tested on 10 anonymous COVID-19 positive patients being treated in a public hospital and the ICU admission results are discussed.
Conclusions
Obtained priorities and ranking is in line with the hospitals’ behavior that potentially depicts the usefulness and validity of the proposed approach.
Keywords: COVID-19, Evaluation, Fuzzy AHP, Intensive care unit admission, MOORA
1. Introduction
The virus disease called COVID-19, which emerged in China in December 2019, was announced by the WHO as a pandemic in January 2020. In the first week of March 2020, more than 400,000 cases have been confirmed globally, in 130 countries, and by January 29, 2021, the confirmed cases had risen a little above 100,819,363 million in 250 countries/regions, with over 2,176,159 deaths of the world [59]. It is also known that the infection is not severe for all patients and may even progress without symptoms for someone who has come into contact with COVID-19. While nearly half of the people infected with COVID-19 develop symptoms that are not serious or may be overlooked, the main symptoms in the other half of patients are fever, fatigue, dry cough, myalgia (muscle pain) and dyspnea [61]. The disease can be severe and mortal in people with advanced age and comorbid disease. More fatality rates have been shown in men. Fatality rate varies around 2-3% worldwide [5]. As the age increases, the rate of fatality increases. In the event that there are diseases requiring urgent or elective treatments in these individuals or in cases of high suspicion, there has been no consensus, despite various reports from various health authorities, about the treatment at home or in the hospital or what treatment methods should be applied.
Since the beginning of the pandemic, a large number of academics have produced significant papers and contributions to struggle with COVID-19. Although the proposed study focuses on the decisions at operational level, the most of studies relevant with COVID-19 has concentrated on strategic level decisions such as spreading models or governments’ policies. For instance, Giordano et al. [21] proposed a new model that predicts the course of the epidemic to help plan an effective control strategy for Italy. Their findings provide policymakers with a tool to assess the consequences of possible strategies, including lockdown and social distancing, as well as testing and contact tracing. To mitigate the COVID-19 outbreak, Carli et al. [13] proposed an optimal control approach that supports governments in defining the most effective strategies to be adopted during post-lockdown mitigation phases in a multi-region scenario. Then, Pare et al. [43] presented a variety of mathematical models that have been proposed to capture the dynamic behavior of epidemic processes and to estimate the spreading parameters of the virus. For an excellent review of COVID-19 forecasting and SIR models, the reader is referred to Rahimi et al. [47].
On the other hand, at the beginning of 2021, the number of countries struggling with the COVID-19 pandemic rose to over 250. The number of cases is increasing rapidly in many countries. One of the most important needs in this period in which the severity of the epidemic increased is the number of beds and ventilators (respirators) in ICUs. However, many countries are worried about the lack of health infrastructure in the face of the rapidly increasing number of cases [58]. While governments apply various protection measures in the process, health units are working to prevent the tsunami caused by a large number of infected individuals to be treated [46]. For instance, Spain and Italy have been hit very hard with tremendous documented cases and deaths [50]. Especially in Italy, critical resources such as protective equipment, ventilators, and even medical staff are becoming deficient. Doctors are being forced to make a choice of whom to priorities caring for [51]. According to the paper of Emanuel et al. [20], the regular approach of treating people on a “first-come, first-served” basis should not apply during these times. They suggest that prioritizing some indicators related with age, respiratory and cardiac system should be a better approach to consider the patients.
While the COVID-19 pandemic, which affects the whole world, caused a noticeable slowdown or even almost complete halt in all businesses and industry, the necessity of overloading the health system and using the health-related resources and health personnel effectively are revealed. It is necessary to act immediately and develop systematical methodologies in order to maintain healthcare system and fight with the current pandemic by protecting valuable and limited resources and the healthcare personnel. In this study, an approach based on multi-criteria decision making (MCDM) is proposed, the COVID-19 suspect patient who comes to the health center/hospital can be evaluated according to the available data to determine/prioritize the condition of the patient and decide which health services should be taken.
This kind of decision problem with conflicting criteria linked to human life should be solved with a proper methodology. In addition the uncertainty and vagueness of the experts’ (doctors, health staff and etc.) opinion is the prominent characteristic of the problem [18]. Therefore, a proper solution methodology must be used considering the uncertain environment. To overcome the aforementioned issues, the applied methodology in this paper includes three main parts. In the first part, the necessary criteria that are considered for ICU admission are determined. Then the criteria are grouped according to their relations such as respiratory-related or cardiovascular-related criteria. It is an expected situation that all the criteria do not have the same priority. For instance, vasopressor need may be more important or urgent than arrhythmia problem of a patient for an ICU admission. For this reason, the criteria weights are determined using F-AHP in the second part. Lastly, the next question is which COVID-19 positive patient will use ICU first in the emergency or limited resource situation. To answer that question, MOORA approach considering the criteria weights is applied to rank the patients who need ICU treatment in the last part.
As of the date of this paper, there is no study applying F-AHP and MOORA approaches to determine/prioritize the condition of the patients for COVID-19 to direct to health services, but there are other studies searching economic impacts of the pandemic on China and the World [4], using behavioral and social science to assist COVID-19 pandemic response [57], food supply chains during the COVID-19 pandemic [29], etc. The readers can easily find various COVID-19 papers related with different subjects from different perspectives. According to the authors’ best knowledge, this paper is the first study based on systematic and modern MCDM techniques to determine criteria and prioritize the condition of the patients for COVID-19 to direct to health services.
The remainder of the paper is organized as follows. The proposed methodology based on F-AHP and MOORA is described in Section 2. The prioritization of the criteria and evaluation of COVID-19 positive patients is given as a case study in Section 3. Discussion of the paper focusing on the relevant literature and conclusion with potential research directions are given in Section 4.
2. Methodology
This section first briefly describes the two proposed methodologies, namely F-AHP and MOORA and then the proposed integrated approach with the stages of the approach and steps to evaluate COVID-19 patients for ICU admission.
2.1. The fuzzy AHP method
The fuzzy logic theory was firstly presented by Zadeh [60]. In classical set theory, an object is either the object of the set or not. An element cannot partially belong to a set. Fuzzy set theory performs graded data modeling using linguistic variables such as low, frequent, medium, low, high and many. To distinguish and solve uncertainty and imprecise real-life issues, fuzzy set would be a valuable technique.
Membership functions characterize the fuzzy logic sets. The membership function of the fuzzy set A, represented by , takes values in the range [0, 1]. means that the number x is doubtless the element of the set, and means that the number x is not the element of the set. Hsieh et al. [30] demonstrated that fuzzy numbers are a fuzzy subset of real numbers, representing the extension of the view of the dependence interval. Triangular fuzzy numbers (TFNs) are a special class of fuzzy numbers. In TFNs expressed by (l/m, m/u) or (l, m, u), l and u stand for the lower and upper limits, respectively, and m for the modarate value. Triangular type membership function is defined in Eq. (1) [38]. The operational laws are used to calculate with TFNs [30].
| (1) |
AHP is one of the methods often used in MCDM. AHP is a mathematical approach that allows a combination of qualitative and quantitative variables to be used in decision making, giving priority to a group or individual. However, the method is weak, especially in the case of uncertain pairwise comparisons are needed [31]. In addition, the AHP method may not fully reflect people's thoughts, even if it contains expert knowledge. The F-AHP method has been introduced as a means of reducing these shortcomings. The method has been applied to a variety of problems, including healthcare service quality [12], renewal of healthcare technologies [17], development of hospital beds [48], and classification of diabetes drugs [42].
The process for determining the priorities of the assessment criteria with F-AHP can be summed up briefly as follows [53]:
Step1: Construct the pairwise comparison matrix.
Pairwise comparison matrices are created between all criteria in the hierarchical structure. Assigned linguistic terms to the pairwise comparisons by demanding which the more important of each two criteria are as in Eq. (2).
| (2) |
where measure denotes, let be (1,1,1) when i equal j (i.e i=j); if criterion i has one of the above linguistic variables assigned to it when compared with criterion j, then j has the reciprocal value when compared with i. If criterion i has one of the above linguistic variables assigned to it when compared with criterion j, then j has the reciprocal value when compared with i. If criterion i is relatively important to criterion j and then that criterion j is relatively important to criterion i. If measure that criterion i is relatively important to criterion j and then measure that criterion j is relatively important to criterion i. The linguistic comparison terms and their equivalent TFNs used in this study are given in Table 1 .
Step 2: Compute the fuzzy geometric mean for each criterion.
Table 1.
Linguistic variables for importance of criteria [23].
| Fuzzy number | Linguistic | Scale of triangular fuzzy number | Scale of triangular reciprocal fuzzy number |
|---|---|---|---|
| 1 | Equal | (1, 1, 1) | (1, 1, 1) |
| 2 | Weak advantage | (1, 2, 3) | (1/3, 1/2, 1) |
| 3 | Not bad | (2, 3, 4) | (1/4, 1/3, 1/2) |
| 4 | Preferable | (3, 4, 5) | (1/5, 1/4, 1/3) |
| 5 | Good | (4, 5, 6) | (1/6, 1/5, 1/4) |
| 6 | Fairly good | (5, 6, 7) | (1/7, 1/6, 1/5) |
| 7 | Very good | (6, 7, 8) | (1/8, 1/7, 1/6) |
| 8 | Absolute | (7, 8, 9) | (1/9, 1/8, 1/7) |
| 9 | Perfect | (8, 9, 10) | (1/10, 1/9, 1/8) |
The use of the geometric mean technique to define the fuzzy geometric mean and the fuzzy weighting of each criterion is described by Buckley [11]. The geometric mean of each row of is calculated as in Eq. (3).
| (3) |
where is the fuzzy value of criterion i compared to criterion n; thus, is the geometric mean of the fuzzy comparison values of criterion i for each criterion.
Step 3: Compute the fuzzy weight for each criterion.
The fuzzy weight of the ith criterion is calculated as in Eq. (4)
| (4) |
where is the fuzzy weighting of the ith criterion and can be indicated by a TFN, , with lwi, mwi and uwi representing the lower, middle and upper values, respectively, of the fuzzy weighting of the ith criterion.
Step 4: Convert fuzzy weight to crisp value.
The result of the fuzzy synthetic decision reached for each alternative is a fuzzy number. Defuzzification is a mathematical process performed to convert fuzzy output into a crisp value. The center of area (COA) method is a simple and practical method and there is no need to introduce the preferences of any evaluators [53]. The best non-fuzzy performance (BNP) value of the fuzzy number, , which is equal to (lwi,mwi,uwi), can be determined as in Eq. (5).
| (5) |
Step 5: The crisp weights of criteria are normalized.
Criterion weights are calculated by normalizing the BNP values to total “1”.
2.2. The MOORA method
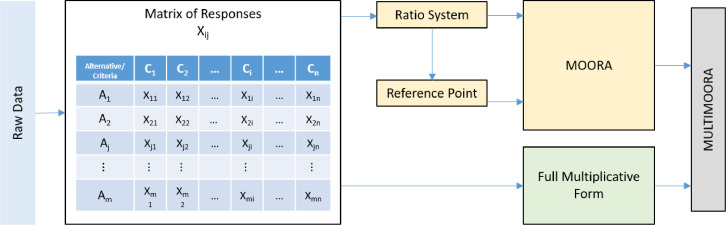
MOORA (Multi Objective Optimization on the basis of Ratio Analysis) method is a multi-purpose optimization method developed by Brauers and Zavadskas [6]. The MOORA method is one of the most frequently used multi-objective optimization methods in decision making problems. The method which is based on the grouping of different predictions is frequently preferred due to its easy operation steps and applicability at the solution of decision-making problems. The most important advantage of the MOORA method is that although the data used in the evaluation of alternatives according to the criteria are in different units, it effectively normalizes these units by using non-subjective non-directional values instead of subjective weighted normalization. The MOORA method is basically a method that is formed by using two different methods: MOORA-Ratio and MOORA-Reference Point methods together. The criteria must have equal weights for these methods which are explained in summarily below. In cases which the criteria do not have equal weights, the methods use the Eqs. (8) and (11) instead of Eqs. (7) and (9), respectively. In 2010, the full Multiplicative Form method is developed by Brauers and Zavadskas [7]. The MULTIMOORA method which is introduced to the literature by Brauers and Zavadskas in 2010 is not a new one. The method combines the results obtained from the MOORA method and the full Multiplicative Form method into a single ranking using the Rank Dominance method. The flow chart of these methods is shown in Fig. 1 . The methods are explained shortly below and the readers can easily find details in different papers ([7], [8], [10], [24]).
Fig. 1.
Diagram of MULTIMOORA [8].
2.2.1. Ratio system of MOORA
The Ratio System method requires initial decision matrix which gives the determined criteria and the performance values of alternatives according to the criteria. The matrix is explained in detail below.
j: 1, 2... m; m is the number of alternatives
i: 1, 2…n; n is the number of criteria
xij:Performance value of alternative j on criterion i
: A normalized number showing the response of alternative j on criterion i
: The total assessment of alternative j according to all criteria
The initial decision matrix is normalized and the total assessment of each alternative is determined by using Eq. (6) and (7), respectively. shows the ordinal ranking of the decision maker who build the matrix.
| (6) |
| (7) |
In some cases, different weights can be assigned to the criteria depending on the nature of the problem. In this case, the dimensionless number could be multiplied with an importance value as shown in the Eq. (8).
| (8) |
where si is the importance value/weight of the criterion.
2.2.2. The Reference Point Approach of MOORA
The MOORA Reference Point method is based on the normalized data obtained by the MOORA-Ratio Method. It firstly requires the determination of reference points (ri) for each criterion. If the goal is the maximization, the highest values; if the goal is minimization, the lowest values are determined as the reference point for each criterion. The alternatives’ distance to the reference point according to each criterion is calculated by using the Eq. (9).
| (9) |
The matrix is calculated using the "Min-Max Metric of Tchebycheff" formula in Eq. (10). The formula used for Tchebycheff's Min-Max metric operation is shown below.
| (10) |
Alternatives are sorted from low value to higher value. The alternative with the lowest value gets the 1st rank and the others are ranked from low value to the high value. Depending on the decision makers’ intend to give more importance to a criterion's response on an alternative, the Reference Point approach the formula would be as Eq. (11).
| (11) |
2.2.3. The full multiplicative form
The maximization data of each alternative is multiplied and divided by the multiplication of the data for minimization purposes. This method uses the following Eqs. (12) to (14). The alternative with the highest value of Uj is considered the most appropriate one.
| (12) |
| (13) |
| (14) |
j: 1, 2..., m; m is the number of alternatives
i: The number of criteria to be maximized
n − i: The number of criteria to be minimized
Uj: The utility of alternative j with criteria to be maximized and criteria to be minimized
2.2.4. The MULTIMOORA approach
The MULTIMOORA is not a stand-alone sorting method; it depends on MOORA methods and full multiplicative form and makes a final evaluation based on their dominance. The theory of dominance is based on propositions such as dominance, being dominated, transitivity, and equability. The researchers can easily find the details about the dominance theory at the different papers [9, 28].
2.3. Proposed approach
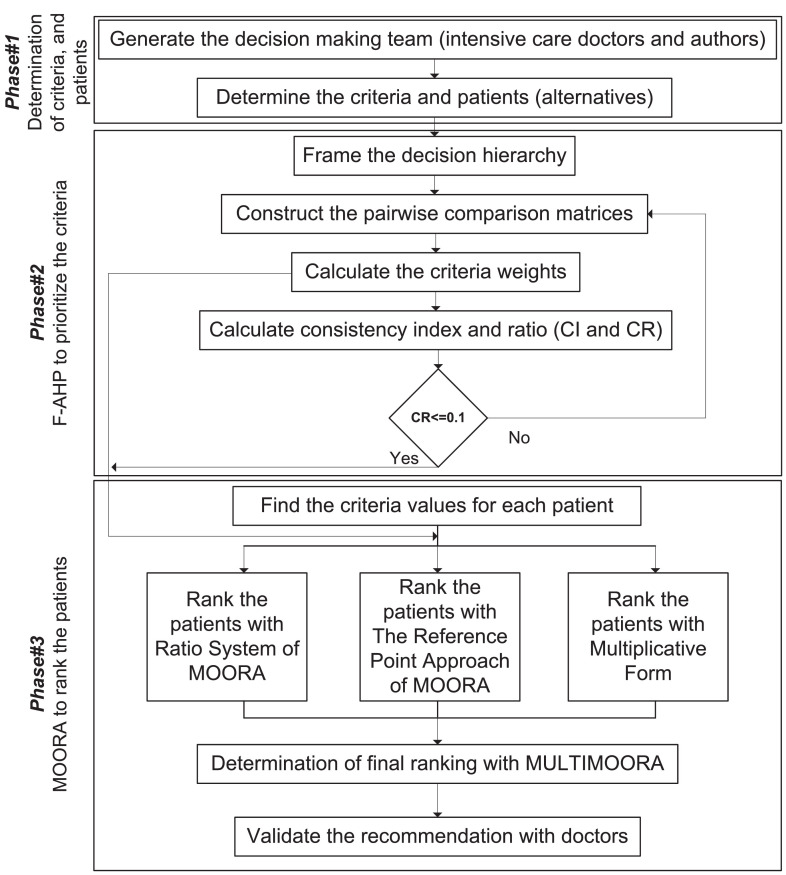
The integrated approach – composed of F-AHP and MOORA methods – for the COVID-19 patients evaluation problem consists of 3 basic stages: (1) Determination of criteria and constructing the hierarchy, (2) F-AHP computations, and (3) MOORA computations and recommendation. In the first stage, alternative COVID-19 patients who may need ICU treatment and the criteria which will be used in their evaluation are determined and the decision hierarchy is formed. This stage is supported by a group of doctors (including fourth author) from Gazi University Hospital and related literature to determine the criteria pool and the problem hierarchy. After the approval of decision hierarchy by the group, the first stage is terminated. In the second stage, criteria used in COVID-19 patients’ evaluation are weighted using F-AHP. In this phase, pairwise comparison matrices are formed to determine the criteria weights. The experts from decision making team make individual evaluations using the scale, provided in Section 3.1, to determine the values of the elements of pairwise comparison matrices to reflect the uncertainty in experts’ options. Computing the geometric mean of the values obtained from individual evaluations, a final pairwise comparison matrix on which there is a consensus is found. The weights of the criteria are calculated based on this final comparison matrix regarding to the consistency ratio. In the last step of this phase, calculated weights of the criteria are approved by decision making team. Patients’ priorities are found by using MOORA computations in the last stage. In the last step of this phase, the most suitable patients for ICU treatment are selected according to the ranking. Details of each stage are explained during the implementation section (next section). Schematic representation of the proposed integrated approach is presented in Fig. 2 .
Fig. 2.
Stepwise procedure of the applied methodology.
3. Results
In this section, the application process is described in detail. This section consists of three sub-sections parallel to the steps of the study.
3.1. Determining the criteria and presentation of data
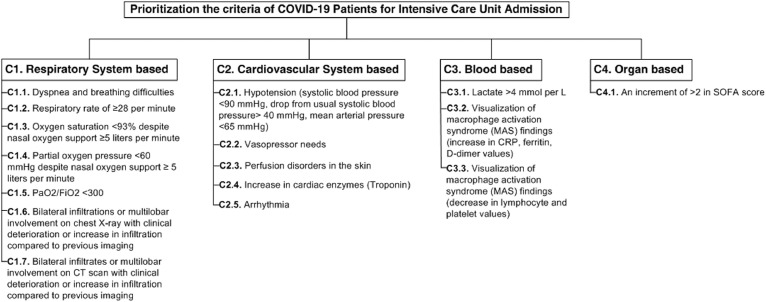
As mentioned in the beginning of study, the criteria are determined by the help of the doctors (one of them is fourth co-author) in Gazi University Hospital and related literature. The experts including doctors determined 16 different criteria to be considered during the ICU admission process. The decision making team consists of three doctors. As mentioned, one of them is the fourth co-author of this study. The second expert is a doctor at Anesthesiology and Reanimation department in Gazi University Hospital, and the last expert is a doctor working at Ankara City Hospital. Due to similarities of the criteria, 16 criteria are classified under four main criteria, namely respiratory system based criteria, cardiovascular system based criteria, blood based criteria and organ based criteria. For instance, vasopressor needs and arrhythmia situations are related with cardiovascular system of the patients. On the other hand, there is only one criterion (the SOFA score) that is related with organ. It must be noted that the considered 16 criteria are not only the criteria that evaluate the ICU admission for COVID-19 patients. Based on the literature and consulting to the doctors, the evaluation part is limited with 16 criteria. With a more accurate description of the COVID-19 in near future, the criteria may change. For instance, the age or the chance of being improved should be also considered. The hierarchy and brief explanations of the criteria are illustrated in Fig. 3 .
Fig. 3.
Considered criteria for ICU admission.
3.2. Prioritization the criteria
The first step of the applied methodology is determining the weights of criteria. By using the scale in Table 1, a pairwise comparison between the evaluation criteria is provided to each decision maker. The linguistic terms obtained after pairwise comparisons are transformed into TFNs (Table 2 ) using the scale given in Table 1.
Table 2.
Pairwise comparison matrix with TFNs for main criteria.
| Decision Maker | Main Criteria | C1 | C2 | C3 | C4 |
|---|---|---|---|---|---|
| DM1 | C1 | (1, 1, 1) | (2, 3, 4) | (2, 3, 4) | (1/5, 1/4, 1/3) |
| C2 | (1/4, 1/3, 1/2) | (1, 1, 1) | (1, 1, 1) | (1/6, 1/5, 1/4) | |
| C3 | (1/4, 1/3, 1/2) | (1, 1, 1) | (1, 1, 1) | (4, 5, 6) | |
| C4 | (3, 4, 5) | (4, 5, 6) | (1/6, 1/5, 1/4) | (1, 1, 1) | |
| DM2 | C1 | (1, 1, 1) | (2, 3, 4) | (2, 3, 4) | (1, 1, 1) |
| C2 | (1/4, 1/3, 1/2) | (1, 1, 1) | (2, 3, 4) | (1/4, 1/3, 1/2) | |
| C3 | (1/4, 1/3, 1/2) | (1/4, 1/3, 1/2) | (1, 1, 1) | (1/8, 1/7, 1/6) | |
| C4 | (1, 1, 1) | (2, 3, 4) | (6, 7, 8) | (1, 1, 1) | |
| DM3 | C1 | (1, 1, 1) | (1, 1, 1) | (1, 1, 1) | (1, 1, 1) |
| C2 | (1, 1, 1) | (1, 1, 1) | (2, 3, 4) | (1, 1, 1) | |
| C3 | (1, 1, 1) | (1/4, 1/3, 1/2) | (1, 1, 1) | (1/8, 1/7, 1/6) | |
| C4 | (1, 1, 1) | (1, 1, 1) | (6, 7, 8) | (1, 1, 1) |
It is necessary to apply the group decision-making process (GDM) to bring together group decisions. The GDM procedure can be carried out in two ways namely Aggregating Individual Judgments and Aggregating Individual Priorities (AIP) [19]. In this study, AIP was applied since each group member acted individually. In order to aggregate the individual decisions of the decision makers, the geometric mean method given in Eq. (3) proposed by Buckley [11] was applied (Table 3 ). For instance, :
, (1/2×1/2×1)1/3)=(0.397, 0.481, 0.630)
Table 3.
Synthetic pairwise comparison matrix for main criteria.
| Main Criteria | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| C1 | (1.000, 1.000, 1.000) | (1.587, 2.080, 2.520) | (1.587, 2.080, 2.520) | (1.000, 1.000, 1.000) |
| C2 | (0.397, 0.481, 0.630) | (1.000, 1.000, 1.000) | (1.587, 2.080, 2.520) | (0.347, 0.405, 0.500) |
| C3 | (0.397, 0.481, 0.630) | (0.397, 0.481, 0.630) | (1.000, 1.000, 1.000) | (0.138, 0.160, 0.191) |
| C4 | (1.000, 1.000, 1.000) | (2.000, 2.466, 2.884) | (5.241, 6.257, 7.268) | (1.000, 1.000, 1.000) |
After the pairwise comparison matrix is transformed into TFNs, firstly value is calculated by using Eq. (3) to calculate the fuzzy weights of criteria. For as example:
, (1 × 2.08 × 2.08 × 1)1/4, (1× 1× 1×1)
Similarly, the remaining values are calculated, there are:
(0.684, 0.798, 0.944), (0.384, 0.438, 0.525), (1.799, 1.982, 2.140)
Then, values are calculated using Eq. (4). For as example:
(1/(1.587 + 0.944 + 0.525 + 2.140),
Similarly, the remaining values are calculated, there are:
(0.132, 0.171, 0.229), (0.074, 0.094, 0.127), (0.346, 0.425, 0.519)
The COA defuzzification method is used to calculate BNP weights of criteria. For BNP 1 as example; BNP 1 = 0.242 + [(0.385 − 0.242) + (0.385 − 0.309)]/3 = 0.312. Similarly, the remaining BNP weights of criteria are calculated, there are:
BNP2 = 0.177, BNP 3 = 0.092, BNP 4 = 0.430
After the BNP values are calculated, the criterion values are normalized to a sum of 1. The steps described above apply to each sub-criteria group. These calculated weights are local weights. Then, the global weights of the criteria are calculated by multiplying each sub criterion by the weight of the main criterion to which it belongs (Table 4 ).
Table 4.
Main and sub-criteria weights.
| Main Criteria | Sub-Criteria | Local | Global |
|---|---|---|---|
| C.1 | 0.307 | ||
| C.1.1 | 0.146 | 0.045 | |
| C.1.2 | 0.129 | 0.040 | |
| C.1.3 | 0.195 | 0.060 | |
| C.1.4 | 0.190 | 0.058 | |
| C.1.5 | 0.113 | 0.035 | |
| C.1.6 | 0.113 | 0.035 | |
| C.1.7 | 0.113 | 0.035 | |
| C.2 | 0.174 | ||
| C.2.1 | 0.118 | 0.021 | |
| C.2.2 | 0.216 | 0.038 | |
| C.2.3 | 0.090 | 0.016 | |
| C.2.4 | 0.467 | 0.081 | |
| C.2.5 | 0.109 | 0.019 | |
| C.3 | 0.096 | ||
| C.3.1 | 0.333 | 0.032 | |
| C.3.2 | 0.333 | 0.032 | |
| C.3.3 | 0.333 | 0.032 | |
| C.4 | 0.423 | ||
| C.4.1 | 1.000 | 0.421 |
According to experts’ evaluation of ICU admission criteria, “an increment of >2 in SOFA score” seems the most dominant factor among others. The criterion of “increase in cardiac enzymes (Troponin)” takes second place, followed by the criterion of “oxygen saturation”. On the contrary, “perfusion disorders in the skin” has the weakest impact on the ICU admission.
3.3. Evaluation the patients
After the weight search is done, the next step is to calculate the MOORA to obtain the ranking of patients so that it is clear which one needs ICU more than others. To test the ranking part of the proposed methodology, 10 patients (alternatives) are considered. It must be noted that the data of 10 patients are anonymous and randomly mixed by the doctors. In MOORA approach, firstly decision matrix is formed as seen in Table 5 . In this table, data of the patients in terms of criteria are given. Four of the patients are male, six of them are female. The youngest patient is 52 years old; the oldest one is 86 years old. While the data for C1.1, C1.6, C1.7, C2.2, C2.3 and C2.5 are binary, rest of them has continuous/integer values. For the binary criteria, “+” means yes, “–” means no. For instance, patient#1 has dyspnea and breathing difficulties (C1.1) however he does not need vasopressors (C2.2). On the other hand, C2.1 represents the blood pressure including diastolic and systolic blood pressure values of the patients, respectively. Table 5 also shows the desired direction of each criterion. While C1.3, C1.4, C1.5, and C3.3 are desired to be maximized, the rest of the criteria are wanted to be minimized.
Table 5.
Data for performance evaluation of alternatives (patients).
| Desired direction | Min | Min | Max | Max | Max | Min | Min | Min | Min | Min | Min | Min | Min | Min | Max | Min | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Patients | Sex/Age | C1.1 | C1.2 | C1.3 | C1.4 | C1.5 | C1.6 | C1.7 | C2.1 | C2.2 | C2.3 | C2.4 | C2.5 | C3.1 | C3.2 | C3.3 | C4.1 |
| P1 | M/80 | + | 25 | 86 | 21´9 | 21/100 | + | + | 163/99 | – | – | 0.168 | – | 1.7 | 0.82 | 162 | 14 |
| P2 | F/72 | + | 22 | 80 | 78 | 100/78 | – | – | 100/56 | – | + | 0.097 | – | 1.1 | 1.86 | 259 | 10 |
| P3 | F/78 | + | 29 | 97 | 29´8 | 10/30 | – | – | 89/47 | + | – | 0.276 | – | 3.9 | 3.60 | 241 | 18 |
| P4 | F/86 | + | 33 | 68 | 70 | 100/68 | + | + | 66/31 | + | + | 24.700 | + | 17.0 | 35.20 | 32 | 24 |
| P5 | M/61 | + | 21 | 83 | 40´1 | 80/40 | + | + | 96/60 | + | + | 13.780 | – | 2.0 | 35.20 | 146 | 20 |
| P6 | F/52 | + | 25 | 81 | 34´9 | 6/34.9 | – | – | 117/70 | – | – | 0.097 | – | 2.3 | 1.73 | 369 | 12 |
| P7 | M/86 | + | 24 | 88 | 92 | 100/90 | + | + | 101/58 | + | + | 22.340 | – | 16.0 | 5.20 | 198 | 22 |
| P8 | M/82 | + | 22 | 100 | 98 | 100/98 | + | + | 137/44 | + | – | 0.097 | – | 0.8 | 1.16 | 291 | 16 |
| P9 | F/81 | + | 23 | 97 | 46 | 8/46 | – | – | 116/82 | – | – | 1.260 | – | 2.4 | 20.67 | 140 | 15 |
| P10 | F/52 | + | 29 | 92 | 54 | 100/54 | + | + | 124/79 | – | – | 0.090 | + | 1.3 | 6.10 | 368 | 10 |
Due to variety of the data structure in Table 5, all data are transformed into quantitative values. In this process, “+” and “–” values of binary criteria (C1.1, C1.6, C1.7, C2.2, C2.3 and C2.5) are assumed as 10 and 1, respectively. For the criterion of hypotension, three conditions are checked. These are (i) systolic blood pressure <90 mmHg, (ii) drop from usual systolic blood pressure >40 mmHg, and (iii) mean arterial pressure <65 mmHg) [14]. If all these conditions are satisfied, the patient's hypotension score is 3. The calculations of all patients’ C2.1 value are shown in Table 6 . The final values of all criteria are given in Table 7 .
Table 6.
Calculations of criterion C2.1.
| Patients | Systolica | Diastolicb | a < 90 mmHg | (a − b) > 40 mmHg | Final value of C2.1 | |||
|---|---|---|---|---|---|---|---|---|
| P1 | 163 | 99 | 0 | 64 | 1 | 120 | 0 | 0+1+0= 1 |
| P2 | 100 | 56 | 0 | 44 | 1 | 71 | 0 | 1 |
| P3 | 89 | 47 | 1 | 42 | 1 | 61 | 1 | 3 |
| P4 | 66 | 31 | 1 | 35 | 0 | 43 | 1 | 2 |
| P5 | 96 | 60 | 0 | 36 | 0 | 72 | 0 | 0 |
| P6 | 117 | 70 | 1 | 47 | 1 | 86 | 0 | 2 |
| P7 | 101 | 58 | 1 | 43 | 1 | 72 | 0 | 2 |
| P8 | 137 | 44 | 1 | 93 | 1 | 75 | 0 | 2 |
| P9 | 116 | 82 | 1 | 34 | 0 | 93 | 0 | 1 |
| P10 | 124 | 79 | 1 | 45 | 1 | 94 | 0 | 2 |
Table 7.
Quantitative values of criteria.
| Desired direction | Min | Min | Max | Max | Max | Min | Min | Min | Min | Min | Min | Min | Min | Min | Max | Min | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Patients | Sex/Age | C1.1 | C1.2 | C1.3 | C1.4 | C1.5 | C1.6 | C1.7 | C2.1 | C2.2 | C2.3 | C2.4 | C2.5 | C3.1 | C3.2 | C3.3 | C4.1 |
| P1 | M/80 | 10 | 25 | 86 | 21.9 | 0.21 | 10 | 10 | 1 | 1 | 1 | 0.168 | 1 | 1.7 | 0.82 | 162 | 14 |
| P2 | F/72 | 10 | 22 | 80 | 78.0 | 1.28 | 1 | 1 | 1 | 1 | 10 | 0.097 | 1 | 1.1 | 1.86 | 259 | 10 |
| P3 | F/78 | 10 | 29 | 97 | 29.8 | 0.33 | 1 | 1 | 3 | 10 | 1 | 0.276 | 1 | 3.9 | 3.60 | 241 | 18 |
| P4 | F/86 | 10 | 33 | 68 | 70.0 | 1.47 | 10 | 10 | 2 | 10 | 10 | 24.700 | 10 | 17.0 | 35.20 | 32 | 24 |
| P5 | M/61 | 10 | 21 | 83 | 40.1 | 2.00 | 10 | 10 | 0 | 10 | 10 | 13.780 | 1 | 2.0 | 35.20 | 146 | 20 |
| P6 | F/52 | 10 | 25 | 81 | 34.9 | 0.17 | 1 | 1 | 2 | 1 | 1 | 0.097 | 1 | 2.3 | 1.73 | 369 | 12 |
| P7 | M/86 | 10 | 24 | 88 | 92.0 | 1.11 | 10 | 10 | 2 | 10 | 10 | 22.340 | 1 | 16.0 | 5.20 | 198 | 22 |
| P8 | M/82 | 10 | 22 | 100 | 98.0 | 1.02 | 10 | 10 | 2 | 10 | 1 | 0.097 | 1 | 0.8 | 1.16 | 291 | 16 |
| P9 | F/81 | 10 | 23 | 97 | 46.0 | 0.17 | 1 | 1 | 1 | 1 | 1 | 1.260 | 1 | 2.4 | 20.67 | 140 | 15 |
| P10 | F/52 | 10 | 29 | 92 | 54.0 | 1.85 | 10 | 10 | 2 | 1 | 1 | 0.090 | 10 | 1.3 | 6.10 | 368 | 10 |
After forming the decision matrix, it is normalized by using Eq. (6) as shown in Table 8 . Then, the weighted normalized decision matrix obtained by multiplying the weights with Table 8 is shown in Table 9 .
Table 8.
Normalized matrix.
| Min | Min | Max | Max | Max | Min | Min | Min | Min | Min | Min | Min | Min | Min | Max | Min | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Patients | C1.1 | C1.2 | C1.3 | C1.4 | C1.5 | C1.6 | C1.7 | C2.1 | C2.2 | C2.3 | C2.4 | C2.5 | C3.1 | C3.2 | C3.3 | C4.1 |
| P1 | 0.316 | 0.309 | 0.310 | 0.112 | 0.057 | 0.407 | 0.407 | 0.177 | 0.044 | 0.050 | 0.005 | 0.069 | 0.070 | 0.015 | 0.211 | 0.264 |
| P2 | 0.316 | 0.272 | 0.288 | 0.399 | 0.346 | 0.041 | 0.041 | 0.177 | 0.044 | 0.496 | 0.003 | 0.069 | 0.046 | 0.034 | 0.338 | 0.189 |
| P3 | 0.316 | 0.359 | 0.350 | 0.152 | 0.089 | 0.041 | 0.041 | 0.530 | 0.445 | 0.050 | 0.008 | 0.069 | 0.162 | 0.066 | 0.314 | 0.340 |
| P4 | 0.316 | 0.408 | 0.245 | 0.358 | 0.397 | 0.407 | 0.407 | 0.354 | 0.445 | 0.496 | 0.685 | 0.693 | 0.705 | 0.644 | 0.042 | 0.453 |
| P5 | 0.316 | 0.260 | 0.299 | 0.205 | 0.540 | 0.407 | 0.407 | 0.000 | 0.445 | 0.496 | 0.382 | 0.069 | 0.083 | 0.644 | 0.190 | 0.378 |
| P6 | 0.316 | 0.309 | 0.292 | 0.178 | 0.046 | 0.041 | 0.041 | 0.354 | 0.044 | 0.050 | 0.003 | 0.069 | 0.095 | 0.032 | 0.481 | 0.227 |
| P7 | 0.316 | 0.297 | 0.317 | 0.470 | 0.300 | 0.407 | 0.407 | 0.354 | 0.445 | 0.496 | 0.619 | 0.069 | 0.663 | 0.095 | 0.258 | 0.415 |
| P8 | 0.316 | 0.272 | 0.361 | 0.501 | 0.276 | 0.407 | 0.407 | 0.354 | 0.445 | 0.050 | 0.003 | 0.069 | 0.033 | 0.021 | 0.379 | 0.302 |
| P9 | 0.316 | 0.285 | 0.350 | 0.235 | 0.046 | 0.041 | 0.041 | 0.177 | 0.044 | 0.050 | 0.035 | 0.069 | 0.100 | 0.378 | 0.182 | 0.283 |
| P10 | 0.316 | 0.359 | 0.332 | 0.276 | 0.500 | 0.407 | 0.407 | 0.354 | 0.044 | 0.050 | 0.002 | 0.693 | 0.054 | 0.112 | 0.480 | 0.189 |
| Reference P. | 0.316 | 0.260 | 0.361 | 0.501 | 0.540 | 0.041 | 0.041 | 0.000 | 0.044 | 0.050 | 0.002 | 0.069 | 0.033 | 0.015 | 0.481 | 0.189 |
Table 9.
Weighted normalized matrix.
| Weights | 0.045 | 0.04 | 0.06 | 0.058 | 0.035 | 0.035 | 0.035 | 0.021 | 0.038 | 0.016 | 0.081 | 0.019 | 0.032 | 0.032 | 0.032 | 0.421 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Patients | C1.1 | C1.2 | C1.3 | C1.4 | C1.5 | C1.6 | C1.7 | C2.1 | C2.2 | C2.3 | C2.4 | C2.5 | C3.1 | C3.2 | C3.3 | C4.1 |
| P1 | 0.000 | 0.002 | 0.003 | 0.023 | 0.017 | 0.013 | 0.013 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.009 | 0.032 |
| P2 | 0.000 | 0.000 | 0.004 | 0.006 | 0.007 | 0.000 | 0.000 | 0.004 | 0.000 | 0.007 | 0.000 | 0.000 | 0.000 | 0.001 | 0.005 | 0.000 |
| P3 | 0.000 | 0.004 | 0.001 | 0.020 | 0.016 | 0.000 | 0.000 | 0.011 | 0.015 | 0.000 | 0.000 | 0.000 | 0.004 | 0.002 | 0.005 | 0.064 |
| P4 | 0.000 | 0.006 | 0.007 | 0.008 | 0.005 | 0.013 | 0.013 | 0.007 | 0.015 | 0.007 | 0.055 | 0.012 | 0.021 | 0.020 | 0.014 | 0.111 |
| P5 | 0.000 | 0.000 | 0.004 | 0.017 | 0.000 | 0.013 | 0.013 | 0.000 | 0.015 | 0.007 | 0.031 | 0.000 | 0.002 | 0.020 | 0.009 | 0.079 |
| P6 | 0.000 | 0.002 | 0.004 | 0.019 | 0.017 | 0.000 | 0.000 | 0.007 | 0.000 | 0.000 | 0.000 | 0.000 | 0.002 | 0.001 | 0.000 | 0.016 |
| P7 | 0.000 | 0.001 | 0.003 | 0.002 | 0.008 | 0.013 | 0.013 | 0.007 | 0.015 | 0.007 | 0.050 | 0.000 | 0.020 | 0.003 | 0.007 | 0.095 |
| P8 | 0.000 | 0.000 | 0.000 | 0.000 | 0.009 | 0.013 | 0.013 | 0.007 | 0.015 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.048 |
| P9 | 0.000 | 0.001 | 0.001 | 0.015 | 0.017 | 0.000 | 0.000 | 0.004 | 0.000 | 0.000 | 0.003 | 0.000 | 0.002 | 0.012 | 0.010 | 0.040 |
| P10 | 0.000 | 0.004 | 0.002 | 0.013 | 0.001 | 0.013 | 0.013 | 0.007 | 0.000 | 0.000 | 0.000 | 0.012 | 0.001 | 0.003 | 0.000 | 0.000 |
To calculate the scores of Ratio System of MOORA, values of each patient are calculated with Eq. (8) using the weighted normalized decision matrix. The ranking of patients with Ratio System of MOORA by considering values are given at the second column of Table 10 .
Table 10.
The health situation of patients based on the MULTIMOORA approach.
| Patients | Ratio System | Reference Point | Multiplicative Form | MULTIMOORA |
|---|---|---|---|---|
| P1 | 6 | 4 | 5 | 5 |
| P2 | 1 | 1 | 1 | 1 |
| P3 | 7 | 7 | 7 | 7 |
| P4 | 10 | 10 | 10 | 10 |
| P5 | 8 | 8 | 8 | 8 |
| P6 | 2 | 3 | 2 | 2 |
| P7 | 9 | 9 | 9 | 9 |
| P8 | 5 | 6 | 3 | 4 |
| P9 | 4 | 5 | 6 | 6 |
| P10 | 3 | 2 | 4 | 3 |
In the Reference Point approach of MOORA, as a first step, reference points are determined for each criterion using the normalized decision matrix. Highest values in maximization criteria (C1.3, C1.4, C1.5 and C3.3) and lowest values in minimization criteria (rest of the criteria) are considered as reference points. The last row of Table 8 indicates the reference points. Using Eq. (9), the distances between the reference points and the alternatives are determined. Then, maximum values of calculated distances (bold values in Table 9) are determined. Later, the best alternative is named by using the Tchebycheff Min-Max metric seen in Eq. (11). The third column of Table 10 shows the final ranking of the alternatives obtained by Reference Point approach of MOORA.
Multiplicative ranking index Ui for each alternative are determined using Eq. (12) in Full Multiplicative Form of MOORA. Then ranking of the alternatives are obtained by ranking Ui values in descending order. The fourth column of Table 10 represents the ranking obtained by Full Multiplicative Form of MOORA.
Eventually, the final ranking of the alternatives are calculated with MULTIMOORA method. One final ranking is obtained from three ranks of Ratio System, Reference Point approach and Full Multiplicative Form using dominance theory. The last column of Table 10 gives the final ranking.
All the ranking shown at Table 10 are done according to the health situations of patients. Patients are ranked from good to poor health conditions. Patient #2 is healthiest person based on the three methods (Ratio System, Reference Point, and Multiplicative Form). Patient #6 gets the 2nd order based on the Ratio System and Multiplicative Form while her ranking 3rd within the Reference Point method. Patients #2, #3, #4, #5, and #7 dominate others according to the whole MOORA methods. The final ranking based on the MULTIMOORA which is the combination of three rankings is more convincing. According to the result of MULTIMOORA, the final ranking of patients (from good to poor health conditions) is obtained as P2>P6>P10>P8>P1>P9>P3>P5>P7>P4. In other words, the patient who has to use ICU firstly is P4, followed by P7.
3.4. Scenario analysis
In this section, two additional analyses are conducted. The former is used to see the effect of criterion weights on ranking, whereas the latter is used to compare different MCDM approaches for ranking part.
Due to the dynamic nature of the COVID-19, the importance values of criteria can be updated by doctors. To reflect this situation, different sub-scenarios including cases where criteria weights vary are generated. In addition to the current situation (Table 4), following scenarios are considered. The weight values taken into account for each scenario are given in Table 11 .
Scenario#1: The main criteria are considered equally weighted in which the sub-criteria is distributed.
Scenario#2: All sub-criteria are equally weighted.
Scenario#3: Only respiratory system based criteria (first main criteria) are considered and weighted.
Scenario#4: Only cardiovascular system based criteria (second main criteria) are considered and weighted.
Scenario#5: Only blood based criteria (third main criteria) are considered and weighted.
Scenario#6: Only organ based criteria (fourth main criteria) are considered and weighted.
Table 11.
The weights of scenarios.
| Main | Sub | Scenario#1 | Scenario#2 | Scenario#3 | Scenario#4 | Scenario#5 | Scenario#6 |
|---|---|---|---|---|---|---|---|
| C1 | C1.1 | 0.0357 | 0.0625 | 0.1429 | 0.0000 | 0.0000 | 0.0000 |
| C1.2 | 0.0357 | 0.0625 | 0.1429 | 0.0000 | 0.0000 | 0.0000 | |
| C1.3 | 0.0357 | 0.0625 | 0.1429 | 0.0000 | 0.0000 | 0.0000 | |
| C1.4 | 0.0357 | 0.0625 | 0.1429 | 0.0000 | 0.0000 | 0.0000 | |
| C1.5 | 0.0357 | 0.0625 | 0.1429 | 0.0000 | 0.0000 | 0.0000 | |
| C1.6 | 0.0357 | 0.0625 | 0.1429 | 0.0000 | 0.0000 | 0.0000 | |
| C1.7 | 0.0357 | 0.0625 | 0.1429 | 0.0000 | 0.0000 | 0.0000 | |
| C2 | C2.1 | 0.0500 | 0.0625 | 0.0000 | 0.2000 | 0.0000 | 0.0000 |
| C2.2 | 0.0500 | 0.0625 | 0.0000 | 0.2000 | 0.0000 | 0.0000 | |
| C2.3 | 0.0500 | 0.0625 | 0.0000 | 0.2000 | 0.0000 | 0.0000 | |
| C2.4 | 0.0500 | 0.0625 | 0.0000 | 0.2000 | 0.0000 | 0.0000 | |
| C2.5 | 0.0500 | 0.0625 | 0.0000 | 0.2000 | 0.0000 | 0.0000 | |
| C3 | C3.1 | 0.0833 | 0.0625 | 0.0000 | 0.0000 | 0.3333 | 0.0000 |
| C3.2 | 0.0833 | 0.0625 | 0.0000 | 0.0000 | 0.3333 | 0.0000 | |
| C3.3 | 0.0833 | 0.0625 | 0.0000 | 0.0000 | 0.3333 | 0.0000 | |
| C4 | C4.1 | 0.2500 | 0.0625 | 0.0000 | 0.0000 | 0.0000 | 1.0000 |
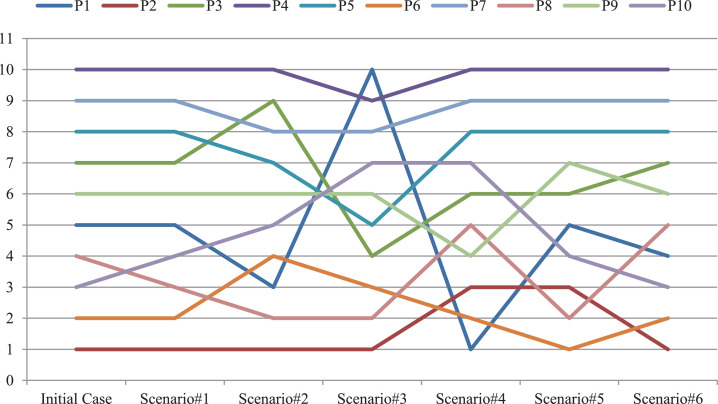
Using the weights in Table 11, MULTIMOORA approach is re-applied as in the previous section. Six new ranking are obtained. The new six rankings are shown in Fig. 4 compared to the initial ranking. It must be noted that this is a ranking according to their health status. So, the first rank means the healthiest patient who is the last person to receive ICU treatment.
Fig. 4.
Health condition ranks of COVID-19 patients based on alternative scenarios.
According to the Fig. 4, it is clear to see that the variability in criterion weight affects patients' ICU queues. There are no patients whose sequence did not change in all analyses. However, some patients have less variability than others. In other words, patient rank robustness is high for some patients such as P4, P2, P5, and P7. For instance, P4 ranks last in all cases (except Scenario#3). It means that the situation of P4 may be interpreted as urgent compared to other patients. Including the initial case, P2 ranks top three in all scenarios. It means that the health condition of P2 seems better than the others. The most interesting situation occurs in patient P1. While P1 ranks last in Scenario#3, he ranks first in Scenario#4. If the respiratory system based criteria are taken into account, P1 needs more ICU treatment than other patients. However, if the cardiovascular system based criteria are dominant, there is no emergency for P1.
In the next analysis, two well-known MCDM approaches namely, Evaluation based on Distance from Average Solution (EDAS) and The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) are also applied to rank the patients and compare the results of MULTIMOORA. For this analysis, the weights given in Table 4 are used. In order not to spoil the whole of the paper and to ensure its readability, the calculations of EDAS and TOPSIS are not given. However, calculation steps of the methods are available upon request. TOPSIS and EDAS provide analytical solutions to decision makers to determine the best alternative in complex decision problems or to rank the alternatives. Although TOPSIS and EDAS methods are among the distance-based methods [19], there are differences in the determination of alternatives. While TOPSIS method determines the best alternative by calculating the distance from ideal and rare solutions; in the EDAS method, the alternative is determined by calculating the distance from the mean solution [35]. The priority order of the patients according to the TOPSIS calculations [33] and EDAS calculations [35] are given in Table 12 . While Ci value represents the TOPSIS output for each alternative, Si value shows the performance of EDAS method.
Table 12.
The health situation of patients based on the TOPSIS and EDAS approach.
| Patients | Ci | TOPSIS | Si | EDAS |
|---|---|---|---|---|
| P1 | 0.707 | 4 | 0.797 | 4 |
| P2 | 0.854 | 2 | 0.908 | 2 |
| P3 | 0.519 | 7 | 0.524 | 7 |
| P4 | 0.168 | 10 | 0.086 | 10 |
| P5 | 0.370 | 8 | 0.406 | 8 |
| P6 | 0.766 | 3 | 0.790 | 5 |
| P7 | 0.268 | 9 | 0.307 | 9 |
| P8 | 0.653 | 5 | 0.800 | 3 |
| P9 | 0.646 | 6 | 0.628 | 6 |
| P10 | 0.875 | 1 | 0.958 | 1 |
According to the Table 12, the highest values of Ci and Si identifies the tenth patient (P10) as non-emergency patient. On the other hand, fourth patient’ (P4) condition is most critical among other. This means that the first person to receive the ICU service is that patient. Except two patients (P6 and P8), EDAS and TOPSIS approaches provide the same result. Due to different working principle of the methods, there is a 50% difference in the ranking with the MULTIMOORA approach. The doctors mentioned in the acknowledgment section stated that the result of the MULTIMOORA method is more reasonable.
4. Discussion
Healthcare decisions are complex and include going up against trade-offs between numerous, frequently clashing, targets. Utilizing organized, express approaches to choices including numerous criteria can make strides in the quality of choice-making, and a set of strategies, known beneath the collective heading MCDM, are valuable for this reason [56]. MCDM methods are widely used in other sectors, and recently there is a growing body of literature in healthcare applications. While the readers are referred to Liberatore and Nydick [39]; Muhlbacher and Kaczynski [41]; Frazão et al. [27] and Glaize et al. [22] for an excellent review of methodological and case-study based MCDM papers in healthcare sector, the reader is referred to Thokala et al. [56] for the MCDM emerging good practices for healthcare decision. We now provide a brief review of the literature that is relevant to the focus of the present paper.
One of the most popular MCDM approaches is AHP in healthcare management. AHP is used to select neonatal ventilators for a new women's health hospital [52]; to measure the performance of ICUs [16]; to manage of rectal cancer [54]; to prioritize multiple outcome measures of antidepressant drug treatment [32]; to produce national guidance relating to the treatment of disease [49]; to prioritize the medical equipment for ICUs [25]; and to select best treatment technique for breast cancer [1]. In addition to AHP, VIšekriterijumsko KOmpromisno Rangiranje (VIKOR) is also preferred to select the most proper vaccination strategy under uncertainty by Lopez and Gunasekaran [40]. While performance evaluation for physicians and nurses of heart failure clinic is studied by Jokar et al. [34] using analytical network process (ANP); a recent method namely best-worst method (BWM) is applied by Fei et al. [26] for the assessment of hospital service quality. Suwantika et al. [55] use strategic multi-attribute ranking tool to prioritize the introduction of new vaccines in Indonesia. As a recent study, weighted sum method (WSM) is applied by Klamer et al. [36] to evaluate the infectious diseases according to their relative importance for surveillance and public health.
Although most of the studies apply a MCDM individually, there are also some papers which use two MCDM methods hierarchically. For instance, the service quality of some Turkish hospitals is measured by Akdag et al. [2]. While the criteria are weighted using AHP, the hospitals are ranked using technique for order preference by similarity to ideal solution (TOPSIS) approach regarding to the weighted criteria. Another hybrid approach is conducted by Parsia and Sorooshian [44]. In their study, the criteria related with the minimization of nosocomial infections risks are weighted using decision-making trial and evaluation laboratory (DEMATEL) and WSM.
One of the relevant and recent studies is conducted by De Nardo et al. [15]. They use PAPRIKA (potentially all pairwise rankings of all possible alternatives) software to prioritize for 11 criteria in order to evaluate non-critical patients for admission to hospital in healthcare settings under scarce resources. Although the paper by De Nardo et al. [15] is close to our paper, they only consider 11 criteria (16 criteria in this paper) and the patients are not ranked in their study.
According to the investigated studies above (see Table 13 ), it can be clearly said that MCDM approaches are commonly used in various sub-sections of healthcare management. To the best knowledge of the authors, no paper which studies F-AHP and MOORA approaches for the ICU admission of COVID-19 is observed in literature. As already mentioned in the study of Angelis et al. [3] that MCDM approaches may give a more comprehensive and straightforward approach in healthcare to efficiently capture decision-makers’ concerns, compare esteem trade-offs and evoke their esteem inclinations. In expansion, MCDM strategies might illuminate the improvement of a choice bolster framework in healthcare, contributing towards more productive, levelheaded, and authentic asset assignment choices.
Table 13.
MCDM approaches in healthcare.
| Authors | MCDM Method(s) | Problem |
|---|---|---|
| Sloane et al. [52] | AHP | Selecting neonatal ventilators for a new women's health hospital. |
| Dey et al. [16] | AHP | Measuring the performance of ICUs in Barbados, Trinidad and India. |
| Suner et al. [54] | AHP | Deciding the foremost suitable strategy for development of a sequential choice tree within the administration of rectal cancer, utilizing different patient-specific criteria and medications such as surgery, chemotherapy, and radiotherapy. |
| Hummel et al. [32] | AHP | Prioritizing multiple outcome measures of antidepressant drug treatment. |
| Reddy et al. [49] | AHP | Creating national direction relating to the advancement of great health and the avoidance and treatment of illness. |
| Akdag et al. [2] | AHP and TOPSIS | Measuring the service quality of some Turkish hospitals. |
| Lopez and Gunasekaran [40] | Fuzzy VIKOR | Selection of vaccination strategy. |
| Faisal and Sharawi [25] | AHP | Prioritization the medical equipment (30 devices in ICU) for replacement. |
| Kolasa et al. [37] | Linear additive model | Pricing and reimbursement process of orphan drugs. |
| Peijia et al. [45] | Intuitionistic fuzzy TOPSIS | Assisting the hierarchical medical system in China. |
| Akdag et al. [1] | AHP | Selection of the best treatment technique for breast cancer. |
| Jokar et al. [34] | ANP | Performance evaluation for physicians and nurses of heart failure clinic. |
| Fei et al. [26] | BWM | Assessment of hospital service quality. |
| Parsia and Sorooshian [44] | DEMATEL and WSM | Minimization of nosocomial infections risks. |
| De Nardo et al. [15] | PAPRIKA | Weighting the criteria for COVID-19 non-critical patients for admission to hospital under scarce resources. |
| Suwantika et al. [55] | Strategic multi-attribute ranking tool | Prioritizing the introduction of new vaccines. |
| Klamer et al. [36] | WSM | Ranking the infectious diseases. |
| Proposed study | F-AHP and MOORA | Weighting the criteria and ranking the COVID-10 patients for ICU admission. |
Regarding to aforementioned findings by Angelis et al. [3], following gaps are tried to be contributed with the proposed paper: (i) an efficient ICU admission in the era of pandemic or scarce resources, (ii) an hybrid approach which integrates F-AHP and MOORA methods and finally (iii) evaluation of COVID-19 patients for the ICU treatment to show the applicability of the proposed approach.
The rapid spread of COVID-19 over the world results to force the healthcare service systems in countries. As a result of pushing the limits of healthcare services, the shortage of available hospital beds and the lack of beds in ICUs for critically ill patients have been among the major challenges faced.
In addition to the current triages for prioritizing admissions to ICUs for general patients, recommendations based on a scientific structure should be also developed to identify which COVID-19 patients are prioritized for ICU admission in emergency or resource limited situations. Due to conflicting factors that affect the admission and number of alternatives (patients), MCDM approaches are proper for such a context. To fill this gap in practice and literature, two different MCDM approaches namely F-AHP and MOORA are applied in this study. While F-AHP is chosen to weight the 16 criteria to reflect the uncertain environment, MOORA approach is used to determine which patient benefits ICU treatment first. The proposed methodology is tested and validated 10 anonymous patients. The results show that priorities and ranking obtained by the proposed approach is in line with the experts’ behavior, which potentially illustrates the validity and usefulness of the proposed approach.
The criteria and their weights to evaluate COVID-19 patients’ ICU status can be determined from different perspectives. So, the decision making team can be expanded from different departments such as administrative staff, support personnel, etc. In addition, the weights of decision makers can be different according to their experience, skills, and departments for future researches.
Although MULTIMOORA method gives guarantee for robustness due to combining the results of three MOORA approaches namely Ratio System, Reference Point Method and Full Multiplicative Form, different MCDM approaches should be applied for prioritizing and ranking in future studies. To reduce the calculation time and provide a dynamic decision-making process, developing a decision support system should be another future research. If large amounts of data related with ICU admission processes are available, stochastic approaches should be applied to represent the uncertainty. Finally, when the number of available hospitals is more than one, the patient assignment problem should be also considered.
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Availability of data and materials
Identified data can be obtained from the corresponding author on request.
Funding
Not applicable.
Authors' contributions
All authors (BÖ, EÖ, MK, and AUD) contributed equally to the development of the study and the writing of the manuscript. All authors read and approved the final manuscript.
Declaration of Competing Interests
The authors declare that they have no competing interests.
Acknowledgements
We would like to thank all the doctors who participated in the providing data process, Prof. Dr. Lale Karabıyık and specialist Dr. Fatih Kayserili for taking part as experts. The authors dedicate this work to all healthcare workers who lost their lives in the fight against COVID-19 pandemic.
References
- 1.Akdag H., Alemdar C., Aydin E. A MCDM model design for Her2+ breast cancer treatment technique using AHP method. Ponte Academic Journal. 2019;75(1):160–172. [Google Scholar]
- 2.Akdag H., Kalayci T., Karagoz S., Zulfikar H., Giz D. The evaluation of hospital service quality by fuzzy MCDM. Appl. Soft Comput. 2014;23:239–248. [Google Scholar]
- 3.Angelis A., Kanavos P., Montibeller G. Resource allocation and priority setting in healthcare: A multi-criteria decision analysis problem of value? Global Policy. 2017;8(2):76–83. [Google Scholar]
- 4.Ayittey F.K., Ayittey M.K., Chiwero N.B., Kamasah J.S., Dzuvor C. Economic impacts of Wuhan 2019-nCoV on China and the World. J. Med. Virol. 2020;92(5):473–475. doi: 10.1002/jmv.25706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Baud D., Qi X., Nielsen-Saines K., Musso D., Pomar L., Favre G. Real estimates of mortality following COVID-19 infection. Lancet Infect. Dis. 2020 doi: 10.1016/S1473-3099(20)30195-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Brauers W.K.M., Zavadskas E.K. The MOORA method and its application to privatization in a transition economy. Control and Cybernetic. 2006;35(2):445–469. [Google Scholar]
- 7.Brauers W.K.M., Zavadskas E.K. Project management by MULTIMOORA as an instrument for transition economies. Technological and Economic Development of Economy. 2010;16(1):5–24. [Google Scholar]
- 8.Brauers W.K.M., Zavadskas E.K. MULTIMOORA optimization used to decide on a bank loan to buy property. Technological and Economic Development of Economy. 2011;17(1):174–188. [Google Scholar]
- 9.Brauers W.K.M., Zavadskas E.K. Robustness of MULTIMOORA: A method for multi-objective optimization. Informatica. 2012;23(1):1–25. [Google Scholar]
- 10.Brauers W.K.M. Multi-objective seaport planning by MOORA decision making. Annals of Operations Research. 2013;206(1):39–58. [Google Scholar]
- 11.Buckley J.J. Fuzzy hierarchical analysis. Fuzzy Sets Syst. 1985;17(3):233–247. [Google Scholar]
- 12.Buyukozkan F.G., Cifci G., Guleryuz S. Strategic analysis of healthcare service quality using fuzzy AHP methodology. Expert Syst. Appl. 2011;38:9407–9424. [Google Scholar]
- 13.Carli R., Cavone G., Epicoco N., Scarabaggio P., Dotoli M. Model predictive control to mitigate the COVID-19 outbreak in a multi-region scenario. Annual Reviews in Control. 2020;50:373–393. doi: 10.1016/j.arcontrol.2020.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chalmers J.D., Singanayagam A., Hill A.T. Systolic blood pressure is superior to other haemodynamic predictors of outcome in community acquired pneumonia. Thorax. 2008;63:698–702. doi: 10.1136/thx.2008.095562. [DOI] [PubMed] [Google Scholar]
- 15.De Nardo P., Gentilotti E., Mazzaferri F., Cremonini E., Hansen P., Goossens H., Tacconelli E. Multi-criteria decision analysis to prioritize hospital admission of patients affected by COVID-19 in low-resource settings with hospital-bed shortage. Int. J. Infect. Dis. 2020;98:494–500. doi: 10.1016/j.ijid.2020.06.082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dey P.K., Hariharan S., Clegg B.T. Measuring the operational performance of intensive care units using the analytic hierarchy process approach. International Journal of Operations & Production Management. 2006;26(8):849–865. [Google Scholar]
- 17.Domínguez S., Carnero M.C. Fuzzy multicriteria modelling of decision making in the renewal of healthcare technologies. Mathematics. 2020;8:944. [Google Scholar]
- 18.Dotoli M., Epicoco N., Falagario M., Sciancalepore F. A cross-efficiency fuzzy data envelopment analysis technique for performance evaluation of decision making units under uncertainty. Computers and Industrial Engineering. 2015;79:103–114. [Google Scholar]
- 19.Dotoli M., Epicoco N., Falagario M. Multi-criteria decision making techniques for the management of public procurement tenders: A case study. Appl. Soft Comput. 2020;88 [Google Scholar]
- 20.Emanuel E.J., Persad G., Upshur R., et al. Fair allocation of scarce medical resources in the time of COVID-19. N. Engl. J. Med. 2020;382:2049–2055. doi: 10.1056/NEJMsb2005114. [DOI] [PubMed] [Google Scholar]
- 21.Giordano G., Blanchini F., Bruno R., Colaneri P., Di Filippo A., Di Matteo A., Colaneri P. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020;26:855–860. doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Glaize A., Duenas A., Di Martinelly C., Fagnot I. Healthcare decision-making applications using multi criteria decision analysis: A scoping review. Journal of Multi-Criteria Decision Analysis. 2019;26:62–83. [Google Scholar]
- 23.Gumus A.T. Evaluation of hazardous waste transportation firms by using a two-step fuzzy-AHP and TOPSIS methodology. Expert Syst. Appl. 2009;36(2):4067–4074. [Google Scholar]
- 24.Fadli S., Imtihan K. Implementation of MOORA method in evaluating work performance of honorary teachers. Journal Publications and Informatics Engineering Research. 2019;4(1):128–135. [Google Scholar]
- 25.Faisal M., Sharawi A. Prioritize medical equipment replacement using analytical hierarchy process. IOSR Journal of Electrical and Electronics Engineering. 2015;10(3):55–63. [Google Scholar]
- 26.Fei L., Lu J., Feng Y. An extended best-worst multi-criteria decision-making method by belief functions and its applications in hospital service evaluation. Comput. Ind. Eng. 2020;142 [Google Scholar]
- 27.Frazão T.D.C., Camilo D.G.G., Cabral E.L.S., Souza R.P. Multi-criteria decision analysis (MCDA) in health care: a systematic review of the main characteristics and methodological steps. BMC Med. Inf. Decis. Making. 2018;18(90):1–16. doi: 10.1186/s12911-018-0663-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hafezalkotob A., Hafezalkotob A. Comprehensive MULTIMOORA method with target-based attributes and integrated significant coefficients for materials selection in biomedical applications. Materials & Design. 2015;87:949–959. [Google Scholar]
- 29.Hobbs J.E. Food supply chains during the COVID-19 pandemic. Canadian Journal of Agricultural Economics. 2020;68(2):171–176. [Google Scholar]
- 30.Hsieh T.Y., Lu S.T., Tzeng G.H. Fuzzy MCDM approach for planning and design tenders selection in public office buildings. Int. J. Project Manage. 2004;22(7):573–584. [Google Scholar]
- 31.Huang CC, Chu P.Y., Chiang Y.H. A fuzzy AHP application in government-sponsored R&D project selection. Omega. 2008;36(6):1038–1052. [Google Scholar]
- 32.Hummel M.J.M., Volz F., Van Manen J.G. Using the analytic hierarchy process to elicit patient preferences prioritizing multiple outcome measures of antidepressant drug treatment. Patient. 2012;5(4):225–237. doi: 10.1007/BF03262495. [DOI] [PubMed] [Google Scholar]
- 33.Hwang C.L., Yoon K. Multiple attribute decision making. Springer; Berlin, Heidelberg: 1981. Methods for multiple attribute decision making; pp. 58–191. [Google Scholar]
- 34.Jokar M., Ardan S., Khalesi N. Designing a method of performance evaluation for physicians and nurses of heart failure clinic based on the analytic network process. Quarterly Journal of Nursing Management. 2020;8(4):54–65. [Google Scholar]
- 35.Keshavarz Ghorabaee M., Zavadskas E.K., Olfat L., Turskis Z. Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS) Informatica. 2015;26(3):435–451. [Google Scholar]
- 36.Klamer S., Goethem N.V., Thomas D., Duysburgh E., Braeye T., Quoilin S. Prioritisation for future surveillance, prevention and control of 98 communicable diseases in Belgium: a 2018 multi-criteria decision analysis study. BMC Public Health. 2021;21(192):1–18. doi: 10.1186/s12889-020-09566-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kolasa K., Zwolinski K.M., Kalo Z., Hermanowski T. Potential impact of the implementation of multiple-criteria decision analysis (MCDA) on the Polish pricing and reimbursement process of orphan drugs. Orphanet. J. Rare. Dis. 2016;11:23. doi: 10.1186/s13023-016-0388-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Laarhoven P.J.M., Pedrycz W. A fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 1983;11(3):229–241. [Google Scholar]
- 39.Liberatore M.J., Nydick R.L. The analytic hierarchy process in medical and health care decision-making: A literature review. European Journal of Operational Research. 2007;189:194–207. [Google Scholar]
- 40.Lopez D., Gunasekaran M. the Proceedings of the Fifth International Conference on Fuzzy and Neuro Computing. 2015. Assessment of vaccination strategies using fuzzy multi-criteria decision making; pp. 195–208. [Google Scholar]
- 41.Muhlbacher A.C., Kaczynski A. Making good decisions in healthcare with multi-criteria decision analysis: The use, current research and future development of MCDA. Appl. Health Econ. Health Policy. 2016;14:29–40. doi: 10.1007/s40258-015-0203-4. [DOI] [PubMed] [Google Scholar]
- 42.Nag K., Helal M. the Proceedings of IEEE International Conference on Industrial Engineering and Engineering Management. 2018. Multicriteria inventory classification of diabetes drugs using a comparison of AHP and fuzzy AHP models; pp. 1456–1460. [Google Scholar]
- 43.Parè P.E., Beck C.L., Basar T. Modeling, estimation, and analysis of epidemics over networks: An overview. Annual Reviews in Control. 2020;50:345–360. [Google Scholar]
- 44.Parsia Y., Sorooshian S. A decision-making algorithm for re-architecting of healthcare facilities to minimize nosocomial infections risks. International Journal of Environmental Research and Public Health. 2020;17(3):855. doi: 10.3390/ijerph17030855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Peijia R., Zeshui X., Huchang L., Xiao-Jun Z. A thermodynamic method of intuitionistic fuzzy MCDM to assist the hierarchical medical system in China. Information Sciences. 2017;420:490–504. [Google Scholar]
- 46.Perc M., Miksić N.G., Slavinec M., Stožer A. Forecasting COVID-19. Front. Phys. 2020 doi: 10.3389/fphy.2020.00127. [DOI] [Google Scholar]
- 47.Rahimi I., Chen F., Gandomi A.H. A review on COVID-19 forecasting models. Neural Computing and Applications. 2021 doi: 10.1007/s00521-020-05626-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ravangard R., Bahadori M., Raadabadi M., Teymourzadeh E., Alimomohammadzadeh K., Mehrabian F. A model for the development of hospital beds using fuzzy analytical hierarchy process (Fuzzy AHP) Iranian Journal of Public Health. 2017;46(11):1555–1562. [PMC free article] [PubMed] [Google Scholar]
- 49.Reddy B.P., Kelly M.P., Thokala P., Walters S.J., Duenas A. Prioritizing public health guidance topics in the National Institute for Health and Care Excellence using the analytic hierarchy process. Public Health. 2014;12(8):896–903. doi: 10.1016/j.puhe.2014.07.003. [DOI] [PubMed] [Google Scholar]
- 50.Remuzzi A, Remuzzi G. COVID-19 and Italy: What next? Lancet North Am. Ed. 2020;395(10231):1225–1228. doi: 10.1016/S0140-6736(20)30627-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Rosenbaum L. Facing Covid-19 in Italy – Ethics, logistics, and therapeutics on the epidemic’s front line. N. Engl. J. Med. 2020;382:1873–1875. doi: 10.1056/NEJMp2005492. [DOI] [PubMed] [Google Scholar]
- 52.Sloane E.B., Liberatore M.J., Nydick R.L., Luo W., Chung Q.B. Using the analytic hierarchy process as a clinical engineering tool to facilitate an iterative, multidisciplinary, microeconomic health technology assessment. Computers & Operations Research. 2003;30:1447–1465. [Google Scholar]
- 53.Sun C.C. A performance evaluation model by integrating fuzzy AHP and fuzzy TOPSIS methods. Expert Syst. Appl. 2010;37(12):7745–7754. [Google Scholar]
- 54.Suner A., Celikoglu C.C., Dicle O., Sokmen S. Sequential decision tree using the analytic hierarchy process for decision support in rectal cancer. Artificial Intelligence in Medicine. 2012;56:59–68. doi: 10.1016/j.artmed.2012.05.003. [DOI] [PubMed] [Google Scholar]
- 55.Suwantika A.A., Purwadi F.V., Zakiyah N., Puspitasari I.M., Abdulah R., Diantini A., Boersma C., Postma M.J. Multi-criteria decision analysis to prioritize the introduction of new vaccines in Indonesia by using the framework of the strategic multi-attribute ranking tool for vaccines (SMART vaccines) Expert Rev. Vaccines. 2021;20(1):83–91. doi: 10.1080/14760584.2021.1874926. [DOI] [PubMed] [Google Scholar]
- 56.Thokala P., Devlin N., Marsh K., et al. Multiple criteria decision analysis for health care decision making – An introduction: Report 1 of the ISPOR MCDA emerging good practices task force. Value in Health. 2016;19(1):1–13. doi: 10.1016/j.jval.2015.12.003. [DOI] [PubMed] [Google Scholar]
- 57.Van Bavel J.J., Boggio P.S., Capraro V., et al. Using social and behavioral science to support COVID-19 pandemic response. Nature Human Behaviour. 2020;4:460–471. doi: 10.1038/s41562-020-0884-z. [DOI] [PubMed] [Google Scholar]
- 58.Wax R.S, Christian M.D. Practical recommendations for critical care and anesthesiology teams caring for novel coronavirus (2019-nCoV) patients. Can. J. Anaesth. 2020;67(5):568–576. doi: 10.1007/s12630-020-01591-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.WHO, 2021, World Health Organization Coronavirus disease (COVID-19) pandemic, https://www.who.int/emergencies/diseases/novel-coronavirus-2019, Access date: 24.06.2021.
- 60.Zadeh L. Fuzzy sets. Information and Control. 1965;8(3):338–353. [Google Scholar]
- 61.Zu Z.Y., Jiang M.D., Xu P.P., Chen W., Ni Q.Q., Lu G.M., Zhang L.J. Coronavirus disease 2019 (COVID-19): A perspective from China. Radiology. 2020;296(2):15–25. doi: 10.1148/radiol.2020200490. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Identified data can be obtained from the corresponding author on request.