Quantifying competitive advantages of mutant strains in a population involving importation and mass vaccination rollout

Abstract

The SARS-CoV-2 Delta variant, known as B.1.617.2 and first identified in India, is becoming a dominant strain in many countries due to its extreme infectiousness. Assessing and quantifying the transmissibility and competitive advantage of the Delta variant is of major significance for countries around the world so that appropriate measures to mitigate and even eliminate the epidemic can be introduced. Aiming at such problems, we proposed a method to model the invasion process of a novel strain and estimate the competitive advantage of the invading strain over the local strain. We applied this method to study the invasion and spread of the Delta variant into England. We have estimated the basic reproduction number of the Delta variant as being 49% higher than that of the Alpha variant (CI: 45–52%), assuming a mean generation interval of 5 days with a standard deviation of 3 days. In the period 11 April to 17 May 2021, the effective reproduction number of the Delta variant was 65% higher than that of the Alpha variant in England (CI: 61–70%). Our results show that the Delta variant has a significantly higher transmission capacity than other strains, which explains the rebound of the epidemic in many countries, even in those with relatively high vaccination coverages.

1. Introduction

The SARS-CoV-2 Delta variant, known as B.1.617.2 and first identified in India, is a variant of the SARS-CoV-2 lineage B.1.617. It was characterized as a VOC (Variant of Concern) on 11 May 2021 and later termed the Delta variant by the World Health Organization (WHO) under a new naming system introduced on 31 May 2021 (WHO, 2021a). The Delta variant has been spreading quickly and had appeared in more than 60 countries by June 2021 (WHO, 2021b). On 18 June 2021 the WHO chief scientist said that the Delta variant is “well on its way to becoming the dominant variant globally” (New Scientist, 2021). There is evidence showing that this variant that has taken over from the Alpha variant (lineage B.1.1.7) is clearly significantly more infectious (WHO, 2021b). Therefore, assessing and quantifying the transmissibility of the Delta variant is of great significance for countries around the world so that they can introduce appropriate measures to mitigate and even eliminate the epidemic.

The most widely used epidemiological measurement of the transmissibility in a given population is the basic reproduction number, R₀, which is defined as the average number of secondary cases generated by a single primary case in a fully susceptible population. This indicator reflects the intensity of non-pharmaceutical interventions needed to control the epidemic and the proportion of the immune population needed to form herd immunity, hence it is of great significance for understanding and controlling the epidemic. The estimation of R₀ should be based on the data during the early stage of the outbreak when there were no prevention/control measures or immunizations. When the Delta variant emerged, however, a proportion of the population had already developed antibodies due to infection or mass vaccination and the contact rate has not recovered to the normal level, thus the time series data for Delta cases was difficult to use directly for estimating its basic reproduction number R₀.

In view of this situation, we proposed a statistical model based on the renewal equation, which describes the process of a variant invading and replacing the local strain, to estimate the competitive advantage of the invading variant over the local strain and consequently obtain the basic reproduction number R₀ for the invading variant indirectly. We then applied this idea to model the process of the Delta variant invading England and estimate the transmissibility of the Delta variant.

2. Methods

As a complement to the basic reproduction number R₀, the effective reproduction number, R_t, which is defined as the actual average number of secondary cases per primary case at time t, can be used to access time-dependent variations in the transmission potential when infection is spreading in a population (Wallinga & Teunis, 2004). Both of these two types of reproduction numbers were used to characterize the spread of the disease in our analysis.

In this section we denote the local strain and the invading strain by strain α and strain δ, respectively. The basic reproduction number and the effective reproduction number of strain i are denoted by $R_0^i$ and $R_t^i$ for i = α, δ.

Let $L_t^{\alpha }$ be the number of new cases with strain α on day t, then we have the following renewal equation which models the transmission of strain α and the relationship between the reproduction number and the infection incidence (Wallinga & Lipsitch, 2007):

$$E[L_t^{\alpha }\mid R_t^{\alpha }]=R_t^{\alpha }\sum _{s=1}^{t-1}{L}_s^{\alpha }{g}_{t-s}^{\alpha },$$ (1)

where ${\{g_t^{\alpha }\}}_{t=1,2,\dots }$ represents the discretized probability distribution of the generation interval (i.e. time from the infection of a primary case to infection of the cases he/she generates) of strain α, which describes the average infectiousness profile after infection. And ${\sum }_{s=1}^{t-1}{L}_s^{\alpha }{g}_{t-s}^{\alpha }$, the sum of cases up to day t − 1, weighted by the infectivity function $g_t^{\alpha }$, indicates the total infectiousness of infected individuals on day t. Here t = 1 is the initial time at which the first local case emerged.

Given that during the early stage of the strain invasion most cases with the invading strain are imported cases, we divided cases with strain δ into three classes, namely 1). imported cases, 2). secondary cases of primary imported cases and 3). local cases (not travel-associated), and denote the number of these three classes of cases on day t by $J_t^{\delta }$, $K_t^{\delta }$ and $L_t^{\delta }$. Again, let ${\{g_t^{\delta }\}}_{t=1,2,\dots }$ be the discretized generation interval distribution of strain δ, from the renewal equation we have

$$E[K_t^{\delta }\mid a,R_t^{\delta }]=a{R}_t^{\delta }\sum _{s=1}^{t-1}{J}_s^{\delta }{g}_{t-s}^{\delta },$$ (2)

and

$$E[L_t^{\delta }\mid R_t^{\delta }]=R_t^{\delta }\sum _{s=1}^{t-1}(K_s^{\delta }+L_s^{\delta })g_{t-s}^{\delta },$$ (3)

with a ∈ (0, 1) indicates the ratio of the transmissibility of imported cases to that of non-imported cases.

In order to parameterize the competitive relationship between strain δ and strain α, we introduce a function F as follows:

$$R_t^{\delta }=F(t,R_t^{\alpha }),$$ (4)

here F describes how the difference in the spreading ability of the two strains changes over time and reflects the competitive advantage of strain δ over strain α.

To obtain the specific form of F under the scenario of mass vaccination, we consider the following SIR model:

$$\begin{array}{c}\left\{\begin{array}{l}\frac{dS}{dt}=-{\beta }_{\alpha }c(t)\frac{S}{N}{I}_{\alpha }-{\beta }_{\delta }c(t)\frac{S}{N}{I}_{\delta }-v_{\text{I}}(t),\\ \frac{d{V}_{\text{I}}}{dt}=-(1-e_{\text{I}}^{\alpha }){\beta }_{\alpha }c(t)\frac{V_{\text{I}}}{N}{I}_{\alpha }-(1-e_{\text{I}}^{\delta }){\beta }_{\delta }c(t)\frac{V_{\text{I}}}{N}{I}_{\delta }+v_{\text{I}}(t)-v_{\text{II}}(t),\\ \frac{d{V}_{\text{II}}}{dt}=-(1-e_{\text{II}}^{\alpha }){\beta }_{\alpha }c(t)\frac{V_{\text{II}}}{N}{I}_{\alpha }-(1-e_{\text{II}}^{\delta }){\beta }_{\delta }c(t)\frac{V_{\text{II}}}{N}{I}_{\delta }+v_{\text{II}}(t),\\ \frac{d{I}_i}{dt}={\beta }_{i}c(t)I_i[S+(1-e_{\text{I}}^i)V_{\text{I}}+(1-e_{\text{II}}^i)V_{\text{II}}]/N-({\gamma }_i+d_i)I_i,i=\alpha ,\delta .\\ \frac{dR}{dt}={\gamma }_{\alpha }{I}_{\alpha }+{\gamma }_{\delta }{I}_{\delta }.\end{array}\right)\end{array}$$ (5)

In which the population is stratified as susceptible (S), vaccinated (V), infected (I) and recovered (R) compartments. Subscripts I, II represent vaccination with only a single dose, and with two doses, respectively. Subscripts i = α, δ represent strain i. N is the total population. $e_{\text{I}}^i$ and $e_{\text{II}}^i$ indicate the efficacy of the first and the second doses of the vaccine to strain i. Parameters β, γ and d are the transmission rate, recovery rate and death rate, respectively.

Following the next generation matrix method (Van den Driessche & Watmough, 2002), we define

$${\mathcal{H}}_i={\beta }_{i}c(t)I_i[S+(1-e_{\text{I}}^i)V_{\text{I}}+(1-e_{\text{II}}^i)V_{\text{II}}]/N$$ (6)

and

$${\mathcal{V}}_i=({\gamma }_i+d_i)I_i$$ (7)

for i = α, δ and

$$H={\left(\frac{\partial {\mathcal{H}}_i}{\partial I_j}\right)}_{2\times 2},V={\left(\frac{\partial {\mathcal{V}}_i}{\partial I_j}\right)}_{2\times 2}.$$ (8)

The matrix HV⁻¹ has two positive eigenvalues corresponding to the reproduction numbers for each strain:

$$R_t^i=\frac{{\beta }_{i}c(t)}{{\gamma }_i+d_i}[S(t)+(1-e_{\text{I}}^i)V_{\text{I}}(t)+(1-e_{\text{II}}^i)V_{\text{II}}(t)]/N(t),i=\alpha ,\delta .$$ (9)

Taking t = 0 and S(0) = N(0), V_I(0) = 0, V_II(0) = 0 we have the basic reproduction numbers for strain i:

$$R_0^i=\frac{{\beta }_{i}c(0)}{{\gamma }_i+d_i},i=\alpha ,\delta .$$ (10)

Define the effective population susceptible to strain i as

$$S_e^i(t)=S(t)+(1-e_{\text{I}}^i)V_{\text{I}}(t)+(1-e_{\text{II}}^i)V_{\text{II}}(t),i=\alpha ,\delta .$$ (11)

and let $b=R_0^{\delta }/R_0^{\alpha }$, $f_t=\frac{S_e^{\delta }(t)}{S_e^{\alpha }(t)}$, then we have

$$R_t^{\delta }=\frac{R_0^{\delta }}{R_0^{\alpha }}\cdot \frac{S_e^{\delta }(t)}{S_e^{\alpha }(t)}\cdot R_t^{\alpha }=b\cdot f_t\cdot R_t^{\alpha }$$ (12)

and

$$F(t,R_t^{\alpha })=b\cdot f_t\cdot R_t^{\alpha }.$$ (13)

It can be verified that the above relationship between reproduction numbers of different strains is valid for general SIR-type or SEIR-type compartmental models.

We estimate the reproduction number for the period t₀ ≤ t ≤ t₁. Set the time window of reproduction numbers to τ days, i.e. for i = α, δ and m = 1, 2, …, the effective reproduction number $R_t^i$ during the period t ∈ [t₀ + (m − 1)τ, t₀ + mτ − 1] is assumed to be a constant $R_{m,\tau }^i$ (Cori et al., 2013). Assume that $L_t^{\alpha }$, $K_t^{\delta }$ and $L_t^{\delta }$ are Poisson-distributed, then we have the following log-likelihood function:

$$L({\left\{R_{m,\tau }^{\alpha }\right\}}_{m=1}^M,a,b)=\ln \left(\prod _{t=t_0}^{t_1}P\left(L_t^{\alpha }\right)P\left(K_t^{\delta }\right)P\left(L_t^{\delta }\right)\right)=\sum _{m=1}^M\sum _{j=t_0+(m-1)\tau }^{t_0+m\tau -1}(l\left(L_j^{\alpha }\right)+l\left(K_j^{\delta }\right)+l\left(L_j^{\delta }\right))$$ (14)

where P(x) = λ^xexp(−λ)/(x!) is the probability mass function of a Poisson distribution with mean λ and l(x) = x ln(E[x]) − E[x] − ln(x!). M is the maximum integer such that t₀ + Mτ − 1 ≤ t₁. Means of $L_t^{\alpha }$, $K_t^{\delta }$ and $L_t^{\delta }$ are given by (1), (2), (3). By maximizing the function L, we can see that the maximum likelihood estimates of ${\{R_{m,\tau }^{\alpha }\}}_{m=1,2,\dots }$ and a, b satisfy

$$\begin{array}{c}\left\{\begin{array}{l}{R}_{m,\tau }^{\alpha }=\frac{\sum _j(L_j^{\alpha }+K_j^{\delta }+L_j^{\delta })}{\sum _j\sum _{s=1}^{j-1}[L_s^{\alpha }{g}_{j-s}^{\alpha }+b{f}_j(a{J}_s^{\delta }+L_s^{\delta }+K_s^{\delta })g_{j-s}^{\delta }]},\\ a=\frac{\sum _{m,j}{K}_j^{\delta }}{\sum _{m,j}(b{f}_j{R}_{m,\tau }^{\alpha }\sum _{s=1}^{j-1}{J}_s^{\delta }{g}_{j-s}^{\delta })},\\ b=\frac{\sum _{m,j}(K_j^{\delta }+L_j^{\delta })}{\sum _{m,j}[f_j{R}_{m,\tau }^{\alpha }\sum _{s=1}^{j-1}(a{J}_s^{\delta }+L_s^{\delta }+K_s^{\delta })g_{j-s}^{\delta }]}.\end{array}\right)\end{array}$$ (15)

In the above equations, the index of summation m ranges from 1 to M and the index of summation j ranges from t₀ + (m − 1)τ to min(t₀ + mτ − 1, t₁).

3. A case study: application to model the invasion of the delta variant into england

Outside India, the UK has recorded the highest number of Delta cases (PANGOlineages, 2021). The Delta variant was first introduced into England in March 2021 when the Alpha variant was the dominant local strain, then it began to spread locally in April and became dominated by the end of May (Public Health England, 2021a). Since the whole process of the Delta variant replacing the Alpha variant was observed in England and the associated sequencing data on such COVID-19 cases are available, our study is based on the epidemic data in England. In the following we use notations α and δ to indicate the Alpha variant and the Delta variant, respectively. The initial time t = 1 is set to 1 March 2021.

3.1. Data

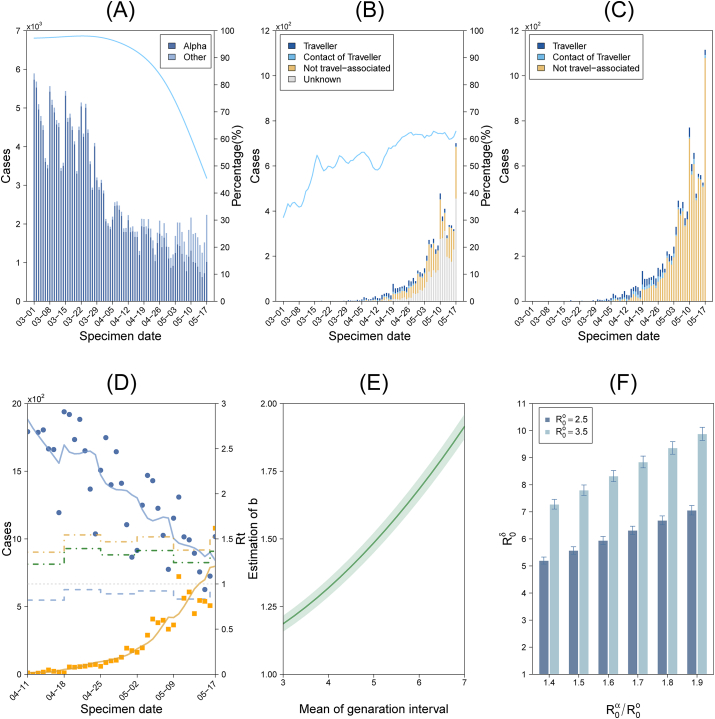
We obtained the daily number of laboratory-confirmed COVID-19 cases in England from (The official UK government website for data and insights on coronavirus (COVID-19), 2021a) (bars in Fig. 1 (A)) and obtained sequencing data on part of these confirmed cases from (Public Health England, 2021a). Sequencing data include the daily percentage of sequenced confirmed cases (blue line in Fig. 1 (B)), the weekly proportion of Alpha cases amongst all sequenced cases (dots in Fig. 1 (A)) and daily travel data for confirmed Delta cases (bars in Fig. 1 (B)). All of the above data are presented by specimen date (the date when the sample was taken from the person being tested). Since sequencing data were released on 31 May 2021, data on the previous 14 days before this day are still accumulating and the proportions are less likely to accurately reflect prevalence, so we only used data up to 17 May 2021.

Fig. 1.

Data and analysis for epidemics in England: (A). Bars represent the daily number of laboratory-confirmed COVID-19 cases, dots represent the proportion of Alpha cases in weekly sequenced cases. The line is the curve fitted to the dots and represents the proportion of Alpha cases in daily newly confirmed cases, which we divided into the daily confirmed Alpha cases (dark bars) and non-Alpha cases (light bars); (B). Data for confirmed Delta cases (bars) and the proportion of sequenced cases in all cases (blue line); (C). Estimated number of Delta cases among all confirmed cases; (D). Estimated effective reproduction number and fitted number of confirmed cases of the Alpha variant (blue) and the Delta variant (yellow). Dots and solid lines represent the number of new cases and its fitted value. Dotted lines in blue and yellow represent estimated effective reproduction numbers. The green dotted line is the blue dotted line multiplied by b = 1.49; (E). Variation of b when the generation interval varies. The shaded region represents the 95% confidence interval; (F). Estimated value of the basic reproduction number of the Delta variant. All dates are in the year 2021.

3.2. Estimation of case numbers

The proportion of cases for the Alpha variant in weekly sequenced cases is shown in blue dots in Fig. 1 (A), and is fitted with a smooth spline function over time, denoted by $h_t^{\alpha }$. Then the daily number of new cases, denoted by C_t is multiplied by the fitting function $h_t^{\alpha }$ to get the daily number of new Alpha cases, denoted by $L_t^{\alpha }$ shown in dark blue bars in Fig. 1 (A), then we have

$$L_t^{\alpha }=C_t{h}_t^{\alpha }.$$ (16)

Fig. 1 (B) shows the daily data for confirmed Delta cases, including travellers (denoted by $C_t^t$), cases due to contact with a traveller ($C_t^c$), not travel-associated cases ($C_t^n$) and cases of unknown origin ($C_t^u$), and the blue curve represents the proportion of daily confirmed cases that were sequenced, denoted by function p_t. It is reasonable to assume that the unknown cases may only contain two groups, that is those resulting from contacts with a traveller or those that are not travel-associated, due to clear information on travelling histories. Suppose that the ratios of confirmed cases that are from contacts with a traveller or not travel-associated are the same as those for the unknown cases, from which we can divide the unknown cases into the group of contacts with a traveller and the group of not travel-associated. As shown in Fig. 1 (C), by using the function p_t, we can further estimate the number of Delta cases among confirmed cases that are travellers (denoted by $J_t^{\delta }$), derived from contact with a traveller (denoted by $K_t^{\delta }$) or not travel-associated (denoted by $L_t^{\delta }$), that is,

$$J_t^{\delta }=C_t^t/p_t,$$ (17)

$$K_t^{\delta }=\left(C_t^c+C_t^u\cdot \frac{C_t^c}{C_t^c+C_t^n}\right)/p_t,$$ (18)

$$L_t^{\delta }=\left(C_t^n+C_t^u\cdot \frac{C_t^n}{C_t^c+C_t^n}\right)/p_t.$$ (19)

3.3. Vaccinations in England and the resistance of the delta variant to vaccines

According to section 2, for the effective reproduction numbers of the Delta and Alpha variants we have

$$R_t^{\delta }=b\cdot f_t\cdot R_t^{\alpha },$$ (20)

where b is the ratio of the basic reproduction number for the Delta variant to that for the Alpha variant and $f_t=S_e^{\delta }(t)/S_e^{\alpha }(t)$. Here $S_e^i$ is calculated as

$$S_e^i(t)=\left(N(0)-V_{\text{I}}(t)-V_{\text{II}}(t)-\sum _{j\le t}{C}_j\right)+(1-e_{\text{I}}^i)V_{\text{I}}(t)+(1-e_{\text{II}}^i)V_{\text{II}}(t)$$ (21)

for i = α, δ and ∑_{j ≤ t}C_j refers to the cumulative number of cases from the beginning of the epidemic up to time t in England.

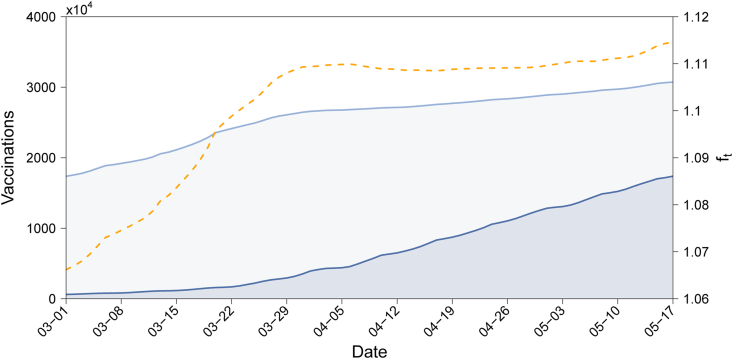
We obtained the data on vaccinations in England from (The official UK government website for data and insights on coronavirus (COVID-19), 2021b). As shown in Fig. 2, the light blue and dark blue lines are the number of people who have been vaccinated with the first, and with the second doses, respectively. The difference between them (the light shaded region) equals V_I(t) and the dark shaded region equals V_II(t). The population of England is N = 56, 287, 000 (Office for National Statistics, 2021). According to the vaccine effectiveness analyses undertaken by (Public Health England, 2021c), we take $e_{\text{I}}^{\alpha }=50\%$, $e_{\text{II}}^{\alpha }=88\%$, $e_{\text{I}}^{\delta }=33\%$, $e_{\text{II}}^{\delta }=81\%$. Then $f_t=S_e^{\delta }(t)/S_e^{\alpha }(t)$ is calculated according to expression (21) and is shown in Fig. 2 (the yellow line), from which we can see that the increase in the effective reproduction number of the Delta variant compared to that of the Alpha variant due to the resistance of the Delta variant to the vaccine.

Fig. 2.

Number of people who have received 1st (light blue line) and 2nd (dark blue line) dose vaccinations, and the ratio of the effective population susceptible to the Delta variant to that of the Alpha variant (yellow dotted line). Dates are in the year 2021.

3.4. The effective reproduction number and estimation of the competitive advantage of the delta variant

On the basis of the model in section 2 we estimate the effective reproduction number of the Alpha variant, and the transmission advantage level of the Delta variant compared to that of the Alpha variant. The starting time for the estimation is chosen as

$$t_0=\underset{t}{\mathrm{arg\; min}}\{L_t^{\delta }\ge 10\},$$ (22)

which is the day when the daily number of confirmed local delta cases was more than 10 for the first time, which was on 11 April 2021. Then, according to the statement in section 3.1, we can select t₁ as 17 May. The value of f_t is given in section 3.3. Recent findings suggest no significant changes in the generation intervals (GI) for SARS-CoV-2 cases infected with the Delta variant (Pung et al., 2021), hence we assume the Delta and Alpha variants have the same GI, which is set to a gamma distribution with a mean of 5 days and standard deviation (std) of 3 days (Nishiura et al., 2020). We set the time window τ of reproduction numbers to be 7 days in likelihood model (14). Then we have 8 parameters in the model, including a, b and ${\{R_{m,7}^{\alpha }\}}_{m=1}^6$. Here $R_{m,7}^{\alpha }$ indicates the effective reproduction number of the Alpha variant over the time interval t₀ + 7(m − 1) ≤ t ≤ t₀ + 7m − 1. The estimated values for these parameters are listed in Table 1. Data fitting results and the estimated effective reproduction numbers for the two strains are shown in Fig. 1 (D). The ratio of the basic reproduction number R₀ for the Delta variant to that for the Alpha variant was estimated as b = 1.486 (95% CI: 1.449–1.522).

Table 1.

Estimates (95% confidence intervals) of parameters for different means of the generation interval.

E[GI][1]	3	4	5 (baseline)	6	7
b	1.19 (1.16,1.22)	1.32 (1.29,1.35)	1.49 (1.45,1.52)	1.68 (1.64,1.73)	1.92 (1.87,1.96)
a	0.35 (0.32,0.38)	0.33 (0.30,0.36)	0.30 (0.27,0.33)	0.28 (0.25,0.30)	0.25 (0.23,0.28)
$R_{m,\tau }^{\alpha }$[2]
m = 1	0.87 (0.35,1.44)	0.85 (0.30,1.44)	0.82 (0.24,1.45)	0.80 (0.19,1.46)	0.78 (0.14,1.47)
m = 2	0.95 (0.70,1.22)	0.95 (0.69,1.21)	0.94 (0.68,1.21)	0.93 (0.66,1.20)	0.91 (0.64,1.20)
m = 3	0.93 (0.78,1.09)	0.91 (0.76,1.07)	0.89 (0.75,1.04)	0.87 (0.73,1.02)	0.85 (0.72,0.99)
m = 4	0.95 (0.88,1.03)	0.94 (0.87,1.01)	0.92 (0.85,1.00)	0.90 (0.83,0.98)	0.88 (0.81,0.96)
m = 5	0.90 (0.85,0.94)	0.86 (0.82,0.91)	0.83 (0.79,0.87)	0.81 (0.77,0.85)	0.79 (0.75,0.83)
m = 6	1.10 (0.98,1.23)	1.00 (0.90,1.12)	0.92 (0.82,1.02)	0.84 (0.76,0.93)	0.79 (0.71,0.87)
$R_{m,\tau }^{\delta }$[3]
m = 1	1.15 (0.46,1.90)	1.24 (0.44,2.11)	1.35 (0.40,2.39)	1.49 (0.36,2.73)	1.66 (0.31,3.12)
m = 2	1.26 (0.93,1.61)	1.39 (1.02,1.78)	1.55 (1.12,1.99)	1.73 (1.24,2.25)	1.94 (1.36,2.55)
m = 3	1.23 (1.02,1.44)	1.33 (1.11,1.57)	1.47 (1.23,1.72)	1.63 (1.36,1.90)	1.81 (1.52,2.11)
m = 4	1.25 (1.16,1.35)	1.37 (1.27,1.49)	1.52 (1.40,1.65)	1.69 (1.55,1.83)	1.88 (1.72,2.04)
m = 5	1.18 (1.12,0.24)	1.26 (1.20,1.33)	1.37 (1.31,1.44)	1.51 (1.44,1.59)	1.68 (1.60,1.76)
m = 6	1.45 (1.29,1.62)	1.47 (1.31,1.64)	1.51 (1.35,1.68)	1.58 (1.41,1.75)	1.67 (1.50,1.85)

[1] The mean of the generation interval (days). [2] The effective reproduction numbers of the Alpha variant with the time window τ = 7 days. [3] The effective reproduction numbers of the Delta variant with the time window τ = 7 days.

As illustrated in (Cori et al., 2013), small values of the time window τ lead to more rapid detection of changes in transmission but also more statistical noise; large values lead to more smoothing, and reductions in statistical noise. Note that the number of virus tests conducted in England has a periodicity of one week, which results in the same periodic fluctuation of the number of confirmed cases. In order to reduce the impact of this system error on our estimations of R_t, in the above estimation we take the time window τ = 7 days which is equal to the period of confirmation time series. To examine the sensitivity of the main results to the parameter, we let τ vary from 1 to 14 days, the estimated value of the parameter b is in the range of 1.48–1.54, therefore the main conclusion of this paper is not greatly influenced by the choice of τ.

Note that GI is not only related to the viral dynamics at the individual level, but it is also affected by isolation and detection measures. A study in mainland China showed that from early January 2020, the estimated GI for COVID-19 decreased from more than 7 days to around 3 days in about a month (Ali et al., 2020). This indicates that GI varies with the intensity of prevention and control measures during the epidemic. To examine variation of the estimated value of parameter b with GI, we carried out sensitivity analysis by changing the mean of GI. Our sensitivity analysis indicates that b increases with respect to GI, shown in Fig. 1 (E), and the range of b is 1.19–1.92 with increasing GI from 3 to 7 days.

Apart from the increase in the basic reproduction number reflected by the parameter b, the competitive advantage of the Delta variant also involves a reduction in vaccine efficacy against infection for the Delta variant compared to that of the Alpha variant (Public Health England, 2021b), which is reflected by the parameter f_t. We illustrate these two parts of the competitive advantage of the Delta variant in Fig. 1 (D), in which the green dotted line is $b{R}_t^{\alpha }$ and the yellow dotted line is $R_t^{\delta }=b{f}_t{R}_t^{\alpha }$. During the period (t₀, t₁), $R_t^{\delta }$ is 64.7–65.6% higher than $R_t^{\alpha }$ (range of 95% CI: 60.7–69.7%), without the reduction in vaccine efficacy against the Delta variant, this number would reduce to 48.6% (95% CI: 44.9–52.2%).

3.5. The basic reproduction number for the delta variant

Note that the estimation of the basic reproduction number R₀ should be based on the data at the beginning of the outbreak when there were no prevention/control measures or immunizations, and then the number of infected people is in the exponential growth stage. When the Alpha and Delta variants appeared in the UK, the contact rate had not yet returned to the original level due to gradually lifting of closure measures, and a considerable proportion of the population had already acquired a certain degree of immunity. This consequently leads to direct estimations of the basic reproduction numbers for the two variants to be no longer feasible. However, based on the previous analysis, we can indirectly estimate the basic reproduction number of the Delta variant through the basic reproduction number of the original strain and the force of transmission of the Alpha and Delta variants relative to that of the original strain.

Note that it is difficult to accurately estimate the basic reproduction number of SARS-CoV-2, which may be influenced by the chosen methods, the available data, various populations/regions etc. For estimation of the basic reproduction number of the original SARS-CoV-2 (denoted by $R_0^o$), the estimated mean value is between 2 and 3 for mainland China (Ahammed et al., 2021; Li et al., 2020; Riou & Althaus, 2020; Wu et al., 2020), and between 3 and 4 for European countries (Flaxman et al., 2020; Gatto et al., 2020; Roques et al., 2020; Yuan et al., 2020). Here we chose $R_0^o=2.5$, $R_0^o=3.5$, and $R_0^{\alpha }/R_0^o$ being in the interval of [1.4, 1.9] (Davies et al., 2021) as the basis for estimating the basic reproduction number of the Delta variant.

We calculated the basic reproduction number for the Delta variant according to the following formula:

$$R_0^{\delta }=R_0^o\cdot \frac{R_0^{\alpha }}{R_0^o}\cdot b$$ (23)

with b = 1.49 (1.45–1.52). Results are shown in Fig. 1 (F). In particular, when the basic reproduction number $R_0^o=2.5$, the estimated value $R_0^{\delta }$ is 5.20–7.06 (range of 95% CI: 5.07–7.23), when $R_0^o=3.5$, the estimated value $R_0^{\delta }$ is 7.28–9.88 (range of 95% CI: 7.10–10.12).

4. Conclusion and discussion

In this study, we proposed a model that describes the process of a variant invading and replacing the local strain, which can be used to estimate the competitive advantage of the variant over the local strain. This model can be applicable for the situation with mass vaccination rollout and different vaccine efficacies for the invading and the local strains. When the vaccine efficacies against the two strains are the same, we can omit the consideration of vaccination and simplify formula (13) to

$$F(t,R_t^{\alpha })=b\cdot R_t^{\alpha }.$$ (24)

Our method can also be used to analyze the competitive advantage of a newly-emerging mutant strain over the original local dominant strain. Assuming that the strain δ is a newly-emerging mutant strain, we only need to replace (2), (3) in section 2 with

$$E[L_t^{\delta }\mid R_t^{\delta }]=R_t^{\delta }\sum _{s=1}^{t-1}{L}_s^{\delta }{g}_{t-s}^{\delta }.$$ (25)

The proposed model in this study is simple and technical, and the parameter estimation is not computationally costly, so the approach is easy to be applied for estimations of and comparisons between the transmission ability of different strains.

As an application, we used case data in England to examine the competitive advantage of the Delta variant of SARS-CoV-2 (lineage B.1.617.2), which is spreading rapidly across the world, compared to that of the Alpha variant (lineage B.1.1.7). We found that the basic reproduction number of the Delta variant is 49% higher than that of the Alpha variant (CI: 45–52%) under the baseline value (mean GI being 5 days with std 3 days). In the period 11 April to 17 May 2021, the effective reproduction number of the Delta variant was 65% higher than that of the Alpha variant in England (CI: 61–70%). Moreover, these two estimates increase with increasing GI. Our results show that competitive advantage of the Delta variant is not only illustrated by its high basic reproduction number, but also by the low efficacy of vaccinations against it compared with vaccination efficacies against other strains. The latter has led to the Delta variant replacing other strains more quickly to become the dominant strain in countries including even those with high vaccination coverages. The findings also show that the Delta variant has a significantly higher transmission capacity than other strains, which explains the rebound of the epidemic in many countries, including the United Kingdom, when the proportion of people vaccinated is high and when some prevention and control measures are still in place.

When many variant strains, including the SARS-CoV-2 Delta variant, were prevalent, a considerable proportion of the population already had antibodies, and prevention and control measures were still in place, making direct estimations of the basic reproduction number for variant strains by classical methods very difficult and challenging. Here we also provided a means of estimating the basic reproduction number indirectly when the classical estimation method is not applicable. In this study, we infer the basic reproduction number ($R_0^{\delta }$) for the Delta variant indirectly by estimating the ratio of the basic reproduction number R₀ for the Delta variant to that for the Alpha variant, parameter b, and using the ratio of R₀ for the Alpha variant to estimates of that for the original strain.

The effective reproduction numbers of Delta and Alpha Variants are estimated and compared based on epidemic data in England, the results coincide with similar studies, e.g. (Campbell et al., 2021) and (Imperial College London, 2021), in which the effective reproduction number of the Delta variant is 53% (with mean GI being 5 days) or 100% (with mean GI being 6.7 days) higher than that of the Alpha variant, respectively. Note that such research generally considered the comparison between the effective reproduction numbers or the growth rates for various strains for a given time, however these results are limited by ignorance of the presence of vaccine. Our study further considered the competitive advantage of the Delta variant against other strains, including the increase in the basic reproductive number (denoted by parameter b) and reduction in immune efficacy (denoted by function f_t). Theoretically our method is not affected by the coverage and efficacy of vaccine. After adjusting the function f_t according to the immune condition of a given population, we can get the competitive and transmission advantage of the Delta variant in other areas. Therefore our model and results are more universal than other similar models.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling editor: CNLOU- Yijun