An Adaptative Steered Molecular Dynamics (ASMD) study of mutagenesis effects on calcium affinity in the regulatory domain of cardiac troponin C

Abstract

Calcium-dependent cardiac muscle contraction is regulated by the protein complex troponin (cTn), and specifically by the regulatory N-terminal domain (N-cTnC) which contains one active Ca²⁺ binding site (site II). It has been previously shown that cardiac muscle contractility and functionality is affected by mutations in N-cTnC which alter calcium binding affinity. Here, we describe the application of adaptive steered molecular dynamics to characterize the influence of N-cTnC mutations on site II calcium binding affinity. We observed the correct trends for all of the studied calcium sensitizing and desensitizing mutants, in conjunction with loop II perturbations. Additionally, the potential of mean force accuracy was shown to increase substantially with increasingly slower speeds and using fewer trajectories. This study presents a novel approach to computationally estimate the Ca²⁺ binding affinity of N-cTnC structures and is a valuable potential tool to support the design and characterization of novel mutations with potential therapeutic benefits.

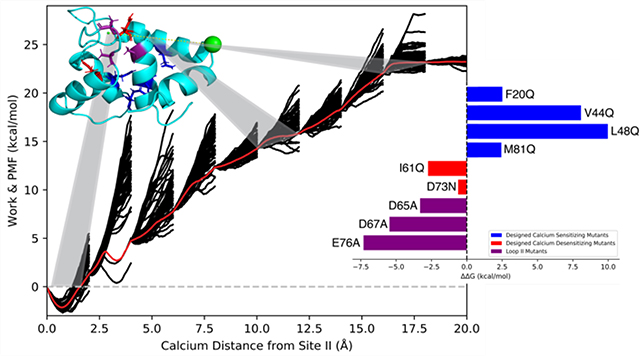
Graphical Abstract

Introduction

Calcium-dependent cardiac muscle contraction occurs through a multitude of proteins and filaments operating cohesively, and is regulated by the protein complex troponin (cTn). Troponin’s functionality is modulated through its three subunits: troponin C (cTnC), troponin I (cTnI), and troponin T (cTnT). cTnT anchors the protein complex to tropomyosin (Tm). cTnI inhibits the actomyosin interaction¹. cTnC, the calcium binding subunit, when bound to Ca²⁺ induces a conformational change in cTnI, dissociating it from actin. Tm is then able to slide along the actin filament away from the myosin binding site, thus allowing myosin to bind to actin, forming a cross bridge, the first step in the cross-bridge cycle. cTnC is a two-domain subunit, with each domain containing two EF-hand (helix-loop-helix) structural motifs. The C-domain, referred to as the structural domain, contains site III and site IV which under physiological conditions are consistently occupied by either Ca²⁺ or Mg^{2+ 2}. The regulatory, N-terminal domain (N-cTnC), contains one active binding site (site II) ³. Site II has been characterized as having low affinity and high selectivity to Ca^{2+ 4, 5}, with a N-cTnC Ca²⁺ K_D=7μM, measured using steady state fluorescence at 15 °C ⁶. The inactivity of site I (residues 28–41) is attributed to non-conserved residue mutations in the Ca²⁺ coordinating sites of the loop, compared to the skeletal isoform which contains two active binding sites in the regulatory domain ⁷.

Cardiac muscle contractility and functionality has been shown to be affected by mutations in the regulatory domain of cTnC. The mutation either increases or decreases Ca²⁺ sensitivity based on the substituted residue identity and its location in the tertiary structure relative to site II ⁶. Recent work has shown success in designing mutations (F20Q, V44Q, L48Q, M81Q) that increase Ca²⁺ sensitivity ⁶. Additionally, designed mutations that decrease Ca²⁺ sensitivity have been reported: I61Q ⁸ and D73N ⁹. It has been shown in vivo that expression of mutant cTn complexes has the potential to restore cardiac muscle contractility and functionality after a myocardial infarction event, thus supporting the claim that mutated cTn structures combined with gene therapy offer a therapeutic strategy for treatment of heart disease ^10–12.

In addition to experimental characterization of mutational effects on N-cTnC Ca²⁺ sensitivity, computational methods to study protein dynamics such as conventional and accelerated Molecular Dynamics (MD)^{8, 13–24}, as well as free energy methods such as Umbrella Sampling (US)^{13, 25–27} and Thermodynamic Integration (TI) ²⁸ have been used to support experimental findings. The free energy studies were partly motivated by the desire to accurately calculate the Ca²⁺ binding affinity of known sensitizing and desensitizing mutations. This could potentially support and accelerate the design and characterization of novel mutations with therapeutic benefits for further experimental validation. However, limitations of free energy methods such as inaccuracies in forcefield descriptions of divalent metal cations^29–31, non-classical electronic effects³², potential insufficient sampling of the thermodynamic ensemble³³, and high computational cost³⁴ have hampered these calculations.

Steered Molecular Dynamics (SMD) has the potential to overcome some of the limitations discussed above. It serves as a biased integration methodology to obtain the potential of mean force (PMF) along a chosen pulling path. In this method a pseudo particle applies a steering force in order to move along the reaction coordinate at a particular velocity. The non-equilibrium work conducted on the system during the SMD simulation can be related to the free energy difference between the initial and final states of the simulation ³⁵. However, the main limitation of this method comes from requiring thousands of individual nonequilibrium trajectories to achieve convergence of the PMF, especially for long distance paths. An improvement upon this method was introduced by Hernandez and coworkers ³⁶ termed Adaptive Steered Molecular Dynamics (ASMD). The strength of ASMD arises from the ability to split the reaction coordinate into a number of smaller stages, where the Jarzynski average (JA) ³⁷ is calculated for each stage over a number of individual trajectories. Then the JA serves as the starting reference point for the next sequential stage of the reaction coordinate. This method has been shown to greatly reduce the number of individual nonequilibrium trajectories needed to converge the PMF from thousands to only a few hundred ^{38, 39}. Thus, ASMD offers a potential solution to the previously described limitations of insufficient sampling and cost efficiency that have been obstacles for other free energy methods.

In this work, we utilized the ASMD method to obtain the PMF of Ca²⁺ binding to wildtype N-cTnC, several designed Ca²⁺ sensitizing and desensitizing mutants, and perturbations in loop II of the regulatory domain of cTnC. We show that based on the ASMD theory with increasingly slower pull speeds, the number of individual nonequilibrium trajectories needed to converge the PMF is greatly reduced. The obtained PMFs of all mutants exhibited the correct trend of either increased or decreased binding affinity, making this a viable computational tool for characterizing cTnC sensitizing and desensitizing mutants.

Methods

Preparation of Initial Structure for Molecular Dynamics

The structure of the Ca²⁺-bound N-terminal domain of cardiac troponin was obtained from PDB 1AP4 ⁴⁰. The representative model was solvated using the tLeap module of AMBER 18 ⁴¹ in a 40 Å TIP3P ⁴² water box and neutralized with Na⁺ ions. The forcefield used for the simulations was ff14SB ⁴³. Energy minimizations were performed on the entire system. The first minimization minimized the solvent with the protein and cations held fixed for a maximum of 10000 cycles, where the first 10 iteration were performed using the steepest descent algorithm and the rest used the conjugate gradient algorithm. The second energy minimization minimized the entire system for a maximum of 10000 cycles, where the first 10 iterations were performed using the steepest descent algorithm and the remaining cycles utilized the conjugate gradient algorithm. The system was subsequently heated to 300 K over a span of 500 ps using the Langevin thermostat ⁴⁴, followed by 500 ps of density equilibration using the Berendsen barostat ⁴⁵. The entire system was then set to equilibrate over a span of 800 ps (with production settings) at constant pressure and temperature (300 K).

Adaptative Steered Molecular Dynamics (ASMD)

To study the unbinding process of Ca²⁺ from N-cTnC site II, we used adaptive steered molecular dynamics (ASMD). The simulations started with the equilibrated system as detailed above. ASMD was performed by restraining the distance between the center of mass of the α carbons in the residues Ser69, Gly70, and Thr71 for a 20Å pull from the original starting distance between the Ca²⁺ ion and the calculated center of mass point. The initial distance between the center of mass of the α carbons and Ca²⁺ of the pulling coordinate was determined using the CPPTRAJ ⁴⁶ distance function. The pulling was performed using a force constant of 7.2 kcal mol⁻¹ Å⁻² and pulling speeds of 1 Å/ns and 0.5 Å/ns. All ASMD simulations were split into ten stages. For a pulling speed of 1 Å/ns, each stage was stimulated for 2 ns with either 100 or 150 trajectories per stage. For a pulling speed of 0.5 Å/ns, each stage was simulated for 4 ns and 50 trajectories per stage. Upon completion of the SMD pulls for any stage (N) of the simulation, the JA was calculated via the “ASMD.py” script provided by Hernandez and colleagues in the AMBER Advanced Tutorial 26. The final coordinates of the trajectory whose work most closely matched the JA were used to initialize the subsequent stage (N+1) of the simulation. All ASMD simulations were performed with the GPU implementation of PMEMD⁴⁷ from the AMBER 18 package.

Mutant N-cTnC Structures

All Ca²⁺ sensitizing mutants (F20Q, V44Q, L48Q, M81Q), Ca²⁺ desensitizing mutants (I61Q, D73N), and loop II mutants (D65A, D67A, E76A, D65A/D67A/E76A, D65A,D67A,S69A,T71A,E76A) were constructed using the protein mutagenesis tool in PyMOL⁴⁸. The 1AP4 representative N-cTnC structure served as the base model to which the mutations were applied. Mutant structures were solvated, minimized, and equilibrated as detailed for the wildtype structure. ASMD simulations were performed with a pull speed of 0.5 Å/ns and 50 trajectories per stage and using the GPU implementation of PMEMD.

Results and Discussion

Validating PMF Accuracy with Slower Pull Speeds and Fewer Trajectories for N-cTnC

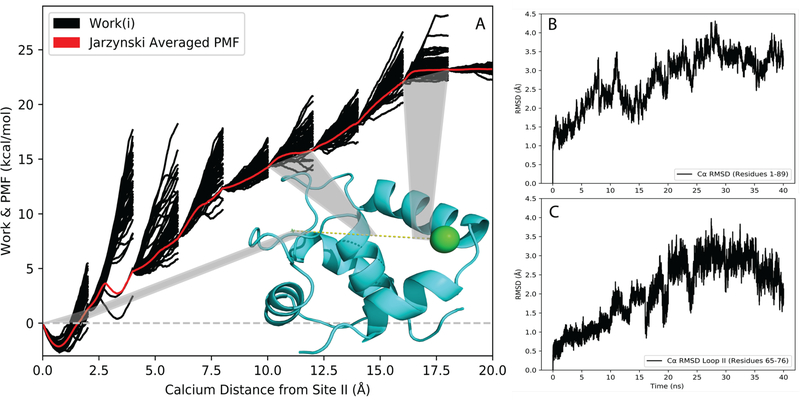
It has been previously shown that ASMD accuracy can be improved via two ways: an infinitely slow pull rate (such that all intermediate states are in thermodynamic equilibrium) and increasing the number of trajectories per stage ^{38, 39}. For Ca²⁺ binding to cTnC, our results support the established notion that an increasingly slow pull rate has a larger impact on increasing the PMF accuracy than increasing the number of trajectories per stage (Figure 1). We conducted ASMD simulations on the regulatory domain of cTnC (N-cTnC) using two different pull speeds (1Å /ns and 0.5 Å/ns) with varying numbers of trajectories per stage (tps) to create the PMF of Ca²⁺ binding to site II. Figure 1 supports the claim that at a constant pull rate, increasing the number of trajectories improves PMF accuracy especially at long distances. The PMF containing 150 tps showed an improvement (−3.5 kcal/mol) over the PMF containing 100 tps. However, with an even slower pull rate we were able to achieve better results with fewer trajectories. The PMF obtained using a pull speed of 0.5 Å/ns and only 50 tps exhibited an improved accuracy with a lower absolute binding energy compared to the PMF obtained from a 1Å /ns pull rate and 150 tps. ASMD utilizes nonequilibrium trajectories to provide an unbiased sampling of the reaction coordinate ⁴⁹. The benefit of slower sampling speeds is that statistically more favorable trajectories are explored more frequently compared to the high energy alternatives (Figure 2A), thus accounting for the improved accuracy of the PMF while using fewer trajectories. The Cα RMSD was calculated for all protein residues (Figure 2B) and for loop II residues (Figure 2C) over the duration of the simulation for the resulting Jarzynski averaged PMF trajectory. These values show that the protein structure remained stable during the course of the simulation, thus ensuring a physiologically relevant structure. GPU acceleration through the PMEMD.cuda program allowed for these slow rate ASMD simulations to be performed at a relatively low computational cost. Based on this data we proceeded with a 0.5 Å/ns pull speed and 50 tps for all mutant ASMD simulations.

Figure 1.

Comparison ofthe PMF of Ca²⁺ binding to site II of N-cTnC at múltiple pulí speeds and number of trajectòries per stage (tps).The solid black Une shows the pulí speed of 0.5 Á/ns using 50 tps, while the red dashed curve shows the pulí speed of 1 Á/ns using 100 tps, and the red dotted curve shows the pulí speed of 1 Á/ns using 150 tps.

Figure 2.

Analysis of Ca²⁺-bound N-cTnC ASMD. (A) The PMF ofwildtype N-cTnC obtained at constant NPT using ASMD in 10 stages with 50tps, and a pulling speed of 0.5 Á/ns.The work traces W(£_t’ )forthe 50 individual trajectòries in each stage are shown in thin black curves, and the PMF W obtained from the Jarzynski Equality is shown asa thin red curve. A representative structure ofWT N-cTnC [PDB 1AP4] is shown with the pulí path of calcium (dashed yellow line) and highlighted sections corresponding to specific ASMD stages. (B)The RMSDof Ca atoms of N-cTnC (residues 1–89) throughout the entirety of the Jarzynski Averaged trajectory. (C)The RMSD of Ca atoms of loop II N-cTnC (residues 65–76) throughout the entirety of the Jarzynski Averaged trajectory.

Adaptive Steered Molecular Dynamics of Ca²⁺ Sensitivity Altering Mutants Successfully Identify Calcium Sensitization and Desensitization

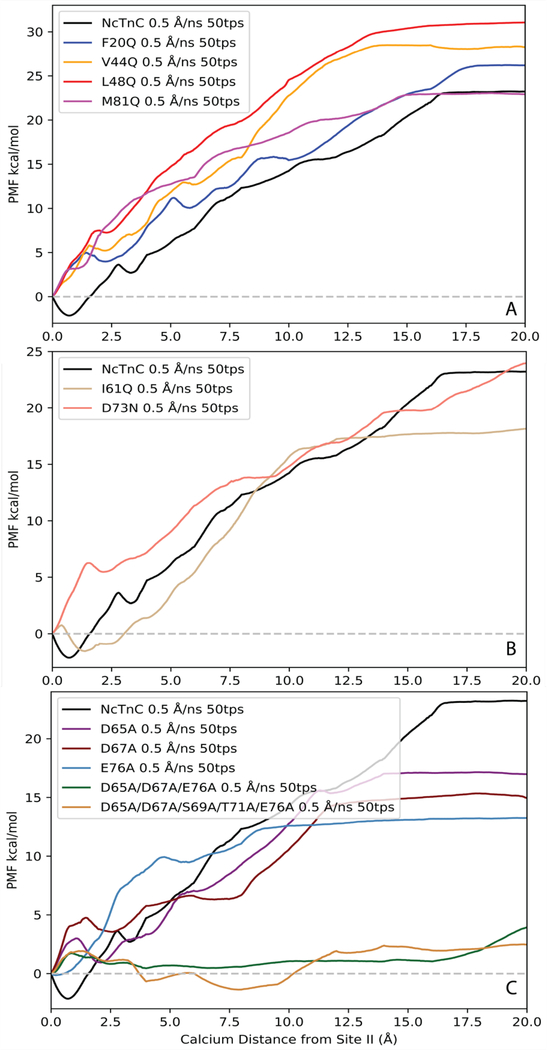
The PMF was obtained for wildtype N-cTnC, calcium sensitizing cTnC mutants (F20Q, V44Q, L48Q, M81Q) [Figure 3A], calcium desensitizing cTnC mutants (I61Q, D73N) [Figure 3B], and loop II cTnC mutants (D65A, D67A, E76A, D65A/D67A/E76A, D65A/D67A/S69A/T71A/E76A) [Figure 3C] using a 0.5 Å/ns pull speed and 50 tps. We successfully predicted the correct trends for mutagenesis effects on N-cTnC Ca²⁺ binding affinity. The ΔG of Ca²⁺ binding was estimated to be the difference between the free energies along the obtained PMF when Ca²⁺ was 15 Å from its initial starting position in site II (x = 15Å) and the initial starting position (x = 0Å). This reference position was chosen instead of the end of the pull length (x = 20Å) due to observed secondary interactions between Ca²⁺ and helix A for pull lengths larger than 15Å. These observed secondary interactions were attributed to be an artifact of the ASMD simulations due to the vector along which Ca²⁺ was pulled. Therefore, these interactions are physiologically unlikely to occur and were ignored. The reference point of 15 Å from the initial starting position was chosen based on having negligible electrostatic interactions between Ca²⁺ and residues in loop II, in addition to being far enough away from helix A such that secondary interactions were minimal.

Figure 3.

PMFs of Ca²⁺ binding to wild type N-cTnC and mutants: (A) designed calcium sensitizing mutations, (B) designed calcium desensitizing mutations, (C) loop II mutations.

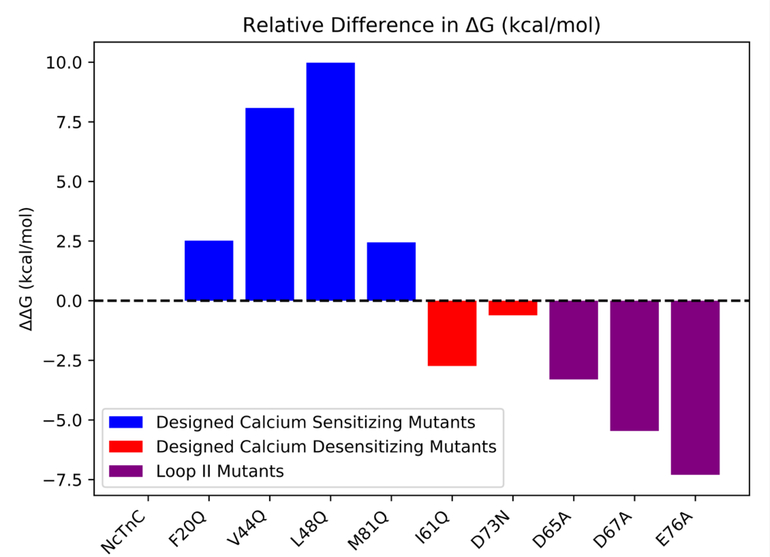
The calculated ΔΔG values for the calcium sensitizing and desensitizing mutants followed the anticipated trends. However, the ΔΔG values of the sensitizing mutations (F20Q, V44Q, L48Q, and M81Q) were consistently overestimated compared to the derived experimental values⁶, with predicted ΔΔG values of 2.5, 8.0, 10.0, and 2.5 kcal/mol respectively. L48Q showed the greatest increase in binding affinity in agreement with experimental findings. The calcium desensitizing mutations (I61Q and D73N) exhibited negative ΔΔG values, correctly reflecting the trend observed in experimental pCa₅₀ measurements ^{8, 9}. The predicted ΔΔG values calculated for I61Q and D73N were −2.7 and −0.6 kcal/mol, respectively. Additionally, three individual mutations of chelating residues in loop II were simulated to characterize the effects of mutating specific Ca²⁺ coordinating residues. Residues Asp65, Asp67, and Glu76 were selected since these residues were expected to have the greatest impact on Ca²⁺ binding affinity. This was supported by the significant difference in predicted ΔΔG values (−3.3, −5.5, and −7.3 kcal/mol respectively). The ΔΔG values between WT N-cTnC and all single mutant N-cTnC structures are summarized in Figure 4. The PMFs of the triple mutant (D65A/D67A/E76A) and quintuple mutant (D65A/D67A/S69A/T71A/E76A) showed that calcium binding was effectively completely removed from loop II. The ΔG of Ca²⁺ binding obtained from the PMFs were 1.13 and 2.25 kcal/mol, respectively. The PMFs also indicated that at the initial pulling distances (distances less than 10Å) the ΔG of binding was essentially 0 kcal/mol (Figure 3C), suggesting that nonbonded ligand-protein interactions within site II were effectively removed. It was not until further distances that work was done on the system, thus supporting the claim that at long distances any work done on the system was an attribute of secondary protein-ligand interactions.

Figure 4.

Relative AAG valúes between mutant and wíld type N-cTnC structures. AG valúes of calcium binding wereobtained from the respective PMFs at a distance of Ca²⁺ 15Áfrom its ¡nitially bound position ¡n site II.

Limitations

ASMD has proven to be a dependable method for characterizing the relative Ca²⁺ binding affinities of mutant N-cTnC structures. The sign of the ΔΔG values was correctly identified for all investigated mutations. However, this method was not without limitations. The discrepancies between in vivo and in silico ΔG values can be attributed to several factors. We speculate that the use of a non-polarizable forcefield contributed to overestimation of the mutational effects on Ca²⁺ binding. Non-polarizable forcefields add nonbonded interactions in a pairwise manner, greatly simplifying the interactions of ligand with protein and solvent. Additionally, the exact reaction coordinate of calcium binding remains unknown, making it exceedingly difficult to accurately and efficiently sample all possible potential binding paths. The explored path has been shown to introduce work onto the system via secondary protein-ligand interactions which presumably do not occur in vivo. Therefore, it is possible that a more biologically relevant pulling path could be explored.

Conclusions

We utilized an adaptive steered molecular dynamics protocol in order to characterize the binding affinity of Ca²⁺ to wildtype and several mutant regulatory domain cTnC structures. It was shown that more accurate PMFs were generated faster and with fewer trajectories per stage with slower pull rates. The pull rate of 0.5 Å/ns with 50 tps proved to have the highest PMF accuracy while still maintaining relatively low computational cost. ASMD of WT N-cTnC and Ca²⁺ sensitivity modulating mutations supported the experimentally confirmed ΔΔG value trends. We also successfully characterized the effects of several loop II perturbations on Ca²⁺ binding affinity. The inclusion of multisite alanine mutations at coordinating residues in loop II proved to effectively minimize any nonbonded ligand-protein interactions, thus resulting in negligible work to be done on the system. In conclusion, we have shown that ASMD is a valuable method for the characterization of ligand binding affinity in cTnC. The sign of the ΔΔG values was correctly identified for all investigated mutations. This positions ASMD as a prime tool to computationally study novel designed calcium sensitivity altering mutants for potential therapeutic application. It is our hope that this method can support and supplement experimental efforts for the design and characterization of novel mutations with therapeutic benefits.

Data and Software Availability

The wildtype cTnC protein structure (1AP4) was available in the Protein Data Bank (PDB) at https://www.rcsb.org/. All mutations were created using the wildtype protein structure as the base model within the PyMOL software using the protein mutagenesis tool. All ASMD simulations were performed within the Amber18 software framework. Initial simulation file preparation scripts were obtained from the AMBER Advanced Tutorial 26 at http://ambermd.org/tutorials/advanced/tutorial26/. Scripts from this tutorial were modified based on the system specifications and for usage on the Ohio Supercomputer Center.